Introduction: Human induced pluripotent stem cells (hiPSCs) have two main properties: pluripotency and self-renewal[1]. Physical cues presented by biomaterial can stimulate differentiation of hiPSCs to neurons[2],[3]. We derive a mathematical model of cell growth and neural differentiation on melt electrospun biomaterial scaffolds. An ordinary differential equation (ODE) model of population size of each cell state (undifferentiated, progenitor, differentiated) was developed based on experimental results and previous literature[4]-[6]. Our model allows the use of mathematical analysis and numerical simulations to determine key factors controlling cell behavior when seeded on melt electrospun scaffolds.
Materials and Methods: A melt electrospinning setup was used to make Poly(ε-Caprolactone) (PCL) biomaterial scaffolds with different topographies[2]. HiPSCs were cultured in defined, xeno-free conditions and treated with STEMdiff™ Neural Induction Medium (NIM) for 5 days to induce neural differentiation[2],[7]. After 5 days, neural aggregates were seeded onto scaffolds and cultured in NIM for 12 days. Neuronal differentiation of hiPSCs was qualitatively assessed by immunocytochemistry[2]. An ODE system was developed to model stem, progenitor, and differentiated cell populations, oxygen and waste concentrations encountered by the cells based on experimental results and previous literature. Scaffold porosity is modeled by cell-scaffold contact rate, C, with high porosity corresponding to low C. Parameters model factors such as oxygen tension, effect of scaffold porosity on cell behavior, and effects of oxygen during cell maturation. These effects are modeled as functional terms on proliferation, apoptosis and differentiation.
Results and Discussion: After 12 days of seeding, green fluorescence intensity was 71.5±1% and 58.4±3% for neural progenitors seeded onto high porosity (~40%) and low porosity (~23%) scaffolds, respectively (Figure 1).
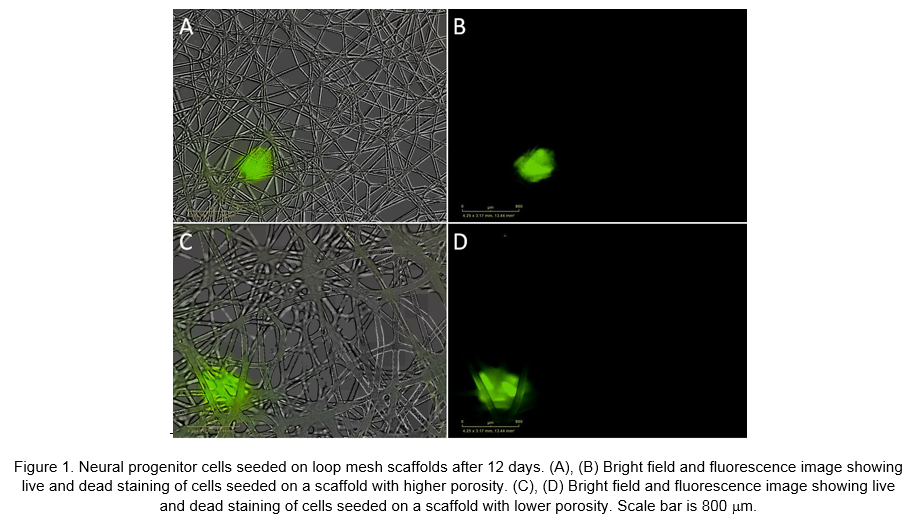
Moreover, cell body cluster area of neural progenitors cultured on more porous scaffolds was larger (~2mm2) than those seeded on less porous scaffolds (~0.9 mm2). Simulations predict increased growth and differentiation at 40% scaffold porosity versus 20%, consistent with experimental results. In agreement with literature, model simulations predict increased growth and differentiation with physiologic oxygen concentrations (~3%) compared to atmospheric levels (~21%) (Figure 2).

Conclusion: We have developed a mathematical model to explore how physical cues affect growth and neuronal differentiation of hiPSCs seeded on fibrous melt electrospun scaffolds. Effects of scaffold contact on proliferation, death and differentiation are derived from Live/Dead staining and cell body cluster area, with quantitative results used for determining functional terms on these processes and model validation. Model simulations successfully reproduce experimental observations, with physiologic oxygen and ~40% scaffold porosity increasing growth and differentiation. Ongoing work will develop our current model to study the effect of scaffold porosity and culture conditions on neuronal differentiation and growth of hiPSCs.
The authors would like to acknowledge the funding support from the Natural Sciences and Engineering Research Council’s Discovery Grant program.; The authors would also like to acknowledge the Advanced Microscopy Facility at the University of Victoria and also the Laboratory of Dr. Martin Jun at the Mechanical Engineering Department, University of Victoria.
References:
[1] Willerth, SM. Neural Tissue Engineering using Embryonic and Induced Pluripotent Stem Cells. Stem Cell Research and Therapy. 2011 Apr 15; 2(2):17.
[2] Mohtaram, et al. Electrospun biomaterial scaffolds with varied topographies for neuronal differentiation of human-induced pluripotent stem cells. Journal of Biomedical Materials Research Part A, DOI: 10.1002/jbm.a.35392.
[3] Mohtaram et al. Development of a glial cell-derived neurotrophic factor-releasing artificial dura for neural tissue engineering applications. J. Mater. Chem. B, DOI: 10.1039/C5TB00871A.
[4] Lo, et al. Feedback regulation in multistage cell lineages. Mathematical Biosciences and Engineering. 2009 Jan; 6(1):59-82.
[5] Sengers, et al. Computational modelling of cell spreading and tissue regeneration in porous scaffolds. Biomaterials, DOI: 10.1016/j.biomaterials.2006.12.008.
[6] Studer, et al. Enhanced proliferation, survival, and dopaminergic differentiation of CNS precursors in lowered oxygen. The Journal of Neuroscience. 2000 Oct 1; 20(19):7377-83.
[7] Braam, et al. Recombinant vitronectin is a functionally defined substrate that supports human embryonic stem cell self-renewal via alpha V beta 5 integrin. Stem Cells. 2008 Sep;26(9):2257-65.