Periodic Motion and Stability of Gravitational Planar Triple Systems

The stability of gravitational triple systems is a well-known problem in celestial mechanics. The basic model used is the general three body problem (GTBP). Many criteria estimated from the integrals of motion and zero velocity curves or from purely numerical simulations have been given in literature. In this paper, we propose a different approach for the study of stability of triple systems based on the numerical computation of manifolds of periodic orbits and their linear stability. Such an approach has been used for the study of two-planet exosolar systems but here, applying the method of continuation with respect to the masses, we refer to systems where all bodies can have similar mass values. In the present work we apply the proposed approach by starting from the circular family of periodic orbits, which is known to exist for the planetary type problem, and we restrict our computations to the case of two equal masses. By considering that the system has a hierarchical structure, the constructed manifold of periodic solutions can be projected on a plane defined by the relative distance and the relative mass of the system. On such a plane a stability map can be constructed showing the stability limits on the manifold of periodic orbits.

1. Introduction

The dynamical evolution of triple systems, where the three bodies are considered as point mass bodies, can be studied by using the classical general three body problem (GTBP). The system is not integrable and when the three bodies have masses of the same order and evolve initially in close distance orbits these become strongly irregular and ejections or collisions should appear. This is not the case for hierarchical systems when the single body moves sufficiently far from the binary formed by the other two bodies. Then, long-term stability can be obtained with the bodies evolving on almost periodic orbits. The conditions for stability between the above mentioned dynamical configurations have been studied quite extensively in literature. However due to the lack of sufficient number of constants of motion and the many parameters involved in the problem it is not possible to express an explicit condition for stability. A review on stability criteria of triple systems is given by Georgakarakos (2008) while a resent extended numerical studies on eccentric and inclined triple star systems is presented in Mylläri et al. (2018) and He and Petrovich (2018).

The analytical criteria are neither necessary nor sufficient for the stability. For example, the Hill type stability (Marchal and Bozis, 1982) guarantees that the bodies cannot show close encounters, which generally destabilize the system, but it cannot strictly prohibit the ejection of the lighter body (Bozis, 1981) or, in case of a planetary system, a close encounter between the star and the inner planet (Gladman, 1993). On the other hand stability criteria obtained by numerical integrations cannot cover all the possible space of parameters and initial conditions and, also, refer to a short period of time. Since the system is Hamiltonian, orbits of long-term stability should be confined to invariant tori in phase space, which, according to the KAM theorem, form foliations centered at linearly stable periodic orbits (see e.g., Siegel and Moser, 1971; Contopoulos, 2002). Therefore, the detection of stable periodic orbits reveals and locates domains of initial conditions for long-term stability and this approach is studied in the present paper. The importance of periodic solutions for understanding the dynamics of the three body problem has been recognized by Poincare. Generally they are associated with resonant motion and for the restricted three body problem (RTBP) the structure of periodic solutions is well-described by Hénon (1997) and Bruno (1994). Applications of periodic orbits of the RTBP may include but not limited to evolution of asteroids and trans-Neptunian objects (see e.g., Winter and Murray, 1997; Hadjidemetriou, 1999; Voyatzis et al., 2018) and orbital spacecraft dynamics (e.g., Xin et al., 2016; Dei Tos et al., 2018).

The computation of periodic orbits of the planar GTBP is addressed by Henon (1974) and Hadjidemetriou (1975), where periodicity refers to the periodic evolution of the mutual distances of the bodies. In the last 15 years many computations of periodic orbits have been performed in the study of the dynamics of exosolar systems (see e.g., Antoniadou and Voyatzis, 2016 and references therein). Of course, in these studies the planetary model is used where the two bodies (planets) have very small mass with respect to the mass of the third body (star). In the present work we start from such periodic planetary orbits and apply continuation with respect to the mass in order for the bodies to become of comparable masses. Our study is restricted to planar and almost circular orbits. Besides the computation of periodic orbits their linear stability is also estimated and, thus, we can conclude about how the limits of stability depends on the masses and the relative distance of the three bodies.

By considering the continuation of periodic orbits, as it is described in this paper, we can approach any physical configuration of three bodies. Apart from triple star systems, the method can be used to approach the dynamics of single star planetary systems with two heavy planets or the planetary motion around a binary star system (Voyatzis, 2017). Here we present particular computations in order to describe the methodology and we do not focus on any particular system. In section 2, we present briefly the model and the basic notions on periodic orbits and also we describe our methodology. In section 3, we present some computations, in order to show how our method is applied, and the results obtained. Finally in section 4, we conclude and discuss about the usefulness of the method and the possible wider computations which could be performed.

2. Model and Methodology

2.1. The Model in a Rotating Frame

We consider three point masses, m₀, m₁, and m₂ moving on the plane and define the inertial frame OXY, where O is the center of mass. For any triple system we assume m₀ ≥ m_i, i = 1, 2, and in the planetary case m₀ indicates the star, m₁ the inner planet and m₂ the outer one. According to Hadjidemetriou (1975) we define the rotating frame Gxy, where G is the center of mass of m₀ and m₁, Gx is the axis along the direction m₀ to m₁ and Gy is perpendicular to Gx. Thus, the position of the system in the rotating frame is given by the variables (r, x, y), where r is the distance between m₀ and m₁ and x, y are the coordinates of m₂ in the rotating system. With θ we indicate the angle between the inertial and the rotating frame. The Lagrangian of the system is written as (Voyatzis, 2017)

$\begin{array}{rc}{L}=\frac{1}{2}{M}_1({ṙ}^2+r^2{\stackrel{·}{\theta }}^2)+\frac{1}{2}{M}_2({ẋ}^2+{ẏ}^2+2\stackrel{·}{\theta }(xẏ-ẋy)+{\stackrel{·}{\theta }}^2(x^2+y^2))-{V},& (1)\end{array}$

with

$\begin{array}{l}{M}_1=\frac{m_1{m}_0}{m_1+m_0},M_2=\frac{(m_1+m_0)m_2}{m_0+m_1+m_2},\\ {V}={\displaystyle \sum _{i,j=0,i\ne j}^2}\frac{G{m}_i{m}_j}{r_{ij}},\end{array}$

where r_ij indicate the mutual distances of the respective bodies and G is the gravitational constant. Since θ is a cyclic variable, the angular momentum, which in the rotating frame is written as

$\begin{array}{rc}L=\partial {L}/\partial \stackrel{·}{\theta }=M_1{r}^2\stackrel{·}{\theta }+M_2(\stackrel{·}{\theta }(x^2+y^2)+xẏ-ẋy),& (2)\end{array}$

is constant. Therefore, r = r(t), x = x(t), and y = y(t) are given by the Lagrangian equations derived from equation (1), while $\stackrel{·}{\theta }$ is provided by equation (2). In the following we consider always the normalization of masses

$\begin{array}{l}{m}_0+m_1+m_2=1\text{ and }G=1.\end{array}$

2.2. Periodic Orbits

Let us symbolize the initial conditions of an orbit by r(0) = r₀, x(0) = x₀, y(0) = y₀ and accordingly, the velocities. For the GTBP of planetary type, the existence of periodic orbits, their classification and initial conditions are described (e.g., by Hadjidemetriou, 1996). In this work we study symmetric periodic orbits, i.e., orbits which show two perpendicular crosses with the axis Gx, at t = 0 and at t = T/2, where T is the period. Their initial conditions are

$\begin{array}{rcl}r(0)=r_{00},x(0)=x_{00},y(0)=0,ṙ(0)& =& 0,ẋ(0)=0,\\ ẏ(0)& =& {ẏ}_{00}& (3)\end{array}$

and imply, in general, a normalization scheme of units. Instead of r₀, we can use the initial position of m₁ given by $x_{10}=\frac{m_0}{m_1+m_0}{r}_0$

By assuming fixed non-zero masses, any periodic solution of initial conditions given by Equation (3) can be continued monoparametrically, for example by varying r₀₀ and determining x₀₀ and ẏ₀₀ in order to satisfy appropriate periodic conditions (Hadjidemetriou, 2006; Voyatzis, 2017). We call this continuation scheme in space as x-continuation. Applying x-continuation, monoparametric families of periodic orbits are obtained in the 3D space of initial conditions Π₃ = {(r₀, x₀, ẏ₀)}. Also, any periodic solution of initial conditions of Equation (3) and non-zero masses is continued by varying the masses, say m₁ and m₂. If the masses do not vary independently, e.g., by fixing the ratio ρ = m₂/m₁, then a monoparametric continuation is applicable, e.g., by varying m₂, and we call this scheme μ-continuation. By combining both the above mentioned continuation schemes we obtain a 2D manifold, ${P}$, of initial conditions for periodic motion as a subset of a 4D space, namely

$\begin{array}{l}{P}\subset {\Pi }_4,\text{ where }{\Pi }_4=\left\{(r_0,x_0,{ẏ}_0,m_2)|\rho =\text{fixed}\right\}.\end{array}$

2.3. Stability of Periodic Orbits

The stability of periodic orbits can be examined by considering the monodromy matrix, Δ(T), of the variational equations of the system computed on a periodic solution of period T (Hadjidemetriou, 1996). For the system (1), Δ(T) is a 6 × 6 constant matrix of unit determinant, and it possesses three pairs of eigenvalues. We always get two unit eigenvalues, λ₁ = λ₂ = 1, while the remaining four form reciprocal pairs providing the following cases

- λ_3,4 = a ± ib ∈ ℂ, ${\lambda }_{5,6}=a^{\prime }\pm i{b}^{\prime }\in ℂ$, |λ_j| = 1,∀j (stability)

- λ₃ = 1/λ₄ ∈ ℝ and λ_{5, 6} = a ± ib ∈ ℂ with |λ₅| = |λ₆| = 1 (single instability)

- λ_j ∈ ℝ, ∀j with λ₃ = 1/λ₄ and λ₅ = 1/λ₆ (double instability)

- λ_3,4,5,6 = ±a ± ib, |λ_j| ≠ 1 (complex instability)

The above possible distributions of eigenvalues on the complex plane is presented in Figure 1. Cases of equal eigenvalues (except the pair λ₁, λ₂) correspond to critical cases of linear stability. Along a family of periodic orbits the monodromy matrix varies and the eigenvalues moves on the complex plane continuously preserving the feature of reciprocal pairs and the stability of orbits may change when critical cases are met. In general, any manifold ${P}$ should be divided in domains of different stability and the borders between the domains consist of critically stable orbits. For computations of stability it is convenient to use the indices of Broucke (1969).

FIGURE 1

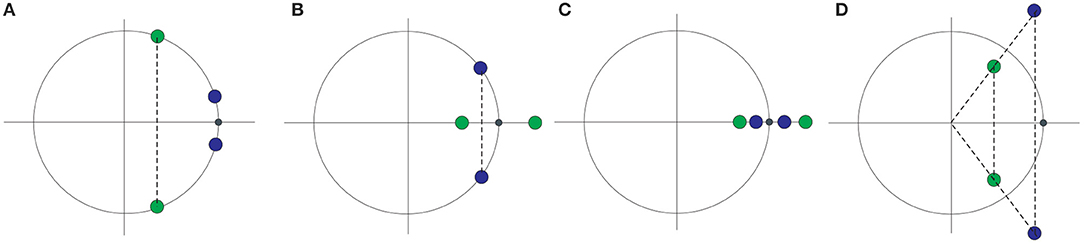
Figure 1. Possible distribution of eigenvalues λ_i, i = 3, 4, 5, 6 on the complex plane and with respect the unit circle (A) stability (B) single (or simple) instability (C) double instability (D) complex instability. For all cases λ₁=λ₂ = 1.

2.4. Methodology

The GTBP described in section 2.1 can model any physical configuration of three bodies (e.g., a star with two planets, two stars and one planet or a triple star system). Starting from the unperturbed planetary model, where m₀ = 1 and m₁ = m₂ = 0, we can increase the masses m₁ and/or m2 continuously to obtain any configuration of three bodies (see Figure 2). We remark that the mass m₀ is decreased accordingly in order to preserve the mass normalization.

FIGURE 2

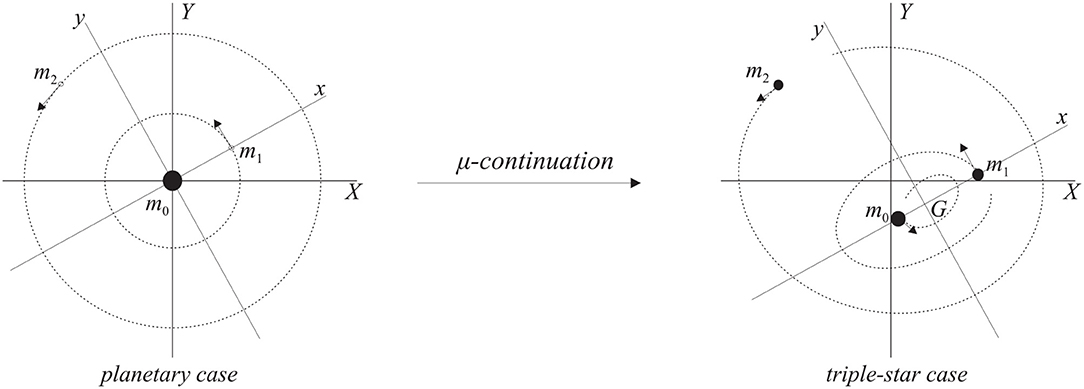
Figure 2. Schematic plot of the initial configuration of the system (planetary case, m₁, m₂ ≪ 1) and its final form (three stars with masses of the same order) obtained after μ-continuation.

We can compute a manifold ${P}$ by starting from known families of periodic orbits of a two-planet system (see e.g., Hadjidemetriou, 2006). Our approach consists of two steps. First, we perform μ-continuation to a particular periodic orbit selected from a family of the planetary case (0 < m₁, m₂ ≪ 1), which corresponds to a particular mass ratio ρ. Thus we obtain periodic orbits for large mass values for the initially small planets. Such a continuation provides a μ-family of orbits which is represented by a curve in the manifold ${P}$. Then, for a set of orbits of the μ-family, which are selected with sufficient resolution, x-continuation is applied in order to cover sufficiently whole ${P}$ or the interesting part of it.

In order to associate the periodic orbits with some physical description, we assume a hierarchical structure of the system, where m₀ and m₁ form the inner binary and m₂ revolves around the center of mass G of the inner binary. We denote with a₁ and e₁ the semimajor axis and the eccentricity of the inner binary and with a₂ and e₂ the same elements of the orbit of m₂ around G. Since we refer to triple systems with strong interactions, the orbits of the inner binary and the outer body may differ from being close to elliptic and the orbital elements are considered as osculating elements computed to the initial conditions of Equation (3) for each periodic orbit. We will use the dimensionless parameters for mass, distance and time defined as

$\begin{array}{l}\alpha =\frac{a_2}{a_1},\mu =\frac{m_1+m_2}{2m_0},\tau =\frac{T}{T_1},\end{array}$

where T is the period of the periodic orbit in the rotating frame and T₁ is the Keplerian period of the inner binary that corresponds to the osculating semimajor axis a₁. For almost circular orbits a is equivalent to the pericenter distance, Q, used in various stability criteria (Mylläri et al., 2018). For μ = 0 we have the unperturbed problem and for μ = 1 it is m₀ = 1/3 and m₁ + m₂ = 2/3. Each point of ${P}$ can be mapped to a pair of values (a, μ) and, provided that the mapping is one-to-one, a stability map can be given on this plane. The smallest values of a or the largest values of μ where stable periodic orbits exist consist the stability limits according to our approach.

3. Computations and Results

It is well-known that for the unperturbed planetary model (m₁ = m₂ = 0), when the two planets revolve on circular orbits of radii a₁ and a₂ and with the same direction, a circular periodic orbit of the system is defined with period T = 2π/(n₂ − n₁), where $n_i=a_i^{-3/2}$ is the mean motion of the planet i. Thus a family of circular orbits, denoted as S₀, is formed with orbits of any value of a > 1. When m_i ≠ 0 (i = 1, 2), the family C₀ generates by μ-continuation and for some μ ≪ 1 the family C, which breaks at the first order resonances n₂/n₁ = (p+1)/p, p = 1, 2, .., and joins smoothly with the resonant families of elliptic periodic orbits (Voyatzis et al., 2009).

Here, our computations are restricted to a particular manifold, called ${{P}}_c$, constructed from the family segment, denoted as C_I, consisting of planetary circular periodic orbits with n₂/n₁ > 2 and m₁ = m₂ (ρ = 1). The family C_I for small non-zero mass values is computed by applying differential corrections to the unperturbed orbits of family C₀. For 0 < m₁ = m₂ ≪ 1 all circular orbits are stable except for a small segment near the 3:1 resonance. Family C_I could generate the manifold ${{P}}_c$ by continuing all of its orbits by increasing the mass parameter μ. However, we found it more convenient for computations to construct the manifold ${{P}}_c$ by first performing μ-continuation starting from a particular periodic orbit of C_I. Then we apply x-continuation to the previously computed periodic orbits and, thus, we cover whole the manifold ${{P}}_c$.

We have chosen as starting orbit for our computations the orbit of C_I at a = a₀ ≈ 2.136 (n₂/n₁ ≈ 3.145), which is stable, and compute the family of symmetric periodic orbits S(μ; a₀) in the parameter interval μ ∈ (0, 1]. Since ρ = 1, we pass along the family from a two-planet system to a triple star system and the family ends with m₀ = m₁ = m₂ = 1/3¹. Along continuation we fix the initial position of m₁, x₁₀ ≈ 1, and increase the value of the angular momentum, given by Equation (2), proportionally to the increasing masses m₁ and m₂ (Voyatzis, 2017). The variation of the distance parameter a along the family is presented in Figure 3A. As μ increases the distance of the outer body from the inner binary also increases while the normalized period τ decreases accordingly. The eccentricities e₁ and e₂, which start from zero, vary along the family as it is shown in Figure 3B. The eccentricity of the inner binary, e₁, increases rapidly in the region up to μ < 0.1 (the maximum appears for μ = 0.17), but it does not take large values along the whole family. The orbit of the outer body seems to preserve its circular shape since its eccentricity remains < 0.01. All orbits of S(μ; a₀) are stable.

FIGURE 3

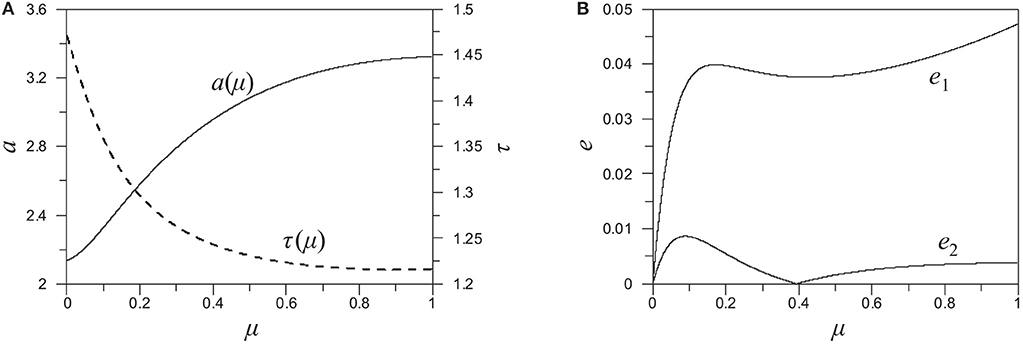
Figure 3. (A) The variation of the distance parameter a and the normalized period τ along the family S(μ; a₀) (B) The variation of the eccentricity of the inner binary (e₁) and the outer body (e₂) along the same family.

The next step in constructing the manifold ${{P}}_c$ is to perform x-continuation for the orbits of the family S(μ; a₀) by varying the distance parameter a (in computations we vary directly the distance x₁₀, so a changes accordingly). For each value of μ we compute the family S′(a; μ) in an interval a ∈ [a_min, a_max]. The family is not bounded from the right, i.e., a_max → ∞ and τ → 1. However, for each value of μ, a takes a minimum value along each family S′(a; μ) as it is shown in Figure 4A where the families for some values of μ are represented in the plane τ − a. The type of stability is also indicated by different colors. For any value of μ the orbits are certainly stable for a > a_s, where a_s = a_s(μ). For τ > τ_*, where τ_* indicates the position of the minimum of a, the periodic orbits are unstable and the continuation procedure becomes very slow as τ increases more. This is caused by the fact that the inner binary becomes very eccentric as it is shown in the top-right panel of Figure 4. In cases of μ = 0.021 and 0.125, the orbit of the outer body also becomes very eccentric when a is close to its minimum value. However as μ increases (e.g., in case μ = 0.75) and the bodies are relatively close to each other, their orbits are strongly perturbed ellipses and they are not described efficiently by the osculating elements e₁ and e₂.

FIGURE 4

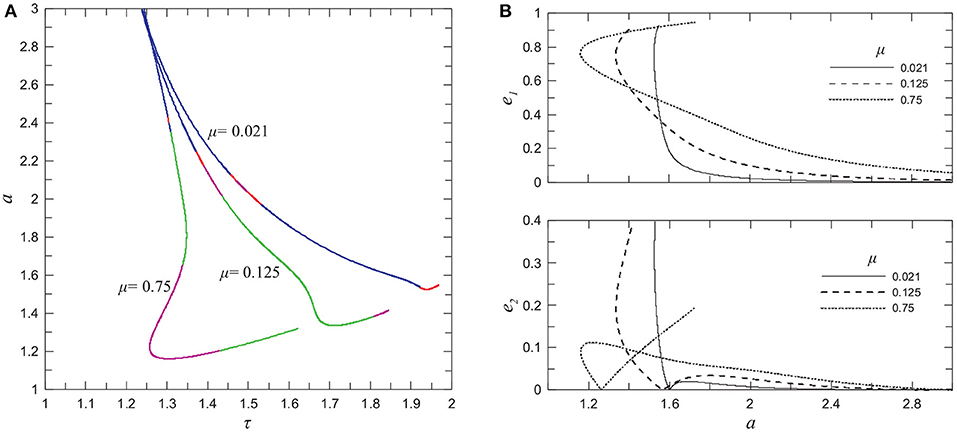
Figure 4. (A) Characteristic curves of families S′(a; μ) for particular mass values presented in the plane τ − a. Segments of blue color indicate stable orbits while red, magenta and green color present single, double, and complex instability, respectively (B) The initial eccentricities of the inner binary and the outer planet, e₁ and e₂ respectively, along the families presented in the left panel.

The manifold ${{P}}_c$ can be mapped one-to-one on the plane a − μ for the domain where τ < τ_*. Namely we consider the segments of the families S′(a; μ) where a descends as τ increases. As we have mentioned, for τ > τ_* the families consist of unstable orbits and are not considered in the definition of the stability limits. Therefore, by taking into account only the segments for τ < τ_*, each orbit of the restricted manifold ${{P}}_c$ is mapped on a point (a, μ). By considering a color coded mapping according to the stability type (see section 3) we form the stability map shown in Figure 5. On the stability map we indicate the border a = a_min on the left of the colored region. For a < a_min there are no periodic orbits belonging to the manifold P_c. For μ ≈ 0, a_min ≈ 1.6 and corresponds to the 2:1 planetary resonance. Also a_min(μ = 1) = 1.1656 and this is the smallest value of the relative distance a obtained among the periodic orbits of ${{P}}_c$.

FIGURE 5

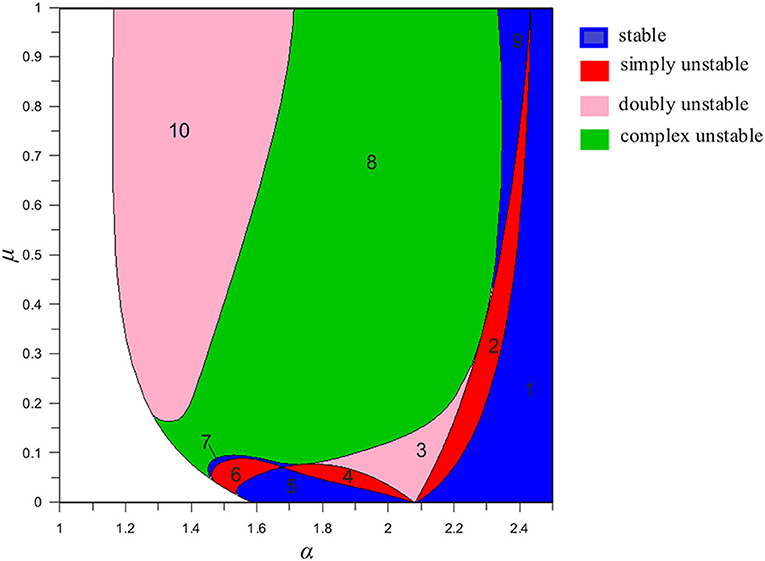
Figure 5. The stability map of the manifold ${{P}}_c$ of periodic orbits, which is projected on the plane a − μ. The manifold is restricted on the right of the white region and extends to a → ∞ (as a blue region).

In the colored domain we distinguish ten regions, indicated in the figure by the numbers 1 to 10. We symbolize the borders between the different regions as B_ij where i and j are the indices of the separated regions. The border B₁₂ is a limit of stability, in the sense that for a > a(B₁₂) all orbits on ${{P}}_c$ are stable (region 1). Nevertheless, the stable regions 5, 7, and 9 exist for a < a(B₁₂). The region 7 is narrow and includes orbits with relatively small distance parameter a but μ does not exceed the value 0.097 (i.e., m₁ = m₂ < 0.081). For μ ≈ 0, the region 5 is extended between the 2:1 and 3:1 resonances (1.59 < a < 2.08). As we mentioned above 2:1 resonance is associated with the value a_min. On the other side, at the 3:1 resonance, three unstable regions (2, 3, and 4) converge. This is in agreement with the instability of the circular family which occurs at the 3:1 resonance in the RTBP and in the GTBP of planetary type (Voyatzis and Hadjidemetriou, 2006). The stable region 9 is found for 0.375 ≤ μ ≤ 1 and close to the border B₈₉ we obtain the stable periodic orbits of the smallest relative distance, a, for large masses, particularly for μ>0.35. For μ = 1 the value a = 2.33 is the smallest one for obtaining a stable periodic orbit in a triple system of equal masses. Finally we mention that it has been proved by Hadjidemetriou (1982) that complex instability cannot occur for sufficiently small μ. In our stability map there is only the region 8 of complex instability. It is the wider region and extends down to μ ≈ 0.05.

4. Conclusions and Discussion

In this paper we addressed the problem of stability of triple systems by computing periodic orbits and their linear stability of the planar GTBP. We examined a particular manifold of periodic solutions, ${{P}}_c$, which is generated from the circular family of the planetary problem by applying continuation with respect to the mass. Here we restricted our computations to the case of m₁ = m₂ starting from m₁ = m₂ = 0 (μ = 0) and ending to the case of equal masses, m₁ = m₂ = m₃ = 1/3 (μ = 1). By considering the system as a hierarchical model, the orbit of the inner binary and the orbit of the outer body are almost circular as the mass parameter μ is small and the relative distance of the orbits, a, is quite large. The manifold ${{P}}_c$ is defined for a > a_min(μ). As μ → 0, a_min ≈ 1.59, which corresponds to the planetary resonance 2:1 and to the first gap of the circular family known from previous studies.

The most interesting subset of the manifold ${{P}}_c$ can be mapped on the plane a − μ and a stability map is formed according to the type of linear stability of the periodic orbit at each point of the plane. This is shown in Figure 5 where ten different distinguished regions appear. The stable region 1 seems to extend up to very distant orbits, a → ∞, while its left border, B₁₂, can be considered as the limit of stability of our study. The known triple star systems² are very hierarchical with very large values of a and therefore belong to the stability domain 1. However we showed that stability can exist for triple star systems with quite nearby orbits (e.g., for stars of equal masses we can have stability for a down to ~2.33). Stable regions 5, 7, and 9 are located on the left of B₁₂ and surrounded by unstable regions. Particularly, region 5 could host planetary systems with very heavy planets (like Kepler-53). We remark that the map indicates the known instability of the 3:1 resonance (a ≈ 2.08) for μ → 0.

In Figure 6 we show on the stability map the stability limits, μ_crit = μ(a), suggested by some previous studies. The criterion of Gladman (curve G) refers to Hill type stability that prevents close encounters (Gladman, 1993). The criterion holds for planetary masses so it is not reliable for large μ. It includes a large portion of the stability region 5, represents fairly the region 1 but includes also many unstable orbits of the regions 2, 3, and 4. The criterion of Donnison and Mikulskis (1992), which is based on numerical computations, seems more conservative than that of Gladman while the numerical criterion of Harrington (1975), which was one of the first numerical criteria for the stability of hierarchical systems, is located between the above mentioned criteria for large μ but deviates strongly from the other criteria for small μ and includes large regions of unstable periodic orbits.

FIGURE 6

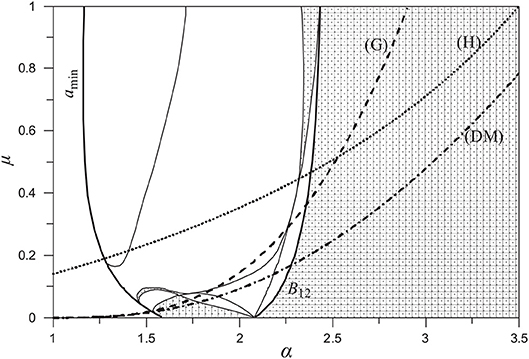
Figure 6. The stable (dotted) regions of the manifold ${{P}}_c$ and limit curves of stability criteria defined by Harrington (H), Donnison&Mikulskis (DM), and Gladman (G).

By assuming reasonably that stable periodic orbits are surrounded by invariant curves, which also support long-term stability, the stable regions obtained in this study are not restricted only on the manifold ${{P}}_c$. We tested this assumption by performing numerical integrations for initial conditions that deviate from the periodic orbit. For the narrow stable region 7, small deviations may cause instability. In regions 5 and 9 we obtain quasi-periodic orbits even by performing relatively large deviations. Certainly region 1 is the most stable region and almost all orbits with small eccentricities seem to remain stable for very long integrations.

The methodology suggested and applied in the presented work can be extended by either considering family segments of circular orbits for n₁/n₂ < 2 or by considering the families of resonant elliptic orbits which bifurcate at any resonance. It is well-known from planetary dynamics that resonances can provide protection of bodies from coming close to each other and, subsequently, can provide stable orbits even of very high eccentricities (Antoniadou and Voyatzis, 2016). Such a stability mechanism could be met also for triple systems of large μ and small a. Although in our computations we considered the mass ratio ρ = 1, μ-continuation can applied for any value of ρ and, thus, different configurations of three body systems can be studied.

Author Contributions

Both authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Footnotes

1. ^The system of a planet around a binary star is not included in this approach. Such a system can be obtained by increasing only the mass m₁ (or m₂) and keeping the m₂ (or m₁) small.

2. ^See e.g., https://www.univie.ac.at/adg/schwarz/multiple.html

References

Antoniadou, K. I., and Voyatzis, G. (2016). Orbital stability of coplanar two-planet exosystems with high eccentricities. Mthly Notic. R. Astron. Soc. 461, 3822–3834. doi: 10.1093/mnras/stw1553

CrossRef Full Text | Google Scholar

Bozis, G. (1981). Escape of the smallest mass of a triple system. Publ. Astron. Soc. Japan 33:67.

Google Scholar

Broucke, R. A. (1969). Stability of Periodic Orbits in the Elliptic, Restricted Three-Body Problem. JPL Technical report 32-1360, Pasadena, CA.

Bruno, A. D. (1994). The Restricted 3-Body Problem: Plane Periodic Orbits. Berlin; New York, NY: Walter de Gruyter.

Google Scholar

Contopoulos, G. (2002). Order and Chaos in Dynamical Astronomy. Berlin: Springer-Verlag.

Google Scholar

Dei Tos, D. A., Russell, R. P., and Topputo, F. (2018). Survey of mars ballistic capture trajectories using periodic orbits as generating mechanisms. J. Guid. Control Dyn. 41, 1227–1242. doi: 10.2514/1.G003158

CrossRef Full Text | Google Scholar

Donnison, J. R., and Mikulskis, D. F. (1992). Three-body orbital stability criteria for circular orbits. Mthly Notic. R. Astron. Soc. 254, 21–26.

Google Scholar

Georgakarakos, N. (2008). Stability criteria for hierarchical triple systems. Celestial Mech. Dyn. Astron. 100, 151–168. doi: 10.1007/s10569-007-9109-2

CrossRef Full Text | Google Scholar

Gladman, B. (1993). Dynamics of systems of two close planets. Icarus 106, 247–263.

Google Scholar

Hadjidemetriou, J. D. (1975). The continuation of periodic orbits from the restricted to the general three-body problem. Celestial Mech. 12, 155–174.

Google Scholar

Hadjidemetriou, J. D. (1982). On the relation between resonance and instability in planetary systems. Celestial Mech. 27, 305–322.

Google Scholar

Hadjidemetriou, J. D. (1996). “Periodic orbits in gravitational systems,” in Chaotic Worlds: From Order to Disorder in Gravitational N-Body Systems, eds B. A. Steves, A. J. Maciejewski, and M. Hendry (Amsterdam: Springer), 43–79.

Google Scholar

Hadjidemetriou, J. D. (1999). A symplectic mapping model as a tool to understand the dynamics of 2/1 resonant asteroid motion. Celestial Mech. Dyn. Astron. 73, 65–76.

Google Scholar

Hadjidemetriou, J. D. (2006). Symmetric and asymmetric librations in extrasolar planetary systems: a global view. Celestial Mech. Dyn. Astron. 95, 225–244. doi: 10.1007/s10569-006-9007-z

CrossRef Full Text | Google Scholar

Harrington, R. S. (1975). Production of triple stars by the dynamical decay of small stellar systems. Astron. J. 80, 1081–1086.

Google Scholar

He, M. Y., and Petrovich, C. (2018). On the stability and collisions in triple stellar systems. Mthly Notic. R. Astron. Soc. 474, 20–31. doi: 10.1093/mnras/stx2718

CrossRef Full Text | Google Scholar

Henon, M. (1974). Families of periodic orbits in the three-body problem. Celestial Mech. 10, 375–388.

Google Scholar

Hénon, M. (1997). Generating Families in the Restricted Three-Body Problem. Berlin: Springer-Verlag.

Google Scholar

Marchal, C., and Bozis, G. (1982). Hill stability and distance curves for the general three-body problem. Celestial Mech. 26, 311–333.

Google Scholar

Mylläri, A., Valtonen, M., Pasechnik, A., and Mikkola, S. (2018). Stability of hierarchical triples - I. Dependence on inner eccentricity and inclination. Mthly Notic. R. Astron. Soc. 476, 830–841. doi: 10.1093/mnras/sty237

CrossRef Full Text | Google Scholar

Siegel, C. L., and Moser, J. (1971). Lectures on Celestial Mechanics. Berlin: Springer.

Google Scholar

Voyatzis, G. (2017). “Periodic orbits of planets in binary systems,” in Proceedings of the First Greek-Austrian Workshop on Extrasolar Planetary Systems, eds T. A. Maindl, H. Varvoglis, and R. Dvorak (North Charleston, SC: Create Space Publishing), 197–224.

Google Scholar

Voyatzis, G., and Hadjidemetriou, J. D. (2006). Symmetric and asymmetric 3:1 resonant periodic orbits with an application to the 55cnc extra-solar system. Celestial Mech. Dyn. Astron. 95, 259–271. doi: 10.1007/s10569-006-9005-1

CrossRef Full Text | Google Scholar

Voyatzis, G., Kotoulas, T., and Hadjidemetriou, J. D. (2009). On the 2/1 resonant planetary dynamics - periodic orbits and dynamical stability. Mthly Notic. R. Astron. Soc. 395, 2147–2156. doi: 10.1111/j.1365-2966.2009.14671.x

CrossRef Full Text | Google Scholar

Voyatzis, G., Tsiganis, K., and Antoniadou, K. I. (2018). Inclined asymmetric librations in exterior resonances. Celestial Mech. Dyn. Astron. 130:29. doi: 10.1007/s10569-018-9821-0

CrossRef Full Text | Google Scholar

Winter, O. C., and Murray, C. D. (1997). Resonance and chaos. I. First-order interior resonances. Astron. Astrophys. 319, 290–304.

Google Scholar

Xin, X., Scheeres, D. J., and Hou, X. (2016). Forced periodic motions by solar radiation pressure around uniformly rotating asteroids. Celestial Mech. Dyn. Astron. 126, 405–432. doi: 10.1007/s10569-016-9701-4

CrossRef Full Text | Google Scholar