Corrigendum: Longitudinal modulation of Marangoni wave patterns in thin film heated from below: instabilities and control
- 1Theoretical Physics Department, Perm State University, Perm, Russia
- 2Department of Mathematics, Technion—Israel Institute of Technology, Haifa, Israel
A corrigendum on
Longitudinal modulation of Marangoni wave patterns in thin film heated from below: instabilities and control
by Samoilova, A., and Nepomnyashchy, A. (2021). Front. Appl. Math. Stat. 7:697332. doi: 10.3389/fams.2021.697332
In the published article, there was an error in Equations 22–23. The substitution of α (given by the expression on page 3 below Equation 12) in Equation 21 provides a coefficient that is opposite in sign to the one in the original paper. Hence there is an opposite sign in front of the expressions of Equations 22–23. The analysis below Equation 24 is perfectly correct in the original paper. However, the change in sign of parameter K1 results in the transformation of Figure 2. The description of Figure 2 in the text must also be corrected. The following corrections are presented in their order of appearance in the text.
A correction has been made to Longitudinal Modulation, “Amplitude Equation,” paragraphs 15–17. The text previously stated:
“For a traveling wave A = A(X1, t1) = A(x1+ω1t1), Eq. 21 gives
hence,
Because of the conservation of the liquid's volume, the value of h20 averaged over a whole region of X1 vanishes, 〈h20(X1, t2)〉X1 = 0; therefore,
and
Thus, Eq. 19 reads as
where .”
The corrected text appears below:
“For a traveling wave A = A(X1, t1) = A(x1+ω1t1), Eq. 21 gives
hence,
Because of the conservation of the liquid's volume, the value of h20 averaged over a whole region of X1 vanishes, 〈h20(X1, t2)〉X1 = 0; therefore,
and
Thus, Eq. 19 reads as
where .”
A correction has been made to Longitudinal Modulation, “Stability of Traveling Wave,” last paragraph. The last sentence previously stated:
“We find that traveling rolls are stable against both the amplitude modulation instability and the phase modulation instability.”
The corrected sentence appears below:
“We find that traveling rolls are unstable against both the amplitude modulation instability and the phase modulation instability.”
A correction has been made to Longitudinal Modulation, “Influence of the Feedback Control,” paragraph four. Sentences 4–6 previously stated:
“One can see from Figures 2D, E that a positive control gain excites the amplitude modulation instability within a small area of parameters. The growth of the positive control gain results in extension of the domain of subcritical instability (see Figure 2F). For ϰq = 0.3, the amplitude modulation instability is replaced by the phase modulation instability.”
The corrected text appears below:
“One can see from Figures 2D, E that a positive control gain suppresses the amplitude modulation instability within a small area of parameters. The growth of the positive control gain results in extension of the domain of subcritical instability (see Figure 2F). For ϰq = 0.3, the domain of stable traveling rolls extends and the area of the phase modulation instability occurs.”
A correction has been made to Figure 2. The corrected Figure 2 appears below.
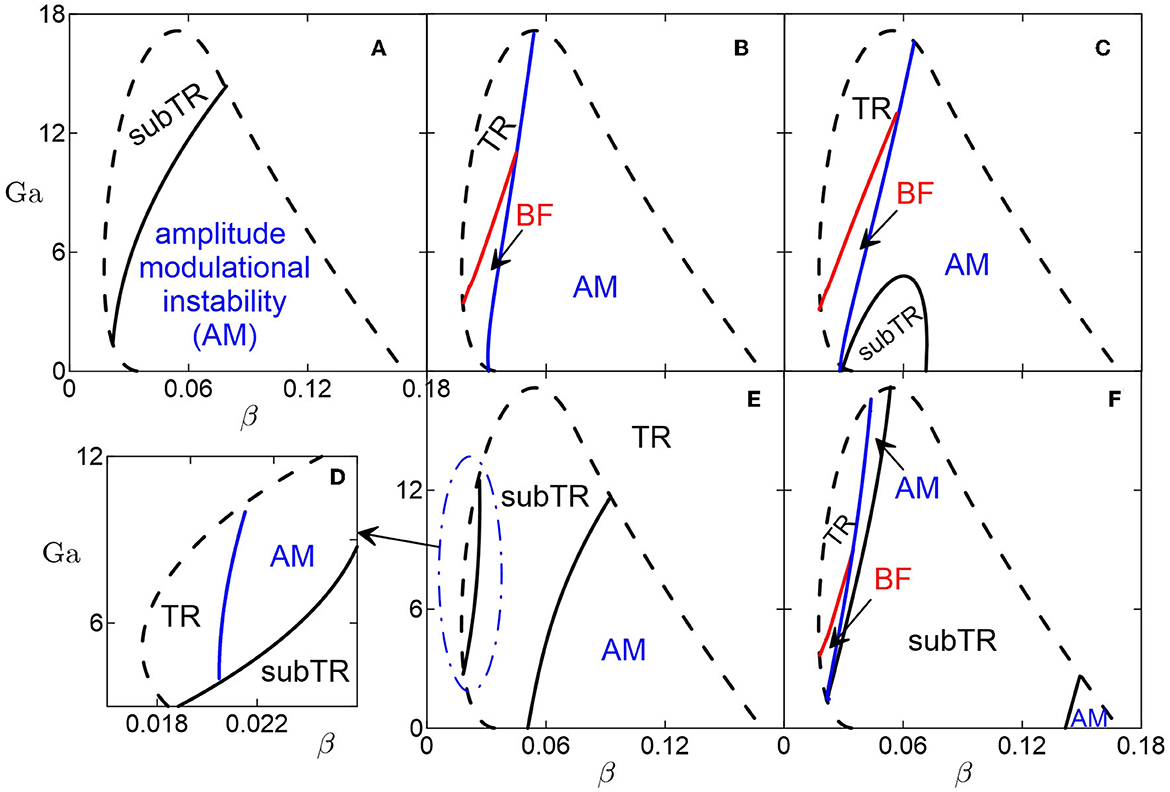
Figure 2. Domains of stability for traveling rolls against the longitudinal modulations for (A) uncontrolled convection; (B, C) negative non-linear feedback control gain ϰq = −0.2, −0.3, (E, F) positive non-linear feedback control gain ϰq = 0.1, 0.3. (D) Zoomed-in fragment of panel (E). Dashed lines indicate the area of the oscillatory convection. Within domains marked “subTR” traveling rolls bifurcate subcritically. “TR” marks domains of stability for traveling rolls. Benjamin-Feir instability and the amplitude modulational instability occurs within domains marked “BF” and “AM,” respectively.
A correction has been made to Discussions, paragraph three. The paragraph previously stated:
“Calculations show that the uncontrolled roll patterns are stable against the perturbations with a slightly different wavelength. However, in the absence of the control, traveling rolls emerge through the subcritical bifurcation within certain parameter domains. Previously, it was demonstrated that one can eliminate subcritical bifurcation by applying the non-linear feedback control [7]. But besides that, non-linear feedback control affects pattern selection as well. In this article, we reveal that the non-linear feedback control with positive gain can produce an amplitude modulation instability, and the control with negative gain can produce a phase modulation instability. Thus, the non-linear feedback control can destabilize traveling rolls against the longitudinal modulation at the same time as it stabilizes traveling rolls against the subcritical excitation.”
The corrected paragraph appears below:
“Calculations show that the uncontrolled roll patterns are unstable against the perturbations with slightly different wavelength. However, in the absence of the control, traveling rolls emerge through the subcritical bifurcation within certain parameter domains. Previously, it was demonstrated that one can eliminate subcritical bifurcation by applying the non-linear feedback control [7]. But besides that, non-linear feedback control affects pattern selection as well. In this article, we reveal that the non-linear feedback control can suppress an amplitude modulation instability or produce a phase modulation instability depending on the parameters. Thus, the non-linear feedback control can destabilize traveling rolls against the longitudinal modulation at the same time as it stabilizes traveling rolls against the subcritical excitation.”
The authors apologize for these errors and state that they do not change the scientific conclusions of the article in any way. The original article has been updated.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Keywords: thin film, Marangoni convection, modulated wave, feedback control, Benjamin–Feir instability
Citation: Samoilova A and Nepomnyashchy A (2023) Corrigendum: Longitudinal modulation of Marangoni wave patterns in thin film heated from below: instabilities and control. Front. Appl. Math. Stat. 9:1229581. doi: 10.3389/fams.2023.1229581
Received: 26 May 2023; Accepted: 06 June 2023;
Published: 26 June 2023.
Edited and reviewed by: Ulrich Parlitz, Max-Planck-Institute for Dynamics and Self-Organisation, Germany
Copyright © 2023 Samoilova and Nepomnyashchy. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Anna Samoilova, annsomeoil@gmail.com
 Anna Samoilova
Anna Samoilova Alexander Nepomnyashchy
Alexander Nepomnyashchy