Promoting the construction of intelligent knowledge with the help of various methods of cognitively activating instruction

1. Introduction

All subjects taught in school aim to foster meaningful learning and conceptual understanding. The knowledge acquired in the classroom is supposed to enable students to better understand the world around them, as well as to develop and achieve short-term and long-term goals. The reality, however, often looks different: Students acquire knowledge that is bound to the narrow context of the classroom, which means they do not achieve a deeper understanding of the content dealt with. Many of them can retrieve the knowledge in the next exam, but its isolated representation in long-term memory makes it unlikely to be activated in new contexts inside and outside of school (Day and Goldstone, 2012). In the past decades, the learning sciences have developed and evaluated means of classroom practice that can promote the construction of flexible and thereby intelligent knowledge that facilitates the transfer of knowledge to new situations. This article gives an overview of the current state of empirical research on methods of cognitively activating teaching that promote conceptual change and flexible application of knowledge in new situations. “Cognitively activating” means that these methods promote the active construction of knowledge by facilitating a better understanding of the problem at hand, by activating relevant prior knowledge, and by fostering a better awareness of the limits of one’s own knowledge. Six methods that have each proven successful in boosting learners’ conceptual understanding in experimental studies are presented in this article. The examples presented in this article as well as the literature referred to come from the STEM fields. On the one hand, this is because our expertise lies in STEM learning, and on the other hand, many principles of human learning have been researched using the example of STEM subjects. There are many reasons for this, including the possibility of creating objective tests to measure learning progress as well as international coherence in curricula. It should, however, be emphasized that all means of classroom practice presented in the following can be adapted to the humanities. Also in these subjects, there is a risk of accumulating unrelated facts instead of creating meaningful conceptual networks, as discussed for the subject of history by Carretero and Perez-Manjarrez (2022).

2. Assessing and utilizing students’ prior knowledge

Since prior knowledge is among the best predictors for learning (Stern, 2009, 2017), instructors should use pretests as means of formative assessment (Black and Wiliam, 2009) to gain information about the learners’ state of knowledge at the beginning and also during the process of learning. Educational researchers nowadays agree that the main barrier to understanding scientific concepts in all content areas is not so much what students lack, but what they have. These are alternative conceptual frameworks, also addressed as naïve concepts or misconceptions, that often work well in everyday life, but differ from or even contradict scientific explanations (e.g., Carey, 2000). It will be shown, how teachers can use information about students’ prior knowledge and misconceptions to support conceptual change.

2.1. Do students actually have the prior knowledge required for understanding the new topics?

In order to prepare lessons for a new content area, teachers are well advised to examine in advance whether students already fulfill the knowledge requirements needed to profit from the planned lessons. Without such an examination teachers do not know why their students did not understand a particular content in a certain lesson: Is it because the content and the learning activities were not comprehensibly presented, or is the real reason for their lack of understanding that in previous lessons they had not understood fundamental concepts underlying this new content? Such uncertainties can be avoided if learners’ prior knowledge is checked by specific pre-tests, which can be carried out anonymously if this encourages learners to honestly report their deficits.

Checking prior knowledge is helpful in all subjects at all age levels, and it is essential in mathematical and science education, since these contents are often strictly built on each other. For example, understanding the mathematical concept of power functions presupposes understanding the mathematical concept of function. Therefore, before starting with lessons on power functions one should find out with questions like those presented in Figure 1, whether students already have an adequate understanding of the mathematical concept of function.

FIGURE 1

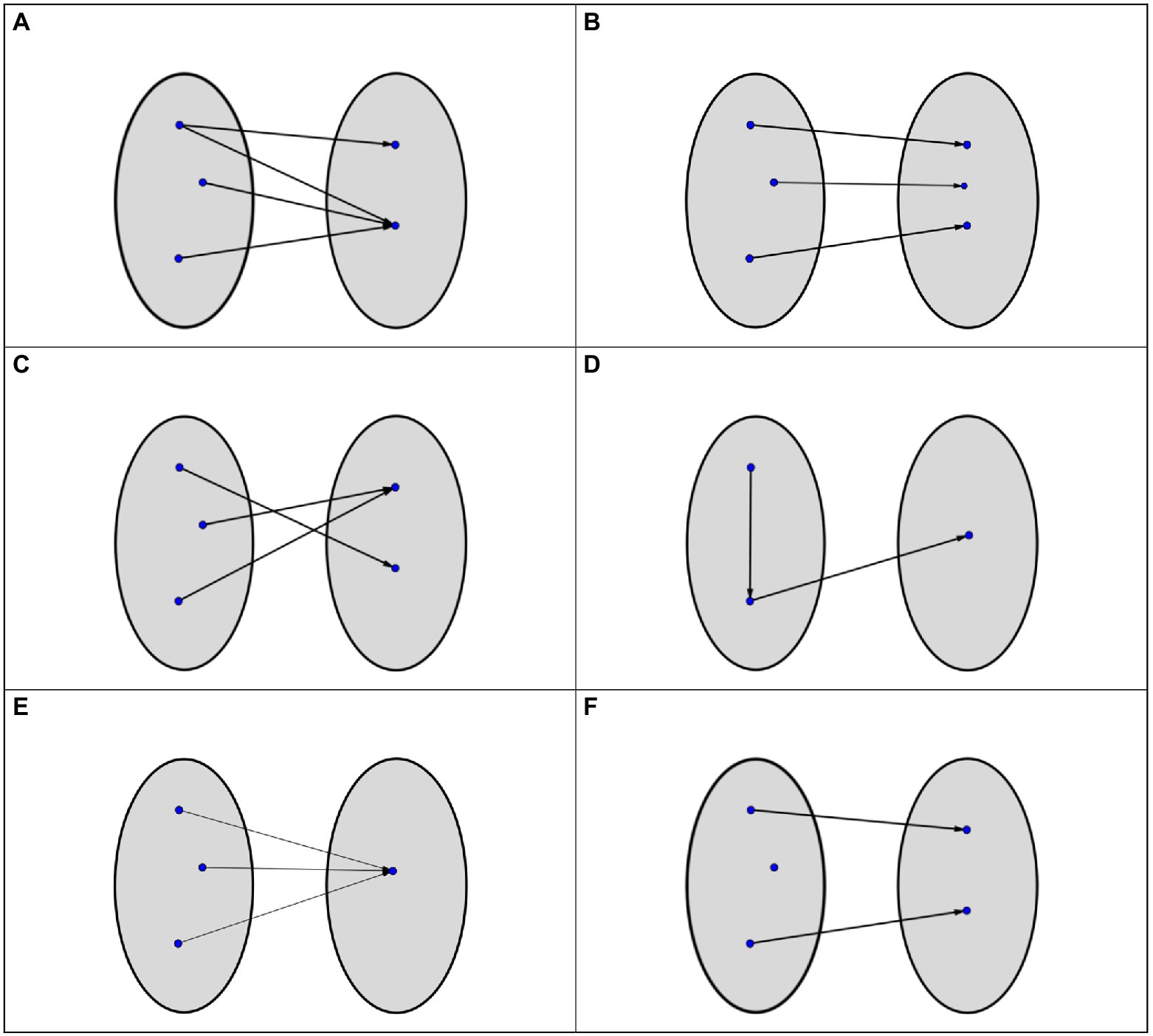
Figure 1. Example of an item to assess prior knowledge on functions by asking “Which of the following diagrams represent a function from the first set (left) to the second set?” (Correct answers: b, c, e).

In chemistry, likewise, one cannot profit from lessons on intermolecular forces without having an adequate understanding of the chemical concept of molecule. Pre-test questions like the one presented in the following example can clarify whether students understand that the concept of molecule exclusively applies to small atomic ensembles connected via covalent bonds, but is not applicable in the case of ionic and metallic bonding or large ensembles of atoms that are all connected via covalent bonds.

FIGURE 2

Figure 2. A demonstration of the increase of the sphere’s surface with increasing radius.

Which of the following substances contain molecules?

A. Iron (Fe).

B. Water (H₂O).

C. Cooking Salt (NaCl).

D. Diamond (C).

E. Glucose (C₆H₁₂O₆).

F. Methane (CH₄).

An exemplary question on understanding the concept of molecule (Correct answers: B, E, F).

If in the question presented in Figure 2 the options A and C are chosen, this indicates a too broad and therefore inaccurate understanding of molecules. In this case, students falsely apply the concept of molecule to all substances indifferent of the bonding situation present. If option D is chosen, this shows that learners are unaware of the fact that a diamond crystal does not consist of separate and small molecules, but of atoms that are all connected via covalent bond forming one huge structure.

Consequently, if it turns out in a pre-test that students lack relevant prior knowledge, teachers should close these gaps before starting the new lessons.

2.2. Using prior knowledge to build meaningful units

A further reason for checking students’ prior knowledge before starting with lessons on a new topic is that thereby teachers learn which of their students’ knowledge could be used for connecting new learning contents to already existing ideas. Learning thus can be facilitated since working memory capacity depends on connecting new information with prior knowledge to build meaningful units (Stern et al., 2016; Stern, 2017). In cognitive psychology, this important process of constructing meaningful units is labeled as “chunking.”

For example, if the following four sentences with randomly chosen names were presented to us:

•  Beat walked over the roof.

•  Urs ate an apple.

•  Dominik set the sail.

•  Peter hid an egg.

it would be significantly more difficult to memorize them than it would be to memorize the following sentences that contain names that facilitate chunking:

•  Father Christmas walked over the roof.

•  Adam ate an apple.

•  Columbus set the sail.

•  The Easter Bunny hid an egg.

The more possibilities one has to connect new information to prior knowledge and, thereby, to construct meaningful units, the more information can be memorized. For this reason, it is important to use prior knowledge to enable chunking.

If teachers know which prior knowledge learners already have, they can present new information in a way that enables learners to connect it to their already existing knowledge. In Switzerland, for instance, students typically learn about the law of Coulomb in chemistry lessons before the law of gravitation is presented to them in physics lessons 1 year later. Activating students’ knowledge about the law of Coulomb is likely to facilitate the understanding of the law of gravitation.

Law of Coulomb:

$F_C=\frac{1}{4\cdot \pi \cdot {\epsilon }_0}\cdot \frac{Q_1\cdot Q_2}{r^2}$

Law of Gravitation:

$F_G=G\cdot \frac{m_1\cdot m_2}{r^2}$

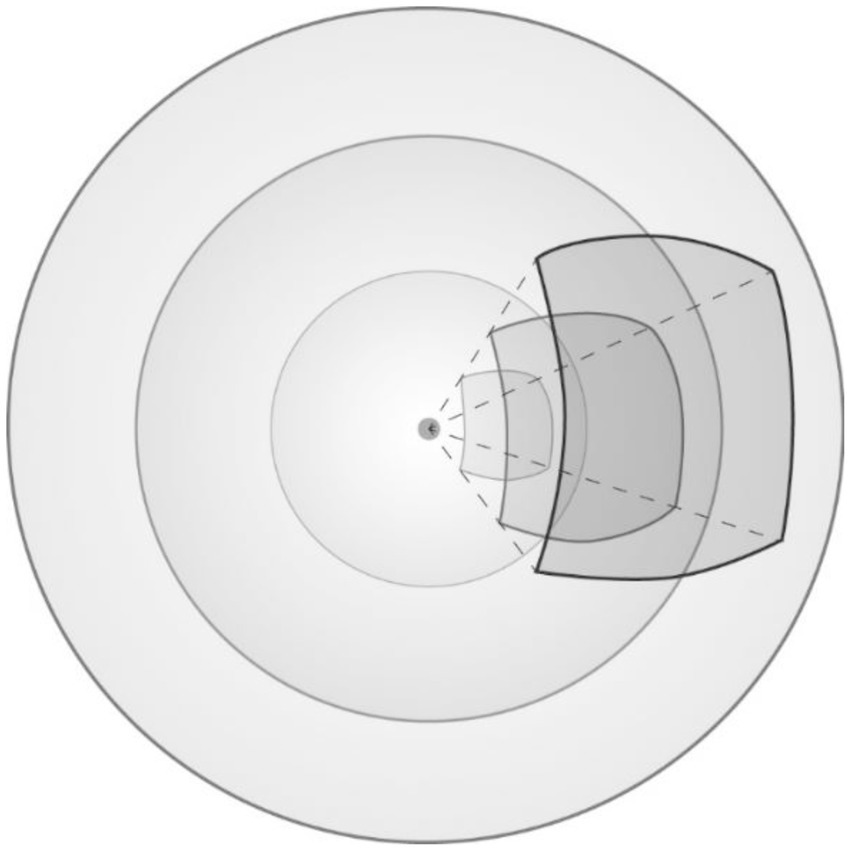
Accordingly, it can be helpful, when introducing the law of gravitation in physics lessons to highlight the similarities with the law of Coulomb, and to emphasize that these similarities are explained by the fact that in both cases a force is distributed on the surface of a sphere. The fact that the surface of the sphere is proportional to the square of the radius, as demonstrated in Figure 2, explains the denominator in both formulas.

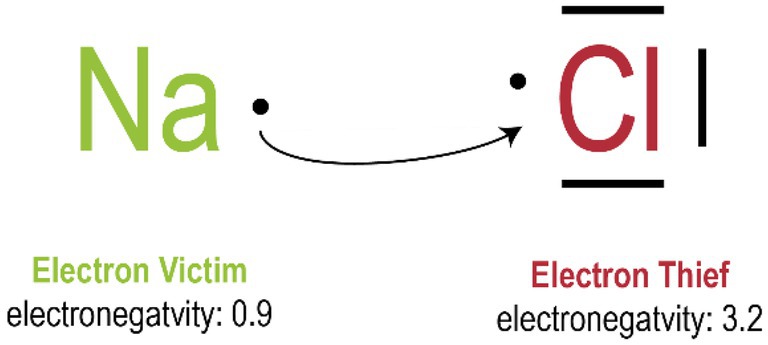
In order to facilitate the understanding of the chemical concept of electronegativity, it might be helpful to introduce the figures of speech of “electron thieves,” “electron victims” and of electrons as “loot.” In this analogy, elements with a high electronegativity like oxygen and chlorine are described as electron thieves because they can snatch away electrons from other elements if these do not sufficiently hold their electrons, as illustrated in Figure 3. Electron victims, i.e., elements like sodium and lithium with a low electronegativity, are particularly endangered by this kind of theft. By this analogy, the chemical concept of electronegativity can be connected to students’ prior knowledge and thereby provides the basis for further reasoning.

FIGURE 3

Figure 3. An illustration of electronegativity.

These examples illustrate how learners could connect new information to prior knowledge by constructing meaningful units. The better they manage to chunk new information in this way, the better this information is available for solving future problems.

2.3. Actively restructuring naïve concepts and misconceptions

As mentioned before, the main barrier to understanding the scientific explanations offered is not so much what students lack, but what they have. Because naïve concepts or misconceptions often work well in everyday life, there is no pressure to revise them, unless students experience their limited or misleading explanatory power in school. For example, an appropriate understanding of the concept of density is impeded by children’s belief that all light objects float in water while all heavy ones sink. Likewise, understanding the buoyancy force is hampered by students’ belief that a ship made of steel floats because the air in the ship’s body pulls it upwards (Hardy et al., 2006). Many of the naïve concepts on matter, motion, inertia, force and other mechanical topics persist even until university and beyond, despite students were offered scientific explanations in physics classes (Mazur, 2015).

Understanding Newton’s mechanics, for instance, is so demanding because many of our naïve ideas about force and inertia initially have a high plausibility although they are not compatible with the concepts of physics. In everyday life, we usually associate the concept of force with effort, and therefore we assume that a small and light person has to apply more force if this person is pressing her hands against the hands of a larger and heavier person (see Figure 4), because the small and light person has to make a greater effort to stay in an equilibrium. However, from the perspective of Newton’s physics the forces between them are not of different magnitude, but active and reactive forces of the same magnitude and with opposite directions.

FIGURE 4

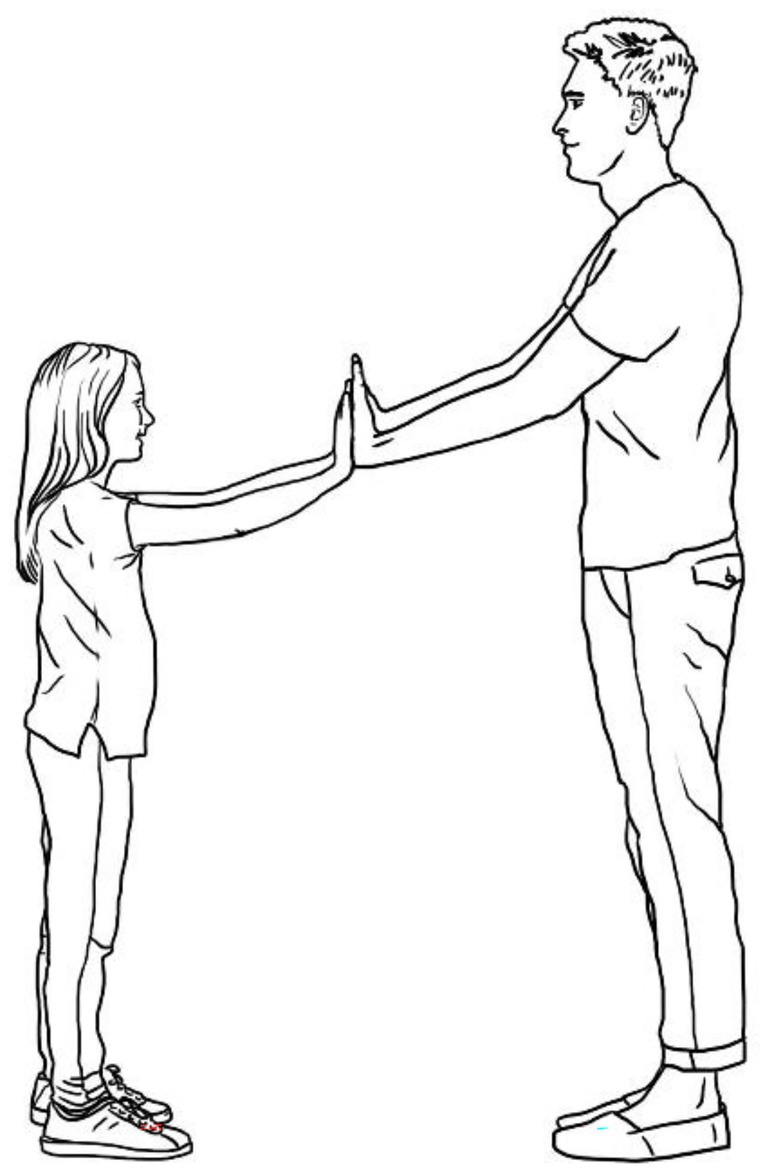
Figure 4. An illustration to show that although the girl has to make a greater effort than the man to keep in an equilibrium, the active and reactive forces between them are of the same magnitude and with opposite directions.

For many students, also the physical concept of inertia is incongruent with their naïve concepts. Consequently, they typically expect that a body that falls from a moving plane (Figure 5) will move along trajectory A instead of trajectory D, as it would be correct.

FIGURE 5

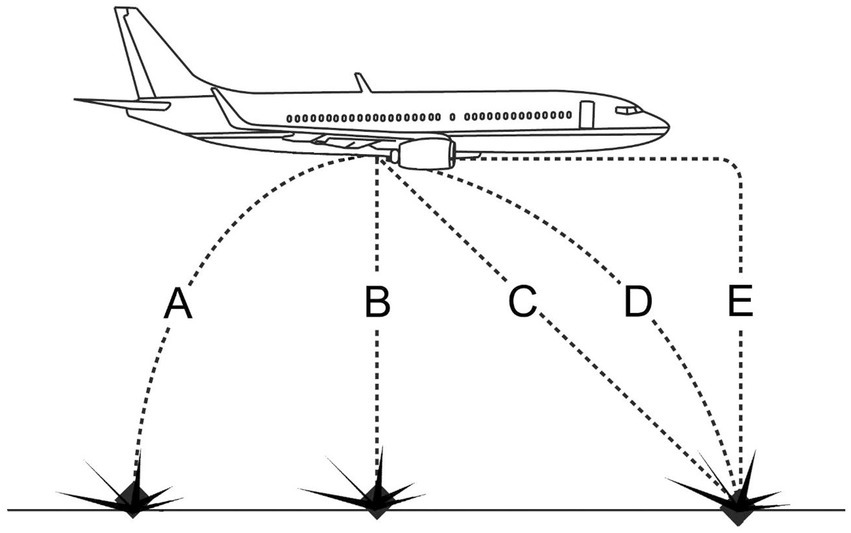
Figure 5. An item to test the concept of inertia by asking “Which option correctly describes the trajectory of a body that falls from the moving plane?”

These examples illustrate that previously checking naïve concepts and misconceptions that might hinder understanding is essential for preparing science lessons. Only based on this information, teachers can specifically address such ideas and design tasks that help learners to replace them by the correct scientific concepts (Schneider and Stern, 2010).

3. Productive failure: Generating solutions to novel problems prior to instruction

Knowledge construction and reorganization starts with the learner’s insight that a given problem cannot be solved by referring to one’s preexisting knowledge. Accordingly, one way to involve students in active knowledge construction consists in challenging them with interesting questions they so far cannot answer. If such tasks have an appropriate level of difficulty, this method may lead to an activation of relevant prior knowledge, and it may also facilitate a better understanding of the problem at hand. In addition, it makes students aware of their own knowledge deficits. Failing in this context can be productive because it reveals the limits of the students’ existing knowledge and can hence initiate conceptual change (e.g., Loibl et al., 2017).

Typically, lessons at school start with the presentation of new concepts, theories and problem-solving strategies which are subsequently elaborated and practiced. In the following, this traditional sequence will be labeled as “tell and practice.” One of its advantages is that students are provided from the beginning with all relevant information and, thus, should be well prepared for the subsequent tasks. Tell and practice is a proven and reliable method of teaching. However, when it comes to abstract and demanding concepts, one might ask whether tell and practice is the most effective way of teaching – or whether learners could be better cognitively activated by different instructions, for instance by reversing the order of the tell and practice sequence. This is the leading question in research on “productive failure.” The underlying idea is that learners should start with a problem for which they so far cannot retrieve a solution strategy. Only after having tried to solve the problem, learners receive the correct explanation resp. solution strategy. It is expected that even after an unsuccessful attempt to solve the problem, learners will activate more relevant prior knowledge, have a deeper understanding of the problem at hand and also a better awareness of the limits of their knowledge. This in turn is intended to direct the learners’ attention to the following instruction. It has been shown in several studies by different research teams that learning by productive failure can outperform learning by tell and practice (for an overview see Darabi et al., 2018; Loibl and Leuders, 2019; Mazziotti et al., 2019).

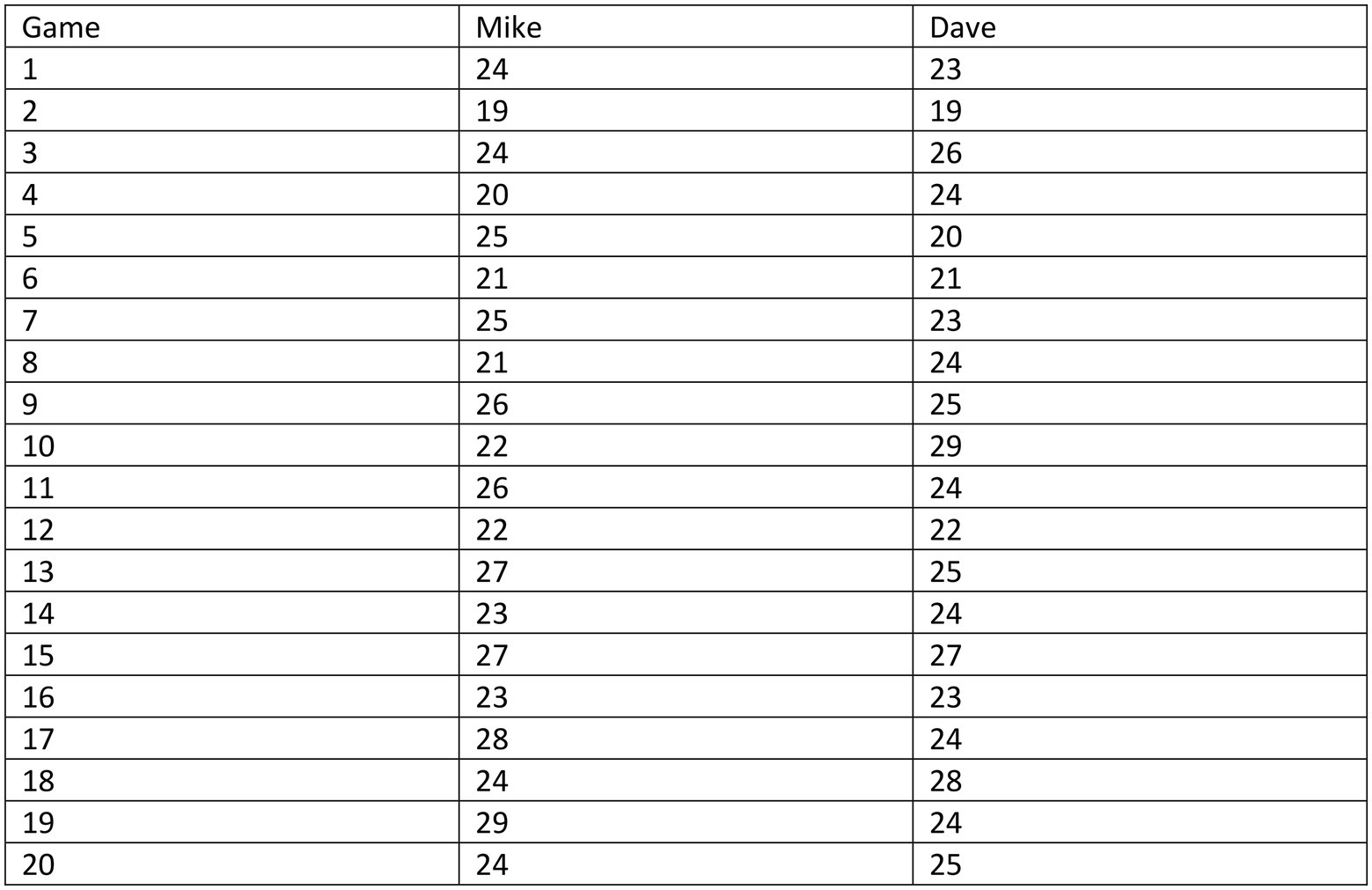
A typical study is on the mathematical concept of standard deviation (Kapur, 2014). Students in the “tell and practice”-group (control group) received all relevant information about the concept of standard deviation at the beginning of the lesson. Subsequently they had to apply their new knowledge by calculating the standard deviations of the scores of two basketball players. In contrast, students in the “productive failure”-group (experimental group) started with the task to develop by themselves mathematical measures for the consistency of the scores of the two basketball players. Thus, they had to construct a mathematical description for the mean variation of the scores:

FIGURE 6

Figure 6. Learning materials for figuring out the concepts of variance and standard deviation.

Mike and Dave are two basketball players. The table in Figure 6 shows the number of points scored by Mike and Dave over the course of 20 games. An award has to be given to the more consistent player of the two. The decision has to be made mathematically. Design as many measures of consistency as you can to determine the more consistent player.

The scores of the two basketball players were selected in a way that they were matching with regard to the arithmetic mean, the median and the mode. Hence, these mathematical concepts were of no help for the students. Therefore, they had to invent something that came close to the concept of standard deviation.

The students in the experimental group received the correct mathematical definition of standard deviation only after they – unsuccessfully – tried to design an appropriate mathematical measure. It turned out that students in the experimental group had higher posttest scores than students in the control group. These results indicate that learning by productive failure was more effective because it was more cognitively activating than the traditional “tell and practice”-teaching.

For successful learning by productive failure it is decisive that the level of difficulty is well chosen. Students should have enough knowledge to understand the question, respectively what kind of solution they are looking for, and they should just lack the specific knowledge that would enable them to construct by themselves the concept in question. In addition, subsequent research emphasizes that – after students’ failure to find the correct solution – it is essential to compare their own suggestions with the correct concept so that they understand it’s advantages (Loibl and Leuders, 2019). According to these authors, failing to solve a problem is not effective if students are not aware of their failure and of the shortcomings of their own suggestions (Loibl et al., 2017). In order for the method to work, the learning material must contain hurdles that need to be overcome.

4. Inventing with contrasting cases: Problem-solving followed by instruction

Stimulating learning material is a precondition for meaningful learning. In some cases, however, the potential of this material can be further improved by rethinking the order of presentation. As discussed in the previous paragraph on productive failure, students first try to solve a problem and afterwards they undergo an instruction. This procedure can be further refined by encouraging the learners to compare and contrast material for differences and similarities. On doing so, learners are expected to extract deeper principles and abstract concepts. Engaging students in such activities before they undergo an instruction is expected to be effective if prior knowledge is available, but its spontaneous activation is unlikely. This can be implemented by presenting learners with several contrasting cases illustrating a specific underlying concept (e.g., linear graphs with different slopes) and instructing them to invent a common index that can be used to describe the slopes of these linear graphs. After the completion of the invention task, the scientific concept is explained to them. This instructional method is cognitively activating since it requires students to actively address a given problem and activate relevant prior knowledge. It helps students process and understand subsequent instruction (e.g., Schalk et al., 2017).

This kind of instruction is labeled as “inventing with contrasting cases” (Schwartz et al., 2011). The major difference to learning by productive failure is that in this case students have a realistic chance to find the solution. In the just mentioned study by Schwartz and his team, for instance, students in the experimental group were guided by instructions to construct the physical concept of density by comparing buses filled with different amounts of clowns. After finishing this task the concept of density was explained to them. In contrast, students in the control group followed the “tell and practice”-sequence. Accordingly, they first received the information about the physical concept of density and, subsequently, applied their new knowledge by calculating the different densities of clowns in buses. In post- and follow up-tests it turned out that students in the experimental group outperformed students in the control group. This advantage is attributed to the factors that students in the experimental group, due to their constructive activity, had a deeper understanding of the problem (“What kind of solution are we looking for?”), a better metacognitive awareness of the limits of their own knowledge, and also activated more relevant prior knowledge.

A study on understanding the mathematical concept of the slope of graphs of linear functions provides further evidence for the effectiveness of this form of learning (Schalk et al., 2017). In this study, students in the control group followed the traditional “tell and practice”-sequence, i.e., they first received information about the mathematical concept of the slope of graphs of linear functions, and subsequently practiced their new knowledge by calculating the slopes of different graphs. Students in the experimental group, in contrast, started with the instruction to construct by themselves a mathematical description of the slope of graphs of linear functions, as presented in Figure 7.

FIGURE 7

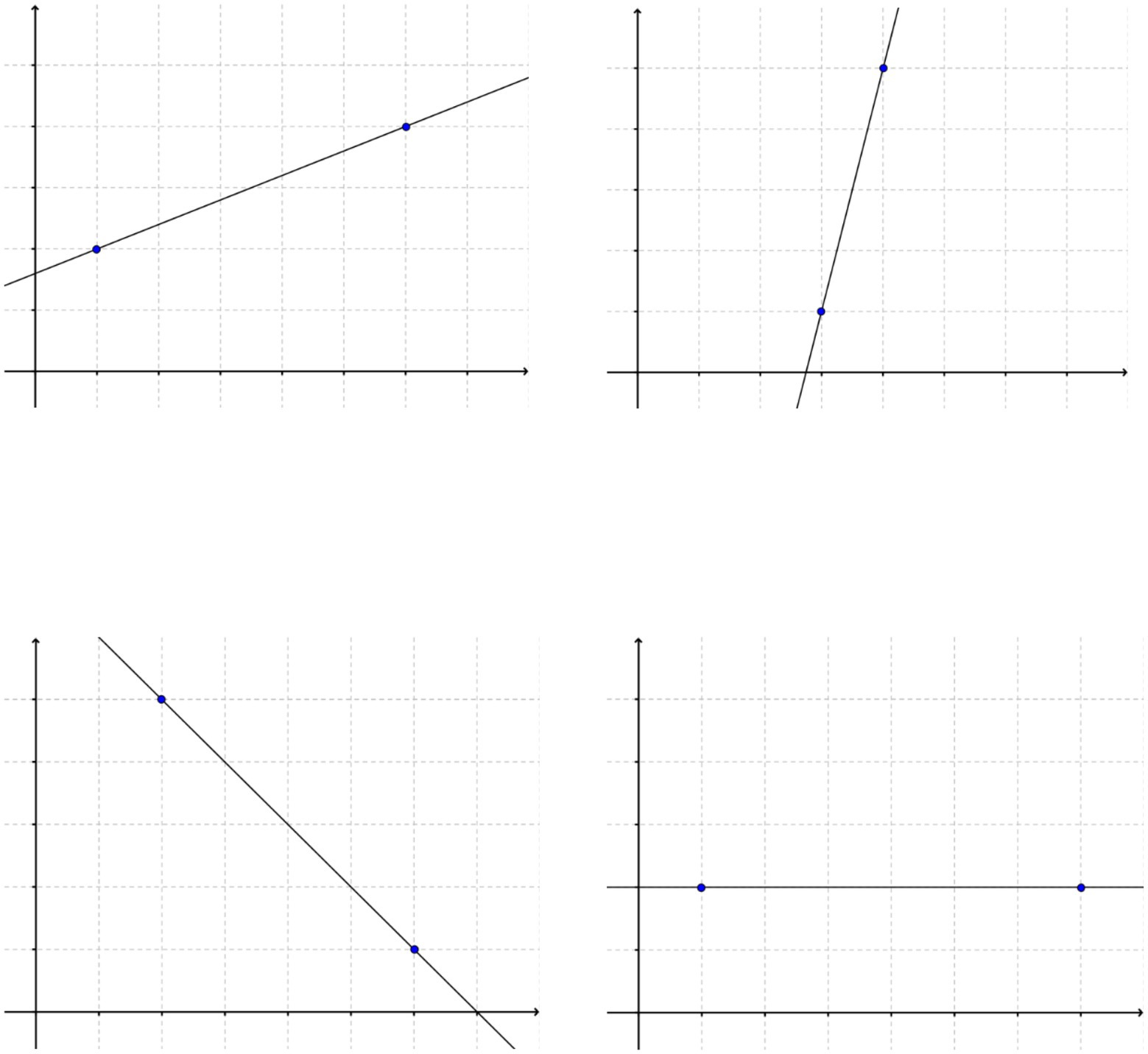
Figure 7. Learning materials for finding out formulae for the slopes of the graphs of linear functions.

Alice has the following graphs in front of her. She calls Bob who cannot see them, and she wants to tell him the different slopes of these graphs. Please invent a mathematical measure for the slope of graphs. This measure should be described by a number that Alice can tell Bob on the telephone. This number must be calculated in all cases by the same rule. Furthermore, it must be possible to determine this number by the information on the diagrams and without further aid. The value of the number should give Bob a clear idea of the graph’s slope.

In the study by Schalk et al. (2017), eight graphs with different slopes were presented to the students. They received the correct information about the mathematical concept of the slope of graphs of linear functions only after constructing their own proposals. Posttests immediately after the lesson and follow up tests 4 weeks later showed that the experimental group clearly outperformed the control group. Inventing with contrasting cases, like learning by productive failure, thus shows how students can be better prepared for future learning by problem-solving followed by instruction.

5. Comparing and contrasting to highlight the differences between easily confusable concepts and problem-solving strategies

By varying the order of presenting learning material, attention can be directed to different aspects of the underlying structure or the superior concept. One can either present learning material in a blocked or in an interleaved order. To differentiate between superficially similar concepts, two or more situations that instantiate the concepts can be juxtaposed and contrasted. Kornell and Bjork (2008) wanted to find out, how art students learn best to distinguish the styles of six different painters. In the blocked condition, six pictures of each artist were presented successively while in the interleaved condition, pictures of the artists were presented in a mixed order, which turned out to be the more effective learning condition. Rohrer (2012) summarized studies from different content areas which demonstrated the benefits of interleaved presentation of learning material. This condition most likely supports the extraction of the specific features of the underlying concepts. Likewise, situations that are superficially different, but represent the same underlying concept can be compared to derive the general principle that connects all cases. Comparing and contrasting are basic operations of knowledge construction. It can, however, not be taken for granted that learners automatically benefit from interleaved presentation. Particularly younger and less experienced learners benefit from an explicit instruction to describe relevant commonalities and differences between the situations (e.g., Ziegler and Stern, 2014, 2016).

Comparing and contrasting is applicable in all fields to support learners in distinguishing concepts and problem-solving strategies that are easily mixed up. Most of the studies were run in mathematics education (Rittle-Johnson and Star, 2007; Rittle-Johnson et al., 2009; Rittle-Johnson and Star, 2011; for an overview see Alfieri et al., 2013; Ziegler et al., 2018, 2019, 2021). To illustrate how instructions should be designed to activate learners to more comparing and contrasting activities than in regular lessons, the studies from Esther Ziegler on teaching algebra are presented in the following.

Ziegler and her collaborators showed in two studies on teaching algebra that comparing and contrasting sustainably promotes the understanding of the algebraic rules of addition and multiplication (Ziegler and Stern, 2014, 2016). Starting point of both studies is the observation that students typically have difficulties to keep both sets of rules separate (see Figure 8). It was assumed that this difficulty is mainly caused by teaching these sets of rules sequentially. Therefore, Ziegler formulated the research hypothesis that the probability of confusion can be reduced by teaching these sets of rules simultaneously instead of sequentially. Accordingly, under these new conditions learners have more opportunities for comparing and contrasting the different sets of rules, and, thereby, to achieve a better understanding of their commonalities and differences.

FIGURE 8

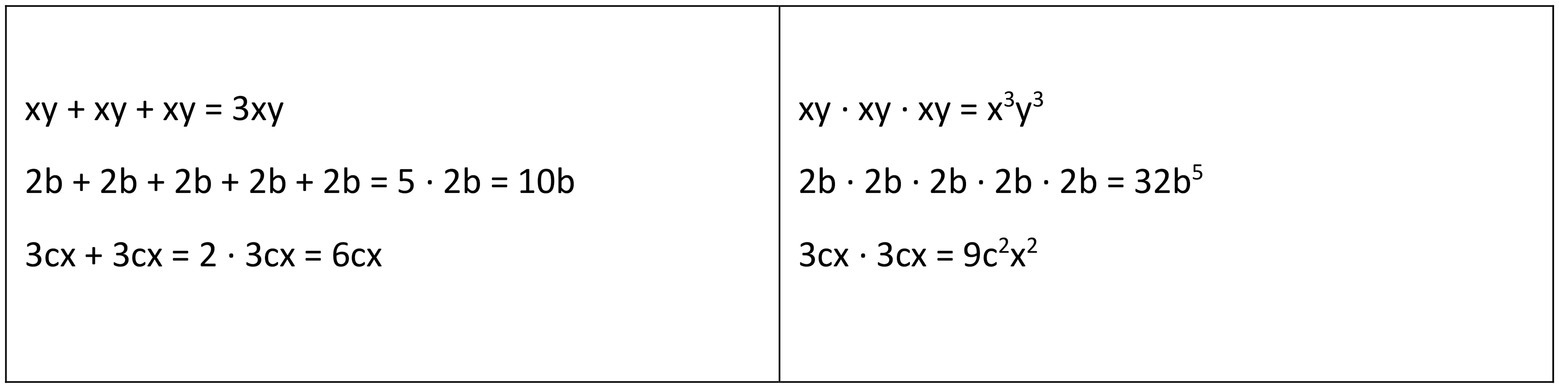
Figure 8. Some examples of algebraic rules for addition and multiplication that are typically confused by students.

In the first study, students in the experimental group received self-learning materials that enabled them to work on addition- and multiplication-problems simultaneously (Ziegler and Stern, 2014). Students in the control group, in contrast, got self-learning materials with which they worked sequentially on addition- and multiplication-problems. In this group, both sets of rules were brought together not until the end of their lessons.

The design of the second study was analogous, with the only difference that the self-learning material was replaced by direct instruction (Ziegler and Stern, 2016). Both studies agreed in showing that students in the experimental groups outperformed students in the control groups immediately after the intervention as well as 3 months later. Among other things, students in the control groups made much more typical mistakes in the follow-up test 3 months later than students in the experimental groups. Thus, both studies confirmed that the probability of confusion can be reduced by teaching these sets of rules simultaneously instead of sequentially. Further confirmation came from an additional study on algebra learning by Ziegler and her colleagues (Ziegler et al., 2019).

These studies are important for two further reasons: First, it turned out that the differences between the experimental and the control groups became larger over time. This means that students in the experimental groups had learned in a much more sustainable way. Second, the beneficial effects of comparing and contrasting were independent of the way in which the learning contents were presented, i.e., by self-learning materials or by direct instruction. Accordingly, what counts are not such differences in the way of presentation, but instead whether learners are prompted by instructions to differentiate between superficially similar concepts.

Comparing and contrasting thus promotes understanding by drawing students’ attention to relevant commonalities and differences. A further means for directing students’ attention to commonalities and differences, for instance, in the strategies for solving addition or multiplication problems in algebra is prompting them to write down the common features and differences instead of just instructing them to practice these strategies by repeated application. Accordingly, the fourth study on understanding algebra focuses on the question of what is more effective: the explicit learning of problem-solving strategies by describing them or the implicit learning by repeatedly applying and practicing them (Ziegler et al., 2021). In this study, students in the experimental group were instructed to distinguish between different kinds of algebra problems and problem-solving strategies and to write down these differences. In contrast, students in the control group were prompted to solve different kinds of algebra problems and to generate new algebra problems of different kinds. It turned out that the experimental group outperformed the control group in three follow-up tests over 10 weeks. Students in the experimental group were not only better in problem-solving, but also had a better conceptual understanding of the problem-solving strategies than students in the control group.

The popular saying “Practice makes perfect” should thus be regarded with reservation. Instead of hoping that students get a better understanding of problem-solving strategies just by repeated application, their understanding should rather be promoted by instructions that direct their attention to relevant commonalities and differences, like prompts for comparing and contrasting as well as prompts for description. Not implicit learning by repetition, but explicit learning by comparisons and descriptions make perfect.

6. Self-explanation prompts: Promoting active knowledge construction

Self-explanations are explanations that are constructed for and addressed to oneself in order to clarify and rethink concepts. Self-explanation prompts ask students to deliberate on central points of the learning content and draw connections to preexisting knowledge. Thereby, self-explanation prompts promote the active construction of knowledge. In the last two decades many studies were published that show that prompting self-explanations by specific questions is an effective way of enhancing students’ understanding (e.g., Schworm and Renkl, 2007; Fiorella and Mayer, 2016; Hofer et al., 2018).

However, without targeted instruction and practice, students rarely construct demanding self-explanations by themselves. For this reason, they have to be prompted to do so. The benefits of prompts for self-explanations are twofold: First, they help students to understand the learning contents at hand. Second, if students receive such prompts regularly, they acquire a certain routine to construct such explanations by themselves. Once this habit is established, they possess a procedure to deepen and check their own understanding.

In one of the first and classic studies on self-explanation prompts students on class level eight received a short text on the human blood circuit (Chi et al., 1994). Students in the experimental group were instructed to write a short explanation after each sentence. In contrast, students in the control group were asked to carefully read the text twice. The test results showed that students in the experimental group had learned significantly more than students in the control group. Learning thus can be promoted by prompting self-explanations.

An example for a self-explanation prompt in physics is the task on the difference between active and reactive forces, on the one hand, and situations with an equilibrium of forces, on the other hand (Hofer et al., 2018). This difference is not easy to understand. Since students typically tend to mix up both situations, it is important to guide them repeatedly by instructions to describe the differences between both cases. In order to do so, it could be helpful to confront them with misconceptions or misunderstandings to which they might be attracted by themselves. In the task presented in Figure 9, they should recognize that the gravitational forces between earth and moon are active and reactive forces:

FIGURE 9

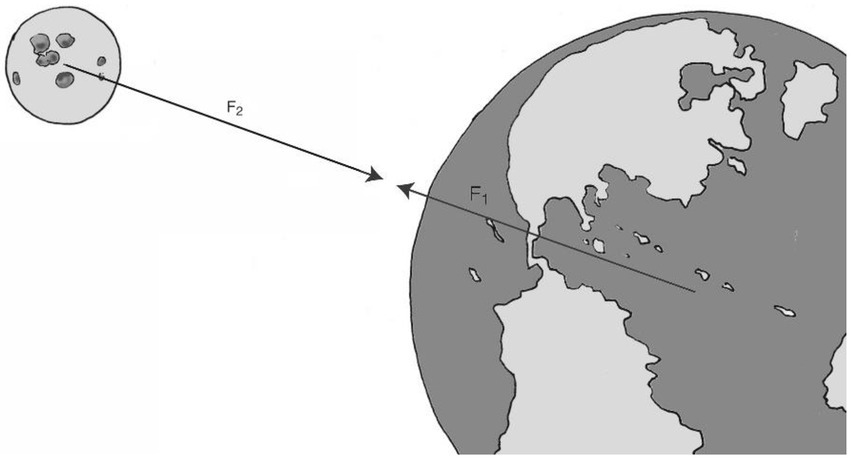
Figure 9. An example of a self-explanation prompt to highlight the gravitational forces between Earth and Moon.

Hugo thinks that earth and moon are in an equilibrium of forces because the gravitational forces between them are of the same size. Is that true? If not, how would you explain to Hugo why his view is incorrect?

In addition, self-explanation prompts can also be used to ask students to explain fundamental concepts and principles, and to adapt their explanation to the perspective of a person with a different state of knowledge, as presented in Figure 10.

FIGURE 10

Figure 10. Example of a self-explanation prompt: How would you explain the difference between mass and weight?

A student in your class has missed the lesson on the difference between mass and weight. How would you explain this difference to her / him, using the following illustration with the astronaut on the moon?

Both examples are from the teaching materials on the basic concepts of mechanics of the MINT Learning Center of the ETH Zurich.¹ They have in common that they activate students to integrate new information into their already existing conceptual knowledge. In an experimental study with 172 students of Swiss Gymnasiums we were able to show that students who received physics lessons with our cognitively activating teaching materials outperformed regular classes in conceptual understanding (Hofer et al., 2018). The cognitively activating classes’ advantage in conceptual understanding was not at the expense of their quantitative problem-solving performance, which exceeded the quantitative problem-solving performance of the regular classes at posttest. Furthermore, female students with above-average intelligence particularly benefited from cognitively activating instruction.

In a nutshell, prompts for self-explanations promote the active construction of conceptual knowledge because students have to describe central learning contents in their own words, draw conclusions to organize the new knowledge in a coherent model, and connect the new contents with their prior knowledge by looking for commonalities and inconsistencies with the knowledge they already have.

7. Metacognitive questions: Monitoring one’s state of knowledge and learning progress

Regularly monitoring one’s state of knowledge and learning progress is an essential part of meaningful learning. Since such control mechanisms cannot be taken for granted, learners have to be guided by questions to build up such routines. Questions that prompt students to reflect on their state of knowledge and on their learning progress are called “metacognitive questions.” They promote students’ awareness of contradictions and shortcomings of their knowledge, and, thereby, contribute to better learning gains (e.g., Mevarech and Fridkin, 2006; Schneider and Artelt, 2010; Donker et al., 2014; Zepeda et al., 2015).

For constructing new knowledge, it is decisive that one knows what is already well understood, and in which areas more elaboration, information or practice is needed. For example, it does not make sense to teach intermolecular forces before students understand the concept of covalent bonding within molecules (Figure 11). Otherwise, they would not understand the difference between the covalent bonding, for instance, within the H₂O molecule (marked in red) and the hydrogen bond between two H₂O molecules (marked in green). This is particularly difficult to understand since in both cases hydrogen and oxygen atoms are connected.

FIGURE 11

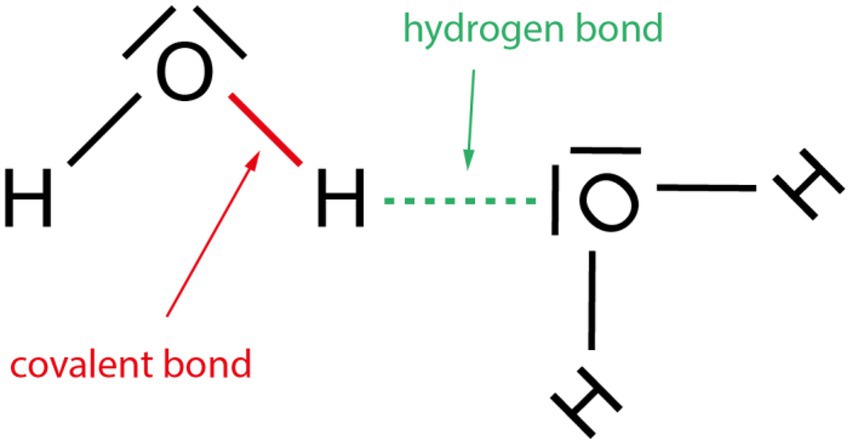
Figure 11. Contrasting the covalent bond with a hydrogen bond present between oxygen and hydrogen atoms.

Accordingly, successful learning requires monitoring one’s state of knowledge and learning progress. In order to establish such routines, students have to be guided by instructions to ask themselves metacognitive questions about what they know and what they learned. Such questions should address central learning contents like concepts and problem-solving strategies. In particular, it is important to address concepts that are typically confounded by students, as in the following metacognitive question: Do I understand the difference between an exponential function (a^x) and a power function (xⁿ)? Am I able to explain this difference to another student who does not know these concepts?

In an exemplary study run in the group of Zemira Mevarech (Mevarech and Fridkin, 2006), 81 university students between 19 and 27 years were randomly assigned to two groups. Both groups had to solve the same math problems during the same amount of time. The difference between the two groups was that students in the experimental group were also instructed to answer metacognitive questions of the following four types:

•  Comprehension questions guide students to describe the main ideas in a problem.

•  Connection questions instruct students to think about similarities between a given problem and problems already solved in the past.

•  Strategic questions focus on the appropriate problem-solving strategies.

•  Reflection questions ask students to monitor their steps in the process of problem-solving as well as their final result.

In the posttests on math problems, students in the experimental group outperformed the control group. Answering metacognitive questions thus contributes to better learning gains.

These results are further supported by other studies on metacognitive questions – mainly on math lessons and on learning from texts. Studies were run in primary school (Zohar and Peled, 2008; Michalsky et al., 2009; Mevarech et al., 2010), secondary school including the Gymnasium (Kramarski and Mevarech, 2003; Mevarech and Amrany, 2008; Mevarech and Kramarski, 1997, 2003; Zion et al., 2005; Michalsky et al., 2007; Schneider and Artelt, 2010) and university (Zohar, 2004). This means, learners at different age levels have in common that their routines for reflecting their state of knowledge and learning progress can still be improved, so that they profit from trainings with metacognitive questions.

That metacognitive questions can be successfully implemented, for instance, in physics lessons in school is shown by the following experimental study (Zepeda et al., 2015). In this study, 46 students on class level eight were randomly assigned to two groups. Both groups received the same amount of lessons over 30 weeks. Whereas students in the control group just received physics lessons, students in the experimental group – during the same time – received physics lessons and six lessons on a training with metacognitive questions. Although students in the experimental group actually received six lessons on physics less than the control group, they showed better results in the posttests on physics than the students from the control group. Moreover, in a subsequent training on a different topic, i.e., on the principle of the control of variables, students from the experimental group also showed higher learning gains than students in the control group because the metacognitive training prepared them better for these new lessons.

To sum up, these results show that trainings with metacognitive questions can have beneficial effects in two dimensions: First, they promote the understanding of the topic at hand, and, second, they are an effective preparation for future learning so that students gain more from new learning opportunities.

8. Concluding remarks on implementing cognitively activating methods in classroom

The six methods presented in this article have been proven successful in promoting meaningful learning by supporting conceptual extension and restructuring. Randomized controlled intervention studies showed that learners who engaged in learning activities with the methods of cognitive activation outperformed learners of the active control groups particularly in transfer tasks that required to use their knowledge in new contexts. In these studies, the active control groups either underwent traditional classroom practice or they got similar material as the intervention group but in different order that made sense. Moreover, sound intervention studies also take into account potential advantages of the control group when designing the outcome measure. For instance in physics, conceptual understanding and quantitative problem solving are two competencies that not always come together. For instance, whether physics instruction with a focus on conceptual understanding is at the expense of quantitative problem solving – a major topic in traditional teaching–is a matter of concern. Hofer et al. (2018) found, that this was not the case.

Once benefits of methods of cognitive activation have been proven, implementing them in real classroom with in-service-teachers can start. This, however, requires extra effort that differs from designing a sound controlled study. In experimental intervention studies, the learning time must be kept strictly constant, otherwise no causal conclusions would be possible. In vivo, however, methods of cognitive activation may even better unfold their potential if more time is granted than in the experimental study. Also more direct interventions by the teachers, which have to be strictly avoided during scientific intervention studies, may be beneficial in classroom and therefore should be allowed. It is utmost important to emphasize that methods of cognitive activation should not be understood as recipes that unfold their potential similar to swallowing a pill. A pill helps even if patients do not know anything about the underlying physiological processes, and the prescribing doctors do not need to understand all details of these processes. This is very different in case of meaningful learning. Methods of cognitive activation are based in the theory of cognitive-constructivist learning (Staub and Stern, 2002), which means that learning is understood as a process of connecting incoming information with existing knowledge rather than filling empty vessels. Teachers have to understand that learning outcomes depend on their student’s prior knowledge, and that their – the teachers’ – responsibility is to support students in activating and restructuring their existing knowledge.

The degree of self-determination that students need for meaningful learning has long been debated in learning sciences (Kirschner et al., 2006). While the efficiency of pure discovery learning has been seriously called into question (Mayer, 2004), the construction of scientifically adequate concepts need more than direct instruction and explanations delivered by teachers (Mazur, 2015). Means of cognitive activation bridge the gap between these two extremes: Teachers stay in control of how students spend their time in class, and students are involved in activities that make them aware of their competencies as well as of their deficits. It is important to realize that in order for means of cognitive activation to work, it also places demands on the students. They have to understand that they have to take control of their learning rather than waiting for silver bullets from their teachers. This can be an emotional challenge in the learning culture, especially when in the past making mistakes was valued as a failure rather than an important learning step. Students need to be encouraged to own up to their mistakes. Methods of cognitive activation can only unfold their potential if both, teachers and learners understand meaningful learning as a process of knowledge construction that is accompanied by obstacles.

Author contributions

RS and ES are long-term collaborators. RS: drafted the manuscript. ES: completed it with additional ideas. All authors contributed to the article and approved the submitted version.

Funding

Open access funding provided by ETH Zurich.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

1. ^https://educ.ethz.ch/lernzentren/mint-lernzentrum/swiss-mint-study.html

References

Alfieri, L., Nokes-Malach, T. J., and Schunn, C. D. (2013). Learning through case comparisons: a meta-analytic review. Educ. Psychol. 48, 87–113. doi: 10.1080/00461520.2013.775712

CrossRef Full Text | Google Scholar

Black, P., and Wiliam, D. (2009). Developing the theory of formative assessment. Educ. Asses. Eval. Acc. 21, 5–31. doi: 10.1007/s11092-008-9068-5

CrossRef Full Text | Google Scholar

Carey, S. (2000). Science education as conceptual change. J. Appl. Dev. Psychol. 21, 13–19. doi: 10.1016/S0193-3973(99)00046-5

CrossRef Full Text | Google Scholar

Carretero, M., and Perez-Manjarrez, E. (2022). “Learning history” in Cambridge Handbook of Learning Sciences. ed. K. Sawyer (Cambridge: Cambridge University Press).

Google Scholar

Chi, M. T. H., de Leeuw, N., Chiu, M. H., and Lavancher, C. (1994). Eliciting self-explanations improves understanding. Cogn. Sci. 18, 439–477.

Google Scholar

Darabi, A., Arrington, T. L., and Sayilir, E. (2018). Learning from failure: a meta-analysis of the empirical studies. Educ. Technol. Res. Dev. 66, 1101–1118. doi: 10.1007/s11423-018-9579-9

CrossRef Full Text | Google Scholar

Day, S. B., and Goldstone, R. L. (2012). The import of knowledge export: connecting findings and theories of transfer of learning. Educ. Psychol. 47, 153–176. doi: 10.1080/00461520.2012.696438

CrossRef Full Text | Google Scholar

Donker, A. S., de Boer, H., Kostons, D., Dignath van Ewijk, C. C., and van der Werf, M. P. C. (2014). Effectiveness of learning strategy instruction on academic performance: a meta-analysis. Educ. Res. Rev. 11, 1–26. doi: 10.1016/j.edurev.2013.11.002

CrossRef Full Text | Google Scholar

Fiorella, L., and Mayer, R. E. (2016). Eight ways to promote generative learning. Educ. Psychol. Rev. 28, 717–741. doi: 10.1007/s10648-015-9348-9

CrossRef Full Text | Google Scholar

Hardy, I., Jonen, A., Möller, K., and Stern, E. (2006). Why does a large ship of iron float? Effects of instructional support in constructivist learning environments for elementary school students’ understanding of ‘floating and sinking’. J. Educ. Psychol. 98, 307–326. doi: 10.1037/0022-0663.98.2.307

CrossRef Full Text | Google Scholar

Hofer, S., Schumacher, R., Rubin, H., and Stern, E. (2018). Enhancing physics learning with cognitively activating instruction: a quasi-experimental classroom intervention study. J. Educ. Psychol. 110, 1175–1191. doi: 10.1037/edu0000266

CrossRef Full Text | Google Scholar

Kapur, M. (2014). Productive failure in learning math. Cogn. Sci. 38, 1–15.

Google Scholar

Kirschner, P. A., Sweller, J., and Clark, R. (2006). Why minimal guidance during instruction does not work: an analysis of the failure of constructivist, discovery, problem-based, experiential, and inquiry-based teaching. Educ. Psychol. 41, 75–86. doi: 10.1207/s15326985ep4102_1

CrossRef Full Text | Google Scholar

Kornell, N., and Bjork, R. A. (2008). Learning concepts and categories: is spacing the "enemy of induction"? Psychol. Sci. 19, 585–592. doi: 10.1111/j.1467-9280.2008.02127.x

CrossRef Full Text | Google Scholar

Kramarski, B., and Mevarech, Z. (2003). Enhancing mathematical reasoning in the classroom: the effects of cooperative learning and metacognitive training. Am. Educ. Res. J. 40, 281–310. doi: 10.3102/00028312040001281

CrossRef Full Text | Google Scholar

Loibl, K., and Leuders, T. (2019). How to make failure productive. Fostering learning from errors through elaboration prompts. Learn. Instr. 62, 1–10. doi: 10.1016/j.learninstruc.2019.03.002

CrossRef Full Text | Google Scholar

Loibl, K., Roll, I., and Rummel, N. (2017). Towards a theory of when and how problem solving followed by instruction supports learning. Educ. Psychol. Rev. 29, 693–715. doi: 10.1007/s10648-016-9379-x

CrossRef Full Text | Google Scholar

Mayer, R. (2004). Should there be a three-strikes rule against pure discovery learning? The case for guided methods of instruction. Am. Psychol. 59, 14–19. doi: 10.1037/0003-066X.59.1.14

PubMed Abstract | CrossRef Full Text | Google Scholar

Mazur, E. (2015). Principles and Practice of Physics. Harlow, England: Pearson.

Google Scholar

Mazziotti, C., Rummel, N., Deiglmayr, A., and Loibl, K. (2019). Probing boundary conditions of productive failure and analyzing the role of young students’ collaboration. Nat. Sci. Learn. 4, 1–9. doi: 10.1038/s41539-019-0041-5

CrossRef Full Text | Google Scholar

Mevarech, Z., and Amrany, C. (2008). Immediate and delayed effects of meta-cognitive instruction on regulation of cognition and mathematics achievement. Metacogn. Learn. 3, 147–157. doi: 10.1007/s11409-008-9023-3

CrossRef Full Text | Google Scholar

Mevarech, Z., and Fridkin, S. (2006). The effects of IMPROVE on mathematical knowledge, mathematical reasoning and meta-cognition. Metacogn. Learn. 1, 85–97. doi: 10.1007/s11409-006-6584-x

CrossRef Full Text | Google Scholar

Mevarech, Z., and Kramarski, B. (1997). IMPROVE: a multidimensional method for teaching mathematics in heterogeneous classrooms. Am. Educ. Res. J. 34, 365–394. doi: 10.3102/00028312034002365

CrossRef Full Text | Google Scholar

Mevarech, Z., and Kramarski, B. (2003). The effects of metacognitive training versus worked out examples on students’ mathematical reasoning. Br. J. Educ. Psychol. 73, 449–471. doi: 10.1348/000709903322591181

PubMed Abstract | CrossRef Full Text | Google Scholar

Mevarech, Z., Terkieltaub, S., Vinberger, T., and Nevet, V. (2010). The effects of meta-cognitive instruction on third and sixth graders solving word problems. ZDM 42, 195–203. doi: 10.1007/s11858-010-0244-y

CrossRef Full Text | Google Scholar

Michalsky, T., Mevarech, Z., and Haibi, L. (2009). Elementary school children Reading scientific texts: effects of metacognitive instruction. J. Educ. Res. 102, 363–376. doi: 10.3200/JOER.102.5.363-376

CrossRef Full Text | Google Scholar

Michalsky, T., Zion, M., and Mevarech, Z. (2007). Developing students’ metacognitive awareness in asymchronous learning networks in comparison to face-to-face discussion groups. J. Educ. Comput. Res. 36, 421–450. doi: 10.2190/320V-8H4W-1123-44R6

CrossRef Full Text | Google Scholar

Rittle-Johnson, B., and Star, J. R. (2007). Does comparing solution methods facilitate conceptual and procedural knowledge? An experimental study on learning to solve equations. J. Educ. Psychol. 99, 561–574. doi: 10.1037/0022-0663.99.3.561

CrossRef Full Text | Google Scholar

Rittle-Johnson, B., and Star, J. R. (2011). The power of comparison in learning and instruction: learning outcomes supported by different types of comparisons. Psychol. Learn. Motiv. 55, 199–225. doi: 10.1016/B978-0-12-387691-1.00007-7

CrossRef Full Text | Google Scholar

Rittle-Johnson, B., Star, J. R., and Durkin, K. (2009). The importance of prior knowledge when comparing examples: influences on conceptual and procedural knowledge of equation solving. J. Educ. Psychol. 101, 836–852. doi: 10.1037/a0016026

CrossRef Full Text | Google Scholar

Rohrer, D. (2012). Interleaving helps students distinguish among similar concepts. Educ. Psychol. 24, 355–367. doi: 10.1007/s10648-012-9201-3

CrossRef Full Text | Google Scholar

Schalk, L., Schumacher, R., Barth, A., and Stern, E. (2017). When problem-solving followed by instruction is superior to the traditional tell-and-practice sequence. J. Educ. Psychol. 110, 596–610. doi: 10.1037/edu0000234

CrossRef Full Text | Google Scholar

Schneider, W., and Artelt, C. (2010). Metacognition and mathematics education. Math. Educ. 42, 149–161. doi: 10.1007/s11858-010-0240-2

CrossRef Full Text | Google Scholar

Schneider, M., and Stern, E. (2010). “The cognitive perspective on learning: ten cornerstone finding.,” in The Nature of Learning: Using Research to Inspire Practice. eds. Organisation for Economic Co-Operation and Development (OECD) (Paris: OECD).

Google Scholar

Schwartz, D. L., Chase, C. C., Oppezzo, M. A., and Chin, D. B. (2011). Practicing versus inventing with contrasting cases: the effects of telling first on learning and transfer. J. Educ. Psychol. 103, 759–775. doi: 10.1037/a0025140

CrossRef Full Text | Google Scholar

Schworm, S., and Renkl, A. (2007). Learning argumentation skills through the use of prompts for self-explaining examples. J. Educ. Psychol. 99, 285–296. doi: 10.1037/0022-0663.99.2.285

CrossRef Full Text | Google Scholar

Staub, F., and Stern, E. (2002). The nature of teachers’ pedagogical content beliefs matters for students’ achievement gains: quasi-experimental evidence from elementary mathematics. J. Educ. Psychol. 94, 344–355. doi: 10.1037/0022-0663.94.2.344

CrossRef Full Text | Google Scholar

Stern, E. (2009). “The development of mathematical competencies: sources of individual differences and their developmental trajectories” in Human Development from Early Childhood to Early adulthood: Evidence from the Munich Longitudinal Study on the Genesis of Individual Competencies (LOGIC). eds. W. Schneider and M. Bullock (Erlbaum: New Jersey).

Google Scholar

Stern, E. (2017). Individual differences in the learning potential of human beings. Nat. Part. J. Sci. Learn. 2, 1–7. doi: 10.1038/s41539-016-0003-0

CrossRef Full Text | Google Scholar

Stern, E., Schalk, L., and Schumacher, R. (2016). “Lernen” in Basiswissen Lehrerbildung: Schule und Unterricht. Lehren und Lernen. eds. J. Möller, M. Köller, and T. Riecke-Baulecke (Seelze: Klett-Verlag).

Google Scholar

Zepeda, C. D., Richey, J. E., Ronevich, P., and Nokes-Malach, T. J. (2015). Direct instruction of metacognition benefits adolescent science learning, transfer, and motivation: an in vivo study. J. Educ. Psychol. 107, 954–970. doi: 10.1037/edu0000022

CrossRef Full Text | Google Scholar

Ziegler, E., Edelsbrunner, P. A., and Star, J. R. (2019). Preventing interference: reordering complexity in the learning of new concepts. J. Educ. Psychol. 111, 1202–1219. doi: 10.1037/edu0000347

CrossRef Full Text | Google Scholar

Ziegler, E., Edelsbrunner, P. A., and Stern, E. (2018). The relative merits of explicit and implicit learning of contrasted algebra principles. Educ. Psychol. Rev. 30, 531–558. doi: 10.1007/s10648-017-9424-4

CrossRef Full Text | Google Scholar

Ziegler, E., Edelsbrunner, P. A., and Stern, E. (2021). The benefits of combining teacher- direction with contrasted presentation of algebra principles. Eur. J. Psychol. Educ. 36, 187–218. doi: 10.1007/s10212-020-00468-3

CrossRef Full Text | Google Scholar

Ziegler, E., and Stern, E. (2014). Delayed benefits of learning elementary algebraic transformations through contrasted comparisons. Learn. Instr. 33, 131–146. doi: 10.1016/j.learninstruc.2014.04.006

CrossRef Full Text | Google Scholar

Ziegler, E., and Stern, E. (2016). Consistent advantages of contrasted comparisons: algebra learning under direct instruction. Learn. Instr. 41, 41–51. doi: 10.1016/j.learninstruc.2015.09.006

CrossRef Full Text | Google Scholar

Zion, M., Michalsky, T., and Mevarech, Z. (2005). The effects of metacognitive instruction embedded within an asynchronous learning network on scientific inquiry skills. Int. J. Sci. Educ. 27, 959–983.

PubMed Abstract | Google Scholar

Zohar, A. (2004). Higher-order thinking in science classrooms: students’ learning and teachers’ professional development. Dordrecht, the Netherlands: Kluwer Academic Press.

Google Scholar

Zohar, A., and Peled, B. (2008). The effects of explicit teaching of metastrategic knowledge on low- and high-achieving students. Learn. Instr. 18, 337–353. doi: 10.1016/j.learninstruc.2007.07.001

CrossRef Full Text | Google Scholar