Decision-making for solar panel selection using Sugeno-Weber triangular norm-based on q-rung orthopair fuzzy information

1 Introduction

The multi-attribute decision-making (MADM) process is used to resolve complicated issues when it is necessary to consider several different factors. The use of MADM is essential in real-world decision-making, particularly when the stakes are high or the decision-maker must select between many equally appealing possibilities. In this article, we will examine the advantages of using MADM in practical terms and in aiding both individuals and organizations to make wiser judgments. Numerous industries, including business, engineering, economics, healthcare, and politics, may benefit from MADM. For instance, MADM is used in business to identify the best supplier, recruit staff, choose the most lucrative investment, or determine the best marketing plan. Engineering uses MADM to identify the optimal design, choose the best material, or enhance a system’s performance. MADM is a tool used in the healthcare industry to determine the efficacy of various therapies, distribute resources, and rate the standard of care. Politicians employ MADM to decide on public policies, rank public projects, and distribute public funds.

One of the key advantages of MADM is that it offers an organized and systematic approach to decision-making, which aids in preventing judgments based on biases, intuition, or personal preferences. In order to use the MADM technique, decision-makers must first identify the decision issue, provide the criteria, assess the options, and then choose the optimal option using a thorough and transparent procedure. This procedure ensures that all pertinent information is considered and a decision is made based on reasonable, impartial standards. Another advantage of MADM is that it enables decision-makers to consider numerous factors at once, which may be difficult to achieve without a structured decision-making process. For instance, when recruiting a new employee, the decision-makers may need to consider several factors, including education, experience, talents, and personality. The decision-makers may assess each candidate based on each criterion using MADM, give weights depending on their relative relevance, and choose the candidate with the highest total score. This strategy ensures that all relevant information about each candidate, instead of only one or two factors, is considered in the selection.

By offering a mechanism to assess the effects of many options under various circumstances, MADM also assists decision-makers in managing risk and uncertainty. Many different outcomes may occur in many real-life decision-making situations, and the consequences of the alternatives are often not known with confidence. For instance, while making an investment choice, the decision-makers may need to consider several factors, including return on investment, risk, liquidity, and diversification. Using MADM, the decision-maker can evaluate the results of many investment alternatives under various circumstances, such as a favorable or adverse market, and choose the best overall performance. Additionally, MADM offers a mechanism to include stakeholders’ beliefs and preferences in decision-making. It may be challenging to meet the stakeholders’ interests in many real-life decision-making scenarios when several parties may have varied preferences and values. Using MADM, the decision-maker may weigh each stakeholder based on their relative significance and consider their priorities and values. This strategy ensures that the selection is made based on a reasonable and equitable inspection of the available options, taking into account of the interests of all parties involved.

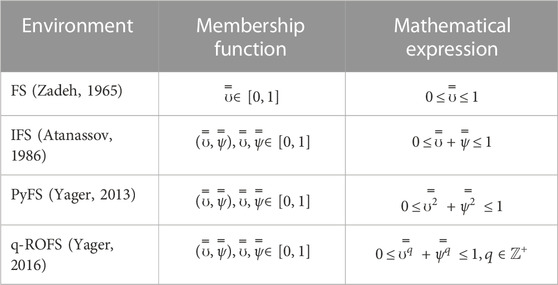
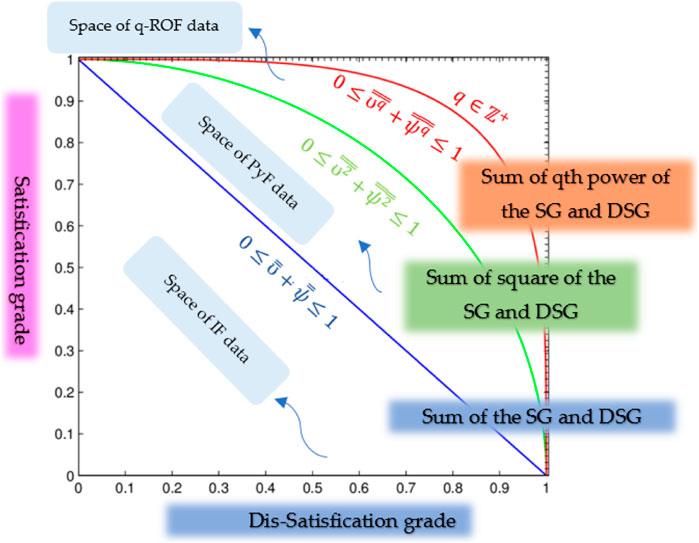
Zadeh (1965) introduced the basic theory of fuzzy set (FS) in 1965 to cope with unclear and redundant information related to human opinions with a single term of satisfaction grade (SG). FS is an efficient aggregation model, and several mathematicians explored the fuzzy set theory in different frameworks. Atanassov (1986) presented a new concept of an intuitionistic fuzzy set (IFS) by expanding the theory of FS. IFS is a powerful structure of FSs and is produced by adding a dissatisfaction grade (DSG) with SG in such a way that the sum of SG and DSG lies in a close interval $\left[\mathrm{0,1}\right]$. Atanassov (1989) also modified some fundamental operations under the system of an IFS, like union, intersection, and relation, among different intuitionistic fuzzy numbers. The concepts of IFSs cannot deal with complex situations due to restricted conditions and insufficient information. To serve this situation, Yager (2013) illustrated a robust idea of a Pythagorean fuzzy set (PyFS) with the sum of the square of SG and DSG bound in a closed interval $\left[\mathrm{0,1}\right]$. After that, Yager (2016) proposed the q-rung orthopair fuzzy set (q-ROFS) theory. The q-ROFS theory provides liberty to decision-makers due to a wide range of uncertain information and enables them to acquire results according to their own preferences. Several mathematicians utilized discussed aggregation models to mitigate the impact of attributes. Some realistic mathematical approaches under the system of different fuzzy circumstances, like Alcantud et al. (2020), discussed the properties of an infinite chain based on intuitionistic fuzzy information. Akram and Shahzadi (2021) presented a novel approach to PyFSs by using operations of Dombi aggregation tools and developed a class of new aggregation models. Hussain et al. (2023) presented Heronian mean models for selecting a suitable solar panel. By utilizing Hamacher triangular norms, Darko and Liang (2020) developed new aggregation operators (AOs) to tackle redundant information related to human opinions.

AOs are essential for the MADM problems to find an appropriate optimal option during decision-making. Several scholars established numerous mathematical aggregation approaches by expanding different fuzzy domains. Riaz and Farid (2022) suggested an effective logistic provider using three components of membership values related to any object. A sustainable approach for energy planning enterprises was demonstrated by Riaz et al. (2020) to overcome the impact of redundant information by taking into account q-rung orthopair fuzzy (q-ROF) circumstances. Senapati et al. (2023) mentioned a sustainable structure for implementing the concept of shared mobility to reduce the negative impacts of traffic congestion and environmental pollution. Senapati et al. (2022) also recommended a robust global partner for the improvement of multinational companies and suggested a class of new approaches. Akram and Shahzadi (2021) developed a series of new AOs using Dombi aggregation tools considering complex Pythagorean fuzzy situations. Akram et al. (2023) proposed the Muirhead mean aggregation model using 2-tuple linguistic fuzzy circumstances. Hussain et al. (2023) classified a suitable optimal option using the Aczel–Alsina aggregation model with an interval-valued Pythagorean fuzzy system. To reduce the impact of fuel and gas, Hussain et al. (2023) evaluated an electric motor car based on the decision-making process and presented new mathematical approaches considering complex spherical fuzzy circumstances. Hussain et al. (2022) also modified Hamy mean aggregation models with some specific properties to check the performance of vendor management enterprises. Wang and Garg (2021) designed an algorithm for the MADM problem using the properties of Archimedean triangular norms to take into account ambiguous information. To eliminate the negative effect of redundant information, Wang and Zhang (2022) developed interactional operational laws by improving traditional rules to propose new approaches. Hussain, Wang, Ullah et al. (2023) anticipated dominant mathematical approaches by exploring the properties of Hamy mean models and operations of Aczel–Alsina t-norms. In a few decades, decision-making techniques became a research hotspot, and a number of mathematicians worked on different environments and developed robust mathematical approaches such as Shafiq et al. (2023), Çolak et al. (2023), and Shafiq et al. (2024).

An interval-valued intuitionistic fuzzy (IVIF) model is an extended framework of an IFS used to handle unpredictable or insufficient information related to any object. Liu and Jiang (2020) utilized the concepts of distance measures by incorporating the theory of IVIF information to develop a new list of AOs. The key components of AOs in the decision-making process are used to evaluate a notable optimal option considering appropriate attributes. The decision-making process is utilized in every field and has gained considerable attention from numerous research scholars. For instance, Liu and Gao (2019) mixed two different theories, intuitionistic fuzzy values and Dempster–Shafer theory, to eliminate the shortcomings of traditional operational laws. They also explored the theory of the Bonferroni mean operator using the properties of incomplete weight vectors. Mahmood and Ali (2023) utilized the operations of Aczel–Alsina aggregation tools to investigate appropriate approaches based on the complex intuitionistic fuzzy framework. Garg (2020) explored some reliable properties of trigonometric functions to overcome the impact of insufficient or redundant information related to real-life applications. After deeply analyzing different mathematical approaches, we conclude that the proposed methodologies play an essential role in the decision support system. For instance, Garg and Kumar (2020) put forward the theory of intuitionistic fuzzy information, Bessa and Matos (2012) classified electric vehicles based on economic and technical management, and Khan et al. (2022) illustrated a power aggregation model based on the complex t-spherical fuzzy system.

Naeem et al. (2023) classified different sources of renewable energy enterprises using Frank aggregation tools and bipolar complex fuzzy theory. Riaz et al. (2021) used a novel approach of interval-valued Pythagorean fuzzy information and advanced decision-making technique to examine reliable energy sources. Al-Barakati et al. (2022) developed some prominent strategies under the q-ROF information system for choosing the best energy source. Motivated by the significance of solar cells and their storage capacity, Zeng et al. (2019) established some interactive aggregation models for the decision-making process. An innovative approach to the analytic hierarchy technique for the decision-making process was illustrated by Kahraman et al. (2009). Using operations of Dombi aggregation tools and T-spherical fuzzy information, Waqar et al. (2022) evaluated a suitable optimal option from different available options. We also studied a list of dominant mathematical strategies, which were designed by numerous research scholars based on different fuzzy domains (Krishankumar et al., 2019; Hussain et al., 2022; Razzaque et al., 2023; Shafiq, 2023).

Menger (1942) developed a robust concept of triangular norms with notable characteristics under the system of statistical measures. Xia et al. (2012) utilized properties of the probabilistic sum of t-conorms and product t-norms considering intuitionistic fuzzy situations. Sugeno (1974) discovered some new results during his PhD by generalizing triangular norms with certain characteristics of nilpotent t-conorms. Weber (1983) also worked on nilpotent t-norms (as well as asymptotic member’s products and drastic products) to investigate the latest research work. Later on, these discoveries were known as the Sugeno–Weber t-norm and t-conorm, or the family of Sugeno–Weber triangular norms. Sugeno–Weber triangular norms are reliable and efficient aggregation tools used to tackle uncertain information of human opinions during decision-making. Hwang et al. (2012) explored the concepts of similarity measures using Sugeno integral properties and established a decision-making process under the IF information system. The theory of fuzzy measures was expanded by Murofushi and Sugeno (1991), with properties of Sugeno integral and Choquet integral. Marichal (2000) and Weber et al. (2015) also presented an effective way to tackle unrealistic information about human opinions when choosing the optimal option under certain criteria or attributes. Recently, Sarkar et al. (2023) explored the concepts of the t-spherical fuzzy hypersoft set using robust aggregation tools of Sugeno–Weber triangular norms to resolve real-life challenges.

However, the discussed strategies have several advantages and are used to handle complex human opinions. Sometimes, the decision-maker cannot deal with awkward and unpredictable situations during evaluation in the decision-making process. However, there is a lack of studies on the q-ROF environment based on dominant operations of the Sugeno–Weber t-norms. Authors also construct new mathematical strategies by combining three different theories for handling imprecision and complex information. Currently, the developed approaches have the additional advantage of dealing with insufficient information without the degree of weight, which is assigned to the characteristics or attributes by the decision-maker. The key feature of this article is to develop a class of mathematical approaches under the system of q-ROF information. Some valuable advantages of the derived theory are stated as follows:

a) By utilizing our proposed research methodologies, we can express uncertainty and complexity more precisely under the system of q-ROF information during the MADM problem evaluation process.

b) We can also evaluate given information about any object without any external weight vectors, which are assigned to the characteristics or attributes by the decision-maker.

The massive contributions of this article are as follows:

a) Based on three different theories, we derived some robust mathematical strategies, namely, q-rung orthopair fuzzy Sugeno–Weber power weighted average (q-ROFSWPWA) and q-rung orthopair fuzzy Sugeno–Weber power weighted geometric (q-ROFSWPWG) operators with notable characteristics and special cases.

b) We evaluated the applicability and effectiveness of the developed AOs and pioneered an advanced decision-making technique to cope with awkward and redundant information of human opinion with the help of derived strategies.

c) A numerical example was also studied to evaluate a suitable renewable energy resource under some dominant features and characteristics with the help of the developed approaches.

d) A comparative study was conducted to demonstrate the superiority of the proposed approaches on existing operators developed by different research scholars. This comparison verifies the capability and effectiveness of the proposed approaches.

The remainder of the article is organized as follows: Section 2 covers the basic notion of Sugeno–Weber triangular norms, IFS, q-ROFSs, and their related fundamental operational laws. Section 3 presents some essential operational laws of Sugeno–Weber triangular norms under the system of q-ROF information. Section 4 presents a class of new AOs based on Sugeno–Weber triangular norms, including q-ROFSWPWA operator with some realistic special cases. Section 5 explores new AOs of the q-ROFSWPW operator with certain characteristics. The MADM problem is established to resolve different real-life situations under the system of q-ROF information in Section 6. To examine the stability of the proposed methodologies, a numerical example is considered to select a suitable solar panel to enhance the storage capacity of electricity. In Section 7,in order to show the reliability and consistency of the proposed research work, a comparative analysis is established to compare the results of the existing approaches with pioneered strategies. Final remarks related to our research work are presented in Section 8.

2 Preliminaries

To verify the proposed research work, we explore some basic notions of Sugeno–Weber triangular norms, q-ROFSs, and their related fundamental rules for developing this research work.

Definition 1. The Sugeno-Weber t-norm and t-conorm are, respectively, expressed as follows (Sarkar et al., 2023):

${\mathcal{T}}^{Ђ}=\left\{\begin{array}{c}\begin{array}{cc}{\mathcal{T}}_D\left(\stackrel{═}{ά},\stackrel{═}{ή}\right),& ifЂ=-1\end{array},\\ \begin{array}{cc}\mathit{max}\left(0,\frac{\stackrel{═}{ά}+\stackrel{═}{ή}-1+Ђ\stackrel{═}{ά}\stackrel{═}{ή}}{1+Ђ}\right),& if-1<Ђ<+\infty ,\end{array}\\ \begin{array}{cc}{\mathcal{T}}_P\left(\stackrel{═}{ά},\stackrel{═}{ή}\right),& Ђ=+\infty \end{array}\end{array}\right.$

and

${\mathcal{S}}^{Ђ}=\left\{\begin{array}{c}\begin{array}{cc}{\mathcal{S}}_D\left(\stackrel{═}{ά},\stackrel{═}{ή}\right),& ifЂ=-1\end{array},\\ \begin{array}{cc}\mathit{min}\left(1,\stackrel{═}{ά}+\stackrel{═}{ή}-\frac{Ђ}{1+Ђ}\stackrel{═}{ά}\stackrel{═}{ή}\right),& if-1<Ђ<+\infty \end{array}\\ \begin{array}{cc}{\mathcal{S}}_P\left(\stackrel{═}{ά},\stackrel{═}{ή}\right),& Ђ=+\infty \end{array},\end{array}\right.,$

where ${\mathcal{T}}_D\left((\stackrel{═}{ά},\stackrel{═}{ή}\right))$ and ${\mathcal{S}}_D\left((\stackrel{═}{ά},\stackrel{═}{ή}\right))$ indicate the drastic t-norm and drastic t-conorm, respectively. Furthermore, ${\mathcal{T}}_P\left((\stackrel{═}{ά},\stackrel{═}{ή}\right))$ and ${\mathcal{S}}_P\left((\stackrel{═}{ά},\stackrel{═}{ή}\right))$ represent the probabilistic sum of t-norm and t-conorm.

Definition 2. A q-ROFS $\stackrel{═}{A}$ on $Ŵ$ is expressed by (Yager, 2016)

$\stackrel{═}{A}=\left\{\sigma ,\left(\stackrel{═}{ʊ}\left(\sigma \right),\stackrel{═}{\psi }\left(\sigma \right)\right)|\sigma \in Ŵ\right\},$

where $\stackrel{═}{ʊ}:Ŵ\to \left[\mathrm{0,1}\right]$ and $\stackrel{═}{\psi }:Ŵ\to \left[\mathrm{0,1}\right]$ indicate the satisfaction grade (SG) and dissatisfaction grade (DSG), respectively, with some realistic constraints:

$0\le \stackrel{═}{{ʊ}^q}\left(\sigma \right)+\stackrel{═}{{\psi }^q}\left(\sigma \right)\le 1,q\in {\mathbb{Z}}^{+}.$

The hesitancy degree of q-ROFS is expressed by $r\left(\sigma \right)=1-\sqrt[q]{\left((\stackrel{═}{{ʊ}^q}\left(\sigma \right)+\stackrel{═}{{\psi }^q}\left(\sigma \right)\right))}$. A q-ROF value (q-ROFV) is denoted by $\stackrel{═}{\zeta }=\left((\stackrel{═}{ʊ},\stackrel{═}{\psi }\right))$. Table 1 and Figure 1 show the mathematical expressions and geometrical behaviors of different fuzzy domains. We take two different notations, namely, $\stackrel{═}{ʊ}$ and $\stackrel{═}{\psi }$, which indicate SG and DSG, respectively.

TABLE 1

TABLE 1. Mathematical structure of different fuzzy domains.

FIGURE 1

FIGURE 1. Geometrical structure of different fuzzy domains.

Definition 3. For any two q-ROFVs, $\stackrel{═}{\zeta }=\left(\stackrel{═}{ʊ}\left(\sigma \right),\stackrel{═}{\psi }\left(\sigma \right)\right),\stackrel{═}{{\zeta }_1}=\left({\stackrel{═}{ʊ}}_1\left(\sigma \right),\stackrel{═}{{\psi }_1}\left(\sigma \right)\right)$, and $\stackrel{═}{{\zeta }_2}=\left(\stackrel{═}{{ʊ}_2}\left(\sigma \right),\stackrel{═}{{\psi }_2}\left(\sigma \right)\right)$. Then, some necessary operations are expressed as follows (Ullah et al., 2023):

 1) $\stackrel{═}{{\zeta }_1}\subseteq \stackrel{═}{{\zeta }_2}$, if ${\stackrel{═}{ʊ}}_1\le {\stackrel{═}{ʊ}}_2,\stackrel{═}{{\psi }_1}\ge \stackrel{═}{{\psi }_2}$.

 2) $\stackrel{═}{{\zeta }_1}=\stackrel{═}{{\zeta }_2}$, if $\stackrel{═}{{\zeta }_1}\subseteq \stackrel{═}{{\zeta }_2}$ and $\stackrel{═}{{\zeta }_1}\supseteq \stackrel{═}{{\zeta }_2}$.

 3) $\stackrel{═}{{\zeta }_1}\cup \stackrel{═}{{\zeta }_2}=\left\{\max \left({\stackrel{═}{ʊ}}_1\left(\sigma \right),{\stackrel{═}{ʊ}}_2\left(\sigma \right)\right),\min \left(\stackrel{═}{{\psi }_1}\left(\sigma \right),\stackrel{═}{{\psi }_2}\left(\sigma \right)\right)|\left(\sigma \right)\in Ŵ\right\}$.

 4) $\stackrel{═}{{\zeta }_1}\cap \stackrel{═}{{\zeta }_2}=\left\{\min \left({\stackrel{═}{ʊ}}_1\left(\sigma \right),{\stackrel{═}{ʊ}}_2\left(\sigma \right)\right),\max \left(\stackrel{═}{{\psi }_1}\left(\sigma \right),\stackrel{═}{{\psi }_2}\left(\sigma \right)\right)|\left(\sigma \right)\in Ŵ\right\}$.

 5) ${\stackrel{═}{\zeta }}^C=\left(\stackrel{═}{\psi }\left(\sigma \right),\stackrel{═}{ʊ}\left(\sigma \right)\right),\forall \left(\sigma \right)\in Ŵ.$

Definition 4. For any two q-ROFVs, $\stackrel{═}{\zeta }=\left((\stackrel{═}{ʊ},\stackrel{═}{\psi }\right)),\stackrel{═}{{\zeta }_1}=\left(({\stackrel{═}{ʊ}}_1,\stackrel{═}{{\psi }_1}\right))$, and $\stackrel{═}{{\zeta }_2}=\left((\stackrel{═}{{ʊ}_2},\stackrel{═}{{\psi }_2}\right))$ with $₵>0$. Then, we have (Ullah et al., 2023)

 1) $\stackrel{═}{{\zeta }_1}\oplus \stackrel{═}{{\zeta }_2}=\left((\sqrt[q]{{\stackrel{═}{{ʊ}^q}}_1+{\stackrel{═}{{ʊ}^q}}_2-{\stackrel{═}{ʊ}}_1^q.{\stackrel{═}{{ʊ}^q}}_2},\stackrel{═}{{\psi }_1}.\stackrel{═}{{\psi }_2}\right))$.

 2) $\stackrel{═}{{\zeta }_1}⨂\stackrel{═}{{\zeta }_2}=\left(({\stackrel{═}{ʊ}}_1.{\stackrel{═}{ʊ}}_2,\sqrt[q]{\stackrel{═}{{\psi }_1^q}+\stackrel{═}{{\psi }_2^q}-\stackrel{═}{{\psi }_1^q}.\stackrel{═}{{\psi }_2^q}}\right))$.

 3) $₵\stackrel{═}{\zeta }=\left((\sqrt[q]{1-{\left(1-\stackrel{═}{{ʊ}^q}\right)}^{₵}},{\stackrel{═}{\psi }}^{₵}\right))$.

 4) ${\stackrel{═}{\zeta }}^{₵}=\left(({\stackrel{═}{ʊ}}^{₵},\sqrt[q]{1-{\left(1-\stackrel{═}{{\psi }^q}\right)}^{₵}}\right))$.

Definition 5. Consider a q-ROFVs $\stackrel{═}{\zeta }=\left(\stackrel{═}{ʊ},\stackrel{═}{\psi }\right)$, and score function and accuracy function are, respectively, expressed as follows (Ateş and Akay, 2020):

$\mathcal{S}\left(\stackrel{═}{\zeta }\right)=\stackrel{═}{{ʊ}^q}\left(\sigma \right)-\stackrel{═}{{\psi }^q}\left(\sigma \right),\mathcal{S}\left(\stackrel{═}{\zeta }\right)\in \left[-\mathrm{1,1}\right]$

and

$\mathcal{A}\left(\stackrel{═}{\zeta }\right)=\stackrel{═}{{ʊ}^q}\left(\sigma \right)+\stackrel{═}{{\psi }^q}\left(\sigma \right),\mathcal{A}\left(\stackrel{═}{\zeta }\right)\in \left[\mathrm{0,1}\right].$

If two q-ROFVs $\stackrel{═}{{\zeta }_1}=\left({\stackrel{═}{ʊ}}_1,\stackrel{═}{{\psi }_1}\right)$ and $\stackrel{═}{{\zeta }_2}=\left(\stackrel{═}{{ʊ}_2},\stackrel{═}{{\psi }_2}\right)$, then we have $\mathcal{S}\left({\stackrel{═}{\zeta }}_1\right)<\mathcal{S}\left({\stackrel{═}{\zeta }}_2\right)$ if $\stackrel{═}{{\zeta }_1}<\stackrel{═}{{\zeta }_2}$ and $\mathcal{S}\left({\stackrel{═}{\zeta }}_1\right)>\mathcal{S}\left({\stackrel{═}{\zeta }}_2\right)$ if $\stackrel{═}{{\zeta }_1}>\stackrel{═}{{\zeta }_2}$. When $\mathcal{S}\left({\stackrel{═}{\zeta }}_1\right)=\mathcal{S}\left({\stackrel{═}{\zeta }}_2\right)$, then $\mathcal{A}\left({\stackrel{═}{\zeta }}_1\right)>\mathcal{A}\left({\stackrel{═}{\zeta }}_2\right)$ if $\stackrel{═}{{\zeta }_1}>\stackrel{═}{{\zeta }_2}$ and $\mathcal{A}\left({\stackrel{═}{\zeta }}_1\right)=\mathcal{A}\left({\stackrel{═}{\zeta }}_2\right)$ if $\stackrel{═}{{\zeta }_1}\approx \stackrel{═}{{\zeta }_2}$.

Definition 6. Suppose $\stackrel{═}{{\zeta }_{Ɣ}},Ɣ=1,2,\dots ,Ɯ$ is a set of positive integers. The power average (PA) operator is expressed as (Yager, 2001)

$PA\left(\stackrel{═}{{\zeta }_1},\stackrel{═}{{\zeta }_2},\dots ,\stackrel{═}{{\zeta }_{Ɯ}}\right)=\frac{\left(1+A\left(\stackrel{═}{{\zeta }_{Ɣ}}\right)\right)\stackrel{═}{{\zeta }_{Ɣ}}}{{\displaystyle \sum _{Ɣ=1}^{Ɯ}}\left(1+A\left(\stackrel{═}{{\zeta }_{Ɣ}}\right)\right)},$

where $A\left(\stackrel{═}{{\zeta }_{Ɣ}}\right)={\displaystyle \sum _{\begin{array}{c}Ɣ=1\\ Ɣ\ne \tau \end{array}}^{Ɯ}}Supp\left(\stackrel{═}{{\zeta }_{Ɣ}},\stackrel{═}{{\zeta }_{\tau }}\right)$.

3 Operations of Sugeno–Weber triangular norm based on q-ROFVs

Some necessary operations of Sugeno–Weber triangular norms are expressed considering q-ROF information. The following aggregation expressions play an important role in our proposed research work.

Definition 7. For three q-ROFVs, $\stackrel{═}{\zeta }=\left(\stackrel{═}{ʊ},\stackrel{═}{\psi }\right),\stackrel{═}{{\zeta }_1}=\left({\stackrel{═}{ʊ}}_1,\stackrel{═}{{\psi }_1}\right)$, and $\stackrel{═}{{\zeta }_2}=\left(\stackrel{═}{{ʊ}_2},\stackrel{═}{{\psi }_2}\right)$ with $\Delta >0$. Basic operations of Sugeno–Weber triangular norms are given by

 a) $\stackrel{═}{{\zeta }_1}⨁\stackrel{═}{{\zeta }_2}=\left((\sqrt[q]{\stackrel{═}{{ʊ}_1^q}+\stackrel{═}{{ʊ}_2^q}-\frac{Ђ}{1+Ђ}\stackrel{═}{{ʊ}_1^q}.\stackrel{═}{{ʊ}_2^q}},\sqrt[q]{\frac{\stackrel{═}{{\psi }_1^q}+\stackrel{═}{{\psi }_2^q}-1+Ђ\stackrel{═}{{\psi }_1^q}.\stackrel{═}{{\psi }_2^q}}{1+Ђ}}\right))$.

 b) $\stackrel{═}{{\zeta }_1}⨂\stackrel{═}{{\zeta }_2}=\left((\sqrt[q]{\frac{\stackrel{═}{{ʊ}_1^q}+\stackrel{═}{{ʊ}_2^q}-1+Ђ\stackrel{═}{{ʊ}_1^q}.\stackrel{═}{{ʊ}_2^q}}{1+Ђ}},\sqrt[q]{\stackrel{═}{{\psi }_1^q}+\stackrel{═}{{\psi }_2^q}-\frac{Ђ}{1+Ђ}\stackrel{═}{{\psi }_1^q}.\stackrel{═}{{\psi }_2^q}}\right))$.

 c) $\Delta \stackrel{═}{\zeta }=\left((\sqrt[q]{\frac{1+Ђ}{Ђ}\left((1-{\left((1-\stackrel{═}{{ʊ}^q}\left(\frac{Ђ}{1+Ђ}\right))\right))}^{\Delta }\right))},\sqrt[q]{\left((\left((1+Ђ\right){\left(\frac{Ђ\stackrel{═}{{\psi }^q}+1}{1+Ђ}\right))}^{\Delta }-1\right))\frac{1}{Ђ}}\right))$.

 d) $\stackrel{═}{{\zeta }^{\Delta }}=\left((\sqrt[q]{\frac{1}{Ђ}\left((\left((1+Ђ\right){\left((\frac{Ђ\stackrel{═}{{ʊ}^q}+1}{1+Ђ}\right))}^{\Delta }-1\right))},\sqrt[q]{\frac{1+Ђ}{Ђ}\left((1-{\left((1-\stackrel{═}{{\psi }^q}\left((\frac{Ђ}{1+Ђ}\right))\right))}^{\Delta }\right))}\right))$.

4 q-rung orthopair fuzzy Sugeno–Weber aggregation operators

Based on the operational laws of Sugeno–Weber t-norms, we established new mathematical strategies of the q-ROF information, such as q-ROFSWPA and q-ROFSWPG operators.

Definition 8. Consider a class of q-ROFVs $\stackrel{═}{{\zeta }_{Ɣ}}=\left({\stackrel{═}{ʊ}}_{Ɣ},\stackrel{═}{{\psi }_{Ɣ}}\right),Ɣ=1,2,\dots ,Ɯ$. The q-ROFSWPA operator is characterized as follows:

$q-ROFSWPA\left(\stackrel{═}{{\zeta }_1},\stackrel{═}{{\zeta }_2},\dots ,\stackrel{═}{{\zeta }_{Ɯ}}\right)=\underset{Ɣ=1}{\overset{Ɯ}{{\displaystyle ⨁}}}{Ɲ}_{Ɣ}\stackrel{═}{{\zeta }_{Ɣ}},$

where ${Ɲ}_{Ɣ}=\frac{\left((1+A\left((\stackrel{═}{{\zeta }_{Ɣ}}\right))\right))}{{\sum }_{Ɣ=1}^{Ɯ}\left((1+A\left((\stackrel{═}{{\zeta }_{Ɣ}}\right))\right))}$ and $A\left(\stackrel{═}{{\zeta }_{Ɣ}}\right)={\sum }_{\begin{array}{c}Ɣ=1\\ Ɣ\ne \tau \end{array}}^{Ɯ}Supp\left(\stackrel{═}{{\zeta }_{Ɣ}},\stackrel{═}{{\zeta }_{\tau }}\right)$.

Theorem 1. For a class of q-ROFVs $\stackrel{═}{{\zeta }_{Ɣ}}=\left({\stackrel{═}{ʊ}}_{Ɣ},\stackrel{═}{{\psi }_{Ɣ}}\right),Ɣ=1,2,\dots ,Ɯ$, the accumulated value of the q-ROFSWPA operator is still a q-ROFV, so we obtain the following:

$q-ROFSWPA\left(\stackrel{═}{{\zeta }_1},\stackrel{═}{{\zeta }_2},\dots ,\stackrel{═}{{\zeta }_{Ɯ}}\right)=\left(\begin{array}{c}\sqrt[q]{\frac{1+Ђ}{Ђ}\left(1-{\displaystyle \prod _{Ɣ=1}^{Ɯ}}{\left(1-\stackrel{═}{{ʊ}_{Ɣ}^q}\left(\frac{Ђ}{1+Ђ}\right)\right)}^{{Ɲ}_{Ɣ}}\right)},\\ \sqrt[q]{\frac{1}{Ђ}\left(\left(1+Ђ\right){\displaystyle \prod _{Ɣ=1}^{Ɯ}}{\left(\frac{Ђ\stackrel{═}{{\psi }_{Ɣ}^q}+1}{1+Ђ}\right)}^{{Ɲ}_{Ɣ}}-1\right)}.\end{array}\right)$

Proof: We can prove the above expression using the induction method for $Ɯ=2$. We can write

${Ɲ}_1\stackrel{═}{{\zeta }_1}=\left(\begin{array}{c}\sqrt[q]{\frac{1+Ђ}{Ђ}\left(1-{\left(1-\stackrel{═}{{ʊ}_1^q}\left(\frac{Ђ}{1+Ђ}\right)\right)}^{{Ɲ}_1}\right)},\\ \sqrt[q]{\left(\left(1+Ђ\right){\left(\frac{Ђ\stackrel{═}{{\psi }_1^q}+1}{1+Ђ}\right)}^{{Ɲ}_1}-1\right)\frac{1}{Ђ}},\end{array}\right)$

${Ɲ}_2\stackrel{═}{{\zeta }_2}=\left(\begin{array}{c}\sqrt[q]{\frac{1+Ђ}{Ђ}\left(1-{\left(1-\stackrel{═}{{ʊ}_2^q}\left(\frac{Ђ}{1+Ђ}\right)\right)}^{{Ɲ}_2}\right)},\\ \sqrt[q]{\left(\left(1+Ђ\right){\left(\frac{Ђ\stackrel{═}{{\psi }_2^q}+1}{1+Ђ}\right)}^{{Ɲ}_2}-1\right)\frac{1}{Ђ}},\end{array}\right)$

$q-ROFSWPA\left(\stackrel{═}{{\zeta }_1},\stackrel{═}{{\zeta }_2}\right)=\underset{Ɣ=1}{\overset{2}{⨁}}{Ɲ}_{Ɣ}\stackrel{═}{{\zeta }_{Ɣ}},$

$q-ROFSWPA\left(\stackrel{═}{{\zeta }_1},\stackrel{═}{{\zeta }_2}\right)=\left(\begin{array}{c}\sqrt[q]{\frac{1+Ђ}{Ђ}\left(1-{\left(1-\stackrel{═}{{ʊ}_1^q}\left(\frac{Ђ}{1+Ђ}\right)\right)}^{{Ɲ}_1}\right)}\\ ⨁\sqrt[q]{\frac{1+Ђ}{Ђ}\left(1-{\left(1-\stackrel{═}{{ʊ}_2^q}\left(\frac{Ђ}{1+Ђ}\right)\right)}^{{Ɲ}_2}\right)},\\ \sqrt[q]{\left(\left(1+Ђ\right){\left(\frac{Ђ\stackrel{═}{{\psi }_1^q}+1}{1+Ђ}\right)}^{{Ɲ}_1}-1\right)\frac{1}{Ђ}}\\ ⨁\sqrt[q]{\left(\left(1+Ђ\right){\left(\frac{Ђ\stackrel{═}{{\psi }_2^q}+1}{1+Ђ}\right)}^{{Ɲ}_2}-1\right)\frac{1}{Ђ}},\end{array}\right)$

$q-ROFSWPA\left(\stackrel{═}{{\zeta }_1},\stackrel{═}{{\zeta }_2}\right)=\left(\begin{array}{c}\sqrt[q]{\begin{array}{c}\frac{1+Ђ}{Ђ}\left(1-{\left(1-\stackrel{═}{{ʊ}_1^q}\left(\frac{Ђ}{1+Ђ}\right)\right)}^{{Ɲ}_1}\right)+\frac{1+Ђ}{Ђ}\left(1-{\left(1-\stackrel{═}{{ʊ}_2^q}\left(\frac{Ђ}{1+Ђ}\right)\right)}^{{Ɲ}_2}\right)\\ -\frac{Ђ}{1+Ђ}\left(\frac{1+Ђ}{Ђ}\left(1-{\left(1-\stackrel{═}{{ʊ}_1^q}\left(\frac{Ђ}{1+Ђ}\right)\right)}^{{Ɲ}_1}\right)\right).\left(\frac{1+Ђ}{Ђ}\left(1-{\left(1-\stackrel{═}{{ʊ}_2^q}\left(\frac{Ђ}{1+Ђ}\right)\right)}^{{Ɲ}_2}\right)\right)\end{array}},\\ \sqrt[q]{\left(\frac{1}{1+Ђ}\right)\left(\begin{array}{c}\left(\left(1+Ђ\right){\left(\frac{Ђ\stackrel{═}{{\psi }_1^q}+1}{1+Ђ}\right)}^{{Ɲ}_1}-1\right)\frac{1}{Ђ}+\left(\left(1+Ђ\right){\left(\frac{Ђ\stackrel{═}{{\psi }_2^q}+1}{1+Ђ}\right)}^{{Ɲ}_2}-1\right)\frac{1}{Ђ}-1+\\ Ђ\left(\left(\left(1+Ђ\right){\left(\frac{Ђ\stackrel{═}{{\psi }_1^q}+1}{1+Ђ}\right)}^{{Ɲ}_1}-1\right)\frac{1}{Ђ}\right).\left(\left(\left(1+Ђ\right){\left(\frac{Ђ\stackrel{═}{{\psi }_2^q}+1}{1+Ђ}\right)}^{{Ɲ}_2}-1\right)\frac{1}{Ђ}\right)\end{array}\right),}\end{array}\right)$

$q-ROFSWPA\left(\stackrel{═}{{\zeta }_1},\stackrel{═}{{\zeta }_2}\right)=\left(\begin{array}{c}\sqrt[q]{\frac{1+Ђ}{Ђ}\left(1-{\displaystyle \prod _{Ɣ=1}^2}{\left(1-\stackrel{═}{{ʊ}_{Ɣ}^q}\left(\frac{Ђ}{1+Ђ}\right)\right)}^{{Ɲ}_{Ɣ}}\right)},\\ \sqrt[q]{\frac{1}{Ђ}\left(\left(1+Ђ\right){\displaystyle \prod _{Ɣ=1}^2}{\left(\frac{Ђ\stackrel{═}{{\psi }_{Ɣ}^q}+1}{1+Ђ}\right)}^{{Ɲ}_{Ɣ}}-1\right).}\end{array}\right)$

Suppose that the above expression is valid for $Ɯ=k$.

$q-ROFSWPA\left(\stackrel{═}{{\zeta }_1},\stackrel{═}{{\zeta }_2},\dots ,\stackrel{═}{{\zeta }_k}\right)=\underset{Ɣ=1}{\overset{k}{⨁}}{Ɲ}_{Ɣ}\stackrel{═}{{\zeta }_{Ɣ}}$

$q-ROFSWPA\left(\stackrel{═}{{\zeta }_1},\stackrel{═}{{\zeta }_2},\dots ,\stackrel{═}{{\zeta }_k}\right)=\left(\begin{array}{c}\sqrt[q]{\frac{1+Ђ}{Ђ}\left(1-{\displaystyle \prod _{Ɣ=1}^k}{\left(1-\stackrel{═}{{ʊ}_{Ɣ}^q}\left(\frac{Ђ}{1+Ђ}\right)\right)}^{{Ɲ}_{Ɣ}}\right)},\\ \sqrt[q]{\frac{1}{Ђ}\left(\left(1+Ђ\right){\displaystyle \prod _{Ɣ=1}^k}{\left(\frac{Ђ\stackrel{═}{{\psi }_{Ɣ}^q}+1}{1+Ђ}\right)}^{{Ɲ}_{Ɣ}}-1\right).}\end{array}\right)$

Next, we can prove $Ɯ=k$ +1.

$q-ROFSWPA\left(\stackrel{═}{{\zeta }_1},\stackrel{═}{{\zeta }_2},\dots ,\stackrel{═}{{\zeta }_k}\right)=\underset{Ɣ=1}{\overset{k}{⨁}}{Ɲ}_{Ɣ}\stackrel{═}{{\zeta }_{Ɣ}}⨁{Ɲ}_{k+1}\stackrel{═}{{\zeta }_{k+1}}$

$=\left(\begin{array}{c}\sqrt[q]{\frac{1+Ђ}{Ђ}\left(1-{\displaystyle \prod _{Ɣ=1}^k}{\left(1-\stackrel{═}{{ʊ}_{Ɣ}^q}\left(\frac{Ђ}{1+Ђ}\right)\right)}^{{Ɲ}_{Ɣ}}\right)}\\ \sqrt[q]{\frac{1}{Ђ}\left(\left(1+Ђ\right){\displaystyle \prod _{Ɣ=1}^k}{\left(\frac{Ђ\stackrel{═}{{\psi }_{Ɣ}^q}+1}{1+Ђ}\right)}^{{Ɲ}_{Ɣ}}-1\right)}\end{array}\right)⨁\left(\begin{array}{c}\sqrt[q]{\frac{1+Ђ}{Ђ}\left(1-{\left(1-\stackrel{═}{{ʊ}_{k+1}^q}\left(\frac{Ђ}{1+Ђ}\right)\right)}^{{Ɲ}_{k+1}}\right)},\\ \sqrt[q]{\frac{1}{Ђ}\left(\left(1+Ђ\right){\left(\frac{Ђ\stackrel{═}{{\psi }_{k+1}^q}+1}{1+Ђ}\right)}^{{Ɲ}_{k+1}}-1\right)},\end{array}\right)$

$q-ROFSWPA\left(\stackrel{═}{{\zeta }_1},\stackrel{═}{{\zeta }_2},\dots ,\stackrel{═}{{\zeta }_{k+1}}\right)=\left(\begin{array}{c}\sqrt[q]{\frac{1+Ђ}{Ђ}\left(1-{\displaystyle \prod _{Ɣ=1}^{k+1}}{\left(1-\stackrel{═}{{ʊ}_{Ɣ}^q}\left(\frac{Ђ}{1+Ђ}\right)\right)}^{{Ɲ}_{Ɣ}}\right)},\\ \sqrt[q]{\frac{1}{Ђ}\left(\left(1+Ђ\right){\displaystyle \prod _{Ɣ=1}^{k+1}}{\left(\frac{Ђ\stackrel{═}{{\psi }_{Ɣ}^q}+1}{1+Ђ}\right)}^{{Ɲ}_{Ɣ}}-1\right)}.\end{array}\right)$

Hence, Theorem 1 is proved. □

Theorem 2. Consider a class of q-ROFVs $\stackrel{═}{{\zeta }_{Ɣ}}=\left({\stackrel{═}{ʊ}}_{Ɣ},\stackrel{═}{{\psi }_{Ɣ}}\right),Ɣ=1,2,\dots ,Ɯ$,which implies that $\stackrel{═}{{\zeta }_{Ɣ}}=\stackrel{═}{\zeta }$. Then we obtain

$q-ROFSWPA\left(\stackrel{═}{{\zeta }_1},\stackrel{═}{{\zeta }_2},\dots ,\stackrel{═}{{\zeta }_{Ɯ}}\right)=\stackrel{═}{\zeta }.$

Proof: Since all q-ROFVs $\stackrel{═}{{\zeta }_{Ɣ}}=\left({\stackrel{═}{ʊ}}_{Ɣ},\stackrel{═}{{\psi }_{Ɣ}}\right),Ɣ=1,2,\dots ,Ɯ$ are identical, $\stackrel{═}{{\zeta }_{Ɣ}}=\stackrel{═}{\zeta }$. Then, we obtain

$q-ROFSWPA\left(\stackrel{═}{{\zeta }_1},\stackrel{═}{{\zeta }_2},\dots ,\stackrel{═}{{\zeta }_{Ɯ}}\right)=\left(\begin{array}{c}\sqrt[q]{\frac{1+Ђ}{Ђ}\left(1-{\displaystyle \prod _{Ɣ=1}^{Ɯ}}{\left(1-\stackrel{═}{{ʊ}_{Ɣ}^q}\left(\frac{Ђ}{1+Ђ}\right)\right)}^{{Ɲ}_{Ɣ}}\right)},\\ \sqrt[q]{\frac{1}{Ђ}\left(\left(1+Ђ\right){\displaystyle \prod _{Ɣ=1}^{Ɯ}}{\left(\frac{Ђ\stackrel{═}{{\psi }_{Ɣ}^q}+1}{1+Ђ}\right)}^{{Ɲ}_{Ɣ}}-1\right)},\end{array}\right)$

$=\left(\begin{array}{c}\sqrt[q]{\frac{1+Ђ}{Ђ}\left(1-{\left(1-\stackrel{═}{{ʊ}^q}\left(\frac{Ђ}{1+Ђ}\right)\right)}^{{\sum }_{Ɣ=1}^{Ɯ}{Ɲ}_{Ɣ}}\right)},\\ \sqrt[q]{\frac{1}{Ђ}\left(\left(1+Ђ\right){\left(\frac{Ђ\stackrel{═}{{\psi }^q}+1}{1+Ђ}\right)}^{{\sum }_{Ɣ=1}^{Ɯ}{Ɲ}_{Ɣ}}-1\right),}\end{array}\right)$

$=\left(\begin{array}{c}\sqrt[q]{\frac{1+Ђ}{Ђ}\left(1-\left(1-\stackrel{═}{{ʊ}^q}\left(\frac{Ђ}{1+Ђ}\right)\right)\right)},\\ \sqrt[q]{\frac{1}{Ђ}\left(\left(1+Ђ\right)\left(\frac{Ђ\stackrel{═}{{\psi }^q}+1}{1+Ђ}\right)-1\right),}\end{array}\right)$

$=\left(\begin{array}{c}\sqrt[q]{\frac{1+Ђ}{Ђ}\left(1-1+\stackrel{═}{{ʊ}^q}\left(\frac{Ђ}{1+Ђ}\right)\right)},\\ \sqrt[q]{\frac{1}{Ђ}\left(Ђ\stackrel{═}{{\psi }^q}+1-1\right)},\end{array}\right)$

$=\left(\begin{array}{c}\sqrt[q]{\frac{1+Ђ}{Ђ}\left(\stackrel{═}{{ʊ}^q}\left(\frac{Ђ}{1+Ђ}\right)\right)},\\ \sqrt[q]{\frac{1}{Ђ}\left(Ђ\stackrel{═}{{\psi }^q}\right)},\end{array}\right)$

$=\left(\stackrel{═}{ʊ},\stackrel{═}{\psi }\right)=\stackrel{═}{\zeta }.$

Hence, Theorem 2 is proved. □

Theorem 3. For any two sets of q-ROFVs, $\stackrel{═}{{\zeta }_{Ɣ}}=\left({\stackrel{═}{ʊ}}_{Ɣ},\stackrel{═}{{\psi }_{Ɣ}}\right)$ and $\stackrel{═}{{\zeta }_{Ɣ}^{\prime }}=\left({\stackrel{═}{ʊ}}_{Ɣ}^{\prime },\stackrel{═}{{\psi }_{Ɣ}^{\prime }}\right),Ɣ=1,2,\dots ,Ɯ$. If $\stackrel{═}{{\zeta }_{Ɣ}}\le \stackrel{═}{{\zeta }_{Ɣ}^{\prime }}$, so we obtain

$q-ROFSWPA\left(\stackrel{═}{{\zeta }_1},\stackrel{═}{{\zeta }_2},\dots ,\stackrel{═}{{\zeta }_{Ɯ}}\right)\le q-ROFSWPA\left(\stackrel{═}{{\zeta }_1^{\prime }},\stackrel{═}{{\zeta }_2^{\prime }},\dots ,\stackrel{═}{{\zeta }_{Ɯ}^{\prime }}\right).$

Proof: The proof is straightforward.

Theorem 4. Consider a class of q-ROFVs $\stackrel{═}{{\zeta }_{Ɣ}}=\left({\stackrel{═}{ʊ}}_{Ɣ},\stackrel{═}{{\psi }_{Ɣ}}\right),Ɣ=1,2,\dots ,Ɯ$. If $\stackrel{═}{{\zeta }^{-}}=\left(\mathit{min}\left\{\stackrel{═}{{ʊ}_{Ɣ}}\right\},\mathit{max}\left\{\stackrel{═}{{\psi }_{Ɣ}}\right\}\right)$ and $\stackrel{═}{{\zeta }^{+}}=\left(\mathit{max}\left\{\stackrel{═}{{ʊ}_{Ɣ}}\right\},\mathit{min}\left\{\stackrel{═}{{\psi }_{Ɣ}}\right\}\right)$, then we obtain

$\stackrel{═}{{\zeta }^{-}}\le q-ROFSWPA\left(\stackrel{═}{{\zeta }_1},\stackrel{═}{{\zeta }_2},\dots ,\stackrel{═}{{\zeta }_{Ɯ}}\right)\le \stackrel{═}{{\zeta }^{+}}.$

Proof: Consider a class of q-ROFVs $\stackrel{═}{{\zeta }_{Ɣ}}=\left({\stackrel{═}{ʊ}}_{Ɣ},\stackrel{═}{{\psi }_{Ɣ}}\right),Ɣ=1,2,\dots ,Ɯ$. Then we obtain

$\min \stackrel{═}{{ʊ}_{Ɣ}}\le \max \stackrel{═}{{ʊ}_{Ɣ}},$

$\min \stackrel{═}{{ʊ}_{Ɣ}^q}\left(\frac{Ђ}{1+Ђ}\right)\le \stackrel{═}{{ʊ}_{Ɣ}^q}\left(\frac{Ђ}{1+Ђ}\right)\le \max \stackrel{═}{{ʊ}_{Ɣ}^q}\left(\frac{Ђ}{1+Ђ}\right),$

$1-\min \stackrel{═}{{ʊ}_{Ɣ}^q}\left(\frac{Ђ}{1+Ђ}\right)\ge 1-\stackrel{═}{{ʊ}_{Ɣ}^q}\left(\frac{Ђ}{1+Ђ}\right)\ge 1-\max \stackrel{═}{{ʊ}_{Ɣ}^q}\left(\frac{Ђ}{1+Ђ}\right),$

${\left(1-\min \stackrel{═}{{ʊ}_{Ɣ}^q}\left(\frac{Ђ}{1+Ђ}\right)\right)}^{{Ɲ}_{Ɣ}}\ge {\left(1-\stackrel{═}{{ʊ}_{Ɣ}^q}\left(\frac{Ђ}{1+Ђ}\right)\right)}^{{Ɲ}_{Ɣ}}\ge {\left(1-\max \stackrel{═}{{ʊ}_{Ɣ}^q}\left(\frac{Ђ}{1+Ђ}\right)\right)}^{{Ɲ}_{Ɣ}},$

${\left(1-\min \stackrel{═}{{ʊ}_{Ɣ}^q}\left(\frac{Ђ}{1+Ђ}\right)\right)}^{{\displaystyle \sum _{Ɣ=1}^{Ɯ}}{Ɲ}_{Ɣ}}\ge {\displaystyle \prod _{Ɣ=1}^{Ɯ}}{\left(1-\stackrel{═}{{ʊ}_{Ɣ}^q}\left(\frac{Ђ}{1+Ђ}\right)\right)}^{{Ɲ}_{Ɣ}}\ge {\left(1-\max \stackrel{═}{{ʊ}_{Ɣ}^q}\left(\frac{Ђ}{1+Ђ}\right)\right)}^{{\displaystyle \sum _{Ɣ=1}^{Ɯ}}{Ɲ}_{Ɣ}},$

$\left(1-\min \stackrel{═}{{ʊ}_{Ɣ}^q}\left(\frac{Ђ}{1+Ђ}\right)\right)\ge {\displaystyle \prod _{Ɣ=1}^{Ɯ}}{\left(1-\stackrel{═}{{ʊ}_{Ɣ}^q}\left(\frac{Ђ}{1+Ђ}\right)\right)}^{{Ɲ}_{Ɣ}}\ge \left(1-\max \stackrel{═}{{ʊ}_{Ɣ}^q}\left(\frac{Ђ}{1+Ђ}\right)\right),$

$\min \stackrel{═}{{ʊ}_{Ɣ}^q}\left(\frac{Ђ}{1+Ђ}\right)\le 1-{\displaystyle \prod _{Ɣ=1}^{Ɯ}}{\left(1-\stackrel{═}{{ʊ}_{Ɣ}^q}\left(\frac{Ђ}{1+Ђ}\right)\right)}^{{Ɲ}_{Ɣ}}\le \max \stackrel{═}{{ʊ}_{Ɣ}^q}\left(\frac{Ђ}{1+Ђ}\right),$

$\min \stackrel{═}{{ʊ}_{Ɣ}^q}\le \sqrt[q]{\frac{1+Ђ}{Ђ}\left(1-{\displaystyle \prod _{Ɣ=1}^{Ɯ}}{\left(1-\stackrel{═}{{ʊ}_{Ɣ}^q}\left(\frac{Ђ}{1+Ђ}\right)\right)}^{{Ɲ}_{Ɣ}}\right)}\le \max \stackrel{═}{{ʊ}_{Ɣ}^q}.$

Similarly, we can write

$\min \stackrel{═}{{\psi }_{Ɣ}}\ge \sqrt[q]{\frac{1}{Ђ}\left(\left(1+Ђ\right){\displaystyle \prod _{Ɣ=1}^{Ɯ}}{\left(\frac{Ђ\stackrel{═}{{\psi }_{Ɣ}^q}+1}{1+Ђ}\right)}^{{Ɲ}_{Ɣ}}-1\right)}\ge \max \stackrel{═}{{\psi }_{Ɣ}}.$

Therefore,

$\stackrel{═}{{\zeta }^{-}}\le q-ROFSWPA\left(\stackrel{═}{{\zeta }_1},\stackrel{═}{{\zeta }_2},\dots ,\stackrel{═}{{\zeta }_{Ɯ}}\right)\le \stackrel{═}{{\zeta }^{+}}.$

Definition 9. For a class of q-ROFVs $\stackrel{═}{{\zeta }_{Ɣ}}=\left({\stackrel{═}{ʊ}}_{Ɣ},\stackrel{═}{{\psi }_{Ɣ}}\right),Ɣ=1,2,\dots ,Ɯ$, the q-ROFSWOPA operator is characterized as follows:

$q-ROFSWOPA\left(\stackrel{═}{{\zeta }_1},\stackrel{═}{{\zeta }_2},\dots ,\stackrel{═}{{\zeta }_{Ɯ}}\right)=\underset{Ɣ=1}{\overset{Ɯ}{{\displaystyle ⨁}}}{Ɲ}_{Ɣ}{\stackrel{═}{\zeta }}_{\wp \left(Ɣ\right)},$

where ${Ɲ}_{Ɣ}=\frac{\left(1+A\left(\stackrel{═}{{\zeta }_{Ɣ}}\right)\right)}{{\sum }_{Ɣ=1}^{Ɯ}\left(1+A\left(\stackrel{═}{{\zeta }_{Ɣ}}\right)\right)}$ and $A\left(\stackrel{═}{{\zeta }_{Ɣ}}\right)={\displaystyle \sum _{\begin{array}{c}Ɣ=1\\ Ɣ\ne \tau \end{array}}^{Ɯ}}Supp\left(\stackrel{═}{{\zeta }_{Ɣ}},\stackrel{═}{{\zeta }_{\tau }}\right)$, and let $\left(\wp \left(1\right),\wp \left(2\right),\dots ,\wp \left(Ɯ\right)\right)$ be the set of permutation of $,Ɣ=1,2,\dots ,Ɯ$ as ${\stackrel{═}{\zeta }}_{\wp \left(Ɣ-1\right)}\ge \stackrel{═}{{\zeta }_{Ɣ}}$.

Theorem 5. Consider a class of q-ROFVs $\stackrel{═}{{\zeta }_{Ɣ}}=\left({\stackrel{═}{ʊ}}_{Ɣ},\stackrel{═}{{\psi }_{Ɣ}}\right),Ɣ=1,2,\dots ,Ɯ$. The accumulated value of the q-ROFSWOPA operator is still a q-ROFV, so we obtain the following:

$q-ROFSWOPA\left(\stackrel{═}{{\zeta }_1},\stackrel{═}{{\zeta }_2},\dots ,\stackrel{═}{{\zeta }_{Ɯ}}\right)=\left(\begin{array}{c}\sqrt[q]{\frac{1+Ђ}{Ђ}\left(1-{\displaystyle \prod _{Ɣ=1}^{Ɯ}}{\left(1-\stackrel{═}{{ʊ}_{\wp \left(Ɣ\right)}^q}\left(\frac{Ђ}{1+Ђ}\right)\right)}^{{Ɲ}_{Ɣ}}\right)},\\ \sqrt[q]{\frac{1}{Ђ}\left(\left(1+Ђ\right){\displaystyle \prod _{Ɣ=1}^{Ɯ}}{\left(\frac{Ђ\stackrel{═}{{\psi }_{\wp \left(Ɣ\right)}^q}+1}{1+Ђ}\right)}^{{Ɲ}_{Ɣ}}-1\right)},\end{array}\right)$

where ${\mathrm{Ɲ}}_{\mathrm{Ɣ}}=\frac{\left(1+\mathrm{A}\left(\stackrel{═}{{\mathrm{\zeta }}_{\mathrm{Ɣ}}}\right)\right)}{{\sum }_{\mathrm{Ɣ}=1}^{\mathrm{Ɯ}}\left(1+\mathrm{A}\left(\stackrel{═}{{\mathrm{\zeta }}_{\mathrm{Ɣ}}}\right)\right)}$ and $\mathrm{A}\left(\stackrel{═}{{\mathrm{\zeta }}_{\mathrm{Ɣ}}}\right)={\displaystyle \sum _{\begin{array}{c}\mathrm{Ɣ}=1\\ \mathrm{Ɣ}\ne \mathrm{\tau }\end{array}}^{\mathrm{Ɯ}}}\text{Supp}\left(\stackrel{═}{{\mathrm{\zeta }}_{\mathrm{Ɣ}}},\stackrel{═}{{\mathrm{\zeta }}_{\mathrm{\tau }}}\right)$, and let $\left(\wp \left(1\right),\wp \left(2\right),\dots ,\wp \left(\mathrm{Ɯ}\right)\right)$ be the set of permutation of $\mathrm{Ɣ}=1,2,\dots ,\mathrm{Ɯ}$ as ${\stackrel{═}{\mathrm{\zeta }}}_{\wp \left(\mathrm{Ɣ}-1\right)}\ge \stackrel{═}{{\mathrm{\zeta }}_{\mathrm{Ɣ}}}$.

Theorem 6. Consider a class of q-ROFVs $\stackrel{═}{{\zeta }_{Ɣ}}=\left({\stackrel{═}{ʊ}}_{Ɣ},\stackrel{═}{{\psi }_{Ɣ}}\right),Ɣ=1,2,\dots ,Ɯ$,which implies that $\stackrel{═}{{\zeta }_{Ɣ}}=\stackrel{═}{\zeta }$. Then we obtain

$q-ROFSWPOA\left(\stackrel{═}{{\zeta }_1},\stackrel{═}{{\zeta }_2},\dots ,\stackrel{═}{{\zeta }_{Ɯ}}\right)=\stackrel{═}{\zeta }.$

Theorem 7. Consider any two sets of q-ROFVs $\stackrel{═}{{\zeta }_{Ɣ}}=\left({\stackrel{═}{ʊ}}_{Ɣ},\stackrel{═}{{\psi }_{Ɣ}}\right)$ and $\stackrel{═}{{\zeta }_{Ɣ}^{\prime }}=\left({\stackrel{═}{ʊ}}_{Ɣ}^{\prime },\stackrel{═}{{\psi }_{Ɣ}^{\prime }}\right),Ɣ=1,2,\dots ,Ɯ$. If $\stackrel{═}{{\zeta }_{Ɣ}}\le \stackrel{═}{{\zeta }_{Ɣ}^{\prime }}$, then we obtain

$q-ROFSWPOA\left(\stackrel{═}{{\zeta }_1},\stackrel{═}{{\zeta }_2},\dots ,\stackrel{═}{{\zeta }_{Ɯ}}\right)\le q-ROFSWPOA\left(\stackrel{═}{{\zeta }_1^{\prime }},\stackrel{═}{{\zeta }_2^{\prime }},\dots ,\stackrel{═}{{\zeta }_{Ɯ}^{\prime }}\right).$

Theorem 8. Consider a class of q-ROFVs $\stackrel{═}{{\zeta }_{Ɣ}}=\left({\stackrel{═}{ʊ}}_{Ɣ},\stackrel{═}{{\psi }_{Ɣ}}\right),Ɣ=1,2,\dots ,Ɯ$. If $\stackrel{═}{{\zeta }^{-}}=\left(\mathit{min}\left\{\stackrel{═}{{ʊ}_{Ɣ}}\right\},\mathit{max}\left\{\stackrel{═}{{\psi }_{Ɣ}}\right\}\right)$ and $\stackrel{═}{{\zeta }^{+}}=\left(\mathit{max}\left\{\stackrel{═}{{ʊ}_{Ɣ}}\right\},\mathit{min}\left\{\stackrel{═}{{\psi }_{Ɣ}}\right\}\right)$, then we obtain

$\stackrel{═}{{\zeta }^{-}}\le q-ROFSWPOA\left(\stackrel{═}{{\zeta }_1},\stackrel{═}{{\zeta }_2},\dots ,\stackrel{═}{{\zeta }_{Ɯ}}\right)\le \stackrel{═}{{\zeta }^{+}}.$

Definition 10. For a class of q-ROFVs $\stackrel{═}{{\zeta }_{Ɣ}}=\left({\stackrel{═}{ʊ}}_{Ɣ},\stackrel{═}{{\psi }_{Ɣ}}\right),Ɣ=1,2,\dots ,Ɯ$, the q-ROFSWPG operator is characterized as follows:

$q-ROFSWPG\left(\stackrel{═}{{\zeta }_1},\stackrel{═}{{\zeta }_2},\dots ,\stackrel{═}{{\zeta }_{Ɯ}}\right)=\underset{Ɣ=1}{\overset{Ɯ}{{\displaystyle ⨂}}}{\stackrel{═}{{\zeta }_{Ɣ}}}^{{Ɲ}_{Ɣ}},$

where ${Ɲ}_{Ɣ}=\frac{\left(1+A\left(\stackrel{═}{{\zeta }_{Ɣ}}\right)\right)}{{\sum }_{Ɣ=1}^{Ɯ}\left(1+A\left(\stackrel{═}{{\zeta }_{Ɣ}}\right)\right)}$ and $A\left(\stackrel{═}{{\zeta }_{Ɣ}}\right)={\displaystyle \sum _{\begin{array}{c}Ɣ=1\\ Ɣ\ne \tau \end{array}}^{Ɯ}}Supp\left(\stackrel{═}{{\zeta }_{Ɣ}},\stackrel{═}{{\zeta }_{\tau }}\right)$.

Theorem 9. Consider a class of q-ROFVs $\stackrel{═}{{\zeta }_{Ɣ}}=\left({\stackrel{═}{ʊ}}_{Ɣ},\stackrel{═}{{\psi }_{Ɣ}}\right),Ɣ=1,2,\dots ,Ɯ$. The accumulated value of the q-ROFSWPG operator is still a q-ROFV, so we obtain

$q-ROFSWPG\left(\stackrel{═}{{\zeta }_1},\stackrel{═}{{\zeta }_2},\dots ,\stackrel{═}{{\zeta }_{Ɯ}}\right)=\left(\begin{array}{c}\sqrt[q]{\frac{1}{Ђ}\left(\left(1+Ђ\right){\displaystyle \prod _{Ɣ=1}^{Ɯ}}{\left(\frac{Ђ\stackrel{═}{{ʊ}_{Ɣ}^q}+1}{1+Ђ}\right)}^{{Ɲ}_{Ɣ}}-1\right)},\\ \sqrt[q]{\frac{1+Ђ}{Ђ}\left(1-{\displaystyle \prod _{Ɣ=1}^{Ɯ}}{\left(1-\stackrel{═}{{\psi }_{Ɣ}^q}\left(\frac{Ђ}{1+Ђ}\right)\right)}^{{Ɲ}_{Ɣ}}\right)}.\end{array}\right)$

Theorem 10. Consider a class of q-ROFVs $\stackrel{═}{{\zeta }_{Ɣ}}=\left({\stackrel{═}{ʊ}}_{Ɣ},\stackrel{═}{{\psi }_{Ɣ}}\right),Ɣ=1,2,\dots ,Ɯ$, which implies that $\stackrel{═}{{\zeta }_{Ɣ}}=\stackrel{═}{\zeta }$. Then we have

$q-ROFSWPG\left(\stackrel{═}{{\zeta }_1},\stackrel{═}{{\zeta }_2},\dots ,\stackrel{═}{{\zeta }_{Ɯ}}\right)=\stackrel{═}{\zeta }.$

Theorem 11. Consider any two sets of q-ROFVs $\stackrel{═}{{\zeta }_{Ɣ}}=\left({\stackrel{═}{ʊ}}_{Ɣ},\stackrel{═}{{\psi }_{Ɣ}}\right)$ and $\stackrel{═}{{\zeta }_{Ɣ}^{\prime }}=\left({\stackrel{═}{ʊ}}_{Ɣ}^{\prime },\stackrel{═}{{\psi }_{Ɣ}^{\prime }}\right),Ɣ=1,2,\dots ,Ɯ$. If $\stackrel{═}{{\zeta }_{Ɣ}}\le \stackrel{═}{{\zeta }_{Ɣ}^{\prime }}$, then we obtain

$q-ROFSWPG\left(\stackrel{═}{{\zeta }_1},\stackrel{═}{{\zeta }_2},\dots ,\stackrel{═}{{\zeta }_{Ɯ}}\right)\le q-ROFSWPG\left(\stackrel{═}{{\zeta }_1^{\prime }},\stackrel{═}{{\zeta }_2^{\prime }},\dots ,\stackrel{═}{{\zeta }_{Ɯ}^{\prime }}\right).$

Theorem 12. Consider a class of q-ROFVs $\stackrel{═}{{\zeta }_{Ɣ}}=\left({\stackrel{═}{ʊ}}_{Ɣ},\stackrel{═}{{\psi }_{Ɣ}}\right),Ɣ=1,2,\dots ,Ɯ$. If $\stackrel{═}{{\zeta }^{-}}=\left(\mathit{min}\left\{\stackrel{═}{{ʊ}_{Ɣ}}\right\},\mathit{max}\left\{\stackrel{═}{{\psi }_{Ɣ}}\right\}\right)$ and $\stackrel{═}{{\zeta }^{+}}=\left(\mathit{max}\left\{\stackrel{═}{{ʊ}_{Ɣ}}\right\},\mathit{min}\left\{\stackrel{═}{{\psi }_{Ɣ}}\right\}\right)$, then we obtain

$\stackrel{═}{{\zeta }^{-}}\le q-ROFSWPG\left(\stackrel{═}{{\zeta }_1},\stackrel{═}{{\zeta }_2},\dots ,\stackrel{═}{{\zeta }_{Ɯ}}\right)\le \stackrel{═}{{\zeta }^{+}}.$

Definition 11. For a class of q-ROFVs $\stackrel{═}{{\zeta }_{Ɣ}}=\left({\stackrel{═}{ʊ}}_{Ɣ},\stackrel{═}{{\psi }_{Ɣ}}\right),Ɣ=1,2,\dots ,Ɯ$, the q-ROFSWPOG operator is characterized as follows:

$q-ROFSWPOG\left(\stackrel{═}{{\zeta }_1},\stackrel{═}{{\zeta }_2},\dots ,\stackrel{═}{{\zeta }_{Ɯ}}\right)=\underset{Ɣ=1}{\overset{Ɯ}{{\displaystyle ⨂}}}{\stackrel{═}{{\zeta }_{\wp \left(Ɣ\right)}}}^{{Ɲ}_{Ɣ}},$

where ${Ɲ}_{Ɣ}=\frac{\left(1+A\left(\stackrel{═}{{\zeta }_{Ɣ}}\right)\right)}{{\displaystyle {\sum }_{Ɣ=1}^{Ɯ}}\left(1+A\left(\stackrel{═}{{\zeta }_{Ɣ}}\right)\right)},A\left(\stackrel{═}{{\zeta }_{Ɣ}}\right)={\displaystyle {\sum }_{\begin{array}{c}Ɣ=1\\ Ɣ\ne \tau \end{array}}^{Ɯ}}Supp\left(\stackrel{═}{{\zeta }_{Ɣ}},\stackrel{═}{{\zeta }_{\tau }}\right)$ and $\left(\wp \left(1\right),\wp \left(2\right),\dots ,\wp \left(Ɯ\right)\right)$ are the set of permutation of $Ɣ=1,2,\dots ,Ɯ$ as $\stackrel{═}{{\zeta }_{\wp \left(Ɣ-1\right)}}\ge \stackrel{═}{{\zeta }_{Ɣ}}$.

Theorem 13. Consider a class of q-ROFVs $\stackrel{═}{{\zeta }_{Ɣ}}=\left({\stackrel{═}{ʊ}}_{Ɣ},\stackrel{═}{{\psi }_{Ɣ}}\right),Ɣ=1,2,\dots ,Ɯ$. The accumulated value of the q-ROFSWPOG operator is still a q-ROFV, so we obtain

$q-ROFSWPOG\left(\stackrel{═}{{\zeta }_1},\stackrel{═}{{\zeta }_2},\dots ,\stackrel{═}{{\zeta }_{Ɯ}}\right)=\left(\begin{array}{c}\sqrt[q]{\frac{1}{Ђ}\left(\left(1+Ђ\right){\displaystyle \prod _{Ɣ=1}^{Ɯ}}{\left(\frac{Ђ\stackrel{═}{{ʊ}_{\wp \left(Ɣ\right)}^q}+1}{1+Ђ}\right)}^{{Ɲ}_{Ɣ}}-1\right)},\\ \sqrt[q]{\frac{1+Ђ}{Ђ}\left(1-{\displaystyle \prod _{Ɣ=1}^{Ɯ}}{\left(1-\stackrel{═}{{\psi }_{\wp \left(Ɣ\right)}^q}\left(\frac{Ђ}{1+Ђ}\right)\right)}^{{Ɲ}_{Ɣ}}\right)}.\end{array}\right)$

Theorem 14. Consider a class of q-ROFVs $\stackrel{═}{{\zeta }_{Ɣ}}=\left({\stackrel{═}{ʊ}}_{Ɣ},\stackrel{═}{{\psi }_{Ɣ}}\right),Ɣ=1,2,\dots ,Ɯ$, which implies that $\stackrel{═}{{\zeta }_{Ɣ}}=\stackrel{═}{\zeta }$. Then we obtain

$q-ROFSWPOG\left(\stackrel{═}{{\zeta }_1},\stackrel{═}{{\zeta }_2},\dots ,\stackrel{═}{{\zeta }_{Ɯ}}\right)=\stackrel{═}{\zeta }.$

Theorem 15. Consider any two sets of q-ROFVs $\stackrel{═}{{\zeta }_{Ɣ}}=\left({\stackrel{═}{ʊ}}_{Ɣ},\stackrel{═}{{\psi }_{Ɣ}}\right)$ and $\stackrel{═}{{\zeta }_{Ɣ}^{\prime }}=\left({\stackrel{═}{ʊ}}_{Ɣ}^{\prime },\stackrel{═}{{\psi }_{Ɣ}^{\prime }}\right),Ɣ=1,2,\dots ,Ɯ$. If $\stackrel{═}{{\zeta }_{Ɣ}}\le \stackrel{═}{{\zeta }_{Ɣ}^{\prime }}$, then we obtain

$q-ROFSWPOG\left(\stackrel{═}{{\zeta }_1},\stackrel{═}{{\zeta }_2},\dots ,\stackrel{═}{{\zeta }_{Ɯ}}\right)\le q-ROFSWPOG\left(\stackrel{═}{{\zeta }_1^{\prime }},\stackrel{═}{{\zeta }_2^{\prime }},\dots ,\stackrel{═}{{\zeta }_{Ɯ}^{\prime }}\right).$

Theorem 16. Consider a class of q-ROFVs $\stackrel{═}{{\zeta }_{Ɣ}}=\left({\stackrel{═}{ʊ}}_{Ɣ},\stackrel{═}{{\psi }_{Ɣ}}\right),Ɣ=1,2,\dots ,Ɯ$. If $\stackrel{═}{{\zeta }^{-}}=\left(\mathit{min}\left\{\stackrel{═}{{ʊ}_{Ɣ}}\right\},\mathit{max}\left\{\stackrel{═}{{\psi }_{Ɣ}}\right\}\right)$ and $\stackrel{═}{{\zeta }^{+}}=\left(\mathit{max}\left\{\stackrel{═}{{ʊ}_{Ɣ}}\right\},\mathit{min}\left\{\stackrel{═}{{\psi }_{Ɣ}}\right\}\right)$, then we obtain

$\stackrel{═}{{\zeta }^{-}}\le q-ROFSWPOG\left(\stackrel{═}{{\zeta }_1},\stackrel{═}{{\zeta }_2},\dots ,\stackrel{═}{{\zeta }_{Ɯ}}\right)\le \stackrel{═}{{\zeta }^{+}}.$

5 q-rung orthopair fuzzy Sugeno–Weber geometric aggregation operators

In this section, some robust mathematical aggregation approaches are illustrated considering q-ROF information.

Definition 12. For a class of q-ROFVs $\stackrel{═}{{\zeta }_{Ɣ}}=\left({\stackrel{═}{ʊ}}_{Ɣ},\stackrel{═}{{\psi }_{Ɣ}}\right),Ɣ=1,2,\dots ,Ɯ$, the q-ROFSWPWA operator is characterized as follows:

$q-ROFSWPWA\left(\stackrel{═}{{\zeta }_1},\stackrel{═}{{\zeta }_2},\dots ,\stackrel{═}{{\zeta }_{Ɯ}}\right)=\underset{Ɣ=1}{\overset{Ɯ}{{\displaystyle ⨁}}}{Ώ}_{Ɣ}\stackrel{═}{{\zeta }_{Ɣ}},$

where ${Ώ}_{Ɣ}=\frac{\left(1+A\left(\stackrel{═}{{\zeta }_{Ɣ}}\right)\right)}{{\displaystyle {\sum }_{Ɣ=1}^{Ɯ}}\left(1+A\left(\stackrel{═}{{\zeta }_{Ɣ}}\right)\right)},A\left(\stackrel{═}{{\zeta }_{Ɣ}}\right)={\displaystyle {\sum }_{\begin{array}{c}Ɣ=1\\ Ɣ\ne \tau \end{array}}^{Ɯ}}{\phi }_{Ɣ}Supp\left(\stackrel{═}{{\zeta }_{Ɣ}},\stackrel{═}{{\zeta }_{\tau }}\right),\phi =\left({\phi }_1,{\phi }_2,\dots ,{\phi }_{Ɯ}\right),{\phi }_{Ɣ}>0$, and ${\displaystyle {\sum }_{Ɣ=1}^{Ɯ}}{\phi }_{Ɣ}=1$.

Theorem 17. Consider a class of q-ROFVs $\stackrel{═}{{\zeta }_{Ɣ}}=\left({\stackrel{═}{ʊ}}_{Ɣ},\stackrel{═}{{\psi }_{Ɣ}}\right),Ɣ=1,2,\dots ,Ɯ$. The accumulated value of the q-ROFSWPWA operator is still a q-ROFV, so we obtain

$q-ROFSWPWA\left(\stackrel{═}{{\zeta }_1},\stackrel{═}{{\zeta }_2},\dots ,\stackrel{═}{{\zeta }_{Ɯ}}\right)=\left(\begin{array}{c}\sqrt[q]{\frac{1+Ђ}{Ђ}\left(1-{\displaystyle \prod _{Ɣ=1}^{Ɯ}}{\left(1-\stackrel{═}{{ʊ}_{Ɣ}^q}\left(\frac{Ђ}{1+Ђ}\right)\right)}^{{Ώ}_{Ɣ}}\right)},\\ \sqrt[q]{\frac{1}{Ђ}\left(\left(1+Ђ\right){\displaystyle \prod _{Ɣ=1}^{Ɯ}}{\left(\frac{Ђ\stackrel{═}{{\psi }_{Ɣ}^q}+1}{1+Ђ}\right)}^{{Ώ}_{Ɣ}}-1\right)},\end{array}\right)$

where ${Ώ}_{Ɣ}=\frac{\left(1+A\left(\stackrel{═}{{\zeta }_{Ɣ}}\right)\right)}{{\displaystyle {\sum }_{Ɣ=1}^{Ɯ}}\left(1+A\left(\stackrel{═}{{\zeta }_{Ɣ}}\right)\right)},A\left(\stackrel{═}{{\zeta }_{Ɣ}}\right)={\displaystyle {\sum }_{\begin{array}{c}Ɣ=1\\ Ɣ\ne \tau \end{array}}^{Ɯ}}{\phi }_{Ɣ}Supp\left(\stackrel{═}{{\zeta }_{Ɣ}},\stackrel{═}{{\zeta }_{\tau }}\right),\phi =\left({\phi }_1,{\phi }_2,\dots ,{\phi }_{Ɯ}\right),{\phi }_{Ɣ}>0$, and ${\displaystyle {\sum }_{Ɣ=1}^{Ɯ}}{\phi }_{Ɣ}=1$.

Theorem 18. Consider a class of q-ROFVs $\stackrel{═}{{\zeta }_{Ɣ}}=\left({\stackrel{═}{ʊ}}_{Ɣ},\stackrel{═}{{\psi }_{Ɣ}}\right),Ɣ=1,2,\dots ,Ɯ$, which implies that $\stackrel{═}{{\zeta }_{Ɣ}}=\stackrel{═}{\zeta }$. Then, we obtain

$q-ROFSWPWA\left(\stackrel{═}{{\zeta }_1},\stackrel{═}{{\zeta }_2},\dots ,\stackrel{═}{{\zeta }_{Ɯ}}\right)=\stackrel{═}{\zeta }.$

Theorem 19. Consider any two sets of q-ROFVs $\stackrel{═}{{\zeta }_{Ɣ}}=\left({\stackrel{═}{ʊ}}_{Ɣ},\stackrel{═}{{\psi }_{Ɣ}}\right)$ and $\stackrel{═}{{\zeta }_{Ɣ}^{\prime }}=\left({\stackrel{═}{ʊ}}_{Ɣ}^{\prime },\stackrel{═}{{\psi }_{Ɣ}^{\prime }}\right),Ɣ=1,2,\dots ,Ɯ$. If $\stackrel{═}{{\zeta }_{Ɣ}}\le \stackrel{═}{{\zeta }_{Ɣ}^{\prime }}$, then we obtain

$q-ROFSWPWA\left(\stackrel{═}{{\zeta }_1},\stackrel{═}{{\zeta }_2},\dots ,\stackrel{═}{{\zeta }_{Ɯ}}\right)\le q-ROFSWPWA\left(\stackrel{═}{{\zeta }_1^{\prime }},\stackrel{═}{{\zeta }_2^{\prime }},\dots ,\stackrel{═}{{\zeta }_{Ɯ}^{\prime }}\right).$

Theorem 20. Consider a class of q-ROFVs $\stackrel{═}{{\zeta }_{Ɣ}}=\left({\stackrel{═}{ʊ}}_{Ɣ},\stackrel{═}{{\psi }_{Ɣ}}\right),Ɣ=1,2,\dots ,Ɯ$. If $\stackrel{═}{{\zeta }^{-}}=\left(\mathit{min}\left\{\stackrel{═}{{ʊ}_{Ɣ}}\right\},\mathit{max}\left\{\stackrel{═}{{\psi }_{Ɣ}}\right\}\right)$ and $\stackrel{═}{{\zeta }^{+}}=\left(\mathit{max}\left\{\stackrel{═}{{ʊ}_{Ɣ}}\right\},\mathit{min}\left\{\stackrel{═}{{\psi }_{Ɣ}}\right\}\right)$, then we obtain

$\stackrel{═}{{\zeta }^{-}}\le q-ROFSWPWA\left(\stackrel{═}{{\zeta }_1},\stackrel{═}{{\zeta }_2},\dots ,\stackrel{═}{{\zeta }_{Ɯ}}\right)\le \stackrel{═}{{\zeta }^{+}}.$

Definition 13. For a class of q-ROFVs $\stackrel{═}{{\zeta }_{Ɣ}}=\left({\stackrel{═}{ʊ}}_{Ɣ},\stackrel{═}{{\psi }_{Ɣ}}\right),Ɣ=1,2,\dots ,Ɯ$, the q-ROFSWPWG operator is characterized as follows:

$q-ROFSWPWG\left(\stackrel{═}{{\zeta }_1},\stackrel{═}{{\zeta }_2},\dots ,\stackrel{═}{{\zeta }_{Ɯ}}\right)=\underset{Ɣ=1}{\overset{Ɯ}{{\displaystyle ⨂}}}{\stackrel{═}{{\zeta }_{Ɣ}}}^{{Ώ}_{Ɣ}},$

where ${Ώ}_{Ɣ}=\frac{\left(1+A\left(\stackrel{═}{{\zeta }_{Ɣ}}\right)\right)}{{\sum }_{Ɣ=1}^{Ɯ}\left(1+A\left(\stackrel{═}{{\zeta }_{Ɣ}}\right)\right)},A\left(\stackrel{═}{{\zeta }_{Ɣ}}\right)={\displaystyle {\sum }_{\begin{array}{c}Ɣ=1\\ Ɣ\ne \tau \end{array}}^{Ɯ}}{\phi }_{Ɣ}Supp\left(\stackrel{═}{{\zeta }_{Ɣ}},\stackrel{═}{{\zeta }_{\tau }}\right),\phi =\left({\phi }_1,{\phi }_2,\dots ,{\phi }_{Ɯ}\right),{\phi }_{Ɣ}>0$, and ${\displaystyle {\sum }_{Ɣ=1}^{Ɯ}}{\phi }_{Ɣ}=1$.

Theorem 21. Consider a class of q-ROFVs $\stackrel{═}{{\zeta }_{Ɣ}}=\left({\stackrel{═}{ʊ}}_{Ɣ},\stackrel{═}{{\psi }_{Ɣ}}\right),Ɣ=1,2,\dots ,Ɯ$. The accumulated value of the q-ROFSWPWG operator is still a q-ROFV, so we obtain

$q-ROFSWPWG\left(\stackrel{═}{{\zeta }_1},\stackrel{═}{{\zeta }_2},\dots ,\stackrel{═}{{\zeta }_{Ɯ}}\right)=\left(\begin{array}{c}\sqrt[q]{\frac{1}{Ђ}\left(\left(1+Ђ\right){\displaystyle \prod _{Ɣ=1}^{Ɯ}}{\left(\frac{Ђ\stackrel{═}{{ʊ}_{Ɣ}^q}+1}{1+Ђ}\right)}^{{Ώ}_{Ɣ}}-1\right)},\\ \sqrt[q]{\frac{1+Ђ}{Ђ}\left(1-{\displaystyle \prod _{Ɣ=1}^{Ɯ}}{\left(1-\stackrel{═}{{\psi }_{Ɣ}^q}\left(\frac{Ђ}{1+Ђ}\right)\right)}^{{Ώ}_{Ɣ}}\right)}.\end{array}\right)$

Theorem 22. Consider a class of q-ROFVs $\stackrel{═}{{\zeta }_{Ɣ}}=\left({\stackrel{═}{ʊ}}_{Ɣ},\stackrel{═}{{\psi }_{Ɣ}}\right),Ɣ=1,2,\dots ,Ɯ$, which implies that $\stackrel{═}{{\zeta }_{Ɣ}}=\stackrel{═}{\zeta }$. Then we obtain

$q-ROFSWPWG\left(\stackrel{═}{{\zeta }_1},\stackrel{═}{{\zeta }_2},\dots ,\stackrel{═}{{\zeta }_{Ɯ}}\right)=\stackrel{═}{\zeta }.$

Theorem 23. For any two sets of q-ROFVs, $\stackrel{═}{{\zeta }_{Ɣ}}=\left({\stackrel{═}{ʊ}}_{Ɣ},\stackrel{═}{{\psi }_{Ɣ}}\right)$ and $\stackrel{═}{{\zeta }_{Ɣ}^{\prime }}=\left({\stackrel{═}{ʊ}}_{Ɣ}^{\prime },\stackrel{═}{{\psi }_{Ɣ}^{\prime }}\right),Ɣ=1,2,\dots ,Ɯ$. If $\stackrel{═}{{\zeta }_{Ɣ}}\le \stackrel{═}{{\zeta }_{Ɣ}^{\prime }}$, then we obtain

$q-ROFSWPWG\left(\stackrel{═}{{\zeta }_1},\stackrel{═}{{\zeta }_2},\dots ,\stackrel{═}{{\zeta }_{Ɯ}}\right)\le q-ROFSWPWG\left(\stackrel{═}{{\zeta }_1^{\prime }},\stackrel{═}{{\zeta }_2^{\prime }},\dots ,\stackrel{═}{{\zeta }_{Ɯ}^{\prime }}\right).$

Theorem 24. Consider a class of q-ROFVs $\stackrel{═}{{\zeta }_{Ɣ}}=\left({\stackrel{═}{ʊ}}_{Ɣ},\stackrel{═}{{\psi }_{Ɣ}}\right),Ɣ=1,2,\dots ,Ɯ$. If $\stackrel{═}{{\zeta }^{-}}=\left(\mathit{min}\left\{\stackrel{═}{{ʊ}_{Ɣ}}\right\},\mathit{max}\left\{\stackrel{═}{{\psi }_{Ɣ}}\right\}\right)$ and $\stackrel{═}{{\zeta }^{+}}=\left(\mathit{max}\left\{\stackrel{═}{{ʊ}_{Ɣ}}\right\},\mathit{min}\left\{\stackrel{═}{{\psi }_{Ɣ}}\right\}\right)$, then we obtain

$\stackrel{═}{{\zeta }^{-}}\le q-ROFSWPWG\left(\stackrel{═}{{\zeta }_1},\stackrel{═}{{\zeta }_2},\dots ,\stackrel{═}{{\zeta }_{Ɯ}}\right)\le \stackrel{═}{{\zeta }^{+}}.$

6 An innovative approach to the MADM problem based on q-ROF information

The objective of this section is to explore notable optimal options using the proposed methodologies under the system of the MADM problem. To serve this purpose, assume a set of finite alternatives $\mathfrak{M}=\left({\mathfrak{M}}_{\mathbf{1}},{\mathfrak{M}}_{\mathbf{2}},\dots ,{\mathfrak{M}}_{\mathit{m}}\right)$ and a class of finite characteristics $\mathfrak{S}=\left({\mathfrak{S}}_{\mathbf{1}},{\mathfrak{S}}_{\mathbf{2}},\dots ,{\mathfrak{S}}_{\mathit{n}}\right)$ with some specific degrees of criteria $\mathbf{\Delta }=\left({\mathbf{\Delta }}_{\mathbf{1}},{\mathbf{\Delta }}_{\mathbf{2}},\dots ,{\mathbf{\Delta }}_{\mathbf{n}}\right)$ as ${\mathbf{\Delta }}_{\mathbf{\iota }}>\mathbf{0}$ and ${\displaystyle {\sum }_{\mathbf{\iota }=\mathbf{1}}^{\mathit{n}}}{\mathbf{\Delta }}_{\mathbf{\iota }}=\mathbf{1}$. The decision-maker acquired information about an object in the form of q-ROF $\mathbf{\Sigma }=\left({\stackrel{═}{\mathit{ʊ}}}_{\mathit{Ɣ}\mathbf{\iota }},\stackrel{═}{{\mathit{\psi }}_{\mathit{Ɣ}\mathbf{\iota }}}\right)$ situations with restricted constraints $\mathbf{0}\le {\stackrel{═}{\mathit{ʊ}}}_{\mathit{Ɣ}\mathbf{\iota }}^{\mathit{q}}+\stackrel{═}{{\mathit{\psi }}_{\mathit{Ɣ}\mathbf{\iota }}^{\mathit{q}}}\le \mathbf{1}$. All collected information is listed in the decision matrix $\mathfrak{R}={\left({\mathbf{\Sigma }}_{\mathit{Ɣ}\mathbf{\iota }}\right)}_{\mathit{m}\times \mathit{n}}={\left({\stackrel{═}{\mathit{ʊ}}}_{\mathit{Ɣ}\mathbf{\iota }},\stackrel{═}{{\mathit{\psi }}_{\mathit{Ɣ}\mathbf{\iota }}}\right)}_{\mathit{m}\times \mathit{n}}$. The evaluation procedure of the q-ROF information is summarized based on the following algorithm of the MADM problem. Figure 2 shows the flowchart of the algorithm.

FIGURE 2

FIGURE 2. Flowchart of the algorithm.

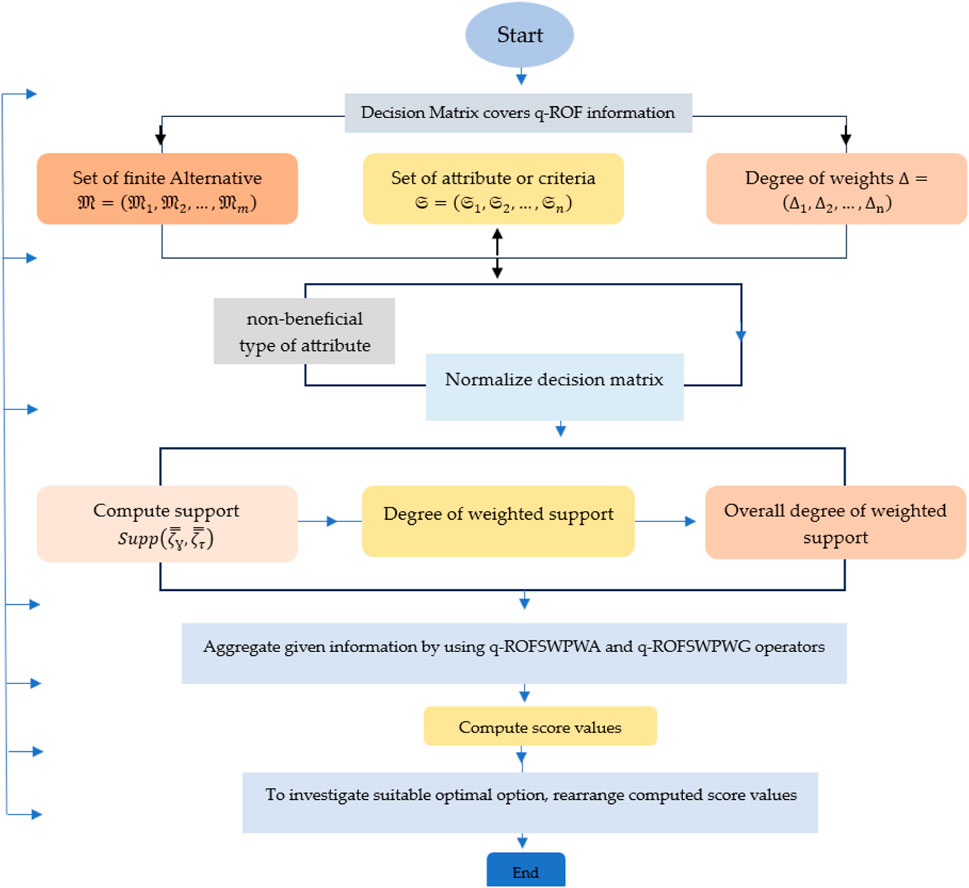
6.1 Algorithm

Step 1: The decision-maker constructs a decision matrix $\mathfrak{R}={\left({\mathrm{\Sigma }}_{Ɣ\mathrm{\iota }}\right)}_{m\times n}={\left({\stackrel{═}{ʊ}}_{Ɣ\mathrm{\iota }},\stackrel{═}{{\psi }_{Ɣ\mathrm{\iota }}}\right)}_{m\times n},Ɣ=1,2,\dots ,m,\mathrm{\iota }=1,2,\dots ,n$ having q-ROF information.

Step 2: Generally, collected information about an object is divided into two types: beneficial and non-beneficial. Before the aggregation process, we must transform the standard decision matrix into a normalized decision matrix using the following formula:

$\mathfrak{R}=\left\{\begin{array}{cc}\left({\stackrel{═}{ʊ}}_{Ɣ\mathrm{\iota }},\stackrel{═}{{\psi }_{Ɣ\mathrm{\iota }}}\right),& ifbeneficialtype,\\ \left(\stackrel{═}{{\psi }_{Ɣ\mathrm{\iota }}},{\stackrel{═}{ʊ}}_{Ɣ\mathrm{\iota }}\right),& ifnon-beneficialtype,\end{array}\right.$

Step 3: Using the following formulas, the support of all individuals is computed:

$Supp\left(\stackrel{═}{{\zeta }_{Ɣ}},\stackrel{═}{{\zeta }_{\tau }}\right)=1-D\left(\stackrel{═}{{\zeta }_{Ɣ}},\stackrel{═}{{\zeta }_{\tau }}\right)$

and

$D\left(\stackrel{═}{{\zeta }_{Ɣ}},\stackrel{═}{{\zeta }_{\tau }}\right)=\frac{1}{2}\left(\left|{\stackrel{═}{{ʊ}^q}}_{Ɣ}-{\stackrel{═}{{ʊ}^q}}_{\tau }\right|+\left|\stackrel{═}{{\psi }_{Ɣ}^q}-\stackrel{═}{{\psi }_{\tau }^q}\right|\right).$

Step 4: The degree of support related to each alternative $Ɣ=1,2,\dots ,m,\mathrm{\iota }=1,2,\dots ,n$ is computed.

$A\left(\stackrel{═}{{\mathcal{F}}_{Ɣ}}\right)={\displaystyle \sum _{\begin{array}{c}Ɣ=1\\ Ɣ\ne \tau \end{array}}^{\mathcal{n}}}{ʊ}_{Ɣ}Supp\left(\stackrel{═}{{\zeta }_{Ɣ}},\stackrel{═}{{\zeta }_{\tau }}\right),$

where $A\left(\stackrel{═}{{\mathcal{F}}_{Ɣ}}\right)={\displaystyle {\sum }_{\begin{array}{c}Ɣ=1\\ Ɣ\ne \tau \end{array}}^{\mathcal{n}}}{ʊ}_{Ɣ}Supp\left(\stackrel{═}{{\zeta }_{Ɣ}},\stackrel{═}{{\zeta }_{\tau }}\right),ʊ=\left({ʊ}_1,{ʊ}_2,\dots ,{ʊ}_{\mathcal{n}}\right),{ʊ}_{Ɣ}>0$, and ${\sum }_{Ɣ=1}^{\mathcal{n}}{ʊ}_{Ɣ}=1$.

Step 5: The degree of weighted support associated with all alternatives is investigated.Here, ${Ώ}_{Ɣ\mathrm{\iota }}=\frac{{ʊ}_{Ɣ}\left(1+A\left(\stackrel{═}{{\zeta }_{Ɣ}}\right)\right)}{{\displaystyle {\sum }_{Ɣ=1}^n}{ʊ}_{Ɣ}\left(1+A\left(\stackrel{═}{{\zeta }_{Ɣ}}\right)\right)},Ɣ=1,2,\dots ,m$.

Step 6: The given information is aggregated using the q-ROFSWPA, q-ROFSWPG, q-ROFSWPWA, and q-ROFSWPWG operators.

Step 7: To find realistic optimal options, the score values of all individuals are investigated.

Step 8: All score values are rearranged considering the ranking and ordering technique.

6.2 Positive impact of renewable energy

The sun provides energy for all life on Earth. This incredible source generates energy and gives out heat and light by fusing hydrogen and helium at its center. It is known as solar radiation. Only approximately half of the total intensity of this solar energy reaches the surface of Earth. The remaining energy is reflected back or absorbed by the atmosphere and clouds. To supply all of the human energy needs, the sun still delivers more than enough energy. The energy that comes from the sun is abundant, unrestricted, and clean.

Numerous industrial and commercial processes, such as solar cooling, hot water heating, and power generation, can directly utilize solar energy. The fact that solar power generation is an environmentally friendly alternative to electricity produced using fossil fuels, with no risk of rise in electricity price, no air or water pollution, and no threat to public health, is essential given the growing concern over climate change.

Harmful substances like carbon dioxide are generated when fossil fuels are burned to create energy. Burning fossil fuels produce more emissions than generating power from renewable sources. The most effective strategy to lessen the risks caused by climate change is to reduce the consumption of fossil fuels, which, at this point, are the main source of emissions. Fossil fuels, such as coal, oil, and natural gas, accounted for approximately 80% of the world’s energy supply at the beginning of the 21st century. Although most estimates show that the proven oil reserves are enough to supply the world’s demand, fossil fuels are scarce resources, at least through the middle of the 21st century. Using fossil fuels has serious repercussions on the environment. In addition, nitrogen oxides, carbon monoxide, particulate matter, and toxic chemicals (including heavy metals, such as mercury, chromium, and arsenic) are released by fossil-fueled power plants and mobile sources, such as fossil-fueled autos. Human exposure to these toxins can develop heart disease, asthma, and other health difficulties. Furthermore, acid rain, which is caused by emissions from burning fossil fuels, has a devastating effect on aquatic life and vegetation and increased soil pollution in or near numerous metropolitan areas. Carbon dioxide (CO2), created from fossil fuel combustion, is one of the main greenhouse gases contributing to global warming.

Numerous research scholars classified different renewable energy resources to handle the energy crisis and introduced an empowered power sector. For instance, Hendiani and Walther (2023) studied some appropriate sources of renewable energy enterprises based on the interval type-2 fuzzy theory and decision-making process. By utilizing previously developed strategies in the literature, Gupta et al. (2023) evaluated reliable energy sources using an advanced decision-making approach based on the VIKOR method. By combining two different theories of t-spherical fuzzy sets and hypersoft sets, Monika et al. (2023) discussed an application of renewable energy sources based on certain characteristics. Riaz et al. (2023) utilized the characteristics of cubic bipolar fuzzy theory and entropy measures based on Einstein t-norms. Recently, numerous research scholars have focused on solar energy and renewable energy to enhance the source of electric power (Li et al., 2013; Kutlu Gündoğdu and Kahraman, 2020; Liu et al., 2021; Seker and Kahraman, 2021; Akram et al., 2022; Naeem and Ali, 2022). To serve this purpose, decision-makers face challenges in choosing an appropriate solar panel or solar cell under specific criteria or characteristics.

6.3 Experimental case study

In this case study, the decision-maker evaluates different types of solar panels considering the discussed algorithm of the MADM problem. The q-ROF environment is an effective and feasible aggregation model, which is the extended version of FSs and IFSs. Consider five different types of solar panels manufactured by different companies which are stated as follows:

${\mathit{T}}_{\mathbf{1}}$: monocrystalline panels,

${\mathit{T}}_{\mathbf{2}}$: polycrystalline panels,

${\mathit{T}}_{\mathbf{3}}$: perovskite panels,

${\mathit{T}}_{\mathbf{4}}$: transparent panels, and

${\mathit{T}}_{\mathbf{5}}$: concentrator photovoltaic panels.

The abovementioned different types of solar panels are evaluated under certain characteristics, which are explained as follows:

${\mathit{J}}_{\mathbf{1}}$: quality of the manufacturing material,

${\mathit{J}}_{\mathbf{2}}$: availability of the solar panel,

${\mathit{J}}_{\mathbf{3}}$: easy to install and high performance at low sunlight, and

${\mathit{J}}_{\mathbf{4}}$: low maintenance rate.

The decision-maker evaluates the information related to solar panels considering the above-discussed properties. Some particular degree of weight is assigned to the criteria $\left(\mathbf{0.17},\mathbf{0.32},\mathbf{0.28},\mathbf{0.23}\right)$ by the decision-maker hypothetically. By utilizing the proposed methodologies, the decision-maker evaluates an appropriate construction material based on the proposed algorithm of the MADM process.

6.4 Evaluation procedure of the decision-making process

Based on the above algorithm of the MADM problem, we applied derived methodologies of the q-ROFSWPWA and q-ROFSWPWG operators for the evaluation of a suitable optimal option considering some reliable characteristics.

Step 1: The decision-maker accumulates information about solar panels and states it in the decision matrix shown in Table 2.

TABLE 2

TABLE 2. Information about green supplier agents.

Step 2: The discussed experimental case study carried only one type of information (beneficial). So there is no need to transform the standard decision matrix into a normalized decision matrix.

Step 3: Support is computed using the following expression:

$Supp\left(\stackrel{═}{{\zeta }_{Ɣ}},\stackrel{═}{{\zeta }_{\tau }}\right)=1-D\left(\stackrel{═}{{\zeta }_{Ɣ}},\stackrel{═}{{\zeta }_{\tau }}\right)$

and

$D\left(\stackrel{═}{{\zeta }_{Ɣ}},\stackrel{═}{{\zeta }_{\tau }}\right)=\frac{1}{2}\left(\left|{\stackrel{═}{{ʊ}^q}}_{Ɣ}-{\stackrel{═}{{ʊ}^q}}_{\tau }\right|+\left|\stackrel{═}{{\psi }_{Ɣ}^q}-\stackrel{═}{{\psi }_{\tau }^q}\right|\right),Ɣ=1,2,\dots ,m,\mathrm{\iota }=1,2,\dots ,n.$

Step 4: Support is computed using the following distance formula.

Step 5: The degree of support related to each alternative $Ɣ=1,2,\dots ,m,\mathrm{\iota }=1,2,\dots ,n$ is investigated.

$A\left(\stackrel{═}{{\mathcal{F}}_{Ɣ}}\right)={\displaystyle \sum _{\begin{array}{c}Ɣ=1\\ Ɣ\ne \tau \end{array}}^{\mathcal{n}}}{ʊ}_{Ɣ}Supp\left(\stackrel{═}{{\zeta }_{Ɣ}},\stackrel{═}{{\zeta }_{\tau }}\right),$

where $A\left(\stackrel{═}{{\mathcal{F}}_{Ɣ}}\right)={\displaystyle {\sum }_{\begin{array}{c}Ɣ=1\\ Ɣ\ne \tau \end{array}}^{\mathcal{n}}}{ʊ}_{Ɣ}Supp\left(\stackrel{═}{{\zeta }_{Ɣ}},\stackrel{═}{{\zeta }_{\tau }}\right),ʊ=\left({ʊ}_1,{ʊ}_2,\dots ,{ʊ}_{\mathcal{n}}\right),{ʊ}_{Ɣ}>0$, and ${\displaystyle {\sum }_{Ɣ=1}^{\mathcal{n}}}{ʊ}_{Ɣ}=1$.

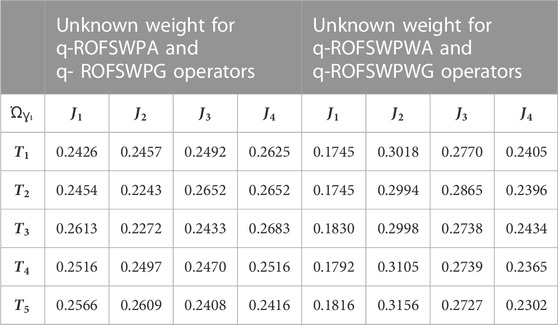
Step 5: Using Steps 3–5, the degree of weighted support related to overall individuals is computed.Here, ${Ώ}_{Ɣ\iota }=\frac{{ʊ}_{Ɣ}\left(1+A\left(\stackrel{═}{{\zeta }_{Ɣ}}\right)\right)}{{\displaystyle {\sum }_{Ɣ=1}^n}{ʊ}_{Ɣ}\left(1+A\left(\stackrel{═}{{\zeta }_{Ɣ}}\right)\right)}$.

Table 3 shows computed degree of unknown weights.

TABLE 3

TABLE 3. Shows computed degree of unknown weights.

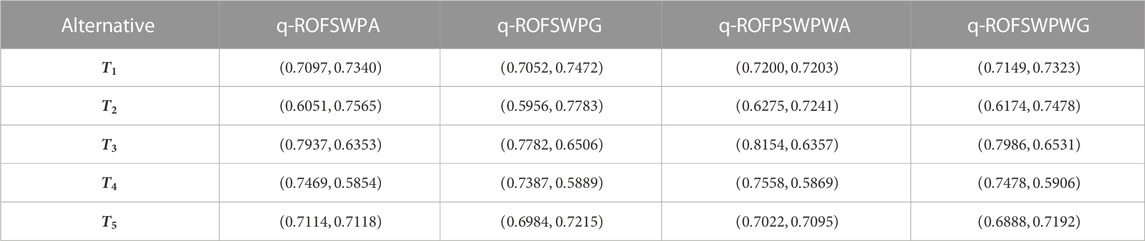
Step 6: Our invented approaches are applied to aggregate the given information, and Table 4 shows all investigated outcomes from the proposed methodologies.

TABLE 4

TABLE 4. Covered computed results from invented approaches.

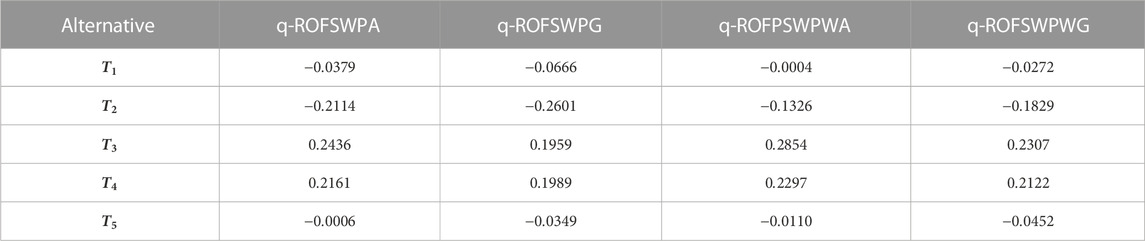
Step 7: Definition 5 is used to compute the score values of all individuals, and the values are listed as shown in Table 5.

TABLE 5

TABLE 5. Covered score values corresponding to each alternative.

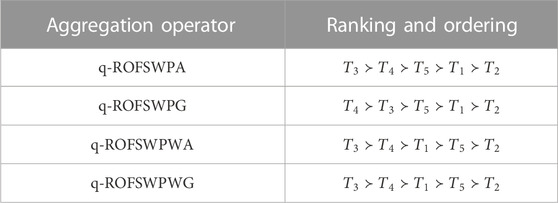
Step 8: To examine an appropriate individual, all score values are rearranged using the ranking and ordering technique. Table 6 shows the ranking and ordering of all individuals, which are investigated using our invented methodologies.

TABLE 6

TABLE 6. Covers the ranking of score values.

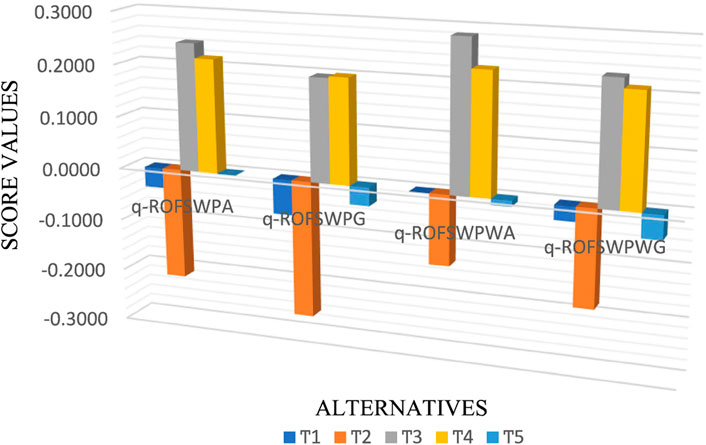
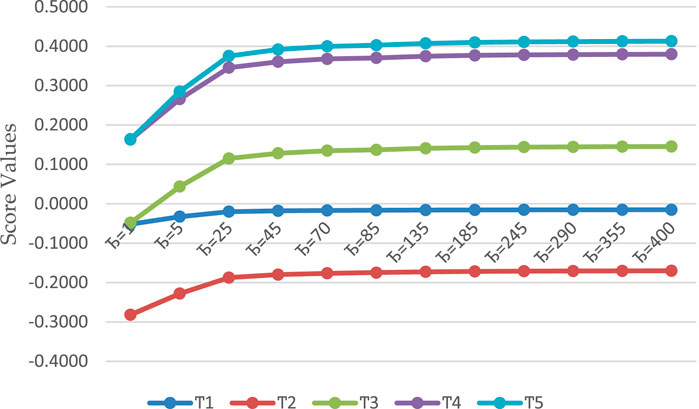
The graphical representation of Figure 3 shows the geometrical behavior of the computed score values, which are listed in Table 5.

FIGURE 3

FIGURE 3. Shows the findings of our proposed aggregation approaches.

6.5 Impact of different parametric values on the results of proposed methodologies

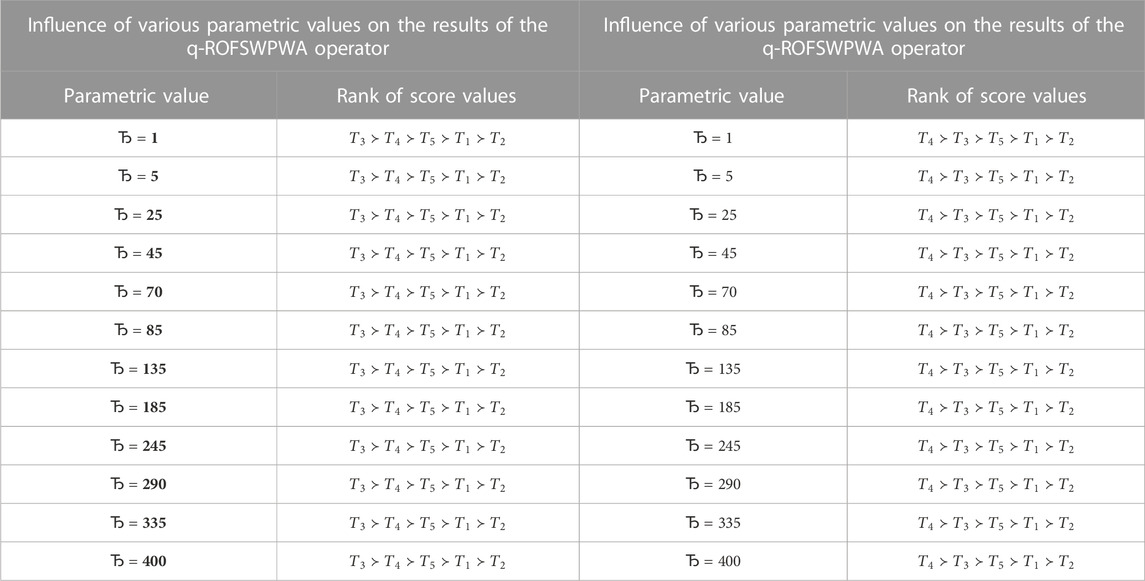
We demonstrate an appropriate optimal option during the decision-making process. In this discussion, we explore the results of the proposed methodologies by assigning different parametric values of the Sugeno–Weber aggregation tools in q-ROFSWPWA and q-ROFSWPWG operators. When we increase the parametric values of the Sugeno–Weber triangular norms, acquired results of the score values using the q-ROFSWPWA operator begin to increase, and the ranking of score values remains unchanged throughout this process: $T_4\succ T_3\succ T_5\succ T_1\succ T_2$. Similarly, we observed the outcomes of the q-ROFSWPWG operator by setting different parametric values of the Sugeno–Weber triangular norm. When we increase the parametric value of the Sugeno–Weber triangular norms in the q-ROFSWPWG operator, investigated results begin to decrease, and the ranking of score values remains the same: ${\mathit{T}}_{\mathbf{4}}\succ {\mathit{T}}_{\mathbf{3}}\succ {\mathit{T}}_{\mathbf{5}}\succ {\mathit{T}}_{\mathbf{1}}\succ {\mathit{T}}_{\mathbf{2}}$. All investigated results of the q-ROFSWPWA and q-ROFSWPWG operators are listed in Table 7.

TABLE 7

TABLE 7. Results of the q-ROFSWPWA operator for different parametric values of $\mathit{Ђ}$.

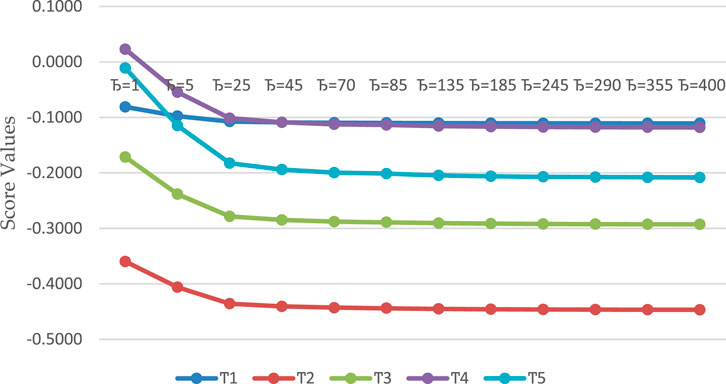
After a deep analysis of the obtained score values using the q-ROFSWPWA and q-ROFSWPWG operators listed in Table 7, our proposed aggregation approaches are shown to be superior to other existing approaches. Figure 4 and Figure 5 show the geometrical behavior of the computed score values using the q-ROFSWPWA and q-ROFSWPWG operators, respectively.

FIGURE 4

FIGURE 4. Influence of various parametric values on the results of the q-ROFSWPWA operator.

FIGURE 5

FIGURE 5. Influence of various parametric values on the results of the q-ROFSWPWG operator.

7 Comparative analysis

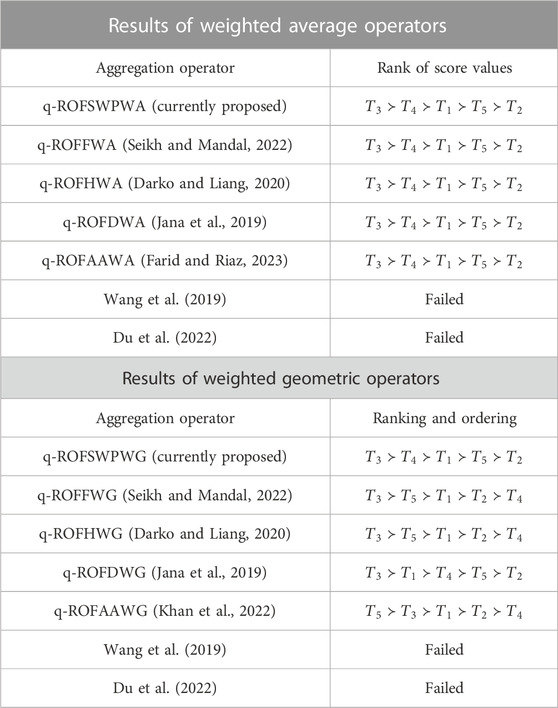
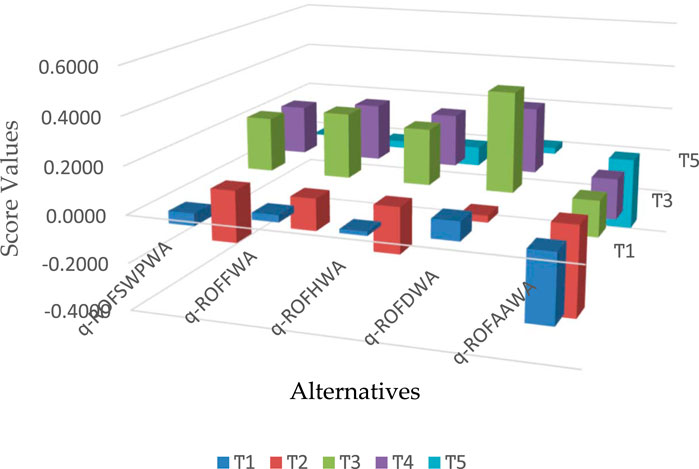
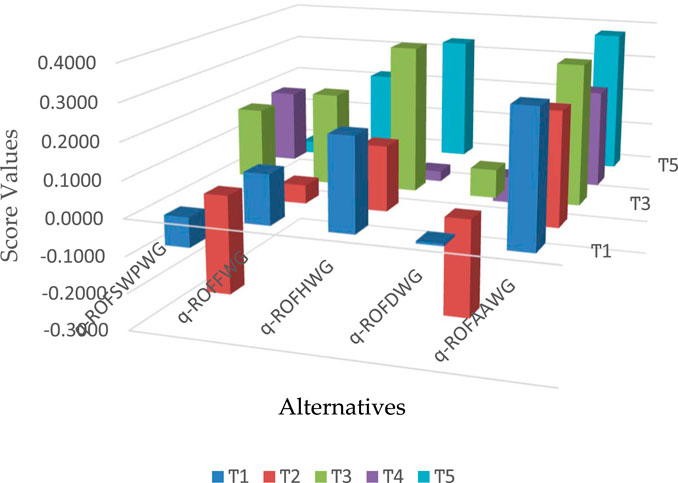
This section covers the advantages of the proposed aggregation approaches by applying the experimental case study. The q-ROFS is a moderate aggregation model, allowing the decision-maker to investigate optimal options during decision-making. In order to verify the applicability of the proposed approaches, we applied existing approaches developed by different mathematicians such as Jana et al. (2019), Wang et al. (2019), Darko and Liang (2020), Du et al. (2022), Khan et al. (2022), Seikh and Mandal (2022), and Farid and Riaz (2023). The Hamacher aggregation tools with some realistic properties were generalized by Darko and Liang (2020), and a list of new approaches based on the q-rung orthopair fuzzy environments was developed. Seikh and Mandal (2022) modified a series of new approaches by expanding the theory of Frank aggregation tools like q-ROF Frank weighted average (q-ROFFWA) and q-ROF Frank weighted geometric (q-ROFFWG) operators. Jana et al. (2019) demonstrated a list of AOs based on Dombi triangular norms such as q-ROF Dombi weighted average (q-ROFDWA) and q-ROF Dombi weighted geometric (q-ROFDWG) operators. Properties of Aczel–Alsina aggregation tools were explored by Farid and Riaz (2023) to develop a list of new approaches, namely, q-ROF Aczel–Alsina weighted average (q-ROFAAWA) operator, and Khan et al. (2022) introduced AOs of the q-ROF Aczel–Alsina weighted geometric (q-ROFAAWG) operator. Wang et al. (2019) extended the theory of q-ROFS in the form of complex q-ROF environments, and Du et al. (2022) utilized the concepts of Frank aggregation tools based on complex q-ROF systems. After the aggregation process, the results are computed using existing methodologies as listed in Table 8. The graphical structure of computed score values using existing weighted average and weighted geometric operators are shown in Figure 6 and Figure 7, respectively.

TABLE 8

TABLE 8. Results of existing approaches.

FIGURE 6

FIGURE 6. Comparison between existing weighted average operators in the comparative study.

FIGURE 7

FIGURE 7. Graphical representation of the score values using existing weighted geometric operators.

We observed that our proposed methodologies are superior to other existing approaches and can greatly reduce the impact of redundant information. Another realistic quality of the discussed approaches is that they provide liberty to the decision-makers for achieving effective results according to their own preferences.

8 Conclusion

This article aims to explore the theory of the MADM problem to resolve unpredictable information in real-life situations. To mitigate the impact of unpredictable information on human opinions, we studied several aggregation methodologies presented by different mathematicians. We also explored the theory of Sugeno–Weber triangular norms to develop some realistic operations of Sugeno–Weber t-norm and t-conorms. The basic operations of Sugeno–Weber t-norms and t-conorms are powerful and efficient aggregation tools, providing authentic estimated information during decision-making. We developed a class of new methodologies considering q-ROF information, including q-ROFSWPWA and q-ROFSWPWG operators with some reliable characteristics. To reveal the efficiency and consistency of the proposed aggregation technique, we illustrated an algorithm for the MADM problem. We demonstrated an experimental case study to select a suitable solar panel considering some dominant criteria or characteristics. The influence study also presented the applicability of the derived approaches and comparative analysis verified by contrasting the results of the existing approaches with currently developed aggregation techniques.

Although there are many advantages of the system of q-ROF environments, they sometimes fail to handle unpredictable information of human opinions. For instance, if information is given in three components like SG, abstinence degree, and DSG, then discussed environments, PyFSs, and IFS cannot deal with such type of information. To overcome this situation, the decision-maker considers robust environments like picture fuzzy sets (PFSs), spherical fuzzy sets (SFSs), and T-spherical fuzzy sets (T-SFSs). Cuong (2013) and Mahmood et al. (2019) introduced the theories of PFSs and spherical FSs. Several mathematicians utilized the notions of PFSs, SFSs, and T-SFSs to develop several mathematical approaches to solving different real-life situations. We try to solve complicated real-life situations like pattern recognition, emerging technologies, renewable energy, medical diagnosis, and artificial intelligence. Furthermore, we will extend our proposed research work in the framework of different fuzzy environments like bipolar soft sets (Mahmood, 2020), complex bipolar soft sets (Mahmood and Ur Rehman, 2022), and linear diophantine fuzzy sets (Riaz and Hashmi, 2019).

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

YW: formal analysis, funding acquisition, project administration, and writing–review and editing. AH: conceptualization, investigation, software, validation, writing–original draft, and writing–review and editing. SY: data curation, project administration, resources, validation, and writing–review and editing. KU: conceptualization, investigation, supervision, validation, and writing–review and editing. DB: investigation, methodology, project administration, visualization, and writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This research was supported by the Top Young Talents Scientific Research Project of Higher Education in Hebei Province under grant number BJ2021084.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Akram, M., Khan, A., and Borumand Saeid, A. (2021). Complex Pythagorean Dombi fuzzy operators using aggregation operators and their decision-making. Expert Syst. 38 (2), e12626. Available at:. doi:10.1111/exsy.12626

CrossRef Full Text | Google Scholar

Akram, M., Naz, S., and Abbas, T. (2023). Complex q-rung orthopair fuzzy 2-tuple linguistic group decision-making framework with Muirhead mean operators. Artif. Intell. Rev. 56, 10227–10274. doi:10.1007/s10462-023-10408-4

CrossRef Full Text | Google Scholar

Akram, M., and Shahzadi, G. (2021). Decision-making approach based on Pythagorean Dombi fuzzy soft graphs. Granul. Comput. 6 (3), 671–689. doi:10.1007/s41066-020-00224-4

CrossRef Full Text | Google Scholar

Akram, M., Ullah, K., and Pamucar, D. (2022). Performance evaluation of solar energy cells using the interval-valued T-spherical fuzzy Bonferroni mean operators. Energies 15 (1), 292. doi:10.3390/en15010292

CrossRef Full Text | Google Scholar

Al-Barakati, A., Mishra, A. R., Mardani, A., and Rani, P. (2022). An extended interval-valued Pythagorean fuzzy WASPAS method based on new similarity measures to evaluate the renewable energy sources. Appl. Soft Comput. 120, 108689. doi:10.1016/j.asoc.2022.108689

CrossRef Full Text | Google Scholar

Alcantud, J. C. R., Khameneh, A. Z., and Kilicman, A. (2020). Aggregation of infinite chains of intuitionistic fuzzy sets and their application to choices with temporal intuitionistic fuzzy information. Inf. Sci. 514, 106–117. Available at:. doi:10.1016/j.ins.2019.12.008

CrossRef Full Text | Google Scholar

Atanassov, K. T. (1986). Intuitionistic fuzzy sets. Fuzzy Sets Syst. 20 (1), 87–96. Available at:. doi:10.1016/S0165-0114(86)80034-3

CrossRef Full Text | Google Scholar

Atanassov, K. T. (1989). More on intuitionistic fuzzy sets. Fuzzy Sets Syst. 33 (1), 37–45. Available at:. doi:10.1016/0165-0114(89)90215-7

CrossRef Full Text | Google Scholar

Ateş, F., and Akay, D. (2020). Some picture fuzzy Bonferroni mean operators with their application to multicriteria decision making. Int. J. Intelligent Syst. 35 (4), 625–649. doi:10.1002/int.22220

CrossRef Full Text | Google Scholar

Bessa, R., and Matos, M. A. (2012). Economic and technical management of an aggregation agent for electric vehicles: a literature survey. Eur. Trans. Electr. Power 22 (3), 334–350. doi:10.1002/etep.565

CrossRef Full Text | Google Scholar

Çolak, A. B., Sindhu, T. N., Lone, S. A., Shafiq, A., and Abushal, T. A. (2023). Reliability study of generalized Rayleigh distribution based on inverse power law using artificial neural network with Bayesian regularization. Tribol. Int. 185, 108544. doi:10.1016/j.triboint.2023.108544

CrossRef Full Text | Google Scholar

Cuong, B. C. (2013). “Picture fuzzy sets-first results. part 1, seminar neuro-fuzzy systems with applications,” in Proceedings of the Third World Congress on Information and Communication Technologies WICT'2013, Hanoi, Vietnam, December, 2013.

Google Scholar

Darko, A. P., and Liang, D. (2020). Some q-rung orthopair fuzzy Hamacher aggregation operators and their application to multiple attribute group decision making with modified EDAS method. Eng. Appl. Artif. Intell. 87, 103259. doi:10.1016/j.engappai.2019.103259

CrossRef Full Text | Google Scholar

Du, Y., Du, X., Li, Y., Cui, J. x., and Hou, F. (2022). Complex q-rung orthopair fuzzy Frank aggregation operators and their application to multi-attribute decision making. Soft Comput. 26 (22), 11973–12008. Available at:. doi:10.1007/s00500-022-07465-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Farid, H. M. A., and Riaz, M. (2023). q-rung orthopair fuzzy Aczel–Alsina aggregation operators with multi-criteria decision-making. Eng. Appl. Artif. Intell. 122, 106105. doi:10.1016/j.engappai.2023.106105

CrossRef Full Text | Google Scholar

Garg, H. (2020). A novel trigonometric operation-based q-rung orthopair fuzzy aggregation operator and its fundamental properties. Neural Comput. Appl. 32 (18), 15077–15099. doi:10.1007/s00521-020-04859-x

CrossRef Full Text | Google Scholar

Garg, H., and Kumar, K. (2020). Power geometric aggregation operators based on connection number of set pair analysis under intuitionistic fuzzy environment. Arabian J. Sci. Eng. 45 (3), 2049–2063. doi:10.1007/s13369-019-03961-0

CrossRef Full Text | Google Scholar

Gupta, P., Mehlawat, M. K., and Ahemad, F. (2023). Selection of renewable energy sources: a novel VIKOR approach in an intuitionistic fuzzy linguistic environment. Environ. Dev. Sustain. 25 (4), 3429–3467. Available at:. doi:10.1007/s10668-022-02172-2

CrossRef Full Text | Google Scholar

Hendiani, S., and Walther, G. (2023). Sustainability performance evaluation of renewable energy systems using a new multi-expert multi-criteria interval type-2 fuzzy distance to ideal solution approach. Appl. Energy 347, 121436. doi:10.1016/j.apenergy.2023.121436

CrossRef Full Text | Google Scholar

Hussain, A., Bari, M., and Javed, W. (2022b). Performance of the multi attributed decision-making process with interval-valued spherical fuzzy Dombi aggregation operators. J. Innovative Res. Math. Comput. Sci. 1 (1), 1–32.

Google Scholar

Hussain, A., Ullah, K., Mubasher, M., Senapati, T., and Moslem, S. (2023c). Interval-valued Pythagorean fuzzy information aggregation based on Aczel-Alsina operations and their application in multiple attribute decision making. IEEE Access 11, 34575–34594. doi:10.1109/access.2023.3244612

CrossRef Full Text | Google Scholar

Hussain, A., Ullah, K., Pamucar, D., Haleemzai, I., and Tatić, D. (2023a). Assessment of solar panel using multiattribute decision-making approach based on intuitionistic fuzzy Aczel Alsina heronian mean operator. Int. J. Intelligent Syst. 2023, 1–22. Available at:. doi:10.1155/2023/6268613

CrossRef Full Text | Google Scholar

Hussain, A., Ullah, K., Pamucar, D., and Vranješ, Đ. (2022a). A multi-attribute decision-making approach for the analysis of vendor management using novel complex picture fuzzy Hamy mean operators. Electronics 11 (23), 3841. doi:10.3390/electronics11233841

CrossRef Full Text | Google Scholar

Hussain, A., Ullah, K., Senapati, T., and Moslem, S. (2023b). Complex spherical fuzzy Aczel Alsina aggregation operators and their application in assessment of electric cars. Heliyon 9 (7), e18100. Available at:. doi:10.1016/j.heliyon.2023.e18100

PubMed Abstract | CrossRef Full Text | Google Scholar

Hussain, A., Wang, H., Ullah, K., and Pamucar, D. (2023d). Novel intuitionistic fuzzy Aczel Alsina Hamy mean operators and their applications in the assessment of construction material. Complex & Intelligent Syst. Available at:. doi:10.1007/s40747-023-01116-1

CrossRef Full Text | Google Scholar

Hwang, C.-M., Yang, M. S., Hung, W. L., and Lee, M. G. (2012). A similarity measure of intuitionistic fuzzy sets based on the Sugeno integral with its application to pattern recognition. Inf. Sci. 189, 93–109. doi:10.1016/j.ins.2011.11.029

CrossRef Full Text | Google Scholar

Jana, C., Muhiuddin, G., and Pal, M. (2019). Some Dombi aggregation of Q-rung orthopair fuzzy numbers in multiple-attribute decision making. Int. J. Intelligent Syst. 34 (12), 3220–3240. doi:10.1002/int.22191

CrossRef Full Text | Google Scholar

Kahraman, C., Kaya, İ., and Cebi, S. (2009). A comparative analysis for multiattribute selection among renewable energy alternatives using fuzzy axiomatic design and fuzzy analytic hierarchy process. Energy 34 (10), 1603–1616. doi:10.1016/j.energy.2009.07.008

CrossRef Full Text | Google Scholar

Khan, M. R., Wang, H., Ullah, K., and Karamti, H. (2022a). Construction material selection by using multi-attribute decision making based on q-rung orthopair fuzzy aczel–alsina aggregation operators. Appl. Sci. 12 (17), 8537. Available at:. doi:10.3390/app12178537

CrossRef Full Text | Google Scholar

Khan, R., Ullah, K., Dragan Pamucar, D., and Bari, M. (2022b). Performance measure using a multi-attribute decision making approach based on complex T-spherical fuzzy power aggregation operators. J. Comput. Cognitive Eng. Available at:. doi:10.47852/bonviewJCCE696205514

CrossRef Full Text | Google Scholar

Krishankumar, R., Ravichandran, K. S., Kar, S., Cavallaro, F., Zavadskas, E. K., and Mardani, A. (2019). Scientific decision framework for evaluation of renewable energy sources under q-rung orthopair fuzzy set with partially known weight information. Sustainability 11 (15), 4202. doi:10.3390/su11154202

CrossRef Full Text | Google Scholar

Kutlu Gündoğdu, F., and Kahraman, C. (2020). A novel spherical fuzzy analytic hierarchy process and its renewable energy application. Soft Comput. 24 (6), 4607–4621. Available at:. doi:10.1007/s00500-019-04222-w

CrossRef Full Text | Google Scholar

Li, J., Guo, Y., Platt, G., and Ward, J. K. (2013). Renewable energy aggregation with intelligent battery controller. Renew. energy 59, 220–228. doi:10.1016/j.renene.2013.03.027

CrossRef Full Text | Google Scholar

Liu, P., and Gao, H. (2019). Some intuitionistic fuzzy power Bonferroni mean operators in the framework of Dempster–Shafer theory and their application to multicriteria decision making. Appl. Soft Comput. 85, 105790. doi:10.1016/j.asoc.2019.105790

CrossRef Full Text | Google Scholar

Liu, Y., and Jiang, W. (2020). A new distance measure of interval-valued intuitionistic fuzzy sets and its application in decision making. Soft Comput. 24 (9), 6987–7003. Available at:. doi:10.1007/s00500-019-04332-5

CrossRef Full Text | Google Scholar

Liu, Z., Mohammadzadeh, A., Turabieh, H., Mafarja, M., Band, S. S., and Mosavi, A. (2021). A new online learned interval type-3 fuzzy control system for solar energy management systems. IEEE Access 9, 10498–10508. doi:10.1109/access.2021.3049301

CrossRef Full Text | Google Scholar

Mahmood, T. (2020). A novel approach towards bipolar soft sets and their applications. J. Math. 2020, 1–11. doi:10.1155/2020/4690808

CrossRef Full Text | Google Scholar

Mahmood, T., and Ali, Z. (2023). Multi-attribute decision-making methods based on Aczel–Alsina power aggregation operators for managing complex intuitionistic fuzzy sets. Comput. Appl. Math. 42 (2), 87–34. doi:10.1007/s40314-023-02204-1

CrossRef Full Text | Google Scholar

Mahmood, T., Ullah, K., Khan, Q., and Jan, N. (2019). An approach toward decision-making and medical diagnosis problems using the concept of spherical fuzzy sets. Neural Comput. Appl. 31 (11), 7041–7053. doi:10.1007/s00521-018-3521-2

CrossRef Full Text | Google Scholar

Mahmood, T., and Ur Rehman, U. (2022). A novel approach towards bipolar complex fuzzy sets and their applications in generalized similarity measures. Int. J. Intelligent Syst. 37 (1), 535–567. doi:10.1002/int.22639

CrossRef Full Text | Google Scholar

Marichal, J.-L. (2000). On Sugeno integral as an aggregation function. Fuzzy sets Syst. 114 (3), 347–365. doi:10.1016/s0165-0114(98)00116-x

CrossRef Full Text | Google Scholar

Menger, K. (1942). Statistical metrics. Proc. Natl. Acad. Sci. U. S. A. 28 (12), 535–537. doi:10.1073/pnas.28.12.535

PubMed Abstract | CrossRef Full Text | Google Scholar

Monika, R., Bajaj, R. K., and Sharma, A. (2023). On some new aggregation operators for T-spherical fuzzy hypersoft sets with application in renewable energy sources. Int. J. Inf. Technol. 15, 2457–2467. doi:10.1007/s41870-023-01258-y

CrossRef Full Text | Google Scholar

Murofushi, T., and Sugeno, M. (1991). Fuzzy t-conorm integral with respect to fuzzy measures: generalization of Sugeno integral and Choquet integral. Fuzzy sets Syst. 42 (1), 57–71. doi:10.1016/0165-0114(91)90089-9

CrossRef Full Text | Google Scholar

Naeem, M., and Ali, J. (2022). A novel multi-criteria group decision-making method based on Aczel–Alsina spherical fuzzy aggregation operators: application to evaluation of solar energy cells. Phys. Scr. 97 (8), 085203. doi:10.1088/1402-4896/ac7980

CrossRef Full Text | Google Scholar

Naeem, M., Mahmood, T., Rehman, U. u., and Mehmood, F. (2023). Classification of renewable energy and its sources with decision-making approach based on bipolar complex fuzzy frank power aggregation operators. Energy Strategy Rev. 49, 101162. doi:10.1016/j.esr.2023.101162

CrossRef Full Text | Google Scholar

Razzaque, A., Masmali, I., Hassan, R., Shuaib, U., Razaq, A., Alhamzi, G., et al. (2023). A modern strategy for the selection of efficacious solar panels at industrial level under an interval-valued picture fuzzy set hybrid environment. Energies 16 (14), 5338. Available at:. doi:10.3390/en16145338

CrossRef Full Text | Google Scholar

Riaz, M., and Farid, H. M. A. (2022). Picture fuzzy aggregation approach with application to third-party logistic provider selection process. Rep. Mech. Eng. 3 (1), 318–327. doi:10.31181/rme20023062022r

CrossRef Full Text | Google Scholar

Riaz, M., Farid, H. M. A., Shakeel, H. M., Aslam, M., and Mohamed, S. H. (2021). Innovative q-rung orthopair fuzzy prioritized aggregation operators based on priority degrees with application to sustainable energy planning: a case study of Gwadar. AIMS Math. 6 (11), 12795–12831. doi:10.3934/math.2021739

CrossRef Full Text | Google Scholar

Riaz, M., Habib, A., Saqlain, M., and Yang, M. S. (2023). Cubic bipolar fuzzy-VIKOR method using new distance and entropy measures and Einstein averaging aggregation operators with application to renewable energy. Int. J. Fuzzy Syst. 25 (2), 510–543. doi:10.1007/s40815-022-01383-z

CrossRef Full Text | Google Scholar

Riaz, M., and Hashmi, M. R. (2019). Linear Diophantine fuzzy set and its applications towards multi-attribute decision-making problems. J. Intelligent Fuzzy Syst. 37 (4), 5417–5439. doi:10.3233/jifs-190550

CrossRef Full Text | Google Scholar

Riaz, M., Sałabun, W., Athar Farid, H. M., Ali, N., and Wątróbski, J. (2020). A robust q-rung orthopair fuzzy information aggregation using Einstein operations with application to sustainable energy planning decision management. Energies 13 (9), 2155. doi:10.3390/en13092155

CrossRef Full Text | Google Scholar

Sarkar, A., Senapati, T., Jin, L., Mesiar, R., Biswas, A., and Yager, R. R. (2023). Sugeno–weber triangular norm-based aggregation operators under T-spherical fuzzy hypersoft context. Inf. Sci. 645, 119305. doi:10.1016/j.ins.2023.119305

CrossRef Full Text | Google Scholar

Seikh, M. R., and Mandal, U. (2022). Q-rung orthopair fuzzy Frank aggregation operators and its application in multiple attribute decision-making with unknown attribute weights. Granul. Comput. 7 (3), 709–730. doi:10.1007/s41066-021-00290-2

CrossRef Full Text | Google Scholar

Seker, S., and Kahraman, C. (2021). Socio-economic evaluation model for sustainable solar PV panels using a novel integrated MCDM methodology: a case in Turkey. Socio-Economic Plan. Sci. 77, 100998. Available at:. doi:10.1016/j.seps.2020.100998

CrossRef Full Text | Google Scholar

Senapati, T., Martínez, L., and Chen, G. (2022). Selection of appropriate global partner for companies using q-rung orthopair fuzzy aczel–alsina average aggregation operators. Int. J. Fuzzy Syst. 25, 980–996. doi:10.1007/s40815-022-01417-6

CrossRef Full Text | Google Scholar

Senapati, T., Simic, V., Saha, A., Dobrodolac, M., Rong, Y., and Tirkolaee, E. B. (2023). Intuitionistic fuzzy power Aczel-Alsina model for prioritization of sustainable transportation sharing practices. Eng. Appl. Artif. Intell. 119, 105716. doi:10.1016/j.engappai.2022.105716

CrossRef Full Text | Google Scholar

Shafiq, A., Çolak, A. B., and Sindhu, T. N. (2023b). Modeling of Darcy-Forchheimer magnetohydrodynamic Williamson nanofluid flow towards nonlinear radiative stretching surface using artificial neural network. Int. J. Numer. Methods Fluids 95 (9), 1502–1520. Available at:. doi:10.1002/fld.5216

CrossRef Full Text | Google Scholar

Shafiq, A., Çolak, A. B., and Sindhu, T. N. (2024). Comparative analysis to study the Darcy–Forchheimer Tangent hyperbolic flow towards cylindrical surface using artificial neural network: an application to Parabolic Trough Solar Collector. Math. Comput. Simul. 216, 213–230. doi:10.1016/j.matcom.2023.09.014

CrossRef Full Text | Google Scholar

Shafiq, A., Çolak, A. B., Sindhu, T. N., Lone, S. A., and Abushal, T. A. (2023a). Modeling and survival exploration of breast carcinoma: a statistical, maximum likelihood estimation, and artificial neural network perspective. Artif. Intell. Life Sci. 4, 100082. doi:10.1016/j.ailsci.2023.100082

CrossRef Full Text | Google Scholar

Sugeno, M. (1974). Theory of fuzzy integrals and its applications. Doctoral Thesis. Tokyo, Japan: Tokyo Institute of Technology.

Google Scholar

Ullah, K., Naeem, M., Hussain, A., Waqas, M., and Haleemzai, I. (2023). Evaluation of electric motor cars based frank power aggregation operators under picture fuzzy information and a multi-attribute group decision-making process. IEEE Access 11, 67201–67219. doi:10.1109/access.2023.3285307

CrossRef Full Text | Google Scholar

Wang, H., and Zhang, F. (2022). Interaction power Heronian mean aggregation operators for multiple attribute decision making with T-spherical fuzzy information. J. Intelligent Fuzzy Syst. 42 (6), 5715–5739. Available at:. doi:10.3233/JIFS-212149

CrossRef Full Text | Google Scholar

Wang, J., Wei, G., Wang, R., Alsaadi, F. E., Hayat, T., Wei, C., et al. (2019). Some q-rung interval-valued orthopair fuzzy Maclaurin symmetric mean operators and their applications to multiple attribute group decision making. Int. J. Intelligent Syst. 34 (11), 2769–2806. doi:10.1002/int.22156

CrossRef Full Text | Google Scholar

Wang, L., and Garg, H. (2021). Algorithm for multiple attribute decision-making with interactive archimedean norm operations under pythagorean fuzzy uncertainty. Int. J. Comput. Intell. Syst. 14 (1), 503–527. doi:10.2991/ijcis.d.201215.002

CrossRef Full Text | Google Scholar

Waqar, M., Ullah, K., Pamucar, D., Jovanov, G., and Vranješ, Ð. (2022). An approach for the analysis of energy resource selection based on attributes by using Dombi T-norm based aggregation operators. Energies 15 (11), 3939. Available at:. doi:10.3390/en15113939

CrossRef Full Text | Google Scholar

Weber, G. W., et al. (2015). Finansal, ekonomik ve çevresel süreçlere ait atlamalı stokastik hibrit sistemler: tanımlama, optimizasyon ve optimal kontrol. Available at: https://open.metu.edu.tr/handle/11511/61690 (Accessed: December 15, 2022).

Google Scholar

Weber, S. (1983). A general concept of fuzzy connectives, negations and implications based on t-norms and t-conorms. Fuzzy sets Syst. 11 (1–3), 115–134. doi:10.1016/s0165-0114(83)80073-6

CrossRef Full Text | Google Scholar

Xia, M., Xu, Z., and Zhu, B. (2012). Some issues on intuitionistic fuzzy aggregation operators based on Archimedean t-conorm and t-norm. Knowledge-Based Syst. 31, 78–88. doi:10.1016/j.knosys.2012.02.004

CrossRef Full Text | Google Scholar

Yager, R. (2013). “Pythagorean fuzzy subsets,” in 2013 Joint IFSA World Congress and NAFIPS Annual Meeting (IFSA/NAFIPS), Edmonton, Canada, June, 2013. doi:10.1109/IFSA-NAFIPS.2013.6608375

CrossRef Full Text | Google Scholar

Yager, R. R. (2001). The power average operator. IEEE Trans. Syst. Man, Cybern. - Part A Syst. Humans 31 (6), 724–731. Available at:. doi:10.1109/3468.983429

CrossRef Full Text | Google Scholar

Yager, R. R. (2016). Generalized orthopair fuzzy sets. IEEE Trans. Fuzzy Syst. 25 (5), 1222–1230. doi:10.1109/tfuzz.2016.2604005

CrossRef Full Text | Google Scholar

Zadeh, L. A. (1965). Fuzzy sets. Inf. Control 8 (3), 338–353. Available at:. doi:10.1016/S0019-9958(65)90241-X

CrossRef Full Text | Google Scholar

Zeng, S., Garg, , Munir, , Mahmood, , and Hussain, (2019). A multi-attribute decision making process with immediate probabilistic interactive averaging aggregation operators of T-spherical fuzzy sets and its application in the selection of solar cells. Energies 12 (23), 4436. Available at:. doi:10.3390/en12234436

CrossRef Full Text | Google Scholar