MHD viscoelastic nanofluid flow across an extended plate using mixed convection and thermal radiation

1 Introduction

Stagnation is a state of zero velocity of the flow field with respect to a body and the fluid particles. In the fluid flow, there comes a point when fluid particles are dragged to rest on the surface for a moment, and this point is known as the stagnation point. According to the Bernoulli equation, stagnant pressure is at its highest level at these points when fluid’s velocity is zero. Nazar et al. (2004) examined the unsteady two-dimensional stagnation point flow of an incompressible viscous fluid across a deformable sheet. Pop et al. (2005) described how radiation has an impact on the flow near a stretching sheet’s stagnation point. They demonstrate the formation of a boundary layer, demonstrating how its thickness changes with variations in temperature, radiation, and velocity, and how it grows with the Prandtl number. Ishak et al. (2006) discussed the full characterization of an incompressible viscid electrically conductive fluid’s flow across an upright stretched sheet during a transverse uniform superconducting magnet instantaneous flow in two dimensions has been published. Layek et al. (2007) investigated the boundary layer stagnated flow with characteristics of heat transfer over an extending pane in a permeable intermediate in the presence of suction injection with internal heat generation/absorption. The stagnation point flow for various fluid models in various shapes and surfaces has been discussed by several writers; see References. The petrochemical manufacturing, polymerization, assembling, classification and features of polymers, and descriptions of key polymers are covered. Metal, metal oxide, carbide, nitride, and even immiscible nanoscale fluid particles can be established. Choi and Eastman (1995) completed the early research for the nanofluid. BUONGIORNO (2006) first proposed the concept of convective transport in nanofluids and demonstrated that nanofluids exhibit a greater thermal conductivity than base fluids. Khanafer et al. (2003) explored how nanofluids can improve heat transport in a two-dimensional enclosure for a variety of important factors. Makinde and Aziz (2011) surveyed the boundary layer flow that is caused in a nanofluid by a sheet that is linearly overextended. Nawaz et al. (2022) suggested that a modified scheme was put into practice for the mass and heat exchange of a chemically active fluid flow in a diagonal funnel. It had distinct orders in space and second orders in time. When various pressure differentials are applied, a stream is produced. The information in their representations demonstrate the mass transfer that occurs in the fluid at various moments as well as the heat transfer that occurs in the fluid due to overheated surfaces. Nawaz et al. (2022) also used the finite element approach to move the energy and mass in a magnetohydrodynamic (MHD) Maxwell nanofluid technology through an extensible sheet while accounting for the interaction of chemicals and thermal radiation.

As a result of random motion with the thermophoretic movement of nanosized fluid particles along with convective heating, the thermal boundary layer thickens when the local temperature increases. Aziz and Khan (2012) studied the naturally convective flow of a nanofluid over a vertical plate that was being heated by convection. The boundary layer stagnation-point flow on an extending pane was studied by Hamad and Ferdows (2012) in a very recent study on heat and mass transfer analysis. Martin and Boyd (2006) examined the momentum with slip effects and heat transfer in a laminar boundary layer. The findings of Uddin et al. (2012) developed a collection scaling conversion for the MHD boundary layer slip flow of a nanofluid on a stretched pane that is convectively heated. In a very recent study by Haq et al. (2015), influences of magnetohydrodynamic with thermal slip limitations on a double-diffusive nanofluid flow with free convection along a semi-infinite horizontal compacted upright plate were examined numerically. A. Shafiq et al. (2022) examined the flow of thermally generated thixotropic nanoparticles by integrating descriptive flow characteristics and also discussed little heat effectiveness for base fluids where a machine learning method has assembled a numerical inquiry on the thermally operation of graphene oxide-containing water/ethylene glycol-based small-molecule fluids with the impact of both the electromagnet hydrodynamic and Darcy–Forchheimer interface (Shafiq et al., 2023). The researchers Khan and Pop (2010), Khan et al. (2013), Nadeem et al. (2013), Nadeem et al. (2013), Akbar et al. (2014), Haq et al. (2014), Nadeem et al. (2014), Nadeem and Hussain (2014), Ramesh and Gireesha (2014), Nawaz et al. (2022b), Nawaz et al. (2022), and Reddy et al. (2022), by utilizing similarity transformation, noticed heat transferal influences on the Maxwell fluid over an extending surface in the presence of nanoparticles. A few more recent studies are listed that describe the characteristics of nanofluid.

The results show that when utilizing nanofluids instead of base fluids, the thermal conductivity and conductive heat transfer coefficients increase. Heat exchangers can be used for a variety of cooling and heating operations since nanofluids have a higher thermal performance than water.

However, there are some instances where this similarity conversion did not work and it was unable to obtain a transformed dimensionless system; this can be solved with a newly introduced transformation called “non-similarity” transformation. In the late 20th century, Sparrow et al. (1970) presented a non-similarity transformation. This method convoluted two independent variables: pseudo-similar and non-similar. This technique is used for reducing partial differential equations (PDEs) to one dimension and to make the problem dimensionless. Merely few choices are available connected to non-similar courses. You et al. (2010) discussed these types of non-similar solutions. Kousar and Mahmood (2013) debated a fluid flow over a wedge-shaped permeable medium and obtained a series solution via the non-similarity method. Farooq et al. (2015) also used non-similarity of the nanofluid flow to obtain a consistent solution. Farooq et al. (2020) considered features of entropy for inhomogeneous 3-D nanofluid flows in the occurrence of magnetic influence. Shukla et al. (2019) established a non-similar result for a non-Newtonian fluid by means of an indigenous non-similar way. Some more related literature studies can be seen (Nawaz et al., 2021; Nawaz et al., 2022; Nawaz et al., 2022a; Nawaz et al., 2022).

Current study’s major goal is to examine how thermal radiation and thermal slip interact to affect the nanofluid flow close to the stagnation point of the MHD boundary layer. Additionally, the impacts of slip velocity and the zero normal flow of a fluid in occurrence with nanoparticles at the surface are considered. The paper’s structure is set down in the following manner: the problem preparation and design are presented in Sections $2-4$. Section $5$ includes the graphical representation of computational solutions with scientific clarification and elaborations. The whole analysis’ summary is included in Section $6$. It is observed that the results regarding the relationship between the MHD factor and the coefficients of skin friction and heat transfer varies depending on the kind of the fluid flow model used and the parameters incorporated. To guarantee that an exact fluid flow prediction can be simulated, a specific inquiry must be represented for a specific application. To the best of our knowledge, no research has been conducted on magnetohydrodynamic mixed convection for nanofluids with thermal radiation configurations along stretched plates. Therefore, the results obtained using non-similarity transformation presented in this work are novel.

2 Formation of a problem

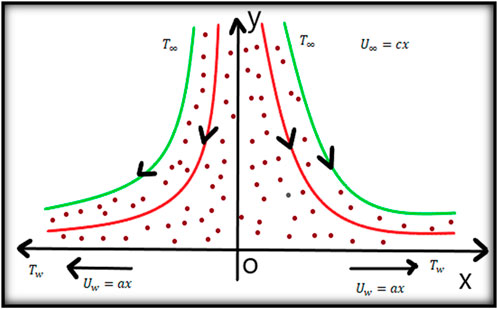
Let us consider the two-dimensional incompressible laminar flow of a non-Newtonian viscid nanofluid approaching a stagnation point at a permeable exterior surface coincides with the horizontal plane $y=0$ and flow occurs at $y\ge 0$. Here, the assumption of the stretching surface with a constant linear speed is taken. Herein, $x$ is a coordinate measured along the extending surface, and $a>0$ is a constant, $U_w\left(x\right)=ax$ (Figure 1). The ambient fluid’s temperature and fluid’s concentration of nanoparticles are $T_{\infty }$ and $C_{\infty }$, respectively. The fluid’s temperature and nanoparticle’s concentration over the stretched plane have fixed quantities, $T_w$ and $C_w$, respectively. Additionally, wall-based hydrodynamic and thermal slip boundary conditions are included. Furthermore, the energy equation incorporates the properties of thermal radiation. The relevant continuity, velocity, momentum, and energy equations are expressed as follows: [40]

$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0,(1)$

$u\frac{\partial u}{\partial x}+v\frac{\partial v}{\partial y}=U_{\infty }\frac{\partial u}{\partial x}+\frac{\partial U_{\infty }}{\partial x}+\upsilon \frac{{\partial }^{2}u}{{\partial y}^2}-\frac{\sigma B_0^2}{\rho }\left(u-U_{\infty }\right)+g{\beta }_T\left(T-T_{\infty }\right)+g{\beta }_C\left(C-C_{\infty }\right),(2)$

$\left(u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}\right)={\alpha }_D\left(\frac{{\partial }^{2}T}{{\partial y}^2}\right)+\tau D_B\left(\frac{\partial T}{\partial y}\frac{\partial C}{\partial y}\right)+\frac{\tau D_T}{T_{\infty }}{\left(\frac{\partial T}{\partial y}\right)}^2-\frac{\partial q_r}{\partial y},(3)$

$\left(u\frac{\partial C}{\partial x}+v\frac{\partial C}{\partial y}\right)=D_B\left(\frac{{\partial }^{2}C}{{\partial y}^2}\right)+\frac{D_T}{T_{\infty }}\left(\frac{{\partial }^{2}T}{{\partial y}^2}\right),(4)$

where $u$ is the velocity in the $x$- direction and $v$ is the velocity in the $y$-direction; $U_{\infty }=cx$ is the ambient velocity with $c>0$, $p$ is the pressure, $\rho$ is the fluid’s density; $\alpha$ is the thermal diffusivity, $\mathrm{\upsilon }$ is the kinematic viscosity, $D_B$ is the Brownian diffusion constant, $D_T$ is the thermophoretic diffusion constant, $\tau$ is the fluid’s heat capacity ratio to nanoparticles, and $c$ is the volumetric extension constant.

FIGURE 1

FIGURE 1. Geometry of the problem.

Using the radiation-based Rosseland approximation, the following equation is obtained:

$q_r=-\frac{4{\sigma }^{*}}{3k^{*}}\frac{\partial T^4}{\partial y},(5)$

where the Stefan–Boltzmann constant ${\sigma }^{*}$ and the mean absorption coefficient $k^{*}$ are both present, with $T^4\cong 4T_{\infty }^{3}T-3T_{\infty }^4$.

The following slip boundary conditions exist:

$\left.\begin{array}{c}u=U_w=ax,v=0,T=T_w,C=C_w,y=0\\ u=U_{\infty }=cx,T=T_{\infty },,C=C_{\infty },y\to \infty \end{array}\right\}.(6)$

2.1 The non-similarity transformation

A non-similarity technique is explored here for the solution of the governed problem by altering the governed dimensional system into a dimensionless system of partial differential equations. For this method, the non-similar flow transformation is considered as follows (40):

$\xi =e^{\frac{x}{l}},\eta =y\sqrt{\frac{U_w}{2l\upsilon }}{e}^{\frac{x}{2l}},\mathrm{\Psi }\left(x,y\right)=\sqrt{2\upsilon l{U}_w}f\left(\xi ,\eta \right),u=U_{w}f,\stackrel{́}{}$

$v=-\frac{\sqrt{2\upsilon l{U}_w}}{2l}f\left(\xi ,\eta \right)-\frac{\sqrt{2\upsilon l{U}_w}}{l}\frac{\partial f}{\partial \xi }\xi -y\frac{U_w}{2l}\frac{\partial f}{\partial \eta }\text{\hspace{0.17em}and\hspace{0.17em}}\theta \left(\xi ,\eta \right)=\frac{\left(T-T_{\infty }\right)}{\left(T_w-T_{\infty }\right)},\phi \left(\xi ,\eta \right)=\frac{\left(C-C_{\infty }\right)}{\left(C_w-C_{\infty }\right)},(7)$

where the variables $\mathrm{\eta }\left(\mathrm{x},\mathrm{y}\right)$ are defined as pseudo-similarity and $\mathrm{\xi }\left(\mathrm{x}\right)$ is the non-similarity variable.

Equations $\left(2\right)-\left(4\right)$ that use non-similarity transformations result in (8)–(10)

${\left(\frac{\partial f}{\partial \eta }\right)}^2+2\xi .\frac{\partial }{\partial \xi }\left(\frac{\partial f}{\partial \eta }\right).\frac{\partial f}{\partial \eta }-f\frac{{\partial }^{2}f}{{\partial \eta }^2}-2\xi \frac{\partial f}{\partial \xi }\frac{{\partial }^{2}f}{{\partial \eta }^2}-r^2+M\left(\frac{\partial f}{\partial \eta }-r\right)-2\theta {Gr}_l-2\phi {Gr}_c-\frac{{\partial }^{3}f}{{\partial \eta }^3}=0,(8)$

$\mathit{Pr}\left[2\xi \frac{\partial \theta }{\partial \xi }\frac{\partial f}{\partial \eta }-f\theta ˊ-2\xi \frac{\partial f}{\partial \xi }\frac{\partial \theta }{\partial \eta }-N_b\theta ˊ\phi ˊ-N_t{\theta ˊ}^2\right]-\left(1+\frac{4}{3}{N}_r\right)\frac{{\partial }^2\theta }{{\partial \eta }^2}=0,(9)$

$2\xi \frac{\partial \phi }{\partial \xi }\frac{\partial f}{\partial \eta }-2\xi \frac{\partial f}{\partial \xi }\frac{\partial \phi }{\partial \eta }-\frac{N_t}{N_b}\theta ˊˊ-\mathit{Pr}.Le.f\phi \mathrm{ˊ}-\frac{{\partial }^2\phi }{{\partial \eta }^2}=0,(10)$

including the modified boundary conditions

$\left.\begin{array}{c}{f}^{ˊ}\left(\xi ,\eta \right)=1,f\left(\xi ,\eta \right)=-2\xi \frac{\partial f}{\partial \xi },\theta \left(\xi ,\eta \right)=1,\phi \left(\xi ,\eta \right)=1at\eta =0\\ f^{ˊ}\left(\xi ,\eta \right)\to \raisebox{1ex}{$c$}\!\left/ \!\raisebox{-1ex}{$a$}\right.=r,\theta \left(\xi ,\eta \right)\to 0,\phi \left(\xi ,\eta \right)\to 0at\eta \to \infty \end{array}\right\}.(11)$

2.2 Local non-similarity procedure

Sparrow et al. [31] applied this technique for the first time to study several non-similar boundary value problems (BVPs). The stepwise formulas are along these lines.

2.3 Truncation at the first level

In leading truncation step terminology $\frac{\partial \left(.\right)}{\partial \xi }$, neglects to consider in Eqs 8–10, assuming that $\xi \partial /\partial \left(\xi .\right)$ can be approximately equal to zero and is relatively little modified when compared to the other components.

By this, we perceive

${\left(fˊ\right)}^2-ffˊˊ-r^2-M\left(r-fˊ\right)-2\theta {Gr}_l-2\phi {Gr}_c-fˊˊˊ=0,(12)$

$\left(1+\frac{4}{3}{N}_r\right)\theta ˊˊ+\mathit{Pr}\left[f\theta ˊ+N_b\theta ˊ\phi ˊ+{N_t\theta }^{ˊ²}\right]=0,(13)$

$\phi ˊˊ+\frac{N_t}{N_b}\theta ˊˊ+\mathit{Pr}.Le.f\phi ˊ=0.(14)$

$N_b=\frac{\tau D_{B\left(C_{w-}{C}_{\infty }\right)}}{\upsilon }$ is the Brownian motion; $N_t=\frac{\tau D_{T\left(T_{w-}{T}_{\infty }\right)}}{T_{\infty }\upsilon }$ is the thermophoresis parameter; $\mathit{Pr}=\frac{\upsilon }{\alpha }$ is the Prandtl number; $N_r=\frac{4{\sigma }^{*}{T}_{\infty }^3}{k^{*}k{\alpha }_D}$ is the radiation parameter; heat and mass transmission, the Grashof numbers are ${Gr}_l=\frac{gl{\beta }_T\left(T_{w-}{T}_{\infty }\right)}{U_w^{²}}$ and ${Gr}_c=\frac{gl{\beta }_C\left(C_{w-}{C}_{\infty }\right)}{U_w^{²}};$ $M=\frac{2l\sigma B_0^2}{\rho U_w}$ is the magnetic parameter; $\frac{\alpha }{D_B}$ is the Lewis number; and $r=\frac{c}{a}$ is the stretching ratio.

2.4 Truncation at the second level

We will use the following functions for the second truncation level.

Then, let $\frac{\partial f}{\partial \xi }=p,\frac{\partial \theta }{\partial \xi }=q,\frac{\partial \phi }{\partial \xi }=g$

$\frac{{\partial }^{2}f}{\partial \xi \partial \eta }=\frac{\partial fˊ}{\partial \xi }=p^{*},\frac{{\partial }^2\theta }{\partial \xi \partial \eta }=\frac{\partial \theta ˊ}{\partial \xi }=q^{*},\frac{{\partial }^2\phi }{\partial \xi \partial \eta }=\frac{\partial \phi ˊ}{\partial \xi }=g^{*}.$

After introducing the new functions, Eqs 8–10 are converted.

${\left(fˊ\right)}^2+2\xi p^{*}-2\xi fˊˊp-ffˊˊ-r^2-M\left(r-fˊ\right)-2\theta {Gr}_l-2\phi {Gr}_c-fˊˊˊ=0,(15)$

$\mathit{Pr}\left[2\xi fˊq-f\theta ˊ-2\xi p\theta ˊ-N_b\theta ˊ\phi ˊ-{N_t\theta }^{ˊ²}\right]-\left(1+\frac{4}{3}{N}_r\right)\theta ˊˊ=0,(16)$

$\left(2\xi gfˊ-2\xi p\phi ˊ-\frac{N_t}{N_b}\theta ˊˊ-PrLef\phi ˊ-\phi ˊˊ\right)=0,(17)$

$\left.\begin{array}{c}{f}^{ˊ}\left(\xi ,\eta \right)=1,f\left(\xi ,\eta \right)=-2\xi p,\theta \left(\xi ,\eta \right)=1,\phi \left(\xi ,\eta \right)=1at\eta =0\\ f^{ˊ}\left(\xi ,\eta \right)\to r,\theta \left(\xi ,\eta \right)\to 0,\phi \left(\xi ,\eta \right)\to 0,at\eta \to \infty \end{array}\right\}.(18)$

Taking the derivatives of Eqs 15–17 with respect to ξ, following equations are obtained:

$\left[2fˊp+2p^{*}+2\xi \frac{\partial p^{*}}{\partial \xi }-3fˊˊp-2\xi p{p}^{**}-2\xi fˊˊ\frac{\partial p}{\partial \xi }-f{p}^{**}-pfˊˊ-2r-M\left(1-p^{*}\right)-2q{Gr}_l-2g{Gr}_c-p^{***}\right.]=0,(19)$

$\mathit{Pr}\left[2fˊq+2\xi p^{*}q+2\xi fˊ\frac{\partial q}{\partial \xi }-3p\theta ˊ-f{q}^{*}-2\xi \frac{\partial p}{\partial \xi }\theta ˊ-2\xi p{q}^{*}\right]-\left(1+\frac{4}{3}{N}_r\right){\theta }^{**}=0,(20)$

$2g{f}^{ˊ}+2\xi \frac{\partial g}{\partial \xi }{f}^{ˊ}+2\xi g{p}^{*}-2p{\phi }^{ˊ}-2\xi \frac{\partial p}{\partial \xi }\phi ˊ-2\xi p{q}^{*}-\frac{N_t}{N_b}{q}^{**}-PrLef{g}^{*}-{\phi }^{**}=0,(21)$

$\left.\begin{array}{c}{p}^{*}\left(\xi ,\eta \right)=0,p\left(\xi ,\eta \right)=0,q\left(\xi ,\eta \right)=0,g\left(\xi ,\eta \right)=0at\eta =0\\ p^{*}\left(\xi ,\eta \right)\to 0,q\left(\xi ,\eta \right)\to 0,g\left(\xi ,\eta \right)\to 0at\eta \to \infty \end{array}\right\}.(22)$

Skin frictions and the local Nusselt number are the relevant physical quantities; they are described as follows:

$C_f=\frac{{\tau }_w}{{\rho }_f\frac{U_w^2}{2}},{Nu}_x=\frac{x{q}_w}{k_f\left(T_{w-}{T}_{\infty }\right)},{Sh}_x=\frac{x{q}_m}{D_B\left(C_w-C_{\infty }\right)},$

$C_f{Re}_x^{1/2}=fˊˊ\left(0\right),\frac{{Nu}_x}{{Re}_x^{1/2}}=-\left(1+\frac{4}{3}{N}_r\right){\theta }^{ˊ}\left(0\right),\frac{{Sh}_x}{{Re}_x^{\frac{1}{2}}}=-{\phi }^{ˊ}\left(0\right).$

Here, ${Re}_x=\frac{U_{w}x}{\upsilon }$ is the Reynolds number.

3 A mathematical procedure

The abovementioned transformation, i.e., the non-similarity technique producing a non-dimensional set of equations, must be determined numerically or analytically for its solution. The finite difference scheme is used here via an appropriate numerical solver like MATLAB to obtain solutions. The three-stage Lobatto III (a) formula is used by the MATLAB solver to solve the scheme of differential equations. The derived equations have two independent variables; hence, one independent variable was kept constant in order to solve these equations, and the remaining equations were transformed into standard differential equations. When using the MATLAB solver to solve equations, functions for solving differential equations along with boundary conditions were used while using the MATLAB.

A renowned numerical technique is the three-stage Lobatto IIIa formula which is being created using the bvp4c finite difference code. Subsequently, the bvp4c solver function is used to investigate stability. A class of continuous results that is consistently precise to the fourth order in the given domain is obtained using the collocation polynomial and this collocation formula. The continuous solution’s residual serves as the basis for both mesh selection and error control. Additionally, the relative error tolerance is set at ${10}^{-5}$. In any event, the values of the solution are obtained from the field-related array sol.y, which is designated as sol.x. The standard protocol for this method is mentioned in the algorithmic form in the following chart.

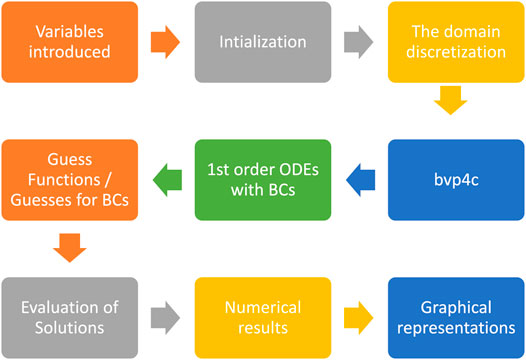
The information about differential equations is provided to the MATLAB solver, and the system of first-order ordinary differential equations with second- or higher-order differential equations must be used. Consequently, transformation into a system of first-order differential equations can be formulated as follows:

$f^{ˊ}=f_2,f^{ˊˊ}=f_3,$

$f^{‴}=f_3^{\prime }=\left[{\left(f_2\right)}^2+2\xi f_9-2\xi f_3{f}_8-f_1{f}_3-2r-M\left(1-f_2\right)-2f_4{Gr}_l-2f_6{Gr}_c\right],(23)$

${\theta }^{ˊ}=f_5,$

${\theta }^{″}=f_5^{\prime }=\frac{\mathit{Pr}}{\left(1+\frac{4}{3}{N}_r\right)}\left[2\xi f_2{f}_{11}-f_1{f}_5-2\xi f_8{f}_5-{N_{b}f}_5{f}_7-{N_t\left(f_5\right)}^{²}\right],(24)$

${\phi }^{ˊ}=f_7,$

${\phi }^{″}=f_7^{\prime }=2\xi f_{13}{f}_2-2\xi f_8{f}_7-\frac{N_t}{N_b}\theta ˊˊ-PrLe{f}_1{f}_7,(25)$

$p^{ˊ}=f_9,p^{ˊˊ}=f_{10},$

$p^{ˊˊˊ}=f_{10}^{\prime }=\left[2f_2{f}_8+2f_9+2\xi f_9-3f_3{f}_8-2\xi f_8{f}_{10}-2\xi f_3{f}_8-f_1{f}_{10}-f_8{f}_3-2r-M\left(1-f_9\right)-2f_{11}{Gr}_l-2f_{13}{Gr}_c\right],(26)$

$q^{ˊ}=f_{12},$

$q^{ˊˊ}=f_{12}^{\prime }=\frac{\mathit{Pr}}{\left(1+\frac{4}{3}{N}_r\right)}\left[2f_2{f}_{11}+2\xi f_9{f}_{11}+2\xi f_2{f}_{11}-3f_8{f}_5-f_1{f}_{12}-2\xi f_8{f}_5-2\xi f_8{f}_{12}\right],(27)$

$g^{ˊ}=f_{14},$

$g^{ˊˊ}=f_{14}^{\prime }=2f_{13}{f}_2+2\xi f_{13}{f}_2+2\xi f_{13}{f}_9-2f_8{f}_7-2\xi f_8{f}_7-2\xi f_8{f}_{12}-\frac{N_t}{N_b}{q}^{**}-PrLe{f}_1{f}_{14},(28)$

Here, ${f=f}_1,\theta =f_4,\phi =f_6,p=f_8,q=f_{11},\text{and\hspace{0.17em}}g=f_{13}$.

4 Physical quantities of interest

The local Sherwood number, local Nusselt number, and local skin friction coefficients are of prior interest of physical quantities of the governed fluid model and highly beneficial in industrial areas.

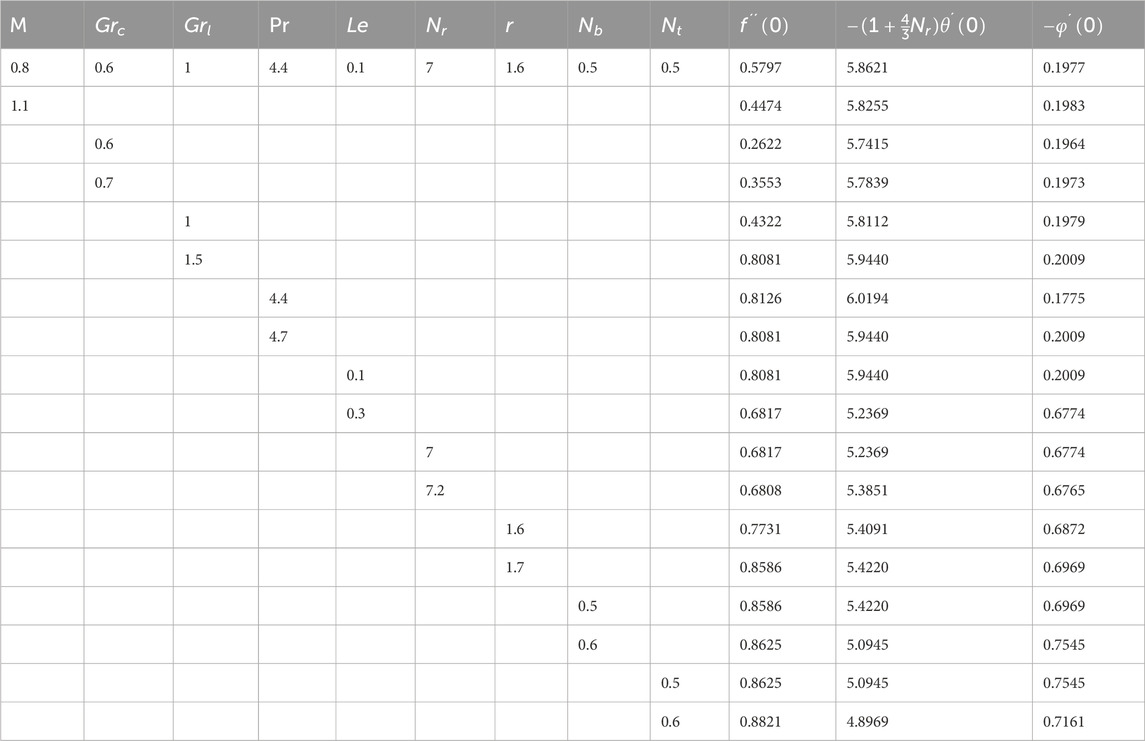
Table 1 describes the numerical values of the skin friction coefficient, the local Nusselt number, and the local Sherwood number regarding the various flow-related factors. It is observed here that the skin friction coefficient ${\mathit{f}}^{ˊˊ}\left(\mathbf{0}\right)$ and local Sherwood number $-{\mathit{\phi }}^{ˊ}\left(\mathbf{0}\right)$ increase as the radiation parameter and Grashof numbers for heat transport increase. The local Sherwood number $-{\mathit{\phi }}^{ˊ}\left(\mathbf{0}\right)$, local Nusselt number ${-\mathit{\theta }}^{ˊ}\left(\mathbf{0}\right)$, and skin friction coefficient ${\mathit{f}}^{ˊˊ}\left(\mathbf{0}\right)$ all augmented when the Grashof number for mass transfer increase. When the Prandtl number increases, the skin friction coefficient ${\mathit{f}}^{ˊˊ}\left(\mathbf{0}\right)$ and local Sherwood number $-{\mathit{\phi }}^{ˊ}\left(\mathbf{0}\right)$ decrease, while the Nusselt number increases. The Nusselt number reduces as thermal conductivity increases, but for this parameter, the skin friction coefficient ${\mathit{f}}^{ˊˊ}\left(\mathbf{0}\right)$ and local Sherwood number $-{\mathit{\phi }}^{ˊ}\left(\mathbf{0}\right)$ increase.

TABLE 1

TABLE 1. Local Sherwood number $-{\mathit{\phi }}^{ˊ}\left(\mathbf{0}\right)$, local Nusselt number ${-\mathit{\theta }}^{ˊ}\left(\mathbf{0}\right)$, and skin friction coefficient ${\mathit{f}}^{ˊˊ}\left(\mathbf{0}\right)$.

TABLE 2

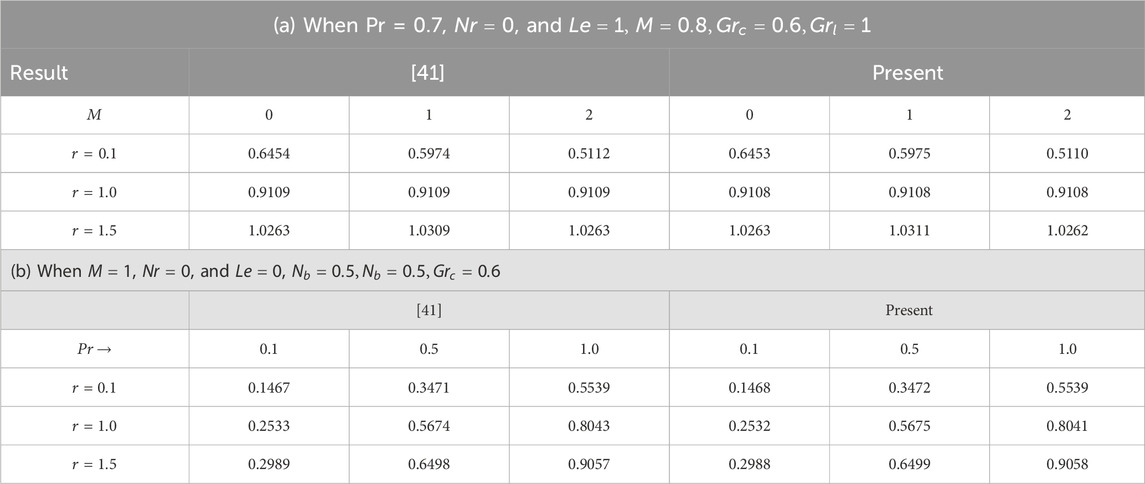
TABLE 2. Comparison of numerical findings for the local Nusselt number for various values of $M,r$, and $P$.

5 Numerical results with their significance

The computational results are illustrated as graphical results (Figures 2–13) to describe the present study’s physical interpretation and significance. Modifications in skin friction, temperature, dimensionless velocities, and heat transfer rate with guiding principles include magnetohydrodynamics $M$ (magnetic parameter), thermal radiation parameter $N_r$, and Grashof numbers ${Gr}_l$ and ${Gr}_c$

FIGURE 2

FIGURE 2. Effect of M on fˊ(η).

FIGURE 3

FIGURE 3. Effect of r on fˊ(η).

FIGURE 4

FIGURE 4. Effects of Grl on fˊ(η).

FIGURE 5

FIGURE 5. Effects of Grc on fˊ(η).

FIGURE 6

FIGURE 6. Effect of Pr on θ(η).

FIGURE 7

FIGURE 7. Effect of Nr on θ(η).

FIGURE 8

FIGURE 8. Effect of Nt on θ(η).

FIGURE 9

FIGURE 9. Effect of Nb on θ(η).

FIGURE 10

FIGURE 10. Effect of Pr on φ(η).

FIGURE 11

FIGURE 11. Effect of Le on φ(η).

FIGURE 12

FIGURE 12. Effect of Nb on φ(η).

FIGURE 13

FIGURE 13. Effect of Nt on φ(η).

Table 2 is provided here to see the validation of results with already existing literature [41] for Magnetic field parameter, radiation parameter and Prandtl number. It is observed ib the Table that all results are found to be in good agreement upto 3 decimal places.

5.1 Effect of $\mathit{M}$ on $\mathit{f}ˊ\left(\mathit{\eta }\right)$

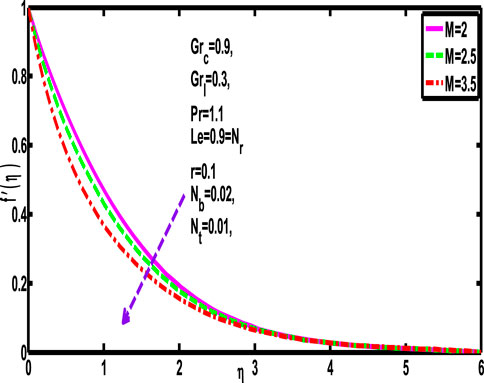
Figure 2 shows the velocity profile for various values of $M$. In the boundary layer, it is discovered that an increase in the magnetic field parameter results in a resistive flow due to the presence of the Lorentz force; as a result, the velocity profile exhibits a declining trend as M is increased because of resistance of molecules. Additionally, the velocity profile in Figure 2 displays the most notable effects of velocity slip parameters.

5.2 Effect of $\mathit{r}$ on $\mathit{f}ˊ\left(\mathit{\eta }\right)$

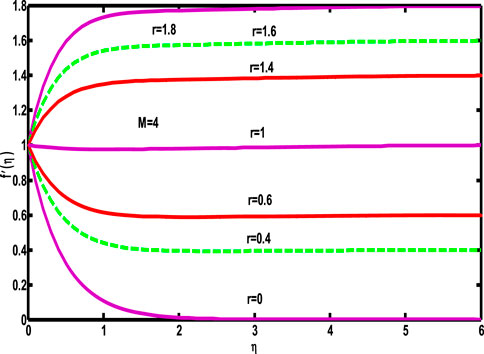
Figure 3 shows the effect of stretching parameter $r$. It is observed here that the velocity profile increased for the stretching ratio parameter $r$; these results are plotted for $r=1$, $r<1$, and $r>1$. When the velocity ratio parameter $r<1$, the velocity decreases, and when $r=1$, the stretching ratio becomes 1, indicating that stretching at the surface and at free stream is the same and for $r>1$, the velocity increases.

5.3 Effects of ${\mathit{G}\mathit{r}}_{\mathit{l}}$ and ${\mathit{G}\mathit{r}}_{\mathit{c}}$ on $\mathit{f}\mathrm{ˊ}\left(\mathit{\eta }\right)$

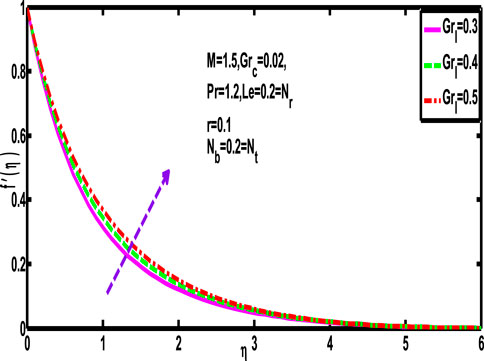
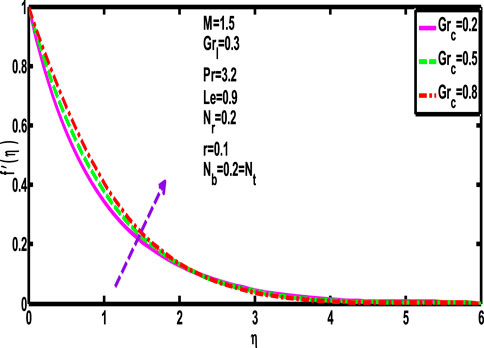
Figures 4, 5 illustrate how Grashof numbers affect the plots ${Gr}_l$ and ${Gr}_c$ on the fluid flow rate. An accelerating velocity profile is produced by increasing the values of the Grashof numbers for both mass and heat transport. The Grashof number, which measures the relationship between the buoyance force and constricting (viscous) force, increases with increasing fluid velocity through reducing viscosity; when the Grashof number increases, viscid forces drop. So, fluid molecules are free to move, and this is why the velocity of fluid increases.

5.4 Effect of $\mathit{Pr}$ on $\mathit{\theta }\left(\mathit{\eta }\right)$

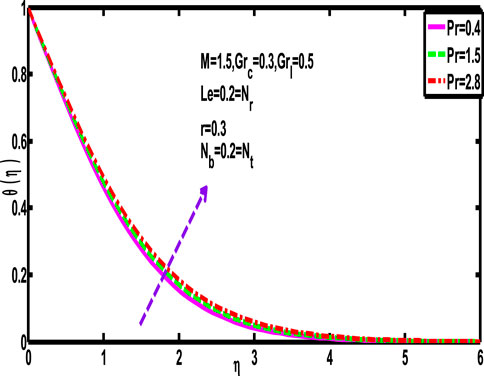
Prandtl numbers’ impact on temperature distribution $\theta \left(\eta \right)$ is explained in Figure 6 The Prandtl number has a positive relationship with the temperature profile. As the Prandtl number increases, the temperature profile decreases. $\mathit{Pr}$ is used to determine the heat transfer between a fluid and a sheet’s surface. The Prandtl number $\mathit{Pr}$ is the ratio of momentum to thermal diffusivity. When the Prandtl number increases, the thermal diffusivity drops, which, in turn, causes the thickness of the thermal boundary layer to decrease along with it, and momentum diffusivity increases, which implies the rapid movement of fluid molecules; hence, the temperature of fluid molecules increases. As a result, the temperature profile has increased.

5.5 Effect of ${\mathit{N}}_{\mathit{r}}$ on $\mathit{\theta }\left(\mathit{\eta }\right)$

$N_r$, radiation parameter; $N_t$, thermophoresis parameter; and $N_b$, Brownian motion are plotted in Figures 7–9, respectively. The temperature profile $\theta \left(\eta \right)$ is reduced using the radiation parameter, as shown in Figure 7. The radiation parameter $N_r$ is defined as the proportional role of conductive transfer of heat to thermal energy transport. It is clear that increasing temperatures within the boundary layer are driven by increasing radiation parameters because when the radiation parameter increases, conduction increases, but thermal radiation transfer drops so the temperature profile drops down [41].

5.6 Effect of ${\mathit{N}}_{\mathit{t}}$ on $\mathit{\theta }\left(\mathit{\eta }\right)$

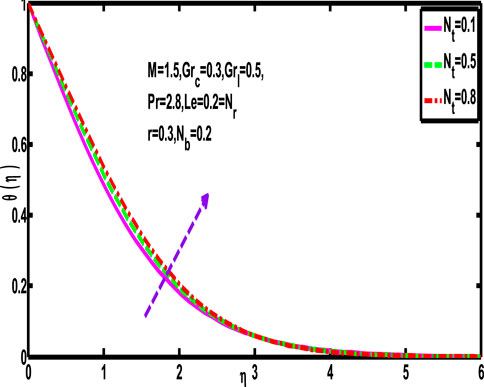
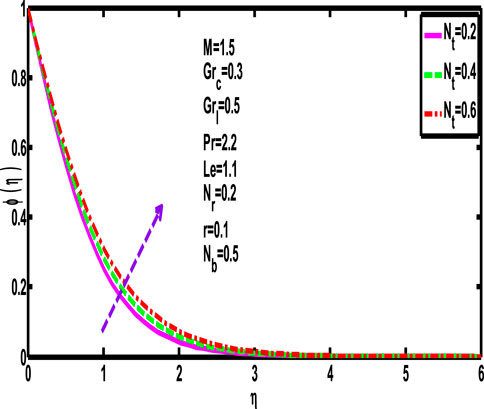
When the thermophoresis parameter $N_t$ is slightly increased, the temperature distribution of the fluid flow is increased sharply. A slight modification in a thermophoresis parameter causes fluid particles to move quickly, greatly increasing the temperature distribution. As a result, the temperature distribution has significantly increased, as shown in Figure 8, although the value of $N_t$ has only slightly increased. The transport force brought about by a temperature gradient is called thermophoresis. At the same temperature, the particles’ kinetic energies are similar, but lighter particles move faster than heavier particles; so, strong kinetic energy of fluid’s particles implies the increase in fluid’s temperature.

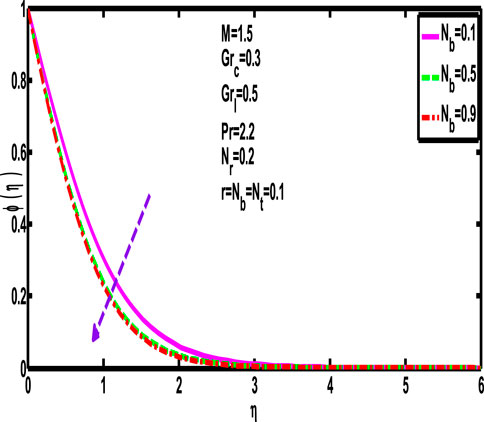
5.7 Effect of ${\mathit{N}}_{\mathit{b}}$ on $\mathit{\theta }\left(\mathit{\eta }\right)$

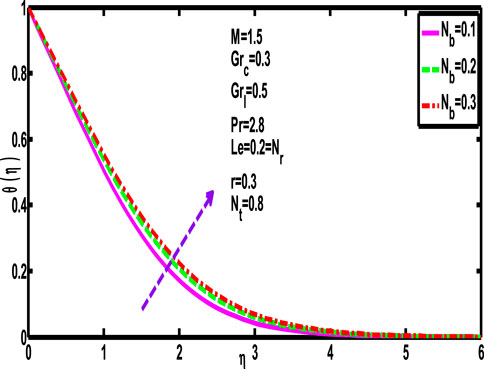
The fluid temperature gradient increases with an increase in the Brownian motion parameter, $N_b$, as a result of the particles moving from an area of low to high temperatures. The fluid particles start moving quickly from regions of lower to higher temperatures as the Brownian motion of the particles grows and as the random acceleration increases the temperature gradient of the fluid flow, as shown in Figure 9. Since heat gives particles energy, the Brownian motion is directly related to temperature as it is the random movement of particles. As a result, it increases when the temperature increases. However, the size of the attached particle and the medium’s viscosity and concentration have an inverse relationship with it.

5.8 Effect of $\mathit{Pr}$ on $\mathit{\phi }\left(\mathit{\eta }\right)$

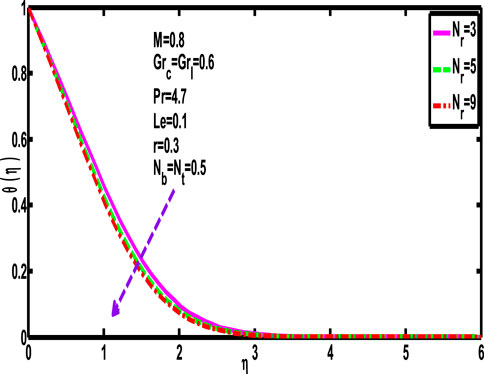
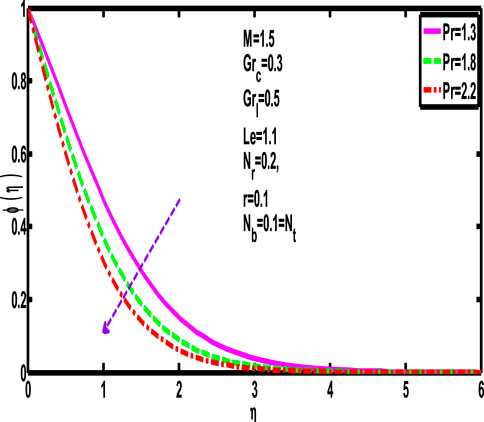
Prandtl numbers’ impact on the concentration distribution $\phi \left(\eta \right)$ is explained in Figure 10. The Prandtl number has a reverse relationship with the concentration profile. As the Prandtl number increases, the concentration profile $\phi \left(\eta \right)$ decreases. Since the Prandtl number is the ratio of momentum diffusivity to thermal diffusivity, when this number increases, the momentum dispersion of molecules increases; however, thermal dispersion drops, so the concentration of nanoparticles become weak and particles disperse more rapidly, as a result of which the concentration profile $\phi \left(\eta \right)$ drops down.

5.9 Effect of $\mathit{L}\mathit{e}$ on $\mathit{\phi }\left(\mathit{\eta }\right)$

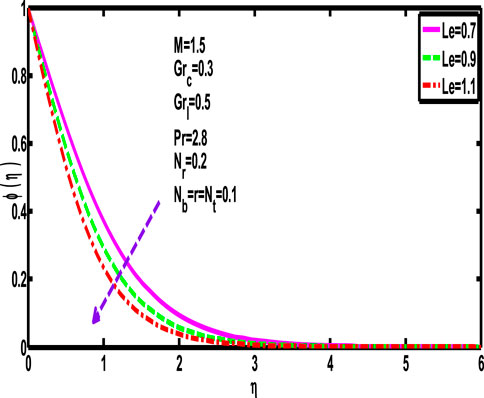
As probable, it is established that the concentration profile $\phi \left(\eta \right)$ is the cumulative profile for the Lewis number $Le$. On the contrary, shrink aging in the Lewis number $Le$ indicates an increase in the nanoparticle segment (Figure 11). Because of the slow movement of particles, the Lewis number actually reflects the relationship between heat and mass transfer. When the Lewis number rises, mass diffusivity and the concentration profile also decrease.

5.10 Effect of ${\mathit{N}}_{\mathit{b}}$ on $\mathit{\phi }\left(\mathit{\eta }\right)$

The fluid concentration gradient $\phi \left(\eta \right)$ declines with an increase in the Brownian motion parameter $N_b$ as a result of particles moving from an area of high to low concentration. Since the Brownian motion of fluid particles is a random movement, they start moving quickly from regions of higher to lower concentration. When the Brownian motion of particles grows, random acceleration decreases the concentration gradient of the fluid flow, as shown in Figure 12.

5.11 Effect of ${\mathit{N}}_{\mathit{t}}$ on $\mathit{\phi }\left(\mathit{\eta }\right)$

When the thermophoresis parameter $N_t$ is slightly increased, the concentration distribution of the fluid flow is increased sharply. A slight modification of a thermophoresis parameter causes fluid particles to move quickly, greatly increasing the concentration distribution among the particles of fluid. As a result, the concentration distribution is significantly increased, as shown in Figure 13.

6 Conclusion

Enhancing heat transfer is a topic of current interest in many fields. A new type of heat transfer fluid called nanofluid may be an effective means of enhancing heat transmission. The flow properties need to be approximated by numerical research. The broad range of applications for MHD, from biological applications to renewable energy generation, has persuaded researchers of the significance of this impact to continue their investigation. In heat transferal infrastructure, mixed convection is a complex state that is essential to enhancing flow mixing and heat transfer operations. Technological and industrial applications in nature that display the mixed convection flow conduct are somewhat solar energy recipients displayed to atmospheric flows, gadgets chilled by fans, nuclear power plant emergency shutdown cooling, exchangers for energy positioned in low-velocity surroundings, and flows in the marine environment and ambiance.

The following significant conclusions can be obtained from the discoveries of the recent study:

• It has been noted that the velocity profile exhibits an increasing trend for the free stream velocity ratio.

• Furthermore, the notable phenomenon occurs when an increase in the Hartmann number causes the resistive flow to occur within the boundary layer; so the velocity profile exhibits a decreasing trend with an increase in M-value.

• The temperature profile is instead caused by radiation factors. We have discovered that the temperature profile is improved using the Hartmann number M and the slip parameter.

• The Lewis number and slip parameter increase and have an undesirable impression on the heat flux.

• Both the thermophoresis and Brownian motion parameters raise the fluid's temperature, but the thermophoresis parameter raises the concentration of nanoparticles while the Brownian motion parameter lowers it.

• The velocity of fluid increases for Grashof numbers and also for the Prandtl number; the temperature of fluid increases, but the concentration of the fluid drops down.

Data availability statement

The original contributions presented in the study are included in the article; further inquiries can be directed to the corresponding author.

Author contributions

SM: funding acquisition, supervision, and writing–review and editing. SR: methodology, conceptualization, validation, and writing–original draft. MM: investigation, methodology, supervision, and writing–review and editing. TA: investigation, methodology, software, and writing–original draft. QU: validation, writing–review and editing, resources, supervision, and visualization. RS: writing–review and editing and validation.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by the Deanship of Scientific Research, Vice Presidency for Graduate Studies and Scientific Research, King Faisal University, Saudi Arabia (Grant No. 5841).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Akbar, N. S., Nadeem, S., Ul Haq, R., and Khan, Z. H. (2014). Nanoparticles fraction on the peristaltic flow of third order fluid. J. Comput. Theor. Nanosci. 11 (1), 47–52. doi:10.1166/jctn.2014.3315

CrossRef Full Text | Google Scholar

Aziz, A., and Khan, W. A. (2012). Natural convective boundary layer flow of a nanofluid past a convectively heated vertical plate. Int. J. Therm. Sci. 52, 83–90. doi:10.1016/j.ijthermalsci.2011.10.001

CrossRef Full Text | Google Scholar

Buongiorno, J. (2006). Convective transport in nanofluids. J. heat Transf. 128 (3), 240–250. doi:10.1115/1.2150834

CrossRef Full Text | Google Scholar

Choi, S. U. S., and Eastman, J. A. (1995). Enhancing thermal conductivity of fluids with nanoparticles. Lemont, IL USA: Argonne National Lab.

Google Scholar

Farooq, U., Hayat, T., Ahmed, A., and Liao, S. J. (2015). Series solutions of non-similarity boundary layer flows of nano-fluids over stretching surfaces. Numer. Algorithms 70 (1), 43–59. doi:10.1007/s11075-014-9934-9

CrossRef Full Text | Google Scholar

Farooq, U., Munir, S., Malik, F., Ahmad, B., and Lu, D. (2020). Aspects of entropy generation for the non-similar three-dimensional bioconvection flow of nanofluids. AIP Adv 10 (7), doi:075110doi:10.1063/1.5142877

CrossRef Full Text | Google Scholar

Hamad, M. A. A., and Ferdows, M. (2012). Similarity solution of boundary layer stagnation-point flow towards a heated porous stretching sheet saturated with a nanofluid with heat absorption/generation and suction/blowing: a Lie group analysis. Commun. Nonlinear Sci. Numer. Simul. 17 (1), 132–140. doi:10.1016/j.cnsns.2011.02.024

CrossRef Full Text | Google Scholar

Haq, R.Ul, Khan, Z. H., and Khan, W. A. (2014). Thermophysical effects of carbon nanotubes on MHD flow over a stretching surface. Phys. E Low-dimensional Syst. Nanostructures 63, 215–222. doi:10.1016/j.physe.2014.06.004

CrossRef Full Text | Google Scholar

Haq, R.U., Nadeem, S., Khan, Z. H., and Noreen Sher Akbar, (2015). Thermal radiation and slip effects on MHD stagnation point flow of nanofluid over a stretching sheet. Phys. E Low-dimensional Syst. nanostructures 65, 17–23. doi:10.1016/j.physe.2014.07.013

CrossRef Full Text | Google Scholar

Ishak, A. R. N., and Pop, I. (2006). Magnetohydrodynamics stagnation point flow towards a stretching vertical sheet. Magnetohydrodynamics 42 (1), 77–90. doi:10.22364/mhd

CrossRef Full Text | Google Scholar

Khan, W. A., and Pop, I. (2010). Boundary-layer flow of a nanofluid past a stretching sheet. Int. J. heat mass Transf. 53 (11-12), 2477–2483. doi:10.1016/j.ijheatmasstransfer.2010.01.032

CrossRef Full Text | Google Scholar

Khan, Z. H., Khan, W. A., Qasim, M., and Shah, I. A. (2013). MHD stagnation point ferrofluid flow and heat transfer toward a stretching sheet. IEEE Trans. Nanotechnol. 13 (1), 35–40. doi:10.1109/tnano.2013.2286991

CrossRef Full Text | Google Scholar

Khanafer, K., Vafai, K., and Lightstone, M. (2003). Buoyancy-driven heat transfer enhancement in a two-dimensional enclosure utilizing nanofluids. Int. J. heat mass Transf. 46 (19), 3639–3653. doi:10.1016/s0017-9310(03)00156-x

CrossRef Full Text | Google Scholar

Kousar, N., and Mahmood, R. (2013). Series solution of non-similarity boundary-layer flow in porous medium. Scientific Research Publishing, Wuhan, China.

Google Scholar

Layek, G. C., Mukhopadhyay, S., and Samad, Sk A. (2007). Heat and mass transfer analysis for boundary layer stagnation-point flow towards a heated porous stretching sheet with heat absorption/generation and suction/blowing. Int. Commun. heat mass Transf. 34 (3), 347–356. doi:10.1016/j.icheatmasstransfer.2006.11.011

CrossRef Full Text | Google Scholar

Makinde, O. D., and Aziz, A. (2011). Boundary layer flow of a nanofluid past a stretching sheet with a convective boundary condition. Int. J. Therm. Sci. 50 (7), 1326–1332. doi:10.1016/j.ijthermalsci.2011.02.019

CrossRef Full Text | Google Scholar

Martin, M. J., and Boyd, I. D. (2006). Momentum and heat transfer in a laminar boundary layer with slip flow. J. Thermophys. heat Transf. 20 (4), 710–719. doi:10.2514/1.22968

CrossRef Full Text | Google Scholar

Nadeem, S., and Hussain, S. T. (2014). Flow and heat transfer analysis of Williamson nanofluid. Appl. Nanosci. 4 (8), 1005–1012. doi:10.1007/s13204-013-0282-1

CrossRef Full Text | Google Scholar

Nadeem, S., Ul Haq, R., and Khan, Z. H. (2014). Numerical solution of non-Newtonian nanofluid flow over a stretching sheet. Appl. Nanosci. 4 (5), 625–631. doi:10.1007/s13204-013-0235-8

CrossRef Full Text | Google Scholar

Nadeem, S., Ul Haq, R., and Noreen Sher, A. (2013). MHD three-dimensional boundary layer flow of Casson nanofluid past a linearly stretching sheet with convective boundary condition. IEEE Trans. Nanotechnol. 13 (1), 109–115. doi:10.1109/tnano.2013.2293735

CrossRef Full Text | Google Scholar

Nadeem, S., Ul Haq, R., Noreen Sher, A., Lee, C., and Khan, Z. H. (2013). Numerical study of boundary layer flow and heat transfer of Oldroyd-B nanofluid towards a stretching sheet. PloS one 8 (8), e69811. doi:10.1371/journal.pone.0069811

PubMed Abstract | CrossRef Full Text | Google Scholar

Nawaz, Y., Abodayeh, K., Muhamamd, S. A., and Muhammad, U. A. (2021). A third-order two-step numerical scheme for heat and mass transfer of chemically reactive radiative MHD power-law fluid. Adv. Mech. Eng. 13 (10), 16878140211054983. doi:10.1177/16878140211054

CrossRef Full Text | Google Scholar

Nawaz, Y., Muhammad, S. A., and Abodayeh, K. (2022). A compact numerical scheme for the heat transfer of mixed convection flow in quantum calculus. Appl. Sci. 12 (10), 4959. doi:10.3390/app12104959

CrossRef Full Text | Google Scholar

Nawaz, Y., Muhammad, S. A., and Abodayeh, K. (2022). A third-order two-stage numerical scheme for fractional Stokes problems: a comparative computational study. J. Comput. Nonlinear Dyn. 17 (10), 101004. doi:10.1115/1.4054800

CrossRef Full Text | Google Scholar

Nawaz, Y., Muhammad, S. A., Abodayeh, K., and Bibi, M. (2022). Finite element method for non-Newtonian radiative maxwell nanofluid flow under the influence of heat and mass transfer. Energies 15 (13), 4713. doi:10.3390/en15134713

CrossRef Full Text | Google Scholar

Nawaz, Y., Muhammad, S. A., Muhammad, U. A., and Abodayeh, K. (2022). A class of unconditionally stable shooting methods with application to radiative Darcy–forchheimer flow. Int. J. Comput. Methods 19 (05), 2250008. doi:10.1142/S0219876222500086

CrossRef Full Text | Google Scholar

Nawaz, Y., Muhammad, S. A., and Shatanawi, W. (2022). A new fourth-order predictor–corrector numerical scheme for heat transfer by Darcy–Forchheimer flow of micropolar fluid with homogeneous–heterogeneous reactions. Appl. Sci. 12 (12), 6072. doi:10.3390/app12126072

CrossRef Full Text | Google Scholar

Nawaz, Y., Muhammad, S. A., Shatanawi, W., and Bibi, M. (2022). A new explicit numerical schemes for time-dependent PDEs with application to pressure driven fluid flow in a rectangular duct. Energies 15 (14), 5145. doi:10.3390/en15145145

CrossRef Full Text | Google Scholar

Nawaz, Y., Muhammad, S. A., Shatanawi, W., and Muhammad Usman Ashraf, (2022). A fourth order numerical scheme for unsteady mixed convection boundary layer flow: a comparative computational study. Energies 15 (3), 910. doi:10.3390/en15030910

CrossRef Full Text | Google Scholar

Nazar, R., Amin, N., Filip, D., and Pop, I. (2004). Unsteady boundary layer flow in the region of the stagnation point on a stretching sheet. Int. J. Eng. Sci. 42 (11-12), 1241–1253. doi:10.1016/j.ijengsci.2003.12.002

CrossRef Full Text | Google Scholar

Pop, S. R., Pop, I., and Grosan, T. (2005). Radiation effects on the flow near the stagnation point of a stretching sheet. Tech. Mechanik-European J. Eng. Mech. 25 (2), 100–106.

Google Scholar

Ramesh, G. K., and Gireesha, B. J. (2014). Influence of heat source/sink on a Maxwell fluid over a stretching surface with convective boundary condition in the presence of nanoparticles. Ain Shams Eng. J. 5 (3), 991–998. doi:10.1016/j.asej.2014.04.003

CrossRef Full Text | Google Scholar

Reddy, T. S., Roja, P., Mohammed Ibrahim, S., Lorenzini, G., and Nor Azwadi Che Sidik, (2022). Characteristic of thermal radiation on MHD fluid stream of nano-fluid over an exponentially elongating sheet by means of warm and mass fluxes. CFD Lett. 14 (4), 80–90. doi:10.37934/cfdl.14.4.8090

CrossRef Full Text | Google Scholar

Shafiq, A., Andaç, B. Ç., and Tabassum, N. S. (2022). Significance of bioconvective flow of MHD thixotropic nanofluid passing through a vertical surface by machine learning algorithm. Chin. J. Phys. 80, 427–444. doi:10.1016/j.cjph.2022.08.008

CrossRef Full Text | Google Scholar

Shafiq, A., Andaç, B. Ç., and Tabassum, N. S. (2023). Significance of EMHD graphene oxide (GO) water ethylene glycol nanofluid flow in a Darcy–Forchheimer medium by machine learning algorithm. Eur. Phys. J. Plus 138 (3), 213. doi:10.1140/epjp/s13360-023-03798-5

CrossRef Full Text | Google Scholar

Shukla, H., Surati, H. C., and Timol, M. G. (2019). Local non-similar solution of powell-eyring fluid flow over a vertical flat plate. Appl. Appl. Math. Int. J. (AAM) 14 (2), 22.

Google Scholar

Sparrow, E. M., Quack, H., and Boerner, C. J. (1970). Local nonsimilarity boundary-layer solutions. AIAA J. 8 (11), 1936–1942. doi:10.2514/3.6029

CrossRef Full Text | Google Scholar

Uddin, Md., Khan, W. A., and Ismail, A. I. (2012). Scaling group transformation for MHD boundary layer slip flow of a nanofluid over a convectively heated stretching sheet with heat generation. Math. problems. Eng. 2012, 1–20. doi:10.1155/2012/934964

CrossRef Full Text | Google Scholar

You, X., Xu, H., and Liao, S. (2010). On the nonsimilarity boundary-layer flows of second-order fluid over a stretching sheet J. Appl. Mech. 77 (2), 021002. doi:10.1115/1.3173764

CrossRef Full Text | Google Scholar