- 1Department of Mathematics, Air University, PAF Complex E-9, Islamabad, Pakistan
- 2Department of Mathematics and Sciences, College of Humanities and Sciences, Prince Sultan University, Riyadh, Saudi Arabia
- 3Stochastic Analysis and Optimization Research Group, Department of Mathematics, Air University, PAF Complex E-9, Islamabad, Pakistan
- 4Department of Electrical and Computer Engineering, COMSATS University Islamabad, Wah Campus, G.T. Road, Wah Cantonment, Pakistan
This paper introduces an exponential time integrator scheme for solving partial differential equations in time, specifically addressing the scalar time-dependent convection-diffusion equation. The proposed second-order accurate scheme is demonstrated to be stable. It is applied to analyze the heat and mass transfer mixed convective flow of power-law nanofluid over flat and oscillatory sheets. The governing equations are transformed into a dimensionless set of partial differential equations, with the continuity equation discretized using a first-order scheme. The proposed time integrator scheme is employed in the time direction, complemented by second-order central discretization in the space direction for the momentum, energy, and nanoparticle volume fraction equations. Quantitative results indicate intriguing trends, indicating that an increase in the Prandtl number and thermophoresis parameter leads to a decrease in the local Nusselt number. This modified time integrator is a valuable tool for exploring the dynamics of unsteady power-law nanofluid flow over moving sheets across various scenarios. Its versatility extends to the examination of unstable fluid flows. This work improves engineering and technological design and operation in nanofluid dynamics. Improving numerical simulations’ precision and computational efficiency deepens our comprehension of fundamental physics, yielding helpful information for enhancing systems that rely on nanofluids.
1 Introduction
Numerous engineering applications can benefit from studying unstable nanofluid flows over moving surfaces, which has garnered much attention in fluid dynamics and heat transfer. The unique properties of nanofluids, which are mixtures of nanoparticles in regular fluids, make them promising tools for enhancing energy efficiency and heat transfer in a wide range of manufacturing operations. In unstable flow situations, fluid and heat transport processes change dynamically over time. Hence, a precise and efficient numerical technique is needed to produce accurate findings.
Various technical and scientific procedures depend on the movement of heat and mass. Recent years have seen a surge in interest in heat and mass transport within the power law of non-Newtonian nanofluid flow. The use of nanofluids has the potential to improve heat transfer efficiency.
A “nanofluid” is a fluid that contains suspended nanoparticles. Due to the nanoparticles’ enhanced thermal conductivity, the base fluid may be able to transmit heat more efficiently. The non-Newtonian behaviour of nanofluids makes it challenging to study their heat and mass transport, despite their intriguing characteristics.
Many people in the field of fluid dynamics have been interested in non-Newtonian nanofluids due to their complex heat and mass transfer features. Since these fluids are used in various contexts, from high-tech manufacturing to healthcare, precise and efficient numerical approaches are required to understand their elusive behavior.
Over the past 35 years, scientists have extensively studied the properties of differential air-heated cavities. These cavities contain two isothermal vertical walls and one adiabatic horizontal wall. Convective laminar and turbulent flows powered by buoyancy were reported by Markatos and Pericleous (Markatos and Pericleous, 1984). Coupled heat conduction across a wall with two-dimensional laminar internal convection was the subject of an early integrated experimental and computational investigation by Kim and Viskanta (Kim and Viskanta, 1984). De Valh Davis (De Vahl Davis, 1987) is credited with one of the seminal numerical research on natural convection in air-filled square cavities; he used the finite difference method to ascertain the initial exact findings concerning fluid mechanics and temperature distribution. The impact of the horizontal top and bottom wall boundary conditions on air natural convection in a cavity with large Rayleigh numbers was described experimentally and numerically by Wu et al. (Wu et al., 2006) and Bari et al. (Baïri et al., 2007), respectively. With internal partitions (Bilski et al., 1983; Kumar-Das and Kumar-Reddy, 2006; Wu and Ching, 2010), conducting solids (House et al., 1990), and local or volumetric heat sources [(Liaqat and Baytas, 2001; Kumar et al., 2022; Asghar et al., 2023; Kuznetsov and Sheremet, 2009)], among other situations, researchers have investigated the impact of solid objects within the cavity on natural convection.
Power law non-Newtonian nanofluid flows have been studied in terms of their heat and mass transport using exponential integrator techniques. Non-Newtonian fluid properties, such as viscosity and power-law index, have been studied (EL-Dabe et al., 2019) for their impacts on the velocities, temperatures, and concentrations of suspended nanoparticles. Researchers have examined the potential effects of the power-law index, nanoparticle volume fraction, nanoparticle type, and permeability parameter on nanofluid flow and heat transfer (Raju et al., 2015; Maleki et al., 2019). It has been found that the friction and heat transfer coefficients are affected by the power-law index and the Reynolds number (Raju et al., 2015). The heat transfer and two-dimensional flow of a non-Newtonian power-law nanofluid over a stretching surface have been the subject of numerical investigations (Afify and El-Aziz, 2017). According to reference (Eid and Mahny, 2017), non-Newtonian nanofluids can experience unstable boundary-layer convective heat and mass movement when a magnetic field is paired with heat generation or absorption.
The natural convection of non-Newtonian fluids is more difficult to understand since viscous forces are calculated using a nonlinear relation between shear stresses and the deformation rate. The effective viscosity is needed to calculate the viscous forces, and this can only be done by locating velocity gradients everywhere and at all times. Non-Newtonian phase change slurries with a power law have been described by Inaba et al. (Inaba et al., 2003) using the Rayleigh-Benard natural convection model. There have been many two-dimensional descriptions of laminar flows of non-Newtonian fluids, including flows in a vertical duct (Lorenzini and Biserni, 2003), from a vertical plate (Kumari and Nath, 2006), inside an enclosure with a micropolar fluid (Aydin and Pop, 2007), inside a power-law fluid with an applied magnetic field (Chen, 2008), inside porous media with viscoelastic fluids (Malashetty et al., 2011; Hirata et al., 2015), inside inclined cavities with Otswald de Waele fluids (Khezzar et al., 2012), and inside circular and square cylinders (Sasmal and Chhabra, 2012; Shyan et al., 2013). Oswald and Waele found that liquid foods had a nonNewtonian fluid character, and their research helped shed light on the part that natural convection plays in the transitory thermal procedures utilized in the food industry for pasteurization and sterilization (Moraga et al., 2011; Moraga and Lemus-Mondaca, 2011). The phenomenon of natural convection and solidification of water juices within inner cavities, induced by a combination of forces involving natural air convection, has been investigated. The study explores different configurations of inlet and outlet for cooling external air. Hershel-Bulkley, Casson, and Power law are the non-Newtonian rheological models used to explain fluid mechanics and heat transmission. The findings of this research have been documented and published in a scientific publication (Lemus et al., 2013).
There are several advantages to using exponential integrators in power law nanofluid flow for mass and heat transfer. The effects of thermophoresis and Brownian motion on heat transmission and nanoparticle volume fraction are investigated (Balaji et al., 2020). An effective way to get self-similar equations by using the right similarity transformation is with exponential integrators. Once these equations are known, they can be numerically solved using the Runge-Kutta method and shooting techniques (Ravnik and Tibaut, 2018). Researchers used the integrators discussed in the paper to understand better how different mass and heat fluxes affected the nanoparticle volume fraction parameter and temperature distribution (Ghosh and Mukhopadhyay, 2018). In addition, they allow us to study how Brownian motion and thermophoresis interact to affect heat transmission and nanoparticle volume fraction (Ellahi et al., 2016). Nevertheless, the abstracts do not address the potential drawbacks of using exponential integrators for this objective.
In (Shafiq et al., 2021), a new approach to solving numerical problems using artificial neural networks (ANN) combines the Levenberg-Marquard algorithm with multilayer perceptron (MLP) feed-forward back-propagation. This approach can be used to understand radiation, heat generation/absorption, and unsteady electrically conducting Williamson liquid flow along porous stretching surfaces. Thermodynamic boundary conditions, velocity, and thermal slip phenomena are all considered in the study of heat. This gap is filled in the article (Sindhu et al., 2023; Çolak et al., 2023) by talking about multilayer ANN with Bayesian regularisation for a generalized exponential model based on inverse power law (IPL) reliability measures. The fundamental goal (Upadhya et al., 2022) is to manage the flow, heat, and mass transfer of Casson and micropolar fluids and hybrid nanofluids (Casson, micropolar, silica, alumina, and water) along a curved stretched sheet. This study (Qureshi et al., 2023) aims to investigate the effects of a morphological nanolayer on the heat transfer characteristics and flow characteristics of a multi-hole-diaphragm (MHD) hybrid nanofluid formed by dispersing a polymer/CNT matrix nanocomposite material through orthogonal permeable discs. This study (Kavya et al., 2022) examines the fluid momentum and thermal energy parameters of a laminar, stable, incompressible, two-dimensional, non-Newtonian pseudo-plastic Williamson hybrid nanofluid flowing across a stretching cylinder. The effects of magnetohydrodynamics, thermal conduction, injection, heat generation, and suction and injection are all considered. The main objective of the (Zeeshan et al., 2023) study is to examine the nanofluid flow that occurs between two horizontal channels that are infinitely rotatable. You can stretch the lower plate because it is porous. We use graphs to discuss how physical parameters like chemical reactions, heat sources and sinks, Hall current, and thermal properties affect concentration, temperature, and velocity profiles. The three-dimensional stable axisymmetric boundary layer over a permeable moving plate is investigated in depth in this study (Lund et al., 2023). As its base liquid, water contains two or more distinct types of nanoparticles in the hybrid nanofluid.
Computational fluid dynamics utilizing an exponential integrator method is the focus of this investigation. This method, famous for its proficiency in handling rigid and very oscillatory systems, elucidates the heat and mass transport phenomena in Power Law non-Newtonian nanofluid flows. This research will combine theoretical analysis with numerical simulations to better understand the intricate interplay between fluid rheology, nanoscale interactions, and heat-mass exchanges. In what follows, we will provide a comprehensive examination of the intricacies of the exponential integrator scheme, shedding light on the intriguing subject of non-Newtonian nanofluid dynamics.
In many contexts, the dynamics of unsteady power-law nanofluid flow over moving sheets can be studied with the help of the modified time integrator. For example, one can use nanofluid flow analysis to understand better how nanofluids behave in systems like heat exchangers and solar panels. Beyond that, it might be used to study the dynamics of nanofluidic flow in the human body, especially in the cardiovascular system. Here are a few concrete instances:
1. By manipulating nanofluids over solar panels, we can enhance the efficiency of solar energy harvesting.
2. By guiding a flow of nanofluids over heat exchangers, it is possible to boost heat transmission efficiency.
3. Drug and other therapeutic agent distribution can be enhanced by harnessing the movement of nanofluids in the circulatory system.
4. Understanding how nanofluids move in an unsteady environment is essential to create cutting-edge cooling systems for high-performance engines, electronic components, and aerospace applications. In industries where lightweight materials and compact designs are prioritized, this research work can improve the accuracy of simulations to aid in the design of more effective cooling solutions.
Our findings can enhance forecasting and design in these practical contexts, leading to savings, efficiencies, and reduced environmental impact. By tackling the challenges of unsteady power-law nanofluid flow over moving sheets, our research could help push forward several engineering disciplines and create cutting-edge, environmentally friendly technology.
The governing equations that describe the unsteady flow of power-law nanofluid over moving sheets are commonly referred to as the Navier-Stokes equations. The abovementioned equations exhibit nonlinearity and coupling, making them challenging to solve by analytical methods. The equations are commonly solved using numerical methods. Numerous numerical methods exist that can solve some particular differential equations. Some numerical methods can be preferred because they give large stability regions. Among the class of numerical methods, the explicit class of finite difference plays a vital role in finding the solution for linear and nonlinear differential equations. One of the advantages of using an explicit scheme is to avoid linearization for nonlinear differential equations. The other advantage is that these schemes can be used without adopting extra iterative schemes for solving difference equations. The class of exponential integrators are those numerical methods that can handle stiff problems. This contribution modifies and applies an exponential time integrator scheme to solve unsteady power-law nanofluid flow over the moving sheets. The modified exponential integrator scheme successfully solves the dimensionless forms of governing equations. The modified time integrator was validated by comparing its results against those obtained from the conventional explicit time integrator and experimental research. Based on the data, it can be concluded that the modified time integrator has higher accuracy and efficiency when compared to the standard explicit time integrator.
The findings of this study, which provide a novel viewpoint, fill a significant gap in the existing body of research on nanofluid dynamics. An exponential time integrator system for solving time-dependent partial differential equations (PDEs) is presented and thoroughly examined in our research. This system is distinct from those presented in earlier works or studies. We demonstrate that this technique is accurate to the second order and stable to a high degree. This method investigates the dynamics of unsteady power-law nanofluid flows over moving sheets in various environments.
This state-of-the-art temporal integrator offers a fresh perspective on non-stationary phenomena in the context of power-law nanofluid flows. A computational tool for researching nanofluid behavior in settings with heat and mass transfer over oscillatory sheets, which answers a need in the literature, is provided by our work.
This study aspires to improve the subject by exploring hitherto unexplored areas regarding the dynamics of unstable nanofluid flows and by enhancing the precision and efficiency of numerical simulations. Our work represents a significant step forward in the ongoing effort to understand nanofluid dynamics and its potential applications in engineering and research.
2 Proposed exponential time integrator scheme
To propose a numerical scheme, one should examine a partial differential equation in the following format:
The first and second stages of the schemes are explicit. For constructing the first stage of the scheme, Eq. 1 can be written as
The first stage of the proposed scheme can be expressed as
Equation 3 can be written as:
where
Re-write Eq. 4 as
Let the second stage of the scheme be expressed as
Where
Equation 6 can be written as
Now consider the Taylor series expansion for
By substituting Taylor series expansion for
Re-write Eq. 9 as:
By substituting Eq. 5 into Eq. 10 it is obtained
Equation 11 can be expressed as;
Equating the coefficients of
Upon solving Eqs. 13–15 it is obtained
Therefore for
Let central difference numerical approximation for
where
3 Stability analysis
This study will use either a Von Neumann stability or Fourier series analysis. For the said purpose, consider a two-dimensional convection-diffusion partial differential equation is expressed as:
The proposed scheme is applied to the time variable of Eq. 21, and space terms are discretized by central difference approximation. Equation 21 is discretized as
where
According to Fourier series analysis, the following transformations can be considered.
where
Some of the transformations are substituted into Eq. 22 and dividing both sides by
Using trigonometric identities, Eq. 25 can be expressed as:
Let
Re-write Eq. 26 as
Now, substituting some of the transformations from (24) into Eq. 23 and dividing both sides by
Using trigonometric identities, Eq. 28 can be expressed as:
Putting the expression for
The amplification factor can be written as:
Therefore, stability condition can be expressed as:
where
The stability analysis of the scalar equation is provided, and now convergence for the partial differential equation system will be provided. To achieve this aim, consider the system of partial differential equations in the vector-matrix equation as:
Discretize Eq. 33 using the first stage of the proposed scheme it is obtained.
Discretizing Eq. 33 using the second stage of the proposed scheme gives
Theorem: The proposed exponential scheme converges conditionally for the system of PDEs (33).
Proof: To prove this Theorem, consider the exact scheme of the exponential scheme as
By subtracting Eq. 34 from Eq. 36 and using
Applying the norm on both sides of Eq. 38 that yields
Since
Now subtracting Eq. 37 from Eq. 35 it is obtained
Applying the norm on both sides of Eq. 41 gives
Re-write Eq. 42 as:
By using inequality (40) into (43), it yields
Rearranging inequality (44) as
where
Put
Since
Put
Similarly, if it is continued, then for finite
For large
4 Problem formulation
Consider a laminar, two-dimensional, unsteady, incompressible non-Newtonian fluid flow over the moving plate. The
Subject to the boundary conditions
and initial conditions are given as
where
By considering the following transformations
where
where
The dimensionless boundary conditions can be expressed as
and dimensionless initial conditions can be expressed as
where
The skin friction coefficient, local Nusselt, and Sherwood numbers are defined as
where
Under the transformations (56) dimensionless skin friction coefficients, local Nusselt number and Sherwood number are expressed as
Physical interoperation of the parameters: Our research seeks to understand the physical effects of these parameters on related profiles, offering critical clues about the intricate relationship between forces and phenomena that control nanofluid dynamics. Each parameter’s effect on fluid behavior, heat transfer, and mass transport can be better understood with the help of the trends that have been noticed.
Hartmann Number
Reynolds Number
Prandtl Number
Schmidt Number
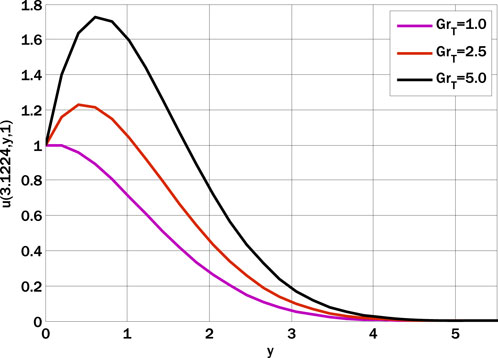
Grashof Numbers
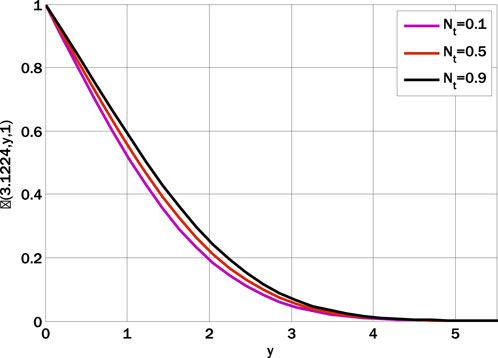
Thermophoresis
Reaction Rate Parameter
5 Results and discussions
A novel approach is presented in this study, wherein an exponential integrator technique is employed to compute numerical solutions for time-dependent partial differential equations. The scheme was proven conditionally stable for time-dependent convection-diffusion equations by employing von Neumann stability analysis. The scheme can be proven consistent because it is constructed using Taylor series expansions. The Lax equivalence theorem can be applied to ensure the convergence of the proposed numerical scheme. Due to the second-order accuracy of the proposed scheme, the result(s) obtained by the scheme is/are more accurate than those produced by the first-order exponential scheme. Since the proposed scheme is explicit, it can solve differential equations without linearising them. So, this explicit scheme can be applied to any linear and nonlinear differential equations without adopting any iterative scheme. So, this is one of the advantages of using the exponential proposed scheme. The time variable is represented in the outermost loop of the Matlab code, as the scheme is explicit. The interior loops denote the spatial directions.
Additionally, the boundary conditions are specified within the circuits. The scheme converges on a solution without needing an additional iterative scheme. One of the primary benefits of employing explicit schemes is this; however, appropriate step sizes must be selected to ensure that the scheme produces stable solutions. Consequently, the time needed to obtain a converged solution from these schemes is reduced. However, implicit schemes occasionally offer the benefit of a large step size; thus, obtaining the solution with a large step size is possible. However, doing so may require considerable time if an iterative scheme is employed.
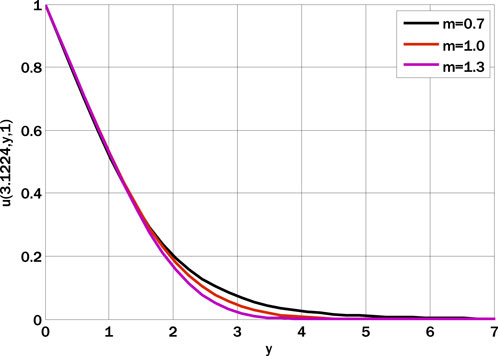
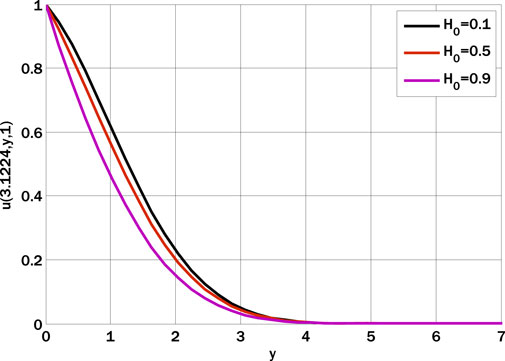
Figure 1 shows the velocity profile by varying
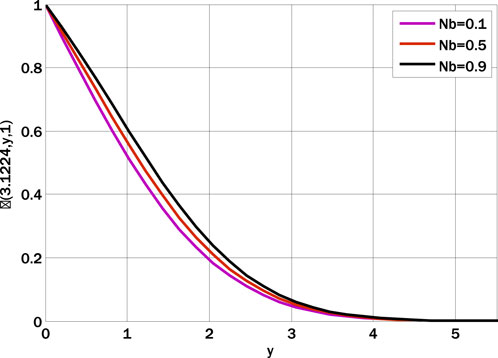
FIGURE 4. Effect of Brownian motion parameter on temperature profile using
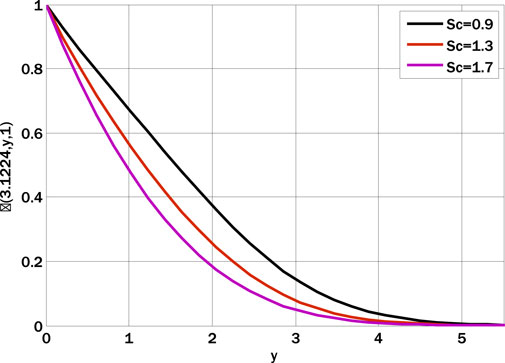
FIGURE 6. Effect of Schmidt number on nanoparticles volume fractions profile using
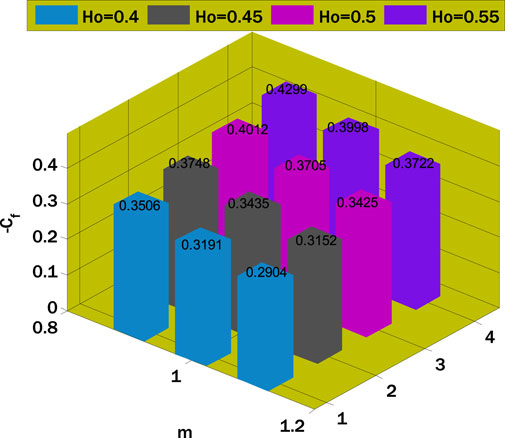
The nanoparticle volume fraction decreases as the Schmidt number increases since the relationship between the two quantities is inversely proportional. Figure 7 shows how the Hartmann number and m affect the negative skin friction coefficient. The negative skin friction coefficient decays by rising
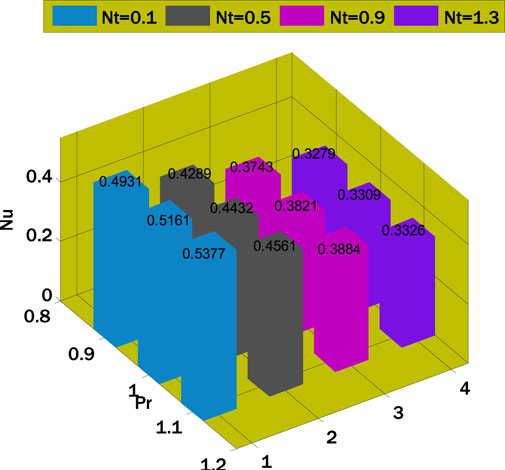
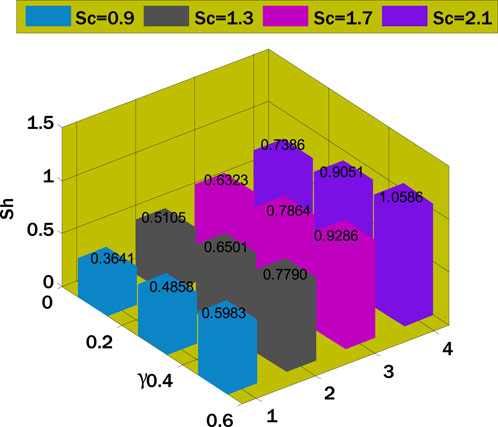
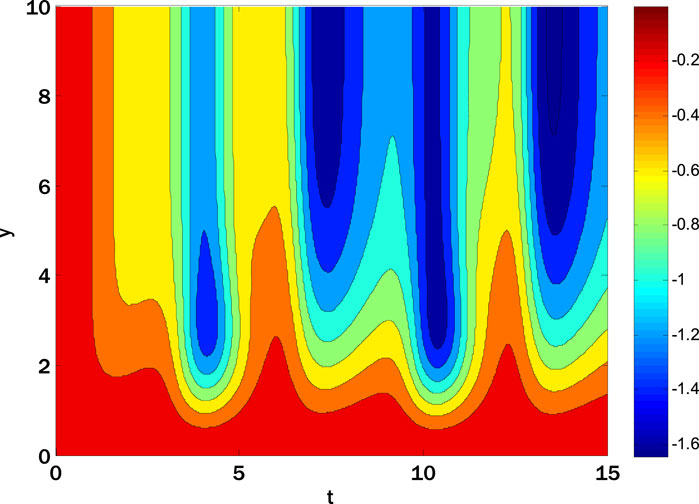
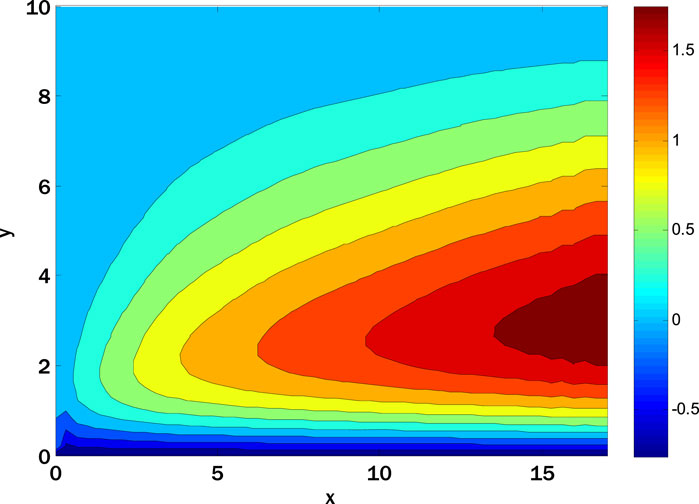
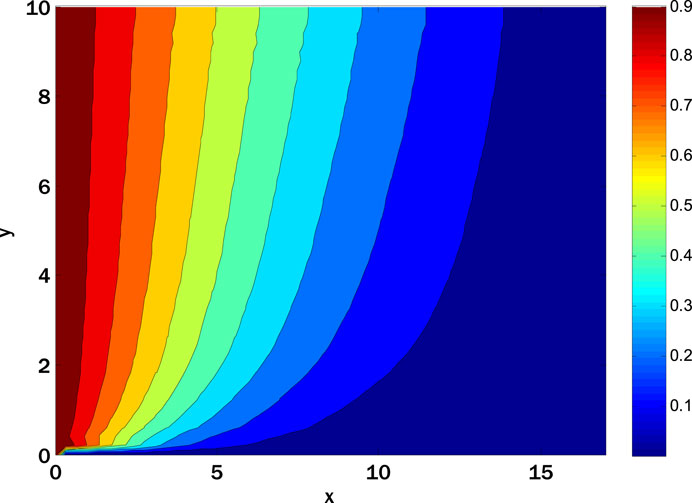
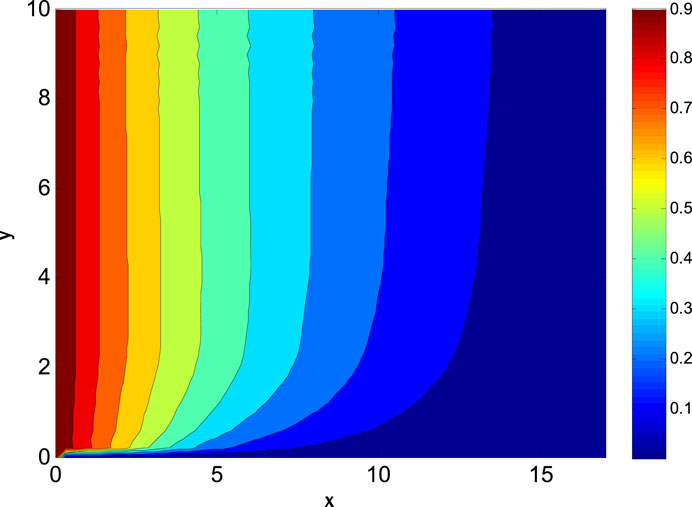
The thermal conductivity rises by enhancing the thermophoresis parameter, and consequently, conductive heat transfer rises, so the local Nusselt number decays. The nanoparticle volume fraction as a function of the reaction rate parameter and the Schmidt number is shown in Figure 9. Figure 9 delves into the complex interplay of the Schmidt number, the reaction rate parameter, and the nanoparticle volume percentage. A noticeable pattern shows that the local Sherwood number increases when the response rate parameter and Schmidt number go up. The mass diffusivity affects the local Sherwood number, which affects the diffusion rate as the Schmidt number increases. For the oscillatory sheet example, the contour plots (Figures 10–14) display the nanoparticle volume velocities, temperatures, and percentages. The second contour map uses geographic and temporal variables, although the first employs spatial coordinates. Looking at these photographs, you can understand the flow dynamics across the oscillatory sheet. The contour plots reveal intricate patterns and variations in the nanoparticle distribution, velocity, and temperature, which provide light on the system’s transient behavior. The dual-variable contour plots offer a new perspective by displaying the changes in these variables over time and space. Visualizations like these aid in painting a clearer image of the complex interplay of factors influencing unstable power-law nanofluid movement. When studying heat and mass transfer phenomena, it is essential to consider numerous factors to comprehend the system’s dynamics fully. The observed patterns and trends demonstrate this.
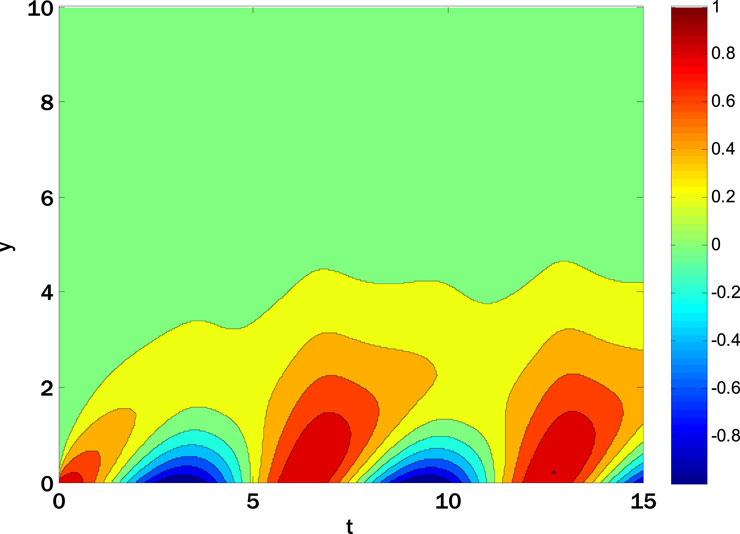
FIGURE 10. Contour plot for the horizontal component of velocity profile over
6 Conclusion
This article discusses how to modify an explicit time integrator to account for unstable power-law nanofluid flow over moving sheets; this work has significant ramifications for many different areas. Since this finding enhances our understanding of the behavior of nanofluids in unsteady flow conditions and the accuracy of numerical models, it has far-reaching consequences for many branches of engineering and technology. We tweaked an exponential time integration technique to deal with PDEs that change over time and used Taylor series expansion to build our new approach. The convergence of the modified exponential scheme has also been provided for a system of parabolic equations. Moreover, a mathematical two-dimensional model for the power-law nanofluid flow over the surfaces has also been presented. The proposed exponential scheme has solved its dimensionless form, and first and second-order difference formulas have been employed for space terms. The modified time integrator can investigate unsteady power-law nanofluid flow over moving sheets. It can also be applied to investigating various forms of non-steady fluid motion. The concluding points can be expressed as
1. Increasing the Hartmann number increased the negative skin friction coefficient.
2. Increasing the Prandtl number and the thermophoresis parameter led to a decline in the local Nusselt number.
3. Both the Schmidt number and the response rate parameter are increasing, which results in a rise in the local Sherwood number.
Our study of unstable power-law nanofluid flow over moving sheets is an essential addition to science and engineering in a world with a rising demand for efficient and sustainable solutions. It paves the way for exploiting nanofluids’ special features to solve some of the most challenging problems in today’s high-tech world. This study lays the groundwork for further research and the expansion of novel applications across various sectors. This research demonstrates that the modified time integrator helps investigate nanofluids’ non-stationary power-law flow over vibrating sheets. The precision and efficiency of the improved time integrator, as well as its potential application to more complex issues, might be further explored in future research.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
YN: Conceptualization, Investigation, Software, Writing–original draft. MA: Methodology, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing. KA: Formal Analysis, Funding acquisition, Project administration, Writing–review and editing. AS: Data curation, Formal Analysis, Resources, Visualization, Writing–review and editing. UJ: Data curation, Investigation, Project administration, Resources, Validation, Writing–review and editing.
Funding
The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.
Acknowledgments
The authors wish to express their gratitude to Prince Sultan University for facilitating the publication of this article through the Theoretical and Applied Sciences Lab.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Afify, A. A., and El-Aziz, M. A. (2017). Lie group analysis of flow and heat transfer of non-Newtonian nanofluid over a stretching surface with convective boundary condition. Pramana 88, 31–10. doi:10.1007/s12043-016-1336-1
Asghar, Z., Khalid, U., Nazeer, M., Rasheed, H. S., and Kausar, A. (2023). Computational study of flow and heat transfer analysis of Ellis fluid model in complicated divergent channel. Mod. Phys. Lett. B, 2450119. doi:10.1142/s0217984924501197
Aydin, O., and Pop, I. (2007). Natural convection in a differentially heated enclosure filled with a micropolar fluid. Int. J. Therm. Sci. 46, 963–969. doi:10.1016/j.ijthermalsci.2006.11.018
Baïri, A., Laraqi, N., and García de María, J. M. (2007). Numerical and experimental study of natural convection in tilted parallelepipedic cavities for large Rayleigh numbers. Exp. Therm. Fluid Sci. 31, 309–324. doi:10.1016/j.expthermflusci.2006.04.017
Balaji, N., Rao, B. M., Kumar, N. S., and Raju, C. S. K. (2020). Heat transfer flow of nanofluid over an exponentially shrinking porous sheet with heat and mass fluxes. AIP Conf. Proc. 2277 (1). doi:10.1063/5.0025216
Bilski, S. M., Lloyd, J. R., and Yang, K. T. (1983). An experimental investigation of the laminar natural convection velocity in square and partitioned enclosures. Proc. 8th Int. Heat. Transf. Conf. San Francisco, CA, August, 1983, 323e9. doi:10.1615/IHTC8.3070
Chen, C. H. (2008). Effects of magnetic field and suction/injection on convection heat transfer of non-Newtonian power-law fluids past a power-law stretched sheet with surface heat flux. Int. J. Therm. Sci. 47, 954–961. doi:10.1016/j.ijthermalsci.2007.06.003
Çolak, A. B., Sindhu, T. N., Lone, S. A., Shafiq, A., and Abushal, T. A. (2023). Reliability study of generalized Rayleigh distribution based on inverse power law using artificial neural network with Bayesian regularization. Tribol. Int. 185, 108544. doi:10.1016/j.triboint.2023.108544
De Vahl Davis, G. (1987). Natural convection of air in a square cavity: a benchmark numerical solution. Int. J. Numer. Methods Fluids 3, 249–264. doi:10.1002/fld.1650030305
Eid, M. R., and Mahny, K. L. (2017). Unsteady MHD heat and mass transfer of a non-Newtonian nanofluid flow of a two-phase model over a permeable stretching wall with heat generation/absorption. Adv. Powder Technol. 28 (11), 3063–3073. doi:10.1016/j.apt.2017.09.021
El-Dabe, N. T., Attia, H. A., Essawy, M. A., Abd-elmaksoud, I. H., Ramadan, A. A., and Abdel-Hamid, A. H. (2019). Nonlinear heat and mass transfer in a thermal radiated MHD flow of a power-law nanofluid over a rotating disk. SN Appl. Sci. 1, 551–620. doi:10.1007/s42452-019-0557-6
Ellahi, R., Hassan, M., and Zeeshan, A. (2016). A study of heat transfer in power law nanofluid. Therm. Sci. 20 (6), 2015–2026. doi:10.2298/tsci150524129e
Ghosh, S., and Mukhopadhyay, S. (2018). Flow and heat transfer of nanofluid over an exponentially shrinking porous sheet with heat and mass fluxes. Propuls. Power Res. 7 (3), 268–275. doi:10.1016/j.jppr.2018.07.004
Hayat, H. U. T., Ahmad, S., Alhodaly, M.Sh., and Alhodaly, M. S. (2021). Entropy generation and heat transfer analysis in power-law fluid flow: finite difference method. Int. Commun. Heat Mass Transf. 122, 105111. doi:10.1016/j.icheatmasstransfer.2021.105111
Hirata, S. C., Ella Eny, G., and Ouarzazi, M. N. (2015). Nonlinear pattern selection and heat transfer in thermal convection of a viscoelastic fluid saturating a porous medium. Int. J. Therm. Sci. 95, 136–146. doi:10.1016/j.ijthermalsci.2015.01.002
House, J., Beckermann, C., and Smith, T. (1990). Effect of a centered conducting body on a natural convection heat transfer in an enclosure. Numer. Heat. Transf. Part A 18, 213–225. doi:10.1080/10407789008944791
Inaba, H., Dai, C., and Horibe, A. (2003). Numerical simulation of Rayleigh–Bénard convection in non-Newtonian phase-change-material slurries. Int. J. Therm. Sci. 42, 471–480. doi:10.1016/s1290-0729(02)00048-0
Kavya, S., Nagendramma, V., Ahammad, N. A., Ahmad, S., Raju, C. S. K., and Shah, N. A. (2022). Magnetic-hybrid nanoparticles with stretching/shrinking cylinder in a suspension of MoS4 and copper nanoparticles. Int. Commun. Heat Mass Transf. 136, 106150. doi:10.1016/j.icheatmasstransfer.2022.106150
Khezzar, L., Siginer, D., and Vinogradov, I. (2012). Natural convection of power law fluids in inclined cavities. Int. J. Therm. Sci. 53, 8–17. doi:10.1016/j.ijthermalsci.2011.10.020
Kim, D., and Viskanta, R. (1984). Study of the effects of wall conductance on natural convection in differently oriented square cavities. J. Fluid Mech. 144, 153–176. doi:10.1017/s0022112084001555
Kumar, G. V., Rehman, K. U., Kumar, R. V. M. S. S. K., and Shatanawi, W. (2022). Unsteady magnetohydrodynamic nanofluid flow over a permeable exponentially surface manifested with non-uniform heat source/sink effects. Waves Random Complex Media, 1–19. doi:10.1080/17455030.2022.2072531
Kumar-Das, M., and Kumar-Reddy, S. (2006). Conjugate natural convection heat transfer in an inclined square cavity containing a conducting block. Int. J. Heat. Mass Transf. 49, 4987–5000. doi:10.1016/j.ijheatmasstransfer.2006.05.041
Kumari, M., and Nath, G. (2006). Conjugate mixed convection transport from a moving vertical plate in a non-Newtonian fluid. Int. J. Therm. Sci. 45, 607–614. doi:10.1016/j.ijthermalsci.2005.06.010
Kuznetsov, G., and Sheremet, M. (2009). Conjugate natural convection in an enclosure with local heat sources. Comput. Therm. Sci. 1, 341–360. doi:10.1615/computthermalscien.v1.i3.60
Lemus, R., Moraga, N., and Riquelme, J. (2013). Unsteady 2D conjugate natural nonNewtonian convection with non-Newtonian liquid sterilization in square cavity. Int. J. Heat. Mass Transf. 61, 73–81. doi:10.1016/j.ijheatmasstransfer.2013.01.079
Liaqat, A., and Baytas, A. (2001). Conjugate natural convection in a square enclosure containing volumetric sources. Int. J. Heat. Mass Transf. 44, 3273–3280. doi:10.1016/s0017-9310(00)00345-8
Lorenzini, G., and Biserni, C. (2003). Numerical investigation on mixed convection in a nonNewtonian fluid inside a vertical duct. Int. J. Therm. Sci. 43, 1153–1160. doi:10.1016/j.ijthermalsci.2004.04.005
Lund, L. A., Yashkun, U., and Shah, N. A. (2023). Magnetohydrodynamics streamwise and cross flow of hybrid nanofluid along the viscous dissipation effect: duality and stability. Phys. Fluids 35 (2). doi:10.1063/5.0135361
Malashetty, M. S., Swamy, M. S., and Sidram, W. (2011). Double diffusive convection in a rotating anisotropic porous layer saturated with viscoelastic fluid. Int. J. Therm. Sci. 50, 1757–1769. doi:10.1016/j.ijthermalsci.2011.04.006
Maleki, H., Safaei, M. R., Alrashed, A. A., and Kasaeian, A. (2019). Flow and heat transfer in non-Newtonian nanofluids over porous surfaces. J. Therm. Analysis Calorim. 135, 1655–1666. doi:10.1007/s10973-018-7277-9
Markatos, N. C., and Pericleous, K. A. (1984). Laminar and turbulent natural convection in an enclosed cavity. Int. J. Heat. Mass Transf. 27, 755–772. doi:10.1016/0017-9310(84)90145-5
Moraga, N., Guarda, A., Galotto, M., and Torres, A. (2011). Non-Newtonian canned liquid food unsteady fluid mechanics and heat transfer prediction for pasteurization and sterilization. J. Food Process Eng. 34, 2000–2025. doi:10.1111/j.1745-4530.2009.00542.x
Moraga, N., and Lemus-Mondaca, R. (2011). Numerical conjugate air mixed convection/non-Newtonian liquid solidification for various cavity configurations and rheological models. Int. J. Heat. Mass Transf. 54, 5116–5125. doi:10.1016/j.ijheatmasstransfer.2011.07.032
Qureshi, M. Z. A., Faisal, M., Raza, Q., Ali, B., Botmart, T., Shah, N. A., et al. (2023). Morphological nanolayer impact on hybrid nanofluids flow due to dispersion of polymer/CNT matrix nanocomposite material. AIMS Math. 8 (1), 633–656. doi:10.3934/math.2023030
Raju, B. L., Rao, V. D., and Krishna, B. B. (2015). Flow and heat transfer of quiescent non-Newtonian power-law fluid driven by a moving plate: an integral approach. Procedia Eng. 127, 485–492. doi:10.1016/j.proeng.2015.11.402
Ravnik, J., and Tibaut, J. (2018). A review of modelling approaches for flow and heat transfer in nanofluids. Adv. Fluid Mech. 12, 9.
Sasmal, C., and Chhabra, R. P. (2012). Effect of orientation on laminar natural convection from a heated square cylinder in power-law liquids. Int. J. Therm. Sci. 57, 112–125. doi:10.1016/j.ijthermalsci.2012.02.008
Shafiq, A., Çolak, A. B., Sindhu, T. N., Al-Mdallal, Q. M., and Abdeljawad, T. (2021). Estimation of unsteady hydromagnetic Williamson fluid flow in a radiative surface through numerical and artificial neural network modeling. Sci. Rep. 11, 14509. doi:10.1038/s41598-021-93790-9
Shyan, R., Sairamu, M., Nirmalkar, N., and Chhabra, R. P. (2013). Free convection from a heated circular cylinder in confined power-law fluids. Int. J. Therm. Sci. 74, 156–173. doi:10.1016/j.ijthermalsci.2013.06.005
Sindhu, T. N., Çolak, A. B., Lone, S. A., and Shafiq, A. (2023). Reliability study of generalized exponential distribution based on inverse power law using artificial neural network with Bayesian regularization. Qual. Reliab. Eng. Int. 39, 2398–2421. doi:10.1002/qre.3352
Upadhya, S. M., Raju, S. S. R., Raju, C. S. K., Shah, N. A., and Chung, J. D. (2022). Importance of entropy generation on Casson, Micropolar and Hybrid magneto-nanofluids in a suspension of cross diffusion. Chin. J. Phys. 77, 1080–1101. doi:10.1016/j.cjph.2021.10.016
Vujanovic, B., Stauss, A. M., and Djukiv, D. J. (1972). A variational solution of the Rayleigh problem for a power law non-Newtonian conducting fluid. Arch. Appl. Mech. 41, 381–386. doi:10.1007/bf00533141
Wu, W., and Ching, C. Y. (2010). Laminar natural convection in an air-filled square cavity with partitions on the top wall. Int. J. Heat. Mass Transf. 53, 1759–1772. doi:10.1016/j.ijheatmasstransfer.2010.01.014
Wu, W., Ewing, D., and Ching, C. Y. (2006). The effect of the top and bottom wall temperatures on the laminar natural convection in an air-filled square cavity. Int. J. Heat. Mass Transf. 49, 1999–2008. doi:10.1016/j.ijheatmasstransfer.2005.11.027
Keywords: exponential time integrator, stability, convergence, power-law fluid, contour plots
Citation: Nawaz Y, Arif MS, Abodayeh K, Soori AH and Javed U (2024) A modification of explicit time integrator scheme for unsteady power-law nanofluid flow over the moving sheets. Front. Energy Res. 12:1335642. doi: 10.3389/fenrg.2024.1335642
Received: 09 November 2023; Accepted: 10 January 2024;
Published: 26 January 2024.
Edited by:
Awadesh Kumar Mallik, Nanyang Technological University, SingaporeReviewed by:
Andaç Batur Çolak, Istanbul Commerce University, TürkiyeNehad Ali Shah, Sejong University, Republic of Korea
Naveed Yaqoob, Majmaah University, Saudi Arabia
Copyright © 2024 Nawaz, Arif, Abodayeh, Soori and Javed. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Muhammad Shoaib Arif, c2hvYWliLmFyaWZAYXUuZWR1LnBr, bWFyaWZAcHN1LmVkdS5zYQ==
 Yasir Nawaz
Yasir Nawaz Muhammad Shoaib Arif
Muhammad Shoaib Arif Kamaleldin Abodayeh
Kamaleldin Abodayeh Atif Hassan Soori1
Atif Hassan Soori1