Opinions on hosting capacity evaluation of distribution network with zonotope power flexibility aggregation

1 Introduction

The installation of solar photovoltaic (PV) systems has been stimulated by governmental incentive mechanisms and the continual reduction in technology costs in recent years (Chattopadhyay and Alpcan, 2015). However, with the substantial integration of distributed PV systems at high penetration levels (Chen et al., 2019a), reverse power flow in the distribution network has been observed, thus triggering issues such as voltage violations and reverse overloads (Ismael et al., 2019; Wu et al., 2021). Therefore, the evaluation of maximum PV hosting capacity of the distribution network can assist distribution network planners in making decisions regarding PV generation (SUN et al., 2021). The current evaluation method considering safe operation constraints is traditional planning method of optimal power flow (Chen et al., 2016) and random scenario simulation method (Ding and Mather, 2016) which can ensure the randomness of PV configuration. To enhance the PV hosting capacity, strategies such as reactive power control (Astero and Söder, 2018), voltage control using OLTC (Wang et al., 2016), energy storage technologies (Hashemi and Østergaard, 2016), and network reconfiguration (Fu and Chiang, 2018) are continuously proposed. With the increasing proliferation of distributed resources, a promising approach to enhancement is also presented by power aggregation (Müller et al., 2017; Wang and Wu, 2021) and proactive control of diversified flexibility resources along feeders. Therefore, this research aims to provide insightful viewpoints and discussions on the assessment method of the maximum PV hosting capacity of the distribution network based on the aggregation of diversified flexibility resources.

The main contributions of this work can be twofold as listed: (1) A highly constrained zonotope aggregation model for diversified flexibility resources is proposed, and a two-stage adaptive robust framework is employed to innerly approximate the projection region of the high-dimensional original space of diversified flexibility resources; (2)A PV hosting capacity evaluation method with flexibility space boundaries is presented to accommodate distributed PV by maximizing the net load during peak PV output on the load side.

2 Highly constrained zonotope aggregation model of diversified flexibility resources

Due to diversified flexibility resources’ small scale, dispersion, and large number, coordinating their control is highly challenging (Chen and Li, 2021). Aggregating flexibility resources on feeders can fully utilize the potential flexibility, reduce invocation difficulty, and lower computational complexity. Specifically, the process of flexibility aggregation can be described as the projection of the power feasible domain of all flexibility resources onto the total power feasible domain of feeders (Wei et al., 2015; Tan et al., 2019; Chen and Li, 2021). Based on the acquisition of the power feasible domain of all flexibility resources on feeders, upon observation of the strong constraints imposed by the network of the distribution network when the aggregation scale is large (Wang and Wu, 2021), the high-dimensional precise original space of flexibility resources is constituted. The analytical form of computing its dimensionality reduction projection onto the precise power flexibility space of the feeder is highly challenging; thus, most studies are focused on approximation methods (Chen and Li, 2021).

Firstly, the power-adjustable range of individual flexibility resources, including energy storage devices, electric vehicles, and HVAC-like energy storage devices, is described through a virtual energy storage model in this paper (Hughes et al., 2016). Given the discrete scheduling decision cycle with N scheduling points and a time interval of $\Delta t$ and a quantity of M flexibility resources, we consider $P_{i,t}^{\text{flx}}$ and $E_{i,t}^{\text{flx}}$ representing the power and energy of individual flexibility resources within the scheduling interval $t\in \left[k\Delta t,\left(k+1\right)\Delta t\right]$, where $\left(k=0,...,N-1\right)$, the corresponding quantification model is established as follews:

${\mathrm{\Omega }}_i=\left\{\begin{array}{l}{P}_{i,t}^{\text{flx},\min }\le P_{i,t}^{\text{flx}}\le P_{i,t}^{\text{flx},\max }\\ E_{i,t}^{\text{flx},\min }\le E_{i,t}^{\text{flx}}\le E_{i,t}^{\text{flx},\max }\\ E_{i,t+1}^{\text{flx}}=E_{i,t}^{\text{flx}}+P_{i,t}^{\text{flx}}\Delta t\end{array}\right\}(1)$

$\chi =\left\{{\mathrm{\Omega }}_1,{\mathrm{\Omega }}_2,...,{\mathrm{\Omega }}_M\right\}(2)$

Where $i\in \left\{\text{EV},\text{ESS},\text{HVAC}\right\}$, $P_{i,t}^{\text{flx},\max }$ and $P_{i,t}^{\text{flx},\min }$ respectively represent the upper and lower limits of the power of flexibility resource i during time period t; and $E_{i,t}^{\text{flx},\min }$ respectively represent the upper and lower limits of the energy; ${\mathrm{\Omega }}_i$ denotes the operational feasible region of flexibility resource i, $\chi$ denotes the operational feasible region of the whole flexibility resource, which can be described as the convex polytope characterized by the aforementioned set of M constraints.

The linear method outlined in (Bernstein et al., 2018) is employed to derive the network power flow model, whereby the magnitudes of node voltage v, branch current i, and feeder line aggregated active power p_agg, can be expressed as the following linear expressions:

$\mathit{v}=\mathit{D}{\mathit{p}}^{\text{flx}}+\mathit{d}(3)$

$\mathit{i}=\mathit{F}{\mathit{p}}^{\text{flx}}+\mathit{f}(4)$

${\mathit{p}}_{\text{agg}}=\mathit{H}{\mathit{p}}^{\text{flx}}+\mathit{h}(5)$

Where D, d, F, f, H, h, J and j are the system parameters. It is necessary to ensure that node voltages and branch currents are not exceeded, as follows:

$\left\{\begin{array}{l}\underset{\_}{\mathit{v}}\le \mathit{v}\le \overline{\mathit{v}}\\ \underset{\_}{\mathit{i}}\le \mathit{i}\le \overline{\mathit{i}}\end{array}\right.(6)$

Where $\underset{\_}{\mathit{v}}$ and $\overline{\mathit{v}}$ represent the upper and lower limits of node voltages respectively, and $\overline{\mathit{i}}$ and $\mathit{i}$ denote the upper and lower limits of branch currents respectively. The convex polytope formed by Eq. 2 is intersected by Eq. 6’s constraints, resulting in irregular polytopes, while the high-dimensional strong constraint primal space Z of flexibility resources is formed by Eqs 1–6.

Then, the feeder power flexibility space P, representing the dimensionality reduction projection of the high-dimensional constrained space Z, is approximately obtained using the zonotope U as shown in Figure 1A. For the N-dimensional zonotope (Müller et al., 2017), its representation can be established with the central point c, a specific generator matrix G, and a scaling factor $\overline{\mathit{\beta }}$. N_g denotes the number of generator vectors. The directions along which the zonotope can be extended are described by the generator matrix $\mathit{G}={\left[g_1,...,g_{N_g}\right]}^T\in {\mathbb{R}}^{N\times N_g}$. The extension range along each generator vector direction is determined by the scaling factor by Eqs 7, 8:

$\mathit{U}=\left\{{\mathit{p}}_{\text{agg}}\in {\mathbb{R}}^N|{\mathit{p}}_{\text{agg}}=\mathit{c}+\mathit{G}\mathit{\beta },-{\mathit{\beta }}_{\max }\le \mathit{\beta }\le {\mathit{\beta }}_{\max }\right\}(7)$

$\mathit{G}=\left\{\begin{array}{l}{g}_i={\left[0,...,0,\begin{array}{c}i\\ 1\end{array},0,...,0\right]}^{\mathrm{T}}\in {\mathbb{R}}^N\\ g^{N+i^{\prime }}={\left[0,...,0,\underset{i^{\prime }}{\underbrace{-1/\sqrt{2}}},\underset{i^{\prime }+1}{\underbrace{1/\sqrt{2}}},0,...,0\right]}^{\mathrm{T}}\in {\mathbb{R}}^N\end{array}\right.(8)$

Figure 1

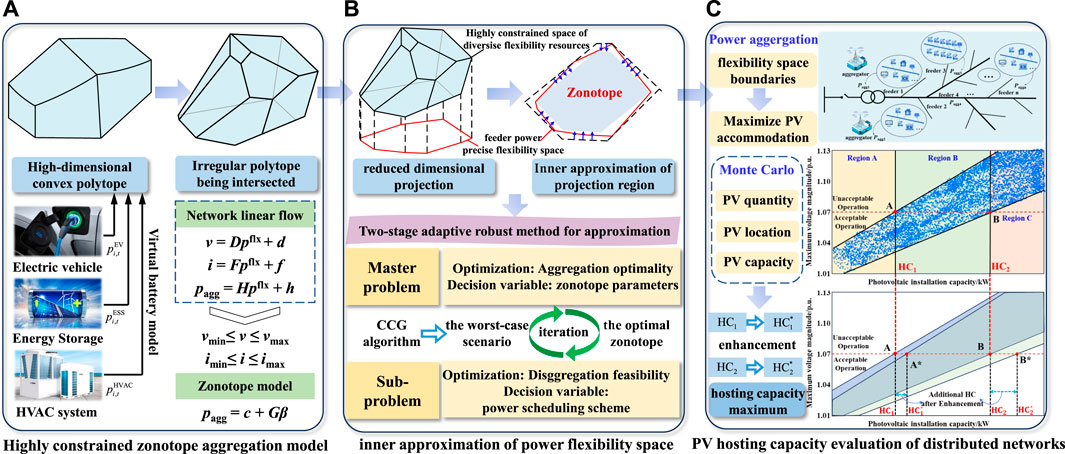
Figure 1. The proposed model, approximation method and PV hosting capacity evaluation. (A) Highly constrained zonotope aggregation model. (B) Inner approximation of power flexibility space. (C) PV hosting capacity evaluation of distributed networks.

The advantage of zonotope projection approximation over ellipsoidal projection (Cui et al., 2021) and cuboidal projection (Chen et al., 2019b) lies in its generator vectors $g_i$ and $g_{N+i^{\prime }}$, which can respectively depict the power and energy constraints of flexibility resources. Therefore, the operationally feasible region of flexibility resources aligns more closely with the characteristics of the zonotope shape.

3 Two-stage adaptive robust method for inner approximation of power flexibility space

The feeder power flexibility space obtained after dimensionality reduction projection becomes more intricate and challenging to obtain. The inner approximation requires ensuring that the approximated flexibility space is optimally bounded internally. Simultaneously, it is imperative to ensure that any aggregated power trajectory within the approximated flexibility space can be realized through scheduling without violating operational constraints, thereby guaranteeing the feasibility of the disaggregation (Chen and Li, 2021).

In this paper, the power flexibility aggregation and disaggregation problem are formulated as a two-stage adaptive robust optimization problem as shown in Figure 1B, where power aggregation is treated as uncertain variables, and the requirement to ensure the feasibility of disaggregation is regarded as adaptive robust constraints (Hua et al., 2024). In the first stage, the objective is to determine the optimal approximation space for the aggregated feeder power. In the second stage, the objective is to ensure the feasibility of disaggregation.

The construction of any S normal vectors, denoted as ${\mathit{\alpha }}_{\mathit{s}}\in {\mathbb{R}}^N\left(s=1,...,S\right)$, is performed. The diameter, denoted as ${\rho }_{\kappa }$, of the zonotope U in the direction of the normal vectors is calculated by Eq. 9. The problem of determining the diameter, denoted as ${\rho }_{\tau }$, of the feeder power flexibility space P in the direction of the normal vectors can be addressed using Eqs 10, 11. Thus, the similarity between the approximate and the original region is defined as shown in Eq. 12. As its value increases, the zonotope’s approximation to the power flexibility space of the feeder becomes larger (Müller et al., 2017).

${\rho }_{\kappa }=2\left|{\mathit{\alpha }}_{\mathit{s}}\mathit{G}\right|{\mathit{\beta }}_{\max }(9)$

${\rho }_{\tau }=\left|\underset{{\mathit{p}}_{\text{agg}}}{\max }\left({\mathit{\alpha }}_{\mathit{s}}{\mathit{p}}_{\text{agg}}-\epsilon \right)-\underset{{\mathit{p}}_{\text{agg}}}{\min }\left({\mathit{\alpha }}_{\mathit{s}}{\mathit{p}}_{\text{agg}}-\epsilon \right)\right|/{‖{\mathit{\alpha }}_{\mathit{s}}‖}_2(10)$

$\mathrm{s}.\mathrm{t}.(11)$

equation (1)–(6)

${\eta }_s=\frac{{\rho }_{\kappa }}{{\rho }_{\tau }}(12)$

The introduction of $\xi$ as an uncertain variable acting on scaling factors applied to each generator vector of the zonontope, the uncertain set is denoted as $\mathbb{C}=\left\{\xi \left|0\le \right|{\xi }_i\le 1,i=1,...,N_g\right\}$. An uncertain zonotope region is constructed, with its parameter feasible domain as $\mathbb{Q}=\left\{{\mathit{p}}_{\text{agg}}\in {\mathbb{R}}^N:{\mathit{p}}_{\text{agg}}=c+\mathit{G}\mathit{\beta }\bullet \xi ,\xi \mathbb{\in }\mathbb{C}\right\}$. Therefore, a two-stage adaptive robust power aggregation solution model is established as shown in Eqs 13–16.

$\text{Obj}.\underset{\mathit{c}、\mathit{\beta }}{\max }\frac{1}{S}{\displaystyle \sum _{s=1}^S}\frac{{\rho }_{\kappa }}{{\rho }_{\tau }}+\underset{\mathit{\xi }\in {\mathrm{U}}_2}{\min }\underset{{\mathit{p}}^{\text{flx}}\left(\mathit{\xi }\right)}{\max }0(13)$

$\mathit{c}+\mathit{G}\mathit{\beta }\cdot \mathit{\xi }=\mathit{H}{\mathit{p}}^{\text{flx}}\left(\mathit{\xi }\right)+\mathit{h}(14)$

$\mathit{E}{\mathit{p}}^{\text{flx}}\left(\mathit{\xi }\right)\le \mathit{\sigma }(15)$

$\mathit{Q}{\mathit{p}}^{\text{flx}}\left(\mathit{\xi }\right)\le \mathit{\gamma }(16)$

In the first stage, the zonotope parameters $\left(\mathit{c}、\mathit{\beta }\right)$ are decision variables, and the optimal inner approximation region is so the uncertain set ught using Eq. 13. In the second stage, the power scheduling scheme ${\mathit{p}}^{\text{flx}}\left(\mathit{\xi }\right)$ is the decision variable, ensuring the feasibility of disaggregation. Eqs 15 and (16) represent the linear compact form of the highly constrained space of diversified flexibility resources p^flx mentioned earlier. Eq. 14 represents the projection of the highly constrained space of diversified flexibility resources p^flx onto the lower-dimensional space of feeder aggregated power p_agg. The solution of this model can be implemented using the column-and-constraint generation algorithm. This process is not further elaborated in this paper (Hua et al., 2024).

4 PV hosting capacity evaluation of distributed networks with flexibility space boundaries

As the penetration rate of PV systems in distribution networks continues to increase, the occurrence of peak PV output not coinciding with peak load power (Xiong et al., 2020) may lead to phenomena such as reverse power flow and overvoltage in low-voltage distribution networks (Zhang et al., 2018; Li et al., 2020). The increase in node voltages within distribution networks becomes the primary factor limiting the integration of distributed PV systems (Lee et al., 2020). Reference (Cao et al., 2024) ensures magnitudes of each bus are maintained within the safety range due to the load shedding. Therefore, effectively increasing the net load during periods of high PV output on the load side helps mitigate the risk of operational constraints exceeding limits, thereby enhancing the hosting capacity of distributed PV systems (Zhou et al., 2021).

In a low-voltage distribution network with H feeders, $p_{\text{agg},i,t}$ represents the aggregated power of the feeder i at time t, while $p_{\text{agg},i,t}^{\min }$ and $p_{\text{agg},i,t}^{\max }$ represent the upper and lower limits of power at that time, respectively. $t_{\text{pv},0}$ and $t_{\text{pv},\text{end}}$ represent the starting and ending times of PV output. During this period, each feeder utilizes the upper boundary of the aggregated power flexibility space, maximizing distributed PV integration (Ding and Mather, 2016). In subsequent periods, the lower boundary is employed to reduce the load on the distribution network, ensuring its stable and safe operation, as depicted in Eqs (17), (18).

$p_{\text{agg},i,t}^{\min }\le p_{agg.i,t}\le p_{\text{agg},i,t}^{\max }(17)$

$p_{agg.i,t}=\left\{\begin{array}{l}{p}_{\text{agg},i,t}^{\max },t\in \left[t_{\text{pv},0},t_{\text{pv},\text{end}}\right]\\ p_{\text{agg},i,t}^{\min },t\notin \left[t_{\text{pv},0},t_{\text{pv},\text{end}}\right]\end{array}\right.(18)$

The PV penetration rate range selected in this paper is 0%–300%, with an incremental step size of 10%. Using the Monte Carlo method, the quantity, location, and capacity of PV grid connections are randomly simulated, with the PV grid connection capacity increasing according to the PV penetration rate (Ding and Mather, 2016). The steady-state power flow of the system is then calculated. For each PV penetration rate ${\lambda }_{\text{PV}}$, multiple samples are drawn to compute the total installed PV capacity and maximum voltage of system nodes for each random scenario. These values serve as the abscissa and ordinate to construct a scatter plot of random simulations, depicted in Figure 1C, where each point represents one simulation result. In the low-voltage distribution network, the voltage per unit value ($V_i^t$) of each feeder line must satisfy the constraint given by Eq. 19, and the scatter plot intersects with the upper voltage constraint of 1.07 per unit at points HC₁ and HC₂.

$0.93\mathrm{p}.\mathrm{u}.\le \left|V_i^t\right|\le 1.07\mathrm{p}.\mathrm{u}.(19)$

Two lines parallel to the vertical axis are drawn respectively at points HC₁ and HC₂ to divide the coordinate graph into three regions: A, B, and C. In region A, points represent scenarios where the capacity of PV systems connected to the distribution network is less than HC₁. Regardless of the node in the distribution network where PV systems are connected, the system voltage remains within the permissible range of the supply voltage. In region B, points represent scenarios where the capacity of PV systems connected to the distribution network falls between HC₁ and HC₂. If the selection of PV integration positions and capacity allocation is unreasonable, it may lead to excessively high or even over-limit system voltage levels. In such cases, the distribution network planner must ensure that the PV systems are appropriately allocated. In region C, points represent scenarios where the capacity of PV systems connected to the distribution network exceeds HC₂. Regardless of the installation scheme employed, it will lead to over-limit system voltage. The aggregation and regulation of flexibility resources on the load side result in the accommodation of distributed photovoltaics, leading to the rightward shift of HC₁ and HC₂, with HC₁ increasing to HC*₁ and HC₂ increasing to HC*₂.

5 Case studies

In this section, the enhancement effect of PV hosting capacity by aggregated and coordinated diversified flexibility resources is demonstrated through numerical simulations based on the proposed method. IEEE 33-bus distribution network system is employed as a case study for simulation verification, with a radial configuration and a standard voltage level set at 12.66 kV. All the algorithms are executed with an AMD Ryzen 7 5800H with Radeon Graphics CPU running at 3.20 GHz, and 16.0 GB RAM. The optimization model involved in the proposed method is programmed and solved using the commercial solver Gurobi 10.0.3. The comparison between results of PV hosting capacity and computational time under different algorithms is shown in Table 1.

Table 1

Table 1. Comparison of PV hosting capacity evaluation method.

As shown in Table 1, it can be seen that the proposed method, compared to the random scenario simulation, can increase the PV hosting capacity by over 9.96%. Due to the necessity of considering flexible resource power aggregation and proactive control, the computational time is comparatively longer. When the scale of flexible resources is large, aggregation can shorten the computational time compared to distributed scheduling. However, our method show a slight decrease in the PV hosting capacity compared to the demand response enhancement method, which is attributed to the approximate feasible domain of the aggregation solution, leading to certain accuracy errors. Overall, the method proposed can effectively assess the PV hosting capacity of the distribution network.

6 Discussion and conclusion

In this paper, the flexibility resource power regulation model, feeder power aggregation model, two-stage robust aggregation solution method, and PV hosting capacity assessment strategy is elaborately investigated. The key findings are summarized as follows: 1) A highly constrained zonotope aggregation model of diversified flexibility resources is proposed, and a two-stage adaptive robust method is introduced to internally approximate the power flexibility space, ensuring the optimality of aggregation and the feasibility of disaggregation; 2) The aggregation and control of flexibility resource power on the load side can accommodate high peak output from distributed PV, thereby enhancing the PV hosting capacity of the distribution network and simultaneously reducing the computational complexity of dispatch decision-making.

Author contributions

ZS: Writing–original draft, Conceptualization. CY: Writing–review and editing, Formal Analysis, Data curation. YL: Writing–review and editing, Visualization. ZM: Writing–review and editing, Investigation.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Astero, P., and Söder, L., Improving PV dynamic hosting capacity using adaptive controller for STATCOMs[J]. IEEE Trans. Energy Convers., 2018, 34(1): 415–425. doi:10.1109/TEC.2018.2873057

CrossRef Full Text | Google Scholar

Bernstein, A., Wang, C., Dall’Anese, E., Le Boudec, J. Y., and Zhao, C. (2018). Load flow in multiphase distribution networks: existence, uniqueness, non-singularity and linear models. IEEE Trans. Power Syst. 33, 5832–5843. doi:10.1109/TPWRS.2018.2823277

CrossRef Full Text | Google Scholar

Cao, Y., Zhou, B., Chung, C. Y., Wu, T., Zheng, L., and Shuai, Z. (2024). A coordinated emergency response scheme for electricity and watershed networks considering spatio-temporal heterogeneity and volatility of rainstorm disasters. IEEE Trans. Smart Grid, 1. doi:10.1109/TSG.2024.3362344

CrossRef Full Text | Google Scholar

Chattopadhyay, D., and Alpcan, T. (2015). Capacity and energy-only markets under high renewable penetration. IEEE Trans. Power Syst. 31, 1692–1702. doi:10.1109/TPWRS.2015.2461675

CrossRef Full Text | Google Scholar

Chen, X., Dall’Anese, E., Zhao, C., and Li, N. (2019b). Aggregate power flexibility in unbalanced distribution systems. IEEE Trans. Smart Grid 11, 258–269. doi:10.1109/TSG.2019.2920991

CrossRef Full Text | Google Scholar

Chen, X., and Li, N. (2021). Leveraging two-stage adaptive robust optimization for power flexibility aggregation. IEEE Trans. Smart Grid 12, 3954–3965. doi:10.1109/TSG.2021.3068341

CrossRef Full Text | Google Scholar

Chen, X., Mcelroy, M. B., Wu, Q., Shu, Y., and Xue, Y. (2019a). Transition towards higher penetration of renewables: an overview of interlinked technical, environmental and socio-economic challenges. J. Mod. Power Syst. Clean Energy 7, 1–8. doi:10.1007/s40565-018-0438-9

CrossRef Full Text | Google Scholar

Chen, X., Wu, W., Zhang, B., and Lin, C. (2016). Data-driven DG capacity assessment method for active distribution networks. IEEE Trans. Power Syst. 32, 3946–3957. doi:10.1109/TPWRS.2016.2633299

CrossRef Full Text | Google Scholar

Cui, B., Zamzam, A., and Bernstein, A. (2021). “Network-cognizant time-coupled aggregate flexibility of distribution systems under uncertainties,” in 2021 American Control Conference (ACC), New Orleans, LA, USA, May, 2021, 1723–1728.

CrossRef Full Text | Google Scholar

Ding, F., and Mather, B. (2016). On distributed PV hosting capacity estimation, sensitivity study, and improvement. IEEE Trans. Sustain. Energy 8, 1010–1020. doi:10.1109/TSTE.2016.2640239

CrossRef Full Text | Google Scholar

Fu, Y. Y., and Chiang, H. D. Toward optimal multiperiod network reconfiguration for increasing the hosting capacity of distribution networks[J]. IEEE Trans. Power Deliv., 2018, 33(5): 2294–2304.doi:10.1109/TPWRD.2018.2801332

CrossRef Full Text | Google Scholar

Hashemi, S., and Østergaard, J. Efficient control of energy storage for increasing the PV hosting capacity of LV grids[J]. IEEE Trans. Smart Grid, 2016, 9(3): 2295–2303. doi:10.1109/TSG.2016.2609892

CrossRef Full Text | Google Scholar

Hua, Z., Zhou, B., Or, S. W., Zhang, J., Li, C., and Wei, J. (2024). Robust emergency preparedness planning for resilience enhancement of energy-transportation nexus against extreme rainfalls. IEEE Trans. Industry Appl. 60, 1196–1207. doi:10.1109/TIA.2023.3274615

CrossRef Full Text | Google Scholar

Hughes, J. T., Domínguez-García, A. D., and Poolla, K. (2016). Identification of virtual battery models for flexible loads. IEEE Trans. Power Syst. 31, 4660–4669. doi:10.1109/TPWRS.2015.2505645

CrossRef Full Text | Google Scholar

Ismael, S. M., Aleem, S. H. E. A., Abdelaziz, A. Y., and Zobaa, A. F. (2019). State-of-the-art of hosting capacity in modern power systems with distributed generation. Renew. energy 130, 1002–1020. doi:10.1016/j.renene.2018.07.008

CrossRef Full Text | Google Scholar

Lee, J., Bérard, J. P., Razeghi, G., and Samuelsen, S. (2020). Maximizing PV hosting capacity of distribution feeder microgrid. Appl. Energy 261, 114400. doi:10.1016/j.apenergy.2019.114400

CrossRef Full Text | Google Scholar

Li, R., Wong, P., Wang, K., and Yuan, F. (2020). Power quality enhancement and engineering application with high permeability distributed photovoltaic access to low-voltage distribution networks in Australia. Prot. Control Mod. Power Syst. 5, 18. doi:10.1186/s41601-020-00163-x

CrossRef Full Text | Google Scholar

Müller, F. L., Szabó, J., Sundström, O., and Lygeros, J. (2017). Aggregation and disaggregation of energetic flexibility from distributed energy resources. IEEE Trans. Smart Grid 10, 1205–1214. doi:10.1109/TSG.2017.2761439

CrossRef Full Text | Google Scholar

Sun, W., Huang, F., and Zhang, W. (2021). Evaluation of feeder available capacity considering demand response. Electr. Power Autom. Equip. 41 (06), 156–165. doi:10.16081/j.epae.202101008

CrossRef Full Text | Google Scholar

Tan, Z., Zhong, H., Wang, J., Xia, Q., and Kang, C. (2019). Enforcing intra-regional constraints in tie-line scheduling: a projection-based framework. IEEE Trans. Power Syst. 34, 4751–4761. doi:10.1109/TPWRS.2019.2913876

CrossRef Full Text | Google Scholar

Wang, S., Chen, S., Ge, L., and Wu, L. Distributed generation hosting capacity evaluation for distribution systems considering the robust optimal operation of OLTC and SVC[J]. IEEE Trans. Sustain. Energy, 2016, 7(3): 1111–1123. doi:10.1109/TSTE.2016.2529627

CrossRef Full Text | Google Scholar

Wang, S., and Wu, W. (2021). Aggregate flexibility of virtual power plants with temporal coupling constraints. IEEE Trans. Smart Grid 12, 5043–5051. doi:10.1109/TSG.2021.3106646

CrossRef Full Text | Google Scholar

Wei, W., Liu, F., and Mei, S. (2015). Real-time dispatchability of bulk power systems with volatile renewable generations. IEEE Trans. Sustain. Energy 6, 738–747. doi:10.1109/TSTE.2015.2413903

CrossRef Full Text | Google Scholar

Wu, H., Yuan, Y., Zhu, J., Qian, K., and Xu, Y. (2021). Potential assessment of spatial correlation to improve maximum distributed PV hosting capacity of distribution networks. J. Mod. Power Syst. Clean Energy 9, 800–810. doi:10.35833/MPCE.2020.000886

CrossRef Full Text | Google Scholar

Xiong, L., Liu, X., Zhang, D., and Liu, Y. (2020). Rapid power compensation-based frequency response strategy for low-inertia power systems. IEEE J. Emerg. Sel. Top. Power Electron. 9, 4500–4513. doi:10.1109/JESTPE.2020.3032063

CrossRef Full Text | Google Scholar

Zhang, D., Li, J., and Hui, D. (2018). Coordinated control for voltage regulation of distribution network voltage regulation by distributed energy storage systems. Prot. Control Mod. Power Syst. 3, 3. doi:10.1186/s41601-018-0077-1

CrossRef Full Text | Google Scholar

Zhou, B., Zou, J., Chung, C. Y., Wang, H., Liu, N., Voropai, N., et al. Multi-microgrid energy management systems: architecture, communication, and scheduling strategies[J]. J. Mod. Power Syst. Clean Energy, 2021, 9(3): 463–476. doi:10.35833/MPCE.2019.000237

CrossRef Full Text | Google Scholar