Construction of a monthly dynamic sediment delivery ratio model at the hillslope scale: a case study from a hilly loess region

1 Introduction

Soil loss is a major and widespread environmental problem that threatens terrestrial ecosystems (Lal, 2003; Van Oost et al., 2007; Borrelli et al., 2017). Sediment transport on hillslopes is a very important part of soil loss, which becomes more complex under the influence of climate change and human activities (Zhang S. et al., 2019; Borrelli et al., 2020; Jin et al., 2021). Clarifying the variation in the hillslope sediment transport and yield is of great significance for the optimization of soil and water conservation measures in watersheds.

The interaction of soil erosion and sediment transport processes with the hydrological and geomorphological processes includes sediment generation, detachment, transport, and deposition (Turnbull and Wainwright, 2019). The sediment delivery ratio (SDR) is the ratio of the sediment yield to the total amount of erosion in a region and an important tool for generalizing the sediment transport (Walling, 1983; Lu et al., 2006). SDR is considered to be a link between the amount of soil erosion and the resulting sediment yield; hence, it plays a key role in sediment yield prediction. In turn, the calculation methods for SDR have attracted the attention of many researchers. Initially, SDR algorithms were mainly based on the definition or empirical formulas of influencing factors (Xie and Li, 2012). Many scholars have proposed empirical single-factor and multi-factor SDR algorithms on the basis of static structural features, such as the watershed area and gully density, or hydrological dynamic indicators, such as rainfall and runoff, for specific watersheds (Xie and Li, 2012; Tao and Chen, 2015; Wu et al., 2018a). Furthermore, Wu et al. (2018b) proposed a segmented dynamic SDR algorithm suitable for most watersheds, achieving improved results in the simulation of the sediment yield at the annual scale. However, the above SDR algorithms still lack a description of spatial distribution and transport processes.

In recent years, sediment connectivity, a newly proposed concept in the study of sediment transport characteristics, has become a research hotspot, owing to its clear spatial variability (Keesstra et al., 2018, Wohl et al., 2019). There is still no consensus on how to quantify and compare connectivity at different spatial and temporal scales and among distinct landscape properties (Hooke et al., 2021; Najafi et al., 2021; Niguse et al., 2023). Many calculation methods of sediment connectivity have been proposed (Lenhart et al., 2005; Borselli et al., 2008; Diodato and Grauso, 2009; Hooke et al., 2021); among these, the index of connectivity (IC) proposed by Borselli et al. (2008) is one of the most widely used. IC, based on structural characteristics, is used to describe sediment transport from hillslopes to the stream network and is also often compared and associated with the SDR. A sigmoidal relationship between the SDR and IC has been identified and applied to sediment yield model construction (Borselli et al., 2008; Vigiak et al., 2012; Jamshidi et al., 2014). Then, various studies applied the Revised Universal Soil Loss Equation (RUSLE)-IC-SDR approach to determine the sediment yield (Michalek et al., 2021). For example, Zhao et al. (2020) used this type of model to explore the effects of land-use change and soil and water conservation measures on the sediment yield. However, the SDR based on the IC has been considered a stationary property assessed for average landscape conditions, which ignores the dynamic mechanism of sediment transport (Vigiak et al., 2016; Najafi et al., 2021; Zhang, 2021). Zhang Y. et al. (2019) pointed out that the SDR algorithm based on the IC characterizes the potential sediment transport capacity on a hillslope but does not reflect the actual variation in sediment transport over time. In many regions, the structural characteristics of a watershed tend not to change in the short term, but sediment transport is mainly caused by several heavy rainfall events during the flood season (Rustomji et al., 2008; Gao et al., 2016). Therefore, the SDR and sediment yield are usually dynamic and depend on both rainfall variation and landscape properties (Liu, 2016). Although the SDR model based on the structural connectivity of sediment has achieved good performance in simulations over long timescales, the dynamic applicability of the model at the monthly scale is poor, owing to the omittance of the influence of the transport threshold. Hence, it is difficult to reflect the changing hillslope sediment yield at a monthly time scale.

Here, we took the Mahuyu watershed on the Loess Plateau (China) as our study area. The objectives of this study are as follows: (i) to propose an SDR model for hillslopes that integrates both structural characteristics and the dynamic sediment transport threshold of rainfall events and verify the applicability of the model and (ii) to analyze spatiotemporal variations in the hillslope sediment yield and explore the response to the rainfall change. The results of this study could provide a reference for understanding sediment transport processes and guidance for optimizing soil and water conservation measures on hillslopes.

2 Materials and methods

2.1 Study area

The Mahuyu watershed is located in the hinterland of the Loess Plateau, a hilly‒gully region covered by loess. The area of the watershed is 372 km², and its elevation ranges from 864 to 1,316 m, with an average of 1,102 m (Figures 1A, C). The Mahuyu River is the first tributary of the middle reaches of the Wuding River, which belongs to the arid and semi-arid climate zone. Affected by monsoons, the annual and inter-annual distribution of rainfall and runoff in the watershed is uneven (Jiao et al., 2017). According to the measured rainfall data, the multi-year average rainfall from 2006 to 2018 was 456.7 mm, with rainfall mainly concentrated in the period from June to September. The Heimutouchuan watershed is also located on the right bank of the middle reaches of the Wuding River, close to the Mahuyu watershed. The Heimutouchuan watershed has a similar underlying surface to that of the Mahuyu watershed; hence, it was selected as the validation area for this study. The spatial location and overview of the Heimutouchuan watershed are shown in Figures 1B, D, respectively.

FIGURE 1

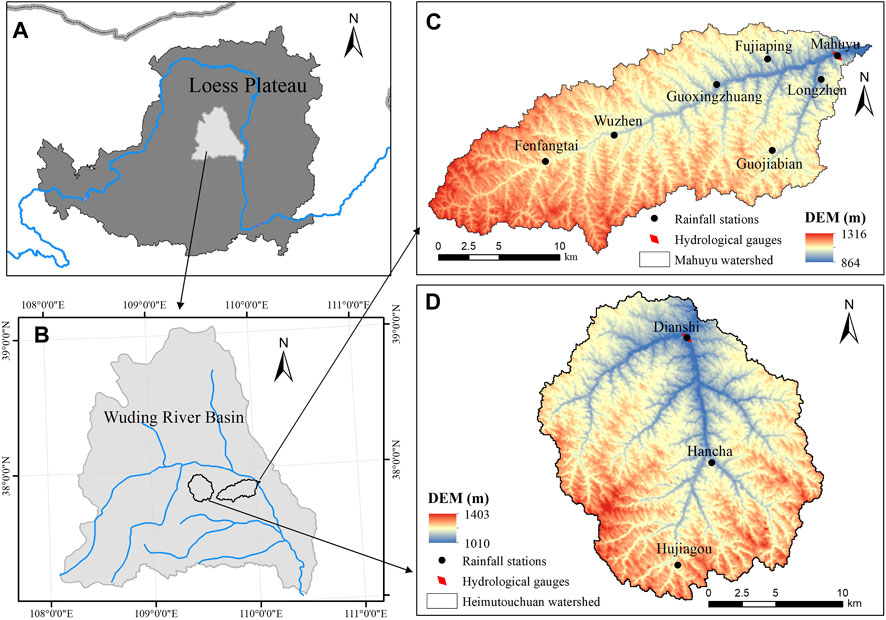
FIGURE 1. Overview of the study area. (A, B) Locations of the Mahuyu and Heimutouchuan watersheds, respectively. (C, D) Overviews of the Mahuyu and Heimutouchuan watersheds, respectively.

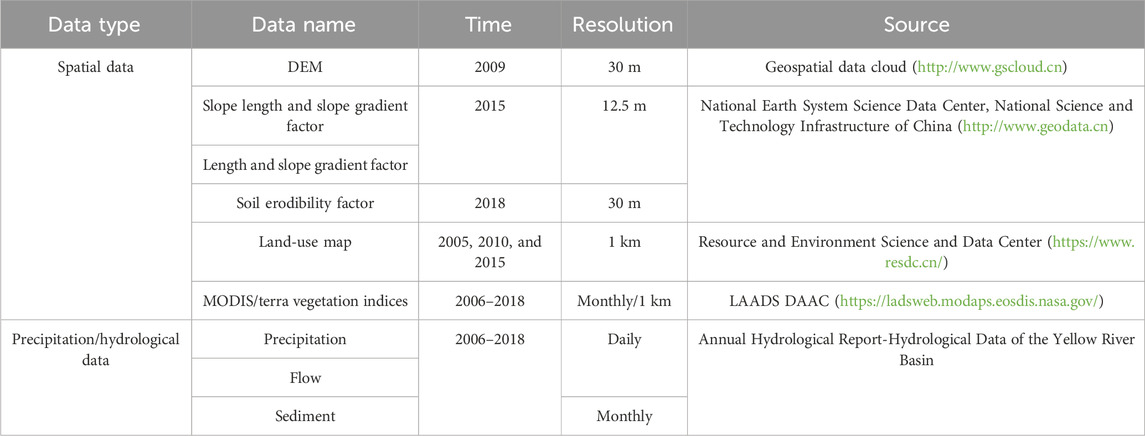
2.2 Data use

Information on the sources of the spatial and attribute data, and details regarding the spatial and temporal resolutions of the data, are provided in Table 1. For spatial data, the raster was unified to 30-m resolution after projection and mosaic processing using ArcGIS software. We obtained meteorological data from seven rainfall stations in the Mahuyu watershed (Fenfangtai, Wuzhen, Guoxingzhuang, Fujiaping, Guojiabian, Longzhen, and Mahuyu stations; Figure 1C) and three rainfall stations in the Heimutouchuan watershed (Hujiagou, Hancha, and Dianshi stations; Figure 1D). Hydrological data were obtained from the Mahuyu and Dianshi hydrological stations, which have watershed areas of 371 and 327 km², respectively.

TABLE 1

TABLE 1. Information on the timeframe, resolution, and sources of our research data.

2.3 Methods

2.3.1 Total erosion (TE) amount

In this study, the soil loss driven by rill and inter-rill erosion was estimated using the Revised Universal Soil Loss Equation (RUSLE) model, which enables the spatial pattern of soil erosion to be estimated (Renard et al., 1991, 1997). This model has been widely used in watersheds throughout the world (Thomas et al., 2018; Batista et al., 2019). Liu et al. (1994) adapted the model to be more applicable to the Loess Plateau region by considering erosion on a steep slope. Researchers have also improved the accuracy of the model under extreme rainfall events by introducing precipitation concentration degree (Xu et al., 2022). To summarize, the total erosion of hillslopes mainly comprises rill, inter-rill, and gully erosion, and the erosion rate can be calculated using the following equation:

${TE}_m={RI}_m*K*LS*C_m*P*\alpha ,(1)$

where TE is the total erosion amount per unit area in a given timestep (t·ha⁻¹); m is the calculation month; RIm is the rainfall erosivity factor introducing the rainfall concentration (MJ·mm·ha⁻¹ h⁻¹); K is the soil erodibility factor (t·h·MJ⁻¹ mm⁻¹); LS is the slope length and gradient factor (dimensionless); and $C_m$ and P are the vegetation cover factor and soil conservation factor, respectively (dimensionless). Cai et al. (2020) determined that multi-year average gully erosion accounted for 49% of the total erosion in the Wuding River basin using a model with a physical mechanism, and α is the amplification coefficient used to represent the gully erosion amount, with a value, in this study, of 1.96. The specific calculations for each factor can be referenced in the Xu et al. (2022).

2.3.2 Structural SDR (HSDR)

Borselli et al. (2008) proposed an index of connectivity (IC) describing the hydrological linkage between sediment sources and sinks. The IC consists of the following two components: an upslope component ($D_{up}$) that represents the potential for down-routing at a given location and a downslope component ($D_{dn}$) that accounts for potential flow sinks between that location and the stream network (Vigiak et al., 2016). The calculation formula is as follows:

$IC={\mathit{log}}_{10}\left(\frac{D_{up}}{D_{dn}}\right)={\mathit{log}}_{10}\left(\frac{\overline{W}*\overline{S}*\sqrt{A}}{{\sum }_{i=1}^n\left(d_i/\left(W_i*S_i\right)\right)}\right).(2)$

The range of the IC is [−∞, +∞], and a higher value indicates a higher degree of connectivity; $\overline{W}$ is the average weight factor of the contributing area, which reflects the surface roughness to measure the resistance of runoff passing through a location; $\overline{S}$ is the average slope of the upslope contributing area (m/m); A is the contributing area (m²); $d_i$ is the flow length to the downstream main channel (m); $W_i$ is the weight factor of the calculated cell; $S_i$ is the slope in the calculated cell (m/m); i refers to the calculated cell; and n is the total cell number from the point to the stream network along the flow path.

The structural SDR (HSDR) is calculated using the IC (in Eq. 2) with the following function, which is now included in the InVEST model (Borselli et al., 2008; Vigiak et al., 2012; Cavalli et al., 2013):

$HSDR=\frac{{SDR}_{\mathit{max}}}{1+\exp \left[\left({IC}_0-{IC}_i\right)/k\right]},(3)$

where ${SDR}_{\mathit{max}}$ is the maximum theoretical structural sediment delivery ratio, which is taken as 1 in this study; ${IC}_i$ is the connectivity index value of each calculated cell; and ${IC}_0$ and k are the calibration parameters.

2.3.3 Transport threshold factor (Er)

In the main sediment yield area of the Yellow River basin, where soil and water conservation measures have been implemented, soil erosion occurred but cannot transport the eroded sediment to the channels. Zhang (2017) pointed out that the eroded sediment can enter the channels when the daily rainfall reaches 25 mm/day; otherwise, it is trapped in the hillslope system. In addition, the benefits of soil and water conservation measures may be reduced and the deposited sediment be transported again when daily rainfall reaches 50 mm/day (Zhang, 2017). Consequently, we developed a transport threshold factor (Er) according to the rainfall thresholds of 25 and 50 mm/day. The definition formulae are as follows:

$\left\{\begin{array}{l}{Er}_j=0P_j<25mm/day,\\ {Er}_j=125mm/day\le P_j<50mm/day,\\ {Er}_j={\left(P_j/50\right)}^{\beta }{P}_j\ge 50mm/day,\end{array}\right.(4)$

where $P_j$ is the daily rainfall; j is the calculation day; and β is the adjustment coefficient. Then, the Er factor is calculated as the ratio of the sum of the daily rainfall erosivity factor multiplied by the ${Er}_j$ during the calculation month to the monthly rainfall erosivity. The Er factor raster is obtained by interpolation, using the inverse distance weighting method.

2.3.4 Dynamic SDR (${\mathit{S}\mathit{D}\mathit{R}}_{\mathit{s}\mathit{l}\mathit{p}}$)

The movement of sediment from the erosion source to channels is influenced by structural factors, such as topography and soil conservation measures, and dynamic factors, such as rainfall (Zhang, 2017). Therefore, we propose a dynamic SDR (${SDR}_{slp}$) model by considering the influence of the structural characteristics of the hillslopes and transport threshold on the sediment. The equation for this is represented as follows:

${SDR}_{slp}=HSDR*Er,(5)$

where HSDR is the structural sediment delivery ratio, reflecting the potential transport capacity of hillslope sediment into the channel system; and Er (in Eq. 4) is the transport threshold factor, reflecting the transport power of rainfall events on eroded soil.

2.3.5 Simulation of sediment yield

The watershed can be divided into hillslopes and channels. In this study, the hillslope sediment yield (${SY}_{slp}$) was defined as the amount of sediment entering the channel system from the hillslope system over a specific period of time. The hillslope SDR is the ratio of ${SY}_{slp}$ to the total erosion amount (TE) on hillslopes. To analyze the applicability of the dynamic SDR model, we coupled the hillslope SDRs (HSDR and ${SDR}_{slp}$) and soil erosion model to simulate the hillslope sediment yield. The potential sediment yield on the hillslope ($P{SY}_{slp}$) was defined based on TE (in Eq. 1) and HSDR (in Eq. 3), represented as follows:

$P{SY}_{slp}={\sum }_{i=1}^N{\left(TE*HSDR\right)}_i.(6)$

${SY}_{slp}$ was calculated based on the TE and ${SDR}_{slp}$ (in Eq. 5) using the following equation:

${SY}_{slp}={\sum }_{i=1}^N{\left(TE*{SDR}_{slp}\right)}_i,(7)$

where i is the calculated raster and N is the total number of the raster.

2.3.6 Calibration and validation

Calibration of hillslope sediment yield models remains a challenge, owing to a lack of long-term measured hillslope data (Wen and Deng, 2020). The measured sediment yield of a watershed (${SY}_{wsd}$), which is the total amount of sediment transported through the observed cross-section in the channel, provides an alternative for calibration and validation. However, deposition and erosion may still occur after the sediment-laden flow in the hillslope enters the channel system. In this study, the values of ${SY}_{wsd}$ were selected for model calibration and validation in the Mahuyu and Heimutouchuan watersheds when only channel erosion occurred based on the sediment-carrying capacity.

As for the sediment-carrying capacity of the channel, many scholars have pointed out that a linear relationship exists between the flow and sediment concentration for saturated flows in hilly loess areas (Zhang et al., 2018; Zheng, 2018). In this study, the observed monthly maximum daily flow (Q) and monthly ${SY}_{wsd}$ were used for curve fitting analysis. The points on the upper side of the fitted curve were then selected for the next fitting analysis until a well-fitted linear curve was obtained, which was regarded as a saturated flow status. The linear relationship was then considered the estimation equation for the sediment-carrying capacity of the channel.

The hillslope sediment yield model based on the ${SDR}_{slp}$ was calibrated using the observed ${SY}_{wsd}$ from 2006 to 2018 at the Mahuyu hydrological station. For validation, the hillslope sediment yield model was applied to the simulation in the Heimutouchuan watershed (Figure 1D). The ${SY}_{wsd}$ from 2006 to 2018 at the Dianshi hydrological station was used as the simulated ${SY}_{slp}$ comparison. Model performance was evaluated using the coefficient of determination (R²), percentage deviation (PBIAS), and Nash–Sutcliffe efficiency (NSE) coefficients (Nash and Sutcliffe, 1970; Gupta et al., 1999; Yesuf et al., 2015).

3 Results

3.1 Variations in structural and dynamic SDRs

The spatial distributions of the HSDR and Er in a typical month (July 2006) are shown in Figures 2A, B. In the Mahuyu watershed, HSDR ranged from 0 to 0.784; values were higher in areas close to the river, indicating that closer to the river there is a greater possibility of the eroded sediment entering the channel system. Er showed notable spatial variability across the Mahuyu watershed, with values ranging from 0 to 1.725, reflecting the spatial heterogeneity of rainfall in this month.

FIGURE 2

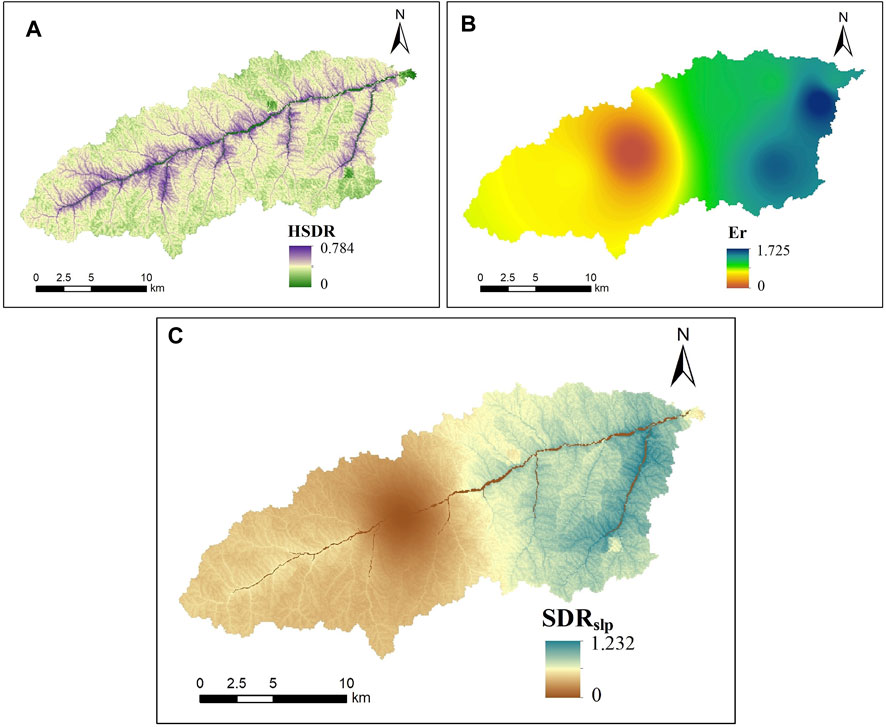
FIGURE 2. Spatial distributions of sediment delivery characteristics of the Mahuyu watershed in July 2006. (A) Structural sediment delivery ratio. (B) Transport threshold factor. (C) Dynamic sediment delivery ratio on the hillslope.

${SDR}_{slp}$ can be obtained by comprehensively considering HSDR and Er and using Eq. 5, as shown in Figure 2C. In July 2006, ${SDR}_{slp}$ ranged from 0 to 1.232. In terms of spatial distribution, ${SDR}_{slp}$ not only mirrors the distribution characteristics of HSDR but also reflects the unevenness of Er distribution across the watershed. It, thus, reflects the influence of rainfall distribution, making it more consistent with the spatial characteristics of the hillslope sediment delivery.

3.2 Model performance

3.2.1 Sediment-carrying capacity

The relationship between the monthly maximum daily flow and sediment-carrying capacity of the channel was evaluated by three-time curve fitting. The fitting process and results are shown in Figures 3A‒C.

FIGURE 3

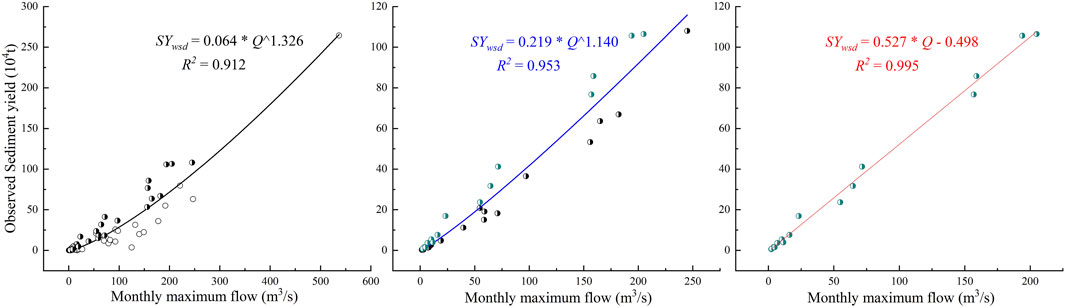
FIGURE 3. Fitting curves of the relationship between monthly maximum flow (Q) and sediment yield of the watershed (${SY}_{wsd}$). (A, B) Power relationship. (C) Linear relationship.

The power relationship between the flow and sediment yield in unsaturated flows is shown in Figures 3A, B, while the linear relationship between the flow and sediment yield in saturated flows is shown in Figure 3C. It can be seen from Figure 3C that 16 points were selected, which is seen as the saturated flow status, and there was a linear relationship between the monthly maximum daily flow and monthly sediment yield of the watershed. The equation was ${SY}_{wsd}$ = 0.527 *Q − 0.498, and the determination coefficient (R²) was 0.995. Therefore, this fitted relationship can be used as a tool for estimating the sediment-carrying capacity.

3.2.2 Performance evaluation

The months with the sediment-carrying capacity greater than simulated ${SY}_{slp}$ in the Mahuyu watershed were selected as calibration months. The model parameters were then calibrated by comparing the observed ${SY}_{wsd}$ in the calibration months during the period 2006–2018. The results are shown in Figure 4A. The main parameters involved in the simulation of the HSDR, IC₀ and k, were −4 and 4, respectively, which are determined by referring to the results of the HSDR in the watershed near the Mahuyu watershed (Zhao et al., 2020), and then, the parameter involved in the Er factor, β, was 1.2.

FIGURE 4

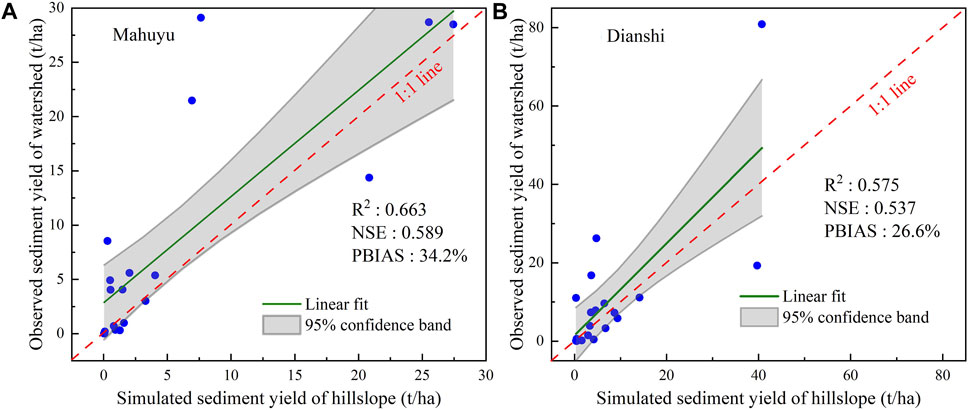
FIGURE 4. Calibration and validation of the hillslope sediment yield model. (A) Calibration in the Mahuyu watershed. (B) Validation in the Heimutouchuan watershed.

It can be seen from Figure 4A that simulated ${SY}_{slp}$ had a good agreement with the observed ${SY}_{wsd}$ in the calibration months. The evaluation index R² was 0.663, NSE was 0.589, and PBIAS was 34.2%, indicating good performance in hillslope sediment yield prediction. For validation of model applicability using the same parameters, the months with the sediment-carrying capacity greater than simulated ${SY}_{slp}$ at the Dianshi station of the Heimutouchuan watershed were selected. The validation results are shown in Figure 4B. The evaluation indices R², NSE, and PBIAS were 0.575, 0.537, and 26.6%, respectively. The values of evaluation indices met the standard, indicating that the parameters were reasonable, and the dynamic hillslope sediment yield model was applicable in this watershed.

3.3 Spatiotemporal variations in the sediment yield

3.3.1 Temporal variations in ${\mathit{P}\mathit{S}\mathit{Y}}_{\mathit{s}\mathit{l}\mathit{p}}$ and ${\mathit{S}\mathit{Y}}_{\mathit{s}\mathit{l}\mathit{p}}$

The watershed average TE, ${PSY}_{slp}$ (in Eq. 6), ${SY}_{slp}$ (in Eq. 7), HSDR, and ${SDR}_{slp}$ were calculated at a monthly scale from 2006 to 2018. To analyze the influence of the Er factor on the hillslope sediment yield, 28 months with erosive rainfall but no transport rainfall events and 9 months with monthly average rainfall >50 mm were selected. The variations in the sediment yield and delivery ratio were plotted, as shown in Figures 5 and 6, respectively.

FIGURE 5

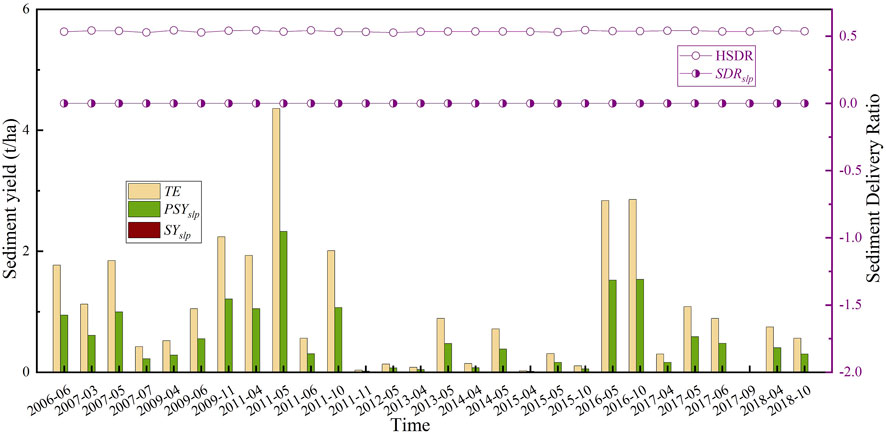
FIGURE 5. Variations in the sediment yield and delivery ratio in months with erosive rainfall but no transport rainfall events.

FIGURE 6

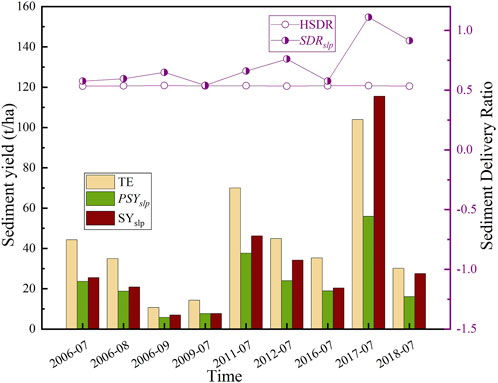
FIGURE 6. Variations in the sediment yield and delivery ratio in months with monthly average rainfall >50 mm.

As shown in Figure 5, the average HSDR of the watershed was 0.535, and this essentially remained unchanged. ${PSY}_{slp}$ was >0, and the maximum value was 2.3 t/ha, while ${SDR}_{slp}$ and ${SY}_{slp}$ were 0, which indicates that there was eroded sediment on the hillslope of the watershed in these months, but not enough transport power. According to the ${SY}_{wsd}$ data obtained from the Mahuyu station, ${SY}_{wsd}$ was 0 in 86% of the months covered by Figure 5, and the maximum value was only 0.06 t/ha, which indicates that the calculated ${SDR}_{slp}$ was rational. The transport rainfall threshold of 25 mm in the Er factor was shown to be acceptable and able to reflect the situation where erosion occurred but no eroded sediment entered the channels.

As shown in Figure 6, the variation in ${SDR}_{slp}$ was striking when the monthly average transport rainfall was >50 mm. ${SDR}_{slp}$ was larger than HSDR, and ${SY}_{slp}$ was larger than ${PSY}_{slp}$. This was especially true for July 2017, where ${PSY}_{slp}$ was 55.9 t/ha, while ${SY}_{slp}$ reached 115.5 t/ha. According to the observed rainfall data, the maximum average daily rainfall of the seven rainfall stations in the Mahuyu watershed was 98 mm in July 2017, and the maximum daily rainfall at the Guoxingzhuang rainfall station was 115.6 mm. Many scholars have obtained hillslope sediment yield via the inversion of dam sediment retention in regions with similar underlying surfaces near the Mahuyu watershed. For example, the hillslope sediment yield in the Chabagou watershed ranged from 107 to 490 t/ha under the heavy rainfall events of 26 July 2017 (Bai et al., 2020), and the ${SY}_{slp}$ in the Wangmaogou watershed reached 253 t/ha under the 148-mm rainfall of the same day (Gao et al., 2018). Comparing the above findings with our simulated results, it can be seen that the simulated ${SY}_{slp}$ based on ${SDR}_{slp}$ is closer to the actual hillslope sediment yield than is the ${PSY}_{slp}$ that is calculated by the HSDR. Thus, ${SDR}_{slp}$ can more accurately reflect the sediment delivery characteristics under key rainfall events in this watershed.

On the basis of the monthly output raster results, the annual TE, ${PSY}_{slp}$, ${SY}_{slp}$, and their accumulated values were tallied, and then the related annual HSDR and ${SDR}_{slp}$ were calculated. The results are shown in Figures 7A, B. In terms of annual variation, ${SY}_{slp}$ was significantly larger than ${PSY}_{slp}$ in 2017, while they were more similar in other years. ${SDR}_{slp}$ varied markedly on the annual scale during the study period, ranging from 0.231 to 0.878. As can be seen from Figure 7B, ${SDR}_{slp}$ had no notable change, indicating that hillslope sediment delivery was relatively stable on the multi-year scale.

FIGURE 7

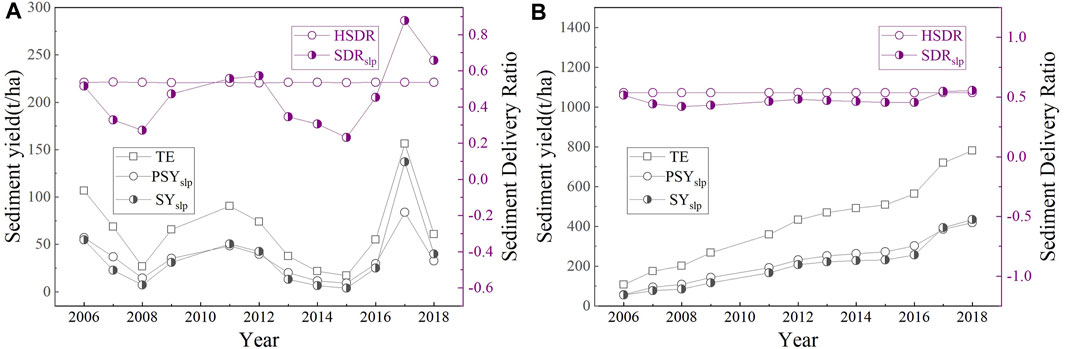
FIGURE 7. Variations in the sediment yield and sediment delivery ratio. (A) Annual variation from 2006 to 2018. (B) Variation in cumulative values.

3.3.2 Spatial distribution of ${\mathit{P}\mathit{S}\mathit{Y}}_{\mathit{s}\mathit{l}\mathit{p}}$ and ${\mathit{S}\mathit{Y}}_{\mathit{s}\mathit{l}\mathit{p}}$

To analyze the influence of the Er factor on the spatial variation in sediment delivery characteristics, we chose July 2006 as the representative month due to its uneven spatial distribution of rainfall. The spatial distributions of TE, ${PSY}_{slp}$, and ${SY}_{slp}$ in July 2006 were plotted, as shown in Figure 8. It can be seen that the amount of soil erosion and sediment yield in the Mahuyu watershed varied dramatically in spatial distribution. The average ${PSY}_{slp}$ and ${SY}_{slp}$ of the watershed were 23.7 and 25.5 t/ha, respectively; and the difference between them was not significant. However, compared with ${PSY}_{slp}$, the percentage of ${SY}_{slp}$ area <10 t/ha and >150 t/ha increased by 4.6% and 1.5%, respectively, indicating that the ${SDR}_{slp}$, which considers the Er factor, can better reflect the key area of sediment yield.

FIGURE 8

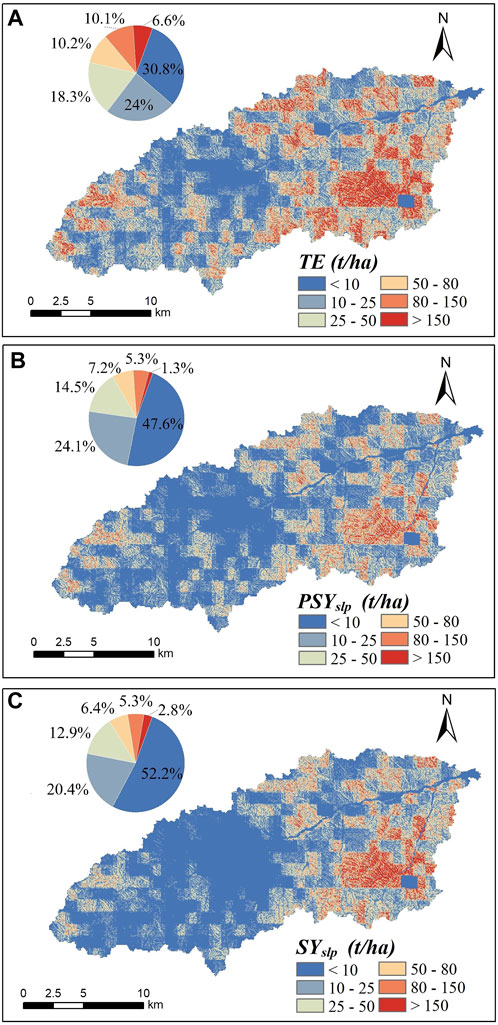
FIGURE 8. Mahuyu watershed (A) total erosion amount, (B) potential sediment yield, and (C) hillslope sediment yield in July 2006.

4 Discussion

In this study, we established a monthly dynamic SDR model by integrating the transport threshold factor and connectivity characteristics of sediment. Hillslope runoff caused by rainfall is a direct driver of sediment delivery. In the context of climate warming, rainfall is unevenly distributed on both spatial and temporal scales (Long et al., 2021). The HSDR can reflect the change in sediment delivery in space; it cannot reflect the change in sediment delivery with time (Borselli et al., 2008). The proposed dynamic SDR can reflect the influence of rainfall variation in both time and space by considering whether rainfall can form sediment-carrying runoff conditions and enter the channels (Figures 2, 8). Perhaps, the thresholds in the Er factor (Eq. 4) need to be appropriately adjusted when applied to watersheds with different underlying surface conditions. However, the annual and monthly variations in ${SDR}_{slp}$ are theoretically more reasonable than the HSDR (Figures 5–7).

${SDR}_{slp}$ was introduced into the simulation of the hillslope sediment yield in the Mahuyu and Heimutouchuan watersheds. The evaluation indices of the simulations show that the ${SDR}_{slp}$ model shows good performance (Figure 4). The simulation performance of the coupled model for small values was better than that for large values. The ${SY}_{wsd}$ was greater than ${SY}_{slp}$ for most large-value cases, which may be a result of ignored erosion in the channels when the sediment-carrying capacity of the channel is greater than ${SY}_{slp}$. In the hilly‒gully region of the Loess Plateau, soil and water conservation measures have been actively used, which has changed the critical rainfall event values that carry the sediment to the channel. This has led to the transport rainfall threshold being significantly higher than the erosive rainfall threshold in the Mahuyu watershed. When the amount of rainfall does not reach the transport threshold, ${SDR}_{slp}$ is 0, so the eroded sediment deposits on the hillslope; this is in line with the actual situation, resulting in the ${SY}_{slp}$ and ${SY}_{wsd}$ of the Mahuyu watershed being 0 (Figure 5). Under heavy rainfall events, hillslope runoff can carry more sediment, and the effects of soil and water conservation measures are reduced. Therefore, ${SDR}_{slp}$ is higher than the HSDR, and ${SY}_{slp}$ is larger than ${PSY}_{slp}$ in months (Figure 6). In addition, ${SDR}_{slp}$ tends to be stable over a multi-year timescale and is similar to the HSDR value (Figure 7B); this is consistent with the view of Jing (2002) who found that the SDR value essentially showed dynamic stability over a long timescale. This is because the effect of the Er factor on the increase or decrease in the sediment yield on the monthly scale is partially offset. Many researchers have also achieved good simulation performance using the HSDR to calculate the hillslope sediment yield over long timescales (Vigiak et al., 2016; Zhao et al., 2020). Similarly, ${PSY}_{slp}$ was similar to ${SY}_{slp}$ at annual (except 2017) and multi-year timescales in our study (Figure 7A). In terms of spatial variation, ${SY}_{slp}$ and ${PSY}_{slp}$ were both in good agreement with the spatial distribution of rainfall (Figures 2B, 8). ${SDR}_{slp}$ in some regions was >1, which can be explained by the sediment deposited before the calculation period entering the channel system under heavy rainfall events (Zhang, 2017). This situation is more common in the region with large-scale hillslope control measures (Li and Li, 2011). In addition, the effect of the spatial difference in the Er factor on the sediment yield was weakened in the average result, resulting in the average ${SY}_{slp}$ being similar to ${PSY}_{slp}$, but the Er factor enhanced the spatial heterogeneity of ${SY}_{slp}$ (Figure 8). Therefore, the ${SDR}_{slp}$ model can be used to identify key regions of sediment delivery. In summary, from the perspective of the dynamic mechanism and spatiotemporal variation characteristics of sediment delivery, the dynamic SDR model, which considers the Er factor, is more reasonable than the structural SDR and can effectively improve the simulation of low and high values of the hillslope sediment yield.

Sediment delivery on hillslopes is a wide-ranging and dynamic process. The characteristics of sediment delivery become more complicated under heavy rainfall events. Although the rationality of the SDR and simulation accuracy of the hillslope sediment yield are improved by considering the transport threshold factor based on the empirical rainfall thresholds, the mechanisms of sediment delivery and the relationship between the threshold and the underlying surface conditions under heavy rainfall require further research. In addition, it is an effective supplement to explore the method to obtain long-term measured sediment yield and investigate the variation in the underlying surface under rainfall in the future.

5 Conclusion

In this study, we have proposed a monthly dynamic SDR model that integrates the structural characteristics of hillslopes and the sediment transport threshold of rainfall events. We calculated the hillslope sediment yield using a coupled model of SDR and soil erosion. We then obtained the relationship between the spatiotemporal variation in sediment delivery and the transport threshold factor. Our conclusions are as follows:

1) The dynamic SDR, which integrates the structural characteristics of a hillslope and the sediment transport threshold of rainfall events, is more reasonable with temporal and spatial variations than the structural SDR. In the application of the dynamic SDR model to the simulation of the hillslope sediment yield in the Mahuyu and Heimutouchuan watersheds, the evaluation indices R² > 0.575, the PBIAS <34.2%, and NSE >0.537. Hence, the results can be used as an effective reference for understanding hillslope sediment transport processes.

2) The dynamic SDR, which considers the transport threshold factor, increases the heterogeneity of monthly and spatial distributions of hillslope sediment yields and effectively improves the simulation accuracy of low and high values of the hillslope sediment yield. The effect of the transport threshold factor on the hillslope sediment yield is essentially in dynamic stability on a multi-year timescale. The dynamic SDR can be used to identify the key regions and rainfall events of sediment delivery.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

ZX: methodology, writing–original draft, and writing–review and editing. SZ: funding acquisition, methodology, project administration, resources, and writing–review and editing. XH: conceptualization, formal analysis, methodology, visualization, and writing–review and editing. YZ: data curation, methodology, validation, and writing–original draft.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This study was supported by the National Key R&D Program of China (grant no. 2022YFC3202004) and the National Natural Science Foundation of China (grant no. U2340204).

Acknowledgments

The authors thank David Wacey, PhD, from Liwen Bianji (Edanz) (www.liwenbianji.cn) for editing the English text of a draft of this manuscript.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bai, L., Wang, N., Jiao, J., Chen, Y., Tang, B., Wang, H., et al. (2020). Soil erosion and sediment interception by check dams in a watershed for an extreme rainstorm on the Loess Plateau, China. Int. J. Sediment Res. 35, 408–416. doi:10.1016/j.ijsrc.2020.03.005

CrossRef Full Text | Google Scholar

Batista, P. V. G., Davies, J., Silva, M. L. N., and Quinton, J. N. (2019). On the evaluation of soil erosion models: are we doing enough? Earth-Science Rev. 197, 102898. doi:10.1016/j.earscirev.2019.102898

CrossRef Full Text | Google Scholar

Borrelli, P., Robinson, D. A., Fleischer, L. R., Lugato, E., Ballabio, C., Alewell, C., et al. (2017). An assessment of the global impact of 21st century land use change on soil erosion. Nat. Commun. 8, 2013–13. doi:10.1038/s41467-017-02142-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Borrelli, P., Robinson, D. A., Panagos, P., Lugato, E., Yang, J. E., Alewell, C., et al. (2020). Land use and climate change impacts on global soil erosion by water (2015-2070). Proc. Natl. Acad. Sci. 117, 21994–22001. doi:10.1073/pnas.2001403117

PubMed Abstract | CrossRef Full Text | Google Scholar

Borselli, L., Cassi, P., and Torri, D. (2008). Prolegomena to sediment and flow connectivity in the landscape: a GIS and field numerical assessment. CATENA 75, 268–277. doi:10.1016/j.catena.2008.07.006

CrossRef Full Text | Google Scholar

Cai, J., Zhou, Z., Liu, J., Wang, H., and Jia, Y. (2020). A distributed soil erosion model based on the three-process of runoff and sediment transport. J. Hydraulic Eng. 51, 140–151. (in Chinese with English Abstract). doi:10.13243/j.cnki.slxb.20190432

CrossRef Full Text | Google Scholar

Cavalli, M., Trevisani, S., Comiti, F., and Marchi, L. (2013). Geomorphometric assessment of spatial sediment connectivity in small Alpine catchments. Geomorphol. Sediment sources, source-to-sink fluxes Sediment. budgets 188, 31–41. doi:10.1016/j.geomorph.2012.05.007

CrossRef Full Text | Google Scholar

De Vente, J., Poesen, J., Verstraeten, G., Van Rompaey, A., and Govers, G. (2008). Spatially distributed modelling of soil erosion and sediment yield at regional scales in Spain. Glob. Planet. Change 60, 393–415. doi:10.1016/j.gloplacha.2007.05.002

CrossRef Full Text | Google Scholar

Diodato, N., and Grauso, S. (2009). An improved correlation model for sediment delivery ratio assessment. Environ. Earth Sci. 59, 223–231. doi:10.1007/s12665-009-0020-x

CrossRef Full Text | Google Scholar

Gao, G., Ma, Y., and Fu, B. (2016). Multi-temporal scale changes of streamflow and sediment load in a loess hilly watershed of China. Hydrol. Process. 30, 365–382. doi:10.1002/hyp.10585

CrossRef Full Text | Google Scholar

Gao, H., Li, Z., Li, P., Ren, Z., Yang, Y., and Wang, J. (2018). Paths and prevention of sediment during storm-runoff on the loess plateau: based on the rainstorm of 2017-07-26 in Wuding river. Sci. Soil Water Conservation 16, 66–72. (in Chinese with English Abstract). doi:10.16843/j.sswc.2018.04.009

CrossRef Full Text | Google Scholar

Gupta, H., Sorooshian, S., and Yapo, P. (1999). Status of automatic calibration for hydrologic models: comparison with multilevel expert calibration. J. Hydrologic Eng. - J HYDROL ENG 4, 135–143. doi:10.1061/(ASCE)1084-0699(1999)4:2(135)

CrossRef Full Text | Google Scholar

Hooke, J., Souza, M., and Marchamalo, M. (2021). Evaluation of connectivity indices applied to a Mediterranean agricultural catchment. Catena 207, 105713. doi:10.1016/j.catena.2021.105713

CrossRef Full Text | Google Scholar

Jamshidi, R., Dragovich, D., and Webb, A. A. (2014). Distributed empirical algorithms to estimate catchment scale sediment connectivity and yield in a subtropical region. Hydrol. Process. 28, 2671–2684. doi:10.1002/hyp.9805

CrossRef Full Text | Google Scholar

Jiao, Y., Lei, H., Yang, D., Huang, M., Liu, D., and Yuan, X. (2017). Impact of vegetation dynamics on hydrological processes in a semi-arid basin by using a land surface-hydrology coupled model. J. Hydrology, Investigation Coast. Aquifers 551, 116–131. doi:10.1016/j.jhydrol.2017.05.060

CrossRef Full Text | Google Scholar

Jin, F., Yang, W., Fu, J., and Li, Z. (2021). Effects of vegetation and climate on the changes of soil erosion in the Loess Plateau of China. Sci. Total Environ. 773, 145514. doi:10.1016/j.scitotenv.2021.145514

PubMed Abstract | CrossRef Full Text | Google Scholar

Jing, K. (2002). Sediment delivery ratio in the upper yangtze river. J. Sediment Res. 1, 53–59. doi:10.16239/j.cnki.0468-155x.2002.01.008

CrossRef Full Text | Google Scholar

Keesstra, S., Nunes, J., Saco, P., Parsons, T., Poeppl, R., Masselink, R., et al. (2018). The way forward: can connectivity be useful to design better measuring and modelling schemes for water and sediment dynamics? Sci. Total Environ. 644, 1557–1572. doi:10.1016/j.scitotenv.2018.06.342

PubMed Abstract | CrossRef Full Text | Google Scholar

Lal, R. (2003). Soil erosion and the global carbon budget. Environ. Int. 29, 437–450. doi:10.1016/S0160-4120(02)00192-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Lenhart, T., Van Rompaey, A., Steegen, A., Fohrer, N., Frede, H.-G., and Govers, G. (2005). Considering spatial distribution and deposition of sediment in lumped and semi-distributed models. Hydrol. Process. 19, 785–794. doi:10.1002/hyp.5616

CrossRef Full Text | Google Scholar

Li, X., and Li, T., 2011. Study of relationship between sediment delivery ratio and watershed scale of Yellow River Basin. (2): 33–38.

Google Scholar

Liu, B. Y., Nearing, M. A., and Risse, L. M. (1994). Slope gradient effects on soil loss for steep slopes. Trans. ASAE 37, 1835–1840. doi:10.13031/2013.28273

CrossRef Full Text | Google Scholar

Liu, Y. (2016). Landscape connectivity in soil erosion research: concepts, implication and quantification. Geogr. Res. 35, 195–202. (in Chinese with English Abstract).

Google Scholar

Long, K., Wang, D., Wang, G., Zhu, J., Wang, S., and Xie, S. (2021). Higher temperature enhances spatiotemporal concentration of rainfall. J. Hydrometeorol. 22, 3159–3169. doi:10.1175/JHM-D-21-0034.1

CrossRef Full Text | Google Scholar

Lu, H., Moran, C. J., and Prosser, I. P. (2006). Modelling sediment delivery ratio over the murray darling basin. Environ. Model. Softw. 21, 1297–1308. doi:10.1016/j.envsoft.2005.04.021

CrossRef Full Text | Google Scholar

Michalek, A., Zarnaghsh, A., and Husic, A. (2021). Modeling linkages between erosion and connectivity in an urbanizing landscape. Sci. Total Environ. 764, 144255. doi:10.1016/j.scitotenv.2020.144255

PubMed Abstract | CrossRef Full Text | Google Scholar

Mishra, K., Sinha, R., Jain, V., Nepal, S., and Uddin, K. (2019). Towards the assessment of sediment connectivity in a large Himalayan river basin. Sci. Total Environ. 661, 251–265. doi:10.1016/j.scitotenv.2019.01.118

PubMed Abstract | CrossRef Full Text | Google Scholar

Najafi, S., Dragovich, D., Heckmann, T., and Sadeghi, S. H. (2021). Sediment connectivity concepts and approaches. CATENA 196, 104880. doi:10.1016/j.catena.2020.104880

CrossRef Full Text | Google Scholar

Nash, J. E., and Sutcliffe, J. V. (1970). River flow forecasting through conceptual models part I — a discussion of principles. J. Hydrology 10, 282–290. doi:10.1016/0022-1694(70)90255-6

CrossRef Full Text | Google Scholar

Niguse, A., Eekhout, J., Vermeulen, B., Boix-Fayos, C., Vente, J., Grum, B., et al. (2023). The potential and challenges of the ‘RUSLE-IC-SDR’ approach to identify sediment dynamics in a Mediterranean catchment. Catena 233, 107480. doi:10.1016/j.catena.2023.107480

CrossRef Full Text | Google Scholar

Renard, K. G., Foster, G. R., Weesies, G. A., and Porter, J. P. (1991). RUSLE: Revised universal soil loss equation. J. Soil Water Conservation 46, 30–33.

Google Scholar

Rustomji, P., Zhang, X. P., Hairsine, P. B., Zhang, L., and Zhao, J. (2008). River sediment load and concentration responses to changes in hydrology and catchment management in the Loess Plateau region of China. Water Resour. Res. 44. doi:10.1029/2007WR006656

CrossRef Full Text | Google Scholar

Tao, M., and Chen, X. (2015). Afforestation influence on soil moisture dynamics and runoff on the Loess Plateau. Yellow River 37 (3), 96–99. (in Chinese with English Abstract).

Google Scholar

Thomas, J., Joseph, S., and Thrivikramji, K. P. (2018). Assessment of soil erosion in a tropical mountain river basin of the southern Western Ghats, India using RUSLE and GIS. Geosci. Front. 9, 893–906. doi:10.1016/j.gsf.2017.05.011

CrossRef Full Text | Google Scholar

Turnbull, L., and Wainwright, J. (2019). From structure to function: understanding shrub encroachment in drylands using hydrological and sediment connectivity. Ecol. Indic. 98, 608–618. doi:10.1016/j.ecolind.2018.11.039

CrossRef Full Text | Google Scholar

Van Oost, K., Quine, T. A., Govers, G., De Gryze, S., Six, J., Harden, J. W., et al. (2007). The impact of agricultural soil erosion on the global carbon cycle. Science 318, 626–629. doi:10.1126/science.1145724

PubMed Abstract | CrossRef Full Text | Google Scholar

Vigiak, O., Beverly, C., Roberts, A., Thayalakumaran, T., Dickson, M., McInnes, J., et al. (2016). Detecting changes in sediment sources in drought periods: the Latrobe River case study. Environ. Model. Softw. 85, 42–55. doi:10.1016/j.envsoft.2016.08.011

CrossRef Full Text | Google Scholar

Vigiak, O., Borselli, L., Newham, L. T. H., McInnes, J., and Roberts, A. M. (2012). Comparison of conceptual landscape metrics to define hillslope-scale sediment delivery ratio. Geomorphology 138, 74–88. doi:10.1016/j.geomorph.2011.08.026

CrossRef Full Text | Google Scholar

Walling, D. E. (1983). The sediment delivery problem. J. Hydrology, Scale Problems Hydrology 65, 209–237. doi:10.1016/0022-1694(83)90217-2

CrossRef Full Text | Google Scholar

Wen, X., and Deng, X. (2020). Current soil erosion assessment in the Loess Plateau of China: a mini-review. J. Clean. Prod. 276, 123091. doi:10.1016/j.jclepro.2020.123091

CrossRef Full Text | Google Scholar

Wu, L., Liu, X., and Ma, X. (2018a). Research progress on the watershed sediment delivery ratio. Int. J. Environ. Stud. 75, 565–579. doi:10.1080/00207233.2017.1392771

CrossRef Full Text | Google Scholar

Wu, L., Yao, W., and Ma, X. (2018b). Using the comprehensive governance degree to calibrate a piecewise sediment delivery ratio algorithm for dynamic sediment predictions: a case study in an ecological restoration watershed of northwest China. J. Hydrology 564, 888–899. doi:10.1016/j.jhydrol.2018.07.072

CrossRef Full Text | Google Scholar

Xie, W., and Li, T. (2012). Research comment on watershed sediment delivery ratio. Acta Sci. Nat. Univ. Pekin. 48 (4), 676–685. (in Chinese with English Abstract). doi:10.13209/j.0479-8023.2012.089

CrossRef Full Text | Google Scholar

Xu, Z., Zhang, S., Zhou, Y., Hou, X., and Yang, X. (2022). Characteristics of watershed dynamic sediment delivery based on improved RUSLE model. CATENA 219, 106602. doi:10.1016/j.catena.2022.106602

CrossRef Full Text | Google Scholar

Yesuf, H. M., Assen, M., Alamirew, T., and Melesse, A. M. (2015). Modeling of sediment yield in Maybar gauged watershed using SWAT, northeast Ethiopia. CATENA 127, 191–205. doi:10.1016/j.catena.2014.12.032

CrossRef Full Text | Google Scholar

Zhang, G. (2021). Understanding sediment connectivity from soil erosion perspective. Adv. water Sci. 32, 295–308. (in Chinese with English Abstract). doi:10.14042/j.cnki.32.1309.2021.02.015

CrossRef Full Text | Google Scholar

Zhang, J. (2017). Discussion on Mechanism and process of sediment moving into the yellow river. Yellow River 39, 8–12+17. (in Chinese with English Abstract).

Google Scholar

Zhang, S., Chen, D., Li, F., He, L., Yan, M., and Yan, Y. (2018). Evaluating spatial variation of suspended sediment rating curves in the middle Yellow River basin, China. Hydrol. Process. 32, 1616–1624. doi:10.1002/hyp.11514

CrossRef Full Text | Google Scholar

Zhang, S., Li, Z., Hou, X., and Yi, Y. (2019a). Impacts on watershed-scale runoff and sediment yield resulting from synergetic changes in climate and vegetation. Catena 179, 129–138. doi:10.1016/j.catena.2019.04.007

CrossRef Full Text | Google Scholar

Zhang, Y., Jiao, J., Tang, B., Chen, Y., Wang, N., Bai, L., et al. (2019b). Channel sediment connectivity and influence factors in small watersheds under extremely rainstorm—a case study at Zizhou county, shaanxi province. Bull. soil water conservation 39, 302–309. (in Chinese with English Abstract). doi:10.13961/j.cnki.stbctb.2019.01.047

CrossRef Full Text | Google Scholar

Zhao, G., Gao, P., Tian, P., Sun, W., Hu, J., and Mu, X. (2020). Assessing sediment connectivity and soil erosion by water in a representative catchment on the Loess Plateau, China. CATENA 185, 104284. doi:10.1016/j.catena.2019.104284

CrossRef Full Text | Google Scholar

Zheng, M. (2018). A spatially invariant sediment rating curve and its temporal change following watershed management in the Chinese Loess Plateau. Sci. Total Environ. 630, 1453–1463. doi:10.1016/j.scitotenv.2018.02.323

PubMed Abstract | CrossRef Full Text | Google Scholar