An undrained dynamic strain-pore pressure model for deep-water soft clays from the South China Sea

1 Introduction

With the development and utilization of deep-sea resources, many engineering structures (e.g., the anchoring foundation of floating production platforms, submarine wellheads, and submarine pipelines) are fixed or laid to seabed soils (Guo et al., 2023a; Wang et al., 2024; Wu et al., 2024). The stability of these structures is closely related to the self-properties and responses of the seabed soils (Nian et al., 2021; Liu et al., 2023). The distribution of soft soils, which have physical and mechanical properties such as high water content, high thixotropy, low strength, and low permeability, is very common in deep-sea areas, according to survey and analysis results (Nian et al., 2018; Huang et al., 2021). Deep-sea soft soils are highly susceptible to destabilization and sliding due to external disturbances (Ren et al., 2018a; Fan et al., 2023; Guo et al., 2023b; Guo et al., 2024), especially for cyclic loading disturbances with high frequencies and load levels (usually caused by frequent seaquakes or earthquakes; for example, Figure 1 shows the seismic distribution situation around the Pacific Ocean). The low permeability of deep-sea soft soils results in the inability of water to drain out of the soils (i.e., in the undrained state) under cyclic loading, which generates excess pore water pressure and reduces the strength and bearing capacity of deep-sea seabed soils, threatening the safety and stability of deep-sea engineering structures (Andersen, 2009). Therefore, it is necessary to study the undrained deformation-pore pressure behavior of deep-sea soft soils under cyclic loading to ensure the safety and normal use of deep-sea engineering structures.

Figure 1

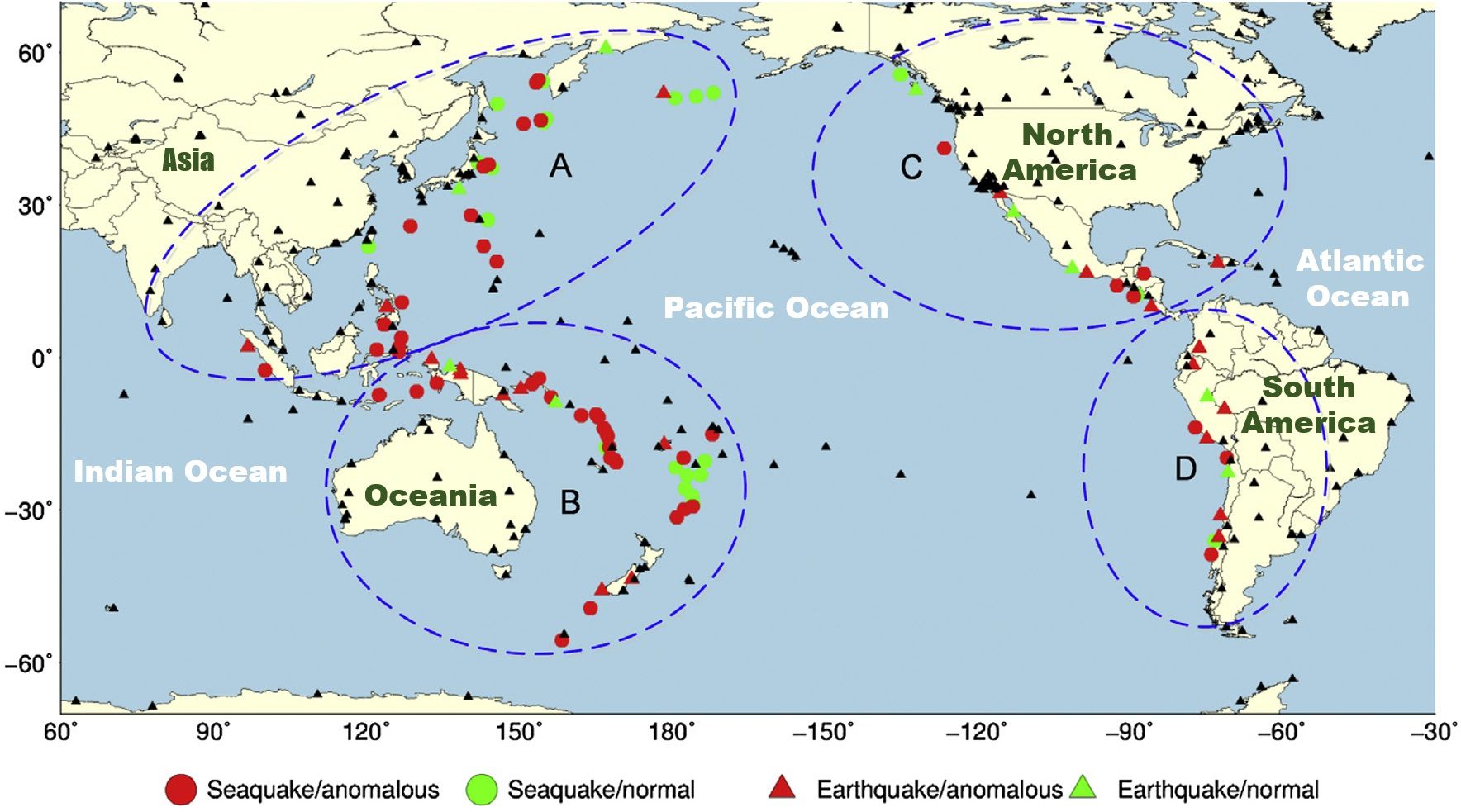
Figure 1 Distribution of 100 M7.0+ earthquakes in the Circum-Pacific seismic belt from 2006 to 2015 (sources from Li et al., 2018, where (A) refers to most parts of Southeast Asia, Taiwan Island, Japan, Kamchatka and the Aleutian Islands; (B) refers to New Guinea, the Solomon Islands, the Fiji Islands and New Zealand; (C) refers to Mexico and the west coast of Canada and America; (D) refers to the west coast of South America; and the black triangles signify the IGS stations).

The dynamic response of soft soils under cyclic loading has been investigated in many studies (e.g., Moses et al., 2003; Li et al., 2011, 2014; Wang et al., 2017). In studies on the dynamic pore water pressure response of soils, several empirical and theoretical models have been proposed to describe the development of pore water pressure under cyclic loading based on cyclic triaxial test results (e.g., Li and Meissner, 2002; Nie et al., 2007; Ni et al., 2015), which can predict the pore pressure accumulation of soft soils under cyclic loading. Considering the low number of cyclic loadings (usually less than 2000) in previous studies, Ren et al. (2018b) conducted long-term low-stress horizontal cyclic loading tests to obtain a new empirical model describing the development of pore pressure in soft marine clay under long-term low-stress horizontal cyclic loading. Wang et al. (2021) carried out several principal stress axis rotation tests and found that the pore water pressure accumulation of soft clay is greatly affected by the intermediate principal stress coefficient. Through a series of dynamic cyclic shear tests, Jin et al. (2023) found that an increase in the cyclic stress ratio and the amplitude ratio of the shear stress accelerates pore water pressure accumulation and proposed a normalized model for predicting the variation in residual pore water pressure with the number of cycles.

Many studies have also been carried out on the strain and deformation behavior of soft soils under cyclic loading. Hyodo et al. (1992) found that the elastic strain of saturated clay was not significantly related to the value of the amplitude of the dynamic stress, but there was a corresponding relationship with the effective stress ratio through cyclic triaxial tests. Muhanna (1994) developed a simple model for assessing the elastic modulus and cumulative permanent strain of soft clay under cyclic loading through similar soil dynamic tests. Yang et al. (2012) revealed that the cyclic stress ratio was a key factor for the development of different deformations of marine soft clay under cyclic loading and proposed the concept of a critical cyclic stress ratio, below which the cumulative plastic deformation of the soil body gradually stabilized. Guo et al. (2013) found that the stress-strain hysteretic loop, resilient modulus, and permanent strain of soils were significantly correlated with the cyclic stress ratio and confining pressure by analyzing the results of a series of monotonic triaxial tests and long-term cyclic triaxial tests. Yang et al. (2012) and Lei et al. (2016) further reported that cyclic loading accelerated the creep behavior of marine soft clay when the cyclic stress ratio was greater than the critical cyclic stress ratio, which adversely affected soil deformation. Lei et al. (2020) investigated the microscopic characteristics and deformation development of soft marine clay under cyclic loading using cyclic triaxial tests and scanning electron microscopy (SEM), discussed the relationship between microscopic parameters and the cumulative plastic strain of marine soft clay, and further established an empirical model of cumulative plastic strain involving microscopic parameters for assessing the deformation of marine soft clay.

In addition, in several previous studies, the pore pressure–deformation behavior of soft soils under cyclic loading and their relationships have also been investigated. For example, Ansal and Erken (1989) investigated the cyclic stress-strain-pore pressure and cyclic shear strength characteristics of clay under undrained conditions and proposed an empirical method for evaluating the cyclic yield strength of normally consolidated soils. Hyde et al. (1993) carried out a series of cyclic undrained triaxial tests on Ariake clay, and based on the results of the tests, relevant stability criteria for pore water pressures and strains at different cyclic stress levels were developed. Wang et al. (2013) conducted a series of high-cycle (50,000 cycles) triaxial tests on Wenzhou marine soft clay under different stress levels and confining pressures to study the development of strain and pore water pressure. These researchers proposed an equation for describing the relationship between the peak axial stress and the peak pore water pressure after 1000 cycles. Dai et al. (2021) found that the development of permanent pore pressure depends on the large initial shear stress ratio (SSR) and overpressure consolidation ratio (OCR), whereas the development of permanent dynamic strain is divided into three stages by a series of cyclic triaxial tests on marine soft clay with large initial SSR and OCR. Zhao et al. (2023) proposed a conceptual model of high-cycle, low-amplitude undrained loading containing shrinkage yield surfaces and swelling boundary surfaces to describe the weakening behavior induced by the increase in excess pore water pressure and the hardening effect induced by shrinkage plastic deformation, respectively.

In summary, although some valuable studies on the behavior of soft soils under cyclic loading have been conducted, to date, there have been relatively few studies on the in situ properties of deep-sea soft soils. In particular, there is still a gap in the studies that reveal the pore pressure-deformation behavior of deep-sea soft soils under cyclic loading, taking into account a more comprehensive stress level and long-term cyclic loading (such as earthquake action). In this study, we aim to reveal the dynamic pore pressure–deformation development behavior of deep-sea soft soils under strong and long-term cyclic loading and further propose a dynamic pore pressure–deformation equation applicable to typical deep-sea soft soils in the South China Sea.

2 Materials and methods

2.1 Soil properties and specimen preparation

The marine clay samples analyzed in this study were collected during a shared voyage in the northeastern part of the South China Sea and the Luzon Strait. This region, characterized by its unique location at the convergence of several tectonic plates, has a rich history of seismic activity and marine events (Liu, 1994; Wang et al., 2014). Its geological features offer a unique opportunity to study interactions between tectonic movements and marine geological processes. The study of these marine clays is pivotal for understanding the mechanics behind seismic occurrences, predicting future seismic activities, and formulating strategies for mitigating disaster risks. The sampling stations are located at the intersection of the Pearl River valley slope (Station S7A-3) and the Dongsha slope (Station D2-1), as depicted in Figure 2. These samples were retrieved by employing the gravity penetration method. The selected region is notably situated in an area characterized by seismic activity and frequent maritime occurrences.

Figure 2

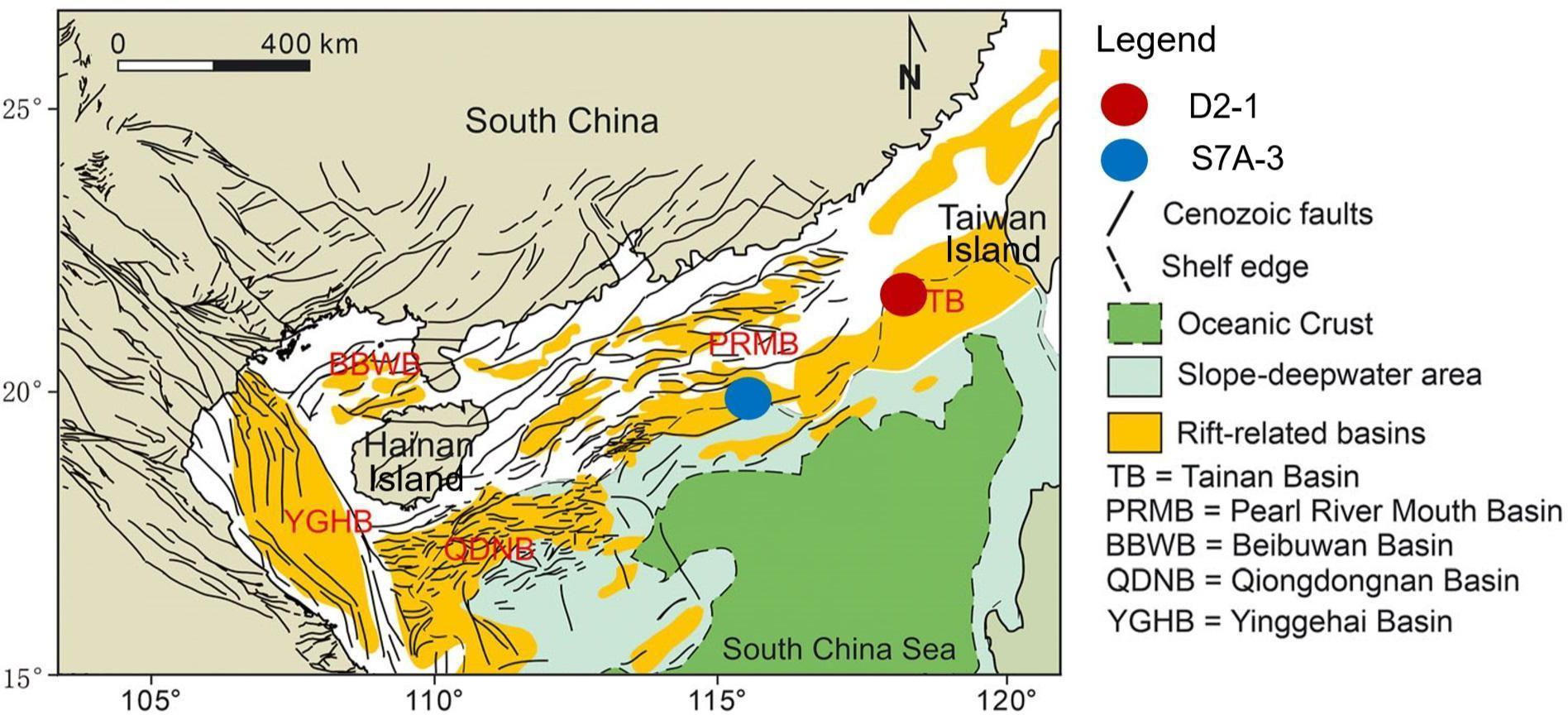
Figure 2 Sampling sites in the northern continental slope area of the South China Sea showing the major tectonic units (modified from Zhang et al., 2020).

The soil samples used in the test were obtained through the 2016 shared voyage plan for the northeastern South China Sea and the Luzon Strait by using the gravity sampling method. This sampling method can ensure that the sampling depth meets the test requirements and ensure the natural state of undisturbed soil samples to the greatest extent. The soil samples obtained by drilling consisted of shallow sensitive clay located at seabed depths ranging from 0 to 2.4 m, beneath water depths of 1,152 m (Station S7A-3) and 1,885 m (Station D2-1). The soil samples obtained by drilling were canned in polyvinyl chloride (PVC) pipes with a diameter of 10 cm. To facilitate transportation, each section was cut to 1 m. The cut soil samples were marked in turn, wrapped with fresh-keeping film, sealed with adhesive tape, and then sealed at both ends with pipe heads to ensure no loss of water. During the test period, the soil samples were kept in a constant temperature room. The collection, cutting, packaging, transportation, storage and other processes of the above soil samples minimize the disturbance caused by objective factors and effectively ensure the undisturbed nature of the soil samples.

The fundamental physical and mechanical properties of these undisturbed soil samples were determined through indoor soil testing, and the results are presented in Table 1. Analysis of these parameters reveals distinctive attributes of deep-sea marine clay in the South China Sea. The specific gravity (G_s) of the S7A-3 sample was found to be 2.62 g/cm³, which was slightly greater than that of the D2-1 sample, which was 2.57 g/cm³. This difference suggests a higher mineral content in the S7A-3 sample, possibly due to the localized geological composition. A remarkable difference was observed in the natural water content (ω₀), with the S7A-3 sample exhibiting a significantly higher value (121.04%) than the D2-1 sample (85.75%). This substantial disparity indicates a greater degree of saturation and potential pore-water interaction in the S7A-3 sample, which could have implications for its mechanical behavior under stress. The initial density (ρ₀) of the S7A-3 sample was 1.354 g/cm³, whereas the D2-1 sample had a notably higher density of 1.523 g/cm³. Correspondingly, the initial void ratio (e₀) for S7A-3 was 3.326, which was significantly greater than the value of 2.191 for Station D2-1. These measurements suggest a more loosely packed structure in the S7A-3 sample, potentially influencing its compressibility and shear strength. The liquid limit (ω_L) and plasticity index (I_p) of the S7A-3 sample were 55.85% and 31.42, respectively, compared to 51.01% and 32.35 for the D2-1 sample. These values indicate that both samples exhibit high plasticity. The compressibility factor (α_v) for S7A-3 was 3.217 MPa⁻¹, which is greater than the 2.283 MPa⁻¹ of D2-1, indicating a greater susceptibility to volume change under load for the S7A-3 sample. Additionally, the undrained strength (S_u,0) of the S7A-3 sample was 19.58 kPa, substantially higher than the 12.31 kPa of D2-1, suggesting a greater resistance to shear under undrained conditions. The sensitivity (S_t) of the S7A-3 sample was 14.34, compared to 10.53 for the D2-1 sample. This higher sensitivity in the S7A-3 sample points to a more delicate structure, which could be more susceptible to disturbances. These characteristics are indicative of the unique structural properties inherent to marine clay under various environmental and loading conditions.

Table 1

Table 1 Index properties of the deep-sea clay.

The meticulous process of preparing and cutting marine clay samples for dynamic triaxial testing is a crucial step in ensuring the accuracy and reliability of the experimental results. As depicted in Figure 3 of the study, this process involves several key stages, each designed to preserve the integrity of the samples while preparing them for precise testing. The process begins with the in situ cylindrical soil samples, which are carefully sectioned into three equal parts. This initial sectioning is critical to ensure uniformity in size and properties across all test specimens. Each of these segments is then meticulously processed into cylindrical specimens. The dimensions of these specimens are strictly controlled, with a diameter of 39.1 mm and a height of 80 mm. These dimensions are chosen to fit the requirements of the dynamic triaxial testing apparatus. The precision in cutting these cylindrical specimens is achieved through the use of specialized equipment. This equipment ensures that each specimen maintains its integrity without inducing any additional stress or alteration to its natural state. Precision cutting is crucial for maintaining the natural structure and properties of marine clay, which are essential for accurate testing and analysis. Throughout the preparation and cutting process, great care is taken to preserve the natural moisture content and structural properties of the samples. This preservation is vital for maintaining the authenticity of the samples under in situ conditions. Once cut to the precise dimensions, the specimens are immediately prepared for dynamic triaxial testing.

Figure 3

Figure 3 Deep-sea in situ clay samples and specimen preparation.

2.2 Test scheme of the automated triaxial testing system

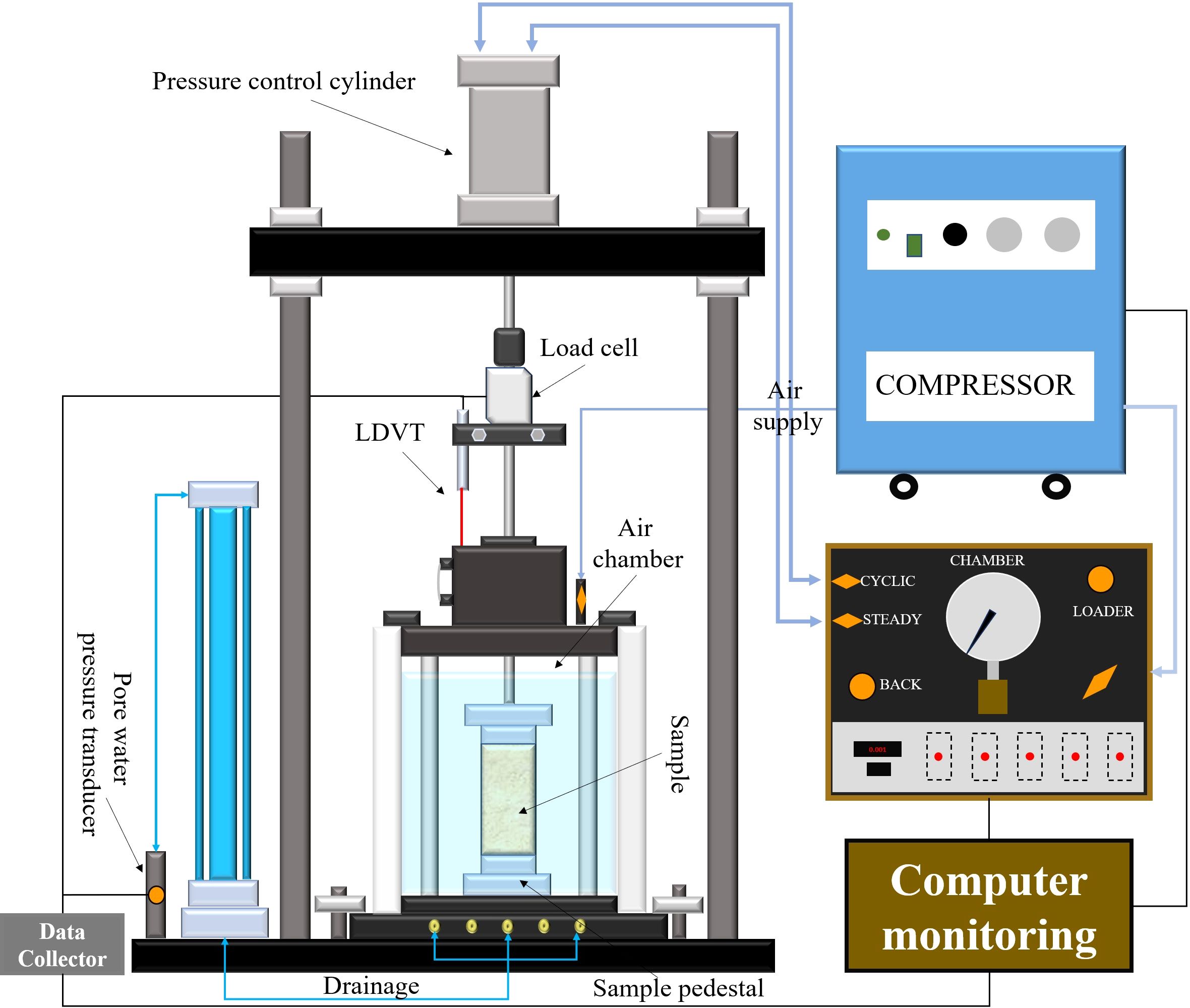
In this study, an automated triaxial testing system (ATTS), as shown in Figure 4, was employed to conduct consolidation and cyclic loading triaxial tests. This system, which is specifically designed and manufactured, accommodates the unique requirements of dynamic triaxial testing under both isotropic and anisotropic consolidation conditions. The ATTS applies vertical pressure through a highly precise load cell. This load cell is a crucial component, providing the necessary force to simulate vertical stress conditions on the soil specimens. The confining pressure, an essential parameter in triaxial testing, is generated within the system using an air pressure-type piston. This method of applying confining pressure allows for accurate simulation of the lateral stress conditions that are prevalent in subsurface environments. The axial displacements during the testing process are meticulously recorded using a linear variable differential transformer (LVDT) axial actuator. The LVDT axial actuator offers high-resolution measurements of the specimen’s deformation. The ATTS is also equipped with a pore water pressure transducer positioned at the center of the specimen’s bottom.

Figure 4

Figure 4 The ATTS testing system.

The experimental scheme is presented in Table 2. A confining pressure of 150 kPa was maintained. The test specimens from Station S7A-3 were subjected to anisotropic consolidation with consolidation stress ratios of 1.0, 1.25, and 1.40, whereas the specimens from D2-1 were tested at a ratio of 1.25. The experiments were conducted using constant-amplitude half-sine wave cyclic loading at a frequency of 1.0 Hz. The condition for the end of the test is that the axial dynamic strain exceeds 25% or the number of loading times exceeds 2000. The number of loading cycles each specimen underwent varied, as indicated in Table 2. To account for varying conditions of biased and isostatic consolidation, the cyclic stress ratio (CSR) was defined as per Formula (1):

Table 2

Table 2 Experimental conditions of the cyclic triaxial tests.

$\begin{array}{ll}CSR=\frac{{\sigma }_{\text{d}}}{2{\sigma }_{\text{c}}}=3{\sigma }_{\text{d}}/[2({\sigma }_1+2{\sigma }_3)]& (1)\end{array}$

where σ_d is the cyclic dynamic stress, σ_c is the average consolidation pressure, σ₁ is the axial consolidation pressure, and σ₃ is the lateral consolidation pressure.

3 Results and discussion

3.1 Cumulative evolution of the undrained dynamic strain

This section assesses the impact of the cyclic stress ratio (CSR), OCR, and consolidation stress ratio (K_c) on the accumulation of dynamic strain during undrained cyclic dynamic tests. Figure 5 illustrates the dynamic strain (ε_d) accumulations as the number of cycles increases under varying K_c and OCR. Overall, the evolution of the dynamic strain (ε_d) is closely linked to the peak value of the cyclic dynamic stress, i.e., the magnitude of the CSR. A higher CSR results in a greater dynamic strain, including resilient strain (ε_r) and permanent strain (ε_p), increasing the likelihood of structural failure of clay samples across all K_c. The critical cyclic stress ratio (CSR_cr) serves to distinguish the developmental trend of dynamic strain (ε_d) (Nian et al., 2020).

Figure 5

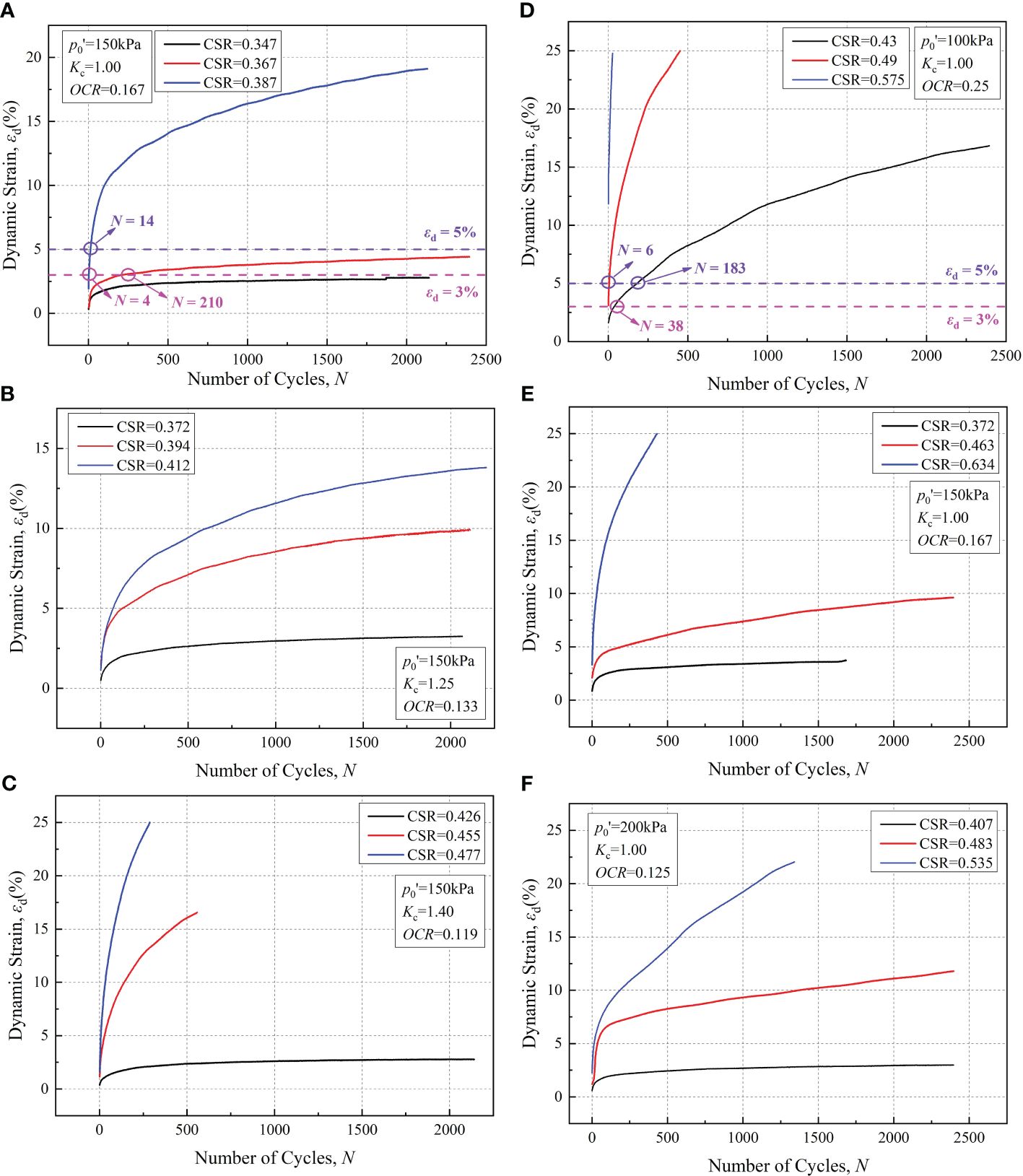
Figure 5 Dynamic strain evolution under different stress magnitudes [(A–C) under different consolidation ratios K_c (Nian et al., 2018); and (D–F) under different overpressure consolidation ratios OCR (Nian et al., 2020)].

When the CSR is less than the CSR_cr, the dynamic strain initially increases and then stabilizes within a very few cycles, well before reaching 100 cycles. Ultimately, ϵ_d stabilizes at a lower level, consistently below 3% (refer to the black trend lines in Figures 5A–C, E, F. However, when the CSR exceeds the CSR_cr, the dynamic strain continues to increase during subsequent cyclic loading, particularly when the CSR is significantly greater than the CSR_cr. In such cases, the ε_d of the specimen rapidly surpasses 5% within the initial 10 cycles (refer to the blue trend lines in Figure 5). The impact of K_c on dynamic strain development during dynamic tests is depicted in Figures 5A–C. For a given CSR, a higher consolidation stress ratio leads to smaller strain growth trends. As illustrated by the black trend lines in Figure 5, a consistent strain growth pattern characterized by slow increases that tend to stabilize is exhibited at approximately 3%. With the same growth trend, as K_c increases from 1.0 to 1.25 and then to 1.40, the corresponding cyclic stress ratio increases from 0.347 to 0.412 and then to 0.426. This implies that under the same dynamic load, greater consolidation ratios result in less structural damage to marine clay and enhanced stability. Figures 5D–F illustrates the influence of the OCR on dynamic strain development during dynamic tests. The influence of CSR on dynamic strain aligns with the earlier discussion. In contrast to the effect of K_c on the dynamic strain, to achieve the same level of dynamic strain, the OCR decreases from 0.25 to 0.167 and further to 0.125, requiring an increase in the CSR from 0.43 to 0.463 or even 0.483. This reveals a converse outcome compared to K_c; under the same dynamic load, a smaller OCR results in reduced structural damage to marine clay and increased clay sample stability.

3.2 Cumulative dynamic strain model

Through fitting and analyzing the dynamic strain data, it is observed that the model (Equation (2)) based on the well-known classical Hardin-Drnevich model (Hardin and Drnevich, 1972) effectively captures the cumulative plastic deformation of deep-sea soft clay caused by dynamic stress:

$\begin{array}{ll}{\epsilon }_d=\frac{N^c}{a+b{N}^c}& (2)\end{array}$

where a, b, and c are parameters dependent on the stress path, stress state, and physical properties of the clay.

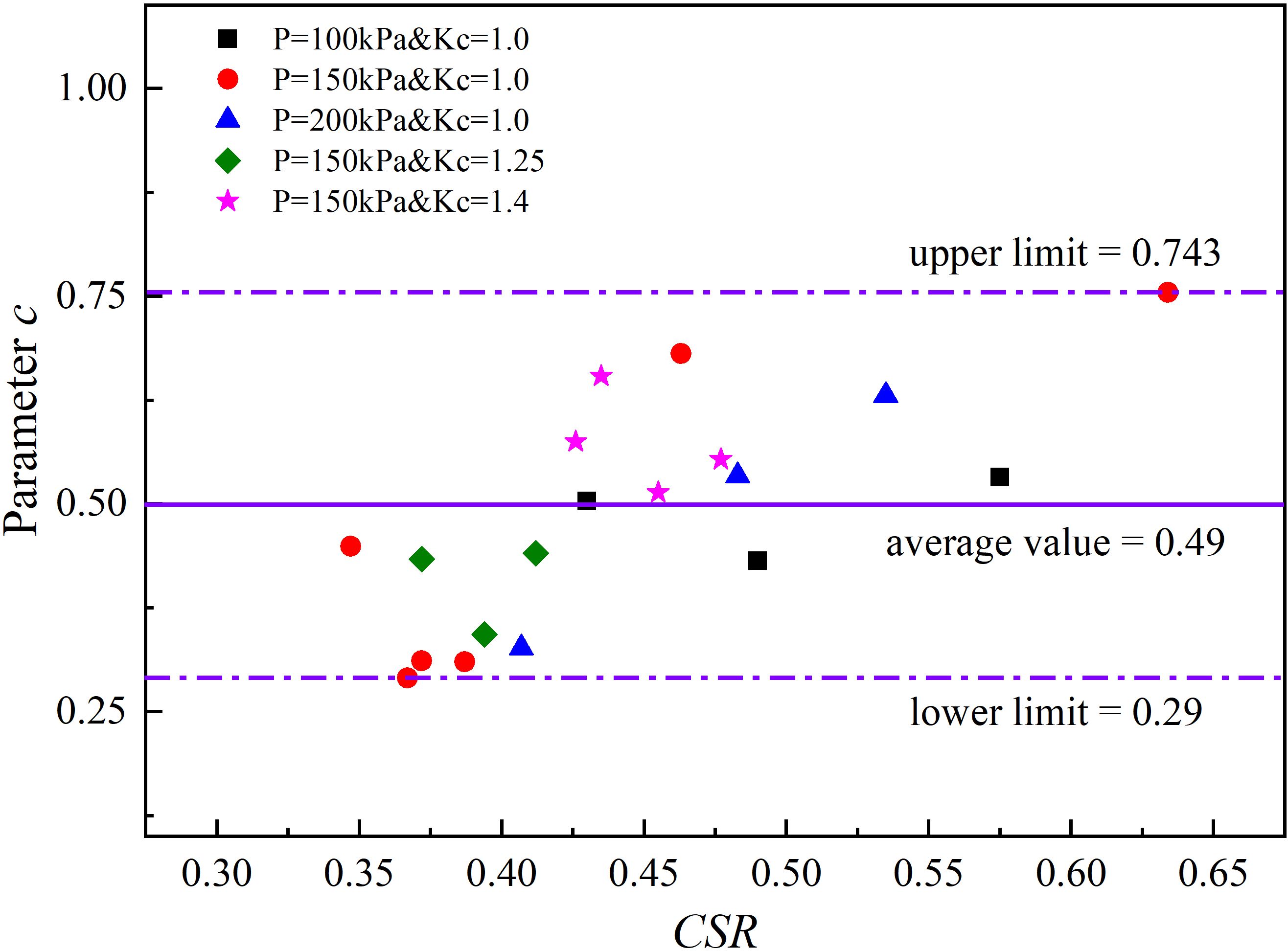
Considering the dynamic strain growth curve, it is reasonable to infer that parameter c depends on the physical properties of the clay, such as the water content, void ratio, particle size, and particle specific surface area. Ren et al. (2018), in conjunction with previous studies (referencing Monismith et al., 1975; Li and Selig, 1996), discovered that most values of parameter c fall within a narrow range of 0.18–0.82, with an average value of approximately 0.5. The fitting results for parameter c of the deep-sea clay in the South China Sea in this article are essentially consistent with previous findings, yielding an average value of 0.49, as illustrated in Figure 6.

Figure 6

Figure 6 Effect of the stress state on parameter c.

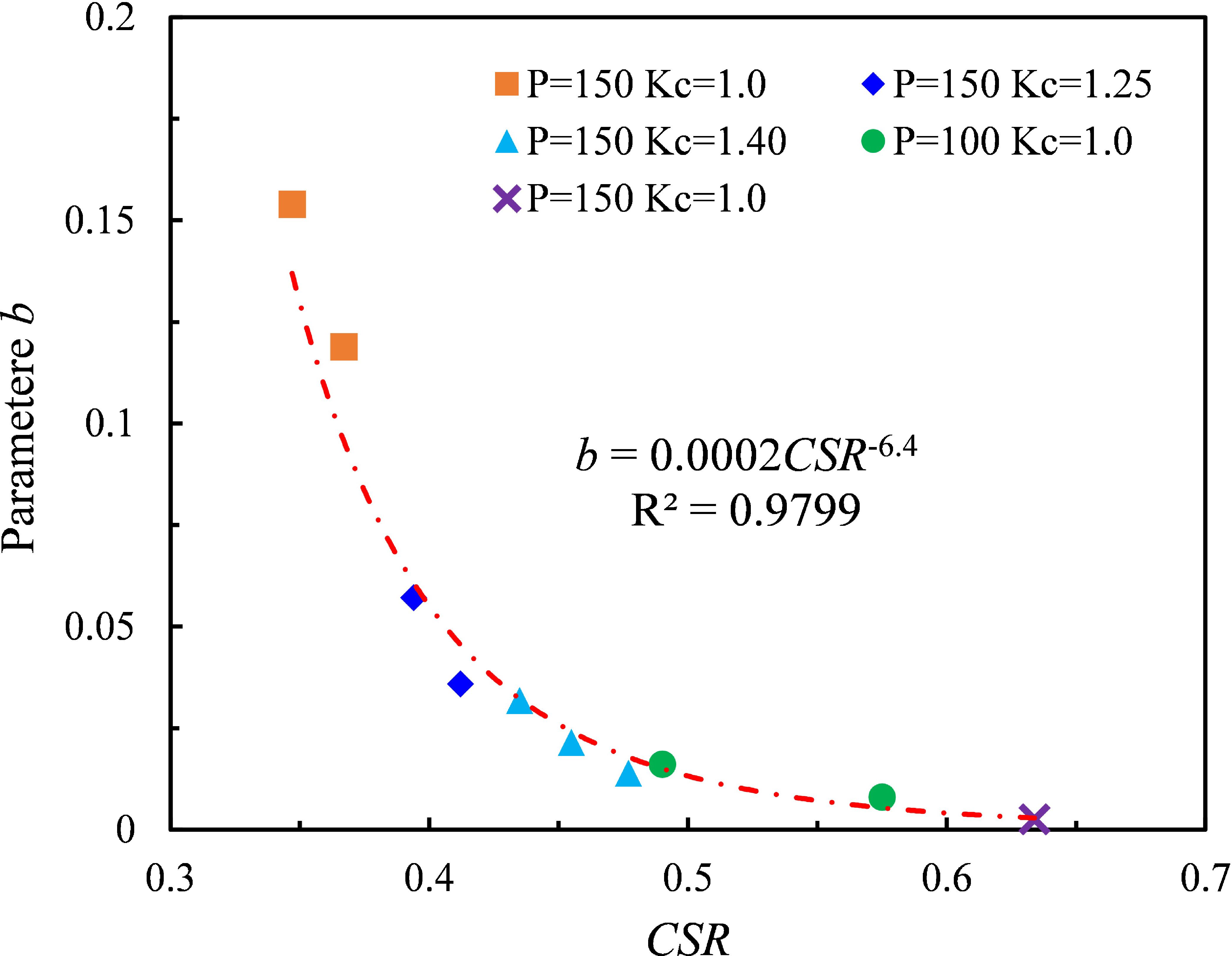
An analysis of the cumulative curve of the corresponding changes shows that parameter a governs the initial strain of the clay, indicating the degree of difficulty for the clay to begin deforming. Additionally, experimental data of ϵ_d under different CSR values, varying initial mean effective stresses P, and different K_c values were utilized to derive parameters a and b in Equation (2) using the least squares method. The fitting revealed a robust correlation between parameter b and CSR (as illustrated in Figure 7), while parameter a exhibited a strong correlation with CSR and K_c. Their relationships were also determined. The influence of the OCR on the dynamic strain was found to be insignificant, and therefore, it is not reflected in the relationship equation. The correlation of parameters a and b in the fitting formula exceeded 90%, and the corresponding Equations (3) and (4) are as follows:

Figure 7

Figure 7 Effect of the stress state on parameter b.

$\begin{array}{ll}a=2(\text{E}-5) CS{R}^{-8.05}{K}_{\text{c}}^{16.30}& (3)\end{array}$

$\begin{array}{ll}b=0.0002CS{R}^{-6.4}& (4)\end{array}$

To validate the applicability of the strain model and the fitting formula for model parameters, laboratory test results from Station-2 were compared with corresponding predicted outcomes from the model. Figure 8 shows the comparison between the model predictions for deep-sea clay and the dynamic strain results obtained from laboratory tests. The validation utilized deep-sea soft clay (Station-2) in the South China Sea, and its fundamental physical and mechanical properties are listed in Table 1. The test carefully considered the physical state, stress conditions, and applied dynamic loads of the clay to maintain consistency with the testing process at Station-1, minimizing human interference. In Figure 9, the experimental results and model predictions are represented by points and dashed lines, respectively. The predicted strain results from the model closely replicate the experimental data, demonstrating a high degree of fitting under sustained cyclic dynamic loading. The conditions corresponding to the four different CSR values encompass various development trends of the clay sample from stability to failure, all achieving a high level of reproducibility. This signifies that the model effectively characterizes the development curve of dynamic strain in deep-sea clay under dynamic loading. The control parameters a and b exhibit robust correlations with CSR and K_c. Furthermore, their relationships in this deep-sea clay are successfully validated.

Figure 8

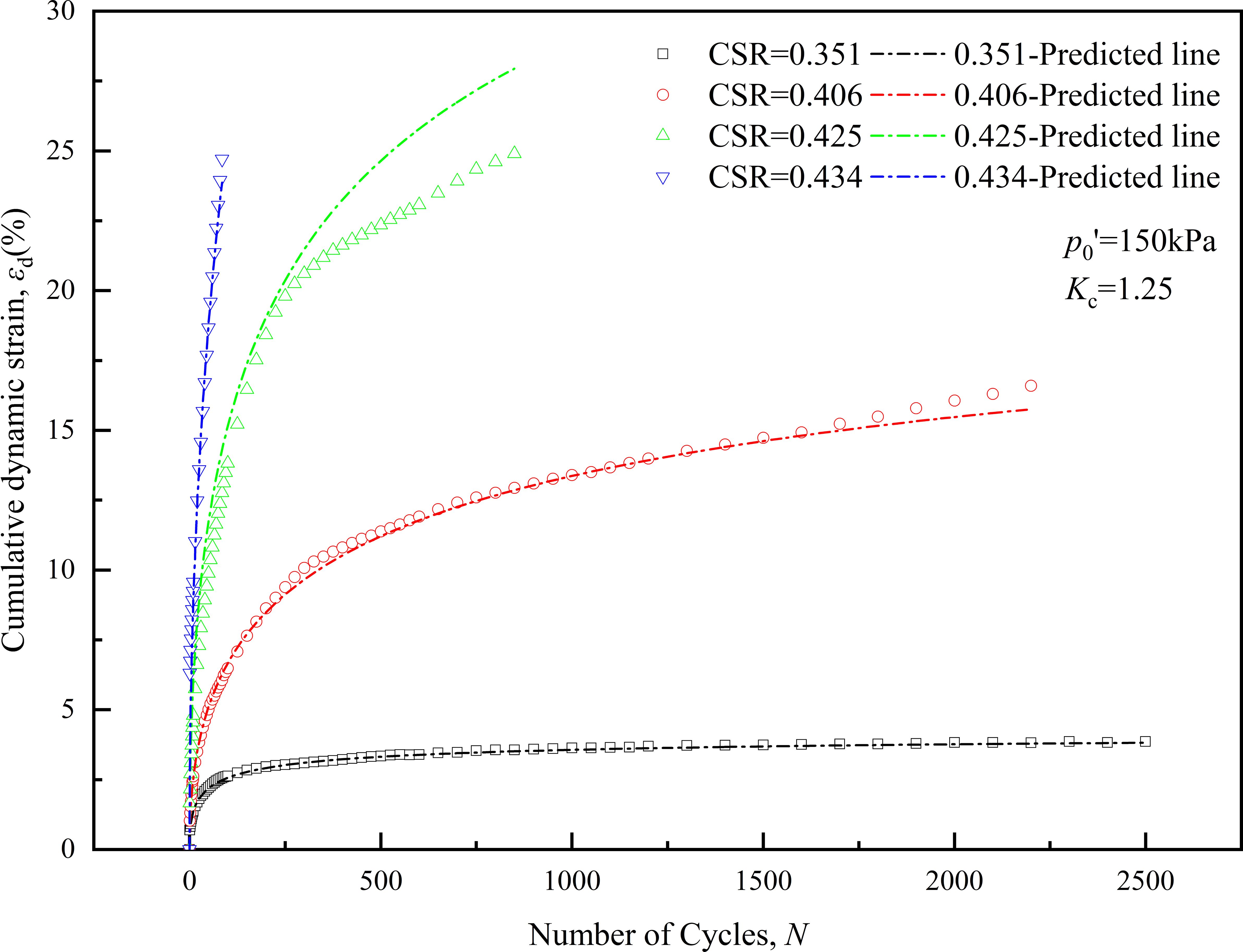
Figure 8 Comparison between model predictions and laboratory test results of cumulative dynamic strain for deep-sea clay.

Figure 9

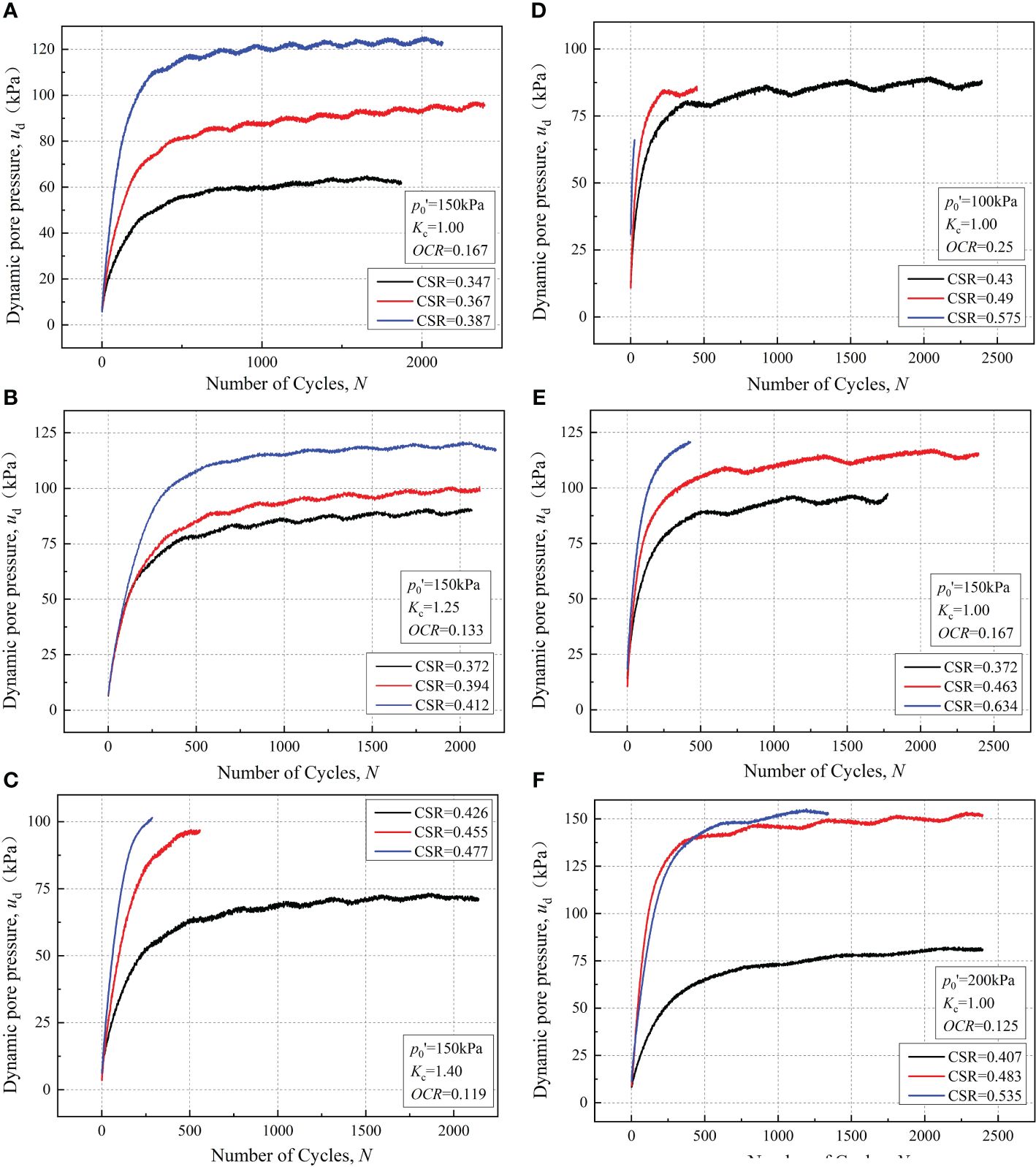
Figure 9 Accumulations of the dynamic pore water pressure under different stress magnitudes [(A–C) Station-1 under different K_c (Nian et al., 2018); D–F Station-2 under different OCRs (Nian et al., 2020)].

3.3 Cumulation evolution of the undrained dynamic pore pressure

Figures 9A–C illustrates the accumulations of dynamic pore water pressure (u_d) with an increasing number of cycles under various K_c. Notably, in correspondence with dynamic strain development, the evolution of dynamic pore water pressure (u_d) is highly dependent on the peak value of cyclic dynamic stress, with minimal influence from the consolidation stress ratio. Across all dynamic triaxial tests, the pore water pressure exhibits rapid initial growth under dynamic loading, followed by a gradual decrease in the growth trend, ultimately stabilizing around a specific value. The final stability value is primarily determined by the peak value of the dynamic load and increases with increasing dynamic load. Moreover, regardless of the increase in the cyclic stress ratio and consolidation stress, the maximum stability value of the pore water pressure can only reach 120 kPa. This limitation arises from the constant confining pressure of 150 kPa applied in all dynamic load tests combined with the unique structural characteristics of the soft clay from the South China Sea.

Figures 9D–F demonstrates the impact of the OCR on the development of u_d during dynamic tests. The influence of CSR on u_d aligns with the earlier discussion. In contrast to the effect of the consolidation stress ratio K_c on u_d, under the same stress level, as the OCR decreases from 0.25 to 0.167 and further to 0.125, the maximum pore pressure ratio achievable by the sample decreases from 0.875 to 0.833 until 0.75. This reveals a starkly different outcome compared to K_c; that is, under the same dynamic load, a smaller OCR results in increased stability in the structural characteristics of marine clay, along with a lower limit for the dynamic pore water pressure u_d that the clay sample can attain.

3.4 Undrained dynamic pore pressure model

To address the issue of conventional pore pressure models showing a perpetual increase rather than reaching a plateau across loading cycles (N), Ren et al. (2018b) introduced a curve model tailored for cyclic dynamic loads to forecast the growth trajectory of undrained dynamic pore pressure. Given that the clay sample utilized in the study originates from soft clay in the deep sea of the South China Sea, which is subjected to an intricate seabed environment during sedimentation, the stress conditions and initial pore pressure characteristics inherent to this clay sample significantly differ from those of normally consolidated clay. To precisely predict the undrained pore pressure of the clay sample, we have made adaptive enhancements to the model proposed by Ren et al. (2018a). Specifically, by addressing the complex cyclic loads and initial pore pressure conditions considered in the experiment, we have derived a dynamic pore pressure model suitable for deep-sea clay in the South China Sea. The formulated model is expressed as follows:

$\begin{array}{ll}{u}_d^{\text{'}}=\frac{u_d}{p_0^{\text{'}}}=D+\frac{N^C}{A+B{N}^C}& (5)\end{array}$

where u_d’ is the dynamic pore pressure ratio; u_d is the dynamic pore pressure; P₀’ is the initial mean effective stress; and A, B, C, and D are parameters that depend on the stress state and physical properties of the clay.

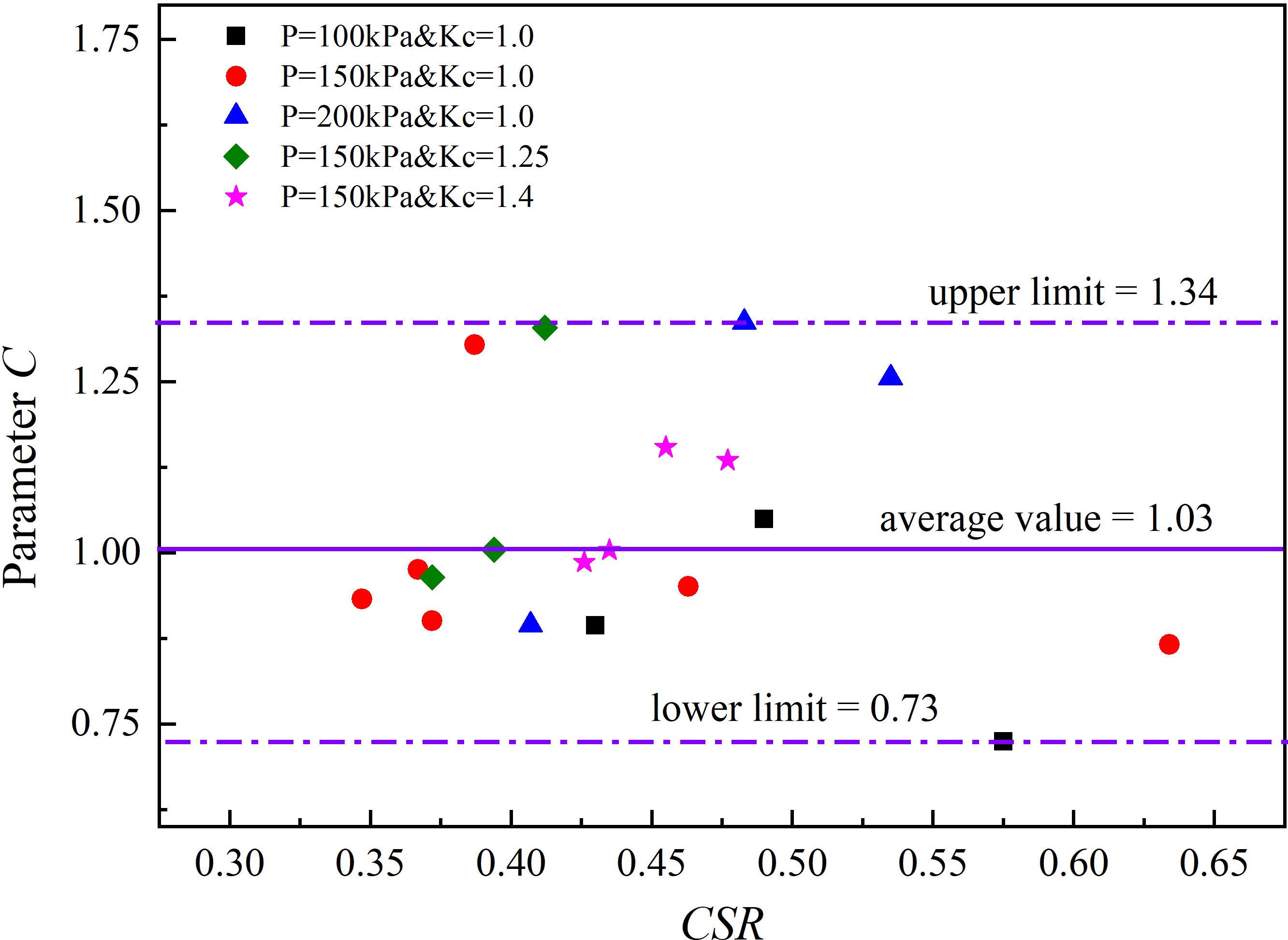
The relationship between the dynamic pore pressure and dynamic strain suggests that the factors governing strain also play a crucial role in determining the pore pressure. These factors include cyclic stress, effective confining pressure, and clay static strength. The model parameters are designed to capture the influence of these factors on the dynamic pore pressure. Ren et al. (2018) emphasized that the exponential parameter C characterizes the rate of pore pressure development, specifically how fast it increases with loading cycles. Importantly, C does not influence the generation of permanent pore pressure. On the other hand, the physical meaning of parameter c in the strain model has consistently maintained its interpretation. This implies that parameter C may solely depend on the inherent physical properties of the clay and should be independent of the stress state. This distinction clarifies the roles of C and c, reinforcing the model’s ability to capture the nuanced behavior of pore pressure under dynamic loading conditions.

An examination of the relationship between parameter C and CSR reveals that parameter C shares the same physical meaning as parameter c in the strain model. It is solely dependent on the clay type and remains independent of the cyclic stress state. Consequently, for a given type of clay sample, parameter C should remain constant. In contrast to the fixed value of C (equal to 0.5) in Ren et al. (2018), the best-fit values for C for the deep-sea soft clay of the South China Sea under dynamic cyclic loading fall within the range of 0.73 to 1.34, as depicted in Figure 10. Their average value is 1.03, which closely aligns with 1.0. As a result, it is recommended that Equation (5) be simplified to the following form (Equation (6)):

Figure 10

Figure 10 Effect of the stress state on parameter C.

$\begin{array}{ll}{u}_d^{\text{'}}=D+\frac{N}{A+BN}& (6)\end{array}$

By employing the same fitting method as that used for the dynamic strain model parameters, the experimental dynamic pore pressure (u_d’) data under various CSR, OCR, and K_c values were utilized to determine parameters A, B, and D in Equation (5) through the least squares method. In contrast to parameters a and b in the dynamic strain fitting formula, the influence of the overpressure consolidation ratio on the dynamic pore pressure is significant. The fitting results reveal that parameters A and D exhibit a robust correlation with CSR and OCR, with correlation coefficients (R²) of 97% and 90%, respectively. Parameter B demonstrates a strong correlation with CSR, with a correlation coefficient exceeding 90%, as depicted in Figure 11. The relationships Equations (7–9) are as follows:

Figure 11

Figure 11 Effect of the stress state on parameter B.

$\begin{array}{ll}A=0.039CS{R}^{1.405}OC{R}^{-5.360}& (7)\end{array}$

$\begin{array}{ll}B=0.574CS{R}^{-1.147}& (8)\end{array}$

$\begin{array}{ll}D=-0.006+0.258CS{R}^2+6.028OC{R}^3& (9)\end{array}$

To validate the applicability of the strain model and the fitting formula for model parameters, the laboratory test results from Station-2 were compared with their corresponding predicted outcomes obtained from the model. Figure 12 shows a comparison between the model predictions for deep-sea clay and the laboratory test results of the dynamic pore pressure. In Figure 12, the experimental results and model predictions are represented by points and dashed lines, respectively. The dynamic pore pressure curves predicted by the model effectively replicate the experimental data, maintaining a high level of fitting under sustained cyclic dynamic loading. The conditions corresponding to four different cyclic stress ratios cover various development trends of the clay sample from stability to failure, all achieving a high level of reproducibility. This indicates that the model is effective in describing the dynamic pore pressure development curve of deep-sea clay under dynamic loading. The control parameters A, B, and D are strongly correlated with the cyclic stress ratio and the overpressure consolidation ratio. Their relationships in this deep-sea clay have been successfully validated.

Figure 12

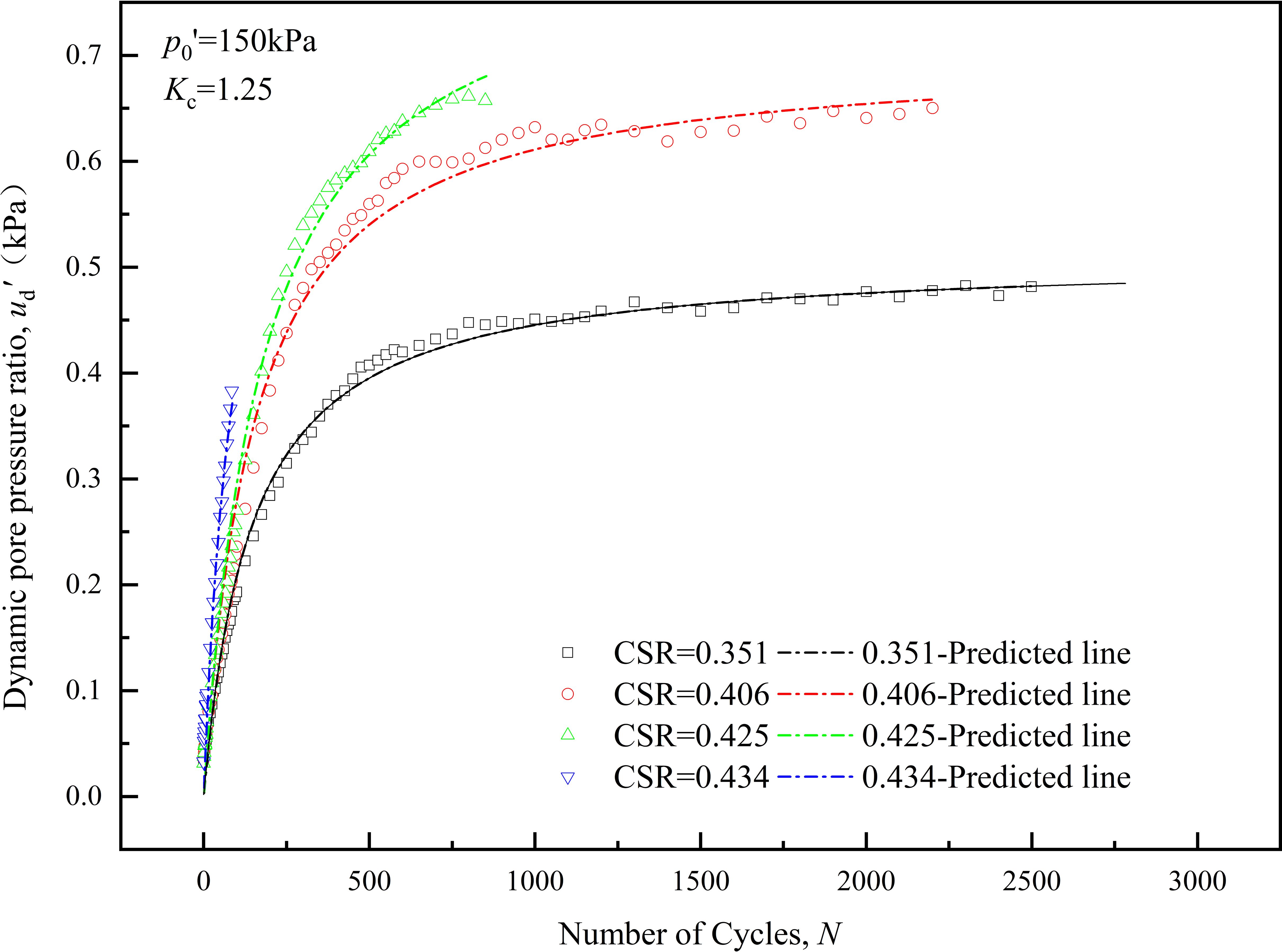
Figure 12 Comparison between model predictions and laboratory test results of dynamic pore pressure ratio for deep-sea clay.

3.5 Undrained dynamic strain–pore pressure model

The parameter c=0.5, derived from fitting cyclic triaxial test data of deep-sea soft clay, is integrated into a universal model capable of describing the cumulative dynamic strain trend under high cyclic dynamic loads. The dynamic strain formula for the South China Sea soft clay is obtained as follows:

$\begin{array}{ll}{\epsilon }_d=\frac{N^{0.5}}{a+b{N}^{0.5}}& (10)\end{array}$

Substituting Equation (10) into Equation (6), the relationship between the dynamic pore pressure ratio and cumulative dynamic strain (ε_d - u_d’) is expressed as:

$\begin{array}{ll}{u}_d^{\text{'}}=q+\frac{{\epsilon }_{\text{d}}^2}{m+n{({\epsilon }_{\text{d}}-p)}^2}& (11)\end{array}$

Equation (11) reveals a hyperbolic relationship between the cumulative dynamic strain and accumulated dynamic pore pressure ratio for deep-sea soft clay under high cyclic dynamic loading conditions. This observation aligns with conclusions drawn by Yasuhara et al. (1982); Hyodo et al. (1992), and Ren et al. (2018). The experimental data support a strong hyperbolic relationship between ε_d and u_d’, with regression analyses consistently yielding correlation coefficients (R²) exceeding 90%. Consequently, it can be concluded that Equation (11) effectively describes the relationship between ε_d and u_d’ for deep-sea soft clay in the South China Sea under high-frequency and strong-load dynamic cyclic loading conditions.

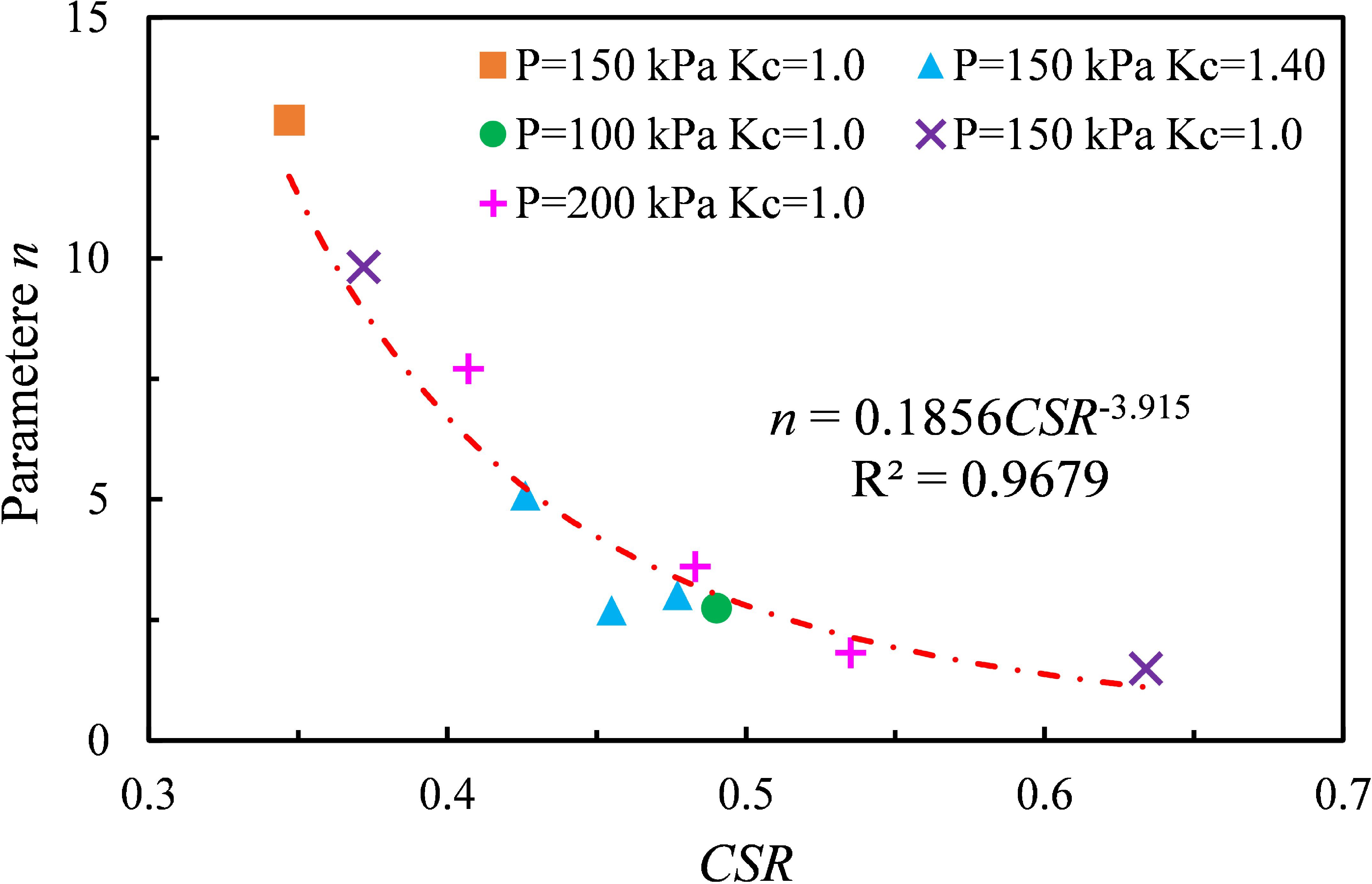
Applying the same fitting method employed for the model parameters in Equations (2) and (5), we utilized experimental data of ϵ_d and u_d’ under varying CSR, OCR, and K_c values to determine the parameters m, n, p, and q in Equation (11) through the least squares method. Unlike the parameters in the dynamic strain and dynamic pore pressure fitting formula, both K_c and OCR exert a significant influence on the parameters. The fitting analysis revealed a robust correlation between parameter n and CSR (as illustrated in Figure 13), while parameter m demonstrated a strong correlation with CSR and K_c, both with correlation coefficients exceeding 96%. Parameters p and q exhibited a robust correlation with CSR and OCR, achieving correlation coefficients (R²) of 92% and 98%, respectively. The relationships Equations (12–15) are expressed as follows:

Figure 13

Figure 13 Effect of the stress state on parameter n.

$\begin{array}{ll}m=1.8\ast {10}^{6}CS{R}^{10.054}-7.55K_c^{11.56}& (12)\end{array}$

$\begin{array}{ll}n=0.186CS{R}^{-3.915}& (13)\end{array}$

$\begin{array}{ll}p=20.372+23.197\text{Ln }CSR+\frac{0.414}{OC{R}^2}& (14)\end{array}$

$\begin{array}{ll}q=-0.492+1.339CS{R}^2+93.674OC{R}^3& (15)\end{array}$

Similarly, the experimental results from Station-2 were utilized to compare and validate the ε_d - u_d’ model along with its parameter fitting formula, as illustrated in Figure 14. In Figure 14, the experimental results and model predictions are denoted by points and dashed lines, respectively. The dynamic strain-pore pressure curves predicted by the model effectively replicate the experimental data, maintaining a high level of fitting under sustained cyclic dynamic loading. The conditions corresponding to four different cyclic stress ratios cover various development trends of the clay sample from stability to failure, all demonstrating a high degree of reproducibility. Notably, the initial fitting deviation of the CSR = 0.425 test group is relatively large, likely due to unavoidable factors such as differences in the undisturbed soil samples and experimental errors. However, overall, the model effectively describes the ε_d - u_d’ curve of deep-sea clay under dynamic loading. The control parameters m, n, p, and q exhibit strong correlations with the consolidation stress ratio, cyclic stress ratio, and overpressure consolidation ratio. These relationships in deep-sea clay have been successfully validated. This implies that with limited deep-sea soil samples, we can predict the deformation and pore pressure development trend of this soil type based on the ε_d - u_d’ model, considering known working conditions such as the determined soil sample category, sedimentary history, stress state, and loading conditions.

Figure 14

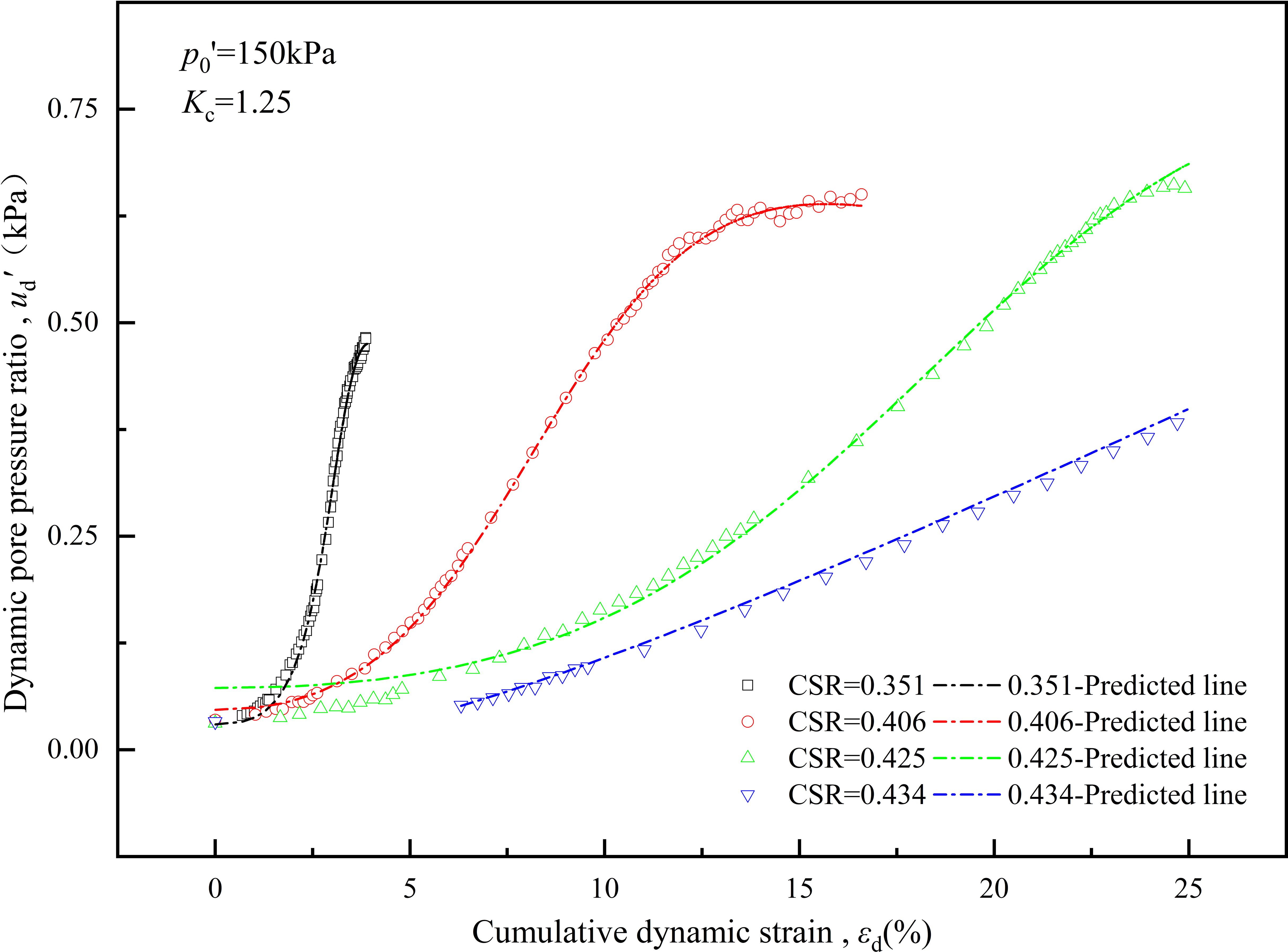
Figure 14 Comparison between the model predictions and laboratory test results of dynamic strain - pore pressure ratio for deep-sea clay.

4 Conclusions

This study comprehensively assessed the influence of CSR, OCR, and K_c on the cumulative evolution of dynamic strain during undrained cyclic dynamic tests in deep-sea soft clay. The key findings and conclusions are summarized as follows:

(1) The evolution of ε_d is closely linked to the peak value of the CSR. Higher CSR values result in greater dynamic strain, including ε_r and ε_p, increasing the likelihood of structural failure of clay samples across all K_c values. The CSR_cr distinguishes the developmental trend of dynamic strain. When the CSR is less than the CSR_cr, the dynamic strain stabilizes at a lower level within a few cycles. However, when the CSR exceeds the CSR_cr, the dynamic strain continues to increase, particularly when the CSR significantly surpasses the CSR_cr.

(2) The cumulative plastic deformation of deep-sea soft clay caused by dynamic stress is effectively captured by a model based on the classical Hardin-Drnevich model. The parameters in the model show strong correlations with CSR and K_c, and their relationships have been successfully validated through laboratory test results.

(3) The evolution of u_d is highly dependent on the peak value of the cyclic dynamic stress, with minimal influence from K_c. Smaller OCR values result in increased stability in the structural characteristics of marine clay, along with a lower limit for u_d that the clay sample can attain.

(4) A dynamic pore pressure model tailored for deep-sea clay under high cyclic dynamic loads is proposed. The model parameters (A, B, and D) show strong correlations with CSR, OCR, and K_c, and the model effectively replicates the experimental data, demonstrating its applicability in describing the dynamic pore pressure development curve.

(5) The proposed model, which integrates the parameter c = 0.5, effectively describes the hyperbolic relationship between the cumulative dynamic strain and dynamic pore pressure ratio (ε_d - u_d’) for deep-sea soft clay under high cyclic dynamic loading conditions. The control parameters (m, n, p, q) exhibit strong correlations with the consolidation stress ratio, cyclic stress ratio, and overpressure consolidation ratio, and the model effectively replicates the experimental data, indicating its potential for predicting the deformation and pore pressure development trend of deep-sea clay under known working conditions.

In conclusion, this comprehensive investigation provides valuable insights into the complex behavior of deep-sea soft clay under cyclic dynamic loading, offering practical implications for engineering applications and further research in geotechnical engineering.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material. Further inquiries can be directed to the corresponding author.

Author contributions

HJ: Data curation, Formal analysis, Methodology, Visualization, Writing – original draft. XG: Investigation, Writing – review & editing. NF: Conceptualization, Writing – review & editing. HW: Conceptualization, Writing – review & editing. TN: Funding acquisition, Resources, Supervision, Writing – review & editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This research is funded by the National Natural Science Foundation of China (Nos. 52079020 and 52108337).

Acknowledgments

We thank the Trial Voyage of Dongfanghong 2 Scientific Research Vessel for providing the clay samples.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Andersen K. H. (2009). Bearing capacity under cyclic loading-offshore, along the coast, and on land. The 21st Bjerrum Lecture presented in Oslo, 23 November 2007. Can. Geotech. J. 46, 513–535. doi: 10.1139/T09-003

CrossRef Full Text | Google Scholar

Ansal M. A., Erken A. (1989). Undrained behavior of clay under cyclic shear stresses. J. Geotech. Eng. 115, 948–955. doi: 10.1061/(ASCE)0733-9410(1989)115:7(968)

CrossRef Full Text | Google Scholar

Dai M., Guo L., Li M. F., Jin T. (2021). The pore pressure generation and deformation of overconsolidated soft marine clay considering initial static shear effect. Mar. Georesour. Geotechnol. 40, 922–935. doi: 10.1080/1064119X.2021.1951406

CrossRef Full Text | Google Scholar

Fan N., Jiang J. X., Nian T. K., Dong Y. K., Guo L., Fu C. W., et al. (2023). Impact action of submarine slides on pipelines: A review of the state-of-the-art since 2008. Ocean Eng. 286, 115532. doi: 10.1016/j.oceaneng.2023.115532

CrossRef Full Text | Google Scholar

Guo L., Wang J., Cai Y. Q., Liu H. L., Gao Y. F., Sun H. L. (2013). Undrained deformation behavior of saturated soft clay under long-term cyclic loading. Soil Dynam. Earthquake Eng. 50, 28–37. doi: 10.1016/j.soildyn.2013.01.029

CrossRef Full Text | Google Scholar

Guo X., Fan N., Liu Y., Liu X., Wang Z., Xie X., et al. (2023b). Deep seabed mining: Frontiers in engineering geology and environment. Int. J. Coal Sci. Technol. 10, 23. doi: 10.1007/s40789-023-00580-x

CrossRef Full Text | Google Scholar

Guo X., Fan N., Zheng D., Fu C., Wu H., Zhang Y., et al. (2024). Predicting impact forces on pipelines from deep-sea fluidized slides: A comprehensive review of key factors. Int. J. Min. Sci. Technol. doi: 10.1016/j.ijmst.2024.02.001

CrossRef Full Text | Google Scholar

Guo X., Liu X., Li M., Lu Y. (2023a). Lateral force on buried pipelines caused by seabed slides using a CFD method with a shear interface weakening model. Ocean Eng. 280, 114663. doi: 10.1016/j.oceaneng.2023.114663

CrossRef Full Text | Google Scholar

Hardin B. O., Drnevich V. P. (1972). Shear modulus and damping in soils: measurement and parameter effects (terzaghi leture). J. Soil mechan. foundations division 98, 603–624. doi: 10.1061/JSFEAQ.0001756

CrossRef Full Text | Google Scholar

Huang J., Jiao W., Liu J., Wan S., Xiong Z., Zhang J., et al. (2021). Sediment distribution and dispersal in the southern South China Sea: Evidence from clay minerals and magnetic properties. Mar. Geol. 439, 106560. doi: 10.1016/j.margeo.2021.106560

CrossRef Full Text | Google Scholar

Hyde A. F. L., Yasuhara K., Hirao K. (1993). Stability criteria for marine clay under one-way cyclic loading. J. Geotech. Eng. 119, 1771–1789. doi: 10.1061/(ASCE)0733-9410(1993)119:11(1771)

CrossRef Full Text | Google Scholar

Hyodo M., Yasuhara K., Hirao K. (1992). Prediction of clay behaviour in undrained and partially drained cyclic triaxial tests. Soils Foundations 32, 117–127. doi: 10.3208/sandf1972.32.4_117

CrossRef Full Text | Google Scholar

Jin H. X., Pan D. M., Guo L., Shi L. (2023). Effect of cyclic shear stress ratio on cyclic behavior of clay under multidirectional shear loading. Mar. Georesour. Geotechnol. 20, 1–9. doi: 10.1080/1064119X.2023.2267042

CrossRef Full Text | Google Scholar

Lei H. Y., Liu J. J., Liu M., Zhang Z. P., Jiang M. J. (2016). Effects of frequency and cyclic stress ratio on creep behavior of clay under cyclic loading. Mar. Georesour. Geotechnol. 35, 281–291. doi: 10.1080/1064119X.2016.1157659

CrossRef Full Text | Google Scholar

Lei H. Y., Xu Y. G., Jiang M. J., Jiang Y. (2020). Deformation and fabric of soft marine clay at various cyclic load stages. Ocean Eng. 195, 106757. doi: 10.1016/j.oceaneng.2019.106757

CrossRef Full Text | Google Scholar

Li J. A., Chen S. X., Jiang L. F., Xiong S. D. (2014). Experimental study on the influence of stress history on the dynamic characteristics of remolded red clay. Chin. J. Geotech. Eng. 36, 1657–1665. doi: 10.11779/CJGE201409012

CrossRef Full Text | Google Scholar

Li L. L., Dan H. B., Wang L. Z. (2011). Undrained behavior of natural marine clay under cyclic loading. Ocean Eng. 38, 1792–1805. doi: 10.1016/j.oceaneng.2011.09.004

CrossRef Full Text | Google Scholar

Li T., Meissner H. (2002). Two-surface plasticity model for cyclic undrained behavior of clays. J. Geotech. Geoenviron. Eng. 128, 613–626. doi: 10.1061/(ASCE)1090-0241(2002)128:7(613)

CrossRef Full Text | Google Scholar

Li D., Selig E. T. (1996). Cumulative plastic deformation for fine-grained subgrade soils. J. geotech. Eng. 122, 1006–1013. doi: 10.1061/(ASCE)0733-9410(1996)122:12(1006)

CrossRef Full Text | Google Scholar

Li W., Yue J. P., Guo J. Y., Yang Y., Zou B., Shen Y., et al. (2018). Statistical seismo-ionospheric precursors of M7.0+ earthquakes in Circum-Pacific seismic belt by GPS TEC measurements. Adv. Space Res. 61, 1206–1219. doi: 10.1016/j.asr.2017.12.013

CrossRef Full Text | Google Scholar

Liu Y. (1994). Neotectonic and Crustal Stableness. Beijing: Science Press, 1–271.

Google Scholar

Liu X., Wang Y., Zhang H., Guo X. (2023). Susceptibility of typical marine geological disasters: an overview. Geoenviron. Disasters 10, 10. doi: 10.1186/s40677-023-00237-6

CrossRef Full Text | Google Scholar

Monismith C. L., Ogawa N., Freeme C. R. (1975). Permanent deformation characteristics of subgrade soils due to repeated loading. Transport. Res. Rec. 537.

Google Scholar

Moses G. G., Rao S. N., Rao P. N. (2003). Undrained strength behaviour of a cemented marine clay under monotonic and cyclic loading. Ocean Eng. 30, 1765–2178. doi: 10.1016/S0029-8018(03)00018-0

CrossRef Full Text | Google Scholar

Muhanna A. S. H. (1994). A testing procedure and a model for resilient modulus and accumulated plastic strain of cohesive subgrade soils. North Carolina State University.

Google Scholar

Ni J., Indraratna B., Geng X., Carter J. P., Chen Y. (2015). Model of soft soils under cyclicloading. Int. J. Geomechan. 5, 1–10. doi: 10.1061/(ASCE)GM.1943-5622.0000411

CrossRef Full Text | Google Scholar

Nian T. K., Jiao H. B., Fan N., Guo X. S. (2020). Microstructure analysis on the dynamic behavior of marine clay in the South China Sea. Mar. Georesour. Geotechnol 38, 349–362. doi: 10.1080/1064119X.2019.1573864

CrossRef Full Text | Google Scholar

Nian T., Jiao H., Fan N., Guo X., Jia Y. (2018). Experiment on dynamic strain-pore pressure of soft clay in the northern slope of south China sea. Yantu Lixue. Rock Soil Mech. 39, 1564–1572. doi: 10.16285/j.rsm.2017.0887

CrossRef Full Text | Google Scholar

Nian T., Shen Y., Zheng D., Lei D. (2021). Research advances on the chain disasters of submarine landslides. J. Eng. Geol. 29, 1657–1675. doi: 10.13544/j.cnki.Jeg.2021-0815

CrossRef Full Text | Google Scholar

Nie Q., Bai B., Hu J., Shang W. (2007). The pore pressure model and undrained shear strength of soft clay under cyclic loading. Rock Soil Mech. 28, 724–729.

Google Scholar

Ren X. W., Xu Q., Teng J., Zhao N., Lv L. (2018a). A novel model for the cumulative plastic strain of soft marine clay under long-term low cyclic loads. Ocean Eng. 149, 194–204. doi: 10.1016/j.oceaneng.2017.12.028

CrossRef Full Text | Google Scholar

Ren X. W., Xu Q., Xu C. B., Teng J. D., Lv S. H. (2018b). Undrained pore pressure behavior of soft marine clay under long-term low cyclic loads. Ocean Eng. 150, 60–68. doi: 10.1016/j.oceaneng.2017.12.045

CrossRef Full Text | Google Scholar

Wang Y. K., Gao Y. F., Guo L., Cai Y. Q., Li B., Qiu Y., et al. (2017). Cyclic response of natural soft marine clay under principal stress rotation as induced by wave loads. Ocean Eng. 129, 191–202. doi: 10.1016/j.oceaneng.2016.11.031

CrossRef Full Text | Google Scholar

Wang J., Guo L., Cai Y. Q., Xu C. J., Gu C. (2013). Strain and pore pressure development on soft marine clay in triaxial tests with a large number of cycles. Ocean Eng. 74, 125–132. doi: 10.1016/j.oceaneng.2013.10.005

CrossRef Full Text | Google Scholar

Wang X., Li S., Gong Y., Liu X., Suo Y., Dai L. (2014). Active tectonics and its effects on gas-hydrates in Northern South China Sea. Journal of Ji Lin University: Earth Science Edition 44 (2), 419–431. doi: 10.13278/j.cnki.jjuese.201402102

CrossRef Full Text | Google Scholar

Wang Y. K., Wan Y. S., Ruan H., Yu X., Shao J. G., Ren D. B. (2021). Pore pressure accumulation of anisotropically consolidated soft clay subjected to complex loads under different stress paths. China Ocean Eng. 35, 465–474. doi: 10.1007/s13344-021-0043-y

CrossRef Full Text | Google Scholar

Wang Z., Zheng D., Guo X., Gu Z., Shen Y., Nian T. (2024). Investigation of offshore landslides impact on bucket foundations using a coupled SPH–FEM method. Geoenviron. Disasters 11, 2. doi: 10.1186/s40677-024-00266-9

CrossRef Full Text | Google Scholar

Wu T., Zhang C., Guo X. (2024). Dynamic responses of monopile offshore wind turbines in cold sea regions: Ice and aerodynamic loads with soil-structure interaction. Ocean Eng. 292, 116536. doi: 10.1016/j.oceaneng.2023.116536

CrossRef Full Text | Google Scholar

Yang G., Yang Q., Liu W. H., Zhang K. (2012). Critical cyclic stress ratio of reconstituted silty clay under the cyclic loading. J. Converge. Inf. Technol. 7, 1–8. doi: 10.4156/jcit.vol7.issue23.1

CrossRef Full Text | Google Scholar

Yasuhara K., Yamanouchi T., Hirao K. (1982). Cyclic strength and deformation of normally consolidated clay. Soils Foundations 22, 77–91. doi: 10.3208/sandf1972.22.3_77

CrossRef Full Text | Google Scholar

Zhang G., Shao L., Qiao P., Cao L., Pang X., Zhao Z., et al. (2020). Cretaceous–Palaeogene sedimentary evolution of the South China Sea region: A preliminary synthesis. Geol J. 55, 2662–2683. doi: 10.1002/gj.3533

CrossRef Full Text | Google Scholar

Zhao C., Liu J. M., Liu H. M., Bian X. C., Chen Y. M. (2023). A conceptual model for the shakedown response of soft clay to high-cycle, low-amplitude undrained loading. Comput. Geotech. 156, 105257. doi: 10.1016/j.compgeo.2023.105257

CrossRef Full Text | Google Scholar