Joint decision-making for tanker deployment and refueling strategies under berthing time and fuel price uncertainties

This study proposes a robust optimization framework for the joint optimization of tanker deployment and refueling strategies under uncertainties in berthing times and fuel prices. Unlike traditional sequential approaches, the model jointly determines vessel assignment and refueling decisions within a unified mathematical formulation, explicitly accounting for interdependencies between operational variables. By incorporating robust optimization techniques, the framework addresses fuel price volatility and stochastic berthing delays, enabling resilient decision-making in dynamic maritime environments. Using real-world data from a leading maritime logistics provider, computational experiments demonstrate that the robust model reduces operational costs by 2.06% compared to deterministic approaches when fuel price fluctuations exceed critical thresholds (e.g., 300 RMB/ton for Heavy Fuel Oil (HFO) and 250 RMB/ton for Light Fuel Oil (LFO)). Sensitivity analyses further reveal the model’s resilience under extreme anchorage time uncertainties (e.g., 16-hour delays), achieving cost savings of up to 8.5%. The framework’s adaptability to diverse fleet configurations and regulatory environments underscores its practical value for enhancing decision-making in volatile markets.

1 Introduction

The refined petroleum products transportation market is experiencing robust growth driven by the global expansion of energy demand and sustained development of the petrochemical industry. While precise figures for 2025 are unavailable, industry reports and observed trends suggest a reasonable estimate of the global market size for that year could range between 250 billion USD and 300 billion USD¹ This projection encompasses the transportation of various refined products―including gasoline, diesel, kerosene, and specialized fuels―via multiple modalities such as pipelines, rail, road, and maritime shipping. The market is projected to expand at a compound annual growth rate (CAGR) of approximately 4-5% between 2025 and 2033, indicating sustained market expansion².

Within market segmentation, maritime transportation is anticipated to maintain its dominant position due to its unparalleled efficiency in moving large volumes over long distances. However, market dynamics are complicated by geopolitical instabilities and volatile crude oil prices, which introduce significant uncertainties and fluctuations. Efficient deployment and refueling strategies are critical components of maritime transportation, especially in the context of tanker operations (Wang et al., 2025b). With the increasing demand for crude oil and refined products, tanker operators must carefully optimize their operations to ensure cost efficiency while meeting delivery schedules. However, maritime logistics is subject to significant uncertainties, including port congestion, weather disruptions, and fluctuating fuel prices. Among these, berthing time uncertainty—the variability in the time a vessel spends waiting for and accessing port facilities—poses a considerable challenge (Zhou et al., 2025a). Delays can lead to higher operational costs, disrupt schedules, and necessitate adjustments to refueling plans (Zhou et al., 2025c, 2024). Therefore, designing a robust decision-making framework that accounts for both tanker deployment and refueling under such uncertainty is of paramount importance.

The problem involves two intertwined decisions: the assignment of tankers to delivery routes (deployment) and the determination of optimal refueling strategies along those routes. Traditionally, these two problems are addressed independently, with tanker deployment focused on minimizing voyage costs and refueling strategies optimized separately based on fuel consumption patterns and price variations. However, ignoring their interdependence may result in suboptimal outcomes. For instance, an inefficient deployment may force a tanker to refuel at ports with higher fuel prices or under less favorable conditions, increasing overall operational costs. Consequently, an integrated approach that simultaneously optimizes both deployment and refueling decisions is essential.

The volatility of fuel prices exerts significant and multifaceted pressures on the refined petroleum products transportation market, particularly within maritime logistics, where operational costs and strategic decisions are inextricably linked to fluctuating fuel costs (Hao et al., 2022). Rising fuel prices directly inflate voyage expenses, compelling tanker operators to reassess route optimization, port selection, and refueling strategies to mitigate financial burdens, while also forcing shippers and carriers to potentially pass on increased costs to consumers or absorb profit margins under price-sensitive market conditions. Conversely, price declines may temporarily alleviate operational expenses, enabling cost savings or competitive pricing adjustments, but they also introduce long-term uncertainties that deter sustained investment in infrastructure modernization or alternative energy transitions. The interdependence of tanker deployment and refueling decisions becomes acute in volatile environments, as suboptimal choices—such as refueling at ports with unexpectedly higher prices due to misaligned scheduling or port congestion—can exacerbate costs and disrupt delivery timelines, thereby necessitating dynamic risk-management frameworks that integrate real-time fuel price data with route planning and inventory control.

Another significant factor complicating tanker operations is the uncertain berthing time at ports. Variations in waiting times can force vessels to spend more time in transit or at anchor, impacting fuel consumption and disrupting delivery schedules (Zhen et al., 2024). This uncertainty introduces an additional layer of complexity to decision-making. Operators need to anticipate possible delays and incorporate them into their planning to avoid penalties and extra fuel costs. Stochastic modeling offers a promising way to address such uncertainties by considering the variability in berthing times and optimizing the deployment and refueling decisions accordingly.

The main contributions of this study can be summarized as follows:

● Integrated Decision-Making Framework: We propose a novel mathematical model that jointly optimizes tanker deployment (vessel-to-route assignment) and refueling strategies (when, where, and how much fuel to bunker) within a single framework. This integrated approach captures the critical interdependencies between these decisions, moving beyond traditional sequential or isolated planning methods.

● Robust Optimization Under Dual Uncertainties: We develop a robust optimization model to specifically address two critical and simultaneous sources of real-world uncertainty in maritime logistics: volatile fuel prices (for both HFO and LFO) and stochastic port berthing times. This enhances the resilience and practical applicability of the proposed strategies.

● Real-World Validation and Managerial Insights: The model is validated using a large-scale, realistic case study based on operational data from a world-leading refined oil shipping company. Our computational results provide practical managerial insights into the specific cost-saving thresholds at which a robust approach becomes more effective than a deterministic one in volatile market conditions.

The remainder of the paper is organized as follows: Section 2 reviews the relevant literature on tanker operations, refueling strategies, and stochastic optimization. Section 3 presents the mathematical model for the joint decision-making problem, including the formulation of the stochastic berthing time uncertainty. Section 4 discusses the solution methodology, and Section 5 provides a detailed computational study to evaluate the proposed framework. Finally, Section 6 concludes the paper with key insights and directions for future research.

2 Literature review

The optimization of shipping operations, particularly in tanker deployment, refueling, and speed strategies, has emerged as a critical area of research in response to the increasing complexity of modern maritime logistics. Traditional methodologies, which often treated these variables in isolation, have been supplanted by integrated decision-making frameworks designed to address the interdependencies among operational parameters (Zhou et al., 2025b; Chen et al., 2025). Recent studies emphasize the necessity of jointly optimizing deployment, refueling, and speed to mitigate suboptimal outcomes such as excess fuel consumption, delayed schedules, and noncompliance with environmental regulations. Nonlinear mixed-integer programming models, for instance, have been developed to minimize operational costs by synchronizing decisions across service routes, refueling quantities, and vessel speeds (Wang and Chen, 2017). These models reveal that fragmented optimization of individual variables can lead to inefficiencies, such as misaligned port stops or unanticipated delays, underscoring the importance of holistic strategies. Gao et al. (2025) considered the vehicle speed and refueling strategy of methanol dual-fuel pipeline with emission control area, and constructed a mixed integer 0–1 programming model with the goal of minimizing the single voyage operating cost.

Environmental regulations, including those in Emission Control Areas (ECAs), further complicate this optimization by imposing constraints on fuel types and emissions (Jiang et al., 2025; Li et al., 2022). Researchers have addressed these challenges through advanced mathematical approaches, such as transforming nonlinear discrete programming models into continuous formulations solvable via convex optimization techniques (Ma et al., 2021). This allows for simultaneous consideration of fuel consumption, emissions, and transportation costs, enabling more sustainable decision-making. For example, studies demonstrate that nonlinear relationships between ship speed, fuel efficiency, and emissions require balanced trade-offs to achieve cost-effective and environmentally responsible outcomes (Lashgari et al., 2021).

Uncertainty in fuel prices, consumption rates, and regulatory policies has driven the adoption of stochas92 tic and dynamic optimization methods. Dynamic programming algorithms, for instance, generate adaptive refueling policies based on real-time fuel price fluctuations across ports Zhen et al. (2017), while scenario-based stochastic programming accounts for potential shifts in carbon taxes and LNG availability (Wu et al., 2022). These approaches not only enhance resilience against market volatility but also reveal that static deterministic models may underestimate risks, particularly in regions with stringent emission controls. Multistage stochastic models further highlight the strategic importance of low-sulfur fuel oil when LNG supplies are limited or prices are volatile, emphasizing the need for flexible refueling strategies (Zhou and Wang, 2025).

The integration of dual-fuel technologies, such as LNG engines, introduces new dimensions to operational planning. While LNG reduces carbon emissions, challenges such as methane slip and port infrastructure limitations necessitate optimization models that account for engine performance, fuel availability, and environmental regulations (Wu et al., 2024). Linearization techniques have enabled practical solutions to these complex, multi-variable problems, demonstrating the feasibility of adopting cleaner fuels without compromising efficiency. Concurrently, studies explore the role of emission trading systems in incentivizing LNG adoption, suggesting that market-based mechanisms could align profitability with environmental goals (Ma et al., 2023).

Dynamic programming and distributionally robust optimization methods have gained traction in addressing demand uncertainty and fluctuating market conditions. These frameworks ensure operational resilience by guaranteeing demand satisfaction while minimizing exposure to adverse scenarios, such as sudden bunker price spikes (Besbes and Savin, 2009). Progressive hedging algorithms further advance computational efficiency, enabling large-scale optimization of refueling and speed decisions (Ghosh et al., 2015).

Recent literature has further advanced this field by focusing on more integrated and complex models. A significant trend is the joint optimization of sailing speed with routing and bunkering, a point of departure from our fixed-speed tactical model. For instance, Aydin et al. (2017) utilized dynamic programming to optimize vessel speed while facing uncertain port service times, demonstrating that considering such uncertainty can noticeably reduce fuel costs. Similarly, several studies have developed mixed-integer linear programming (MILP) models to co-optimize speed and bunkering for vessels using alternative fuels, such as LNG (He et al., 2024) and biofuels with storage limitations (Li et al., 2025). Wang et al. (2025a) also jointly optimized speed and bunkering, focusing on both cost and carbon emission reductions by incorporating practical constraints like fuel inspection processes.

The drive for sustainability and resilience has also spurred new methodologies. De et al. (2020) addressed sustainable ship routing with bunker management using a hybrid variable neighborhood search and particle swarm optimization algorithm. To handle uncertainty, researchers have moved towards more sophisticated techniques. Zhou and Wang (2025), for example, applied a distributionally robust optimization method to 124 manage stochastic shipping demand and ECA regulations, jointly determining the optimal route, speed, and refueling strategy. In a different approach, Sun and Chou (2025) introduced a data-driven method that combines machine learning with traditional optimization to learn the optimal refueling policy directly from market data, moving beyond price prediction to policy prescription. These studies underscore the complexity and multi-faceted nature of modern maritime logistics optimization.

Despite the extensive research on vessel routing, speed optimization, and bunkering, a specific research gap remains. While many studies focus on the operational level for a single vessel’s voyage (often including variable speed), less attention has been paid to the tactical, fleet-wide problem of simultaneously optimizing vessel deployment and refueling strategies. Furthermore, few models have incorporated a robust optimization framework to specifically handle the combined and simultaneous impact of fuel price volatility and port berthing time uncertainty.

This study aims to fill this gap by proposing an integrated, robust optimization model tailored for this joint tactical decision-making problem. While our work simplifies the problem by assuming a fixed economical speed, it contributes by focusing on the tactical joint deployment and refueling problem for an entire fleet, using a robust optimization framework to specifically address simultaneous fuel price and port time uncertainties. Our contribution is to provide a resilient decision-support tool that enhances fleet-wide operational planning in the face of these critical real-world uncertainties, a focus distinct from single-voyage, speed-centric optimization models.

3 Base model formulations

We consider the operational decision-making process within a refined oil transportation company. Let S denote the set of ships owned by the company, indexed by s, with each ship s having a capacity denoted by q_s. The company ensures the supply of refined petroleum products downstream in the supply chain through coastal shipping. The set of routes utilized for this purpose is R, indexed by r, with a transportation demand on each route represented by W_r. Let L_r represent the set of leg of route r, and l_r,i denote the i-th leg on route r, where l_r,i ∈ L_r. The route distance of leg l_r,i is d_r,i.

The deployment of ships on each route must be considered first to ensure that service demands are met. Secondly, a ship refueling strategy must be devised to ensure the successful completion of the entire voyage. The deployment of product tankers and their refueling strategies is complex, involving multiple factors: First, product tankers typically have separate tanks for heavy and light fuel oils, with heavy fuel oil (HFO) primarily consumed during coastal navigation and light fuel oil (LFO) required in restricted areas such as ports, anchorage, and cargo operations. This makes route complexity a significant challenge in formulating refueling strategies. However, it is worth noting that the type of fuel used is often related to the vessel’s characteristics. For instance, some ships are not equipped with LFO tanks, allowing them to use HFO throughout the entire voyage. Second, the initial quantities of HFO and LFO onboard critically influence vessel deployment along the route, and the refueling strategy also depends on the fuel price differences at various ports along the route.

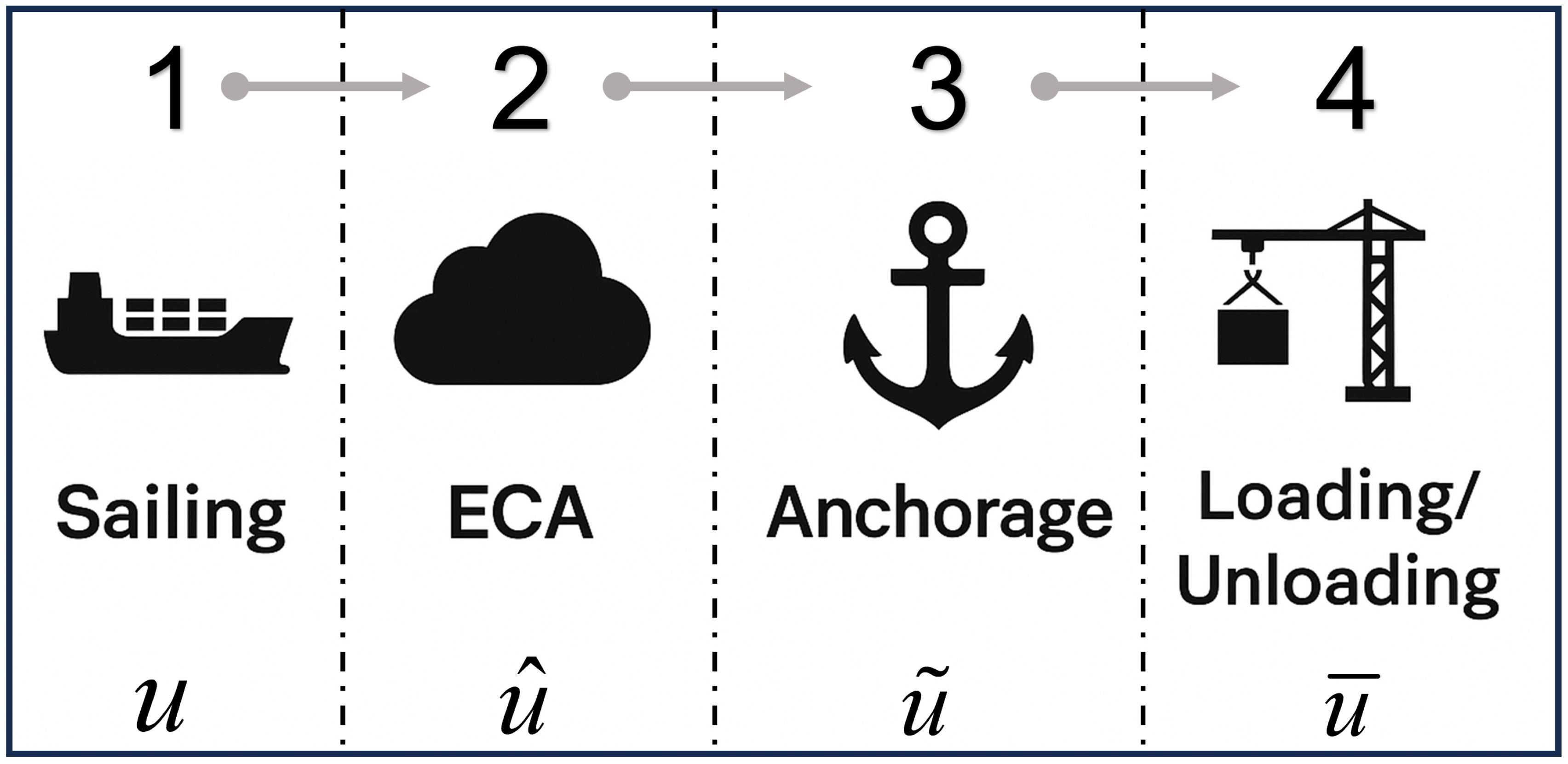
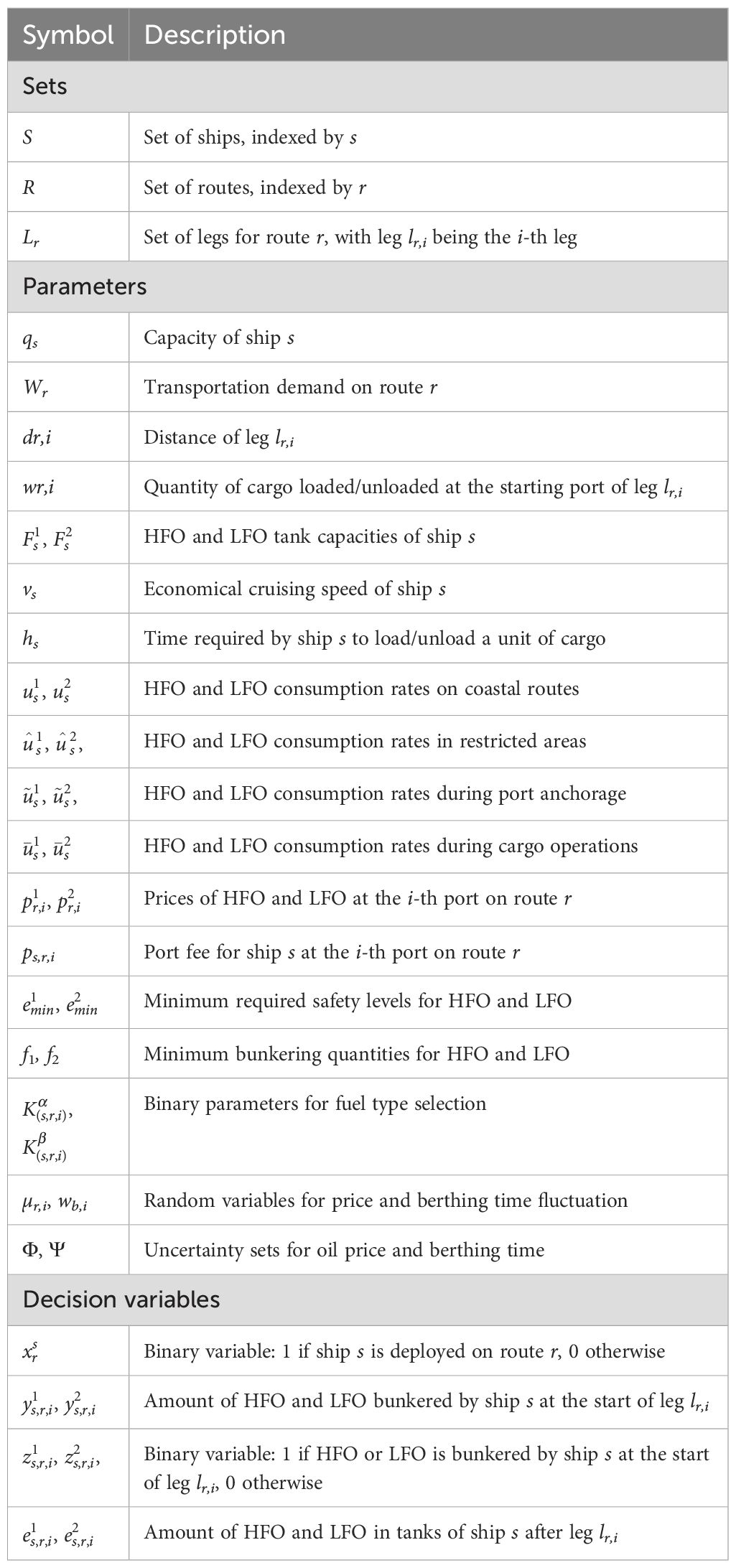
The following introduces the parameters related to fuel consumption for product tankers. Let $F_s^1$ and $F_s^2$ denote the heavy fuel oil (HFO) and light fuel oil (LFO) tank capacities, respectively, for vessel s. The vessel’s economical cruising speed on coastal routes is represented by v_s. It is important to clarify the assumptions regarding vessel speed in our model. The vessel speed v_s is treated as a fixed parameter representing the economical cruising speed. This assumption is rooted in the ex-ante, tactical nature of the decision problem, which focuses on optimizing fleet deployment and refueling strategies over a planning horizon. Real-time operational decisions, such as in-voyage speed adjustments, are considered outside the scope of this planning model. At this level, operators often prioritize fuel efficiency by adhering to a steady economical speed due to the prohibitive costs associated with speeding up. Our framework captures the impact of port time uncertainties by incorporating the variable anchorage time directly into the operational cost function. Thus, the objective is to find a plan that is robust against the financial impact of delays. The resulting costs can be viewed as a robust baseline; any costs or savings from exceptional operational speed adjustments made during the voyage could then be benchmarked against this baseline to evaluate actual performance. The variables $u_s^1$ and $u_s^2$ signify the consumption rates of HFO and LFO per unit time for vessel s on coastal routes. Meanwhile, ${\widehat{u}}_s^1$ and ${\widehat{u}}_s^2$ indicate the consumption rates of HFO and LFO per unit time in restricted areas. Additionally, ${\tilde{u}}_s^1$ and ${\tilde{u}}_s^2$ correspond to the consumption rates of HFO and LFO per unit time during port anchorage. Finally, ${\overline{u}}_s^1$ and ${\overline{u}}_s^2$ represent the consumption rates of HFO and LFO per unit time for vessel s during cargo loading and unloading operations at the port. These fuel consumption value are derived from historical data statistics of the shipping company. Figure 1 illustrates the typical operational sequence of a tanker between two consecutive ports, highlighting the four distinct phases and their corresponding fuel consumption notations. This schematic helps to intuitively connect the mathematical formulation to real operational contexts. t_s,r,i is the time spent at anchoring and bunkering at the starting port of leg l_r,i Let w_r,i denote the total quantity of crude oil loaded or unloaded at the starting port of the leg l_r,i. Let h_s denote the time required by vessel s to load or unload a unit of cargo. Table 1 offers a detailed explanation of all symbols used in this paper.

Figure 1

Figure 1. Operational phases and corresponding fuel consumption between consecutive ports.

Table 1

Table 1. Nations.

Based on the above notation, the consumption of heavy and light fuel oil for ship s during leg l_r,i, as well as during anchorage and loading/unloading processes, can be expressed as follows:

$\begin{array}{ll}{\text{HFO}}_{(s,r,i)}^{\alpha }=K_{(s,r,i)}^{\alpha }{u}_s^1\left(\frac{d_{r,i}}{v_s}\right)\forall s\in S,\forall r\in R,\forall i\in I_r& (1)\end{array}$

$\begin{array}{ll}{\text{LFO}}_{(s,r,i)}^{\alpha }=(1-K_{(s,r,i)}^{\alpha })u_s^2\left(\frac{d_{r,i}}{v_s}\right)\forall s\in S,\forall r\in R,\forall i\in I_r& (2)\end{array}$

$\begin{array}{ll}{\text{HFO}}_{(s,r,i)}^{\beta }=K_{(s,r,i)}^{\beta }\left[{\widehat{u}}_s^1{t}_{s,r,i}+{\overline{u}}_s^1\left(\frac{w_{r,i}}{h_s}\right)\right]\forall s\in S,\forall r\in R,\forall i\in I_r& (3)\end{array}$

$\begin{array}{ll}{\text{LFO}}_{(s,r,i)}^{\beta }=(1-K_{(s,r,i)}^{\beta })\left[{\widehat{u}}_s^2{t}_{s,r,i}+{\overline{u}}_s^2\left(\frac{w_{r,i}}{h_s}\right)\right]\forall s\in S,\forall r\in R,\forall i\in I_r& (4)\end{array}$

Equations 1, 2 represent the consumption of HFO and LFO for the ship during navigation. Here, $K_{(s,r,i)}^{\alpha }$ is a binary variable that ensures the ship uses only one type of fuel during navigation. $K_{(s,r,i)}^{\alpha }=1$ indicates that ship s uses HFO on the i-th leg of route r, denoted as l_r,i. Otherwise, $K_{(s,r,i)}^{\alpha }=0$. Equations 3 and 4 represent the consumption of HFO and LFO for the ship during anchorage. Similarly, $K_{(s,r,i)}^{\beta }=1$ indicates that ship s uses HFO during anchorage and loading/unloading at the starting port of the i th leg of route r. Otherwise, $K_{(s,r,i)}^{\beta }=0$. Here, $K_{(s,r,i)}^{\alpha }$ is a binary parameter indicating the fuel choice during navigation (1 for HFO, 0 for LFO), and $K_{(s,r,i)}^{\beta }$ is a binary parameter for fuel choice during port and anchorage operations. These are external input parameters determined by the shipping company based on the vessel’s characteristics and ECA regulations to derive the most economical choice for each leg. The fuel consumption of HFO and LFO for ship s on leg l_r,i can be derived as follows:

$\begin{array}{ll}\begin{array}{l}{\text{HFO}}_{(s,r,i)}={\text{HFO}}_{(s,r,i)}^{\alpha }+{\text{HFO}}_{(s,r,i)}^{\beta }\\ {\text{LFO}}_{(s,r,i)}={\text{LFO}}_{(s,r,i)}^{\alpha }+{\text{LFO}}_{(s,r,i)}^{\beta }\end{array}& (5)\end{array}$

The shipping company aims to minimize costs through decisions on fleet deployment and refueling strategies. The binary decision variable $x_r^s$ indicates whether ship s is deployed on route r; it is 1 if deployed, otherwise 0. The non-negative decision variable $y_{s,r,i}^1$ represents the amount of HFO bunkered by ship s at the starting port of leg l_r,i. Similarly, the non-negative decision variable $y_{s,r,i}^2$ represents the amount of LFO bunkered by ship s at the starting port of leg l_r,i. Furthermore, to account for minimum purchase requirements often imposed by fuel suppliers, we introduce the binary decision variables $z_{s,r,i}^1$ and $z_{s,r,i}^2$. These variables are equal to 1 if vessel s bunkers HFO or LFO, respectively, at the starting port of leg l_r,i, and 0 otherwise. The company’s primary costs include: (1) vessel operating costs, (2) fuel bunkering costs, and (3) Port Fees.

The vessel operating cost C_o is a non-decreasing function of the total voyage time. In this equation, c_o represents the vessel’s daily operating cost.

$\begin{array}{ll}{C}_o=\sum _{r\in R}\sum _{s\in S}\sum _{i\in I_r}{x}_r^s\left(\frac{d_{r,i}}{v_s}+t_{s,r,i}+\frac{w_{r,i}}{h_s}\right)c_o& (6)\end{array}$

In Equation 6, t_s,r,i represents the total time spent at port, which is the sum of the anchorage time t_r,i and the time spent bunkering HFO and LFO.

$\begin{array}{ll}{t}_{s,r,i}=t_{r,i}+\text{max }\left\{\frac{y_{s,r,i}^1}{h_{s,1}},\frac{y_{s,r,i}^2}{h_{s,2}}\right\}& (7)\end{array}$

The second term in Equation 7 represents the time required to simultaneously bunker HFO and LFO. The total cost of bunkering HFO and LFO for the ship C_f is given by:

$\begin{array}{ll}{C}_f=\sum _{r\in R}\sum _{s\in S}\sum _{i\in I_r}\left(y_{s,r,i}^1{p}_{r,i}^1+y_{s,r,i}^2{p}_{r,i}^2\right)& (8)\end{array}$

In Equation 8, $p_{r,i}^1$ and $p_{r,i}^2$ represent the prices of HFO and LFO, respectively, at the i-th port on route r. Due to the varying charges and size restrictions imposed by different ports based on the scale of the vessels, the total port fees are expressed as follows:

$\begin{array}{ll}{C}_p=\sum _{r\in R}\sum _{s\in S}\sum _{i\in I_r}{x}_r^s{p}_{s,r,i}& (9)\end{array}$

In Equation 9, p_s,r,i represents the fee charged to ship s at the i-th port on route r. It is worth noting that some ports are unable to accommodate larger vessels due to berth size limitations. In such cases, the port charges for these vessels should be set to a significantly higher value to reflect practical constraints.

Based on the above description, the mathematical model is as follows:

$\begin{array}{ll}\underset{x,y,z}{\min }C=\sum _{r\in R}\sum _{s\in S}\sum _{i\in I_r}{x}_r^s\left(\frac{d_{r,i}}{v_s}+t_{s,r,i}+\frac{w_{r,i}}{h_s}\right)c_o+\sum _{r\in R}\sum _{s\in S}\sum _{i\in I_r}(y_{s,r,i}^1{p}_{r,i}^1+y_{s,r,i}^2{p}_{r,i}^2)+\sum _{r\in R}\sum _{s\in S}\sum _{i\in I_r}{x}_r^s{p}_{s,r,i}& (10)\end{array}$

$\begin{array}{ll}\sum _{s\in S}{x}_r^s{q}_s\ge W_r \forall r\in R& (11)\end{array}$

$\begin{array}{ll}\sum _{r\in R}{x}_r^s\le 1 \forall s\in S& (12)\end{array}$

$\begin{array}{ll}{e}_{s,r,i+1}^1=e_{s,r,i}^1+y_{s,t,i}^1-{\text{HFO}}_{(s,r,i)}\forall s\in S,\forall r\in R,\forall i\in I_r& (13)\end{array}$

$\begin{array}{ll}{e}_{s,r,i+1}^2=e_{s,r,i}^2+y_{s,t,i}^2-{\text{LFO}}_{(s,r,i)}\forall s\in S,\forall r\in R,\forall i\in I_r& (14)\end{array}$

$\begin{array}{ll}{e}_{s,r,i}^1\ge e_{min}^1-(1-x_r^s)M\forall s\in S,\forall r\in R,\forall i\in I_r& (15)\end{array}$

$\begin{array}{ll}{e}_{s,r,i}^2\ge e_{min}^2-(1-x_r^s)M\forall s\in S,\forall r\in R,\forall i\in I_r& (16)\end{array}$

$\begin{array}{ll}{e}_{s,r,i}^1+y_{s,t,i}^1\le F_s^1\forall s\in S,\forall r\in R,\forall i\in I_r& (17)\end{array}$

$\begin{array}{ll}{e}_{s,r,i}^2+y_{s,t,i}^2\le F_s^2\forall s\in S,\forall r\in R,\forall i\in I_r& (18)\end{array}$

$\begin{array}{ll}{y}_{s,r,i}^1\ge z_{s,r,i}^1{f}_1\forall s\in S,\forall r\in R,\forall i\in I_r& (19)\end{array}$

$\begin{array}{ll}{y}_{s,r,i}^2\ge z_{s,r,i}^2{f}_2\forall s\in S,\forall r\in R,\forall i\in I_r& (20)\end{array}$

$\begin{array}{ll}{y}_{s,r,i}^1\le z_{s,r,i}^1{F}_s^1\forall s\in S,\forall r\in R,\forall i\in I_r& (21)\end{array}$

$\begin{array}{ll}{y}_{s,r,i}^2\le z_{s,r,i}^2{F}_s^2\forall s\in S,\forall r\in R,\forall i\in I_r& (22)\end{array}$

$\begin{array}{ll}{x}_r^s-z_{s,r,i}^1\ge 0\forall s\in S,\forall r\in R,\forall i\in I_r& (23)\end{array}$

$\begin{array}{ll}{x}_r^s-z_{s,r,i}^2\ge 0\forall s\in S,\forall r\in R,\forall i\in I_r& (24)\end{array}$

$\begin{array}{ll}{x}_r^s=\left\{0,1\right\}\forall s\in S,\forall r\in R& (25)\end{array}$

$\begin{array}{ll}{y}_{s,r,i}\ge 0\forall s\in S,\forall r\in R,\forall i\in I_r& (26)\end{array}$

$\begin{array}{ll}{z}_{s,r,i}=\left\{0,1\right\}\forall s\in S,\forall r\in R,\forall i\in I_r& (27)\end{array}$

The objective function Equation 10, represents the minimization of the sum of fleet operating costs, fuel costs, and port fees. Constraint Equation 11 ensures that the transportation demand for refined oil on each route is met. Constraint Equation 12 ensures that each ship serves at most one route. Constraints Equations 13, 14 are continuity constraints for the 219 ship’s fuel consumption. Constraints Equations 15, 16 restrict the amount of HFO and LFO in the fuel tanks during navigation to not fall below the minimum levels. Constraints Equations 17, 18 ensure that the fuel volume in the tanks does not exceed the maximum capacity during refueling. Constraints Equations 19–22 are linearization constraints that enforce minimum bunkering quantities, a common requirement from fuel suppliers. For instance, constraint Equation 19 states that if a decision to bunker HFO is made ($z_{s,r,i}^1=1$), the amount bunkered ($y_{s,r,i}^1$) must be at least the minimum required quantity f₁. Conversely, if $z_{s,r,i}^1=0$, constraint Equation 21 forces ($y_{s,r,i}^1$) to be zero. Constraints Equations 23 and 24 are logical constraints that link the bunkering and deployment decisions, ensuring that a vessel can only bunker at a port on a route to which it has been assigned ($x_r^s=1$). Finally, constraints Equations 25–27 define the domains of the decision variables, specifying which are binary ($x_r^s,z_{s,r,i}$), and which are non-negative continuous variables ($y_{s,r,i}^1,y_{s,r,i}^2$).

4 Advanced models and solving algorithms

4.1 Robust model

During the actual operation of refined oil shipping, various uncertainty factors can significantly impact both vessel deployment and refueling strategies. Among these, fluctuations in oil prices and the unpredictability of berth availability stand out as key challenges. The volatility of oil prices directly influences operational costs, making it difficult for shipping companies to optimize refueling schedules and manage fuel reserves efficiently. Sudden price hikes can force companies to adjust routes or delay refueling, thereby increasing the overall complexity of voyage planning. In addition to fuel price volatility, uncertain berth times at ports contribute to operational inefficiencies. Delays in docking due to port congestion, adverse weather conditions, or logistical bottlenecks can lead to longer waiting periods, which in turn affect shipping schedules and fuel consumption. This unpredictability complicates the coordination of vessel arrivals and departures, leading to further disruptions in the supply chain.

To address these challenges, we developed a robust optimization model based on our foundational framework, explicitly accounting for the two key uncertainties: oil price fluctuations and berth time unpredictability. This model incorporates stochastic elements to capture the variability in fuel costs and port conditions, allowing for more resilient decision-making in ship deployment and refueling strategies. By integrating these uncertainty factors, the model enhances operational flexibility, ensuring that shipping companies can minimize disruptions and maintain efficiency under varying conditions. Consider transforming two external input parameters, oil price and berthing time at each port, into random variables. The random oil price is given by:

$\begin{array}{ll}{p}_{r,i}+{\rho }_{r,i}{\mu }_{r,i},{\mu }_{r,i}\in [-1,1]& (28)\end{array}$

indicating that the oil price follows an arbitrary distribution in the interval [p_r,i − ρ_r,i, p_r,i + ρ_r,i]. Similarly, the random berthing time is expressed as:

$\begin{array}{ll}{t}_{r,i}+{\tau }_{r,i}{w}_{b,i}, w_{b,i}\in [-1,1]& (29)\end{array}$

suggesting a distribution in the interval [t_r,i − τ_r,i, t_r,i + τ_r,i]. The uncertainty sets 𝒵 and 𝒲 capturing the constraints are defined as:

$\begin{array}{ll}\begin{array}{l}\text{Φ}=\left\{\mu :\parallel \mu {\parallel }_{\infty }\le 1,\parallel \mu {\parallel }_1\le {\text{Γ}}_p\right\}\hfill \\ \text{Ψ}=\left\{w :\parallel w{\parallel }_{\infty }\le 1,\parallel w{\parallel }_1\le {\text{Γ}}_t\right\}\hfill \end{array}& (30)\end{array}$

The robust model is presented below.

$\begin{array}{ll}\begin{array}{l}\underset{\text{x},\text{y},\text{z}}{\min }\underset{\mu \in \text{Φ},w\in \text{Ψ}}{\max }C=C_o+C_f+C_p\\ s.t. \end{array}& (31)\end{array}$

Equations 11–27.

In these definitions, Φ and Ψ represent the uncertainty sets for oil price and berthing time, respectively. The parameter Γ_p is the budget of uncertainty for price, which limits the total number of ports where prices can deviate from their nominal values simultaneously. Similarly, Γ_t is the budget of uncertainty for berthing time. This formulation creates a robust model that hedges against a limited number of worst-case deviations, which is more practical than protecting against the highly unlikely scenario where all prices and times deviate simultaneously.

It is important to acknowledge that the prices of HFO and LFO are often highly correlated in the real world. Our model utilizes separate uncertainty sets for each fuel type, which does not explicitly model this correlation. This approach is chosen for modeling tractability and to ensure a more conservative solution, as it prepares for a wider range of scenarios. Critically, this structure allows the model to effectively capture the significant uncertainty in the price spread (differential) between HFO and LFO, which can be independently volatile due to regulatory changes or supply imbalances. While the framework is flexible enough to model correlated price movements by setting proportional deviation parameters, the independent approach was chosen for this study to guarantee greater robustness. Explicitly modeling price correlations represents a meaningful avenue for future research.

4.2 Solving algorithms

The proposed Algorithm 1 aims to solve a mixed-integer optimization model involving decision variables $x_r^s$, $y_{s,r,i}^1$, $y_{s,r,i}^2$, $z_{s,r,i}^1$, and $z_{s,r,i}^2$. This algorithm systematically explores a search tree to identify the global optimal solution while leveraging bounds to prune non-promising branches, enhancing computational efficiency. The algorithm begins by initializing the root node with the linear relaxation of the original problem and solving it to determine a lower bound L and the relaxed solution. The best known feasible solution C^* is initialized to infinity. A priority queue is maintained to manage the nodes in the search tree, with the node having the smallest objective value being selected for processing. For each node, the linear relaxation is solved. If the solution is both feasible and integer, it is compared with C^*. If the solution improves C^*, the optimal value and the associated decision variables are updated. If the solution is infeasible, the node is discarded. Otherwise, branching is performed on fractional variables.

Algorithm 1. Branch and Bound Algorithm with Variable Bounds.

The branching process involves selecting variables among $x_r^s$, $z_{s,r,i}^1$, $z_{s,r,i}^2$, $y_{s,r,i}^1$, and $y_{s,r,i}^2$ that hold fractional values in the current solution. For each selected variable, two subproblems are created by imposing bounds on the variable (v = 1 and v = 0 for binary variables, or v ≥ 1 and v ≤ 0 for bounded continuous variables). These subproblems are then added to the search tree for further exploration. To ensure computational efficiency, the bounding step is employed. For each node, the algorithm computes an upper bound U and compares it with the best-known solution C^*. If the lower bound L of the node is greater than or equal to C^*, the node and its descendants are pruned from the search tree, as they cannot yield better solutions. The algorithm terminates when all nodes in the search tree are either processed or pruned. At the end, the algorithm returns C^* as the optimal objective value and the corresponding decision variables $(x_r^s,y_{s,r,i}^1,y_{s,r,i}^2,z_{s,r,i}^1,z_{s,r,i}^2)$. By combining relaxation, branching, and bounding strategies, this method efficiently handles the complexity of mixed-integer optimization problems.

The branch-and-bound algorithm serves as the fundamental solution method for deterministic base models. This Algorithm 1 systematically explores a search tree to identify the global optimal solution by combining relaxation, branching, and bounding strategies, efficiently handling the complexity of the mixed-integer optimization problem. This method provides the solution for our deterministic benchmark case. For the robust optimization model with its min-max structure and uncertainty sets, a more specialized approach is required. We employ RSOME (Robust Stochastic Optimization Made Easy) (Chen et al., 2020; Chen and Xiong, 2023), a powerful Python package designed for such problems. The RSOME platform automatically reformulates the robust problem into its tractable robust counterpart, which is a large-scale deterministic mixed-integer program. This reformulated problem is then solved by a state-of-the-art solver that RSOME calls internally. These solvers are themselves built upon advanced implementations of the Branch and Bound framework. Therefore, Algorithm 1 serves two roles: it is the direct solver for the deterministic model, and it illustrates the fundamental solution logic that is ultimately used by the specialized tools that solve the reformulated robust model.

5 Case study

5.1 Parameter settings

In this section, we use the actual transportation network of a world-leading refined oil shipping company as a case study to illustrate the effectiveness of our model. China COSCO Shipping Energy Transportation Co., Ltd., the sole carrier for China’s domestic refined oil maritime transportation under PetroChina, handles an annual transport volume of 20 million tons with over 2,400 voyages, accounting for approximately 23% of the country’s total seaborne refined oil transportation. The company wields significant market influence and industry impact, managing the transportation of five major product categories: -10 diesel, 0 diesel, 92 gasoline, 95 gasoline, and 98 gasoline. The company’s specific shipping routes include loading ports located in five major regions: Dalian, Bayuquan, Jinzhou, Qinhuangdao, and Tianjin. The unloading ports cover more than 30 key ports across 11 provinces and cities, ranging from Yantai in Shandong to Qinzhou in Guangxi. Currently, the company operates with its own fleet of 16 vessels with a combined capacity of 420,000 DWT (Deadweight Tonnage) and an annual operational cost exceeding 600 million RMB. Additionally, it accesses a charter market fleet of 238 vessels with a total capacity of 2.02 million DWT, approximately 40% of the active domestic refined oil shipping fleet. These vessels range in size from 2,000 tons to 40,000 tons, with an annual charter cost exceeding 1.3 billion RMB.

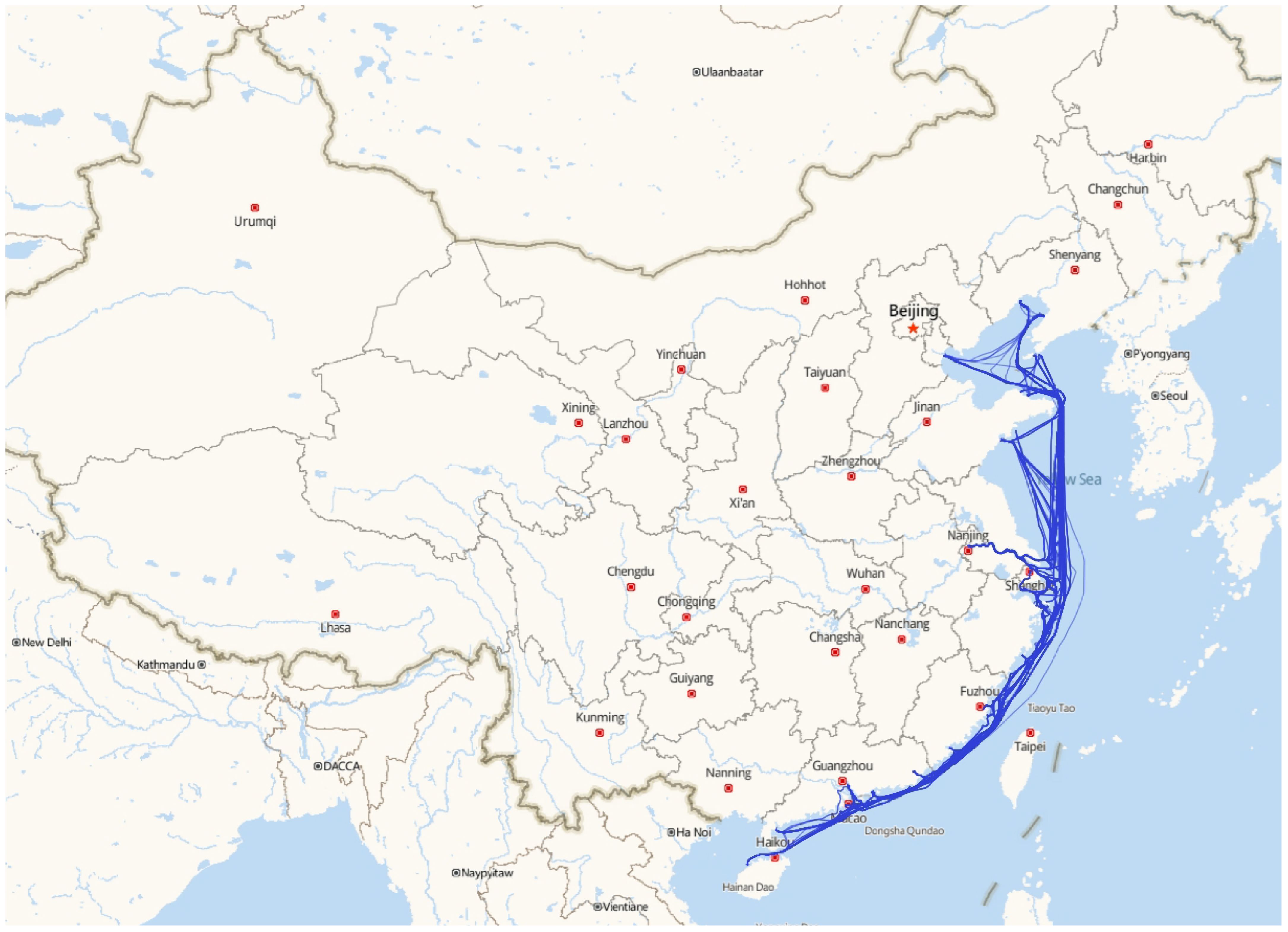
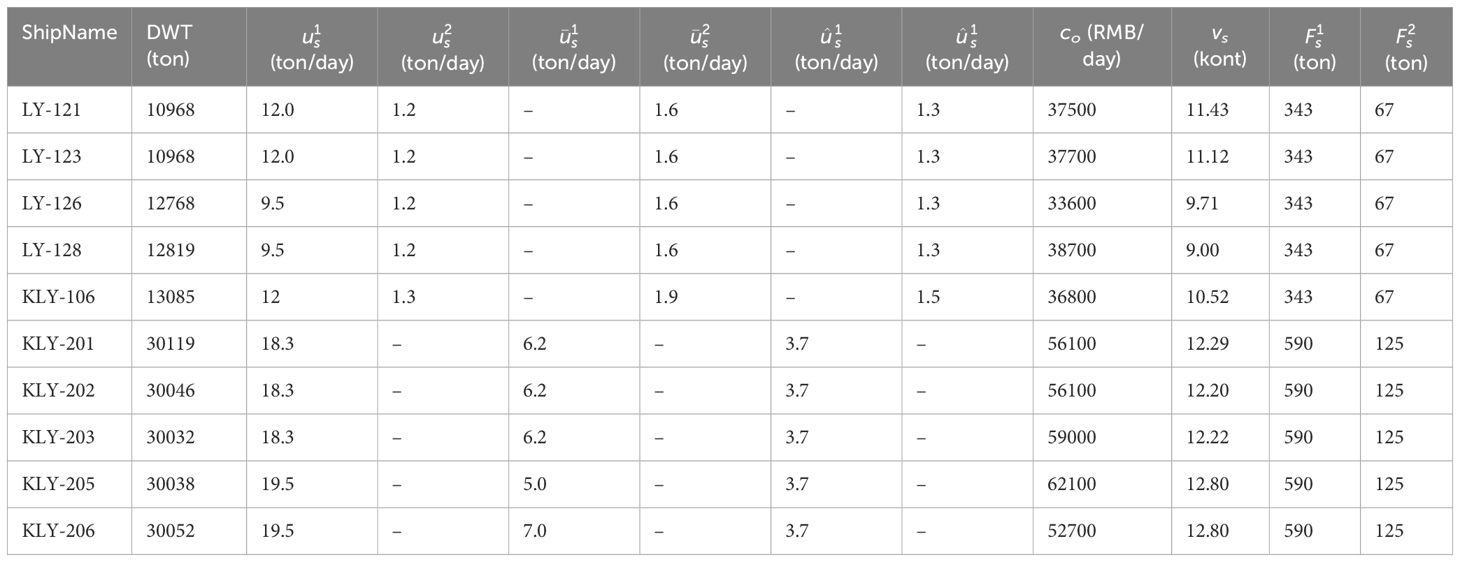
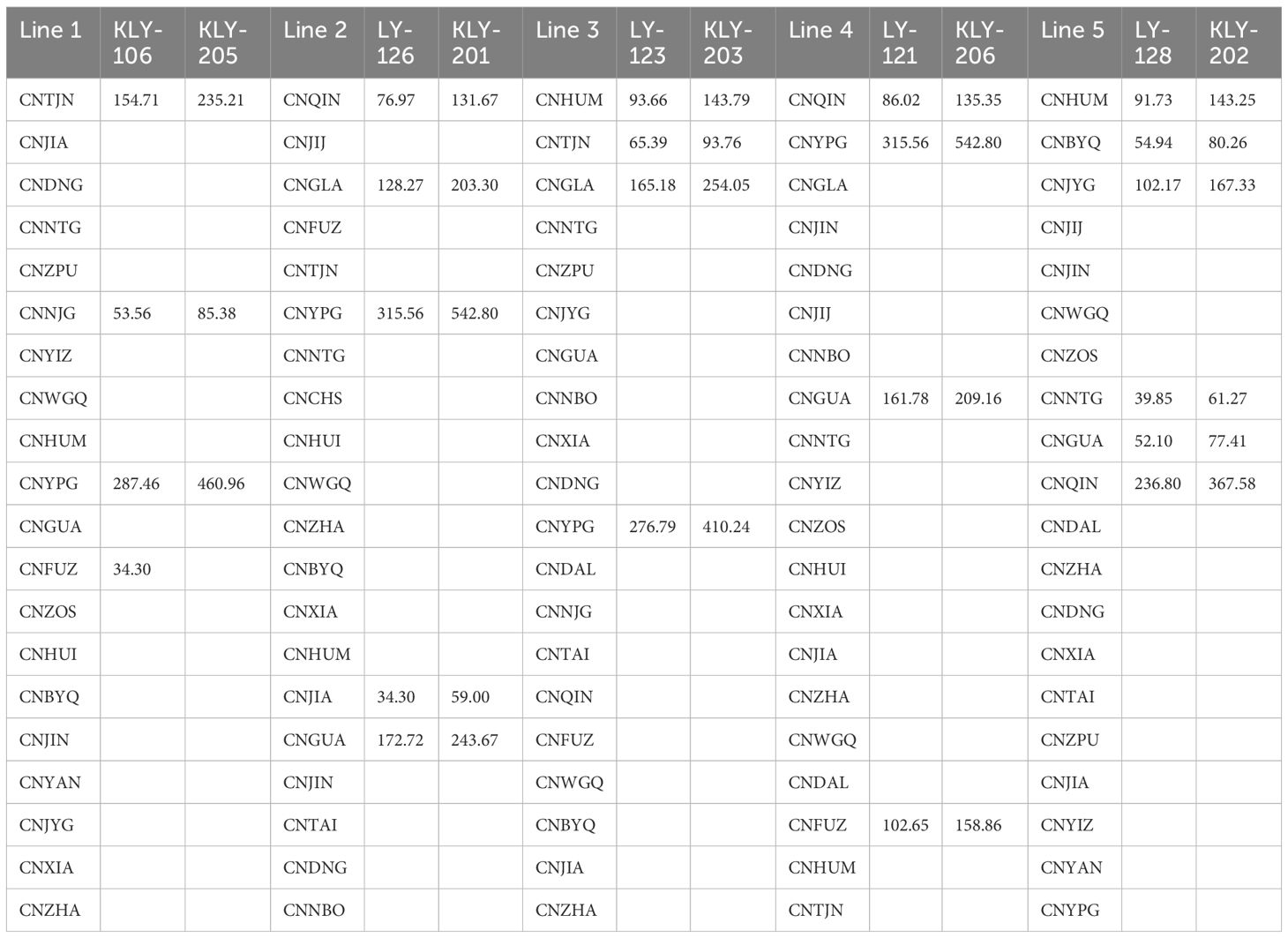
The routes served by the company are shown in Figure 2. These routes connect 27 ports along China’s coastal and inland waterways. The company owns 10 refined oil tankers, with their technical specifications detailed in Table 2.

Figure 2

Figure 2. Refined oil transportation service areas and routes.

Table 2

Table 2. Ship cost and fuel tank parameters.

The case study presented in Table 2 examines the operational and fuel-related parameters of nine vessels (LY-121 to KLY-206), providing critical insights into cost optimization and fuel management across different ship classes. The table details key metrics such as Deadweight Ton (DWT), fuel consumption rates for High-Sulfur Fuel Oil (HFO) and Low-Sulfur Fuel Oil (LFO) under three operational modes—sailing (SC), port (PC), and anchoring (AC)—alongside fuel tank capacities (HFO-Cap and LFO-Cap), daily operational costs (OC in RMB), and cruising speed (kont). Notably, smaller vessels like the LY-series (e.g., LY-121, LY-123) rely on LFO for port and anchoring operations but consume HFO during navigation, while larger KLY-series ships (e.g., KLY-201, KLY-205) prioritize HFO for sailing due to its cost efficiency, despite higher daily operational expenses (e.g., KLY-205 incurs 62,100 RMB/day). Fuel tank capacities scale with vessel size, with KLY-series 331 ships accommodating up to 590 tons of HFO compared to 343 tons in LY-series vessels, reflecting strategic trade-offs between fuel storage and cargo capacity. The data also reveals variations in speed and DWT, such as KLY-205’s higher cruising speed (12.80 knots) and triple the cargo capacity of LY-121, underscoring the need for operators to balance fuel choice, route planning, and compliance with environmental regulations (e.g., using LFO in emission control areas).

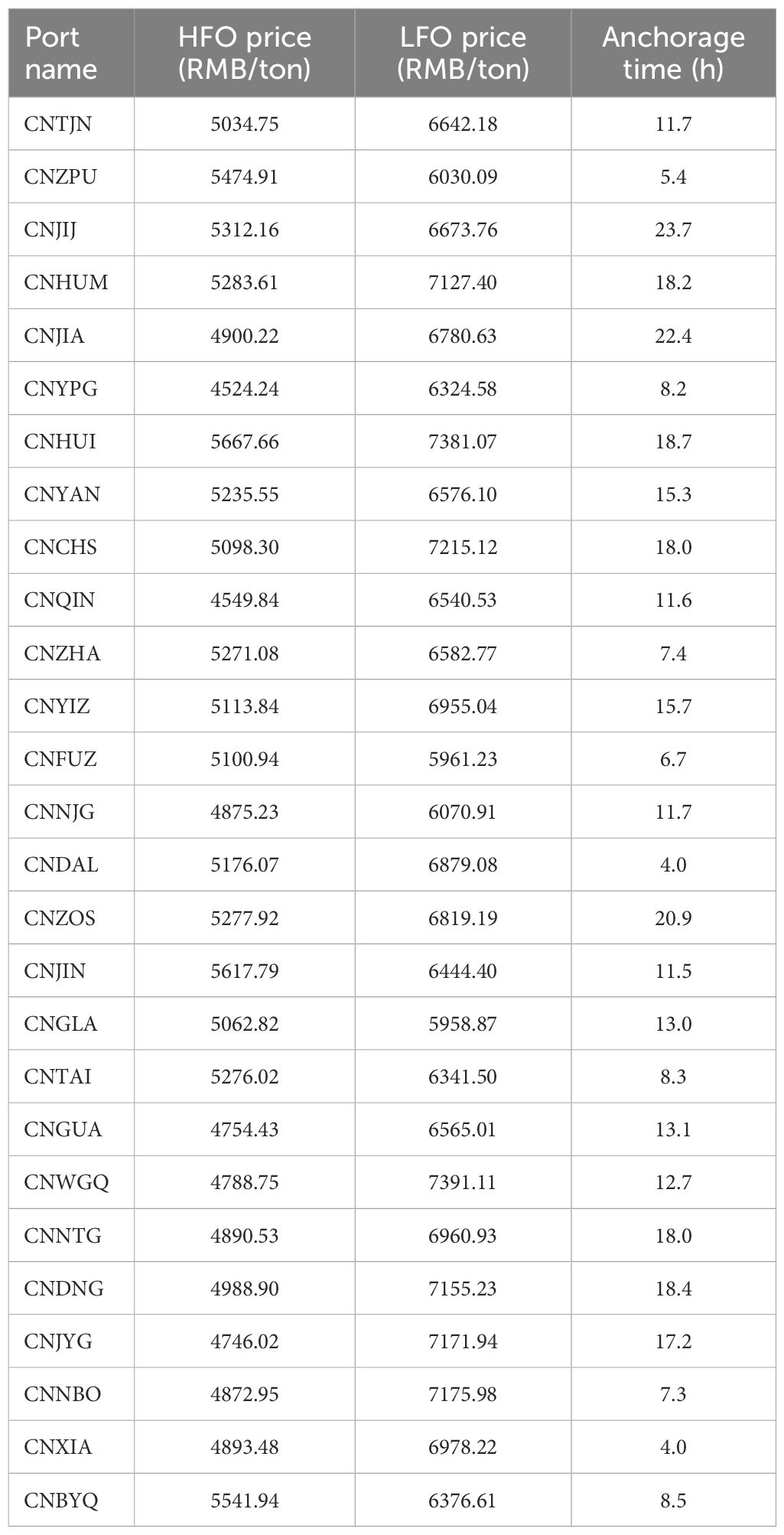
The table presents port-specific parameters for 26 Chinese ports (e.g., CNTJN, CNZPU), focusing on fuel cost dynamics and operational constraints critical to maritime logistics optimization. Key metrics include the price of High-Sulfur Fuel Oil (HFO) and Low-Sulfur Fuel Oil (LFO) in RMB per ton, alongside the average anchorage time required (in hours). Notably, significant price variations exist between ports: HFO costs range from 4,524.24 RMB/ton (CNYPG) to 7,391.11 RMB/ton (CNWGQ), while LFO prices span from 5,958.87 RMB/ton (CNGLA) to 7,381.07 RMB/ton (CNHUI). For instance, CNFUZ offers the lowest LFO price (5,961.23 RMB/ton), contrasting with CNHUI’s premium LFO rate, which exceeds HFO prices in some ports (e.g., CNGLA’s LFO is cheaper than its HFO). Anchorage time also varies widely, from as little as 4.0 hours in CNDAL and CNXIA to 23.7 hours in CNJIJ, directly impacting vessel operational timelines and associated costs. These disparities highlight strategic implications for route planning–operators may prioritize ports like CNFUZ or CNGLA for cost-effective LFO procurement, while shorter anchorage times (e.g., CNDAL) reduce downtime. Conversely, ports with high fuel prices or lengthy anchorage periods (e.g., CNWGQ, CNJIJ) may deter frequent calls unless offset by cargo demand or regulatory requirements. The dataset underscores the need for nuanced cost-benefit analyses when selecting ports, balancing fuel expenses, time sensitivity, and compliance with emission control regulations (e.g., favoring LFO in sulfur-emission control areas despite price premiums). In addition to the data in the Tables 2, 3, several key parameters were configured. The minimum fuel safety level was set to 0.08 of a tank’s total capacity. The minimum bunkering quantity was set to 0.1 of a tank’s capacity. The vessel’s speed in restricted areas was assumed to be 0.8 of its economical cruising speed at sea. A value of 10⁸ was used for the ‘Big M’ in linearization constraints. The case study is based on five distinct shipping routes, each with a transportation demand of 41000 tons. The order of stops for each route is shown in Table 4. The complete port-to-port distance matrix, which details both total and ECA-specific distances in nautical miles for all voyage legs, is provided as Supplementary Material to ensure full reproducibility. This information serves as a foundational input for optimizing fuel purchasing strategies, voyage scheduling, and overall fleet efficiency across diverse port networks.

Table 3

Table 3. Port parameters.

Table 4

Table 4. Deterministic ship deployment and HFO refueling strategy results.

5.2 Comparison of model results

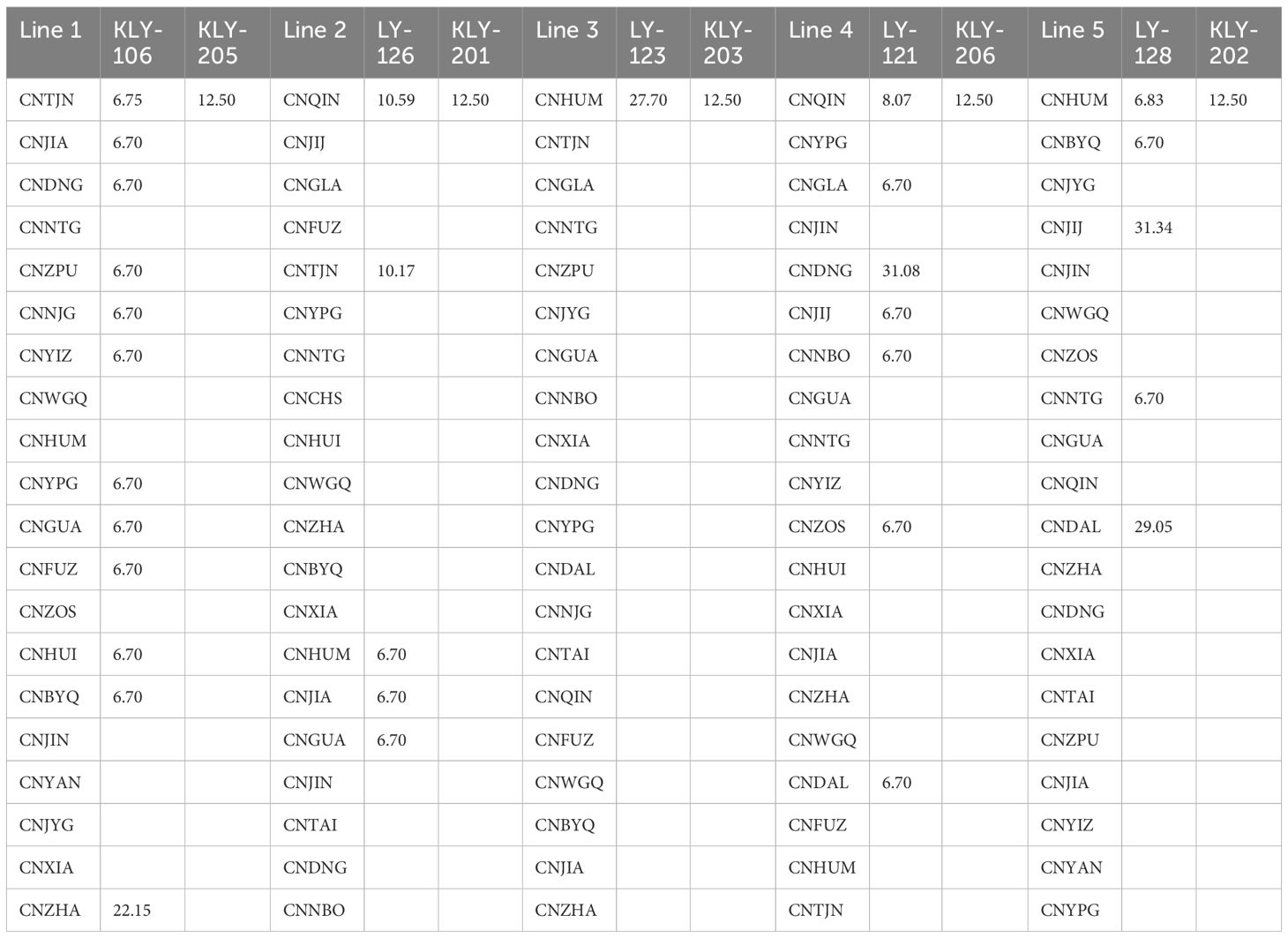
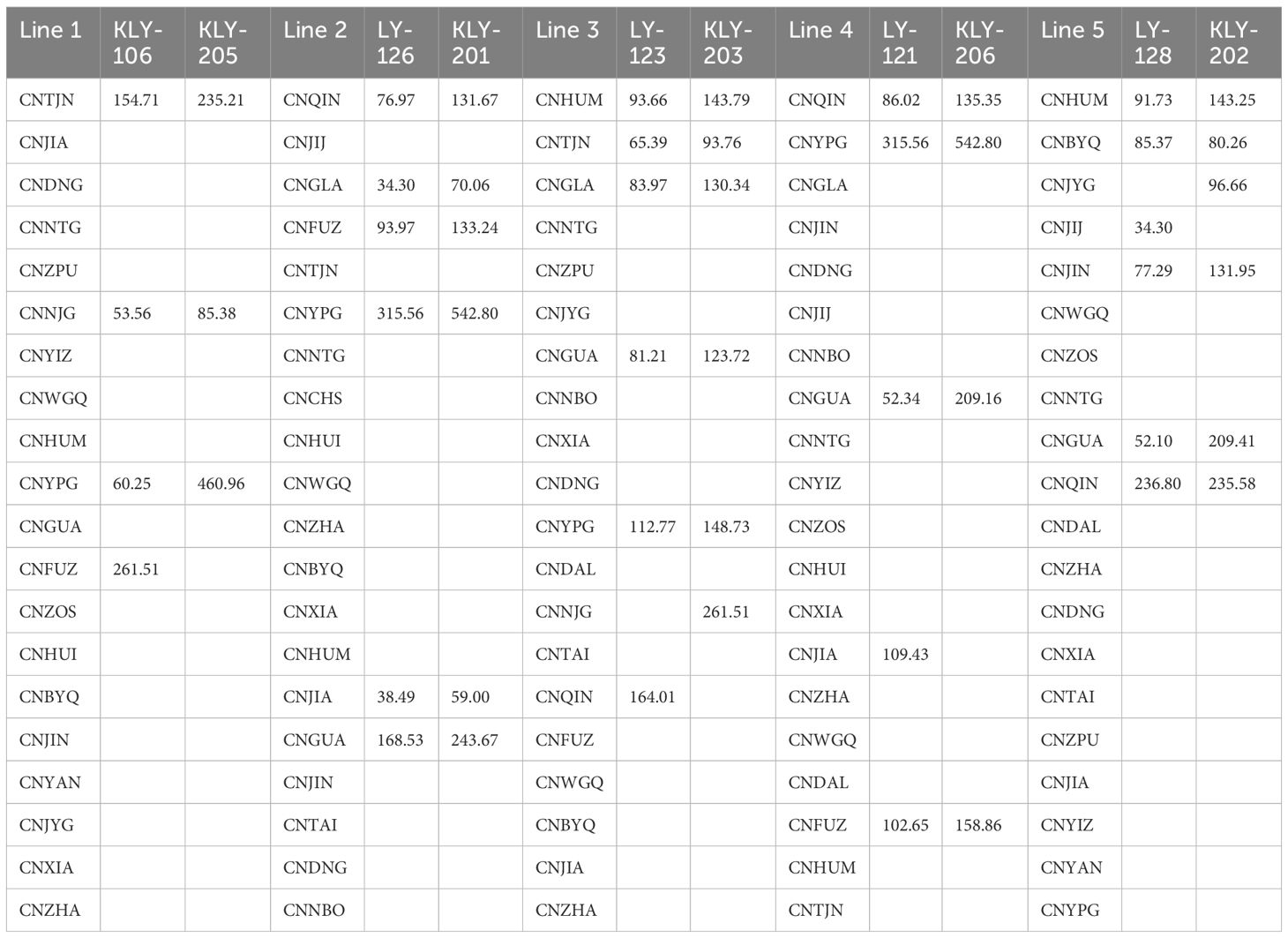
The comparison between deterministic and robust optimization models for ship deployment and fuel refueling strategies (Tables 4–7) reveals distinct trade-offs in fuel allocation, cost efficiency, and operational flexibility under certainty versus uncertainty. The results for the robust optimization model shown in Table 6 and Table 7 were generated by considering the uncertainties in HFO price, LFO price, and anchorage time simultaneously. The specific uncertainty sets, based on the formulation in Section 4.1, were configured as follows. For HFO prices, the maximum deviation (ρ) was set to 100 RMB/ton with a budget of uncertainty (Γ) of 10. For LFO prices, the maximum deviation was 300 RMB/ton with a budget of 10. For anchorage time, the maximum deviation was 6 hours with a budget of 10. The resulting robust strategy is therefore resilient against the combined impact of these potential disruptions. The subsequent sensitivity analysis in Section 5.3 explores the effects of varying these uncertainty parameters individually.

Table 5

Table 5. Deterministic ship deployment and LFO refueling strategy results.

Table 6

Table 6. Robust ship deployment and HFO refueling strategy results.

Table 7

Table 7. Robust ship deployment and LFO refueling strategy results.

The comparison of deterministic and robust optimization models under uncertainty in HFO/LFO fuel prices and anchorage times highlights how each approach addresses volatility in critical operational parameters. The deterministic model assumes fixed fuel costs and port dwell times (e.g., HFO prices like 5034.75 RMB/ton in CNTJN and 11.7-hour anchorage in CNTAI), leading to rigid fuel procurement strategies prioritizing cost minimization—such as heavy reliance on HFO for large vessels (e.g., KLY-205’s 235.21 tons in Line 1 of the deterministic HFO model) and minimal LFO use (e.g., fixed 12.50-ton allocations in most ports). However, this approach becomes vulnerable to disruptions: sudden HFO price spikes (e.g., CNWGQ’s 7,391.11 RMB/ton) or unexpected delays (e.g., CNJIJ’s 23.7-hour anchorage) could disrupt planned routes and budgets.

In contrast, the robust model explicitly accounts for price and time uncertainties by diversifying fuel choices and port selections. For instance, it increases LFO allocations in critical routes (e.g., LY-123’s LFO use rises to 31.34 tons in Line 3 of the robust LFO model) to hedge against HFO price volatility, while expanding port options to avoid over-reliance on high-risk hubs (e.g., incorporating CNJIJ and CNDNG for LFO refueling). The model also adjusts anchorage time impacts by reserving contingency fuel (e.g., KLY-106’s HFO increases to 261.51 tons in Line 11) and selecting shorter-anchorage ports (e.g., prioritizing CNDAL’s 4-hour dwell time over CNJIJ’s 23.7 hours). These adjustments come at a cost: robust strategies incur higher expenses (e.g., LFO’s premium pricing) but ensure operational continuity amid fluctuating conditions, such as avoiding delays caused by unanticipated anchorage extensions.

The trade-offs between cost and resilience are stark. The deterministic model achieves lower fuel expenses but risks failure if assumptions about prices or anchorage times prove inaccurate—e.g., a sudden surge in HFO costs at CNWGQ could strand ships relying on fixed budgets. The robust model, while more expensive (e.g., LFO usage expands to cover 22.42 tons in Line 9 of the LFO: RO model), provides a buffer against disruptions, ensuring compliance with emission regulations and minimizing delays. Decision-makers must balance these factors: short-term cost-sensitive operations may favor the deterministic approach in stable markets, while the robust model is critical in regions with erratic fuel prices (e.g., CNHUI’s 7,381.07 RMB/ton LFO) or unpredictable port congestion, where flexibility outweighs minor cost savings.

An important observation from the results is that the vessel-to-route assignments remain identical be397 tween the deterministic (Tables 4, 5) and robust (Tables 6, 7) solutions. This stability is primarily a consequence of the case study’s structural constraints. With a fixed demand of 41,000 tons per route and a fleet composed of two distinct vessel size classes (12,000 DWT and 30,000 DWT), any feasible solution must pair one vessel from each class to meet the demand. Within this constrained solution space, the optimal assignment is determined by inherent deterministic characteristics of the vessels, such as daily operating costs and fuel efficiency. The uncertainties in fuel price and anchorage time, while impacting total cost, were not sufficient in this instance to alter the fundamental cost hierarchy of the vessel pairings. It is important to note, however, that the model’s main response to uncertainty is reflected in the significant adjustments to the refueling strategies, which represent the most flexible operational decision for hedging against cost volatility.

It is crucial to understand how the cost of robustness is incurred, particularly in low-volatility environments where the deterministic model may appear to outperform the robust one. This cost is not a flaw, but rather the price paid for operational resilience. The robust optimization model makes decisions to hedge against the worst-case scenarios defined within the uncertainty set. In practice, this leads to more conservative operational strategies.

For example, to guard against potential fuel price spikes, the robust model might decide to bunker a larger quantity of more expensive but price-stable LFO, even when HFO prices are nominally lower. To avoid the risk of costly delays, it might favor a port with shorter, more reliable anchorage times over a port that is cheaper but historically more congested. Furthermore, the model may opt to carry a larger buffer of fuel throughout 415 the voyage to mitigate the impact of unforeseen delays, which could slightly reduce the available deadweight for cargo or necessitate less optimal routing. When these worst-case scenarios do not materialize in a stable, low-volatility environment, these prudent, hedging decisions are more expensive in hindsight than the strategy from the deterministic model, which perfectly capitalized on the favorable conditions. This difference in cost is the price of insuring the voyage against disruptions.

5.3 Sensitivity analysis

In this section, we conduct a sensitivity analysis to evaluate the impact of the magnitude of uncertainty on the performance of the deterministic and robust models. The analysis is performed by systematically varying 423 the maximum deviation parameter (ρ_r,i for price or τ_r,i for time) for one source of uncertainty at a time, while the other two uncertainty parameters are held constant at the base values defined in Section 5.2. The ranges for these deviations were selected in consultation with industry experts to reflect plausible market and operational conditions.

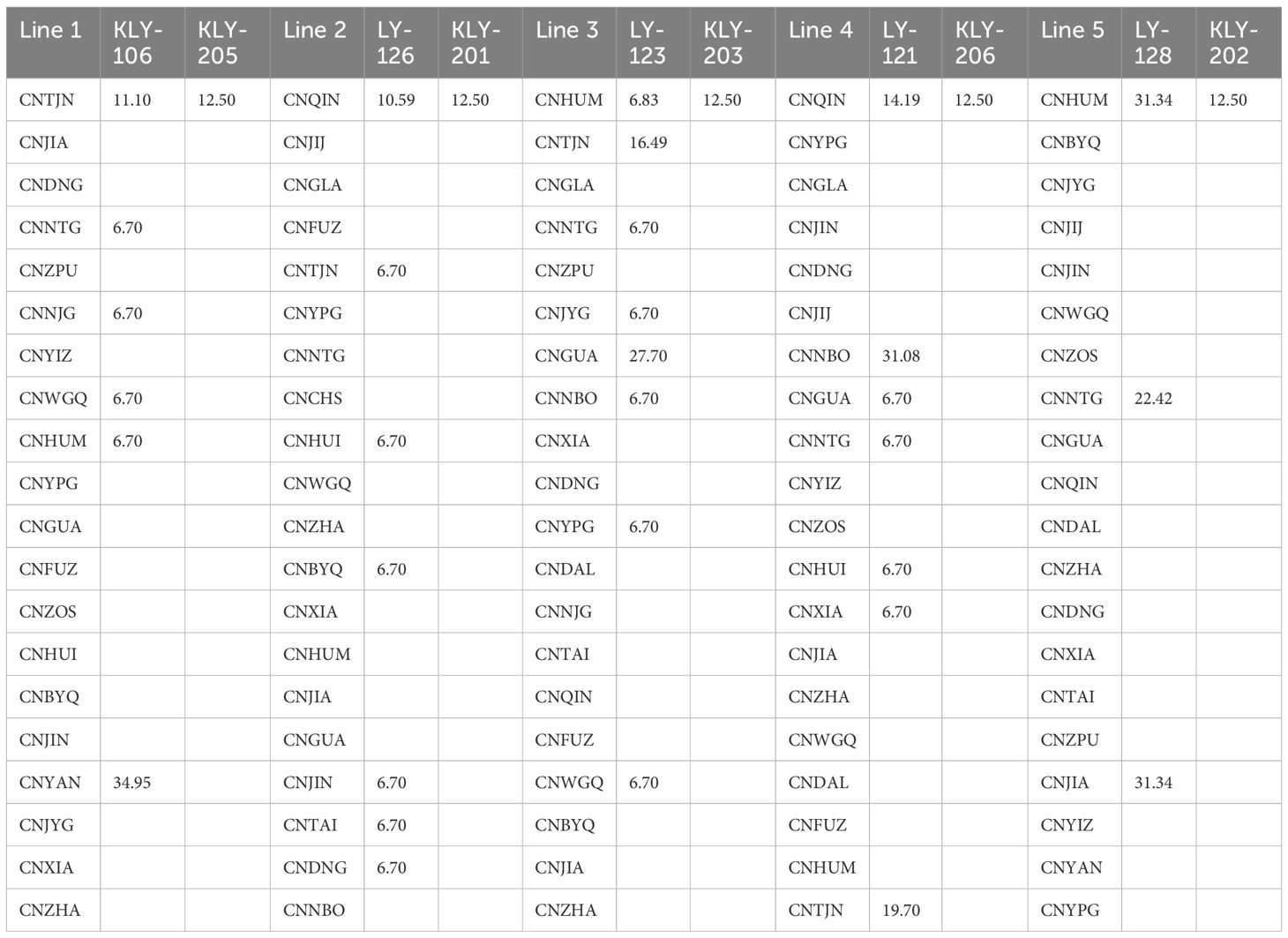
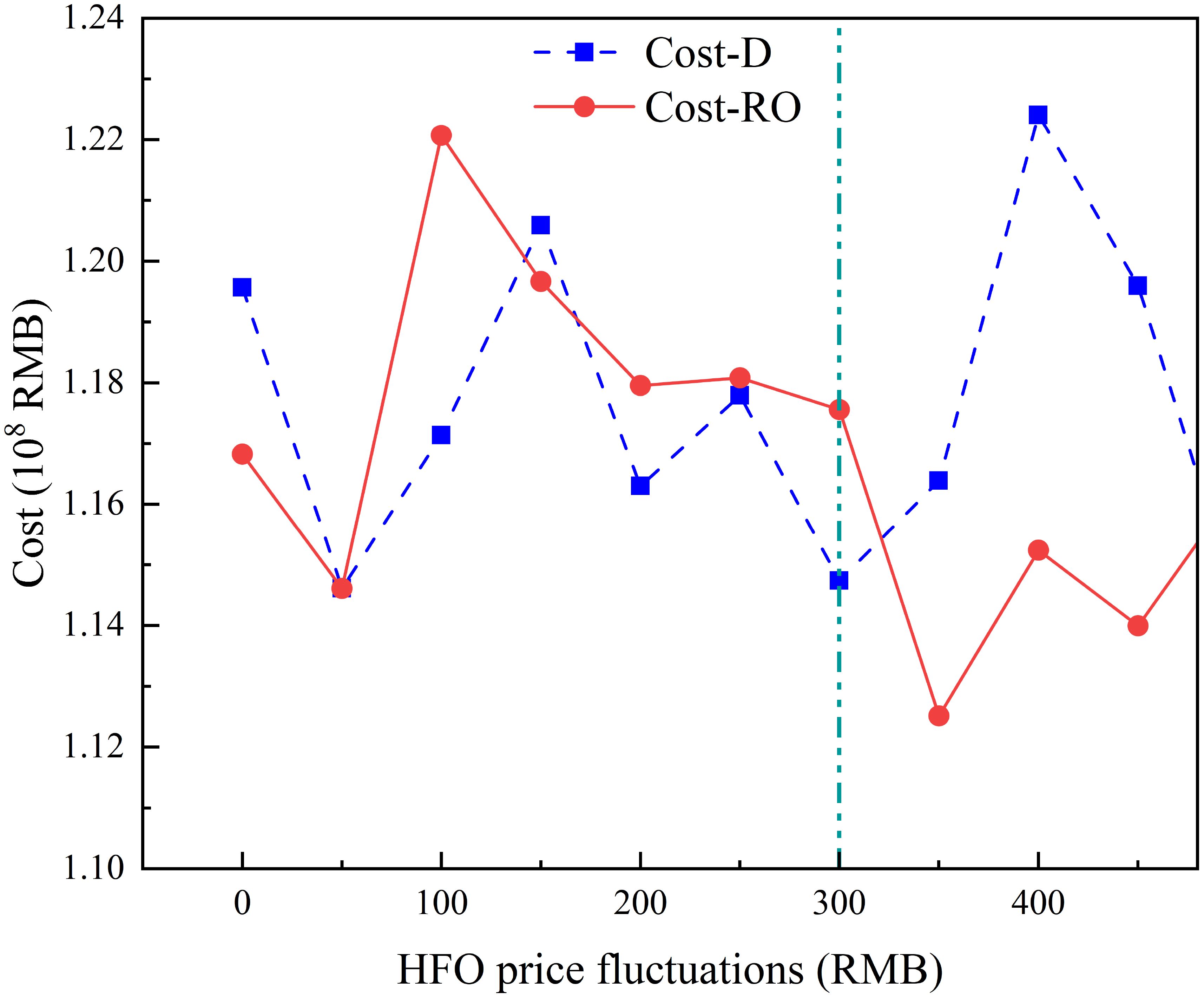
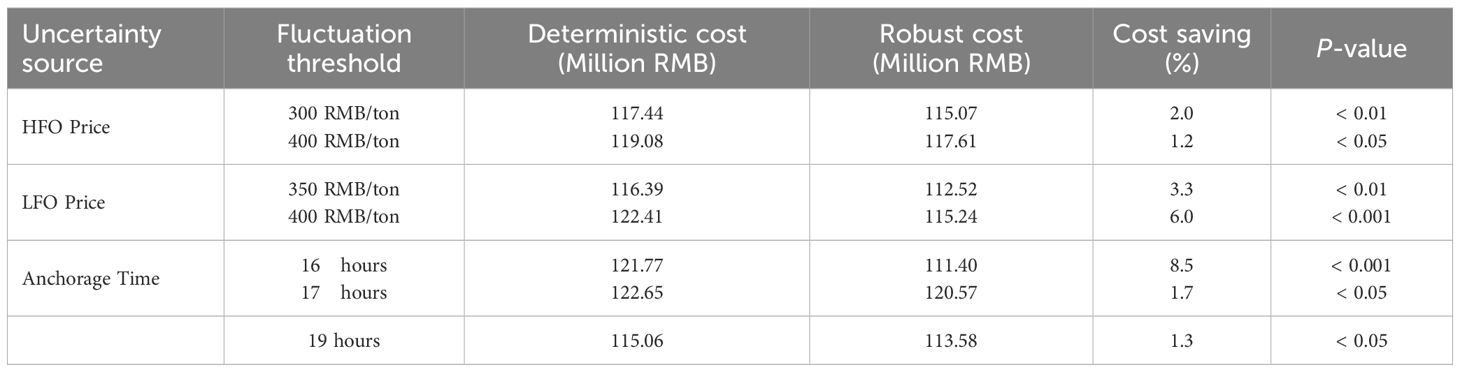
The cost curves presented in Figures 3–5 illustrate the fundamental trade-off of robust optimization. We define the ‘fluctuation threshold’ as the point where the cost of the robust solution falls below that of the deterministic solution. Below this threshold, the robust model may incur a higher cost due to its conservative nature—this is often referred to as the ‘price of robustness.’ However, once the level of uncertainty surpasses this threshold, the proactive hedging strategy of the robust model yields significant cost savings, demonstrating its economic value in volatile environments. The non-monotonic fluctuations in the cost curves can be attributed to the complex interplay of the three simultaneous uncertainties active within the robust model, where the structure of the worst-case scenario shifts as the parameters are varied. Under varying price fluctuations of HFO and LFO, the robust optimization model (RO) demonstrates superior performance compared to the deterministic model (D) when price volatility exceeds critical thresholds. Figures 3 and 4 present cost comparisons between robust optimization and deterministic models under varying price fluctuation ranges for HFO and LFO, respectively, demonstrating the robust model’s superior cost stability in high-volatility scenarios exceeding predefined thresholds.

Figure 3

Figure 3. Comparison of costs under different fluctuation ranges of HFO prices.

Figure 4

Figure 4. Comparison of costs under different fluctuation ranges of LFO prices.

Figure 5

Figure 5. Comparison of costs under different fluctuation ranges of anchorage time.

For HFO refueling strategies, when HFO price fluctuations exceed 300 (Figure 3 green line) units (e.g., at 300 and 400 units), the robust model consistently outperforms the deterministic approach by stabilizing costs. At 300 units of HFO volatility, the deterministic cost rises to 117437000, while the robust model reduces costs to 115071000 (a 2.0% decrease). At 400 units of volatility, the deterministic cost further increases to 119076000, whereas the robust model maintains lower costs at 117607000 (1.2% reduction).

For LFO refueling strategies, the robust model’s advantage becomes pronounced when LFO price fluctuations exceed 250 (Figure 4 green line) units (e.g., 350, 400, and 450 units). At 350 units of LFO volatility, the deterministic cost reaches 116390000, while the robust model lowers costs to 112517000 (a 3.3% reduction). At 400 units of volatility, the deterministic cost spikes to 122407000, but the robust model controls costs at 115242000 (6.0% lower). This resilience stems from the robust model’s ability to hedge against HFO price shocks through diversified fuel procurement and contingency port selection, minimizing exposure to volatile markets.

By dynamically adjusting fuel ratios and optimizing route flexibility, the robust model mitigates risks from extreme price swings, particularly at higher volatility levels. Even when deterministic costs temporarily outperform at lower volatility (e.g., 250 units), the robust model’s long-term stability and ability to handle extreme scenarios make it the preferred choice in unpredictable markets. These results underscore the value of robust optimization in safeguarding operational costs against price instabilities, especially when volatility exceeds predefined thresholds.

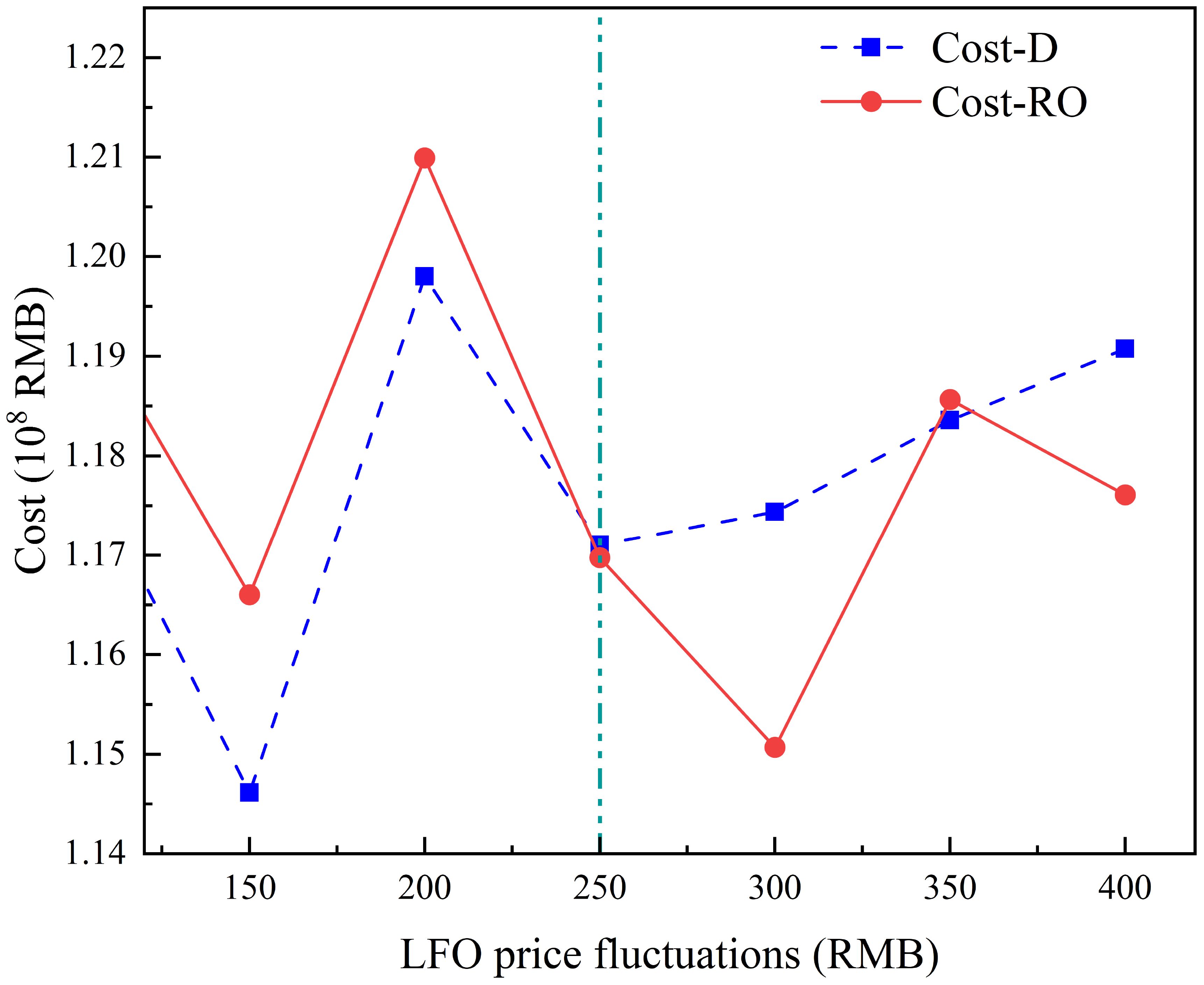
Figure 5 presents a comparison of the costs between the robust optimization and deterministic models across different anchorage time fluctuations. When anchor time fluctuations exceed 12 hours (Figure 5 green line), the robust optimization model (RO) demonstrates a clear cost advantage over the deterministic model (D) in high-volatility scenarios. For fluctuations exceeding 12 hours (e.g., 1319 hours), the robust model consistently achieves lower or more stable costs. Notably, at a 16-hour fluctuation, the deterministic cost spikes to 121.773 million, while the robust model mitigates risks through optimized scheduling and contingency planning, reducing costs to 111.4 million (an 8.5% decrease). At 17 hours, the deterministic cost reaches 122.646 million, whereas the robust model further lowers it to 120.57 million (1.7% reduction). This performance gap widens in extreme scenarios, such as a 19-hour fluctuation, where the robust model reduces costs to 113.582 million compared to the deterministic model’s 115.064 million (1.3% reduction). These results highlight the robust model’s ability to dynamically adjust vessel schedules and fuel reserves to counteract anchorage time uncertainties, ensuring cost stability in volatile operational environments where deterministic models fail due to rigid parameter assumptions.

To provide a clearer quantitative summary of the sensitivity analysis, Table 8 presents a comparison of the cost performance of the deterministic and robust models at the key fluctuation thresholds identified. This table directly addresses the need for statistical validation and highlights the value of robust optimization in highly volatile conditions. The Cost Saving (%) column quantifies the advantage of the robust model, showing savings of up to 8.5% in extreme scenarios.

Table 8

Table 8. Statistical summary of key sensitivity analysis results.

To rigorously validate that the performance improvements of the robust model are statistically significant, we developed a Monte Carlo simulation framework to evaluate the cost savings reported in Table 8. This approach allows us to test the performance of the fixed deterministic and robust solutions against a wide range of randomly generated, plausible future scenarios. The validation process for each sensitivity case (e.g., an anchorage time fluctuation of 16 hours) is as follows:

● Solution Generation: We first solve the deterministic and robust optimization models under the baseline conditions to obtain two distinct, fixed decision plans (D_det and D_rob). Each plan contains a complete set of vessel-to-route assignments and detailed refueling strategies. These plans are the objects of our evaluation.

● Scenario Generation via Monte Carlo Simulation: We conduct 1,000 independent simulation trials. In each trial, we generate a unique what-if scenario by randomly sampling values for the uncertain parameters (fuel prices and anchorage times) from their predefined uncertainty sets. For instance, for the anchorage time scenario with a budget of uncertainty Γ_t = 10 and a maximum deviation of 16 hours, each trial involves:

- Randomly selecting up to 10 ports that will experience a delay.

- For each selected port, randomly assigning a delay time drawn from a uniform distribution between 0 and 16 hours.

A similar process is applied to fuel prices. This ensures each of the 1,000 trials represents a distinct, valid realization of a possible future.

● Performance Evaluation: For each of the 1,000 generated scenarios, we calculate the total operational cost that would have been incurred by applying both the deterministic plan (C_det) and the robust plan (C_rob). The cost saving for that specific trial is then calculated as S_i = C_det,i − C_rob,i, where i is the trial number.

● Hypothesis Testing: After completing all trials, we obtain a sample distribution of 1,000 cost-saving values (S₁,S₂,…,S₁₀₀₀). We then perform a one-sample, one-tailed t-test on this sample. Our hypotheses are:

- Null Hypothesis (H₀): The mean cost saving is zero (µ_S =0). This implies there is no statistically significant difference between the two plans.

- Alternative Hypothesis (H₁): The mean cost saving is greater than zero (µ_S > 0). This implies the robust plan is statistically superior.

The Table 8 final column reports the p-values from our Monte Carlo simulation. The resulting p-value represents the probability of observing our sample’s mean cost saving (or a greater one) purely by random chance if the null hypothesis were true. All reported values are well below the conventional significance level of 0.05, providing strong statistical evidence that the cost savings are not coincidental but are a significant result of the robust model’s hedging strategy.

It is important to contextualize that the fluctuation ranges tested in this analysis are representative of real-world phenomena. The volatility in bunker fuel markets is driven by a multitude of factors, including geopolitical events, global supply chain disruptions, and local port dynamics. Similarly, anchorage time uncertainty is a persistent operational challenge caused by port congestion, adverse weather, and logistical delays. Therefore, the performance gains shown by the robust model at higher levels of uncertainty are not merely theoretical but reflect a tangible advantage in navigating the genuine volatilities inherent in maritime logistics.

5.4 Managerial implications

The results of our sensitivity analysis offer several practical managerial insights for tanker operators navigating volatile market conditions. The identification of specific cost-saving thresholds provides a quantitative basis for dynamic decision-making.

First, the findings can be used to establish a more sophisticated fuel procurement policy. Instead of relying on a static strategy, managers can use the thresholds identified in Figures 3 and 4 as triggers. For instance, if market forecasts predict that fuel price volatility will exceed the identified threshold (e.g., 300 RMB/ton for HFO), a pre-defined policy could dictate a shift towards the robust refueling strategy. This might involve bunkering larger quantities of fuel at ports with historically stable prices or strategically utilizing more of the (often more expensive) but less volatile LFO to hedge against extreme HFO price spikes. This data-driven approach moves the company from a reactive to a proactive stance on fuel cost management.

Second, the model serves as a powerful tool for contingency and risk planning, particularly regarding port congestion. If intelligence suggests that a key port is likely to experience extreme berthing delays (e.g., exceeding the 12-hour fluctuation threshold shown in Figure 5), managers can use the robust model to simulate alternative scenarios. This might lead to a decision to preemptively reroute a vessel, swap vessel assignments to use a smaller, more versatile ship, or adjust the cargo-loading schedule. By quantifying the financial impact of such delays, the model allows decision-makers to make informed trade-offs between accepting a delay or taking costly preventative action.

Finally, our integrated framework encourages a shift in mindset from siloed decision-making to holistic operational management. It demonstrates that vessel deployment and refueling are not independent problems. A suboptimal vessel assignment can create unavoidable high-cost refueling situations down the line. By considering these decisions jointly, especially under uncertainty, companies can develop more resilient and cost-effective operational plans that are robust to the compounding effects of market and operational disruptions.

6 Conclusion

This study presents a robust optimization framework for joint decision-making in tanker deployment and refueling strategies under berthing time and fuel price uncertainties. By integrating operational decisions that are traditionally addressed separately, the proposed model captures the interdependencies between vessel assignment and fuel management, thereby mitigating suboptimal outcomes caused by isolated planning. The incorporation of stochastic berthing times and fuel price fluctuations enables adaptive refueling strategies, enhancing resilience against disruptions such as port congestion and market volatility. Computational experiments, based on a realistic case study constructed with operational data from a leading maritime logistics provider, illustrate the specific value of the robust optimization approach. The findings do not show that one model universally outperforms the other, but rather highlight a critical trade-off. The robust model demonstrates a significant cost-saving advantage—reducing operational costs by 2.06.0% but only when price and time volatility exceeds certain thresholds. Below these levels, the deterministic model is often preferable. This highlights the robust model’s capability to balance economic efficiency with operational flexibility specifically in highly uncertain environments.

The findings underscore the practical value of adopting integrated decision-making frameworks in maritime transportation, particularly for companies navigating volatile fuel markets and unpredictable port conditions. By optimizing tanker deployment and refueling strategies holistically, operators can achieve substantial cost savings while ensuring schedule adherence and regulatory compliance. Future research could extend this framework to incorporate dynamic routing adjustments, multi-objective optimization for emission reduction, and machine learning techniques for real-time uncertainty prediction. Furthermore, future research could extend this framework to incorporate dynamic routing adjustments and treat voyage speed as a decision variable. This extension would involve treating vessel speed for each leg of a voyage as a continuous decision variable. Such a model would need to incorporate the well-established non-linear, convex relationship between vessel speed and fuel consumption directly into the objective function. Consequently, the constraints would also require reformulation to account for variable transit times, directly linking speed choices to arrival schedules and port windows. By co-optimizing deployment, refueling, and speed, such a model could provide deeper insights into the critical trade-o between fuel expenditure, operational costs, and schedule adherence. This would significantly enhance the model’s applicability at the operational level and offer a more holistic solution for cost-efficient and sustainable logistics, especially when considering time-sensitive cargo or carbon emission reduction targets. Investigating these complex dynamics represents a challenging but highly promising extension of the current work. It is important to justify our selection of RO over other frameworks like Stochastic Programming (SP). While SP is a powerful tool, its requirement for precise probability distributions is a significant challenge in our real-world context. Through industry consultations, we confirmed that variables like port berthing time and fuel prices are subject to high distributional ambiguity and heterogeneity, making it impractical to t reliable distributions. Given this, we chose RO for its “distribution-free” nature, which allows us to hedge against worst-case scenarios without assuming specific probabilistic models, thus aligning better with the practical need for operational resilience in a volatile market. We acknowledge, however, that a comparative study with SP is a valuable direction for future research, contingent on the future availability of more granular data for accurate distribution fitting. Such advancements would further bridge the gap between theoretical models and industry needs, fostering sustainable and adaptive solutions for global maritime logistics.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

LD: Software, Writing – original draft, Visualization, Data curation, Resources, Conceptualization, Formal Analysis, Investigation, Project administration, Funding acquisition, Writing – review & editing, Methodology, Validation, Supervision. XY: Data curation, Conceptualization, Investigation, Writing – original draft, Writing – review & editing. MW: Writing – original draft, Software, Funding acquisition, Writing – review & editing. SS: Resources, Methodology, Writing – review & editing, Investigation, Funding acquisition, Conceptualization. ZT: Writing – original draft, Resources, Funding acquisition, Conceptualization, Validation, Writing – review & editing, Supervision.

Funding

The author(s) declare financial support was received for the research and/or publication of this article. Funded by the following projects: National Natural Science Foundation of China (71871037), National Natural Science Foundation of China (72501254), Natural Science Foundation of Hebei Province (G2025203015), China Scholarship Council (No. 202406570041), and COSCO PETROCHINA SHIPPING CO., LTD.

Conflict of interest

Authors LD was employed by the company COSCO Petrochina Shipping CO., LTD. Author XY was employed by the company COSCO Shipping Energy Transportation Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The authors declare that this study received funding from COSCO PETROCHINA SHIPPING CO., LTD. The funder had the following involvement in the study: data collection.

The reviewer ZW declared a shared affiliation with the authors LD, MW and ZT to the handling editor at the time of review.

Generative AI statement

The author(s) declare that Generative AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmars.2025.1677919/full#supplementary-material.

Footnotes

1. ^ https://www.archivemarketresearch.com/reports/refined-oil-transportation-63550
2. ^ https://dataintelo.com/report/refined-oil-transportation-market

References

Aydin N., Lee H., and Mansouri S. (2017). Speed optimization and bunkering in liner shipping in the presence of 583 uncertain service times and time windows at ports. Eur. J. Operational Res. 259, 143154. doi: 10.1016/j.ejor.2016.10.002

Crossref Full Text | Google Scholar

Besbes O. and Savin S. (2009). Going bunkers: The joint route selection and refueling problem. Manufacturing Service Operations Manage. 11, 694711. doi: 10.1287/msom.1080.0249

Crossref Full Text | Google Scholar

Chen X., Ma F., Wu Y., Han B., Luo L., and Biancardo S. A. (2025). Mfmdepth: Metaformer-based monocular metric depth estimation for distance measurement in ports. Comput. Ind. Eng. 207, 111325. doi: 10.1016/j.cie.2025.111325

Crossref Full Text | Google Scholar

Chen Z., Sim M., and Xiong P. (2020). Robust stochastic optimization made easy with RSOME. Manage. Sci. 66, 33293339. doi: 10.1287/mnsc.2020.3603

Crossref Full Text | Google Scholar

Chen Z. and Xiong P. (2023). RSOME in Python: An open-source package for robust stochastic optimization made easy. INFORMS J. Computing 35, 717724. doi: 10.1287/ijoc.2023.1291

Crossref Full Text | Google Scholar

De A., Wang J., and Tiwari M. K. (2020). Hybridizing basic variable neighborhood search with particle swarm optimization for solving sustainable ship routing and bunker management problem. IEEE Trans. Intelligent Transportation Syst. 21, 986997. doi: 10.1109/TITS.2019.2900490

Crossref Full Text | Google Scholar

Gao T., Tian J., Liu C., Huang C., Wu H., and Yuan Z. (2025). A model for speed and fuel refueling strategy of methanol dual-fuel liners with emission control areas. Transport Policy 161, 116. doi: 10.1016/j.tranpol.2024.11.015

Crossref Full Text | Google Scholar

Ghosh S., Lee L. H., and Ng S. H. (2015). Bunkering decisions for a shipping liner in an uncertain environment with service contract. Eur. J. Operational Res. 244, 792802. doi: 10.1016/j.ejor.2015.02.012

Crossref Full Text | Google Scholar

Hao J., Feng Q., Yuan J., Sun X., and Li J. (2022). A dynamic ensemble learning with multi-objective optimization for oil prices prediction. Resour. Policy 79, 102956. doi: 10.1016/j.resourpol.2022.102956

Crossref Full Text | Google Scholar

He P., Jin J. G., Pan W., and Chen J. (2024). Route, speed, and bunkering optimization for lng-fueled tramp ship with alternative bunkering ports. Ocean Eng. 305, 117957. doi: 10.1016/j.oceaneng.2024.117957

Crossref Full Text | Google Scholar

Jiang G., Fan Q., Zhang Y., Xiao Y., Xie J., and Zhou S. (2025). A tradable carbon credit incentive scheme based on the public-private-partnership. Transportation Res. Part E: Logistics Transportation Rev. 197, 104039. doi: 10.1016/j.tre.2025.104039

Crossref Full Text | Google Scholar

Lashgari M., Akbari A. A., and Nasersarraf S. (2021). A new model for simultaneously optimizing ship route, sailing speed, and fuel consumption in a shipping problem under different price scenarios. Appl. Ocean Res. 113, 102725. doi: 10.1016/j.apor.2021.102725

Crossref Full Text | Google Scholar

Li Y., Jin J. G., He P., and Lu C. (2025). Optimizing bunkering and speed for dry bulk carriers considering biofuel storage period limitation. Ocean Coast. Manage. 260, 107482. doi: 10.1016/j.ocecoaman.2024.107482

Crossref Full Text | Google Scholar

Li S., Wu W., Ma X., Zhong M., and Safdar M. (2022). Modelling medium- and long-term purchasing plans for environment-orientated container trucks: a case study of Yangtze river port. Transportation Saf. Environ. 5, tdac043. doi: 10.1093/tse/tdac043

Crossref Full Text | Google Scholar

Ma D., Ma W., Hao S., Jin S., and Qu F. (2021). Ship’s response to low-sulfur regulations: From the perspective of route, speed and refueling strategy. Comput. Ind. Eng. 155, 107140. doi: 10.1016/j.cie.2021.107140

Crossref Full Text | Google Scholar

Ma W., Zhang J., Han Y., Mao T., Ma D., Zhou B., et al. (2023). A decision-making optimization model for ship energy system integrating emission reduction regulations and scheduling strategies. J. Ind. Inf. Integration 35, 100506. doi: 10.1016/j.jii.2023.100506

Crossref Full Text | Google Scholar

Sun Q. and Chou M. C. (2025). Express: Data-driven bunker refueling under price uncertainty. Production Operations Manage. 0, 10591478251376781. doi: 10.1177/10591478251376781

Crossref Full Text | Google Scholar

Wang C. and Chen J. (2017). Strategies of refueling, sailing speed and ship deployment of containerships in the low-carbon background. Comput. Ind. Eng. 114, 142150. doi: 10.1016/j.cie.2017.10.012

Crossref Full Text | Google Scholar

Wang W., Wang H., Pang K. W., Zhen L., and Wang S. (2025a). Optimizing bunkering and sailing strategies for sustainable shipping: a decision model for reducing costs and carbon emissions. Ann. Operations Res. 119, 2287–2305. doi: 10.1007/s10479-025-06650-4

Crossref Full Text | Google Scholar

Wang Y., Zhang H., Wang T., and Liu J. (2025b). Heterogeneous vessel fleet co-management for liner alliances under profit-sharing agreement and weekly-dependent demand. Transportation Res. Part E: Logistics Transportation Rev. 194, 103880. doi: 10.1016/j.tre.2024.103880

Crossref Full Text | Google Scholar

Wu Y., Guo H., Qi J., Wang S., and Zhen L. (2024). Ship refueling optimization for dual-fuel ships considering carbon intensity indicator rating limit and uncertain fuel prices. Multimodal Transportation 3, 100138. doi: 10.1016/j.multra.2024.100138

Crossref Full Text | Google Scholar

Wu Y., Huang Y., Wang H., and Zhen L. (2022). Joint planning of fleet deployment, ship refueling, and speed optimization for dual-fuel ships considering methane slip. J. Mar. Sci. Eng. 10 (11), 1690. doi: 10.3390/jmse10111690

Crossref Full Text | Google Scholar

Zhen L., He X., Zhuge D., and Wang S. (2024). Primal decomposition for berth planning under uncertainty. Transportation Res. Part B: Methodological 183, 102929. doi: 10.1016/j.trb.2024.102929

Crossref Full Text | Google Scholar

Zhen L., Wang S., and Zhuge D. (2017). Dynamic programming for optimal ship refueling decision. Transportation Res. Part E: Logistics Transportation Rev. 100, 6374. doi: 10.1016/j.tre.2016.12.013

Crossref Full Text | Google Scholar

Zhou S., Guo Z., Chen J., and Jiang G. (2025a). Large containership stowage planning for maritime logistics: A novel meta-heuristic algorithm to reduce the number of shifts. Advanced Eng. Inf. 64, 102962. doi: 10.1016/j.aei.2024.102962

Crossref Full Text | Google Scholar

Zhou S., Liao Q., Xiong C., Chen J., and Li S. (2024). A novel metaheuristic approach for agvs resilient scheduling problem with battery constraints in automated container terminal. J. Sea Res. 202, 102536. doi: 10.1016/j.seares.2024.102536

Crossref Full Text | Google Scholar

Zhou S., Liu X., Chen J., Zhao M., Wang F., and Wu L. (2025b). Joint optimization of slot and empty container co-allocation for liner alliances with uncertain demand in the maritime logistics industry. Transportation Res. Part E: Logistics Transportation Rev. 204, 104437. doi: 10.1016/j.tre.2025.104437

Crossref Full Text | Google Scholar

Zhou Y. and Wang C. (2025). Decisions on ship route, refueling, and sailing speed considering eca regulation and demand uncertainty. J. Operational Res. Soc. 76, 1433. doi: 10.1080/01605682.2024.2324139

Crossref Full Text | Google Scholar

Zhou S., Yu Y., Zhao M., Zhuo X., Lian Z., and Zhou X. (2025c). A reinforcement learning based agv scheduling for automated container terminals with resilient charging strategies. IET Intelligent Transport Syst. 19, e70027. doi: 10.1049/itr2.70027

Crossref Full Text | Google Scholar