- 1Departamento de Nutrición y Salud Pública, Universidad del Bío-Bío, Chillán, Chile
- 2Residue Chemistry and Predictive Microbiology Research Unit, Eastern Regional Research Center, Agricultural Research Service, United States Department of Agriculture, Wyndmoor, PA, USA
- 3Laboratorio de Microbiología y Probióticos, Instituto de Nutrición y Tecnología de los Alimentos, Universidad de Chile, Santiago, Chile
- 4Departamento de Nutrición, Bromatología y Tecnología de los Alimentos, Facultad de Veterinaria, Universidad Complutense, Madrid, Spain
Cronobacter spp. have been responsible for severe infections in infants associated with consumption of powdered infant formula and follow-up formulae. Despite several risk assessments described in published studies, few approaches have considered the tremendous variability in cell response that small micropopulations or single cells can have in infant formula during storage, preparation or post process/preparation before the feeding of infants. Stochastic approaches can better describe microbial single cell response than deterministic models as we prove in this study. A large variability of lag phase was observed in single cell and micropopulations of ≤50 cells. This variability increased as the heat shock increased and growth temperature decreased. Obviously, variability of growth of individual Cronobacter sakazakii cell is affected by inoculum size, growth temperature and the probability of cells able to grow at the conditions imposed by the experimental conditions should be taken into account, especially when errors in bottle-preparation practices, such as improper holding temperatures, or manipulation, may lead to growth of the pathogen to a critical cell level. The mean probability of illness from initial inoculum size of 1 cell was below 0.2 in all the cases and for inoculum size of 50 cells the mean probability of illness, in most of the cases, was above 0.7.
Introduction
Cronobacter spp. are members of the family Enterobacteriaceae and can cause serious infection of all human age groups (Farmer et al., 1980; van Acker et al., 2001; Iversen and Forsythe, 2003; FAO/WHO, 2006; Holý and Forsythe, 2014), but infants of less than 1 year are at particular risk (Bowen and Braden, 2006; Pagotto and Farber, 2009) mainly the neonates, who are less than 4 weeks old (Yan et al., 2012). Severe symptoms related to Cronobacter spp., include necrotizing enterocolitis and meningitis (Simmons et al., 1989; van Acker et al., 2001; Himelright et al., 2002; FAO/WHO, 2004, 2006, 2008; O’Brien et al., 2009). The overall mortality rate caused by the microorganism is between 20 and 80% in infected infants (Lai, 2001; Hunter and Bean, 2013). The incidence of Cronobacter spp. infection among infants is relatively low (8.7 per 100 000 low birth weight neonates) (Cawthorn et al., 2008; Tóthová et al., 2011), however, it is assumed that the number of infections caused by Cronobacter is underreported (Tóthová et al., 2011).
Occasional contamination of powdered infant formula (PIF) and follow-up formulae (FUF) during manufacture is an important source of the microorganism’s occurrence in reconstituted product (FAO/WHO, 2008). However, Cronobacter spp. have been also detected in other foods (Friedemann, 2007) and environments such as food processing plants, hospital equipment and households (Kandhai et al., 2004; Guillaume-Gentil et al., 2005; Hurrell et al., 2009).
Powdered infant formula/follow-up formulae are not sterile (Farber, 2004; FAO/WHO, 2008). At least two outbreaks demonstrated a relationship between Cronobacter isolates from infected patients and the isolated cultured from unopened cans of PIF consumed by these same patients (Clark et al., 1990; Block et al., 2002). Although the levels of Cronobacter spp. are generally very low (<1 CFU/g) (Osaili and Forsythe, 2009), reconstituted infant formula is a good medium for growth (Parra et al., 2015). Furthermore, Cronobacter spp. may be recovered after, at least, 2.5 years from a dairy formula (Barron and Forsythe, 2007). When this bacterium contaminates one of these formulae, it may grow during preparation, cooling, storage, and holding of the reconstituted infant formula in bottles, Cronobacter spp. may grow resulting in an increased probability of illness. According to FAO/WHO (2006), the incidence rate among infants weighting less than 2500 g at birth was 8.7 per 100,000 infants in the United States of America during their 1st year of life. Other group of concern is the elderly who have experienced strokes that cause dysphagia and, therefore, may require reconstituted powdered supplements as part of their diet (FAO/WHO, 2006).
Recalls of infant formula contaminated with Cronobacter sakazakii have occurred in the United States, Europe, and other countries (Simmons et al., 1989; van Acker et al., 2001; Weir, 2002; Drudy et al., 2006; Schreck, 2010; Tomasulo, 2012; Herriman, 2015). This has resulted in increased efforts to implement appropriate strategies to reduce the health risks associated with the use of reconstituted infant formula and to provide guidance to risk-based management decisions (Reij et al., 2009; Pina-Pérez et al., 2014).
A microbial risk assessment (MRA) for E. sakazakii and other micro-organisms in PIF was developed in 2004 during a FAO/WHO expert meeting (FAO/WHO, 2004). This MRA was estimated in terms of relative risk, comparing different “what-if” scenarios regarding contamination levels and risk mitigation measures. During a second expert consultation in 2006, a more elaborate risk assessment model was presented, that allows comparing scenarios to a baseline scenario to be chosen by the user (FAO/WHO, 2006). In these MRAs risk estimates were made using the average response of microbial cells based on deterministic approaches, however, deterministic models are not effective in describing the behavior of small microbial populations or individual cells (Baranyi, 1998) since they ignore the proven variability between individual cells (Elfwing et al., 2004; Métris et al., 2005, 2008; Pin and Baranyi, 2006; Koutsoumanis, 2008; Niven et al., 2008; Dupont and Augustin, 2009; Aguirre et al., 2009; Cuevas-Muñoz et al., 2013; Lianou and Koutsoumanis, 2013; Aspridou and Koutsoumanis, 2015). Stochastic modeling approaches seem to solve the above problem since they are able to deal with more “realistic” food contamination events with few cells (Ross and McMeekin, 2003; Koutsoumanis, 2008; Koutsoumanis and Lianou, 2013; Alonso et al., 2014; Skandamis and Jeanson, 2015).
Cronobacter spp., especially the most virulent ones, may be present in reconstituted infant formula and possibly survive the mild heat stress associated with reconstitution because clinical strains appeared to be more thermotolerant than their environmental counterparts (Yan et al., 2012). On the other hand, as cross contamination can occur at any point, cells present in reconstituted infant formula may not be heat damaged. Despite the advice of FAO/WHO (2006) to use water at 70°C to reconstitute PIF, instructions for reconstitution may suggest use of water at temperatures as low as 40°C (Xu et al., 2015; Parra-Flores et al., 2015) due to the undesirable effects on the organoleptic, nutritional, and functional properties (Pina-Pérez et al., 2015) or risk of burns during preparation and feedings (Agence Francaise de Securite Sanitaire Des Aliments [AFSSA], 2005).
In both cases of contamination, it may lead to the PIF becoming unsafe, as untreated and mildly heat treated Cronobacter spp. present in the PIF may have the potential to recover and grow during the holding time. The assumption, in these cases, that all cells (treated and untreated cell survivors) will have the same lag phase and that all services will have the same dose per service (number of cells) can lead to unrealistic and inaccurate predictions, which is unlikely to be a sufficient basis for management decisions on the safety risk (European Commission [EC], 2002; Lammerding and Todd, 2006).
In contrast to extensive studies on individual lag for other microorganisms (Elfwing et al., 2004; Métris et al., 2005, 2008; Pin and Baranyi, 2006; Koutsoumanis, 2008; Niven et al., 2008; Aguirre et al., 2009; Cuevas-Muñoz et al., 2013; Aspridou and Koutsoumanis, 2015), few data are available on variability of single cell lag time of Cronobacter spp. (Miled et al., 2011; Xu et al., 2015).
In this study we compared both lag phases, estimated by deterministic and stochastic approaches of two inoculum sizes (individual single cell and fifty cells) of untreated or sublethal heat treated C. sakazakii at four storage and abuse temperatures. In addition, the effect of both approaches on the probability of illness was assessed.
Materials and Methods
Culture Preparation
Cronobacter sakazakii ATCC 29544 was used. The strain was kept frozen at -20°C in tryptic soy broth (TSB; Pronadisa, Madrid, Spain) supplemented with 20% glycerol. The strain was subcultured twice in sterile TSB at 37°C for 24 h to reach the stationary phase, with a concentration of ca. 109 CFU/ml. Cells were harvested by centrifugation at 10,000×g, 15 min at 4°C in a Sorvall RC5B refrigerated centrifuge. The final pellets were resuspended in sterile saline solution (0.75% NaCl). Cell suspensions were then used to inoculate sterile TSB solution.
Heat Shock
Cells were treated at 50° C during 5 and 10 min, based on the experiments described by Parra-Flores et al. (2015) and Xu et al. (2015).
To apply the heat treatments, the protocol described by Aguirre et al. (2009) was used with few modifications. Briefly, 10 tubes for each time of treatment containing 9.9 ml of sterile TSB were immersed in a temperature-controlled water baths (model TFB, Bunsen S.A., Madrid, Spain) set at the target temperature which was monitored using a thermocouple (Testo AG 720, Kirchzarten, Germany). Once tubes reached the target temperature, 100 μl of the bacterial suspension were inoculated. When the heat treatment was complete, at each sampling time (5 and 10 min), aliquots of 100 μl were removed and immediately mixed with 900 μl of cold sterile TSB in a tube immersed in an ice water bath. Surviving bacteria were properly diluted and plated on tryptic soy agar (TSA, Pronadisa, Spain) for counting. Initial inoculum size (non-heated cells) was also estimated to determine the degree of inactivation achieved.
Based on the methodology of Koutsoumanis (2008), from the above suspensions and untreated ones, a dilution containing around 100 cells (by previous plate counting) was plated in TSA to estimate the cell growth probability (Pg) of treated and untreated ones. Plates were incubated at 5, 10, 15, or 25°C for 30, 20, 10, and 5 days, respectively. Before storage, plates were covered with Parafilm (Parafilm ‘M’, American National Can, Greenwich, CT, USA) to avoid dehydration.
Inoculum Size, Growth Rate, Growth Temperature, and Lag Phase
From the above two treated and untreated suspensions (50° C by 5 and 10 min of exposure), serial-dilutions in TSB were prepared in order to obtain several inoculum sizes from 106 to 101 cells/ml as described in Aguirre et al. (2013).
The specific growth rate (μmax) was estimated in TSB at 5, 10, 15, and 25°C from turbidity growth curves in three replicate experiments using an automated spectrophotometer (Bioscreen C, Labsystems, Helsinki, Finland) kept in a controlled temperature room as described in several studies (Guillier et al., 2005; Métris et al., 2005; Aguirre et al., 2013).
Briefly, from the above mentioned inoculum sizes, 20 replicate samples (350 ml) from each dilution were inoculated into wells of Bioscreen microplates (honeycomb plates, Thermo Fisher Scientific, Basingstoke, UK). The plates were loaded into the Bioscreen C at incubation temperatures of 5, 10, 15, or 25°C. After shaking at medium intensity for 10 s, turbidity measurements were determined using a wide band filter at 420 to 580 nm at 15-min intervals. Plates were incubated for enough time to reach stationary phase in the most diluted samples [for up to 1 month or enough time to observed optical density (OD) above 0.35]. The reading chamber of the Bioscreen was pre-heated to a set-point temperature 1 day before the experiment to allow equilibration.
Dilutions of each initial inoculum were plated by spreading onto TSA, then they were incubated at 5, 10, 15, or 25°C in a controlled incubator for the same time as the Bioscreen experiment’s and finally colonies were counted. Using the Bioscreen device, the time to detection (Td), defined as the time required to reach an absorbance of 0.20 (Aguirre et al., 2012, 2013), was obtained from each well, and a mean value was calculated for each dilution. μmax was estimated from the reciprocal of the absolute value of the regression slope of the Td versus Ln (N), where N is the initial number of cells. The experiment was carried out at least three times.
To estimate the lag time (λ) in TSB from the solutions mentioned above (heat shocked at 50°C during 5 and 10 min and untreated ones), the same protocol described by Aguirre et al., 2013 was followed using the Bioscreen C equipment with few modifications. To do this, 350 μl from the dilution expecting that contain 101 and 100 CFU/ml (100 samples per dilution) were transferred to the two microplates of the Bioscreen (100 wells per dilution) and incubated at 5, 10, 15, or 25°C, kept in at a controlled room temperature. The increase in OD was tracked by measuring it in the wavelength range from 420 to 580 nm using the Bioscreen C every 30 min for up to 30, 25, 15, and 10 days for 5, 10, 15, or 25°C, respectively. Cultures were shaken for 10 s at medium intensity before OD was measured.
Lag times were estimated using the detection time (Td), defined as the time required for the OD in the wavelength range between 420 and 580 nm to reach 0.2 units, which corresponds to an average concentration of 1.57∗ 107 CFU/well obtained by OD calibration curve (data not shown) as described in previous studies (Métris et al., 2005, 2006; Aguirre et al., 2013). More specifically, lag times were estimated based on the following equation (Baranyi and Pin, 1999):
where Nd is the bacterial number (CFU) at Td, N0 the initial number of cells (CFU), and μ (h-1) is the specific growth rate determined from the growth curve obtained under the experimental conditions described above.
To estimate the initial average number of cells (N0) per well that were able to grow at each growth temperature, 350 μl from each dilution were mixed with molten TSA in plates and incubated at 5, 10, 15, or 25°C in a controlled incubator for the same time as the lag time experiments and then colonies were counted. Approximately 20 plates were counted for each dilution and treatment. To be considered, Guillier et al. (2005) stated that if 35% of samples (microplates) show growth, this should not significantly affect individual cell lag phase distributions because at least 80% of samples contain one cell, according to the Poisson distribution function (Francois et al., 2003). Finally, number of cells per well was assessed based on the number of positives as described in Aguirre et al. (2012) and each experiment was replicated two or three times to obtain at least 80 individual cell lag times. A similar protocol was used to estimate the kinetic parameters of 50 cells per well.
Data Analysis and Modeling
The data of λ and μmax were fitted to various distributions using the @Risk 4.5 for Excel software (Palisade Corporation, Newfield, NY, USA). The goodness of fit was compared using three different methods: X2, Anderson–Darling (A–D) and Kolmogorov–Smirnov (K–S). The best-fitted distributions based on the mentioned criteria were further introduced into an exponential model with lag to describe the growth of individual treated and untreated cells using Monte Carlo simulations as described by Koutsoumanis and Lianou (2013):
where Nt is the total number of cells in a population at time t, N0 is the initial number of cells in the population at t = 0, Ng∼Binomial (N0, Pg) is the initial number of cells in the population at t = 0 that are able to grow and form a colony, Pg is the mean probability of growth at each condition (heat shock and growth temperature) determined as described by Koutsoumanis (2008), μmax and λ are introduced as probability distributions from the best fit, respectively, of a microcolony originating from an untreated and a treated single cell, respectively. The output of the model was assessed for N0 of 1 and 50 cells using Monte Carlo simulation with 10,000 iterations and with a uniform distribution for t [t∼Uniform (0, tn)], with tn 250, 600 and 900 h for each temperature of cells untreated and heat treated at 50°C for 5 or 10 min, respectively.
The above approach takes into account the heterogeneity (variability) in the growth dynamics of single cells by introducing the kinetic parameters in the model as probability distributions using Monte Carlo simulation. In addition, this approach predicts the probability of growth of individual cells as a function of prior heat treatment.
Growth in PIF
To test the applicability of the model in commercial PIF, packages of infant product from the same batch were bought locally. Before use, they were checked for absence of anaerobic and aerobic microorganisms, including Cronobacter spp, based on the method of Chap et al. (2009). The PIF was reconstituted using sterile water at 50°C and 900 ml of the reconstituted milk were distributed in 100 Eppendorf tubes for each growth temperature (5, 10, 15, and 25°C). Once stabilized the temperature, tubes were inoculated with 100 μl of 1 or 50 Cronobacter cells that survived heat treatment at 50°C for 5 or 10 min or that were not subjected to prior heat treatment. Tubes were incubated at 5, 10, 15, and 25°C for up to 1 month and everyday duplicate samples were mixed in molten TSA in plates and incubated at 5, 10, 15, and 25°C.
The obtained growth curves were then fitted to the deterministic primary model of Baranyi and Roberts (1994) for the estimation of λ and μmax. As suggested by Koutsoumanis and Lianou (2013), in order to describe the abrupt transition from the lag to the exponential phase characterizing the observed growth, the values of the parameters m and n of the model were fixed to 0 and 20, respectively.
Probability of Illness of Infants by Cronobacter sakazakii from Consumption of PIF
Through the consideration of the storage stages between preparation of the formula and feeding of the infant, we used the Risk Assessment Model for Enterobacter sakazakii in PIF designed by FAO/WHO (2006) although including the probability distribution provided by our data as an input of the model, hence the risk characterization provides the level of contamination, the ingested dose, and the probability of illness resulting from feeding PIF.
To include the uncertainty in our results and since infants can take different amounts of milk, we fitted a distribution to the weight of the infant and the expected consumptions provided by FAO/WHO (2006) which are shown in Table 1.
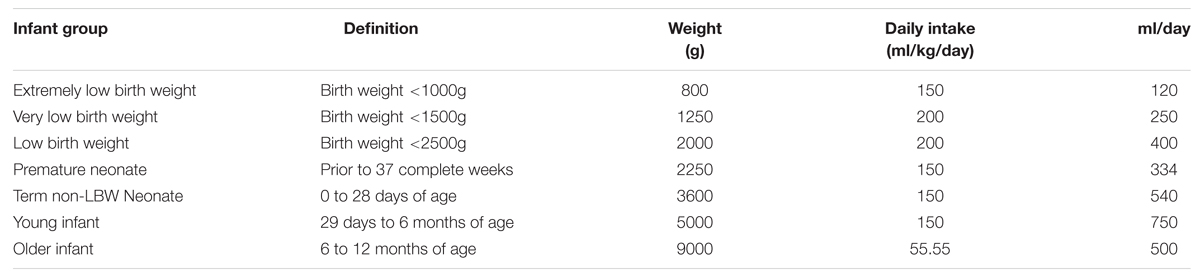
TABLE 1. Infant group definitions presents as options in the risk assessment model (modified from FAO/WHO, 2006).
To estimate the probability of illness (Pill), the exponential dose-response model was used (Haas et al., 1999).
where r is the exponential dose-response parameter and dc is the dose at consumption that results from an initial contamination level of 1 or 50 cells of Cronobacter spp per serving.
As mentioned by FAO/WHO (2006), there are no data currently available to estimate the parameter r, however, in the report they proposed six options for r, ranging from 1∗10-5 to 1∗10-10. In our approach, a Uniform distribution was used with these values. To estimate dc, the volume of consumption and the concentration of Cronobacter spp. at the time of consumption have to be considered. A Normal distribution (413.39; 206.61) was fitted to the estimated milk consumption, which was obtained by the product between weight of the infant and the daily intake shown in Table 1.
To estimate the concentration of Cronobacter at the time of consumption, two approaches (probabilistic and deterministic) were assessed based on our data, considering the time to reach a hypothetical infected dose of 1000 CFU (Iversen and Forsythe, 2004; Mittal et al., 2009) with an initial concentration of 1 or 50 untreated cells or heat treated at 50°C for 5 or 10 min and the concentration reached after 50 h of incubation at 15°C for a single cell survivors to heat treatment at 50°C for 5 or 10 min.
Finally, to have an idea of the probability of illness in real a situation, Eq. 3 was multiply by the prevalence of Cronobacter in PIF obtained from the literature (Iversen and Forsythe, 2004; FAO/WHO, 2008; Chap et al., 2009; Siqueira et al., 2013), from 3 to 30%. To do this, we assumed a Uniform distribution (0.03, 0.3).
Results
Experimentally obtained lag phase and specific growth rate values are shown in Table 2. As expected, the higher the growth temperature, the shorter the lag phase was, reflecting the known mesophilic character of this species (Nazarowec-White and Farber, 1997). At the same growth temperature, the lag phase increased as the time of exposure to heat treatment increased with untreated cells showing the shortest lag phases. For example, at 25°C, lag phase was 3.9 h for an untreated single cell whereas it was 424 h for a single cell that survived at 50°C for 10 min. In the case of the inoculum size of 50 cells, the shorter lag was 1.75 h and the higher was 272 h in the same conditions as those of 1 cell.
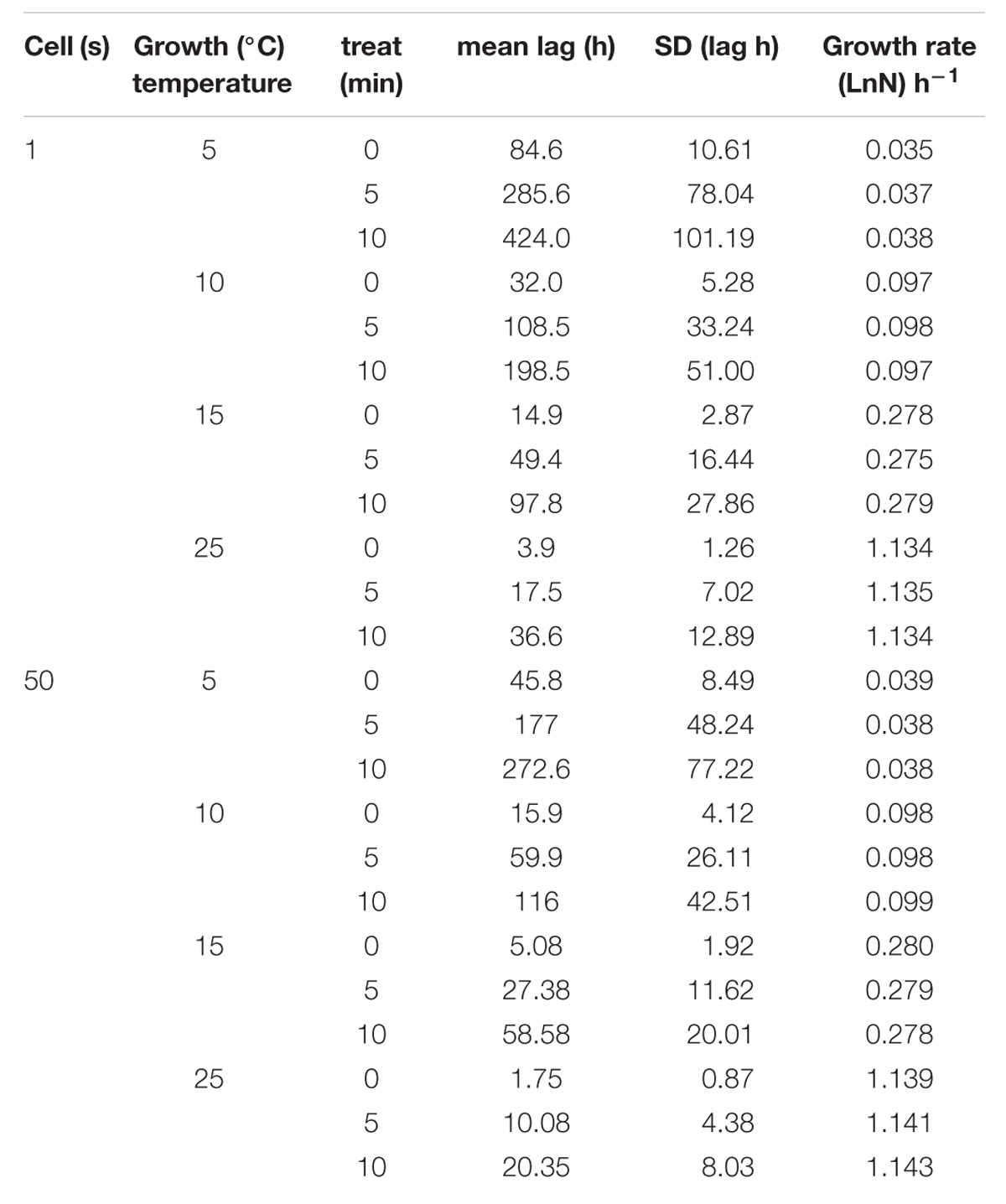
TABLE 2. Kinetic parameter (lag and umax) of 1 and 50 cells of Cronobacter sakazakii growth of cells able to growth at three different temperatures in tryptic soy broth (TSB).
Inoculum size also affected the lag phase (Table 2). Lag phase of single cells were longer on average than lag phase for samples that contained 50 cells. In contrast, growth rates did not show substantial differences between treated and untreated cells at the same growth temperature. In addition, the specific growth rate was not affected significantly by inoculum size. However, as expected, temperature did affect the growth rate; the higher the temperature the higher the growth rate. For example, the highest mean growth rate (1.134 h-1) was obtained with cells grown at 25°C, and the lowest mean growth rate (0.035 h-1) was observed with cells grown at 5°C, a decrease of approximately 97%.
Figure 1 shows the fitted Gamma distributions for lag phase of single cells of Cronobacter sakazakii as a function of temperature and heat treatments. For the same growth temperature, the variability of the lag phase increased as the severity of heat shock increased. For example, at 5°C, the lag phase of the untreated samples ranged from 45 to 125 h whereas it ranged from 80 to 420 h for cells heat shocked at 50°C for 5 min and from 176 to 650 h for cells heat shocked at 50°C for 10 min. As the growth temperature increased, the distributions for lag phase became less variable (Figure 1). Similar results were obtained for the higher inoculum size (i.e., 50 cells) although the distributions were narrower; reflecting the smaller standard deviations than those of 1 cells (data not shown).
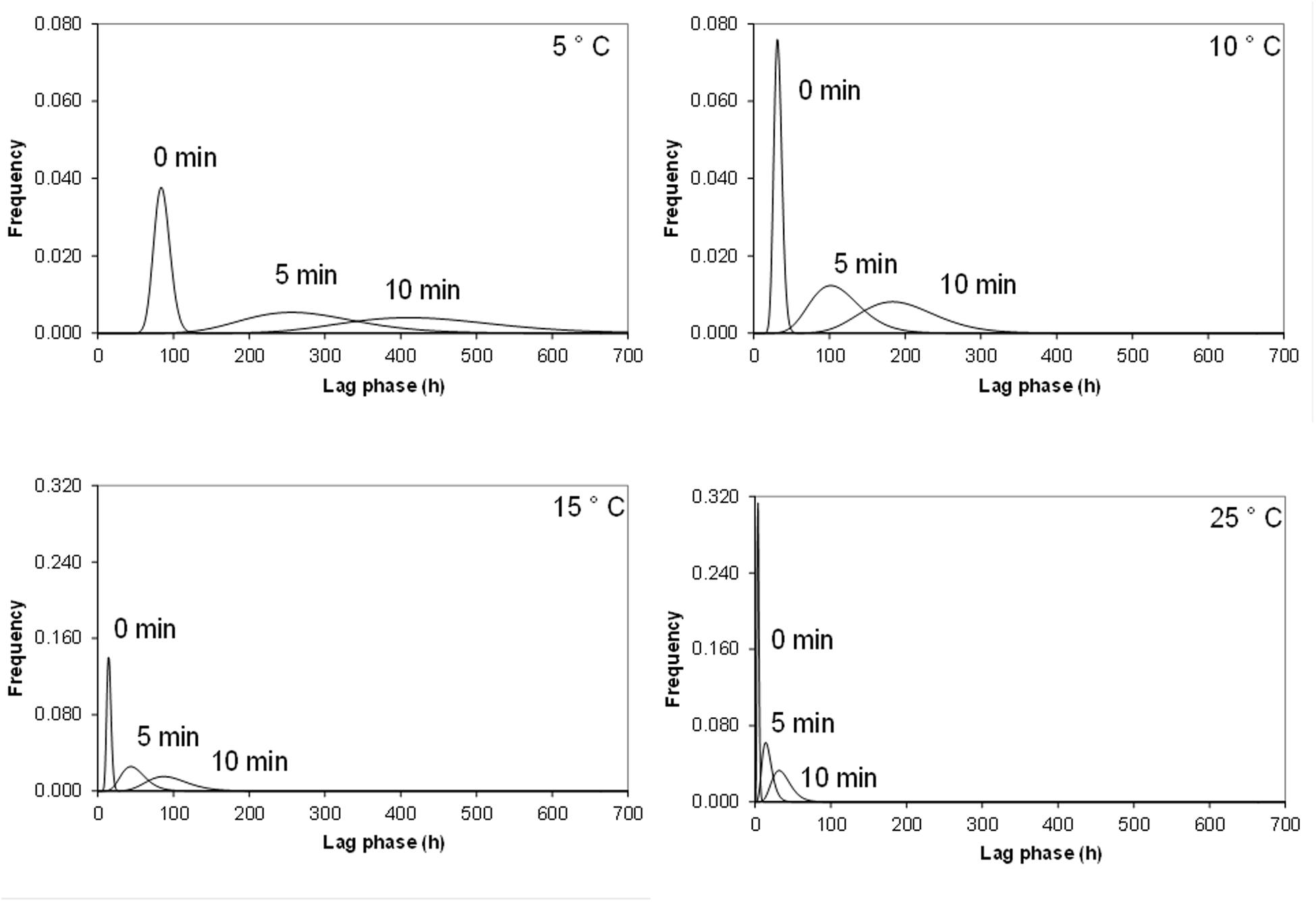
FIGURE 1. Frequency distribution of individual Cronobacter sakazakii lag phases fitted by gamma distribution at different growth temperatures after 50°C heat shock by 0, 5, and 10 min.
Figure 2 shows the mean probability of cell able to growth (Pg) as a function of the time of heat treatment and temperature. It was observed that as the heat treatment increased, Pg decreased; in addition, the higher the temperature, the higher was the Pg, indicating a significant variation in the number cells with growth ability. For example, at 25°C, the Pg was 0.05 for cells that survived heating at 50°C for 10 min, whereas the Pg was 0.97 for cells treated for 10 min at 50°C.
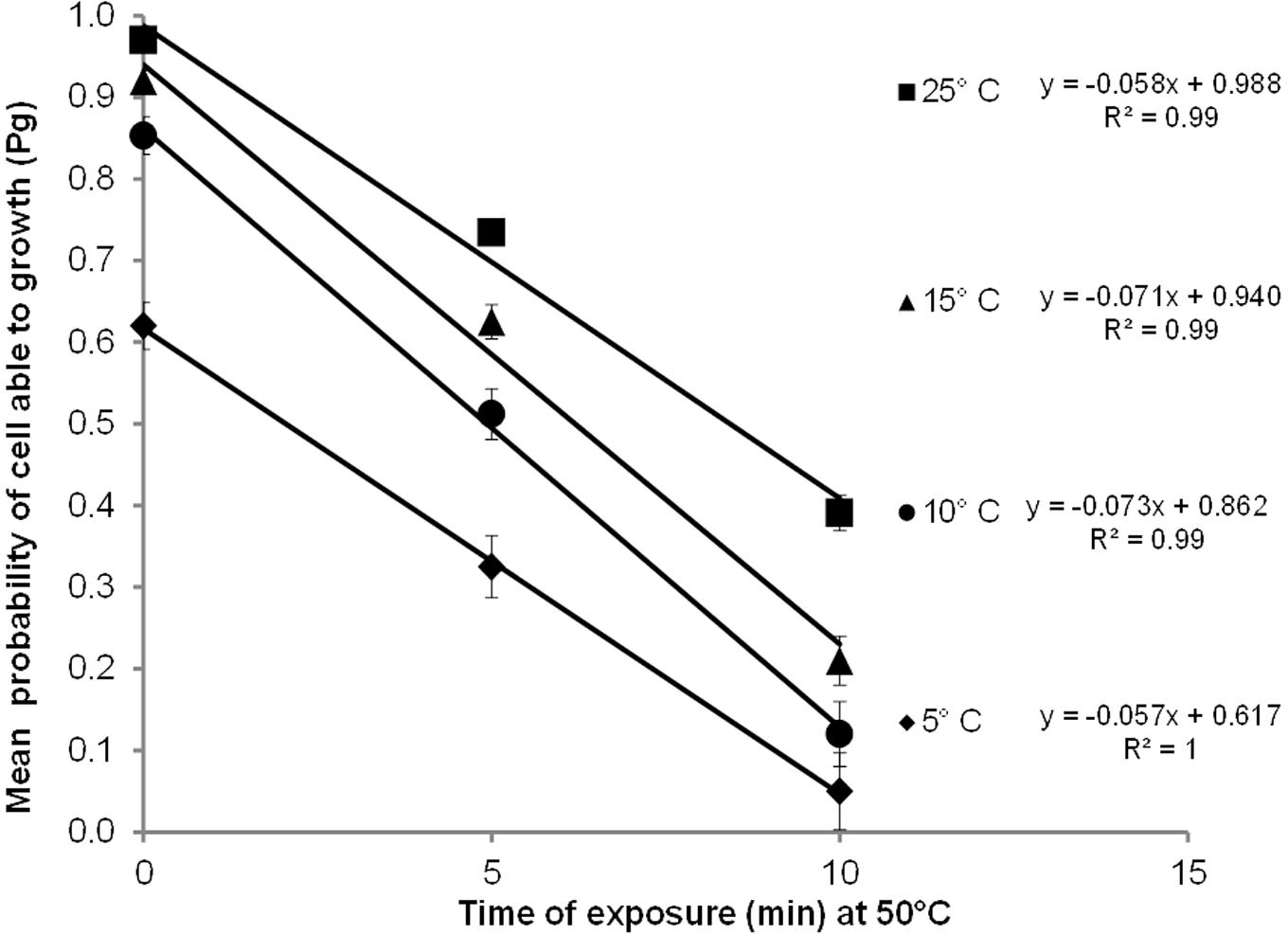
FIGURE 2. Probability of growth (Pg) of C. sakazakii as a function of exposure time at 50°C by 0, 5, and 10 min and growth temperatures of 5, 10, 15, and 25°C. The continuous black lines, for which equations are shown in the figure, show the relationships found in our experiments.
We found an explicit linear relationship (Figure 2) between Pg and the heat treatment at the three different growth temperatures with a high coefficient of determination (R2 ≥ 0.99). We also observed variability in the Pg within the same time of treatment. This variability increased when the heat treatment increased and the growth temperature decreased (presented in the Figure 2 as bar of standard deviation). However, the standard deviation come from 10 observations, that the authors consider not enough to result in robust results and to affirm that the probability of growth is more variable when growth is less probable, hence, we continued working with the mean Pg, but this observation can be important for further research.
Table 3 describes the estimated parameters of the distribution fitted to the experimental data and the variables used in Monte Carlo simulations. The best fitted distribution (according to X2, A–D, or K–S test, data not shown) to the experimental lag phases and specific growth rate were gamma and normal, respectively.
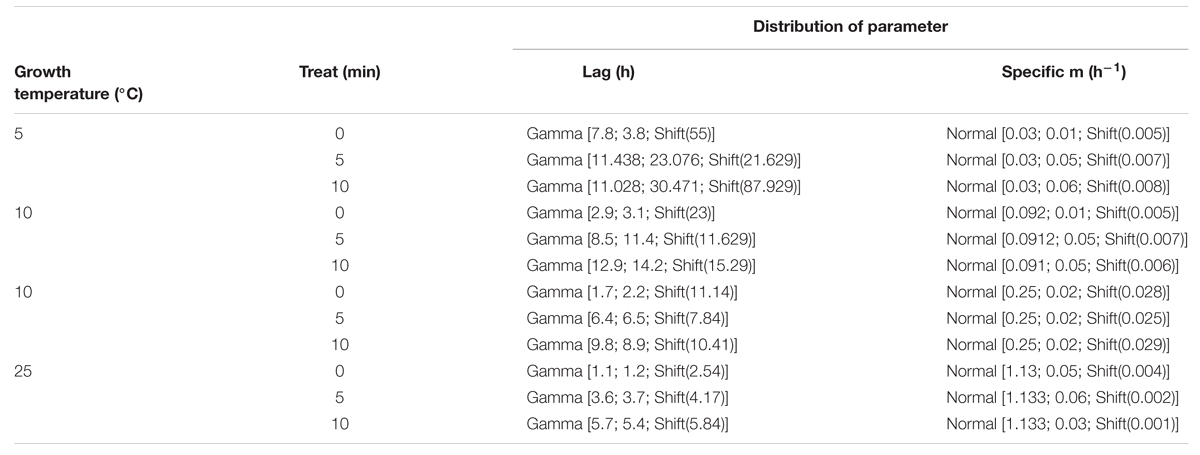
TABLE 3. Incubation temperature, duration of heat treatments, fitted distribution and parameters used to simulate growth of untreated and heat treated cells of a single cell of C. sakazakii.
Figure 3 shows the fitted distributions together with the density data for λ and μmax of one cell based on the stochastic growth model (Eq. 2) in TSB at 5 (A), 10 (B), 15 (C), and 25°C (D) and simulated using Monte Carlo approach with 10.000 iterations and the deterministic growth model of Baranyi and Roberts (1994) fitted to data of C. sakazakii in PIF. From the stochastic approach it can be observed that the higher the heat treatment, the higher the dispersion of the data [from right (3) to the left (1)]. This dispersion decreased as the growth temperature increased [from 5°C (A) to 25°C (D], indeed deterministic and stochastic approaches were similar at 25°C (Figures 3D1–D3). In addition, it can be observed that the tendency of the fitted model is situated in the average of the stochastic outputs. For example, at 5°C, the stochastic growth model predicted that the dangerous dose level of 1000 CFU/ml was reached at 250 min (discontinuous black line Figure 3A2), while the deterministic approach indicated that this concentrations was reached after 490 min (discontinuous gray line Figure 3A2) from a single survivor that was heat shocked at 50°C for 5 min and growing at 5°C. A similar tendency was observed in the simulations of an inoculum size of 50 cells (results not shown). In addition, it can be observed in the vertical discontinuous gray line in Figure 3B2, the differences in the concentrations at the time 190 min (when deterministic model reaches 1000 CFU/ml), the stochastic growth model at the same time can have concentrations ranging from 0 to 107 CFU/ml.
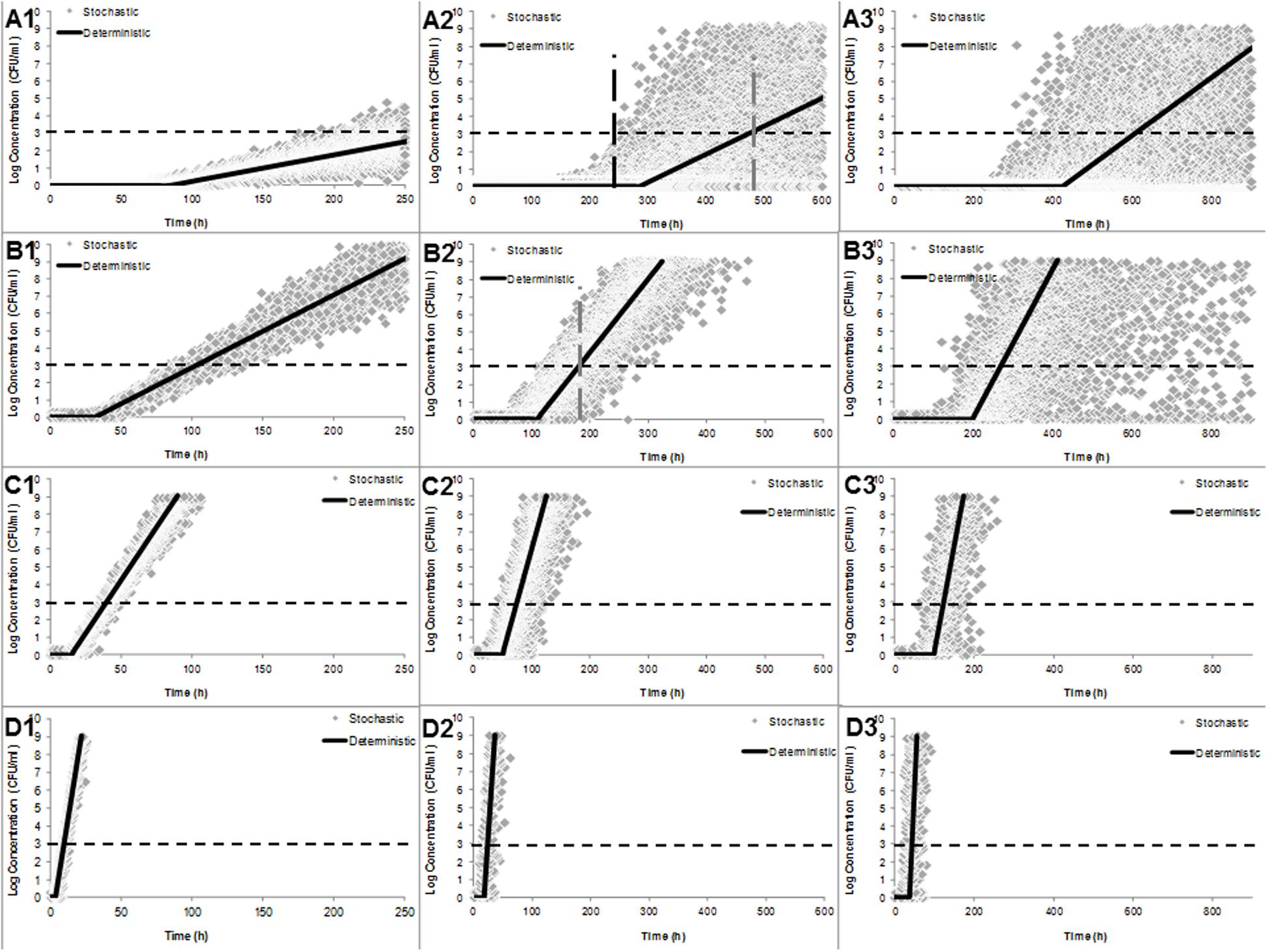
FIGURE 3. Simulation output of stochastic (gray diamonds) and deterministic (continuos black lines) growth models of an individual C. sakazakii at 5 (A), 10 (B), 15 (C), and 25 °C (D) and treated with 50°C by 0, 5, and 10 min (numbers 1, 2, and 3, respectively). Discontinuous vertical lines (A2) represent the time at which deterministic and stochastic models reach the concentration of 103 CFU/ml. Stochastic predictions for the growth of a single cell using Monte Carlo simulation with 10,000 iterations.
The comparison between stochastic and deterministic approaches showed a relevant difference between the probabilities of illness determined by both approaches. For example, the deterministic approach predicted (using Eq. 3) a probability of illness of 0.144 for a dose of 1000 CFU/ml, in contrast, the probabilistic approach predicts a probability of illness ranging from 0 to 0.285 for untreated cells, 0 to 0.071 for cell treated for 5 min at 50°C and from 0 to 0.002 (95% of the cases) when deterministic growth model reached 1000 CFU/ml (Concentrations are taken from Figures 3C1–C3, respectively). Note that for every case the time to reach 1000 CFU/h was different.
As expected the previous finding was affected by growth conditions and previous history of the cells (heat treatment intensity). The higher the previous heat treatment the lower the probability of illness, indeed the predicted mean probability of illness in this conditions was close to 0 (0.0006) as shows Figure 4, in contrast, untreated cells showed the higher mean probability of illness (0.165), while heat treated cells for 5 min had a mean probability of 0.003. These estimation are affected directly by the concentration of cells at the time of consumption, in this example, after 50 h of keeping the PIF at 15°C, the stochastic growth model of untreated cells (Figure 3C1–C3) predicted concentration ranged from 2282 to 32205 cells/ml (95% CI) while heat treated cells by 50°C for 10 min there were no growth (1 cell) to 3 cells/ml (95% CI), in the other hand, at 5 min of heat treatment the concentration observed was 1 to 873 cells/ml (95% CI).
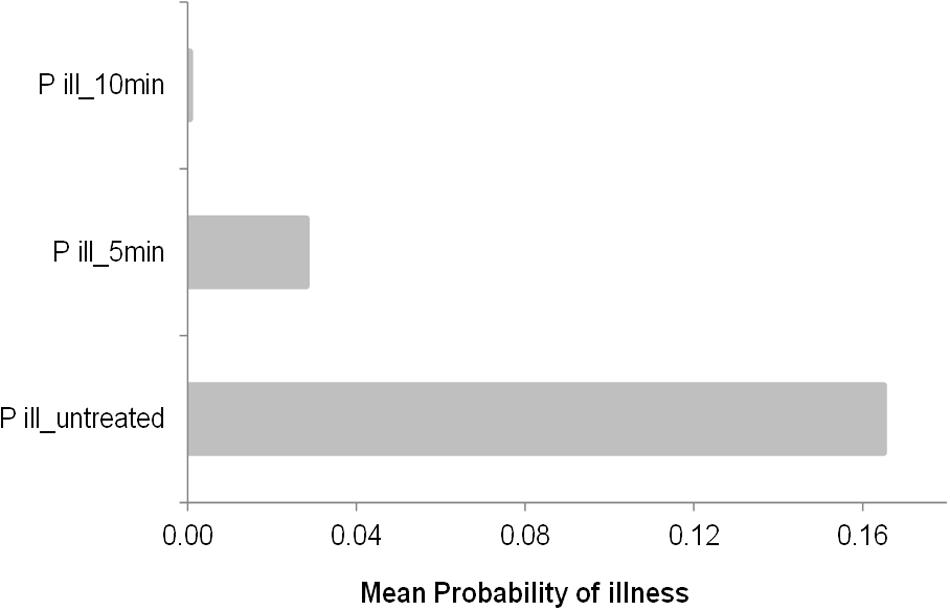
FIGURE 4. Mean probability of illness by consumption of PIF contaminated with a concentration of cells (taken from Figures 3C1–C3, stochastic approach at 50 h of incubation at 15°C of a single cell survivor to 50°C for 5 and 10 min). The control is also showed as untreated cells and the prevalence is included as a uniform distribution between 3 and 30%.
In contrast, deterministic growth model predicted a concentration after 50 h at 15°C of 16384 cells/ml for untreated cells, 2 and 1 cells/ml for cells heat treated at 50°C for 5 and 10 min, respectively. These concentrations resulted in probability of illness of 0.165, 0.0007 and 0.0003, respectively.
Figure 5 shows the mean probability of illness by consumption of PIF contaminated with an initial inoculum of 1 (Figure 5A) and 50 (Figure 5B) cells growing at four different temperatures with the input of the stochastic growth model at the concentrations when the deterministic model reached 1000 CF/ml (Figure 3). It can be observed that the effect of the temperature and the inoculum size in the probability of illness. As expected the higher inoculum size and growth temperature were, the higher the mean probability of illness. The probability of illness from initial inoculum size of 1 cell were below 0.2 in all the cases and for inoculum size of 50 cells the probability of illness were, in most of the cases, above 0.7; the probability of illness was 0.68 and 0.69 by consumption of PIF with cell survivor to 50°C by 5 and 10 min, respectively (Figure 5B).
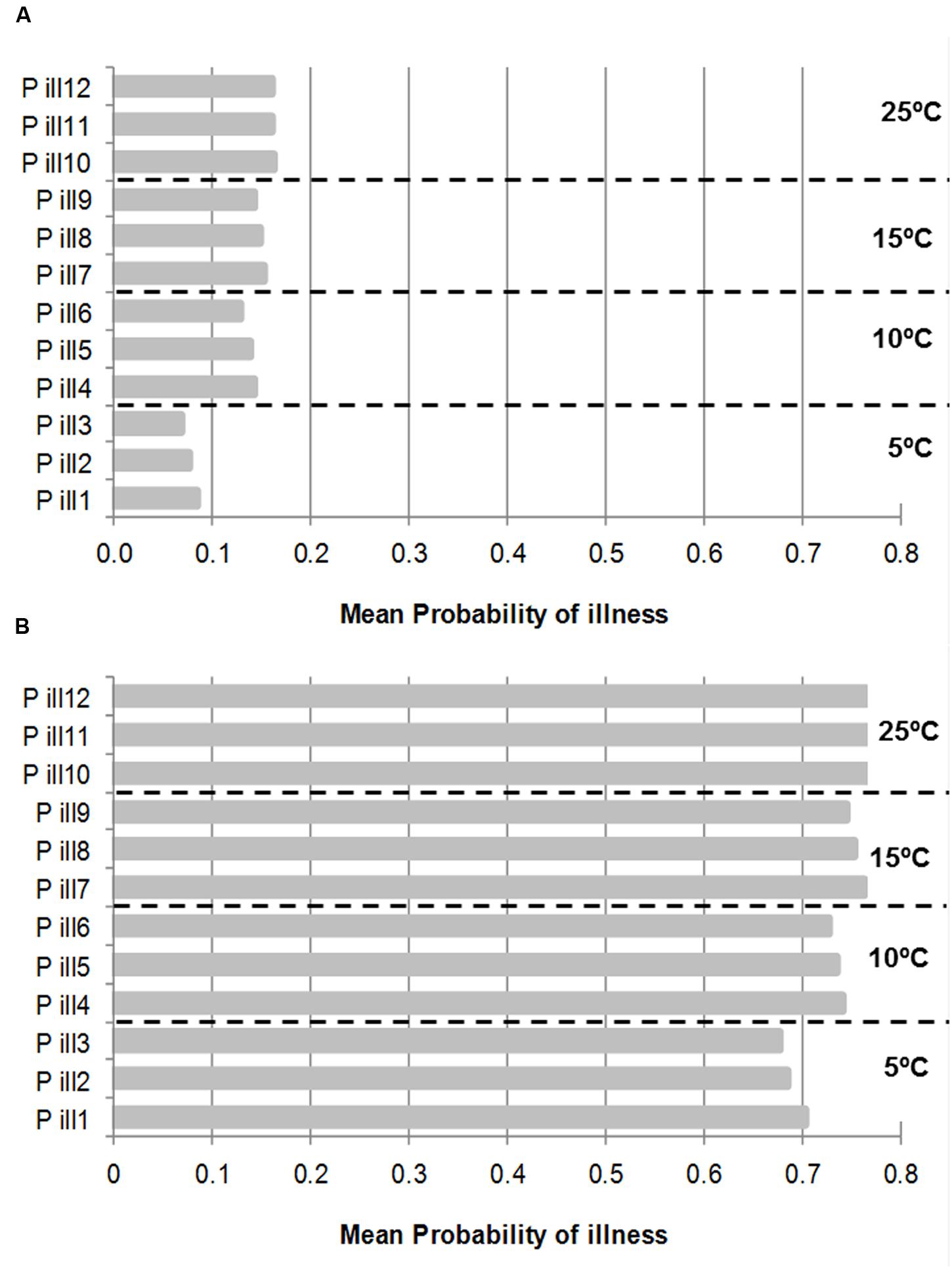
FIGURE 5. Mean Probability of illness by consumption of PIF contaminated with an initial inoculum of 1 cell (A) and 50 (B) cells and growth at four different temperatures. Each temperature has three probability of illness according to cells treated with 50°C by 0 (P ill 1), 5 min (P ill 2), and 10 min (P ill 3) and so on, respectively. The concentration to estimate the probabilities were taken from stochastic growth model using the cut-off point when the deterministic growth model reached 1000 CFU/ml (See Figure 3).
In contrast, it can be observed that there were no differences among untreated or heat treated probabilities of illness for the two times considered (5 and 10 min) within the same growth temperature and inoculum size. To note that, to estimate the probability of illness it was used the output of the stochastic growth model but when the deterministic model reached 1000 CFU/ml, in this point of cut-off, the distribution of cells of treated and untreated cells were similar (See Figure 3).
Discussion
A major goal of scientists, industry, public health, and regulatory authorities is to control pathogenic microorganisms and improve food products hygiene and safety within a country and internationally (Sofos and Geomaras, 2010). However, in reality, it would be impossible to measure all parameters and conditions under which food pathogens, such as Cronobacter spp. can growth. Deterministic models for the behavior of microorganism are not effective in describing the behavior of small microbial populations or individual cells (Baranyi, 1998), since they ignore the observed variability between individual cells (Nauta, 2000; Koutsoumanis, 2008; Niven et al., 2008; Métris et al., 2008; Aguirre et al., 2009; Lianou and Koutsoumanis, 2011; Cuevas-Muñoz et al., 2013; Aspridou and Koutsoumanis, 2015). Stochastic modeling approaches seem to solve the above problem since they are able to deal with more “realistic” food contamination events with few cells (Koutsoumanis, 2008).
In this study we compare both lag phases, estimated by deterministic and stochastic approaches of two inoculum sizes (individual single cell and fifty cells) of untreated or sublethally heat treated C. sakazakii at four temperatures and the effect of both approaches on the probability of illness was assessed.
We observed considerable variability in the lag phase in our experiments (Figure 1), with a remarkable influence of the previous heat shock, the inoculum size and the growth temperatures (Table 2); in addition, we observed an effect of the heat shock and growth temperature on the probability (Pg) of cells able to growth (Figure 2). Both findings are in agreement with similar results in previous studies (Koutsoumanis, 2008; Métris et al., 2008; Aguirre et al., 2011, 2013; Lianou and Koutsoumanis, 2011). Miled et al. (2011) confirmed that the variability of individual cell lag times has a major impact on the growth of Cronobacter; however, the microorganism was subjected to dry stress, rather than mild heating. Recently, Xu et al. (2015) also observed that lag phase of individual C. turicensis cells was variable after mild heat treatment. They stated that an increase in the stress on cells resulted in increases in lag variability, as mentioned also by other authors (Stephens et al., 1997; Smelt et al., 2002; Métris et al., 2006; Rasch et al., 2007).
Generally, the specific growth rate in TSB (Table 2) in this study is in agreement with previous studies (Nazarowec-White and Farber, 1997; Iversen et al., 2004; Kandhai et al., 2004; Ghassem et al., 2011; Miled et al., 2011; Xu et al., 2015), the higher the growth temperature, the higher the growth rate.
In the published scientific literature, many researchers have characterized and explained the reason of kinetic variability from a biological point of view. Since this aspect is beyond the scope of this study, we direct the readers to different references for further information on the explanation of biological variability (Nauta, 2000; Robinson et al., 2001; Korobkova et al., 2004; Stewart et al., 2005; Avery, 2006; Lianou et al., 2006; Koutsoumanis and Lianou, 2013; Jackson et al., 2014; Huertas et al., 2015). However, we point out the information provided by Pin and Baranyi, (2006) who mentioned the presence of fast-growing cells and their subsequent subpopulations which have a dominant effect on the growth of the total culture (Pin and Baranyi, 2006), denoting the presence of different types of subpopulations, in this case, sensitive, less sensitive and resistant to environmental stressor, which can be supported by the several D values and its variation reported in the literature (Huertas et al., 2015). The presence of different types of cells will affect to the adaptation to the environmental condition, in the recovery and the ability to initiate growth. Also, it is important to mention that, not all cells within a population have the same probability to grow which is affected by the inoculum size (Koutsoumanis, 2008) and the growth temperature (Aguirre et al., 2013), which are expressed as genotype (Noma et al., 2006) or non-genotypic differences (den Besten et al., 2006), which is one of the biggest assumptions used in predictive microbiology models when survivors are counted at optimum growth conditions rather than at the temperature of the “real growth conditions”, which is demonstrated here. Although other factors may have a large impact on the exposure to Cronobacter spp., the initial level of the micro-organism in PIF is one of the key to its impact on public health and thus insight in this level is important for governmental risk managers as well as for PIF manufacturers (Reij et al., 2009).
We found that a gamma distribution described well the distribution of lag times whereas a normal distribution described well the distribution of μmax for both heat stressed and unstressed C. sakazakii cells (Table 3). These findings are in agreement with those reported by others authors (Métris et al., 2008; Aguirre et al., 2013; Koutsoumanis and Lianou, 2013; Xu et al., 2015). In conditions of very low contamination, individual cell variability can have an important impact on pathogen growth (Guillier and Augustin, 2006). Knowing how their long term presence in PIF, and subsequent stress, affect the variability of single-cell lag times is important in assessing the risk of cell recovery and growth in reconstituted milk, where low numbers of stressed cells of pathogenic bacteria may be distributed among PIF samples (Miled et al., 2011) or may enter into the infant formula post preparation, during the manipulation or storage (Reich et al., 2010; Kucerova et al., 2011; Parra et al., 2015). Moreover, the heterogeneous distribution of Cronobacter cells in PIF makes this even more the case. In a real situation, a distribution of the inoculum size can be observed in a batch of food, which markedly influences public health risk. This heterogeneity can be due to the structural heterogeneity of the food matrix, incomplete mixing, incidental (post-processing) contamination, and/or localized microbial growth (Jongenburger et al., 2011). It is critical to take into account variability in microbial response because the credibility of a microbial risk assessment is based on its ability to consider the variability and uncertainty of each parameter involved in estimating final risk (Delignette-Muller and Rosso, 2000). The presence of a few atypical cells with short lag phase can unexpectedly shorten population lag time (Baranyi, 2002), which may shorten food shelf-life or, if pathogens are present in the food, increase the health risk to consumers.
The probabilistic approach proposed by Koutsoumanis and Lianou (2013) and replicated in the present study (Figure 3) is a stochastic growth curve in which the number of cells in the population at any time is a probability distribution based on a Monte Carlo simulation for describing the variability of parameters. For example, the number of cells in a microcolony generated from a single untreated cell after 100 h of growth at 10°C (Figure 3B1) can be either 155 (1st percentile) or 5252 (99th percentile); in contrast the deterministic model predicts a number of cell in average of 777, or from a heat shocked single cell (50°C for 5 min, Figure 3B2) growth at 10°C, the number of cells can be either 1 (1st percentile) or 76 (99th percentile), while the deterministic model predict no growth (1 cell with no duplication yet). The above variation in concentration of Cronobacter spp. at the time of consumption can affect the response of the host, however, in the case of this pathogen several aspects need more work to establish a proper dose-response model for premature newborns.
Here, it is easy to understand and visualize the impact of the variability of the kinetic parameters in the estimation of the concentration at certain time of growth and the impact between stochastic and deterministic approaches in our estimations, indeed, if we graph an imaginary line (Figure 3A2) we can observe that after 250 min the stochastic model predicted a concentration of 1000 CFU/ml while in the deterministic model, this concentration is reached after 490 min from a single cell growth sublethaly injured at 50°C for 5 min and grown at 10°C. Hence, the impact of individual cell variability on the growth of Cronobacter as affected by inoculum size, growth temperature, and the probability of growth should be taken into account, especially when errors in feeding bottle-preparation practices, such as improper holding temperatures, may lead to growth of the pathogen to a critical cell level (Miled et al., 2011). In addition, to better estimate risk (Aguirre et al., 2013) the above variability should be used in a dose response model, in contrast to providing the mean average probability of illness (Figures 4 and 5), however, care should be taken with the effect of the inoculum size, because even the best studied host–pathogen systems, the exact relation between the inoculum size and the probability of disease is unclear (Cornforth et al., 2015).
Current manufacturing processes are not capable of producing a sterile PIF (Kent et al., 2015), in addition, intrinsic contamination of PIF can occur at any stage during manufacture at the factory before distribution of product for retail; also, extrinsic contamination of product can occur after the factory container is first opened by the user; at any stage of reconstitution through the use of contaminated water, utensils, work surfaces; at the time of feeding (e.g., using contaminated feeding bottles or enteral tubing with existing biofilm); or because of inappropriate storage conditions (e.g., poor refrigeration or storage for too long at room temperature) (Kalyantanda et al., 2015).
In this study, we established the importance of assessing the impact of some factors (heat treatment, inoculum size, growth temperature) on the variability response of Cronobacter and its impact in the probability of illness by PIF consumption contaminated with it, however, several aspects need more work and scrutiny before being conclusive and able to us to performance a sensitivity analysis (Poschet et al., 2004; Membré et al., 2008; Ellouze et al., 2010). Additionally, the stress response factors identified previously in Cronobacter species, such as heat-shock, cold-stresses, survival in dry conditions, water activity (aw), and pH need to be re-assessed using novel approaches that are currently under development (Yan and Fanning, 2015).
Conclusion
Extensive variation of lag phase was observed for C. sakazakii. The inoculum size also affected the lag phase, as the inoculum size decreased the mean lag phase and its variability increased. The μmax was primarily affected by growth conditions and not by inoculum size. Results of this study highlight the risks associated with mean estimation rather stochastic approaches. Furthermore, the information provided here demonstrates that the effect of the growth environment and previous stress on the variability of the kinetic behavior of the microorganism survivors to a treatment is not negligible, and should, therefore, be characterized and taken into account in the development of stochastic approaches utilized in predictive microbiology and microbial risk assessment for food safety plans.
Author Contributions
JP-F: He is an expert in Cronobacter spp., he was involved dose response model assess and risk assessment. VJ: Expert in food safety and predictive microbiology, he support the growth model approach. GF: Expert in food microbiology and predict microbiology, he was involved in experimental designing. JA: Risk assessment and predictive microbiology approach in this work and data processing.
Funding
This work was partially supported by DIUBB Chile, project 143720 and the Program Consolider CARNISENUSA Spain CSD2007-0016.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgment
The authors wish to thank William Chalmers for technical assistance with the manuscript.
References
Agence Francaise de Securite Sanitaire Des Aliments [AFSSA] (2005). Hygiene Recommendations for the Preparation, Handling and Storage of Feeding Bottles. Available at: https://www.anses.fr/fr/system/files/MIC-Ra-BIB.pdf
Aguirre, J., Bravo, C., Ordóñez, J. A., and García de Fernando, G. (2012). The poisson distribution is applied to improve the estimation of individual cell and micropopulation lag phases. Advan. Microbiol. 2, 146–161. doi: 10.4236/aim.2012.22020
Aguirre, J. S., González, A., Özçelik, N., Rodríguez, M. R., and Garcia de Fernando, G. D. (2013). Modeling the Listeria innocua micropopulation lag phase and its variability. Int. J. Food Microbiol. 164, 60–69. doi: 10.1016/j.ijfoodmicro.2013.03.003
Aguirre, J. S., Pin, C., Rodriguez, M. R., and Garcia de Fernando, G. D. (2009). Analysis of the variability in the number of viable bacteria after mild heat treatment of food. Appl. Environ. Microbiol. 75, 6992–6997. doi: 10.1128/AEM.00452-09
Aguirre, J. S., Rodriguez, M. R., and García Fernando, G. D. (2011). Effects of electron beam irradiation on variability of the number of survivors and on duration of lag phase of four food-borne organisms. Int. J. Food Microbiol. 149, 236–246. doi: 10.1016/j.ijfoodmicro.2011.07.003
Alonso, A., Molina, I., and Theodoropoulos, C. (2014). Modeling bacterial population growth from stochastic single-cell dynamics. Appl. Environ. Microbiol. 80, 5241–5253. doi: 10.1128/AEM.01423-14
Aspridou, Z., and Koutsoumanis, K. (2015). Individual cell heterogeneity as variability source in population dynamics of microbial inactivation. Food Microbiol. 45, 216–221. doi: 10.1016/j.fm.2014.04.008
Avery, S. V. (2006). Microbial cell individuality and the underlying sources of heterogeneity. Nat. Rev. Microbiol. 4, 577–587. doi: 10.1038/nrmicro1460
Baranyi, J. (1998). Comparison of stochastic and deterministic concepts of bacterial lag. J. Theor. Biol. 192, 403–408. doi: 10.1006/jtbi.1998.0673
Baranyi, J. (2002). Stochastic modeling of bacterial lag phase. Int. J. Food Microbiol. 73, 203–206. doi: 10.1016/S0168-1605(01)00650-X
Baranyi, J., and Pin, C. (1999). Estimating bacterial growth parameter by means of detection times. Appl. Environ. Microbiol. 65, 732–736.
Baranyi, J., and Roberts, T. A. (1994). A dynamic approach to predicting bacterial growth in food. Int. J. Food Microbiol. 23, 277–294. doi: 10.1016/0168-1605(94)90157-0
Barron, J. C., and Forsythe, S. J. (2007). Dry stress and survival time of Enterobacter sakazakii and other Enterobacteriaceae in dehydrated powdered infant formula. J. Food Prot. 70, 2111–2117.
Block, C., Peleg, O., Minster, N., Simhon, A., Arad, I., and Shapiro, M. (2002). Cluster of neonatal infections in Jerusalem due to unusual biochemical variant of Enterobacter sakazakii. Eur. J. Clin. Microbiol. Infect. Dis. 21, 613–616. doi: 10.1007/s10096-002-0774-5
Bowen, A. B., and Braden, C. R. (2006). Invasive Enterobacter sakazakii disease in infants. Emerg. Infect. Dis. 12, 1185–1189. doi: 10.3201/eid1208.051509
Cawthorn, D. M., Botha, S., and Witthuhn, C. (2008). Evaluation of different methods for the detection and identification of Enterobacter sakazakii isolated from South African infant formula milks and the processing environment. Int. J. Food Microbiol. 127, 129–138. doi: 10.1016/j.ijfoodmicro.2008.06.024
Chap, J., Jackson, P., Siqueira, R., Gaspar, N., Quintas, C., Park, J., et al. (2009). International survey of Cronobacter sakazakii and other Cronobacter spp. in follow up formulas and infant foods. Int. J. Food Microbiol. 136, 185–188. doi: 10.1016/j.ijfoodmicro.2009.08.005
Clark, N. C., Hill, B. C., O’Hara, C. M., Steingrimsson, O., and Cooksey, R. C. (1990). Epidemiologic typing of Enterobacter sakazakii in two neonatal nosocomial outbreaks. Diagn. Microbiol. Infect. Dis. 13, 467–472. doi: 10.1016/0732-8893(90)90078-A
Cornforth, D. M., Matthews, A., Brown, S. P., and Raymond, B. (2015). Bacterial cooperation causes systematic errors in pathogen risk assessment due to the failure of the independent action hypothesis. PLoS Pathog. 11:e1004775. doi: 10.1371/journal.ppat.1004775
Cuevas-Muñoz, M., Guevara, L., Aznar, A., Martínez, A., Periago, P. M., and Fernández, P. S. (2013). Characterization of the resistance and the growth variability of Listeria monocytogenes after high hydrostatic pressure treatments. Food Control. 29, 409–415. doi: 10.1016/j.foodcont.2012.05.047
Delignette-Muller, M. L., and Rosso, L. (2000). Biological variability and exposure assessment. Int. J. Food Microbiol. 58, 203–212. doi: 10.1016/S0168-1605(00)00274-9
den Besten, H. M., Mataragas, M., Moezelaar, R., Abee, T., and Zwietering, M. H. (2006). Quantification of the effects of salt stress and physiological state on thermotolerance of Bacillus cereus ATCC 10987 and ATCC 14579. Appl. Environ. Microbiol. 72, 5884–5894. doi: 10.1128/AEM.00780-06
Drudy, D., Mullane, N. R., Quinn, T., Wall, P. G., and Fanning, S. (2006). Enterobacter sakazakii: an emerging pathogen in powdered infant formula. Clin. Infect Dis. 42, 996–1002. doi: 10.1086/501019
Dupont, C., and Augustin, J. C. (2009). Influence of stress on single-cell lag time and growth probability for Listeria monocytogenes in half fraser broth. Appl. Environ. Microbiol. 75, 3069–3076. doi: 10.1128/AEM.02864-08
Elfwing, A., LeMarc, Y., Baranyi, J., and Ballagi, A. (2004). Observing growth and division of large numbers of individual bacteria by image analysis. Appl. Environ. Microbiol. 70, 675–678. doi: 10.1128/AEM.70.2.675-678.2004
Ellouze, M., Gauchi, J.-P., and Augustin, J.-C. (2010). Global sensitivity analysis applied to a contamination assessment model of Listeria monocytogenes in cold smoked salmon at consumption. Risk Anal. 30, 841–852. doi: 10.1111/j.1539-6924.2010.01380.x
European Commission [EC] (2002). Risk Assessment of Food Borne Bacterial Pathogens: Quantitative Methodology Relevant for Human Exposure Assessment. Preliminary report in: HEALTH & CONSUMER PROTECTION DIRECTORATE-GENERAL. [Internet Document]. Available at: http://ec.europa.eu/food/fs/sc/ssc/out252_en.pdf [accessed December 1, 2015].
Farber, J. M. (2004). Enterobacter sakazakii- new foods for thought? Lancet 363, 5–6. doi: 10.1016/S0140-6736(03)15244-0
Farmer, J. J., Asbury, M. A., Hickman, F. W., and Brenner, D. J. (1980). Enterobacter sakazakii: a new species of “Enterobacteriaceae” isolated from clinical specimens. Int. J. Syst. Bacteriol. 30, 569–584. doi: 10.1099/00207713-30-3-569
Food and Agriculture Organization of the United Nations and the World Health Organization (FAO/WHO). (2004). Enterobacter sakazakii and Other Organisms in Powdered Infant Formula. Meeting Report in: MRA Series 6. [Internet Document] Available at: http://www.fao.org/3/a-y5502e.pdf [accessed November 07, 2015].
Food and Agriculture Organization of the United Nations and the World Health Organization (FAO/WHO). (2006). Enterobacter sakazakii and Salmonella in Powdered Infant Formula: Meeting Report in: Mra Series 10. [Internet Document]. Available at: ftp://ftp.fao.org/docrep/fao/009/ a0707e/a0707e00.pdf [accessed December 1, 2015].
Food and Agriculture Organization of the United Nations and the World Health Organization (FAO/WHO). (2008). Enterobacter sakazakii (Cronobacter spp.) in Powdered Follow up Formulae: Meeting report in: MRA series 15. [Internet Document]. Available at: http://www.fao.org/fileadmin/templates/agns/pdf/jemra/mra15_sakazaki.pdf [accessed December 9, 2015].
Francois, K., Devlieghere, F., Standaert, A. R., Geeraerd, A. H., van Impe, J. F., and Debevere, J. (2003). Modelling the individual lag phase. Isolating single cells: protocol development. Lett. Appl Microbiol. 37, 26–30. doi: 10.1046/j.1472-765X.2003.01340.x
Friedemann, M. (2007). Enterobacter sakazakii in food and beverages (other than infant formula and milk powder). Int. J. Food Microbiol. 116, 1–10. doi: 10.1016/j.ijfoodmicro.2006.12.018
Ghassem, M., Babji, A. S., Forsythe, S. J., and Norrakiah, A. S. (2011). Growth and survival of Cronobacter species as measured by media performance. Int. Food. Res. J. 18, 367–372.
Guillaume-Gentil, O., Sonnard, V., Kandhai, M. C., Marugg, J. D., and Joosten, H. (2005). A simple and rapid cultural method for detection of Enterobacter sakazakii in environmental samples. J. Food Prot. 68,k64–69.
Guillier, L., and Augustin, J. C. (2006). Modelling the individual cell lag time distributions of Listeria monocytogenes as a function of the physiological state and the growth conditions. Int. J. Food Microbiol. 111, 241–251. doi: 10.1016/j.ijfoodmicro.2006.05.011
Guillier, L., Pardon, P., and Augustin, J. C. (2005). Influence of stress on individual lag time distributions of Listeria monocytogenes. Appl. Environ. Microbiol. 71, 2940–2948. doi: 10.1128/AEM.71.6.2940-2948.2005
Haas, C. N., Rose, J. B., and Gerba, C. P. (1999). Quantitative Microbial Risk Assessment. Nueva York, NY: John Wiley and Sons Inc, 464.
Herriman, R. (2015). SanCor Infant Formula Recalled Due to Cronobacter sakazakii Contamination. Outbreak News Today. [Internet Document]. Available at: http://outbreaknewstoday.com/sancor-infant-formula-recalled-due-to-cronobacter-sakazakii-contamination-70996/ [accessed December 9, 2015].
Himelright, I., Harris, E., Lorch, V., Anderson, M., Jones, T., Craig, A., et al. (2002). Enterobacter sakazakii infections associated with the use of powdered infant formula-Tennessee, 2001. MMWR Morb. Mortal. Wkly Rep. 51, 297–300.
Holý, O., and Forsythe, S. J. (2014). Cronobacter spp. as emerging causes of health care associated infection. J. Hosp. Infect. 86, 169–177. doi: 10.1016/j.jhin.2013.09.011
Huertas, J. P., Álvarez-Ordóñez, A., Morrissey, R., Ros-Chumillas, M., Esteban, M. D., Maté, J., et al. (2015). Heat resistance of Cronobacter sakazakii DPC 6529 and its behavior in reconstituted powdered infant formula. Food Res. Int. 69, 401–409. doi: 10.1016/j.foodres.2015.01.010
Hunter, C. J., and Bean, J. F. (2013). Cronobacter: an emerging opportunistic pathogen associated with neonatal meningitis, sepsis and necrotizing enterocolitis. J. Perianatol. 33, 581–585. doi: 10.1038/jp.2013.26
Hurrell, E., Kucerova, E., Loughlin, M., Caubilla-Barron, J., Hilton, A., Armstrong, R., et al. (2009). Neonatal enteral feeding tubes as loci for colonisation by members of the Enterobacteriaceae. BMC Infect. Dis. 9:146. doi: 10.1186/1471-2334-9-146
Iversen, C., and Forsythe, S. J. (2003). Risk profile of Enterobacter sakazakii, an emergent pathogen associated with infant milk formula. Trends Food Sci. Technol. 14, 443–454. doi: 10.1016/S0924-2244(03)00155-9
Iversen, C., and Forsythe, S. J. (2004). Isolation of Enterobacter sakazakii and other Enterobacteriaceae from powdered infant formula milk and related products. Food Microbiol. 21, 771–776. doi: 10.1016/j.fm.2004.01.009
Iversen, C., Lane, M., and Forsythe, S. (2004). The growth profile, thermotolerance, and biofilm formation of Enterobacter sakazakii grown in infant formula milk. Lett. Appl. Microbiol. 28, 378–382. doi: 10.1111/j.1472-765X.2004.01507.x
Jackson, E. E., Sonbol, H., Masood, N., and Forsythe, S. J. (2014). Genotypic and phenotypic characteristics of Cronobacter species, with particular attention to the newly reclassified species Cronobacter helveticus, Cronobacter pulveris, and Cronobacter zurichensis. Food Microbiol. 44, 226–235. doi: 10.1016/j.fm.2014.06.013
Jongenburger, I., Reij, M., Boer, E., Gorris, L., and Zwietering, M. (2011). Random or systematic sampling to detect a localised microbial contamination within a batch of food. Food Control. 22, 1448–1455. doi: 10.1016/j.foodcont.2011.03.009
Kalyantanda, G., Shumyak, L., and Archibald, L. K. (2015). Cronobacter species contamination of powdered infant formula and the implications for neonatal health. Front. Pediatr. 3:56. doi: 10.3389/fped.2015.00056
Kandhai, M. C., Reij, M. W., Gorris, L. G. M., Guillaume-Gentil, O., and van Schothorst, M. (2004). Occurrence of Enterobacter sakazakii in food production environments and households. Lancet 363, 39–40. doi: 10.1016/S0140-6736(03)15169-0
Kent, R. M., Fitzgerald, G. F., Hill, C., Stanton, C., and Ross, R. P. (2015). Novel approaches to improve the intrinsic microbiological safety of powdered infant milk formula. Nutrients 7, 1217–1244. doi: 10.3390/nu7021217
Korobkova, E., Emonet, T., Vilar, J. M. G., Shimizu, T. S., and Cluzel, P. (2004). From molecular noise to behavioural variability in a single bacterium. Nature 428, 574–578. doi: 10.1038/nature02404
Koutsoumanis, K. (2008). A study on the variability in the growth limits of individual cells and its effect on the behavior of microbial populations. Int. J. Food Microbiol. 128, 116–121. doi: 10.1016/j.ijfoodmicro.2008.07.013
Koutsoumanis, K., and Lianou, A. (2013). Stochasticity in colonial growth dynamics of individual bacterial cells. Appl. Environ. Microbiol. 79, 2294–2301. doi: 10.1128/AEM.03629-12
Kucerova, E., Joseph, S., and Forsythe, S. J. (2011). The Cronobacter genus: ubiquity and diversity. Qual. Assur. Safety Foods Crops. 3, 104–122. doi: 10.1111/j.1757-837X.2011.00104.x
Lai, K. K. (2001). Enterobacter sakazakii infections among neonates, infants, children, and adults. Case reports and review of the literature. Medicine 80, 113–122.
Lammerding, A., and Todd, E. C. D. (2006). “Microbial food safety risk assessment, chapter 2 at forborne infections and intoxicantions,” in Food Science and Technology, International Series, eds H. P. Riemann and D. O. Cliver (Amsterdam: Elsevier).
Lianou, A., and Koutsoumanis, K. P. (2011). Effect of the growth environment on the strain variability of Salmonella enteric kinetic behaviour. Food Microbiol. 28, 828–837. doi: 10.1016/j.fm.2010.04.006
Lianou, A., and Koutsoumanis, K. P. (2013). Strain variability of the behavior of foodborne bacterial pathogens: a review. Int. J. Food Microbiol. 167, 310–321. doi: 10.1016/j.ijfoodmicro.2013.09.016
Lianou, A., Stopforth, J. D., Yoon, Y., Wiedmann, M., and Sofos, J. N. (2006). Growth and stress resistance variation in culture broth among Listeria monocytogenes strains of various serotypes and origins. J. Food Prot. 69, 2640–2647.
Membré, J. M., Kan-King-Yu, D., de, W., and Blackburn, C. (2008). Use of sensitivity analysis to aid interpretation of a probabilistic Bacillus cereus spore lag time model applied to heat-treated chilled foods (REPFEDs). Int. J. Food Microbiol. 128, 28–33. doi: 10.1016/j.ijfoodmicro.2008.06.029
Métris, A., George, S. M., and Baranyi, J. (2006). Use of optical density detection times to assess the effect of acetic acid on single cell kinetics. Appl. Environ. Microbiol. 72, 6674–6679. doi: 10.1128/AEM.00914-06
Métris, A., George, S. M., Mackey, B. M., and Baranyi, J. (2008). Modeling the variability of single-cell lag times for Listeria innocua populations after sublethal and lethal heat treatments. Appl. Environ. Microbiol. 74, 6949–6955.
Métris, A., Le Marc, Y., Elfwing, A., Ballagi, A., and Baranyi, J. (2005). Modelling the variability of lag times and the first generation times of single cells of E. coli. Int. J. Food Microbiol. 100, 13–19. doi: 10.1016/j.ijfoodmicro.2004.10.004
Miled, R. B., Guillier, L., Neves, S., Augustin, J. C., Colin, P., and Gnanou Besse, N. (2011). Individual cell lag time distributions of Cronobacter (Enterobacter sakazakii) and impact of pooling samples on its detection in powdered infant formula. Food Microbiol. 28, 648–655. doi: 10.1016/j.fm.2010.08.005
Mittal, R., Wang, Y., Hunter, C., Gonzalez-Gomez, I., and Prasadarao, N. (2009). Brain damage in newborn rat model of meningitis by Enterobacter sakazakii: a role for outer membrane protein A. Lab. Invest. 89, 263–277. doi: 10.1038/labinvest.2008.164
Nauta, M. J. (2000). Separation of uncertainty and variability in quantitative microbial risk assessment models. Int. J. Food Microbiol. 57, 9–18. doi: 10.1016/S0168-1605(00)00225-7
Nazarowec-White, M., and Farber, J. M. (1997). Incidence, survival and growth of Enterobacter sakazakii in infant formula. J. Food Prot. 5, 226–230.
Niven, G. W., Morton, J. S., Fuks, T., and Mackey, B. M. (2008). Influence of environmental stress on distributions of times to first division in Escherichia coli populations, as determined by digital-image analysis of individual cells. Appl. Environ. Microbiol. 74, 3757–3763.
Noma, S., Kajiyama, D., Igura, N., Shimoda, M., and Hayakawa, I. (2006). Mechanisms behind tailing in the pressure inactivation curve of a clinical isolate of Escherichia coli O157:H7. Int. J. Food Microbiol. 109, 103–108. doi: 10.1016/j.ijfoodmicro.2006.01.018
O’Brien, S., Healy, B., Negredo, C., Anderson, W., Faning, S., and Iversen, C. (2009). Prevalence of Cronobacter species (Enterobacter sakazakii) in follow-on infant formulae and infant drinks. Lett. Appl. Microbiol. 48, 536–541. doi: 10.1111/j.1472-765X.2009.02562.x
Osaili, T. M., and Forsythe, S. J. (2009). Desiccation resistance and persistence of Cronobacter species in infant formula. Int. J. Food Microbiol. 136, 214–220. doi: 10.1016/j.ijfoodmicro.2009.08.006
Pagotto, F. J., and Farber, J. M. (2009). Cronobacter spp. (Enterobacter sakazakii): advice, policy and research in Canada. Int. J. Food Microbiol. 136, 238–245. doi: 10.1016/j.ijfoodmicro.2009.05.010
Parra, J., Oliveras, L., Rodriguez, A., Riffo, F., Jackson, E., and Forsythe, S. (2015). Risk of Cronobacter Sakazakii contamination in powdered milk for infant nutrition. Rev. Chil. Nutr. 42, 83–89.
Parra-Flores, J., Rodriguez, A., Riffo, F., Arvizu, S., Arias-Rios, E., and Aguirre, J. (2015). Investigation on the factors affecting Cronobacter sakazakii contamination levels in reconstituted powdered infant formula. Front. Pediatr. 3:72. doi: 10.3389/fped.2015.00072
Pin, C., and Baranyi, J. (2006). Kinetics of single cells: observation and modeling of a stochastic process. Appl. Environ. Microbiol. 72, 2163–2169. doi: 10.1128/AEM.72.3.2163-2169.2006
Pina-Pérez, M. C., Benlloch-Tinoco, M., Rodrigo, D., and Martinez, A. (2014). Cronobacter sakazakii inactivation by microwave processing. Food Bioproc. Tech. 7, 821–828. doi: 10.1007/s11947-013-1063-2
Pina-Pérez, M. C., Rodrigo, D., and Martínez, A. (2015). Non-thermal inactivation of Cronobacter Sakazakii in infant formula milk: a review. Crit. Rev. Food Sci. Nutr. doi: 10.1080/10408398.2013.781991 [Epub ahead of print].
Poschet, F., Bernaerts, K., Geeraerd, A. H., Scheerlinck, N., Nicola, B. M., and Van Impe, J. F. (2004). Sensitivity analysis of microbial growth parameter distributions with respect to data quality and quantity by using Monte Carlo analysis. Math Comput. Simul. 65, 231–243. doi: 10.1016/j.matcom.2003.12.002
Rasch, M., Métris, A., Baranyi, J., and Budde, B. B. (2007). The effect of reuterin on the lag time of single cells of Listeria innocua grown on a solid agar surface at different pH and NaCl concentrations. Int. J. Food Microbiol. 113, 35–40. doi: 10.1016/j.ijfoodmicro.2006.07.012
Reich, F., Konig, R., von Wiese, W., and Klein, G. (2010). Prevalence of Cronobacter spp. in a powdered infant formula processing environment. Int. J. Food Microbiol. 140, 214–217. doi: 10.1016/j.ijfoodmicro.2010.03.031
Reij, M., Jongerburger, I., Gkogka, E., Gorris, L., and Zwietering, M. (2009). Perspective on the risk to infants in the Netherlands associated with Cronobacter spp. occurring in powdered infant formula. Int. J. Food Microbiol. 136, 232–237. doi: 10.1016/j.ijfoodmicro.2009.07.011
Robinson, T. P., Aboaba, O. O., Kaloti, A., Ocio, M. J., Baranyi, J., and Mackey, B. M. (2001). The effect of inoculum size on the lag phase of Listeria monocytogenes. Int. J. Food Microbiol. 70, 163–173.
Ross, T., and McMeekin, T. A. (2003). Modeling microbial growth within food safety risk assessments. Risk Anal. 23, 179–197. doi: 10.1111/1539-6924.00299
Schreck, S. (2010). Baby Formula Recalled in Middle East. Food Safety News [Internet Document]. Available at: http://www.foodsafetynews.com/2010/02/baby-formula-recalled-in-middle-east/#.VmhGfXYvdD8 [accessed December 9, 2015].
Simmons, B. P., Gelfand, M. S., Haas, M., Metts, L., and Ferguson, J. (1989). Enterobacter sakazakii infections in neonates associated with intrinsic contamination of a powdered infant formula. Infect. Control Hosp. Epidemiol. 10, 398–401. doi: 10.2307/30144207
Siqueira, R. F., da Silva, N., Junqueira, V., Kajsik, M., Forsythe, S., and Pereira, J. (2013). Screening for Cronobacter species in powdered and reconstituted infant formulas and from equipment used in formula preparation in maternity hospitals. Ann. Nutr. Met. 63, 62–68. doi: 10.1159/000353137
Skandamis, P. N., and Jeanson, S. (2015). Colonial vs. planktonic type of growth: mathematical modeling of microbial dynamics on surfaces and in liquid, semi-liquid and solid foods. Front. Microbiol. 6:1178. doi: 10.3389/fmicb.2015.01178
Smelt, J. P., Otten, G. D., and Bos, A. P. (2002). Modelling the effect of sublethal injury on the distribution of the lag times of individual cells of Lactobacillus plantarum. Int. J. Food Microbiol. 73, 207–212. doi: 10.1016/S0168-1605(01)00651-1
Sofos, J., and Geomaras, I. (2010). Overview of current meat hygiene and safety risks and summary of recent studies on biofilms, and control of Escherichia coli O157:H7 in nonintact, and Listeria monocytogenes in ready-to-eat, meat products. Meat Sci. 86, 2–14. doi: 10.1016/j.meatsci.2010.04.015
Stephens, P. J., Joynson, J. A., Davies, K. W., Holbrook, R., Lappin-Scott, H. M., and Humphrey, T. J. (1997). The use of an automated growth analyser to measure recovery times of single heat-injured Salmonella cells. J. Appl. Microbiol. 83, 445–455. doi: 10.1046/j.1365-2672.1997.00255.x
Stewart, E. J., Madden, R., Paul, G., and Taddei, F. (2005). Aging and death in an organism that reproduces by morphologically symmetric division. PLoS Biol. 3:e45. doi: 10.1371/journal.pbio.0030045
Tomasulo, A. (2012). Update on Enfamil, Infants and Cronobacter Infections. The Disease Daily [Internet Document]. Available at: http://www.healthmap.org/site/diseasedaily/article/update-enfamil-infants-and-cronobacter-infections-1512 [accessed December 9, 2015].
Tóthová, L., Celec, P., Bábíčková, J., Gajdošová, J., Al-Alami, H., Kamodyova, N., et al. (2011). Phage therapy of Cronobacter-induced urinary tract infection in mice. Med. Sci. Monit. 17, BR173–BR178.
van Acker, J., de Smet, F., Muyldermans, G., Bougatef, A., Naessens, A., and Lauwers, S. (2001). Outbreak of necrotizing enterocolitis associated with Enterobacter sakazakii in powdered milk formula. J. Clin. Microbiol. 39, 293–297. doi: 10.1128/JCM.39.1.293-297.2001
Weir, E. (2002). Powdered infant formula and fatal infection with Enterobacter sakazakii. CMAJ 166, 1570.
Xu, Y., Métris, A., Stasinopoulos, D. M., Forsythe, S. J., and Sutherland, J. P. (2015). Effect of heat shock and recovery temperature on variability of single cell lag time of Cronobacter turicensis. Food Microbiol. 45, 195–204. doi: 10.1016/j.fm.2014.04.003
Yan, Q. Q., Condell, O., Power, K., Butler, F., Tall, B. D., and Fanning, S. (2012). Cronobacter species (formerly known as Enterobacter sakazakii) in powdered infant formula: a review of our current understanding of the biology of this bacterium. J. Appl. Micrtobiol. 113, 1–15. doi: 10.1111/j.1365-2672.2012.05281.x
Keywords: Cronobacter sakazakii, PIF/FUF, food safety, variability, risk assessment, heat treatment
Citation: Parra-Flores J, Juneja V, Garcia de Fernando G and Aguirre J (2016) Variability in Cell Response of Cronobacter sakazakii after Mild-Heat Treatments and Its Impact on Food Safety. Front. Microbiol. 7:535. doi: 10.3389/fmicb.2016.00535
Received: 30 January 2016; Accepted: 01 April 2016;
Published: 19 April 2016.
Edited by:
Andrea Gomez-Zavaglia, Center for Research and Development in Food Cryotechnology, Consejo Nacional de Investigaciones Científicas y Técnicas, ArgentinaReviewed by:
Laurent Guillier, Agence nationale de sécurité sanitaire de l’alimentation, de l’environnement et du travail, FrancePablo S. Fernandez, Polytechnic University of Cartagena, Spain
Copyright © 2016 Parra-Flores, Juneja, Garcia de Fernando and Aguirre. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Juan Aguirre, juaguirr@vet.ucm.es; juan.aguirre@inta.uchile.cl
 Julio Parra-Flores1
Julio Parra-Flores1 Vijay Juneja
Vijay Juneja Gonzalo Garcia de Fernando
Gonzalo Garcia de Fernando Juan Aguirre
Juan Aguirre