Learning and the development of contexts for action

Introduction

An important question in neurophysiological studies of human cognition is how limbic circuits regulate cortical networks in the motivational control of learning and memory (Tucker and Luu, 2007). Animal studies have identified two separate circuits underlying discriminative learning: one supports the rapid acquisition of new skills under changing conditions, and a second system supports gradual development of the animal’s cognitive representation of the environmental context, allowing fast, and efficient regulation of actions that are congruent with the context model (Gabriel et al., 2002). The early and late systems allow learning to be graded: there is a progression from intensive monitoring and control early in the learning cycle, when stimulus–response contingencies remain undeveloped, toward more efficient and automated control once the stimulus–response contingencies have been sufficiently mapped. The first stage is marked by rapid learning, in which considerable improvement in performance can be seen within a single training session, whereas the second stage is characterized by gradual improvements in performance, as the practiced behavior is incorporated within the animal’s “neuronal model” of the environmental context (Gabriel et al., 2002).

Lesion studies in animals have suggested that the fast or early learning system includes the anterior cingulate cortex (ACC), amygdala, and mediodorsal nucleus of the thalamus. The unique properties of the fast learning system, specifically its contribution to overcoming habitual responses, led Gabriel et al. (2002) to suggest that this circuit is integral to what has been called the executive control of cognition. Bussey et al. (2001) have shown that the ventral and orbital prefrontal cortices should also be included as part of this fast learning system. Lesion evidence suggested that the slow learning system is centered on the posterior cingulate cortex (PCC) and anterior thalamic nucleus (Gabriel et al., 2002), integrating hippocampal contributions to the dorsal cortical pathway for both spatial cognition and the pragmatic control of actions (Tucker and Luu, 2007).

Perhaps consistent with the animal studies, results from human imaging studies have also converged to identify brain structures involved in the early and late stages of learning (Chein and Schneider, 2005). For example, the prefrontal lobes (including the inferior prefrontal cortex, dorsolateral prefrontal cortex, and medial prefrontal cortex) and ACC are engaged early in learning. During the later stage of learning, however, the frontal structures of cognitive control exhibit a reduction in activity. In contrast, in the later stage the posterior regions, including PCC, precuneus, cuneus, superior parietal lobule, and intraparietal sulcus were found to show increased activity in the functional magnetic resonance (fMRI) observations (Chein and Schneider, 2005). The accumulated evidence led Chein and Schneider to propose a dual-processing model underlying human learning that has interesting parallels with the neurophysiology of animal learning (Tucker and Luu, 2007).

Event-related potential research on repetition suppression (RS), wherein repeated presentation of the same stimulus produces attenuated cortical responses, can be used to understand plasticity induced changes associated with learning (see Garrido et al., 2008; Race et al., 2010; Summerfield et al., 2011). Different forms of learning, such as stimulus–decision and stimulus–response, produce RS effects in different cortical regions (Race et al., 2010). Chein and Schneider’s (2005) proposed that learning-related brain changes reflect reduced dependencies on brain regions involved in controlled processes and the formation of local associations in brain regions that are specifically engaged by the task, such as visual areas for visual learning. Consistent with this proposal Garrido et al. showed that RS can be accounted for by changes in both extrinsic (between brain regions) and intrinsic connections.

Based on the dual-stage model of learning, we conducted two studies that were guided by the hypothesis that initial learning requires greater executive control from frontolimbic networks (centered on the ACC) and that more automated processing engages posterior corticolimbic networks (centered on the PCC; Luu et al., 2007, 2009). In a simple code-learning task in which subjects read a number on the screen and had to learn which finger to press, we examined cortical activity in response to both the number target (Luu et al., 2007) and the feedback stimulus (Luu et al., 2009) using dense-array (128 channel) EEG. The results revealed that in response to the target stimulus, several neural response changes with learning matched the theoretical predictions. As predicted, posterior cortical regions (including parietal, PCC, and mediotemporal cortices, indexed by the P3) became progressively engaged as participants discovered and learned stimulus–response mappings.

Surprisingly, activity in the medial prefrontal cortex (indexed by the medial frontal negativity, MFN) increased as learning progressed, even after the early stage was completed. The MFN is distinct from other negativities recorded along the midline, such as the feedback-related negativity (FRN) and error-related negativity (ERN). As shown by Luu et al. (2009), the FRN is localizable to the very rostral aspects of the ACC whereas the MFN is generated by more dorsal and caudal cortical areas (such as ACC, medial premotor cortex, and mid-cingulate cortex). Unlike the MFN, the FRN shows marked reduction after learning. The MFN is also distinguishable from the ERN in these previous studies because it is defined relative to correct targets; the ERN is a response-locked component that is elicited by erroneous responses and localizable to more rostral aspects of the ACC than the MFN (see Luu et al., 2003; Luu et al., 2007).

These previous results (Luu et al., 2007, 2009) were obtained within single-session studies wherein early learning was defined as the period before, and late learning as the period after learning was achieved, in other words, after the participants’ consistent performance demonstrated knowledge of the code. Consistent performance was indicated by reduced variability in reaction times (RTs), a characteristic of automated cognition and well-integrated learning (Segalowitz and Segalowitz, 1993). Nonetheless, although learning the code was achieved, it could be argued that the MFN persisted because participants did not have enough practice to acquire fully automated performance. Would the responses of frontal corticolimbic circuits, including the MFN, decrease if learning progressed to a more fully automatic stage, wherein controlled processes of the frontal lobe would be more fully disengaged?

We addressed this question in the present study by examining the MFN during the number code-learning task across four sessions. In the first three sessions, participants learned, and then practiced, the task with the same stimulus–response mappings. This allowed us to broaden our definition of the late learning stage and to explore the influence of extended practice (in sessions 2 and 3) on the MFN and P3 components. In a fourth session, participants were required to learn new stimulus–response mappings, but within a task context that was now fully familiar. This design allowed us to test the hypothesis, predicted by the theory that frontal controlled processes decrease with practice, that the extended practice of sessions 2 and 3 would lead to decreases in MFN amplitude. Under this hypothesis, the MFN component would reappear with the new code mapping (and effortful control) to be learned in session 4.

We also examine the P3 response to understand the uniqueness of the MFN changes. We hypothesize that P3 amplitude would increase during learning and that it will decrease when new stimulus–response mappings must be learned.

Materials and Methods

Participants

Participants were recruited from the general student population at the University of Oregon. Fifteen right-handed participants completed the study (nine males), with ages ranging between 18 and 37 years of age (mean = 22.8, SD = 5.5) and education ranging between 12 and 18 years (mean = 15, SD = 1.7). All participants had normal or corrected-to-normal vision. Participants reported no history of seizures or head injuries that resulted in loss of consciousness, nor the taking medications that could affect the EEG (e.g., anticonvulsants) or illicit drugs. Informed written consent was obtained from each participant prior to participation in the studies. The protocol was approved by the EGI and University of Oregon institutional review boards.

Task

The task was a variant of the go/no-go discrimination task developed by Newman et al. (1990). On each trial, 1 of 16 two-digit codes (“targets,” e.g., 15, 23, 47) was presented centrally on a computer screen (1500 ms maximum duration). Targets were presented using 18-point, bold Courier New font type. Participants were seated 65 cm from the center of the computer screen. Targets were randomly presented, with the constraint that the same target could not occur on consecutive trials. Half of the targets were pre-designated as “go” stimuli and the other half were pre-designated as “no-go” stimuli. Participants were required either to press a button or to withhold a button-press response upon the presentation of a target. For go stimuli, which required a response, participants had to learn to respond with the appropriate finger of the appropriate hand. There were four response choices (the index and middle finger of each hand) and each of the eight targets was consistently mapped to one of these four fingers (two targets per finger). This mapping was arbitrarily determined. The target was terminated when participants made a response or 1500 ms elapsed. After each response (or non-response) contingent feedback was provided immediately.

The feedback provided participants with all the information needed to learn the stimulus–response rules, through shaping correct responses in an approximation sequence. The feedback stimuli were: (1) ErrorGo (error of omission in response to go target), (2) ErrorNG (error of commission in response to no-go target), (3) Correct (correct response to go target but response committed with wrong hand), (4) CorrectH (correct response with correct hand to go target but response committed with wrong finger), (5) CorrectNG (correct withholding of response to no-go target), and (6) CorrectF (correct response with correct hand and finger to go target). The feedback was presented for a maximum duration of 10 s, unless terminated by the participant with a button press. The inter-trial interval varied between 1500 and 2500 ms. A total of 800 trials was presented in each session, grouped into 100-trial blocks.

Participants were informed that correct performance (CorrectNG and CorrectF) would earn eight points, errors (ErrorGo and ErrorNG) would result in a loss of eight points, and partially correct responses (Correct and CorrectH) would result in losses of four and two points, respectively. Participants started the study with zero points. To motivate participants to learn the task, participants were informed they would be paid a monetary bonus according to the number of points they accumulated by the end of the study. At the end of each block, participants were presented with the cumulative earned points and recorded them on a paper form.

All participants completed four study sessions. The average time between the first and fourth session was 9 days (range 3–17, SD = 3.5). In sessions 1–3, participants were presented with the same target–response mappings. In the fourth session, participants were presented with new target–response mappings to learn. Note that new target stimuli were used in the fourth session (i.e., the target–response mappings were not simply switched).

For each session, participants were paid $15 for their participation and an additional amount, ranging between $25 and $45, depending on task performance. On average they earned $40 per session.

EEG Recording

The EEG was acquired using a 256-channel HydroCel Geodesic Sensor Net (Electrical Geodesics, Inc., Eugene, OR, USA). All electrodes impedances were kept below 70 kΩ (Ferree et al., 2001). Recordings were referenced to Cz. The EEG was bandpass filtered (0.1–100 Hz) prior to being sampled at 250 s/s with a 16-bit analog-to-digital converter.

Procedure

Participants completed several mood questionnaires prior to the EEG recording for each session. Once fitted with the 256-channel HCGSN, participants were seated 65 cm in front of the computer monitor. A chin rest was used to minimize head movements and to maximize consistency of gaze distance and alignment to the monitor. Participants were explicitly instructed that there were a total of 16 two-digit codes, half of which required a response and half of which required no response. For those digits that required a response, participants were told they had to figure out the correct hand and finger mappings and that each of the four designated fingers had two two-digit codes associated with it. The feedback stimuli were described on a sheet of paper for participants to review prior to task performance. They were explicitly informed that they must learn the stimulus–response mappings through trial-and-error based on these feedback stimuli. No mention of context learning was made by the experimenter.

Once participants understood the nature of the task and feedback stimuli, they performed a simplified, 32-trial task training session, during which they learned to associate the hand/finger mappings to 4 two-digit numbers through use of feedback information. They were explicitly informed that only 1 two-digit code would be associated with each finger for the practice session, unlike the actual task. The training stimuli were not used in any subsequent part of the study. All participants showed proficiency for the target-response mappings by the end of the training session. After this initial training in session 1, participants did not engage in any other training or rehearsal tasks for sessions 2 and 3. In session 4, participants were informed that they will perform the same learning task as in sessions 1–3 with new stimuli. The instructions were identical to those provided at the beginning of session 1, and they were provided with a training block using a new set of training stimuli. In other words, all parameters were kept constant between sessions 1 and 4 except for the stimuli. Each experimental session, including recording set up, lasted approximately 2.5 h.

Learning Criterion

Bayesian state-space analysis was employed to categorize pre-learning vs post-learning trials for each participant (Smith et al., 2007). By computing a learning curve and its corresponding 95% confidence intervals, the state-space analysis identified, with 95% confidence, the first trial at which the learner was performing above chance. This estimate was based on the ideal observer. That is, it used the outcomes of all the trials in the experiment to compute the learning curve (the learning state process). The learning curve was constructed by determining at each trial the likelihood of a correct response given the prior response history. In a second step, confidence intervals were computed in order to determine the trial at which the learner began to respond above chance. The Bayesian approach applies Monte Carlo Markov Chain methods to compute the posterior probability densities of the model parameters and the learning state, thereby enabling the model to handle interleaved responses to the 16 different stimuli and to correct for any initial response bias.

Experimental Factors

Stimulus (Go vs No-Go), Learning (Pre vs Post-learning criterion), Learning Session (1 vs 4), Practice Session (1, 2, 3), and Accuracy (Error vs Correct) served as repeated factors in the behavioral and ERP analyses. “Learning” is the contrast between not knowing the code-finger mapping, and demonstrating knowledge through consistent use, as described in the next section. “Learning Session” is the first, inexperienced learning session contrasted with the fourth session in which the task context is well known, even though new codes and response mappings are introduced. “Practice” refers to the continued transition toward automated performance in sessions 2 and 3, after demonstration of knowledge of the code and mappings in session 1. Greenhouse–Geisser correction was applied to all ANOVAs involving the Practice Session factor.

EEG Processing

The continuous EEG data were digitally filtered with a 30-Hz low pass finite impulse response filter and then segmented relative to target onset (200 ms before and 1000 ms after) and sorted according to pre and post-learning criteria. A segment of the EEG was excluded from signal averaging if it was contaminated by ocular artifacts (e.g., blinks or lateral eye movements) or if it contained 10 or more channels of data that exceeded a voltage threshold of 200 μV (absolute) or a transition threshold of 100 μV (sample to sample). After averaging, the data were re-referenced to the average reference.

Source Estimates

Source estimates, describing the neural sources of the measured scalp potentials, were estimated with GeoSource (version 1.0) electrical source imaging software (EGI, Eugene, OR, USA). GeoSource uses a finite difference model (FDM) of head tissue conductivity for accurate computation of the lead field in relation to head tissues, where the primary resistive component is the skull. The FDM allows accurate characterization of the cranial orifices, primarily the optical canals and foramen magnum. Tissue compartments of the FDM were constructed from whole head MRI and CT scans of a single individual (Colin27) whose head shape closely matches the Montreal Neurological Institute (MNI) average MRI (MNI305). The MRI and CT images were co-registered prior to segmentation of the brain and cerebral spinal fluid (identified from MRI data) and skull and scalp (identified from CT images). This individual’s MRI and CT images were aligned with the cortex volume from the MNI atlas with Talairach registration. The tissue volumes were parcellated using 2-mm voxels to form the computational elements of the FDM.

Conductivity values used in the FDM model are as follows: 0.25 S/m (Siemens/meter) for brain, 1.8 S/m for cerebral spinal fluid, 0.018 S/m for skull, and 0.44 S/m for scalp (see Ferree et al., 2001). These values reflect recent evidence that the skull-to-brain conductivity ratio is about 1:15 (e.g., Ryynanen et al., 2006), compared to the 1:80 ratio traditionally assumed. Source locations were derived from the probabilistic map of the MNI305 average (to which the typical subject matches closely). Based on the probabilistic map, gray matter volume was parcellated into 7-mm voxels; each voxel served as a source location with three orthogonal orientation vectors. This resulted in a total of 2447 source triplets whose anatomic identities were estimated through use of a Talairach daemon (Lancaster et al., 2000). Once the head model was constructed, an average of the 256-channel sensor positions was registered to the scalp surface. To compute estimates of the sources, a minimum norm solution with the LAURA (local autoregressive average) constraint (Grave de Peralta Menendez et al., 2004) was used. All source estimates were performed on the grand-averaged scalp data.

Results

Behavioral Data

In order to reduce the influence of outlier RTs for behavioral analyses, the top and bottom 10% of the RT distribution (i.e., the tails) within each condition were winsorized (Wilcox, 1997) prior to analysis.

Learning effects (trials to learn)

A repeated-measures ANOVA, with Stimulus and Learning Sessions as factors, was performed on the total number of trials it took participants to learn the stimulus–response mappings. A significant effect was obtained for Learning Session, F(1,14) = 35.1, p < 0.001 (see Figure 1). A significant trend was observed for Stimulus, F(1,14) = 3.8, p < 0.08. The results show that learning was much faster in session 4 and that No-Go stimuli required fewer trials to learn than Go trials. Of particular significance is that the total trials it took to learn Go stimuli in session 4 was substantially reduced compared to session 1.

FIGURE 1

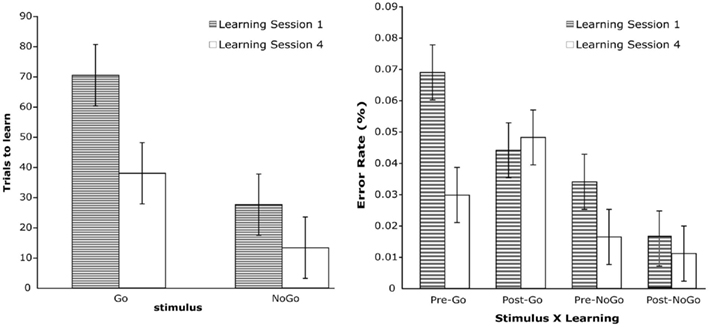
Figure 1. Left: average of total trials to learn for stimulus type and learning session. Right: error rate for stimulus type, learning, and learning session.

Learning effects (error rate)

A repeated-measures ANOVA was conducted with Stimulus, Learning, and Learning Session as independent variables and error rate as the dependent variable. For No-Go stimuli, error rates were computed for errors of commission; for Go stimuli, error rates were computed for errors of omission as well as partial errors (i.e., responses with the wrong finger or hand).

The results revealed significant main effects for Stimulus, F(1,14) = 61.3, p < 0.001, and Learning Session, F(1,14) = 30.2, p < 0.001. There was also a significant Learning × Learning Session interaction, F(1,14) = 17.3, p < 0.002. All of these significant effects were qualified by a Stimulus × Learning × Learning Session effect, F(1,14) = 17.1, p < 0.002 (see Figure 1). This three-way interaction was examined by performing separate Learning × Learning Session analyses for Go and No-Go stimuli. The Learning × Learning Session interaction was significant for both Go, F(1,14) = 21.0, p < 0.001, and No-Go stimuli, F(1,14) = 5.6, p < 0.04. Analysis of the simple effects for each stimulus revealed that for Go targets, participants made fewer errors prior to learning the stimulus–response mappings in Learning Session 4 compared to Learning Session 1, t(1,14) = 6.1, p < 0.001, and that after learning, error rates did not differ between the two learning sessions. For No-Go stimuli, the results revealed that the number of errors committed in Learning Session 4 did not differ from Session 1 either before or after learning.

Learning effects (RT)

In this analysis only data from 11 participants were included; four participants did not make enough errors in the pre-learned error condition to provide reliable RT data. That is, they exhibited a fast learning rate. A repeated-measures ANOVA with Learning, Learning Session, and Accuracy as independent factors and RT as dependent variable revealed significant main effects of Learning, F(1,10) = 34.0, p < 0.01, and Accuracy, F(1,10) = 104.0, p < 0.001. These main effects were qualified by a significant Learning × Accuracy interaction, F(1,12) = 17.1, p < 0.003. Examination of the significant interaction revealed that participants’ RTs decreased with learning for correct responses, t(1,10) = 7.7, p < 0.001, but that RTs for error trials after learning did not differ from error trials prior to learning. Moreover, error trials after learning had longer RTs than correct trials after learning, t(1,10) = 11.4, p < 0.001. This suggests that errors after learning were not “slips” (mistaken actions in the context of accurate knowledge), but rather may have resulted from memory retrieval failures that produced ambiguity (and thus response conflict) in generating appropriate responses.

Practice effects (error rate)

Stimulus and Practice Session served as within-subjects factors. There were significant Stimulus, F(1,14) 33.3, p < 0.001, and Practice Session, F(2,28) = 55.9, p < 0.001, effects that were qualified by a significant interaction between these two factors, F(2,28) = 8.9, p < 0.005. Figure 2 illustrates the nature of this interaction. As participants gained practice in the task, their error rates dropped significantly, particularly between sessions 1 and 2.

FIGURE 2

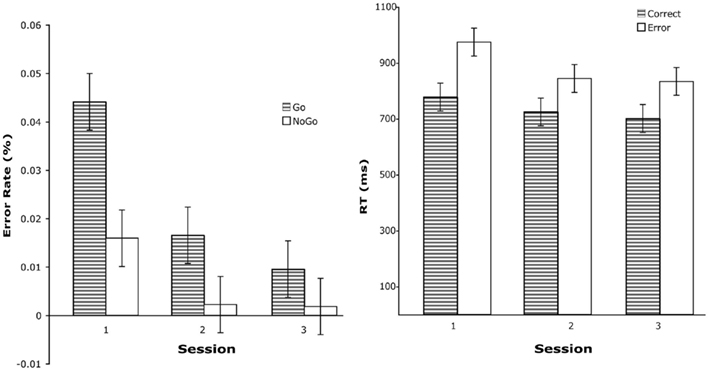
Figure 2. Left: error rate for stimulus type and practice session. Error rates are for post-learned trials. Right: mean RT for practice session and accuracy.

Practice effects (RT)

Reaction times were analyzed with Practice Session and Accuracy serving as repeated-measures factors. Thirteen participants were included in this analysis (two were excluded because they did not make enough errors after learning to provide stable RT measures). Significant results were obtained for Practice Session, F(2,24) = 7.9, p < 0.007, and Accuracy, F(2,24) = 60.5, p < 0.001. The reduction in error RT as a function of practice was particularly large between sessions 1 and 2 (see Figure 2) and error responses were associated with longer RTs than correct responses.

Practice effects (development of automaticity)

To assess whether participants developed skilled performance to automated levels, we computed the coefficient of variation (CV), the ratio of the SD to the (winsorized) mean RT (CV = SD/RT; Segalowitz and Segalowitz, 1993). The logic is that controlled processes, such as those required early in learning, are inherently more variable than the processes underlying automatic performance (also see Logan, 1988). Therefore, a reduction in controlled processes should result in a reduction in the CV. For this analysis, CV values were only obtained for correct responses.

We performed two analyses using the CV measure. The first analysis aimed to replicate our previous findings of significant CV changes within the first session (Luu et al., 2009). For this analysis post-learning trials from session 1 were grouped into four equal bins. A trend analysis revealed a significant linear trend, F(1,14) = 8.5, p < 0.02 (see Figure 3); CV decreased within the first learning session as participants practiced the task. The decrease was most notable between the first and second bins. This fully replicated our previous findings. We also analyzed CV changes across sessions 1–3. For this analysis, CV was determined for each session. Although participants’ CVs continued to decrease across sessions, the reductions were small and the analysis did not reveal significant trends. These results show that progression toward automated performance was most dramatic within the first session.

FIGURE 3

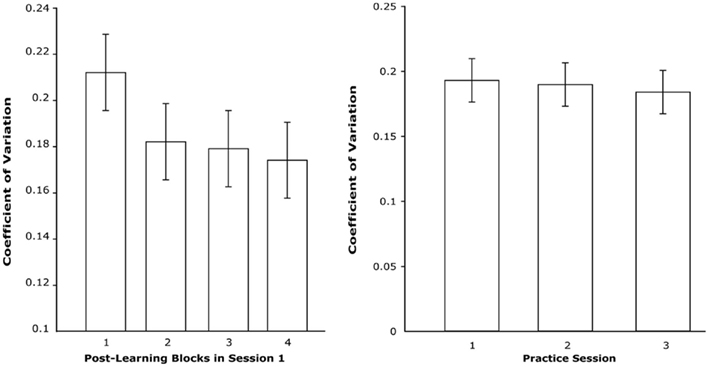
Figure 3. Left: CV across four blocks of post-learned trials in session 1. Right: CV of post-learned trials across first three sessions.

ERP Data

In order to examine the neural mechanisms associated with learning arbitrary visuomotor mappings, as opposed to response inhibition, we focused the ERP analysis on Correct Go trials. Because pre-learning represents the performance stage during which stimulus–response mappings are not known, we combined all pre-learning trials (correct and error Go and No-Go trials) into a single “pre-learning” condition to contrast against the post-learned CorrectGo trials. Prior to combining all pre-learned trials, we examined whether differences exist between go and no-go trials. The results revealed no significant differences. This combination permitted more trials to be included, resulting in a more stable average ERP. We focused the analyses on two ERP components: MFN and P3. Note that researchers have used the labels MFN and N2 to refer to the same component. Because we have used the MFN label in previous publications of work employing this experimental paradigm, we will use the MFN label to maintain consistency.

Channels that were used to quantify the MFN and P3 are illustrated in Figure 4. For all ERP components, the data from each channel was first quantified (see below) and then averaged across the channel groups. To quantify the MFN, a negative peak was identified between 295 and 427 ms after target onset (yellow box in Figure 5) and an average amplitude was calculated for a 44-ms interval around this peak. The MFN was referenced to the preceding positive peak (i.e., the P2). The P2 was quantified as the average amplitude around a 44-ms window centered on the most positive peak within a 167- to 283-ms post-target interval. The P3 was quantified by first indentifying positive peak between 440 and 760 ms after target onset (yellow box in Figure 6) and then averaging over a 44-ms interval centered on this peak. The average was then referenced to the average of the −200 to 0 ms pre-stimulus baseline. This method for quantifying the MFN and P3 amplitude was applied separately for each participant and condition, thereby allowing for small variations in peak latency across individuals and conditions.

FIGURE 4

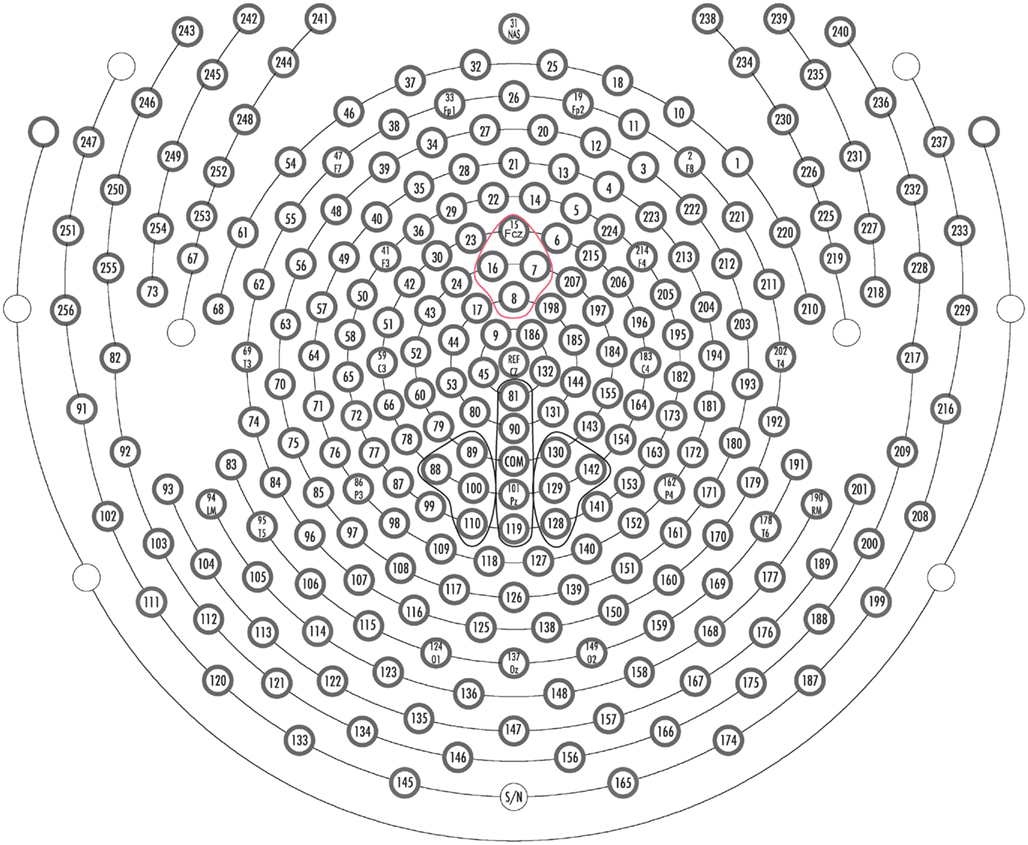
Figure 4. Sensor layout for 256-channel Hydrocel Geodesic Sensor Net. Orientation of layout is top looking down with the nose at the top of the page. Channel groups used to quantify ERP components: Red: MFN, Black: P3.

FIGURE 5

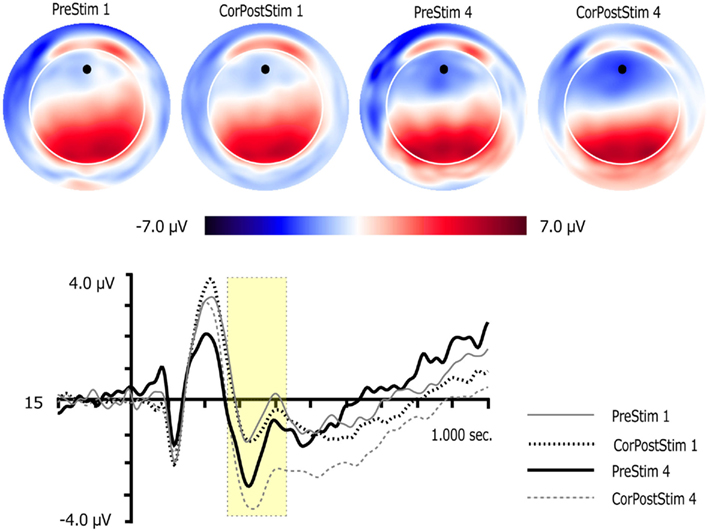
Figure 5. Two dimensional topographic maps and waveform plots for pre-learned targets and correct post-learned go targets for sessions 1 and 4. Topographic maps are presented for the peak of the MFN. Orientation of maps is top looking down with nose at the front. Black circles on 2D maps represent channel locations of the waveform plots. Yellow boxes in waveform plots mark the time window used to quantify the MFN. Vertical lines in waveform plots mark onset of targets.

FIGURE 6

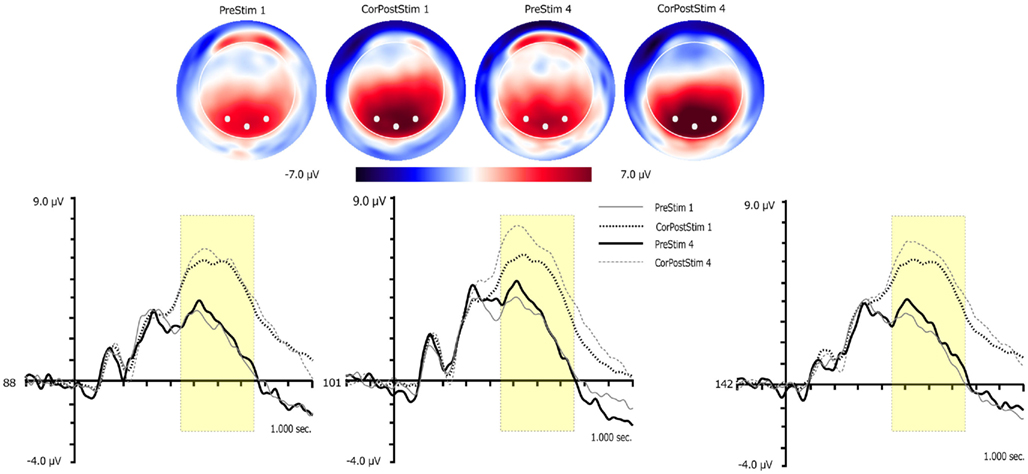
Figure 6. Three dimensional topographic maps and waveform plots for pre-learned targets and correct post-learned go targets for sessions 1 and 4. Topographic maps are presented for the peak of the P3. White circles on 3D maps represent channel locations of the waveform plots. Yellow boxes in waveform plots mark the time window used to quantify the P3. Vertical lines in waveform plots mark onset of targets.

MFN (learning effects)

Learning and Learning Session served as within-subject factors. Significant main effects for Learning, F(1,14) = 7.3, p < 0.02, and Learning Session, F(1,14) = 8.0, p < 0.02 were observed. These were qualified by a significant Learning × Learning Session interaction, F(1,14) = 6.4, p < 0.03. Paired t-tests showed that MFN amplitude was substantially more negative post-learning in session 4 than pre-learning in session 4, t(14) = 3.0, p < 0.02, or post-learning in session 1, t(14) = 3.5, p < 0.01.

P3 (learning effects)

Learning, Learning Session, and Laterality (left, midline, right) served as within-subject factors. Significant effects were found for Learning, F(1,14) = 79.9, p < 0.001, and Learning Session, F(1,14) = 5.7, p < 0.04. P3 amplitude was larger after learning and it was also larger in session 4.

MFN (practice effects)

A one-way repeated-measures ANOVA was conducted with Practice Session as the factor. The results revealed that the MFN amplitude increased with practice, F(2,28) = 6.5, p > 0.01. This was also confirmed by a significant linear trend, F(1,14) = 8.8, p < 0.02.

P3 (practice effects)

Practice Session and Laterality (left, midline, right) served as within-subject factors. No significant results were obtained.

Predictors of facilitated learning

The behavioral results revealed that participants required fewer trials to reach learning criterion (henceforth, “trials to learn”) in session 4 than session 1, indicating that they did indeed acquire a task set that facilitated learning a new group of code-finger mappings. Based on our theoretical model that the MFN tracks the gradual development of a contextual model that guides learning (Luu et al., 2007, 2009), we examined whether the post-learning MFN amplitude in sessions 1–3 could predict learning rate during the fourth session. Moreover, to control for individual differences in learning rate, we included the trials to learn in session 1 as a covariate. We conducted a statistical stepwise regression (p-to-enter = 0.05, p-to-remove = 1.0) with MFN amplitude in session 1–3 as predictors and session 4 learning rate as the criterion. As covariate, trials to learn in session 1 was entered first. R² = 0.617, F(1,13) = 23.5, p < 0.001. Based on the criterion set for variable inclusion, MFN amplitude in session 3 entered next; R² change = 0.115, F(1,12) = 5.7, p < 0.04. Because the P3 also increases with learning (reported previously in Luu et al., 2007, 2009), we explored whether P3 amplitude (from session 1–3) may predict learning rate in session 4. The analysis revealed that P3 amplitudes did not contribute significantly as predictors of learning rate in session 4.

ERP source estimates

For source estimates of the MFN, a difference between the waveforms from session 3 and the pre-learned waveforms in session 1 was derived. The source estimate was then obtained during the peak (∼339 ms) difference. The results revealed sources along the mediodorsal aspect of the frontal lobe, including the ACC (BA 24), medial frontal gyrus (BA 8 and 6), and mid-cingulate cortex and paracentral lobule (BA 31, see Figure 7). These results are consistent with source estimates for the MFN in our previous studies (Luu et al., 2007, 2009). Source estimates were also derived for MFNs obtained at different stages of post-learning (i.e., sessions 1, 2, 3, and 4) to examine differences. The results for each estimate were very similar to the solution shown in Figure 7.

FIGURE 7

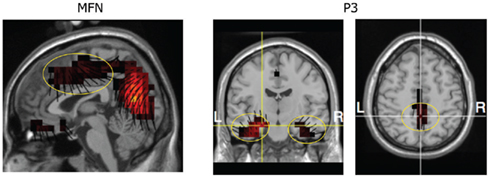
Figure 7. Estimate of source generator for MFN and P3. Lines at each voxel represent orientation vectors (pointing in the positive direction). The vectors indicate the scalp topography features that are accounted by the source voxels (see orientation of these sources relative to the scalp topography of the MFN in Figure 5 and P3 in Figure 6).

Source estimates of the P3, derived from post-learning sessions 1, 2, 3, and 4 were performed at the peak (∼500 ms). The source locations are similar across all post-learning sessions and is illustrated for session 3 in Figure 7. Consistent with our previous findings (Luu et al., 2007, 2009), the generators of the P3 are located in the medial temporal lobes (stronger in the left for the stimuli used in the present study) and PCC.

Discussion

Participants took more trials to learn correct response (Go) stimulus–response mappings than correct (No-Go) response suppressions. This is not surprising because No-Go stimuli require a single category (inaction) whereas Go stimuli have four possible response mappings (four finger alternatives) that must be learned depending on the codes. Participants made fewer errors after they learned the task, and error RTs did not decrease after learning, in contrast to the significant reduction in RTs associated with correct responses after learning. Apparently, in this paradigm, the speeding of responses with automaticity after learning applies only to correct responses, and the residual errors are not quick “slips” but rather trials in which problems of attention, memory retrieval, response programming or other underlying mechanisms lead to extended processing preceding the error.

These learning-related behavioral results are consistent with our previous findings (Luu et al., 2007, 2009). Furthermore, there was evidence of improved automaticity with continued practice. With continued practice in sessions 2 and 3, participants made faster responses and fewer errors (particularly between the first and second sessions). Analysis of the CV measure revealed that variability in performance decreased substantially after learning within the first session, and then remained quite stable thereafter (across sessions 2–3). According to CV rationale, stable CV after learning implies that automaticity did not further increase with practice.

These behavioral results can be understood using Logan’s (1988) Instance Theory of automaticity. This theory proposes that during the initial stages of learning, participants’ performance is based on algorithmic computations and/or response strategies. Through learning and practice, a single-step, direct-access retrieval of the stimulus–response mapping is established to produce automaticity. This may be described as obligatory retrieval. The transition to automaticity and obligatory retrieval explains the reduction in RT as well as reduction in the variability of RT. These behavioral findings suggest that the experimental manipulations were successful, and they provide the psychological framework for understanding the neurophysiological results.

A unique effect in the present study was the improvement in learning rate after participants had learned the general requirements of the task, even as they were challenged with new codes in session 4. The participants required fewer trials to learn in the fourth session than they did in the first session.

Medial Frontal Negativity

Initially, based on well known findings of decreased ACC activation after learning and practice (e.g., Chein and Schneider, 2005) we predicted that MFN amplitude would decrease after learning has been achieved (Luu et al., 2007). The MFN is localized to the medial frontal cortex, including the ACC, and should reflect similar effects as fMRI studies showing ACC decreases in learning. Furthermore, studies have shown a similar component (the frontal N2) to be involved in cognitive control (Folstein and Van Petten, 2008). However, we found that the amplitude of the MFN continued to increase as learning progressed, even during the practice sessions when P3 amplitude remained stable. Recently, Schapkin et al. (2007) also found that the MFN (referred to as an N2 in that study) increased with practice. How should we understand this increase?

Based on a review of the literature, Folstein and Van Petten (2008) argued that there are at least two types of N2 components: one related to cognitive control and the other to detection of novelty or mismatch. If the MFN of the present study indexes cognitive control, we would expect it to decrease with learning and practice, similar to what is observed in RS studies (e.g., Race et al., 2009, 2010). Whereas the ACC has been the focus of many studies and theories of cognitive control, and whereas the ERN in motor tasks is consistently localized to the ACC (Luu et al., 2003), the MFN often includes sources in the supplementary motor area (SMA) and mid-cingulate cortex (MCC; Tucker et al., 2003; Luu et al., 2007, 2009). In fact, sources in both the SMA and MCC were major contributors to the MFN in the present experiment (Figure 7). Several studies now show that the SMA and MCC are progressively engaged during learning (Eliassen et al., 2003; Lee and Quessy, 2003) and that increases of neural activity within these regions correlate with improvements in performance (Salimpoor et al., 2010). These findings are not consistent with fMRI findings of reduced activity based on repetition of stimulus–response mappings (the RS effect, Garrido et al., 2008; Race et al., 2009). They are also inconsistent with a simple model of reduced cognitive control (at least in relation to cingulate cortex) with increase learning.

It is possible that the MFN examined in the present study is related to novelty-mismatch processes rather than cognitive control processes. Novelty or mismatch detection depends on the existence of a “mental template” (Folstein and Van Petten, 2008). Schapkin et al. (2007) also interpreted their findings of increased N2 amplitude with practice as reflecting improved stimulus–response classification supported by a mental template. We think that the notion of a mental template may be reinterpreted within learning theory as a context model that organizes the relations of actions with the environmental situation (Luu et al., 2009).

Based on the finding by Elliott and Dolan (1998) that fMRI activation of the dorsal ACC reflects the formation of hypotheses to guide actions, we proposed that dorsal aspects of the ACC track the monitoring of actions in relation to task parameters (such as feedback and conflicting task demands, Luu et al., 2003). More recently, based on the findings of increased MFN amplitudes with learning and practice, we proposed that the dorsal ACC is involved in the early representation of action contexts (Luu et al., 2009). Conceptually, generating hypotheses about future events and generating temporary action contexts could be seen as differing ways of describing the same cognitive process; an internal model is formed to guide the selection of action. We suggest that framing the role of the dorsal ACC as early context-formation may serve as a generic theoretical model that subsumes more specific contemporary theories of ACC function. These include a role for the ACC as a motor control filter (Holroyd and Coles, 2002), a conflict detector (Botvinick et al., 2004), and an integrator of actions with values (Rushworth et al., 2004).

Results from several recent studies point to a key role of the MCC in contextual representation during learning and decision-making. For example, Behrens et al. (2007) found the MCC to be active during decision-making phases of a probability tracking task, wherein the goal is to maximize rewards. In a task that involves making decisions about how many monetary points to send to another participant (who then returns a portion of received points), Chiu et al. (2008) found that activity in the MCC was associated with making the decision to send points. These results may be interpreted as demonstrating MCC contributions to context representations (specific to each task) that were required to direct an optimal course of action.

Takehara-Nishiuchi and McNaughton (2008) examined neuronal responses in the dorsal aspects of the prelimbic region of rats during conditional association learning. Based on their report, the electrodes were positioned in the caudal aspects of the prelimbic region, appearing to us to be in close proximity to the MCC. They showed that activity of neurons in this region became selective for task-relevant information during the course of learning. Of particular importance are the findings that (1) the neurons were responsive to more than just the stimulus (they also responded to the spatial and behavioral context), and (2) task performance depended on the integrity of these neurons after 2 weeks (lesions to this region before this time result only in minor impairment in task performance). Additionally, they found that during the first session of reconditioning (i.e., retraining on the same learning task after a 6-week interval during which no training occurred) there was a decrement in the conditioned response, although not to the initial unlearned levels, and that it took the animal about half the time, relative to original learning, to reacquire the condition response. Examination of the neuronal response revealed that during reconditioning, excitatory responses were similar to the overtraining (i.e., practice) sessions rather than the initial learning sessions. These results can be interpreted as analogous to our finding that MFN amplitude reflects the cingulate cortex contribution to context representation that efficiently frames new learning in a similar context.

In order to differentiate the SMA and MCC involvement from the findings and literature on the ACC, we propose the following distinction. Generating new hypotheses (action contexts) initially engages the ACC, because this is the limbic (motivational) base of the frontal motor planning system. As learning progresses, action contexts that accurately dictate the course of action are extended and supported by the SMA and MCC. Action context here refers to the configuration of external features and internal states, including action values organized in the visceral limbic cortex (Luu and Tucker, 2003; Rushworth et al., 2004; Tucker and Luu, 2007), and not just the stimulus–response mappings (see Balsam, 1985). The activity indexed by the MFN thus appears to provide a transitional mechanism, a conceptual representation of action contexts in the SMA and MCC, that mediates between the temporary representation and monitoring of action contexts (i.e., a hypotheses) in the dorsal ACC (Luu et al., 2003, 2007) and the more enduring representation of the environmental context model by the PCC and hippocampus.

P3

As in previous dense-array EEG studies (Luu et al., 2007, 2009), we found that P3 amplitude increased as participants demonstrated learning of the task, consistent with our previous findings as well as results reported by other researchers (e.g., Barceló et al., 2000; Race et al., 2010). However, unlike MFN amplitude, with continued practice in sessions 2 and 3, P3 amplitude did not increase but remained constant. Perhaps most importantly, P3 amplitudes did not predict new learning rate in session 4, whereas MFN amplitude did.

On the other hand, the P3 amplitude did parallel the MFN amplitude increase with new learning in session 4: P3 amplitude post-learning in session 4 was significantly larger than P3 amplitudes for post-learning in session 1. We propose that this pattern of results is consistent with the classical context-updating theory of the P3 (Donchin and Coles, 1988) and that it reveals the more passive, late-stage operation of the posterior dorsal corticolimbic networks in generating the P3 (including the PCC and medial temporal lobes, Luu et al., 2007, 2009), in contrast to the more active context-model generation supported by the ACC and MCC.

According to the context-updating model of the P3, this electrophysiological measure tracks a cognitive system that forms a representation of the environmental context that is restored and reinforced on a trial-by-trial basis during task performance (Donchin and Coles, 1988; Gonsalvez et al., 1999; Polich, 2007). P3 amplitude appears to reflect both the extent to which a template is restored (i.e., updated) and the processing resources that are available during restoration (Gonsalvez et al., 1999; Gonsalvez and Polich 2002). Based on the context-updating model, we interpreted learning-related P3 amplitude increases as reflecting the representation and restoration of action contexts that support skilled performance, specifically during the late stages of learning (Luu et al., 2007, 2009). With a stable representation of action contexts, skilled performance can be achieved through a more automatic, implicit mode of control, with a concomitant reduction in processing resource requirements.

Limitations of the Present Study

One limitation of the present study is that the EEG reflects brain activity generated by the cortex, and yet there is substantial evidence, from both animal and human studies, that subcortical structures (such as the caudate nucleus and amygdala) are central to learning (e.g., Grol et al., 2006). These subcortical structures and circuits work in concert with cortical structures during both early and late stages of learning (Brovelli et al., 2008). Studies with techniques that have ms time resolution and subcortical sensitivities (such as joint dense-array EEG–fMRI) will be required to delineate a comprehensive account of the brain’s learning systems and stages.

A second limitation of the present study is the spatial resolution of the source estimate procedure. Although not yet demonstrated to achieve the spatial resolution of fMRI, recent research shows that, given 256-channel sampling and realistic head models, source estimates can be quite accurate, allowing localization to sub-lobule resolution (approximately several centimeters) even in deep cortical structures, such as the medial temporal lobe (e.g., Michel et al., 2004; Yamazaki et al., in press). Thus, distinguishing between the various brain regions implicated for the MFN and P3 (e.g., medial prefrontal cortex, PCC, and medial temporal lobes) is well within the resolution of dense-array EEG. However, it is possible that the lack of any difference in MFN sources for different stages of learning and practice is due to the spatial resolution afforded by the “Atlas” FDM and the use of the grand-averaged data. Ideally, source estimates should be performed using FDMs from MRI segmentation for each participant and applied to their individual dEEG source localization.

A third limitation of the present study is that direct manipulation of contextual information was not performed (aside from keeping all parameters except stimulus–response mappings the same between sessions 1 and 4) and yet context representation is the key concept for understanding the findings. This is mainly due to the fact that the results reported here are novel and needed to be replicated and confirmed with systematic manipulations of the original paradigm. The results are interpreted in light of recent findings from EEG and fMRI studies in humans as well as results from animal studies and provide a foundation from which clear hypotheses can be formulated for future studies. Such studies might involve the manipulation of learning context while keeping stimulus–response mappings consistent.

Conclusion

Based on the present findings, we propose a graded model of learning that emphasizes a progression across ACC, MCC, PCC, and medial temporal lobes in the contextual representation functions of the dorsal corticolimbic network. In the earliest stage of learning, the key cognitive representation of context is an action hypothesis formed within the dorsal ACC as a temporary guide for actions. Although the term “hypothesis” implies a rational process, this temporary action context model can be understood in more primitive terms, such as impulses related to current urges and affordances, or impulses related to associates triggered with past experiences (also see Mitchell et al., 2009). These temporary contexts are tested through trial-and-error, and outcomes of actions are evaluated for motive significance by the rostroventral division of the ACC (e.g., Luu et al., 2003; Taylor et al., 2006), such that outcomes are integrated with actions (Williams et al., 2004) to form action values (Rushworth et al., 2004). This cycle is reiterated and new temporary contexts are generated to guide rapid learning. With this dorsal frontolimbic circuitry providing the key substrate of motivated action, the actual association between stimulus and response is supported by ventrolateral corticolimbic structures, such as the inferior frontal gyrus (Passingham et al., 2000; Luu et al., 2009; Race et al., 2009).

When an action hypothesis is confirmed through repeated successful performance, it is consolidated within the SMA and MCC. This context is still amenable to rapid modification, and it can be used to facilitate relearning of the task or new learning when the new learning situation resembles the existing context. When a behavioral context model is further stabilized through extensive experience, it is then consolidated in the PCC, precuneus, hippocampal network through the process of context updating. This more passive context-updating process slowly adapts changes to the context.

As Gabriel et al. (2002) noted, a system that is organized for rapid learning cannot easily or efficiently deal with the requirement for coding of consistent and enduring stimulus–response contingencies. Here we emphasize that there appears to be an intermediate stage that may overlap with both the early and late learning stages, permitting current context to guide learning of new responses in similar situations while supporting the gradual context-updating process that must occur to support skilled performance.

Conflict of Interest Statement

Some authors of this paper are employes of a commercial EEG company. The research and results presented in this paper were conducted in the absence of any commercial or financial conflicts with their employer, Electrical Geodesics, Inc.

Acknowledgments

This project was supported by the Office of Naval Research, Human Performance, Training, and Education program and NIMH grant RO1 MH070911 to Phan Luu.

References

Balsam, P. D. (1985). “The functions of context in learning and performance,” in Context and Learning, eds P. D. Balsam and A. Tomie (Hillsdale: Lawrence Earlbaum), 1–22.

Barceló, F., Muñoz-Céspedes, J. M., Pozo, M. A., and Rubia, F. J. (2000). Attentional set shifting modulates the target P3b response in the Wisconsin card sorting test. Neuropsychologia 38, 1342–1355.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Behrens, T. E. J., Woolrich, M. W., Walton, M. E., and Rushworth, M. F. S. (2007). Learning the value of information in an uncertain world. Nat. Neurosci. 10, 1214–1221.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Botvinick, M. W., Cohen, J. D., and Carter, C. S. (2004). Conflict monitoring and anterior cingulate cortex: and update. Trends Cogn. Sci. (Regul. Ed.) 8, 539–546.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Brovelli, A., Laksiri, N., Nazarian, B., Meunier, M., and Boussaoud, D. (2008). Understanding the neural computations of arbitrary visuomotor learning through fMRI and associative learning theory. Cereb. Cortex 18, 1485–1495.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Bussey, T. J., Wise, S. P., and Murray, E. A. (2001). The role of ventral and orbital prefrontal cortex in conditional visuomotor learning and strategy use in rhesus monkeys (Macaca mulatta). Behav. Neurosci. 115, 971–982.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Chein, J. M., and Schneider, W. (2005). Neuroimaging studies of practice-related change: fMRI and meta-analytic evidence of a domain general control network for learning. Cogn. Brain Res. 25, 607–623.

CrossRef Full Text

Chiu, P. H., Kayali, M. A., Kishida, K. T., Tomlin, D., Klinger, L. G., Klinger, M. R., and Montague, P. R. (2008). Self responses along cingulate cortex reveal quantitative neural phenotype for high-functioning autism. Neuron 57, 463–473.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Donchin, E., and Coles, M. G. H. (1988). Is the P300 component a manifestation of context updating? Behav. Brain Sci. 11, 357–374.

CrossRef Full Text

Eliassen, J. C., Souza, T., and Sanes, J. N. (2003). Experience-dependent activation patterns in human brain during visual-motor associative learning. J. Neurosci. 23, 10540–10547.

Pubmed Abstract | Pubmed Full Text

Elliott, R., and Dolan, R. J. (1998). Activation of different anterior cingulate foci in association with hypothesis testing and response selection. Neuroimage 8, 17–29.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Ferree, T., Luu, P., Russel, J. S., and Tucker, D. M. (2001). Scalp electrode impedance, infection risk, and EEG data quality. Clin. Neurophysiol. 112, 536–544.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Folstein, J. R., and Van Petten, C. (2008). Influence of cognitive control and mismatch on the N2 component of the ERP: a review. Psychophysiology 45, 152–170.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Gabriel, M., Burhans, L., Talk, A., and Scalf, P. (2002). “Cingulate cortex,” in Encyclopedia of the Human Brain, ed. V. S. Ramachandran (Elsevier Science), 775–791.

Garrido, M. I., Friston, K. J., Kiebel, S. J., Stephan, K. E., Baldeweg, T., and Kilner, J. M. (2008). The functional anatomy of the MMN: a DCM study of the roving paradigm. Neuroimage 42, 936–944.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Gonsalvez, C. J., Gordon, E., Grayson, S., Barry, R. J., Lazzaro, I., and Bahramali, H. (1999). Is the target-to-target interval a critical determinant of P3 amplitude? Psychophysiol. 36, 643–654.

CrossRef Full Text

Gonsalvez, C. L., and Polich, J. (2002). P300 amplitude is determined by target-to-target interval. Psychophysiology 39, 388–396.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Grave de Peralta Menendez, R., Murray, M. M., Michel, C. M., Martuzzi, R., and Gonzalez Andino, S. L. (2004). Electrical neuroimaging based on biophysical constraints. Neuroimage 21, 527–539.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Grol, M. J., de Lange, F. P., Verstraten, F. A. J., Passingham, R. E., and Toni, I. (2006). Cerebral changes during performance of overlearned arbitrary visuomotor associations. J. Neurosci. 26, 117–125.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Holroyd, C. B., and Coles, M. G. H. (2002). The basis of human error processing: reinforcement learning, dopamine, and the error-related negativity. Psychol. Rev. 109, 679–709.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Lancaster, J. L., Woldorff, M. G., Parsons, L. M., Liotti, M., Freitas, C. S., Rainey, L., Kochunov, P. V., Nickerson, D., Mikiten, S. A., and Fox, P. T. (2000). Automated Talairach Atlas labels for functional brain mapping. Hum. Brain Mapp. 10, 120–131.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Lee, D., and Quessy, S. (2003). Activity in the supplementary motor area related to learning and performance during a sequential visuomotor task. J. Neurophysiol. 89, 1039–1056.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Logan, G. (1988). Toward an instance theory of automatization. Psychol. Rev. 95, 492–527.

CrossRef Full Text

Luu, P., Shane, M., Pratt, N. L., and Tucker, D. M. (2009). Corticolimbic mechanisms in the control of trial and error learning. Brain Res. 1247, 100–113.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Luu, P., and Tucker, D. M. (2003). “Self-regulation and the executive functions: electrophysiological clues,” in The Cognitive Electrophysiology of Mind and Brain, Eds. A. Zani and A. M. Preverbio (San Diego: Academic Press), 199–223.

Luu, P., Tucker, D. M., Derryberry, D., Reed, M., and Poulsen, C. (2003). Electrophysiological responses to errors and feedback in the process of action regulation. Psychol. Sci. 14, 47–53.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Luu, P., Tucker, D. M., and Stripling, R. (2007). Neural mechanisms for learning actions in context. Brain Res. 1179, 89–105.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Michel, C. M., Murray, M. M., Lantz, G., Gonzalez, S., Spinelli, L., and Grave de Peralta, R. (2004). EEG source imaging. Clin. Neurophysiol. 115, 2195–2222.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Mitchell, C. J., De Houwer, J., and Lovibond, P. F. (2009). The propositional nature of human associative learning. Behav. Brain Sci. 32, 198–246.

CrossRef Full Text

Newman, J. P., Patterson, M. C., Howland, E. W., and Nichols, S. L. (1990). Passive avoidance in psychopaths: the effects of reward. Pers. Individ. Diff. 11, 1101–1114.

CrossRef Full Text

Passingham, R. E., Toni, I., and Rushworth, M. F. S. (2000). Specialisation within the prefrontal cortex: the ventral prefrontal cortex and associative learning. Exp. Brain Res. 133, 103–113.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Polich, J. (2007). Updating P300: an integrative theory of P3a and P3b. Clin. Neurophysiol. 118, 2128–2148.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Race, E. A., Badre, D., and Wagner, A. D. (2010). Multiple forms of learning yeald temporally distinct electrophysiological repetition effects. Cereb. Cortex 20, 1726–1738.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Race, E. A., Shanker, S., and Wagner, A. D. (2009). Neural priming in human frontal cortex: multiple forms of learning reduce demands on prefrontal executive system. J. Cogn. Neurosci. 21, 1766–1781.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Rushworth, M. F. S., Walton, M. E., Kennerley, S. W., and Bannerman, D. M. (2004). Action sets and decisions in the medial frontal cortex. Trends Cogn. Sci. (Regul. Ed.) 8, 410–417.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Ryynanen, O. R., Hyttinen, J. A., and Malmivuo, J. A. (2006). Effect of measurement noise and electrode density on the spatial resolution of cortical potential distribution with different resistivity values for the skull. IEEE Trans. Biomed. Eng. 53, 1851–1858.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Salimpoor, V. N., Chang, C., and Menon, V. (2010). Neural basis of repetition priming during mathematical cognition: repetition suppression or repetition enhancement? J. Cogn. Neurosci. 22, 790–805.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Schapkin, S. E., Falkenstein, M., Marks, A., and Griefahn, B. (2007). Practice-related effects in a go-nogo task. Percept. Mot. Skills 105, 1275–1288.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Segalowitz, N., and Segalowitz, S. J. (1993). Skilled performance, practice, and the differentiation of speed-up from automatization effects: evidence from second language word recognition. Appl. Psycholinguist. 14, 369–385.

CrossRef Full Text

Smith, A. C., Wirth, S., Suzuki, W. A., and Brown, E. N. (2007). Bayesian analysis of interleaved learning and response bias in behavioral experiments. J. Neurophysiol. 97, 2516–2524.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Summerfield, C., Wyart, V., Johnen, V. M., and de Gardelle, V. (2011). Human scalp electroencephalography reveals that repetition suppression varies with expectation. Front. Hum. Neurosci. 5:67. doi:10.3389/fnhum.2011.00067

CrossRef Full Text

Takehara-Nishiuchi, K., and McNaughton, B. L. (2008). Spontaneous changes of neocortical code for associative memory during consolidation. Science 322, 960–963.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Taylor, S. F., Martis, B., Fitzgerald, K. D., Welsh, R. C., Abelson, J. L., Liberzon, I., Himle, J. A., and Gehring, W. J. (2006). Medial frontal cortex activity and loss-related responses to errors. J. Neurosci. 26, 4063–4070.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Tucker, D. M., and Luu, P. (2007). Neurophysiology of motivated learning: adaptive mechanisms underlying cognitive bias in depression. Cognit. Ther. Res. 31, 189–209.

CrossRef Full Text

Tucker, D. M., Luu, P., Desmond, R. E., Hartry-Speiser, A. L., Davey, C., and Flaisch, T. (2003). Corticolimbic mechanisms in emotional decisions. Emotion 3, 127–149.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Wilcox, R. R. (1997). Introduction to Robust Estimation and Hypothesis Testing. San Diego: Academic.

Williams, Z. M., Bush, G., Rauch, S. L., Cosgrove, G. R., and Eskander, E. N. (2004). Human anterior cingulate neurons and the integration of monetary reward with motor responses. Nat. Neurosci. 7, 1370–1375.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Yamazaki, M., Tucker, D. M., Fujimoto, A., Yamazoe, T., Okanishi, T., Yokota, T., Enoki, H., and Yamamoto, T. (in press). Comparison of dense array EEG with simultaneous intracranial EEG for interictal spike detection and localization. Epilepsy Res. doi:10.1016/j.eplepsyres.2011.09.007. [Epub ahead of print].

CrossRef Full Text