Damping of Alfvén Waves in MHD Turbulence and Implications for Cosmic Ray Streaming Instability and Galactic Winds

1 Propagation of Alfvén Waves in MHD Turbulence

Astrophysical media are turbulent and magnetized (see a collection of relevant reviews in [1]). The propagation of Alfvén waves in turbulent magnetized media is an important astrophysical problem that influences fundamental astrophysical processes (see e.g., [2–5]). This review focuses on the damping of Alfvén waves in MHD turbulence. The Alfvén waves can arise from instabilities induced by cosmic rays (CRs), e.g., from the streaming of CRs [6–9], and the gyroresonance instability related to the compression of magnetic field and CRs (see [10]). They can also be generated by large scale perturbations of magnetic field (see [11] and ref. therein [12]).

Turbulent damping suppresses its growth and affects the streaming speed of CRs. As a result, turbulent damping of streaming instability is important for studies on the diffusion and acceleration of CRs in shocks, galaxies, and galaxy clusters ([13–15], [3,16–18]), stellar wind launching (e.g., [19,20]), and galaxy evolution (e.g., [21]).

It should be noted that the well-known study of Alfvén wave damping by turbulent plasmas performed by Silimon and Sudan [22] employed an unrealistic model of isotropic MHD turbulence. Later, turbulent damping of Alfvén waves was mentioned as a process for suppressing CR streaming instability in Yan and Lazarian [23], henceforth YL02. This process was quantified by Farmer and Goldreich [24], henceforth FG04, where the Goldreich and Sridhar [25]; henceforth, GS95 model of Alfvénic turbulence with scale-dependent anisotropy was adopted. The limitation of the aforementioned study was that for the calculations it was assumed that turbulence is injected isotropically with the turbulent velocity u_L exactly equal to the Alfvén velocity V_A, i.e., Alfvén Mach number M_A equal to unity. In addition, only turbulent damping of streaming instability was considered.

Following the study in Lazarian [26], we will seperately discuss the turbulent damping of Alfvén waves that are generated by streaming instability and by large-scale magnetic perturbations. We will demonstrate the strong dependence of turbulent damping on M_A in various turbulence regimes and astrophysical media with different levels of medium magnetization. In §2 we provide the derivation of the Alfvénic turbulent scaling. In §3 we describe the turbulent damping of Alfvén waves generated by streaming instability in the reference system aligned with the local direction of turbulent magnetic field. In §4 we discuss the turbuelnt damping of Alfvén waves induced by large-scale magnetic perturbations in a global system of reference. We compare the turbulent damping with ion-neutral collisional damping of streaming instability in a partially ionized medium in §5. The numerical testing of the theoretical predictions is provided in §6. The discussion of the astrophysical implications on propagation of CRs in galaxies and launching of winds follows in §7. The summary is given in §8.

2 Derivation of Alfvénic Turbulent Scaling

In Alfvénic turbulence the relative perturbations of velocities and magnetic fields are related as follows:

$\frac{\delta B_l}{B}=\frac{\delta B_l}{B_L}\frac{B_L}{B}=\frac{u_l}{u_L}{M}_A=\frac{u_l}{V_A},(1)$

where B_l is the fluctuation of the magnetic field B at scale l, B_L is the fluctuation of the magnetic field at the driving scale L of turbulence. Correspondingly, u_l is the turbulent velocity fluctuation at the scale l and u_L is the turbulent velocity at L. M_A = u_L/V_A is the Alfvén Mach number.

One way to understand the non-linear interactions of Alfvén waves within the MHD turbulent cascade is to consider colliding Alfvén wave packets with parallel scales l_‖ and perpendicular scales l_⊥. The collision of a wave packet induces an energy change.

$\mathrm{\Delta }E˜\left(d{u}_l^2/dt\right)\mathrm{\Delta }t,(2)$

where the term in brackets manifests the change of the energy of a wave packet induced by its interaction with the oppositely moving Alfvén wave packet. The time of this interaction is equal to the time of the passage of these wave packets through each other. As the size of the packet is l_‖, the interaction time is simply Δt ∼ l_‖/V_A.

The rate of turbulent energy cascade is related to the rate of structure change of the oppositely moving wave packet. The latter is u_l/l_⊥. As a result, Eq. 2 provides

$\mathrm{\Delta }E˜{\mathbf{u}}_l\cdot {\dot{\mathbf{u}}}_l\mathrm{\Delta }t˜\left(u_l^3/l_{\perp }\right)\left(l_{\Vert }/V_A\right),(3)$

The fractional change of packet energy taking place per collision is ΔE/E. This characterises the strength of the nonlinear turbulent interaction:

$f\equiv \frac{\mathrm{\Delta }E}{u_l^2}˜\frac{u_l{l}_{\Vert }}{V_A{l}_{\perp }}.(4)$

In Eq. 4, f is the ratio of the shearing rate of the wave packet, i.e., u_l/l_⊥, to its propagation rate, i.e., V_A/l_‖.

One can identify two distinct cases. If f ≪ 1, the shearing rate is significantly smaller than the propagation rate, and the cascade presents a random walk process. Therefore

$\aleph =f^{-2}(5)$

steps are required for the energy cascade, and therefore the cascading time is

$t_{cas}˜\aleph \mathrm{\Delta }t.(6)$

ℵ > 1 corresponds to the weak turbulent cascade. Naturally, ℵ cannot become less than unity. Therefore, the limiting case is ℵ ≈ 1. This is the case of strong MHD turbulence.

Traditionally, the wavevectors are defined in the system of reference related to the mean field. However, the system of reference related to a wave packet with given parallel and perpendicular dimensions is more relevant when dealing with strong MHD turbulence. We take this into account by considering Alfvén wave packets having the dispersion relation ω = V_A|k_‖|, where we use $k_{\Vert }˜l_{\Vert }^{-1}$ as the component of wavevector parallel to the local background magnetic field. As the result of interaction the increase of $k_{\perp }˜l_{\perp }^{-1}$ occurs. In the rest of the discussion we use l_‖ and l_⊥ that are defined in the local frame of wave packets.

In weak turbulence, the decrease of l_⊥ while l_‖ does not change signifies the increase of the energy change per collision. This forces ℵ to be of the order of unity. In this case one gets

$u_l{l}_{\perp }^{-1}\approx V_A{l}_{\Vert }^{-1}(7)$

in strong turbulence, which signifies the cascading time being equal to the wave period $\sim \mathrm{\Delta }t$. Any further decrease of l_⊥ inevitably results in the corresponding decrease of l_‖ and Eq. 7 is still satisfied. The change of l_‖ entails the increase of the frequencies of interacting waves. This is compatible with the conservation of energy condition above, as the cascade introduces the uncertainty in wave frequency ω of the order of 1/t_cas.

The cascade of turbulent energy satisfies the relation [27]:

$ϵ\approx u_l^2/t_{cas}=const,(8)$

which for the hydrodynamic cascade provides

${ϵ}_{hydro}\approx u_l^3/l\approx u_L^3/L=const,(9)$

where the relation for the cascading time t_cas ≈ l/u_l is employed.

For the weak turbulent cascade with ℵ≫ 1, we have (LV99)

${ϵ}_w\approx \frac{u_l^4}{V_A^2\mathrm{\Delta }t{\left(l_{\perp }/l_{\Vert }\right)}^2}\approx \frac{u_L^4}{V_{A}L},(10)$

where Eqs 6, 8 are used. The isotropic turbulence injection at scale L results in the second relation in Eq. 10. Taking into account that for the weak turbulence l_‖ is constant, it is easy to see that Eq. 10 provides

$u_l˜u_L{\left(l_{\perp }/L\right)}^{1/2},(11)$

which is different from the hydrodynamic $˜l^{1/3}$ scaling¹.

It was shown in LV99 that for turbulence with isotropic injection at scale L with V_L < V_A the transition to the strong regime corresponding to ℵ ≈ 1 happens at the scale

$l_{trans}˜L{\left(u_L/V_A\right)}^2\equiv L{M}_A^2.(12)$

As a result, the inertial range of weak turbulence is limited, i.e., $[L,L{M}_A^2]$, and at l_trans the turbulence transits into the regime of strong MHD turbulence. At the transition, the velocity is

$u_{trans}\approx V_A\frac{l_{trans}}{L}\approx V_A{M}_A^2,(13)$

which follows from ℵ ≈ 1 condition given by Eqs 4, 5.

The scaling relations for the strong turbulence with V_L < V_A can be easily obtained. The turbulence is strong and cascades over one wave period, which according to Eq. 7 is equal to l_⊥/u_l. Substituting the latter in Eq. 8 one gets

${ϵ}_s\approx \frac{u_{trans}^3}{l_{trans}}\approx \frac{u_l^3}{l}=const.(14)$

The latter energy cascading rate is analogous to that in an ordinary hydrodynamic Kolmogorov cascade. However, this cascading takes place in the direction perpendicular to the local direction of the magnetic field².

This strong MHD turbulence cascade starts at l_trans and its injection velocity is given by Eq. 13. This provides another way to obtain the Alfvénic turbulent scaling in strong turbulence regime (LV99).

$u_l\approx V_A{\left(\frac{l_{\perp }}{L}\right)}^{1/3}{M}_A^{4/3},(15)$

which can be rewritten in terms of the injection velocity u_L (see Eq. 15).

$\delta u_l\approx u_L{\left(\frac{l_{\perp }}{L}\right)}^{1/3}{M}_A^{1/3}.(16)$

Substituting this in Eq. 7 we get the relation between the parallel and perpendicular scales of the eddies (LV99):

$l_{\Vert }\approx L{\left(\frac{l_{\perp }}{L}\right)}^{2/3}{M}_A^{-4/3}.(17)$

The relations Eqs 15, 17 reduce to the GS95 scaling for transAlfvénic turbulence if M_A ≡ 1.

In the opposite case we deal with superAlfvénic turbulence, i.e., with u_L > V_A. As a result, at scales close to the injection scale the turbulence is essentially hydrodynamic as the influence of magnetic forces is marginal. Therefore, the velocity is Kolmogorov.

$u_l=u_L{\left(l/L\right)}^{1/3}.(18)$

The magnetic field becomes more important at smaller scales and the cascade changes its nature at the scale.

$l_A=L{M}_A^{-3},M_A>1,(19)$

at which the turbulent velocity becomes equal to the Alfvén velocity [28]. The rate of cascade for l < l_A is:

${ϵ}_{superA}\approx u_l^3/l\approx M_A^3{V}_A^3/L=const.(20)$

Unlike the case of subAlfvénic turbulence, the case of superAlfvénic turbulence can be reduced to the case of transAlfvénic turbulence, but with l_A acting as the injection scale. At scales l < l_A.

$l_{\Vert }\approx L{\left(\frac{l_{\perp }}{L}\right)}^{2/3}{M}_A^{-4/3},(21)$

$u_l\approx u_L{\left(\frac{l_{\perp }}{L}\right)}^{1/3}{M}_A^{1/3}.(22)$

The relations for subAlfvénic and superAlfvénic tubulence that we obtain above coincide with the expressions first obtained in Lazarian and Vishniac [29] using a different approach. These expressions will be used below in our discussion on turbulent damping of Alfvén waves.

3 Turbulent Damping of Streaming Instability

Linear Alfvén waves undergo non-linear cascading when they propagate through Alfvénic turbulence. This process is of MHD nature and the non-linear damping of Alfvén waves does not depend on plasma microphysics. The interaction between CR-driven Aflven waves and turbulence is similar to that of oppositely moving wave packets of turbulent cascade.

The Alfvén waves emitted parallel to the local magnetic field experiences the least distortions from the oppositely moving eddies. Thus the least distorted Alfvén waves are those with the largest value of l_⊥. Indeed, the larger l_⊥, the longer time it takes for the evolution of the oppositely moving wave packets. For instance, for strong GS95 turbulence the time corresponds to $l_{\perp }/v_l˜l_{\perp }^{2/3}$.

The case of Alfvén waves parallel to the local direction of magnetic field corresponds to streaming and gyroresonance instabilities. In what follows, we will focus on the streaming instability. The dispersion of magnetic field directions with respect to the mean magnetic field determines the corresponding l_⊥. Naturally, the turbulent damping of Alfvén waves is different for weak turbulence and strong turbulence. Thus we will separately discuss turbulent damping of streaming instability in different turbulence regimes.

3.1 Streaming Instability and Local System of Reference

The streaming instability of CRs happens as CR particles moving in one direction scatter back from a magnetic field perturbation and thus increase the amplitude of the perturbation. The induced perturbations are Alfvén waves. If the Alfvén waves are severely damped, the CR particles can stream freely along the magnetic field.

Physically, the generation of Alfvén waves takes place as CRs stream along the local magnetic field. During the process the sampling scale for the magnetic field is the CR Larmor radius r_L. In this setting one should consider the process in the system of reference related to the local direction³ of the wondering magnetic field (LV99, [31–33]).

In the direction parallel to the local magnetic field, the growth rate of the streaming instability is (see [7]):

${\mathrm{\Gamma }}_{cr}\approx {\mathrm{\Omega }}_B\frac{n_{cr}\left(>\gamma \right)}{n_i}\left(\frac{v_{stream}}{V_A}-1\right),(23)$

where Ω_B = eB/mc is the nonrelativistic gyrofrequency, n_cr is the number density of CRs with gyroradius r_L > λ = γmc²/eB, and γ is the Lorentz factor. If the growth rate given by Eq. 23 is less than the rate of turbulent damping, the streaming instability is suppressed.

3.2 Damping by SubAlfvénic Strong Turbulence

Our first approach is based on calculating the distortion of Alfvén waves by MHD turbulence as the waves propagate along magnetic field. The cause of the wave distortion is the field line wandering over angle θ_x. This angle is determined by the amplitude of magnetic field fluctuations δB_x that are induced by turbulent eddies with perpendicular scale x. One can see that the distortion induced during the time t is

${\delta }_x\approx V_{A}t{\sin }^2{\theta }_x\approx V_{A}t{\left(\frac{\delta B_x}{B}\right)}_t^2,(24)$

where the fluctuation induced by turbulence evolves as

${\left(\frac{\delta B_x}{B}\right)}_t\approx \left(\frac{u_x}{V_A}\right)\left(\frac{t}{x/u_x}\right).(25)$

In the above expression u_x denotes the velocity corresponding to the magnetic field fluctuation δB_x. The time t in Eq. 25 is chosen to be less than the eddy turnover time x/u_x. As a result, the ratio reflects the partial sampling of the magnetic perturbation by the wave. By using the velocity scaling of strong subAlfvénic turbulence for u_x in Eq. 25, it is easy to rewrite Eq. 24 as

${\delta }_x\approx \frac{V_A^3{M}_A^{16/3}{t}^3}{x^{2/3}{L}^{4/3}}.(26)$

The wave damping corresponds to the “resonance condition” δ_x = λ, where λ is the wavelength. Inserting this in Eq. 26 we obtain the perpendicular scale of the “resonance” magnetic fluctuations that distort the Alfvén waves:

$x\approx \frac{V_A^{9/2}{t}^{9/2}{M}_A^8}{{\lambda }^{3/2}{L}^2}.(27)$

The time required to damp the Alfvén waves is equal to the turnover time of the “resonant” eddy:

$t\approx \frac{x}{u_l}\approx \frac{V_A^2{t}^3{M}_A^4}{\lambda L}.(28)$

This provides the rate of non-linear damping of the Alfvén waves,

${\mathrm{\Gamma }}_{subA,s}\approx t^{-1},(29)$

or

${\mathrm{\Gamma }}_{subA,s}\approx \frac{V_A{M}_A^2}{{\lambda }^{1/2}{L}^{1/2}},(30)$

where the subsscript “s” denotes “strong turbulence.” For transAlfvénic turbulence, i.e., M_A = 1, this result was obtained in FG04. The square of the Alfvén Mach number dependence presented in Eq. 30 means a significant change of the damping rate compared to the transAlfvénic case⁴.

If the injection of turbulence is isotropic, the maximal perpendicular scale of strong subAlfvénic motions is $x_{\max }=L{M}_A^2$. Substituting this in Eq. 27 and using Eq. 29 and Eq. 30 to express t, we get

${\lambda }_{\mathit{max},s}\approx L{M}_A^4.(31)$

The streaming CRs generate Alfvén waves at a scale comparable to the gyroradius r_L. Thus it requires that

$r_L<L{M}_A^4,(32)$

which is a notable limitation on CR energy if M_A is small. The CRs with larger energies interact with weak turbulence as we will discuss in Section 3.3.

Due to the importance of turbulent damping of streaming instability, it is advantageous to provide another derivation of Eq. 30. This alternative derivation is based on the picture of propagating wave packets that we used while obtaining Eq. 3. Consider two oppositely moving Alfvén wave packets with the perpendicular scale $x^{\prime }˜k_{\perp }^{\prime -1}$. As we discussed earlier, each wave packet induces the distortion ${\theta }_x^{\prime }$ of the oppositely moving waves. Consider an Alfvén wave with wavenumber $k_{\Vert }^{-1}˜\lambda$ moving parallel to the local direction of magnetic field. Such a wave is mostly distorted when interacting with turbulent perturbations with the perpendicular wavenumber $k_{\perp }˜k_{\Vert }\sin {\theta }_x^{\prime }$. The interactions are most efficient if they are “resonant,” i.e., a wave with k_⊥ interacts with the oppositely moving packets and $k_{\perp }^{\prime }=k_{\perp }$⁵. Thus the perpendicular scale of the “resonant” wave packet is determined by the relation k_‖ sin θ_x = k_⊥, which results in

$\lambda \approx x\sin {\theta }_x\approx x\frac{\delta B_x}{B}.(33)$

Using the scaling in Eqs 15, 25, we derive the “resonant” perpendicular scale x:

$x=L^{1/4}{\lambda }^{3/4}{M}_A^{-1}.(34)$

This can be used to determine the rate of damping defined as Γ_subA,s ≈ u_x/x. This coincides with the earlier result given by Eq. 30. Then the maximal wavelength of the non-linearly damped Alfvén waves can be obtained from Eq. 33 if the scale l_trans is used instead of x, i.e.

${\lambda }_{\mathit{max},s}\approx \left(\frac{u_{trans}}{V_A}\right)l_{trans}\approx L{M}_A^4.(35)$

Naturally, the latter coincides with the result given by Eq. 31. The minimal scale of non-linearly damped waves depends on the perpendicular scale of the smallest Alfvénic eddies l_min. The full range of r_L for which turbulent damping is essential can be obtained by using Eq. 33 and the scaling of strong turbulence given by Eq. 15:

$\frac{l_{\mathit{min}}^{4/3}}{L^{1/3}}{M}_A^{4/3}<r_L<L{M}_A^4.(36)$

The value of l_min depends on the particular damping process of MHD turbulent cascade, which can be relatively large in a weakly ionized gas (see [34]). Due to the differences of r_L for protons and electrons, Eq. 36 presents a possible situation when the streaming instability of CR electrons is not damped by turbulence, while it is damped for CR protons.

We note that the turbulent damping of streaming instability for $r_L<\frac{l_{\mathit{min}}^{4/3}}{L^{1/3}}{M}_A^{4/3}$ is still present, although it is reduced. We can get an estimate of it by considering the distortion δ_x ≪ λ given by Eq. 26 for the time period of the wave λ/V_A. This time is significantly less than the period of the eddy at the scale l_min, $t_{eddy}\approx l_{\mathit{min}}^{2/3}{L}^{1/3}/(V_A{M}_A^{4/3})$. The distortions act in a random walk fashion with the time step given by t_eddy. The damping requires λ/δ_x steps, which induces the damping rate.

${\mathrm{\Gamma }}_{sub,s,r_L\ll l_{\mathit{min}}}\approx \frac{M_A^{12}{V}_A{r}_L^4}{l_{\mathit{min}}^2{L}^3}.(37)$

The latter clearly illustrates the inefficiency of damping when turbulence has the perpendicular scale larger than the “resonant” scale.

3.3 Damping by SubAlfvénic Weak Turbulence

In many instances the weak turbulence is not important. It has a limited inertial range and transfers to strong turbulence at smaller scales. However, as we show below, this may not be true for wave damping by turbulence. For wavelengths longer than λ_max ,s the wave is non-linearly damped through interactions with the wave packets of the weak turbulence, having perpendicular scales given by Eq. 33. Naturally, the scaling of weak turbulence given by Eq. 11 should be used. This provides the relation between the Alfvén wave wavelength and the perpendicular scale of the “resonant” weak turbulence perturbation.

$\lambda =l_{\perp }{\left(\frac{l_{\perp }}{L}\right)}^{1/2}{M}_A.(38)$

This delivers the perpendicular scale

$l_{\perp }\approx {\lambda }^{2/3}{L}^{1/3}{M}_A^{-2/3}.(39)$

According to Eqs 5, 6, the weak turbulence packets cascade ℵ times slower compared to the case of strong turbulence. Taking into account that the parallel scale of weak turbulence wave packets is equal to the injection scale L, we have

$\aleph \approx {\left(\frac{V_A{l}_{\perp }}{u_{l}L}\right)}^2.(40)$

The rate of turbulent damping of the wave is therefore

${\mathrm{\Gamma }}_{subA,w}\approx {\left(\aleph \mathrm{\Delta }t\right)}^{-1}={\aleph }^{-1}\frac{V_A}{L},(41)$

which gives

${\mathrm{\Gamma }}_{subA,w}\approx \frac{V_A{M}_A^{8/3}}{{\lambda }^{2/3}{L}^{1/3}},(42)$

where the subsscript “w” denotes “weak turbulence.” Note that compared to the case of damping given by Eq. 30 we now have a stronger dependence on M_A, as well as a different scaling with the wavelength λ.

The maximal wavelength of the Alfvén waves that is cascaded by the weak cascade we derive by substituting l_⊥ = L, i.e., using the energy injection scale in Eq. 38. This gives:

${\lambda }_{\mathit{max},w}\approx L{M}_A.(43)$

Thus for CRs that generate Alfvén waves, their r_L should satisfy

$L{M}_A^4<r_L<L{M}_A(44)$

to interact with weak Alfvénic turbulence. The underlying assumption here is that $L{M}_A^4$ is larger than the turbulent damping scale l_min. Otherwise the lower boundary in Eq. 44 is determined by l_min.

Waves with λ > λ_max ,w can interact with the turbulent motions at the injection scale L. The cascade of such waves is induced by the largest wave packets at a rate ${\aleph }^{-1}\frac{V_A}{L}$, i.e.,

${\mathrm{\Gamma }}_{outer}\approx {\aleph }^{-1}\frac{V_A}{L}\approx M_A^2\frac{V_A}{L},(45)$

which does not depend on wavelength. Physically, this means that all waves in the range LM_A < λ < L decay at the same rate that is determined by the restructuring of the magnetic field at the injection scale.

The above expression is valid for λ < L. In the case of λ ≫ L the rate is reduced due to the random walk, which results in a factor (L/λ)², i.e.,

${\mathrm{\Gamma }}_{outer,extreme}\approx {\aleph }^{-1}\frac{V_A}{L}\frac{L^2}{{\lambda }^2}\approx M_A^2\frac{V_A}{L}\frac{L^2}{{\lambda }^2}.(46)$

The latter result is relevant for the damping induced by turbulence injected at scales smaller than the wavelength.

In terms of the dependence of damping rate on λ for subAlfvénic turbulence, we observe that the dependence becomes stronger with the increase of λ up to λ = LM_A. For λ less than $L{M}_A^4$, the waves interact with strong Alfvénic turbulence and the damping rate Γ is proportional to λ^−1/2. The scaling changes for waves longer than $L{M}_A^4$ but shorter than LM_A. The scaling of Γ gets to λ^−2/3 as Alfvén waves interact with weak turbulence. For smaller M_A the range for which weak Alfvénic turbulence damps Alfvén waves increases. A further increase of the wavelength, i.e., for λ from LM_A to L, introduces a flat regime of damping, i.e., no dependence on λ. The damping at this regime is determined by the evolution of turbulence at the injection scale. In its turn, this regime proceeds untill λ gets of the order of L. Finally, if λ is much larger than L, the damping modifies further that it transfers to λ⁻². In that regime the Alfvén waves have so large λ that they only feel the distortions that are introduced by turbulence at the outer scale. In comparison, the FG04 study considered only transAlfvénic turbulence and provided only λ^−1/2 scaling for all scales.

In terms of the dependence of turbulent damping rate on M_A, it changes from $M_A^2$ for strong turbulence to $M_A^{8/3}$ for weak turbulence. The case of no damping naturally follows as M_A → 0. As for FG04 study, it only provided the result for M_A = 1.

3.4 Damping by SuperAlfvénic Turbulence

As we discussed earlier, if turbulence is superAlfvénic, at large scales the effects of magnetic field are marginal and turbulence is hydrodynamic-like. However, the turbulent velocity decreases with the decreasing scale and at a scale l_A becomes equal to the Alfvén velocity. This scale can be considered as the injection scale of transAlfvénic turbulence. Therefore, the case of Alfvén wave damping by superAlfvénic turbulence at scales less than l_A can be related to the case of damping by transAlfvénic turbulence considered in FG04. Indeed, a simple substitution of L by l_A provides the required rate of magnetic structure evolution on scales less than l_A. This gives:

${\mathrm{\Gamma }}_{super}\approx \frac{V_A}{l_A^{1/2}{\lambda }^{1/2}}=\frac{V_A{M}_A^{3/2}}{L^{1/2}{\lambda }^{1/2}}.(47)$

Treating l_A as the effective injection scale and using Eq. 31, it is easy to obtain the maximal wavelength up to which our treatment of the non-linear damping is applicable:

${\lambda }_{\mathit{max},super}\approx l_A=L{M}_A^{-3}.(48)$

Associating λ with r_L, we define the corresponding range of r_L

$\frac{l_{\mathit{min}}^{4/3}}{L^{1/3}}{M}_A<r_L<L{M}_A^{-3},(49)$

assuming that the minimal/damping scale of turbulent motions l_min is less than $L{M}_A^{-3}$.

For Alfvén waves with λ larger than that given by Eq. 48 and therefore for $r_L>L{M}_A^{-3}$, the damping is induced by Kolmogorov-type isotropic hydrodynamic turbulence. The characteristic damping rate in this case is expected to coincide with the eddy turnover rate, i.e.,

${\mathrm{\Gamma }}_{hydro}\approx \frac{u_{\lambda }}{\lambda }\approx \frac{V_A}{l_A^{1/3}{\lambda }^{2/3}}\approx \frac{V_A{M}_A}{L^{1/3}{\lambda }^{2/3}},(50)$

where we use Eq. 18.

Similar to the case of sub-Alfvénic turbulence, in superAlfvénic case, we observe the change of the rate of Alfvén wave damping changing from λ^−1/2 for short wavelengths to λ^−2/3 for λ longer than $L{M}_A^{-3}$. The turbulent damping rate of Alfvén waves increases with M_A.

3.5 Other Forms of Presenting Our Results

The scaling of weak turbulence is different from that of strong turbulence that starts at the transition scale $l_{trans}=L{M}_A^2$ of subAlfvénic turbulence. However, what is the same in the two regimes of turbulence is the cascading rate. Indeed, the energy cascades at the same rate without accumulating at any scale and dissipates only at the small dissipation scale. Therefore, by expressing the dissipation rate of Alfvén waves through the cascading rate of turbulence, we will demonstrate a higher degree of universality of the obtained expressions.

The cascading rate of the weak turbulence is given by Eq. 10 and we can write it as

${ϵ}_w\approx \frac{V_A^3{M}_A^4}{L}.(51)$

This reflects the decrease of energy dissipation by $M_A^4$ compared to the case of transAlfvénic turbulence in FG04. If $r_L<L{M}_A^4$, the rate of Alven wave damping can be obtained by combining Eq. 51 and Eq. 30:

${\mathrm{\Gamma }}_{subA,s}\approx \frac{{ϵ}_w^{1/2}}{V_A^{1/2}{r}_L^{1/2}}.(52)$

The peculiar feature of Eq. 52 is that if one formally substitutes instead of ϵ_w the cascading rate of strong turbulence, one will get the expression in FG04. This is exactly the universality of expressions that we sought. Nevertheless, this analogy is only formal as the cascading rate for weak turbulence is $M_A^4$ times lower compared to the transAlfvénic case. Therefore, the obtained damping rate for subAlfvénic turbulence is $M_A^2$ times less than the case of trans-Alfvénic turbulence (see also Eq. 30).

For wavelengths in the range $L{M}_A^4<\lambda <L{M}_A$ the weak turbulence is responsible for the Alfvén wave damping. Thus, expressing M_A from Eq. 51 and substituting it in Eq. 42 we can get

${\mathrm{\Gamma }}_{subA,w}\approx \frac{{ϵ}_w^{1/3}{L}^{1/3}}{V_A{r}_L^{2/3}}\approx \frac{{ϵ}_w^{1/3}{M}_A^{4/3}}{r_L^{2/3}}.(53)$

The expression given by Eq. 53 demonstrates a slower damping rate in comparison to Eq. 52. The decrease of damping rate by the factor $M_A^{8/3}$ (see Eq. 42) is significant. It is important to note that for M_A ≪ 1 it provides the smooth transition to the regime of marginal Alfvén wave damping as the magnetic field perturbations get smaller and smaller. Naturally, this expression is very different from that in FG04, as the latter study did not consider the damping induced by weak Alfvénic turbulence.

For damping of Alfvén waves generated by CRs with larger r_L, i.e. LM_A < r_L < L (see Eq. 38) we obtain:

${\mathrm{\Gamma }}_{outer}\approx \frac{{ϵ}_w^{1/2}}{L^{1/2}{V}_A^{1/2}}.(54)$

For superAlfvénic turbulence at scales less than l_A, by expressing M_A from Eq. 20 and substituting it in Eq. 47, we obtain

${\mathrm{\Gamma }}_{super}\approx \frac{{ϵ}_{super}^{1/2}}{V_A^{1/2}{r}_L^{1/2}}.(55)$

Formally, the above expression coincides with the expression for the damping by subAlfvénic strong turbulence given by Eq. 52. Nevertheless, the subAlfvénic turbulence demonstrates the significant reduction of the cascading rate compared to the transAlfvénic turbulence. On the contrary, the superAlfvénic strong MHD turbulence corresponds to a significant increase of dissipation rate in comparison with the transAlfvénic case. Thus, for the same injection scale L and the same injection velocity V_L, the damping of Alfvén waves depends on the magnetization of media. At a lower magnetization, e.g., for superAlfvénic turbulence, the damping of Alfvén waves is more efficient than that at a higher medium magnetization, i.e., for the subAlfvénic case.

As we discussed earlier, in superAlfvénic turbulence, the long Alfvén waves with λ larger than $l_A=L{M}_A^{-3}$ interact with hydrodynamic turbulence and the corresponding damping rate is

${\mathrm{\Gamma }}_{hydro}\approx \frac{{ϵ}_{hydro}^{1/3}}{r_L^{2/3}},(56)$

where the hydrodynamic dissipation rate is ${ϵ}_{hydro}\approx V_L^3/L$.

Below we present a few more forms of presenting the damping rates that we obtained above. For instance, it could be sometimes useful to rewrite the expressions given by Eqs 30, 42 in terms of λ_max ,s given by Eq. 35. We remind the reader that the physical meaning of λ_max ,s is the longest wavelength that still interacts with strong turbulent cascade. Then,

${\mathrm{\Gamma }}_{subA,s}\approx \frac{V_A}{L}{\left(\frac{{\lambda }_{\mathit{max},s}}{r_L}\right)}^{1/2},r_L<{\mathit{\lambda }}_{\mathit{max},s},(57)$

and

${\mathrm{\Gamma }}_{subA,w}\approx \frac{V_A}{L}{\left(\frac{{\lambda }_{\mathit{max},s}}{r_L}\right)}^{2/3},r_L>{\lambda }_{\mathit{max},s}.(58)$

It is easy to see that Eq. 57 demonstrates that the damping by strong MHD turbulence Γ_subA,s happens faster than the Alfvén crossing rate of the injection scale eddies. In the case of weak turbulence, Eq. 58 demonstrates that Γ_subA,w is slower than the above rate.

4 Turbulent Damping of Alfvén Waves Generated in the Global System of Reference

The turbulent damping of Alfvén waves generated by streaming CRs is an important special case of turbulent damping as the streaming instability induces Alfvén waves that are aligned with the local direction of magnetic field. Another case arises if we consider the damping of a flux of Alfvén waves generated by an extended source. The difference between the two cases is that in the latter setting the waves are generated irrespectively to the local direction of magnetic field. Therefore, such Alfvén waves should be viewed in the global system of reference related to the mean magnetic field. As a result, our earlier treatment of the Alfvén wave damping by MHD turbulence should be modified.

4.1 Case of Strong SubAlfvénic Turbulence

Consider an Alfvén wave generated at an angle θ ≫ δB/B with respect to the global mean magnetic field. In this situation it is natural to disregard the dispersion of angles that arises from magnetic wandering induced by turbulence⁶. To distinguish these two cases we use sin θ instead of sin θ_x in Eq. 33. In this case the perpendicular scale of eddies that the waves interact with is given by:

$x\approx \frac{\lambda }{\sin \theta }.(59)$

For strong turbulence the rate of the wave damping is equal to the turnover rate of subAlfvénic eddies. Therefore using Eq. 59, we find

${\mathrm{\Gamma }}_{subA,s,\theta }\approx \frac{V_A{M}_A^{4/3}{\sin }^{2/3}\theta }{{\lambda }^{2/3}{L}^{1/3}}.(60)$

This provides the non-linear damping rate of an Alfvén wave moving at the angle θ with respect to the mean field.

Using the expression of weak turbulent cascading rate ϵ_w (see Eq. 10), one can write:

${\mathrm{\Gamma }}_{subA,s,\theta }\approx \frac{{ϵ}_w^{1/3}{\sin }^{2/3}\theta }{{\lambda }^{2/3}}.(61)$

The turbulent damping given by Eq. 61 is applicable to

$l_{\mathit{min}}\sin \theta <\lambda <L{M}_A^2\sin \theta ,(62)$

where l_min is the perpendicular damping scale, and $L{M}_A^2=l_{trans}$ is the transition scale from strong to weak MHD turbulence.

Naturally, the adopted approximation θ ≫ δB/B fails if the wave is launched parallel to the mean magnetic field. The directions of the local magnetic field deviates from the mean field and this makes the actual θ₀ different from zero. In the global system of reference the dispersion is dominated by the magnetic field variations presented at the injection scale (see [33]). Therefore

${\theta }_0\approx \frac{B_L}{B}\approx M_A.(63)$

Substituting this into Eq. 60 we get

${\mathrm{\Gamma }}_{subA,s,0}\approx \frac{{ϵ}_w^{1/3}{M}_A^{2/3}}{{\lambda }^{2/3}}.(64)$

The above expression is different from Eqs 30, 52. The difference stems from the different properties of Alfvén waves generated in the local system versus the global system of reference. The damping rate in Eq. 64 is applicable to the range of wavelength.

$l_{\mathit{min}}{M}_A<\lambda <L{M}_A^3,(65)$

the latter result trivially follows from Eqs 62, 63.

4.2 The Case of Weak SubAlfvénic Turbulence

For weak subAlfvénic turbulence, in the case θ ≫ δB/B, one should use Eq. 59 to relate λ to the scale of perpendicular motions that the wave strongly non-linearly interacts with. To obtain the damping rate, Eq. 41 should be used:

${\mathrm{\Gamma }}_{weak,global,\theta }\approx \frac{V_A\sin \theta M_A^2}{\lambda }\approx \frac{{ϵ}^{1/2}{L}^{1/2}\sin \theta }{V_A^{3/2}\lambda },(66)$

where we use the weak cascading rate ϵ_w. The range of wavelength for this type of damping is

$L{M}_A^2\sin \theta <\lambda <L{M}_A\sin \theta .(67)$

The last inequality is obtained by substituting the maximal perpendicular eddy scale LM_A for x in Eq. 59.

In the case of Alfvén wave propagation along the mean magnetic field, one should use Eq. 63 to get

${\mathrm{\Gamma }}_{weak,global,0}\approx \frac{V_A{M}_A^3}{\lambda }\approx \frac{V_A{ϵ}^{3/4}{L}^{3/4}}{\lambda V_A^{5/4}}.(68)$

Using Eqs 63, 67, we find the range of wavelength that is subject to the turbulent damping:

$L{M}_A^3<\lambda <L{M}_A^2.(69)$

4.3 Other Cases

After illustrating the difference of non-linear damping for waves generated in the local reference system of magnetic field and in the global reference system of the mean field, we can provide results for other cases. More detailed discussion was presented in Lazarian [26]. For instance, for superAlfvénic turbulence, there is

${\mathrm{\Gamma }}_{super,global,\theta }\approx \frac{V_A{M}_A{\sin }^{2/3}\theta }{{\lambda }^{2/3}{L}^{1/3}},(70)$

where in superAlfvénic turbulence angle θ varies from one turbulent eddy of size l_A to another. As a result, the corresponding averaging over such changing directions should be performed. For the random distribution of the relevant directions, the corresponding geometric factor is ⟨ sin^2/3θ⟩ = 3/5.

On scales larger than l_A, MHD turbulence is marginally affected by magnetic fields. As a result, no difference between local and global frames is present in terms of Alfvén wave damping. This difference also disappears for the damping by turbulent fluctuations at the injection scale.

4.4 Summary of Main Results in Sections 3 and 4 on Turbulent Damping

Some of our results for non-linear turbulent damping of Alfvén waves in different turbulence regimes are summarized in Table 1.

TABLE 1

TABLE 1. Regimes of MHD turbulence and turbulent Alfvén wave damping.

We show results relevant both to the damping of waves in the local system of reference, e.g., corresponding to the waves generated by streaming instability (fifth column in Table 1 with the name “Instability damping rate”), and the damping of waves generated by external sources parallel to the mean magnetic field (sixth column in Table 1 with the name “Wave damping rate”). The table illustrates that the rate of damping and the ranges of wavelengths for which damping is applicable are very different for the two situations. At the first glance, this seems strange. However, the difference stems from the fact that in the case of streaming instability the waves are aligned with the local magnetic field, while the waves generated by an extended source are sent parallel to the mean magnetic field.

We did not cover in Table 1 the general case of Alfvén waves generated at an arbitrary angle relative to the mean magnetic field, as well as damping of Alfvén waves by outer-scale turbulence. It is also necessary to stress again the important role of weak turbulence for the suppression of streaming instability at low M_A. While the weak turbulence is frequently disregarded due to its limited inertial range $[L{M}_A^2,L]$, it can affect CR streaming for r_L in the range $[L{M}_A^4,L{M}_A]$, which can be extensive for sufficiently small M_A.

5 Ion-Neutral Collisional Damping of Streaming Instability

In the presence of partial ionization, an additional effect of damping by ion-neutral collisions becomes important. This effect was discussed originally by Kulsrud and Pearce [7] for Alfvén waves. The damping of turbulent motions in partially ionized gas was recently summarized in Xu and Lazarian [34].

In the presence of neutrals, a slippage between them and ions induces the dissipation. In a mostly neutral medium, at wave frequencies ω = V_Ak_‖ less than the neutral-ion collisional frequency ν_ni, both species move together and the dissipation is minimal. As the wave frequency increases, not all neutrals get the chance to collide with ions and the relative motions of ions and neutrals induce significant dissipation. For strongly coupled ions and neutrals, the ion-neutral collisional (IN) damping rate is [7].

${\mathrm{\Gamma }}_{IN}=\frac{{\xi }_n{V}_A^2{k}_{\Vert }^2}{2{\nu }_{ni}},(71)$

where ξ_n = ρ_n/ρ, and ρ_n and ρ are the neutral and total mass densities. For weakly coupled ions and neutrals with ω = V_Aik_‖ > ν_in, where V_Ai is the Alfvén speed in ions and ν_in is the ion-neutral collisional frequency, there is

${\mathrm{\Gamma }}_{IN}=\frac{{\nu }_{in}}{2}.(72)$

We note that both turbulent and wave motions are subject to the IN damping. Strong Alfvénic turbulence injected in the strong coupling regime cannot cascade into the weak coupling regime due to the severe damping effect [35,36].

IN damping is sensitive to the ionization fraction and becomes weak at a high ionization fraction. For strongly coupled ions and neutrals with V_Ak_‖ < ν_in, Γ_IN is still given by Eq. 71. For decoupled ions with V_Aik_‖ > ν_in, there is [36].

${\mathrm{\Gamma }}_{IN}=\frac{{\nu }_{ni}\chi V_{Ai}^2{k}_{\Vert }^2}{2\left[{\left(1+\chi \right)}^2{\nu }_{ni}^2+V_{Ai}^2{k}_{\Vert }^2\right]},(73)$

where χ = ρ_n/ρ_i and ρ_i is the ion mass density. Furthermore, when neutrals are also decoupled from ions with V_Aik_‖ > ν_ni, the above expression is reduced to Eq. 72. Because of the weak damping effect, Alfvénic cascade in a highly ionized medium is not dissipated by IN damping [18].

Naturally, to understand whether turbulent damping or IN damping is more important for damping the streaming instability, Γ_IN should be compared with the turbulent damping rate Γ that we provided earlier. This comparison has been recently carried out in detail by Xu and Lazarian [18]. Here we selectively review some of their results.

In a weakly ionized interstellar medium, e.g., molecular clouds, CR-driven Alfvén waves are likely in the weak coupling regime with

$\frac{V_{Ai}}{r_L{\nu }_{in}}\approx 2\times 10^3{\left(\frac{B_0}{10\mu \text{G}}\right)}^2{\left(\frac{n_H}{100{\text{cm}}^{-3}}\right)}^{-\frac{3}{2}}{\left(\frac{n_e/n_H}{10^{-4}}\right)}^{-\frac{1}{2}}{\left(\frac{E_{CR}}{1\text{GeV}}\right)}^{-1}\gg 1,(74)$

where B₀ is the mean magnetic field strength, n_e and n_H are number densities of electrons and atomic hydrogen, and E_CR is the CR energy. As already mentioned above, strong Alfvénic turbulence injected at a large scale in the strong coupling regime is severely damped and its cascade cannot persist in the weak coupling regime. Therefore, there is

$\mathrm{\Gamma }<{\mathrm{\Gamma }}_{IN}=\frac{{\nu }_{in}}{2}.(75)$

So the damping of streaming instability in a weakly ionized medium is dominated by IN damping.

In a highly ionized interstellar medium, e.g., the warm ionized medium, CR-generated Alfvén waves are still in the weak coupling regime and have

$\frac{V_{Ai}}{r_L{\nu }_{ni}}=7.6\times 10^3{\left(\frac{B_0}{1\mu \text{G}}\right)}^2{\left(\frac{n_i}{0.1{\text{cm}}^{-3}}\right)}^{-\frac{3}{2}}{\left(\frac{E_{CR}}{1\text{GeV}}\right)}^{-1}\gg 1.(76)$

To have the turbulent damping dominate over IN damping, there should be

$\frac{\mathrm{\Gamma }}{{\mathrm{\Gamma }}_{IN}}=\frac{\mathrm{\Gamma }}{\frac{{\nu }_{in}}{2}}>1,(77)$

which can be rewritten as

$\begin{array}{cc}\hfill M_A& >{\left(\frac{{\nu }_{in}}{2}{V}_{Ai}^{-1}{L}^{\frac{1}{2}}{r}_L^{\frac{1}{2}}\right)}^{\frac{2}{3}}\hfill \\ \hfill & =0.2{\left(\frac{B_0}{1\mu \text{G}}\right)}^{-1}{\left(\frac{n_i}{0.1{\text{cm}}^{-3}}\right)}^{\frac{1}{3}}{\left(\frac{n_n}{0.01{\text{cm}}^{-3}}\right)}^{\frac{2}{3}}{\left(\frac{L}{100\text{pc}}\right)}^{\frac{1}{3}}{\left(\frac{E_{CR}}{1\text{GeV}}\right)}^{\frac{1}{3}}\hfill \end{array}(78)$

for superAlfvénic turbulence, where n_i and n_n are the number densities of ions and neutrals, and

$\begin{array}{cc}\hfill M_A& >{\left(\frac{{\nu }_{in}}{2}{V}_{Ai}^{-1}{L}^{\frac{1}{2}}{r}_L^{\frac{1}{2}}\right)}^{\frac{1}{2}}\hfill \\ \hfill & =0.3{\left(\frac{B_0}{1\mu \text{G}}\right)}^{-\frac{3}{4}}{\left(\frac{n_i}{0.1{\text{cm}}^{-3}}\right)}^{\frac{1}{4}}{\left(\frac{n_n}{0.01{\text{cm}}^{-3}}\right)}^{\frac{1}{2}}{\left(\frac{L}{100\text{pc}}\right)}^{\frac{1}{4}}{\left(\frac{E_{CR}}{1\text{GeV}}\right)}^{\frac{1}{4}}\hfill \end{array}(79)$

for subAlfvénic turbulence. We see that the condition in Eq. 78 is naturally satisfied for superAlfvénic turbulence. In a highly ionized medium, as the IN damping is weak, streaming instability is predominantly damped by the turbulent damping.

6 Numerical Testing of Turbulent Damping of Alfvén Waves

Numerical testing of Lazarian [26] is essential in a variety of regimes. By using 3D MHD turbulence simulations [33], the results of numerical testing on turbulent damping of externally driven Alfvén waves are presented in Figure 1. The observed scaling is consistent with Lazarian [26] predictions, but inconsistent with FG04 prediction.

FIGURE 1

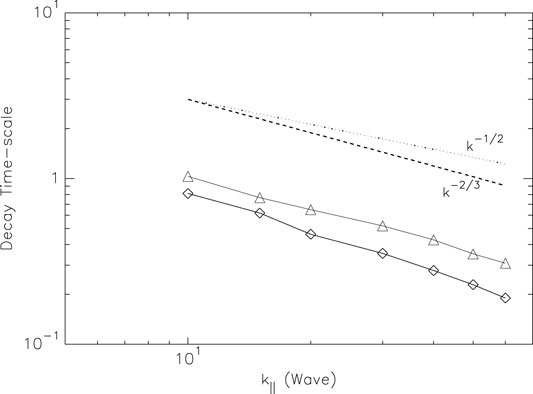
FIGURE 1. The damping time-scale Γ⁻¹ of Alfvén waves that are injected at k_‖ = 10 in 3D MHD turbulence, where the parallel direction is chosen with respect to the mean magnetic field. In one approach the Alfvén wave energy E_w decays in the turbulent medium over the time scale τ₁ =  ln(E(t₁)/E(t₂))/(t₂ − t₁). The values of τ₁ are given by triangular symbols. In the other approach the wave energy is continuously injected at k_‖ = 10 until it reaches a saturation level E_w. The corresponding damping time scale is given by τ₂ = E_w/ϵ_driving, where ϵ_driving is the wave energy injection rate. τ₂ is denoted by diamond symbols. The two measurements are both consistent with k^−2/3 scaling. From Cho and Lazarian (in prep)’.

The reason for this difference arises from the global reference frame adopted in the numerical experiment. Launching of Alfvén waves with respect to the local direction of magnetic field is complicated in turbulent fluid. Therefore, the testing presented in Figure 1 was carried out with Alfvén waves launched with respect to the mean magnetic field. This is the setting corresponding to turbulent damping of Alfvén waves generated in the global system of reference that we considered in §4. As a result, the numerical simulations confirmed the scaling of inverse of damping rate Γ⁻¹, i.e., damping time scale, which is measured at different λ as ${\lambda }^{2/3}˜k_{\Vert }^{-2/3}$. This result is different from the prediction of ${\mathrm{\Gamma }}^{-1}˜k_{\Vert }^{-1/2}$ of streaming instability in FG04 for transAlfvénic turbulence and in Lazarian [26] for the strong Alfvénic turbulence part of the cascade for a wide range of M_A. Numerical testing on turbulent damping of streaming instability in the local reference frame requires a more complicated setup and has not been performed so far.

7 Astrophysical Implications

7.1 Propagation of CRs

For decades the study on CR propagation was performed within a simple model, the so-called “leaky box model” (see [38]). In this model Galactic CRs propagate freely within the partially ionized disk of the Galaxy. The Alfvén waves experience damping in the partially ionized gas [7,34,36,39] and thus the streaming instability is suppressed. On the contrary, in fully ionized plasmas of the Galactic halo, the damping of Alfvén waves is significantly reduced and the streaming instability is present. Therefore, in this classical simplistic picture that ignores turbulence, Galactic CRs stream freely through the Galactic disk and are scattered backwards in the Galactic halo.

This classical “leaky box model” is problematic, as it is well known now that the Galactic disk is not fully filled with partially ionized gas. In fact, a significant fraction of the Galactic disk material is warm ionized gas [40,41]. Therefore, CRs cannot zoom through the Galactic disk due to the streaming instability.

FG04 quantified the idea of turbulent damping of streaming instability mentioned in Yan and Lazarian [23] and came to a paradoxical conclusion by applying their theory to the propagation of CRs in the Galaxy. By assuming homogeneous transAlfvénic turbulence in the Galaxy, they found significant turbulent damping of streaming instability and thus poor confinement of CRs. This would entail problems with explaining, e.g., the observed isotropy of CRs and their residence time in the Galaxy.

In Lazarian [26] the gist of the “leaky box model” was preserved, but instead of damping by ion-neutral collisional friction, the study appealed to the turbulent damping of streaming instability in the Galactic disk and proposed a “turbulent leaky box model.” Different from FG04, by considering inhomogeneous turbulence properties in the Galaxy and the strong M_A dependence of turbulent damping, they found that the damping by weak subAlfvénic turbulence is marginal in the Galactic halo and thus CRs, even at high energies, can still be confined by streaming instability.

In a recent study by Xu and Lazarian [18], they identified the important role of turbulent damping of streaming instability in the warm ionized medium (WIM). Figure 2 shows the diffusion coefficient D of streaming CRs. The M_A dependence comes from both turbulent damping of streaming instability and wandering of turbulent magnetic field lines. In particular, the smaller D in superAlfvénic turbulence is caused by the tangling of turbulent magnetic fields, which results in an effective mean free path l_A of the CRs streaming along turbulent magnetic fields [42].

FIGURE 2

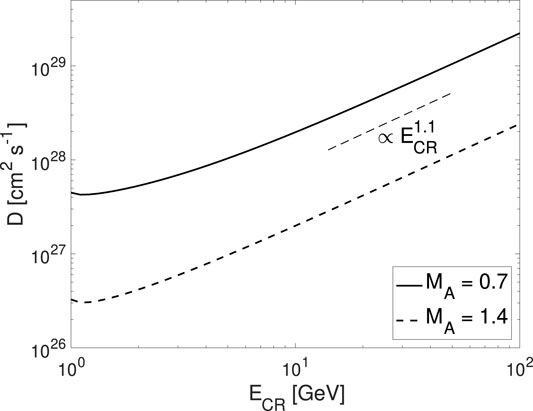
FIGURE 2. Diffusion coefficient vs. E_CR of streaming CRs in super and subAlfvénic turbulence in the WIM. From Xu and Lazarian [18].

The M_A-dependent diffusion of CRs is important for a realistic modeling of inhomogeneous CR diffusion in the Galaxy [43]. The actual values of M_A in the Galaxy can be measured from observations using a newly developed gradient technique ([44], see also [45]) or with more traditional magnetic field and turbulent velocity measurements.

7.2 Launching of Winds and Heating

While the damping of Alfvén waves by turbulence is an accepted process in the field of CR research, we would like to point out that the turbulent damping of Alfvén waves can be responsible for many fundamental astrophysical processes. For instance, different processes of damping were discussed for heating of stellar corona by Alfvén waves, as well as for launching of stellar winds (see [19,46–50]). It is clear that the turbulent damping of Alfvén waves can be very important in these settings. More recently, launching galactic winds by turbulent damping of the Alfvén waves generated by galactic activity was considered in Suzuki and Lazarian [51]. Accounting for the dependence of turbulent damping on M_A is important for the quantitative modeling of the process. A similar process is important for launching winds from other types of active disk systems, e.g., circumstellar disks.

Apart from launching galactic winds by turbulent damping of Alfvén waves generated by the galaxy, the turbulent damping of streaming instability also plays a very important role in coupling CRs and magnetized galactic matter. The pressure of CRs in galactic settings is significant and it can modify interstellar dynamics. Galactic winds driven by CRs present an important example of this modification.

In general, the importance of galactic winds is easy to understand. For galaxies of the Milky Way luminosity, about 20 percent of baryons are accounted for when matching the observed luminosity to the halo mass function. Observing absorption lines in spectra of background quasars testifies for the efficient expulsion of galactic baryons from the galaxies. In fact there is evidence that galaxies with significant star formation can drive mass outflows up to 10 times the rate of star formation [52].

Numerical simulations have demonstrated that CRs indeed influence the generation of global outflows and the local structure of the interstellar medium (ISM) (see [53]). The exact properties of the simulated outflows depend sensitively on how CR transport is modeled. Recent simulations by Holguin et al. [54] employed Lazarian [26] model of turbulent damping and obtained the results that differ significantly from the earlier modeling in, e.g., Ruszkowski et al. [53]. The difference stemmed from the fact that the earlier calculations employed the model by FG04, which is only applicable to transAlfvénic turbulence, i.e., M_A = 1. However, the actual M_A of gas can vary significantly in simulations.

The results of the numerical simulations in Holguin et al. [54] are presented in Figure 3. Some of the implications include, fist of all, when turbulent damping of CR streaming instability is included, there is an increase of star formation rate, and the increase is more significant at a higher level of turbulence. The reason is that the turbulent damping increases the average CR streaming speed. This allows CRs to leave the dense mid-plane, reducing the pressure support from CRs to the gas. As a result, the gas in the disk collapses and stars form more efficiently. Furthermore, the higher efficiency of star formation results in more CRs produced in the mid-plane. The increased streaming speed of CRs leads to a more extended CR distribution away from the mid-plane. It is also important that the escape of CRs from the dense regions allows them to interact with lower-density gas. This widens the gas distribution in height and accelerates the gas to form CR-driven galactic winds.

FIGURE 3

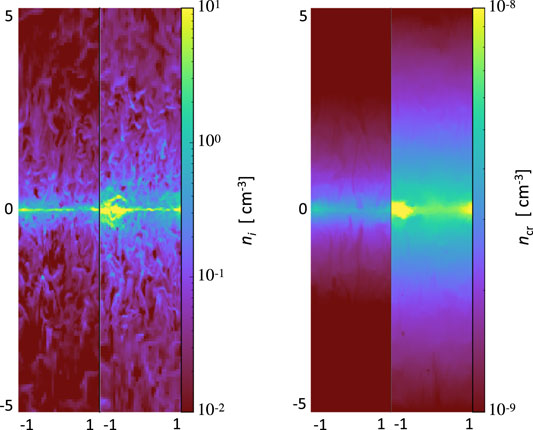
FIGURE 3. Simulations of the galactic ISM evolution in the presence of star formation and CR driven outflows. The figure shows the gas (n_i) and CR (n_cr) density slices ± 5 kpc along z direction perpendicular to the midplane obtained in two simulations over time 200 Myr. The CR streaming is affected by turbulent damping of streaming instability with the turbulent velocity σ = 10 km/s. The results obtained in the absence of turbulent damping on the left side of each pair of plots are clearly different from those with turbulent damping on the right side. The distribution of both gas and CRs is more extended in the presence of turbulent damping. From Holguin et al. [54].

In addition, the theory of Alfvén wave damping by turbulence suggests that Alfvén waves can propagate across longer distances in highly magnetized regions of solar atmosphere (small M_A) compared to the regions with higher M_A. This prediction can be observationally tested. This effect should be accounted in both modelling of solar wind launching and modelling of plasma heating. For instance, it is likely that the turbulent damping can be important in order to explain the observed “unexpected” damping of Alfvén waves in the regions above the Sun’s polar coronal holes [55].

8 Summary

Alfvén waves are damped in turbulent media and the damping depends on the Alfvén Mach number M_A of the turbulence. At the same wavelength, the wave damping depends on whether the waves are generated in the local reference system of magnetic eddies by the CR streaming or they are injected at an angle relative to the large-scale mean magnetic field from an extended astrophysical source. The latter is, e.g., the case of the Alfvén waves arising from magnetic reconnection, or oscillations in accretion disks and stellar atmospheres. The difference in their damping rates arises from the difference between the local and global systems of reference where the Alfvén waves are generated.

The dependence of damping rate on the wavelength λ of the Alfvén waves in the local system of reference is λ^−1/2, as opposed to a stronger dependence λ^−2/3 for the waves in the global reference system.

The turbulent damping also depends on whether Alfvén waves interact with weak or strong Alfvénic turbulence. For M_A < 1, the turbulence from the injection scale L to the scale $L{M}_A^2$ is weak and is strong at smaller scales. Weak turbulence can play an important role in turbulent damping of streaming instability driven by high-energy CRs at a small M_A.

In a partially ionized gas, the turbulent damping still dominates the damping of streaming instability when the ionization fraction is sufficiently high, e.g., in the warm ionized medium [18]. In star burst galaxies, the ionization fraction is low and the ion-neutral collisional damping can be more important (e.g., [56]).

The turbulent damping of streaming instability has important implications on propagation of CRs in the Galaxy, star formation, coupling between CRs and magnetized gas and thus driving galactic winds. In addition, the turbulent damping of Alfvén waves results in heating of the medium and transfer of the momentum from Alfvénic flux to the medium. The latter is also important for launching winds.

Author Contributions

The article was devised and written by AL and SX.

Funding

The research is supported by NASA TCAN 144AAG1967. SX acknowledges the support for this work provided by NASA through the NASA Hubble Fellowship grant # HST-HF2-51 473.001-A awarded by the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Incorporated, under NASA contract NAS5-26 555.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

AL thank Jungyeon Cho for discussing the paper.

Footnotes

¹Using the relation $kE(k)˜u_k^2$ it is easy to show that the energy spectrum of weak turbulence is $E_{k,weak}˜k_{\perp }^{-2}$ (LV99, [30]).

²There is an intuitive way of presenting the Alfvénic cascade in terms of eddies mixing the magnetic field in the direction perpendicular to the magnetic field surrounding the eddies. The existence of such magnetic eddies is possible due to the fact that, as shown in LV99, the turbulent magnetic reconnection happens within one eddy turnover. As a result, the existence of magnetic field does not constrain magnetic eddies, if they are aligned with the magnetic field in their vicinity, i.e., with the local magnetic field. This eddy representation of MHD turbulence vividly demonstrates the importance of the local system of reference, where l_⊥ and l_‖ are defined.

³The fact that MHD turbulence is formulated in terms of the local quantities is required for describing the interaction of MHD turbulence with CRs. Indeed, perturbations in the local system of reference are exactly what CRs interact with.

⁴We note that in FG04 the injection scale for turbulence was defined not as the actual injection scale, but the scale at which the turbulent velocity becomes equal to the Alfvén one. Such scale does not exist for subAlfvénic turbulence.

⁵Simple estimates demonstrate that the interactions with smaller and larger turbulent scales are subdominant compared with the interaction with the “resonant” scale.

⁶In the case θ ∼ δB/B, one should average the final expressions over the θ dispersion that arises from magnetic field wandering.

References

1. Lazarian A, de Gouveia Dal Pino EM, Melioli C Magnetic Fields in Diffuse Media. In: Astrophysics and Space Science Library, Vol. 407. 978-3-662-44624-9. Berlin: Springer-Verlag Berlin Heidelberg (2015). doi:10.1007/978-3-662-44625-6

CrossRef Full Text | Google Scholar

2. Uhlig M, Pfrommer C, Sharma M, Nath BB, Enßlin TA, Springel V Galactic Winds Driven by Cosmic ray Streaming. MNRAS (2012) 423:2374–96. doi:10.1111/j.1365-2966.2012.21045.x

CrossRef Full Text | Google Scholar

3. Wiener J, Oh SP, Guo F Cosmic ray Streaming in Clusters of Galaxies. MNRAS (2013) 434:2209–28. doi:10.1093/mnras/stt1163

CrossRef Full Text | Google Scholar

4. van der Holst B, Sokolov IV, Meng X, Jin M, Manchester WB, Tóth G, et al. Alfven Wave Solar Model (AWSoM): Coronal Heating. ApJ (2014) 782:81. doi:10.1088/0004-637x/782/2/81

CrossRef Full Text | Google Scholar

5. Lynch BJ, Edmondson JK, Li Y Interchange Reconnection Alfvén Wave Generation. Sol Phys (2014) 289:3043–58. doi:10.1007/s11207-014-0506-x

CrossRef Full Text | Google Scholar

6. Lerche I Unstable Magnetosonic Waves in a Relativistic Plasma. ApJ (1967) 147:689. doi:10.1086/149045

CrossRef Full Text | Google Scholar

7. Kulsrud R, Pearce WP The Effect of Wave-Particle Interactions on the Propagation of Cosmic Rays. ApJ (1969) 156:445. doi:10.1086/149981

CrossRef Full Text | Google Scholar

8. Wentzel DG. ApJ (1969) 156:303

CrossRef Full Text

9. Skilling J Cosmic Rays in the Galaxy: Convection or Diffusion? ApJ (1971) 170:265. doi:10.1086/151210

CrossRef Full Text | Google Scholar

10. Lazarian A, Beresnyak A Cosmic ray Scattering in Compressible Turbulence. MNRAS (2006) 373:1195–202. doi:10.1111/j.1365-2966.2006.11093.x

CrossRef Full Text | Google Scholar

11. Königl A Astrophysics Space Sci Proc (2009) 13:67.

12. Suzuki TK Evolution of Solar-type Stellar Winds. Astron nachr (2013) 334:81–4. doi:10.1002/asna.201211751

CrossRef Full Text | Google Scholar

13. Bell AR The Acceleration of Cosmic Rays in Shock Fronts - I. Monthly Notices R Astronomical Soc (1978) 182:147–56. doi:10.1093/mnras/182.2.147

CrossRef Full Text | Google Scholar

14. Kulsrud RM Plasma Physics for Astrophysics / Russell M. Kulsrud. Princeton, N.J., USA: Princeton University Press (2005). (Princeton series in astrophysics).

Google Scholar

15. Enßlin T, Pfrommer C, Miniati F, Subramanian K. A&A (2011) 527:A99

16. Blasi P, Amato E, Serpico PD PhRvL (2012) 109:061101. doi:10.1103/physrevlett.109.061101

CrossRef Full Text

17. Badruddin and Kumar A. Study of the Cosmic-Ray Modulation during the Passage of ICMEs and CIRs. Sol Phys (2016) 291:559–80. doi:10.1007/s11207-015-0843-4

CrossRef Full Text | Google Scholar

18. Xu S, Lazarian A Submitted. ApJ (2022). arXiv:2112.06941.

Google Scholar

19. Suzuki TK, Inutsuka S-i Making the Corona and the Fast Solar Wind: A Self-Consistent Simulation for the Low-Frequency Alfvén Waves from the Photosphere to 0.3 AU. ApJ (2005) 632:L49–L52. doi:10.1086/497536

CrossRef Full Text | Google Scholar

20. van Ballegooijen AA, Asgari-Targhi M arXiv:1602.06883 (2016).

21. Hopkins PF, Squire J, Chan TK, Quataert E, Ji S, Kereš S, et al. MNRAS (2021) 501:4184. doi:10.1093/mnras/staa3691

CrossRef Full Text

22. Similon PL, Sudan RN. ApJ (1989) 336:442

CrossRef Full Text

23. Yan H, Lazarian A Scattering of Cosmic Rays by Magnetohydrodynamic Interstellar Turbulence. Phys Rev Lett (2002) 89:281102. doi:10.1103/physrevlett.89.281102

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Farmer AJ, Goldreich P Wave Damping by Magnetohydrodynamic Turbulence and its Effect on Cosmic‐Ray Propagation in the Interstellar Medium. ApJ (2004) 604:671–4. doi:10.1086/382040

CrossRef Full Text | Google Scholar

25. Goldreich P, Sridhar S Toward a Theory of Interstellar Turbulence. 2: Strong Alfvenic Turbulence. ApJ (1995) 438:763. doi:10.1086/175121

CrossRef Full Text | Google Scholar

26. Lazarian A Damping of Alfvén Waves by Turbulence and its Consequences: from Cosmic-ray Streaming to Launching Winds. ApJ (2016) 833:131. doi:10.3847/1538-4357/833/2/131

CrossRef Full Text | Google Scholar

27. Batchelor GK The Theory of Homogeneous Turbulence. Cambridge: George Batchelor (1953).

Google Scholar

28. Lazarian A Enhancement and Suppression of Heat Transfer by MHD Turbulence. ApJ (2006) 645:L25–L28. doi:10.1086/505796

CrossRef Full Text | Google Scholar

29. Lazarian A, Vishniac ET Reconnection in a Weakly Stochastic Field. ApJ (1999) 517:700–18. doi:10.1086/307233

CrossRef Full Text | Google Scholar

31. Cho J, Vishniac ET The Anisotropy of Magnetohydrodynamic Alfvenic Turbulence. ApJ (2000) 539:273–82. doi:10.1086/309213

CrossRef Full Text | Google Scholar

30. Galtier S, Nazarenko SV, Newell AC, Pouquet A. JPlPh (2000) 63:447

32. Maron J, Goldreich P. ApJ (2001) 554:1175.

CrossRef Full Text

33. Cho J, Lazarian A, Vishniac ET Simulations of Magnetohydrodynamic Turbulence in a Strongly Magnetized Medium. Vishniac ETApJ (2002) 564:291–301. doi:10.1086/324186

CrossRef Full Text | Google Scholar

34. Xu S, Lazarian A Magnetohydrodynamic Turbulence and Turbulent Dynamo in Partially Ionized Plasma. New J Phys (2017) 19:065005. doi:10.1088/1367-2630/aa6ec9

CrossRef Full Text | Google Scholar

35. Xu S, Lazarian A, Yan H The Line Width Difference of Neutrals and Ions Induced by Mhd Turbulence. ApJ (2015) 810:44. doi:10.1088/0004-637x/810/1/44

CrossRef Full Text | Google Scholar

36. Xu S, Yan H, Lazarian A Damping of Magnetohydrodynamic Turbulence in Partially Ionized Plasma: Implications for Cosmic Ray Propagation. ApJ (2016) 826:166. doi:10.3847/0004-637x/826/2/166

CrossRef Full Text | Google Scholar

37. Cho J, Lazarian A Compressible Magnetohydrodynamic Turbulence: Mode Coupling, Scaling Relations, Anisotropy, Viscosity-Damped Regime and Astrophysical Implications. MNRAS (2003) 345:325–39. doi:10.1046/j.1365-8711.2003.06941.x

CrossRef Full Text | Google Scholar

38. Longair MS In: MS Longair, editor. High Energy Astrophysics. Cambridge, UK: Cambridge University Press (2011).

Google Scholar

39. Lithwick Y, Goldreich P Compressible Magnetohydrodynamic Turbulence in Interstellar Plasmas. ApJ (2001) 562:279–96. doi:10.1086/323470

CrossRef Full Text | Google Scholar

40. McKee CF, Ostriker JP A Theory of the Interstellar Medium - Three Components Regulated by Supernova Explosions in an Inhomogeneous Substrate. ApJ (1977) 218:148. doi:10.1086/155667

CrossRef Full Text | Google Scholar

41. Draine BT Physics of the Interstellar and Intergalactic Medium by Bruce T. Draine. 978-0-691-12214-4. Princeton, N.J., USA: Princeton University Press (2011).

Google Scholar

42. Brunetti G, Lazarian A Compressible Turbulence in Galaxy Clusters: Physics and Stochastic Particle Re-acceleration. Monthly Notices R Astronomical Soc (2007) 378:245–75. doi:10.1111/j.1365-2966.2007.11771.x

CrossRef Full Text | Google Scholar

43. Xu S Proceedings of Science, PoS(ICRC2021)041. arXiv:2110.08282 (2021).

Google Scholar

44. Lazarian A, Yuen KH, Ho KW, Chen J, Lazarian V, Lu Z, et al. ApJ (2018) 865:46

45. Xu S, Hu Y Measuring Magnetization with Rotation Measures and Velocity Centroids in Supersonic MHD Turbulence. ApJ (2021) 910:88. doi:10.3847/1538-4357/abe403

CrossRef Full Text | Google Scholar

46. Verdini A, Velli M, Oughton S Propagation and Dissipation of Alfvén Waves in Stellar Atmospheres Permeated by Isothermal Winds. A&A (2005) 444:233–44. doi:10.1051/0004-6361:20052748

CrossRef Full Text | Google Scholar

47. Evans RM, Opher M, Jatenco-Pereira V, Gombosi TI Surface Alfvén Wave Damping in a Three-Dimensional Simulation of the Solar Wind. IApJ (2009) 703:179–86. doi:10.1088/0004-637x/703/1/179

CrossRef Full Text | Google Scholar

48. Vidotto AA, Jatenco-Pereira V Alfvén Waves as a Driving Mechanism in Stellar Winds. Adv Space Res (2010) 46:509–13. doi:10.1016/j.asr.2008.12.025

CrossRef Full Text | Google Scholar

49. Verdini A, Velli M, Matthaeus WH, Oughton S, Dmitruk P A Turbulence-Driven Model for Heating and Acceleration of the Fast Wind in Coronal Holes. ApJ (2010) 708:L116–L120. doi:10.1088/2041-8205/708/2/l116

CrossRef Full Text | Google Scholar

50. Suzuki TK Numer Model Space Plasma Flows ASTRONUM-2014 (2015) 498:22.

51. Suzuki TK, Lazarian A arXiv:1710.03930 (2017).

53. Ruszkowski M, Yang H-YK, Zweibel E Global Simulations of Galactic Winds Including Cosmic-ray Streaming. ApJ (2017) 834:208. doi:10.3847/1538-4357/834/2/208

CrossRef Full Text | Google Scholar

54. Holguin F, Ruszkowski M, Lazarian A, Farber R, Yang H-YK Role of Cosmic-ray Streaming and Turbulent Damping in Driving Galactic Winds. MNRAS (2019) 490:1271–82. doi:10.1093/mnras/stz2568

CrossRef Full Text | Google Scholar

55. Hahn M, Landi E, Savin DW Evidence of Wave Damping at Low Heights in a Polar Coronal Hole. ApJ (2012) 753:36. doi:10.1088/0004-637x/753/1/36

CrossRef Full Text | Google Scholar

56. Bland-Hawthorn J, Veilleux S, Cecil G Ap&SS (2007) 311:87

CrossRef Full Text

57. Krumholz MR, Crocker RM, Xu S, Lazarian A, Rosevear MT, Bedwell-Wilson J Cosmic ray Transport in Starburst Galaxies. MNRAS (2020) 493:2817–33. doi:10.1093/mnras/staa493

CrossRef Full Text | Google Scholar