Characterization of the Induced Magnetic Field on Third-Grade Micropolar Fluid Flow Across an Exponentially Stretched Sheet

1 Introduction

Magnetohydrodynamics (MHD) is a branch of fluid mechanics that studies the movement of an electrically conductive liquid in the existence of the magnetic field. Alfven [1] was the first who found that the movement of conducting fluid between magnetic field lines generates potential differences, that, in turn induces the flow of electric currents. The magnetic fields coupled with these electric currents alter the magnetic force that generates them. Alternatively, the fluid stream modifies the system’s electromagnetic structure. The propagation of electric current through a magnetic field, on the other hand, is coupled with a body force, known as the Lorentz force, which affects fluid motion. Scientists and researchers in the field of fluid dynamics have identified its use in metal dispersion, mining, fusion reactors, targeted drug delivery, MHD-based laser beam scanning, construction of MHD pumps, MHD generators, and MHD flow meters. Andersson [2] probed the MHD stream of a viscoelastic liquid past over an expanding sheet and showed that external magnetic field affects the flow similar as viscoelasticity. Hayat and Abbas [3] investigated the radiation impacts on the MHD stream of a viscoelastic liquid across a permeable surface. Nadeem and Hussain [4] explored the shrinking solutions in the existence of MHD stream of a viscous liquid toward a non-linear contracting surface. The effects of an exponentially stretched surface on MHD boundary layer stream and heat transmission characteristics in a permeable medium have been investigated by Ahmad et al. [5]. Hayat et al. [6] discussed the MHD boundary layer stream of a viscous fluid due to non-linear extending cylinder with thermal slip stratification and radiation. Sohail et al. [7] probed the boundary layer stream of the steady MHD Carreau liquid with bioconvection across the heated disk. They determined that the intensity of the magnetic field reduces fluid’s particle velocity, although mass transfer and fluid temperature increase with increasing magnetic field values. Riaz et al. [8] probed the MHD and entropy formation modeling of nanoliquid with three-dimensional (3-D) peristaltic cylindrical confinement. Employing molecular dynamical modeling, AbdulHussein et al. [9] investigated the boiling mechanism of several fluids in micro-channels in the existence of an exterior electromagnetic field.

The study of fluid flow across an expanding sheet is crucial for a variety of applications including, extrusion, glass blowing, cord depiction, copper spiraling, strengthening and tinning of copper wires, glass blowing, warm progressing, thermal conductivity of heat sinks, and melts of high molecular weight polymers. Hussain et al. [10] explored the influences on the boundary layer stream of a micropolar liquid flowing on the stretched surface. Abbas et al. [11] inspected the micropolar fluid flow behavior across the stretched sheet due to a variety of significant applications. Awan et al. have investigated different types of flows over the stretching surface and porous media, with various physical implications [12, 13]. Nadeem and Khan [14] studied the rotating Maxwell nanofluid flow between linear and exponential expanding sheets. Riaz et al. [15] exposed the bioconvection mechanism in the stream of magnetically polarized Williamson nanoparticles along with activating energy and heat source/sink.

Many scientists from all over the world are eager to learn more about non-Newtonian fluid flow. The reason for such a motivation in the study of these fluids is as a result of their use in industries and technologies including suspension fabrication, detergent and paint production, skincare creams, polymer production, spinning of metal etc. The non-Newtonian fluids in comparison to the Newtonian fluids are rheological in structure having non-linear correlation between shearing stress and velocity gradient. Non-Newtonian liquids are classified into three kinds depending upon their characteristics: rate type, differential type, and integral type fluids. The differential type liquid models have found to be well known among them. The second-grade fluid is the most basic subclass of these viscoelastic models, capturing typical stress variations but not anticipating shear thinning/thickening processes. In contrast, the third-grade liquid model can predict both ordinary stress and shear thinning/expanding processes. Abbasbandy et al. [16] investigated the both exact and series approaches for third-grade fluid by using thin film. Hayat et al. [17] probed the rotating stream of third-grade liquid among two permeable sheets by applying MHD effects. Hayat et al. [18] probed the MHD nanofluid stream of second-grade fluid caused by a non-linear stretched surface. In the vicinity of nanoparticles, the non-transient motions of a third-grade fluid driven by a pressure sort die are investigated by Mahanthesh and Joseph [19]. The characteristics of an applied magnetism and entropy formation on Jeffrey nanoliquid in between an annulus region of two small non-concentric pipes was disclosed by Riaz et al. [20]. Mondal et al. [21] discussed nanoliquid stream across a permeable vertical plate along with interior heat production and non-linear thermal radiations. Sangeetha and De [22] analyzed the bioconvection in nanoliquid stream with viscous losses and Ohmic heating. Riaz et al. [23] presented a comparative analysis of entropy assessment on a (3-D) wavy stream of Eyring–Powell nanoliquid.

Micropolar fluids have a microstructure and are coupled to fluids with a non-symmetrical stress tensor. Because of the liquid particles’ localized composition and micro-motions, micropolar liquids display particular microscopic features. They characterize fluids composed of stiff, arbitrarily oriented, or cylindrical particles dispersed in a viscous material, where fluid’s particle distortion is neglected. Eringen [24] was the first to investigate the hypothesis of micropolar fluids. In this hypothesis, the continuum is defined as the set of systematic particles that have not only momentum but also a sub-structure. In other words, each material volume element is made up of micro volume components that can translate and twist independently of each other. Gorla et al. [25] scrutinized the impacts of buoyancy on driven convection in an axially symmetric stagnation stream of micropolar fluids across a vertically placed cylinder. Rehman and Sattar [26] explained the MHD convective stream of a micropolar liquid over the consistently moving permeable sheet. The temperature boundary layer stream caused by a linearly stretched surface submerged in a constant density micropolar liquid together with radiation effects is probed by [27]. Gaffar et al. [28] examined the free convective boundary layer stream of viscoelastic third-grade micropolar liquid passing over a vertically positioned isothermal cone. Ali et al. [29] revealed the significance of MHD on the micropolar nanoliquid stream across an expanding surface along with radiation and heat stratification influences. Jiang et al. [30] conducted the numerical assessment of the passive usage of phase-change elements and the active usage of nanoliquid inside a rectangular channel.

To the extent of the writer’s insights, no research has been conducted to investigate the magnetohydrodynamics (MHD), and heat transmission effects of a viscous, micropolar, and third-grade fluid passed across an exponentially stretched sheet. The current research is presented to analyze the consequences of third-grade fluid parameters, thermophoresis and Brownian motion, induced magnetic field, micro-polarity, and micro-inertia density on the stream of an electrically conductive fluid. The primary purpose of this extensive study is to improve thermal transportation subject to the existence of micro-rotations of tiny nanoparticles. The mathematical model is built under considered flow assumptions and Buongiorno model. The similarity transformation is a technique that is commonly used for solving various flow problems, in which the system of partial differential equations (PDEs) is modified into ordinary differential equations (ODEs) to solve them analytically or numerically. The current model is simplified by applying similarity transformation. The resultant ODEs are numerically tackled in MATLAB using the bvp4c algorithm, and the numerical tables are constructed to ensure the validity of results. The obtained findings have significant engineering and technological applications.

2 Mathematical Analysis and Flow Geometry

2.1 Constitutive Model for Third-Grade Fluid

For an incompressible fluid, the equations of motion and continuity are as follows:

$\nabla .\mathbf{V}=0,(1)$

$\mathit{d}\mathit{i}\mathit{v}\mathbf{T}=-\mathbf{J}\times \mathbf{B}+\rho \frac{D\mathbf{V}}{Dt}-\rho \mathbf{b}.(2)$

Here, ρ, V, T, b, J, and B are density of the fluid, velocity vector, Cauchy stress tensor, body force, electric current, and external magnetic field, respectively. Following Rajagopal and Fosdick [31], the third-grade fluid’s stress tensor is as follows:

$\mathbf{T}+p\mathbf{I}=\mathbf{S},(3)$

$\mathbf{S}=\mu {\mathbf{B}}_{\mathbf{1}}+\widehat{{\alpha }_1}{\mathbf{B}}_{\mathbf{2}}+\widehat{{\alpha }_2}{\mathbf{B}}_{\mathbf{1}}^{\mathbf{2}}+\widehat{{\beta }_1}{\mathbf{B}}_{\mathbf{3}},(4)$

$+\widehat{{\beta }_2}({\mathbf{B}}_{\mathbf{1}}{\mathbf{B}}_{\mathbf{2}}+{\mathbf{B}}_{\mathbf{2}}{\mathbf{B}}_{\mathbf{1}})+\widehat{{\beta }_3}{\mathbf{B}}_{\mathbf{1}}\left(trc{\mathbf{B}}_{\mathbf{1}}^{\mathbf{2}}\right).$

Here, p, I, T, and S are the pressure, identity tensor, Cauchy stress tensor, and the extra stress tensor, respectively. Furthermore, $\widehat{{\alpha }_k}(k=\mathrm{1,2}),\widehat{{\beta }_j}(j=\mathrm{1,2,3})$ are metallic constants and B_i(i = 1, 2, 3) is the kinematic tensor defines as:

$\begin{array}{ll}\hfill {\mathbf{B}}_{\mathbf{1}}& ={\left(\mathbf{L}\right)}^T+\mathbf{L},\hfill \\ \hfill {\mathbf{B}}_{\mathbf{n}}& =\frac{D{\mathbf{B}}_{\mathbf{n-1}}}{Dt}+{\mathbf{B}}_{\mathbf{n-1}}\mathbf{L}+{\left(\mathbf{L}\right)}^T{\mathbf{B}}_{\mathbf{n-1}},n=\mathrm{2,3}\hfill \\ \hfill \text{where},\mathbf{L}& =\nabla \mathbf{V}.\hfill \end{array}$

Here, $\frac{D}{Dt}$ represents the substantial derivative, and it is stated as:

$\frac{D\mathrm{()}\left(\right)}{Dt}\equiv \mathbf{V}.\nabla \mathrm{()}\left(\right)+\frac{\partial \mathrm{()}\left(\right)}{\partial t}.$

In the case of third-grade fluid, the material moduli satisfy Clausius–Duhem inequality stated as:

$\widehat{{\beta }_1}=\widehat{{\beta }_2}=0,\widehat{{\alpha }_1}\ge 0,\mu \ge 0,\widehat{{\beta }_3}\ge 0,(5)$

$\mid \widehat{{\alpha }_2}+\widehat{{\alpha }_1}\mid \le \sqrt{24\mu \widehat{{\beta }_3}}.(6)$

So, the stress tensor takes the following form.

$\mathbf{T}=\mu {\mathbf{B}}_{\mathbf{1}}+\widehat{{\alpha }_1}{\mathbf{B}}_{\mathbf{2}}+\widehat{{\alpha }_2}{\mathbf{B}}_{\mathbf{1}}^{\mathbf{2}}+\widehat{{\beta }_3}{\mathbf{B}}_{\mathbf{1}}\left(trc{\mathbf{B}}_{\mathbf{1}}^{\mathbf{2}}\right).(7)$

2.2 Constitutive Model for Micropolar Fluid

The field equations for the micropolar fluid following Papautsky et al. [32] are stated as follows:

$\nabla .\left(\rho \mathbf{V}\right)+\frac{\partial \rho }{\partial t}=0,(8)$

$\left({\lambda }^{\ast }+\kappa +2\mu \right)\nabla \left(\nabla .\mathbf{V}\right)+\kappa \left(\nabla \times \mathbf{G}\right)-\left(\kappa +\mu \right)\nabla \times \nabla \times \mathbf{V}+\rho \mathbf{f}=\rho {\mathbf{V}}^{\prime }+\nabla p,(9)$

$\left(\bar{\alpha }+{\gamma }^{\ast }+\bar{\beta }\right)\nabla \left(\nabla .\mathbf{G}\right)+\kappa \left(\nabla \times \mathbf{V}\right)--2\kappa \mathbf{G}-{\gamma }^{\ast }\nabla \times \nabla \times \mathbf{G}=-\rho \mathbf{l}+\rho j{\mathbf{G}}^{\prime }.(10)$

Eqs. 8–10, respectively, denote conservation of mass, linear momentum, and angular momentum. Furthermore, ρ represents the micropolar fluid density, G is the (gyration) micro-rotation vector, V depicts velocity vector, j represents micro-inertia, p is the pressure, l denotes body couple per unit mass vector , λ∗ reflects Eringen second-degree viscosity parameter, f depicts the body strength per unit mass vector, κ represents coefficient of vortex viscosity, μ denotes dynamic viscosity, and $\bar{\alpha }$, γ∗, and $\bar{\beta }$ denote the swirl gradient viscosity coefficient. Also, (′) denotes the time derivative. For $\bar{\alpha }=\kappa =\bar{\beta }={\gamma }^{\ast }=0$ and in the absence of l and f, the micro-rotation vector G approaches zero, and Eq. 9 is simplified to the Navier–Stokes equations. For κ = 0, the gyration vector G and velocity vector V become detached, and the micro-movements have no influence on the entire motion of the fluid.

2.3 Problem Formulation

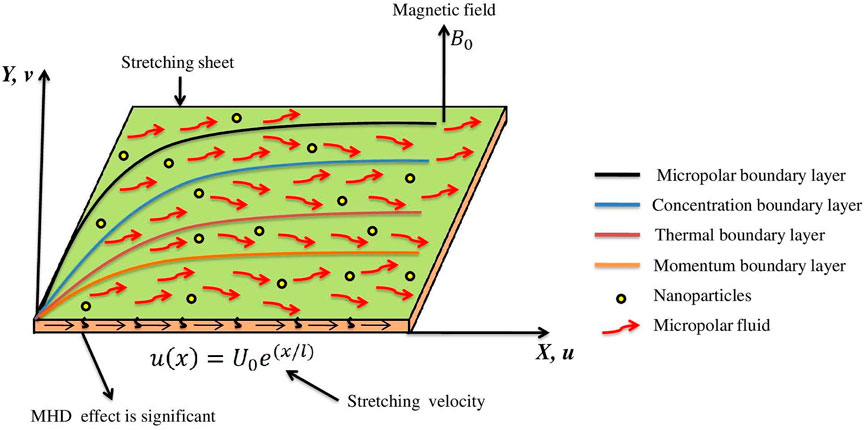
In this section, the steady, laminar, two-dimensional, and incompressible third-grade viscoelastic micropolar fluid stream along with thermal radiation caused by an exponentially stretched surface is reported. The x-axis is marked parallel to the sheet, while the y-axis is directed orthogonal to the sheet. The uniform magnetic field is supplied to the surface in a normal direction, and the fluid is believed to be electrically conductive. The sheet and the third-grade micropolar liquid are both originally maintained at the identical temperature. The temperature is elevated to T_f, and T_f > T_∞ where T_∞ is the ambient temperature, which remains constant as (see Figure 1). The concentration at the sheet is taken as C_f, while the ambient concentration is C_∞ (C_f > C_∞). This is supposed that the flow’s magnetic Reynolds number is not low in magnitude, and thus the produced magnetic field is not negligible. The evoked magnetic field H₂ is also assumed to be supplied along the x-axis. The parallel component H₁ of the induced magnetic field tends to H_e(x) in the free stream flow, and the slope of the magnetic field approaches zero along y-axis.

FIGURE 1

FIGURE 1. Geometry of the flow.

Using Eq. 7 in Eq. of motion (Eq. 2) along with the boundary layer estimations [33–36] in case of third-grade fluid, notably, inside the boundary layer $\frac{\partial p}{\partial x},\frac{{\partial }^{2}u}{\partial x},\frac{\partial u}{\partial x}$, and u are O(1), v and y are O(δ), $\frac{\widehat{{\alpha }_j}}{\rho }(j=\mathrm{1,2})$ and ν be O(δ²), and $\frac{\widehat{{\beta }_k}}{\rho }(k=\mathrm{1,2,3})$ being O(δ⁴), and the components of O(δ) are ignored (δ is boundary layer width). The equations for conservation of mass, magnetic field, and momentum are given as Eqs. 11–12. Equations 13–14 rise from the conservation of energy and concentration. Eq. 15 rises from micropolar boundary layer approximation by Papautsky et al. [32], and Eq. 16 resulted from the conservation of induced magnetic field. Hence, the mathematical model overseeing the considered flow problem is as follows:

$\frac{\partial v}{\partial y}+\frac{\partial u}{\partial x}=0,\frac{\partial H_1}{\partial x}+\frac{\partial H_2}{\partial y}=0,(11)$

$v\frac{\partial u}{\partial y}+u\frac{\partial u}{\partial x}=\frac{\widehat{{\alpha }_1}}{\rho }\left(\frac{\partial u}{\partial x}\frac{{\partial }^{2}u}{\partial y^2}+3\frac{\partial u}{\partial y}\frac{{\partial }^{2}v}{\partial y^2}+v\frac{{\partial }^{3}u}{\partial y^3}+u\frac{{\partial }^{3}u}{\partial x\partial y^2}\right)+2\frac{\widehat{{\alpha }_2}}{\rho }\frac{\partial u}{\partial y}\frac{{\partial }^{2}v}{\partial y^2}(12)$

$+\frac{6\widehat{{\beta }_3}}{\rho }\frac{{\partial }^{2}u}{\partial y^2}{\left(\frac{\partial u}{\partial y}\right)}^2+\frac{k}{\rho }\frac{\partial N}{\partial y}+\frac{\left(k+\mu \right)}{\rho }\frac{{\partial }^{2}u}{\partial y^2}-\frac{\sigma B_0^2}{\rho }u,$

$v\frac{\partial T}{\partial y}+u\frac{\partial T}{\partial x}=\frac{1}{\rho C_p}\frac{\partial }{\partial y}\left[\frac{\partial T}{\partial y}k\left(T\right)\right]+\left(\frac{k+\mu }{\rho C_p}\right){\left(\frac{\partial u}{\partial y}\right)}^2-\frac{1}{\rho C_p}\frac{\partial q_r}{\partial y}(13)$

$+{\tau }^{\ast }\left[D_B\frac{\partial C}{\partial y}\frac{\partial T}{\partial y}+{\left(\frac{\partial T}{\partial y}\right)}^2\frac{D_T}{T_{\infty }}\right]$

$v\frac{\partial C}{\partial y}+u\frac{\partial C}{\partial x}=D_B\frac{{\partial }^{2}C}{\partial y^2}+\frac{D_T}{T_{\infty }}\frac{{\partial }^{2}T}{\partial y^2},(14)$

$v\frac{\partial N}{\partial y}+u\frac{\partial N}{\partial x}=\frac{{\gamma }^{\ast }}{\rho j}\frac{{\partial }^{2}N}{\partial y^2}-\frac{k}{j\rho }\left(\frac{\partial u}{\partial y}+2N\right),(15)$

$v\frac{\partial H_1}{\partial y}+u\frac{\partial H_1}{\partial x}=H_2\frac{\partial u}{\partial y}+H_1\frac{\partial u}{\partial x}+{\eta }_o\frac{{\partial }^2{H}_1}{\partial y^2}.(16)$

The concerned boundary conditions are as follows:

$N=-m\frac{\partial u}{\partial y},u=U_w\left(x\right)=U_{0}exp\left(x/l\right),T=k\left(\frac{\partial T}{\partial y}\right)+T_f,$

$H_2=0,D_B\frac{\partial C}{\partial y}+\frac{D_T}{T_{\infty }}\frac{\partial T}{\partial y}=0,v=0,\frac{\partial H_1}{\partial y}=0,\text{for}y\to 0,(17)$

$C\to C_{\infty },H_1\to H_e\left(x\right)T\to T_{\infty },N\to 0,u\to 0,\frac{\partial u}{\partial y}\to 0\text{for}y\to \infty .(18)$

Here, u, v are the velocity coefficients in x and y directions, ρ depicts the liquid’s density , k denotes the vertex viscosity, μ represents dynamic viscosity, N denotes the micropolar fluid’s angular velocity, T represents the temperature, U₀ depicts the reference velocity, C depicts the concentration, B₀ denotes the uniform magnetic field, η₀ denotes the magnetic diffusivity, σ denotes the electrical conductance, C_p represents specific heat, and τ* reveals the quotient of the latent heat of the nanoparticles to the latent heat of the base liquid. Furthermore, D_B reflects the coefficient of Brownian motion, D_T denotes the coefficient of thermophoresis diffusion, and the micro-inertial density is depicted by j. The viscosity of the spin gradient γ* is given as follows:

${\gamma }^{\ast }=j\left(\mu +\frac{k}{2}\right)=\mu j\left(1+\frac{K}{2}\right),\text{and}j=\frac{2l\mu }{\rho U_0}\mathit{exp}\left(-x/l\right),(19)$

where $K=\frac{k}{\mu }$ is the micropolar parameter. Temperature-based thermal conductivity is defined as follows:

$k\left(T\right)=\left(1+ϵ\frac{T_{\infty }-T}{T_{\infty }-T_f}\right)k.(20)$

The Rosseland radiative heat flow (q_r) along y-axis is defined as:

$q_r=\frac{-4{\sigma }^{\ast }}{3k^{\ast }}\frac{\partial T^4}{\partial y},\text{and}{T}^4\approx 4T_{\infty }^{3}T-3T_{\infty }^4.(21)$

Here, Stefan–Boltzman constant and average absorption coefficient are expressed by σ∗ and k∗, respectively.

$\frac{\partial q_r}{\partial y}=\frac{-16T_{\infty }^3{\sigma }^{\ast }}{3k^{\ast }}\frac{{\partial }^{2}T}{\partial y^2}.(22)$

To simplify the analysis, the following appropriate similarity transformations are implemented.

$\begin{array}{c}\hfill \psi \left(x,y\right)=\sqrt{2\nu l{U}_0}f\left(\eta \right)exp\left(\frac{x}{2l}\right),{\psi }_1\left(x,y\right)=H_0\sqrt{\frac{\nu }{U_0}}g\left(\eta \right)exp\left(\frac{x}{2l}\right),\hfill \\ \hfill \varphi \left(\eta \right)=\frac{C-C_{\infty }}{C_f-C_{\infty }},N\left(\eta \right)=U_0\sqrt{\frac{U_0}{2\nu l}}exp\left(\frac{3x}{2l}\right)h\left(\eta \right),\theta \left(\eta \right)=\frac{T-T_{\infty }}{T_f-T_{\infty }},\eta =y\sqrt{\frac{U_0}{2\nu l}}exp\left(\frac{x}{2l}\right).\hfill \end{array}(23)$

Here, ψ and ψ₁ are stream functions and can be represented as:

$\begin{array}{c}\hfill u=\frac{\partial \psi }{\partial y}=U_0{f}^{\prime }\left(\eta \right)exp\left(x/l\right),v=-\frac{\partial \psi }{\partial x}=-\sqrt{\frac{\nu U_0}{2l}}\left(f+\eta f^{\prime }\right)exp\left(x/2l\right),\hfill \\ \hfill H_1=\frac{\partial {\psi }_1}{\partial y}=\frac{H_0}{\sqrt{2l}}exp\left(x/l\right)g^{\prime }\left(\eta \right),H_2=-\frac{\partial {\psi }_1}{\partial x}=-H_0\sqrt{\frac{\nu }{4l^2{U}_0}}exp\left(x/2l\right)\left(g+\eta g^{\prime }\right).\hfill \end{array}(24)$

where η denotes the dimensionless variable, and f′(η), θ(η), ϕ(η), h(η), and g(η) are the dimensionless velocity curve, temperature curve, concentration curve, micropolar curve, and induced magnetic field curve, respectively. Implying Eqs. 23, 24, the continuity equation and magnetic flux equation holds true, and the Eqs. 12–16 are modified into the non-dimensional ODEs as stated:

$\begin{array}{c}\hfill \left(1+K\right)f^{‴}+3\beta f^{‴}{\left(f^{″}\right)}^2+K{h}^{\prime }+f{f}^{″}+{\alpha }_1\left[-2\eta f^{″}{f}^{‴}-f{f}^{\left(iv\right)}-9{\left(f^{″}\right)}^2+6f^{\prime }{f}^{‴}\right]\hfill \\ \hfill -2{\left(f^{\prime }\right)}^2-2M{f}^{\prime }-{\alpha }_2\left[\eta f^{″}{f}^{‴}+3{\left(f^{″}\right)}^2\right]=0,\hfill \end{array}(25)$

$\frac{1}{Pr}\left[{\theta }^{″}+ϵ\theta {\theta }^{″}+ϵ{\left({\theta }^{\prime }\right)}^2\right]+f{\theta }^{\prime }+Ec\left(1+K\right){\left(f^{″}\right)}^2+\frac{4}{3}Rd{\theta }^{″}+Nt{\left({\theta }^{\prime }\right)}^2+Nb{\theta }^{\prime }{\varphi }^{\prime }=0,(26)$

${\varphi }^{″}+\frac{Nt}{Nb}{\theta }^{″}+Lef{\varphi }^{\prime }=0,(27)$

$\left(1+\frac{K}{2}\right)h^{″}+f{h}^{\prime }-3h{f}^{\prime }-2KB\left(f^{″}+2h\right)=0,(28)$

$g^{‴}+P{r}_m\left(f{g}^{″}-g{f}^{″}\right)=0.(29)$

The associated non-dimensional boundary constraints are given as:

$\begin{array}{c}\hfill Nb{\varphi }^{\prime }\left(0\right)+Nt{\theta }^{\prime }\left(0\right)=0,g^{″}\left(0\right)=0,f\left(0\right)=0,h\left(0\right)=-m{f}^{″}\left(0\right),h\left(\infty \right)=0,\varphi \left(\infty \right)=0,\hfill \\ \hfill \theta \left(0\right)=\delta {\theta }^{\prime }\left(0\right)+1,\theta \left(\infty \right)=0,f^{\prime }\left(\infty \right)=0,f^{\prime }\left(0\right)=1,f^{″}\left(\infty \right)=0,g^{\prime }\left(\infty \right)=1,g\left(0\right)=0.\hfill \end{array}(30)$

The non-dimensional parameters are defined as:

$\begin{array}{c}\hfill {\alpha }_1=\frac{\widehat{{\alpha }_1}{U}_0}{2\rho \nu l}exp\left(x/l\right),{\alpha }_2=\frac{\widehat{{\alpha }_2}{U}_0}{\rho \nu l}exp\left(x/l\right),\beta =\frac{{\beta }_3{U}_0^3}{\rho {\nu }^{2}l}exp\left(3x/l\right),\hfill \\ \hfill Pr=\frac{\mu C_p}{k},Ec=\frac{U_0^{2}exp\left(2x/l\right)}{C_p\left(T_f-T_{\infty }\right)},Rd=\frac{4{\sigma }^{\ast }{T}_{\infty }^3}{\mu C_p{k}^{\ast }},Nt=\frac{D_T\left(T_f-T_{\infty }\right){\tau }^{\ast }}{\nu T_{\infty }},\hfill \\ \hfill Nb=\frac{D_B{\tau }^{\ast }}{\nu }\left(C_f-C_{\infty }\right),Le=\frac{\nu }{D_B},B=\frac{\nu l}{U_{0}j}exp\left(-x/l\right),P{r}_m=\frac{\nu }{{\eta }_0},\hfill \\ \hfill \delta =k\sqrt{\frac{U_0}{2\nu l}}exp\left(x/2l\right)M=\frac{\sigma B_0^{2}l}{\rho U_0}exp\left(-x/l\right),K=\frac{k}{\mu }.\hfill \end{array}$

Here, α₁, α₂ are the non-dimensional viscoelastic coefficients, β is the third-grade fluid constant, M depicts the magnetic parameter, δ denotes the thermal slip parameter , Ec represents the Eckert no, Rd is the radiation constant, Nt represents the thermophoresis constant, K denotes the micropolar fluid coefficient, Pr stands for Prandtl number, Nb indicates the Brownian diffusivity coefficient, Le denotes the Lewis no, B is the micro-inertia density coefficient, and Pr_m denotes the magnetic Prandtl number. Physical variables of interest, such as local couple stress (M_s), Sherwood number (Sh_x), Nusselt number (Nu_x), and skin friction coefficient (Cf_x) are defined as follows:

$S{h}_x=\frac{x{j}_w}{D_B\left(C_f-C_{\infty }\right)},C{f}_x=\frac{{\tau }_w}{\frac{1}{2}\rho U_w^2},N{u}_x=\frac{x{q}_w}{k\left(T_f-T_{\infty }\right)},M_s=\frac{{\gamma }^{\ast }}{U_w^2\rho l}{\left.\left(\frac{\partial N}{\partial y}\right)\right|}_{y=0},(31)$

where

$j_w=-D_B{\left.\left(\frac{\partial C}{\partial y}\right)\right|}_{y=0},q_w=-\left(\frac{16T_{\infty }^3{\sigma }^{\ast }}{3k^{\ast }}+k\right){\left.\frac{\partial T}{\partial y}\right|}_{y=0},$

${\tau }_w={\left[\left(\mu +k\right)\frac{\partial u}{\partial y}+\widehat{{\alpha }_1}\left(v\frac{{\partial }^{2}u}{\partial y^2}+2\frac{\partial u}{\partial y}\frac{\partial u}{\partial x}+u\frac{{\partial }^{2}u}{\partial y\partial x}\right)+2{\beta }_3{\left(\frac{\partial u}{\partial y}\right)}^3+kN\right]}_{y=0}.$

Utilizing the similarity transformation (Eq. 22), the aforementioned expressions in non-dimensional aspects are stated as follows:

$\frac{1}{\sqrt{2}}{\left(R{e}_x\right)}^{1/2}C{f}_x=\left(1+K\right)f^{″}\left(0\right)+Kh\left(0\right)+\beta {\left[f^{″}\left(0\right)\right]}^3+{\alpha }_1\left[-f\left(0\right)f^{‴}\left(0\right)+7f^{\prime }\left(0\right)f^{″}\left(0\right)\right],(32)$

$\frac{\sqrt{2}}{X}{\left(R{e}_x\right)}^{-1/2}N{u}_x=-\left(1+\frac{4}{3}Rd\right){\theta }^{\prime }\left(0\right),(33)$

$\frac{\sqrt{2}}{X}{\left(R{e}_x\right)}^{-1/2}S{h}_x=-{\varphi }^{\prime }\left(0\right),(34)$

$R{e}_x{M}_s=\left(1+\frac{K}{2}\right)h^{\prime }\left(0\right),(35)$

where X = x/l and $R{e}_x=\frac{l{U}_w(x)}{\nu }$ is the local Reynolds number.

3 Numerical Procedure

Due to the extreme non-linearity, the coupled ODEs Eqs. 25–29 along with the boundary constraints (Eq. 30) are unable to solve analytically. To address non-linear boundary value problems, different numerical techniques are applied in MATLAB. The bvp4c approach is a useful technique to solve such problems numerically. The underlying partial differential equations (PDEs) are transfigured into ODEs utilizing the similarity analysis. The resulting system of ODEs is resolved numerically employing the built-in bvp4c technique in MATLAB. The solution strategy is described as follows:

$\begin{array}{c}\hfill f\left(\eta \right)=y\left(1\right);f^{\prime }\left(\eta \right)=y\left(2\right);f^{″}\left(\eta \right)=y\left(3\right);f^{‴}\left(\eta \right)=y\left(4\right);f^{\left(iv\right)}\left(\eta \right)=yy1;\theta \left(\eta \right)=y\left(5\right);\hfill \\ \hfill {\theta }^{\prime }\left(\eta \right)=y\left(6\right);{\theta }^{″}\left(\eta \right)=yy2;\varphi \left(\eta \right)=y\left(7\right);{\varphi }^{\prime }\left(\eta \right)=y\left(8\right);{\varphi }^{″}\left(\eta \right)=yy3;h\left(\eta \right)=y\left(9\right);\hfill \\ \hfill h^{\prime }\left(\eta \right)=y\left(10\right);h^{″}\left(\eta \right)=yy4;g\left(\eta \right)=y\left(11\right);g^{\prime }\left(\eta \right)=y\left(12\right);g^{″}\left(\eta \right)=y\left(13\right);g^{‴}\left(\eta \right)=yy5\hfill \end{array}.$

Utilizing the aforementioned notations, the coupled ODEs are transformed into the following first-order ODEs:

$\begin{array}{c}\hfill yy1={\left({\alpha }_1\ast y\left(1\right)\right)}^{-1}\ast \left(\left(1+K\right)\ast y\left(4\right)-2\ast y\left(2\right)\ast y\left(2\right)+y\left(3\right)\ast y\left(1\right)-2\ast M\ast y\left(2\right)\right.\hfill \\ \hfill +3\ast \beta \ast y\left(3\right)\ast y\left(3\right)\ast y\left(4\right)+K\ast y\left(10\right)-\left(9\ast {\alpha }_1+3\ast {\alpha }_2\right)\ast y\left(3\right)\ast y\left(3\right)\hfill \\ \hfill \left.-\left({\alpha }_2+2\ast {\alpha }_1\right)\ast y\left(4\right)\ast x\ast y\left(3\right)+6\ast {\alpha }_1\ast y\left(4\right)\ast y\left(2\right)\right);\hfill \end{array},(36)$

$\begin{array}{c}\hfill yy2=\left(-3\ast Pr\right)\ast {\left(3+3\ast ϵ\ast y\left(5\right)+4\ast Pr\ast Rd\right)}^{-1}\ast \left(y\left(1\right)\ast y\left(6\right)+\left(1+K\right)\ast y\left(3\right)\ast Ec\ast y\left(3\right)\right.\hfill \\ \hfill \left.+y\left(6\right)\ast Nt\ast y\left(6\right)+Nb\ast y\left(6\right)\ast ,y\left(8\right)+\frac{ϵ}{Pr}\ast y\left(6\right)\ast y\left(6\right)\right);\hfill \end{array}(37)$

$yy3=-Le\ast y\left(1\right)\ast y\left(8\right)-\left(\frac{Nt}{Nb}\right)\ast yy2,(38)$

$yy4=2\ast {\left(2+K\right)}^{-1}\ast \left(2\ast K\ast B\ast \left(2\ast y\left(9\right)+y\left(3\right)\right)+3\ast y\left(2\right)\ast y\left(9\right)-y\left(1\right)\ast y\left(10\right)\right),(39)$

$yy5=P{r}_m\ast \left(-y\left(1\right)\ast y\left(13\right)+y\left(11\right)\ast y\left(3\right)\right).(40)$

The concerned boundary constraints in MATLAB script are stated as:

$\begin{array}{ccc}\hfill y0\left(1\right);y0\left(2\right)-1;y0\left(5\right)-\delta \ast y0\left(6\right)-1;y0\left(9\right)+m\ast y0\left(3\right);yinf\left(5\right);yinf\left(2\right);& \hfill & \hfill \\ \hfill Nb\ast y0\left(8\right)+Nt\ast y0\left(6\right);yinf\left(9\right);yinf\left(7\right);y0\left(11\right);y0\left(13\right);yinf\left(12\right)-1;yinf\left(3\right).& \hfill & \hfill \end{array}(41)$

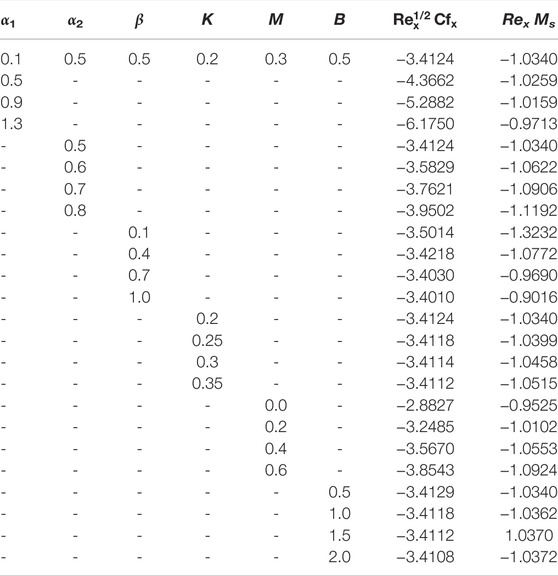
The MATLAB code is processed to get the numerical solutions. In order to determine the validity of numerical technique, we have analyzed our outcomes for limiting cases with already existing research work. The outcomes are reported to be in excellent concordance as shown in Tables 1, 2. It is also probed that for β = α₂ = 0, the mathematical model reduces to the second-grade fluid model, and for β = α₁ = α₂ = 0, we get the equations of motion for the classical viscous liquid.

TABLE 1

TABLE 1. Comparative results of − f^″(0) for diverse values of M, setting all other parameters zero.

TABLE 2

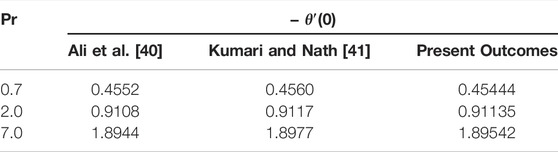
TABLE 2. Comparative outcomes of − θ′(0) for diverse values of Pr, setting all other parameters zero.

4 Computational Results

In this article, the micropolar, third-grade, nanofluid flow past across an exponentially expanding surface is considered. The mathematical model is built by analyzing fluid flow assumptions. The system of dimensionless ODEs (Eqs. 25–29) are solved numerically, utilizing the bvp4c strategy in MATLAB in addition to the boundary constraints (Eq. 30), and the impacts of numerous physical variables are explored. The significance of these coefficients on the temperature curve θ(η), micro-rotation curve h(η), velocity curve f′(η), produced magnetic field profile g(η), and concentration profile ϕ(η) is highlighted via tables and figures.

4.1 Velocity Profile f′(η)

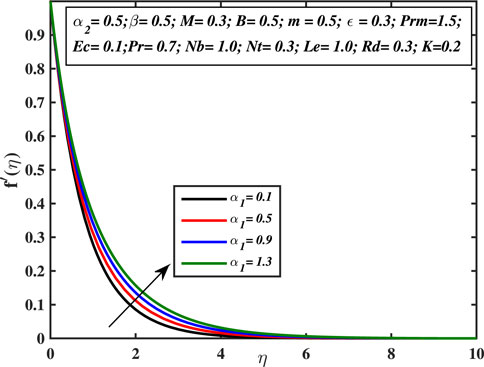
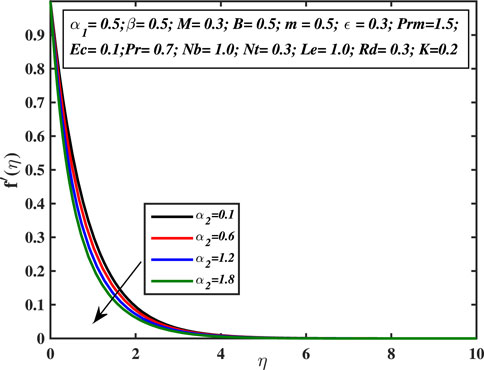
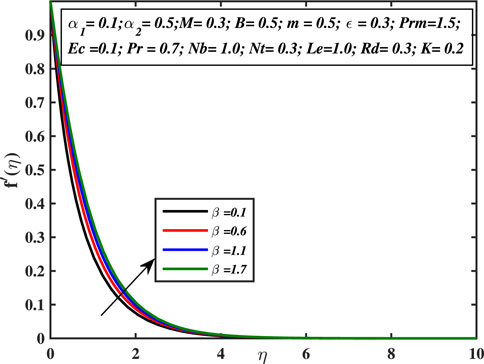
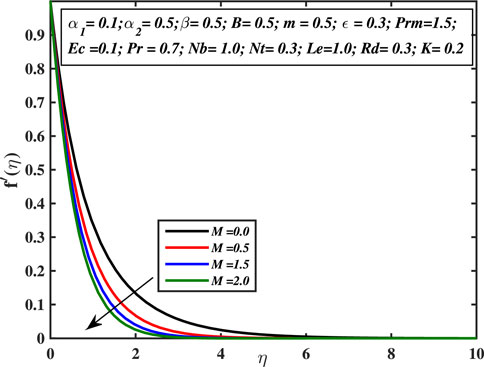
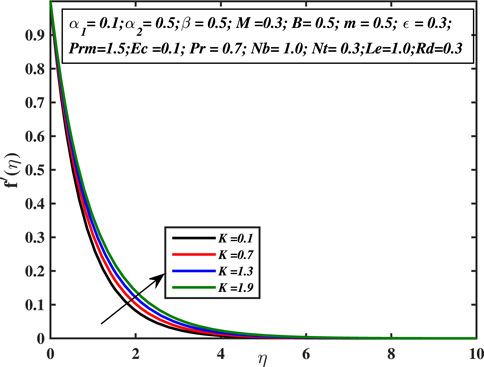
Figure 2 depicts the tendency of velocity distribution with the rising values of material constant α₁. It is clear that velocity and momentum boundary layer thickness increases for the higher values of viscoelastic constant α₁. Physically, the viscosity of the liquid is inversely proportional to the material constant α₁ because of that when the stress is applied, it reduces the strain and strengthens the elastic effects between the adjacent layers, and hence the velocity profile enhances. Figure 3 denotes the impact of second material constant α₂ on the velocity profile. The velocity curve is the decreasing function for larger values of α₂. This parameter causes shear thickening of the fluid and an increase in resistance that reduces the boundary layer flow, and originates a decrement in the size of the momentum boundary layer width. Figure 4 exhibits the ascending behavior of velocity with the augmentation of the third-grade fluid coefficient β. This coefficient is inversely proportionate to the square of the liquid viscosity. Alternatively, higher β readings indicate superior third-grade material characteristics (higher liquid elasticity) and smaller fluid viscosity. This causes the boundary layer stream to accelerate, resulting in higher f′(η) values. As this value is raised, the fluid needs less stress to flow, encouraging flow acceleration. In Figure 5, the influence of the magnetic field coefficient on velocity profile is examined. It is analyzed that the velocity curve declines monotonically with the augmented values of M ,and the velocity diminishes far away from the sheet. This process assists in controlling the size of the boundary layer. This is because of the fact that the existence of magnetism in an electrically conductive liquid generates a force known as the Lorentz force that operates opposite to the flow direction and forces velocity profile to decline. The velocity diminishes as the retardation to the flow enhances. In Figure 6 the influence of micropolar fluid parameter on the structure of velocity distribution is noticed. The increase in vortex viscosity strongly accelerates the fluid flow. The results show that the momentum transfer layer-by-layer is significantly affected by the rise in viscosity caused by the micro-rotation of the molecules. The micro-elements rotate more strongly, which helps to accelerate the liquid motion in the boundary layer. As a result, linear momentum diffusion is enhanced by micro-polarity, which explains why suspension fluids have thinner boundary layers than regular fluids.

FIGURE 2

FIGURE 2. Effect of α₁ on the velocity curve.

FIGURE 3

FIGURE 3. Effect of α₂ on the velocity curve.

FIGURE 4

FIGURE 4. Effect of β on the velocity curve.

FIGURE 5

FIGURE 5. Effect of M on the velocity curve.

FIGURE 6

FIGURE 6. Effect of K on the velocity curve.

4.2 Temperature Profile θ(η)

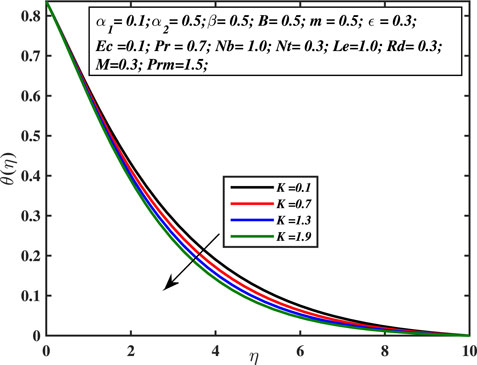
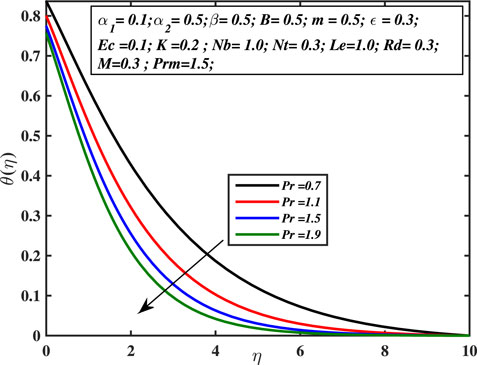
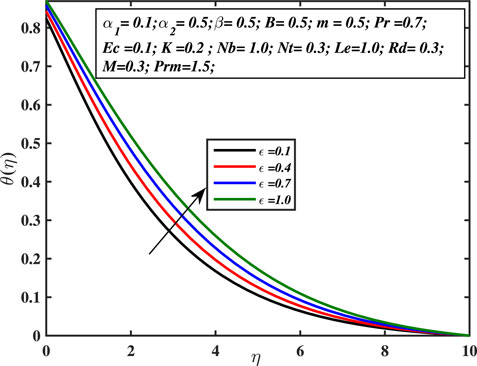
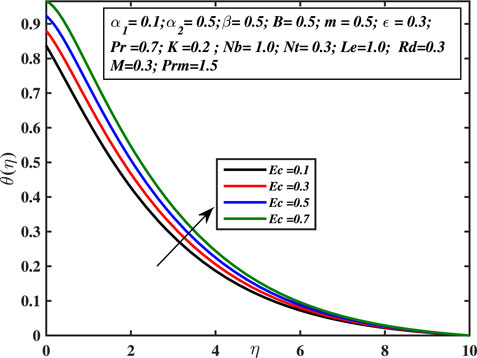
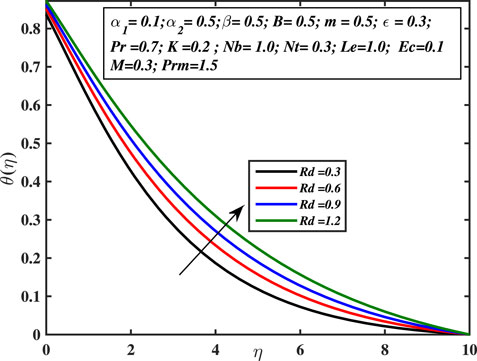
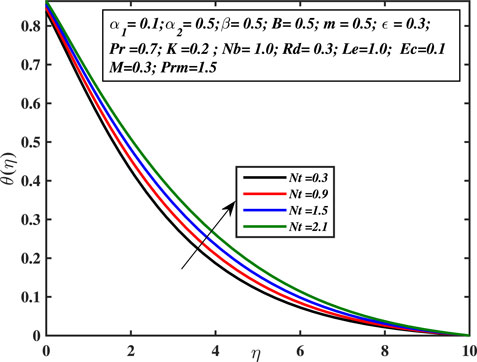
Figure 7 explains that temperature in the boundary layer increases with progressing micropolar coefficient, that is, higher K values. The regime is greatly heated, and the size of the temperature boundary layer enhances. The vortex’s enhanced viscosity promotes thermal diffusion and serves as a rotator. This boosts up the capacity of thermal diffusion within the fluid’s regime from the micro to the macro level and rapidly carries heat from the sheet boundary into the liquid body with greater intensity. Figure 8 depicts the relationship between the temperature profile and the Prandtl number Pr. The fraction of the momentum diffusion coefficient to heat diffusion coefficient is called the Prandtl number. This is examined that the temperature curve declines with increasing the Prandtl number. The higher values of Prandtl number affect the thermal diffusion. Prandtl number is inversely proportionate to the thermal diffusion; hence, higher Pr values indicate lower thermal diffusion, leading in lower temperature and a weaker temperature boundary layer. When the Prandtl number increases, rate of thermal conductivity gets lower. Consequently, heat is dissipated more quickly, and hence, the temperature boundary layer width and temperature of the liquid both diminish. As a result, the Prandtl number is employed to enhance the cooling tendency of fluids. The temperature-dependent thermal conductivity parameter’s effect over the temperature curve is explored in Figure 9. This is evident that the temperature curve is increasing with the augmentation of ϵ. The consequence of various Eckert number values over the temperature curve is explored in Figure 10. Ec is known as the quotient of the kinetic energy and enthalpy of heat transfer. As the Eckert number (Ec) increases, the liquid’s temperature rises. The fluctuation in the thermal curve θ(η) is examined in Figure 11 in respect to distinct amounts of the radiation parameter Rd. It is identified that a higher thermal radiation constant is related to a greater temperature and a wider temperature boundary layer. As the temperature field grows, the enhanced radiation transfers a significant amount of heat to the fluid. Physically, the involved radiation produces more heat which raises the fluid’s temperature. The influence of thermophoresis coefficient over the thermal distribution is probed in Figure 12. Thermophoresis is a phenomenon that occurs in mixture of sub-micron sized particles, in which the different particles respond differently to the force of a thermal gradient. The particle’s velocity is known as the thermophoretic velocity, and the stress exerted on the dispersed particles because of the temperature difference is known as the thermophoretic force. The thermophoretic force increases as the value of Nt grows, causing the temperature to increase.

FIGURE 7

FIGURE 7. Impact of K on the θ(η) curve.

FIGURE 8

FIGURE 8. Impact of Pr on the θ(η) curve.

FIGURE 9

FIGURE 9. Impact of ϵ on the θ(η) curve.

FIGURE 10

FIGURE 10. Impact of Ec on the θ(η) curve.

FIGURE 11

FIGURE 11. Impact of Rd on the θ(η) curve.

FIGURE 12

FIGURE 12. Impact of Nt on the θ(η) curve.

4.3 Concentration Profile ϕ(η)

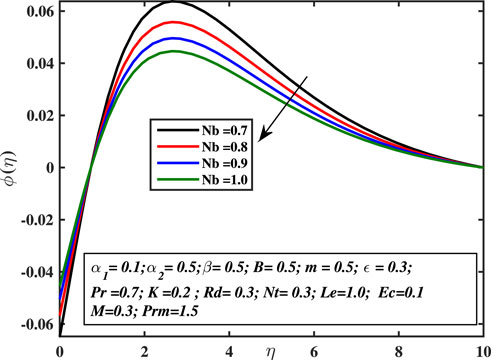
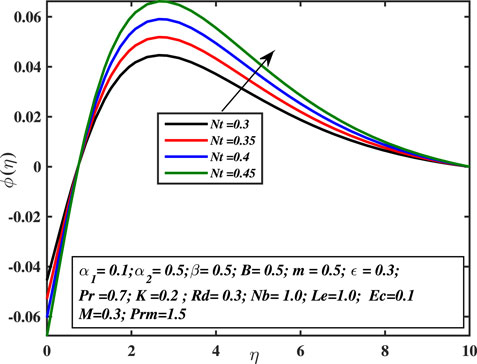
The influence of Brownian diffusivity and thermophoresis coefficients over the concentration distribution ϕ(η) is portrayed in Figures 13, 14. According to these graphs, nanofluid constants have opposite impacts on concentration distributions. Particularly, as the thermophoresis constant rises, the width of the concentration boundary layer enhances; nevertheless, as the Brownian motion constant increases, the ϕ(η) values decrease. The thermophoresis constant amplifies the thermophoretic force, resulting in the transfer of nanoparticles from warm to cool locations and an increment in nanoparticle volume. Thermophoresis has numerous uses, including radioactive particle deposition in nuclear reactors, silicon thin film deposition, and aerosol technologies. Furthermore, the progressing amount of the Brownian motion coefficient reduces the micro-mixing of nanoparticles into the fluid’s zone, which diminishes the boundary layer thickness of concentration distribution.

FIGURE 13

FIGURE 13. Effect of Nb on the ϕ(η) profile.

FIGURE 14

FIGURE 14. Effect of Nt on the ϕ(η) profile.

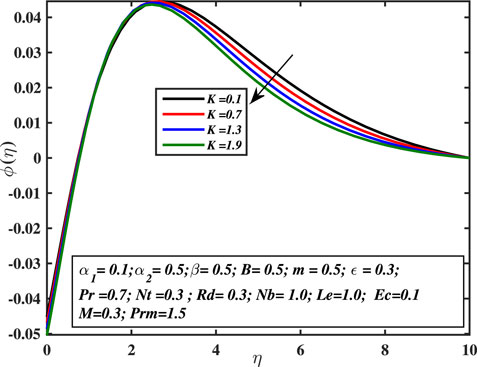
The behavior of ϕ(η) for the numerous values of Lewis number (Le) is examined in Figure 15. The Lewis number is stated as the rate of heat-to-mass diffusion coefficient. It is utilized to express the flow of liquid, in which heat and momentum transfer occur simultaneously. The concentration distribution becomes steeper when Lewis number is increased. The higher values of ‘Le’ imply the lesser values of mass diffusivity ‘D_B,’ which causes a weaker penetration depth for the concentration boundary layer. In Figure 16, the concentration curve for the various amounts of the micropolar coefficient is explored. However, when K increases, the micro-rotation velocity ϕ(η) drops down within a shorter range in the concentration boundary layer.

FIGURE 15

FIGURE 15. Effect of Le on the ϕ(η) profile.

FIGURE 16

FIGURE 16. Effect of K on the ϕ(η) profile.

4.4 Micropolar Profile h(η)

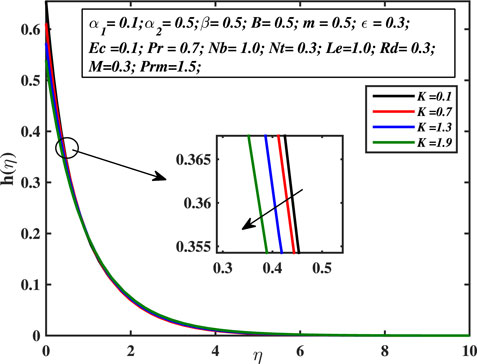
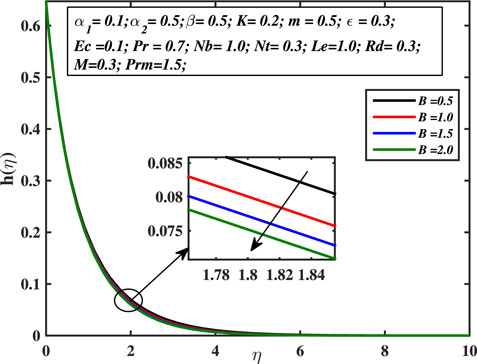
Figures 17, 18 are portrayed for the different values of micro-inertia density coefficient B and micropolar coefficient K. This is clear that the micropolar (angular) speed of the sub-micron sized particles decreases with the increase in the micro-polarity of the fluid. Similarly, the micro-inertia density coefficient B serves as a restricting force for the micro-rotation profile h(η). So, for the progressing amounts of B, the micropolar boundary layer width declines. This is possible because micropolar fluids provide a high barrier to fluid motion.

FIGURE 17

FIGURE 17. Effect of K on the h(η) profile.

FIGURE 18

FIGURE 18. Effect of B on the h(η) profile.

4.5 Induced Magnetic Field Profile h(η)

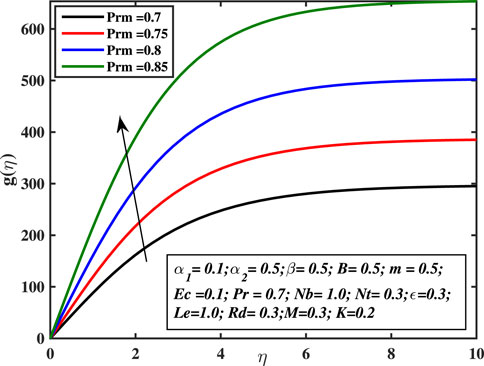
The influence of magnetic Prandtl number Pr_m over induced magnetic field curve g(η) is exhibited in Figure 19 , where a rise in Pr_m leads to an improvement in the produced magnetic field distribution. This is because the magnetic diffusivity over the boundary layer’s surface decreased while the fluid viscous dispersion rate enhanced. Magnetic Prandtl no.(Pr_m) is a non-dimensional quantity in Magnetohydrodynamics that estimates the ratio of momentum diffusion coefficient (ν) to magnetic diffusion coefficient (η).

FIGURE 19

FIGURE 19. Influence of Prm on induced magnetic velocity.

4.6 Numerical Results

The influence of all the non-dimensional coefficients used in the considered article on the skin friction parameter $(R{e}_x^{1/2}C{f}_x)$, Nusselt number. $(R{e}_x^{-1/2}N{u}_x)$, Sherwood number. $(R{e}_x^{-1/2}S{h}_x)$, and coupled wall stress (Re_x M_s) are presented in Tables 3, 4. Table 3 probes the significance of involved coefficients on the skin friction. The values of the coefficients other than used in Table 3 are taken to be fixed Pr = 0.7, ϵ = 0.3, Ec = 0.1, K = 0.2, Rd = 0.3, Nt = 0.3, Nb = 1.0, and Le = 1.0. By increasing the value of material parameters α₁ and α₂, the skin friction coefficient reduces. It is because of the reason that the viscosity near the surface of sheet is enhanced with the progression in material constant, which causes the decline in $R{e}_x^{1/2}C{f}_x$ values. As the rise in shear thickening coefficient β, improves the boundary layer thickness that give rise to the skin friction coefficient. The increase in micropolar parameter K, give rise to the value of $R{e}_x^{1/2}C{f}_x$, but the opposite behavior is seen for couple stress Re_x M_s. A reduction is caused by a rise in the magnetic field constant M in both $R{e}_x^{1/2}C{f}_x$ and Re_x M_s values. By increasing the micro-inertia density B, the values of $R{e}_x^{1/2}C{f}_x$ get enhanced but reverse behavior is seen for couple stress Re_x M_s.

TABLE 3

TABLE 3. Numerical findings of Re_xM_s and $\mathbf{R}{\mathbf{e}}_{\mathbf{x}}^{\mathbf{1}/\mathbf{2}}\mathbf{C}{\mathbf{f}}_{\mathbf{x}}$ for various values of parameters

TABLE 4

TABLE 4. Numerical findings of $\mathbf{S}{\mathbf{h}}_{\mathbf{x}}{(\mathbf{R}{\mathbf{e}}_{\mathbf{x}})}^{-\mathbf{0.5}}$ and $\mathbf{N}{\mathbf{u}}_{\mathbf{x}}{(\mathbf{R}{\mathbf{e}}_{\mathbf{x}})}^{-\mathbf{0.5}}$ for diverse values of parameters.

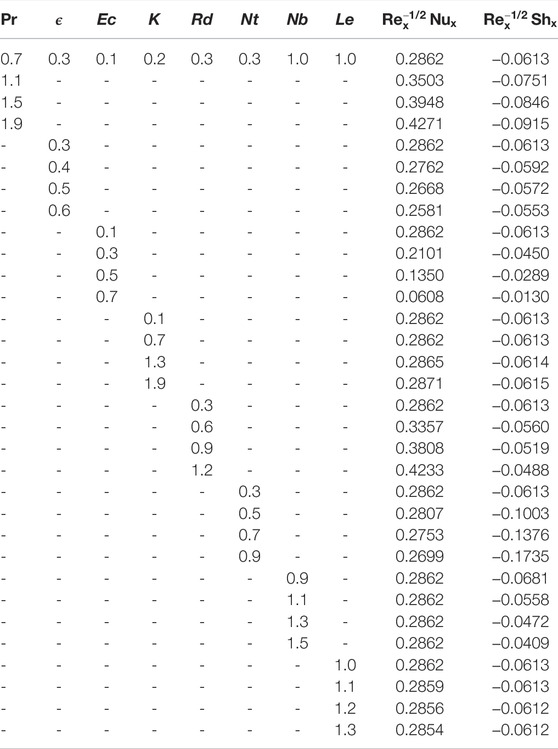
Table 4 depicts the influence of different parameters on the Nusselt number and Sherwood number. The other parameters are taken to be fixed β = 0.5, α₁ = 0.1, B = 0.5, α₂ = 0.5, K = 0.2, and M = 0.3. The increment in the values of Prandtl number causes a decline in the thermal diffusivity, and hence resists the rise in the heat transmission rate at the boundary. Boosting the Prandtl number raises the average Nusselt number at the heated surface, while a reverse effect is examined for the $R{e}_x^{-1/2}S{h}_x$. As ϵ is enhanced, the Nusslet number decreases while the Sherwood number increases. The increase in the value of Ec causes the Nusselt number to decrease while the Sherwood number increases. The boosting values of micropolar parameter K enhances the Nusselt number but declines the Sherwood number. Higher values of the Rd parameter improve convective heat and matter transmission, which ultimately increases the average Nusselt and Sherwood numbers values.

The higher values of thermophoresis coefficient Nt causes a decline in both the $N{u}_{x}R{e}_x^{-1/2}$ and $S{h}_{x}R{e}_x^{-1/2}$ values. The increment in the Nb values results in the enhancement of Sherwood number because the mass transfer rate from higher to lower concentration area get increased. The growth in the values of Lewis number Le improves the thermal diffusion and declines the mass conductivity. Thus, the values of $N{u}_{x}R{e}_x^{-1/2}$ decrease and that of $S{h}_{x}R{e}_x^{-1/2}$ increase.

5 Conclusion

The third-grade micropolar fluid flowing over an exponentially stretched sheet is probed in this research article. The underlying PDEs are transfigured into a system of ODEs using the appropriate similarity analysis, and the subsequent ODEs are settled in MATLAB using the bvp4c technique. The graphical explanation for the velocity curve f′(η), concentration curve ϕ(η), micropolar curve h(η), temperature curve θ(η), and induced magnetic field curve g(η) is portrayed via graphs. The key points under the aforementioned study are:

• Nanofluid constants have reverse effects over the concentration distribution. Concentration distribution ϕ(η) continues to increase for the greater values of Nt. It is due to the fact that the thermophoretic force increases causing an increase in concentration. On the other hand, an opposing trend is seen for Nb.

• Fluid’s velocity enhances with increasing the viscoelastic parameter α₁, micropolar parameter K, and third-grade fluid coefficient β. The reverse trend is analyzed for magnetic field parameter M and α₂.

• The thermal boundary layer width declines with the increment in the micropolar coefficient K and Prandtl number Pr. But the temperature gradient show ascending behavior for higher values of ϵ, radiation parameter Rd, Eckert number Ec, and thermophoresis constant Nt.

• The micropolar distribution h(η) tends to decline with increasing micropolar parameter K and micro-rotation constant B. With increasing the magnetic Prandtl number Pr_m, the induced magnetic field’s velocity remains going up.

• The skin friction coefficient remains diminishing for the larger values of α₁, α₂, and M, while, reverse behavior is observed for β, K, and B values.

• Couple stress coefficient continues to decline with rising the parameters α₂, K, M, and B. The ascending trend is noted for the higher values of α₁ and β.

• Nusselt number continuous to increase with boosting the parameters Pr , K, and Rd, while, the decreasing trend is examined for the parameters ϵ, Ec, Nt, and Le.

• Sherwood number depreciates for higher values of Pr , K, and Nt, and grows up for the higher values of ϵ, Ec, Rd, Nb, and Le.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

AUA: methodology and conceptualization. AAA: writing—original draft and validation. FG: funding acquisition, software, and revision. EMT-E: validation and funding acquisition. AmA: software and funding acquisition. HH contributed in revision and validation.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors would like to extend their appreciation to the Deanship of Scientific Research at King Khalid University, Saudi Arabia for funding this work through the Research Group Program under Grant No. RGP. 2/12/43. We will be thankful to you for your kind favor.

References

1. Alfvén H. Existence of Electromagnetic-Hydrodynamic Waves. Nature (1942) 150(3805):405–6. doi:10.1038/150405d0

CrossRef Full Text | Google Scholar

2. Andersson HI. MHD Flow of a Viscoelastic Fluid Past a Stretching Surface. Acta Mech (1992) 95(1):227–30. doi:10.1007/bf01170814

CrossRef Full Text | Google Scholar

3. Abbas Z, Hayat T. Radiation Effects on MHD Flow in a Porous Space. Int J Heat Mass Transf (2008) 51(5-6):1024–33. doi:10.1016/j.ijheatmasstransfer.2007.05.031

CrossRef Full Text | Google Scholar

4. Nadeem S, Hussain A. MHD Flow of a Viscous Fluid on a Nonlinear Porous Shrinking Sheet with Homotopy Analysis Method. Appl Math Mech.-Engl Ed (2009) 30(12):1569–78. doi:10.1007/s10483-009-1208-6

CrossRef Full Text | Google Scholar

5. Ahmad I, Sajid M, Awan W, Rafique M, Aziz W, Ahmed M, et al. MHD Flow of a Viscous Fluid over an Exponentially Stretching Sheet in a Porous Medium. J Appl Maths (2014) 2014:1–8. doi:10.1155/2014/256761

CrossRef Full Text | Google Scholar

6. Khan MI, Tamoor M, Hayat T, Alsaedi A. MHD Boundary Layer thermal Slip Flow by Nonlinearly Stretching cylinder with Suction/blowing and Radiation. Results Phys (2017) 7:1207–11. doi:10.1016/j.rinp.2017.03.009

CrossRef Full Text | Google Scholar

7. Sohail M, Nazir U, Chu YM, Al-Kouz W, Thounthong P. Bioconvection Phenomenon for the Boundary Layer Flow of Magnetohydrodynamic Carreau Liquid over a Heated Disk. Sci Iran (2021) 28(3):1896–907. doi:10.24200/SCI.2021.53970.3518

CrossRef Full Text | Google Scholar

8. Riaz A, Abbas T, Zeeshan A, Doranehgard MH. Entropy Generation and MHD Analysis of a Nanofluid with Peristaltic Three Dimensional Cylindrical Enclosures. Hff (2021) 31:2698–714. doi:10.1108/HFF-11-2020-0704

CrossRef Full Text | Google Scholar

9. AbdulHussein WA, Abed AM, Mohammed DB, Smaisim GF, Baghaei S. Investigation of Boiling Process of Different Fluids in Microchannels and Nanochannels in the Presence of External Electric Field and External Magnetic Field Using Molecular Dynamics Simulation. Case Stud Therm Eng (2022) 35:102105. doi:10.1016/j.csite.2022.102105

CrossRef Full Text | Google Scholar

10. Hussain M, Ashraf M, Nadeem S, Khan M. Radiation Effects on the thermal Boundary Layer Flow of a Micropolar Fluid towards a Permeable Stretching Sheet. J Franklin Inst (2013) 350(1):194–210. doi:10.1016/j.jfranklin.2012.07.005

CrossRef Full Text | Google Scholar

11. Abbas N, Saleem S, Nadeem S, Alderremy AA, Khan AU. On Stagnation point Flow of a Micro Polar Nanofluid Past a Circular cylinder with Velocity and thermal Slip. Results Phys (2018) 9:1224–32. doi:10.1016/j.rinp.2018.04.017

CrossRef Full Text | Google Scholar

12. Awan AU, Abid S, Ullah N, Nadeem S. Magnetohydrodynamic Oblique Stagnation point Flow of Second Grade Fluid over an Oscillatory Stretching Surface. Results Phys (2020) 18:103233. doi:10.1016/j.rinp.2020.103233

CrossRef Full Text | Google Scholar

13. Awan AU, Abid S, Abbas N. Theoretical Study of Unsteady Oblique Stagnation point Based Jeffrey Nanofluid Flow over an Oscillatory Stretching Sheet. Adv Mech Eng (2020) 12(11):1687814020971881. doi:10.1177/1687814020971881

CrossRef Full Text | Google Scholar

14. Khan MN, Nadeem S. A Comparative Study between Linear and Exponential Stretching Sheet with Double Stratification of a Rotating Maxwell Nanofluid Flow. Surf Inter (2021) 22:100886. doi:10.1016/j.surfin.2020.100886

CrossRef Full Text | Google Scholar

15. Abdelmalek Z, Khan SU, Waqas H, Riaz A, Khan IA, Tlili I. A Mathematical Model for Bioconvection Flow of Williamson Nanofluid over a Stretching cylinder Featuring Variable thermal Conductivity, Activation Energy and Second-Order Slip. J Therm Anal Calorim (2021) 144(1):205–17. doi:10.1007/s10973-020-09450-z

CrossRef Full Text | Google Scholar

16. Abbasbandy S, Hayat T, Mahomed FM, Ellahi R. On Comparison of Exact and Series Solutions for Thin Film Flow of a Third-Grade Fluid. Int J Numer Meth Fluids (2009) 61(9):987–94. doi:10.1002/fld.1994

CrossRef Full Text | Google Scholar

17. Hayat T, Naz R, Alsaedi A, Rashidi MM. Hydromagnetic Rotating Flow of Third Grade Fluid. Appl Math Mech.-Engl Ed (2013) 34(12):1481–94. doi:10.1007/s10483-013-1761-7

CrossRef Full Text | Google Scholar

18. Hayat T, Aziz A, Muhammad T, Ahmad B. On Magnetohydrodynamic Flow of Second Grade Nanofluid over a Nonlinear Stretching Sheet. J Magnetism Magn Mater (2016) 408:99–106. doi:10.1016/j.jmmm.2016.02.017

CrossRef Full Text | Google Scholar

19. Mahanthesh B, Joseph TV. Dynamics of magneto-nano third-grade fluid with Brownian motion and thermophoresis effects in the pressure type die. J Nanofluids (2019) 8(4):870–5. doi:10.1166/jon.2019.1642

CrossRef Full Text | Google Scholar

20. Riaz A, Ellahi R, Sait SM, Muhammad T. Magnetized Jeffrey Nanofluid with Energy Loss in between an Annular Part of Two Micro Non-concentric Pipes. Energy Sourc A: Recovery, Utilization, Environ Effects (2020) 2020:1–20. doi:10.1080/15567036.2020.1798568

CrossRef Full Text | Google Scholar

21. Mondal H, De P, Goqo S, Sibanda P. A Numerical Study of Nanofluid Flow over a Porous Vertical Plate with Internal Heat Generation and Nonlinear thermal Radiation. J Por Media (2020) 23(6):517–29. doi:10.1615/JPorMedia.2020026624

CrossRef Full Text | Google Scholar

22. Sangeetha E, De P. Bioconvection in Nanofluid Flow Embedded in Non-darcy Porous Medium with Viscous Dissipation and Ohmic Heating. J Por Media (2021) 24(1):15–23. doi:10.1615/JPorMedia.2020036165

CrossRef Full Text | Google Scholar

23. Riaz A, Zeeshan A, Bhatti MM. Entropy Analysis on a Three-Dimensional Wavy Flow of Eyring-Powell Nanofluid: A Comparative Study. Math Probl Eng (2021) 2021:1–14. doi:10.1155/2021/6672158

CrossRef Full Text | Google Scholar

24. Eringen A. Theory of Micropolar Fluids. Indiana Univ Math J (1966) 16(1):1–18. doi:10.1512/iumj.1967.16.16001

CrossRef Full Text | Google Scholar

25. Subba Reddy Gorla R, Mansour MA, Mohammedien AA. Combined Convection in an Axisymmetric Stagnation Flow of Micropolar Fluid. Int J Numer Methods Heat Fluid Flow (1996) 6(4):47–55. doi:10.1108/09615539610123441

CrossRef Full Text | Google Scholar

26. Rahman MM, Sattar MA. Magnetohydrodynamic Convective Flow of a Micropolar Fluid Past a Continuously Moving Vertical Porous Plate in the Presence of Heat Generation/absorption. J Heat Transfer (2006) 128(2):142–52. doi:10.1115/1.2136918

CrossRef Full Text | Google Scholar

27. Ishak A. Thermal Boundary Layer Flow over a Stretching Sheet in a Micropolar Fluid with Radiation Effect. Meccanica (2010) 45(3):367–73. doi:10.1007/s11012-009-9257-4

CrossRef Full Text | Google Scholar

28. Gaffar SA, Bég OA, Prasad VR. Mathematical Modeling of Natural Convection in a Third-Grade Viscoelastic Micropolar Fluid from an Isothermal Inverted Cone. Iran J Sci Technol Trans Mech Eng (2020) 44(2):383–402. doi:10.1007/s40997-018-0262-x

CrossRef Full Text | Google Scholar

29. Ali L, Liu X, Ali B, Mujeed S, Abdal S, Mutahir A. The Impact of Nanoparticles Due to Applied Magnetic Dipole in Micropolar Fluid Flow Using the Finite Element Method. Symmetry (2020) 12(4):520. doi:10.3390/sym12040520

CrossRef Full Text | Google Scholar

30. Jiang Y, Smaisim GF, Mahmoud MZ, Li Z, Aybar HŞ, Abed AM. Simultaneous Numerical Investigation of the Passive Use of Phase-Change Materials and the Active Use of a Nanofluid inside a Rectangular Duct in the thermal Management of Lithium-Ion Batteries. J Power Sourc (2022) 541:231610. doi:10.1016/j.jpowsour.2022.231610

CrossRef Full Text | Google Scholar

31. Fosdick RL, Rajagopal KR. Thermodynamics and Stability of Fluids of Third Grade. Proc R Soc Lond A (1980) 369(1738):351–77. doi:10.1098/rspa.1980.0005

CrossRef Full Text | Google Scholar

32. Papautsky I, Brazzle J, Ameel T, Frazier AB. Laminar Fluid Behavior in Microchannels Using Micropolar Fluid Theory. Sens Actuator A Phys (1999) 73(1-2):101–8. doi:10.1016/S0924-4247(98)00261-1

CrossRef Full Text | Google Scholar

33. Sajid M, Hayat T, Asghar S. Non-similar Analytic Solution for MHD Flow and Heat Transfer in a Third-Order Fluid over a Stretching Sheet. Int J Heat Mass Transfer (2007) 50(9-10):1723–36. doi:10.1016/j.ijheatmasstransfer.2006.10.011

CrossRef Full Text | Google Scholar

34. Pakdemirli M. The Boundary Layer Equations of Third-Grade Fluids. Int J Non-Linear Mech (1992) 27(5):785–93. doi:10.1016/0020-7462(92)90034-5

CrossRef Full Text | Google Scholar

35. Loganathan K, Mohana K, Mohanraj M, Sakthivel P, Rajan S. Impact of Third-Grade Nanofluid Flow across a Convective Surface in the Presence of Inclined Lorentz Force: an Approach to Entropy Optimization. J Therm Anal Calorim (2021) 144(5):1935–47. doi:10.1007/s10973-020-09751-3

CrossRef Full Text | Google Scholar

36. Bég OA, Bakier AY, Prasad VR, Zueco J, Ghosh SK. Nonsimilar, Laminar, Steady, Electrically-Conducting Forced Convection Liquid Metal Boundary Layer Flow with Induced Magnetic Field Effects. Int J Therm Sci (2009) 48(8):1596–606. doi:10.1016/j.ijthermalsci.2008.12.007

CrossRef Full Text | Google Scholar

37. Chaudhary S, Singh S, Chaudhary S. Thermal Radiation Effects on MHD Boundary Layer Flow over an Exponentially Stretching Surface. Appl Maths (2015) 06(02):295–303. doi:10.4236/am.2015.62027

CrossRef Full Text | Google Scholar

38. Hayat T, Khan MI, Waqas M, Alsaedi A, Yasmeen T. Diffusion of Chemically Reactive Species in Third Grade Fluid Flow over an Exponentially Stretching Sheet Considering Magnetic Field Effects. Chin J Chem Eng (2017) 25(3):257–63. doi:10.1016/j.cjche.2016.06.008

CrossRef Full Text | Google Scholar

39. Elbashbeshy E. Heat Transfer over an Exponentially Stretching Continuous Surface with Suction. Arch Mech (2001) 53(6):643–51.

Google Scholar

40. Ali B, Naqvi RA, Hussain D, Aldossary OM, Hussain S. Magnetic Rotating Flow of a Hybrid Nano-Materials Ag-MoS2 and Go-MoS2 in C2H6O2-H2o Hybrid Base Fluid over an Extending Surface Involving Activation Energy: FE Simulation. Mathematics (2020) 8(10):1730. doi:10.3390/math8101730

CrossRef Full Text | Google Scholar

41. Kumari M, Nath G. Transient Rotating Flow over a Moving Surface with a Magnetic Field. Int J Heat Mass Transfer (2005) 48(14):2878–85. doi:10.1016/j.ijheatmasstransfer.2005.02.009

CrossRef Full Text | Google Scholar

Nomenclature

v Velocity in y-direction (m/s)

u Velocity in x-direction (m/s)

C_p Specific heat (J/kg.K)

C_∞ Ambient concentration (kg/m³)

T_∞ Ambient temperature (K)

Rd Radiation parameter (–)

k Vortex viscosity (Pa.s)

q_r Radiative heat flux (W/m²)

p Pressure (N/m²)

Re Reynolds number (–)

T Temperature (K)

N Angular velocity (1/s)

Nt Thermophoresis diffusion parameter (–)

Ec Eckert number (–)

Pr_m Magnetic Prandtl number (–)

Cf_x Skin friction coefficient (–)

Greek Symbols

τ* Ratio of latent heat capacities (–)

σ* Stepan–Boltzmann constant (W/m².K⁴)

μ Viscosity (kgm⁻¹s⁻¹)

θ(η) Dimensionless temperature (–)

η_o Magnetic diffusivity (m²/s)

ρ Density (kg.m⁻³)

η Dimensionless variable

j Micro-inertia density (m²)

α₁, α₂, β Dimensionless fluid parameters (–)

(x, y) Cartesian coordinates (m)

T_f Temperature at wall (K)

C Fluid’s concentration (kg/m³)

U_o Reference velocity (m/s)

B Micro-inertia density coefficient (–)

D_B Brownian diffusivity coefficient (m²/s)

D_T Thermophoresis diffusivity coefficient (m²/s)

B_o Applied magnetic field (kg/s².A)

Pr Prandtl number (–)

Le Lewis number (–)

K micro-polarity parameter (–)

Nb Brownian diffusion parameter (–)

M Magnetic parameter

H₁, H₂ Induced magnetism components (A/m)

C_f Concentration at sheet (kg/m³)

Nu_x Heat transfer coefficient (–)

f(η) Non-dimensional velocity (–)

ϕ(η) Non-dimensional concentration curve (–)

δ Thermal slip parameter (–)

g(η) Dimensionless induced field (–)

k* Average absorption coefficient (1/m)

h(η) Dimensionless micro-rotation curve (–)

γ* Fluid’s spin gradient viscosity (kg.m/s)

σ Electrical conductance (A².s³/kg.m³)

Ψ(x, y) Stream function (m/s)