Linear and quadratic convection significance on the dynamics of MHD Maxwell fluid subject to stretched surface

Introduction

Background study

Magnetohydrodynamics (MHD) is a subfield of fluid mechanics that analysis how an electrically conductive liquid moves in the vicinity of magnetism. Liao [1] inspected the exact solutions for the MHD stream of non-Newtonian fluid over an enlarging sheet. Datti et al. [2] explored the MHD stream and thermal transmission in a visco-elastic liquid across a non-isothermal expanding surface. Ishak et al. [3] analyzed the MHD stagnating point stream across an expanding sheet. Ahmad et al. [4] examined the MHD stream of a viscous liquid in a permeable medium across an exponentially stretched layer. Hayat et al. [5] provided an analytical solution for the MHD stream of a micropolar liquid caused by a curved elongating surface under the impact of homogeneous-heterogeneous reactions. The transient MHD transportation of spinning Maxwell nanofluid stream over an extending surface with doubled diffusion and activating potential was exposed by Ali et al. [6]. Dawar et al. [7] explored the Lorentz forces and their effects on the Jaffrey nano liquid stream across a convectively warmed plain surface. Numerous researchers [8–11] have probed the MHD influence on fluid flow behavior.

The applications of non-Newtonian fluids cover a wide range of fundamental challenges in pharmaceutical, crude oil, polymer, and food production industries. Viscoelastic fluids are non-Newtonian fluids in which the imposed tension distribution is non-linearly related to velocity gradient. The Navier-Stokes equations and Newton’s law of viscosity are insufficient for characterizing non-Newtonian liquids. Generally, the mathematical issues in non-Newtonian liquids are more complex than in Newtonian fluids because of severe non-linearity and higher-order differential equations. As a result, several modern scientists are exploring various non-Newtonian liquid models under varied flow conditions. Exact solutions for the rotational stream of a modified Burgers fluid over cylindrical regions were proposed by Jamil and Fetecau [12]. Kamran et al. [13] disclosed the unstable rotating stream of fractional Oldroyd-B liquid between two infinite concentric cylinders. Ali et al. [14] performed the numerical assessment of MHD boundary layer stream and heat transport in micropolar liquids across a shrinkable sheet. Rehman et al. [15] probed the numerical solutions for a stream of Casson fluid caused by the rotating disk. Riaz et al. [16–19] have studied numerous non-Newtonian liquids and a detailed analysis of entropy production considering different flow configurations. Ali et al. [20] discussed Maxwell’s unsteady (3-D) stream and tangentially hyperbolic nano liquid across a stretchy surface in the rotational frame.

Boundary layer flows across the stretchable sheet are essential for various applications, including glass blowing, cord depiction, copper spiraling, paper manufacture, glass blowing, extrusion, warm progressing, thermal conductivity of heat sinks, and melts of high molecular weight polymers. Sakiadis [21] illustrated the boundary layer stream at a continuous elongated surface having consistent speed. Wang [22] explored the viscid stream produced by a horizontally extended surface, considering suction and sliding phenomena. Khan et al. [23] scrutinized the two-dimensional stream of Prandtl liquid across a stretchy surface and the influence of homogeneous-heterogeneous reactions. In the vicinity of a heat source, the MHD boundary layer stream and heating flux of nano liquid across a vertically expanded sheet was scrutinized by Ali et al. [24]. Awan et al. [25] inspected second-grade liquid’s MHD stagnation point stream over the oscillating extending sheet. Ali et al. [26] inspected the influence of bio-convection and chemical reaction over MHD nano liquid stream caused by exponentially enlarging surface. Awan et al. [27] performed the thermal inspection of an oblique stagnation point stream of second-grade liquid over an elongating surface with slip constraints.

The general form of convection is mixed (combined) convection, which is a composite of natural and driven convection in which a stream is governed concurrently by both an outer driving system and interior volumetric (body) stresses. They are used in various applications, including climatic boundary-layer streams, thermal radiators, solar cells, nuclear plants, and auto-electronic devices. Earlier researchers assumed a linear density change in the buoyancy force factor, which is typically appropriate with minor temperature variations. The interplay of forced and natural convection is most noticeable where the driven flow rate is low and temperature variations are enormous. Karwe and Jaluria [28] disclosed the transportation of fluid stream and combined convection from a movable plate in sliding and erosion processes. Vajravelu et al. [29] revealed the heat transmission from a dike using nonlinear convection across a permeable flat plate. Kumar and Sood [30] disclosed the combined impact of MHD and nonlinear convection in the stagnation point stream across a shrinkable surface. Hayat et al. [31] investigated the MHD influence on (3-D) nonlinear buoyancy stream of Oldroyd-B nano liquid across an extending sheet. Sampath Kumar et al. [32] inspected the stream of Jaffrey nano liquid, considering the impact of quadratic convection, MHD, nonlinear radiations, and multiple convected constraints. Patil and Kulkarni [33] probed the impact of surface ruggedness on MHD nonlinear convective nano liquid stream above a vertically moving plate. The comparative analysis for the linear and nonlinear buoyancy stream of hybrid nano liquid was explored by Kumar et al. [34].

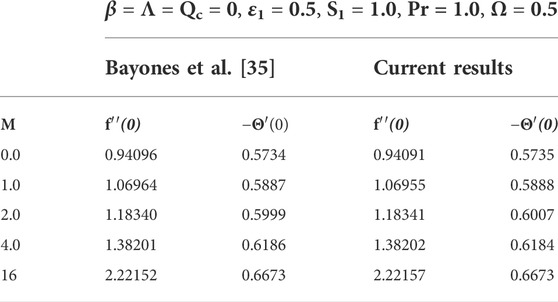
After the aforementioned literature review, it is observed that no initiative has been taken to explore the energy and mass transport behavior of nonlinear mixed convection flow with nonhomogeneous material features and linear heat production around the boundary layer of a stretchy surface. Furthermore, nonlinear convection occurs due to nonlinear density temperature differences in the buoyant force term, which substantially influences flow behavior. Motivated by the Bayones et al. [35], the present analysis is carried out to 1) analyze the rheology attributes of Maxwell fluid, 2) the significance of variable thermal conductance on the fluid temperature, 3) incorporate the influence of MHD, nonlinear convection, and heat absorption/generation. The underlying problem is solved numerically with the bvp4c technique in MATLAB. For linear and quadratic convection and varying temperature-dependent attributes, the velocity and temperature distributions and the coefficient of skin friction and heat flux are graphically explored. The validity of the numerical technique is probed by comparative tables with the existing research work. It is found that flow velocity enhances quadratic convection versus linear convection. On the other hand, the thermal boundary layer size and heat transport rate are higher for linear convection than in the quadratic model. The lower temperature for the quadratic convection model versus the linear model offers applications in manufacturing improved lubricants to minimize machinery degradation. Moreover, thermal designers can employ the current numeric outcomes in the industry because varying thermal conductance achieves higher efficiency than uniform thermal conductance.

Mathematical model

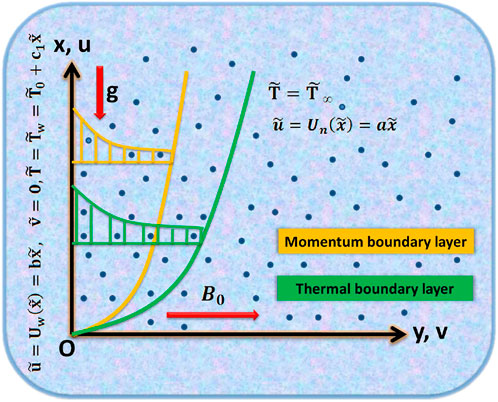
A time-independent, incompressible, two-dimensional, laminar, MHD flow of the Maxwell fluid across the stretched surface has been analyzed in the current flow problem. The impacts of varying thermal conductance, quadratic convection, and heat source/sink have also been incorporated. The cartesian coordinates are chosen with the horizontal axis pointing in the direction of the stretched surface and the vertical axis normal to the stretchy surface. The flow’s composition is portrayed in Figure 1. To stabilize the boundary layer flow, a constant magnetic field B₀ is provided perpendicular to the sheet. The produced magnetic field is ignored since the magnetic Reynolds number is considered to be quite small. The enlarging velocity is supposed to be $U_w\left(\tilde{x}\right)=b\tilde{x}$ with b > 0, and the stream velocity is taken as $U_n(\tilde{x})=a\tilde{x}$ with a > 0. The governing equations for the considered problem following [34–36] are stated as:

$\frac{\partial \tilde{u}}{\partial \tilde{x}}+\frac{\partial \tilde{v}}{\partial \tilde{y}}=0,(1)$

$\begin{array}{ll}\hfill & \tilde{u}\frac{\partial \tilde{u}}{\partial \tilde{x}}+\tilde{v}\frac{\partial \tilde{u}}{\partial \tilde{y}}=\nu \frac{{\partial }^2\tilde{u}}{\partial {\tilde{y}}^2}+U_n\frac{d{U}_n}{d\tilde{x}}+\left(g{\beta }_1\right)\left(\tilde{T}-{\tilde{T}}_{\infty }\right)+\left(g{\beta }_2\right){\left(\tilde{T}-{\tilde{T}}_{\infty }\right)}^2\hfill \\ \hfill & -{\lambda }_1\left[{\tilde{u}}^2\frac{{\partial }^2\tilde{u}}{\partial {\tilde{x}}^2}+{\tilde{v}}^2\frac{{\partial }^2\tilde{u}}{\partial {\tilde{y}}^2}+2\tilde{u}\tilde{v}\frac{{\partial }^2\tilde{u}}{\partial \tilde{x}\partial \tilde{y}}\right]-\frac{\sigma B_o^2}{\rho }\left(\tilde{u}-U_n\right),\hfill \end{array}(2)$

$\tilde{u}\frac{\partial \tilde{T}}{\partial \tilde{x}}+\tilde{v}\frac{\partial \tilde{T}}{\partial \tilde{y}}=\frac{1}{\left(\rho C_p\right)}\left[\frac{\partial }{\partial \tilde{y}}\left(k\left(\tilde{T}\right)\frac{\partial \tilde{T}}{\partial \tilde{y}}\right)\right]+\frac{Q_o}{\left(\rho C_p\right)}\left(\tilde{T}-{\tilde{T}}_{\infty }\right).(3)$

FIGURE 1

FIGURE 1. Flow configuration.

The suitable boundary constraints are stated as follows:

$\left.\begin{array}{c}\hfill \tilde{u}\left(\tilde{x},\tilde{y}\right)=U_w\left(\tilde{x}\right),\tilde{T}\left(\tilde{x},\tilde{y}\right)={\tilde{T}}_w\left(\tilde{x}\right)={\tilde{T}}_{\infty }+c_1\tilde{x},\tilde{v}\left(\tilde{x},\tilde{y}\right)=0,\text{for}\tilde{y}=0,\hfill \\ \hfill \tilde{u}\left(\tilde{x},\tilde{y}\right)\to U_n\left(\tilde{x}\right),\tilde{T}\left(\tilde{x},\tilde{y}\right)\to {\tilde{T}}_{\infty }\text{for}\tilde{y}\to \infty .\hfill \end{array}\right\}(4)$

Where the velocity coefficients along $\tilde{x}$ and $\tilde{y}$ axes are indicated by $\tilde{u}$ and $\tilde{v}$, respectively. The density of fluid is ρ, B_o is the intensity of applied magnetism, λ₁ is the fluid’s relaxation time, σ is electrical conductance of fluid, (β₁, β₂) depict the coefficients of thermal expansion, the fluid’s temperature is $\tilde{T}$, g stands for gravity, the heat diffusivity is $\widehat{\alpha }$, (ρC_p) is the volumetric thermal capability, and Q_o reflect the heat generating coefficient. The ambient temperature and surface temperature are symbolized by ${\tilde{T}}_{\infty }$ and ${\tilde{T}}_w$ respectively. The variable thermal conductance is defines as follows:

$k\left(\tilde{T}\right)=\left(1+\mathrm{\Lambda }\frac{{\tilde{T}}_{\infty }-\tilde{T}}{{\tilde{T}}_{\infty }-{\tilde{T}}_w}\right)k.(5)$

The problem is simplified by using similarity variables following [35, 37, 38]:

$\tilde{u}=f^{\prime }\left(\xi \right)a\tilde{x},\tilde{v}=-\sqrt{a\nu }f\left(\xi \right),\mathrm{\Theta }\left(\xi \right)=\frac{\tilde{T}-{\tilde{T}}_{\infty }}{{\tilde{T}}_w-{\tilde{T}}_{\infty }},\xi =\tilde{y}\sqrt{\frac{a}{\nu }}.(6)$

where ξ is non-dimensional constraint, f′(ξ) and Θ(ξ) are the dimensionless velocity and temperature distributions respectively. Using above mentioned transformation Eq. 1 is satisfied, and Eqs 2, 3 are altered into dimensionless ODEs.

$f^{‴}+1+f{f}^{″}-{\left(f^{\prime }\right)}^2+\beta \left(2f{f}^{\prime }{f}^{″}-f^2{f}^{‴}\right)+\mathrm{\Omega }\left(\mathrm{\Theta }+Q_c{\mathrm{\Theta }}^2\right)-M^2\left(f^{\prime }-1\right)=0,(7)$

${\mathrm{\Theta }}^{″}\left(1+\mathrm{\Lambda }\mathrm{\Theta }\right)+\mathrm{\Lambda }{\left({\mathrm{\Theta }}^{\prime }\right)}^2+Prf{\mathrm{\Theta }}^{\prime }+Pr{S}_1\mathrm{\Theta }-Pr\mathrm{\Theta }{f}^{\prime }=0.(8)$

The associated non-dimensional boundary conditions are stated as:

$\left.\begin{array}{c}\hfill f\left(\xi \right)=0,f^{\prime }\left(\xi \right)={\epsilon }_1,\mathrm{\Theta }\left(\xi \right)=1,\text{for}\xi \to 0,\hfill \\ \hfill f^{\prime }\left(\xi \right)=1,\mathrm{\Theta }\left(\xi \right)=0,\text{for}\xi \to \infty .\hfill \end{array}\right\}(9)$

In above mentioned equations, the prime (′) denotes the differentiation with regard to the similarity variable ξ. Furthermore, M² denotes magnetic parameter, β is the Deborah number, Ω the mixed convection parameter, S₁ represents the heat generating/absorbing parameter, Pr is the Prandtl number, the heat conductance parameter is Λ, Q_c depicts quadratic convection parameter, and ɛ₁ is the velocity ratio coefficient. These parameters are stated as follows:

$\begin{array}{l}\hfill M^2=\frac{\sigma B_o^2}{\rho a}\mathrm{\Omega }=\frac{G{r}_{\tilde{x}}}{{\left(R{e}_{\tilde{x}}\right)}^2},G{r}_{\tilde{x}}=\frac{g{\beta }_1\left({\tilde{T}}_w-{\tilde{T}}_{\infty }\right){\tilde{x}}^3}{{\nu }^2},R{e}_{\tilde{x}}=\frac{a{\left(\tilde{x}\right)}^2}{\nu },\\ \hfill Q_c=\left(\frac{{\beta }_2}{{\beta }_1}\right)\left({\tilde{T}}_w-{\tilde{T}}_{\infty }\right),Pr=\frac{\mu C_p}{k},S_1=\frac{Q_o}{\left(\rho C_p\right)a},{\epsilon }_1=\frac{b}{a},\beta ={\lambda }_{1}a.\end{array}$

It would be observed that $\left(Q_c>0\right)$ reflects the non-linear convection, and $\left(Q_c=0\right)$ represents linear mixed convection. Further, $\left({\epsilon }_1>0\right)$ for a stretching case, and $\left({\epsilon }_1=0\right)$ for the stationary surface. The skin frictional coefficient and Nusselt number are two important physical attributes. These quantities are stated as follows:

${Cf}_{\tilde{x}}=\frac{{\tilde{\tau }}_w}{\rho U_n^2},N{u}_{\tilde{x}}=\frac{\tilde{x}{q}_w}{k\left(\tilde{T}\right)\left({\tilde{T}}_w-{\tilde{T}}_{\infty }\right)},(10)$

where ${\tilde{\tau }}_w$ the wall shear stress, and q_w the wall heat influx are stated as:

$q_w={\left.-k\left(\frac{\partial \tilde{T}}{\partial \tilde{y}}\right)\right|}_{\tilde{y}=0},{\tilde{\tau }}_w={\left.\mu \left(\frac{\partial \tilde{u}}{\partial \tilde{y}}\right)\right|}_{\tilde{y}=0}.(11)$

By using Eqs 6, 11 in Eq. 10, the dimensionless forms of physical quantities are stated as:

${Cf}_{\tilde{x}}{\left(R{e}_{\tilde{x}}\right)}^{1/2}=f^{″}\left(0\right),N{u}_{\tilde{x}}{\left(R{e}_{\tilde{x}}\right)}^{-1/2}=-\frac{1}{\left(1+\mathrm{\Lambda }\mathrm{\Theta }\right)}{\mathrm{\Theta }}^{\prime }\left(0\right).(12)$

where $R{e}_{\tilde{x}}=\frac{a{\tilde{x}}^2}{\nu }$ depicts the local Reynolds number.

Numerical method

Due to the high non-linearity of the coupled ODEs (7–8), the analytical solution is not feasible. Various numerical methods are utilized in MATLAB to obtain a valid numerical solution. One of most significant method is bvp4c technique. The solution strategy is given as:

$f\left(\xi \right)=Z_1,f^{\prime }\left(\xi \right)=Z_2,f^{″}\left(\xi \right)=Z_3,f^{‴}\left(\xi \right)=Z_4,\mathrm{\Theta }\left(\xi \right)=Z_5,{\mathrm{\Theta }}^{\prime }\left(\xi \right)=Z_6,{\mathrm{\Theta }}^{″}\left(\xi \right)=Z_7,$

Using the above substitution, the subsequent ODEs are defined as:

$Z_4=\frac{1}{\left(1-\beta Z_1^2\right)}\left[{\left(Z_2\right)}^2-Z_1{Z}_3+M^2\left(Z_2-1\right)-1-\mathrm{\Omega }\left(Z_5+Q_c{\left(Z_5\right)}^2\right)-2\beta Z_1{Z}_2{Z}_3\right],(13)$

$Z_7=\frac{1}{\left(1+\mathrm{\Lambda }{Z}_5\right)}\left[Pr\left(Z_5{Z}_2-Z_1{Z}_6-S_1{Z}_5\right)-\mathrm{\Lambda }{\left(Z_6\right)}^2\right].(14)$

The boundary constraints are stated as:

$\left.\begin{array}{c}\hfill Z_1=0,Z_2={\epsilon }_1,Z_5=1,\text{for}\xi \to 0,\hfill \\ \hfill Z_2=1,Z_5=0,\text{for}\xi \to \infty .\hfill \end{array}\right\}(15)$

Numerical findings and discussion

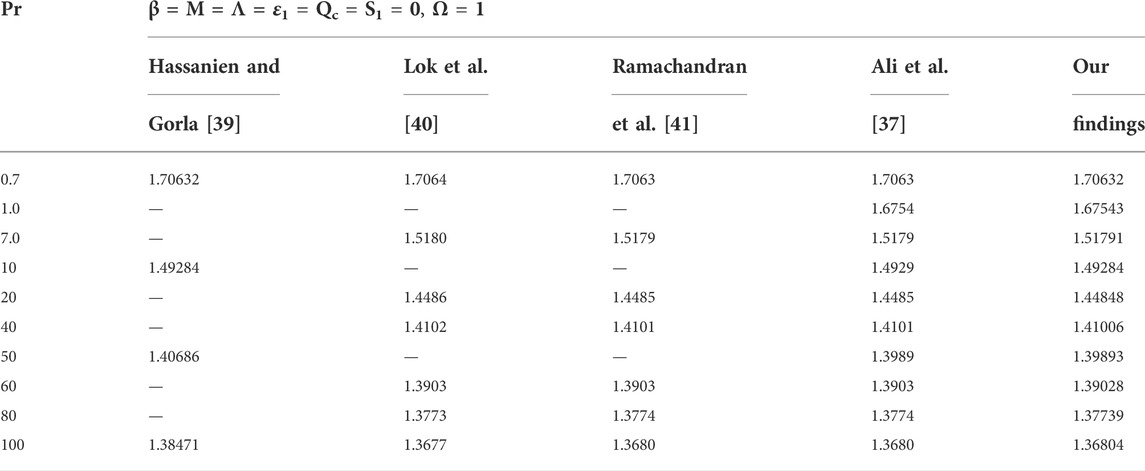
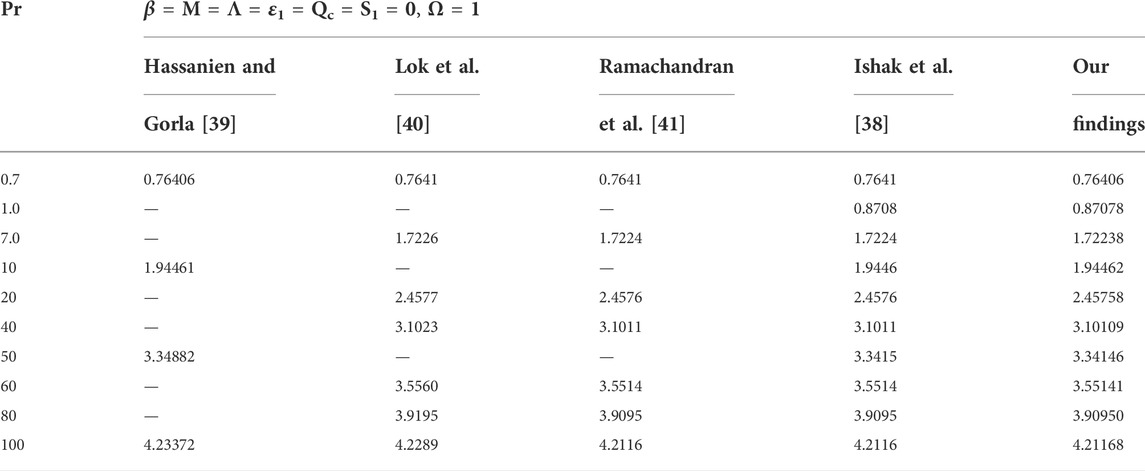
In current article, the flow phenomena arising due the linear stretching of expanding sheet for two-dimensional Maxwell fluid with variable thermal conductivity is studied. The numerical outcomes for the current study are calculated by solving the dimensionless ODEs (7–8) along with the boundary and initial constraints (9). The bvp4c method in MATLAB software is applied to obtain the numeric results. The estimation for the current analysis is settled by using the specified values for parameters: Pr = 2.0, M = 0.3, β = 0.2, Ω = 1.0, ɛ₁ = 0.3, S₁ = 0.2, Λ = 0.2. The ranges for the involved parameters are: 0.2 ≤ β ≤ 2.6, 0.2 ≤ Λ ≤ 2.2, 0.2 ≤ ɛ₁ ≤ 1.4, 0 ≤ M ≤ 8.6, −8 ≤ S₁ ≤ 2, 0.2 ≤ Ω ≤ 1.4 and 0.7 ≤ Pr ≤ 3 are chosen to observe the smooth behavior of velocity and temperature curves. Tables 1–3 are constructed to compare our findings with already published papers. A notable coincidence has occurred, displaying the validity of the bvp4c method. Figures 2–8 are plotted to show the significance of distinct parameters over velocity f′(ξ) and temperature Θ(ξ) profiles for two cases: (i) linear convection (Ω = 1, Q_c = 0) (ii) quadratic convection (Ω = 1, Q_c = 2).

TABLE 1

TABLE 1. Numerical evaluations for f′′(0) with fluctuation in Pr.

TABLE 2

TABLE 2. Numerical evaluations for − Θ′(0) with fluctuation in Pr.

TABLE 3

TABLE 3. Numerical evaluations for − Θ′(0) and f′′(0) with fluctuation in M.

FIGURE 2

FIGURE 2. The Θ(ξ) and f′(ξ) curves for distinct β values.

FIGURE 3

FIGURE 3. The Θ(ξ) and f′(ξ) curves for distinct Λ values.

FIGURE 4

FIGURE 4. The Θ(ξ) and f′(ξ) curves for distinct ɛ₁ values.

FIGURE 5

FIGURE 5. The Θ(ξ) and f′(ξ) curves for distinct M values.

FIGURE 6

FIGURE 6. The Θ(ξ) and f′(ξ) curves for distinct S₁ values.

FIGURE 7

FIGURE 7. The Θ(ξ) and f′(ξ) curves for distinct Ω values.

FIGURE 8

FIGURE 8. The Θ(ξ) and f′(ξ) curves for distinct Pr values.

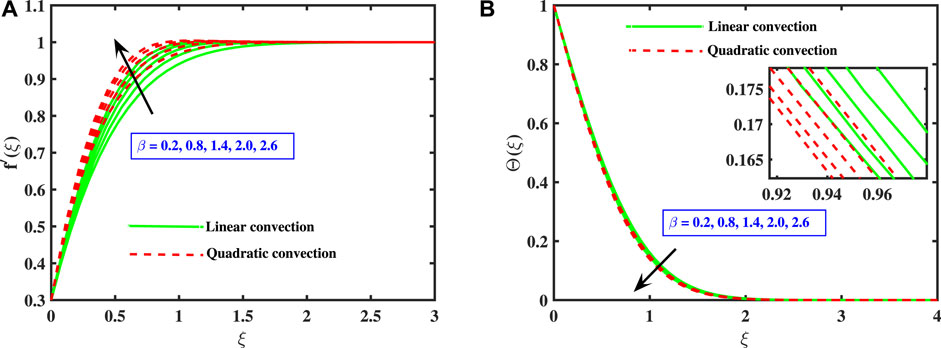
Figure 2A,B reveal the influence of Deborah no. (β) on the dimensionless velocity f′(ξ) and temperature Θ(ξ) profiles for both the linear and non-linear convection. Deborah no. is the quotient of fluids relaxation time and the time of observation. It is used to assess the fluidity of the substances under specified flow regimes. The case (β = 0) reduces to Newtonian fluid model. Raising the value of β enhances the velocity and thus the width of the boundary layer. The velocity fluctuates from zero to a maximal positive value, then gradually declines taking zero value outside the boundary layer. It is observed that the fluid accelerates more strongly for quadratic convection in comparison to the linear convection. An reverse effect is visualized for the temperature Θ(ξ), which descends slightly for the boosting β values. In the temperature boundary layer, it is depicted that the linear buoyancy (Q_c = 0) provides more heat transfer than the quadratic buoyancy (Q_c ≠ 0).

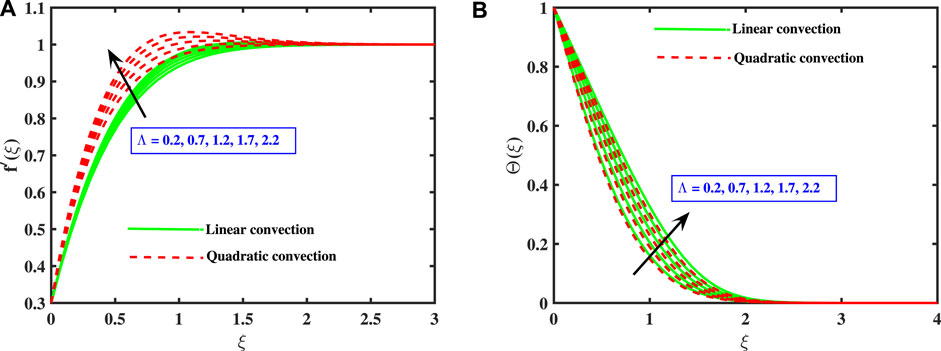
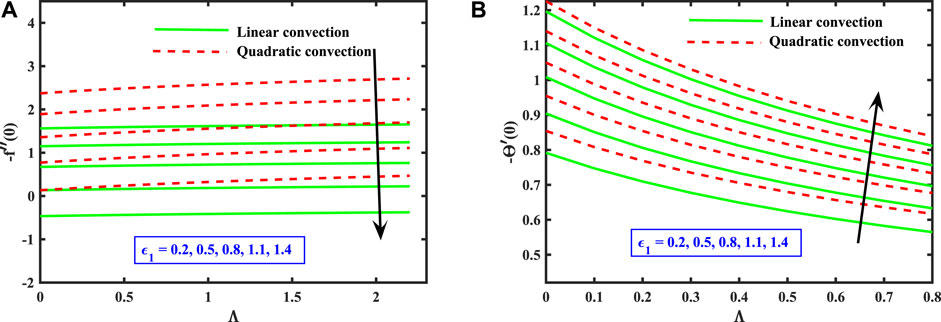
Figures 3A,B exhibit the non-dimensional velocity and temperature curves for both the linear and quadratic convection terms for different values of variable thermal conductivity parameter Λ. The higher values of Λ improves the peak velocity of the fluid. Hence, the linear convection model performs as a lower bound. The thermal conductance of the liquid rises the non-dimensional temperature as a function of ξ, as illustrated in Figure 3B, for both linear and quadratic buoyancy terms. This is due to the fact that thermal conductivity measures the efficiency with which heat escapes from a fluid. As a result, heat from the sheet is estimated to be transmitted quickly into the primary stream due to an elevation in the thermal conductance value. The heat transmission at the boundary layer is found to be greater for the linear convection than for the quadratic convection model.

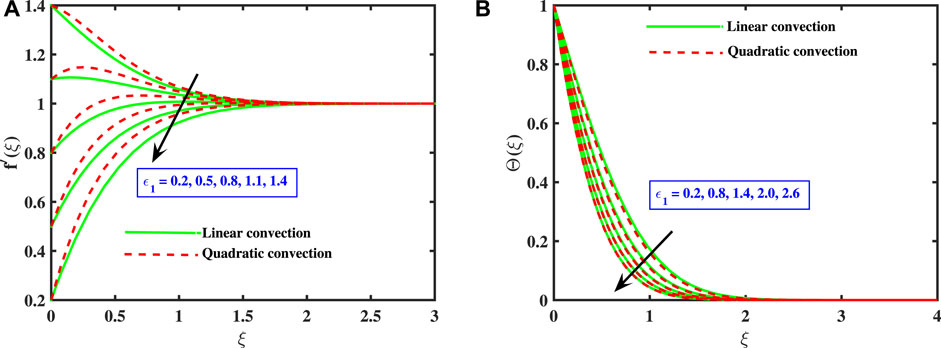
Figures 4A,B depict the impact of velocity ratio coefficient ɛ₁ for both linear and non-linear buoyancy parameters. For larger values of ɛ₁ (when the stretching velocity U_w is greater than the free stream speed U_n), the fluid’s speed decelerates in the boundary layers for both the linear and non-linear models. Figure 4B indicates the impact of ɛ₁ on Θ(ξ). It is noted that as ɛ₁ grows, the temperature curve and temperature boundary layer size for both linear and non-linear convection diminish. Also, linear buoyancy model generates more heat in comparison to the quadratic model.

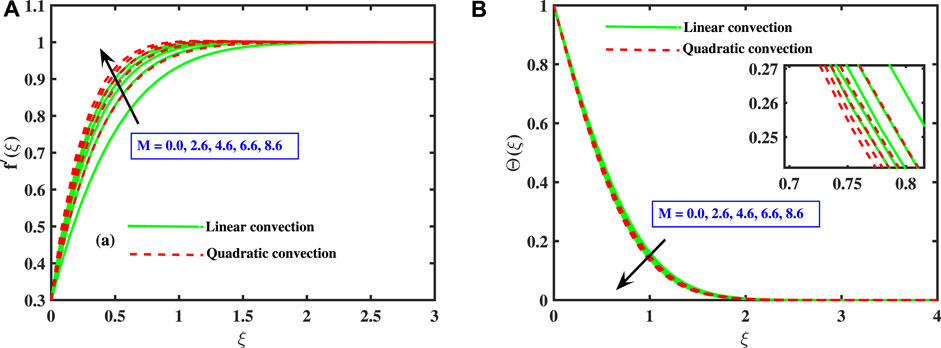
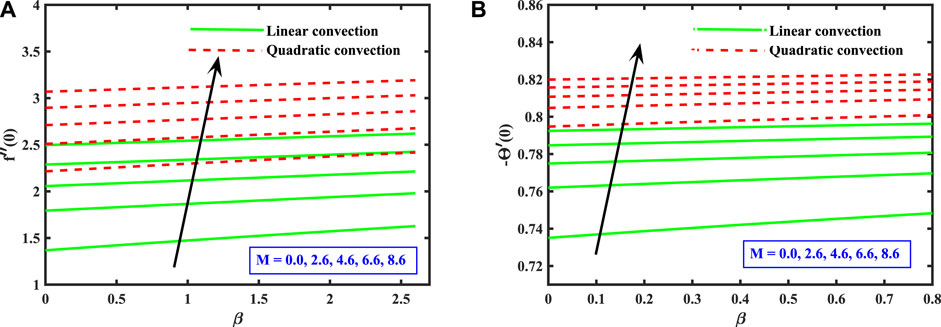
Figures 5A,B are displayed to highlight the effect of magnetic coefficient M over the f′(ξ) and Θ(ξ) profiles for both linear and non-linear convection. This is probed that the velocity of liquid improves for progressing amounts of M, which holds for both the linear and quadratic buoyancy models. However, in an electrically conductive liquid, the transverse magnetic flux leads to a retardation force termed as the Lorentz force, that restricts the motion of the liquid in boundary layer. The opposite impact of M over the velocity profile, on the other hand, indicates that the free stream velocity exceeds the stretched surface speed. The temperature curve Θ(ξ) declines for higher amounts of magnetic coefficient M. It is noted that quadratic buoyancy model works as the lower bound for the heat transport than the linear convection model.

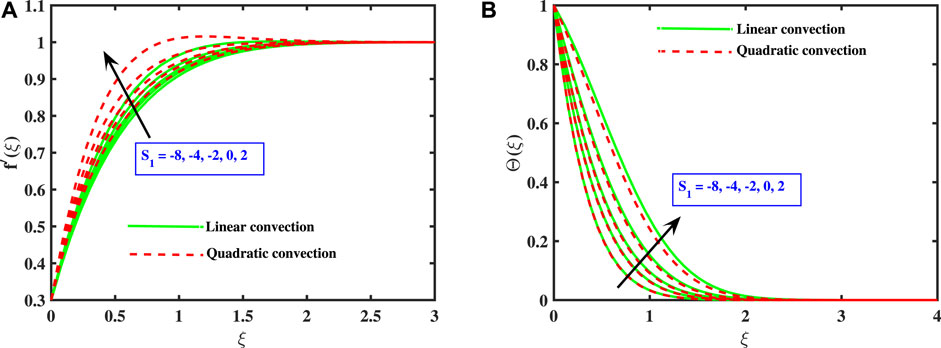
Figures 6A,B capture the trend of velocity and temperature curves for heat generation/absorbtion coefficient S₁ for the quadratic and linear buoyancy terms. It is explored that enhancing the heat generating coefficient improves both the velocity and the heat propagation of the fluid. The heat generating coefficient enables fluid surface to absorb this heat and so remain effective. This consequence illustrates that the energy of the heating source is rather high, and the maximum temperature of the liquid is measured on the surface. As depicted in Figure 6B, the participation of a heat sink (S₁ < 0) causes decline in the thermal efficiency of the fluid, resulting in the formation of smaller thermal boundary layers. Furthermore, the linear convection model acquires higher heat transport rate in comparison to the quadratic convection model.

Figures 7A,B are plotted to depict the behavior of f′(ξ) and Θ(ξ) for both linear and non-linear buoyancy terms along with diverse values of mixed convective coefficient Ω. Increasing values of the combined convection coefficient Ω indicate a stronger buoyant force, which results in more kinetic energy and an elevation in fluid speed, as plotted in Figure 7A, the velocity has growing impacts. As the quadratic convective coefficient grows (Q_c > 0), the maximum velocity improves, and the linear case (Q_c = 0) acts as the lowest limit. On the other hand, Figure 7B depicts a very minor reduction in temperature profile as the combined convection parameter is enhanced. Furthermore, the linear buoyancy model serves as a upper bound in case of heat transport as compared to the quadratic buoyancy.

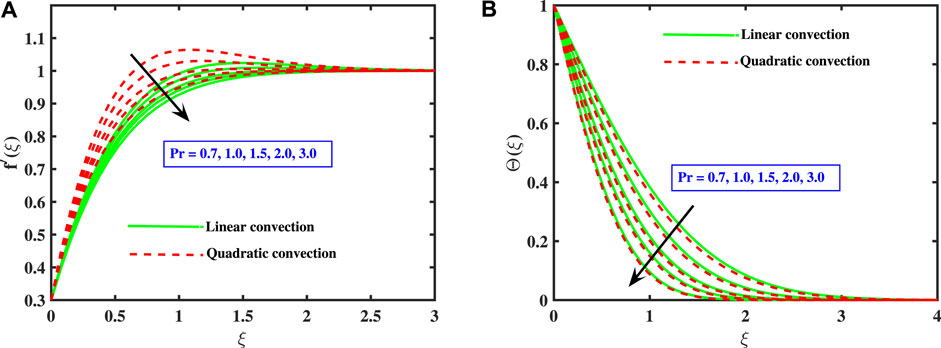
The tendency of velocity and temperature curve for distinct values of Prandtl no. is described in Figures 8A,B for the linear and non-linear Boussinesq estimations. The velocity curve depicts a declining trend for higher Pr values. However, quadratic buoyancy model attains larger thickness of boundary layer in comparison to the linear convection. Physically, as the Prandtl number raises, the heat diffuseness reduces, resulting in a reduction in power capacity, which lessens the temperature boundary layer, as displayed in Figure 8B. Consequently, heat is dissipated more quickly, and hence, temperature boundary layer width and temperature of the liquid both diminish. As a result, the Prandtl number is employed to enhance the cooling tendency of fluids. It is examined that linear convection gains more heat exchange rate than the quadratic convection model.

Numerical assessment of skin friction and nusselt number

Figures 9A,B are plotted to signify the importance of Deborah no. (β) and magnetic coefficient (M) on coefficient of skin friction $C{f}_{\tilde{x}}{(R{e}_{\tilde{x}})}^{0.5}$ and Nusselt no. $N{u}_{\tilde{x}}{(R{e}_{\tilde{x}})}^{-0.5}$. It is exposed that f′′(0) and − Θ′(0) grow up for higher values of M and β. It is visualized that quadratic convection gains higher values of f′′(0) and − Θ′(0) as compared to linear buoyancy model. Figures 10A,B characterize the behavior of $C{f}_{\tilde{x}}{(R{e}_{\tilde{x}})}^{0.5}$ and $N{u}_{\tilde{x}}{(R{e}_{\tilde{x}})}^{-0.5}$ for progressing values of Λ and ɛ₁. It is probed that coefficient of skin friction has descending trend for accelerating values of ɛ₁ and Λ for both the linear and quadratic convection. However, the linear buoyancy model acts as lower bound against higher values of ɛ₁ and Λ in comparison to the quadratic buoyancy model. Figure 10B depicts the increasing fashion of wall heat transfer coefficient for the enhancing values of ɛ₁ and Λ. The heat flux coefficient accelerates more quickly for quadratic convection as compared to linear convection.

FIGURE 9

FIGURE 9. The f′′(0) and − Θ′(0) curves against M and β.

FIGURE 10

FIGURE 10. The f′′(0) and − Θ′(0) curves against ɛ₁ and Λ.

Concluding remarks

This research has investigated Maxwell fluid’s boundary layer stream and thermal efficiency across a linear stretchy surface along with MHD, nonlinear convection, and varying thermal conductance. The dimensionless nonlinear ODEs are tackled numerically in MATLAB utilizing the bvp4c technique. The numerical findings for the non-dimensional velocity curve, temperature curve, skin friction, and Nusselt number are displayed via graphs and verified through tables. Some crucial outcomes are listed here:

• Increment in the magnetic coefficient (M), varying thermal conductance (Λ), and Deborah number (β) value amplified the axial velocity field for both the linear and quadratic convection. However, the fluid temperature diminishes for higher inputs of β and M but amplifies for larger values of Λ in both linear and nonlinear convection.

• When the velocity ratio coefficient ɛ₁ is raised, the extending velocity becomes greater than the free streaming speed, reducing the temperature and velocity fields.

• Higher inputs of Ω depict stronger buoyant force. Hence, the velocity field boosts, and temperature declines for larger inputs of Ω.

• As the heat-generating parameter S₁ is elevated, the velocity and thermal profiles increase for both linear and quadratic buoyancy.

• The thermal boundary layer width declines with increment in Pr no. values due to the reduction in thermal diffuseness for both linear and nonlinear buoyancy.

• The coefficient of skin friction $C{f}_{\tilde{x}}{(R{e}_{\tilde{x}})}^{1/2}$ and Nusselt no. $N{u}_{\tilde{x}}{(R{e}_{\tilde{x}})}^{-1/2}$ enhance for the larger inputs of M and β for both linear and quadratic convection. However, the elevating fashion of Λ and ɛ₁ has decreased the skin friction but increased the Nusselt number.

• The linear convection model attains a higher heat transport rate than the quadratic convection model.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication. AAA: Formal analysis, investigation and writing-original draft. AUA: Formal analysis and supervision. MZB-F: Funding acquisition, software and revision. EMT-E: Funding acquisition, validation and revision. KG: Funding acquisition, resources and revision. MFY: Funding acquisition, validation and revision. BA: Conceptualization, editing and revision.

Acknowledgments

The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work through research groups program under grant number R.G.P. 2/76/43. The authors would like to thank the Deanship of Scientific Research at Umm Al-Qura University for supporting this work by Grant Code: 22UQU4331317DSR34.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Liao S-J. On the analytic solution of magnetohydrodynamic flows of non-Newtonian fluids over a stretching sheet. J Fluid Mech (2003) 488:189–212. doi:10.1017/s0022112003004865

CrossRef Full Text | Google Scholar

2. Datti P, Prasad K. V., Abel MS, Joshi A. MHD visco-elastic fluid flow over a non-isothermal stretching sheet. Int J Eng Sci (2004) 42(8-9):935–46. doi:10.1016/j.ijengsci.2003.09.008

CrossRef Full Text | Google Scholar

3. Ishak A, Jafar K, Nazar R, Pop I. MHD stagnation point flow towards a stretching sheet. Physica A: Stat Mech its Appl (2009) 388(17):3377–83. doi:10.1016/j.physa.2009.05.026

CrossRef Full Text | Google Scholar

4. Ahmad I, Sajid M, Awan W, Rafique M, Aziz W, Ahmed M, et al. MHD flow of a viscous fluid over an exponentially stretching sheet in a porous medium. J Appl Math (2014) 2014:256761. doi:10.1155/2014/256761

CrossRef Full Text | Google Scholar

5. Hayat T, Sajjad R, Ellahi R, Alsaedi A, Muhammad T. Homogeneous-heterogeneous reactions in MHD flow of micropolar fluid by a curved stretching surface. J Mol Liq (2017) 240:209–20. doi:10.1016/j.molliq.2017.05.054

CrossRef Full Text | Google Scholar

6. Ali B, Nie Y, Hussain S, Manan A, Sadiq MT. Unsteady magneto-hydrodynamic transport of rotating Maxwell nanofluid flow on a stretching sheet with Cattaneo–Christov double diffusion and activation energy. Therm Sci Eng Prog (2020) 20:100720. doi:10.1016/j.tsep.2020.100720

CrossRef Full Text | Google Scholar

7. Dawar A, Wakif A, Saeed A, Shah Z, Muhammad T, Kumam P, et al. Significance of Lorentz forces on Jeffrey nanofluid flows over a convectively heated flat surface featured by multiple velocity slips and dual stretching constraint: A homotopy analysis approach. J Comput Des Eng (2022) 9(2):564–82. doi:10.1093/jcde/qwac019

CrossRef Full Text | Google Scholar

8. Ali L, Liu X, Ali B, Abdal S, Zulqarnain RM. Finite element analysis of unsteady MHD Blasius and Sakiadis flow with radiation and thermal convection using Cattaneo-Christov heat flux model. Phys Scr (2021) 96(12):125219. doi:10.1088/1402-4896/ac25a3

CrossRef Full Text | Google Scholar

9. Ali L, Ali Finite element analysis on transient. doi:10.1016/j.camwa.2022.01.009

CrossRef Full Text

10. Ali L, Ali B, Liu X, Iqbal T, Zulqarnain RM, Javid M, et al. A comparative study of unsteady MHD Falkner–Skan wedge flow for non-Newtonian nanofluids considering thermal radiation and activation energy. Chin J Phys (2022) 77:1625–38. doi:10.1016/j.cjph.2021.10.045

CrossRef Full Text | Google Scholar

11. Ali L, Ali B, Liu X, Ahmed S, Shah MA. Analysis of bio-convective MHD Blasius and Sakiadis flow with Cattaneo-Christov heat flux model and chemical reaction. Chin J Phys (2022) 77:1963–75. doi:10.1016/j.cjph.2021.12.008

CrossRef Full Text | Google Scholar

12. Jamil M, Fetecau C. Some exact solutions for rotating flows of a generalized Burgers fluid in cylindrical domains. J Nonnewton Fluid Mech (2010) 165(23-24):1700–12. doi:10.1016/j.jnnfm.2010.08.004

CrossRef Full Text | Google Scholar

13. Kamran M, Imran M, Athar M, Imran M. On the unsteady rotational flow of fractional Oldroyd-B fluid in cylindrical domains. Meccanica (2012) 47(3):573–84. doi:10.1007/s11012-011-9467-4

CrossRef Full Text | Google Scholar

14. Hussain S, Ali B, Ahmad F. MHD boundary layer flow and heat transfer for micropolar fluids over a shrinking sheet. J Appl Environ Biol Sci (2015) 5(5):330–8.

Google Scholar

15. Rehman KU, Malik M, Khan WA, Khan I, Alharbi SO. Numerical solution of non-Newtonian fluid flow due to rotatory rigid disk. Symmetry (2019) 11(5):699. doi:10.3390/sym11050699

CrossRef Full Text | Google Scholar

16. Riaz A, Ellahi R, Bhatti MM, Marin M. Study of heat and mass transfer in the Eyring–Powell model of fluid propagating peristaltically through a rectangular compliant channel. Heat Transf Res (2019) 50(16):1539–60. doi:10.1615/heattransres.2019025622

CrossRef Full Text | Google Scholar

17. Riaz A, Zeeshan A, Bhatti M, Ellahi R. Peristaltic propulsion of Jeffrey nano-liquid and heat transfer through a symmetrical duct with moving walls in a porous medium. Physica A: Stat Mech its Appl (2020) 545:123788. doi:10.1016/j.physa.2019.123788

CrossRef Full Text | Google Scholar

18. Riaz A, Bhatti MM, Ellahi R, Zeeshan A, Sait SM. Mathematical analysis on an asymmetrical wavy motion of blood under the influence entropy generation with convective boundary conditions. Symmetry (2020) 12(1):102. doi:10.3390/sym12010102

CrossRef Full Text | Google Scholar

19. Riaz A, Zeeshan A, Bhatti M. Entropy analysis on a three-dimensional wavy flow of eyring–powell nanofluid: A comparative study. Math Probl Eng (2021) 2021:6672158. doi:10.1155/2021/6672158

CrossRef Full Text | Google Scholar

20. Ali B, Thumma T, Habib D, Salamat N, Riaz S Finite element analysis on transient MHD 3D rotating flow of Maxwell and tangent hyperbolic nanofluid past a bidirectional stretching sheet with Cattaneo Christov heat flux model. Therm Sci Eng Prog (2022) 28:101089. doi:10.1016/j.tsep.2021.101089

CrossRef Full Text | Google Scholar

21. Sakiadis BC. Boundary-layer behavior on continuous solid surfaces: I. Boundary-Layer equations for two-dimensional and axisymmetric flow. AICHE J (1961) 7(1):26–8. doi:10.1002/aic.690070108

CrossRef Full Text | Google Scholar

22. Wang C. Stagnation flow towards a shrinking sheet. Int J Non Linear Mech (2008) 43(5):377–82. doi:10.1016/j.ijnonlinmec.2007.12.021

CrossRef Full Text | Google Scholar

23. Khan I, Malik M, Hussain A, Salahuddin T. Effect of homogenous-heterogeneous reactions on MHD Prandtl fluid flow over a stretching sheet. Results Phys (2017) 7:4226–31. doi:10.1016/j.rinp.2017.10.052

CrossRef Full Text | Google Scholar

24. Abbas Z, Abdal S, Hussain N, Hussain F, Adnan M, Ali B, et al. Mhd boundary layer flow and heat transfer of nanofluid over a vertical stretching sheet in the presence of a heat source. Sci Inq Rev. (2019) 3(4):60–73. doi:10.32350/sir.34.05

CrossRef Full Text | Google Scholar

25. Awan AU, Abid S, Ullah N, Nadeem S. Magnetohydrodynamic oblique stagnation point flow of second grade fluid over an oscillatory stretching surface. Results Phys (2020) 18:103233. doi:10.1016/j.rinp.2020.103233

CrossRef Full Text | Google Scholar

26. Asjad MI, Sarwar N, Ali B, Hussain S, Sitthiwirattham T, Reunsumrit J, et al. Impact of bioconvection and chemical reaction on MHD nanofluid flow due to exponential stretching sheet. Symmetry (2021) 13(12):2334. doi:10.3390/sym13122334

CrossRef Full Text | Google Scholar

27. Awan AU, Aziz M, Ullah N, Nadeem S, Abro KA. Thermal analysis of oblique stagnation point flow with slippage on second-order fluid. J Therm Anal Calorim (2022) 147(5):3839–51. doi:10.1007/s10973-021-10760-z

CrossRef Full Text | Google Scholar

28. Karwe MV, Jaluria Y. Fluid flow and mixed convection transport from a moving plate in rolling and extrusion processes. J Heat Transfer (1988) 110(3):655–61. doi:10.1115/1.3250542

CrossRef Full Text | Google Scholar

29. Vajravelu K, Cannon J, Leto J, Semmoum R, Nathan S, Draper M, et al. Nonlinear convection at a porous flat plate with application to heat transfer from a dike. J Math Anal Appl (2003) 277(2):609–23. doi:10.1016/s0022-247x(02)00634-0

CrossRef Full Text | Google Scholar

30. Kumar R, Sood S. Interaction of magnetic field and nonlinear convection in the stagnation point flow over a shrinking sheet. J Eng (2016) 2016:6752520. doi:10.1155/2016/6752520

CrossRef Full Text | Google Scholar

31. Hayat T, Qayyum S, Shehzad SA, Alsaedi A. Magnetohydrodynamic three-dimensional nonlinear convection flow of Oldroyd-B nanoliquid with heat generation/absorption. J Mol Liq (2017) 230:641–51. doi:10.1016/j.molliq.2017.01.045

CrossRef Full Text | Google Scholar

32. Sampath Kumar P, Mahanthesh B, Gireesha B, Shehzad S. Quadratic convective flow of radiated nano-Jeffrey liquid subject to multiple convective conditions and Cattaneo-Christov double diffusion. Appl Math Mech (2018) 39(9):1311–26. doi:10.1007/s10483-018-2362-9

CrossRef Full Text | Google Scholar

33. Patil P, Kulkarni M. Nonlinear mixed convective nanofluid flow along moving vertical rough plate. Rev Mex Fis (2020) 66(2):153–61. doi:10.31349/revmexfis.66.153

CrossRef Full Text | Google Scholar

34. Kumar MD, Raju C, Sajjan K, El-Zahar ER, Shah NA. Linear and quadratic convection on 3D flow with transpiration and hybrid nanoparticles. Int Commun Heat Mass Transfer (2022) 134:105995. doi:10.1016/j.icheatmasstransfer.2022.105995

CrossRef Full Text | Google Scholar

35. Bayones F, Nisar KS, Khan KA, Raza N, Hussien NS, Osman M, et al. Magneto-hydrodynamics (MHD) flow analysis with mixed convection moves through a stretching surface. AIP Adv (2021) 11(4):045001. doi:10.1063/5.0047213

CrossRef Full Text | Google Scholar

36. Ramesh G, Gireesha B. Influence of heat source/sink on a Maxwell fluid over a stretching surface with convective boundary condition in the presence of nanoparticles. Ain Shams Eng J (2014) 5(3):991–8. doi:10.1016/j.asej.2014.04.003

CrossRef Full Text | Google Scholar

37. Ali FM, Nazar R, Arifin NM, Pop I. Mixed convection stagnation-point flow on vertical stretching sheet with external magnetic field. Appl Math Mech (2014) 35(2):155–66. doi:10.1007/s10483-014-1780-8

CrossRef Full Text | Google Scholar

38. Ishak A, Nazar R, Arifin NM, Pop I. Dual solutions in mixed convection flow near a stagnation point on a vertical porous plate. Int J Therm Sci (2008) 47(4):417–22. doi:10.1016/j.ijthermalsci.2007.03.005

CrossRef Full Text | Google Scholar

39. Hassanien I, Gorla RSR. Combined forced and free convection in stagnation flows of micropolar fluids over vertical non-isothermal surfaces. Int J Eng Sci (1990) 28(8):783–92. doi:10.1016/0020-7225(90)90023-c

CrossRef Full Text | Google Scholar

40. Lok YY, Amin N, Pop I. Unsteady mixed convection flow of a micropolar fluid near the stagnation point on a vertical surface. Int J Therm Sci (2006) 45(12):1149–57. doi:10.1016/j.ijthermalsci.2006.01.015

CrossRef Full Text | Google Scholar

41. Ramachandran N, Chen T, Armaly BF. Mixed convection in stagnation flows adjacent to vertical surfaces. J Heat Transfer (1988) 110(2):373–7. doi:10.1115/1.3250494

CrossRef Full Text | Google Scholar

Nomenclature

$\tilde{\mathit{x}},\tilde{\mathit{y}}$ Cartesian coordinates (m)

$\tilde{\mathit{u}},\tilde{\mathit{v}}$ Velocity components along x and y − axes (m/s)

${\mathit{U}}_{\mathit{n}}(\tilde{\mathit{x}})$ Free stream velocity (m/s)

${\mathit{U}}_{\mathit{w}}(\tilde{\mathit{x}})$ Stretching velocity at the surface (m/s)

g Gravity acceleration (m/s²)

$\tilde{\mathit{T}}$ Temperature of the fluid (K)

${\tilde{\mathit{T}}}_{\mathit{w}}$ Temperature at wall (K)

${\tilde{\mathit{T}}}_{\infty }$ Ambient temperature (K)

Pr Prandtl no. (−−)

B₀ Applied magnetism (kg/s².A)

Q₀ Heat source/sink (J/K.m³.s)

$\mathit{N}{\mathit{u}}_{\tilde{\mathit{x}}}$ Nusselt number (−−)

M² Magnetic parameter (−−)

Q_c Quadratic convection parameter (−−)

C_p Specific heat (J/kg.K)

$\mathit{R}{\mathit{e}}_{\tilde{\mathit{x}}}$ Reynolds number (−−)

$\mathit{G}{\mathit{r}}_{\tilde{\mathit{x}}}$ Grashof number (−−)

${\mathit{C}\mathit{f}}_{\tilde{\mathit{x}}}$ Coefficient of skin friction (−−)

f Non-dimensional velocity

q_w Wall heat flux (W/m²)

Greek symbols

μ Viscosity of fluid (kg/m.s)

ρ Density of fluid (kg/m³)

λ₁ Fluid’s relaxation time (s)

(β₁, β₂) Coefficients of thermal expansion (1/K)

σ Electric conductivity (A².s³/kg.m³)

$\widehat{\alpha }$ Heat diffusivity (m²/s)

ξ Dimensionless variable (−−)

β Deborah number (−−)

ɛ₁ Velocity ratio parameter (−−)

Ω Mixed convection parameter (−−)

${\tilde{\tau }}_{\mathit{w}}$ Shear stress at wall (kg/m.s²)

Θ Non-dimensional temperature (−−)