Motion of an active bent rod with an articulating hinge: exploring mechanical and chemical modes of swimming

1 Introduction

Microscale entities orchestrate physical and biological phenomena. Bacteria play a key role in the spread of infection [1], macrophages have the capacity to affect tumor malignancy [2], T cells can infiltrate solid tumors and kill tumor cells [3], and subsurface microparticles influence contaminant transport in groundwater [4]. Inspired by these natural systems, efforts have been made to create artificial micron-sized objects endowed with programmable actions to influence phenomena at the microscale. Commonly called microrobots, these micron-sized objects are capable of treating diseases [5–9], acting as biological sensors [10, 11], and removing microplastics [12], among others. A key factor that influences the efficacy of microrobots is how capable they are at swimming in fluid environments. Due to the small length scales, viscous forces dominate over inertial forces, such that the Reynolds number (Re) $\mathrm{R}\mathrm{e}=\frac{\text{Inertial\hspace{0.17em}forces}}{\text{Viscous\hspace{0.17em}forces}}\ll 1$. In the low Re regime, microrobots must adapt strategies for locomotion that differ when compared to their macroscopic counterparts [13–15].

The two modes of swimming commonly used to impart motility at the microscale are, taxonomically, mechanical propulsion and propulsion due to field interactions. In the mechanical swimming mode, motility is induced by continuous geometric reconfiguration [16–20]. In field-driven propulsion, the geometry typically remains unchanged, but body forces due to interactions with a field induce motility [21–24]. In this paper, we explore how chemical fields leading to self-diffusiophoretic propulsion, i.e., a chemical mode of swimming, can be employed in concert with a mechanical mode of swimming to alter the motion of a bent rod actuator.

We first focus on the mechanical mode of swimming. In the seminal paper “Life at low Reynolds number,” Purcell outlined the scallop theorem and described the mechanical strategies that microscopic entities use to swim [15]. Purcell argued that any body with Re ≪ 1 experiences zero net displacement under reciprocal geometric reconfigurations, i.e., geometry changes that are identical when viewed forward or backward in time [15, 19]. Purcell illustrated this through the example of a microscopic scallop, whereupon opening and closing its shell, the scallop experienced zero net displacement [15]. More detailed mathematical works have confirmed the scallop theorem [25–27]. A consequence of the scallop theorem is that microscopic objects, both synthetic and biological, must use non-reciprocal swimming strokes to achieve non-zero net displacement. The simplest swimmer that Purcell described is a two-hinge swimmer that is able to achieve net displacement while still returning to the original configuration [15, 28]. In fact, microscopic biological organisms, such as Escherichia coli or spermatozoon, have developed strategies to swim by either rotating slender helical flagellar filaments or beating flexible flagella [29–33]. Advances in microfabrication and external field actuation techniques have enabled many of these biological swimming techniques to be replicated in synthetic systems [34–39].

In the field-driven mode of swimming, phoretic mechanisms, e.g., diffusiophoresis (the focus of this work) [40–52], thermophoresis [53–55], electrophoresis [56–64], and electrodiffusiophoresis [65, 66], are used to achieve directed motion at the microscale. Diffusiophoresis, the movement of particles in chemical gradients [67–80], has been a particularly rich area of research due to similarities with cell chemotaxis [81, 82]. Active diffusiophoretic particles use reactive patches on the particle surface, enabling the particle to generate local concentration gradients and achieve locomotion [40, 51, 83]. One key factor that influences self-diffusiophoretic particle motion is particle geometry [84–90]. Recently, Ganguly and Gupta have explored the effect of geometry on the diffusiophoretic motion of bent rod microparticles [42]. They found that bent rod particles with uniform or nonuniform surface activity, when constrained to move in two dimensions, have trajectories that are always circular, consistent with experimental reports [40, 55].

The aforementioned studies focus only on one mode of swimming. To the best of our knowledge, no study has explored low Re swimming due to a combination of a field-driven motion and mechanical reconfiguration. To this end, we extend the results from Ganguly and Gupta [42] by allowing the hinge connecting the self-propelling bent rod to articulate (Figure 1). We distinguish the articulating bent rod from the non-reconfigurable version by calling it a bent rod actuator. Here, hinge articulations facilitate the mechanical swimming mode, enabling the actuator to alter its geometry, whereas the surface reaction provides the field-driven mode via self-diffusiophoresis, herein called chemical swimming. The bent rod geometry is particularly useful because its configuration can be fully characterized by two dimensionless parameters, the length ratio of the two arms and the angle between the arms. In our framework, the mechanical mode is characterized by a normal surface velocity, whereas the chemical mode introduces a tangential surface velocity, see Figure 1, providing a convenient means to analyze the motion of the bent rod actuator.

FIGURE 1

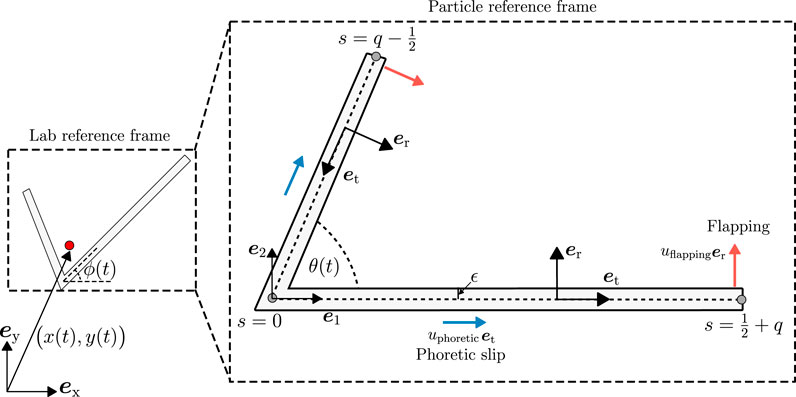
FIGURE 1. Non-dimensional geometry of a bent rod actuator. We consider the motion of a bent rod actuator with an angle θ(t) between the positive (s > 0) and negative (s < 0) arms. The angle θ(t) is allowed to vary in time via an articulating hinge at s = 0 that connects the positive and negative arms. Hinge articulations induce a normal velocity u_flappinge_r on the surface of the actuator arms. We also consider the motion of the bent rod actuator due to a self-diffusiophoretic slip velocity u_phoretice_t in the direction tangential to the arms. The diffusiophoretic velocity is caused by a solute flux j(s) into the fluid surrounding the bent rod actuator imposing concentration gradients in the solution. We determine the velocity U and angular velocity Ω of the bent rod actuator in the particle frame of reference, as described with the e₁ − e₂ unit basis vectors. After calculating U and Ω, we integrate Eq. 14 to find the trajectory and orientation of the bent rod actuator in the laboratory frame of reference.

First, in Section 2, we expand the theoretical framework developed by Roggeveen and Stone [91] and Ganguly and Gupta [42] to compute the motion of the actuator due to both self-diffusiophoresis as well as hinge articulations. In Section 3.1 and Section 3.2, we calculate the trajectories of the actuator moving due to reciprocal hinge articulations (Figure 4) and non-reciprocal hinge articulations (Figure 5). We present an intuitive understanding of the trajectories by considering free-body diagrams (Figure 6). Lastly, we study the motion due to self-diffusiophoresis with hinge articulations to determine particle trajectories that combine mechanical and chemical modes of swimming (Section 3.3; Figures 7, 8).

2 Methods

2.1 Problem setup

We adapt the hydrodynamic calculations outlined by Roggeveen and Stone [91] and Ganguly and Gupta [42] to study the motion of a bent rod actuator, Figure 1. We employ the non-dimensional particle geometry as described by Ganguly and Gupta [42]. The bent rod actuator is composed of two arms connected with a hinge that articulates, allowing for the angle θ between the two arms to be varied in time. The two arms have a combined length ℓ, with each arm having a length of $(\frac{1}{2}+q)\ell$ and $(\frac{1}{2}-q)\ell$, where q is a length asymmetry parameter. We consider the arms to have equal radius a and a small aspect ratio, i.e., $ϵ=\frac{a}{\ell }\ll 1$. A non-dimensional schematic diagram of the particle geometry can be seen in Figure 1.

The position along the center-line of the bent rod actuator is described by the non-dimensional arc-length s (scaled by ℓ), where $s\in \left[q-\frac{1}{2},q+\frac{1}{2}\right]$. s = 0 describes the location of the hinge connecting the two actuator arms that is allowed to articulate. We call the arm with s < 0 the negative arm and the arm with s ≥ 0 the positive arm. When q = 0, both arms have the same length; when q < 0, the negative arm is longer; and when q > 0, the positive arm is longer. We define a coordinate system with unit basis vectors e₁ − e₂ in the particle frame of reference and assume the bent rod actuator propels in the e₁ − e₂ plane and rotates about the e₁ × e₂ axis. We also define local normal e_r and tangential e_t unit vectors to the surface of the bent rod actuator. In terms of e₁ − e₂, e_t − e_r are defined as

${\mathit{e}}_{\text{t}}=\left\{\begin{array}{cc}-\cos \left(\theta \right){\mathit{e}}_1-\sin \left(\theta \right){\mathit{e}}_2\hfill & s<0\hfill \\ {\mathit{e}}_1\hfill & s\ge 0\hfill \end{array}\right.,(\mathrm{1a})$

${\mathit{e}}_{\text{r}}=\left\{\begin{array}{cc}\sin \left(\theta \right){\mathit{e}}_1-\cos \left(\theta \right){\mathit{e}}_2\hfill & s<0\hfill \\ {\mathit{e}}_2\hfill & s\ge 0\hfill \end{array}\right..(\mathrm{1b})$

We extend the results of Ganguly and Gupta [42] to determine the dimensionless velocity U (scaled by $U_{\text{ref}}=\frac{k_{\text{b}}Ta{J}_{\text{ref}}{\lambda }^2}{\mu D\ell }$) and angular velocity Ω (scaled by $\frac{U_{\text{ref}}}{\ell }$) in response to both self-diffusiophoresis [42, 90, 92–94] and hinge articulations. In our non-dimensionalization, k_b is the Boltzmann constant, T is the ambient fluid temperature, J_ref is the reference solute surface flux, λ is the phoretic interaction length scale, D is the solute diffusivity, and μ is the fluid viscosity. The self-diffusiophoretic motion is caused by a surface flux j(s) (scaled by J_ref) on the surface of the bent rod actuator. The surface activity creates a concentration field c(s, r) (scaled by $\frac{a{J}_{\text{ref}}}{D}$) in the surrounding solution. Gradients along the length of the rod in the solute concentration field cause the bent rod actuator to move by inducing a diffusiophoretic slip velocity u_phoretice_t on the surface of the rod. In addition to the self-diffusiophoretic motion, we also consider bent rod actuator motion due to the hinge altering the angle θ between both arms, denoted as hinge articulations or flapping. As the hinge articulates, the arms move with an angular velocity, ω_n for the negative arm and ω_p for the positive arm, which induces a normal fluid velocity u_flappinge_r on the surface of the bent rod actuator.

2.2 Slender-body theory

The velocity U and angular velocity Ω of the bent rod actuator, in the particle frame of reference, can be determined via the mobility relation,

$\left[\begin{array}{c}\hfill \mathit{U}\hfill \\ \hfill \mathbf{\Omega }\hfill \end{array}\right]={\underline{\underline{\mathit{R}}}}^{-1}\cdot \left[\begin{array}{c}\hfill {\mathit{F}}_{\text{eff}}\hfill \\ \hfill {\mathit{T}}_{\text{eff}}\hfill \end{array}\right],(2)$

where ${\underline{\underline{\mathit{R}}}}^{-1}$ is the 6 × 6 mobility matrix and F_eff and T_eff are the effective force and torque acting on the center of mass of the bent rod actuator due to self-diffusiophoresis and hinge articulations. Assuming that the bent rod actuator is only able to translate in the e₁ − e₂ plane and rotate about the e₁ × e₂ axis, we write Eq. 2 as

$\left[\begin{array}{c}\hfill U_1\hfill \\ \hfill U_2\hfill \\ \hfill {\mathrm{\Omega }}_3\hfill \end{array}\right]=\underline{\underline{\mathit{M}}}\cdot \left[\begin{array}{c}\hfill F_1\hfill \\ \hfill F_2\hfill \\ \hfill T_3\hfill \end{array}\right].(3)$

The bent rod actuator can move with a velocity U₁ in the e₁ direction, U₂ in the e₂ direction, and angular velocity Ω₃ about the e₁ × e₂ axis. The motion is caused by an effective force F₁ in the e₁ direction, F₂ in the e₂ direction, or an effective torque T₃ about the e₁ × e₂ axis. The mobility coefficients $\underline{\underline{\mathit{M}}}$ are determined by numerically inverting the resistance coefficients (multiplied by a minus sign) determined by Roggeveen and Stone (Eq. 3.5 in their work) [91] using the Python module Scipy with the linalg.inv function. Using the results from Ganguly and Gupta [42], calculated with the reciprocal theorem, we express the effective force and torque in terms of a velocity on the surface of the bent rod actuator,

$\left[\begin{array}{c}\hfill U_1\hfill \\ \hfill U_2\hfill \\ \hfill {\mathrm{\Omega }}_3\hfill \end{array}\right]=\underline{\underline{\mathit{M}}}\cdot \left[\begin{array}{c}\hfill \int {\mathit{u}}_{\text{surf}}\cdot \left(\mathit{I}-\frac{1}{2}{\mathit{e}}_{\text{t}}{\mathit{e}}_{\text{t}}\right)\cdot {\mathit{e}}_{1}ds\hfill \\ \hfill \int {\mathit{u}}_{\text{surf}}\cdot \left(\mathit{I}-\frac{1}{2}{\mathit{e}}_{\text{t}}{\mathit{e}}_{\text{t}}\right)\cdot {\mathit{e}}_{2}ds\hfill \\ \hfill \int {\mathit{u}}_{\text{surf}}\cdot \left(\mathit{I}-\frac{1}{2}{\mathit{e}}_{\text{t}}{\mathit{e}}_{\text{t}}\right)\cdot {\mathit{e}}_3\times \left({\mathit{x}}_{\text{h}}\left(s\right)-{\mathit{r}}_{\text{com}}\right)ds\hfill \end{array}\right],(4)$

where x_h(s) = se_t is the position of a point along the center-line of the bent rod and ${\mathit{r}}_{\text{com}}={\int }_{q-1/2}^{q+1/2}s{\mathit{e}}_{\text{t}}ds=\left(\frac{1}{2}\cos \theta {\left(q-\frac{1}{2}\right)}^2+\frac{1}{2}{\left(q+\frac{1}{2}\right)}^2\right){\mathit{e}}_1+\frac{1}{2}\sin \theta {\left(q-\frac{1}{2}\right)}^2{\mathit{e}}_2$ is the center of mass of the bent rod. We consider the surface velocity to be composed of a tangential component due to self-diffusiophoresis and a normal component due to hinge articulations,

${\mathit{u}}_{\text{surf}}=u_{\text{phoretic}}{\mathit{e}}_{\text{t}}+u_{\text{flapping}}{\mathit{e}}_{\text{r}}.(5)$

Following similar treatments in the literature [42, 90, 94], we model the velocity induced by solute concentration gradients with

$u_{\text{phoretic}}=\mathrm{\Gamma }\left(s\right)\frac{d{c}_{\text{s}}\left(s\right)}{ds},(6)$

where Γ(s) is a lumped phoretic mobility parameter, c_s(s) = c(s, ϵ), and $\frac{d{c}_{\text{s}}(s)}{ds}$ is the surface concentration gradient. For simplicity, we consider Γ(s) = ±1, a value representative for diffusiophoretic systems [72]. Considering the slip velocity to be composed of only a phoretic component, Eq. 4 can be integrated and written as

$\left[\begin{array}{c}\hfill U_{1,\mathrm{p}\mathrm{h}\mathrm{o}\mathrm{r}\mathrm{e}\mathrm{t}\mathrm{i}\mathrm{c}}\hfill \\ \hfill U_{2,\mathrm{p}\mathrm{h}\mathrm{o}\mathrm{r}\mathrm{e}\mathrm{t}\mathrm{i}\mathrm{c}}\hfill \\ \hfill {\mathrm{\Omega }}_{3,\mathrm{p}\mathrm{h}\mathrm{o}\mathrm{r}\mathrm{e}\mathrm{t}\mathrm{i}\mathrm{c}}\hfill \end{array}\right]=\mathrm{sign}\left(\mathrm{\Gamma }\right)\underline{\underline{\mathit{M}}}\cdot \left[\begin{array}{c}\hfill \frac{1}{2}\mathrm{\Delta }{c}_0^{q+\frac{1}{2}}-\frac{\cos \theta }{2}\mathrm{\Delta }{c}_{q-\frac{1}{2}}^0\hfill \\ \hfill -\frac{\sin \theta }{2}\mathrm{\Delta }{c}_{q-\frac{1}{2}}^0\hfill \\ \hfill \frac{\sin \theta }{4}\left({\left(q-\frac{1}{2}\right)}^2\mathrm{\Delta }{c}_0^{q+\frac{1}{2}}+{\left(q+\frac{1}{2}\right)}^2\mathrm{\Delta }{c}_{q-\frac{1}{2}}^0\right)\hfill \end{array}\right],(7)$

where $\mathrm{\Delta }{c}_0^{q+\frac{1}{2}}=c_{\text{s}}(q+\frac{1}{2})-c_{\text{s}}(0)$ and $\mathrm{\Delta }{c}_{q-\frac{1}{2}}^0=c_{\text{s}}(0)-c_{\text{s}}(q-\frac{1}{2})$ [42]. The phoretic motion is driven by the concentration difference between the hinge and ends of the bent rod actuator arms. As we are considering bent rod actuators with a small aspect ratio ϵ ≪ 1, we use boundary layer theory [42, 95] to determine the concentration profile along the bent rod actuator by numerically solving

$c_{\text{s}}\left(s\right)=\frac{1}{2}{\int }_{q-\frac{1}{2}}^{q+\frac{1}{2}}\frac{j\left(s^{\prime }\right)}{\left|{\mathit{x}}_{\text{h}},\left(s^{\prime }\right),+,ϵ,{\mathit{e}}_r,\left(s\right),-,{\mathit{x}}_{\text{h}},\left(s\right)\right.|}d{s}^{\prime }.(8)$

We note that all results shown are calculated with ϵ = 10^–3. The framework is agnostic to the flux profile used; however, we use a uniform flux profile j(s) = 1 for simplicity. The concentration profile is derived for the case of small Péclet number, i.e., $\mathrm{P}\mathrm{e}=\frac{U_{\text{ref}}\ell }{D}\sim \mathcal{O}\left(10^{-3}\right)$ [42]. The numerical solution of Eq. 8 is difficult to resolve near s = 0 due to a singularity in the concentration profile at s = 0 (Figure 2) caused by the sharp turn in the bent rod actuator at the hinge, see Figure 3A.

FIGURE 2

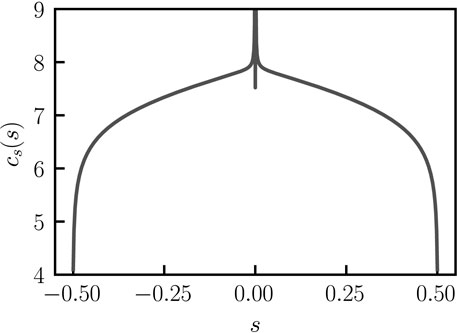
FIGURE 2. Concentration profile across the bent rod actuator. Concentration profile across the bent rod actuator for q = 0, θ = π/4, and j(s) = 1, as determined by solving Eq. 8 with Eq. 1 using the Scipy.integrate.quad function.

FIGURE 3

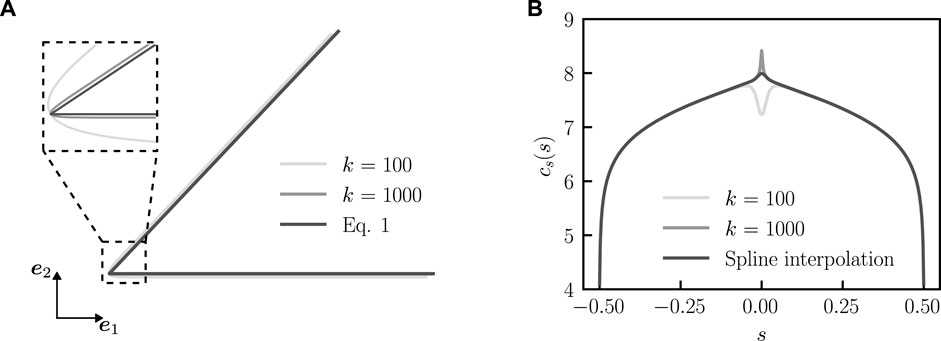
FIGURE 3. Determination of the concentration profile with approximated bent rod actuator geometry. (A) Comparison between bent rod actuator geometry, as approximated by Eq. 9 for k = 100 and k = 1,000 and Eq. 1. (B) Concentration profiles (q = 0, θ₀ = π/4, and j(s) = 1) for the approximated bent rod actuator with k = 100 and k = 1,000 as well as the spline interpolated concentration profile near s = 0.

To achieve a numerical solution, we approximate the entire bent rod actuator center-line with the smooth continuous function ${\mathit{x}}_{\text{h}}(s)=\mathcal{X}(s){\mathit{e}}_1+\mathcal{Y}(s){\mathit{e}}_2$, where

$\mathcal{X}\left(s\right)=-s\cos \theta +\frac{1+\cos \theta }{k}\ln \left(\frac{1+e^{ks}}{2}\right),(\mathrm{9a})$

$\mathcal{Y}\left(s\right)=-s\sin \theta +\frac{\sin \theta }{k}\ln \left(\frac{1+e^{ks}}{2}\right),(\mathrm{9b})$

and k is a smoothness parameter that controls the curvature of the approximate bent rod actuator near s = 0. A larger k corresponds to a corner with higher curvature and a better approximated bent rod actuator, while a smaller k corresponds to a corner with lower curvature and a worse approximation of the bent rod actuator, see Figure 3A. To approximate the concentration profile near the hinge, we use Eq. 9 to calculate Eq. 8 with k = 100 and k = 1,000 (Figure 3B). We determine the values of s for s < 0 and s > 0, where the value of concentration profiles differs by 5% and fit the concentration profile for k = 1,000 with a fourth-order spline using the Scipy. interpolate.UnivariateSpline function (Figure 3B) between the two s values.

In addition to the phoretic contribution, we consider the motion of the bent rod actuator due to hinge articulations, θ → θ(t). The articulation of the hinge induces an angular velocity ω_n for the negative arm and ω_p for the positive arm. The angular velocity of each arm is related to the hinge articulation via

$\frac{d\theta }{dt}=-\left({\omega }_{\text{n}}+{\omega }_{\text{p}}\right)=-\omega .(10)$

We write the flapping velocity as

$u_{\text{flapping}}=\left\{\begin{array}{cc}-{\omega }_{\text{n}}s\hfill & s<0,\hfill \\ {\omega }_{\text{p}}s\hfill & s\ge 0.\hfill \end{array}\right.(11)$

Inserting Eq. 11 into Eq. 4 and integrating yields

$\left[\begin{array}{c}\hfill U_{1,\mathrm{fl}\mathrm{a}\mathrm{p}\mathrm{p}\mathrm{i}\mathrm{n}\mathrm{g}}\hfill \\ \hfill U_{2,\mathrm{fl}\mathrm{a}\mathrm{p}\mathrm{p}\mathrm{i}\mathrm{n}\mathrm{g}}\hfill \\ \hfill {\mathrm{\Omega }}_{3,\mathrm{fl}\mathrm{a}\mathrm{p}\mathrm{p}\mathrm{i}\mathrm{n}\mathrm{g}}\hfill \end{array}\right]=\underline{\underline{\mathit{M}}}\cdot \left[\begin{array}{c}\hfill \frac{1}{2}{\omega }_{\text{n}}\sin \theta {\left(q-\frac{1}{2}\right)}^2\hfill \\ \hfill -\frac{1}{2}{\omega }_{\text{n}}\cos \theta {\left(q-\frac{1}{2}\right)}^2+\frac{1}{2}{\omega }_{\text{p}}{\left(q+\frac{1}{2}\right)}^2\hfill \\ \hfill \frac{1}{192}\left\{{\left(2q-1\right)}^3\left(6q+5\right){\omega }_{\text{n}}-{\left(2q+1\right)}^3\left(6q-5\right){\omega }_{\text{p}}+3\cos \theta \left({\omega }_{\text{n}}-{\omega }_{\text{p}}\right){\left(1-4q^2\right)}^2\right\}\hfill \end{array}\right].(12)$

The total velocity and angular velocity of the bent rod actuator is determined by a linear combination of Eqs. 7, 12:

$\left[\begin{array}{c}\hfill U_1\hfill \\ \hfill U_2\hfill \\ \hfill {\mathrm{\Omega }}_3\hfill \end{array}\right]=\left[\begin{array}{c}\hfill U_{1,\mathrm{p}\mathrm{h}\mathrm{o}\mathrm{r}\mathrm{e}\mathrm{t}\mathrm{i}\mathrm{c}}\hfill \\ \hfill U_{2,\mathrm{p}\mathrm{h}\mathrm{o}\mathrm{r}\mathrm{e}\mathrm{t}\mathrm{i}\mathrm{c}}\hfill \\ \hfill {\mathrm{\Omega }}_{3,\mathrm{p}\mathrm{h}\mathrm{o}\mathrm{r}\mathrm{e}\mathrm{t}\mathrm{i}\mathrm{c}}\hfill \end{array}\right]+\left[\begin{array}{c}\hfill U_{1,\mathrm{fl}\mathrm{a}\mathrm{p}\mathrm{p}\mathrm{i}\mathrm{n}\mathrm{g}}\hfill \\ \hfill U_{2,\mathrm{fl}\mathrm{a}\mathrm{p}\mathrm{p}\mathrm{i}\mathrm{n}\mathrm{g}}\hfill \\ \hfill {\mathrm{\Omega }}_{3,\mathrm{fl}\mathrm{a}\mathrm{p}\mathrm{p}\mathrm{i}\mathrm{n}\mathrm{g}}\hfill \end{array}\right].(13)$

We note that in order to use the combined phoretic and flapping contributions to the bent rod actuator motion, the Péclet number due to flapping must also be small. To justify, we briefly restore dimensions and note that ${\mathrm{P}\mathrm{e}}_{\mathrm{fl}\mathrm{a}\mathrm{p}\mathrm{p}\mathrm{i}\mathrm{n}\mathrm{g}}=\frac{\omega \ell \frac{U_{\text{Ref}}}{\ell }\ell }{D}=\frac{\omega U_{\text{ref}}\ell }{D}$. In our simulations, $\omega \sim \frac{{\theta }_a}{T}$, where θ_a ∈ [0, 2π] is the amplitude of an articulation and T is a typical period for a given articulation. By constraining our results to $T\sim \mathcal{O}(1)$, we ensure that ${\mathrm{P}\mathrm{e}}_{\mathrm{fl}\mathrm{a}\mathrm{p}\mathrm{p}\mathrm{i}\mathrm{n}\mathrm{g}}\sim \mathcal{O}\left(10^{-3}\right)\ll 1$. In addition to the dependence of Eq. 13 on geometric parameters, the phoretic velocities and flapping velocities also linearly depend on j(s) and ω, respectively. Therefore, the relative contribution of each velocity can be tuned by either changing j(s) or by changing ω through θ_a or T.

2.3 Numerical procedure

To calculate the bent rod actuator trajectory, we convert from the particle (e₁ − e₂) to the laboratory (e_x − e_y) frame of reference by employing the rotation matrix

$\frac{d}{dt}\left[\begin{array}{c}\hfill x\left(t\right)\hfill \\ \hfill y\left(t\right)\hfill \\ \hfill \varphi \left(t\right)\hfill \end{array}\right]=\left[\begin{array}{ccc}\hfill \cos \varphi \left(t\right)\hfill & \hfill -\sin \varphi \left(t\right)\hfill & \hfill 0\hfill \\ \hfill \sin \varphi \left(t\right)\hfill & \hfill \cos \varphi \left(t\right)\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right]\cdot \left[\begin{array}{c}\hfill U_1\hfill \\ \hfill U_2\hfill \\ \hfill {\mathrm{\Omega }}_3\hfill \end{array}\right]+\left[\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \\ \hfill {\omega }_{\text{p}}\hfill \end{array}\right],(14)$

where ϕ(t) is the angle between e₁ and e_x and t is the dimensionless timescale (scaled by $\frac{\ell }{U_{\text{Ref}}}$). Additionally, as e₁ in the particle frame of reference aligns with the tangential direction of the positive arm, we need to account for changes in ϕ(t) due to the angular velocity ω_p of the positive arm about the hinge at s = 0. To do so, we add ω_p to $\frac{d\varphi (t)}{dt}$. Eq. 14 is evaluated use an eighth-order Runge–Kutta integration scheme (DOP853) as implemented in the Python Scipy package via the Solve-IVP function. We use initial conditions x(0) = y(0) = ϕ(0) = 0. We note that x(t) and y(t) correspond to the center of mass of the bent rod actuator in the laboratory reference frame. To determine the coordinates of the hinge and end points of the bent rod actuator at each time point in the laboratory reference frame, we first determine the position of the hinge point r_hinge(t) and two end points, ${\mathit{r}}_{\text{s\hspace{0.17em}}=\text{\hspace{0.17em}q}-\frac{1}{2}}(t)$ and ${\mathit{r}}_{\text{s\hspace{0.17em}}=\text{\hspace{0.17em}q}+\frac{1}{2}}(t)$, relative to the center of mass in the particle frame of reference.

${\mathit{r}}_{\text{hinge}}\left(t\right)=-{\mathit{r}}_{\text{com}},(\mathrm{15a})$

${\mathit{r}}_{\text{s\hspace{0.17em}}=\text{\hspace{0.17em}q}-\frac{1}{2}}\left(t\right)=-\left(q-\frac{1}{2}\right)\cos \theta \left(t\right){\mathit{e}}_1-\left(q-\frac{1}{2}\right)\sin \theta \left(t\right){\mathit{e}}_2-{\mathit{r}}_{\text{com}},(\mathrm{15b})$

${\mathit{r}}_{\text{s\hspace{0.17em}}=\text{\hspace{0.17em}q}+\frac{1}{2}}\left(t\right)=\left(q+\frac{1}{2}\right){\mathit{e}}_1-{\mathit{r}}_{\text{com}}.(\mathrm{15c})$

We apply the rotation matrix and translate the hinge and end points to determine the coordinates of the hinge and end points of the bent rod actuator in the laboratory frame of reference at each instant of time.

${\mathit{r}}_{\text{hinge}}^{\prime }\left(t\right)=\left[\begin{array}{cc}\hfill \cos \varphi \left(t\right)\hfill & \hfill -\sin \varphi \left(t\right)\hfill \\ \hfill \sin \varphi \left(t\right)\hfill & \hfill \cos \varphi \left(t\right)\hfill \end{array}\right]\cdot {\mathit{r}}_{\text{hinge}}\left(t\right)+\left[\begin{array}{c}\hfill x\left(t\right)\hfill \\ \hfill y\left(t\right)\hfill \end{array}\right],(\mathrm{16a})$

${\mathit{r}}_{\text{s\hspace{0.17em}}=\text{\hspace{0.17em}q}-\frac{1}{2}}^{\prime }\left(t\right)=\left[\begin{array}{cc}\hfill \cos \varphi \left(t\right)\hfill & \hfill -\sin \varphi \left(t\right)\hfill \\ \hfill \sin \varphi \left(t\right)\hfill & \hfill \cos \varphi \left(t\right)\hfill \end{array}\right]\cdot {\mathit{r}}_{\text{s\hspace{0.17em}}=\text{\hspace{0.17em}q}-\frac{1}{2}}\left(t\right)+\left[\begin{array}{c}\hfill x\left(t\right)\hfill \\ \hfill y\left(t\right)\hfill \end{array}\right],(\mathrm{16b})$

${\mathit{r}}_{\text{s\hspace{0.17em}}=\text{\hspace{0.17em}q}+\frac{1}{2}}^{\prime }\left(t\right)=\left[\begin{array}{cc}\hfill \cos \varphi \left(t\right)\hfill & \hfill -\sin \varphi \left(t\right)\hfill \\ \hfill \sin \varphi \left(t\right)\hfill & \hfill \cos \varphi \left(t\right)\hfill \end{array}\right]\cdot {\mathit{r}}_{\text{s\hspace{0.17em}}=\text{\hspace{0.17em}q}+\frac{1}{2}}\left(t\right)+\left[\begin{array}{c}\hfill x\left(t\right)\hfill \\ \hfill y\left(t\right)\hfill \end{array}\right].(\mathrm{16c})$

We then sequentially solve 14 and 16 to determine the trajectories of the bent rod actuator. Trajectories shown in Figure 4, Figure 5, Figure 6, and Figure 7 are ascertained from Eq. 16a, with the coordinates of the hinge and end points of the bent rod actuator drawn according to Eqs. 16b, 16c.

FIGURE 4

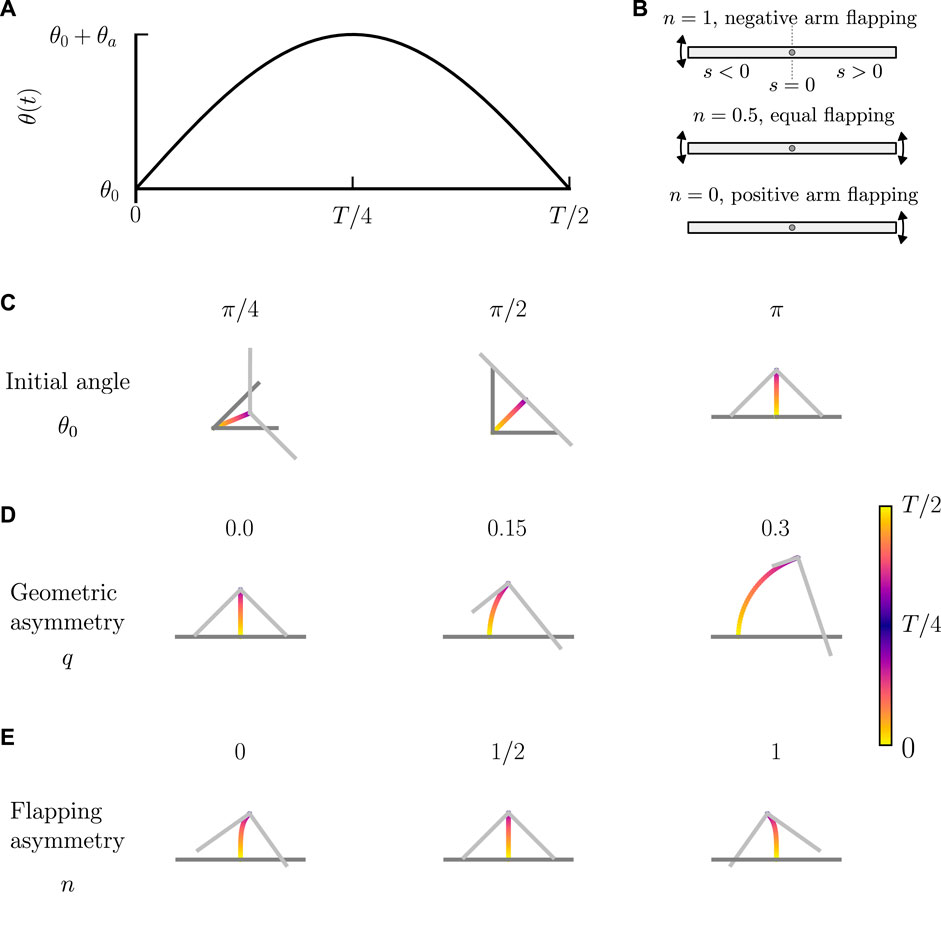
FIGURE 4. Motion of a bent rod actuator due to reciprocal hinge articulations. (A) θ(t) used for a bent rod actuator with reciprocal hinge articulations. θ(t) is characterized by an initial angle θ₀, flapping amplitude θ_a, and period T. (B) Schematic illustration of flapping distribution between arms, as characterized by n. n = 1 describes a bent rod actuator where all changes in θ(t) are ascribed to the negative arm. n = 0.5 describes a bent rod actuator where the positive and negative arms are equally responsible for changes in θ(t). n = 0 describes a bent rod actuator where the positive arm is responsible for all changes in θ(t). Trajectory plots of r_hinge over one half period for (C) θ₀ ∈[π/4, π/2, π], θ_a = π/2, T = 1, q = 0, and n = 0.5. (D) θ₀ = π, θ_a = π/2, T = 1, q ∈[0, 0.15, 0.3], and n = 0.5. (E) θ₀ = π, θ_a = π/2, T = 1, q = 0, and n ∈[0, 1/2, 1].

FIGURE 5

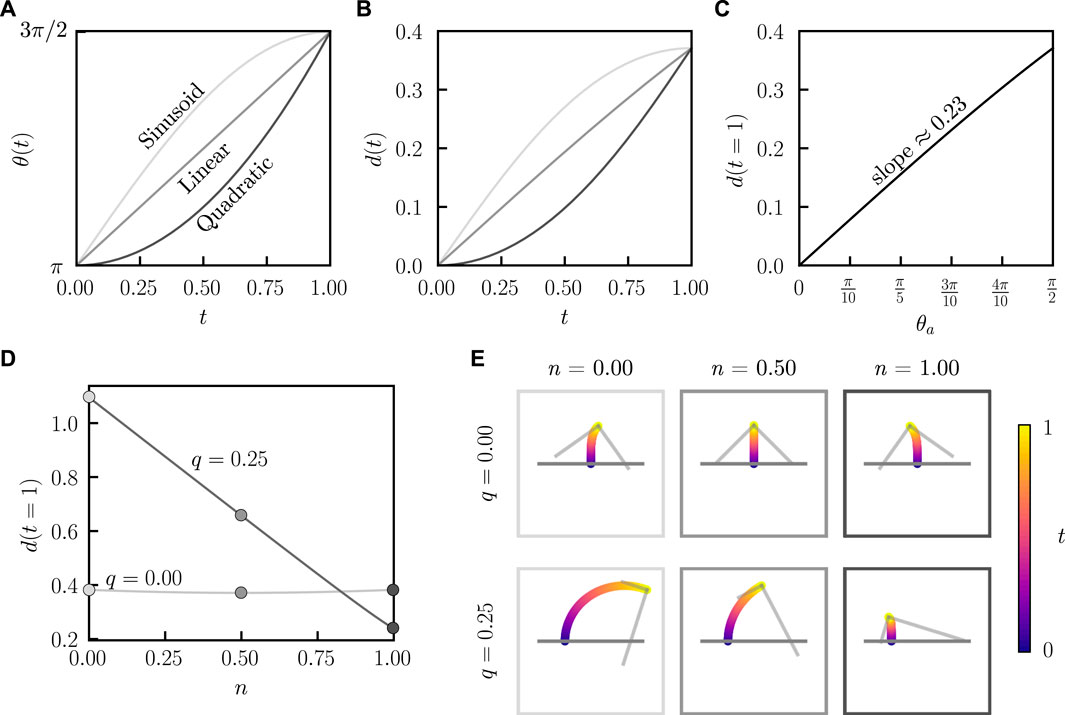
FIGURE 5. Distance traveled for a bent rod actuator with a single hinge articulation. (A) Variation of θ for a single hinge articulation from an initial angle π to a final angle 3π/2 under sinusoidal, linear, and quadratic temporal evolutions. (B) Distance traveled as a function of time for a bent rod actuator (q = 0, n = 0.5) undergoing a single hinge articulation from θ(t) = π to 3π/2 for sinusoidal, linear, and quadratic evolutions of θ(t). (C) Distance traveled at the end of a single articulation as a function of θ_a for linear hinge articulations (q = 0, n = 0.5, θ₀ = π). (D) Distance traveled at the end of a single articulation for q = 0 and q = 0.25 as a function of n. (E) Bent rod actuator trajectories resulting from a single hinge articulation with an initial angle π and a final angle 3π/2 for q = 0, 0.25 and n = 0, 0.5, 1.

FIGURE 6

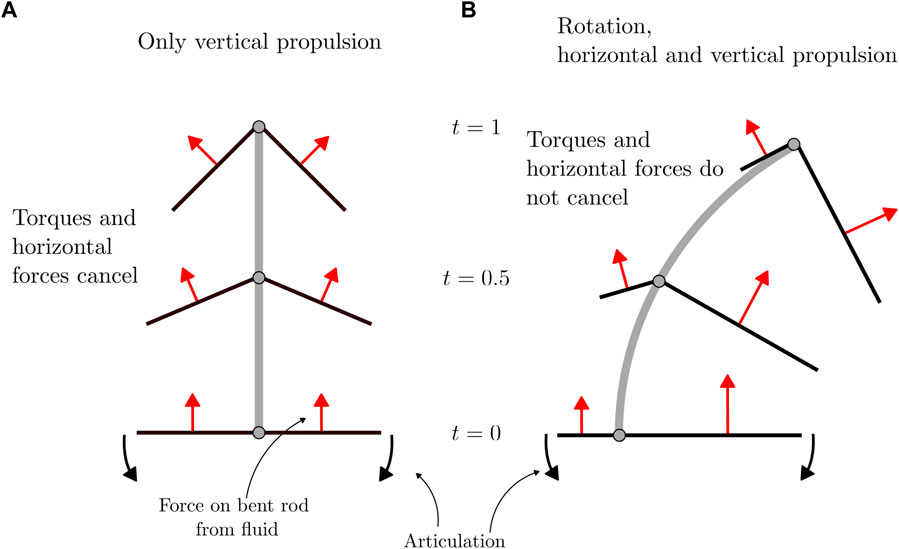
FIGURE 6. Free-body diagram of forces applied to a bent rod actuator due to hinge articulations. (A) Forces acting on a bent rod with geometric and flapping symmetry. (B) Forces acting on a bent rod with geometric asymmetry and flapping symmetry. The trajectories and bent rod are not to scale.

FIGURE 7

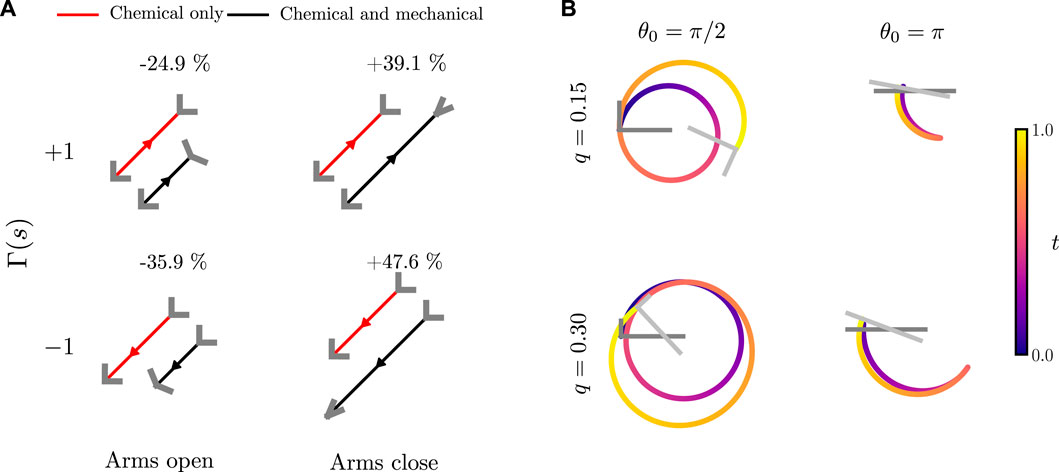
FIGURE 7. Trajectories of an active bent rod actuator undergoing hinge articulations. (A) Comparison between bent rod actuator motion due to a uniform surface activity (j(s) = 1) with a phoretic mobility Γ(s) = ±1, θ₀ = π/2, q = 0, n = 0.5 and arms either opening or closing by θ_a = ±π/4 over t = 1 of linear temporal variation. (B) Trajectories for an active bent rod actuator undergoing sinusoidal hinge articulations, Γ(s) = 1, T = 1, ${\theta }_a=\frac{\pi }{4}$, and n = 0.5 for q ∈[0.15, 0.30] and θ₀ ∈ [π/2, π].

3 Results and discussion

3.1 Reciprocal motion

We first show that the bent rod actuator experiences zero net displacement while undergoing reciprocal hinge articulations without the contribution of diffusiophoresis (see Figure 4A). At t = 0, the hinge initiates articulation, changing θ(t) from an initial angle of θ₀ to a final angle of θ₀ + θ_a over a time $\frac{T}{4}$. The hinge then changes θ from θ₀ + θ_a back to θ₀ over a time $\frac{T}{4}$. Therefore, by $\frac{T}{2}$, the bent rod actuator has reciprocally articulated the hinge. To determine the angular velocity of the positive and negative arms (ω_p and ω_n), we use Eq. 10. First, we note that θ(t) is piece-wise defined as

$\theta \left(t\right)=\left\{\begin{array}{cc}{\theta }_0+{\theta }_a\sin \left(2\pi \frac{t}{T}\right)\mathcal{H}\left(t\right)\hfill & t\le \frac{T}{2}\hfill \\ 0\hfill & t>\frac{T}{2}\hfill \end{array}\right.,(17)$

where $\mathcal{H}(t)$ is the Heaviside function. By using Eq. 17 and Eq. 10, we write the angular velocities as

${\omega }_{\text{p}}=\left\{\begin{array}{cc}-\left(1-n\right)\frac{2\pi {\theta }_a}{T}\cos \left(2\pi \frac{t}{T}\right)\mathcal{H}\left(t\right)\hfill & t\le \frac{T}{2}\hfill \\ 0\hfill & t>\frac{T}{2}\hfill \end{array}\right.,(\mathrm{18a})$

${\omega }_{\text{n}}=\left\{\begin{array}{cc}-n\frac{2\pi {\theta }_a}{T}\cos \left(2\pi \frac{t}{T}\right)\mathcal{H}\left(t\right)\hfill & t\le \frac{T}{2}\hfill \\ 0\hfill & t>\frac{T}{2}\hfill \end{array}\right.,(\mathrm{18b})$

where n ∈ [0, 1] describes the distribution of angular velocities between the positive and negative arms, Figure 4B. When n = 1, only the articulation of the negative arm contributes to the changes in θ. When n = 0, only the positive arm articulates. When n = 0.5, both arms equally articulate. Thus, n = 0.5 distinguishes symmetric flapping, where both arms have the same angular velocity, and n ≠ 0.5 describes asymmetric flapping, where one arm has a larger angular velocity than the other. We solve Eq. 14, including no phoretic contributions, using Eq. 18. Figure 4C shows the trajectories of the hinge as well as the orientation of the bent rod actuator with an asymmetry parameter q = 0, flapping distribution n = 0.5, flapping amplitude ${\theta }_a=\frac{\pi }{2}$, flapping period T = 1, and initial angles ${\theta }_0\in [\frac{\pi }{4},\frac{\pi }{2},\frac{3\pi }{4},\pi ]$. For a symmetric bent rod with symmetric flapping (q = 0, n = 0.5), the trajectory makes an angle of $\frac{{\theta }_0}{2}$ with e_x. This is a consequence of Ω₃ identically going to 0 for a bent rod actuator with symmetric flapping and geometry. In contrast, rotation and curved trajectories can be induced by either introducing geometric asymmetry via q (Figure 4D) or flapping asymmetry via n (Figure 4E). As geometric asymmetry is introduced, the bent rod actuator moves in the positive e_x direction, toward the longer arm, and rotates counter-clockwise up to $t=\frac{T}{4}$ before retracing the same trajectory in reverse to attain the original position and orientation of the bent rod actuator. See Supplementary Video S1 for a movie of a bent rod actuator moving due to sinusoidal hinge articulations, described by $\theta (t)={\theta }_0+{\theta }_a\sin (2\pi \frac{t}{T})$, with q = 0.3, n = 0.5, ${\theta }_0=\frac{\pi }{2}$, ${\theta }_a=\frac{\pi }{4}$, and T = 1. A similar behavior is observed when the flapping asymmetry is introduced (Figure 4E). Both the direction of rotation, clockwise or counter-clockwise, and the direction of translation depend on which arm has a larger angular velocity. When n > 0.5, the negative arm has a larger angular velocity and the entire bent rod actuator rotates clockwise and translates in the negative e_x direction during the first half of the articulation. Inversely, when n < 0.5, the positive arm has a larger angular velocity and the entire bent rod actuator rotates counter-clockwise and translates in the positive e_x direction during the first half of the articulation. An intuitive understanding of this motion based on free-body diagrams will be explored in Sec. 3.2.

We also note that the bent rod actuator does return to its original position after undergoing a reciprocal hinge articulation. While known mathematically, to our knowledge, this is the first time where the trajectories of the bent rod actuator have been calculated numerically. It can be shown analytically via our framework that the bent rod actuator must return to its original location, as given in Eq. 14 and 12. We note that Eq. 12 can be expressed as

$\left[\begin{array}{c}\hfill U_{1,\mathrm{fl}\mathrm{a}\mathrm{p}\mathrm{p}\mathrm{i}\mathrm{n}\mathrm{g}}\hfill \\ \hfill U_{2,\mathrm{fl}\mathrm{a}\mathrm{p}\mathrm{p}\mathrm{i}\mathrm{n}\mathrm{g}}\hfill \\ \hfill {\mathrm{\Omega }}_{3,\mathrm{fl}\mathrm{a}\mathrm{p}\mathrm{p}\mathrm{i}\mathrm{n}\mathrm{g}}\hfill \end{array}\right]=\left[\begin{array}{c}\hfill \mathcal{A}\left(q,n,\theta \right)\hfill \\ \hfill \mathcal{B}\left(q,n,\theta \right)\hfill \\ \hfill \mathcal{C}\left(q,n,\theta \right)\hfill \end{array}\right]\frac{d\theta }{dt},(19)$

where $\mathcal{A},\mathcal{B}\&\mathcal{C}$ are functions of q, n, and θ only. Upon inserting into Eq. (14), we write

$\frac{d}{dt}\left[\begin{array}{c}\hfill x\left(t\right)\hfill \\ \hfill y\left(t\right)\hfill \\ \hfill \varphi \left(t\right)\hfill \end{array}\right]=\left[\begin{array}{c}\hfill \cos \varphi \left(t\right)\mathcal{A}\left(q,n,\theta \right)-\sin \varphi \left(t\right)\mathcal{B}\left(q,n,\theta \right)\hfill \\ \hfill \sin \varphi \left(t\right)\mathcal{A}\left(q,n,\theta \right)+\cos \varphi \left(t\right)\mathcal{B}\left(q,n,\theta \right)\hfill \\ \hfill \mathcal{C}\left(q,n,\theta \right)+n-1\hfill \end{array}\right]\frac{d\theta }{dt}.(20)$

By integrating Eq. 20, we see that ϕ is a unique function of θ only (up to an arbitrary choice of ϕ(0), q, and n). Therefore, any trajectory characterized by a reciprocal choice of θ, i.e., θ(t = 0) = θ(t_final), implies that $x(t=0)=x(t=t_{\text{final}}),y(t=0)=y(t=t_{\text{final}}),\mathrm{a}\mathrm{n}\mathrm{d}\varphi (t=0)=\varphi (t=t_{\text{final}})$.

In summary, our framework using slender-body theory is able to recapitulate Purcell’s scallop theorem both numerically and analytically. In addition, we are able to numerically determine the trajectories taken by the bent rod actuator due to reciprocal hinge articulations. Either geometric or flapping asymmetry can be used to introduce rotation and motion along a curved trajectory.

3.2 Non-reciprocal articulation

To further understand the relationship between geometric and flapping asymmetry, we calculate the trajectories and cumulative distance traveled d(t) by a bent rod undergoing non-reciprocal hinge articulations, Figure 5A. In these simulations, the bent rod actuator starts with an initial angle of θ = π and the hinge articulates to a final angle of $\theta =\frac{3\pi }{2}$, representing a total increase in the angle of $\frac{\pi }{2}$ over a time period t = 1. We vary the time rate of change of θ(t) using a sinusoidal, linear, and quadratic function, Figure 5A. Figure 5B shows that the total distance traveled remains equal among the three temporal variations by t = 1. Additionally, Figure 5C shows that the total distance traveled is linearly dependent on the amplitude of the hinge articulation. We also determine the total distance traveled by the bent rod actuator when both geometric and flapping asymmetries are introduced. Figure 5D shows the total distance traveled by a bent rod actuator undergoing displacements from an initial angle π to a final angle $\frac{3\pi }{2}$ as a function of n for q = 0 and q = 0.25. When q = 0, the variation in total distance traveled is weakly dependent on n. Interestingly, we find a minimum at n = 0.5. To better understand why a minimum exists at n = 0.5, we plot the trajectories that the bent rod actuators undergo, Figure 5D. When n = 0 and n = 1, we see that the bent rod actuator turns during the trajectory, while the bent rod actuator with n = 0.5 moves in a straight line. In this way, the projected surface area along the direction of the trajectory is smaller for n = 0 and n = 1, allowing these bent rod actuators to travel slightly further. The relationship between d(t = 1) and n is more distinct for the q = 0.25 case. In these cases, d(t = 1) decreases with n. This shows that for a bent rod actuator with geometric asymmetry, articulating the longer arm leads to a larger distance traveled. In addition to traveling further, the bent rod actuator also traces a circular trajectory.

An intuition for the motion of the bent rod actuator under non-reciprocal articulations can be understood by considering how forces are distributed across the bent rod arms as a function of geometric and flapping asymmetry, Figure 6. In the case of a bent rod actuator with both geometric (q = 0) as well as flapping (n = 0.5) symmetry, as the hinge articulates, the force applied to the bent rod actuator arms from the fluid is distributed across both arms, see Figure 6A. This leads to a net effective force in the e_y direction. While the force does have a component in the e_x direction, the contributions from the positive and negative arms cancel, leading to no net force in the e_x direction. The same is true for the effective torque about the e₁ × e₂ axis applied to the center of mass of the bent rod actuator. As the arms are of the same length and flapping is symmetric, the torque produced by both arms is equal and opposite, leading to a net zero effective torque. When geometric (or similarly flapping) asymmetry is introduced (q > 0.5, Figure 6B), the effective force applied to the bent rod actuator due to hinge articulations is biased toward the longer arm. In this case, the effective force in the e_y direction remains non-zero; however, the contributions to effective force in the e_x direction as well as the effective torque about the e₁ × e₂ axis no longer cancels between the two arms.

In summary, an intuitive picture of bent rod actuator motion can be built by considering how forces acting on the bent rod from the fluid are distributed at each instant of time. In the case of flapping, this is done by considering normal force components distributed across the arms and decomposing the forces into their constitutive laboratory frame of reference components.

3.3 Phoretic motion with hinge articulations

To investigate interactions between the chemical mode of swimming from self-diffusiophoresis and the mechanical mode of swimming due to hinge articulations, we begin by comparing trajectories and the change in total distance traveled due to either a positive or negative Γ(s) when the arms open and close, Figure 7A. We notice that the bent rod actuator always moves further when closing its arms, independent of whether the phoretic mobility is positive or negative. This is due to two effects. First, as the angle between the arms decreases, the concentration difference between the hinge and end points increases [42]. As the effective phoretic forces, see Eq. 7, are proportional to the concentration differences, this leads to a larger effective force and, thus, a larger velocity. The inverse is true for the scenario when the arms are opening. As the arms open, the concentration difference between the hinge and end points decreases, leading to a smaller effective phoretic force and a shorter distance traveled. Second, as the arms close, the projected surface area along the direction of motion decreases, decreasing the drag and leading to a larger distance traveled over a given period of time.

While changes to phoretic motion are the primary reason for changes in the total distance traveled, a subtle effect involving the competition between mechanical and chemical swimming can also be noticed. When the arms open, the bent rod with a positive phoretic mobility experiences a smaller decrease in the total distance traveled when compared to the bent rod with a negative phoretic mobility. This is because the effective force acting on the bent rod actuator due to a positive phoretic mobility and the arms opening are in the same direction. Similarly, the bent rod actuator with a negative phoretic mobility and arms that close experiences a larger increase in the total distance traveled.

We also investigate how θ₀ and q affect the motion of a self-diffusiophoretic bent rod actuator undergoing sinusoidal hinge articulations described by $\theta (t)={\theta }_0+{\theta }_a\sin (2\pi \frac{t}{T})$, Figure 7B. First, we notice that when θ₀ = π/2, the bent rod actuator travels in a circular trajectory (see Supplementary Video S3), while the bent rod actuator with θ₀ = π travels in trajectories that map circular arcs. Additionally, we notice that the bent rod actuator no longer experiences zero net displacement upon reciprocal articulations. This is due to the fact that the effective phoretic forces, Eq. 7, do not depend on $\frac{d\theta }{dt}$ and instead are functions of θ (as well as q and j(s)). Therefore, upon integrating, the time dependence of θ matters. This leads to trajectories that do not end and start at the same location.

We briefly discuss how the relative contributions of hinge articulations and diffusiophoresis impact the trajectory of the bent rod actuator. By increasing j(s), the contribution of diffusiophoresis relative to hinge articulations increases. Conversely, by increasing the articulation amplitude θ_a, the contribution of diffusiophoresis relative to hinge articulations decreases. Figure 8 shows the trajectories of a bent rod actuator moving due to both hinge articulations and diffusiophoresis, with j(s) increasing while keeping θ_a constant. As j(s) increases, the bent rod actuator traces a larger distance (though not necessarily displacement) during a given time period. This is attributed to the increase in the effective force and torque acting on the bent rod caused by the increasing j(s). Additionally, increasing j(s) causes the trajectories to become more circular and approach the trajectory of a self-diffusiophoretic bent rod without hinge articulations (refer to Supplementary Video S2) [42].

FIGURE 8

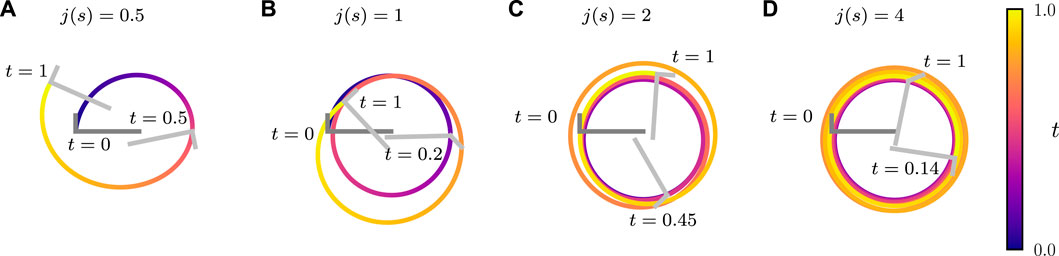
FIGURE 8. Trajectories of an active bent rod actuator undergoing sinusoidal hinge articulations with ${\theta }_a=\frac{\pi }{4}$, q = 0.3, n = 0.5, T = 1, and ${\theta }_0=\frac{\pi }{2}$ for (A–D) j(s) ∈ [0.5, 1, 2, 4].

4 Applications to biomedical microrobots

An improved understanding of the motion of a bent rod actuator with both mechanical and chemical swimming modes has direct applicability to the growing field of biomedical microrobots. Biomedical microrobots have found use in the delivery of small-molecule drugs, living cells, and contrast agents through complex biological media for precision medicine [8]. Primarily, the ability to enact real-time geometric changes and predict the resultant motion can have implications for the design of biomedical microrobots. First, real-time changes to microrobot geometry may allow the robot to switch between characteristic trajectories. In one sense, the ability to switch between straight-line trajectories and circular trajectories could enable enhanced motion through porous media [61]. In a similar manner, the direction of the microrobot for a given propulsion mechanism can be changed through flapping asymmetry and geometry alterations, for instance, by flapping a single arm to induce rotation that alters the direction of propulsion (Figure 5). This may be particularly useful for microrobots traversing through complex environments with multiple barriers, wherein real-time changes to trajectories may allow the swimmer to move around barriers and potentially escape confinement [96]. We note that the proposed hydrodynamic model of the bent rod actuator would need to be significantly modified to account for the presence of boundaries and is currently limited to two-dimensional motion. This warrants further studies that expand motion to three dimensions and include the effects of boundaries.

Experimental realizations of microrobots with similar geometries to the bent rod actuators exist [97–100]. These systems use polymeric cubes, typically fabricated at the micron scale with photolithography, coated with a ferromagnetic patch, that assemble into linear chains with hinges in a constant uniform magnetic field [97–99]. Systems could also be fabricated at the nanoscale using electron-beam lithography [101]. Upon turning the external magnetic field on and off, the assemblies open and close, allowing them to propel in non-Newtonian fluids, such as xanthan gum solutions for shear thinning fluids or fumed silica suspensions for shear thickening fluids, by using time asymmetric hinge articulations [97, 100]. Endowing such microrobots with a chemical mode of propulsion could be enabled by conjugating enzymes, such as urease, to the particles, allowing the microrobot to generate propulsion by converting urea, a chemical commonly found in the human body, to CO₂ and NH₃ [102]. In summary, our results will encourage scientists and engineers aiming to design microrobots with multiple swimming modalities for biomedical applications.

5 Conclusion

In this article, we have developed a mobility framework to calculate the trajectories taken by a bent rod actuator under chemical and mechanical modes of swimming. In the mechanical mode, where propulsion is induced by hinge articulations, we show numerically and analytically that Purcell’s Scallop theorem holds. To better understand the role of geometry on the bent rod actuator motion, we calculate the trajectories traced under non-reciprocal hinge articulations. Rotation and curved trajectories can be induced either through geometric or flapping asymmetry. This is explained through free-body diagrams that consider how forces are distributed across the bent rod actuator’s arms. To further explore the bent rod actuator’s motion, we also include self-diffusiophoresis to study the interplay between chemical and mechanical modes of swimming. We find that hinge articulations either aid or hinder self-diffusiophoretic motion. These effects are caused by changes to mobility, increasing or decreasing the effective phoretic force, and by the interference between the effective phoretic and flapping forces. Our work invites future studies to expand to swimmers with more than one hinge [28, 98, 99], to study swimmers in non-Newtonian fluids [48, 97, 103, 104], and to incorporate optimization schemes to control microrobot trajectories via hinge articulations. One intriguing direction is to extend the analysis to non-Newtonian fluids by scaling the applied forces in response to a viscosity that depends on the hinge articulation rate [100]. Another interesting possibility is to explore simultaneous mechanical reconfiguration with other methods of field-driven propulsion, such as electrochemical reactions [105], where the time dependence of the reactive flux [65, 66, 106] is known to impact the directed assembly of particles [107]. This may further influence the ability of swimmers to transport through confined porous media [108, 109], where it is known that both motion [110, 111] and the distribution of electrochemical species are altered [112, 113].

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

RR: writing–original draft and writing–review and editing. ArG: writing–review and editing. CB: writing–review and editing. CS: writing–review and editing. AnG: writing–original draft and writing–review and editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. RR thanks the National Science Foundation (DGE—2040434) Graduate Research Fellowship for financial support. CB thanks the Discovery Learning Apprenticeship program for financial support. AG thanks the National Science Foundation (CBET—2238412) CAREER award for financial support. The authors acknowledge the donors of the American Chemical Society Petroleum Research Fund for partial support of this research. CS thanks the National Science Foundation (CBET—2143419) CAREER award for financial support. CS is a Pew Scholar in the Biomedical Sciences, supported by the Pew Charitable Trusts. He thanks the Packard Foundation for their support of this project.

Acknowledgments

The authors would like to acknowledge Filipe Henrique, Collin Kemper, and Gesse Roure for their insightful discussions leading to the completion of this work.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2023.1307691/full#supplementary-material

References

1. Ribet D, Cossart P. How bacterial pathogens colonize their hosts and invade deeper tissues. Microbes Infect (2015) 17:173–83. doi:10.1016/j.micinf.2015.01.004

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Williams CB, Yeh ES, Soloff AC. Tumor-associated macrophages: unwitting accomplices in breast cancer malignancy. NPJ Breast Cancer (2016) 2:15025. doi:10.1038/npjbcancer.2015.25

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Lanitis E, Dangaj D, Irving M, Coukos G. Mechanisms regulating T-cell infiltration and activity in solid tumors. Ann Oncol (2017) 28:xii18–32. doi:10.1093/annonc/mdx238

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Kanti Sen T, Khilar KC. Review on subsurface colloids and colloid-associated contaminant transport in saturated porous media. Adv Colloid Interf Sci (2006) 119:71–96. doi:10.1016/j.cis.2005.09.001

CrossRef Full Text | Google Scholar

5. Cong Z, Tang S, Xie L, Yang M, Li Y, Lu D, et al. Magnetic-powered Janus cell robots loaded with oncolytic adenovirus for active and targeted virotherapy of bladder cancer. Adv Mater (2022) 34:2201042. doi:10.1002/adma.202201042

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Gwisai T, Mirkhani N, Christiansen MG, Nguyen TT, Ling V, Schuerle S. Magnetic torque–driven living microrobots for increased tumor infiltration. Sci Robotics (2022) 7:eabo0665. doi:10.1126/scirobotics.abo0665

CrossRef Full Text | Google Scholar

7. Lee JG, Raj RR, Thome CP, Day NB, Martinez P, Bottenus N, et al. Bubble-based microrobots with rapid circular motions for epithelial pinning and drug delivery. Small (2023) 19:2300409. doi:10.1002/smll.202300409

CrossRef Full Text | Google Scholar

8. Lee JG, Raj RR, Day NB, Shields IVCW. Microrobots for biomedicine: unsolved challenges and opportunities for translation. ACS Nano (2023) 17:14196–204. doi:10.1021/acsnano.3c03723

PubMed Abstract | CrossRef Full Text | Google Scholar

9. De Ávila BEF, Angsantikul P, Li J, Angel Lopez-Ramirez M, Ramírez-Herrera DE, Thamphiwatana S, et al. Micromotor-enabled active drug delivery for in vivo treatment of stomach infection. Nat Commun (2017) 8:272. doi:10.1038/s41467-017-00309-w

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Thome CP, Hoertdoerfer WS, Bendorf JR, Lee JG, Shields IVCW. Electrokinetic active particles for motion-based biomolecule detection. Nano Lett (2023) 23:2379–87. doi:10.1021/acs.nanolett.3c00319

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Mohagheghian E, Luo J, Yavitt FM, Wei F, Bhala P, Amar K, et al. Quantifying stiffness and forces of tumor colonies and embryos using a magnetic microrobot. Sci Robotics (2023) 8:eadc9800. doi:10.1126/scirobotics.adc9800

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Zhou H, Mayorga-Martinez CC, Pumera M. Microplastic removal and degradation by mussel-inspired adhesive magnetic/enzymatic microrobots. Small Methods (2021) 5:2100230. doi:10.1002/smtd.202100230

CrossRef Full Text | Google Scholar

13. Sitti M. Mobile microrobotics. Cambridge: MIT Press (2017).

Google Scholar

14. Abbott JJ, Peyer KE, Lagomarsino MC, Zhang L, Dong L, Kaliakatsos IK, et al. How should microrobots swim? Int J Robotics Res (2009) 28:1434–47. doi:10.1177/0278364909341658

CrossRef Full Text | Google Scholar

15. Purcell EM. Life at low Reynolds number. Am J Phys (1977) 45:3–11. doi:10.1119/1.10903

CrossRef Full Text | Google Scholar

16. Elfring GJ, Lauga E. Theory of locomotion through complex fluids. Complex Fluids Biol Syst Exp Theor Comput (2015) 283–317. doi:10.1007/978-1-4939-2065-5_8

CrossRef Full Text | Google Scholar

17. Elfring GJ. A note on the reciprocal theorem for the swimming of simple bodies. Phys Fluids (2015) 27. doi:10.1063/1.4906993

CrossRef Full Text | Google Scholar

18. Nasouri B, Khot A, Elfring GJ. Elastic two-sphere swimmer in Stokes flow. Phys Rev Fluids (2017) 2:043101. doi:10.1103/physrevfluids.2.043101

CrossRef Full Text | Google Scholar

19. Lauga E. Life around the scallop theorem. Soft Matter (2011) 7:3060–5. doi:10.1039/c0sm00953a

CrossRef Full Text | Google Scholar

20. Lauga E, Powers TR. The hydrodynamics of swimming microorganisms. Rep Prog Phys (2009) 72:096601. doi:10.1088/0034-4885/72/9/096601

CrossRef Full Text | Google Scholar

21. Moran JL, Posner JD. Phoretic self-propulsion. Annu Rev Fluid Mech (2017) 49:511–40. doi:10.1146/annurev-fluid-122414-034456

CrossRef Full Text | Google Scholar

22. Michelin S, Lauga E. Phoretic self-propulsion at finite péclet numbers. J Fluid Mech (2014) 747:572–604. doi:10.1017/jfm.2014.158

CrossRef Full Text | Google Scholar

23. Saha S, Yariv E. Phoretic self-propulsion of a slightly inhomogeneous disc. J Fluid Mech (2022) 940:A24. doi:10.1017/jfm.2022.237

CrossRef Full Text | Google Scholar

24. Domínguez A, Popescu MN. A fresh view on phoresis and self-phoresis. Curr Opin Colloid Interf Sci (2022) 61:101610. doi:10.1016/j.cocis.2022.101610

CrossRef Full Text | Google Scholar

25. Ishimoto K, Yamada M. A coordinate-based proof of the scallop theorem. SIAM J Appl Math (2012) 72:1686–94. doi:10.1137/110853297

CrossRef Full Text | Google Scholar

26. Shapere A, Wilczek F. Geometry of self-propulsion at low Reynolds number. J Fluid Mech (1989) 198:557–85. doi:10.1017/S002211208900025X

CrossRef Full Text | Google Scholar

27. Yariv E. Self-propulsion in a viscous fluid: arbitrary surface deformations. J Fluid Mech (2006) 550:139–48. doi:10.1017/S002211200500830X

CrossRef Full Text | Google Scholar

28. Becker LE, Koehler SA, Stone HA. On self-propulsion of micro-machines at low Reynolds number: purcells three-link swimmer. J Fluid Mech (2003) 490:15–35. doi:10.1017/S0022112003005184

CrossRef Full Text | Google Scholar

29. Lauga E. The fluid Dynamics of cell motility. Cambridge: Cambridge University Press (2020).

Google Scholar

30. Berg HC. E. coli in motion. New York: Springer Science+Business Media (2003).

Google Scholar

31. Berg HC. Motile behavior of bacteria. Phys Today (2000) 53:24–9. doi:10.1063/1.882934

CrossRef Full Text | Google Scholar

32. Lowe G, Meister M, Berg HC. Rapid rotation of flagellar bundles in swimming bacteria. Nature (1987) 325:637–40. doi:10.1038/325637a0

CrossRef Full Text | Google Scholar

33. Ishijima S, Oshio S, Mohri H. Flagellar movement of human spermatozoa. Gamete Res (1986) 13:185–97. doi:10.1002/mrd.1120130302

CrossRef Full Text | Google Scholar

34. Medina-Sánchez M, Schwarz L, Meyer AK, Hebenstreit F, Schmidt OG. Cellular cargo delivery: toward assisted fertilization by sperm-carrying micromotors. Nano Lett (2016) 16:555–61. doi:10.1021/acs.nanolett.5b04221

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Gu H, Boehler Q, Cui H, Secchi E, Savorana G, De Marco C, et al. Magnetic cilia carpets with programmable metachronal waves. Nat Commun (2020) 11:2637. doi:10.1038/s41467-020-16458-4

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Hou Y, Wang H, Zhong S, Qiu Y, Shi Q, Sun T, et al. Design and control of a surface-dimple-optimized helical microdrill for motions in high-viscosity fluids. IEEE/ASME Trans Mechatronics (2022) 28:429–39. doi:10.1109/TMECH.2022.3201012

CrossRef Full Text | Google Scholar

37. Dillinger C, Nama N, Ahmed D. Ultrasound-activated ciliary bands for microrobotic systems inspired by starfish. Nat Commun (2021) 12:6455. doi:10.1038/s41467-021-26607-y

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Orbay S, Ozcelik A, Bachman H, Huang TJ. Acoustic actuation of in situ fabricated artificial cilia. J Micromechanics Microengineering (2018) 28:025012. doi:10.1088/1361-6439/aaa0ae

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Huang HW, Uslu FE, Katsamba P, Lauga E, Sakar MS, Nelson BJ. Adaptive locomotion of artificial microswimmers. Sci Adv (2019) 5:eaau1532. doi:10.1126/sciadv.aau1532

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Venkateshwar Rao D, Reddy N, Fransaer J, Clasen C. Self-propulsion of bent bimetallic Janus rods. J Phys D: Appl Phys (2019) 52:014002. doi:10.1088/1361-6463/aae6f6

CrossRef Full Text | Google Scholar

41. Zhou C, Zhang H, Tang J, Wang W. Photochemically powered AgCl Janus micromotors as a model system to understand ionic self-diffusiophoresis. Langmuir (2018) 34:3289–95. doi:10.1021/acs.langmuir.7b04301

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Ganguly A, Gupta A. Going in circles: slender body analysis of a self-propelling bent rod. Phys Rev Fluids (2023) 8:014103. doi:10.1103/physrevfluids.8.014103

CrossRef Full Text | Google Scholar

43. Golestanian R, Liverpool TB, Ajdari A. Propulsion of a molecular machine by asymmetric distribution of reaction products. Physcial Rev Lett (2005) 94:220801. doi:10.1103/PhysRevLett.94.220801

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Howse JR, Jones RAL, Ryan AJ, Gough T, Vafabakhsh R, Golestanian R. Self-motile colloidal particles: from directed propulsion to random walk. Physcial Rev Lett (2007) 99:048102. doi:10.1103/PhysRevLett.99.048102

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Rückner G, Kapral R. Chemically powered nanodimers. Physcial Rev Lett (2007) 98:150603. doi:10.1103/PhysRevLett.98.150603

CrossRef Full Text | Google Scholar

46. Paxton WF, Kistler KC, Olmeda CC, Sen A, St Angelo SK, Cao Y, et al. Catalytic nanomotors: autonomous movement of striped nanorods. J Am Chem Soc (2004) 126:13424–31. doi:10.1021/ja047697z

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Tătulea-Codrean M, Lauga E. Artificial chemotaxis of phoretic swimmers: instantaneous and long-time behaviour. J Fluid Mech (2018) 856:921–57. doi:10.1017/jfm.2018.718

CrossRef Full Text | Google Scholar

48. Datt C, Natale G, Hatzikiriakos SG, Elfring GJ. An active particle in a complex fluid. J Fluid Mech (2017) 823:675–88. doi:10.1017/jfm.2017.353

CrossRef Full Text | Google Scholar

49. Natale G, Datt C, Hatzikiriakos SG, Elfring GJ. Autophoretic locomotion in weakly viscoelastic fluids at finite péclet number. Phys Fluids (2017) 29. doi:10.1063/1.5002729

CrossRef Full Text | Google Scholar

50. Uspal W, Popescu MN, Dietrich S, Tasinkevych M. Self-propulsion of a catalytically active particle near a planar wall: from reflection to sliding and hovering. Soft Matter (2015) 11:434–8. doi:10.1039/c4sm02317j

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Popescu MN, Uspal WE, Bechinger C, Fischer P. Chemotaxis of active Janus nanoparticles. Nano Lett (2018) 18:5345–9. doi:10.1021/acs.nanolett.8b02572

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Davis AM, Yariv E. Self-diffusiophoresis of Janus particles at large Damköhler numbers. J Eng Math (2022) 133:5. doi:10.1007/s10665-022-10213-y

CrossRef Full Text | Google Scholar

53. Lin X, Si T, Wu Z, He Q. Self-thermophoretic motion of controlled assembled micro-/nanomotors. Phys Chem Chem Phys (2017) 19:23606–13. doi:10.1039/c7cp02561k

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Jiang HR, Yoshinaga N, Sano M. Active motion of a Janus particle by self-thermophoresis in a defocused laser beam. Phys Rev Lett (2010) 105:268302. doi:10.1103/physrevlett.105.268302

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Kümmel F, Ten Hagen B, Wittkowski R, Buttinoni I, Eichhorn R, Volpe G, et al. Circular motion of asymmetric self-propelling particles. Physcial Rev Lett (2013) 110:198302. doi:10.1103/physrevlett.110.198302

CrossRef Full Text | Google Scholar

56. Shields IVCW, Han K, Ma F, Miloh T, Yossifon G, Velev OD. Supercolloidal spinners: complex active particles for electrically powered and switchable rotation. Adv Funct Mater (2018) 28:1803465. doi:10.1002/adfm.201803465

CrossRef Full Text | Google Scholar

57. Gangwal S, Cayre OJ, Bazant MZ, Velev OD. Induced-charge electrophoresis of metallodielectric particles. Physcial Rev Lett (2008) 100:058302. doi:10.1103/physrevlett.100.058302

PubMed Abstract | CrossRef Full Text | Google Scholar

58. Squires TM, Bazant MZ. Breaking symmetries in induced-charge electro-osmosis and electrophoresis. J Fluid Mech (2006) 560:65–101. doi:10.1017/s0022112006000371

CrossRef Full Text | Google Scholar

59. Bazant MZ, Squires TM. Induced-charge electrokinetic phenomena. Curr Opin Colloid Interf Sci (2010) 15:203–13. doi:10.1016/j.cocis.2010.01.003

CrossRef Full Text | Google Scholar

60. Pascall AJ, Squires TM. Induced charge electro-osmosis over controllably contaminated electrodes. Physcial Rev Lett (2010) 104:088301. doi:10.1103/physrevlett.104.088301

PubMed Abstract | CrossRef Full Text | Google Scholar

61. Lee JG, Brooks AM, Shelton WA, Bishop KJ, Bharti B. Directed propulsion of spherical particles along three dimensional helical trajectories. Nat Commun (2019) 10:2575. doi:10.1038/s41467-019-10579-1

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Lee JG, Al Harraq A, Bishop KJ, Bharti B. Fabrication and electric field-driven active propulsion of patchy microellipsoids. The J Phys Chem B (2021) 125:4232–40. doi:10.1021/acs.jpcb.1c01644

PubMed Abstract | CrossRef Full Text | Google Scholar

63. Brooks AM, Tasinkevych M, Sabrina S, Velegol D, Sen A, Bishop KJ. Shape-directed rotation of homogeneous micromotors via catalytic self-electrophoresis. Nat Commun (2019) 10:495. doi:10.1038/s41467-019-08423-7

PubMed Abstract | CrossRef Full Text | Google Scholar

64. Brooks AM, Sabrina S, Bishop KJ. Shape-directed dynamics of active colloids powered by induced-charge electrophoresis. Proc Natl Acad Sci (2018) 115:E1090–E1099. doi:10.1073/pnas.1711610115

PubMed Abstract | CrossRef Full Text | Google Scholar

65. Wang K, Leville S, Behdani B, Batista CAS. Long-range transport and directed assembly of charged colloids under aperiodic electrodiffusiophoresis. Soft Matter (2022) 18:5949–59. doi:10.1039/d2sm00631f

PubMed Abstract | CrossRef Full Text | Google Scholar

66. Jarvey N, Henrique F, Gupta A. Asymmetric rectified electric and concentration fields in multicomponent electrolytes with surface reactions. Soft Matter (2023) 19:6032–45. doi:10.1039/D3SM00823A

PubMed Abstract | CrossRef Full Text | Google Scholar

67. Velegol D, Garg A, Guha R, Kar A, Kumar M. Origins of concentration gradients for diffusiophoresis. Soft Matter (2016) 12:4686–703. doi:10.1039/C6SM00052E

PubMed Abstract | CrossRef Full Text | Google Scholar

68. Shim S. Diffusiophoresis, diffusioosmosis, and microfluidics: surface-flow-driven phenomena in the presence of flow. Chem Rev (2022) 122:6986–7009. doi:10.1021/acs.chemrev.1c00571

PubMed Abstract | CrossRef Full Text | Google Scholar

69. Shin S, Um E, Sabass B, Ault JT, Rahimi M, Warren PB, et al. Size-dependent control of colloid transport via solute gradients in dead-end channels. Proc Natl Acad Sci (2016) 113:257–61. doi:10.1073/pnas.1511484112

PubMed Abstract | CrossRef Full Text | Google Scholar

70. Shin S, Ault JT, Feng J, Warren PB, Stone HA. Low-cost zeta potentiometry using solute gradients. Adv Mater (2017) 29:1701516. doi:10.1002/adma.201701516

CrossRef Full Text | Google Scholar

71. Gupta A, Rallabandi B, Stone HA. Diffusiophoretic and diffusioosmotic velocities for mixtures of valence-asymmetric electrolytes. Phys Rev Fluids (2019) 4:043702. doi:10.1103/physrevfluids.4.043702

CrossRef Full Text | Google Scholar

72. Gupta A, Shim S, Stone HA. Diffusiophoresis: from dilute to concentrated electrolytes. Soft Matter (2020) 16:6975–84. doi:10.1039/d0sm00899k

PubMed Abstract | CrossRef Full Text | Google Scholar

73. Alessio BM, Shim S, Mintah E, Gupta A, Stone HA. Diffusiophoresis and diffusioosmosis in tandem: two-dimensional particle motion in the presence of multiple electrolytes. Phys Rev Fluids (2021) 6:054201. doi:10.1103/PhysRevFluids.6.054201

CrossRef Full Text | Google Scholar

74. Alessio BM, Shim S, Gupta A, Stone HA. Diffusioosmosis-driven dispersion of colloids: a taylor dispersion analysis with experimental validation. J Fluid Mech (2022) 942:A23. doi:10.1017/jfm.2022.321

CrossRef Full Text | Google Scholar

75. Raj RR, Shields IVCW, Gupta A. Two-dimensional diffusiophoretic colloidal banding: optimizing the spatial and temporal design of solute sinks and sources. Soft Matter (2023) 19:892–904. doi:10.1039/d2sm01549h

PubMed Abstract | CrossRef Full Text | Google Scholar

76. Banerjee A, Squires TM. Long-range, selective, on-demand suspension interactions: combining and triggering soluto-inertial beacons. Sci Adv (2019) 5:eaax1893. doi:10.1126/sciadv.aax1893

PubMed Abstract | CrossRef Full Text | Google Scholar

77. Banerjee A, Williams I, Azevedo RN, Helgeson ME, Squires TM. Soluto-inertial phenomena: designing long-range, long-lasting, surface-specific interactions in suspensions. Proc Natl Acad Sci (2016) 113:8612–7. doi:10.1073/pnas.1604743113

PubMed Abstract | CrossRef Full Text | Google Scholar

78. Banerjee A, Vogus DR, Squires TM. Design strategies for engineering soluto-inertial suspension interactions. Phys Rev E (2019) 100:052603. doi:10.1103/PhysRevE.100.052603

PubMed Abstract | CrossRef Full Text | Google Scholar

79. Alessio BM, Gupta A. Diffusiophoresis-enhanced turing patterns. Sci Adv (2023) 9:eadj2457. doi:10.1126/sciadv.adj2457

PubMed Abstract | CrossRef Full Text | Google Scholar

80. Ganguly A, Alessio BM, Gupta A. Diffusiophoresis: a novel transport mechanism - fundamentals, applications, and future opportunities. Front Sensors manuscript under final Rev Publ (2023). doi:10.3389/fsens.2023.1322906

CrossRef Full Text | Google Scholar

81. Kalinin YV, Jiang L, Tu Y, Wu M. Logarithmic sensing in Escherichia coli bacterial chemotaxis. Biophysical J (2009) 96:2439–48. doi:10.1016/j.bpj.2008.10.027

PubMed Abstract | CrossRef Full Text | Google Scholar

82. Alessio BM, Gupta A. Diffusiophoresis-enhanced turing patterns (2023). arXiv preprint arXiv:2305.11372.

Google Scholar

83. Sharifi-Mood N, Koplik J, Maldarelli C. Diffusiophoretic self-propulsion of colloids driven by a surface reaction: the sub-micron particle regime for exponential and van der Waals interactions. Phys Fluids (2013) 25:012001. doi:10.1063/1.4772978

CrossRef Full Text | Google Scholar

84. Poehnl R, Popescu MN, Uspal WE. Axisymmetric spheroidal squirmers and self-diffusiophoretic particles. J Phys Condensed Matter (2020) 32:164001. doi:10.1088/1361-648x/ab5edd

PubMed Abstract | CrossRef Full Text | Google Scholar

85. Ebbens SJ, Howse JR. Direct observation of the direction of motion for spherical catalytic swimmers. Langmuir (2011) 27:12293–6. doi:10.1021/la2033127

PubMed Abstract | CrossRef Full Text | Google Scholar

86. Shemi O, Solomon MJ. Self-propulsion and active motion of Janus ellipsoids. J Phys Chem B (2018) 122:10247–55. doi:10.1021/acs.jpcb.8b08303

PubMed Abstract | CrossRef Full Text | Google Scholar

87. Hsu JP, Luu XC, Hsu WL. Diffusiophoresis of an ellipsoid along the axis of a cylindrical pore. J Phys Chem B (2010) 114:8043–55. doi:10.1021/jp1039157

PubMed Abstract | CrossRef Full Text | Google Scholar

88. Daddi-Moussa-Ider A, Nasouri B, Vilfan A, Golestanian R. Optimal swimmers can be pullers, pushers or neutral depending on the shape. J Fluid Mech (2021) 922:R5. doi:10.1017/jfm.2021.562

CrossRef Full Text | Google Scholar

89. Shklyaev S, Brady JF, Córdova-Figueroa UM. Non-spherical osmotic motor: chemical sailing. J Fluid Mech (2014) 748:488–520. doi:10.1017/jfm.2014.177

CrossRef Full Text | Google Scholar

90. Poehnl R, Uspal W. Phoretic self-propulsion of helical active particles. J Fluid Mech (2021) 927:A46. doi:10.1017/jfm.2021.801

CrossRef Full Text | Google Scholar

91. Roggeveen JV, Stone HA. Motion of asymmetric bodies in two-dimensional shear flow. J Fluid Mech (2022) 939:A23. doi:10.1017/jfm.2022.203

CrossRef Full Text | Google Scholar

92. Schnitzer O, Yariv E. Osmotic self-propulsion of slender particles. Phys Fluids (2015) 27. doi:10.1063/1.4914417

CrossRef Full Text | Google Scholar

93. Yariv E. Self-diffusiophoresis of slender catalytic colloids. Langmuir (2019) 36:6903–15. doi:10.1021/acs.langmuir.9b02393

PubMed Abstract | CrossRef Full Text | Google Scholar

94. Katsamba P, Michelin S, Montenegro-Johnson TD. Slender phoretic theory of chemically active filaments. J Fluid Mech (2020) 898:A24. doi:10.1017/jfm.2020.410

CrossRef Full Text | Google Scholar

95. Bender CM, Orszag SA. Advanced mathematical methods for scientists and engineers I: asymptotic methods and perturbation theory. Berlin, Germany: Springer Science and Business Media (1999).

Google Scholar

96. Bechinger C, Di Leonardo R, Löwen H, Reichhardt C, Volpe G, Volpe G. Active particles in complex and crowded environments. Rev Mod Phys (2016) 88:045006. doi:10.1103/RevModPhys.88.045006

CrossRef Full Text | Google Scholar

97. Han K, Shields IVCW, Bharti B, Arratia PE, Velev OD. Active reversible swimming of magnetically assembled “microscallops” in non-Newtonian fluids. Langmuir (2020) 36:7148–54. PMID: 32011137. doi:10.1021/acs.langmuir.9b03698

PubMed Abstract | CrossRef Full Text | Google Scholar

98. Shields IVCW, Kim YK, Han K, Murphy AC, Scott AJ, Abbott NL, et al. Control of the folding dynamics of self-reconfiguring magnetic microbots using liquid crystallinity. Adv Intell Syst (2020) 2:1900114. doi:10.1002/aisy.201900114

CrossRef Full Text | Google Scholar

99. Han K, IV CWS, Diwakar NM, Bharti B, López GP, Velev OD. Sequence-encoded colloidal origami and microbot assemblies from patchy magnetic cubes. Sci Adv (2017) 3:e1701108. doi:10.1126/sciadv.1701108

PubMed Abstract | CrossRef Full Text | Google Scholar

100. Qiu T, Lee TC, Mark AG, Morozov KI, Münster R, Mierka O, et al. Swimming by reciprocal motion at low Reynolds number. Nat Commun (2014) 5:5119. doi:10.1038/ncomms6119

PubMed Abstract | CrossRef Full Text | Google Scholar

101. Vieu C, Carcenac F, Pepin A, Chen Y, Mejias M, Lebib A, et al. Electron beam lithography: resolution limits and applications. Appl Surf Sci (2000) 164:111–7. doi:10.1016/s0169-4332(00)00352-4

CrossRef Full Text | Google Scholar

102. Walker D, Käsdorf BT, Jeong HH, Lieleg O, Fischer P. Enzymatically active biomimetic micropropellers for the penetration of mucin gels. Sci Adv (2015) 1:e1500501. doi:10.1126/sciadv.1500501

PubMed Abstract | CrossRef Full Text | Google Scholar

103. Qin K, Pak OS. Purcell’s swimmer in a shear-thinning fluid. Phys Rev Fluids (2023) 8:033301. doi:10.1103/PhysRevFluids.8.033301

CrossRef Full Text | Google Scholar

104. Shaik VA, Elfring GJ. Hydrodynamics of active particles in viscosity gradients. Phys Rev Fluids (2021) 6:103103. doi:10.1103/physrevfluids.6.103103

CrossRef Full Text | Google Scholar

105. Jarvey N, Henrique F, Gupta A. Ion transport in an electrochemical cell: a theoretical framework to couple dynamics of double layers and redox reactions for multicomponent electrolyte solutions. J Electrochem Soc (2022) 169:093506. doi:10.1149/1945-7111/ac908e

CrossRef Full Text | Google Scholar

106. Rath M, Weaver J, Wang M, Woehl T. pH-mediated aggregation-to-separation transition for colloids near electrodes in oscillatory electric fields. Langmuir (2021) 37:9346–55. doi:10.1021/acs.langmuir.1c00671

PubMed Abstract | CrossRef Full Text | Google Scholar

107. Wang K, Behdani B, Silvera Batista CA. Visualization of concentration gradients and colloidal dynamics under electrodiffusiophoresis. Langmuir (2022) 38:5663–73. doi:10.1021/acs.langmuir.2c00252

PubMed Abstract | CrossRef Full Text | Google Scholar

108. Alonso-Matilla R, Chakrabarti B, Saintillan D. Transport and dispersion of active particles in periodic porous media. Phys Rev Fluids (2019) 4:043101. doi:10.1103/physrevfluids.4.043101

CrossRef Full Text | Google Scholar

109. Modica KJ, Xi Y, Takatori SC. Porous media microstructure determines the diffusion of active matter: experiments and simulations. Front Phys (2022) 10:232. doi:10.3389/fphy.2022.869175

CrossRef Full Text | Google Scholar

110. Caprini L, Marconi UMB. Active particles under confinement and effective force generation among surfaces. Soft Matter (2018) 14:9044–54. doi:10.1039/c8sm01840e

PubMed Abstract | CrossRef Full Text | Google Scholar

111. Lee CF. Active particles under confinement: aggregation at the wall and gradient formation inside a channel. New J Phys (2013) 15:055007. doi:10.1088/1367-2630/15/5/055007

CrossRef Full Text | Google Scholar

112. Henrique F, Zuk PJ, Gupta A. Kirchhoff’s laws for electric-double-layer charging in arbitrary porous networks (2023). arXiv preprint arXiv:2308.13100.

Google Scholar

113. Henrique F, Zuk PJ, Gupta A. Impact of asymmetries in valences and diffusivities on the transport of a binary electrolyte in a charged cylindrical pore. Electrochimica Acta (2022) 433:141220. doi:10.1016/j.electacta.2022.141220

CrossRef Full Text | Google Scholar