Generalized connectivity in cubic fuzzy graphs with application in the trade deficit problem

1 Introduction

Graph theory plays a vital role in numerous disciplines, including mathematics, engineering, physical sciences, social sciences, biology, computer science, linguistics, and more. The concept of fuzzy graphs emerges from the recognition that networks can exhibit ambiguity or uncertainty. This constitutes a crucial area of research. Traditional graphs face limitations in adequately capturing the uncertain attributes of network measurements, such as robust connections, accomplished individuals, and influential figures within social networks. In contrast, fuzzy graphs offer a more effective representation of these less-defined aspects. The acknowledgment of uncertainty in specific aspects of graph theory problems has spurred the evolution of fuzzy theory. The concept of fuzzy set (FS) theory, an extension of the classical set notion, was introduced by Zadeh [1] in 1965. Building upon this theory, Zadeh proposed a mathematical approach that enables decision-making problems through the use of fuzzy descriptions. In 1975, Rosenfeld [2] introduced fuzzy graph theory, combining the concepts of FS theory and graph theory. Around the same time, Yeh and Bang [3] also introduced the concept of fuzzy graphs (FGs). FGs find application in various scientific and engineering fields, such as broadcast communications, artificial reasoning, data hypothesis, and neural systems. Akram et al. [4] presented the idea of m-polar fuzzy hypergraphs, m-polar fuzzy line graphs, dual m-polar fuzzy hypergraphs, and 2-section of m-polar fuzzy hypergraphs.

FG theory is a significant and extensive area of research with a primary focus on connectivity. Different fuzzy connectivity measures were discussed in [5–14], 15–19. Mathew and Sunitha [20, 21] examined the concepts of edge connectivity, vertex connectivity, and cycle connectivity in FGs. Banerjee [22] and Tong and Zheng proposed various algorithms for analyzing connectivity in FGs. Ali et al. [23] discussed the notion of t-connected fuzzy graphs and average fuzzy vertex connectivity. Ahmad and Nawaz [24] explored the application of connectivity in directed rough graphs for trade networking. Shang [25] introduced some asymptotic results on r-super connectedness for classical Erdos–Rényi random graphs as the number of nodes tends to infinity. Su et al. [26] presented sufficient conditions in terms of the forgotten topological index for a graph to be l-connected, l-deficient, l-Hamiltonian, and l-independent, respectively. Binu et al. investigated the connectivity index of FGs and its application in the context of human trafficking. Mandal and Pal [27] introduced the concept of the connectivity index of m-polar fuzzy graphs and discussed the boundedness of the connectivity index. Amer et al. [28] calculated the edge-based counterparts of several notable topological degree-based indices, including the Randic index, sum-connectivity index, Zagreb indices, atom–bond connectivity (ABC) index, harmonic index, and geometric–arithmetic (GA) index for Boron triangular nanotubes. Irfan et al. [29] derived closed forms for M-polynomials pertaining to the line graphs of H-naphthalenic nanotubes and chain silicate networks. Using these M-polynomials, various topological indices based on degrees were obtained. The characteristics of fuzzy trees were studied by Sunitha and Vijayakumar [30] in 1999, while Mathew et al. [31] examined the characterization of fuzzy trees and cycles using saturation counts. Mordeson et al. [32] analyzed the properties of different types of fuzzy bridges and fuzzy cut vertices in FGs. Bhutani et al. introduced the concept of strong edges in fuzzy graphs and also discussed fuzzy end nodes in [33]. Talebi et al. [34] presented the idea of weak isomorphism, self-weak complementary, and co-weak isomorphism on vague graphs. Talebi et al. [35] investigated relations among union, join, and complement operations on bipolar fuzzy graphs. Mathew and Sunitha proposed various types of arcs, such as α-strong, β-strong, and δ-edges, in FGs [36]. Karunambigai et al. [37] introduced different types of arcs in intuitionistic FGs. Akram et al. [38] presented the idea of strong edges for m-polar fuzzy graphs in 2021. Naeem et al. [39] proposed the connectivity index for intuitionistic FGs. Last, Binu et al. [40] introduced the concept of the cyclic connectivity index in 2020.

Zadeh [41] proposed interval-valued fuzzy sets (IVFSs) as an extension of FSs, where membership degrees are represented by interval numbers instead of single points. Akram [42] presented the idea of interval-valued fuzzy line graphs and discussed some of their properties. Talebi et al. [43] introduced novel concepts of interval-valued intuitionistic fuzzy graphs (IVIFGs). Talebi et al. [44] introduced the concept of interval-valued intuitionistic fuzzy competition graphs of an interval-valued intuitionistic fuzzy digraph and investigated their properties. Rashmanlou et al. [45] introduced the concept of several types of interval-valued intuitionistic (S, T)-fuzzy graphs and also introduced different kinds of arc interval-valued intuitionistic (S, T)-fuzzy graphs.

In 2012, Jun et al. [46] introduced cubic fuzzy sets (CFSs) as a combination of IVFSs and FSs, offering a more generalized approach for handling uncertainty. They also provided an explanation of basic properties and operations.

Jun et al. [27] further extended the CFS by merging it with the neutrosophic complex, giving rise to the neutrosophic CFS. Cubic fuzzy sets present clear advantages compared to other fuzzy set types, such as interval-valued or general fuzzy sets. Their distinctive shape and parameters offer exceptional flexibility for modeling uncertainty. This flexibility allows for a more precise representation of complex relationships within a specific domain. The enhanced decision-making and reasoning capabilities of cubic fuzzy sets make them invaluable tools in various fields that depend on accurately modeling uncertainty. In 2018, Rashid et al. [47] introduced cubic fuzzy graphs (CFGs) based on CFSs. However, the initial definition of CFGs proposed by Rashid et al. [47] was later found to be incorrect, and a revised definition was provided by Muhiuddin et al. [48] in 2020. Fang et al. [49] discussed the planarity in cubic intuitionistic graphs and also introduced the concept of the degree of planarity in cubic intuitionistic planar graphs. Muhiuddin et al. [50] worked on cubic Pythagorean fuzzy graphs (CPFGs) and introduced certain fundamental operations, such as the lexicographical product, semi-strong product, and symmetric difference of two CPFGs. Muhiuddin et al. [51] discussed the concept of strong and weak edges for cubic planar graphs in 2022. In real-world scenarios, fuzzy graph ideas prove effective in describing certain phenomena, while interval-valued graph concepts excel in others. However, for more intricate phenomena that cannot be adequately represented by either of these approaches alone, a combination of both becomes valuable, referred to as cubic fuzzy graphs. An example illustrating the utility of this combined modeling approach is in addressing the trade deficit problem. When decisions require consideration of the past, present, and future simultaneously, cubic fuzzy graphs prove quite advantageous. They serve as a valuable tool for visually representing information spanning multiple time dimensions, offering a comprehensive view of the situation at hand.

1.1 Motivation and contribution

CFGs offer a more advantageous representation by integrating the membership degree of vertices and edges in both interval and fuzzy number forms. This enhanced representation fosters a more profound and detailed understanding of the connections and uncertainties inherent in the graph’s structure. The following features of edge cuts and cut nodes in CFG theory serve as the motivation for presenting this paper:

• While FGs or IVFGs may suffice for resolving certain practical problems, more intricate issues often demand a fusion of both. CFGs present a valuable approach for tackling such complex problems. Examples encompass traffic flow modeling, trade deficit modeling, and earthquake modeling, where CFGs can offer insightful perspectives.

• The motivation behind our research stems from the fact that the concepts of edge cuts and cut nodes have been well documented in the literature for crisp and fuzzy graphs, and their counterparts in CFGs are not widely known. Investigating their relevance and implications in the context of CFGs is, therefore, a worthwhile endeavor.

• The analysis of edge cuts and cut nodes holds significant potential in various decision-making problems, offering valuable insights and aiding in informed decision-making processes.

This paper introduces the notions of partial cubic fuzzy edge cuts, partial cubic fuzzy cut nodes, generalized partial cubic fuzzy edge cuts, and generalized partial cubic fuzzy cut nodes for CFGs. It builds upon the substantial significance and wide-ranging applications of edge cuts and cut nodes in fuzzy networks. Generalized partial cubic fuzzy edge cuts are particularly advantageous in addressing practical issues where the concept of fuzzy edge cuts may not be applicable. In particular, these concepts become relevant when the IVF-connectivity experiences a strict decrease upon the removal of a specific edge or any edge, while the F-connectivity remains equivalent to the F-connectivity of an edge after its removal or the removal of any specific edge and vice versa. In scenarios where we have information about the past, future, and current conditions of a model or problem, we can represent the past condition as a lower IVF-membership, the future condition as an upper IVF-membership, and the present condition as an F-membership value. Our objective is to scrutinize the problem by deducing lower IVF-connectivity, upper IVF-connectivity, and F-connectivity. Furthermore, we aim to make new predictions based on this analysis. In these situations, IVF-connectivity strictly decreases the IVF-connectivity of an edge after removing that edge or any specific edge, while the F-connectivity equates to the F-connectivity of an edge after removing that edge or any specific edge and vice versa. To tackle this issue effectively, we can apply the concept of generalized partial cubic fuzzy edge cuts. Such problems frequently arise in the analysis of transportation networks, trading, and decision making under uncertainty and optimization scenarios. Using the generalized partial cubic fuzzy edge cuts allows for a more accurate and detailed depiction of the connections between nodes or edges, enabling better modeling and evaluation of uncertain or imprecise relationships. It is important to note that throughout this study, we specifically focused on simple connected CFGs. The main contributions of this paper can be summarized as follows:

• The primary objective is to investigate the behavior of edge cuts and cut nodes in CFGs

• This paper examines the behavior of edge cuts and cut nodes in specific graph problems, aiming to gain insights into their properties and applications

• It introduces the concepts of partial cubic fuzzy edge cuts, partial cubic fuzzy cut nodes, generalized partial cubic fuzzy edge cuts, and generalized partial cubic fuzzy cut nodes for CFGs, providing a more comprehensive framework for analysis

• This paper applies the concept of generalized partial cubic fuzzy edge cuts to determine centrality in street crime problems, offering a practical application of the proposed concepts

• This research aims to enhance the understanding of complex systems modeled by CFGs and develop effective strategies for addressing real-world problems, such as analyzing trade deficits in specific regions through the use of generalized partial cubic fuzzy edge cuts

The organization of this research is structured as follows: Section 2 presents the necessary definitions and key findings that contribute to the development of the concept. In Section 3, an in-depth exploration is conducted on vertex and edge connectivity in CFGs and their corresponding outcomes. Section 4 specifically addresses the concept of generalized cubic fuzzy vertex and edge connectivity. The discussion in Section 5 focuses on the use of generalized partial cubic fuzzy edge cuts for examining regions impacted by trade congestion resulting from street crimes. Section 6 offers a comprehensive analysis of the research conducted. Finally, Section 7 serves as the conclusion of our investigation. Throughout the paper, we use the abbreviations given in Table 1.

Table 1

Table 1. Abbreviations.

2 Preliminaries

This section is composed of elementary ideas affiliated with CFGs.

Definition 2.1. [46]. A CFS X on a non-empty set V is described as

$X=\left\{⟨\left[{\sigma }^{-}\left(d_w\right),{\sigma }^{+}\left(d_w\right)\right],{\sigma }^{\mathbb{F}}\left(d_w\right)⟩|d_w\in V\right\},$

where [σ⁻(d_w), σ⁺(d_w)] is named as the IVF-membership value and ${\sigma }^{\mathbb{F}}(t_w)$ is named as the F-membership value of d_w. The CFS X is referred to as an internal CFS if ${\sigma }^{\mathbb{F}}(d_w)\in [{\sigma }^{-}(d_w),{\sigma }^{+}(d_w)]$ for d_w ∈ V; otherwise, it is called an external CFS.

Definition 2.2. [48]. A CFG over the set V is a pair $\mathbb{R}=(A,B)$, where A is a CFS in V and B is a CFS in V × V so that for all (d_w−1, d_w) ∈ B,

$\begin{array}{ccc}\hfill {\mu }^{-}\left(d_{w-1},d_w\right)& \le \hfill & \wedge \left\{{\sigma }^{-}\left(d_{w-1}\right),{\sigma }^{-}\left(d_w\right)\right\},\hfill \\ \hfill {\mu }^{+}\left(d_{w-1},d_w\right)& \le \hfill & \wedge \left\{{\sigma }^{+}\left(d_{w-1}\right),{\sigma }^{+}\left(d_w\right)\right\},\hfill \\ \hfill {\mu }^{\mathbb{F}}\left(d_{w-1},d_w\right)& \le \hfill & \wedge \left\{{\sigma }^{\mathbb{F}}\left(d_{w-1}\right),{\sigma }^{\mathbb{F}}\left(d_w\right)\right\}.\hfill \end{array}$

Definition 2.3. [48]. A CFG $\mathbb{Q}=(\tau ,\omega )$ is called a partial cubic fuzzy subgraph of $\mathbb{R}=(\sigma ,\nu )$ if

• ${\tau }^{-}(g)\le {\sigma }^{-}(g),{\tau }^{+}(g)\le {\sigma }^{+}(g),{\tau }^{\mathbb{F}}(g)\le {\sigma }^{\mathbb{F}}(g)\forall g\in {\tau }^{\star }$

• ${\omega }^{-}(gs)\le {\nu }^{-}(gs),{\omega }^{+}(gs)\le {\nu }^{+}(gs),{\omega }^{\mathbb{F}}(gs)\le {\nu }^{\mathbb{F}}(gs)\forall gs\in {\omega }^{\star }$

Definition 2.4. [48]. A CFG $\mathbb{R}=(A,B)$ is said to be complete if

$\begin{array}{ccc}\hfill {\mu }^{-}\left(d_{w-1},d_w\right)& =\hfill & \wedge \left\{{\sigma }^{-}\left(d_{w-1}\right),{\sigma }^{-}\left(d_w\right)\right\},\hfill \\ \hfill {\mu }^{+}\left(d_{w-1},d_w\right)& =\hfill & \wedge \left\{{\sigma }^{+}\left(d_{w-1}\right),{\sigma }^{+}\left(d_w\right)\right\},\hfill \\ \hfill {\mu }^{\mathbb{F}}\left(d_{w-1},d_w\right)& =\hfill & \wedge \left\{{\sigma }^{\mathbb{F}}\left(d_{w-1}\right),{\sigma }^{\mathbb{F}}\left(d_w\right)\right\},\hfill \end{array}$

∀d_w−1, d_w ∈ B.

Definition 2.5. [48]. A cubic fuzzy path $\mathbb{P}$ of length n is a sequence of distinct vertices $d_0,d_1,d_2,\dot{\dots },d_n$ with μ⁺(d_w−1, d_w) > 0, μ⁻(d_w−1, d_w) > 0, and ${\mu }^{\mathbb{F}}(d_{w-1},d_w)>0$ for $w=\mathrm{1,2,3},\dot{\dots },n$. A cubic fuzzy path $\mathbb{P}$ is called a cycle if d₀ = d_n.

The strength of cubic fuzzy path $\mathbb{P}=d_1,d_2,d_3,\dot{\dots },d_n$ is defined as

$\mathbb{S}\left(\mathbb{P}\right)=⟨\left[L^{-}\left(\mathbb{P}\right),L^{+}\left(\mathbb{P}\right)\right],L^{\mathbb{F}}\left(\mathbb{P}\right)⟩,$

where

$L^{+}\left(\mathbb{P}\right){=\wedge }_{w=1}^n{\mu }^{+}\left(d_{w-1},d_w\right),L^{-}\left(\mathbb{P}\right){=\wedge }_{w=1}^n{\mu }^{-}\left(d_{w-1},d_w\right),L^{\mathbb{F}}\left(\mathbb{P}\right){=\wedge }_{w=1}^n{\mu }^{\mathbb{F}}\left(d_{w-1},d_w\right).$

The strength of connectedness ${\mathbb{CONN}}_{\mathbb{R}}^{\infty }$ among the vertices d_w−1 and d_w is defined as

${\mathbb{CONN}}_{\mathbb{R}}^{\infty }\left(d_{w-1},d_w\right)=⟨\left[{\mathbb{CONN}}_{\mathbb{R}}^{-}\left(d_{w-1},d_w\right),{\mathbb{CONN}}_{\mathbb{R}}^{+}\left(d_{w-1},d_w\right)\right],{\mathbb{CONN}}_{\mathbb{R}}^{\mathbb{F}}\left(d_{w-1},d_w\right)⟩,$

where

$\begin{array}{ccc}\hfill {\mathbb{CONN}}_{\mathbb{R}}^{+}\left(d_{w-1},d_w\right)& =\hfill & \vee L^{+}\left(\mathbb{P}\right):\left.\mathbb{P}\text{is\hspace{0.17em}a\hspace{0.17em}path\hspace{0.17em}between}{d}_{w-1}\text{and\hspace{0.17em}}{d}_w\right\},\hfill \\ \hfill {\mathbb{CONN}}_{\mathbb{R}}^{-}\left(d_{w-1},d_w\right)& =\hfill & \vee L^{-}\left(\mathbb{P}\right):\left.\mathbb{P}\text{is\hspace{0.17em}a\hspace{0.17em}path\hspace{0.17em}between}{d}_{w-1}\text{and\hspace{0.17em}}{d}_w\right\},\hfill \\ \hfill {\mathbb{CONN}}_{\mathbb{R}}^{\mathbb{F}}\left(d_{w-1},d_w\right)& =\hfill & \vee L^{\mathbb{F}}\left(\mathbb{P}\right):\left.\mathbb{P}\text{is\hspace{0.17em}a\hspace{0.17em}path\hspace{0.17em}between}{d}_{w-1}\text{and\hspace{0.17em}}{d}_w\right\}.\hfill \end{array}$

The path $\mathbb{P}$ between d_w−1 and d_w with $L^{+}(\mathbb{P})={\mathbb{CONN}}_{\mathbb{R}}^{+}(d_{w-1},d_w)$ is referred to as the L⁺-stronger path. Similarly, the L⁻-stronger and $L^{\mathbb{F}}$-stronger paths are defined. The L⁺-stronger, L⁻-stronger, and $L^{\mathbb{F}}$-stronger paths are denoted by ${\mathbb{P}}^{+},{\mathbb{P}}^{-}$, and ${\mathbb{P}}^F$, respectively.

Definition 2.6. [52]. Let $\mathbb{R}=(A,B)$ be a CFG and (d_w−1, d_w) ∈ B.

1. If ${\mu }^{+}(d_{w-1}{d}_w)>{\mathbb{CONN}}_{\mathbb{R}-d_{w-1}{d}_w}^{+}(d_{w-1},d_w)$, ${\mu }^{-}(d_{w-1}{d}_w)>{\mathbb{CONN}}_{\mathbb{R}-d_{w-1}{d}_w}^{-}(d_{w-1},d_w)$, and ${\mu }^{\mathbb{F}}(d_{w-1}{d}_w)>{\mathbb{CONN}}_{\mathbb{R}-d_{w-1}{d}_w}^{\mathbb{F}}(d_{w-1},d_w)$, then d_w−1d_w is called a cubic α-strong edge

2. If ${\mu }^{+}(d_{w-1}{d}_w)={\mathbb{CONN}}_{\mathbb{R}-d_{w-1}{d}_w}^{+}(d_{w-1},d_w)$, ${\mu }^{-}(d_{w-1}{d}_w)={\mathbb{CONN}}_{\mathbb{R}-d_{w-1}{d}_w}^{-}(d_{w-1},d_w)$, and ${\mu }^{\mathbb{F}}(d_{w-1}{d}_w)={\mathbb{CONN}}_{\mathbb{R}-d_{w-1}{d}_w}^{\mathbb{F}}(d_{w-1},d_w)$, then d_w−1d_w is called a cubic β-strong edge

3. If ${\mu }^{+}(d_{w-1}{d}_w)<{\mathbb{CONN}}_{\mathbb{R}-d_{w-1}{d}_w}^{+}(d_{w-1},d_w)$, ${\mu }^{-}(d_{w-1}{d}_w)<{\mathbb{CONN}}_{\mathbb{R}-d_{w-1}{d}_w}^{-}(d_{w-1},d_w)$, and ${\mu }^{\mathbb{F}}(d_{w-1}{d}_w)<{\mathbb{CONN}}_{\mathbb{R}-d_{w-1}{d}_w}^{\mathbb{F}}(d_{w-1},d_w)$, then d_w−1d_w is called a cubic δ-weak edge

Definition 2.7. [52]. A CFG $\mathbb{R}$ is referred to be

• α-saturated if at each node of σ*, there are incident n ≥ 1 α-strong edges to it

• β-saturated if at each node of σ*, there are incident n ≥ 1 β-strong edges to it

• saturated if it is α- as well as β-saturated

• unsaturated if it is neither α- nor β-saturated

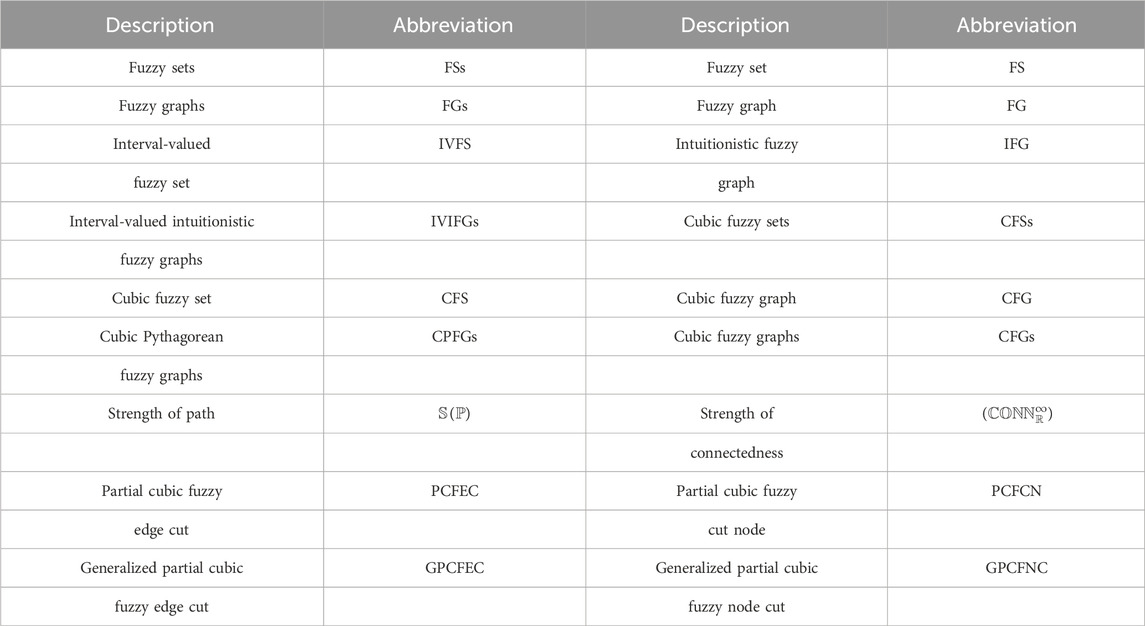
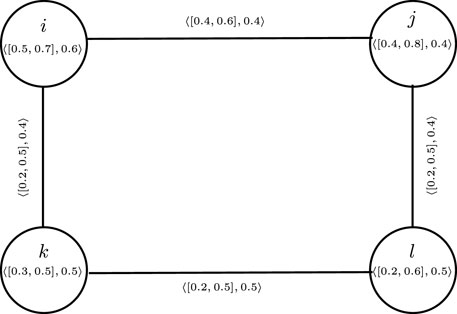
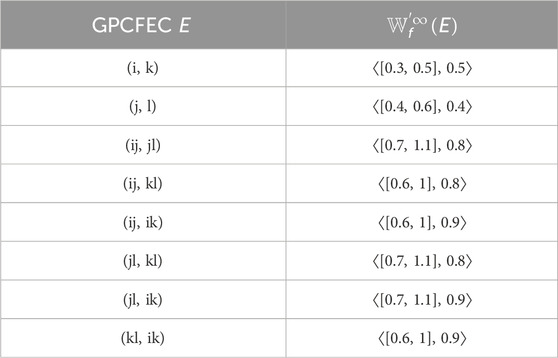
Example 2.8. consider a CFG $\mathbb{T}=(L,K)$ (Figure 1) with

$\begin{array}{ccc}\hfill L& =\hfill & \left(\frac{i}{\langle \left[0.4,0.5\right],0.4\rangle },\frac{j}{\langle \left[0.3,0.9\right],0.5\rangle },\frac{k}{\langle \left[0.3,0.5\right],0.5\rangle },\frac{l}{\langle \left[0.2,0.8\right],0.6\rangle }\right),\hfill \\ \hfill K& =\hfill & \left(\frac{ij}{\langle \left[0.3,0.5\right],0.3\rangle },\frac{ik}{\langle \left[0.1,0.3\right],0.2\rangle },\frac{jl}{\langle \left[0.1,0.3\right],0.2\rangle },\frac{kl}{\langle \left[0.2,0.5\right],0.4\rangle }\right).\hfill \end{array}$

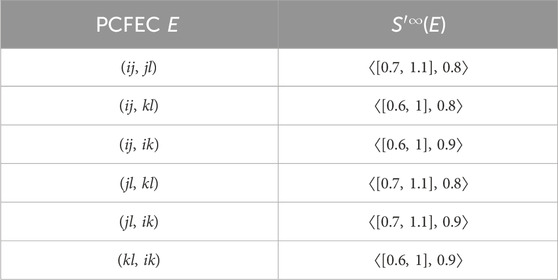
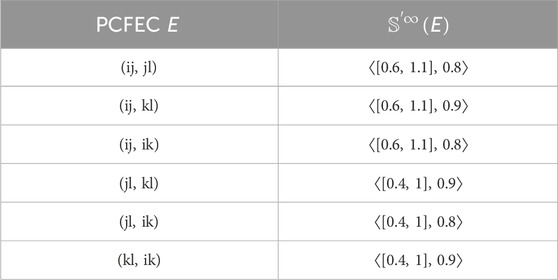
The connectivity among the pairs (i, j), (k, l), (j, l), and (i, k) is computed as follows:

$\begin{array}{ccc}\hfill & \hfill & \hfill \langle \left[{\mathbb{CONN}}_{\mathbb{T}-\left(ij\right)}^{-}\left(i,j\right),{\mathbb{CONN}}_{\mathbb{T}-\left(ij\right)}^{+}\left(i,j\right)\right],{\mathbb{CONN}}_{\mathbb{T}-\left(ij\right)}^{\mathbb{F}}\left(i,j\right)\rangle =\langle \left[0.1,0.3\right],0.2\rangle ,\\ \hfill & \hfill & \hfill \langle \left[{\mathbb{CONN}}_{\mathbb{T}-\left(kl\right)}^{-}\left(k,l\right),{\mathbb{CONN}}_{\mathbb{T}-\left(kl\right)}^{+}\left(k,l\right)\right],{\mathbb{CONN}}_{\mathbb{T}-\left(kl\right)}^{\mathbb{F}}\left(k,l\right)\rangle =\langle \left[0.1,0.3\right],0.2\rangle ,\\ \hfill & \hfill & \hfill \langle \left[{\mathbb{CONN}}_{\mathbb{T}-\left(ik\right)}^{-}\left(i,k\right),{\mathbb{CONN}}_{\mathbb{T}-\left(ik\right)}^{+}\left(i,k\right)\right],{\mathbb{CONN}}_{\mathbb{T}-\left(ik\right)}^{\mathbb{F}}\left(i,k\right)\rangle =\langle \left[0.1,0.3\right],0.2\rangle ,\\ \hfill & \hfill & \hfill \langle \left[{\mathbb{CONN}}_{\mathbb{T}-\left(jl\right)}^{-}\left(j,l\right),{\mathbb{CONN}}_{\mathbb{T}-\left(jl\right)}^{+}\left(j,l\right)\right],{\mathbb{CONN}}_{\mathbb{T}-\left(jl\right)}^{\mathbb{F}}\left(j,l\right)\rangle =\langle \left[0.1,0.3\right],0.2\rangle .\end{array}(1)$

From Equation 1, if we follow Definition 2.6, it is clear that ij and kl are α-strong edges and ik and jl are β-strong edges. If we follow Definition 2.7 CFG $\mathbb{T}=(L,K)$ is saturated because all the vertices of $\mathbb{T}$ are incident to at least one α-strong edge and at least one β-strong edge. Definition 2.6 specifically addresses strong edges, but by following 2.7, we can also discern the saturation status of the graph. Moreover, it enables us to understand the extent to which our graph is interconnected with both strong and weak edges.

Figure 1

Figure 1. $\mathbb{T}=(L,K)$.

3 Vertex and edge connectivity in a CFG

In this section, we present the notion of a partial cubic fuzzy cut node, cubic fuzzy vertex connectivity, partial cubic fuzzy edge cut, and cubic fuzzy edge connectivity and engage in a thorough exploration of their pertinent findings.

Definition 3.1. A collection of cubic fuzzy vertices denoted as X = v₁, v₂, … , v_n ⊂ σ* within a cubic fuzzy graph $\mathbb{R}=(\sigma ,\mu )$ is referred to as a partial cubic fuzzy cut node (PCFCN) if either the removal of X from $\mathbb{R}$ leads to the disconnection of the remaining graph or for some pair of the vertices t, v ∈ σ* (where t, v ≠ v_i for i = 1, 2, … , n), at least one of the following statements holds:

$\begin{array}{c}\hfill \left[{\mathbb{CONN}}_{\mathbb{R}}^{-}\left(t,v\right),{\mathbb{CONN}}_{\mathbb{R}}^{+}\left(t,v\right)\right]>\left[{\mathbb{CONN}}_{\mathbb{R}-X}^{-}\left(t,v\right),{\mathbb{CONN}}_{\mathbb{R}-X}^{+}\left(t,v\right)\right]\text{and}\\ \hfill {\mathbb{CONN}}_{\mathbb{R}}^{\mathbb{F}}\left(t,v\right)\ge {\mathbb{CONN}}_{\mathbb{R}-X}^{\mathbb{F}}\left(t,v\right),\end{array}(2)$

$\begin{array}{c}\hfill \left[{\mathbb{CONN}}_{\mathbb{R}}^{-}\left(t,v\right),{\mathbb{CONN}}_{\mathbb{R}}^{+}\left(t,v\right)\right]\ge \left[{\mathbb{CONN}}_{\mathbb{R}-X}^{-}\left(t,v\right),{\mathbb{CONN}}_{\mathbb{R}-X}^{+}\left(t,v\right)\right]\text{and}\\ \hfill {\mathbb{CONN}}_{\mathbb{R}}^{\mathbb{F}}\left(t,v\right)>{\mathbb{CONN}}_{\mathbb{R}-X}^{\mathbb{F}}\left(t,v\right).\end{array}(3)$

If Eq. (2) holds, then a set of cubic fuzzy vertices is referred to as an IVF cut node, whereas if Eq. (2) and Eq. (3) is satisfied, then it is referred to as an F cut node. If both Eq. (2) are satisfied for the same pair of vertices, then it is referred to as a strict cubic fuzzy cut node. If X contains n vertices, then X is referred to as an n-PCFCN.

Definition 3.2. Let X be a partial cubic fuzzy cut node in $\mathbb{R}$. The strong weight of X is denoted as ${\mathbb{S}}^{\infty }(X)$ and is defined as

${\mathbb{S}}^{\infty }\left(X\right)=⟨\left[{\displaystyle \sum _{t\in X}}{\mu }^{-}\left(t,z\right),{\displaystyle \sum _{t\in X}}{\mu }^{+}\left(t,z\right)\right],{\displaystyle \sum _{t\in X}}{\mu }^{\mathbb{F}}\left(t,z\right)⟩,$

where μ⁻(t, z), μ⁺(t, z) and ${\mu }^{\mathbb{F}}t,z$) is the minimum weight of strong edges incident at t.

Definition 3.3. The cubic fuzzy vertex connectivity of $\mathbb{R}$ denoted by ${\kappa }^{\infty }(\mathbb{R})$ and ${\kappa }^{\infty }(\mathbb{R})=⟨[{\kappa }^{-}(\mathbb{R}),{\kappa }^{+}(\mathbb{R})],{\kappa }^{\mathbb{F}}(\mathbb{R})⟩$ is defined as

${\kappa }^{\infty }\left(\mathbb{R}\right){=\wedge }_X\left({\mathbb{S}}^{\infty }\left(X\right)\right).$

Definition 3.4. Considering $\mathbb{R}$ as a cubic fuzzy graph and {V₁, V₂} as a partition of its vertex set, the set of edges connecting vertices from V₁ to vertices in V₂ is referred to as a cut set of $\mathbb{R}$, denoted as (V₁, V₂) with respect to the partition {V₁, V₂}. The weight assigned to the cut-set (V₁, V₂) is defined as

$⟨\left[{\displaystyle \sum _{c\in V_1,z\in V_2}}{\mu }^{-}\left(c,z\right),{\displaystyle \sum _{c\in V_1,z\in V_2}}{\mu }^{+}\left(c,z\right)\right],{\displaystyle \sum _{c\in V_1,z\in V_2}}{\mu }^{\mathbb{F}}\left(c,z\right)⟩.$

Considering $\mathbb{R}$ as a cubic fuzzy graph, the edge connectivity of $\mathbb{R}$ is represented by ${\lambda }^{\infty }(\mathbb{R})$, and ${\lambda }^{\infty }(\mathbb{R})=⟨[{\lambda }^{-}(\mathbb{R}),{\lambda }^{+}(\mathbb{R})],{\lambda }^{\mathbb{F}}(\mathbb{R})⟩$ is defined as

${\lambda }^{\infty }\left(\mathbb{R}\right){=\wedge }_{\left(V_1,V_2\right)}⟨\left[{\displaystyle \sum _{c\in V_1,z\in V_2}}{\mu }^{-}\left(c,z\right),{\displaystyle \sum _{c\in V_1,z\in V_2}}{\mu }^{+}\left(c,z\right)\right],{\displaystyle \sum _{c\in V_1,z\in V_2}}{\mu }^{\mathbb{F}}\left(c,z\right)⟩.$

Definition 3.5. For a CF edge d_w−1d_w in a CFG, if one of the following holds, then d_w−1, d_w is called a partial cubic α-strong edge.

1. $[{\mu }_{\mathbb{R}}^{-}(d_{w-1},d_w),{\mu }_{\mathbb{R}}^{+}(d_{w-1},d_w)]\ge [{\mathbb{CONN}}_{\mathbb{R}-d_{w-1}{d}_w}(d_{w-1},d_w),{\mathbb{CONN}}_{\mathbb{R}-d_{w-1}{d}_w}^{+}(d_{w-1},dw)]$ and ${\mu }_{\mathbb{R}}^{\mathbb{F}}(d_{w-1}{d}_w)>{\mathbb{CONN}}_{\mathbb{R}-d_{w-1}{d}_w}^{\mathbb{F}}(d_{w-1},d_w)$

2. $[{\mu }_{\mathbb{R}}^{-}(d_{w-1},d_w),{\mu }_{\mathbb{R}}^{+}(d_{w-1},d_w)]>[{\mathbb{CONN}}_{\mathbb{R}-d_{w-1}{d}_w}^{-}(d_{w-1},d_w),{\mathbb{CONN}}_{\mathbb{R}-d_{w-1}{d}_w}^{+}(d_{w-1},dw)]$ and ${\mu }_{\mathbb{R}}^{\mathbb{F}}(d_{w-1}{d}_w)\ge {\mathbb{CONN}}_{\mathbb{R}-d_{w-1}{d}_w}^{\mathbb{F}}(d_{w-1},d_w)$

The CF α-strong is defined in [52]. However, we note that there are CFGs which contain edges which are either IVF α-strong and F β-strong or IVF β-strong and F α-strong but not CF α-strong. These types of edges seem very close to CF α-strong edges and may be more useful in different CF connectivity problems. The following example is helpful to understand this situation:

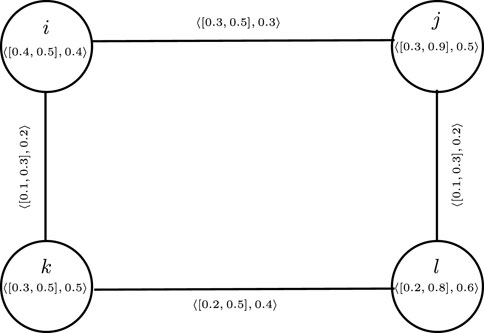
Example 3.6. consider a CFG $\mathbb{T}=(E,S)$ (Figure 2) with

$\begin{array}{c}E=\left(\frac{l}{⟨\left[0.3,0.5\right],0.3⟩},\frac{j}{⟨\left[0.5,0.9\right],0.8⟩},\frac{k}{⟨\left[0.2,0.7\right],0.5⟩},\frac{i}{⟨\left[0.4,0.8\right],0.6⟩}\right),\hfill \\ S=\left(\frac{ij}{⟨\left[0.3,0.7\right],0.5⟩},\frac{ik}{⟨\left[0.2,0.5\right],0.5⟩},\frac{jk}{⟨\left[0.2,0.5\right],0.5⟩},\frac{jl}{⟨\left[0.3,0.4\right],0.3⟩},\frac{kl}{⟨\left[0.1,0.4\right],0.3⟩})\right..\hfill \end{array}$

The connectivity for the pair i, j is computed as

$\begin{array}{ccc}\hfill & \hfill & \left[{\mathbb{CONN}}_{\mathbb{T}-\left(ij\right)}^{-}\left(i,j\right),{\mathbb{CONN}}_{\mathbb{T}-\left(ij\right)}^{+}\left(i,j\right)\right]=\left[0.2,0.5\right],{\mathbb{CONN}}_{\mathbb{T}-\left(ij\right)}^{\mathbb{F}}\left(i,j\right)=0.5,\hfill \\ \hfill & \hfill & \left[{\mu }^{-}\left(ij\right),{\mu }^{+}\left(ij\right)\right]=\left[0.3,0.7\right],{\mu }^{\mathbb{F}}\left(ij\right)=0.5.\hfill \end{array}$

It is clear that the edge ij is an IVF α-strong edge but an F β-strong edge. We can see that if we slightly increase the value of the F-membership of edge ij, then it becomes a CF α-strong edge. So, we can say that it is very close to a CF α-strong edge. This example motivates us to define the concept of partial cubic α-strong edge.

Figure 2

Figure 2. $\mathbb{T}=(E,S)$.

Definition 3.7. For a CF edge d_w−1d_w in a CFG, if one of the following holds, then d_w−1d_w is called a partial cubic δ-weak edge.

1. $[{\mu }_{\mathbb{R}}^{-}(d_{w-1}{d}_w),{\mu }_{\mathbb{R}}^{+}(d_{w-1}{d}_w)]\le [{\mathbb{CONN}}_{\mathbb{R}-d_{w-1}{d}_w}^{-}(d_{w-1},d_w),{\mathbb{CONN}}_{\mathbb{R}-d_{w-1}{d}_w}^{+}(d_{w-1},d_w)]$ and ${\mu }_{\mathbb{R}}^{\mathbb{F}}(d_{w-1}{d}_w)<{\mathbb{CONN}}_{\mathbb{R}-d_{w-1}{d}_w}^{\mathbb{F}}(d_{w-1},d_w)$

2. $[{\mu }_{\mathbb{R}}^{-}(d_{w-1}{d}_w),{\mu }_{\mathbb{R}}^{+}(d_{w-1}{d}_w)]<[{\mathbb{CONN}}_{\mathbb{R}-d_{w-1}{d}_w}^{-}(d_{w-1},d_w),{\mathbb{CONN}}_{\mathbb{R}-d_{w-1}{d}_w}^{+}(d_{w-1},d_w)]$ and ${\mu }_{\mathbb{R}}^{\mathbb{F}}(d_{w-1}{d}_w)\le {\mathbb{CONN}}_{\mathbb{R}-d_{w-1}{d}_w}^{\mathbb{F}}(d_{w-1},d_w)$

Definition 3.8. A CFG $\mathbb{R}$ is referred to be

• partial α-saturated if at each node of σ*, there are incident n ≥ 1 partial α-strong edges to it

• β-saturated if at each node of σ*, there are incident n ≥ 1 β-strong edges to it

• partial saturated if it is partial α-saturated as well as β-saturated

Definition 3.9. Considering $\mathbb{R}=(\sigma ,\mu )$ as a CFG, let E = {e₁, e₂, … , e_n} be a set of strong edges, where each edge e_i can be categorized as either a partial α-strong or β-strong edge and is represented as e_i = b_ic_i for i = 1, 2, … , n. Then, E is considered as a partial cubic fuzzy edge cut (PCFEC) if either $\mathbb{R}-E$ becomes disconnected or at least one of the following conditions is satisfied for a pair of vertices t and v in σ*, with the requirement that t or v must differ from both b_i and c_i.

$\begin{array}{c}\hfill \left[{\mathbb{CONN}}_{\mathbb{R}}^{-}\left(t,v\right),{\mathbb{CONN}}_{\mathbb{R}}^{+}\left(t,v\right)\right]>\left[{\mathbb{CONN}}_{\mathbb{R}-E}^{-}\left(t,v\right),{\mathbb{CONN}}_{\mathbb{R}-E}^{+}\left(t,v\right)\right]\text{and}\\ \hfill {\mathbb{CONN}}_{\mathbb{R}}^{\mathbb{F}}\left(t,v\right)\ge {\mathbb{CONN}}_{\mathbb{R}-E}^{\mathbb{F}}\left(t,v\right),\end{array}(4)$

$\begin{array}{c}\hfill \left[{\mathbb{CONN}}_{\mathbb{R}}^{-}\left(t,v\right),{\mathbb{CONN}}_{\mathbb{R}}^{+}\left(t,v\right)\right]\ge \left[{\mathbb{CONN}}_{\mathbb{R}-E}^{-}\left(t,v\right),{\mathbb{CONN}}_{\mathbb{R}-E}^{+}\left(t,v\right)\right]\text{and}\\ \hfill {\mathbb{CONN}}_{\mathbb{R}}^{\mathbb{F}}\left(t,v\right)>{\mathbb{CONN}}_{\mathbb{R}-E}^{\mathbb{F}}\left(t,v\right).\end{array}(5)$

If Eq. (4) holds, then a set of strong edges is referred to as an IVF edge cut, whereas if Eq. (5) is satisfied, then it is referred to as an F edge cut. If both Eq. (4) and Eq. (5) are satisfied for the same pair of vertices, then it is referred to as a strict cubic fuzzy edge cut. If E contains n edges, then E is referred to as an n-PCFEC.

Definition 3.10. Let E be a partial cubic fuzzy edge cut in $\mathbb{R}$. The strong weight of E denoted as ${\mathbb{S}}^{\prime \infty }(E)$ is defined as

${\mathbb{S}}^{\prime \infty }\left(E\right)=⟨\left[{\displaystyle \sum _{e_i\in E}}{\mu }^{-}\left(e_i\right),{\displaystyle \sum _{e_i\in E}}{\mu }^{+}\left(e_i\right)\right],{\displaystyle \sum _{e_i\in E}}{\mu }^{\mathbb{F}}\left(e_i\right)⟩.$

Definition 3.11. The cubic fuzzy edge connectivity of $\mathbb{R}$ denoted by ${\kappa }^{\prime \infty }(\mathbb{R})$ and ${\kappa }^{\prime \infty }(\mathbb{R})=⟨[{\kappa }^{\prime -}(\mathbb{R}),{\kappa }^{\prime +}(\mathbb{R})],{\kappa }^{\prime \mathbb{F}}(\mathbb{R})⟩$ is defined as

${\kappa }^{\prime \infty }\left(\mathbb{R}\right){=\wedge }_E\left({\mathbb{S}}^{\prime \infty }\left(E\right)\right).$

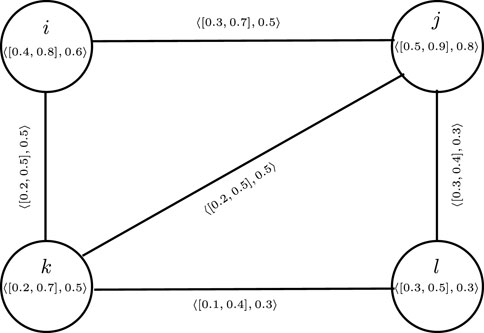
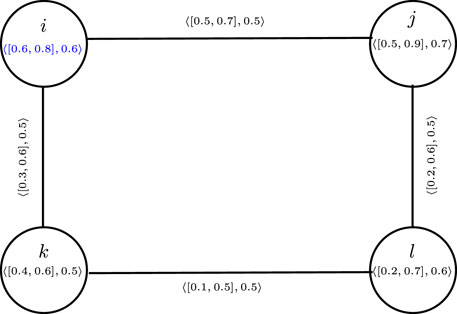
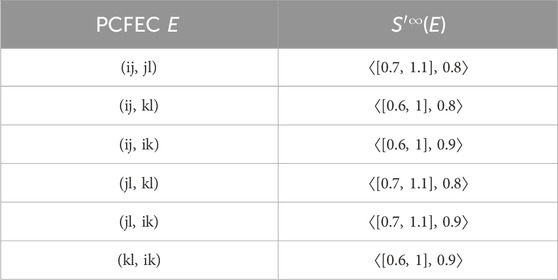
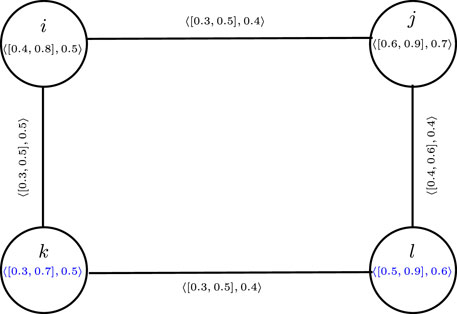
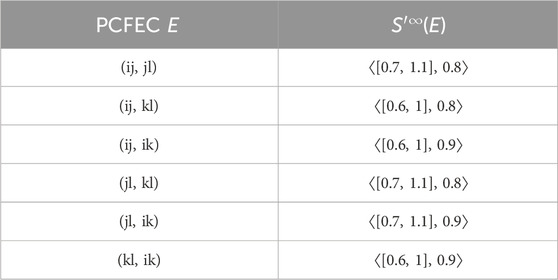
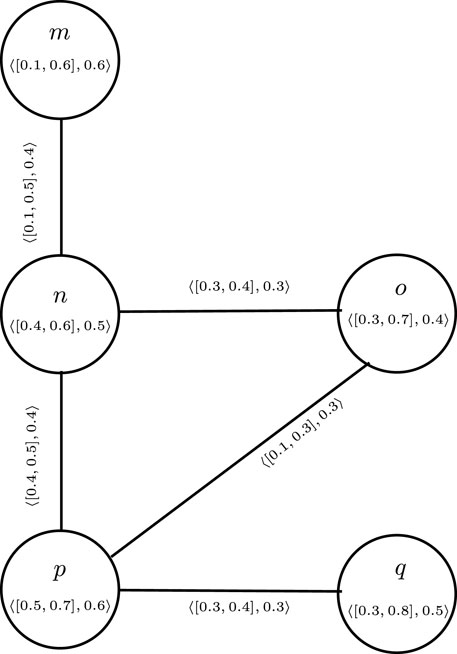
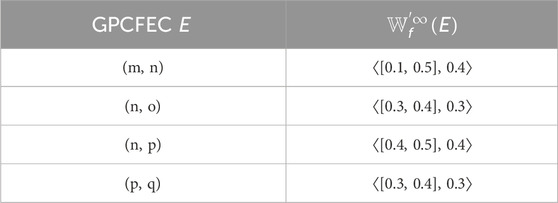
Example 3.12. consider a CFG $\mathbb{R}=(D,F)$ given in Figure 3 with

$\begin{array}{ccc}\hfill D& =\hfill & \left(\frac{i}{\langle \left[0.4,0.8\right],0.5\rangle },\frac{j}{\langle \left[0.6,0.9\right],0.7\rangle },\frac{k}{\langle \left[0.3,0.7\right],0.5\rangle },\frac{l}{\langle \left[0.5,0.9\right],0.6\rangle }\right),\hfill \\ \hfill F& =\hfill & \left(\frac{ij}{\langle \left[0.3,0.5\right],0.4\rangle },\frac{ik}{\langle \left[0.3,0.5\right],0.5\rangle },\frac{kl}{\langle \left[0.3,0.5\right],0.4\rangle },\frac{jl}{\langle \left[0.4,0.6\right],0.4\rangle }\right).\hfill \end{array}$

Thus, from Table 2, the cubic fuzzy edge connectivity is

${\kappa }^{\prime \infty }\left(\mathbb{R}\right)=⟨\left[0.6,1\right],0.8⟩.$

Figure 3

Figure 3. $\mathbb{R}=(D,F)$.

Table 2

Table 2. PCFEC of $\mathbb{R}=(D,F)$.

Definition 3.13. Let $\mathbb{R}$ be a cubic fuzzy connected graph, and $t^{\infty }=⟨[t^{-},t^{+}],t^{\mathbb{F}}⟩\in (0,\infty )$, $\mathbb{R}$ is called a partial t^∞ vertex connected graph if either

$\left[{\kappa }^{-}\left(\mathbb{R}\right),{\kappa }^{-}\left(\mathbb{R}\right)\right]>\left[t^{-},t^{+}\right],{\kappa }^{\mathbb{F}}\left(\mathbb{R}\right)\ge t^{\mathbb{F}}(6)$

or

$\left[{\kappa }^{-}\left(\mathbb{R}\right),{\kappa }^{-}\left(\mathbb{R}\right)\right]\ge \left[t^{-},t^{+}\right],{\kappa }^{\mathbb{F}}\left(\mathbb{R}\right)>t^{\mathbb{F}}.(7)$

If Eq. (6) holds, then $\mathbb{R}$ is referred to as an IVF t^∞ vertex connected graph, whereas if Eq. (7) is satisfied, then it is referred to as an F t^∞ vertex connected graph. If both (Eq. 6) and (Eq. 7) are satisfied, then it is referred to as a strict t^∞ cubic fuzzy vertex connected graph. Similarly, $\mathbb{R}$ is called a partial t^∞ − edge connected graph if either

$\left[{\kappa }^{\prime -}\left(\mathbb{R}\right),{\kappa }^{\prime -}\left(\mathbb{R}\right)\right]>\left[t^{-},t^{+}\right],{\kappa }^{\prime \mathbb{F}}\left(\mathbb{R}\right)\ge t^{\mathbb{F}}(8)$

or

$\left[{\kappa }^{\prime -}\left(\mathbb{R}\right),{\kappa }^{\prime -}\left(\mathbb{R}\right)\right]\ge \left[t^{-},t^{+}\right],{\kappa }^{\prime \mathbb{F}}\left(\mathbb{R}\right)>t^{\mathbb{F}}.(9)$

If Eq. (8) holds, then $\mathbb{R}$ is referred to as an IVF t^∞ edge connected graph, whereas if Eq. (9) is satisfied, then it is referred to as an F t^∞ edge connected graph. If both Eq. (8) and Eq. (9) are satisfied, then it is referred to as a strict t^∞ cubic fuzzy edge connected graph.

Definition 3.14. A CFG graph $\mathbb{R}$ is referred to as a CF cycle if its crisp graph $\mathbb{R^\{\backslash star\; \}}$ is a cycle and $\mathbb{R}$ contains no partial δ-weak edge.

Theorem 3.15. Considering $\mathbb{R}=(\sigma ,\mu )$ as a CFG with |σ*| = n, if $\mathbb{Q}=(\sigma ,\nu )$ is a partial cubic fuzzy subgraph that shares the same vertex set as $\mathbb{R}$, then

$1.[{\kappa }^{\prime -}(\mathbb{Q}),{\kappa }^{\prime +}(\mathbb{Q})]\le [{\kappa }^{\prime -}(\mathbb{R}),{\kappa }^{\prime +}(\mathbb{R})]\mathrm{a}\mathrm{n}\mathrm{d}{\kappa }^{\prime \mathbb{F}}(\mathbb{Q})\le {\kappa }^{\prime \mathbb{F}}(\mathbb{R})$

Proof. Let S be any partial cubic fuzzy edge cut in Q. If Q−S becomes disconnected, then clearly R−S will also become disconnected. Thus, in this case, each partial cubic fuzzy edge cut of Q is also a partial cubic fuzzy edge cut of R with ${\mathbb{S}}_Q^{\prime \infty }(S)\le {\mathbb{S}}_R^{\prime \infty }(S)$. Now, we assume that there exists a pair of vertices a and b in Q such that

$\begin{array}{c}\hfill \left[{\mathbb{CONN}}_{\mathbb{Q}}^{-}\left(a,b\right),{\mathbb{CONN}}_{\mathbb{Q}}^{+}\left(t,v\right)\right]>\left[{\mathbb{CONN}}_{\mathbb{Q}-S}^{-}\left(a,b\right),{\mathbb{CONN}}_{\mathbb{Q}-S}^{+}\left(a,b\right)\right]\text{and}\\ \hfill {\mathbb{CONN}}_{\mathbb{R}}^{\mathbb{F}}\left(a,b\right)\ge {\mathbb{CONN}}_{\mathbb{Q}-E}^{\mathbb{F}}\left(a,b\right),\end{array}(10)$

$\begin{array}{c}\hfill \left[{\mathbb{CONN}}_{\mathbb{R}}^{-}\left(a,b\right),{\mathbb{CONN}}_{\mathbb{Q}}^{+}\left(a,b\right)\right]\ge \left[{\mathbb{CONN}}_{\mathbb{Q}-S}^{-}\left(a,b\right),{\mathbb{CONN}}_{\mathbb{Q}-S}^{+}\left(a,b\right)\right]\text{and}\\ \hfill {\mathbb{CONN}}_{\mathbb{Q}}^{\mathbb{F}}\left(a,b\right)>{\mathbb{CONN}}_{\mathbb{Q}-S}^{\mathbb{F}}\left(a,b\right).\end{array}(11)$

If the pair a, b or any other pair satisfied Eq. (10) and Eq. (11) in R, then again ${\mathbb{S}}_Q^{\prime \infty }(S)\le {\mathbb{S}}_R^{\prime \infty }(S)$. Thus, we may consider the case when the removal of any partial cubic fuzzy edge cut in Q does not affect the connectivity (IVF-connectivity or F-connectivity) of any pair of vertices in Q. Clearly, in this case, the strong weight of any partial cubic fuzzy edge cut in R is greater than the strong weight of any partial cubic fuzzy edge cut in Q.

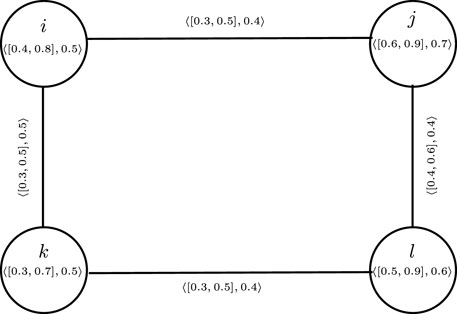
Example 3.16. consider a CFG $\mathbb{R}=(V,B)$ given in Figure 4 with

$\begin{array}{ccc}\hfill V& =\hfill & \left(\frac{i}{\langle \left[0.6,0.8\right],0.6\rangle },\frac{j}{\langle \left[0.5,0.9\right],0.7\rangle },\frac{k}{\langle \left[0.4,0.6\right],0.5\rangle },\frac{l}{\langle \left[0.2,0.7\right],0.6\rangle }\right),\hfill \\ \hfill B& =\hfill & \left(\frac{ij}{\langle \left[0.5,0.7\right],0.5\rangle },\frac{ik}{\langle \left[0.3,0.6\right],0.5\rangle },\frac{kl}{\langle \left[0.1,0.5\right],0.5\rangle },\frac{jl}{\langle \left[0.2,0.6\right],0.5\rangle }\right).\hfill \end{array}$

E = {ij} is a 1-PCFEC because for the pair kl,

$\begin{array}{ccc}\hfill \langle \left[{\mathbb{CONN}}_{\mathbb{R}}^{-}\left(kl\right),{\mathbb{CONN}}_{\mathbb{R}}^{+}\left(kl\right)\right],{\mathbb{CONN}}_{\mathbb{R}}^{\mathbb{F}}\left(kl\right)\rangle & =\hfill & \hfill \langle \left[0.2,0.6\right],0.5\rangle ,\\ \hfill \langle \left[{\mathbb{CONN}}_{\mathbb{R}-E}^{-}\left(kl\right),{\mathbb{CONN}}_{\mathbb{R}-E}^{+}\left(kl\right)\right],{\mathbb{CONN}}_{\mathbb{R}-E}^{\mathbb{F}}\left(kl\right)\rangle & =\hfill & \hfill \langle \left[0.1,0.5\right],0.5\rangle .\end{array}(14)$

From Equation 14, $\mathbb{R}-E$ satisfies the following condition: $[{\mathbb{CONN}}_{\mathbb{R}-E}^{-}(kl),{\mathbb{CONN}}_{\mathbb{R}-E}^{+}(kl)]<[{\mathbb{CONN}}_{\mathbb{R}}^{-}(kl),{\mathbb{CONN}}_{\mathbb{R}}^{+}(kl)]$ and ${\mathbb{CONN}}_{\mathbb{\{R\}}-E}^{\mathbb{F}}(kl)={\mathbb{CONN}}_{\mathbb{R}}^{\mathbb{F}}(kl)$ with weight ${\mathbb{S}}^{\prime \infty }(E)=⟨[0.5,0.7],0.5⟩$. Similarly, E = {jl} is a 1-PCFEC because for the pair kl,

$\begin{array}{ccc}\hfill \langle \left[{\mathbb{CONN}}_{\mathbb{R}}^{-}\left(kl\right),{\mathbb{CONN}}_{\mathbb{R}}^{+}\left(kl\right)\right],{\mathbb{CONN}}_{\mathbb{R}}^{\mathbb{F}}\left(kl\right)\rangle & =\hfill & \hfill \langle \left[0.2,0.6\right],0.5\rangle ,\\ \hfill \langle \left[{\mathbb{CONN}}_{\mathbb{R}-E}^{-}\left(kl\right),{\mathbb{CONN}}_{\mathbb{R}-E}^{+}\left(kl\right)\right],{\mathbb{CONN}}_{\mathbb{R}-E}^{\mathbb{F}}\left(kl\right)\rangle & =\hfill & \hfill \langle \left[0.1,0.5\right],0.5\rangle .\end{array}(15)$

From Equation 15, $\mathbb{R}-E$ satisfies $[{\mathbb{CONN}}_{\mathbb{R}-E}^{-}(kl),{\mathbb{CONN}}_{\mathbb{R}-E}^{+}(kl)]<[{\mathbb{CONN}}_{\mathbb{R}}^{-}(kl),{\mathbb{CONN}}_{\mathbb{R}}^{+}(kl)]$ and ${\mathbb{CONN}}_{\mathbb{R}-E}^{\mathbb{F}}(kl)={\mathbb{CONN}}_{\mathbb{R}}^{\mathbb{F}}(kl)$ with weight ${\mathbb{S}}^{\prime \infty }(E)=⟨[0.2,0.6],0.5⟩$. Now, E = {ik} is also a 1-PCFEC because for the pair kl,

$\begin{array}{ccc}\hfill \langle \left[{\mathbb{CONN}}_{\mathbb{R}}^{-}\left(kl\right),{\mathbb{CONN}}_{\mathbb{R}}^{+}\left(kl\right)\right],{\mathbb{CONN}}_{\mathbb{R}}^{\mathbb{F}}\left(kl\right)\rangle & =\hfill & \hfill \langle \left[0.2,0.6\right],0.5\rangle ,\\ \hfill \langle \left[{\mathbb{CONN}}_{\mathbb{R}-E}^{-}\left(kl\right),CON{N}_{\mathbb{R}-E}^{+}\left(kl\right)\right],{\mathbb{CONN}}_{\mathbb{R}-E}^{\mathbb{F}}\left(kl\right)\rangle & =\hfill & \hfill \langle \left[0.1,0.5\right],0.5\rangle .\end{array}(16)$

From Equation 16, $\mathbb{R}-E$ satisfies $[CON{N}_{\mathbb{R}-E}^{-}(kl),{\mathbb{CONN}}_{\mathbb{R}-E}^{+}(kl)]<[CON{N}_{\mathbb{R}}^{-}(kl),{\mathbb{CONN}}_{\mathbb{R}}^{+}(kl)]$ and ${\mathbb{CONN}}_{\mathbb{R}-E}^{\mathbb{F}}(kl)={\mathbb{CONN}}_{\mathbb{R}}^{\mathbb{F}}(kl)$ with weight ${\mathbb{S}}^{\prime \infty }(E)=⟨[0.3,0.6],0.5⟩$. Thus,

${\kappa }^{\prime \infty }\left(\mathbb{R}\right)=⟨\left[0.2,0.6\right],0.5⟩.(17)$

Now, we consider $\mathbb{S}=(D,C)$, a CF subgraph of $\mathbb{R}$, given in Figure 5 with

$\begin{array}{ccc}\hfill D& =\hfill & \left(\frac{i}{⟨\left[0.6,0.8\right],0.6⟩},\frac{j}{⟨\left[0.5,0.9\right],0.7⟩}\right),\hfill \\ \hfill C& =\hfill & \left(\frac{ij}{⟨\left[0.5,0.7\right],0.5⟩}\right).\hfill \end{array}$

E = {ij} is a unique 1-PCFEC because $\mathbb{R}-E$ is disconnected. Its weight is ${\mathbb{S}}^{\prime \infty }(E)=⟨[0.5,7],0.5⟩$. Thus,

${\kappa }^{\prime \infty }\left(\mathbb{S}\right)=⟨\left[0.5,0.7\right],0.5⟩.(18)$

From Equations 17 and 18, it can be seen that Theorem 3.15 does not generally hold for every partial cubic fuzzy subgraph.

Figure 4

Figure 4. $\mathbb{R}=(V,B)$.

Figure 5

Figure 5. $\mathbb{S}=(D,C)$.

Theorem 3.17. consider a cubic fuzzy cycle $\mathbb{R}=(\sigma ,\mu )$ with |σ*|≥ 3. If $\mathbb{R}$ is β-saturated, then

${\kappa }^{\prime \infty }\left(\mathbb{R}\right)=2⟨\left[{\mu }^{-}\left(tv\right),{\mu }^{+}\left(tv\right)\right],{\mu }^{\mathbb{F}}\left(tv\right)⟩,$

where tv is the β-strong edge of $\mathbb{R}$.

Proof. Suppose $\mathbb{R}=(\sigma ,\mu )$ represents a cubic fuzzy cycle that is β-saturated, where |σ*|≥ 3 and no vertex is incident with more than two edges. In such a scenario, it can be concluded that each vertex of the cubic fuzzy cycle is connected to at least one edge that is β-strong. We consider $\mathbb{R}\backslash \{s_1{s}_2\}$. If s₁s₂ is a β-strong edge, then it does not have any impact on the connectivity among any pair of vertices in $\mathbb{R}$. Thus, we may suppose that s₁s₂ is not beta-strong. Since $\mathbb{R}$ is a β-saturated cycle, it is adjacent to a unique beta-strong edge, say s₂s₃. This implies that

$\begin{array}{ccc}\hfill & \hfill & <\left[{\mathbb{CONN}}_{\mathbb{R}\backslash s_2{s}_3}^{-}\left(s_2,s_3\right),{\mathbb{CONN}}_{\mathbb{R}\backslash s_2{s}_3}^{-}\left(s_2,s_3\right)\right],{\mathbb{CONN}}_{\mathbb{R}\backslash s_2{s}_3}^{\mathbb{F}}\left(s_2,s_3\right)>\hfill \\ \hfill & =\hfill & <\left[{\mu }^{-}\left(s_2{s}_3\right),{\mu }^{+}\left(s_2{s}_3\right)\right],{\mu }^F\left(s_2{s}_3\right)>.\hfill \end{array}$

Since $\mathbb{R}$ is a cycle, s₁s₂ lies on the unique path between s₂ and s₃ in $\mathbb{R}\backslash s_2{s}_3$; therefore,

$\begin{array}{ccc}\hfill & \hfill & <\left[{\mathbb{CONN}}_{\mathbb{R}\backslash s_2{s}_3}^{-}\left(s_2,s_3\right),{\mathbb{CONN}}_{\mathbb{R}\backslash s_2{s}_3}^{-}\left(s_2,s_3\right)\right],{\mathbb{CONN}}_{\mathbb{R}\backslash s_2{s}_3}^{\mathbb{F}}\left(s_2,s_3\right)>\hfill \\ \hfill & \le \hfill & <\left[{\mu }^{-}\left(s_1{s}_2\right),{\mu }^{+}\left(s_1{s}_2\right)\right],{\mu }^F\left(s_1{s}_2\right)>.\hfill \end{array}$

This implies that

$<\left[{\mu }^{-}\left(s_2{s}_3\right),{\mu }^{+}\left(s_2{s}_3\right)\right],{\mu }^F\left(s_2{s}_3\right)>\le \left[{\mu }^{-}\left(s_1{s}_2\right),{\mu }^{+}\left(s_1{s}_2\right)\right],{\mu }^F\left(s_1{s}_2\right)>.$

This shows that s₁s₂ is either IVF α-strong or F α-strong. This, along with the fact that $\mathbb{R}$ does not contain any partial δ-weak edges, further implies that any edge other than beta-strong is either IVF α-strong or F α-strong in a cubic fuzzy cycle $\mathbb{R}$. When removing an IVF α-strong edge from the cubic fuzzy cycle $\mathbb{R}$, it affects only the IVF-connectivity of its end vertices, while the F-connectivity remains unchanged. Similarly, removing an F α-strong edge affects only the F-connectivity of its end vertices, while the IVF-connectivity remains unchanged.

Thus, removing a single edge within $\mathbb{R}$ does not disrupt the edge connectivity between any pair of vertices other than the end vertices of that edge. Therefore, ${\kappa }^{\prime \infty }(\mathbb{R})\ge 2$. However, removing any two edges from $\mathbb{R}$ will result in the graph becoming disconnected. Now, as $\mathbb{R}$ is β-saturated with |σ*| > 2, it contains at least two β-strong edges. The set of these two beta-strong edges with the same membership is required for a partial cubic fuzzy cut set.

${\kappa }^{\prime \infty }\left(\mathbb{R}\right)=2⟨\left[{\mu }^{-}\left(tv\right),{\mu }^{+}\left(tv\right)\right],{\mu }^{\mathbb{F}}\left(tv\right)⟩.$

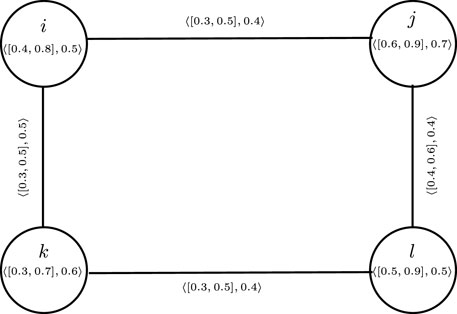
Example 3.18. consider a CFG $\mathbb{R}=(D,F)$ given in Figure 6 with

$\begin{array}{ccc}\hfill D& =\hfill & \left(\frac{i}{\langle \left[0.4,0.8\right],0.5\rangle },\frac{j}{\langle \left[0.6,0.9\right],0.7\rangle },\frac{k}{\langle \left[0.3,0.7\right],0.6\rangle },\frac{l}{\langle \left[0.5,0.9\right],0.5\rangle }\right),\hfill \\ \hfill F& =\hfill & \left(\frac{ij}{\langle \left[0.3,0.5\right],0.4\rangle },\frac{ik}{\langle \left[0.3,0.5\right],0.5\rangle },\frac{kl}{\langle \left[0.3,0.5\right],0.4\rangle },\frac{jl}{\langle \left[0.4,0.6\right],0.4\rangle }\right).\hfill \end{array}$

Thus, from Table 3, we have

${\kappa }^{\prime \infty }\left(\mathbb{R}\right)=⟨\left[0.6,1\right],0.8⟩.(19)$

ij and kl are both the same weakest edge in a given graph $\mathbb{R}=(D,F)$, and they also satisfy the condition of Theorem 3.17 because from Equation 19, we have

${\kappa }^{\prime \infty }\left(\mathbb{R}\right)=2⟨\left[{\mu }^{-}\left(ij\right),{\mu }^{+}\left(ij\right)\right],{\mu }^{\mathbb{F}}\left(ij\right)⟩.$

Figure 6

Figure 6. $\mathbb{R}=(D,F)$.

Table 3

Table 3. PCFEC of $\mathbb{R}=(D,F)$.

Theorem 3.19. consider $\mathbb{R}=(\sigma ,\mu )$ as an even partial saturated cubic fuzzy cycle, where |σ*| > 3. Then,

${\kappa }^{\prime \infty }\left(\mathbb{R}\right)=2⟨\left[{\mu }^{-}\left(bc\right),{\mu }^{+}\left(bc\right)\right],{\mu }^{\mathbb{F}}\left(bc\right)⟩,$

where bc is the β-strong edge in $\mathbb{R}$.

Proof. We consider $\mathbb{R}=(\sigma ,\mu )$ as an even partial saturated cubic fuzzy cycle with |σ*| > 3. In such a case, it can be stated that each vertex within $\mathbb{R}$ is adjacent to at least one β-strong edge as well as at least one partial α-strong edge. When removing an IVF α-strong edge from the cubic fuzzy cycle $\mathbb{R}$, it affects only the IVF-connectivity of its end vertices, while the F-connectivity remains unchanged. Similarly, removing an F α-strong edge affects only the F-connectivity of its end vertices, while the IVF-connectivity remains unchanged. On the other hand, if a β-strong edge is removed from $\mathbb{R}$, it does not have any impact on the connectivity among any pair of vertices in $\mathbb{R}$. Therefore, removing a single edge within $\mathbb{R}$ does not disrupt the edge connectivity between any pair of vertices. However, any collection of two edges in $\mathbb{R}$ will form a minimal PCFEC. Among all possible PCFECs, the one with the minimum weights forms a minimum PCFEC. Hence,

${\kappa }^{\prime \infty }\left(\mathbb{R}\right)=2⟨\left[{\mu }^{-}\left(bc\right),{\mu }^{+}\left(bc\right)\right],{\mu }^{\mathbb{F}}\left(bc\right)⟩.$

Example 3.20. consider a CFG $\mathbb{R}=(Z,Y)$ given in Figure 7 with

$\begin{array}{ccc}\hfill Z& =\hfill & \left(\frac{i}{\langle \left[0.5,0.7\right],0.6\rangle },\frac{j}{\langle \left[0.4,0.8\right],0.4\rangle },\frac{k}{\langle \left[0.3,0.5\right],0.5\rangle },\frac{l}{\langle \left[0.2,0.6\right],0.5\rangle }\right),\hfill \\ \hfill Y& =\hfill & \left(\frac{ij}{\langle \left[0.4,0.6\right],0.4\rangle },\frac{ik}{\langle \left[0.2,0.5\right],0.4\rangle },\frac{kl}{\langle \left[0.2,0.5\right],0.5\rangle },\frac{jl}{\langle \left[0.2,0.5\right],0.4\rangle }\right).\hfill \end{array}$

Thus, from Table 4, we have

${\kappa }^{\prime \infty }\left(\mathbb{R}\right)=⟨\left[0.4,1\right],0.8⟩.(20)$

ik and jl are both strong edges with the same minimum cubic membership in a given graph $\mathbb{R}=(Z,Y)$, and they also satisfy the condition of Theorem 3.19 because from Equation 20, we have

${\kappa }^{\prime \infty }\left(\mathbb{R}\right)=2⟨\left[{\mu }^{-}\left(ij\right),{\mu }^{+}\left(ij\right)\right],{\mu }^{\mathbb{F}}\left(ij\right)⟩.$

Figure 7

Figure 7. $\mathbb{R}=(Z,Y)$.

Table 4

Table 4. PCFEC of $\mathbb{R}=(D,F)$.

4 Generalized cubic fuzzy vertex and edge connectivity

The concepts of cubic fuzzy cut node and cubic fuzzy edge cut are generalized in this section. It is evident that not only strong edges but also non-strong edges play a significant role in maintaining the connectivity of cubic fuzzy graphs. Additionally, the requirement that both t and v should differ from the endpoints of edges in E renders a cubic fuzzy edge cut invalid, as it extends beyond the conventional set of edges. Consequently, the definitions of cubic fuzzy vertex connectivity and cubic edge connectivity have been revised, as indicated in Definition 4.1 and Definition 4.4, respectively.

Definition 4.1. Let X be a partial cubic fuzzy cut node in $\mathbb{R}$. The generalized strong weight of X denoted as ${\mathbb{W}}_f^{\infty }(X)$ is defined as

${\mathbb{W}}_f^{\infty }\left(X\right)=⟨\left[{\displaystyle \sum _{t\in X}}{\mu }^{-}\left(t,z\right),{\displaystyle \sum _{t\in X}}{\mu }^{+}\left(t,z\right)\right],{\displaystyle \sum _{t\in X}}{\mu }^{\mathbb{F}}\left(t,z\right)⟩,$

where μ⁻(t, z), μ⁺(t, z) and ${\mu }^{\mathbb{F}}(t,z)$ is the minimum weight of edges incident at t. Then, the generalized cubic fuzzy vertex connectivity of $\mathbb{R}$ denoted by ${\kappa }_f^{\infty }(\mathbb{R})$ and ${\kappa }_f^{\infty }(\mathbb{R})=⟨[{\kappa }_f^{-}(\mathbb{R}),{\kappa }_f^{+}(\mathbb{R})],{\kappa }_f^{\mathbb{F}}(\mathbb{R})⟩$ is defined as

${\kappa }_f^{\infty }\left(\mathbb{R}\right){=\wedge }_X\left({\mathbb{W}}_f^{\infty }\left(X\right)\right).$

Definition 4.2. Let $\mathbb{R}=(\sigma ,\mu )$ be a CFG. A set of edges E = {e₁, e₂, … , e_n} with e_i = b_ic_i i = 1, 2, … , n is said to be a generalized partial cubic fuzzy edge cut (GPCFEC) if either $\mathbb{R}-E$ is disconnected or one of the following holds for some pair of vertices t, v ∈ σ*:

$\begin{array}{c}\hfill \left[{\mathbb{CONN}}_{\mathbb{R}}^{-}\left(t,v\right),{\mathbb{CONN}}_{\mathbb{R}}^{+}\left(t,v\right)\right]>\left[{\mathbb{CONN}}_{R-E}^{-}\left(t,v\right),{\mathbb{CONN}}_{\mathbb{R}-E}^{+}\left(t,v\right)\right]\text{and}\\ \hfill {\mathbb{CONN}}_{\mathbb{R}}^{\mathbb{F}}\left(t,v\right)\ge {\mathbb{CONN}}_{\mathbb{R}-E}^{\mathbb{F}}\left(t,v\right),\end{array}(21)$

$\begin{array}{c}\hfill \left[{\mathbb{CONN}}_{\mathbb{R}}^{-}\left(t,v\right),{\mathbb{CONN}}_{\mathbb{R}}^{+}\left(t,v\right)\right]\ge \left[{\mathbb{CONN}}_{\mathbb{R}-E}^{-}\left(t,v\right),{\mathbb{CONN}}_{\mathbb{R}-E}^{+}\left(t,v\right)\right]\text{and}\\ \hfill {\mathbb{CONN}}_{\mathbb{R}}^{\mathbb{F}}\left(t,v\right)>{\mathbb{CONN}}_{\mathbb{R}-E}^{\mathbb{F}}\left(t,v\right).\end{array}(22)$

If Eq. (21) holds, then a set of edges is referred to as an IVF edge cut, whereas if Eq. (22) is satisfied, then it is referred to as an F edge cut. If both Eq. (21) and Eq. (22) are satisfied for the same pair of vertices, then it is referred to as a strict generalized cubic fuzzy edge cut (GCFEC). If there are n edges in E, then E is called an n-GPCFEC.

Definition 4.3. Let E be a generalized partial cubic fuzzy edge cut in $\mathbb{R}$. The strong weight of E denoted as ${\mathbb{W}}_f^{\prime \infty }(E)$ is defined as

${\mathbb{W}}_f^{\prime \infty }\left(E\right)=⟨\left[{\displaystyle \sum _{e_i\in E}}{\mu }^{-}\left(e_i\right),{\displaystyle \sum _{e_i\in E}}{\mu }^{+}\left(e_i\right)\right],{\displaystyle \sum _{e_i\in E}}{\mu }^{\mathbb{F}}\left(e_i\right)⟩.$

Definition 4.4. The generalized cubic fuzzy edge connectivity of $\mathbb{R}$ denoted by ${\kappa }_f^{\prime \infty }(\mathbb{R})$ and ${\kappa }_f^{\prime \infty }(\mathbb{R})=⟨[{\kappa }_f^{\prime -}(\mathbb{R}),{\kappa }_f^{\prime +}(\mathbb{R})],{\kappa }_f^{\prime \mathbb{F}}(\mathbb{R})⟩$ is defined as

${\kappa }_f^{\prime \infty }\left(\mathbb{R}\right){=\wedge }_X\left({\mathbb{W}}_f^{\prime \infty }\left(E\right)\right).$

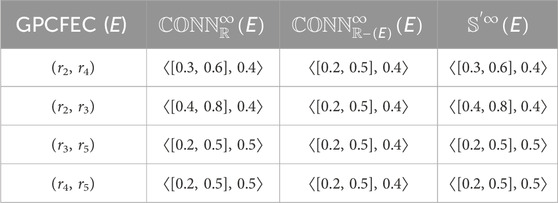
Example 4.5. consider a CFG $\mathbb{R}=(D,F)$ given in Figure 8 with

$\begin{array}{ccc}\hfill D& =\hfill & \left(\frac{i}{\langle \left[0.4,0.8\right],0.5\rangle },\frac{j}{\langle \left[0.6,0.9\right],0.7\rangle },\frac{k}{\langle \left[0.3,0.7\right],0.5\rangle },\frac{l}{\langle \left[0.5,0.9\right],0.6\rangle }\right),\hfill \\ \hfill F& =\hfill & \left(\frac{ij}{\langle \left[0.3,0.5\right],0.4\rangle },\frac{ik}{\langle \left[0.3,0.5\right],0.5\rangle },\frac{kl}{\langle \left[0.3,0.5\right],0.4\rangle },\frac{jl}{\langle \left[0.4,0.6\right],0.4\rangle }\right).\hfill \end{array}$

Thus, from Table 5, the cubic fuzzy edge connectivity is given in Eq. (23)

${\kappa }^{\prime \infty }\left(\mathbb{R}\right)=⟨\left[0.6,1\right],0.8⟩.(23)$

Thus, from Table 6, the generalized cubic fuzzy edge connectivity is given in Eq. (24)

${\kappa }_f^{\prime \infty }\left(\mathbb{R}\right)=⟨\left[0.3,0.5\right],0.4⟩.(24)$

Figure 8

Figure 8. $\mathbb{R}=(D,F)$.

Table 5

Table 5. PCFEC of $\mathbb{R}=(D,F)$.

Table 6

Table 6. PCFEC of $\mathbb{R}=(D,F)$.

Definition 4.6. A connected CFG $\mathbb{R}=(\sigma ,\mu )$ is a cubic fuzzy tree if $\mathbb{R}$ has a cubic spanning fuzzy subgraph $\mathbb{Q}=(\sigma ,\nu )$, which is a tree such that for $tv\in \mathbb{R}$ but $tv\notin \mathbb{Q}$, one of the following holds:

1. $[{\mu }^{-}(tv),{\mu }^{+}(tv)]<[{\mathbb{CONN}}_{\mathbb{Q}}^{-}(t,v),{\mathbb{CONN}}_{\mathbb{Q}}^{+}(t,v)]$ and ${\mu }^{\mathbb{F}}(tv)\le {\mathbb{CONN}}_{\mathbb{Q}}^{\mathbb{F}}(t,v)$

2. $[{\mu }^{-}(tv),{\mu }^{+}(tv)]\le [{\mathbb{CONN}}_{\mathbb{Q}}^{-}(t,v),{\mathbb{CONN}}_{\mathbb{Q}}^{+}(t,v)]$ and ${\mu }^{\mathbb{F}}(tv)<{\mathbb{CONN}}_{\mathbb{Q}}^{\mathbb{F}}(t,v)$

Theorem 4.7. For a cubic fuzzy tree $\mathbb{R}=(\sigma ,\mu )$,

${\kappa }_f^{\prime \infty }\left(\mathbb{R}\right)=\wedge \left\{⟨\left[{\mu }^{+}\left(b,c\right),{\mu }^{-}\left(b,c\right)\right],{\mu }^{\mathbb{F}}\left(b,c\right)⟩\right\},(25)$

where bc in Eq. (25) is a strong edge (partial α-strong or β-strong edge) in $\mathbb{R}$.

Proof. We consider a cubic fuzzy tree $\mathbb{R}=(\sigma ,\mu )$. Then, $\mathbb{R}$ contains a cycle denoted as C. Within this cycle, there exists an edge xy, which can be identified as the weakest edge and is categorized as a partial δ-weak edge. All other edges (e₁, e₂, … , e_n) where e_i = b_ic_i for i = 1, 2, … , n in C are considered strong. Thus, removing any edge from C, except for xy, satisfies one of the following conditions:

1. $[{\mathbb{CONN}}_{\mathbb{R}-e_i}^{-}(x,y),{\mathbb{CONN}}_{\mathbb{R}-e_i}^{+}(x,y)]<[{\mathbb{CONN}}_{\mathbb{R}}^{-}(x,y),{\mathbb{CONN}}_{\mathbb{R}}^{+}(x,y)]$ and ${\mathbb{CONN}}_{\mathbb{R}-e_i}^{\mathbb{F}}(x,y)\le {\mathbb{CONN}}_{\mathbb{R}}^{\mathbb{F}}(x,y)$

2. $[{\mathbb{CONN}}_{\mathbb{R}-e_i}^{-}(x,y),{\mathbb{CONN}}_{\mathbb{R}-e_i}^{+}(x,y)]\le [{\mathbb{CONN}}_{\mathbb{R}}^{-}(x,y),{\mathbb{CONN}}_{\mathbb{R}}^{+}(x,y)]$ and ${\mathbb{CONN}}_{\mathbb{R}-e_i}^{\mathbb{F}}(x,y)<{\mathbb{CONN}}_{\mathbb{R}}^{\mathbb{F}}(x,y)$

A non-cyclic edge in $\mathbb{R}$, which is not a part of any cycle in $\mathbb{R}$, is referred to as a bridge and is considered a GPCFEC. Consequently, we can deduce that ${\kappa }_f^{\prime \infty }(\mathbb{R})$ is equivalent to the minimum membership value among the strong edges present in $\mathbb{R}$.

Example 4.8. consider a cubic fuzzy tree $\mathbb{R}=(L,Q)$ given in Figure 9 with

$\begin{array}{c}L=\left(\frac{m}{\langle \left[0.1,0.6\right],0.6\rangle },\frac{n}{\langle \left[0.4,0.6\right],0.5\rangle },\frac{o}{\langle \left[0.3,0.7\right],0.4\rangle },\frac{p}{\langle \left[0.5,0.7\right],0.6\rangle },\frac{q}{\langle \left[0.3,0.8\right],0.5\rangle }\right),\hfill \\ Q=\left(\frac{mn}{\langle \left[0.1,0.5\right],0.4\rangle },\frac{no}{\langle \left[0.3,0.4\right],0.3\rangle },\frac{np}{\langle \left[0.4,0.5\right],0.4\rangle },\frac{op}{\langle \left[0.1,0.3\right],0.3\rangle },\frac{pq}{\langle \left[0.3,0.4\right],0.3\rangle }\right).\hfill \end{array}$

Thus, from Table 7, the generalized cubic fuzzy edge connectivity is given in Eq. (26)

${\kappa }_f^{\prime \infty }\left(\mathbb{R}\right)=⟨\left[0.1,0.4\right],0.3⟩.(26)$

Figure 9

Figure 9. $\mathbb{R}=(L,Q)$.

Table 7

Table 7. GPCFEC of $\mathbb{R}=(L,Q)$.

Theorem 4.9. Let $\mathbb{R}=(\sigma ,\mu )$ be a cubic fuzzy cycle. Then,

${\kappa }_f^{\prime \infty }\left(\mathbb{R}\right)=\wedge \left\{m,2⟨\left[{\mu }^{+}\left(b,c\right),{\mu }^{-}\left(b,c\right)\right],{\mu }^{\mathbb{F}}\left(b,c\right)⟩\right\},(27)$

where bc in Eq. (27) is a β-strong edge in $\mathbb{R}$ and m is the minimum membership value of partial α-strong edges in $\mathbb{R}$.

Proof. We consider $\mathbb{R}=(\sigma ,\mu )$ as a cubic fuzzy cycle. In this case, every edge within $\mathbb{R}$ is categorized as strong, which means it is either partially α-strong or β-strong. It is clear that a set containing a single partial α-strong or two β-strong edges forms the GPCFEC. Let m denote the minimum membership value among the partial α-strong edges in $\mathbb{R}$, and let bc be an edge that has the lowest values of μ⁺, μ⁻, and ${\mu }^{\mathbb{F}}$. It should be noted that any β-strong edge within $\mathbb{R}$ will possess a membership value denoted by $⟨[{\mu }^{+}(b,c),{\mu }^{-}(b,c)],{\mu }^{\mathbb{F}}(b,c)⟩$. Moreover, if a GPCFEC consists of two β-strong edges, its strength will be equal to $2⟨[{\mu }^{+}(b,c),{\mu }^{-}(b,c)],{\mu }^{\mathbb{F}}(b,c)⟩$. Then, the generalized cubic fuzzy edge connectivity is given in Eq. (28)

${\kappa }_f^{\prime \infty }\left(\mathbb{R}\right)=\wedge \left\{m,2⟨\left[{\mu }^{+}\left(b,c\right),{\mu }^{-}\left(b,c\right)\right],{\mu }^{\mathbb{F}}\left(b,c\right)⟩\right\}.(28)$

Theorem 4.10. Let $\mathbb{R}=(\sigma ,\mu )$ be a β-saturated cubic fuzzy cycle. Then, ${\kappa }_f^{\prime \infty }(\mathbb{R}-b)={\kappa }_f^{\prime \infty }(\mathbb{R}-bc)=k\forall b\in {\sigma }^{*}$, bc ∈ μ*, where k is the membership value of the β-strong edge in $\mathbb{R}$.

Proof. We consider $\mathbb{R}=(\sigma ,\mu )$ as a β-saturated cubic fuzzy cycle. In this case, it can be concluded that every vertex in $\mathbb{R}$ is adjacent to at least one β-strong edge. It is evident that removing a vertex from $\mathbb{R}$ leads to the formation of a tree. Since $\mathbb{R}$ is β-saturated, the graph $\mathbb{R}-b$ obtained by removing a vertex b must have at least one edge denoted as bc. This edge bc satisfies the condition $⟨[{\mu }^{-}(bc),{\mu }^{+}(bc)],{\mu }^{\mathbb{F}}(bc)⟩=k$, where k represents the minimum membership value among the weakest strong edges (partial α-strong or β-strong) present in $\mathbb{R}$. In the graphs $\mathbb{R}-b$ or $\mathbb{R}-bc$, every edge becomes a bridge and, consequently, a GPCFEC. Therefore, it can be concluded that ${\kappa }_f^{\prime \infty }(\mathbb{R}-b)$ or ${\kappa }_f^{\prime \infty }(\mathbb{R}-bc)$ is equal to the minimum membership value among the strong edges (partial α-strong or β-strong) present in $\mathbb{R}$. Hence, the generalized cubic fuzzy edge connectivity after removal of edge bc is given in Eq. (29)

${\kappa }_f^{\prime \infty }\left(\mathbb{R}-b\right)={\kappa }_f^{\prime \infty }\left(\mathbb{R}-bc\right)=k.(29)$

5 Application

Street crimes stem from various underlying causes, including socioeconomic disparities, unemployment, drug addiction, and inadequate law enforcement. These crimes, such as mugging, theft, and drug dealing, create an environment of insecurity and instability, which hampers trade relations between different regions. The occurrence of street crimes can lead to decreased investment, hinder economic growth, and result in a trade deficit between regions. Business operating in areas with high crime rates may experience decreased sales and increased costs due to theft, property damage, and heightened security measures. This can result in a decline in exports and an increase in imports, further widening the trade deficit. To improve trade flow, it is crucial to address the root causes of street crimes. This can be achieved through socioeconomic development initiatives, job creation, rehabilitation programs for offenders, and strengthening law enforcement. Furthermore, fostering community engagement, enhancing public safety measures, and promoting awareness campaigns can help to create a secure environment that encourages trade and fosters economic cooperation between regions.

5.1 Trade deficit model

This article presents the development of an application that specifically addresses the trade deficit resulting from street crimes. It explores the factors contributing to trade congestion and delves into the causes of street crimes. Furthermore, it proposes several strategies to prevent crimes and enhance trade flow. To achieve this, this study identifies regions that are particularly susceptible to trade congestion. Here, we analyze the impact of street crimes on these specific regions by using the GPCFEC. By using the CFG methodology, a trade deficit model is constructed to examine the impact of street crimes. The model assigns vertices to different regions, with lower IVF-membership values indicating past trade deficits caused by street crimes and upper IVF-membership values, suggesting the potential for future trade deficits. The F-membership value represents the current trade deficit situation resulting from street crimes. Edges in the model signify potential trade deficit zones, indicating the possibility of trade imbalances between adjacent vertices. The strength of connectedness among various regions can be used to categorize trade deficit zones. These zones can be classified as GPCFEC zones and secure zones. A secure zone indicates an area where the occurrence of a trade deficit due to street crimes is negligible; on the other hand, a GPCFEC zone represents an area where the possibility of a trade deficit resulting from street crimes exists.

A fuzzy graph is a model that visually represents the relationships among elements and their degrees of membership using vertices and edges in a two-dimensional space. However, dealing with ambiguous data using fuzzy graph theory can often be challenging. On the other hand, a CFG is an extension of the FG concept. While the memberships of vertices and edges in fuzzy graphs range from 0 to 1, a CFG holds greater significance as it assigns both lower and upper IVF-membership and F-membership values to its vertices and edges. Each membership value can be any real number within the range of [0,1], making the CFG more versatile and flexible compared to the FG. A CFG proves to be a valuable instrument for handling partial knowledge relationships among regions and effectively managing knowledge loss within a given system. In this regard, an algorithm has been devised specifically for identifying the regions impacted by trade deficits. The algorithm is provided in Table 8.

Table 8

Table 8. Algorithm.

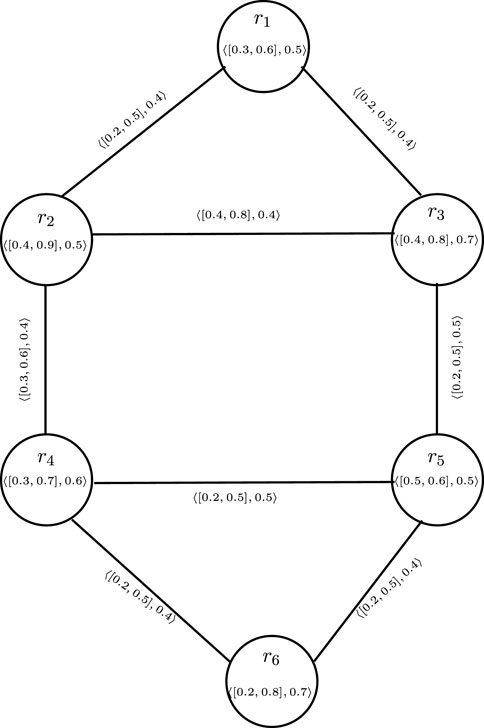
Let us consider the group of regions denoted as Y = (r₁, r₂, r₃, r₄, r₅, r₆), where street crimes occur. These regions can potentially be affected by trade deficits. A CFG denoted as $\mathbb{R}=(M,K)$, depicted in Figure 10, is developed to model the trade deficit scenario. The IVF-membership and F-membership values of the vertices and edges in $\mathbb{R}=(M,K)$ are provided in Table 9 and Table 10, respectively.

Figure 10

Figure 10. $\mathbb{R}=(M,K)$.

Table 9

Table 9. Membership values of each vertex in CFG $\mathbb{R}=(M,K)$.

Table 10

Table 10. Membership values of each edge in CFG $\mathbb{R}=(M,K)$.

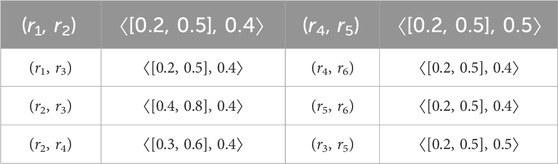
Table 11 provides a list of all possible paths between r₂ and r₄ in the CFG, along with the strengths and strength of connections among them. Specifically, the edge (r₂, r₄) in the CFG is represented as the GPCFEC. It is recommended to explore the nature of other edges among regions as well. Analyzing the characteristics of each edge in the CFG will further highlight the importance and effectiveness of our research. By referring to Figure 10 and using conventional computations, the connectivity between vertices in $\mathbb{R}=(M,K)$ can be determined as in (Table 12).

Table 11

Table 11. All paths from r₂ to r₄ in $\mathbb{R}$.

Table 12

Table 12. Generalized partial cubic fuzzy edge cut of $\mathbb{R}$.

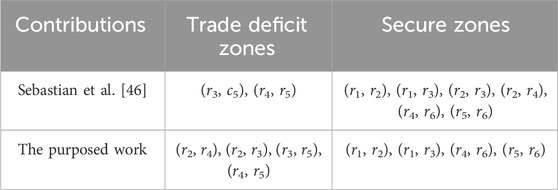
The GPCFEC zones are determined based on specific edge conditions. In this system, the zones (r₂, r₄), (r₂, r₃), (r₃, r₅), and (r₄, r₅) satisfy the criteria for GPCFEC zones, and these zones are characterized by meeting the conditions set for the generalized partial cubic fuzzy edge cut. On the other hand, the remaining edges (r₁, r₂), (r₁, r₃), (r₄, r₆), and (r₅, r₆) do not fulfill the conditions required for GPCFEC zones and are referred to as secure zones within this specific CFG system. The categorization of regions experiencing a trade deficit into various zones can be beneficial in understanding the trade deficit situation in those regions caused by street crimes. In regions classified as the GPCFEC zone, where trade deficits are influenced by street crimes, effective planning is essential. Emergency response planning should be prioritized to ensure swift actions in addressing street crimes and their impact on trade. Additionally, enhancing public safety measures, such as increasing police presence and improving surveillance systems, can contribute to reducing criminal incidents. Promoting awareness among the public about the consequences of street crimes on trade and encouraging citizen engagement in reporting suspicious activities are important measures. In secure zones, where regions have no trade deficits, planning efforts should focus on maintaining favorable conditions and further enhancing trade flow through streamlined customs procedures, trade facilitation measures, and fostering a business-friendly environment. Overall, by planning efforts for each zone, trade regions can effectively address trade deficits caused by street crimes, promoting trade flow, economic growth, and sustainable trade surpluses.

6 Comparative analysis

The generalized partial cubic fuzzy edge cut introduces a novel extension to the existing concept of generalized fuzzy edge cut in the context of trade deficit modeling caused by street crimes. In this comparative analysis, it can be argued that the generalized partial cubic fuzzy edge cut offers certain advantages over the generalized fuzzy edge cut.

From Table 13, it can be seen that when applying the concept of generalized partial cubic fuzzy edge cut to the trade deficit model given in Figure 10, specific zones can be identified with precision. The generalized partial cubic fuzzy edge cut zones, such as (r₂, r₄), (r₂, r₃), (r₃, r₅), and (r₄, r₅), are determined based on the satisfaction of the generalized partial cubic fuzzy edge cut condition by the corresponding edges, and the remaining edges (r₁, r₂), (r₁, r₃), (r₄, r₆), and (r₅, r₆) do not satisfy this condition and are considered secure zones. On the other hand, generalized fuzzy edge cut zones such as (r₃, r₅) and (r₄, r₅) are identified through the generalized fuzzy edge cut condition, and the remaining edges (r₁, r₂), (r₁, r₃), (r₂, r₃), (r₂, r₄), (r₄, r₆), and (r₅, r₆) do not satisfy this condition and are referred to as secure zones. The generalized partial cubic fuzzy edge cut allows for a more comprehensive analysis of trade conditions. In the concept of generalized fuzzy edge cuts, only the F-membership of edges is considered. This concept assesses trade deficit conditions, taking into account either the past, present, or future. However, when discussing generalized partial cubic fuzzy edge cuts, additional factors come into play, including upper IVF-membership, lower IVF-membership, and F-membership for edges. Consequently, when we use the generalized partial cubic fuzzy edge cut concept to solve our model, we consider all these membership values concurrently, encompassing trade deficit conditions for the past, present, and future, and provide insights into trade deficit zones and secure zones. Generalized partial cubic fuzzy edge cuts surpass these limitations by encompassing all three time periods, allowing for a more comprehensive understanding of trade deficit conditions from a comparative point of view; the concept of generalized partial cubic fuzzy edge cuts offers distinct advantages over generalized fuzzy edge cuts in terms of precise zone identification and a comprehensive analysis of trade conditions in past, present, and future scenarios.

Table 13

Table 13. Trade deficit zones and secure zones.

7 Conclusion

The CFG is a vital model that adeptly addresses vagueness and ambiguity in dealing with incomplete information. By incorporating lower and upper memberships, the CFG excels beyond both the fuzzy model and the interval-valued model in terms of compatibility, precision, and flexibility. This model finds extensive applications in various fields, including social circuits, machine intelligence, traffic networks, and decision-making problems. The assessment of connectivity or the strength of connectivity remains a fundamental aspect of network theory, and the CFG provides valuable insights in this regard. This paper introduces the notions of vertex and edge connectivity within cubic fuzzy graphs, accompanied by discussions on partial cubic fuzzy cut nodes and partial cubic fuzzy edge cuts. Several associated results are presented, supported by illustrative examples to facilitate comprehension. Furthermore, this research article delves into the concept of partial cubic α-strong and partial cubic δ-weak edges. An example is also presented to elucidate the rationale behind partial cubic α-strong edges. In situations where we possess information regarding the past, future, and current states of a model or problem, we can depict the past condition as a lower interval-valued fuzzy membership, the future condition as an upper interval-valued fuzzy membership, and the present condition as a fuzzy membership value. Our goal is to examine the problem by deriving lower interval-valued fuzzy connectivity, upper interval-valued fuzzy connectivity, and fuzzy connectivity. Additionally, we aspire to formulate new predictions based on this analytical approach. Moreover, it delves into the introduction of generalized vertex and edge connectivity in cubic fuzzy graphs, along with generalized partial cubic fuzzy cut nodes and generalized partial cubic fuzzy edge cuts. Relevant results pertaining to these concepts are also discussed. Furthermore, this article introduces an application that employs generalized partial cubic fuzzy edge cuts to examine the impacts of trade congestion on different regions and address vagueness and uncertainty in business-related contexts. Throughout this paper, we considered simple connected CFGs. In the realm of future research, a promising avenue for exploration lies in the amalgamation of graph theory with recent advancements in fuzzy set models. This integration could encompass the assimilation of concepts and methodologies from various fuzzy set models, including (i) (2,1)-fuzzy sets, emphasizing their properties, weighted aggregated operators, and applications in multi-criteria decision-making methods; (ii) generalized frame for orthopair fuzzy sets, investigating (m,n)-fuzzy sets and their relevance in multi-criteria decision making; and (iii) SR-fuzzy sets and their potential in weighted aggregated operators for decision making. This interdisciplinary approach holds substantial potential for advancing both graph theory and fuzzy set theory, paving the way for novel solutions to complex problems and the optimization of decision-making processes. Looking forward, this study aims to delve deeper into vertex connectivity and edge connectivity in cubic intuitionistic fuzzy graphs (CIFGs) as an expansion of the research scope.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

YR: formal analysis, funding acquisition, investigation, methodology, resources, and writing–review and editing. RC: conceptualization, formal analysis, funding acquisition, investigation, resources, and writing–review and editing. UA: conceptualization, formal analysis, investigation, methodology, resources, and writing–review and editing. AG: conceptualization, formal analysis, investigation, methodology, writing–original draft, and writing–review and editing.

Funding

The authors declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by the National Natural Science Foundation of China (No. 62172116).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Zadeh LA. Fuzzy sets. Inf Control (1965) 8(3):338–53. doi:10.1016/s0019-9958(65)90241-x

CrossRef Full Text | Google Scholar

2. Rosenfeld A. Fuzzy graphs. fuzzy Sets their Appl Cogn Decis Process (1975) 77–95.

CrossRef Full Text | Google Scholar

3. Yeh RT, Bang SY. Fuzzy relations, fuzzy graphs and their applications to clustering analysis. Fuzzy Sets their Appl Cogn Decis Process (1975) 125–49.

CrossRef Full Text | Google Scholar

4. Akram M, Sarwar M. Novel applications of m-polar fuzzy hypergraphs. J Intell Fuzzy Syst (2017) 32(3):2747–62. doi:10.3233/jifs-16859

CrossRef Full Text | Google Scholar

5. Ahmad U, Batool T. Domination in rough fuzzy digraphs with application. Soft Comput (2023) 27(5):2425–42. doi:10.1007/s00500-022-07795-1

CrossRef Full Text | Google Scholar

6. Ahmad U, Khan NK, Saeid AB. Fuzzy topological indices with application to cybercrime problem. Granular Comput (2023) 8:967–80. doi:10.1007/s41066-023-00365-2

CrossRef Full Text | Google Scholar

7. Ahmad U, Nawaz I. Wiener index of a directed rough fuzzy graph and application to human trafficking. J Intell Fuzzy Syst (2023) 44:1479–95. doi:10.3233/jifs-221627

CrossRef Full Text | Google Scholar

8. Ahmad U, Sabir M. Multicriteria decision making based on the degree and distance based indices of fuzzy graphs. Granular Comput (2022) 8:793–807. doi:10.1007/s41066-022-00354-x

CrossRef Full Text | Google Scholar

9. Kou Z, Kosari S, Akhoundi M. A novel description on vague graph with application in transportation systems. J Math (2021) 2021:1–11. doi:10.1155/2021/4800499

CrossRef Full Text | Google Scholar

10. Shao Z, Kosari S, Shoaib M, Rashmanlou H. Certain concepts of vague graphs with applications to medical diagnosis. Front Phys (2020) 8:357. doi:10.3389/fphy.2020.00357

CrossRef Full Text | Google Scholar

11. Qiang X, Akhoundi M, Kou Z, Liu X, Kosari S. Novel concepts of domination in vague graphs with application in medicine. Math Probl Eng (2021) 2021:1–10. doi:10.1155/2021/6121454

CrossRef Full Text | Google Scholar

12. Shao Z, Kosari S, Rashmanlou H, Shoaib M. New concepts in intuitionistic fuzzy graph with application in water supplier systems. Mathematics (2020) 8:1241. doi:10.3390/math8081241

CrossRef Full Text | Google Scholar

13. Shi X, Kosari S, Talebi AA, Sadati SH, Rashmanlou H. Investigation of the main energies of picture fuzzy graph and its applications. Int J Comput Intelligence Syst (2022) 15(1):31. doi:10.1007/s44196-022-00086-5

CrossRef Full Text | Google Scholar

14. Rao Y, Kosari S, Anitha J, Rajasingh I, Rashmanlou H. Forcing parameters in fully connected cubic networks. Mathematics (2022) 10(8):1263. doi:10.3390/math10081263

CrossRef Full Text | Google Scholar

15. Akram M, Davvaz B. Strong intuitionistic fuzzy graphs. Filomat (2012) 26(1):177–96. doi:10.2298/fil1201177a

CrossRef Full Text | Google Scholar

16. Harary F, Norman RZ. Graph theory as a mathematical model in social science, Ann Arbor: University of Michigan, Institute for Social Research (1953).

Google Scholar

17. Kosari S, Rao Y, Jiang H, Liu X, Wu P, Shao Z. Vague graph Structure with Application in medical diagnosis. Symmetry (2020) 12(10):1582. doi:10.3390/sym12101582

CrossRef Full Text | Google Scholar

18. Mandal S, Pal M. Connectivity index of m-polar fuzzy graph with application (2021). https://www.researchsquare.com/article/rs-737239/v11.

Google Scholar

19. Sebastian A, Mordeson JN, Mathew S. Generalized fuzzy graph connectivity parameters with application to human trafficking. Mathematics (2020) 8(3):424. doi:10.3390/math8030424

CrossRef Full Text | Google Scholar

20. Mathew S, Sunitha MS. Node connectivity and arc connectivity of a fuzzy graph. Inf Sci (2010) 180(4):519–31. doi:10.1016/j.ins.2009.10.006

CrossRef Full Text | Google Scholar

21. Mathew S, Sunitha MS. Cycle connectivity in fuzzy graphs. J Intell Fuzzy Syst (2013) 24(3):549–54. doi:10.3233/ifs-2012-0573

CrossRef Full Text | Google Scholar

22. Banerjee S. An optimal algorithm to find the degrees of connectedness in an undirected edge-weighted graph. Pattern Recognition Lett (1991) 12(7):421–4. doi:10.1016/0167-8655(91)90316-e

CrossRef Full Text | Google Scholar

23. Ali S, Mathew S, Mordeson JN, Rashmanlou H. Vertex connectivity of fuzzy graphs with applications to human trafficking. New Math Nat Comput (2018) 14(03):457–85. doi:10.1142/s1793005718500278

CrossRef Full Text | Google Scholar

24. Ahmad U, Nawaz I. Directed rough fuzzy graph with application to trade networking. Comput Appl Math (2022) 41(8):366. doi:10.1007/s40314-022-02073-0

CrossRef Full Text | Google Scholar

25. Shang Y. Super connectivity of erdos-rényi graphs. Mathematics (2019) 7(3):267. doi:10.3390/math7030267

CrossRef Full Text | Google Scholar

26. Su G, Wang S, Du J, Gao M, Das KC, Shang Y. Sufficient conditions for a graph to Be ℓ-connected, ℓ-deficient, ℓ-Hamiltonian and ℓ−-independent in terms of the forgotten topological index. Mathematics (2022) 10(11):1802. doi:10.3390/math10111802

CrossRef Full Text | Google Scholar

27. Jun YB, Smarandache F, Kim CS. Neutrosophic cubic sets. New Math Nat Comput (2017) 13(01):41–54. doi:10.1142/s1793005717500041

CrossRef Full Text | Google Scholar

28. Amer A, Naeem M, Rehman HU, Irfan M, Saleem MS, Yang H. Edge version of topological degree based indices of Boron triangular nanotubes. J Inf Optimization Sci (2020) 41(4):973–90. doi:10.1080/02522667.2020.1743505

CrossRef Full Text | Google Scholar

29. Irfan M, Rehman HU, Almusawa H, Rasheed S, Baloch IA. M-polynomials and topological indices for line graphs of chain silicate network and h-naphtalenic nanotubes. J Math (2021) 2021:1–11. doi:10.1155/2021/5551825

CrossRef Full Text | Google Scholar

30. Sunitha MS, Vijayakumar A. A characterization of fuzzy trees. Inf Sci (1999) 113:293–300. doi:10.1016/s0020-0255(98)10066-x

CrossRef Full Text | Google Scholar

31. Mathew S, Yang HL, Mathew JK. Saturation in fuzzy graphs. New Math Nat Comput (2018) 14(01):113–28. doi:10.1142/s1793005718500084

CrossRef Full Text | Google Scholar

32. Mordeson JN, Yao YY. Fuzzy cycles and fuzzy trees. J Fuzzy Math (2002) 10(1):189–202.

Google Scholar

33. Bhutani KR, Rosenfeld A. Fuzzy end nodes in fuzzy graphs. Inf Sci (2003) 152:323–6. doi:10.1016/s0020-0255(03)00078-1

CrossRef Full Text | Google Scholar

34. Talebi AA, Rashmanlou H, Mehdipoor N. Isomorphism on vague graphs. Ann Fuzzy Math Inform (2013) 6(3):575–88.

Google Scholar

35. Talebi AA, Rashmanlou H. Complement and isomorphism on bipolar fuzzy graphs. Fuzzy Inf Eng (2014) 6(4):505–22. doi:10.1016/j.fiae.2015.01.007

CrossRef Full Text | Google Scholar

36. Mathew S, Sunitha MS. Types of arcs in a fuzzy graph. Inf Sci (2009) 179(11):1760–8. doi:10.1016/j.ins.2009.01.003

CrossRef Full Text | Google Scholar

37. Karunambigai MG, Parvathi R, Buvaneswari R. Arcs in intuitionistic fuzzy graphs. Notes on Intuitionistic Fuzzy Sets (2011) 17(4):37–47.

Google Scholar

38. Akram M, Siddique S, Ahmad U. Menger’s theorem for m-polar fuzzy graphs and application of m-polar fuzzy edges to road network. J Intell Fuzzy Syst (2021) 41(1):1553–74. doi:10.3233/jifs-210411

CrossRef Full Text | Google Scholar

39. Naeem T, Gumaei A, Kamran Jamil M, Alsanad A, Ullah K. Connectivity indices of intuitionistic fuzzy graphs and their applications in internet routing and transport network flow. Math Probl Eng (2021) 2021:1–16. doi:10.1155/2021/4156879

CrossRef Full Text | Google Scholar

40. Binu M, Mathew S, Mordeson JN. Cyclic connectivity index of fuzzy graphs. IEEE Trans Fuzzy Syst (2020) 29(6):1340–9. doi:10.1109/tfuzz.2020.2973941

CrossRef Full Text | Google Scholar

41. Zadeh LA. The concept of a linguistic variable and its application to approximate reasoning-I. Inf Sci (1975) 8(3):199–249. doi:10.1016/0020-0255(75)90036-5

CrossRef Full Text | Google Scholar

42. Akram M. Interval-valued fuzzy line graphs. Neural Comput Appl (2012) 21:145–50. doi:10.1007/s00521-011-0733-0

CrossRef Full Text | Google Scholar

43. Talebi AA, Rashmanlou H, Sadati SH. New concepts on m-polar interval-valued intuitionistic fuzzy graph. TWMS J Appl Eng Math (2020) 10(3):806–18.

Google Scholar

44. Talebi AA, Rashmanlou H, Sadati SH. Interval-valued intuitionistic fuzzy competition graph. J Multiple-Valued Logic Soft Comput (2020) 34:335–64.

Google Scholar

45. Rashmanlou H, Borzooei RA. New concepts of interval-valued intuitionistic (S, T)-fuzzy graphs. J Intell Fuzzy Syst (2016) 30(4):1893–901. doi:10.3233/ifs-151900

CrossRef Full Text | Google Scholar

46. Jun YB, Kim CS, Yang KO. Cubic sets. Ann Fuzzy Math Inform (2012) 4(1):83–98.

Google Scholar

47. Rashid S, Yaqoob N, Akram M, Gulistan M. Cubic graphs with application. Int J Anal Appl (2018) 16(5):733–50. doi:10.28924/2291-8639

CrossRef Full Text | Google Scholar

48. Muhiuddin G, Takallo MM, Jun YB, Borzooei RA. Cubic graphs and their application to a traffic flow problem. Int J Comput Intelligence Syst (2020) 13(1):1265–80. doi:10.2991/ijcis.d.200730.002

CrossRef Full Text | Google Scholar

49. Fang G, Ahmad U, Rasheed A, Khan A, Shafi J. Planarity in cubic intuitionistic graphs and their application to control air traffic on a runway. Front Phys (2023) 11. doi:10.3389/fphy.2023.1254647

CrossRef Full Text | Google Scholar

50. Muhiuddin G, Hameed S, Maryam A, Ahmad U. Cubic Pythagorean fuzzy graphs. J Math (2022) 2022:1–25. doi:10.1155/2022/1144666

CrossRef Full Text | Google Scholar

51. Muhiuddin G, Hameed S, Rasheed A, Ahmad U. Cubic planar graph and its application to road network. Math Probl Eng (2022) 2022:1–12. doi:10.1155/2022/5251627

CrossRef Full Text | Google Scholar

52. Shi X, Akhoundi M, Talebi AA, Sadati SH. Some properties of cubic fuzzy graphs with an application. Symmetry (2022) 14(12):2623. doi:10.3390/sym14122623

CrossRef Full Text | Google Scholar