Single-photon-based quantum secure protocol for the socialist millionaires’ problem

1 Introduction

Since Bennett and Brassard [1] introduced the pioneering quantum key distribution (QKD) protocol in 1984, leveraging the distinctive properties of quantum mechanics instead of relying on computational complexity problems and demonstrating its unconditional security, a multitude of quantum cryptographic protocols have since been developed. These include quantum secret sharing [2–4], quantum secure direct communication [5–7], and quantum key agreement [8, 9], aiming to address various cryptographic tasks. Quantum cryptography offers significant security advantages compared to classical cryptography, which is vulnerable to attacks from quantum algorithms (e.g., Shor’s algorithm [10]).

In 1982, Andrew Yao [11] proposed the concept of the millionaires’ problem, with the aim of solving the following task: two millionaires, each possessing their own wealth, seek to ascertain the wealthier party without revealing their financial status. Boudot et al. [12] introduced an efficient scheme for the socialist millionaires’ problem, relying on three standard assumptions: discrete logarithm, the Diffie–Hellman, and the Decision Diffie–Hellman. In this problem, two millionaires aim to ascertain the equality of their wealth. Nevertheless, as noted by Lo [13], securely evaluating an equality function in a two-party setting is deemed impossible. Consequently, the involvement of a third party (TP) becomes imperative to address the millionaires’ problem. Indeed, addressing the socialist millionaires’ problem is tantamount to formulating a private comparison protocol for confidentially comparing secrets. The reliability of the third party (TP) can be categorized into three types: completely honest, semi-honest, and dishonest. Since completely honest TP involvement in real life is hard to find, and implementing dishonest TP is difficult, semi-honest TP, who may misbehave but cannot collude with the participants, is a more reasonable and widely used approach in designing private comparison protocols up to now.

Quantum private comparison (QPC), which combines quantum mechanics and classical private comparison, can be used to solve the socialist millionaires’ problem that achieves the comparison of the equality or inequality of two secrets while ensuring the security of information transmission. The first QPC protocol, incorporating EPR pairs and decoy photons, was suggested by Yang et al. [14] in 2009, which allows the equality relationship of two secrets to be determined by involving a TP who is barred from accessing either the comparison result or the private inputs. To conserve quantum resources, Chen et al. [15] introduced a QPC protocol using triplet entangled states. In this protocol, the classical message can be divided into multiple groups, and comparison results can be obtained even if not all data are completely compared. Lin et al. [16] identified vulnerabilities in the protocol described in Ref. [15], noting its susceptibility to intercept-resend attacks and emphasizing the need for improvements. Afterward, several QPC protocols were proposed using different quantum states as carriers of quantum information, such as single photons [17], Bell states [18, 19], multi-qubit entangled states [20–24], and multi-qubit cluster states [25–28]. In addition, Ye [29] proposed a QPC protocol using cavity quantum electrodynamics (QED), which requires two-atom product states as carriers of quantum information, and one two-atom product state can be utilized to perform the equality comparison of 1 bit in each round. Chen et al. [30] introduced a QPC protocol utilizing quantum walks on a circle. This protocol requires a two-particle quantum walk state and a quantum walk operator, and it can improve efficiency by allowing private inputs to be compared all at once rather than bit by bit. In order to compare the relationship of arbitrary single-qubit states, Huang et al. [31] constructed a QPC protocol by utilizing the special property of rotation encryption and swap test.

The QPC protocols mentioned above mainly utilize low-dimensional quantum states as carriers of quantum information, with the classical message encoded on these quantum states. In most quantum states, a single quantum state can only convey 1 bit of information, limiting the transmission efficiency of quantum states. To address the issue, some scholars have focused on developing QPC protocols based on high-dimensional quantum states instead of low-dimensional quantum states since high-dimensional quantum states can encode a greater amount of information. In 2011, Jia et al. [32] introduced d-level GHZ states to solve the millionaire problem. The private inputs are encoded into the phase of the initial quantum entangled states by performing local operations, and the phase information can be obtained by performing collective measurements. In 2013, Yu et al. [33] introduced d-level single particles to construct the QPC protocol, with the aim of comparing the size relationship of private inputs. Guo et al. [34] used entanglement swapping of d-level Bell states to determine the equality and size relationship of two secrets. Since the particles can be used multiple times, the scheme has an advantage in efficiency. After that, Li and Shi [35] proposed a QPC protocol utilizing quantum Fourier transforms, wherein the encoding of private inputs into the phase of the quantum state sent from the third party is employed. This protocol achieves higher communication efficiency by employing secret-by-secret comparisons rather than bit-by-bit comparisons. Ji et al. [36] used (n+1)-qubit GHZ states as quantum resources to compare the participants’ secrets, and the requirement of quantum devices can be reduced as the protocol only employs quantum states and quantum measurements without the need for any entanglement swapping and unitary operations. Wu and Zhao [37] proposed a QPC based on d-level Bell states to determine the equality and size relationship of two secrets.

Based on the analysis of the aforementioned protocols, it can be deduced that QPC protocols utilizing low-dimensional quantum states as quantum information carriers, have lower transmission efficiency. In contrast, implementing high-dimensional quantum states-based QPC protocols poses challenges with current quantum technologies. In this paper, we introduce a practical QPC protocol to address the socialist millionaires’ problem utilizing single photons, as they are easier to implement and manipulate with current technology. This protocol utilizes single photons as carriers of quantum information, with TP tasked with preparing groups of quantum sequences and transmitting them to Alice who performs Identity or Hadamard operations on the received quantum sequences via her private inputs and the secret keys to obtain new quantum sequences, which are then sent to Bob. Similarly, Bob encodes his private inputs into the received quantum sequences to produce new quantum sequences, which are then sent to TP. By conducting single-particle measurements on the quantum sequence received from Bob, TP can ascertain the equality of private inputs between Alice and Bob, and subsequently communicate the comparison results to them. Two simulation experiments are conducted on IBM Quantum Experience to showcase the feasibility of the proposed protocol. Additionally, the incorporation of decoy photons enables the detection of any potential eavesdropping during the eavesdropping detection process.

The remaining sections of this paper are structured as follows: Section 2 introduces preliminary knowledge, Section 3 outlines the detailed steps of the proposed quantum secure protocol for the socialist millionaires’ problem, Section 4 conducts two simulation experiments, and Section 5 provides the corresponding analysis for the proposed protocol. Finally, Section 6 concludes the paper.

2 Preliminary knowledge

In this section, we will primarily introduce the Identity and Hadamard operations, which are equivalent to two quantum gates. In essence, a quantum gate can be represented as a unitary matrix. When performing a quantum gate on an n-qubit quantum state, the unitary matrix is of size $2^n\times 2^n$. For a single photon, also known as a single qubit, the unitary matrix is of size $2\times 2$. Therefore, Identity or Hadamard operations can be represented as a $2\times 2$ unitary matrix, as shown in the following equation.

$I=\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right),H=\frac{1}{\sqrt{2}}\left(\begin{array}{cc}1& 1\\ 1& -1\end{array}\right)(1)$

For a single qubit, performing the Identity operation will not change its state, while the state will change when performing the Hadamard operation. That is $\left|0\right.〉\leftrightarrow \left|+\right.〉,\left|1\right.〉\leftrightarrow \left|-\right.〉$.

Theorem 1. When using the Z-basis to measure $\left|0\right.〉$ and $\left|1\right.〉$ respectively, the measurement results yield $\left|0\right.〉$ and $\left|1\right.〉$ respectively with a probability of 1. However, when using Z-basis to measure $\left|+\right.〉$ and $\left|-\right.〉$ respectively, the measurement results yield $\left|0\right.〉$ and $\left|1\right.〉$ respectively, with an equal probability of 0.5.

Proof. The measurement operators of Z-basis can be represented as $M_0=\left|0\right.〉〈\left.0\right|$ and $M_1=\left|1\right.〉〈\left.1\right|$, where $M_0$ and $M_1$ are Hermitian matrices and satisfy the completeness equation, that is,

$I=M_0^{†}{M}_0+M_1^{†}{M}_1(2)$

When performing the measurement on $\left|0\right.〉$ with the Z-basis, the probabilities that the measurement results yield $\left|0\right.〉$ and $\left|1\right.〉$ respectively can be given by

$p_1\left(\left|0\right.〉\right)=〈\left.0\right|M_0^{†}{M}_0\left|0\right.〉=〈\left.0\right|\left|0\right.〉〈\left.0\right|\left|0\right.〉=1(3)$

$p_1\left(\left|1\right.〉\right)=〈\left.0\right|M_1^{†}{M}_1\left|0\right.〉=〈\left.0\right|\left|1\right.〉〈\left.1\right|\left|0\right.〉=0(4)$

When performing the measurement on $\left|1\right.〉$ with the Z-basis, the probabilities that the measurement results yield $\left|0\right.〉$ and $\left|1\right.〉$ respectively can be given by

$p_2\left(\left|0\right.〉\right)=〈\left.1\right|M_0^{†}{M}_0\left|1\right.〉=〈\left.1\right|\left|0\right.〉〈\left.0\right|\left|1\right.〉=0(5)$

$p_2\left(\left|1\right.〉\right)=〈\left.1\right|M_1^{†}{M}_1\left|1\right.〉=〈\left.1\right|\left|1\right.〉〈\left.1\right|\left|1\right.〉=1(6)$

When performing the measurement on $\left|+\right.〉$ with the Z-basis, the probabilities that the measurement results yield $\left|0\right.〉$ and $\left|1\right.〉$ respectively can be given by

$p_3\left(\left|0\right.〉\right)=〈\left.+\right|M_0^{†}{M}_0\left|+\right.〉=\frac{〈\left.0\right|+〈\left.1\right|}{\sqrt{2}}\left|0\right.〉〈\left.0\right|\frac{\left|0\right.〉+\left|1\right.〉}{\sqrt{2}}=\frac{1}{2}(7)$

$p_3\left(\left|1\right.〉\right)=〈\left.+\right|M_1^{†}{M}_1\left|+\right.〉=\frac{〈\left.0\right|+〈\left.1\right|}{\sqrt{2}}\left|1\right.〉〈\left.1\right|\frac{\left|0\right.〉+\left|1\right.〉}{\sqrt{2}}=\frac{1}{2}(8)$

When performing the measurement on $\left|-\right.〉$ with the Z-basis, the probabilities that the measurement results yield $\left|0\right.〉$ and $\left|1\right.〉$ respectively can be given by

$p_4\left(\left|0\right.〉\right)=〈\left.-\right|M_0^{†}{M}_0\left|-\right.〉=\frac{〈\left.0\right|-〈\left.1\right|}{\sqrt{2}}\left|0\right.〉〈\left.0\right|\frac{\left|0\right.〉-\left|1\right.〉}{\sqrt{2}}=\frac{1}{2}(9)$

$p_4\left(\left|1\right.〉\right)=〈\left.-\right|M_1^{†}{M}_1\left|-\right.〉=\frac{〈\left.0\right|-〈\left.1\right|}{\sqrt{2}}\left|1\right.〉〈\left.1\right|\frac{\left|0\right.〉-\left|1\right.〉}{\sqrt{2}}=\frac{1}{2}(10)$

From Eqs 3–6, we can conclude that when using the Z-basis to measure $\left|0\right.〉$ and $\left|1\right.〉$ respectively, the measurement results are $\left|0\right.〉$ and $\left|1\right.〉$ respectively with a probability of 1. From Eqs 7–10, we can also conclude that when using the Z-basis to measure $\left|+\right.〉$ and $\left|-\right.〉$ respectively, the measurement results are $\left|0\right.〉$ and $\left|1\right.〉$ respectively with the same probability of 0.5.

Theorem 2. When using the X-basis to measure $\left|0\right.〉$ and $\left|1\right.〉$ respectively, the measurement results are $\left|+\right.〉$ and $\left|-\right.〉$ respectively with an equal probability of 0.5. However, when using the X-basis to measure $\left|+\right.〉$ or $\left|-\right.〉$ respectively, the measurement results yield $\left|+\right.〉$ and $\left|-\right.〉$ respectively with a probability of 1.

Proof. The measurement operators of X-basis can be represented as ${\mathit{M}}_{+}=\left|+\right.〉〈\left.+\right|$ and $M_{-}=\left|-\right.〉〈\left.-\right|$, where $M_{+}$ and $M_{-}$ are also Hermitian matrices and satisfy the completeness equation as well, that is,

$I=M_{+}^{†}{M}_{+}+M_{-}^{†}{M}_{-}(11)$

When performing the measurement on $\left|0\right.〉$ with the X-basis, the probabilities that the measurement results yield $\left|+\right.〉$ and $\left|-\right.〉$ respectively can be given by

$p_5\left(\left|+\right.〉\right)=〈\left.0\right|M_{+}^{†}{M}_{+}\left|0\right.〉=〈\left.0\right|\left|+\right.〉〈\left.+\right|\left|0\right.〉=\frac{1}{2}(12)$

$p_5\left(\left|-\right.〉\right)=〈\left.0\right|M_{-}^{†}{M}_{-}\left|0\right.〉=〈\left.0\right|\left|-\right.〉〈\left.-\right|\left|0\right.〉=\frac{1}{2}(13)$

When performing the measurement on $\left|1\right.〉$ with the X-basis, the probabilities that the measurement results yield $\left|+\right.〉$ and $\left|-\right.〉$ respectively can be given by

$p_6\left(\left|+\right.〉\right)=〈\left.1\right|M_{+}^{†}{M}_{+}\left|1\right.〉=〈\left.1\right|\left|+\right.〉〈\left.+\right|\left|1\right.〉=\frac{1}{2}(14)$

$p_6\left(\left|-\right.〉\right)=〈\left.1\right|M_{-}^{†}{M}_{-}\left|1\right.〉=〈\left.1\right|\left|-\right.〉〈\left.-\right|\left|1\right.〉=\frac{1}{2}(15)$

When performing the measurement on $\left|+\right.〉$ with the X-basis, the probabilities that the measurement results yield $\left|+\right.〉$ and $\left|-\right.〉$ respectively can be given by

$p_7\left(\left|+\right.〉\right)=〈\left.+\right|M_{+}^{†}{M}_{+}\left|+\right.〉=〈\left.+\right|\left|+\right.〉〈\left.+\right|\left|+\right.〉=1(16)$

$p_7\left(\left|-\right.〉\right)=〈\left.+\right|M_{-}^{†}{M}_{-}\left|+\right.〉=〈\left.+\right|\left|-\right.〉〈\left.-\right|\left|+\right.〉=0(17)$

When performing the measurement on $\left|-\right.〉$ with the X-basis, the probabilities that the measurement results yield $\left|+\right.〉$ and $\left|-\right.〉$ respectively can be given by

$p_8\left(\left|+\right.〉\right)=〈\left.-\right|M_{+}^{†}{M}_{+}\left|-\right.〉=〈\left.-\right|\left|+\right.〉〈\left.+\right|\left|-\right.〉=0(18)$

$p_8\left(\left|-\right.〉\right)=〈\left.-\right|M_{-}^{†}{M}_{-}\left|-\right.〉=〈\left.-\right|\left|-\right.〉〈\left.-\right|\left|-\right.〉=1(19)$

From Eqs 12–15, we can also conclude that when using the X-basis to measure $\left|0\right.〉$ and $\left|1\right.〉$ respectively, the measurement results are $\left|+\right.〉$ and $\left|-\right.〉$ respectively with the same probability of 0.5. From Eqs 16–19, we can also conclude that when using the X-basis to measure $\left|+\right.〉$ and $\left|-\right.〉$ respectively, the measurement results are $\left|+\right.〉$ and $\left|-\right.〉$ respectively with a probability of 1.

3 Quantum secure protocol for the socialist millionaires’ problem

The quantum secure protocol for the socialist millionaires’ problem is run between two participants, each of whom possesses two secret inputs, A and B, respectively. The two participants aim to determine the equality relationship between A and B. The binary representations of A and B in $F_2^L$ can be represented as $A^{\prime }=\left(a_1,a_2,\cdots ,a_L\right)$ and $B^{\prime }=\left(b_1,b_2,\cdots ,b_L\right)$, where L is the length of $A^{\prime }$ and $B^{\prime }$. If the length of $A^{\prime }$ and $B^{\prime }$ is less than L, Alice and Bob fill in the high digit with adequate zeros. A semi-honest third party is engaged in the preparation of the sequence of single photons. In the entire process, TP may have access to some immediate computation processes, but she cannot collude with any participant. Before the protocol is executed, TP shares a secret key $TA=\left(t{a}_1,t{a}_2,\cdots ,t{a}_L\right)$ and $TB=\left(t{b}_1,t{b}_2,\cdots ,t{b}_L\right)$ between Alice and Bob via a secure QKD protocol, respectively. Additionally, Alice and Bob also share a secret key $AB=\left(a{b}_1,a{b}_2,\cdots ,a{b}_L\right)$ using a secure QKD protocol.

The detailed steps of the proposed protocol are described in the following procedure.

Step 1. TP prepares $\lambda$ groups of quantum sequences denoted as $S=\left({\otimes }_{i=1}^L{s}_i^1;{\otimes }_{i=1}^L{s}_i^2;\cdots {\otimes }_{i=1}^L{s}_i^{\lambda }\right)$, with each group being equivalent and containing L photons randomly selected from $\left\{\left|0\right.〉,\left|1\right.〉,\left|+\right.〉,\left|-\right.〉\right\}$. Then, she prepares $\delta$ decoy photons and inserts them into the sequence $S$ at random positions to produce a new sequence $S^{\prime }$ and notes the positions of the decoy photons in $S^{\prime }$ and each quantum state in sequence $S$. Finally, TP sends $S^{\prime }$ to Alice.

Step 2. Upon receiving $S^{\prime }$, Alice and TP perform the eavesdropping detection to identify the presence of any eavesdropper. When TP knows that Alice has received $S^{\prime }$, TP securely conveys the positions of the decoy photons and their corresponding measurement bases to Alice through a classical channel. Subsequently, Alice measures the decoy photons using the provided measurement bases and communicates the measurement results back to TP. TP then compares these results with the originally prepared $\delta$ decoy photons. If they are different, the process is returned to Step 1. Otherwise, they proceed with the following steps.

Step 3. Alice discards the decoy photons to get $S$. If $a_i\oplus t{a}_i\oplus a{b}_i=0$, Alice applies the Identity operation to each photon within the $\lambda$ groups in $S$. Otherwise, Alice applies the Hadamard operation to each photon within the $\lambda$ groups in $S$. Let the resultant sequence be $S_A$. To detect the eavesdropper, Alice adds $\delta$ decoy photons into $S_A$ to produce a fresh sequence $S_A^{\prime }$ , which is then sent to Bob.

Step 4. Upon receiving $S_A^{\prime }$, Alice and Bob perform the eavesdropping detection in the same manner as TP. If no eavesdropper is detected, Bob removes the decoy photons from $S_A^{\prime }$ to get $S_A$. If $b_i\oplus t{b}_i\oplus a{b}_i=0$, Bob performs the Identity operation. Otherwise, Bob performs the Hadamard operation. Let the resultant sequence be $S_B$. To prevent eavesdropping, Bob adds $\delta$ decoy photons into $S_B$ to produce a fresh sequence $S_B^{\prime }$, which is then sent to TP.

Step 5. Upon receiving $S_B^{\prime }$, TP interacts with Bob in the same manner as Alice and Bob to check whether the eavesdropper exists. If not, TP gets $S_B$ by removing the decoy photons from $S_B^{\prime }$. In the following, TP applies the Identity or Hadamard operation to each photon within the $\lambda$ groups in $S_B$ to produce a new sequence $S_{TP}$. If $t{a}_i\oplus t{b}_i=0$, TP performs the Identity operation. Otherwise, TP performs the Hadamard operation. TP measures each photon of the $\lambda$ groups in $S_{TP}$ with the measurement basis determined by the initial prepared quantum state in $S$ to get the measurement results. If the photon stays in $\left|0\right.〉$ or $\left|1\right.〉$, the measurement basis is the Z-basis, Otherwise, the measurement basis is the X-basis.

Step 6. TP communicates the comparison results to both Alice and Bob. If all measurement results in $S_{TP}$ are the same as the initially prepared quantum state in $S$, A and B are identical. Otherwise, A and B are different.

4 Simulation experiments

Since single photons are easier to implement and manipulate compared to low-dimensional and high-dimensional quantum states, we simulate the aforementioned protocol on IBM Quantum Experience using two concrete examples to demonstrate its feasibility and correctness. The specifics of two simulation experiments are outlined below.

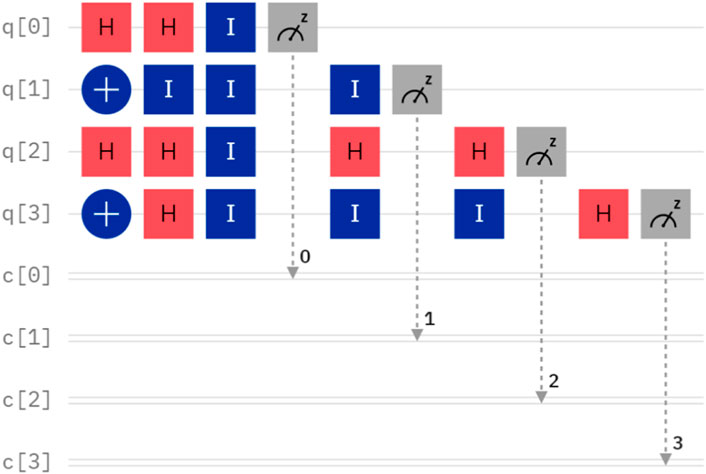
4.1 Simulation I. Alice and Bob desire to compare their private inputs, with A = 12 and B = 12, respectively

A and B can be denoted as $A^{\prime }=1100$ and $B^{\prime }=1100$ in the form of binary representations in $F_2^L$. For the sake of simplicity, any eavesdropping or attacks will not be considered in the simulation experiments. We assume that TP shares the secret keys $TA=1011$ and $TB=1001$ respectively, and then Alice and Bob also share a secret key $AB=1101$.

Suppose that the initial quantum sequence prepared by TP is $S=\left\{\left|0\right.〉,\left|1\right.〉,\left|+\right.〉,\left|-\right.〉\right\}$. After that, Alice performs the operators $\left\{H,I,H,I\right\}$ on each photon of $S$ to get $S_A=\left\{H\left|0\right.〉,I\left|1\right.〉,H\left|+\right.〉,I\left|-\right.〉\right\}$ and then she sends $S_A$ to Bob. In the same way, Bob performs the operator $\left\{H,I,I,I\right\}$ on each photon of $S_A$ to get $S_B=\left\{HH\left|0\right.〉,II\left|1\right.〉,IH\left|+\right.〉,II\left|-\right.〉\right\}$ and then she sends $S_B$ to TP. Finally, TP performs the operators $\left\{I,I,H,I\right\}$ on each photon of $S_B$ to get $S_{TP}=\left\{IHH\left|0\right.〉,III\left|1\right.〉,HIH\left|+\right.〉,III\left|-\right.〉\right\}=\left\{\left|0\right.〉,\left|1\right.〉,\left|+\right.〉,\left|-\right.〉\right\}$ and then measures $S_{TP}$ with the measurement bases determined by the initially prepared quantum state in $S$ to get the measurement results. That is, TP measures $S_{TP}$ with basis $\left\{Z,Z,X,X\right\}$ to get the measurement results denoted as $\left\{\left|0\right.〉,\left|1\right.〉,\left|+\right.〉,\left|-\right.〉\right\}$. Therefore, we can see that all measurement results are the same as the initially prepared quantum state, indicating that A and B are identical.

The quantum circuit for Case I is depicted in Figure 1. By executing the quantum circuit on IBM Quantum Experience, we can obtain the measurement results shown in Figure 2. In Figure 2, the string on the horizontal axis represents the measurement outcome, corresponding to q [0]-q [3] from right to left. The value on the vertical axis represents the quasiprobability. It is important to note that both the measurement bases selected in q [2] and q [3] are the X basis, and the measurement outcome 1 and 0 are considered as $\left|+\right.〉$ and $\left|-\right.〉$ respectively. From Figure 2, we can see that the final measurement outcome is $\left\{\left|0\right.〉,\left|1\right.〉,\left|+\right.〉,\left|-\right.〉\right\}$, which is the same as the initial prepared quantum state. This indicates that A and B are identical.

FIGURE 1

FIGURE 1. The quantum circuit of Simulation I.

FIGURE 2

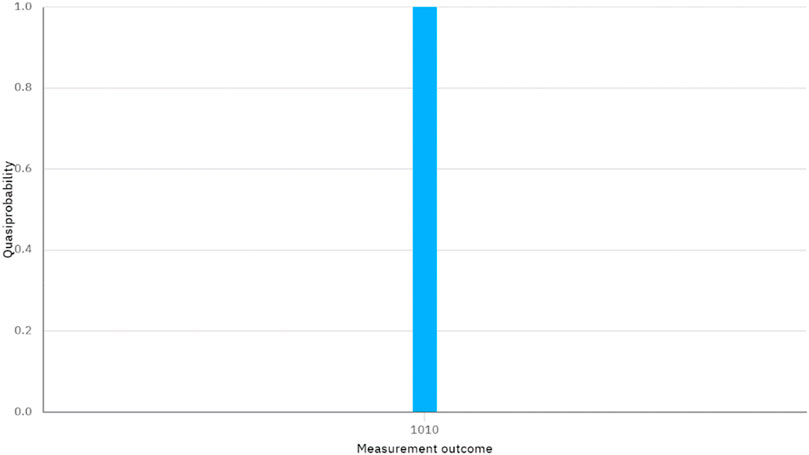
FIGURE 2. The measurement outcome in Figure 1.

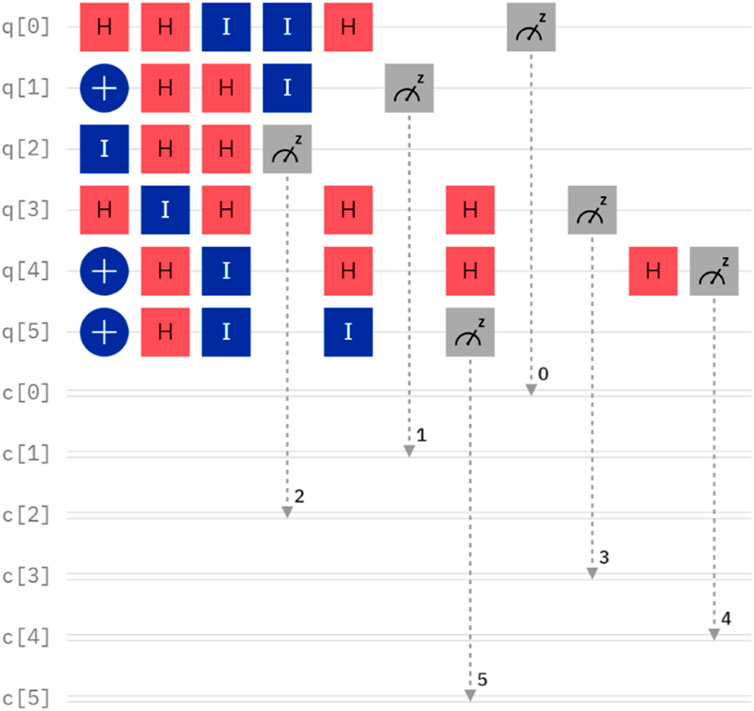
4.2 Simulation II. Alice and Bob desire to compare their private inputs, with A = 55 and B = 22, respectively

A and B can be represented as $A^{\prime }=110111$ and $B^{\prime }=10110$ in the form of binary representations in $F_2^L$. Suppose that L = 6, we can see that the length of $B^{\prime }$ is less than L, Bob will fill in the necessary 0s at the higher digits and thus $B^{\prime }=010110$. We assume that TP shares the secret keys $TA=101011$ and $TB=100101$ between Alice and Bob, respectively, and Alice and Bob also share a secret key $AB=101101$.

Suppose that the initial quantum sequence prepared by TP is $S=\left\{\left|+\right.〉,\left|1\right.〉,\left|0\right.〉,\left|+\right.〉,\left|-\right.〉,\left|1\right.〉\right\}$. Afterward, Alice performs the operators $\left\{H,H,I,I,I,H\right\}$ on each photon of $S$ to get $S_A=\left\{H\left|+\right.〉,H\left|1\right.〉,I\left|0\right.〉,I\left|+\right.〉,I\left|-\right.〉,H\left|1\right.〉\right\}$ , which is then sent to Bob. In the same way, Bob performs the operators $\left\{I,H,H,H,H,I\right\}$ on each photon of $S_A$ to get $S_B=\left\{IH\left|+\right.〉,HH\left|1\right.〉,HI\left|0\right.〉,HI\left|+\right.〉,HI\left|-\right.〉,IH\left|1\right.〉\right\}$, which is then sent to TP. Finally, TP performs the operators $\left\{I,I,H,H,H,I\right\}$ on each photon of $S_B$ to get $S_{TP}=\left\{IIH\left|+\right.〉,IHH\left|1\right.〉,HHI\left|0\right.〉,HHI\left|+\right.〉,HHI\left|-\right.〉,IIH\left|1\right.〉\right\}=\left\{\left|0\right.〉,\left|1\right.〉,\left|0\right.〉,\left|+\right.〉,\left|-\right.〉,\left|-\right.〉\right\}$ and then TP measures $S_{TP}$ using the measurement bases determined by the initially prepared quantum state in $S$ to obtain the measurement results. That is, TP measures $S_{TP}$ with basis $\left\{X,Z,Z,X,X,Z\right\}$ to get the measurement results denoted as $\left\{\left|+\right.〉or\left|-\right.〉,\left|1\right.〉,\left|0\right.〉,\left|+\right.〉,\left|-\right.〉,\left|0\right.〉or\left|1\right.〉\right\}$. Therefore, we can see that not all measurement results are the same as the initially prepared quantum state, indicating that A and B are different.

The quantum circuit for Case II is depicted in Figure 3. By executing the quantum circuit on IBM Quantum Experience, we can obtain the measurement results shown in Figure 4. It is important to note that the measurement basis selected in q [0], q [3], and q [4] are all based on the X basis. The measurement outcome 1 and 0 can be considered as $\left|+\right.〉$ and $\left|-\right.〉$ respectively. From Figure 2, we can see that the measurement outcome is $\left\{\left|+\right.〉or\left|-\right.〉,\left|1\right.〉,\left|0\right.〉,\left|+\right.〉,\left|-\right.〉,\left|0\right.〉or\left|1\right.〉\right\}$, which corresponds to the measurement outcome q [0]-q [5] from right to left. Since the measurement outcome is not the same as the initial quantum state, A and B are different.

FIGURE 3

FIGURE 3. The quantum circuit of Simulation II.

FIGURE 4

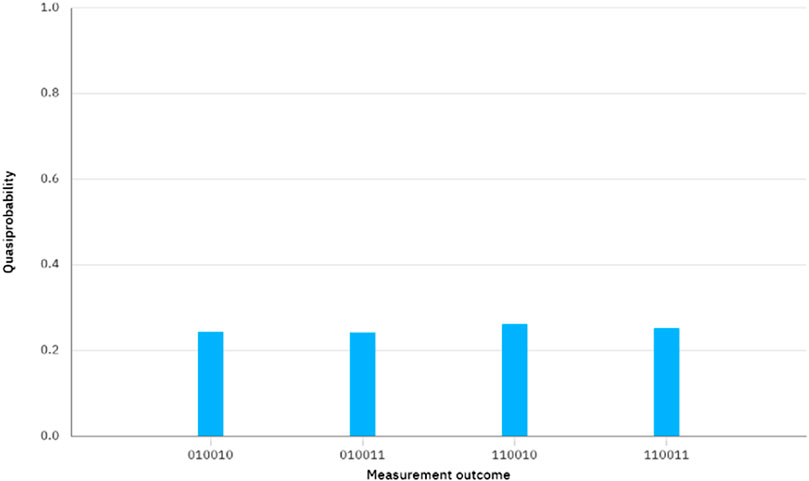
FIGURE 4. The measurement outcome in Figure 3.

5 Analysis

5.1 Correctness analysis

In the proposed protocol, TP prepares $\lambda$ groups of quantum sequences denoted as $S=\left({\otimes }_{i=1}^L{s}_i^1;{\otimes }_{i=1}^L{s}_i^2;\cdots {\otimes }_{i=1}^L{s}_i^{\lambda }\right)$, which is sent to Alice. Then, Alice applies the Identity or Hadamard operation to each photon within the $\lambda$ groups in $S_{TP}$ according to her private inputs and the secret keys. Thus, we can get

$S_A=\left({\otimes }_{i=1}^L\left(IorH\right)s_i^1;{\otimes }_{i=1}^L\left(IorH\right)s_i^2;\cdots {\otimes }_{i=1}^L\left(IorH\right)s_i^{\lambda }\right)(20)$

After that, $S_A$ is sent to Bob. Bob also applies the Identity or Hadamard operation to each photon within the $\lambda$ groups in $S_A$ according to her private inputs and the secret keys. Thus, we can also get

$S_B=\left({\otimes }_{i=1}^L\left(IorH\right)\left(IorH\right)s_i^1;{\otimes }_{i=1}^L\left(IorH\right)\left(IorH\right)s_i^2;\cdots {\otimes }_{i=1}^L\left(IorH\right)\left(IorH\right)s_i^{\lambda }\right)(21)$

After that, $S_B$ is sent to TP. TP also applies the Identity or Hadamard operation to each photon within the $\lambda$ groups in $S_B$ to produce a new sequence $S_{TP}$. If $t{a}_i\oplus t{b}_i=0$, Bob performs the Identity operation. Otherwise, Bob performs the Hadamard operation.

There are four cases that should be considered.

Case I: If $a_i=0$ and $b_i=0$, then

$S_{TP}=\left({\otimes }_{i=1}^L{s}_i^1;{\otimes }_{i=1}^L{s}_i^2;\cdots {\otimes }_{i=1}^L{s}_i^{\lambda }\right)(22)$

When TP measures each group of quantum states in $S_{TP}$ with the measurement bases determined by the initially prepared quantum state in $S$. We can easily observe that all the ith qubits in each group of $S_{TP}$ are the same as the initially prepared ith qubits in each group of $S$, indicating that A and B are identical.

Case II: If $a_i=1$ and $b_i=0$, then

$S_{TP}=\left({\otimes }_{i=1}^{L}H{s}_i^1;{\otimes }_{i=1}^{L}H{s}_i^2;\cdots {\otimes }_{i=1}^{L}H{s}_i^{\lambda }\right)(23)$

When TP measures each group of quantum states in $S_{TP}$ with the measurement bases determined by the initially prepared quantum state in $S$. It is easy to see that not all the ith qubits in each group of $S_{TP}$ are the same as the initially prepared ith qubits in each group of $S$, indicating that A and B are not identical.

Case III: If $a_i=0$ and $b_i=1$, then

$S_{TP}=\left({\otimes }_{i=1}^{L}H{s}_i^1;{\otimes }_{i=1}^{L}H{s}_i^2;\cdots {\otimes }_{i=1}^{L}H{s}_i^{\lambda }\right)(24)$

We can see that $S_{TP}$ in Case III is the same as in the Case II, and thus we can deduce that A and B are not identical.

Case IV: If $a_i=1$ and $b_i=1$, then

$S_{TP}=\left({\otimes }_{i=1}^L{s}_i^1;{\otimes }_{i=1}^L{s}_i^2;\cdots {\otimes }_{i=1}^L{s}_i^{\lambda }\right)(25)$

Similarly, we can also observe that $S_{TP}$ in Case VI is the same as in Case I, and thus we can deduce that A and B are not identical.

Therefore, the above results reveal that our protocol is correct.

5.2 Security analysis

5.2.1 External attacks

External attacks involve an outsider eavesdropper, Eve, who may attempt to obtain valuable information about Alice’s or Bob’s private inputs during the transmission of the quantum sequence between the participants. Unfortunately, decoy photons are used during the transmission of each quantum sequence. Both the sender and receiver of the quantum sequences will perform the eavesdropping detection to verify the presence of any eavesdropper. This technique guarantees the security of the quantum sequence transmission, and any external attacks including intercept-resend attack, auxiliary particle attack, the man-in-the-middle attack and denial-of-service (Dos) attacks are invalid. In this context, we primarily delve into the security aspects of the proposed protocol concerning intercept-resend attacks, entanglement-measure attacks, and Trojan-Horse attacks in detail.

5.2.1.1 The intercept-resend attack

The intercept-resend attack refers to the outsider eavesdropper, Eve, intercepting the sequence sent from the previous participant during the transmission of each quantum sequence. Once Eve obtains the quantum sequence that carries the private inputs, she has the option to measure them using the Z-basis and send a fake sequence whose states match the measurement results instead of the initial quantum sequences to the original receiver. We assume that when a sender’s initial quantum state is $\left|0\right.〉$ or $\left|1\right.〉$, and Eve intercepts and measures it with the Z-basis, she will evade eavesdropping detection. If Eve measures it using the X-basis, she will successfully evade eavesdropping detection with a probability of 1/2. For any selected decoy photon, the probability that Eve can correctly choose the measurement basis is 1/2. Therefore, the error rate of a decoy state that Eve introduced in the eavesdropping detection is $\left(1-\frac{1}{2}\times 1-\frac{1}{2}\times \frac{1}{2}\right)=\frac{1}{4}$. Since the number of decoy photons is $\delta$, the probability of detecting the decoy states that Eve resends incorrectly is $1-{\left(\frac{3}{4}\right)}^{\delta }$. It is important to note that if $\delta$ is sufficiently large, the error rate introduced by Eve in the eavesdropping detection will approach 1, indicating that Eve’s eavesdropping will be detected by the sender and the receiver, and the entire protocol process will need to be restarted. Therefore, the intercept-resend attack carried out by Eve is invalid, and her attempts to pilfer any valuable information regarding Alice’s or Bob’s private inputs prove futile.

5.2.1.2 The entanglement-measure attack

The entanglement-measure attack involves an outsider eavesdropper, Eve, intercepting the sequence sent from the previous participant during the transmission of each quantum sequence. She then performs unitary operations to entangle the prepared auxiliary particle sequence $E=\left\{\left|E_0\right.〉,\left|E_1\right.〉,\cdots ,\left|E_n\right.〉\right\}$ with the intercepted single-photon sequence. And the unitary operations performed on each single photon can be denoted as

$U\left|E_i\right.〉\left|0\right.〉=a\left|e_{00}\right.〉\left|0\right.〉+b\left|e_{01}\right.〉\left|1\right.〉(26)$

$U\left|E_i\right.〉\left|1\right.〉=c\left|e_{10}\right.〉\left|0\right.〉+d\left|e_{11}\right.〉\left|1\right.〉(27)$

$\begin{array}{l}U\left|E_i\right.〉\left|+\right.〉=U\left|E_i\right.〉\otimes \frac{\left|0\right.〉+\left|1\right.〉}{\sqrt{2}}\\ =\frac{1}{\sqrt{2}}\left(a\left|e_{00}\right.〉\left|0\right.〉+b\left|e_{01}\right.〉\left|1\right.〉+c\left|e_{10}\right.〉\left|0\right.〉+d\left|e_{11}\right.〉\left|1\right.〉\right)\\ =\frac{1}{\sqrt{2}}\left(\begin{array}{l}a\left|e_{00}\right.〉\otimes \frac{\left|+\right.〉+\left|-\right.〉}{\sqrt{2}}+b\left|e_{01}\right.〉\otimes \frac{\left|+\right.〉-\left|-\right.〉}{\sqrt{2}}\\ +c\left|e_{10}\right.〉\otimes \frac{\left|+\right.〉+\left|-\right.〉}{\sqrt{2}}+d\left|e_{11}\right.〉\otimes \frac{\left|+\right.〉-\left|-\right.〉}{\sqrt{2}}\end{array}\right)\\ =\frac{1}{2}\left[\begin{array}{l}\left|+\right.〉\left(a\left|e_{00}\right.〉+b\left|e_{01}\right.〉+c\left|e_{10}\right.〉+d\left|e_{11}\right.〉\right)\\ +\left|-\right.〉\left(a\left|e_{00}\right.〉-b\left|e_{01}\right.〉+c\left|e_{10}\right.〉-d\left|e_{11}\right.〉\right)\end{array}\right]\end{array}(28)$

$\begin{array}{l}U\left|E_i\right.〉\left|-\right.〉=U\left|E_i\right.〉\otimes \frac{\left|0\right.〉-\left|1\right.〉}{\sqrt{2}}\\ =\frac{1}{\sqrt{2}}\left(a\left|e_{00}\right.〉\left|0\right.〉+b\left|e_{01}\right.〉\left|1\right.〉-c\left|e_{10}\right.〉\left|0\right.〉-d\left|e_{11}\right.〉\left|1\right.〉\right)\\ =\frac{1}{\sqrt{2}}\left(\begin{array}{l}a\left|e_{00}\right.〉\otimes \frac{\left|+\right.〉+\left|-\right.〉}{\sqrt{2}}+b\left|e_{01}\right.〉\otimes \frac{\left|+\right.〉-\left|-\right.〉}{\sqrt{2}}\\ -c\left|e_{10}\right.〉\otimes \frac{\left|+\right.〉+\left|-\right.〉}{\sqrt{2}}-d\left|e_{11}\right.〉\otimes \frac{\left|+\right.〉-\left|-\right.〉}{\sqrt{2}}\end{array}\right)\\ =\frac{1}{2}\left[\begin{array}{l}\left|+\right.〉\left(a\left|e_{00}\right.〉+b\left|e_{01}\right.〉-c\left|e_{10}\right.〉-d\left|e_{11}\right.〉\right)\\ +\left|-\right.〉\left(a\left|e_{00}\right.〉-b\left|e_{01}\right.〉-c\left|e_{10}\right.〉+d\left|e_{11}\right.〉\right)\end{array}\right]\end{array}(29)$

$\left\{\left|e_{00}\right.〉,\left|e_{01}\right.〉,\left|e_{10}\right.〉,\left|e_{11}\right.〉\right\}$ are four pure quantum states that are determined by the unitary operations U, and they satisfy the following condition.

${\displaystyle \sum _{\alpha ,\beta }}〈e_{\alpha ,\beta }|e_{\alpha ,\beta }〉=1(30)$

Moreover, the parameters a, b, c, and d satisfy the condition, e.g., ${\left|a\right|}^2+{\left|b\right|}^2=1$ and ${\left|c\right|}^2+{\left|d\right|}^2=1$. In the proposed protocol, the eavesdropping detection is performed between each transmission of the quantum sequence. If the decoy photon is in state $\left|0\right.〉$ or $\left|1\right.〉$ and Eve wants to avoid detection, the parameters b and c must satisfy $b=c=0$. Similarly, if the decoy photon is in state $\left|+\right.〉$ or $\left|-\right.〉$ and Eve wants to avoid detection, then $a\left|e_{00}\right.〉-b\left|e_{01}\right.〉+c\left|e_{10}\right.〉-d\left|e_{11}\right.〉=\overrightarrow{0}$ and $a\left|e_{00}\right.〉+b\left|e_{01}\right.〉-c\left|e_{10}\right.〉-d\left|e_{11}\right.〉=\overrightarrow{0}$. Therefore, we can easily deduce that

$a\left|e_{00}\right.〉=d\left|e_{11}\right.〉(31)$

When Substituting Eq. 31 and $b=c=0$ into Eqs 26–29, we can get

$U\left|E_i\right.〉\left|0\right.〉=a\left|e_{00}\right.〉\left|0\right.〉(32)$

$U\left|E_i\right.〉\left|1\right.〉=a\left|e_{00}\right.〉\left|1\right.〉(33)$

$U\left|E_i\right.〉\left|+\right.〉=a\left|e_{00}\right.〉\left|+\right.〉(34)$

$U\left|E_i\right.〉\left|-\right.〉=a\left|e_{00}\right.〉\left|-\right.〉(35)$

From Eqs 32–35, we can easily see that the auxiliary particles are not related to the intercepted ones. No matter what the intercept particles are, the auxiliary particles will always be in $\left|e_{00}\right.〉$. As a result, Eve will fail to evade eavesdropping detection by performing the entanglement-measure attack, and her attempts to pilfer any valuable information regarding Alice’s or Bob’s private inputs also prove futile.

5.2.1.3 The Trojan-Horse attacks

The Trojan-Horse attacks [38] mainly include the delay-photon attack and the invisible photon eavesdropping attack. These attacks may occur in a two-way communication protocol where quantum states are returned to the sender. Since our protocol is a two-way communication protocol, the initial quantum sequence prepared by TP is returned to TP and the quantum sequence is transmitted in a circular mode. Therefore, the Trojan-Horse attacks should be considered. In order to prevent these attacks, both the Wavelength Quantum Filter (WQF) and the Photons Number Splitter (PNS) should be equipped to remove invisible photons and separate legitimate photons from delayed photons, respectively.

5.2.2 Participants’ attack

Since the participants have the legal capacity to access more information compared to an outside eavesdropper, the dishonest individual has a high probability of obtaining the private input of the dishonest participant without being detected. Therefore, participants’ attack as high security risk should be prevented by taking appropriate measures. Here, we analyze three types of attacks by participants that are aimed at obtaining the private input of the participants.

5.2.2.1 The attack from TP

As a semi-honest party, TP may exhibit improper behavior, but she cannot collude with either Alice or Bob. If TP intends to usurp the private input of Alice or Bob, she may perform external attacks similar to Eve. Unfortunately, this action will be detected, as discussed in Section 5.2.1, and TP cannot avoid detection by eavesdropping. Although TP has some advantages in generating the initial quantum sequences used for information transmission and receiving the sequences encoded with private inputs and secret keys, TP can only gain knowledge about the comparison result. In other words, TP is able to determine whether a bit of Alice and Bob is identical or not, but it will not disclose whether the bit of Alice or Bob is 0 or 1. In addition, both $S_A$ and $S_B$ are encoded with the private inputs and the secret keys shared, TP remains unable to access any information regarding the private inputs of Alice and Bob without knowledge of the key $AB$. Therefore, the proposed protocol is resistant to TP’s attack.

5.2.2.2 The attack from Alice

When TP sends $S$ to Alice, Alice can intercept and measure it directly. And then she sends carefully prepared quantum sequences denoted as ${S_A}^{″}$ to Bob. When Bob applies the Identity or Hadamard operation to each photon within ${S_A}^{″}$ via his private inputs and the secret keys to obtain new quantum sequences denoted as ${S_B}^{\prime }$, which is sent to TP. Afterward, Alice launches the intercept-resend attack on ${S_B}^{\prime }$ that Bob sends to TP. In other words, Alice can intercept ${S_B}^{\prime }$ and send a fake sequence ${S_B}^{″}$ to TP. Once TP receives the counterfeit sequence ${S_B}^{″}$, Bob will convey the positions of the decoy photons and their corresponding measurement bases. Simultaneously, Alice is aware of the positions of the decoy photons in ${S_B}^{″}$ and she can discard them. Then Alice measures the remaining particles in ${S_B}^{″}$ to obtain the measurement result. Although this attack can be identified through the eavesdropping detection mechanism, Alice has already obtained the final states, allowing her to deduce the operations that Bob performs. However, Bob’s actions are influenced by his private inputs and the confidential key $TB$ shared exclusively between TP and Bob. Alice remains unable to access any information regarding Bob’s secrets without knowledge of the key $TB$.

5.2.2.3 The attack from Bob

When Alice sends $S_A$ to Bob, Bob can measure each particle in $S_A$ directly and obtain the measurement result. Bob can also infer which operations that Alice performs. However, this attack will not work. Firstly, the sequence $S$ prepared by TP will not be disclosed to Bob due to the simi-honesty of TP. Once Bob intends to know $S$ by performing outside attacks just like Eve does, he will be detected in the eavesdropping detection. In addition, $S_A$ is encoded with the private inputs of Alice and the secret key $TA$ shared between TP and Alice, and Alice also remains unable to access any information regarding Alice’s secrets without knowledge of the key $TA$.

In summary, the proposed protocol remains resilient against attacks from the participants, ensuring that the secrets of both Alice and Bob are not compromised.

5.3 Efficiency analysis and comparison

In most of QPC protocol, the qubit efficiency is an important indicator for evaluating the utilization rate of quantum states. However, it does not take into account the decoy photons used in eavesdropping detection, which can be considered as an independent process.

The qubit efficiency [39] ${\eta }_e$ is given by

${\eta }_e=\frac{{\eta }_c}{{\eta }_t}(36)$

Where ${\eta }_c$ represents the total number of bits that Alice and Bob want to compare, and ${\eta }_t$ represents the total number of qubits used, excluding the decoy photons. In our protocol, L-length classical-bit information needs to be encoded using $\lambda L$ single photons as the information carriers to encode them. Therefore, the qubit efficiency of the proposed protocol is ${\eta }_e=\frac{1}{\lambda }$, where $\lambda$ represents the number of repetitively prepared quantum sequences.

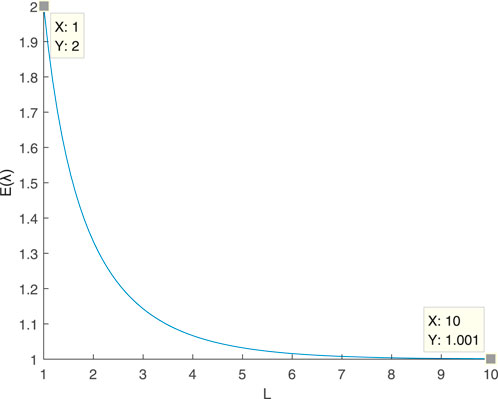
Next, we will discuss the value of $E\left(\lambda \right)$, which represents the average number of times the quantum sequences are repetitively prepared. In Section 5.1, we can conclude that for all ith qubits in each group of quantum states in $S_{TP}$, the measurement result of $S_{TP}$ is the same as the initial prepared quantum state S if and only if $a_i=0$ and $b_i=0$ as well as $a_i=1$ and $b_i=1$. Therefore, the probability that the measurement result matches the initial prepared quantum state for a qubit is $\frac{1}{2}$. We denote the measurement result of one qubit being different from the initially prepared quantum state as Situation I. For a L-length sequence, the probability of Situation I appearing once is $1-{\left(\frac{1}{2}\right)}^L$. How many times should TP prepare the initial quantum state to make Situation I appear once? We denote X as the event. Suppose that in Situation I, when preparing $\lambda$ groups of quantum sequences, the distribution of X is denoted as

$P\left(X=\lambda \right)={\left({\left(\frac{1}{2}\right)}^L\right)}^{\lambda -1}\left(1-{\left(\frac{1}{2}\right)}^L\right)(37)$

$E\left(\lambda \right)$ can be calculated as

$\begin{array}{l}E\left(\lambda \right)={\displaystyle \sum _{\lambda =1}^{\infty }}\lambda P\left(X=\lambda \right)={\displaystyle \sum _{\lambda =1}^{\infty }}\lambda {\left({\left(\frac{1}{2}\right)}^L\right)}^{\lambda -1}\left(1-{\left(\frac{1}{2}\right)}^L\right)\\ =\frac{\left(1-{\left(\frac{1}{2}\right)}^L\right)}{{\left(\frac{1}{2}\right)}^L}\underset{n\to \infty }{\lim }{\displaystyle \sum _{\lambda =1}^n}\lambda {\left({\left(\frac{1}{2}\right)}^L\right)}^{\lambda }=\frac{1}{1-{\left(\frac{1}{2}\right)}^L}\end{array}(38)$

When L is large, we can obtain ${\left(\frac{1}{2}\right)}^L\to 0$ and $E\left(\lambda \right)\to 1$. The relationship between $E\left(\lambda \right)$ and L can be seen in Figure 5. From Fig.8, it is evident that $E\left(\lambda \right)=2$ when $L=1$, and $E\left(\lambda \right)=1.001$ when $L=10$. Meanwhile, as L gradually increases, $E\left(\lambda \right)$ approaches 1. Therefore, the value of $E\left(\lambda \right)=(\left.1,2\right]$, and $\left.{\eta }_e=\frac{1}{E\left(\lambda \right)}=\left[0.5,1\right.\right)$.

FIGURE 5

FIGURE 5. The relationship between L and E(λ).

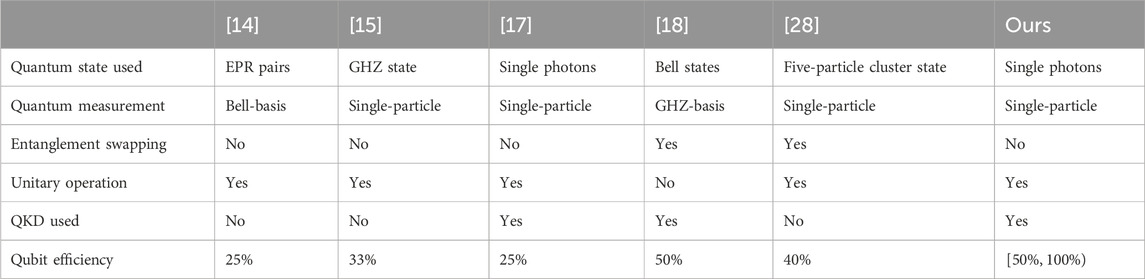
Table 1 illustrates a comparison between the proposed protocol and previous two-party QPC protocols.

TABLE 1

TABLE 1. Comparison among some typical two-party QPC protocols.

Table 1 reveals that our protocol utilizes single photons as carriers of quantum information, which is more feasible than Bell states and multi-particle states. Although both Ref. [17] and our protocol utilize single photons as quantum resources, the qubit efficiency in Ref. [17] is only 25%, which is lower with our protocol with the qubit efficiency of $\left[0.5,1\right)$. Additionally, our protocol only utilizes unitary operations, which are relatively easier to implement compared to the entanglement swapping technology. The QKD technology does not used in Refs. [14, 15, 28] to share the secret key, but it is performed before the protocol begins and its cost can be ignored. Therefore, our protocol is more practical and efficient compared to the previous protocols [14, 15, 17, 18, 28].

6 Conclusion

A single-photon-based quantum secure protocol for the socialist millionaires’ problem is presented in this article. By utilizing single photons as quantum information carriers, encoding the private input through Identity or Hadamard operations, and obtaining the classical outcome via single-particle measurement, the protocol is easier to implement and manipulate compared to other existing protocols. By executing the protocol, TP can ascertain the equality of Alice and Bob’s private inputs and subsequently communicates the result to them. Furthermore, the protocol’s feasibility is tested through simulation on IBM Quantum Cloud Platform. Security analysis demonstrates that any attempt by eavesdroppers or insider parties to grab the private input of another participant is invalid. Currently, the quantum protocols for the socialist millionaires’ problem are primarily designed assuming that all users, including TP, have complete quantum capabilities. In the future, we aim to investigate the development of a quantum protocol that accommodates classical users who can only reflect or measure the received quantum states.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

MH: Formal Analysis, Investigation, Methodology, Writing–original draft. YW: Funding acquisition, Writing–review and editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work is supported by the Gongga Plan for the “Double World-class Project”.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Bennett CH, Brassard G. Quantum cryptography: public key distribution and coin tossing. Theor Comput Sci (2014) 560:7–11. doi:10.1016/j.tcs.2014.05.025

CrossRef Full Text | Google Scholar

2. Hillery M, Bužek V, Berthiaume A. Quantum secret sharing. Phys Rev A (1999) 59(3):1829–34. doi:10.1103/PhysRevA.59.1829

CrossRef Full Text | Google Scholar

3. Li F, Hu H, Zhu S, Yan J, Ding J. A verifiable (k, n)-threshold dynamic quantum secret sharing schemen-threshold dynamic quantum secret sharing scheme. Quan Inf Process (2022) 21(7):259. doi:10.1007/s11128-022-03617-3

CrossRef Full Text | Google Scholar

4. Kuo SY, Tseng KC, Yang CC, Chou YH. Efficient multiparty quantum secret sharing based on a novel structure and single qubits. EPJ Quan Tech (2023) 10(1):29. doi:10.1140/epjqt/s40507-023-00186-x

CrossRef Full Text | Google Scholar

5. Sheng YB, Zhou L, Long GL. One-step quantum secure direct communication. Sci Bull (2022) 67(4):367–74. doi:10.1016/j.scib.2021.11.002

CrossRef Full Text | Google Scholar

6. Zhou L, Sheng YB. One-step device-independent quantum secure direct communication. Sci China Phys Mech Astron (2022) 65(5):250311. doi:10.1007/s11433-021-1863-9

CrossRef Full Text | Google Scholar

7. Huang X, Zhang S, Chang Y, Yang F, Hou M, Chen W. Quantum secure direct communication based on quantum homomorphic encryption. Mod Phys Lett A (2021) 36(37):2150263. doi:10.1142/S0217732321502631

CrossRef Full Text | Google Scholar

8. Yang YG, Gao S, Li D, Zhou YH, Shi WM. Two-party quantum key agreement over a collective noisy channel. Quan Inf Process (2019) 18:74–17. doi:10.1007/s11128-019-2187-8

CrossRef Full Text | Google Scholar

9. Huang X, Zhang SB, Chang Y, Qiu C, Liu DM, Hou M. Quantum key agreement protocol based on quantum search algorithm. Int J Theor Phys (2021) 60:838–47. doi:10.1007/s10773-020-04703-x

CrossRef Full Text | Google Scholar

10. Shor PW. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM Rev (1999) 41(2):303–32. doi:10.1137/S0036144598347011

CrossRef Full Text | Google Scholar

11. Yao AC. Protocols for secure computations. In: 23rd annual symposium on foundations of computer science (sfcs 1982); 03-05 November 1982; Chicago, IL, USA. IEEE (1982). p. 160–4. doi:10.1109/SFCS.1982.38

CrossRef Full Text | Google Scholar

12. Boudot F, Schoenmakers B, Traore J. A fair and efficient solution to the socialist millionaires’ problem. Discrete Appl Maths (2001) 111(1-2):23–36. doi:10.1016/S0166-218X(00)00342-5

CrossRef Full Text | Google Scholar

13. Lo HK. Insecurity of quantum secure computations. Phys Rev A (1997) 56(2):1154–62. doi:10.1103/PhysRevA.56.1154

CrossRef Full Text | Google Scholar

14. Yang YG, Wen QY. An efficient two-party quantum private comparison protocol with decoy photons and two-photon entanglement. J Phys A: Math Theor (2009) 42(5):055305. doi:10.1088/1751-8113/42/5/055305

CrossRef Full Text | Google Scholar

15. Chen XB, Xu G, Niu XX, Wen QY, Yang YX. An efficient protocol for the private comparison of equal information based on the triplet entangled state and single-particle measurement. Opt Commun (2010) 283(7):1561–5. doi:10.1016/j.optcom.2009.11.085

CrossRef Full Text | Google Scholar

16. Lin J, Tseng HY, Hwang T. Intercept–resend attacks on Chen et al.'s quantum private comparison protocol and the improvements. Opt Commun (2011) 284(9):2412–4. doi:10.1016/j.optcom.2010.12.070

CrossRef Full Text | Google Scholar

17. Huang W, Wen QY, Liu B, Gao F, Sun Y. Robust and efficient quantum private comparison of equality with collective detection over collective-noise channels. Sci China Phys Mech Astron (2013) 56:1670–8. doi:10.1007/s11433-013-5224-0

CrossRef Full Text | Google Scholar

18. Huang X, Zhang SB, Chang Y, Hou M, Cheng W. Efficient quantum private comparison based on entanglement swapping of bell states. Int J Theor Phys (2021) 60:3783–96. doi:10.1007/s10773-021-04915-9

CrossRef Full Text | Google Scholar

19. Liu W, Wang YB, Cui W. Quantum private comparison protocol based on Bell entangled states. Commun Theor Phys (2012) 57(4):583–8. doi:10.1088/0253-6102/57/4/11

CrossRef Full Text | Google Scholar

20. Lin S, Guo GD, Liu XF. Quantum private comparison of equality with χ-type entangled states. Int J Theor Phys (2013) 52(11):4185–94. doi:10.1007/s10773-013-1731-z

CrossRef Full Text | Google Scholar

21. Ye TY, Ji ZX. Two-party quantum private comparison with five-qubit entangled states. Int J Theor Phys (2017) 56:1517–29. doi:10.1007/s10773-017-3291-0

CrossRef Full Text | Google Scholar

22. Ji ZX, Zhang HG, Fan PR. Two-party quantum private comparison protocol with maximally entangled seven-qubit state. Mod Phys Lett A (2019) 34(28):1950229. doi:10.1142/S0217732319502298

CrossRef Full Text | Google Scholar

23. Ji Z, Zhang H, Wang H. Quantum private comparison protocols with a number of multi-particle entangled states. IEEE Access (2019) 7:44613–21. doi:10.1109/ACCESS.2019.2906687

CrossRef Full Text | Google Scholar

24. Fan P, Rahman AU, Ji Z, Ji X, Hao Z, Zhang H. Two-party quantum private comparison based on eight-qubit entangled state. Mod Phys Lett A (2022) 37(05):2250026. doi:10.1142/S0217732322500262

CrossRef Full Text | Google Scholar

25. Sun Z, Long D. Quantum private comparison protocol based on cluster states. Int J Theor Phys (2013) 52:212–8. doi:10.1007/s10773-012-1321-5

CrossRef Full Text | Google Scholar

26. Zha XW, Yu XY, Cao Y, Wang SK. Quantum private comparison protocol with five-particle cluster states. Int J Theor Phys (2018) 57:3874–81. doi:10.1007/s10773-018-3900-6

CrossRef Full Text | Google Scholar

27. Xu GA, Chen XB, Wei ZH, Li MJ, Yang YX. An efficient protocol for the quantum private comparison of equality with a four-qubit cluster state. Int J Quan Inf (2012) 10(04):1250045. doi:10.1142/S0219749912500451

CrossRef Full Text | Google Scholar

28. Chang Y, Zhang WB, Zhang SB, Wang HC, Yan LL, Han GH, et al. Quantum private comparison of equality based on five-particle cluster state. Commun Theor Phys (2016) 66(6):621–8. doi:10.1088/0253-6102/66/6/621

CrossRef Full Text | Google Scholar

29. Ye TY. Quantum private comparison via cavity QED. Commun Theor Phys (2017) 67(2):147. doi:10.1088/0253-6102/67/2/147

CrossRef Full Text | Google Scholar

30. Chen FL, Zhang H, Chen SG, Cheng WT. Novel two-party quantum private comparison via quantum walks on circle. Quan Inf Process (2021) 20(5):178. doi:10.1007/s11128-021-03084-2

CrossRef Full Text | Google Scholar

31. Huang X, Chang Y, Cheng W, Hou M, Zhang SB. Quantum private comparison of arbitrary single qubit states based on swap test. Chin Phys B (2022) 31(4):040303. doi:10.1088/1674-1056/ac4103

CrossRef Full Text | Google Scholar

32. Jia HY, Wen QY, Song TT, Gao F. Quantum protocol for millionaire problem. Opt Commun (2011) 284(1):545–9. doi:10.1016/j.optcom.2010.09.005

CrossRef Full Text | Google Scholar

33. Yu CH, Guo GD, Lin S. Quantum private comparison with d-level single-particle states. Physica Scripta (2013) 88(6):065013. doi:10.1088/0031-8949/88/06/065013

CrossRef Full Text | Google Scholar

34. Guo FZ, Gao F, Qin SJ, Zhang J, Wen QY. Quantum private comparison protocol based on entanglement swapping of d-level Bell states. Quan Inf Process (2013) 12(8):2793–802. doi:10.1007/s11128-013-0536-6

CrossRef Full Text | Google Scholar

35. Li L, Shi R. A novel and efficient quantum private comparison scheme. J Korean Phys Soc (2019) 75:15–21. doi:10.3938/jkps.75.15

CrossRef Full Text | Google Scholar

36. Ji Z, Fan P, Zhang H, Wang H. Greenberger-Horne-Zeilinger-based quantum private comparison protocol with bit-flipping. Physica Scripta (2020) 96(1):015103. doi:10.1088/1402-4896/abc980

CrossRef Full Text | Google Scholar

37. Wu WQ, Zhao YX. Quantum private comparison of size using d-level Bell states with a semi-honest third party. Quan Inf Process (2021) 20(4):155. doi:10.1007/s11128-021-03059-3

CrossRef Full Text | Google Scholar

38. Gisin N, Fasel S, Kraus B, Zbinden H, Ribordy G. Trojan-horse attacks on quantum-key-distribution systems. Phys Rev A (2006) 73(2):022320. doi:10.1103/PhysRevA.73.022320

CrossRef Full Text | Google Scholar

39. Huang X, Zhang WF, Zhang SB. Efficient multiparty quantum private comparison protocol based on single photons and rotation encryption. Quan Inf Process (2023) 22(7):272. doi:10.1007/s11128-023-04027-9

CrossRef Full Text | Google Scholar