- 1Department of Biology, University of West Georgia, Carrollton, GA, USA
- 2Department of Physics, University of West Georgia, Carrollton, GA, USA
To explain disparate decay rates of cytosolic Ca2+ and structural changes in the thin filaments during a twitch, we model the time course of Ca2+-bound troponin (Tn) resulting from the free Ca2+ transient of fast skeletal muscle. In fibers stretched beyond overlap, the decay of Ca2+ as measured by a change in fluo-3 fluorescence is significantly slower than the intensity decay of the meridional 1/38.5 nm−1 reflection of Tn; this is not simply explained by considering only the Ca2+ binding properties of Tn alone (Matsuo et al., 2010). We apply a comprehensive model that includes the known Ca2+ binding properties of Tn in the context of the thin filament with and without cycling crossbridges. Calculations based on the model predict that the transient of Ca2+-bound Tn correlates with either the fluo-3 time course in muscle with overlapping thin and thick filaments or the intensity of the meridional 1/38.5 nm−1 reflection in overstretched muscle. Hence, cycling crossbridges delay the dissociation of Ca2+ from Tn. Correlation with the fluo-3 fluorescence change is not causal given that the transient of Ca2+-bound Tn depends on sarcomere length, whereas the fluo-3 fluorescence change does not. Transient positions of tropomyosin calculated from the time course of Ca2+-bound Tn are in reasonable agreement with the transient of measured perturbations of the Tn repeat in overlap and non-overlap muscle preparations.
Introduction
During a twitch of striated muscle, the intracellular fluorescence probe fluo-3 reveals two types of calcium transients (Minta et al., 1989). Owing to its high affinity for Ca2+, fluo-3 detects and contributes to a cytosolic pool of Ca2+ that rises rapidly and persists longer than 150 ms after stimulation of frog striated muscle at 16°C (Harkins et al., 1993; Caputo et al., 1994; Matsuo et al., 2010). The long decay time can be explained by Ca2+ exchange with binding molecules in the cytosol, which may be immobilized molecules such as troponin (Tn) or diffusive molecules such as ATP and parvalbumin, during sequestration of Ca2+ by the sarcoplasmic reticulum (Baylor and Hollingworth, 2011). A transient of free Ca2+, well described by the low-affinity probe furaptra (Hollingworth et al., 2009), can also be calculated from the fluo-3 record (Caputo et al., 1994). The transient of free Ca2+ rises to a peak in 5–7 ms and decays to baseline in about 50 ms at 16°C (Konishi et al., 1991; Hollingworth and Baylor, 2013). This brief pulse of Ca2+ produced by Ca2+ sparks (Cannell et al., 1995) constitutes the intracellular excitation signal for myofilament contraction (Baylor et al., 2002; Baylor and Hollingworth, 2007).
The Ca2+ regulatory sites of Tn (Potter and Gergely, 1975) mediate excitation contraction coupling (Robertson et al., 1981). Based on the binding characteristics of purified Tn (Baylor and Hollingworth, 1998), the decay of Ca2+-bound Tn is expected to follow the long process of fluo-3 decay (Matsuo and Yagi, 2008). However, a simple Ca2+ dissociation rate of Tn is difficult to reconcile with the modeling of the furaptra transient (Baylor et al., 2002). In muscle preparations stretched to average sarcomere lengths of 2.8 and 4.0 μm (overlap and non-overlap preparations, respectively), decays of fluo-3 signals are remarkably similar, but, in the non-overlap preparation, the intensity of the meridional 1/38.5 nm−1 reflection corresponding to the repeat of Tn in the thin filament decays significantly faster than the fluo-3 signal (Matsuo and Yagi, 2008). If Ca2+-bound Tn is a function of the pool of Ca2+ represented by the fluo-3 signal then a significant fraction of Tn remains in the Ca2+-bound state after the Tn-related structure fully relaxes (Matsuo and Yagi, 2008). Our aim is to provide a theoretical framework for the alternative hypothesis, namely, the structure represented by the meridional 1/38.5 nm−1 reflection has a direct relationship with Ca2+-bound Tn.
The properties of Ca2+ binding to the regulatory sites of the C-subunit of Tn (TnC) depend on interactions of Tn with actin in a 7:1:1 molar complex of actin, tropomyosin (Tm), and Tn (regulated actin). Studies using both 45Ca2+ and fluorescence change techniques with native and covalently modified preparations, respectively, consistently demonstrate that the Ca2+ affinity of regulated actin is substantially lower than the Ca2+ affinity of isolated Tn (Wnuk et al., 1984; Rosenfeld and Taylor, 1987; Zot, H. G. and Potter, J. D., 1987). Kinetic measurements of Ca2+-dependent fluorescence changes show slow and fast rates of Ca2+ dissociation from regulated actin; the slow rate correlates with the Ca2+ dissociation rate of isolated Tn, while the other rate is about 10-fold faster (Rosenfeld and Taylor, 1987). Rigor myosin shifts the affinity of regulated actin (myosin:actin:Tm:Tn in a 7:7:1:1 complex with no ATP) to the higher Ca2+ affinity of isolated Tn and reduces the kinetic measurement to one rate, which matches the slow rate of Ca2+ dissociation (Rosenfeld and Taylor, 1987). Tropomyosin can occupy three different positions relative to actin: blocking (B), central (C), and myosin dependent (M) positions. Tn in association with Tm can interact with actin only when Tm is in position B (Lehman et al., 2000). A competition between the open conformation of TnC and actin for the same internal structure of Tn in position B (Gagné et al., 1995; Takeda et al., 2003) could lower the apparent Ca2+ affinity and increase the Ca2+ off rate of Tn in position B by energy coupling. By the same energetic principle, when Tm is in either position C or M and Tn cannot interact with actin, the regulatory sites of TnC should have the higher Ca2+ affinity and slower Ca2+ off rate of isolated Tn.
Cooperative changes associated with Ca2+ binding to TnC depend on not only the context of regulated actin but also the context of rigor and steady-state conditions. Although, some preparations of fluorescently modified TnC display cooperative Ca2+-dependent fluorescence changes (Grabarek et al., 1983; Zot, H. G. and Potter, J. D., 1987; Davis et al., 2002), only a single class of non-interacting Ca2+-binding sites is found for the regulatory sites of native and fluorescently modified TnC in regulated actin by techniques using 45Ca2+ and fluorescence change, respectively (Wnuk et al., 1984; Rosenfeld and Taylor, 1987; Zot, H. G. and Potter, J. D., 1987). Likewise, a non-cooperative fluorescence change in response to Ca2+ is observed for regulated actin saturated with rigor myosin (Rosenfeld and Taylor, 1987). However, in the presence of ATP, muscle fibers and myofibrils reconstituted with fluorescent TnC display steeply cooperative Ca2+-dependent activation and fluorescence changes (Zot et al., 1986; Zot, A. S. and Potter, J. D., 1987; Brandt and Poggesi, 2014). Hence, cooperative Ca2+ binding requires steady-state crossbridges.
Here we link the well-described transient of free Ca2+ to a comprehensive model of contraction (Zot et al., 2009). This model accounts for Ca2+-bound Tn in association with Tm in the three principle structural states of the thin filament (Lehman et al., 2000). As with regulated actin, the muscle fiber is expected to display both slow and fast Ca2+ dissociation rates, which should be evident in the decay rates of structural changes related to Tn and also depend on cycling crossbridges. We apply the model to transient changes in the fluo-3 fluorescence and meridional 1/38.5 nm−1 reflection intensities measured in preparations of frog skeletal muscle at 16°C, with the sarcomere length maintained at overlap or non-overlap of myofilaments (Matsuo et al., 2010), which promotes or prohibits cycling crossbridges, respectively. The model presented here predicts that Ca2+-bound Tn follows the slow decays of fluo-3 fluorescence and meridional 1/38.5 nm−1 reflection intensities of the overlap preparation and only the faster decay of meridional 1/38.5 nm−1 reflection intensity of the non-overlap preparation. The pool of Ca2+ represented by the fluo-3 fluorescence intensity and Ca2+-bound Tn lack a predictable relationship.
Materials and Methods
Description of Model
The model we employ accounts for the relative distributions of thin filament states (Figure 1). The B, C, and M states of Tm refer to Tm's interactions with actin in these respective positions (Lehman et al., 2000). State C is the equilibrium position (Phillips et al., 1986; Lehman et al., 2000), and states B and M are modeled as competing for Tm in state C. To stabilize the non-equilibrium positions B and M, Tm-bound Tn forms an interaction with actin (Greaser and Gergely, 1973) in position B, and Tm forms a ternary complex with crossbridges and actin in position M (Eaton, 1976; Tobacman and Butters, 2000). The interaction of Tn in state B accounts for the states of Tn that are energetically coupled to the states of Tm. Movement of Tm away from B energetically uncouples Tn from possible interactions with actin (Figure 1).
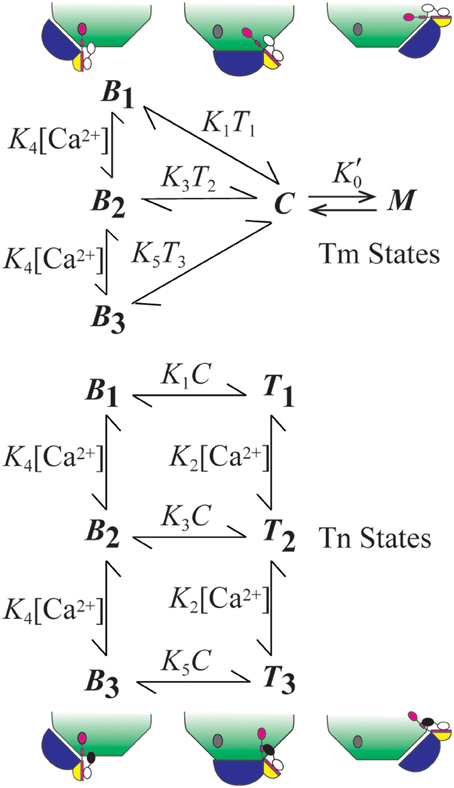
Figure 1. Summary of model. The model consists of two subsystems that partially overlap. The states of Tm (blue) include central (C), myosin-dependent (M), and blocking (Bi, i = 1–3). States of Tn (TnT, yellow; TnI, magenta; TnC, black-white) include energetically coupled (Bi) and uncoupled (Ti) states each having regulatory sites of TnC that can be Ca2+-free (i = 1; white), singly Ca2+-bound (i = 2; black), and doubly Ca2+-bound (i = 3; black). The diagram shows how Tn is isolated from a site of interaction with actin (gray oval) by the movement of Tm from position B to positions C and M. All constants depicted in the figure represent the ratio of component rate constants (Table 1) used to calculate the relative abundance or probability of each state as a function of a transient change in calcium concentration.
Coupled and uncoupled states of Tn are designated B and T, respectively (Figure 1). Calcium-dependent states of Tn are designated Bi and Ti, where i represents 1 (Ca2+ free), 2 (singly bound), or 3 (doubly bound). Affinity for actin is progressively reduced as i increases. Based on conservation of the mass for two partially overlapping subsystems (Tm and Tn), B + C + M = 1 for Tm and B + T = 1 for Tn.
In the system we describe, M can arise by either rigor or cycling crossbridges, but cooperativity derives solely from cycling crossbridges, as seen in the records of Ca2+ binding measurements. With overlapping thin and thick filaments and ATP, M is a state in constant flux (steady-state) rather than at equilibrium; this is readily observed by Ca2+-dependent in vitro sliding of regulated actin filaments. Steady-state cooperativity is achieved if crossbridge turn-over generates additional opportunities (second chances) for M formation (Zot et al., 2009, 2012). By analogy, the M state operates like a man whose feet are bound to a ceiling by adhesion: changing positions quickly relative to the rate of deadhesion improves the odds of remaining bound by re-establishing the initial binding conditions. A statistical treatment of a second chance mechanism applied to data from biological systems is available (Zot et al., 2016a). In practice, a second chance mechanism is given in the following rate equation
where parameters , k−0, α, and n are derived elsewhere (Zot et al., 2009, 2012). The parameter α expresses second chance opportunities for reestablishing equilibrium before the decay of M. As steady-state or equilibrium approach, dM/dt → 0. Because Equation (1) acts on the C-M transition (Figure 1), cooperativity does not directly involve Ca2+ binding to Tn. Although, Equation (1) performs adequately, any logistic function operating on C can be compatible with our model.
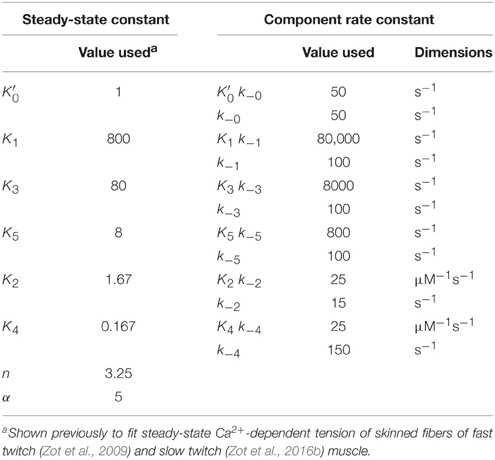
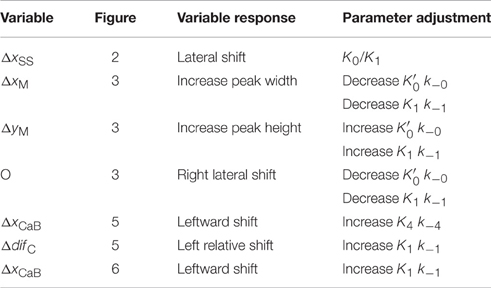
As applied to transient and steady-state striated muscle regulation, the parameters of Equation (1) may have the following interpretations. The equilibrium potential of M as a function of the population of strong binding myosin at any moment of steady-state is expressed by . The forward rate of ensemble M formation is the product k−0. Ensemble size, n, expresses the number of Tm subunits acting in concert to form a ternary complex as described above. The orchestrating event could be a lateral stretch imposed on contiguous Tm subunits by an axial force acting on the thin filament (Zot et al., 2009). The parameter α is an expression of the crossbridges poised to replace crossbridges disrupted by internal chemomechanical forces or by active sliding. The value of α may be related to the average number of crossbridges in a target zone (Tregear et al., 2004), as has been described (Zot et al., 2009). We give unit value to for simplicity and recycle previously discussed values for α, and n (Zot et al., 2009; Table 1) for consistency.
Computational Methods
Transitions other than C-M are spontaneous processes governed by simple mass action (Figure 1). Although the model has eight states, only six are independent. If we choose to calculate states C and T1 by mass conservation (see above), the relative abundances or probabilities of the other six states (Figure 1) as a function of an independent calcium transient are calculated by solving a system of six ordinary differential equations (ODE), i.e., in addition to Equation (1), we have
This system of ODE is solved for each free Ca2+ concentration of a given transient. The free Ca2+ transient of a muscle fiber (Matsuo et al., 2010) is reproduced by a linear rise from the origin to the peak (time to peak is 0.005 s), followed by an exponential decay (rate constant is 100 s−1; Figure 2). We use the same Ca2+ transient for all calculations as a control. Hence, the model varies only the contribution of crossbridges in fitting data from overlap and non-overlap preparations. A Matlab program is provided to reproduce calculations presented here (see Supplementary Materials).
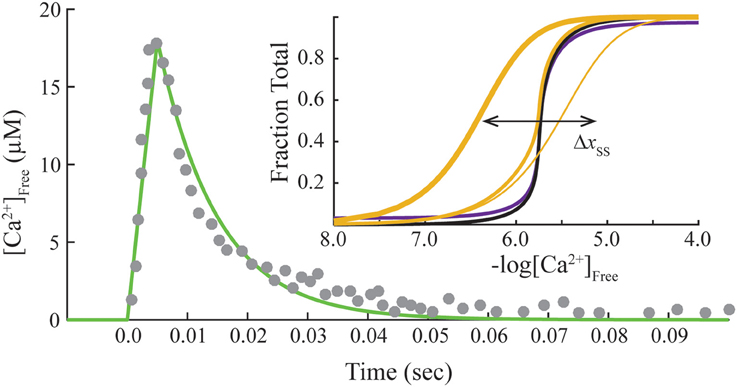
Figure 2. Standard transient of free Ca2+ and final steady-state conditions. Transient free Ca2+ data (dots) reproduced from Matsuo et al. (2010) are fit empirically by a mathematical function (green). Inset, Steady-state activation (M state) is plotted as a function of free Ca2+ concentration on absolute (purple) and normalized (black) scales. Adjusting steady-state constants (Table 2) shifts the curves for activation laterally (Δxss). Predicted Ca2+-bound Tn curves (gold) that simulate no crossbridges (1 pt. line), saturating rigor crossbridges (3 pt. line), and cycling crossbridges (2 pt. gold line) are calculated with set to 0, 106, and 1, respectively, under the standard equilibrium/steady-state conditions of Table 1. Hill coefficients (Hill, 1910) of unity are determined for curves representing no crossbridges and rigor crossbridges.
Standard conditions refer to a set of constants governing steady-state potentials (upper case, “K”), α, and n that we hold constant (Table 1). Thermodynamic principles dictate that K1/K3 = K3/K5 = K2/K4, which allows , K1, K2, and K4 to be selected independently. The values used here for these four parameters, α, and n (Table 1) are the same shown elsewhere to fit steady-state activation of skinned fibers of fast muscle (Zot et al., 2009) and cardiac muscle (Zot et al., 2016b) by Ca2+. Component rate constants (lower case, “k”) are varied to fit transient data. Slow and fast dissociation rates of Ca2+ from Tn (k−2 and k−4; Table 1), are taken from Rosenfeld and Taylor (1987).
Results
Steady-State and Equilibrium Behavior of the Model
Steady-state or equilibrium calculations are produced for standard conditions (Table 1) by nullifying the system of ODE (cf. Matlab program in Zot et al., 2016b). Calculated Ca2+-dependent activation curves on absolute and normalized scales (inset, Figure 2) reproduce fits of steady-state tension and ATPase data of diverse native and mutant protein preparations of fast skeletal and cardiac muscles (Zot et al., 2009, 2016b). To verify that the model reproduces established Ca2+ binding properties of Tn, Ca2+-bound Tn (B2 + B3 + T2 + T3) is calculated as a function of constant concentrations of Ca2+. With cycling crossbridges, the mathematical solution is a cooperative function of Ca2+ (inset, Figure 2), which reproduces the distinctive binding-activation relationship observed previously with fluorescently labeled Tn in reconstituted myofibrils (Zot et al., 1986; Zot, A. S. and Potter, J. D., 1987; Brandt and Poggesi, 2014). To model equilibrium achieved by non-overlap or rigor, is set either to zero or to a relatively large value (106), respectively. Both solutions predict simple mass action (non-cooperative) calcium binding (inset, Figure 2), and both simulations reproduce published simple mass action Ca2+ binding curves for regulated actin and regulated actin with rigor myosin binding, respectively (Rosenfeld and Taylor, 1987). Hence, the model is able to reproduce cooperative and non-cooperative Ca2+ binding measurements of both steady-state and equilibrium preparations, respectively.
Transient Response with Overlap
The transient of calcium-bound troponin, which is modeled as the sum of B2, B3, T2, and T3, is compared with the transient change measured by fluo-3 fluorescence (Matsuo et al., 2010) in overlap muscle preparations. Rather than choosing parameters to fit the fluo-3 data, we fit tension data (Figure 3) from the same preparation with calculated value of M (Equation 1) by adjusting the rate constants (Table 2) that comprise standard conditions (Table 1). Decreasing k−0 shifts the calculated tension transient rightward, and k−0 is decreased in tandem to maintain constant . The same constraint is used throughout to maintain standard conditions. Although adjusting either k−0 or K1k−1 changes the tension transient equivalently, using k−0 for lateral adjustments and K1k−1 for vertical adjustments yields the best shape of the tension transient relative to the data. Given the optimum fit of the tension data, the predicted Ca2+-bound Tn transient is seen to fit most of the fluo-3 fluorescent data (Figure 3). If we accept a slightly faster time to peak tension, the model predicts slower decay of Ca2+-bound Tn, which may better capture the entire trend of fluo-3 data (see Supplementary Materials).
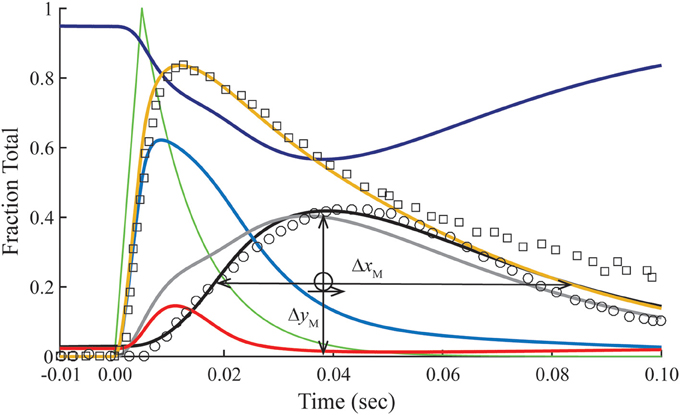
Figure 3. Time courses of principle states of the thin filament with overlap. Plotted as a function of a pulse of free calcium (green) are calculated transients of states B (dark blue), C (red), and M (black). Total Ca2+-bound Tn (B2 + B3 + T2 + T3; gold) is broken down into components, i.e., fast (B2 + B3; blue) and slow (T2 + T3; gray). Plotted on the same scale are measured tension (circles) and fluo-3 fluorescence (squares) transients of muscle fibers of average sarcomere length of 2.8 μm and stimulated by a single impulse (reproduced from Matsuo et al., 2010). Adjustments in standard conditions (Table 1) alter the width (ΔxM), height (ΔyM), and center of the M peak (O) as described in Table 2.
The dissociation of Ca2+ from the Ca2+ regulatory sites of Tn is not uniform over time. Owing to a faster off-rate, Ca2+-bound B states (B2 + B3) release Ca2+ faster than Ca2+-bound T states (T2 + T3; Figure 3). Hence, a significant fraction of Tn has released Ca2+ before tension reaches a peak. A protracted dissociation of residual Ca2+ comes mainly from T states, which represent a pool of Tn molecules held away from interaction with actin in the B position owing to crossbridges (crossbridge-dependent Ca2+-bound Tn).
Transient Response with Non-overlap
The relationship between calculated Ca2+-bound Tn and fluo-3 data differs dramatically in muscle fibers stretched beyond overlap. To simulate no overlap, we nullify k−0 in Equation (1), but otherwise preserve the rates established for the overlap condition (Table 1). Absent crossbridges, the decays of calculated Ca2+-bound troponin, whether expressed as a total or separated into components B and T, are much faster than the decay of fluo-3 fluorescence (Figure 4). No combinations of rate constants will allow the model to fit the tension data of the overlap preparation and the fluo-3 data of overlap and non-overlap preparations. By contrast, the decay of fluo-3 fluorescence is constant for overlap and non-overlap conditions (Figures 3, 5). Therefore, there is not a causal relationship between the calculated Ca2+-bound state of troponin and fluo-3 fluorescence.
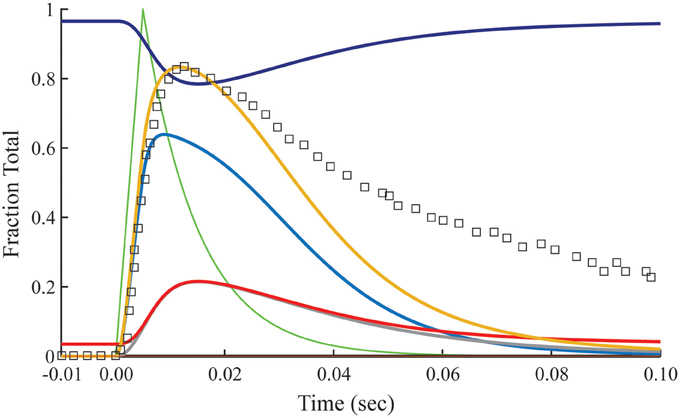
Figure 4. Time courses of principle states of the thin filament with no overlap. Plotted as a function of a pulse of free calcium (green) are calculated transients of states B (dark blue), C (red), and M (black). Total Ca2+-bound Tn (B2 + B3 + T2 + T3; gold) is broken down into fast (B2 + B3; blue) and slow (T2 + T3; gray) components. For comparison, the measured fluo-3 fluorescence transient (squares) is reproduced from Figure 3.
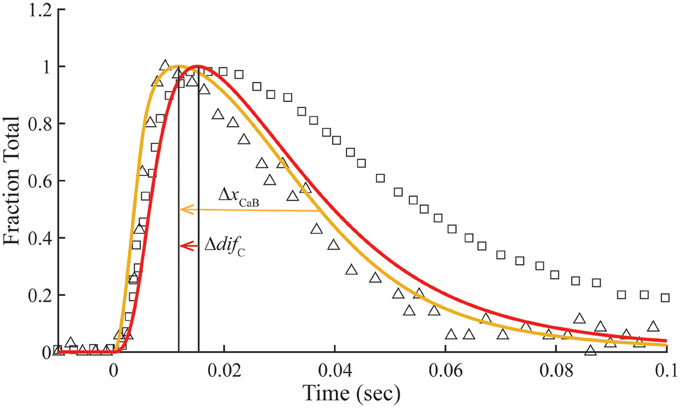
Figure 5. Time courses of fluo-3 fluorescence and transient structural changes of troponin in nonoverlap sarcomeres. Changes in intensity of the meridional 1/38.5 nm−1 reflection (triangles) and of fluo-3 fluorescence (squares) in response to a single calcium pulse are reproduced for muscle stretched beyond overlap (Matsuo et al., 2010). Plotted on the same scale in response to a simulated calcium pulse (Figure 2) are the calculated temporal change of state C (red) and calcium bound to troponin (gold) under standard conditions (Table 1) with set to null. Other adjustments in standard conditions (Table 2) alter the decay rate of Ca2+-bound Tn (ΔxCaB) and the relationship with the state C transient (Δdif C).
Matsuo et al. (2010) show that in a non-overlap sarcomere preparation, the fluo-3 fluorescence decay is slower than the decay of meridional 1/38.5 nm−1 reflection intensity, which corresponds to the troponin repeat in the thin filament (Figure 5). We find that the calculated time courses of Ca2+-bound Tn and the C position of Tm correlate with the transient of meridional 1/38.5 nm−1 reflection intensity (Figure 5). A systematic sensitivity test of all rate constants shows that the decay of Ca2+-bound Tn is limited only by k−4 of the model (Figure 5, Table 2). This is the faster of two dissociation rates determined for Ca2+ from regulated actin (Rosenfeld and Taylor, 1987). Increasing k−4 by a factor of 1.33, which is within the range of measured values (Rosenfeld and Taylor, 1987), and maintaining the same steady-state conditions (inset, Figure 2) bring the decay rate of Ca2+-bound Tn closer in alignment with the decay of meridional 1/38.5 nm−1 reflection intensity (see Supplementary Materials). Furthermore, the decays of Ca2+-bound Tn and state C of Tm align more closely by increasing K1k−1 (Figure 5, Table 2; see Supplementary Materials). Hence, the model predicts that the decay rate of meridional 1/38.5 nm−1 reflection intensity in the non-overlap preparation gives an in vivo measure of the rate of Ca2+ dissociation from Tn. A characteristic intensity increase in response to Ca2+ represents Tn-dependent structural changes of the thin filament (Yagi, 2003). Modeling suggests that Ca2+-bound Tn regulates completely the structural changes related to the movement of Tm to position C in the non-overlap preparation.
Transient Structural Changes with Overlap
In the overlap preparation, the structural changes related to meridional 1/38.5 nm−1 reflection intensity are more complex (Matsuo et al., 2010), showing intensity changes with positive and negative slopes over the time course of a twitch (Figure 6). The early rise in reflection intensity correlates with a brief period at the beginning of the Ca2+ pulse in which the model predicts a rise in Ca2+-bound Tn and state C of Tm before the transition to state M of Tm begins. The large negative change in reflection intensity has roughly the same time course as the calculated fraction of Tm in the M position (Figure 6). The minimum reflection intensity comes at a time after the Ca2+ transient has decayed and the calculated M state has peaked.
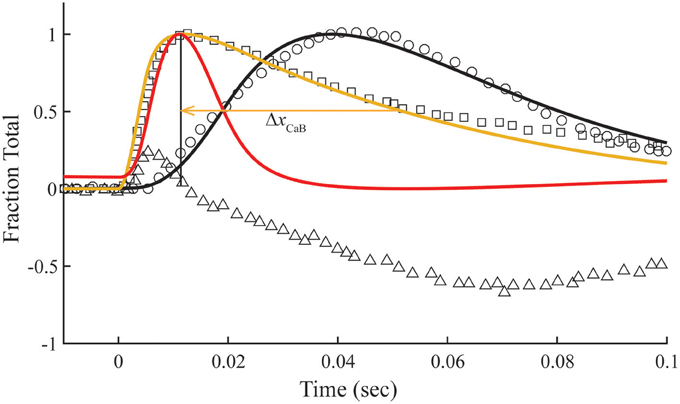
Figure 6. Model compared with temporal responses measured in overlap sarcomeres. Intensities of the meridional 1/38.5 nm−1 reflection (triangles), tension (circles), and fluo-3 fluorescence (squares) for average sarcomere length of 2.8 μm in response to a single calcium pulse are reproduced (Matsuo et al., 2010). Plotted on the same scale in response to a simulated calcium pulse (Figure 2) are the calculated temporal changes of states C (red) and M (black) and Ca2+-bound Tn (gold) under standard conditions (Table 1). Adjustments in standard conditions (Table 2) alter the decay rate of Ca2+-bound Tn (ΔxCaB).
The calculated decay rate of Ca2+-bound Tn can be made more rapid than the measured decay of fluo-3 fluorescence by increasing rate constants, K1 k−1, at fixed K1 (Figure 6, Table 2). However, both absolute rates and the competition between states M and B for Tm in state C (Figure 1) must be made more extreme to hold constant the calculated tension transient (Figure 3). Thus, a balance of competing factors explains the correlation between the calculated Ca2+-bound state of Tn and the fluo-3 fluorescence transient in the overlap preparation (Figure 6).
Predicted Time Course of Crossbridge-Dependent Ca2+-Bound Tn
Crossbridge-dependent Ca2+-bound Tn is the difference between Ca2+-bound Tn calculated for overlap and non-overlap conditions, holding the transient of free Ca2+ constant (Figure 7). The residue is a pool of crossbridge-dependent Ca2+-bound Tn, which represents about 30% of the total area under the curve. The rise in the pool of crossbridge-dependent Ca2+-bound Tn begins near the end of the free Ca2+ transient and continues during the decay of the tension transient. Peaking at ~60 ms, the time course of rising crossbridge-dependent Ca2+-bound Tn correlates most closely with the time course of the declining phase in meridional 1/38.5 nm−1 reflection intensity, which reaches a minimum at ~70 ms.
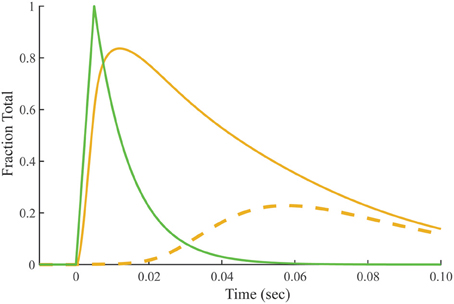
Figure 7. Predicted time course of crossbridge-dependent Ca2+-bound Tn. Crossbridge-dependent Ca2+-bound Tn is the residual (dashed line) obtained by subtracting Ca2+-bound Tn calculated for the non-overlap preparation (Figure 4) from Ca2+-bound Tn calculated for the overlap preparation (solid gold line; Figure 3). The stimulus for both conditions (green) is taken from Figure 2.
Discussion
A comprehensive model of thin filament regulation presented here supports the hypothesis that Ca2+-bound Tn has a causal relationship with the structure of Tn in the thin filament and not with the pool of Ca2+ represented by the intensity of fluo-3 fluorescence. Rather than recapitulating the decay of the fluo-3 fluorescence change in the non-overlap preparation of frog muscle, the model presented here generates transients for Ca2+-bound Tn and position C of Tm-Tn that match transient changes in intensity of the meridional 1/38.5 nm−1 reflection in response to Ca2+ stimulus. The model predicts similar rates of Ca2+ dissociation from the regulatory sites of Tn in the first 50 ms following stimulation of both preparations, overlap and non-overlap. After this period, the model predicts that decays of Ca2+-bound Tn in the two preparations diverge, hence demonstrating a fraction of Ca2+-bound Tn that persists owing to crossbridge interaction. Given the same free Ca2+ transient for both overlap and nonoverlap conditions, calculations of Ca2+-bound Tn, and crossbridge-dependent Ca2+-bound Tn correlate with the time courses of positive and negative changes in intensity of the meridional 1/38.5 nm−1 reflection, respectively, suggestive of a causal relationship. By reproducing the twitch of a well-studied physiologic system given a highly reproducible experimental Ca2+ transient, we achieve a proof of concept for the model presented here.
Fluo-3 may be responding to an exchangeable pool of Ca2+ bound to Ca2+ buffers in the sarcoplasm (Cannell and Allen, 1984; Baylor and Hollingworth, 1998). Small diffusible Ca2+ binding molecules such as ATP and parvalbumin in the myofilaments can facilitate the diffusion of Ca2+ (Feher, 1984) and thereby possibly reduce random non-uniform reactivation events in relaxing myofibrils. However, a fixed Ca2+ buffer also prolongs elevated Ca2+ in the cytosol at all sarcomere lengths, regardless of the status of Ca2+-bound Tn. The decay of the fluo-3 fluorescence may represent a compromise based on the Ca2+ requirements of the working and relaxed muscle.
We assume that the Ca2+ sequestration apparatus has the capacity to prevent a significant rise in free Ca2+ resulting from a pool of crossbridge-dependent Ca2+-bound Tn during a twitch. Aside from equilibrium binding of Ca2+ to buffering agents represented by the fluo-3 fluorescence intensity, Ca2+ is actively transported from the sarcoplasm by the Ca2+ pump of the sarcoplasmic reticulum (SR Ca2+-ATPase). Previous results from amphibian fast skeletal muscle using inhibitors of SR Ca2+-ATPase have shown that the decay and not the peak in free Ca2+ depends on active Ca2+ transport (Jiang et al., 1996; Westerblad and Allen, 1996; Même et al., 1998; Caputo et al., 1999). The delay in onset argues against a significant contribution to the rise and decay process of free Ca2+ sparks by Ca2+ dissociating from the pool of crossbridge-dependent Ca2+-bound Tn. We suggest the rate and load of Ca2+ dissociating from crossbridge-dependent Ca2+-bound Tn is within the capacity of Ca2+ buffers and SR Ca2+-ATPase to move into the SR without effecting a significant increase in sarcoplasmic free Ca2+.
One assumption of the model is that cooperative activation depends exclusively on cycling crossbridges. Although, Equation (1) has the distinction of being a more general form of the Hill equation (Zot et al., 2012), the resulting system of ODE we derive here are mathematically compatible with any logistic function. Hence, the model presented here is limited to a mechanism of regulation in which a steady-state process fully accounts for cooperative transitions between C and M states.
A second assumption of the model is that activated state, M, is proportional to the fraction of maximum tension. This simplification is consistent with the proposal that tension bearing crossbridges are excluded from thin filament states C and B (Lehman et al., 2000).
A third assumption of the model is that Ca2+ binding to the regulatory sites of TnC is uncoupled from the process of activation when the complex of Tm-Tn is in positions C and M. Consequently, we model the C position as favored at equilibrium. Tm occupies either C or B positions in reconstructions of skeletal and cardiac filaments, respectively, but the complex of Tm-Tn is positioned exclusively in C with Ca2+ present (Lehman et al., 2000). There is general agreement that Ca2+ is required to release Tm-Tn from the B position. A possible, albeit more complicated, mechanism is for Ca2+ to have a second, independent action, namely, to perturb the equilibrium position of the Tm-Tn complex. This latter possibility is difficult to reconcile with an uncoupling mechanism.
Although, we do not address a specific myopathy, we suggest that results presented here can be extrapolated to mechanisms underlying disease. By employing a model that accounts for the Ca2+ regulatory properties of Tn, we provide a satisfying explanation for the events of contraction arising from a transient of free Ca2+. The model presented here is consistent with previous experimental results showing non-cooperative Ca2+ binding to regulated actin in the presence or absence of rigor crossbridges and recapitulates the complex cooperative relationship between Ca2+-binding and force in the steady-state (Figure 2). Of the eight adjustable parameters (Table 2), we have consistently published results in which K1 alone is freely adjusted and K3 and K5 vary in a prescribed manner. A recent study shows that the model presented here can inform experiments that explain how a mutation in TnC alters the Ca2+ sensitivity of cardiac myofilaments associated with the hypertrophic state of the heart (Zot et al., 2016b). A previous study shows that the model presented here can fully explain the depressing effect of Ca2+-insensitive mutant TnC on cooperative activation of skeletal muscle fibers (Zot et al., 2009). Hence, a growing body of experimental results in cardiac and skeletal muscle, mutant and wild type preparations, reconstituted and intact systems, and steady-state and transient conditions are explained by the same model and highly constrained parameters of this model. As a robust and reliable predictor of transient and steady-state changes in thin filament structure related to Ca2+-bound Tn, the model presented here is capable of guiding future experiments to uncover mechanisms by which mutations in excitation-contraction coupling lead to pathological conditions.
Author Contributions
Each of the authors contributed significantly to the conception and design of the work, drafting and revision of the manuscript, and final approval of the version to be published. Both authors agree to be accountable for all aspects of the work.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Supplementary Material
The Supplementary Material for this article can be found online at: http://journal.frontiersin.org/article/10.3389/fphys.2016.00406
Abbreviations
Troponin, Tn; tropomyosin, Tm; B, state of Tm in the blocking position; C, state of Tm in the central position; M, state of Tm in the myosin-dependent position.
References
Baylor, S. M., and Hollingworth, S. (1998). Model of sarcomeric Ca2+ movements, including ATP Ca2+ binding and diffusion, during activation of frog skeletal muscle. J. Gen. Physiol. 112, 297–316. doi: 10.1085/jgp.112.3.297
Baylor, S. M., and Hollingworth, S. (2007). Simulation of Ca2+ movements within the sarcomere of fast-twitch mouse fibers stimulated by action potentials. J. Gen. Physiol. 130, 283–302. doi: 10.1085/jgp.200709827
Baylor, S. M., and Hollingworth, S. (2011). Calcium indicators and calcium signalling in skeletal muscle fibres during excitation-contraction coupling. Prog. Biophys. Mol. Biol. 105, 162–179. doi: 10.1016/j.pbiomolbio.2010.06.001
Baylor, S. M., Hollingworth, S., and Chandler, W. K. (2002). Comparison of simulated and measured calcium sparks in intact skeletal muscle fibers of the frog. J. Gen. Physiol. 20, 349–368. doi: 10.1085/jgp.20028620
Brandt, P. W., and Poggesi, C. (2014). Clusters of bound Ca2+ initiate contraction in fast skeletal muscle. Arch. Biochem. Biophys. 552–553, 60–67. doi: 10.1016/j.abb.2013.12.013
Cannell, M. B., and Allen, D. G. (1984). Model of calcium movements during activation in the sarcomere of frog skeletal muscle. Biophys. J. 45, 913–925. doi: 10.1016/S0006-3495(84)84238-1
Cannell, M. B., Cheng, H., and Lederer, W. J. (1995). The control of calcium release in heart muscle. Science 268, 1045–1049. doi: 10.1126/science.7754384
Caputo, C., Bolaños, P., and Escobar, A. L. (1999). Fast calcium removal during single twitches in amphibian skeletal muscle fibres. J. Mus. Res. Cell Motil. 20, 555–567. doi: 10.1023/A:1005526202747
Caputo, C., Edman, K. A., Lou, F., and Sun, Y. B. (1994). Variation in myoplasmic Ca2+ concentration during contraction and relaxation studied by the indicator fluo-3 in frog muscle fibres. J. Physiol. 478(Pt 1), 137–148. doi: 10.1113/jphysiol.1994.sp020237
Davis, J. P., Rall, J. A., Reiser, P. J., Smillie, L. B., and Tikunova, S. B. (2002). Engineering competitive magnesium binding into the first EF-hand of skeletal troponin C. J. Biol. Chem. 277, 49716–49726. doi: 10.1074/jbc.M208488200
Eaton, B. L. (1976). Tropomyosin binding to F-actin induced by myosin heads. Science 192, 1337–1339. doi: 10.1126/science.131972
Feher, J. J. (1984). Measurement of facilitated calcium diffusion by a soluble calcium-binding protein. Biochim. Biophys. Acta 773, 91–98. doi: 10.1016/0005-2736(84)90553-4
Gagné, S. M., Tsuda, S., Li, M. X., Smillie, L. B., and Sykes, B. D. (1995). Structures of the troponin C regulatory domains in the apo and calcium-saturated states. Nat. Struct. Biol. 2:784–789. doi: 10.1038/nsb0995-784
Grabarek, Z., Grabarek, J., Leavis, P. C., and Gergely, J. (1983). Cooperative binding to the Ca2+-specific sites of troponin C in regulated actin and actomyosin. J. Biol. Chem. 258, 14098–14102.
Greaser, M. L., and Gergely, J. (1973). Purification and properties of the components from troponin. J. Biol. Chem. 248, 2125–2133.
Harkins, A. B., Kurebayashi, N., and Baylor, S. M. (1993). Resting myoplasmic free calcium in frog skeletal muscle fibers estimated with fluo-3. Biophys. J. 65, 865–881. doi: 10.1016/S0006-3495(93)81112-3
Hill, A. V. (1910). The possible effects of the aggregation of the molecules of haemoglobin on its dissociation curves. J. Physiol. 40, iv–vii.
Hollingworth, S., and Baylor, S. M. (2013). Comparison of myoplasmic calcium movements during excitation-contraction coupling in frog twitch and mouse fast-twitch muscle fibers. J. Gen. Physiol. 141, 567–583. doi: 10.1085/jgp.201310961
Hollingworth, S., Gee, K. R., and Baylor, S. M. (2009). Low-affinity Ca2+, indicators compared in measurements of skeletal muscle Ca2+, transients. Biophys. J. 97, 1864–1872. doi: 10.1016/j.bpj.2009.07.021
Jiang, Y., Johnson, J. D., and Rall, J. A. (1996). Parvalbumin relaxes frog skeletal muscle when sarcoplasmic Ca2+-ATPase inhibited. Am. J. Physiol. 270, C411–C417.
Konishi, M., Hollingworth, S., Harkins, A. B., and Baylor, S. M. (1991). Myoplasmic calcium transients in intact frog skeletal muscle fibers monitored with the fluorescent indicator furaptra. J. Gen. Physiol. 97, 271–301. doi: 10.1085/jgp.97.2.271
Lehman, W., Hatch, V., Korman, V., Rosol, M., Thomas, L., Maytum, R., et al. (2000). Tropomyosin and actin isoforms modulate the localization of tropomyosin strands on actin filaments. J. Mol. Biol. 302, 593–606. doi: 10.1006/jmbi.2000.4080
Matsuo, T., Iwamoto, H., and Yagi, N. (2010). Monitoring the structural behavior of troponin and myoplasmic free Ca2+ concentration during twitch of frog skeletal muscle. Biophys. J. 99, 193–200. doi: 10.1016/j.bpj.2010.04.021
Matsuo, T. Yagi, N. (2008). Structural changes in the muscle thin filament during contractions caused by single and double electrical pulses. J. Mol. Biol. 383, 1019–1036. doi: 10.1016/j.jmb.2008.09.007
Même, W., Huchet-Cadiou, C., and Léoty, C. (1998). Cyclopiazonic acid-induced changes in the contraction and Ca2+ transient of frog fast-twitch skeletal muscle. Am. J. Physiol. 274, C253–C261.
Minta, A., Kao, J. P., and Tsien, R. Y. (1989). Fluorescent indicators for cytosolic calcium based on rhodamine and fluorescein chromophores. J. Biol. Chem. 264, 8171–8178.
Phillips, G. N. Jr., Fillers, J. P., and Cohen, C. (1986). Tropomyosin crystal structure and muscle regulation. J. Mol. Biol. 192, 111–131. doi: 10.1016/0022-2836(86)90468-7
Potter, J. D., and Gergely, J. (1975). The calcium and magnesium binding sites on troponin and their role in the regulation of myofibrillar adenosine triphosphatase. J. Biol. Chem. 250, 4628–4633.
Robertson, S. P., Johnson, J. D., and Potter, J. D. (1981). The time-course of Ca2+ exchange with calmodulin, troponin, parvalbumin, and myosin in response to transient increases in Ca2+. Biophys. J. 34, 559–569. doi: 10.1016/S0006-3495(81)84868-0
Rosenfeld, S. S., and Taylor, E. W. (1987). The mechanism of regulation of actomyosin subfragment 1 ATPase. J. Biol. Chem. 262, 9984–9993.
Takeda, S., Yamashita, A., Maeda, K., and Maeda, Y. (2003). Structure of the core domain of human cardiac troponin in the Ca2+-saturated form. Nature 424:35–41. doi: 10.1038/nature01780
Tobacman, L. S., and Butters, C. A. (2000). A new model of cooperative myosin-thin filament binding. J. Biol. Chem. 275, 27587–27593. doi: 10.1074/jbc.m003648200
Tregear, R. T., Reedy, M. C., Goldman, Y. E., Taylor, K. A., Winkler, H., Franzini-Armstrong, C., et al. (2004). Cross-bridge number, position, and angle in target zones of cryofixed isometrically active insect flight muscle. Biophys. J. 86, 3009–3019. doi: 10.1016/S0006-3495(04)74350-7
Westerblad, H., and Allen, D. G. (1996). Slowing of relaxation and [Ca2+]i during prolonged tetanic stimulation of single fibres from Xenopus skeletal muscle. J. Physiol. Lond. 492, 723–736. doi: 10.1113/jphysiol.1996.sp021341
Wnuk, W., Schoechlin, M., and Stein, E. A. (1984). Regulation of actomyosin ATPase by a single calcium-binding site on troponin C from crayfish. J. Biol. Chem. 259, 9017–9023.
Yagi, N. (2003). An x-ray diffraction study on early structural changes in skeletal muscle contraction. Biophys. J. 84, 1093–1102. doi: 10.1016/S0006-3495(03)74925-X
Zot, A. S., and Potter, J. D. (1987). The effect of [Mg2+] on the Ca2+ dependence of ATPase and tension development of fast skeletal muscle. The role of the Ca2+-specific sites of troponin C. J. Biol. Chem. 262, 1966–1969.
Zot, H. G., Güth, K., and Potter, J. D. (1986). Fast skeletal muscle skinned fibers and myofibrils reconstituted with N-terminal fluorescent analogues of troponin C. J. Biol. Chem. 261, 15883–15890.
Zot, H. G., Hasbun, J. E., Michell, C. A., Landim-Vieira, M., and Pinto, J. R. (2016b). Enhanced troponin I binding explains the functional changes produced by the hypertrophic cardiomyopathy mutation A8V of cardiac troponin C. Arch. Biochem. Biophys. 601, 97–104. doi: 10.1016/j.abb.2016.03.011
Zot, H. G., Hasbun, J. E., and Minh, N. V. (2012). Second-chance signal transduction explains cooperative flagellar switching. PLoS ONE 7:e41098. doi: 10.1371/journal.pone.0041098
Zot, H. G., Hasbun, J. E., and Van Minh, N. (2016a). Common basis for cellular motility. arXiv:1511.00123.
Zot, H. G., Hasbun, J. E., and Van Minh, N. (2009). Striated muscle regulation of isometric tension by multiple equilibria. PLoS ONE 4:e8052. doi: 10.1371/journal.pone.0008052
Keywords: contraction, calcium, troponin, excitation, muscle, EC-coupling, model, kinetics
Citation: Zot HG and Hasbun JE (2016) Modeling Ca2+-Bound Troponin in Excitation Contraction Coupling. Front. Physiol. 7:406. doi: 10.3389/fphys.2016.00406
Received: 25 June 2016; Accepted: 30 August 2016;
Published: 21 September 2016.
Edited by:
P. Bryant Chase, Florida State University, USAReviewed by:
Corrado Poggesi, University of Florence, ItalyJohn Jeshurun Michael, Cornell University, USA
Copyright © 2016 Zot and Hasbun. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Henry G. Zot, hzot@westga.edu
 Henry G. Zot
Henry G. Zot Javier E. Hasbun2
Javier E. Hasbun2