Market size asymmetry and strategic environmental policy in a Cournot model

1. Introduction

The introduction in the mid-1970s of monopolistic market structures in the study of international trade allowed for the possibility that a given government policy can shape a country's (or firm's) comparative advantage in the international markets (see Stegemann, 1989). The introduction of the “strategic trade policy” term characterized then a branch that studies the policy implications in trade models that incorporate international interdependence of policy measures in the framework of a monopolistic environment. The seminal works of Spencer and Brander (1983), Krugman (1984), and Brander and Spencer (1985) constitute the main references on strategic trade policy.

In the field of international environmental problems, strategic trade models have been widely used to study the choice of the level of a given environmental policy. Some examples are Krutilla (1991), Barrett (1994), Kennedy (1994), and Ulph (1994) and, more recently, Xepapadeas (2000), Burguet and Sempere (2003), Lai and Hu (2008), Baksi and Chaudhuri (2009), and Buccella et al. (2021). Ulph and Ulph (1996) provides a good literature review. The main conclusion of this literature is that when firms operate in an oligopolistic international market, the governments have incentives to adopt lower than optimal levels of environmental policies. This effect is particularly relevant when individual countries can establish unilateral industrial policies and firms engage in Cournot (quantity) competition. Instead, if firms engage in Bertrand (price) competition, governments will set strict environmental policies.

The strategic trade literature also focuses on modeling policy choice in an oligopolistic international trade environment. Ulph (1992) proposes a duopoly model of firms located in two different countries, where governments should choose between a pollution tax or ceiling. The author studies three cases: one-stage Cournot model, two-stage Stackelberg model, and a two-stage Cournot model. The conclusion from this model is that in a one-stage Cournot model, the instrument choice becomes a purely domestic decision, whereas, in the two-stage models, the leader will prefer ceilings, whereas the follower is indifferent between the two instruments under Stackelberg competition, and in the Cournot model the two countries have an incentive to set ceilings. Later on, the generalizations in Ulph (1996) allow for strategic behavior by producers and governments and show that strategic behavior by producers and governments is higher when governments use emission taxes compared to the case where they use emission standards. Gautier (2014) also studies the policy reforms of emission taxes and environmental R&D subsidies in a two-country Cournot model with product differentiation.

With the opening up of markets, the impact of trade liberalization on the environment has become a focus of debate. Many previous studies have focused on internalizing pollution externalities by using an environmental tax (Krutilla, 1991). In the trade-pollution literature, Duval and Hamilton (2002), Burguet and Sempere (2003), Zhao et al. (2005), and Bárcena-Ruiz and Garzón (2006) used a reciprocal-markets model with pollution generated by production to examine the welfare implications of trade liberalization when governments behave strategically using pollution taxes and tariffs on imports. Several studies have since extended the literature on strategic environmental and trade policy to include endogenous entry in response to changes in policy (Katsoulacos and Xepapadeas, 1995; Bhattacharjea, 2002; Bayındır-Upmann, 2003; Greaker, 2003; Fujiwara, 2009; Haufler and Wooton, 2010; Etro, 2011). This literature focuses almost exclusively on pollution externalities in production and the emission fees and standards used to control them.

Melitz and Ottaviano (2008), in the framework of strategic trade literature, studied the effect of the market size in different aspects of international trade by developing a monopolistic competitive model of trade. They assume firm heterogeneity using a linear demand system with horizontal product differentiation (see Ottaviano et al., 2002), and differences in terms of the number and average productivity of competing firms. They investigate the effect of market size on the entry and exit rates of heterogeneous firms, including an analysis of asymmetric trade liberalization scenarios. They conclude that productivity and average mark-ups depend on the market size and the level of trade liberalization.

In this context, this research aims to analyze how (international) market asymmetry might be a determinant in the choice of a given policy in a model of imperfect competition and bilateral trade, where both, firms and governments act strategically, such that government policy choice might shift gains from trade from foreign to domestic firms. We consider an economy with two countries, assuming the foreign country to be larger than the home country in terms of market size. There are two firms, a domestic firm and a foreign firm; each firm produces two different products, one to be sold in the domestic market and one to be sold in the foreign market. The government in each country acts strategically and chooses between two different policies: an emission tax (giving firms incentives to invest in cleaner technologies) or a production subsidy. We are aware that taxes and subsidies have different purposes, and even separate departments in the government are in charge of their design, which can result in implementation or coordination problems. In particular, subsidies can be problematic due to the associated opportunity cost; moreover, subsidizing highly polluting production activities generates social discomfort.

Our paper studies the effect of market size asymmetry on welfare when governments act strategically and decide on the policy instrument to implement: an emission tax or a production subsidy. The assumption of market size asymmetry is closer to reality since international trade often takes place among heterogeneous-sized markets. We believe, therefore, that incorporating this asymmetry assumption into the model will contribute to the existing theoretical studies.

Using a simple duopoly model, we find that when both countries have small and similar market sizes, governments have an incentive to apply emission taxes. As the market size asymmetry increases, the government in the foreign country (large market size) will have incentives to shift to production subsidies. When this asymmetry is very large, the home country (small market size) will have incentives to provide a production subsidy to maintain firms' competitiveness if the government in the foreign country (large market size) decides to subsidize firms. These results are to be considered, since SDG 12 shows that sustainable consumption and production play an essential and transversal role in sustainable development.

The rest of the paper is structured as follows. Section 2 presents the model. Section 3 shows the normal form of the game at Stage 1 and offers some results. Section 4 presents a numerical example. Section 5 shows an extension of the model. Finally, Section 6 offers some concluding remarks.

2. The model

Consider an economy with two countries and two firms, one located in the home country (H) and the other one located in the foreign country (F). Each firm produces two differentiated, tradable goods; that is, one good to the domestic market and another to the foreign market. We assume that country H has a small market size, and country F has a large market size.

The inverse demand function for the differentiated product in the home (foreign) country is as follows:

$\begin{array}{l}{p}_H={\alpha }_H-(q_{hH}+q_{fH})\end{array}$

$\begin{array}{l}{p}_F={\alpha }_F-(q_{fF}+q_{hF})\end{array}$

where p_H (p_F) is the price of the final product in country H (F) and α_H (α_F) is country H's (F) market size. As F is the country with the large market size, α_F = α_H+Δ, where Δ≥0 denotes the market size asymmetry between the two countries, q_hH (q_hF) is the quantity produced by firm h for country H (F), and q_fH (q_fF) is the quantity produced by firm f and sold in country H (F). For simplicity, from now on we denote α_H = α, and thus, α_F = α+Δ.

Firms compete á la Cournot both in their domestic and foreign markets. In each country there is a government whose goal is to maximize national welfare by deciding the type and level of a policy instrument: an environmental tax, τ_H (τ_F), or a production subsidy, σ_H (σ_F). Environmental regulation tackles local pollution.

During the production process, firms generate local emissions:

$\begin{array}{l}{E}_H=q_{hH}+q_{hF}-I_h\end{array}$

$\begin{array}{l}{E}_F=q_{fF}+q_{fH}-I_f\end{array}$

We further simplify the analysis by assuming linear damage function for pollution in the home (foreign) country, denoted as D_H (D_F). We also assume it coincides with the emissions level in the home (foreign) country, D_H = E_H (D_F = E_F). Note therefore that the marginal damage is constant, $D_H^{\prime }=1$ and $D_H^{″}=0$ ($D_F^{\prime }=1$ and $D_F^{″}=0$),¹ and the damage function depends on the total production in the home (foreign) country minus the reduction in emissions if firm h (f) invests in a cleaner technology, denoted as I_h (I_f), when appropriate. Duval and Hamilton (2002) also assume a constant marginal damage, which allows for global damage to be expressed in terms of the amount of produced and consumed pollution in each country. Note that when the government provides a production subsidy, firms do not have incentives to invest in cleaner technologies, thus, I_h = 0 (I_f = 0). We explain this with more detail in subsection 3.2.

We model a four stage game. We assume that the two firms and the two governments decide simultaneously and independently in each stage. In the first stage, the home and foreign governments decide on the type of policy instrument to use, either a production subsidy or an emission tax. Allowing governments to combine both an emission tax and a production subsidy will be equivalent to use only one instrument with a different level. As an example, if the country decides to set a tax, the simultaneous use of a subsidy would be equivalent to modifying the tax level, compared to a situation where the government only uses a tax. In particular, we compare the strategic incentives of firms under four (international) policy scenarios: (i) domestic and foreign governments use an emission tax, (ii) the government of the foreign country (large market size) uses a production subsidy, while the home-country government (small market size) uses an emission tax, (iii) domestic and foreign governments establish a production subsidy, and (iv) the foreign country's government (large market size) uses an emission tax, while the home-country government (small market size) implements a production subsidy. In the second stage, governments choose the level of their policy instrument. In the third stage, only if the corresponding government decides to introduce an emission tax, the firm decides whether to invest in a cleaner technology and on the investment level. In the fourth stage, and after observing the policy choices, firms decide on their output for the home market and their output for the foreign market.

In the Fourth Stage, firms decide the output levels that maximize their profits. Let us define the profit of firm h:

$\begin{array}{ll}{\pi }_h=\{\begin{array}{l}{p}_H{q}_{hH}+(p_F-d)q_{hF}-(q_{hH}^2+q_{hF}^2)-{\tau }_H{D}_H-\frac{I_h^2}{2}\text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}if a tax is applied}\\ p_H{q}_{hH}+(p_F-d)q_{hF}-(q_{hH}^2+q_{hF}^2)+{\sigma }_H(q_{hH}+q_{hF})\text{\hspace{0.17em}\hspace{0.17em}if\hspace{0.17em}a\hspace{0.17em}subsidy\hspace{0.17em}is\hspace{0.17em}provided}\end{array}& (1)\end{array}$

where d is the transportation cost applied to exported output (for analytical simplicity, we assume that d= 2); we also assume quadratic production costs; and $\frac{I_h^2}{2}$ $(\frac{I_f^2}{2})$ is the amount that firm h (f) needs to invest in the cleaner technology in order to reduce emissions in I_h (I_f) units, that is, the abatement cost.

Equivalently, the profit for firm f located in the foreign country F can be written as follows:

$\begin{array}{ll}{\pi }_f=\{\begin{array}{l}{p}_F{q}_{fF}+(p_H-d)q_{fH}-(q_{fF}^2+q_{fH}^2)-{\tau }_F{D}_F-\frac{I_f^2}{2}\text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}if\hspace{0.17em}a\hspace{0.17em}tax\hspace{0.17em}is\hspace{0.17em}applied}\\ p_F{q}_{fF}+(p_H-d)q_{fH}-(q_{fF}^2+q_{fH}^2)+{\sigma }_F(q_{fF}+q_{fH})\text{ if\hspace{0.17em}a\hspace{0.17em}subsidy\hspace{0.17em}is\hspace{0.17em}provided}\end{array}& (2)\end{array}$

Therefore, from the profit function, we see that it is only when the government has set an emission tax, that the firm has an incentive to invest in the new technology, and therefore reduce emissions.²

In the Fist Stage, governments decide their policies to maximize national welfare, defined as the sum of consumer surplus, firms' profit, and government revenue, minus environmental damage. Thus, governments maximize:

$\begin{array}{l}S{W}_H=C{S}_H+{\pi }_h+G{R}_H-D_H\end{array}$

$\begin{array}{l}S{W}_F=C{S}_F+{\pi }_f+G{R}_F-D_F\end{array}$

where

• $C{S}_H=\frac{{(q_{hH}+q_{fH})}^2}{2}$ $(C{S}_F=\frac{{(q_{fF}+q_{hF})}^2}{2})$ is the consumer surplus in the home (foreign) country as a function of the total consumption of final goods in that country, i.e. q_hH+q_fH (q_fF+q_hF),

• GR_H = τ_H(q_hH+q_hF−I_h)>0 (GR_F = τ_F(q_fF+q_fH−I_f)>0) is the government revenue in the home (foreign) country if the country applies an emission tax,

• GR_H = −σ_H(q_hH+q_hF) < 0 (GR_F = −σ_F(q_fF+q_fH) < 0) is the government revenue if the home (foreign) country establishes a production subsidy.

3. Subgame perfect nash equilibrium

In this section, we show the computation of the subgame perfect Nash equilibrium (SPNE) of the game using backward induction.

3.1. Firms' output decision (Stage 4)

In Stage 4, each firm decides on the output level for the two different products to maximize profits.

The first-order conditions imply that output always increases with market size:

• Scenario 1: the governments in both countries H and F apply an emission tax:

$\begin{array}{l}{q}_{hH}^{TT}=\frac{1}{15}(3\alpha -4{\tau }_H+{\tau }_F+2)\end{array}$

$\begin{array}{l}{q}_{hF}^{TT}=\frac{1}{15}(3\alpha +3\Delta -4{\tau }_H+{\tau }_F-8)\end{array}$

$\begin{array}{l}{q}_{fF}^{TT}=\frac{1}{15}(3\alpha +3\Delta +{\tau }_H-4{\tau }_F+2)\end{array}$

$\begin{array}{l}{q}_{fH}^{TT}=\frac{1}{15}(3\alpha +{\tau }_H-4{\tau }_F-8)\end{array}$

• Scenario 2: the home country's government sets an emission tax, and the foreign country's government uses a production subsidy:

$\begin{array}{l}{q}_{hH}^{TS}=\frac{1}{15}(3\alpha -4{\tau }_H-{\sigma }_F+2)\end{array}$

$\begin{array}{l}{q}_{hF}^{TS}=\frac{1}{15}(3\alpha +3\Delta -4{\tau }_H-{\sigma }_F-8)\end{array}$

$\begin{array}{l}{q}_{fF}^{TS}=\frac{1}{15}(3\alpha +3\Delta +{\tau }_H+4{\sigma }_F+2)\end{array}$

$\begin{array}{l}{q}_{fH}^{TS}=\frac{1}{15}(3\alpha +{\tau }_H+4{\sigma }_F-8)\end{array}$

• Scenario 3: the governments in both countries H and F use a production subsidy:

$\begin{array}{l}{q}_{hH}^{SS}=\frac{1}{15}(3\alpha +4{\sigma }_H-{\sigma }_F+2)\end{array}$

$\begin{array}{l}{q}_{hF}^{SS}=\frac{1}{15}(3\alpha +3\Delta +4{\sigma }_H-{\sigma }_F-8)\end{array}$

$\begin{array}{l}{q}_{fF}^{SS}=\frac{1}{15}(3\alpha +3\Delta -{\sigma }_H+4{\sigma }_F+2)\end{array}$

$\begin{array}{l}{q}_{fH}^{SS}=\frac{1}{15}(3\alpha -{\sigma }_H+4{\sigma }_F-8)\end{array}$

• Scenario 4: the home country's government uses a production subsidy, and the foreign country's government an emission tax:

$\begin{array}{l}{q}_{hH}^{ST}=\frac{1}{15}(3\alpha +4{\sigma }_H+{\tau }_F+2)\end{array}$

$\begin{array}{l}{q}_{hF}^{ST}=\frac{1}{15}(3\alpha +3\Delta +4{\sigma }_H+{\tau }_F-8)\end{array}$

$\begin{array}{l}{q}_{fF}^{ST}=\frac{1}{15}(3\alpha +3\Delta -{\sigma }_H-4{\tau }_F+2)\end{array}$

$\begin{array}{l}{q}_{fH}^{ST}=\frac{1}{15}(3\alpha -{\sigma }_H-4{\tau }_F-8)\end{array}$

When both countries apply an emission tax, the home country's total output decreases if the home government chooses to apply an emission tax, whereas it increases if the foreign government is the one using an emission tax. The opposite holds when both countries use a production subsidy: the home country's total output increases with the size of the home country's production subsidy, and it decreases when the foreign country provides a production subsidy. On the other hand, when a country's government uses an emission tax and the foreign government uses a production subsidy, the production of the country that uses emission taxes decreases due to both the domestic tax and the foreign subsidy, while the opposite effect is observed in the production of the country that uses a production subsidy.

3.2. Firms' investment decision (Stage 3)

If a government decides to use an emission tax in Stage 1, firms have incentives to invest in a cleaner technology.

• Scenario 1: the governments in both countries H and F apply an emission tax:

$\begin{array}{l}{I}_h^{TT}={\tau }_H\end{array}$

$\begin{array}{l}{I}_f^{TT}={\tau }_F\end{array}$

• Scenario 2: the home country's government sets an emission tax, and the foreign country's government establishes a production subsidy:

$\begin{array}{l}{I}_h^{TS}={\tau }_H\end{array}$

$\begin{array}{l}{I}_f^{TS}=0\end{array}$

• Scenario 3: the governments in both countries H and F establish a production subsidy:

$\begin{array}{l}{I}_h^{SS}=0\end{array}$

$\begin{array}{l}{I}_f^{SS}=0\end{array}$

• Scenario 4: the home country's government establishes a production subsidy, and the foreign country's government sets an emission tax:

$\begin{array}{l}{I}_h^{ST}=0\end{array}$

$\begin{array}{l}{I}_f^{ST}={\tau }_F\end{array}$

From these first-order conditions, we know that the level of investment is equal to the tax level when governments use a pollution tax, and null if governments use a production subsidy.

3.3. Governments decisions on policy level (Stage 2)

In the second stage of the game, for the given policy instrument chosen in Stage 1, each country's government chooses the level of policy instrument that maximizes social welfare, considering as given the decision of the other country.

From the maximization of social welfare, we obtain the best response function for each of the governments regarding the other country's decision, and if the first-order conditions are met, we obtain the equilibrium policy rates. We verify the second-order conditions for welfare maximization for Scenarios 1–4.

• Scenario 1: the governments in both countries H and F apply an emission tax:

$\begin{array}{ll}{\tau }_H^{TT}=\frac{1}{328}(-24\alpha -3\Delta +7{\tau }_F+369)& (3)\end{array}$

$\begin{array}{ll}{\tau }_F^{TT}=\frac{1}{328}(-24\alpha -21\Delta +7{\tau }_H+369)& (4)\end{array}$

If we solve the system for Eq (3) and (4), we obtain:

$\begin{array}{l}{\tau }_H^{TT}=-0.07\alpha -0.01\Delta +1.15\end{array}$

$\begin{array}{l}{\tau }_F^{TT}=-0.07\alpha -0.06\Delta +1.15\end{array}$

• Scenario 2: the home country's government sets an emission tax, and the foreign country's government establishes a production subsidy:

$\begin{array}{ll}{\tau }_H^{TS}=\frac{1}{328}(-24\alpha -3\Delta -7{\sigma }_F+369)& (5)\end{array}$

$\begin{array}{ll}{\sigma }_F^{TS}=\frac{1}{103}(24\alpha +21\Delta -7{\tau }_H-144)& (6)\end{array}$

If we solve the system for Eq (5) and (6) we obtain:

$\begin{array}{l}{\tau }_H^{TS}=-0.08\alpha -0.01\Delta +1.16\end{array}$

$\begin{array}{l}{\sigma }_F^{TS}=0.24\alpha +0.2\Delta -1.48\end{array}$

• Scenario 3: the governments in both countries H and F establish a production subsidy:

$\begin{array}{ll}{\sigma }_H^{SS}=\frac{1}{103}(24\alpha +3\Delta +7{\sigma }_F-144)& (7)\end{array}$

$\begin{array}{ll}{\sigma }_F^{SS}=\frac{1}{103}(24\alpha +21\Delta +7{\sigma }_H-144)& (8)\end{array}$

If we solve the system for Eq (7) and (8), we obtain:

$\begin{array}{l}{\sigma }_H^{SS}=0.25\alpha +0.04\Delta -1.5\end{array}$

$\begin{array}{l}{\sigma }_F^{SS}=0.25\alpha +0.21\Delta -1.5\end{array}$

• Scenario 4: the home country's government establishes a production subsidy, and the foreign country's government sets an emission tax:

$\begin{array}{ll}{\sigma }_H^{ST}=\frac{1}{103}(24\alpha +3\Delta -7{\tau }_F-144)& (9)\end{array}$

$\begin{array}{ll}{\tau }_F^{ST}=\frac{1}{328}(-24\alpha -21\Delta -7{\sigma }_H+369)& (10)\end{array}$

If we solve the system for Eq (9) and (10), we obtain:

$\begin{array}{l}{\sigma }_H^{ST}=0.24\alpha +0.03\Delta -1.48\end{array}$

$\begin{array}{l}{\tau }_F^{ST}=-0.08\alpha -0.06\Delta +1.16\end{array}$

From these first-order conditions, we can see that the level of taxes (subsidies) decreases (increases) with market size; in other words, the larger the market size, the lower (higher) the equilibrium level of taxes (subsidies). When both countries apply the same (different) type of policy instrument, the higher the tax or subsidy level of the foreign country, the greater the incentive of governments to increase (decrease) the emission tax or the production subsidy.

Figure 1 shows the area with an interior and positive solution for quantities, taxes, and subsidies, i.e., the governments can behave strategically:

FIGURE 1

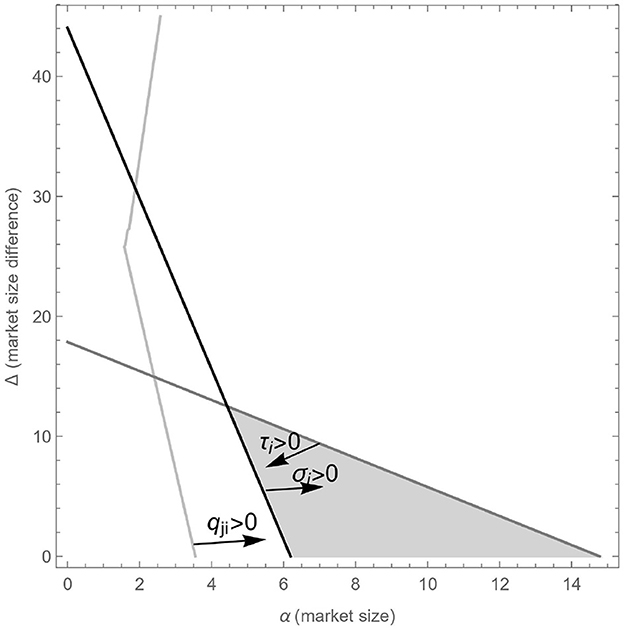
Figure 1. Area in which quantities, taxes and subsidies are interior and positive, where i = H, F and j = h, f.

$A\equiv \left\{(\alpha ,\Delta )\in {\Re }_{+}^2/q_{ji}^{PO}\ge 0,{\tau }_i^{PO}\ge 0,{\sigma }_i^{PO}\ge 0\right\}\equiv \left\{(\alpha ,\Delta )\in {\Re }_{+}^2/{\tau }_F^{ST}\ge 0,{\sigma }_H^{ST}\ge 0\right\}$

where i∈{H, F} , where j∈{h, f} and P, O∈{T, S}

This area shows the values for market size (α) and asymmetry (Δ) that guarantees interior and positive quantities, taxes and subsidies.

3.4. Government decisions on policy instruments (Stage 1)

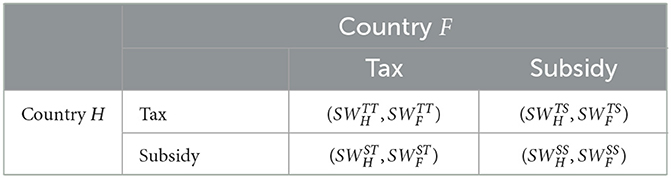
To obtain the SPNE in Stage 1, we compare each country's social welfare levels, considering as given the policy decision of the government in the other country. After solving the game by backward induction, the normal form of the game at Stage 1, in which governments decide on the policy instruments, is shown in Table 1.

TABLE 1

Table 1. Normal form of the game at stage 1.

$S{W}_H^{TT}$ ($S{W}_F^{TT}$) denotes social welfare in country H (F) if the two governments set an emission tax; $S{W}_H^{SS}$ ($S{W}_F^{SS}$) denotes social welfare in country H (F) if the two governments establish a production subsidy; $S{W}_H^{TS}$ ($S{W}_F^{TS}$) denotes social welfare in country H (F) if the home country's government sets an emission tax and the foreign country's government establishes a production subsidy; finally, $S{W}_H^{ST}$ ($S{W}_F^{ST}$) denotes social welfare in country H (F) if the home country's government establishes a production subsidy and the foreign country's government sets an emission tax.

We examine four different subgames: (i) subgame in which both countries apply an emission tax (subgame TT); (ii) subgame in which the home country applies an emission tax, and the foreign country provides a production subsidy (subgame TS); (iii) subgame in which both countries provide a production subsidy (subgame SS); and (iv) subgame in which the home country provides a production subsidy, and the foreign country applies an emission tax (subgame ST).

We first consider the best response of the foreign country when the home country applies an emission tax. If we compare the social welfare of two countries whose governments apply an emission tax to that of a home country's government which applies an emission tax together with that of a foreign country's government which provides a production subsidy, the government in country F is indifferent between setting an emission tax or providing a production subsidy if:

$\begin{array}{l}S{W}_F^{TS}-S{W}_F^{TT}=15.37\Delta (\alpha -2)+8.85\alpha (\alpha -4)-464.59+6.67{\Delta }^2=0\end{array}$

If we solve Δ, we obtain the positive root:

$\begin{array}{ll}{F}_1(\alpha )=0.01\sqrt{(\alpha -4)\alpha +550644}-1.15\alpha +2.3& (11)\end{array}$

$\begin{array}{ll}0\le \Delta \le F_1(\alpha )\Rightarrow S{W}_F^{TS}-S{W}_F^{TT}\le 0& (12)\end{array}$

$\begin{array}{ll}\Delta \ge F_1(\alpha )\Rightarrow S{W}_F^{TS}-S{W}_F^{TT}\ge 0& (13)\end{array}$

Secondly, we consider the best response of the home country when the foreign country provides a production subsidy. If we compare the social welfare of two countries when the home country's government applies an emission tax and the foreign country's government provides a production subsidy with that of two countries whose governments grant production subsidies, the government in country H is indifferent between setting an emission tax or providing a production subsidy if:

$\begin{array}{l}S{W}_H^{SS}-S{W}_H^{TS}=2.94\Delta (\alpha -2)+9.75\alpha (\alpha -4)-464.02+0.22{\Delta }^2=0\end{array}$

If we solve for Δ, we obtain the positive root:

$\begin{array}{ll}{F}_2(\alpha )=1.02\sqrt{(\alpha -4)\alpha +2233}-6.78\alpha +13.56& (14)\end{array}$

$\begin{array}{ll}0\le \Delta \le F_2(\alpha )\Rightarrow S{W}_H^{SS}-S{W}_H^{TS}\le 0& (15)\end{array}$

$\begin{array}{ll}\Delta \ge F_2(\alpha )\Rightarrow S{W}_H^{SS}-S{W}_H^{TS}\ge 0& (16)\end{array}$

Next, we consider the best response for the foreign country when the home country provides a production subsidy. If we compare the social welfare of two countries when the home country's government provides a production subsidy and the foreign country's government applies an emission tax with that of two countries whose governments provide a production subsidy, the government in country F is indifferent between setting an emission tax or providing a production subsidy if:

$\begin{array}{l}S{W}_F^{SS}-S{W}_F^{ST}=16.55\Delta (\alpha -2)+9.75\alpha (\alpha -4)-461.02+7.02{\Delta }^2=0\end{array}$

If we solve for Δ, we get the positive root:

$\begin{array}{ll}{F}_3(\alpha )=0.03\sqrt{86290+\alpha (\alpha -4)}-1.18\alpha +2.4& (17)\end{array}$

$\begin{array}{ll}0\le \Delta \le F_3(\alpha )\Rightarrow S{W}_F^{SS}-S{W}_F^{ST}\le 0& (18)\end{array}$

$\begin{array}{ll}\Delta \ge F_3(\alpha )\Rightarrow S{W}_F^{SS}-S{W}_F^{ST}\ge 0& (19)\end{array}$

Finally, we consider the best response of the home country when the foreign country applies an emission tax. If we compare the social welfare in two countries where governments apply an emission tax with that of two countries where the foreign country's government applies an emission tax and the home country's government provides a production subsidy, the government in country H is indifferent between setting an emission tax or providing a production subsidy if:

$\begin{array}{l}S{W}_H^{TT}-S{W}_H^{ST}=-2.23\Delta (\alpha -2)-8.85\alpha (\alpha -4)+464.59-0.15{\Delta }^2=0\end{array}$

If we solve Δ, we obtain the positive root:

$\begin{array}{ll}{F}_4(\alpha )=2.14\sqrt{703-\alpha (\alpha -4)}-7.29\alpha +14.59& (20)\end{array}$

$\begin{array}{ll}0\le \Delta \le F_4(\alpha )\Rightarrow S{W}_H^{TT}-S{W}_H^{ST}\ge 0& (21)\end{array}$

$\begin{array}{ll}\Delta \ge F_4(\alpha )\Rightarrow S{W}_H^{TT}-S{W}_H^{ST}\le 0& (22)\end{array}$

Comparing Δ with F₁(α), F₂(α), F₃(α) and F₄(α), our results are as follows (find all the proofs in Supplementary material):

Proposition 1.

1. If (α, Δ)∈A and Δ ≤ min{F₁(α), F₄(α)}, the best response of the governments in each country when the government in the other country has set an emission tax is to set an emission tax.

2. If (α, Δ)∈A and F₁(α) ≤ Δ ≤ F₂(α), the best response when the government at the home country applies an emission tax, is that the government at the foreign country establishes a production subsidy.

3. If (α, Δ)∈A and Δ≥max{F₂(α), F₃(α)}, the best response of each government when the government in the other country has set production subsidy is to set a production subsidy.

4. There is no value for Δ such that F₃(α)≥Δ≥F₄(α), therefore, the government in the home country will never apply a production subsidy as a best response when the government in the foreign country sets an emission tax.

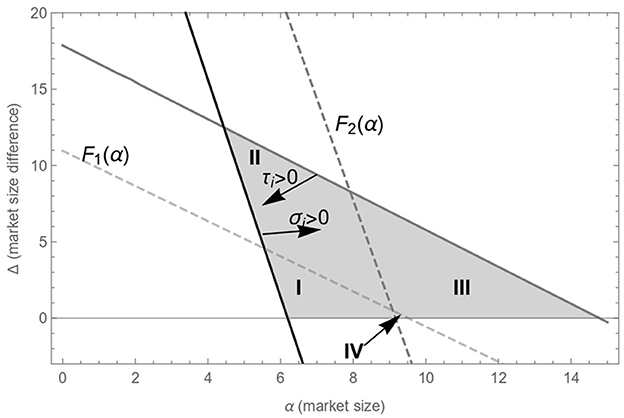
From this solution, we obtain that the two relevant functions are F₁(α) in Eq (11) and F₂(α) in Eq (14). These two functions divide area A into four subareas (see the shaded area in Figure 2). We find areas like A(I), A(II) and A(III) with a single SPNE, whereas in area A(IV) we obtain a multiplicity of equilibria. We define the areas as follows:

A(I) ≡{(α, Δ)∈A/Δ ≤ min{F₁(α), F₂(α)}}

A(II) ≡{(α, Δ)∈A/F₁(α) ≤ Δ ≤ F₂(α)}

A(III) ≡{(α, Δ)∈A/Δ≥max{F₁(α), F₂(α)}}

A(IV) ≡{(α, Δ)∈A/F₁(α)≥Δ≥F₂(α)}

FIGURE 2

Figure 2. Definition of the four subareas in area A.

We summarize our results as follows. Find all proofs in Supplementary material.

Theorem 2.

1. If (α, Δ)∈A(I)≡{(α, Δ)∈A/Δ ≤ min{F₁(α), F₂(α)}} then

$\left[(\mathbf{\text{tax}},{\tau }_H^{*}),(\mathbf{\text{tax}},{\tau }_F^{*}),(I_h^{*},q_{hH}^{*},q_{hF}^{*}),(I_f^{*},q_{fF}^{*},q_{fH}^{*})\right]$ is the unique SPNE of the game.

2. If (α, Δ)∈A(II)≡{(α, Δ)∈A/F₁(α) ≤ Δ ≤ F₂(α)} then

$\left[(\mathbf{\text{tax}},{\tau }_H^{*}),(\mathbf{\text{subsidy}},{\sigma }_F^{*}),(I_h^{*},q_{hH}^{*},q_{hF}^{*}),(I_f^{*},q_{fF}^{*},q_{fH}^{*})\right]$ is the unique SPNE of the game.

3. If (α, Δ)∈A(III)≡{(α, Δ)∈A/Δ≥max{F₁(α), F₂(α)}} then

$\left[(\mathbf{\text{subsidy}},{\sigma }_H^{*}),(\mathbf{\text{subsidy}},{\sigma }_F^{*}),(I_h^{*},q_{hH}^{*},q_{hF}^{*}),(I_f^{*},q_{fF}^{*},q_{fH}^{*})\right]$ is the unique SPNE of the game.

4. If (α, Δ)∈A(IV)≡{(α, Δ)∈A/F₁(α)≥Δ≥F₂(α)} there are two SPNE: $\left[(\mathbf{\text{tax}},{\tau }_H^{*}),(\mathbf{\text{tax}},{\tau }_F^{*}),(I_h^{*},q_{hH}^{*},q_{hF}^{*}),(I_f^{*},q_{fF}^{*},q_{fH}^{*})\right]$ and

$\left[(\mathbf{\text{subsidy}},{\sigma }_H^{*}),(\mathbf{\text{subsidy}},{\sigma }_F^{*}),(I_h^{*}{q}_{hH}^{*},q_{hF}^{*}),(I_f^{*},q_{fF}^{*},q_{fH}^{*})\right]$.

In Area I, in which home and foreign markets are small enough, and there is low market size asymmetry, there is a unique SPNE, and the governments of both countries are better off setting an emission tax. This result explains why in small countries whose industries compete in international and local markets, an environmental industrial policy can be sustained in equilibrium.

If there is an increase of the market size asymmetry between the two countries but the market size in the home country is small enough (area II), there is a unique SPNE: the government in the small (home) country maintains a policy based on emission taxes, while the government in the large (foreign) country has incentives to switch to an industrial policy based on production subsidies to improve firm competitiveness in the home and foreign market.

In area III, (i) if the home country's market size is not very large, but markets are very asymmetric, or (ii) if the two markets are large enough, then there is a unique SPNE: the governments of both countries are better off using production subsidies. In other words, we demonstrate that the home country's government removes the emission tax and subsidizes firms' production if the home country's firms are competing with firms of a country with a large market size that also receive production subsidies.

We also observe a special case in which both home and foreign countries have medium-sized markets that are almost symmetric (area IV). In this case, there are two SPNE: it is part of the equilibrium that governments in the two countries decide to use the same type of instrument, either an environmental tax or a production subsidy.

Therefore, in the symmetric case, (i.e. if the markets in the two countries have the same size, Δ≃0), when markets are sufficiently small, the equilibrium is that the two governments set emission taxes. On the contrary, when market sizes in the two countries are sufficiently large, the governments are better off setting production subsidies. However, when markets are medium-sized, we find two equilibria: the governments in the two countries set emission taxes or both set production subsidies. See A(I), A(III), and A(IV), respectively, in Figure 2 over the X axis.

Our model shows, therefore, how market asymmetry might be a determinant in the SPNE government policies in economies with international trade.

4. A numerical example

4.1. A numerical example in scenarios with a unique equilibrium

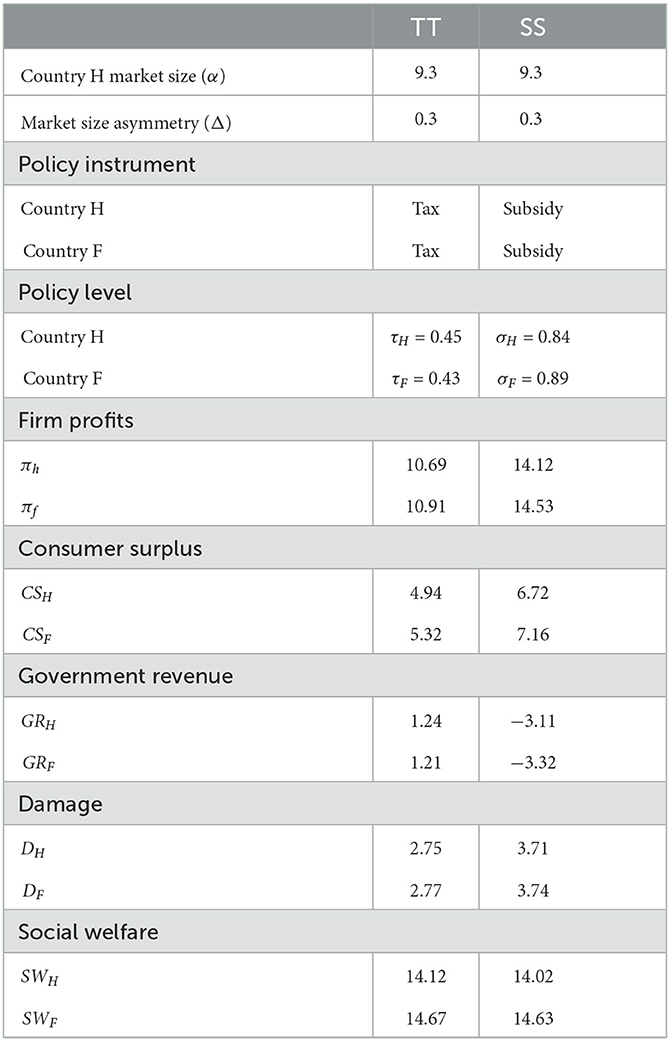
In this section, we provide a numerical example of comparative statics for three different scenarios in which the SPNE is unique. More specifically, in Table 2, we present a numerical example in which the home country faces three possible scenarios. Given a value for the home market size (α = 8.5), we introduce different degrees of asymmetry between the markets (Δ) and compute the equilibrium magnitudes for taxes, subsidies, global damage and social welfare for the two countries. In other words, the table represents a vertical line in Figure 2 over Area I, II, and III (fixing α and increasing Δ), for this reason, 8 < α < 9.

TABLE 2

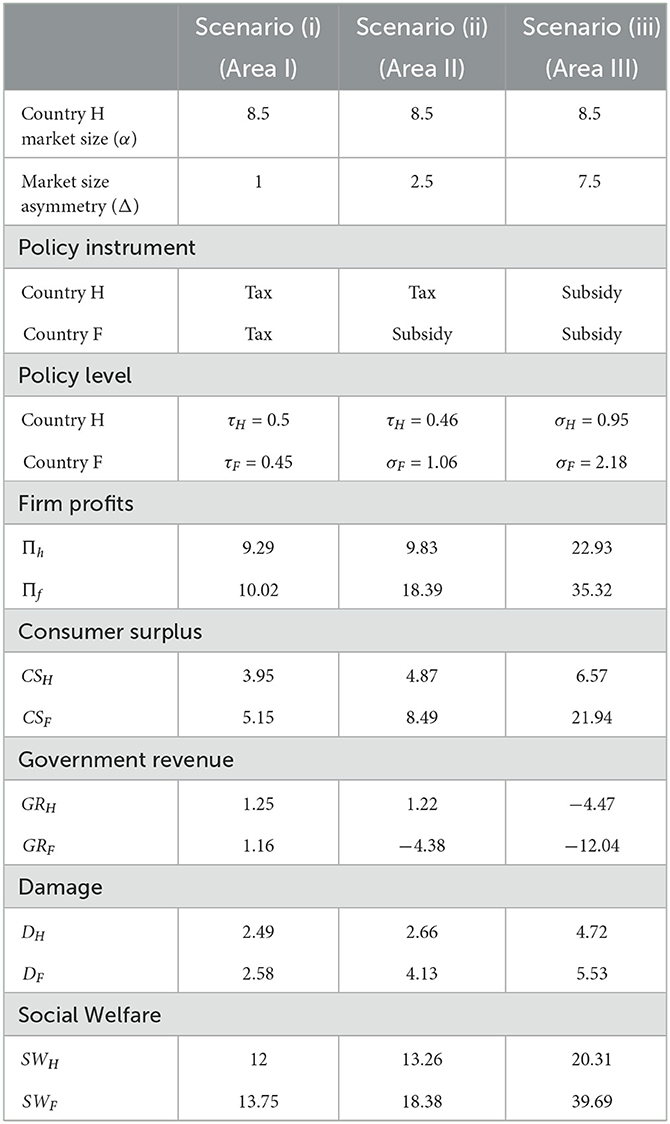
Table 2. Comparative statics for three different scenarios comparing the components of social welfare.

Following Theorem 2, in scenario (i) the two countries have a small, similar market size (α = 8.5, α_F = 9.5); consequently, the SPNE for the governments in the two countries is to apply an emission tax (see Area I in Figure 2). In scenario (ii) the difference in market size increases (α = 8.5, α_F = 11); thus, the home country's government applies an emission tax, and the foreign country's government establishes a production subsidy (see in Area II in Figure 2). Finally, in scenario (iii), the market size of the foreign country almost doubles that of the home country (α = 8.5, α_F = 16); hence, the SPNE for the governments in the two countries is to establish a production subsidy (see Area III in Figure 2).

If we compare scenarios (i) and (ii), we infer that the home country goes from competing with a country whose government has set an emission tax to competing with a country whose government provides a production subsidy. This makes the home country's social welfare increase by 10.5%, while the two countries face a damage almost 34% higher.

Comparing scenarios (i) and (iii), the difference in market size between the two countries is so large that the home country is better off using a production subsidy to be able to compete with the foreign country. As a consequence, social welfare in the home country increases by more than 69%. However, the home country is worse off in environmental terms due to a significant increase in global damage. We can conclude, therefore, that countries are better off but at the expense of increased pollution and environmental damage.

Table 2 also shows the breakdown of social welfare, i.e., the results for firm profits, consumer surplus, government revenue, and damage. If we compare scenarios (i) to (ii) where market size asymmetry increases so that the government in the foreign country is better off switching from an emission tax (in scenario (i)) to a production subsidy (in scenario (ii)), we observe that the increase in social welfare in the home country is mainly due to an increase in firm profits. The home country's consumer surplus increases by 23%, while government revenue decreases. Finally, damage in the home country is larger.

If we compare scenario (i) to (iii), we can see that the increase in social welfare in the home country occurs because firm profits are almost three times higher. The home country's consumer surplus is 66% higher, while government revenue is lower (since in scenario (iii) governments subsidize firms). Finally, the amount of damage in the home country almost doubles.

The conclusion is that when a country with a small market size competes with a country with a large market size and the two governments use production subsidies, although firms are indeed better off, this is not the case for consumers, since the increase in consumer surplus does not compensate the important increase in environmental damage.

Moreover, under the three scenarios, the foreign country (large market size) is better off than the home country in terms of firms' profits, consumer surplus, and social welfare, although suffering from a more polluted environment and a lower government revenue.

4.2. A numerical example for the scenario with multiple equilibria

In this section, we provide a numerical example where there are multiple equilibria. More specifically, we offer a numerical example for area IV (i.e., where areas I and III intersect, see Figure 2, in which markets are medium-sized, and asymmetry is almost null (Δ≃0); for this reason 9 < α < 9.5. Following Theorem 2, governments can choose between two different SPNEs, i.e., both governments set an emission tax, or they establish a production subsidy.

Table 3 shows that, at the aggregate level, social welfare in the two countries is slightly higher under an environmental tax, mainly due to a significant reduction in damage and a higher government revenue that offset the reduction in firms' profits and consumer surplus, compared to a scenario in which the governments in the two countries subsidize firms' production.

TABLE 3

Table 3. Comparative statics for the two possible SPNE.

Under both scenarios, the foreign country (large market size) is better off than the home country in terms of firms' profits, consumer surplus, and social welfare, although it suffers from a slightly more polluted environment and a lower government revenue.

5. Extensions of the model

In the following, we include some extensions of our baseline model.

5.1. Coordination

In our model, the governments' decision on the type and level of policy instrument is made sequentially in Stages 1 and 2 respectively. This means that the government in each country observes each other's decisions on the type of policy instrument (tax vs. subsidy) before deciding on the level. This would allow countries to coordinate on the policy instrument but choose the exact level. We might find corner solutions if the market size difference is very large. For instance, under emission taxes for large market sizes, the government in the foreign country will never use a tax, leading to a corner solution. On the contrary, in the case of production subsidies, the government in the country with smaller market size cannot put a subsidy when the market size is small and/or there is little difference.

5.2. Optimal outcome

The appropriately computed optimal outcome requires the governments in the two countries to decide both the type of instrument and policy level to maximize their joint social welfare. In a setting where governments decide optimizing aggregate welfare, the resulting optimal policy instrument implies that governments in the two countries set either an emission tax or a production subsidy, as well as the same level for the chosen policy instrument depending on the market size (see Figure 3). In this framework, it does not emerge as optimal solution that the government in a country with a small market size sets an emission tax, and that the country with a large market size sets a production subsidy.

FIGURE 3

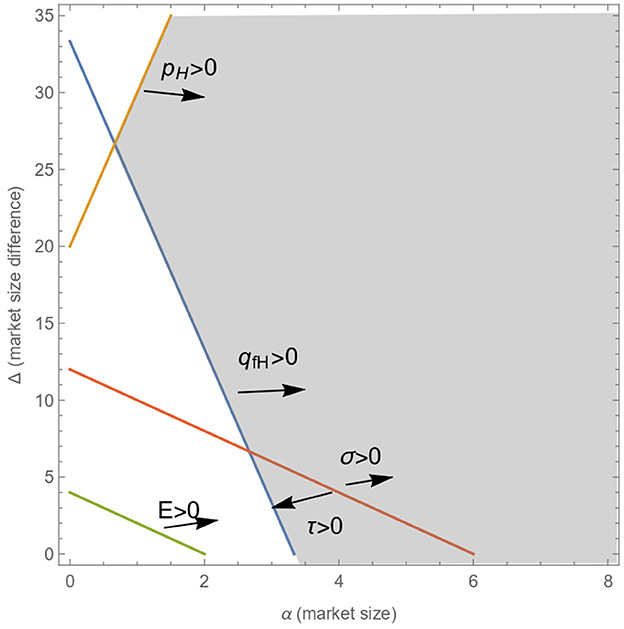
Figure 3. Area in which quantities, prices, emissions, taxes, and subsidies are interior and positive.

5.3. Generalization

In this section, we focus on the new insights we can obtain from a more general demand model. We tried different options for a linear demand function. See, for example, Hamilton (1999) who examined the structural implications of demand shifts in free-entry oligopoly equilibria. To simplify the analysis, we removed the possibility to invest in the cleaner technology.

5.3.1. Linear demand

To generalize the analysis results under a linear demand function, we studied different settings varying shift parameters that captured both shifts and rotations of the demand function (α and b).

Asymmetric market size (α) and equal slope of demand (b)

We allow the demand parameter α to differ across the markets but with a common b for the two of them (and different from 1). That is, home country's market size is α, while foreign country's market size is α+Δ.

$\begin{array}{l}{p}_H=\alpha -b(q_{hH}+q_{fH})\end{array}$

$\begin{array}{l}{p}_F=\alpha +\Delta -b(q_{fF}+q_{hF})\end{array}$

Figure 4 assumes that b = 10.

FIGURE 4

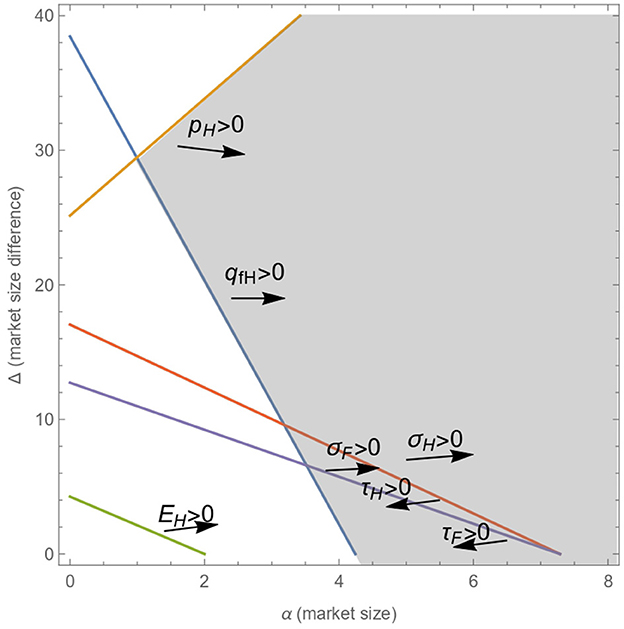
Figure 4. Area in which quantities, prices, emissions, taxes, and subsidies are interior and positive under linear demand with asymmetric market size (α) and equal slope of demand (b).

The simulations we have run show that as b increases, (i) the shaded area shifts to the right, and (ii) the area in which the governments in the two countries use emission taxes increases.

Symmetric market size (α) and different slopes of demand (b)

Alternatively, we also discuss the possibility of different b across the markets with a common α. In other words, the market size is the same in the two countries, but now we assume that in the foreign country b = 1, while in the home country, it can take different values.

$\begin{array}{l}{p}_H=\alpha -b(q_{hH}+q_{fH})\end{array}$

$\begin{array}{l}{p}_F=\alpha -(q_{fF}+q_{hF})\end{array}$

Figure 5 assumes that b = 10.

FIGURE 5

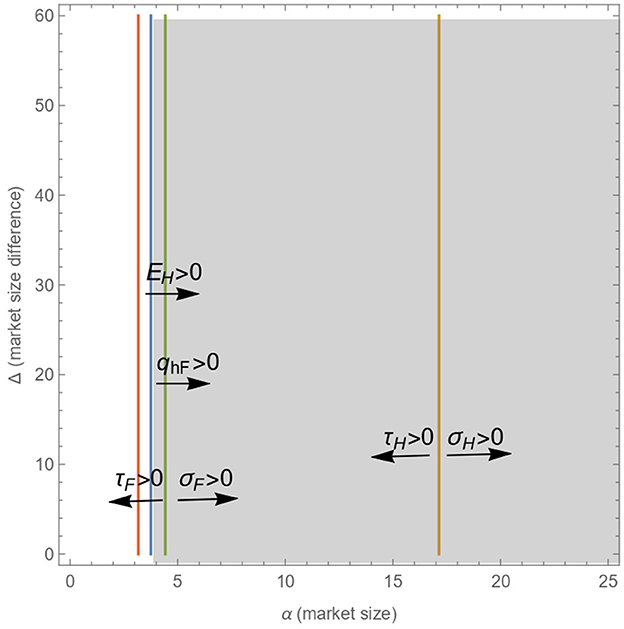
Figure 5. Area in which quantities, prices, emissions, taxes, and subsidies are interior and positive under linear demand with symmetric market size (α) and different slopes of demand (b).

The simulations we have run show that as b increases, (i) the shaded area shifts to the right, and (ii) the area in which both countries set emission taxes increases.

6. Conclusions

Using a simple duopoly model, we study how market size asymmetry can affect the environmental policy implemented by governments. We analyze a scenario in which both firms and governments act strategically when deciding on their production and environmental policy, respectively. We find that the domestic government has an incentive to set emission taxes, as long as the asymmetry between the markets remains sufficiently low. Conversely, in the case of a significant market size asymmetry between home and foreign countries, our results confirm that governments abandon the environmental policy to improve their industrial competitiveness. Our model proves that a policy based on emission taxes is less effective than one based on production subsidies as an instrument for improving industrial competitiveness in the home country.

These results illustrate the potential loss of competitiveness of the European industries, whose manufacturing costs for the same product, e.g. steel, are higher because of CO2 pricing. This could lead to them being outpriced on the world market and eventually to their demise. As a response, the European Union aims to set a carbon border adjustment mechanism, better know as a carbon border tax, on foreign pollution-intensive goods in order to pursue its climate target at the European Green Deal. Such a levy would add the same CO2 costs to a product when it crosses the border into the EU that the manufacturer of a domestically produced item would have to pay. However, this might not be a solution, since it is taxing end consumers for purchasing a foreign product, rather than the exporter itself. Furthermore, Zachmann and McWilliams (2020) claim that a carbon border tax is difficult to implement because of legal, domestic and foreign political issues. They suggest that “the EU must first begin to develop a series of more effective climate policies, such as a higher price on carbon, applied more widely, and broader support for low-carbon technologies. Through such a strategy, Europe will be better placed to decarbonize internally and to spread this decarbonization globally via the export of green technologies and know-how” (p. 17).

Although globalization provides opportunities for sustainable development, it also creates a wide range of challenges. As we have shown in our paper, globalization forces countries to compete with each other and, to remain competitive, the government often provides subsidies to support industries to improve productivity and efficiency. As a result, subsidies often lead to overproduction and increased pollution. To achieve the Sustainable Development Goals (SDGs) and, more specifically, sustainable production as stated by SDG 12, these emerging challenges to sustainable production must be appropriately addressed. From our results, we can make a few recommendations. First, encourage firms, especially those in large markets, to adopt sustainable practices (SDG 12.6). Second, support firms in small markets (usually in developing countries) to strengthen their scientific and technological capacity to move toward more sustainable production patterns (SDG 12.A). All in all, we still have to see if governments are willing to reduce emissions in the detriment of their countries' economic growth.

So far, our results have focused on local pollution; however, under transboundary pollution, our intuition is that the country with a small market size will be worse off, since, in this new scenario, it will be suffering the environmental impact from the neighbor country (large market size). On the one hand, to face this situation, the firm in the country with a small market size might reduce production to decrease emissions. On the other hand, the best decision could be setting production subsidies to stay competitive and put aside the environment. Secondly, if we assume price competition, we conjecture that the two firms would cut the competitor's prices (race to the bottom) to keep the whole demand, so exportation is not profitable, and each firm sells only in the domestic market.

We can use the results of this study to illustrate the effects of international trading on the countries' environmental policy. Taken together, the findings support the evidence that in oligopolistic international markets, the market conditions (in particular the size of the market it is trading with) might drive the regulators' decision on the equilibrium policy. Yet, further research should provide evidence on the generalizable of our findings under different situations, e.g., dynamics, competition issues, or alternative timings.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

LV-M, EC-C, and MG-V contributed to conception and design of the study. LV-M and MG-V performed the model analysis. LV-M wrote the first draft of the manuscript. LV-M and EC-C wrote sections of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

The authors are grateful for the funding from the Universitat Jaume I under Projects UJI-B2021-66 and GACUJI/2022/09, the Spanish Ministry of Science and Technology under Project PID2021-123053OB-I00, the Generalitat Valenciana for the financial support under the Project AICO/2021/005, and the Cátedra de Nueva Transición Verde.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frevc.2023.1099336/full#supplementary-material

Footnotes

1. ^Considering local environmental damage in line with Barcena-Ruiz and Garzon (2014), our model is a particular case of Duval and Hamilton (2002) (see page 263, second paragraph).

2. ^Under an emission tax, firms face a tradeoff between the cost of emissions (through the tax) and reducing emissions (through the investment in the clean technology); indeed, in section 3.2 we show that, in this case, optimal investment equals the emission tax. Note that when the policy is not an emission tax then τ = 0, that is, there are no incentives to invest.

References

Baksi, S., Chaudhuri, A. R. (2009). On trade liberalization and transboundary pollution. Econ. Bull. 29, 2605–2612

Google Scholar

Bárcena-Ruiz, J. C., Garzón, M. B. (2006). Mixed oligopoly and environmental policy. Spanish Econ. Rev. 8, 139–160. doi: 10.1007/s10108-006-9006-y

CrossRef Full Text | Google Scholar

Barcena-Ruiz, J. C., Garzon, M. B. (2014). Multiproduct firms and environmental policy coordination. Environ. Resour. Econ. 59, 407–431. doi: 10.1007/s10640-013-9736-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Barrett, S. (1994). Strategic environmental policy and international trade. J. Public Econ. 54, 325–338. doi: 10.1016/0047-2727(94)90039-6

CrossRef Full Text | Google Scholar

Bayındır-Upmann, T. (2003). Strategic environmental policy under free entry of firms. Rev. Int. Econ. 11, 379–396. doi: 10.1111/1467-9396.00389

CrossRef Full Text | Google Scholar

Bhattacharjea, A. (2002). Foreign entry and domestic welfare: lessons for developing countries. J. Int. Trade Econ. Dev. 11, 143–162. doi: 10.1080/09638190010110721

CrossRef Full Text | Google Scholar

Brander, J. A., Spencer, B. J. (1985). Export subsidies and international market share rivalry. J. Int. Econ. 18, 83–100. doi: 10.1016/0022-1996(85)90006-6

CrossRef Full Text | Google Scholar

Buccella, D., Fanti, L., Gori, L. (2021). To abate, or not to abate? A strategic approach on green production in cournot and bertrand duopolies. Energy Econ. 96, 105–164. doi: 10.1016/j.eneco.2021.105164

CrossRef Full Text | Google Scholar

Burguet, R., Sempere, J. (2003). Trade liberalization, environmental policy, and welfare. J. Environ. Econ. Manag. 46, 25–37. doi: 10.1016/S0095-0696(02)00032-3

CrossRef Full Text | Google Scholar

Duval, Y., Hamilton, S. F. (2002). Strategic environmental policy and international trade in asymmetric oligopoly markets. Int. Tax Public Fin. 9, 259–271. doi: 10.1023/A:1016268213772

CrossRef Full Text | Google Scholar

Etro, F. (2011). Endogenous market structures and strategic trade policy. Int. Econ. Rev. 52, 63–84. doi: 10.2139/ssrn.2192015

CrossRef Full Text | Google Scholar

Fujiwara, K. (2009). Environmental policies in a differentiated oligopoly revisited. Resour. Energy Econ. 31, 239–247. doi: 10.1016/j.reseneeco.2009.03.002

CrossRef Full Text | Google Scholar

Gautier, L. (2014). Policy reform of emission taxes and environmental research and development incentives in an international Cournot model with product differentiation. Environ. Dev. Econ. 19, 440–465. doi: 10.1017/S1355770X13000521

CrossRef Full Text | Google Scholar

Greaker, M. (2003). Strategic environmental policy; eco-dumping or a green strategy? J. Environ. Econ. Manag. 45, 692–707. doi: 10.1016/S0095-0696(02)00053-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Hamilton, S. F. (1999). Demand shifts and market structure in free-entry oligopoly equilibria. Int. J. Indus. Organiz. 17, 259–275. doi: 10.1016/S0167-7187(97)00038-6

CrossRef Full Text | Google Scholar

Haufler, A., Wooton, I. (2010). Competition for firms in an oligopolistic industry: the impact of economic integration. J. Int. Econ. 80, 239–248. doi: 10.1016/j.jinteco.2009.10.002

CrossRef Full Text | Google Scholar

Katsoulacos, Y., Xepapadeas, A. (1995). Environmental policy under oligopoly with endogenous market structure. Scand. J. Econ. 411–420. doi: 10.2307/3440871

CrossRef Full Text | Google Scholar

Kennedy, P. W. (1994). Equilibrium pollution taxes in open economies with imperfect competition. J. Environ. Econ. Manag. 27, 49–63. doi: 10.1006/jeem.1994.1025

CrossRef Full Text | Google Scholar

Krugman, P. (1984). “Import protection as export promotion: international competition in the presence of oligopoly and economies of scale,” in Monopolistic Competition and International Trade ed H. Kierzkowski (Oxford University Press), 75–86.

Krutilla, K. (1991). Environmental regulation in an open economy. J. Environ. Econ. Manag. 20, 127–142. doi: 10.1016/0095-0696(91)90046-L

CrossRef Full Text | Google Scholar

Lai, Y.-B., Hu, C.-H. (2008). Trade agreements, domestic environmental regulation, and transboundary pollution. Resour. Energy Econ. 30, 209–228. doi: 10.1016/j.reseneeco.2007.06.003

CrossRef Full Text | Google Scholar

Melitz, M. J., Ottaviano, G. I. (2008). Market size, trade, and productivity. Rev. Econ. Stud. 75, 295–316. doi: 10.1111/j.1467-937X.2007.00463.x

CrossRef Full Text | Google Scholar

Ottaviano, G., Tabuchi, T., Thisse, J.-F. (2002). Agglomeration and trade revisited. Int. Econ. Rev. 409–435. doi: 10.1111/1468-2354.t01-1-00021

CrossRef Full Text | Google Scholar

Spencer, B. J., Brander, J. A. (1983). International R&D rivalry and industrial strategy. Rev. Econ. Stud. 50, 707–722. doi: 10.2307/2297771

CrossRef Full Text | Google Scholar

Stegemann, K. (1989). Policy rivalry among industrial states: what can we learn from models of strategic trade policy? Int. Organiz. 43, 73–100. doi: 10.1017/S0020818300004562

CrossRef Full Text | Google Scholar

Ulph, A. (1992). “The choice of environmental policy instruments and strategic international trade,” in Conflicts and Cooperation in Managing Environmental Resources (Berlin; Heidelberg: Springer), 111–132. doi: 10.1007/978-3-642-46765-3_6

CrossRef Full Text | Google Scholar

Ulph, A. (1994). “Strategic environmental policy, international trade and the single European market,” in Environmental Policy with Political and Economic Integration (Edward Elgar Publishing). 235–258. doi: 10.1007/978-1-349-23989-4_6

CrossRef Full Text | Google Scholar

Ulph, A. (1996). Environmental policy and international trade when governments and producers act strategically. J. Environ. Econ. Manag. 30, 265–281. doi: 10.1006/jeem.1996.0018

CrossRef Full Text | Google Scholar

Ulph, A., Ulph, D. (1996). “Trade, strategic innovation and strategic environmental policy'a general analysis,” in Environmental Policy and Market Structure (Springer), 181–208. doi: 10.1007/978-94-015-8642-9_10

CrossRef Full Text | Google Scholar

Xepapadeas, A. (2000). International dimensions of environmental policy. Environ. Dev. Econ. 5, 519–524. doi: 10.1017/S1355770X00290281

CrossRef Full Text | Google Scholar

Zachmann, G., McWilliams, B. (2020). A European Carbon Border Tax: Much Pain, Little Gain. Brussels: Bruegel.

Zhao, L., Yu, Z., Onuma, Y. (2005). A theory of mutual migration of polluting firms. Can. J. Econ., 900–918. doi: 10.1111/j.0008-4085.2005.00308.x

CrossRef Full Text | Google Scholar