Higher Dimensional Bianchi Type-I Cosmological Models With Massive String in General Relativity

1 Introduction

Nowadays, there has been drastic interest in string cosmology because of its important role in the study of the origin of the Universe and its very early phases before the formation of particles. It is an interesting concept for cosmologists to study and discover its unknown phenomena that have yet to be observed to study and explore the hidden information of the Universe. So cosmologists have taken an enormous interest to understand the past evolution, present state, and future evolution of the Universe. The general relativistic study of string was started by Letelier (Letelier, 1983) and Stachel (Stachel, 1980), who developed a classical concept of the geometric strings. Due to the key role of strings in describing the evolution of the early stage of our Universe, these days, many distinguished authors are inquisitive about cosmic strings within the framework of general relativity (Kibble (Kibble, 1976; Kibble, 1980)) and it is believed that strings give rise to density perturbations leading to the creation of the massive scale structures (like galaxies) of the Universe (Zel’dovich (Zel’dovich et al., 1974; Zel’dovich, 1980)). These strings have stress-energy and they are classified as geometric strings and massive strings. The occurrence of strings in the Universe results in anisotropy in space-time, though the strings cannot be seen in the latest epoch. These strings are not harmful to the cosmological models, alternatively they can result in plenty of very interesting astrophysical outcomes. There was a spontaneous symmetry breaking of the Universe during the phase transition in the early stage of the Universe after the big-bang explosion and those cosmic strings which are very important topological defects arose in the early epoch as the cosmic temperature went down below a few critical temperature points which are consistent with grand unified theories (Everett (Everett, 1981), Vilenkin (Vilenkin, 1981a; Vilenkin, 1981b)).

The study of cosmological models in higher dimensional space-time provides us with an idea that our present Universe is much greater than the Universe at the early stage of evolution due to the accelerated expansion of the Universe. So, nowadays it is becoming very interesting to study string cosmology in higher-dimensional space-time in the framework of general relativity. The possibility of space-time possessing more than 4D (Higher Dimensions) has attracted many authors to study higher dimensional models to study cosmology. The higher dimensional model was introduced by Kaluza (Kaluza, 1921)and Klein (Klein, 1926) in an effort to unify gravity with electromagnetism. Higher-dimensional models can be regarded as a tool to illustrate the late time expedited expanding paradigm (Banik and Bhuyan (Banik and Bhuyan, 2017)). Investigation of higher-dimensional space-time can be regarded as a task of paramount importance as the Universe might have come across a higher dimensional era during the initial epoch (Singh et al.(Singh et al., 2004)). Marciano (Marciano, 1984) asserts that the detection of a time-varying fundamental constant can possibly show us the proof for extra dimensions. According to Alvax and Gavela (Alvarez and Gavela, 1983) and Guth (Guth, 1981), extra dimensions generate a huge amount of entropy which gives a possible solution to the fitness and horizon problems. Since we are living in a 4D space-time, the hidden extra dimension in 5D is highly likely to be associated with the invisible Dark Matter and Dark Energy (Chakraborty and Debnath (Chakraborty and Debnath, 2010)). Many researchers have investigated various Bianchi type models in the field of five -dimensional space-time to explore the hidden information of the Universe. Chatterjee (Chatterjee, 1993) constructed a cosmological model in higher dimensional inhomogeneous space-time with massive strings.

From the observational data, we found that our Universe is homogeneous and isotropic on a large scale, however, no physical evidence denies the chance of an anisotropic Universe. In fact, theoretical arguments are presently promoting the existence of an anisotropic phase of the Universe that approaches the isotropic phase as suggested by Charles (Charles, 1968), Hinshaw et al. (Hinshaw et al., 2003), Page et al. (Page et al., 2007). Anisotropy plays a vital role in the early phase of the evolution of the Universe and so studying homogeneous and anisotropic cosmological models is considered important. Generally, the Bianchi-type models are spatially homogeneous and are in general anisotropic. The simplicity of the field equations made Bianchi type space-time useful in constructing models which are spatially homogeneous and isotropic. For the Bianchi type I cosmological models the corresponding anisotropy parameters are time-dependent. As time increases, for a suitable choice of the scalars, the Universe which was initially anisotropic starts to become isotropic and finally attains isotropy after some large cosmic time, which agrees with the present-day observational data such as cosmic microwave background (CMB) and type Ia supernovae.

We can find fascinating studies considering the anisotropic Universe in Bianchi type-I space-time by Mohanty et al. (Mohanty et al., 2002), Sahoo et al. (Sahoo et al., 2017). A Bianchi type-I cosmological model in higher dimensional space-time with string was investigated by Krori et al. (Krori et al., 1994) where they found that the strings and matter coexist throughout the evolution of the Universe. Rahaman et al.(Rahaman et al., 2003) obtained the exact solutions of the field equations of a five-dimensional space-time within the framework of Lyra manifold with massive string as a source of gravitational field. Mohanty and Samanta (Mohanty and Samanta, 2010a) constructed an LRS Bianchi type-I inflationary string cosmological model in five-dimensional space-time with massive scalar field in general relativity and obtained that the sum of energy density and tension density is zero. Also, Mohanty and Samanta (Mohanty and Samanta, 2010b) constructed string cosmological models with massive scalar field in five dimensional space-time considering Lyra manifold and obtained that the models avoid the initial singularity. Bianchi type-III cosmological models in five-dimensional space-time in general relativity with massive string as an origin of gravitational field were constructed by Samanta et al. (Samanta et al., 2011). Bianchi type-III string cosmological models in general relativity in presence of magnetic field were investigated by Kandalker et al. (Kandalkar et al., 2012), where they solved the field equations by using the Reddy string condition (ρ + λ = 0). Samanta and Debata (Samanta and Debata, 2011) constructed a five dimension Bianchi type-I string cosmological model in the framework of Lyra manifold. Singh and Mollah (Sing and Mollah, 2016) studied an LRS Bianchi type-I cosmological model with perfect fluidity in the framework of Lyra geometry in five dimensional space-time by using constant deceleration parameter. Kaiser (Kaiser and Stebbins, 1984), Banerjee (Banerjee et al., 1990), Wang (Wang, 2005), Bali et al. (Bali et al., 2007), Power and Deshmukh (Pawar and Deshmukh, 2010), Sahoo and Mishra (Sahoo and Mishra, 2015), Singh (Singh, 2013), Goswami (Goswami et al., 2016), Reddy (Reddy and Naidu, 2007), Khadekar (Khadekar et al., 2005; Khadekar et al., 2007; Khadekar and Tade, 2007), Yadav (Yadav et al., 2011), Ladke (Ladke, 2014), Singh and Baro (Singh and Baro, 2020), Baro and Singh (Baro and Singh, 2020) are some of the authors who studied different string cosmological models within the general relativity in a different contexts in various space-times. In addition to the above mentioned authors, recently Choudhury (Choudhury, 2017), Tripathi (Tripathi et al., 2017), Dubey et al. (Dubey et al., 2018), Tiwari et al. (Tiwari et al., 2019), Ram et al. (Ram and Verma, 2019), Mollah et al. (Mollah et al., 2019), and Baro et al.(Baro et al., 2021) investigated different string cosmological models in various space times.

The above discussion motivated us to investigate here the five-dimensional string cosmological models with particles attached to them in Bianchi type-I space-time in general relativity to investigate the different possibilities of the Bianchi type model Universe which transitions from anisotropic in early evolution to isotropic at a later time point where the survival field equations are solved by making some simplifying assumptions. Also, the physical and geometrical properties of some parameters of our model Universe are discussed in detail.

2 The Metric and Field Equations

We consider the Bianchi type-I metric in five dimensional space-time in the form of

$d{s}^2=-d{t}^2+a^{2}d{x}^2+b^{2}d{y}^2+c^{2}d{z}^2+D^{2}d{m}^2(1)$

where a, b, c and D are the metric functions of cosmic time ‘t′ only. Here the extra (fifth) coordinate ‘m’ is taken to be space-like.

The Einstein’s field equation in general relativity is given by

$R_{ij}-\frac{1}{2}R{g}_{ij}=-8\pi T_{ij}(2)$

The energy-momentum tensor for a cloud string is taken as

$T_{ij}=\rho u_i{u}_j-\lambda x_i{x}_j(3)$

where ρ, λ, ρ_p are the energy density of cloud of strings, tension density, particle density of the string respectively and they satisfy the equation ρ = ρ_p + λ. The co-ordinates are co-moving, x_i is a unit space-like vector towards the direction of strings and u_i is the five velocity vector which satisfies the conditions given below.

$u^i{u}_i=-x^i{x}_i=-1(4)$

$and{u}^i{x}_i=0(5)$

$u^i=\left(\mathrm{0,0,0,0,1}\right)and{x}^i=\left(a^{-1},\mathrm{0,0,0,0}\right)(6)$

For the metric 1 by using Equations 3–6 in the field Equation 2 yields

$\frac{\ddot{b}}{b}+\frac{\ddot{c}}{c}+\frac{\ddot{D}}{D}+\frac{\dot{b}\dot{c}}{bc}+\frac{\dot{b}\dot{D}}{bD}+\frac{\dot{c}\dot{D}}{cD}=8\pi \lambda (7)$

$\frac{\ddot{a}}{a}+\frac{\ddot{c}}{c}+\frac{\ddot{D}}{D}+\frac{\dot{a}\dot{c}}{ac}+\frac{\dot{a}\dot{D}}{aD}+\frac{\dot{c}\dot{D}}{cD}=0(8)$

$\frac{\ddot{a}}{a}+\frac{\ddot{b}}{b}+\frac{\ddot{D}}{D}+\frac{\dot{a}\dot{b}}{ab}+\frac{\dot{a}\dot{D}}{aD}+\frac{\dot{b}\dot{D}}{bD}=0(9)$

$\frac{\ddot{a}}{a}+\frac{\ddot{b}}{b}+\frac{\ddot{c}}{c}+\frac{\dot{a}\dot{b}}{ab}+\frac{\dot{a}\dot{c}}{ab}+\frac{\dot{b}\dot{c}}{bc}=0(10)$

$\frac{\dot{a}\dot{b}}{ab}+\frac{\dot{a}\dot{c}}{ac}+\frac{\dot{a}\dot{D}}{aD}+\frac{\dot{b}\dot{c}}{bc}+\frac{\dot{b}\dot{D}}{bD}+\frac{\dot{c}\dot{D}}{cD}=8\pi \rho (11)$

where an over dot and double over dot denote the first derivative and the second derivative w.r.t. cosmic time ‘t’ respectively.

3 Solution of the Field Equations

In this section we find physically meaningful solutions of the set of field Equations 7–11 by taking some simplifying assumptions.

3.1 Case-I(Isotropic Model)

Let us consider the Isotropic Model as

$a=b=c=t^{l_1}andD=t^{l_2}(12)$

where l₁ and l₂ are arbitrary constants.

By using Eq. 12 in Equations 7–11, we get

$\frac{1}{t^2}\left(3l_1^2+2l_1{l}_2-2l_1-l_2+l_2^2\right)=8\pi \lambda (13)$

$\frac{1}{t^2}\left(3l_1^2+2l_1{l}_2-2l_1-l_2+l_2^2\right)=0(14)$

$\frac{1}{t^2}\left(2l_1^2-l_1\right)=0(15)$

$\frac{1}{t^2}\left(3l_1^2+3l_1{l}_2\right)=8\pi \rho (16)$

Now from Equation 15 we get.

$l_1=0or{l}_1=\frac{1}{2}$

For l₁ = 0, from (14) we obtained

For $l_1=\frac{1}{2}$, from (14) we obtained.

$l_2=\frac{1}{2}or{l}_2=-\frac{1}{2}$

Eq. 12 shows that, with the increases of time t the Universe expands indefinitely if l₁ > 0 and the extra dimension “m” contract to a Planckian length as t → ∞ if l₂ < 0. The string cosmological model will be physically realistic only if we take $l_1=\frac{1}{2}>0$ and $l_2=-\frac{1}{2}<0$.

In this case the geometry of the model is described by the metric

$d{s}^2=-d{t}^2+t\left(d{x}^2+d{y}^2+d{z}^2\right)+t^{-1}d{m}^2(17)$

Using $l_1=\frac{1}{2}$ and $l_2=-\frac{1}{2}$ in Equation 13, the string tension density is obtained as

$\lambda =0(18)$

Using $l_1=\frac{1}{2}$ and $l_2=-\frac{1}{2}$ in Equation 16, the energy density is obtained as

$\rho =0(19)$

And using 18 and 19, the particle density is obtained as

${\rho }_p=0(20)$

This shows that the five-dimensional isotropic Bianchi type-I model in general relativity with strings do not survive and so it results in the five-dimensional vacuum Universe in the context of the general theory of relativity.

3.2 Case-II(Anisotropic Model)

The models with the anisotropic background are the most suitable models to describe the early stages of the Universe. Bianchi type-I models are among the simplest models with the anisotropic backgrounds.

In this case, let us consider

$a=t^{k_1},b=t^{k_2},c=t^{k_3}andD=t^{k_4}(21)$

Where k₁, k₂, k₃ and k₄ are arbitrary constants.

Now from Equations 7, 11, by the use of 21, we find

$\lambda =\frac{1}{8\pi t^2}\left[k_2^2+k_3^2+k_4^2+k_2{k}_3+k_3{k}_4+k_4{k}_2-\left(k_2+k_3+k_4\right)\right](22)$

$\rho =\frac{1}{8\pi t^2}\left[k_1\left(k_2+k_3+k_4\right)+k_2{k}_3+k_3{k}_4+k_4{k}_2\right](23)$

and particle density is

${\rho }_p=\frac{1}{8\pi t^2}\left[\left(k_1+1\right)\left(k_2+k_3+k_4\right)-\left(k_2^2+k_3^2+k_4^2\right)\right](24)$

We observed that the anisotropic three space will expand as t → ∞ when k₁, k₂ and k₃ are all positive and the extra dimension will contract as t → ∞ if k₄ < 0.

The Geometry of the model is described by the metric

$d{s}^2=-d{t}^2+t^{2k_1}d{x}^2+t^{2k_2}d{y}^2+t^{2k_3}d{z}^2+t^{2k_4}d{m}^2(25)$

The Scalar Expansion θ for model 25 is given by

$\theta =\frac{l}{t}(26)$

Where, l = k₁ + k₂ + k₃ + k₄

The Hubble Parameter is given by

$H=\frac{l}{4t}(27)$

The Spatial Volume of the Universe is obtained as

$V=t^l(28)$

The Shear Scalar is obtained as

${\sigma }^2=\frac{1}{2t^2}\left[k_1^2+k_2^2+k_3^2+k_4^2-\frac{1}{4}\right](29)$

Deceleration Parameter q is given by

$q=\frac{4}{l}-1(30)$

In this case, it is observed that the value of the deceleration parameter q is a positive constant when l < 4 which implies that our model Universe 25 decelerates in the standard way and the value of the deceleration parameter q is a negative constant when l > 4 which implies that our model Universe accelerates in the standard way. However, in the early stage of the evolution of the Universe the Bianchi type models represent the cosmos and though the Universe decelerates in the standard way in the early Universe, it will accelerate in finite time because of cosmic recollapse where the Universe in turns inflates “decelerates and then accelerates” (Kandalkar and Samdurkar (Kandalkar and Samdurkar, 2015)).

4 Physical Interpretations of the Solutions

Case I: From the case I, it is observed that ρ = λ = ρ_p = 0, which results in the five-dimensional vacuum Universe in general relativity. So, the isotropic Bianchi type-I five dimensional cosmic strings Universe do not survive in general Relativity.

Case II: In case II, we have constructed the anisotropic Bianchi type-I string cosmological model in general relativity in five-dimensional space-time given by Equation 25. Taking $k_1=\frac{2}{5},k_2=\frac{3}{5}$, $k_3=\frac{1}{4}$ and $k_4=\frac{-1}{4}$, the variation of the parameters of model 25 are shown by Figures 1, 2. The physical and geometrical behavior of the model can be discussed as.

1) We observed that our model expanded along x, y, and z axes as t → ∞ when, k₁, k₂ and k₃ are all positive and the extra dimension contracts and becomes unobservable at t → ∞, when k₄ < 0.

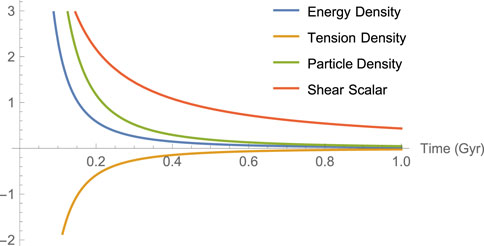
2) It is observed that at the initial epoch, i.e., t = 0, the energy density ρ → ∞ and ρ → 0 as t → ∞(shown by Figure 1) and it satisfies the reality condition when, $k_1+k_2{k}_3+k_3{k}_4+k_4{k}_2>k_1^2$

3) It is also observed that at the initial epoch, i.e., t = 0, the string tension density λ → − ∞ and λ → 0 as t → ∞ (Figure 1). From Eqs. 22, 23, we obtained an equation of state ρ + λ = 0, which occurs naturally in our case.

4) Also from Figure 1, it is observed that the particle density (ρ_p) is infinite when t = 0 and as time increases it decreases and finally it becomes 0 as t → ∞. It satisfies the reality condition when, $(k_1^2+k_2^2+k_3^2+k_4^2)<1$

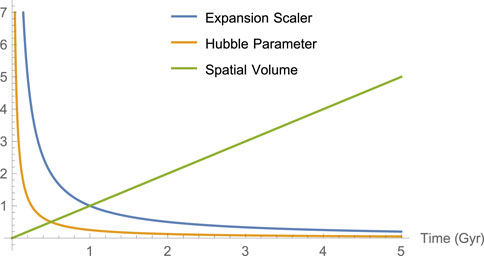
5) The spatial volume V in this model is 0 at initial epoch t = 0, and it increases w. r.t time which shows that our model Universe is expanding with the evolution of time, which is clearly shown in Figure 2.

6) The expansion scalar θ → ∞ at initial epoch t = 0, and as the time progresses gradually it decreases and finally it becomes 0 when t → ∞(as shown in Figure 2). Hence the model shows that the Universe is expanding with the increase of time but the rate of expansion is slower as time increases and the expansion stops at t → ∞.

7) It is observed that the value of deceleration parameter q is positive when l < 4 which implies that our model Universe decelerates for an instant. It is also observed that the value of deceleration parameter q is negative when l > 4, which implies that our model Universe accelerates in the standard way which is in accordance with the present-day observational scenario of accelerating Universe. Here, for our proposed model it may be noted that Bianchi type models represent the cosmos in its initial stage of evolution and there may be some possibilities to have an anisotropic Universe for some finite duration but the initial anisotropy of the Bianchi type -I Universe quickly dies away and the Universe turns to an isotropic one in the late Universe. However, though the Universe decelerates in the standard way for an instant, it will accelerate in finite time because of cosmic recollapse where the Universe in turns inflates “decelerates and then accelerates” (Kandalkar and Samdurkar (Kandalkar and Samdurkar, 2015)). The decelerating behavior of the expansion in the early stage and the accelerating behavior of the expansion of the present Universe has been indicated by many cosmological observations such as cosmic microwave background (CMB), clusters of galaxies, and type Ia supernovae, etc. which have suggested that the reason for this transition from deceleration to acceleration may be due to the presence of an anti-self attraction of matter. This shows that the Universe attains isotropy at late times and transits to the accelerating Universe which is consistent with the present day observational data such as cosmic microwave background (CMB) and type Ia supernovae. We may note that according to CMB and Planck results, our Universe is homogeneous and isotropic on a large scale, however, no physical evidence denies the chances of an anisotropic Universe. In fact, theoretical arguments are presently promoting the existence of an anisotropic phase of the Universe that approaches the isotropic phase as suggested by Charles (Charles, 1968), Hinshaw et al. (Hinshaw et al., 2003), Page et al. (Page et al., 2007).

FIGURE 1

FIGURE 1. Variation of ρ, λ, ρ_p, σ vs time t.

FIGURE 2

FIGURE 2. Variation of θ, H, V vs time t.

5 Conclusion

Here we investigated an anisotropic five dimensional Bianchi type-I string cosmological model in the context of the general theory of relativity. The model represents an expanding Universe that starts at the time t = 0 with a volume V = 0 and expands with acceleration after an epoch of deceleration. Our model Universe satisfies the energy conditions ρ ≥ 0 and ρ_p ≥ 0. The model Universe can represent a stage of evolution from deceleration to acceleration. The deceleration parameter “q” is decelerating at the initial stage of the evolution of the Universe and then accelerates after some finite time because of the cosmic recollapse, indicating inflation in the model after an epoch of deceleration which is in accordance with the present-day observational scenario of the accelerated expansion of our Universe as claimed by type Ia supernovae [Riess et al. (Riess et al., 1998) and Perlmutter et al. (Perlmutter et al., 1999)]. It is observed that our model Universe is anisotropic, expanding, shearing, and the sum of the energy density (ρ) and the string tension density (λ) vanishes (ρ + λ = 0) for this model.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alvarez, E., and Gavela, M. B. (1983). Entropy from Extra Dimensions. Phys. Rev. Lett. 51, 931–934. doi:10.1103/physrevlett.51.931

CrossRef Full Text | Google Scholar

Bali, R., Pareek, U. K., and Pradhan, A. (2007). Bianchi Type-I Massive String Magnetized Barotropic Perfect Fluid Cosmological Model in General Relativity. Chin. Phys. Lett. 24, 2455–2458. doi:10.1088/0256-307x/24/8/082

CrossRef Full Text | Google Scholar

Banerjee, A., Sanyal, A. K., and Chakraborty, S. (1990). String Cosmology in Bianchi I Space-Time. Pramana - J. Phys. 34, 1–11. doi:10.1007/bf02846104

CrossRef Full Text | Google Scholar

Banik, S. K., and Bhuyan, K. (2017). Dynamics of Higher-Dimensional FRW Cosmology in R P exp(λR) Gravity. Pramana - J. Phys. 88, 26. doi:10.1007/s12043-016-1335-2

CrossRef Full Text | Google Scholar

Baro, J., and Singh, K. P. (2020). Higher Dimensional Bianchi Type-III String Universe with Bulk Viscous Fluid and Constant Deceleration Parameter(DP). Adv. Math. Sci. J. 9 (10), 8779–8787. doi:10.37418/amsj.9.10.101

CrossRef Full Text | Google Scholar

Baro, J., Singh, P. K., and Singh, T. A. (2021). Mathematical Analysis on Anisotropic Bianchi Type-III Inflationary String Cosmological Models in Lyra Geometry. Indian J. Sci. Technol. 14 (1), 46–54. doi:10.17485/IJST/v14i1.1705

CrossRef Full Text | Google Scholar

Chakraborty, S., and Debnath, U. (2010). Higher Dimensional Cosmology with Normal Scalar Field and Tachyonic Field. Int. J. Theor. Phys. 49, 1693–1698. doi:10.1007/s10773-010-0348-8

CrossRef Full Text | Google Scholar

Charles, W. (1968). Misner,The Isotropy of the Universe. Astrophysical J. 151, 431–457.

Google Scholar

Chatterjee, S. (1993). Massive Strings in Higher-Dimensional Inhomogeneous Spacetime. Gen. Relat. Gravit. 25, 1079–1087. doi:10.1007/bf00763555

CrossRef Full Text | Google Scholar

Choudhury, S. (2017). Bianchi Type I Universe in Brane World Scenario with Non-Zero Weyl Tensor of the Bulk. Eur. Phys. J. C 77, 619–622. doi:10.1140/epjc/s10052-017-5175-0

CrossRef Full Text | Google Scholar

Dubey, R. K., Shukla, B. V., and Yadav, N. (2018). On Mathematical Analysis for Bianchi Type-I String Cosmological Model in Modified Theory of Relativity. Phys.Astron. Int.J. 2, 143–146. doi:10.15406/paij.2018.02.00058

CrossRef Full Text | Google Scholar

Everett, A. E. (1981). Cosmic Strings in Unified Gauge Theories. Phys. Rev. D 24, 858–868. doi:10.1103/physrevd.24.858

CrossRef Full Text | Google Scholar

Goswami, G. K., Dewangan, R. N., Yadav, A. K., and Pradhan, A. (2016). Anisotropic String Cosmological Models in Heckmann-Schucking Space-Time. Astrophys. Space Sci. 361, 1–10. doi:10.1007/s10509-015-2629-4

CrossRef Full Text | Google Scholar

Guth, A. H. (1981). Inflationary Universe: A Possible Solution to the Horizon and Flatness Problems. Phys. Rev. D 23, 347–356. doi:10.1103/physrevd.23.347

CrossRef Full Text | Google Scholar

Hinshaw, G., Barnes, C., Bennett, C. L., Greason, M. R., Halpern, M., Hill, R. S., et al. (2003). First-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Data Processing Methods and Systematic Error Limits. Astrophys Suppl. Ser. 148, 63–95. doi:10.1086/377222

CrossRef Full Text | Google Scholar

Kaiser, N., and Stebbins, A. (1984). Microwave Anisotropy Due to Cosmic Strings. Nature 310, 391–393. doi:10.1038/310391a0

CrossRef Full Text | Google Scholar

Kaluza, T. (1921). Zum Unitätsproblem in der Physik. Sitzungsber. Preuss Akad. Wiss. Berlin Math. Phys. K1, 966.

Google Scholar

Kandalkar, S. P., Samdurkar, S. W., and Gawande, S. P. (2012). Bianchi Type-III String Cosmological Models in the Presence of Magnetic Field in General Relativity. Int. J. Sci.Eng. Res. 3, 1–7.

Google Scholar

Kandalkar, S. P., and Samdurkar, S. (2015). LRS Bianchi Type-I Cosmological Model with Bulk Viscosity in Lyra Geometry. Bulg. J. Phys 42, 42–52.

Google Scholar

Khadekar, G. S., Patki, V. A., and Radha, R. (2007). String Cosmological Model with Bulk Viscosity in Higher Dimensional Space Time. J. Dynamical Syst. Geometric Theories 5, 117–123. doi:10.1080/1726037x.2007.10698531

CrossRef Full Text | Google Scholar

Khadekar, G. S., Patki, V., and Radha, R. (2005). String Dust Cosmological Model in Higher-Dimensional Space-Time. Int. J. Mod. Phys. D 14, 1621–1634. doi:10.1142/s0218271805007292

CrossRef Full Text | Google Scholar

Khadekar, G. S., and Tade, S. D. (2007). String Cosmological Models in Five Dimensional Bimetric Theory of Gravitation. Astrophys. Space Sci. 310, 47–51. doi:10.1007/s10509-007-9410-2

CrossRef Full Text | Google Scholar

Kibble, T. W. B. (1980). Some Implications of a Cosmological Phase Transition. Phys. Rep. 67, 183–199. doi:10.1016/0370-1573(80)90091-5

CrossRef Full Text | Google Scholar

Kibble, T. W. B. (1976). Topology of Cosmic Domains and Strings. J. Phys. A: Math. Gen. 9, 1387–1398. doi:10.1088/0305-4470/9/8/029

CrossRef Full Text | Google Scholar

Klein, O. (1926). Quantentheorie und fünfdimensionale Relativitätstheorie. Z. Physik 37, 895–906. doi:10.1007/bf01397481

CrossRef Full Text | Google Scholar

Krori, K. D., Chaudhury, T. C. R., and Mahanta, C. R. (1994). Strings in Some Bianchi Type Cosmologies. Gen. Relat. Gravit. 26, 265–274. doi:10.1007/bf02108006

CrossRef Full Text | Google Scholar

Ladke, L. S. (2014). Five Dimensional Bianchi Type-I(Kasner Form) Cosmological Models. Int.J.Scientific Innov. Math. Res. 2, 453–459.

Google Scholar

Letelier, P. S. (1983). String Cosmologies. Phys. Rev. D 28, 2414–2419. doi:10.1103/physrevd.28.2414

CrossRef Full Text | Google Scholar

Marciano, W. J. (1984). Time Variation of the Fundamental "Constants" and Kaluza-Klein Theories. Phys. Rev. Lett. 52, 489–491. doi:10.1103/physrevlett.52.489

CrossRef Full Text | Google Scholar

Mohanty, G., Sahoo, P. K., and Mishra, B. (2002). On Bianchi Type-I Mesonic Cosmological Model in Bimetric Theory. Astrophysics Space Sci. 281, 609–612. doi:10.1023/A:1015868106122

CrossRef Full Text | Google Scholar

Mohanty, G., and Samanta, G. C. (2010). Five Dimensional LRS Bianchi Type-I String Cosmological Model in General Relativity. FIZIKA B 19, 239–246.

Google Scholar

Mohanty, G., and Samanta, G. C. (2010). Five Dimensional String Cosmological Models with Massive Scalar Field. FIZIKA B 19, 43–52.

Google Scholar

Mollah, M. R., Singh, P. K., and Singh, P. S. (2019). On Bianchi Type III Cosmological Model with Quadratic EoS in Lyra Geometry. Int. J. Geom. Methods Mod. Phys. 15, 185–194. doi:10.1142/S0219887818501943

CrossRef Full Text | Google Scholar

Page, L., Hinshaw, G., Komatsu, E., Nolta, M. R., Spergel, D. N., Bennett, C. L., et al. (2007). Three-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Polarization Analysis. Astrophys Suppl. Ser. 170, 335–376. doi:10.1086/513699

CrossRef Full Text | Google Scholar

Pawar, D. D., and Deshmukh, A. G. (2010). Bulk Viscous Fluid Plane Symmetric String Cosmological Model in General Relativity. Bulg. J. Phys. 37, 56–63.

Google Scholar

Perlmutter, S., Aldering, G., Goldhaber, G., Knop, R. A., Nugent, P., Castro, P. G., et al. (1999). Measurements of Ω and Λ from 42 High‐Redshift Supernovae. Astrophys. J. 517, 565–586. doi:10.1086/307221

CrossRef Full Text | Google Scholar

Rahaman, F., Chakraborty, S., Das, S., Hossain, M., and Bera, J. (2003). Higher-dimensional String Theory in Lyra Geometry. Pramana - J. Phys. 60, 453–459. doi:10.1007/bf02706151

CrossRef Full Text | Google Scholar

Ram, S., and Verma, M. K. (2019). Spatially Homogeneous Bianchi Type I Mesonic Models in Two-Fluid Cosmology. Prespacetime J. 10, 293–300.

Google Scholar

Reddy, D. R. K., and Naidu, R. L. (2007). Five Dimensional String Cosmological Models in a Scalar-Tensor Theory of Gravitation. Astrophys. Space Sci. 307, 395–398. doi:10.1007/s10509-007-9387-x

CrossRef Full Text | Google Scholar

Riess, A. G., Filippenko, A. V., Challis, P., Clocchiatti, A., Diercks, A., Garnavich, P. M., et al. (1998). Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant. Astron. J. 116, 1009–1038. doi:10.1086/300499

CrossRef Full Text | Google Scholar

Sahoo, P. K., and Mishra, B. (2015). Higher-Dimensional Bianchi Type-III Universe with Strange Quark Matter Attached to String Cloud in General Relativity. Turk J. Phys. 39, 43–53. doi:10.3906/fiz-1403-5

CrossRef Full Text | Google Scholar

Sahoo, P. K., Sahoo, P., and Bishi, B. K. (2017). Anisotropic Cosmological Models in f(R,T) Gravity with Variable Deceleration Parameter. Int. J. Geom. Methods Mod. Phys. 14, 1750097. doi:10.1142/s0219887817500979

CrossRef Full Text | Google Scholar

Samanta, G. C., Biswal, S. K., and Mohanty, G. (2011). Some Five Dimensional Bianchi Type-III String Cosmological Models in General Relativity. Bulg. J. Phys. 38, 380–389.

Google Scholar

Samanta, G. C., and Debata, S. (2011). Five Dimensional Bianchi Type-I String Cosmological Models in Lyra Manifold. J. Mod. Phys 3, 180–183. doi:10.4236/jmp.2012.32024

CrossRef Full Text | Google Scholar

Sing, K. P., and Mollah, M. R. (2016). Higher Dimensional LRS Bianchi Type-I Cosmological Model Universe Interacting with Perfect Fluid in Lyra Geometry. Afr. Rev. Phys. 11, 33–38.

Google Scholar

Singh, C. P. (2013). String Cosmology with Magnetized Bulk Viscous Fluid in Bianchi I Universe. Astrophys Space Sci. 343, 773–781. doi:10.1007/s10509-012-1236-x

CrossRef Full Text | Google Scholar

Singh, G. P., Deshpande, R. V., and Singh, T. (2004). Higher-Dimensional Cosmological Model with Variable Gravitational Constant and Bulk Viscosity in Lyra Geometry. Pramana - J. Phys. 63, 937–945. doi:10.1007/bf02704332

CrossRef Full Text | Google Scholar

Singh, K. P., and Baro, J. (2020). Bulk Viscous Fluid Bianchi Type-I String Cosmological Model with Negative Constant Deceleration Parameter. Adv. Math. Sci. J. 9 (7), 4907–4916. doi:10.37418/amsj.9.7.55

CrossRef Full Text | Google Scholar

Stachel, J. (1980). Thickening the String. I. The String Perfect Dust. Phys. Rev. D 21, 2171–2181. doi:10.1103/physrevd.21.2171

CrossRef Full Text | Google Scholar

Tiwari, R. K., Shukla, B. K., and Mishra, S. (2019). Bianchi Typpe-III String Cosmological Model in f(R,T) Modified Gravity Theory. Prespacetime J. 10, 306–315.

Google Scholar

Tripathi, B. R., Tyagi, A., and Parikh, S. (2017). Bianchi Type-I Inhomogeneous String Cosmological Model with Electromagnetic Field in General Relativity. Prespacetime J. 8, 474–483.

Google Scholar

Vilenkin, A. (1981). Cosmic Strings. Phys. Rev. D 24, 2082–2089. doi:10.1103/physrevd.24.2082

CrossRef Full Text | Google Scholar

Vilenkin, A. (1981). Gravitational Field of Vacuum Domain Walls and Strings. Phys. Rev. D 23, 852–857. doi:10.1103/physrevd.23.852

CrossRef Full Text | Google Scholar

Wang, X. X. (2005). Bianchi Type-III String Cosmological Model with Bulk Viscosity in General Relativity. Chin. Phys. Lett. 22, 29–32. doi:10.1088/0256-307X/22/1/009

CrossRef Full Text | Google Scholar

Yadav, A. K., Yadav, V. K., and Yadav, L. (2011). Bianchi Type-V String Cosmological Models in General Relativity. Pramana - J. Phys. 76, 681–690. doi:10.1007/s12043-011-0061-z

CrossRef Full Text | Google Scholar

Zel’dovich, Y. B. (1980). Cosmological Fluctuations Produced Near a Singularity. Mon. Not. R. Astron. Soc. 192, 663–667.

Google Scholar

Zel’dovich, Y. B., Kobzarev, I. Y., and Okun, L. B. (1974). Cosmological Consequences of the Spontaneous Breakdown of Discrete Symmetry. Zh. Eksp. Teor. Fiz. 67, 3–11.

Google Scholar