Theory of Fluid Instabilities in Partially Ionized Plasmas: An Overview

Introduction

The study of partially ionized plasmas (PIP) in the astrophysical context has received a tremendous boost in the recent years. A rich variety of astrophysical environments are made of PIP with an ionization degree that may vary from very weak ionization to almost full ionization. For instance, PIP can be found in molecular clouds, accretion disks, cometary tails, planet ionospheres, and the atmosphere of the Sun and other stars, just to give a few examples. Effects driven by partial ionization play a fundamental role in the physics of those plasmas. A recent summary on PIP dynamics in astrophysics can be found in Ballester et al. (2018) and references therein.

Fluid instabilities of different kind commonly occur in astrophysical plasmas, including those that are partially ionized. In many cases, the instabilities are essential to understand the dynamics of the plasmas and have a dramatic impact on their evolution. Thus, partial ionization effects need to be taken into account in the studies of instabilities in astrophysical PIP that aim to describe their relevant physics in detail. In this regard, the analytical and numerical studies of fluid instabilities in astrophysical plasmas have traditionally been made within the theoretical framework of ideal magnetohydrodynamics (MHD) (see, e.g., Goedbloed et al., 2019). Ideal MHD applies to situations where the temporal and spatial scales are much larger than the corresponding scales of the interactions between the different species that compose the plasma. The applicability of ideal MHD in the case of PIP is more limited because, typically, the collisions with neutral species introduce scales that are significantly larger than those in fully ionized plasmas. Theories beyond ideal MHD are required to fully describe the physics of instabilities in PIP when the temporal and spatial scales of the instabilities approach those of collisions with neutrals (see, e.g., Khomenko et al., 2014a).

The purpose of this review paper is to give a general discussion about the effects and modifications caused by partial ionization on some classic fluid instabilities that frequently appear in astrophysical plasmas. We do not aim to perform an exhaustive account of all the works that have investigated fluid instabilities. That would be far beyond the scope of this paper. For the interested reader, there are many books with a more general account of instabilities than this paper aims to provide (e.g., Chandrasekhar, 1961b; Bateman, 1978; Drazin and Reid, 1981; Melrose, 1989; Goedbloed et al., 2019). Instead, we shall focus on discussing the unique effects driven by partial ionization. To this end, for every considered instability we shall first summarize their basic physics. Then, we shall explore how the presence of neutrals affects the triggering, growth, and nonlinear evolution of the instabilities, providing references to the original works where these relevant studies have been made. The case of the solar atmosphere will receive predominant attention throughout the paper. The reason is that some of the instabilities discussed here have actually been observed in PIP of the solar atmosphere as, e.g., solar prominences, so that some of the theoretical results discussed here have direct applications in the solar case. Because of its proximity, the solar plasma offers a unique opportunity to test theory and simulations against observations. Thus, the present review emphasizes the solar application.

This paper is organized as follows. Section 2 discuses the single-fluid and two-fluid mathematical models that are frequently used to investigate instabilities in PIP, including some hints of their numerical implementation. Then, the following sections are devoted to the discussion of several major instabilities: the Kelvin-Helmholtz instability (Section 3), the Rayleigh-Taylor instability (Section 4), the thermal or condensational instability (Section 5), the Farley-Buneman instability (Section 6), the magneto-rotational instability (Section 7), and the Jeans instability (Section 8). Finally, a general discussion and some concluding remarks are given in Section 9.

Fluid Models for Partially Ionized Solar Plasmas

In this section, we briefly summarize the two different but complementary strategies beyond ideal MHD that are typically used to investigate PIP dynamics in the solar atmosphere: the single-fluid and two-fluid models. General derivations of these equations can be found in, e.g., Lehnert (1959), Braginskii (1965), Draine (1986), Helander et al. (1994), Zaqarashvili et al. (2011), Meier and Shumlak (2012), Leake et al. (2014), Khomenko et al. (2014a), and Ballester et al. (2018). Modifications of these equations applicable to other astrophysical PIP are also discussed in Ballester et al. (2018). Although not strictly applicable to the case of partially ionized collisional plasmas, the recent works by Hunana et al. (2019b,a) explore in detail the link between kinetic theory and collisionless fluid models.

Single-Fluid Approximation

In the single-fluid MHD approximation, the distinction between the different species that compose the plasma, namely ions, electrons, and neutrals, is lost. The governing equations are written in terms of total or averaged quantities that represent the plasma as a whole (see, e.g., Goedbloed et al., 2019). Therefore, the single-fluid approximation is applicable to situations in which the temporal and spatial scales of interest are much larger than the corresponding scales of the interactions between the individual plasma components. In the case of PIP, the relevant temporal scale is the ion-neutral (or neutral-ion) collision time, i.e., the average time required for an ion (neutral) to encounter a neutral (ion). The corresponding length scale is the ion-neutral (neutral-ion) collision length, i.e., the average distance that an ion (neutral) needs to travel to encounter a neutral (ion). Although the details of the ion-neutral interactions are lost in the single-fluid approximation, effective remnants of those interactions remain in the form of nonideal terms in the MHD equations. Thus, the usual expressions of the single-fluid MHD equations for a PIP are

$\begin{array}{ccc}\hfill \frac{\mathrm{D}\rho }{\mathrm{D}t}& =\hfill & -\rho \nabla \cdot \mathbf{v},\hfill \end{array}(1)$

$\begin{array}{ccc}\hfill \rho \frac{\mathrm{D}\mathbf{v}}{\mathrm{D}t}& =\hfill & -\nabla p+\frac{1}{\mu }\left(\nabla \times \mathbf{B}\right)\times \mathbf{B}+\rho \mathbf{g}-\nabla \cdot \widehat{\pi },\hfill \end{array}(2)$

$\begin{array}{ccc}\hfill \frac{\partial \mathbf{B}}{\partial t}& =\hfill & \nabla \times \left(\mathbf{v}\times \mathbf{B}\right)-\nabla \times \left(\eta \nabla \times \mathbf{B}\right)+\nabla \times \left\{\left[{\eta }_{\text{A}}\left(\nabla \times \mathbf{B}\right)\times \mathbf{B}\right]\times \mathbf{B}\right\}\hfill \\ \hfill & \hfill & -\nabla \times \left[{\eta }_{\text{H}}\left(\nabla \times \mathbf{B}\right)\times \mathbf{B}\right],\hfill \end{array}(3)$

$\begin{array}{ccc}\hfill \frac{\mathrm{D}p}{\mathrm{D}t}& =\hfill & -\gamma p\nabla \cdot \mathbf{v}+\left(\gamma -1\right)\mathcal{L},\hfill \end{array}(4)$

$\begin{array}{ccc}\hfill p& =\hfill & \rho R\frac{T}{\tilde{\mu }}.\hfill \end{array}(5)$

In these equations, D/Dt = ∂/∂t + v ⋅∇ is the total or Lagrangian derivative, ρ is the plasma total density, p is the plasma total gas pressure, v is the center-of-mass velocity, B is the magnetic field, μ is the magnetic permeability, g is the acceleration of gravity, $\widehat{\pi }$ is the viscosity tensor, η is Ohm’s diffusion coefficient, η_A is the ambipolar diffusion coefficient, η_H is Hall’s coefficient, γ is the adiabatic coefficient, $\mathcal{L}$ is the total heat-loss function of the plasma, R is the ideal gas constant, T is the plasma common temperature, and $\tilde{\mu }$ is the mean molecular weight. Expressions of the coefficients that appear in these equations are not given here for the sake of simplicity and can be found elsewhere (see, e.g., Khomenko et al., 2014a; Ballester et al., 2018)

Eq. 1 is the usual continuity equation for the whole fluid. Eq. 2 is the momentum equation, which includes the pressure force, Lorentz’s force, gravity, and viscosity. The full viscosity tensor, $\widehat{\pi }$, should include contributions from ion, electron, and neutral viscosities. The full treatment of viscosity in a collisional partially ionized plasma is rather cumbersome (see Vranjes, 2014). A common approximation is considering the classic Braginskii (1965) viscosity for ions and electrons, together with an isotropic viscosity for neutrals (see, e.g., Leake et al., 2012; Soler et al., 2015a). In the lower solar atmosphere, neutral viscosity is several orders of magnitude larger than ion viscosity (see Soler et al., 2015b). Eq. 3 is the induction equation, which includes the ideal inductive term followed by several nonideal terms: Ohm’s diffusion term, ambipolar diffusion term, and Hall’s term. Ohm’s diffusion is generally caused by collisions between charge-carriers and neutrals. In the solar atmosphere, Ohm’s diffusion is essentially caused by electron-ion collisions and is greatly enhanced by electron-neutral collisions in the weakly ionized solar chromosphere (see, e.g., Soler et al., 2019). Ambipolar difussion is caused by ion-neutral collisions and typically is the dominant dissipation mechanism in a PIP with strong magnetic fields (Zweibel, 2015). Hall’s term is not a dissipative but a dispersive term that arises because of the imperfect magnetization of ions. In a PIP, ion-neutral collisions enhance this mechanism by further decoupling ions from the magnetic field (see Pandey and Wardle, 2008). The importance of Ohm’s, ambipolar, and Hall’s terms in the lower solar atmosphere was explored by Khomenko and Collados (2012, see their Figure 1), who showed that Ohm’s and Hall’s terms are relevant at lower heights, while the importance of the ambipolar term grows with height and becomes the dominant term in the middle and higher chromosphere. Other terms that could be included in the induction equation are the diamagnetic current term and Biermann’s battery term, which couple pressure gradients with the magnetic field (see, e.g., Khomenko et al., 2014a; Ballester et al., 2018). These terms are omitted here because they are generally less relevant than the included terms (see also a discussion in Cowling, 1956).

FIGURE 1

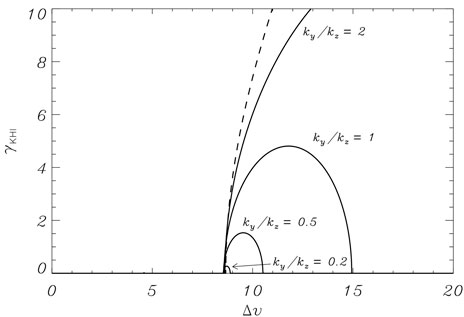
FIGURE 1. KHi growth rate in normalized units as a function of the dimensionless shear flow velocity in a fully ionized plasma interface. The dashed line corresponds to the incompressible case. The various solid lines correspond to the compressible case for different values of the ratio of the perpendicular, k_y, to the longitudinal, k_z, components of the wavevector (indicated within the figure). Compressibility can entirely suppress the KHi for a sufficiently small value of the ratio k_y/k_z. Adapted from Soler et al. (2012b). © AAS. Reproduced with permission.

On the other hand, Eq. 4 is the internal energy equation, which is written here as an equation for the pressure. All sources and sinks of energy are enclosed within the heat-loss function, namely

$\mathcal{L}=\nabla \cdot \left(\widehat{\kappa }\cdot \nabla T\right)-\mathrm{\Lambda }+\mathbf{J}\cdot \mathbf{E}*-\widehat{\pi }:\nabla \mathbf{v}+H_{\text{other}},(6)$

where the various terms, in order from left to right, represent thermal conduction, radiative cooling, Joule heating (with J and E* the current density and the effective electric field, respectively), viscous heating, and other unspecified sources of heating. In Eq. 6, $\widehat{\kappa }$ is the thermal conductivity tensor that, as happens for the viscosity tensor, should include contributions from ion, electron, and neutral thermal conductivities. Again, a common approximation is considering the classic Braginskii (1965) thermal conductivity for electrons (ion thermal conductivity is usually negligible), but a simple isotropic thermal conductivity for neutrals (see, e.g., Leake et al., 2012; Soler et al., 2015a). As in the case of viscosity, neutral thermal conductivity is also larger than electron thermal conductivity in the lower solar atmosphere (see Soler et al., 2015b). The cooling function, Λ, accounts for radiative losses. Assuming optically-thin plasma, several parametrizations of the cooling function are available for solar atmospheric plasmas (see, e.g., Hildner, 1974; Athay, 1986; Klimchuk and Cargill, 2001; Schure et al., 2009; Soler et al., 2012a). The Joule heating can be split in the following way

$\mathbf{J}\cdot {\mathbf{E}}^{*}=\mu \eta {\left|{\mathbf{J}}_{\parallel }\right|}^2+\mu {\eta }_{\mathrm{C}}{\left|{\mathbf{J}}_{\perp }\right|}^2,(7)$

where ${\eta }_{\text{C}}=\eta +{\left|\mathbf{B}\right|}^2{\eta }_{\text{A}}$ is the so-called Cowling’s total coefficient (Cowling, 1956) and J_∥ and J_⊥ denote the components of the current density parallel and perpendicular to the magnetic field direction. Thus, in a PIP the dissipation of perpendicular currents is more efficient than that of parallel currents because of the effect of ambipolar diffusion (see also Cowling, 1956; Khomenko and Collados, 2012). Finally, the ideal gas law is considered as equation of state (Eq. 5) to close the system, where the mean molecular weight, $\tilde{\mu }$, depends on the ionization degree. In a pure hydrogen plasma, it varies from $\tilde{\mu }=0.5$ for a fully ionized plasma to $\tilde{\mu }=1$ for a neutral gas.

Two-Fluid Approximation

The single-fluid MHD approximation breaks down when the spatial and temporal scales of interest approach the characteristic ion-neutral or neutral-ion scales. In that scenario, the plasma cannot longer be treated as a single fluid and a multi-fluid treatment is needed (see, e.g., Martínez-Gómez et al., 2016, 2017). A specific version of the multi-fluid theory is the two-fluid approximation, in which neutrals are treated as a separate fluid while ions and electrons are still assumed to remain strongly coupled and to form another fluid (see, e.g., Zaqarashvili et al., 2011; Leake et al., 2012; Maneva et al., 2017; Popescu Braileanu et al., 2019). The neutral fluid and the ion-electron fluid interact with each other by means of ion-neutral and electron-neutral collisions, along with ionization and recombination. The two-fluid model is justified by the fact that the frequency of collisions between ions and electrons is typically much higher than the frequency of collisions between ions and neutrals. This is the realistic situation in many astrophysical plasmas, including the solar atmosphere (see, e.g., Figure 11 of Ballester et al., 2018). The basic equations in the two-fluid approximation are

$\begin{array}{ccc}\hfill \frac{\mathrm{D}{\rho }_{\text{c}}}{\mathrm{D}t}& =\hfill & -{\rho }_{\text{c}}\nabla \cdot {\mathbf{v}}_{\text{c}}-S,\hfill \end{array}(8)$

$\begin{array}{ccc}\hfill \frac{\mathrm{D}{\rho }_{\text{n}}}{\mathrm{D}t}& =\hfill & -{\rho }_{\text{n}}\nabla \cdot {\mathbf{v}}_{\text{n}}+S,\hfill \end{array}(9)$

$\begin{array}{ccc}\hfill {\rho }_{\text{c}}\frac{\mathrm{D}{\mathbf{v}}_{\text{c}}}{\mathrm{D}t}& =\hfill & -\nabla p_{\text{c}}+\frac{1}{\mu }\left(\nabla \times \mathbf{B}\right)\times \mathbf{B}+{\rho }_{\text{c}}\mathbf{g}-\nabla \cdot {\widehat{\pi }}_{\text{c}}-\mathbf{R},\hfill \end{array}(10)$

$\begin{array}{ccc}\hfill {\rho }_{\text{n}}\frac{\mathrm{D}{\mathbf{v}}_{\text{n}}}{\mathrm{D}t}& =\hfill & -\nabla p_{\text{n}}+{\rho }_{\text{n}}\mathbf{g}-\nabla \cdot {\widehat{\pi }}_{\text{n}}+\mathbf{R},\hfill \end{array}(11)$

$\begin{array}{ccc}\hfill \frac{\partial \mathbf{B}}{\partial t}& =\hfill & \nabla \times \left({\mathbf{v}}_{\text{c}}\times \mathbf{B}\right)-\nabla \times \left(\eta \nabla \times \mathbf{B}\right)-\nabla \times \left[{\eta }_{\mathrm{H}}\left(\nabla \times \mathbf{B}\right)\times \mathbf{B}\right]\hfill \\ -\nabla \times \left[\chi \left({\mathbf{v}}_{\text{c}}-{\mathbf{v}}_{\text{n}}\right)\right],\hfill \end{array}(12)$

$\begin{array}{ccc}\hfill \frac{\mathrm{D}{p}_{\text{c}}}{\mathrm{D}t}& =\hfill & -\gamma p_{\text{c}}\nabla \cdot {\mathbf{v}}_{\text{c}}+\left(\gamma -1\right){\mathcal{L}}_{\text{c}},\hfill \end{array}(13)$

$\begin{array}{ccc}\hfill \frac{\mathrm{D}{p}_{\text{n}}}{\mathrm{D}t}& =\hfill & -\gamma p_{\text{n}}\nabla \cdot {\mathbf{v}}_{\text{n}}+\left(\gamma -1\right){\mathcal{L}}_{\text{n}},\hfill \end{array}(14)$

$\begin{array}{ccc}\hfill p_{\text{c}}& =\hfill & n_{\text{c}}{k}_{\text{B}}{T}_{\text{c}},\hfill \end{array}(15)$

$\begin{array}{ccc}\hfill p_{\text{n}}& =\hfill & n_{\text{n}}{k}_{\text{B}}{T}_{\text{n}},\hfill \end{array}(16)$

where all symbols have the same meaning as before, with the subscripts “c” and “n” explicitly denoting quantities related to the charged (ion-electron) fluid and the neutral fluid, respectively. Quantities that have not been defined before are the number densities of charges and neutrals, namely n_c and n_n, and Boltzmann’s constant, k_B. We note that because of the small electron mass, ρ_c ≈ ρ_i, with ρ_i the ion density.

There are some terms in the two-fluid equations that were absent from the equivalent single-fluid equations. The term S in the two continuity equations (Eqs 8, 9) represents ionization/recombination, namely

$S={\rho }_{\text{c}}{\mathrm{\Gamma }}^{\text{rec}}-{\rho }_{\text{n}}{\mathrm{\Gamma }}^{\text{ion}},(17)$

with Γ^ion/rec the ionization/recombination rates. Explicit expressions for these rates in terms of the plasma properties can be found in, e.g., Meier and Shumlak (2012); Leake et al. (2012); Maneva et al. (2017); Popescu Braileanu et al. (2019) and references therein. The term R in the two momentum equations (Eqs. 10, 11) represents collisional momentum transfer and can be cast as

$\mathbf{R}={\alpha }_{\text{cn}}\left({\mathbf{v}}_{\text{c}}-{\mathbf{v}}_{\text{n}}\right)+{\rho }_{\text{c}}{\mathrm{\Gamma }}^{\text{rec}}{\mathbf{v}}_{\text{c}}-{\rho }_{\text{n}}{\mathrm{\Gamma }}^{\text{ion}}{\mathbf{v}}_{\text{n}},(18)$

where the first term is the momentum transfer due to collisions (that may include both elastic collisions and charge exchange collisions) and the last two terms are associated to the loss or gain of momentum during ionization/recombination processes. We note that Eq. 18 assumes that the velocity drift, v_c − v_n, is much smaller than the thermal speed (Draine, 1986). In Eq. 18, α_cn is the total friction coefficient, which is computed as the sum of the friction coefficients for ion-neutral, α_in, and electron-neutral, α_en, collisions, namely

${\alpha }_{\text{cn}}={\alpha }_{\text{in}}+{\alpha }_{\text{en}}.(19)$

For simplicity, expressions for the friction coefficients are not given here and can be found elsewhere (see, e.g., Braginskii, 1965; Draine, 1986, among others). The collision frequency of two species β and β′ is computed from the corresponding friction coefficient as

${\nu }_{\beta {\beta }^{\prime }}=\frac{{\alpha }_{\beta {\beta }^{\prime }}}{{\rho }_{\beta }},(20)$

where ρ_β is the mass density of species β. Although the friction coefficients are symmetric, i.e., α_ββ′ = α_β′β, in general ν_ββ′ ≠ ν_β′β because of the different densities that the two colliding species may have. These collision frequencies introduce the relevant time scales for the interactions between fluids.

The frictional term (Eq. 18) is one of the major forces behind the district dynamics that a PIP displays compared to a fully ionized plasma. In the two-fluid formalism, the frictional term appears explicitly in the momentum equations of charges and neutrals, while in the single-fluid equations this frictional effect was hidden behind the ambipolar diffusion term. Many effects that are caused by ambipolar diffusion of the magnetic field in the single-fluid approximation become more physically transparent in the two-fluid case, where the coupling between charges and neutrals is mediated by a more plain frictional force. For instance, the damping of MHD waves that propagate in a PIP is caused by this friction (see, e.g., Kulsrud and Pearce, 1969; Balsara, 1996; Soler et al., 2013a,b), while such a damping is attributed to ambipolar diffusion of the magnetic field perturbations in the single-fluid model. An analysis of the differences between the two-fluid and single-fluid models using analytical results of MHD waves was performed by Zaqarashvili et al. (2011). The ion-neutral friction is also fundamental to understand the properties of shocks in astrophysical PIP like molecular clouds. In this regard, the formation of C-shocks in which all hydrodynamic variables are continuous is a good example (see, e.g., Draine, 1980; Draine et al., 1983). In connection to the topic on this review, the reader should not be surprised that the frictional term is also relevant for the development of instabilities.

To summarize, the two-fluid induction equation (Eq. 12) contains three differences with respect to its single-fluid equivalent (Eq. 13). Firstly, in the ideal term the whole fluid centre-of-mass velocity, v, is replaced by the velocity of charges, v_c. Secondly, as a consequence of the previous difference, the ambipolar term is absent from the two-fluid induction equation, but this does not mean that the physical effect of ambipolar diffusion is missing form the equations. Indeed, as explained before, the effect of ambipolar difusion consistently remains in the form of the collisional terms in the two momentum equations (Eqs 10, 11). Thirdly, a new term that accounts for electron-neutral collisions is present. This term depends on the coefficient χ given in Ballester et al. (2018) and is equivalent to the coefficient η_D given in Popescu Braileanu et al. (2019). However, this additional term is usually negligible. We note again that some terms that couple pressure gradients with the magnetic field evolution have been omitted from the induction equation because of their minor importance (see, e.g., Popescu Braileanu et al., 2019, for the full expression of the induction equation).

The two energy equations (Eqs 13, 14) now contain separate heat-loss functions for charges and for neutrals, namely

$\begin{array}{ccc}\hfill {\mathcal{L}}_{\text{c}}& =\hfill & Q_{\text{c}}^{\text{c,\hspace{0.17em}n}}+\nabla \cdot \left({\widehat{\kappa }}_{\text{c}}\cdot \nabla T_{\text{c}}\right)-{\mathrm{\Lambda }}_{\text{c}}+\mu \eta {\left|\mathbf{J}\right|}^2-{\widehat{\pi }}_{\text{c}}:\nabla {\mathbf{v}}_{\text{c}}+H_{\text{c,\hspace{0.17em}other}},\hfill \end{array}(21)$

$\begin{array}{ccc}\hfill {\mathcal{L}}_{\text{n}}& =\hfill & Q_{\text{n}}^{\text{n,\hspace{0.17em}c}}+\nabla \cdot \left({\widehat{\kappa }}_{\text{n}}\cdot \nabla T_{\text{n}}\right)-{\mathrm{\Lambda }}_{\text{n}}-{\widehat{\pi }}_{\text{n}}:\nabla {\mathbf{v}}_{\text{n}}+H_{\text{n,\hspace{0.17em}other}},\hfill \end{array}(22)$

where the meaning of the symbols is the same as in Eq. 6. Importantly, we see that the Joule heating term is only included in the charges heat-loss function (see the fourth term on the right-hand side of Eq. 21), and this term is now isotropic because of Ohm’s diffusion. In addition, both ${\mathcal{L}}_{\text{c}}$ and ${\mathcal{L}}_{\text{n}}$ contain an additional term that accounts for heating and heat exchange due to the interactions with the other fluid, i.e., collisions and ionization/recombination. These terms can be cast as (see, e.g., Martínez-Gómez et al., 2016, 2017; Popescu Braileanu et al., 2019)

$\begin{array}{ccc}\hfill Q_{\text{c}}^{\text{c,\hspace{0.17em}n}}& =\hfill & \frac{2{\alpha }_{\text{cn}}}{m_{\text{i}}+m_{\text{n}}}\left[\frac{1}{2}{m}_{\text{n}}{\left({\mathbf{v}}_{\text{n}}-{\mathbf{v}}_{\text{c}}\right)}^2+\frac{1}{\gamma -1}{k}_{\text{B}}\left(T_{\text{n}}-T_{\text{c}}\right)\right]+\frac{1}{2}{\rho }_{\text{n}}{\mathrm{\Gamma }}^{\text{ion}}{\left({\mathbf{v}}_{\text{n}}-{\mathbf{v}}_{\text{c}}\right)}^2\hfill \\ +\frac{1}{\gamma -1}\frac{2k_{\text{B}}}{m_{\text{i}}+m_{\text{n}}}\left({\rho }_{\text{n}}{T}_{\text{n}}{\mathrm{\Gamma }}^{\text{ion}}-{\rho }_{\text{c}}{T}_{\text{c}}{\mathrm{\Gamma }}^{\text{rec}}\right),\hfill \end{array}(23)$

$\begin{array}{ccc}\hfill Q_{\text{n}}^{\text{n,\hspace{0.17em}c}}& =\hfill & \frac{2{\alpha }_{\text{cn}}}{m_{\text{i}}+m_{\text{n}}}\left[\frac{1}{2}{m}_{\text{i}}{\left({\mathbf{v}}_{\text{c}}-{\mathbf{v}}_{\text{n}}\right)}^2+\frac{1}{\gamma -1}{k}_{\text{B}}\left(T_{\text{c}}-T_{\text{n}}\right)\right]+\frac{1}{2}{\rho }_{\text{c}}{\mathrm{\Gamma }}^{\text{rec}}{\left({\mathbf{v}}_{\text{c}}-{\mathbf{v}}_{\text{n}}\right)}^2\hfill \\ \hfill & \hfill & +\frac{1}{\gamma -1}\frac{2k_{\text{B}}}{m_{\text{i}}+m_{\text{n}}}\left({\rho }_{\text{c}}{T}_{\text{c}}{\mathrm{\Gamma }}^{\text{rec}}-{\rho }_{\text{n}}{T}_{\text{n}}{\mathrm{\Gamma }}^{\text{ion}}\right),\hfill \end{array}(24)$

where m_i and m_n are the masses of ions and neutrals, respectively. The terms proportional to α_cn in Eqs 23, 24 are related with collisions, while the terms proportional to Γ^ion/rec are related with ionization/recombination. Among these terms, those involving the temperatures, T_c and T_n, represent heat exchange between the fluids and their role is to equalize both temperatures, whereas those involving the square of the velocity drift, ${\left({\mathbf{v}}_{\text{n}}-{\mathbf{v}}_{\text{c}}\right)}^2$, produce a net heating of the two fluids and so a global increase of the temperature. In particular, the terms proportional to both α_cn and ${\left({\mathbf{v}}_{\text{n}}-{\mathbf{v}}_{\text{c}}\right)}^2$ are the two-fluid version of the ambipolar heating term, $\mu {\left|\mathbf{B}\right|}^2{\eta }_{\text{A}}{\left|{\mathbf{J}}_{\perp }\right|}^2$, that appears in the single-fluid approximation. We again note that Eqs 23, 24 are obtained in the limit that the velocity drift is much smaller than the thermal speed (Draine, 1986).

Numerical Implementation

The numerical implementation of the PIP equations is a challenging task because of the presence of diffusive (parabolic) terms and the dispersive (hyperbolic) Hall’s term, which impose extremely small time steps if the temporal evolution is done with standard explicit schemes. For this reason, different strategies are adopted to allow high-resolution numerical simulations to be practical. For instance, a convenient strategy is that of operator splitting, in which the ideal and nonideal terms are evolved separately. Ideal terms can be evolved with regular explicit schemes as in ideal MHD simulations, in which the time step is essentially determined by the largest value of the Alfvén/sound velocity in a low-β/high-β plasma. Then, different methods are used to deal with the nonideal terms.

On the other hand, diffusive terms can be advanced with the super time stepping technique (Alexiades et al., 1996; O’Sullivan and Downes, 2006, 2007), which is able to accelerate the explicit computations by using a mixture of large (unstable) time steps and short (stable) time steps that are determined by Chebyshev polynomials. Globally, the super time stepping scheme remains stable. Alternatively, the super time stepping method can also be implemented with Legendre polynomials, which might offer better stability properties (see Meyer et al., 2014). Other methods to deal with diffusive terms are, e.g., the heavy ion approximation (e.g., Li et al., 2006; McKee et al., 2010; Li et al., 2012) and the use of implicit or mixed implicit-explicit schemes (e.g., Falle, 2003).

Concerning the dispersive Hall’s term, the treatment of this term is even more problematic. The Hall term imposes explicit time steps that tend to zero in situations where it is dominant over diffusive terms (Falle, 2003). To solve this problem, the hyper-diffusivity method (see, e.g., Tóth et al., 2008) introduces a sort of artificial diffusion (or hyper-diffusion) with the aim of stabilizing the Hall term, which is advanced with standard explicit schemes. On the contrary, O’Sullivan and Downes (2006, 2007) proposed the Hall diffusion scheme, in which no arbitrary hyper-diffusivity is required. The Hall diffusion scheme relies on the fact that, because of Hall’s term, the instantaneous rate of change of any one component of the magnetic field depends only on the spatial gradients of the other two components. With this in mind, one can advance one component of the magnetic field explicitly, followed by an implicit-like discretization of the other components. However, if the different magnetic field components are updated in a particular order, then the difference equations are explicit in the sense that no matrix inversions, or approximations of matrix inversions, are required. The Hall diffusion scheme is does not lead to instability unless the Courant condition is not satisfied.

Readers interested in the benefits and limitations of these strategies and methods are referred to Section 3 of Ballester et al. (2018) and references therein for detailed explanations.

Kelvin-Helmholtz Instability

The Kelvin–Helmholtz instability (KHi), named after Thomson (1871) and von Helmholtz (1868), is a classic instability that arises at the interface between two fluids in relative motion. Well-known textbooks where the basics of the KHi are discussed in detail are, e.g., Chandrasekhar (1961b) and Drazin and Reid (1981). The KHi is important in many astrophysical plasmas where unstable velocity shears result in the formation of vortices, mixing of plasmas with different densities, and generation of turbulence (see, e.g., Keppens et al., 1999; Ryu et al., 2000; Matsumoto and Hoshino, 2004; Hillier, 2019). The literature abounds in studies of the KHi in different astrophysical contexts such as, e.g., the magnetopause (e.g., Nagano, 1979; Hasegawa et al., 2006; Masson and Nykyri, 2018), planetary magnetospheres (e.g., Miura, 1984; Johnson et al., 2014), Earth’s aurora (e.g., Farrugia et al., 1994), cometary tails (e.g., Ershkovich et al., 1986), protoplanetary disks (e.g., Gómez and Ostriker, 2005), jets and outflows (e.g., Keppens et al., 1999; Baty and Keppens, 2006), molecular clouds (Berné et al., 2010), among many other environments. The case of the KHi in the solar atmosphere is of special relevance because recent observations have confirmed the ubiquitous presence of this instability. For instance, the KHi has been observed in the solar coronal plasma (Foullon et al., 2011; Ofman and Thompson, 2011; Möstl et al., 2013; Yuan et al., 2019), solar prominences (Berger et al., 2008, 2010; Ryutova et al., 2010; Berger et al., 2017; Hillier and Polito, 2018; Yang et al., 2018), coronal streamers (Feng et al., 2013), blowout jets (Li X. et al., 2018), and the solar wind (Kieokaew et al., 2021). The importance of the KHi in the solar plasma motivated a very rich theoretical literature on the topic, even before the instability was first observed (see, e.g. Zhelyazkov, 2015). The confirmed presence of the KHi in solar prominences is of special relevance for the present work because the plasma in prominences is only partially ionized (see, e.g., Labrosse et al., 2010).

Onset of the KHi in a Fully Ionized Plasma

In the spirit of the classic treatment of Chandrasekhar (1961b), the simplest situation in which the onset of the KHi can be studied corresponds to the case of two fully ionized unbounded plasmas with uniform densities ρ₁ and ρ₂ and separated by an abrupt interface. Both plasmas are permeated by a straight and constant magnetic field, which is orientated parallel to the interface. The magnetic field strength at the two sides of the interface is denoted by B₁ and B₂, respectively. In addition, the two plasmas are assumed to be in relative motion, with v₁ and v₂ the constant flow velocities at the two sides of the interface. The flow is assumed to be along the background magnetic field direction and the velocity shear across the interface is $\mathrm{\Delta }v=\left|v_1-v_2\right|$. We note that this set-up composed of an infinitely thin shear layer is ill-defined from a numerical point of view, but it is very convenient from an analytic perspective. A stability analysis of the interface can be done using the linearized single-fluid ideal MHD equations. Considering incompressible perturbations, a temporal dependence of the form $\exp \left(-i\omega t\right)$, where ω is the frequency, and a Fourier-analysis in space, the following dispersion relation of the surface waves propagating on the plasma interface can be derived, namely

${\rho }_1{\left(\omega -k_{\parallel }{v}_1\right)}^2+{\rho }_2{\left(\omega -k_{\parallel }{v}_2\right)}^2-k_{\parallel }^2\frac{B_1^2+B_2^2}{\mu }=0,(25)$

where k_∥ is the component of the wavevector parallel to the magnetic field and the flow. The analytic solution for the frequency is

$\omega =\frac{{\rho }_1{v}_1+{\rho }_2{v}_2}{{\rho }_1+{\rho }_2}{k}_{\parallel }\pm {\left[\frac{B_1^2+B_2^2}{\mu \left({\rho }_1+{\rho }_2\right)}-{\left(\mathrm{\Delta }v\right)}^2\frac{{\rho }_1{\rho }_2}{{\left({\rho }_1+{\rho }_2\right)}^2}\right]}^{1/2}{k}_{\parallel }.(26)$

The + and − signs in Eq. 26 correspond to parallel propagating (forward) waves and anti-parallel propagating (backward) waves, respectively, with respect to the magnetic field direction. There is a critical velocity shear, Δv_crit., denoted by

$\mathrm{\Delta }{v}_{\text{crit.}}={\left(\frac{{\rho }_1+{\rho }_2}{{\rho }_1{\rho }_2}\frac{B_1^2+B_2^2}{\mu }\right)}^{1/2},(27)$

which determines the stability of the wave modes. When Δv < Δv_crit. the frequency is real and the modes are stable regardless of the presence of the velocity shear. This is so because of the stabilizing influence of magnetic tension. However, when Δv > Δv_crit. magnetic tension is not able to stabilize the shear flow any more. The physical reason is that the kinetic energy associated with the shear flow becomes larger than the background magnetic energy. Then, the frequency becomes complex. The imaginary part of the frequency of the mode with the + sign is positive and, according to the prescribed dependence $\exp \left(-i\omega t\right)$, the amplitude of this mode grows with time. This corresponds to the onset and exponential growth of the KHi. The growth rate of the instability is given by

${\gamma }_{\text{KHi}}=k_{\parallel }\frac{\sqrt{{\rho }_1{\rho }_2}}{{\rho }_1+{\rho }_2}{\left[{\left(\mathrm{\Delta }v\right)}^2-{\left(\mathrm{\Delta }{v}_{\text{crit.}}\right)}^2\right]}^{1/2}.(28)$

The growth rate is proportional to k_∥, which means that small scales grow faster than large scales. In addition, for Δv ≫Δv_crit. the growth rate is approximately linear in the velocity shear. Eq. 27 can be rewritten as

$\mathrm{\Delta }{v}_{\text{crit.}}={\left[\frac{{\rho }_1+{\rho }_2}{{\rho }_1{\rho }_2}\left({\rho }_1{v}_{\text{A,}1}^2+{\rho }_2{v}_{\text{A,}2}^2\right)\right]}^{1/2},(29)$

where $v_{\text{A}}=B/\sqrt{\mu \rho }$ is the Alfvén velocity. Eq. 29 evidences that the critical shear flow is a sort of root-mean-square average of the Alfvén velocities at the two sides of the interface. This points out that the shear flow velocities needed for the onset of the KHi are necessarily super-Alfvénic. We note that the condition that the densities at the two sides of the interface are different is not actually needed for the triggering of the KHi; only a shear flow is needed. We also note that if the fluid is unmagnetized so that B₁ = B₂ = 0, this results in Δv_crit. = 0. In other words, there is no shear flow threshold for the triggering of the KHi in the absence of the stabilizing effect of the magnetic field. It would be the case of a fluid exclusively composed of neutrals. As seen later, this has a very important implication in the case of PIP, where only the charges are directly affected by the magnetic field.

The simple configuration explored above suffices for our later purpose to illustrate the effect of partial ionization. Additional ingredients in the background configuration as, e.g., compressibility, dissipation, flows not strictly parallel to the magnetic field, time-dependent flows, nonplanar geometry, a smooth transition, etc., cause refinements to the theory described above at the expense of a more involved mathematical analysis. It is not our goal to analyze all these additional effects, whose discussion can be found elsewhere. For instance, the effect of dissipation has been discussed in, e.g., Ryutova (2015); Ballai et al. (2015). The effect of replacing the abrupt interface by a smooth transition of thickness δ was explored in, e.g., Miura and Pritchett (1982); Berlok and Pfrommer (2019), who found that modes with k_∥δ ≳ 2 become stable because of the presence of the inhomogeneity. The KHi driven by time-dependent flow patterns was investigated in, e.g., Browning and Priest (1984). The role of compressibility is worth to mention in more detail because of its relevant influence on the stability of the shear flow. For a flow parallel to the magnetic field, compressibility has a destabilizing effect when the velocity shear is small and the ratio of densities is large, but a strong stabilizing influence for large velocity shear, so that the KHi can even be completely suppressed for sufficiently large Δv (see, e.g., Fejer, 1964; Sen, 1964; Gerwin, 1968; Miura and Pritchett, 1982; Ferrari and Trussoni, 1983; Rae, 1983; Soler et al., 2012b). Importantly, Δv_crit. is not affected by compressibility, so that Eq. 27 obtained in the incompressible limit remains valid. The value of Δv needed for the compressible stabilization depends upon the plasma β and the orientation of the wavevector with respect to the magnetic field direction, with the most stable situation being that of a low-β plasma with the wavevector parallel to the magnetic field (Miura and Pritchett, 1982; Soler et al., 2012b). In that case, compressible stabilization may happen for a velocity shear smaller than Δv_crit., so that the KHi cannot grow. However, a small perpendicular component of the wavevector is enough to allow the development of the KHi for a restricted range of shear flow velocities between Δv_crit. and the value for the compressible stabilization (see Figure 1). More details about the effect of compressibility can be checked in, e.g., Miura and Pritchett (1982); Soler et al. (2012b).

Onset of the KHi in a Partially Ionized Plasma

The stability of a shear flow in the case of a magnetized plasma composed by a mixture of charges and neutrals poses a fundamental problem. Considering again the same simple scenario discussed in the previous section, we anticipate that charges and neutrals would have different stability properties. On the one hand, charges are subjected to the stabilizing effect of the magnetic field, so that the KHi would only be possible for super-Alfvénic shear flow velocities larger than Δv_crit.. On the other hand, neutrals do not feel the magnetic force, so that there should not be a threshold velocity shear for the KHi. In the paradigmatic case that charges and neutrals do not interact, a sub-Alfvénic velocity shear may be unstable for the neutrals but stable for the charges. Therefore, the KHi may be triggered in the plasma for a sub-Alfvénic shear because of the presence of a neutral component. However, in a real PIP charges and neutrals interact through collisions. Then, the question arises: Do neutrals remain unstable for Δv < Δv_crit. even when they are collisionally coupled with charges? What is the effect of collisions between charges and neutrals on the onset of the KHi?

The question of whether the KHi can be triggered in a PIP for sub-Alfvénic shear is not only relevant from the theoretical point of view, but it also has important observational implications. Again we restrict ourselves to the solar context. Observations of turbulent flow and vortex structures in solar prominences (see Berger et al., 2008, 2010; Ryutova et al., 2010; Berger et al., 2017) already suggested the presence of the KHi, which was confirmed by recent direct observations (Li D. et al., 2018; Hillier and Polito, 2018; Yang et al., 2018). The typical flow velocities measured in quiescent prominences are in the range 10–70 km s⁻¹ (see Mackay et al., 2010), which are typically sub-Alfvénic. The value of the Alfvén velocity for typical values of the magnetic field strength, $\sim 10$ G, and the mass density, $\sim 5\times 10^{-11}$ kg m⁻³, in quiescent prominences is $\sim 126$ km s⁻¹. Assuming that the flows are along the magnetic field direction, the observed flow velocities should be stable according to the classic theory for a fully ionized plasma. It has been proposed that partial ionization effects are responsible for the development of the KHi in solar prominence conditions when slow flows are present (Soler et al., 2012b; Martínez-Gómez et al., 2015).

The onset and initial exponential growth of the KHi in a PIP has theoretically been investigated in a number of different astrophysical contexts by, e.g., Hans (1968); Ershkovich et al. (1986); Prialnik et al. (1986); Chhajlani and Vyas (1990); Birk and Wiechen (2002); Watson et al. (2004); Michikoshi and Inutsuka (2006); Shadmehri and Downes (2007, 2008); Kunz (2008); Soler et al. (2012b); Martínez-Gómez et al. (2015). For this problem, the two-fluid approximation offers a more transparent physical picture because the different stability properties of charges and neutrals can be better described than with the single-fluid model. In particular, the work by Watson et al. (2004) is relevant for our present discussion because the case of field-aligned shear flows at a sharp interface is explored. See, e.g., Kunz (2008) for a detailed study in the single-fluid case. In the analysis of Watson et al. (2004), collisions between charges and neutrals are considered in the two-fluid momentum equations, but ionization and recombination are neglected. Also, diffusion mechanisms other than collisions are omitted. In the incompressible limit, Watson et al. (2004) derived a dispersion relation in the two-fluid approximation, which was reobtained by Soler et al. (2012b) with a slightly different notation. The dispersion relation was also recovered in some limits by Shadmehri and Downes (2007) and Martínez-Gómez et al. (2015), who considered a plasma layer and a cylindrical tube, respectively. In the notation of Soler et al. (2012b), the dispersion relation can conveniently be cast as

${\mathcal{D}}_{\text{c}}{\mathcal{D}}_{\text{n}}+{\mathcal{D}}_{\text{cn}}^2=0,(30)$

with

$\begin{array}{ccc}\hfill {\mathcal{D}}_{\text{c}}& =\hfill & {\rho }_{\text{c,\hspace{0.17em}}1}\left(\omega -k_{\parallel }{v}_1\right)\left(\omega -k_{\parallel }{v}_1+i{\nu }_{\text{cn,\hspace{0.17em}}1}\right)+{\rho }_{\text{c,\hspace{0.17em}}2}\left(\omega -k_{\parallel }{v}_2\right)\left(\omega -k_{\parallel }{v}_2+i{\nu }_{\text{cn,\hspace{0.17em}}2}\right)\hfill \\ \hfill & \hfill & -k_{\parallel }^2\frac{B_1^2+B_2^2}{\mu }\hfill \end{array}(31)$

$\begin{array}{ccc}\hfill {\mathcal{D}}_{\text{n}}& =\hfill & {\rho }_{\text{n,\hspace{0.17em}}1}\left(\omega -k_{\parallel }{v}_1\right)\left(\omega -k_{\parallel }{v}_1+i{\nu }_{\text{nc,\hspace{0.17em}}1}\right)+{\rho }_{\text{n,\hspace{0.17em}}2}\left(\omega -k_{\parallel }{v}_2\right)\left(\omega -k_{\parallel }{v}_2+i{\nu }_{\text{nc,\hspace{0.17em}}2}\right)\hfill \end{array}(32)$

$\begin{array}{ccc}\hfill {\mathcal{D}}_{\text{cn}}& =\hfill & {\rho }_{\text{n,\hspace{0.17em}}1}\left(\omega -k_{\parallel }{v}_1\right){\nu }_{\text{nc,\hspace{0.17em}}1}+{\rho }_{\text{n,\hspace{0.17em}}2}\left(\omega -k_{\parallel }{v}_2\right){\nu }_{\text{nc,\hspace{0.17em}}2}.\hfill \end{array}(33)$

Here, ${\mathcal{D}}_{\text{c}}$ is the dispersion relation associated with the charged fluid (see Eq. 25), which is modified by collisions between charges and neutrals through the terms with ν_{cn, 1} and ν_{cn, 2}. In turn, ${\mathcal{D}}_{\text{n}}$ is the dispersion relation associated with the neutral fluid (note the absence of the magnetic field term), which is modified by collisions between neutrals and charges through the terms with ν_{nc, 1} and ν_{nc, 2}. Finally, ${\mathcal{D}}_{\text{cn}}$ is a coupling term. Eq. 30 is a forth-order polynomial, so it has four different solutions: two associated with the charges and other two with the neutrals. The role of the coupling term ${\mathcal{D}}_{\text{cn}}$ is to entangle the modes associated with charges and neutrals, so that they become global modes of the whole PIP. Numerical investigation of the solutions of Eq. 30 reveals that collisions are not able to completely stabilize the neutral fluid unstable mode for sub-Alfvénic shear (Watson et al., 2004; Soler et al., 2012b; Martínez-Gómez et al., 2015). Collisions reduce the growth rate compared with the collisionless case but a instability is always present for small, sub-Alfvénic shear. Under the approximation of immobile charges and in the case that the densities at the two sides of the interface are the same, Watson et al. (2004) found an approximate dependence of the neutral unstable mode growth rate with the shear flow velocity as $\sim {\left(\mathrm{\Delta }v\right)}^2$ instead of a linear dependence with Δv as in the hydrodynamic collisionless case that would result from Eq. 28 with Δv_crit. = 0. Martínez-Gómez et al. (2015) obtained a similar quadratic dependence of the growth rate with the flow velocity by considering a perturbation analysis in the full Eq. 30 and the particular cases of v₂ = 0, v₁ ≪ v_A,1, and a strong coupling. The approximate growth rate derived by Martínez-Gómez et al. (2015) is

${\gamma }_{\text{KHi}}\approx \frac{2{\rho }_{\text{n,\hspace{0.17em}}1}{\rho }_{\text{n,\hspace{0.17em}}2}}{{\rho }_{\text{n,\hspace{0.17em}}1}+{\rho }_{\text{n,\hspace{0.17em}}2}}\frac{k_{\parallel }^2{v}_1^2}{{\rho }_{\text{n,\hspace{0.17em}}1}{\nu }_{\text{nc,\hspace{0.17em}}1}+{\rho }_{\text{n,\hspace{0.17em}}2}{\nu }_{\text{nc,\hspace{0.17em}}2}}.(34)$

In addition to the quadratic dependence with the flow velocity already found by Watson et al. (2004), Eq. 34 also evidences that the growth rate is inversely proportional to the neutral-charge collision frequencies. Collisions tend to stabilize the KHi in the neutral fluid, but they never manage to suppress it completely. A general investigation for arbitrary coupling strength, showing the transition from the linear dependence to the quadratic dependence in the velocity shear, can be checked in Soler et al. (2012b); Martínez-Gómez et al. (2015), but still in the incompressible case. Martínez-Gómez et al. (2015) applied Eq. 34 to the case of thin threads in solar prominences and computed KHi growth rates compatible with the observations (see Figure 2).

FIGURE 2

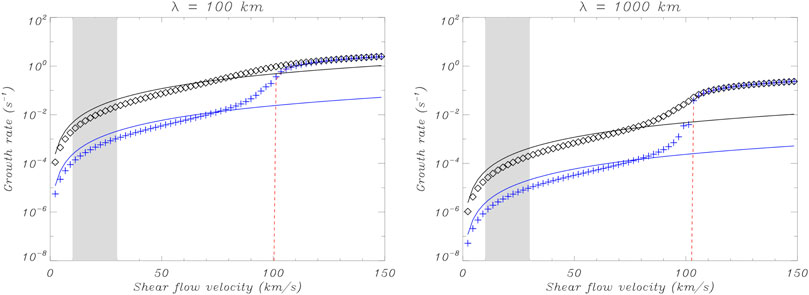
FIGURE 2. KHi growth rate in a solar prominence thread as a function of the shear flow velocity at the thread boundary for two values of the longitudinal wavelength: 100 km (left panel) and 1,000 km (right panel). In both panels, the red dashed lines correspond to the case of a fully ionized plasma, the blue crosses to a partially ionized case, and the black diamonds to a weakly ionized case. The solid lines are the analytical approximation of Eq. 34. The shaded zone denotes the region of flow velocity values that have been frequently measured in solar prominences. Credit: Martínez-Gómez et al. (2015), A&A 578, A104, reproduced with permission © ESO.

The derivation of a dispersion relation in the partially ionized case becomes much more cumbersome when compressibility is taken into account. A simple, approximate expression for the growth rate is no longer easy to obtain. Soler et al. (2012b) obtained a dispersion relation in the compressible case, whose solutions were numerically investigated. Soler et al. (2012b) found that the domain of instability becomes strongly dependent on the plasma parameters, especially the values of the collision frequencies and the density jump across the interface (see their Figures 6, 7). Soler et al. (2012b) found that, in general, compressibility tends to stabilize the neutral component of the plasma. If charges and neutrals are strongly coupled and the density jump is large, the results from Soler et al. (2012b) suggest that the threshold velocity slightly increases when the density jump increases (see their Figure 7B). For realistic physical properties in solar prominences, the threshold velocity shear for the onset of the KHi remains sub-Alfvénic under certain conditions. In particular, modes with a wavevector forming a sufficiently oblique angle with the magnetic field remain unstable and behave, approximately, as in the incompressible limit (see Figure 3).

FIGURE 3

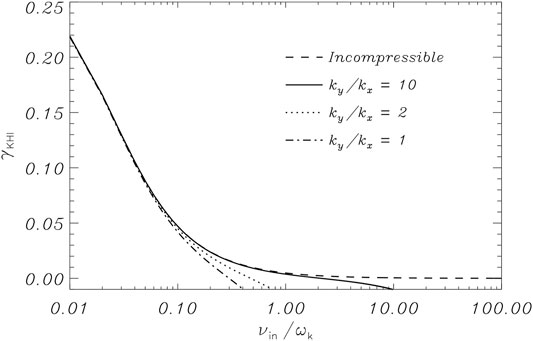
FIGURE 3. KHi growth rate in normalized units as a function of the dimensionless ion-neutral collision frequency for a sub-Alfvénic value of the shear flow velocity so that Δv < Δv_crit.. The dashed line corresponds to the incompressible case in which γ_KHi > 0 even for large values of the collision frequency. The other lines correspond to the compressible case for various values of the ratio of the perpendicular, k_y, to the longitudinal, k_z, components of the wavevector (indicated within the figure). Perturbations with a sufficiently large value of the ratio k_y/k_z can trigger the KHi even in the compressible case. Adapted from Soler et al. (2012b). © AAS. Reproduced with permission.

Compressible effects in the presence of partial ionization were previously investigated by Ershkovich et al. (1986) and Prialnik et al. (1986), but in both studies the flow of neutrals was assumed to be perpendicular to the interface and not parallel to it as in our exemplary configuration. In their case, compressibility was also found to have either a stabilizing or destabilizing effect on the KHi growth rate depending on the parameters considered.

The case investigated by Watson et al. (2004) and Soler et al. (2012b) neglects all nonideal terms in the induction equation. Pandey (2018) and Pandey and Vladimirov (2019) have explored the triggering of the KHi in the presence of Hall’s term in the induction equation using the single-fluid equations. In the case of fully ionized plasmas, the effect of Hall’s term has been explored by, e.g., Zhelyazkov et al. (2020). Pandey (2018) showed that Hall’s effect opens up a new way through which the fluid can become Kelvin–Helmholtz unstable sub-Alfvénic flows. Pandey (2018) have explored the applicability of this mechanism in different astrophysical contexts, including the solar atmosphere, protoplanetary discs, molecular clouds, and Earth’s ionosphere. As Hall’s effect is enhanced by the presence of neutrals (Pandey and Wardle, 2008), this alternative mechanism may be of relevance in PIP. Readers are referred to Pandey (2018) for details. Recently, Martínez-Gómez et al. (2021) have numerically studied the KHi evolution due to shear flow in an initially unmagnetized plasma including the Biermann battery term in the induction equation. The presence of this term does not seem to strongly affect the linear growth of the KHi because similar growth rates than those predicted by the ideal theory are found in the simulations of Martínez-Gómez et al. (2021). However, the Biermann battery term heavily impacts on the nonlinear evolution by generating a magnetic field (see more details in Section 3.3).

Nonlinear Evolution Through Numerical Simulations

While linear theory is very useful to understand the onset of the KHi, full nonlinear numerical simulations are requiered to study its later evolution. In fully ionized astrophysical plasmas, the nonlinear phase of the KHi has been investigated in detail in both 2D and 3D simulations (see, e.g., Frank et al., 1996; Malagoli et al., 1996; Keppens et al., 1999; Keppens and Tóth, 1999; Ryu et al., 2000; Baty et al., 2003; Baty and Keppens, 2006; Matsumoto and Hoshino, 2004; Matsumoto and Seki, 2010, just to name a few representative papers among many other works). Important results obtained from the simulations are that the nonlinear development of the KHi leads to the formation of vortices, mixing of plasmas, and eventual generation of turbulence. Particularly important is the transition from the laminar to the turbulent regime associated with the later evolution of the plasma mixing (Matsumoto and Hoshino, 2004; Matsumoto and Seki, 2010) and its implications concerning the energy cascade towards the dissipative scales. The magnetic field plays an important role in this process. For moderate shear flow velocities, the magnetic field can nonlinearly inhibit the formation of vortices, thus making the system nonlinearly stable although being linearly unstable (Ryu et al., 2000; Hillier, 2019). During the vortex formation, the winding of the magnetic field can cause field amplification, formation of current sheets, and field line reconnection. Another common feature of the KHi nonlinear evolution obtained from simulations is the formation of magnetic islands (see, e.g., Keppens et al., 1999; Nakamura et al., 2008). Readers are referred to the papers cited above, and references therein, for further details.

Considering nonlinear simulations of the KHi in multi-fluid plasmas, the effects of the interactions between the various species have been explored in the last decade in a relatively small number of publications. Most of the studies (see, e.g., Birk and Wiechen, 2002; Johansen et al., 2006; Wiechen, 2006; Barranco, 2009; Hendrix and Keppens, 2014) deal with the case of partially ionized dusty plasmas and focus on analyzing the effect of dust. Typically, the dust grains are treated as particles with a certain mass and charge (they may be neutral) that collide with ions, electrons, and neutrals that may also be present in the plasma. As in the single-fluid fully ionized simulations, these works show that once unstable modes are excited they evolve relatively quickly nonlinearly and result in the formation of vortices, current sheets, and turbulence. Wiechen (2006) concludes that the mass and charge of the dust particles affect the stability, so that a higher mass of the dust grains has a stabilizing effect, while a higher charge number of the dust has a destabilizing effect. With hydrodynamic simulations, Hendrix and Keppens (2014) also found a stabilizing effect of dust when the dust-to-gas ratio is high. Also, Hendrix and Keppens (2014) showed that during the formation of vortices, filamentary high density dust structures can be formed, which may be relevant in molecular clouds. However, none of these studies analyse in detail the role to collisions between charges and neutrals.

The works by Jones and Downes (2011, 2012) are more related with the present discussion. Jones and Downes (2011) performed 2.5D simulations of the KHi in weakly ionized plasmas composed of ions, electrons, and neutrals. The governing equations solved by Jones and Downes (2011) consider the neutral fluid velocity as the centre-of-mass velocity, neglect the inertia of charges, and use a generalized Ohm’s law. Jones and Downes (2011) investigated the ambipolar-dominated and Hall-dominated regimes. They find in their simulations that partial ionization effects do not significantly influence the growth rate of the instability in the linear phase, which seem to be in contradiction with the linear results of the two-fluid model of Watson et al. (2004) and may be a consequence of the different models used by Watson et al. (2004) and Jones and Downes (2011). On the other hand, Jones and Downes (2011) obtain that ambipolar diffusion, which is caused by charge-neutral collisions, significantly decreases the growth of magnetic energy during the nonlinear phase of the instability compared with the evolution in ideal simulations, while the Hall effect, when dominant, causes the system to fail to settle to a quasi-steady state after saturation of the instability. Subsequently, Jones and Downes (2012) performed a specific application to molecular cloud conditions and also added the presence of dust. As in their previous paper, ambipolar diffusion leads to less amplification of the magnetic energy as the instability develops and, therefore, a stronger wind-up of the neutral fluid is possible during vortex formation. However, in molecular cloud conditions Hall’s term does not appear to have an important effect. As explained by Jones and Downes (2012), ambipolar diffusion largely suppresses the influence of Hall’s term. While the simulations of Jones and Downes (2011, 2012) are relevant in molecular clouds, their results cannot easily translated to the case of the partially ionized solar plasma, as solar prominences, where the weakly-ionized version of the governing equations is not applicable.

A thoughtful 2D numerical study of the nonlinear evolution of the KHi in a partially ionized medium has been performed by Hillier (2019). The considered configuration was the classic set-up: a sharp interface with a velocity shear between two partially ionized plasmas with different densities. A straight magnetic field was assumed parallel to the interface. A white noise perturbation was imposed initially. Hillier (2019) evolved in time the nonlinear two-fluid equations, explicitly solving the dynamics of both charges (ions) and neutrals, which were collisionaly coupled in the equations. By using a very high resolution, Hillier (2019) was able to study the different scales where the strength of the ion-neutral coupling varies. Hillier (2019) finds that at the small scales where neutrals are decoupled from ions, fully formed neutral vortices are present, whereas the ion velocity remains laminar in nature. However, and despite the very different velocity patters, similar density structures are found in both neutral and ion fluids because of the role of frictional heating and heat transfer between fluids (see Figure 4). At larger scales, neutrals become coupled with ions and the magnetic field, although secondary, smaller vortices can remain decoupled. The effect of the magnetic field may cause the nonlinear suppression of the instability even when the shear flow is linearly unstable (the same effect but in ideal MHD simulations was already discussed by Ryu et al., 2000). Hillier (2019) concludes that the turbulent energy cascade should probably show a transition from MHD turbulence at the coupled scales to neutral fluid HD turbulence at the smallest scales. This should be confirmed by future 2D and 3D high-resolution simulations.

FIGURE 4

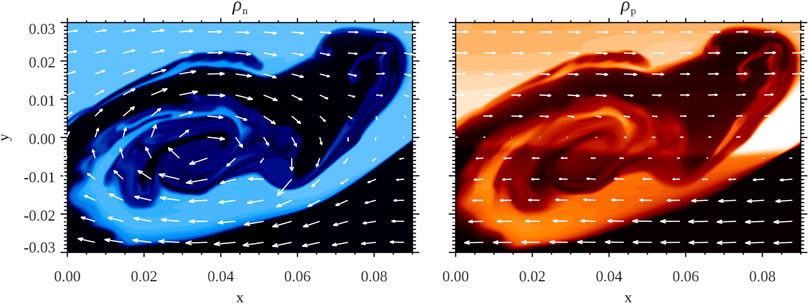
FIGURE 4. Neutrals (left) and charges (right) density structures in a small-scale KHi vortex. The white arrows are the corresponding velocity fields. The neutral fluid shows a clear vortex pattern in velocity that is not seen in the charged fluid. However, the density distributions are similar in the two fluids because of thermal coupling. Reprinted from Hillier (2019), with the permission of AIP Publishing.

Recently, 2D numerical simulations of the KHi in a partially ionized two-fluid plasma have been presented by Martínez-Gómez et al. (2021). These authors considered an initially unmagnetized medium composed of a dense partially ionized plasma slab embedded in a lighter environment. A constant flow longitudinal to the slab was assumed, with different flow velocities inside and outside the slab and a continuous transition between the two regions. The Biermann battery term was included in the Ohm’s Law. The simulations showed that the KHi grows after applying a small perturbation on the slab boundaries. During the KHi nonlinear development, the collisional interaction between the charges and neutrals drives the generation of a magnetic field through the Biermann battery mechanism (see, e.g., Kulsrud et al., 1997). The magnetic field is predominantly generated in the direction perpendicular to the flow, so it has no important influence on the development of the KHi. It is found that the strength of the generated magnetic field increases when the ionisation degree of the plasma decreases. Variations in the charges temperature are produced because of collisions with the neutrals. This increases the charges baroclinic term and enhances the Biermann battery effect (see detailed explainations in Martínez-Gómez et al., 2021). The results of the numerical experiments by Martínez-Gómez et al. (2021) are a good example of how interesting physical effects are driven by partial ionization.

Rayleigh-Taylor Instability

The Rayleigh-Taylor instability (RTi), named after Strutt (1882) and Taylor (1950), is another of the most classic fluid instabilities that are present in astrophysical plasmas. The RTi generally occurs at an interface between two fluids of different densities when the lighter fluid is pushing (accelerating into) the heavier fluid. The typical example for the occurrence of this instability is when, in the presence of gravity, a heavier fluid is put on top of a lighter fluid. Such configuration is unstable to perturbations of the interface and, eventually, the system evolves developing “plumes” of the lighter fluid that flow upwards and “fingers” of the heavier fluid that fall downwards. The Richtmyer–Meshkov instability, named after Richtmyer (1960) and Meshkov (1969), is a sister instability to the RTi that occurs when the two fluids are impulsively accelerated by, e.g., a shock wave. Interested readers are referred to the recent review by Zhou et al. (2021) where the similarities between the RTi and the Richtmyer–Meshkov instability are discussed.

The solar atmosphere and, in particular, solar prominences where the plasma is partially ionized, again represent a paradigmatic case in which the RTi has been observed in detail (see Berger et al., 2008; Ryutova et al., 2010; Berger et al., 2010, 2011, 2017). A comprehensive review of the RTi in solar prominences, including both observations and theoretical efforts, can be checked in Hillier (2018). Beyond the solar context, other well-known astrophysical environments where the RTi is believed to occur are, e.g., supernovae (see, e.g., Hachisu et al., 1992; Hester et al., 1996; Jun et al., 1996; Porth et al., 2014), accretion disks (see, e.g., Wang and Nepveu, 1983; Kulkarni and Romanova, 2008), relativistic jets (e.g., Matsumoto and Masada, 2013), hydrogen clouds in the local bubble (e.g., Breitschwerdt et al., 2000), envelopes of red giants (e.g., Eggleton et al., 2006), among other examples found in a vast literature.

Onset of the RTi in a Fully Ionized Plasma

Chandrasekhar (1961b) presents the simplest configuration in which the onset of the RTi can be studied (see also Sharp, 1984). Let us consider the case of two fully ionized unbounded plasmas with uniform densities laying one above the other in the presence of gravity. The two plasmas are separated by an abrupt interface and the plasma with density ρ₁ is on top of the plasma with density ρ₂, with ρ₁ > ρ₂. A straight and constant magnetic field that is orientated parallel to the interface, i.e., in the horizontal direction, permeates both plasmas. The direction of the magnetic field is assumed to be the same at both sides of the interface. The magnetic field strength at the two sides of the interface is denoted by B₁ and B₂, respectively. Using the linearized single-fluid ideal MHD equations and incompressible perturbations, we can perform a stability analysis of the interface by assuming a temporal dependence of the form   exp( − iωt), where ω is the frequency, and a Fourier-analysis in space. A dispersion relation for the surface waves propagating on the interface can be derived, whose analytic solution for the square of frequency yields,

${\omega }^2=\frac{B_1^2+B_2^2}{\mu \left({\rho }_1+{\rho }_2\right)}{k}_{\parallel }^2-\frac{{\rho }_1-{\rho }_2}{{\rho }_1+{\rho }_2}gk,(35)$

where k_∥ is the component of the wavevector along the background magnetic field, k is the modulus of the wavevector, g is the acceleration of gravity, and the factor $\left({\rho }_1-{\rho }_2\right)/\left({\rho }_1+{\rho }_2\right)$ is the Atwood number. Eq. 35 neglects fluid surface tension. The first term on the right-hand side of Eq. 35 is the square of the frequency of the incompressible surface Alfvén wave. The second term contains the effect of gravity and is related to the so-called interchange mode (see, e.g., Hillier, 2016). The RTi appears when ω² < 0. This is always the case in the absence of a magnetic field, i.e., the HD case, so that for B₁ = B₂ = 0 the first term on the right-hand side of Eq. 35 vanishes. However, in the presence of a magnetic field, magnetic tension plays a stabilizing influence on the interface through the presence of a surface Alfvén wave, which is also called the undular mode in the literature. Perturbations whose wavevector is mostly parallel to the direction of the magnetic field are stable. Conversely, perturbations propagating with a sufficiently oblique angle remain unstable. The critical longitudinal wavenumber for stabilization due to magnetic tension is

$k_{\parallel ,\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}.}=\sqrt{\frac{\mu \left({\rho }_1-{\rho }_2\right)}{B_1^2+B_2^2}gk}.(36)$

We note that Eq. 36 depends on the modulus of the full wavenumber, k, so that the perpendicular lengthscale of the perturbations also influence the longitudinal lengthscales that are stable or unstable, making the stability properties of the interface to be rather complex. Readers are referred to Hillier (2016), who provides a more detailed account of the properties of the ideal RTi in its linear regime beyond the simple discussion provided here.

Terradas et al. (2012) investigated the triggering of the RTi in a model where the interface was replaced by a slab with a finite thickness (see Figure 5). The slab was meant to represent a thin thread of a solar prominence. They found that two different modes appear in the slab configuration, owing the presence of two separate interfaces. One mode is always stable and its character varies from being localised at the upper interface of the slab when the magnetic field is weak, to having a global nature and resembling the transverse kink mode of the whole slab when the magnetic field is strong. On the other hand, there is another mode that is unstable and localised at the lower interface when the magnetic field is weak, but it becomes a stable sausage magnetic mode when the magnetic field is increased. The criterion to know whether the magnetic field is weak or strong comes, again, from the comparison of the gravity force with the magnetic tension force. Ruderman et al. (2014) investigated the RTi in the presence of a sheared magnetic field (see also Hillier, 2016). They considered both the interface and slab scenarios. They showed that magnetic shear can have a strong effect on the growth rates of the instability. For small shear angles the RTi growth rate is linearly proportional to the shear angle, while in the limit of large angles the growth rate becomes independent of the shear angle.

FIGURE 5

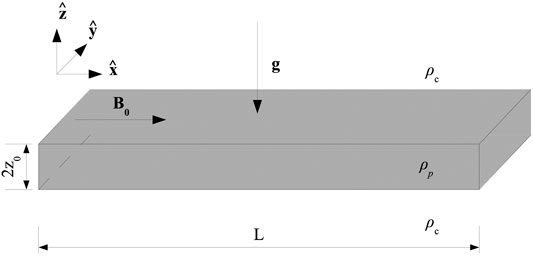
FIGURE 5. Sketch of the slab model used by Terradas et al. (2012). The grey zone denotes the prominece slab of width 2z₀, length L, and density ρ_p embedded in a coronal plasma of density ρ_c, with ρ_p > ρ_c. A uniform magnetic field, B₀, is assumed in the horizontal direction. Gravity, g, acts towards the negative vertical direction. Credit: Terradas et al. (2012), A&A 541, A102, reproduced with permission © ESO.

As in the case of the KHi, the effect of compressibility on the onset of the RTi has been long under debate in both HD and MHD (see. e.g., Vandervoort, 1961; Shivamoggi, 1982; Bernstein and Book, 1983; Ribeyre et al., 2004; Livescu, 2004; Liberatore and Bouquet, 2008, among others). The complexity of the dispersion relation in the compressible case makes it necessary to resort to numerical solutions unless some heavy simplifications are made (see, e.g., Shivamoggi, 2012). Studies by, e.g., Ribeyre et al. (2004); Livescu (2004); Liberatore et al. (2009); Díaz et al. (2012); Ruderman (2017) point out that compressibility has a complex influence, so that the linear growing rates in the compressible case are smaller or larger than those obtained in incompressible approximation depending on the wavenumber range and the plasma β. However, the critical longitudinal wavenumber for magnetic tension stabilization (Eq. 36) appears to be unaltered by compressibility. Detailed studies of the RTi triggering and evolution in more realistic configurations necessarily require the use of numerical simulations (see Section 4.3).

Onset of the RTi in a Partially Ionized Plasma

As in the case of the KHi, the presence of a neutral species may have a relevant effect on the RTi. Neutrals are not affected by the stabilizing influence of magnetic tension. Therefore, a PIP composed of both charges and neutrals should be, in principle, more unstable regarding the RTi than a fully ionized plasma. Of course, ion-neutral collisions couple neutrals and charges, so that neutrals do feel the magnetic field influence in an indirect way. Again, the relevant question is whether collisions are able to fully stabilize the neutral fluid when the classic stability threshold is verified (Eq. 36) or, on the contrary, neutrals remain unstable.

The work by Hans (1968) is probably the first study of the role of ion-neutral collisions on the onset of the RTi in a PIP. Hans (1968) considered the classic setup of a denser fluid located on top of a lighter fluid and separated by an abrupt interface in the presence of a horizontal magnetic field. Both fluids are partially ionized. This author considered an incompressible two-fluid model that included collisions between charges and neutrals and finite Larmor radius effects expressed through a gyro-viscosity term for the charges. However, the gas pressure term was absent from the neutrals momentum equation and the induction equation only contained the ideal term. After performing a linear stability analysis, Hans (1968) concludes that the resulting dispersion relation has always an unstable root, whose growth rate decreases as the collision frequency increases. Ogbonna and Bhatia (1984) revisited the same configuration of Hans (1968) but performed a more in-depth paramenter study. In agreement with the previous results, Ogbonna and Bhatia (1984) conclude that friction between charges and neutrals decrease the growth rate of the RTi compared to the purely HD case, but an instability always remains. The problem was explored once again by Chhajlani and Vaghela (1989), who also included surface tension in their analysis (see Chandrasekhar, 1961b). They found that the conditions for the occurrence of the RTi, i.e., the instability threshold because of surface tension, remain unaffected by the presence of neutrals, but the growth rate is reduced by collisions.

All the works cited in the above paragraph ignored the role of neutral gas pressure and only included the ion-neutral coupling term in the neutrals momentum equation. Such a simplification forces the dynamics of neutrals to be entirely dependent to that of charges. The first study where the dynamics of neutrals was consistently described was done by Díaz et al. (2012). They considered a two-fluid model with collisions between charges and neutrals and included the gas pressure term in the neutrals momentum equation, but neglected all nonideal terms in the induction equation for simplicity. Again, the simple interface configuration was adopted. Díaz et al. (2012) considered both the incompressible and compressible cases. Shadmehri et al. (2013) performed a similar study to that of Díaz et al. (2012) but only in the incompressible limit. The dispersion relation derived in the incompressible case (Eq. 47 of Díaz et al. (2012) and Eq. 23 of Shadmehri et al. (2013)) can be written with a similar structure to that of the KHi dispersion relation (see Eq. 30), i.e., a dispersion relation associated with the neutral fluid multiplied by a dispersion relation associated with the charges, plus an additional term that couples both relations. The coupling term owes its existence to collisions. Unfortunately, unlike in the KHi case, the full dispersion relation is a rather complicated expression even in the incompressible limit, so that no simple analytic approximation for the growth rate was obtained by Díaz et al. (2012) and a numerical study of the solutions was necessary. Díaz et al. (2012) found two unstable modes that are related to the RTi in the neutral and charged fluids separately, with the neutral unstable mode having a larger growth rate. Díaz et al. (2012) computed their results as function of their parameter ϒ = ν_inL/c_s, where ν_in is ion-neutral collision frequency, L is a length scale, and c_s is the sound speed. Hence, large values of ϒ correspond to strong coupling. Díaz et al. (2012) found that collisions between ions and neutrals decrease the growth rates as ϒ increases (see Figure 6). The charges unstable mode can be stabilized by magnetic tension for a sufficiently large longitudinal wavenumber that is independent from the collision frequency (Eq. 36). However, the neutrals-related solution remains always unstable for finite ϒ. So, the results of the more complete model of Díaz et al. (2012) confirmed the previous tentative conclusions obtained in more simplified works (Hans, 1968; Ogbonna and Bhatia, 1984; Chhajlani and Vaghela, 1989): collisional coupling with the charges is not able to fully suppress the RTi of the neutral fluid even when the longitudinal wavenumber is larger than the critical one.

FIGURE 6

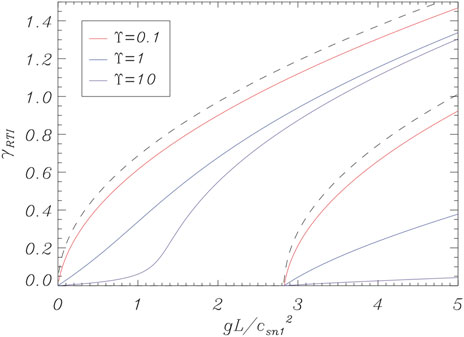
FIGURE 6. RTi growth rate as a function of the dimensionless gravitational acceration obtained from the two-fluid linear analysis of Díaz et al. (2012) in the incompressible case. Two unstable modes are present, with the one related with the neutral fluid being present in whole range and having a larger growth rate. The dashed lines correspond to the colisionless limit, while the different solid lines denote different degrees of ion-neutral coupling indicated through the parameter ϒ (defined in the text). Adapted from Díaz et al. (2012). © AAS. Reproduced with permission.

Díaz et al. (2012) extended their results to the compressible case and showed that the stability thresholds are not modified by compressibility: the mode related with the neutral fluid is always unstable. Compressibility appears to have a largely stabilizing effect, since smaller growth rates are obtained in the compressible case compared to those in the incompressible limit. However, the exact influence of compressibility depends upon the values of some parameters as, e.g., the density contrast and the ratio of the perpendicular to longitudinal wavenumbers. Therefore, although compressibility does not seem to have a relevant influence on the actual triggering of the RTi, it may be relevant for the subsequent growth of the perturbations towards the nonlinear development of the instability.

Díaz et al. (2014) revisited the same problem studied in Díaz et al. (2012) but considering the single-fluid approximation instead of the two-fluid approach. In the single-fluid model, the role of the ion-neutral collisions remains in the form of the ambipolar diffusion term of the induction equation. Regarding the properties of the RTi, the results of the single-fluid model consistently agreed to those previously obtained in the two-fluid formalism. The main difference between the single-fluid and two-fluid cases is that in the single-fluid case it is not possible to disentangle the nature of the two unstable modes, since the single-fluid approximation already assumes a strong coupling between charges and neutrals, so that only one unstable “global” mode is found. Díaz et al. (2014) also considered other nonideal terms in the induction equation as Ohm’s diffusion, Hall’s term, and the battery term that were ignored in Díaz et al. (2012). However, for typical conditions of solar prominences, Díaz et al. (2014) found that the ambipolar term is by far the dominant term in the induction equation, while the other terms are largely negligible, thus confirming the appropriateness of the ideal induction equation used in the two-fluid model of Díaz et al. (2012). Later, Ruderman et al. (2018) expanded the work of Díaz et al. (2014) and performed a detailed mathematical study of the effect of magnetic shear. Ruderman et al. (2018) found that the larger the shear angle, the smaller the maximum RTi growth rate. In addition, Ruderman et al. (2018) concluded that ambipolar diffusion only affects the growth rate when the plasma β is small.

Astrophysical applications of the linear theory discussed above include solar prominences and local clouds. Díaz et al. (2012) argue that the obtained growth rates for physical conditions in partially ionized prominences may explain the existence of fine structures with lifetimes of the order of 30 min, while the timescales derived from the classical theory for fully ionized plasma are about one order of magnitude shorter and incompatible with the observed lifetimes. In addition, Díaz et al. (2014) conclude that their partially ionized model provides an instability timescale comparable to observed lifetimes of RTi plumes in prominences. On the other hand, Shadmehri et al. (2013) explained that, owing to two-fluid effects, the RTi may operate less effectively in local clouds than previously though according to classical theory.

Nonlinear Evolution Through Numerical Simulations

Valuable but limited information is provided by the analysis of the linear regime of the RTi. The linear theoretical analysis must necessarily be complemented with nonlinear numerical simulations to understand the later evolution of the instability. An extensive literature on the nonlinear evolution of the RTi exists. Here we only discuss a few representative works.

Early attempts to simulate with low resolutions the development of the RTi in ideal MHD include, e.g., the works by Wang and Robertson (1985) and Jun et al. (1995), among other relevant papers. Wang and Robertson (1985) considered 2D compressible simulations with the goal to study the mixing process occurring at later stages of the instability. Their simulations show how the interface is deformed by the formation of mushroom-like structures (fingers and plumes) that ultimately lead to the presence of swirling motions and plasma mixing. An energy cascade towards small scales occurs during the nonlinear phase. An inverse cascade towards large scales is found later in the evolution owing to the merging of smaller structures. Jun et al. (1995) performed quasi-incompressible simulations in 2D and 3D. The quasi-incompressible regime was achieved by considering a high gas pressure. They found that turbulence associated with the nonlinear evolution of the RTi amplifies the magnetic field, preferentially on small scales. This effect is more important in 3D than in 2D. The growth of fingers and plumes display the generation of vortex structures associated with secondary KHi. The fully developed structures appear to be sensitive to the initial magnetic field strength and orientation. The growth of instabilities across the magnetic field is more prominent, a result already anticipated by the theoretical linear analysis.

Subsequent 3D simulations with higher resolutions provided more in-depth information of the small-scale evolution of the perturbations. Isobe et al. (2005) performed 3D simulations of magnetic flux emergence in the solar atmosphere in which the RTi is shown to develop. The instability leads to the formation of filamentary structure and small-scale current sheets. Dissipation of the current sheets produces plasma heating, which may me relevant in the solar corona. The simulations also indicate that magnetic reconnection is initiated locally by the RTi, while in turn the reconnection process affects the growth of the instability, resulting in a spatially intermittent reconnection. Thus, the simulations of Isobe et al. (2005) clearly show that reconnection is an essential ingredient of the nonlinear evolution of the RTi.

Stone and Gardiner (2007) performed a rather general numerical study of the RTi in 3D by considering different initial configurations for the magnetic field. They show that uniform magnetic fields cannot suppress the instability in 3D. As linear theory predicts, interchange modes perpendicular to the field can grow at the same rate as in HD, while the magnetic field only stabilizes modes with large longitudinal wavenumbers. In the nonlinear simulations, this results in a highly anisotropic structure as the RTi evolves, as already anticipated by, e.g., Jun et al. (1995). The magnetic tension can inhibit secondary instabilities and reduce the growth of small scales and the mixing of plasmas. As a consequence of the restrained turbulent mixing, the fingers and plumes associated with the primary RTi can grow faster. However, a sheared magnetic field can significantly delay the instability and modify the structures that are formed in the full nonlinear regime. Later results by Ruderman et al. (2014) in the linear regime seem to support the importance of magnetic shear for the RTi growth rate. Stone and Gardiner (2007) used their results to explain the morphology of the optical filaments observed in the Crab nebula. However, more recent adaptive mesh refinement simulations by Porth et al. (2014) indicate that with very high resolutions, the filamentary structure driven by the RTi becomes less similar to the one observed in the Crab nebula.

Due to its observational importance (see Berger et al., 2008; Ryutova et al., 2010; Berger et al., 2010, 2011, 2017), the nonlinear development of the RTi in solar prominences has been intensely studied in the last decade. Also in the solar context, Moschou et al. (2015) showed indications of the RTi or interchange instability during numerical simulations or coronal rain formation and downfall. From here on, we shall put the focus of our discussion to the case of simulations in solar prominences. Again, we refer readers to Hillier (2018) for a comprehensive review on RTi simulations in prominences. What follows is a brief summary of some relevant results.

Hillier et al. (2011) performed the first attempt to simulate the RTi in a quiescent prominence. They considered a modification of the classic Kippenhahn-Schlüter model (Kippenhahn and Schlüter, 1957) in which a high-temperature, low-density tube was placed in the center of the model. The RTi drives upflows that interact with each other and create larger plumes through an inverse cascade process. The upflows advect the magnetic field lines through the structure, but the field line curvature is not heavily affected. The dynamics of the simulations compares qualitatively well with the observations, but the obtained upflow velocities in the model are lower than those observed.

Hillier et al. (2012a,b) revisited the same Kippenhahn-Schlüter configuration and performed an improved analysis of the simulations. Hillier et al. (2012a) carried out a detailed parameter study. They showed that the instability creates low-density filaments inside the prominence that are aligned with the direction of the magnetic field. This implies that a 3D RTi mode, i.e., a mode with both parallel and perpendicular components of the wavenumber, grows inside the prominence. For some range of parameters and initial conditions, the velocity and width of the simulated upflows can match the observed values. Subsequently, Hillier et al. (2012b) investigated a particular aspect of the simulations related to the process of magnetic reconnection. The RTi fingers and plumes and their associated shear flows resulted in the formation of current sheets that can reconnect. This reconnection allows the formation of downflowing blobs that may be related to the observed knots in prominences (see, e.g., Chae, 2010).

The Kippenhahn-Schlüter model used in Hillier et al. (2011, 2012a,b) can be understood as a local model of the prominence. Other works have studied the RTi in prominences considering more global models. Using a 3D arcade model for the prominence magnetic field, Terradas et al. (2015a) showed that the RTi can also grow in fully detached prominences suspended above the photosphere. The chromosphere was not included in the model. The magnetic field structure was anchored at the photosphere by means of the line-tying condition. The downflows developed in the model of Terradas et al. (2015a) may or may not reach the photosphere depending on the strength of the magnetic field in the prominence. For sufficiently intense magnetic fields, an oscillatory behavior of the flow is obtained, suggesting that the magnetic field is nonlinearly suppressing the RTi. The photospheric line-tying may also play a role. Magnetic shear is able to reduce or even to suppress the RTi completely for the considered spatial resolution. Indeed, further simulations by Terradas et al. (2016) using a twisted flux rope model display a much more stable behaviour than the arcade model regarding the RTi.

The development of the RTi in a whole-prominence model was also explored in the numerical simualtions by Keppens et al. (2015). They performed ideal MHD simulations at high resolution with an adaptive mesh refinement code. A horizontal background magnetic field nonuniform in the vertical direction was assumed, which introduces a local magnetic shear inside the prominence. The considered vertical profiles for the density and temperature aimed to represent a suspended prominence mass above the photosphere and chromosphere. The simulations show the quick generation of nonlinear magnetoconvective motions. The downflows associated with the RTi impact and reflect on the chromosphere, so that chromospheric plasma gets mixed with the prominence plasma suspended high in the corona. The results of Keppens et al. (2015) suggest that the nonlinear RTi may be intimately involved in the mass cycle of prominences and the interchange of material between prominences and the chromosphere.

An extension of the work by Keppens et al. (2015) was done in Xia and Keppens (2016). The main difference with the previous work was that the prominence was assumed to be formed by two parallel slab-like layers instead of a single monolitic mass. The simulations show that the two layers of the prominence evolve coherently due to their magnetic connectivity, since the mainly horizontal magnetic field transversely crosses both slabs. The RTi similarly evolves in the two layers following an equivalent dynamics to that discussed in Keppens et al. (2015). A detail of the strongly nonlinear evolution can be seen in Figure 7. Interestingly, the vertical density structures formed during the nonlinear evolution of the RTi may appear as horizontal thread-like structures when seen from the top of the prominence, which may explain the different structures observed in prominences above the solar limb and filaments on the solar disk.

FIGURE 7

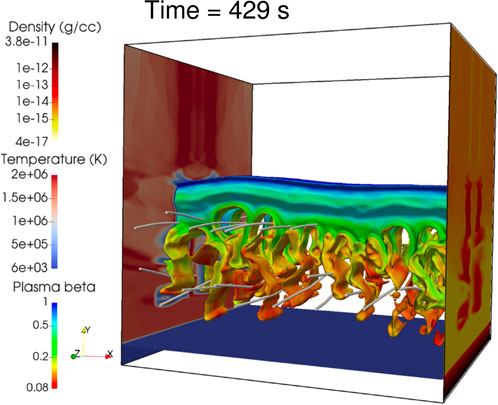
FIGURE 7. A 3D view of a snapshot of the simulations by Xia and Keppens (2016) on the RTi development in a two-layer prominence. The snapshot shows a later stage of the evolution deep into the nonlinear regime of the instability. Adapted from Xia and Keppens (2016). © AAS. Reproduced with permission

All the papers cited above performed MHD simulations and none considered the effect of partial ionization. Hillier et al. (2010) investigated the evolution of the Kippenhahn-Schlüter prominence model under the presence of Cowling’s diffusion. However, they were only concerned with the diffusion of the magnetic field and their simplified model neglected all coupling with the plasma dynamics. A pioneering work where the role of partial ionization effects on RTi simulations was explored was done by Khomenko et al. (2014b), who considered the single-fluid equations for a PIP including the ambipolar diffusion term. Khomenko et al. (2014b) performed 2.5D simulations of the RTi initiated at the corona–prominence interface with a constant magnetic field perpendicular or almost perpendicular to the plane. They found that the configuration is always unstable, which agrees with the expected behavior based on linear theory (Díaz et al., 2012; Díaz et al., 2014). The growth rate of the small-scale modes in the non-linear regime is up to 50% larger than that obtained in equivalent ideal MHD simulations. Significant ion-neutral drift occurs at the corona–prominence interface (drift differences between ions and neutrals have been detected in prominences, see Khomenko et al., 2016). A faster downward motion of the neutral component with respect to the ionized component is obtained (see also Terradas et al., 2015b). The differences in temperature of the RTi bubbles between the ideal and ambipolar cases can be as large as 30% because of the additional heating associated with the dissipation of perpendicular currents by ambipolar diffusion (see Figure 8). The results of Khomenko et al. (2014b) clearly show that partial ionization effects have a measurable influence of the RTi onset and evolution in prominences, particularly in the small scales.

FIGURE 8

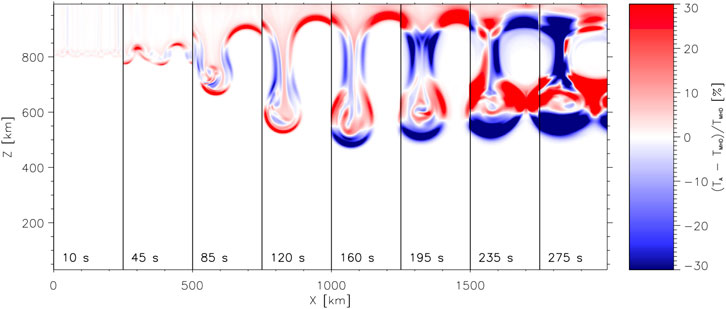
FIGURE 8. Difference between the temperature variations in a RTi simulation including ambipolar diffusion and an equivalent ideal simulation. The time elapsed is given at the bottom of each panel. Red/blue colors mean hotter/cooler plasma in the simulations with ambipolar diffusion. Credit: Khomenko et al. (2014b), A&A 565, A45, reproduced with permission © ESO.

Recently, Popescu Braileanu et al. (2021a), Popescu Braileanu et al. (2021b) have extended the single-fluid simulations of Khomenko et al. (2014b) to the two-fluid case. Although their simulations remained 2.5D as in Khomenko et al. (2014b), the background model was improved by considering a smooth interface instead of a sharp transition and by including magnetic shear. The two-fluid simulations took into account viscosity, thermal conduction, ionization/recombination, and energy and momentum transfer through collisions between neutrals and charges. In Popescu Braileanu et al. (2021a) the study focused on assessing the effects of a smooth interface and magnetic shear. They showed that magnetic shear reduces or even suppresses the instability growth rate, as previous theoretical studies in the single-fluid approximation already anticipated (see, e.g., Ruderman et al., 2014). In turn, the inclusion of a continuous transition affects the length scales of the perturbations that develop due to the RTi, especially for wavelengths comparable to the density gradient length scale. In Popescu Braileanu et al. (2021b) the emphasis was put in investigating the effects of collisions within the framework of the two-fluid model. For prominence conditions, ionization and recombination do not significantly influence the development of the RTi main structures. Secondary structures formed during the later nonlinear development and mixing seem to be more affected by ionization and recombination processes. Ion-neutral collisions play a role in determining the evolution and dissipation of small structures during the nonlinear stage of the RTi. Ion-neutral decoupling affects smaller scales than viscosity. The nonlinear development of the RTi drives decoupling between neutrals and charges. The decoupling is more pronounced on small spatial scales and at locations of strong gradients in density and/or magnetic field. The ion-neutral flow decoupling is more pronounced in the horizontal direction. So, compared with the single-fluid simulations of Khomenko et al. (2014b), the two-fluid simulations of Popescu Braileanu et al. (2021a), Popescu Braileanu et al. (2021b) display a more complex and rich behaviour at small scales, where two-fluid effects become of relevance and the ion-neutral decoupling takes place (see Figure 9). Another important difference between the models of Khomenko et al. (2014b) and Popescu Braileanu et al. (2021a), Popescu Braileanu et al. (2021b) is that the latter papers considered a sheared magnetic configuration. For sufficiently large shear, the cutoff in the linear growth rate disappears, so that the dissipative effect of the collisions can be better observed at small scales.

FIGURE 9

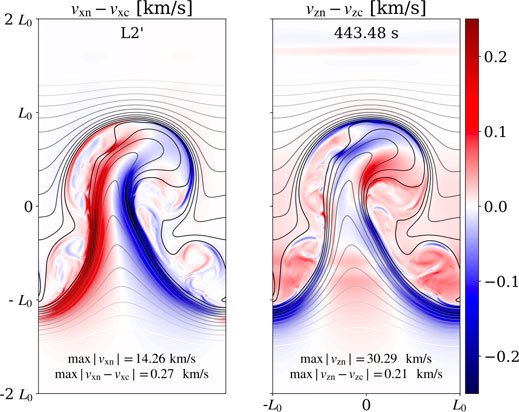
FIGURE 9. Snapshots of the ion-neutral decoupling in horizontal and vertical velocities from a two-fluid simulation of RTi. The image displays a close-up view of a well-developed ascending plume. The back lines are isocontours of the magnetic potential. Credit: Popescu Braileanu et al. (2021b), A&A 565, A45, reproduced with permission © ESO.

Thermal Instability

The first study of thermal instability in an infinite homogeneous medium goes back to the paper by Parker (1953). Starting from a balance between a temperature-independent heating and a temperature-dependent radiative losses, the instability appears when radiative losses increase as temperature decreases. The consequence is that in regions which are cooler than the surroundings, the temperature drops rapidly below the equilibrium temperature in a catastrophic way, giving place to a cool condensation. Zanstra (1955a,b) argued that in order to have a pressure equilibrium, cool regions are compressed while hot ones are expanded, which leads to the formation of cool condensations, obtaining instability criterion different from Parker’s criterion. However, Field (1965) pointed out the incorrectness of the criteria obtained by those authors due to incompleteness of both studies. Weymann (1960) seems to have been the first to give the correct criterion when studying chromospheric heating due to shock waves. Unfortunately, and such as it is mentioned by Field (1965), the importance of this paper was not fully appreciated.

Field (1965) studied the stability of a gas in mechanical and thermodynamical equilibrium in an infinite, uniform and static medium with a fixed density and temperature. In absence of gravity and assuming a generalized heat-loss function, $\mathcal{L}$, which balances heating and cooling, Field’s well-known isochoric, isobaric, and isentropic criteria were introduced, namely

${\left(\frac{\partial \mathcal{L}}{\partial T}\right)}_{\rho }<0,(37)$

for an isochoric process, which is equivalent to Parker’s criterion,

${\left(\frac{\partial \mathcal{L}}{\partial T}\right)}_p={\left(\frac{\partial \mathcal{L}}{\partial T}\right)}_{\rho }-\frac{{\rho }_0}{T_0}{\left(\frac{\partial \mathcal{L}}{\partial \rho }\right)}_T<0,(38)$

for an isobaric process that governs condensation modes, and

${\left(\frac{\partial \mathcal{L}}{\partial T}\right)}_S={\left(\frac{\partial \mathcal{L}}{\partial T}\right)}_{\rho }+\frac{1}{\gamma -1}\frac{{\rho }_0}{T_0}{\left(\frac{\partial \mathcal{L}}{\partial \rho }\right)}_T<0,(39)$

for an isentropic process. In these expressions, ρ₀ and T₀ are the equilibrium density and temperature, and γ is the adiabatic coefficient. In all the cases above mentioned, only hydrodynamic equations in infinite and fully ionized plasmas were considered. In a further extension of this study, Field (1965) considered the inclusion of a magnetic field, which modifies the momentum equation, and thermal conduction. The linear analysis leads to a fifth-order dispersion relation, since two additional wave modes, which correspond to Alfvén waves, appear in addition to the magnetoacoustic and thermal modes. Field (1965) pointed out that under a wide range of conditions thermal equilibrium is unstable and, for instance, can lead to the formation of condensations of higher density and lower temperature than the surrounding medium. These results were applied to the solar chromosphere and corona, planetary nebulae, the galactic halo, and galaxy formation, which evidences that, apart from solar plasmas, thermal instability is also of great interest for astrophysical plasmas. Heyvaerts (1974) extended Field’s study by including Joule dissipation in the energy equation and a magnetized medium, which led to consider the anisotropy of the transport coefficients and to take into account the effect of Joule heating in the energy balance. An in-depth study of all the involved modes was performed and applied to chromospheric and coronal conditions.

Thermal Instability in Fully Ionized Plasmas

In the solar context, and related with prominences, thermal modes were studied in detail in non-homogeneous and fully ionized plasmas (e.g., van der Linden and Goossens, 1991b,a; van der Linden, 1993; Ireland et al., 1995; Carbonell et al., 2004; Soler et al., 2011, 2012a, and references therein). Furthermore, Hildner (1974); Oran et al. (1982); Dahlburg and Mariska (1988); Karpen et al. (1989b,a); Cargill and Hood (1989); Carbonell et al. (2004) investigated both linear and nonlinear thermal instabilities since this instability represents a key guide to understand the formation of prominences and coronal rain in the solar corona. Effects like thermal conduction across magnetic field lines and resistivity, could play an important role in the development of prominence fine structure (van der Linden, 1993; Ireland et al., 1998). Field’s analysis has been recently revised in a thorough study made by Waters and Proga (2019) who, together with a discussion about the stability of acoustic and condensation modes between the two wavelengths corresponding to isobaric and isochoric instabilities, included a numerical analysis of the non-linear evolution of condensation modes with applications to active galactic nuclei (AGNs) and giant molecular clouds (GCM). In solar corona conditions, Claes and Keppens (2019) have also revisited Field’s treatment and have combined it with numerical simulations in order to check the predicted growth rates and to study the non-linear regime. Claes et al. (2020) have investigated the formation of threads by non-linear thermal instability, obtaining that the threads are misaligned with the underlying magnetic structure. This study reveals intricate multidimensional processes that occur through in situ condensations in a low plasma β regime representative of the coronal medium. Falle et al. (2020) have also done another re-analysis of Field’s results using a new approach based on Whitham’s theory of wave hierarchies (Whitham, 1974), which simplifies calculations and establishes relationships between dispersion relations and the involved physical processes. On the other hand, nonlinear thermal instabilities in magnetized solar plasmas have also been studied by Dahlburg et al. (1987); Karpen et al. (1988, 1989b) and the nonlinear dynamics of radiative condensations in the case of optically thin plasmas was reviewed by Meerson (1996). Readers are referred to the cited papers for details on the physics of the instability.

In the case of fully ionized astrophysical plasmas beyond the solar case, there is an extense literature about the role of thermal instability in the interstellar medium and star formation. As a matter of example (Gomez-Pelaez and Moreno-Insertis, 2002), considered the linear thermal stability of an expanding and cooling medium with thermal conduction and self-gravity included, and the obtained results were applied to the case of a hot optically thin interstellar medium such as supernova remnants. Wareing et al. (2016); Ji et al. (2018); Fragile et al. (2018); Choi and Stone (2012) showed that the thermal instability mechanism can be responsible for the formation of molecular loops in the galactic central region, the appearance of higher-density filaments in star-forming clouds, the cold gas found in galactic haloes, the vertical collapse of the accretion disk around stellar-mass black holes, and that, together with anisotropic thermal conduction, thermal instability can significantly affect the shapes and sizes of cold clouds of the interstellar medium. For a thorough review on thermal instability in the interstellar medium, see Inutsuka et al. (2005) and references therein. These examples point out the relevance of the thermal instability in the astrophysical context. The importance of all these studies rests in the fact that thermal instability can explain the formation of dense and cool localized structures in astrophysical and laboratory plasmas, when their masses are less than those required for gravitational contraction i.e. smaller than the Jean’s mass. (See Section 8).

Thermal Instability in Partially Ionized Plasmas

The study of thermal instability in partially ionized plasmas is a topic of great interest in astrophysics, however, the first studies were performed with laboratory plasmas. The first demonstration of thermal instability in fluids giving place to thermal convection was done by Benard (1900). The theoretical interpretation was made by Rayleigh who established that for any Rayleigh number, R, greater than a critical one, R_c, thermal instability sets in. Chandrasekhar (1961a) studied the thermal instability of a layer of fluid in which an adverse temperature gradient is maintained by heating the layer from below, and different situations such as the Bénard problem, the presence of rotation and/or magnetic field were considered. Following the approach by Chandrasekhar (1961a), Sharma (1976) studied the collisional effects between ions and neutrals on the thermal instability of a horizontal layer of finite thickness made of a partially ionized plasma, assumed incompressible, and permeated by a vertical magnetic field. This layer is heated from below in such a way that a steady temperature gradient is maintained. The boundaries of the layer were assumed to be free and the limiting fluid was considered non-conducting. After linearizing a simplified version of the two-fluid equations, including thermal conduction, viscosity, resistivity, gravity, and collisions between neutrals and charges, a dispersion relation was obtained that was expressed in terms of the Rayleigh number. For stationary convection, it was shown that collisions do not have any effect on thermal instability. The possibility that the instability appeared as an overstability was examined and conditions for the non-existence of overstability were obtained. Furthermore, the effect of the magnetic field on the thermal instability was studied by considering the variation of the Rayleigh number with the Chandrasekhar number, which includes the magnetic field. It was found that the magnetic field has an stabilizing effect on thermal instability. Later, Sharma and Sharma (1978), Sharma and Sharma (1985) extended the previous study to the case in which the fluid is rotating and arrived at the same conclusions for the case of stationary convection. Regarding overstability, they studied the variation of the Rayleigh number with respect to the Taylor number, which includes rotation, and with respect to the Chandrasekhar number, finding that rotation and magnetic field have an stabilizing effect on thermal instability. Next, rotation was removed and the Hall term was taken into account in the calculations. As before, for stationary convection collisions have no effect on thermal instability in a partially ionized Hall plasma, however, they found that the Hall currents have a destabilizing effect on thermal hydromagnetic instability when the variation of the Rayleigh number with respect to the Hall parameter was studied. In summary, the obtained results are similar to those of Chandrasekhar (1961a) since collisions between ions and neutrals do not have any influence on stationary convection. Finally, Sharma and Misra (1986) considered the same configuration as before but assuming that the fluid is compressible, and studied the effect of compressibility on thermal instability. Following a linear analysis, they found that the main effect of compressibility is to delay the onset of the instability, therefore, compressibility has an stabilizing influence.

On the other hand, observations have pointed out that small-scale structures pervade the interstellar medium (ISM). In order to understand the formation of these small-scale structures in the weakly ionized cold HI and molecular clouds of the ISM, Fukue and Kamaya (2007) made a thorough study of thermal instability in a magnetized and weakly ionized plasma, based on the idea that thermal instability could be a mechanism for further fragmentation in molecular clouds. The reason is that even in systems stable against gravitational instability, the systems can become thermally unstable because the critical wavelength for thermal instability is smaller than that for gravitational (Jeans) instability, which means that the size of the critical length is smaller than Jean’s length. Using the two-fluid approach (see Subsection 2.2), Fukue and Kamaya (2007) studied the effect of ion-neutral friction on the growth of thermal instability, focusing in the condensation mode rather than in the oscillatory modes. After linearizing the two-fluid equations, a sixth order dispersion relation was obtained, which describes two sets of three modes: one of the modes in each set is the condensation mode and the other two are oscillatory modes. From the dispersion relation it can be seen that the critical wavelength for the condensation mode, which is obtained by setting the growth rate equal to zero, is not affected by ion-neutral friction. In order to study the importance of the condensation mode for structure formation, it is necessary to solve numerically the full dispersion relation, and this was done for different values of the strength of magnetic field and friction. In absence of magnetic field and friction, two independent pure modes for ion and neutrals are present [see thin curves in Figure 2 of Fukue and Kamaya (2007)], however, when friction is allowed pure ion or neutral modes do not exist and, for both components, the growth rate at larger scales decreases because friction is more efficient at these scales [see thick curves in Figure 2 of Fukue and Kamaya (2007)]. This figure also shows that, when friction is allowed, the curves representing the behaviour of the modes originate from the curves corresponding to the case in which magnetic field and friction are not considered [see thin curves in Figure 2 of Fukue and Kamaya (2007)]. When magnetic field is taken into account, the critical wavelength for the ion mode is enlarged, as the criterion for thermal instability in a fully ionized magnetized plasma indicates. However, the critical wavelength for the neutral mode is not affected [see Figure 3 of Fukue and Kamaya (2007)]. When the strength of the magnetic field is strongly increased, the magnetic field completely stabilizes the ion mode, and only the neutral mode appears in the thermal instability diagram [see Figure 5 of Fukue and Kamaya (2007)]. When the strength of ion-neutral friction increases, ion mode remains stabilized for sufficiently intense magnetic fields, while the neutral mode remains unstable but with a reduced growth rate [see Figure 6 of Fukue and Kamaya (2007)]. Baruah et al. (2010) investigated thermal instability in a weakly ionized plasma with ionization and recombination such as in the envelopes of planetary nebulae that surround red giant stars. The presence of ionization and recombination affects the instability behaviour and limits the size of the small structures which can be formed by this instability.

As it is well-known, instability of thermal modes play an important role in the solar context, in particular in solar prominences or coronal rain, since it provides a mechanism for plasma condensation in the solar corona. Following the instability criteria introduced by Field (1965), it is straightforward to conclude that the radiative loss function is of great importance to determine the stability of thermal modes. However, an accurate description of radiative losses in cool plasmas, like prominences, is not an easy task because solutions of the radiative transfer problem in non-local thermodynamic equilibrium are needed. Taking into account partial ionization effects, Soler et al. (2012a) studied the stability of thermal modes in unbounded and uniform plasmas with physical properties akin to those of solar prominences. The single-fluid approximation was used. They considered three different parametrizations for the radiative loss function: the function proposed by Hildner (1974), the Raymond-Klimchuk function (Klimchuk and Cargill, 2001), and a radiative loss function derived from the CHIANTI atomic database (Parenti et al., 2006; Parenti and Vial, 2007). Starting from single-fluid equations (see Subsection 2.1) with ambipolar diffusion and non-adiabatic terms included, a linear analysis was performed in order to obtain a dispersion relation that describes two damped slow modes, two damped fast modes, and one thermal mode. From the full dispersion relation, and after performing a first-order expansion for a low-β plasma, an approximate dispersion relation for slow and thermal modes can be obtained. Since for the thermal mode in a static plasma the real part of the frequency is equal to zero, we can write ω = is, therefore, due to the temporal dependence exp( − iωt) assumed by Soler et al. (2012a), thermal mode perturbations are proportional to exp(is), where s is the growth rate. An approximate growth rate was obtained, which depends on the non-adiabatic terms and Cowling’s diffusion. When Cowling’s diffusion is set to zero, the growth rate of the thermal mode in the case of a fully ionized plasma is recovered. Next, the full dispersion relation was solved numerically. Figure 10 shows a plot of the growth rate versus wavelength for the case of fully and partially ionized plasma and different temperatures and ionization degrees. In both plots, the approximate and the full numerical solution of the dispersion relation are compared. For the considered temperatures, it is found that the approximate and full numerical solutions are in good agreement which points out that magnetic diffusion plays a negligible role in the value of the growth rate. On the other hand, Figure 10 also shows that for fully or partially ionized plasma the thermal mode is stabilized at short wavelengths which is due to the fact that thermal conduction is stronger for short wavelengths. On the opposite, for long wavelengths the growth rate saturates becoming independent from the wavelength. Furthermore, the growth rate decreases with the temperature. When Cowling’s diffusion and thermal conduction by neutrals are taken into account together, we can observe that the growth rate increases when the ionization degree decreases. This is due to an increase of the effective density of the plasma because, in the constant pressure calculations of Soler et al. (2012a), the number density of neutrals is increased when the ionization degree decreases. In addition, when the ionization degree decreases the critical wavelength increases due to the effect of thermal conduction by neutrals. As in the case of fully ionized plasma, the effect of magnetic diffusion on the growth rate is negligible.

FIGURE 10

FIGURE 10. (A) Numerically computed thermal instability growth rate (solid) and approximate value (dashed) vs wavelength for the CHIANTI-based loss function and different values of the temperature in the case of a fully ionized plasma, i.e., ξ_i = 1. (B) Same as panel a) for T = 16,000 K but in the partially ionized case with different values of ξ_i. Credit: Soler et al. (2012a), A&A 540, A7, reproduced with permission © ESO.

Finally, the effect of thermal instability on the onset of the gravitational or Jeans instability, described in subsect 8, has been also considered.

Farley-Buneman Instability

The Farley-Buneman instability (FBi), named after Farley (1963) and Buneman (1963), and also called type I electrojet instability (see Rogister and D’Angelo, 1970), is a low-frequency cross-field two-stream instability that is of much relevance in the E region of the ionosphere. The energy source of the instability resides in the relative motions of ions and electrons in the direction perpendicular to the ambient magnetic field. A strong enough electric field, E, perpendicular to the background magnetic field, B₀, can drive a cross-field drift of particles, E × B₀. The FBi in the ionospheric E region is basically electrostatic, and the presence of neutrals plays a fundamental role in setting the conditions for the instability to be possible. In the ionospheric E region, the electron gyrofrequency is much larger than the electron-neutral collision frequency, while the ion gyrofrequency is much smaller than the ion-neutral collision frequency. This means that electrons are strongly magnetized while ions are very weakly magnetized because of their frequent collisions with neutrals. In addition, electron-ion collisions are negligible in the E region. The different Hall mobility of ions and electrons produces a net current and, in the lowest-order approximation, the FBi is triggered when the drift velocity, U, exceeds the ion acoustic velocity, namely (see, e.g., Fejer et al., 1984; Dimant and Milikh, 2003)

$U\gtrsim c_s\left(1+{\psi }_{\perp }\right),(40)$

where $c_s=\sqrt{k_{\text{B}}\left(T_{\text{i}}+T_{\text{e}}\right)/m_{\text{i}}}$ is the ion acoustic speed, and ψ_⊥ = ν_enν_in/Ω_eΩ_i is a parameter related with the electron and ion magnetization, with Ω_{e, i} the electron/ion cyclotron frequencies. If ion magnetization is taken into account, an additional requirement for the instability is that Ω_i/ν_in < 1, i.e., weak ion magnetization (see Fejer et al., 1984). Predominantly, the ionospheric FBi gives rise to field-aligned (type I) irregularities that were first detected with radar techniques (see references in Kelley, 2009) and was also observed in plasma laboratory experiments (John and Saxena, 1975).

There is an abundant literature on ionospheric FBi. Owing to the low-frequency nature of the instability, it can be studied using multi-fluid or kinetic models describing the dynamics of ions and electrons, but a single-fluid approach is not adequate because the origin of the instability fundamentally resides in the different response of ions and electrons. Most of the works, while assuming the presence of neutrals, do not explicitly solve their dynamics. Detailed studies of the triggering, linear stage, and nonlinear saturation of the FBi in ionospheric conditions can be checked in, e.g., Sudan et al. (1973); Keskinen (1981); Fejer et al. (1984); Dimant and Sudan (1995); Oppenheim et al. (1996); Otani and Oppenheim (1998); Rosenberg and Chow (1998); Volokitin and Atamaniuk (2010); Litt et al. (2016); Young et al. (2020), among many other papers.

Although most of the work on the FBi has been done in the ionospheric context, the instability has also been proposed to play a role in the lower solar atmosphere, where the conditions of electron and ion magnetization are analogous to those in the ionospheric E region (see Leake et al., 2014). Research on the FBi in the solar chromosphere has experienced a recent boost because of its alleged relevance for plasma heating. Liperovsky et al. (2000) first explored the prospects of the FBi excitation in the solar chromosphere and discussed that, contrary to the case of the ionosphere, electron-ion collisions may be important in the solar chromosphere. Fontenla (2005) further discussed the importance of the FBi in the chromosphere and explained that upward-propagating fast MHD waves could trigger the FBi in regions with horizontal magnetic fields. Following this idea, a mechanism to generate a cross-field ion-electron drift that would drive the FBi in the chromosphere has been proposed by Fontenla et al. (2008). This is based on the presence of a stream of neutrals across the magnetic field that would drag the partially magnetized ions, while electrons would remain tight to the magnetic field lines. So, a cross-field ion-electron drift would also be generated. A similar neutral-flow driving mechanism has been discussed by, e.g., Petrović et al. (2007) and Pandey et al. (2012). A neutral flow velocity larger than the ion acoustic speed is required for the onset of the FBi. Fontenla et al. (2008) suggest that convective over-shoot motions may provide the necessary neutral flows. Fontenla et al. (2008) explain that the nonlinear saturation of the FBi would drive turbulence that would greatly enhance the dissipation in the chromosphere.

Another environment in the solar atmosphere where a cross-field flow of neutrals takes place is in solar prominences (see Gilbert et al., 2002; Terradas et al., 2015b). The magnetic structure of prominences, formed by quasi-horizontal dips, holds ions and electrons against gravity, whereas neutrals continuously fall towards the solar surface. Ion-neutral collisions slow down the neutral drainage, but a net downward neutral flow remains. The inferred neutral flow velocities are, in principle, much lower than the required velocities for the onset of the FBi and the condition of weak ion magnetization would not be applicable in prominences. Nevertheless, the prospects of the FBi occurrence in prominences have not been explored in detail.

Again in the chromosphere, Gogoberidze et al. (2009) explored the physics of the FBi onset by including the finite magnetization of the ions and Coulomb (ion-electron) collisions. Importantly, they showed that owing to the effect of Coulomb collisions, the FBi can be triggered in the chromophere even in regions where Ω_i/ν_in > 1, so that the ion magnetization is not negligible (see also Liperovsky et al., 2000). However, contrary to the conclusions of Fontenla et al. (2008), Gogoberidze et al. (2009) claim that plasma heating associated with the FBi would be minor in the chromosphere. Later, Gogoberidze et al. (2014) expanded the previous work by including ion and electron thermal effects. They conclude that destabilization by ion thermal effects is not important because it is effectively suppressed by Coulomb collisions. However, electron thermal effects are able to reduce the threshold velocity drift for the FBi in the middle and high chromosphere. Gogoberidze et al. (2014) conclude that the FBi may produce density irregularities in the chromosphere, but its role in chromospheric heating is less clear.

Madsen et al. (2014) further expanded the theory of chromospheric FBi by considering a multi-ion approach, but ion magnetization and Coulomb collisions were ignored. They consider a chromospheric model including all abundant ion species from hydrogen to zinc. Their multi-ion model predicts that the FBi may be triggered by velocities as low as 4 km s⁻¹, lower than the neutral acoustic speed (see Figure 11), so that neutral flows rising from the photosphere may easily make the FBi common in the chromosphere. The effect of ion magnetization in the multi-ion chromospheric model was discussed by Fletcher et al. (2018), who find that ion magnetization reduces that extent of the FB-unstable regions in the chromosphere. Depending on the magnetic field strength, the minimum trigger speed can occur near the temperature minimum.

FIGURE 11

FIGURE 11. FBi trigger velocity in the solar chromosphere for several magnetic field strengths. The plot is limited to pressures near the temperature minimum. The trigger velocity decreases near the temperature minimum, reaching speeds as low as 4 km s⁻¹. The neutral acoustic speed is plotted with a dashed line for reference. Adapted from Madsen et al. (2014). © AAS. Reproduced with permission.

The papers on chromospheric FBi cited above mostly rely on linearized theory, but the nonlinear evolution of the FBi has not been explored in detail. Recently, Oppenheim et al. (2020) have performed fully kinetic simulations in chromospheric conditions. They show that a new kind of instabilities, called “thermal instabilities” by Oppenheim et al. (2020), can easily generate small-scale turbulence and heating in the plasma. We note that, despite of having the same name, the thermal instabilities of Oppenheim et al. (2020) have a different physical nature than those discussed in Section 5. The mechanism underlying this new thermal instability is closely related to the FBi, but has distinctly different characteristics from the usual FBi, since electron and ion thermal effects dominate the instability growth. The physical picture of this FB-related thermal instability is explained in detail by Oppenheim et al. (2020). As electrons drift across the magnetic field, they collide with neutrals, becoming hotter. If an acoustic-like compressional wave develops mostly in the plane perpendicular to the magnetic field, it will cause a local wave-induced electric field. This field will modify the electron drift speed and, as a consequence, the amount of electron heating. Heating would either increase if the new electron drift speed is faster than the initial one, or heating would decrease otherwise. If the heating is reduced on the wave crests, then the pressure gradient will push plasma into regions of already high density and the perturbations amplitude will grow exponentially. The threshold neutral flow to drive the usual FBi is considerably higher than that required for this FB-related thermal instability. Then Oppenheim et al. (2020) conclude that the thermal instability grows first and dominates the wave growth and ultimately, the nonlinear behavior of the plasma, although the FBi can still be present. The results of Oppenheim et al. (2020) indicate that nonlinear simulations are needed to fully understand the nature of the FBi and related instabilities in the chromosphere. Hence, future works should go in this direction.

Magnetorotational Instability

One of the most important processes in astrophysics is accretion, in which a fluid element describing orbits in a central field of force loses angular momentum and spirals inwards. In order to take place, an efficient mechanism to extract angular momentum is needed. Hoyle (1960) suggested that only a MHD model could explain the needed outward transport of angular momentum. Many different physical mechanisms have been proposed (see Julien and Knobloch, 2010, for a complete set of references), but except one of them, the magnetorotational instability (MRi), the rest of mechanisms do not provide an efficient extraction of the angular momentum. However, it is also worth to point out that magneto-centrifugally launched jets from accretion disks around central objects like YSOs (Young Stellar Objects) or supermassive black holes (SMBH) in galactic nucleus can be another mechanism to remove energy and angular momentum, although it is not an instability. The MRi is a fluid instability known since, e.g., Velikhov (1959) and Chandrasekhar (1960). Balbus and Hawley (1991) were the first to provide a simple physical explanation for the process in the case of a fully ionized, ideal MHD medium, in which magnetic field and matter are well coupled. Essentially, it occurs when the angular velocity of a conducting fluid in a weak poloidal magnetic field decreases outwards. The MRi is fundamentally axisymmetric, grows on a dynamical timescale τ ∼ (Ω)⁻¹, is local, and its occurrence is independent of field strength and orientation. The strength of the magnetic field simply establishes the length of the fastest growing mode (Balbus and Hawley, 1991).

Following Balbus (2003), the MRi instability can be described as an spring-like instability. The simplest fluid system displaying this spring-like instability is an axisymmetric gas disk in the presence of a weak vertical magnetic field and the disk equilibrium is due to a balance of gravitational and rotational forces. If a fluid element is displaced in the orbital plane by an amount ξ with a spatial dependence exp(ikz), where z is the magnetic field direction, the ideal induction equation gives

$\delta \mathbf{B}=ikB\xi ,(41)$

where δB denotes the variation of the magnetic field, and the tension force is given by

$\frac{ikB}{\mu }\delta \mathbf{B}=-k^2{v}_A^2\xi ,(42)$

where v_A denotes the Alfvén velocity vector, ${\mathbf{v}}_{\mathbf{A}}=\mathbf{B}/\sqrt{\mu \rho }$, and k is the wavenumber vector. Eq. 42 is the form of a spring-like force, linearly proportional to the displacement ξ. The oscillatory frequency, ω, for small displacements in the plane of rotation of a disk with a uniform vertical magnetic field satisfies a dispersion relation such as

${\omega }^4-{\omega }^2\left({\kappa }^2+2k^2{v}_A^2\right)+k^2{v}_A^2\left(k^2{v}_A^2+R\frac{\mathrm{d}{\mathrm{\Omega }}^2}{\mathrm{d}R}\right)=0,(43)$

where κ is the epicyclic frequency, which is the rate at which a point of mass disturbed in the plane of its orbit would oscillate about its average radial location, Ω is the angular velocity, and R is the radius. If $\frac{\mathrm{d}{\mathrm{\Omega }}^2}{\mathrm{d}R}<0$, there is an exponentially growing root (instability) for wavenumbers k which satisfy the instability criterion given by

$k^2{v}_A^2<-R\frac{d{\mathrm{\Omega }}^2}{dR}.(44)$

The maximum unstable growth rate of the instability is,

$|\omega |=\frac{1}{2}\left|\frac{\mathrm{d}\mathrm{\Omega }}{\mathrm{d}\ln R}\right|,(45)$

and the maximun growth rate occurs for wavenumbers such as

${\left(k^2{v}_A^2\right)}_{\text{max}}=\left(\frac{1}{4}+\frac{{\kappa }^2}{16{\mathrm{\Omega }}^2}\right)\frac{\mathrm{d}{\mathrm{\Omega }}^2}{\mathrm{d}\ln R}.(46)$

From Eq. 43 we can observe that the magnetic field appears enclosed within the terms proportional to $k^2{v}_A^2$, thus, even if B is very small, and so v_A is small, for very large wavenumbers the magnetic tension can be important. This is the reason why the MRi is very sensitive to very weak magnetic fields since their effect is amplified once multiplied by the wavenumber, k. The MRi mechanism has deserved a lot of attention and has been extensively studied in the context of astrophysical fluid dynamics since differentially rotating systems with magnetic fields are abundant in the Universe. Because of the extensive literature on the MRi, here we have limited ourselves to review only a few representative papers describing the research done on MRi in some astrophysical topics. We shall put our focus on those works that explored partial ionization effects.

As stated before, Balbus and Hawley (1991) considered the case of a fully ionized, ideal MHD medium, in which magnetic field and matter were well coupled. However, often other effects such as Ohm’s and ambipolar diffusion and Hall’s dispersion can be of importance. In addition, in some astrophysical environments where the MRi can occur, plasmas are partially ionized. In the case of weak ionization, charges can slip through magnetic field due to collisions with neutral particles (Mestel and Spitzer, 1956). Therefore, the MRi theory was generalized to weakly ionized disks (Blaes and Balbus, 1994). From a purely theoretical point of view without any specific astrophysical application, most studies of the instability have used in the single-fluid model, which is accurate enough at low frequencies and in the long wavelength limit. However, to account for high frequencies and short wavelengths, the study of the MRi with the two-fluid model is necessary and the first attempt to do so was preformed by Blaes and Balbus (1994).

More recently, Ren et al. (2011) investigated the MRi using a two-fluid model in a rotating plasma permeated by a magnetic field following an analytical approach. They derived a linear dispersion relation for axisymmetric MRi in collisionless and inviscid plasma, while non-ideal dissipation effects were neglected. From the obtained dispersion relation, two different cases were considered, non-magnetized case and weakly magnetized case, and instability criteria were derived. The results showed that the instability criteria in the non-magnetized and weakly magnetized cases remarkably differ from those predicted by the single-fluid model. Later, Ren et al. (2012) considered the dynamical behaviour of a three-component weakly ionized plasma in order to examine the effect of collisions between charged species and neutrals on the MRi. They considered a background magnetic field and a differential rotation in the azimuthal direction. After linearizing the set of equations and performing a normal mode analysis, a highly complex dispersion relation was obtained which was analyzed in different limits: no collisions, the MHD limit, and high-frequency modes. For instance, in the limit of no collisions, the dispersion relation can be greatly simplified and the results show that collisions are indeed very important for the instability criterion. On the contrary, when collisions are allowed and the MHD limit is considered, the MRi behaviour is the same as for a fully ionized plasma, as expected.

Astrophysical environments where the MRi is of great importance range from protoplanetary and protostellar disks to supernovae, neutron stars, and black holes. Related with these astrophysical objects, an extensive research, considering ideal and non-ideal effects, like Ohm’s diffusion (Mikhailovskii et al., 1999), has been developed. However, of these astrophysical scenarios only protoplanetary or protostellar disks can be considered as partially ionized plasmas. Regarding protoplanetary disks (PPDs), the MRi in weakly ionized and uniformly magnetized accretion disks was studied by Sano and Miyama (1999). They started from the MHD equations including magnetic diffusivity in the induction equation and magnetic dissipation in the energy equation. They considered an axisymmetric equilibrium disk rotating with a Keplerian angular velocity profile. Along the vertical direction they assumed an isothermal disk in hydrostatic equilibrium with constant sound speed, and a constant magnetic field with azimuthal and vertical components. They performed a normal mode analysis searching for axisymmetric modes with growth rate, ω. Assuming that magnetic diffusivity and density are spatially uniform, and in order to ponder the effect of Ohmic dissipation, they performed a local analysis considering axisymmetric perturbations proportional to k_r and k_z, corresponding to the radial and vertical wavenumbers, respectively. The obtained dispersion relation for this case was analyzed in two different limits: incompressible (c_s → ∞) and compressible. In the incompressible limit, the corresponding dispersion relation was solved and Figure 12 shows the growth rate of the unstable mode versus the vertical wavenumber, for different values of the magnetic Reynolds number (R_m) when k_r = 0. It can be observed that the MRi growth rate is inversely proportional to the magnetic diffusivity, therefore, an increase of the magnetic diffusivity stabilizes small-scale perturbations. In the compressible case, the general dispersion relation depends on three parameters: the magnetic Reynolds number, the plasma beta, and the direction of the magnetic field. Figure 13 shows the behaviour of the growth rate in the compressible case versus the radial and vertical wavenumbers for a particular set of parameters. For all the parameters, the maximum growth rate exists on the axis where k_r = 0. When the strength of the azimuthal component of the magnetic field is increased, the effect is to suppress the unstable growth. According to Sano and Miyama (1999), the effect of plasma beta is negligible. The results of the linear analysis were applied to PPDs like the solar nebula. Sano and Miyama (1999) concluded that the MRi happens in a region with a radius greater than 15 AU, but it is suppressed inside this critical radius owing to the effect of magnetic dissipation.

FIGURE 12

FIGURE 12. MRi growth rate as a function of the vertical wavenumber. The modes shown in this figure are on the unstable branch for the case of k_r = 0. The result of the ideal MHD case is shown as a solid curve. Other curves are diffusive cases that have different values of the magnetic Reynolds number. Adapted from Sano and Miyama (1999). © AAS. Reproduced with permission

FIGURE 13

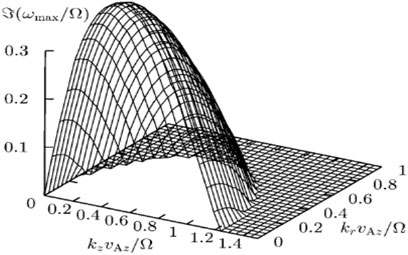
FIGURE 13. Surface plot of the MRi growth rate in the compressible case in the k_r − k_z plane with R_m = 1 and a particular set of parameters. Adapted from Sano and Miyama (1999). © AAS. Reproduced with permission

Later, Sano et al. (2000) showed how the unstable region is modified for a variety of models of PPDs, taking into account recombination of ions and electrons at grain surfaces. The stable region shrinks as the grain size increases or the sedimentation proceeds. Therefore, in the late evolutionary stages, PPDs can be magnetorotationally unstable even in the inner regions. Following with the consideration of different effects, Wardle (1999); Balbus and Terquem (2001) investigated how the inclusion of the Hall effect influences the stability of protostellar disks, and they found that the maximum growth rate and the characteristic wavelength of the MRi are both strongly modified by the Hall effect. For instance, Balbus and Terquem (2001) considered Hall-modified Alfvén waves in a uniformly rotating disk threaded by a vertical magnetic field and plane wave perturbations with z-dependence. After linearizing, azimuthal and radial equations for velocity and magnetic field perturbations can be obtained and the dispersion relation is,

${\omega }^2\pm 2\mathrm{\Omega }\omega \left(1-\frac{k^2{v}_H^2}{4{\mathrm{\Omega }}^2}\right)-k^2\left(v_A^2+c_s^2\right)=0,(47)$

where c_s is the sound velocity, v_H is the Hall velocity (see Balbus and Terquem, 2001), and the rest of parameters have the same meaning as before. In Eq. 47, the plus sign corresponds to left-hand polarization with respect to the magnetic field direction, and the minus sign to right-hand polarization. From the above dispersion relation it can be concluded that there are no instabilities in a uniformly rotating disk. Balbus and Terquem (2001) also considered differential rotation in a disk threaded by a vertical magnetic field, including resistivity and the Hall effect. Assuming the same type of disturbances as in the previous case, azimuthal and radial equations for velocity and magnetic field perturbations can also be obtained. The transition between stability and instability proceeds when ω = 0. Imposing this condition in the perturbed equations, an stability criterion can be derived, namely

$k^2{v}_A^2\left[\left(1+\frac{v_H^2}{v_A^2}\right)\left(1+\frac{{\kappa }^2\frac{v_H^2}{v_A^2}}{4{\mathrm{\Omega }}^2}\right)+\frac{{\kappa }^2{\eta }^2}{v_A^4}\right]<-\left[\left(1+\frac{{\kappa }^2\frac{v_H^2}{v_A^2}}{4{\mathrm{\Omega }}^2}\right)\right]\frac{\mathrm{d}{\mathrm{\Omega }}^2}{\mathrm{d}\ln R}.(48)$

When v_H → 0 and η → 0 in Eq. 48, the standard criterion for the MRi is recovered (Eq. 44). It is found that the Hall effect allows that disks with either decreasingly outward or increasingly outward angular velocity profiles become unstable while, on the contrary, the standard ideal MRi affects only those disks with a decreasingly outward profile.

Sano and Stone (2002) investigated the nonlinear evolution of the MRi using 3D non-ideal MHD simulations for different initial magnetic field geometries. They found that the accretion rate depends on how efficient Hall’s and Ohmic’s terms are. Also, they found that when the magnetic Reynolds number is larger than a critical value, the MRi develops into MHD turbulence. When the opposite happens, Ohmic dissipation suppresses the MRi. The critical value for the magnetic Reynolds number depends on the initial field configuration and is unaffected by the Hall effect. When PPD conditions are considered, the obtained results suggest that the outer regions of the disk, with a radius greater than a critical one, are unstable to the MRi and can become turbulent with an efficient transport of angular momentum. However, for values of the radius smaller than the critical one the MRi is suppressed by Ohmic dissipation. This critical radius is of the order of few AU while the typical size of PPDs is about 100 AU.

Pandey and Wardle (2012) made an exhaustive analysis of the stability of a partially ionized, differentially rotating, diffusive disk permeated by azimuthal and vertical magnetic fields including Ohm, Hall and ambipolar terms. They used the single-fluid model and the main obtained conclusions were: diffusive disks are unstable to radial fluctuations, the upper and middle layers of PPDs are susceptible to MRi and diffusive MRi, the MRi works closer to the midplane of PPDs when the magnetic field is not vertical, and a vertical magnetic field together with transverse fluctuations are fundamental for the MRi in a disk dominated by Hall’s and Ohm’s effects.

Simon et al. (2013b) used the single-fluid equations to perform numerical simulations with the ATHENA code exploring the effect of ambipolar diffusion on the MRi in the outer region of PPDs, including vertical stratification and assuming a zero vertical magnetic flux. In the case of idealized stratified simulations with a spatially constant ambipolar Elsässer number, turbulence induced by the MRi is similar to that in the case without stratification and becomes stronger when the effect of ambipolar diffusion is decreased. Also, the effect of ambipolar diffusion on disk accretion was considered including a vertical profile for the ambipolar Elsässer number. They found that the levels of surface turbulence were strong while the accretion rates did not agree with those observed in T Tauri stars. This discrepancy was attributed to the lack of a vertical magnetic field. Later, Simon et al. (2013a) included ambipolar diffusion together with a vertical magnetic field in the simulations. The results suggested that there is a strong and direct dependence of the accretion rates on the strength of the vertical magnetic field, and that the MRi disappears for a certain field strength. O’Keeffe and Downes (2014) carried out three-fluid simulations of a weakly ionized disk examining the linear and non-linear development of the MRi with and without flux. They also explored the importance of its orientation with respect to the net angular momentum vector. They used the multifluid MHD code HYDRA suitable for weakly ionized plasmas and studied the role of non-ideal effects, like ohmic dissipation, ambipolar diffusion and the Hall effect, on the non-linear development of the MRi in the region of the disk where the Hall effect is dominant over the rest of non-ideal effects. The results point out that the angular momentum transport is significantly enhanced by the inclusion of all the non-ideal effects, and that the Hall effect seems to be responsible for the enhancement of the MRi where a net field (with appropriate orientation) is present. Furthermore, when Ω ⋅ B is negative, the MRi is suppressed and lower rates of angular momentum transport are found. Regarding the same problem, Rodgers-Lee et al. (2016) performed multifluid simulations including ohmic dissipation, ambipolar diffusion and the Hall effect, and focused on the turbulence arising from the non-linear development of the MRi in radially stratified PPDs. They also used the multifluid MHD code HYDRA and compared the obtained results with those of ideal and non-ideal single-fluid simulations. The main conclusion was that the obtained results from the multifluid simulations were similar to those obtained using single-fluid non-ideal simulations. On the other hand, Béthune et al. (2016) have focused on the study of the organised structures observed in PPDs, searching an explanation based on the MRi. They investigated the behaviour of global MRi-unstable disc models that are dominated by the Hall effect. Using the PLUTO code, they carried 3D unstratified Hall-MHD simulations of Keplerian discs with Hall, Ohmic, and ambipolar Elsässer numbers. The results show that when the strength of the Hall effect is increased, a transition from a turbulent to a organised state develops and magnetised vortices are formed, which means that self-organisation by the Hall effect could explain the observed structures in PPDs. Finally, Bai and Stone (2017) have done two-dimensional simulations including the Hall effect and ambipolar diffusion using the ATHENA++ code. These simulations show that when a large-scale poloidal field is aligned with the rotation axis of the disk, the Hall effect drags magnetic flux inward at the midplane region, while flux is pushed outward above and below the midplane. On the opposite, for anti-aligned field polarity, the Hall effect transports magnetic flux outward and produces a large vertical field configuration in the midplane region. In this case, the net rate of outward flux transport is two times faster than in the aligned case.

Nonideal effects on the MRi development have been studied also in the context of massive stars and supernovae. If the core collapse supernovae contains a weak magnetic field and has differential rotation, the MRi instability should also be present. Kotake et al. (2004) performed two-dimensional hydrodynamic simulations of the magnetorotational collapse of a supernova core and found that, once combined with anisotropic neutrino radiation, the growth of the instability may enhance the heating near the axis, which suggests that the formation of extreme neutron stars like magnetars can be accompanied by jet-like explosions. On the other hand, Wheeler et al. (2015) used an stellar evolution code to study the magnetic effects of the MRi and the Spruit-Tayler instability in models of rotating massive stars which naturally develop very strong shear at composition boundaries, a necessary condition for the MRi. An interesting feature of this study is that the MRi can play a key role in the mixing of internal layers, an effect that is not pointed out by models neglecting MRi. In the final stages of stellar evolution, Masada et al. (2007) studied how the neutrino radiation affects the MRi in proto-neutron stars since neutrino radiation plays an important role in the momentum, heat, and lepton transports in proto–neutron stars. These diffusive processes affect the growth rate of the MRi. The study was performed using linear perturbation theory and the results indicated that, even in these conditions, the MRi can grow and when the toroidal magnetic component dominates over the poloidal one, nonaxisymmetric MRi modes grow much faster than axisymmetric modes. Therefore, a complete understanding of the three-dimensional nonlinear evolution of the MRi is needed in order to understand the explosion mechanism of core-collapse supernovae leading to the formation of neutron stars (see Rembiasz et al., 2017, for a review).

The MRi is also relevant in black holes, since the gas orbiting black holes looses angular momentum via MRi. As in any viscous fluid, the transport of angular momentum by the MRi must be accompanied by dissipative heating and the outward transport of energy through the gas. If the gas is able to radiate away the dissipated energy, it will settle into a geometrically thin Keplerian accretion disk. Gas in such a disk spirals inward gradually through a sequence of nearly circular orbits until it reaches the innermost stable circular orbit. Once inside, gas can fall into the black hole without any further loss of angular momentum. Therefore, MRi also plays an important role in accretion disks around stellar and supermassive black holes (Begelman, 2003)

The MRi instability is highly relevant in different astrophysical situations. However, in the solar context only a few studies have been performed and none is related with partially ionized plasmas. From here on, we focus on those works that considered the solar case. Menou et al. (2004) studied the local stability of stratified, differentially rotating fluids, to axisymmetric perturbations in the presence of a weak magnetic field and several nonideal effects, generalizing a previous double diffusive case. As usual, they started from the single-fluid MHD equations including gravity, resistivity, viscosity, and thermal conduction. Using the Boussinesq approximation and after linearization, a fifth-order dispersion relation was obtained. The complexity of the dispersion relation prevents general necessary and sufficient conditions for stability to be derived. In order to simplify the study, they considered two separate limits, namely a perfectly conducting plasma and inviscid plasma. Then, imposing that the five coefficients of the dispersion relation be greater than zero, some inequalities can be obtained and a condition for stability can be derived from each inequality. Finally, the dispersion relation was solved numerically assuming a standard model of the Sun (Bahcall et al., 2001). The results show that in the case of a triple-diffusive situation, the weakest diffusion process can sometimes play a stabilizing role. In a specific numerical application to the Sun upper radiative zone, which is seismologically known to nearly rotate as a solid body, it was found that moderate to strong levels of differential rotation would indeed be unstable. This suggests that magnetized and multidiffusive modes may have played an important role in establishing the current solar internal rotation.

Also in the case of the Sun, Parfrey and Menou (2007) considered, for the first time, the stability of the solar tachocline with respect to the diffusive MRi for general field geometry. To investigate whether instability exists for physically reasonable scales and fields, and to confirm that the MRi is not stabilized by a realistic entropy stratification, the triple-diffusive dispersion relation (Menou et al., 2004) was numerically solved for axisymmetric modes. For each considered magnetic configuration, the fastest growing mode was considered (see Figure 14). From the results of Parfrey and Menou (2007) it can be inferred that the solar tachocline is magnetorotationally unstable for latitutes such that θ ≤ 53° and stable close to the equator.

FIGURE 14

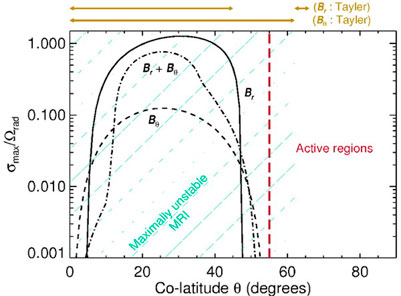
FIGURE 14. Results of the MRi in the solar tachocline. Growth rate of the fastest growing mode in units of the rotation rate as a function of the co-latitude angle for radial (B_r; black solid curve), latitudinal (B_θ; dashed curve), and both radial and latitudinal (B_r + B_θ; dot-dashed curve) magnetic fields. The hatching indicates the maximally unstable region, as determined by the Balbus stability criterion. The arrows above the plot delimit the areas potentially subject to Tayler instability for radial and latitudinal fields. Active regions are found to the right of the vertical long-dashed line. Adapted from Parfrey and Menou (2007). © AAS. Reproduced with permission.

The role MHD turbulence driven by the MRi was studied by Masada (2011) assuming a solar rotation profile obtained from helioseismic data and a standard solar model. Using linear theory, the location where the MRi should be active in the convective zone and tachocline was determined. It was found that the MRi is confined to the higher latitude tachocline and lower latitude near-surface shear layer. Considering an axisymmetric WKB plane wave perturbation in the Boussinesq approximation, the stability of the system to the MRI is governed by a local dispersion equation similar to that investigated by Menou et al. (2004). By numerically solving the linear dispersion equation, the most rapidly growing MRi mode at an arbitrary meridian point (r, θ) in the solar interior was searched for. Potential locations for the MRi development are shown in the colour map in Figure 15. The colour scale represents the maximum growth rate of the MRi at each local meridian point. The vertical and horizontal axes denote polar and equatorial radii normalized by the solar radius. The rotation profile adopted in this analysis is overplotted on the MRi map with solid contours which increase from 330 to 480 nHz by steps of 15 nHz. The MRi location is not drastically changed due to the field strength and structure as long as a weak, vertical component of the magnetic field is present. In this study, the destabilizing effect arising from the unstable internal gravity wave was eliminated to focus better on the destabilizing effect of the MRi modes. In contrast, the stabilizing effect due to the density stratification was consistently introduced in the analysis.

FIGURE 15

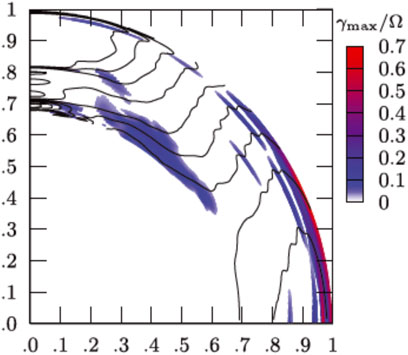
FIGURE 15. Maximum growth rate of the MRi, γ_max, is shown by the colour map. The normalization is the local angular velocity Ω. The region with the positive growth rate is the promising MRI location. The rotation profile is overplotted by the solid contour lines. They increase by 15 nHz from 330 to 480 nHz. Note that the region with zero growth rate of the MRI is filled with white. Reproduced from Masada (2011) by permission of Oxford University Press.

Finally, Kagan and Wheeler (2014) made a comprehensive study of the MRi in the Sun. A dispersion relation for nonaxisymmetric instability including the effects of shear, convective buoyancy, and three diffusivities (thermal conductivity, resistivity, and viscosity) was obtained. In order to determine the unstable modes present at each location in the Sun and the associated growth rates, a solar model was evolved with the stellar evolution code MESA and angular velocity profiles determined by GONG helioseismology. The comparison with previous studies (Masada et al., 2007; Parfrey and Menou, 2007; Masada, 2011) pointed out that the obtained results were equivalent to those of Masada et al. (2007) for proto-neutron stars with the difference that in the considered outer convective region, the nonaxisymmetric MRi modes always grow much faster than axisymmetric modes, in particular when poloidal fields are very large or very small.

Jeans Instability

In the astrophysical context, the Jeans instability is of great importance since it plays a relevant role in gravitational collapse and fragmentation of gaseous structures. The gravitational instability of an infinite homogeneous medium was initially studied by Jeans (1902), who gave a criterion for this instability based on a critical length, or Jean’s length. A thorough study of this problem was made by Chandrasekhar (1961a) showing that Jean’s criterion was neither affected by uniform rotation nor by a uniform magnetic field. Later, many studies have investigated whether Jeans’s criterion is affected by different physical effects in non-rotating and rotating plasmas. Among others, the effects considered have been: the Hall effect, viscosity and thermal conductivity, finite resistivity, finite Larmor radius (FLR), porosity, and radiative heat-loss function, considering either each effect separately or several of them together (e.g., Kalra and Talwar, 1964; Sharma, 1974a; Sharma, 1974b; Sharma and Prakash, 1974; Vyas and Chhajlani, 1989; Kaothekar and Chhajlani, 2012; Kaothekar et al., 2016; Kaothekar, 2020). In all these studies, the approach was similar: start from MHD equations including the considered physical effects, linearize these equations, and assume that perturbations behave as plane waves to obtain a dispersion relation. The dispersion relation was then analyzed with the aim to discriminate the influence of the different physical effects on Jean’s criterion. In most of these studies, the main conclusion was that Jean’s criterion was very robust in the sense that it remained unaffected by the different physical effects considered. Only in some particular cases, like that explored by Kaothekar and Chhajlani (2012), it was found that radiative losses and thermal conduction modify Jean’s criterion for gravitational instability.

The aim of most of these studies was to understand the formation of astrophysical objects through gravitational collapse, but in all these studies the considered astrophysical plasmas were assumed to be fully ionized. However, it is well known that, for instance, molecular clouds, HI regions and the ISM are weakly ionized media made of a mixture of neutrals and ionized species interacting through mutual collisions. Therefore, it became of great interest to study the behaviour of gravitational instability in partially ionized plasmas, containing ions and neutrals, and considering different physical situations. First of all, the presence of magnetic fields was taken into account by different authors. For instance, Mestel and Spitzer (1956) analyzed star formation in clouds containing magnetic fields, and the derived stability criterion was written in terms of Jean’s length. In this case, ion-neutral collisions provide the coupling of magnetic field to the neutrals. Also, the stability of interstellar clouds against gravitational collapse and fragmentation in the presence of magnetic fields was studied by Langer (1978) showing that magnetic pressure provides with additional support against collapse in the case of strong coupling between ions and neutrals. As a consequence, the collapse of the gas is retarded. In the magnetic support model for molecular clouds, a fundamental quantity is the ratio between the self-gravitational and the magnetic energies of a certain parcel of the fluid. When the self-gravity of the cloud does not dominate the magnetic support, the cloud is magnetically subcritical. When the opposite happens, the clouds are supercritical. In the magnetic-support model, clouds are assumed to be globally magnetically subcritical, and thus absolutely supported against their self-gravity as long as the ideal MHD regime is applicable. If some fraction of the mass has to undergo gravitational collapse, material needs to loose magnetic support. This can be accomplished through ambipolar diffusion and, then, a dynamical collapse can take place. Furthermore, the heating released by the friction between ions and neutrals can contribute to heat clouds cores. The description of the standard single-fluid approximation of this process can be found in a review by Shu et al. (1987). See also Ballester et al. (2018).

Apart of including a magnetic field, other physical effects were also considered. In general, to perform these studies a similar procedure as for the case of fully ionized plasmas was used, starting from linearized perturbed two-fluid equations and assuming that perturbations behave as plane waves, a general dispersion relation was derived. Once obtained, the behaviour of its roots were thoroughly analyzed allowing to determine the influence of the different considered physical effect on the instability. Following this approach, the same physical effects as in the case of fully ionized plasmas were considered: finite Larmor radius (FLR) introduced through a pressure tensor, finite conductivity, Hall current, and frictional effects with neutrals, inclusion of an oblique instead of a horizontal or vertical magnetic field, rotating plasma carrying a uniform magnetic field with Hall effect, oblique magnetic field and ion viscosity, large scale magnetic field, non-Boltzmann distribution for electrons and ions, radiation and thermal conduction, and porosity (Bhatia, 1969, 1972; Kumar and Srivastava, 1990; Ali and Bhatia, 1992b,a; Kumar et al., 1993; Bhatia and Rajib Hazarika, 1995; Jacobs and Shukla, 2005; Borah and Sen, 2007; Kaothekar and Chhajlani, 2012). As before, the general conclusion was the same: no modification of Jean’s criterion. However, Kaothekar et al. (2016) considered viscosity, thermal conduction, radiative effects, porosity, magnetic field, and FLR, and found that some of these physical effects affect the gravitational mode in the transverse and longitudinal directions of wave propagation, thus modifying Jean’s condition in those directions. These results were similar to those obtained by Prajapati et al. (2010). Finally, it is worth to remark that while all these studies are of relevance in the astrophysical context in general, when we focus on the solar case these studies are not applicable.

Discussion and Concluding Remarks

The purpose of this paper has been to give a general overview of the role of partial ionization effects on some major fluid instabilities that frequently appear in astrophysical plasmas. The field of plasma instabilities in astrophysics is so vast and the literature is so extensive that we can only aim to offer readers a shallow grasp of this topic. Interested readers should resort to the original works cited throughout the paper, where more detailed explanations of the relevant results briefly discussed here can be found.

The results included in the increasingly large body of literature about partially ionization effects on instabilities, which has mostly been developed during the last decade, allows us to summarize some basic and common features:

• Partial ionization effects are relevant at sufficiently small scales where the decoupling between charges and neutrals can be effective.

• At those small scales, the different responses of charges and neutrals to the influence of the magnetic field is what fundamentally determines the distinct dynamics that a PIP displays compared to a fully ionized plasma.

• The linear stage of the instabilities in a PIP is characterized by a combination of the properties of the equivalent instabilities in the MHD case (for the charged species) and the HD case (for the neutral species). In this regard, the presence of critical thresholds, owing to the magnetic field, for the triggering of the instabilities only appear in the charged components. At small scales, the neutral components remain largely unaffected and only feel the magnetic field indirectly through collisions with the charges. Thus, a PIP is generally more prone to be unstable than a fully ionized plasma.

• The instabilities growth rate in a PIP are typically reduced compared with the growth rates obtained in pure MHD or HD cases. The reason is that collisions between charges and neutrals, besides coupling both components, also act as a dissipation mechanism.

• During the nonlinear development of the instabilities, partial ionization effects that originally show up at small scales, can have a measurable influence on the large-scale evolution. Therefore, partial ionization can indeed affect the large scales when the instabilities enter deeply into the nonlinear regime.

• Dissipation mechanisms already present in fully ionized plasmas as, e.g., Ohmic diffusion and viscosity, are typically enhanced by the collisions between neutrals and charges. As a consequence of this, the plasma heating during the nonlinear evolution of the instabilities may be more important in the presence of partial ionization. Non-dissipative effects as, e.g., Hall’s effect, are also enhanced by collisions.

• The single-fluid model with a generalized Ohm’s law, although very useful and informative, misses part of the rich dynamics of the instabilities at small scales, which are more accurately described by the multi-fluid models. This is especially relevant during the nonlinear evolution of the instabilities.

Thanks to the extensive analytical and numerical research, the triggering and linear stage of the instabilities can be considered as well understood in most cases. Recently, nonlinear numerical simulations including partial ionization effects have also been undertaken in the research of some instabilities. However, due to the computational complexity and cost of the simulations, they are still mostly restricted to simplified 2D or 2.5D set-ups, while large-scale 3D simulations remain a challenge. Thus, the research in the following years should focus on 3D simulations with the goal of understanding the later evolution of the instabilities and their impact on the plasma dynamics and energetics. In this regard, in most cases the evolution of the instabilities leads to the generation of turbulence and enhanced energy dissipation. Understanding the processes of turbulence generation, exploring the form of the turbulence spectra, and determining the dissipation rates in a PIP are issues of great importance not only in astrophysics but in plasma physics in general.

Only a selected number of classic fluid instabilities is discussed here. In addition, the main emphasis of the review has been put on solar physics. However, we are aware that many other types of instabilities are also relevant in astrophysical plasmas and may be affected by partial ionization effects. Readers may find more information elsewhere. This paper aimed to be an introductory and general guide to this topic with the goal of helping interested readers to navigate through the huge literature available.

Author Contributions

The two authors, RS and JLB, have contributed equally to this work.

Funding

This publication is part of the R + D + i project PID2020-112791GB-I00, financed by MCIN/AEI/10.130 39/501 100 011 033.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We thank the reviewers for their constructive comments that helped to improve the paper. We also thank the original authors of the included figures for kindly giving permission for their reproduction.

References

Alexiades, V., Amiez, G., and Gremaud, P.-A. (1996). Super-time-stepping Acceleration of Explicit Schemes for Parabolic Problems. Commun. Numer. Meth. Engng. 12, 31–42. doi:10.1002/(sici)1099-0887(199601)12:1<31:aid-cnm950>3.0.co;2-5

CrossRef Full Text | Google Scholar

Ali, A., and Bhatia, P. K. (1992a). Gravitational Instability of Partially-Ionized Plasma in an Oblique Magnetic Field. Astrophys Space Sci. 195, 389–400. doi:10.1007/BF00646770

CrossRef Full Text | Google Scholar

Ali, A., and Bhatia, P. K. (1992b). Instability of a Gravitating Partially-Ionized Plasma. Astrophys Space Sci. 191, 89–100. doi:10.1007/BF00644198

CrossRef Full Text | Google Scholar

Athay, R. G. (1986). Radiation Loss Rates in Lyman-alpha for Solar Conditions. ApJ 308, 975. doi:10.1086/164565

CrossRef Full Text | Google Scholar

Bahcall, J. N., Pinsonneault, M. H., and Basu, S. (2001). Solar Models: Current Epoch and Time Dependences, Neutrinos, and Helioseismological Properties. ApJ 555, 990–1012. doi:10.1086/321493

CrossRef Full Text | Google Scholar

Bai, X.-N., and Stone, J. M. (2017). Hall Effect-Mediated Magnetic Flux Transport in Protoplanetary Disks. ApJ 836, 46. doi:10.3847/1538-4357/836/1/46

CrossRef Full Text | Google Scholar

Balbus, S. A. (2003). Enhanced Angular Momentum Transport in Accretion Disks. Annu. Rev. Astron. Astrophys. 41, 555–597. doi:10.1146/annurev.astro.41.081401.155207

CrossRef Full Text | Google Scholar

Balbus, S. A., and Hawley, J. F. (1991). A Powerful Local Shear Instability in Weakly Magnetized Disks. I - Linear Analysis. II - Nonlinear Evolution. ApJ 376, 214. doi:10.1086/170270

CrossRef Full Text | Google Scholar

Balbus, S. A., and Terquem, C. (2001). Linear Analysis of the Hall Effect in Protostellar Disks. ApJ 552, 235–247. doi:10.1086/320452

CrossRef Full Text | Google Scholar

Ballai, I., Oliver, R., and Alexandrou, M. (2015). Dissipative Instability in Partially Ionised Prominence Plasmas. A&A 577, A82. doi:10.1051/0004-6361/201423973

CrossRef Full Text | Google Scholar

Ballester, J. L., Alexeev, I., Collados, M., Downes, T., Pfaff, R. F., Gilbert, H., et al. (2018). Partially Ionized Plasmas in Astrophysics. Space Sci. Rev. 214, 58. doi:10.1007/s11214-018-0485-6

CrossRef Full Text | Google Scholar

Balsara, D. S. (1996). Wave Propagation in Molecular Clouds. ApJ 465, 775. doi:10.1086/177462

CrossRef Full Text | Google Scholar

Barranco, J. A. (2009). Three-Dimensional Simulations of Kelvin-Helmholtz Instability in Settled Dust Layers in Protoplanetary Disks. ApJ 691, 907–921. doi:10.1088/0004-637X/691/2/907

CrossRef Full Text | Google Scholar

Baruah, M. B., Chatterjee, S., and Bora, M. P. (2010). Radiation Condensation Instability in a Plasma with Ionization and Recombination. Astrophys Space Sci. 325, 217–225. doi:10.1007/s10509-009-0179-3

CrossRef Full Text | Google Scholar

Bateman, G. (1978). MHD Instabilities (Cambridge).

Google Scholar

Baty, H., Keppens, R., and Comte, P. (2003). The Two-Dimensional Magnetohydrodynamic Kelvin-Helmholtz Instability: Compressibility and Large-Scale Coalescence Effects. Phys. Plasmas 10, 4661–4674. doi:10.1063/1.1624076

CrossRef Full Text | Google Scholar

Baty, H., and Keppens, R. (2006). Kelvin-Helmholtz Disruptions in Extended Magnetized Jet Flows. A&A 447, 9–22. doi:10.1051/0004-6361:20053969

CrossRef Full Text | Google Scholar

Begelman, M. C. (2003). Evidence for Black Holes. Science 300, 1903–1904. 1898. doi:10.1126/science.1085334

PubMed Abstract | CrossRef Full Text | Google Scholar

Benard, H. (1900). Cellular Vortices in a Liquid Layer. Part 1. Gen. description phenomena 11.

Google Scholar

Berger, T. E., Shine, R. A., Slater, G. L., Tarbell, T. D., Title, A. M., Okamoto, T. J., et al. (2008). Hinode SOT Observations of Solar Quiescent Prominence Dynamics. ApJ 676, L89–L92. doi:10.1086/587171

CrossRef Full Text | Google Scholar

Berger, T. E., Slater, G., Hurlburt, N., Shine, R., Tarbell, T., Title, A., et al. (2010). Quiescent Prominence Dynamics Observed with the Hinode Solar Optical Telescope. I. Turbulent Upflow Plumes. ApJ 716, 1288–1307. doi:10.1088/0004-637X/716/2/1288

CrossRef Full Text | Google Scholar

Berger, T., Hillier, A., and Liu, W. (2017). Quiescent Prominence Dynamics Observed with theHinodeSolar Optical Telescope. II. Prominence Bubble Boundary Layer Characteristics and the Onset of a Coupled Kelvin-Helmholtz Rayleigh-Taylor Instability. ApJ 850, 60. doi:10.3847/1538-4357/aa95b6

CrossRef Full Text | Google Scholar

Berger, T., Testa, P., Hillier, A., Boerner, P., Low, B. C., Shibata, K., et al. (2011). Magneto-thermal Convection in Solar Prominences. Nature 472, 197–200. doi:10.1038/nature09925

PubMed Abstract | CrossRef Full Text | Google Scholar

Berlok, T., and Pfrommer, C. (2019). On the Kelvin-Helmholtz Instability with Smooth Initial Conditions - Linear Theory and Simulations. Monthly Notices R. Astronomical Soc. 485, 908–923. doi:10.1093/mnras/stz379

CrossRef Full Text | Google Scholar

Berné, O., Marcelino, N., and Cernicharo, J. (2010). Waves on the Surface of the Orion Molecular Cloud. Nature 466, 947–949. doi:10.1038/nature09289

PubMed Abstract | CrossRef Full Text | Google Scholar

Bernstein, I. B., and Book, D. L. (1983). Effect of Compressibility on the Rayleigh-Taylor Instability. Phys. Fluids 26, 453–458. doi:10.1063/1.864158

CrossRef Full Text | Google Scholar

Béthune, W., Lesur, G., and Ferreira, J. (2016). Self-organisation in Protoplanetary Discs. A&A 589, A87. doi:10.1051/0004-6361/201527874

CrossRef Full Text | Google Scholar

Bhatia, P. K. (1972). Frictional Effects with Neutrals and the Gravitational Instability of a Plasma. Beiträge aus der Plasmaphysik 24, 375. doi:10.1002/ctpp.19760160404

CrossRef Full Text | Google Scholar

Bhatia, P. K. (1969). Gravitational Instability of a Plasma with Finite. Larmor Radius 1, 372.

Google Scholar

Bhatia, P. K., and Hazarika, A. B. R. (1995). Gravitational Instability of Partially-Ionized Plasma in an Oblique Magnetic Field. Phys. Scr. 51, 775–779. doi:10.1088/0031-8949/51/6/012

CrossRef Full Text | Google Scholar

Birk, G. T., and Wiechen, H. (2002). Shear Flow Instabilities in Magnetized Partially Ionized Dense Dusty Plasmas. Phys. Plasmas 9, 964–970. doi:10.1063/1.1445424

CrossRef Full Text | Google Scholar

Blaes, O. M., and Balbus, S. A. (1994). Local Shear Instabilities in Weakly Ionized, Weakly Magnetized Disks. ApJ 421, 163. doi:10.1086/173634

CrossRef Full Text | Google Scholar

Borah, A. C., and Sen, A. K. (2007). Gravitational Instability of Partially Ionized Molecular Clouds. J. Plasma Phys. 73, 831–838. doi:10.1017/S0022377806006295

CrossRef Full Text | Google Scholar

Braginskii, S. I. (1965). Transport Processes in a Plasma. Rev. Plasma Phys. 1, 205.

Google Scholar

Breitschwerdt, D., Freyberg, M. J., and Egger, R. (2000). Origin of H I Clouds in the Local Bubble. I. A Hydromagnetic Rayleigh-Taylor Instability Caused by the Interaction between the Loop I and the Local Bubble, 361, 303–320.

Google Scholar

Browning, P. K., and Priest, E. R. (1984). Kelvin-Helmholtz Instability of a Phased-Mixed Alfven Wave, 131, 283–290.

Google Scholar

Buneman, O. (1963). Excitation of Field Aligned Sound Waves by Electron Streams. Phys. Rev. Lett. 10, 285–287. doi:10.1103/PhysRevLett.10.285

CrossRef Full Text | Google Scholar

Carbonell, M., Oliver, R., and Ballester, J. L. (2004). Time Damping of Linear Non-adiabatic Magnetohydrodynamic Waves in an Unbounded Plasma with Solar Coronal Properties. A&A 415, 739–750. doi:10.1051/0004-6361:20034630

CrossRef Full Text | Google Scholar

Cargill, P. J., and Hood, A. W. (1989). Magnetic and Boundary Effects on thermal Instabilities in Solar Magnetic fields: Localized Modes in a Slab Geometry. Sol. Phys. 124, 101–127. doi:10.1007/BF00146522

CrossRef Full Text | Google Scholar

Chae, J. (2010). Dynamics of Vertical Threads and Descending Knots in a Hedgerow Prominence. ApJ 714, 618–629. doi:10.1088/0004-637X/714/1/618

CrossRef Full Text | Google Scholar

Chandrasekhar, S. (1961a). A Theorem on Rotating Polytropes. ApJ 134, 662–664. doi:10.1086/147192

CrossRef Full Text | Google Scholar

Chandrasekhar, S. (1961b). Hydrodynamic and Hydromagnetic Stability.

Google Scholar

Chandrasekhar, S. (1960). The Stability of Non-dissipative Couette Flow in Hydromagnetics. Proc. Natl. Acad. Sci. 46, 253–257. doi:10.1073/pnas.46.2.253

PubMed Abstract | CrossRef Full Text | Google Scholar

Chhajlani, R. K., and Vaghela, D. S. (1989). Rayleigh-Taylor Instability of Ionized Viscous Fluids with FLR-Corrections and Surface-Tension. Astrophys Space Sci. 155, 257–269. doi:10.1007/BF00643863

CrossRef Full Text | Google Scholar

Chhajlani, R. K., and Vyas, M. K. (1990). Kelvin-Helmholtz Instability of Composite Plasma in an Oblique Magnetic Field with Resistivity. Astrophys Space Sci. 173, 109–125. doi:10.1007/BF00642567

CrossRef Full Text | Google Scholar

Choi, E., and Stone, J. M. (2012). The Effect of Anisotropic Conduction on the Thermal Instability in the Interstellar Medium. ApJ 747, 86. doi:10.1088/0004-637X/747/2/86

CrossRef Full Text | Google Scholar

Claes, N., and Keppens, R. (2019). Thermal Stability of Magnetohydrodynamic Modes in Homogeneous Plasmas. A&A 624, A96. doi:10.1051/0004-6361/201834699

CrossRef Full Text | Google Scholar

Claes, N., Keppens, R., and Xia, C. (2020). Thermal Instabilities: Fragmentation and Field Misalignment of Filament fine Structure. A&A 636, A112. doi:10.1051/0004-6361/202037616

CrossRef Full Text | Google Scholar

Cowling, T. G. (1956). The Dissipation of Magnetic Energy in an Ionized Gas. Monthly Notices R. Astronomical Soc. 116, 114–124. doi:10.1093/mnras/116.1.114

CrossRef Full Text | Google Scholar

Dahlburg, R. B., DeVore, C. R., Picone, J. M., Mariska, J. T., and Karpen, J. T. (1987). Nonlinear Evolution of Radiation-Driven Thermally Unstable Fluids. ApJ 315, 385. doi:10.1086/165142

CrossRef Full Text | Google Scholar

Dahlburg, R. B., and Mariska, J. T. (1988). Influence of Heating Rate on the Condensational Instability. Sol. Phys. 117, 51–56. doi:10.1007/BF00148571

CrossRef Full Text | Google Scholar

Díaz, A. J., Khomenko, E., and Collados, M. (2014). Rayleigh-Taylor Instability in Partially Ionized Compressible Plasmas: One Fluid Approach. A&A 564, A97. doi:10.1051/0004-6361/201322147

CrossRef Full Text | Google Scholar

Díaz, A. J., Soler, R., and Ballester, J. L. (2012). Rayleigh-Taylor Instability in Partially Ionized Compressible Plasmas. ApJ 754, 41. doi:10.1088/0004-637x/754/1/41

CrossRef Full Text | Google Scholar

Dimant, Y. S., and Milikh, G. M. (2003). Model of Anomalous Electron Heating in theEregion: 1. Basic Theory. J. Geophys. Res. 108, 1350. doi:10.1029/2002JA009524

CrossRef Full Text | Google Scholar

Dimant, Y. S., and Sudan, R. N. (1995). Kinetic Theory of the Farley-Buneman Instability in theEregion of the Ionosphere. J. Geophys. Res. 100, 14605–14624. doi:10.1029/95JA00794

CrossRef Full Text | Google Scholar

Draine, B. T. (1980). Interstellar Shock Waves with Magnetic Precursors. ApJ 241, 1021–1038. doi:10.1086/158416

CrossRef Full Text | Google Scholar

Draine, B. T. (1986). Multicomponent, Reacting MHD Flows. Monthly Notices R. Astronomical Soc. 220, 133–148. doi:10.1093/mnras/220.1.133

CrossRef Full Text | Google Scholar

Draine, B. T., Roberge, W. G., and Dalgarno, A. (1983). Magnetohydrodynamic Shock Waves in Molecular Clouds. ApJ 264, 485–507. doi:10.1086/160617

CrossRef Full Text | Google Scholar

Drazin, P. G., and Reid, W. H. (1981). Hydrodynamic Stability. NASA STI/Recon Tech. Rep. A 82, 17950.

Google Scholar

Eggleton, P. P., Dearborn, D. S. P., and Lattanzio, J. C. (2006). Deep Mixing of 3 He: Reconciling Big Bang and Stellar Nucleosynthesis. Science 314, 1580–1583. doi:10.1126/science.1133065

PubMed Abstract | CrossRef Full Text | Google Scholar

Ershkovich, A. I., Prialnik, D., and Eviatar, A. (1986). Instability of a Comet Ionopause: Consequences of Collisions and Compressibility. J. Geophys. Res. 91, 8782–8788. doi:10.1029/JA091iA08p08782

CrossRef Full Text | Google Scholar

Falle, S. A. E. G. (2003). A Numerical Scheme for Multifluid Magnetohydrodynamics. Monthly Notices RAS 344, 1210–1218. doi:10.1046/j.1365-8711.2003.06908.x

CrossRef Full Text | Google Scholar

Falle, S. A. E. G., Wareing, C. J., and Pittard, J. M. (2020). Thermal Instability Revisited. Therm. instability revisited 492, 4484–4499. doi:10.1093/mnras/staa131

CrossRef Full Text | Google Scholar

Farley, D. T. (1963). A Plasma Instability Resulting in Field-Aligned Irregularities in the Ionosphere. J. Geophys. Res. 68, 6083–6097. doi:10.1029/JZ068i022p06083

CrossRef Full Text | Google Scholar

Farrugia, C. J., Sandholt, P. E., and Burlaga, L. F. (199419412). Auroral Activity Associated with Kelvin-Helmholtz Instability at the Inner Edge of the Low-Latitude Boundary Layer. J. Geophys. Res. 99, 19403. doi:10.1029/94JA00926

CrossRef Full Text | Google Scholar

Fejer, B. G., Providakes, J., and Farley, D. T. (1984). Theory of Plasma Waves in the auroralEregion. J. Geophys. Res. 89, 7487–7494. doi:10.1029/JA089iA09p07487

CrossRef Full Text | Google Scholar

Fejer, J. A. (1964). Hydromagnetic Stability at a Fluid Velocity Discontinuity between Compressible Fluids. Phys. Fluids 7, 499–503. doi:10.1063/1.1711229

CrossRef Full Text | Google Scholar

Feng, L., Inhester, B., and Gan, W. Q. (2013). Kelvin-helmholtz Instability of a Coronal Streamer. ApJ 774, 141. doi:10.1088/0004-637X/774/2/141

CrossRef Full Text | Google Scholar

Ferrari, A., and Trussoni, E. (1983). Magnetohydrodynamic Kelvin-Helmholtz Instabilities in Astrophysics - IV. Single Shear Layer in MHD Flows. Monthly Notices R. Astronomical Soc. 205, 515–524. doi:10.1093/mnras/205.2.515

CrossRef Full Text | Google Scholar

Field, G. B. (1965). Thermal Instability. ApJ 142, 531. doi:10.1086/148317

CrossRef Full Text | Google Scholar

Fletcher, A. C., Dimant, Y. S., Oppenheim, M. M., and Fontenla, J. M. (2018). Effects of Ion Magnetization on the Farley-Buneman Instability in the Solar Chromosphere. ApJ 857, 129. doi:10.3847/1538-4357/aab71a

CrossRef Full Text | Google Scholar

Fontenla, J. M. (2005). Chromospheric Plasma and the Farley-Buneman Instability in Solar Magnetic Regions. A&A 442, 1099–1103. doi:10.1051/0004-6361:20053669

CrossRef Full Text | Google Scholar

Fontenla, J. M., Peterson, W. K., and Harder, J. (2008). Chromospheric Heating by the Farley-Buneman Instability. A&A 480, 839–846. doi:10.1051/0004-6361:20078517

CrossRef Full Text | Google Scholar

Foullon, C., Verwichte, E., Nakariakov, V. M., Nykyri, K., and Farrugia, C. J. (2011). Magnetic Kelvin-Helmholtz Instability at the Sun. ApJ 729, L8. doi:10.1088/2041-8205/729/1/L8

CrossRef Full Text | Google Scholar

Fragile, P. C., Etheridge, S. M., Anninos, P., Mishra, B., and Kluźniak, W. (2018). Relativistic, Viscous, Radiation Hydrodynamic Simulations of Geometrically Thin Disks. I. Thermal and Other Instabilities. ApJ 857, 1. doi:10.3847/1538-4357/aab788

CrossRef Full Text | Google Scholar

Frank, A., Jones, T. W., Ryu, D., and Gaalaas, J. B. (1996). The Magnetohydrodynamic Kelvin-Helmholtz Instability: A Two-Dimensional Numerical Study. ApJ 460, 777. doi:10.1086/177009

CrossRef Full Text | Google Scholar

Fukue, T., and Kamaya, H. (2007). Small Structures via Thermal Instability of Partially Ionized Plasma. I. Condensation Mode. ApJ 669, 363–377. doi:10.1086/521268

CrossRef Full Text | Google Scholar

Gerwin, R. A. (1968). Stability of the Interface between Two Fluids in Relative Motion. Rev. Mod. Phys. 40, 652–658. doi:10.1103/RevModPhys.40.652

CrossRef Full Text | Google Scholar

Gilbert, H. R., Hansteen, V. H., and Holzer, T. E. (2002). Neutral Atom Diffusion in a Partially Ionized Prominence Plasma. ApJ 577, 464–474. doi:10.1086/342165

CrossRef Full Text | Google Scholar

Goedbloed, J., Keppens, R., and Poedts, S. (2019). Magnetohydrodynamics: Of Laboratory and Astrophysical Plasmas. Cambridge University Press.

Google Scholar

Gogoberidze, G., Voitenko, Y., Poedts, S., and De Keyser, J. (2014). Electrostatic Plasma Instabilities Driven by Neutral Gas Flows in the Solar Chromosphere. Monthly Notices R. Astronomical Soc. 438, 3568–3576. doi:10.1093/mnras/stt2469

CrossRef Full Text | Google Scholar

Gogoberidze, G., Voitenko, Y., Poedts, S., and Goossens, M. (2009). Farley-buneman Instability in the Solar Chromosphere. ApJ 706, L12–L16. doi:10.1088/0004-637X/706/1/L12

CrossRef Full Text | Google Scholar

Gómez, G. C., and Ostriker, E. C. (2005). The Effect of the Coriolis Force on Kelvin‐Helmholtz-Driven Mixing in Protoplanetary Disks. ApJ 630, 1093–1106. doi:10.1086/432086

CrossRef Full Text | Google Scholar

Gomez‐Pelaez, A. J., and Moreno‐Insertis, F. (2002). Thermal Instability in a Cooling and Expanding Medium Including Self‐Gravity and Conduction. ApJ 569, 766–779. doi:10.1086/339396

CrossRef Full Text | Google Scholar

Hachisu, I., Matsuda, T., Nomoto, K. i., and Shigeyama, T. (1992). Mixing in Ejecta of Supernovae. I - General Properties of Two-Dimensional Rayleigh-Taylor Instabilities and Mixing Width in Ejecta of Supernovae. ApJ 390, 230. doi:10.1086/171274

CrossRef Full Text | Google Scholar

Hans, H. K. (1968). Larmor Radius and Collisional Effects on the Combined taylor and Kelvin Instabilities in a Composite Medium. Nucl. Fusion 8, 89–92. doi:10.1088/0029-5515/8/2/002

CrossRef Full Text | Google Scholar

Hasegawa, H., Fujimoto, M., Takagi, K., Saito, Y., Mukai, T., and Rème, H. (2006). Single-spacecraft Detection of Rolled-Up Kelvin-Helmholtz Vortices at the Flank Magnetopause. J. Geophys. Res. 111, A09203. doi:10.1029/2006JA011728

CrossRef Full Text | Google Scholar

Helander, P., Krasheninnikov, S. I., and Catto, P. J. (1994). Fluid Equations for a Partially Ionized Plasma. Phys. Plasmas 1, 3174–3180. doi:10.1063/1.870470

CrossRef Full Text | Google Scholar

Hendrix, T., and Keppens, R. (2014). Effect of Dust on Kelvin-Helmholtz Instabilities. A&A 562, A114. doi:10.1051/0004-6361/201322322

CrossRef Full Text | Google Scholar

Hester, J. J., Stone, J. M., Scowen, P. A., Jun, B.-I., Gallagher, J. S. I., Norman, M. L., et al. (1996). WFPC2 Studies of the Crab Nebula. III. Magnetic Rayleigh-Taylor Instabilities and the Origin of the Filaments. ApJ 456, 225. doi:10.1086/176643

CrossRef Full Text | Google Scholar

Heyvaerts, J. (1974). The thermal Instability in a Magnetohydrodynamic Medium, 37, 65–73.

Google Scholar

Hildner, E. (1974). The Formation of Solar Quiescent Prominences by Condensation. Sol. Phys. 35, 123–136. doi:10.1007/BF00156962

CrossRef Full Text | Google Scholar

Hillier, A., Berger, T., Isobe, H., and Shibata, K. (2012a). Numerical Simulations of the Magnetic Rayleigh-taylor Instability in the Kippenhahn-Schlüter Prominence Model. I. Formation of Upflows. ApJ 746, 120. doi:10.1088/0004-637X/746/2/120

CrossRef Full Text | Google Scholar

Hillier, A. (2019). Ion-neutral Decoupling in the Nonlinear Kelvin-Helmholtz Instability: Case of Field-Aligned Flow. Phys. Plasmas 26, 082902. doi:10.1063/1.5103248

CrossRef Full Text | Google Scholar

Hillier, A., Isobe, H., Shibata, K., and Berger, T. (2011). Numerical Simulations of the Magnetic Rayleigh-taylor Instability in the Kippenhahn-Schlüter Prominence Model. ApJ 736, L1. doi:10.1088/2041-8205/736/1/L1

CrossRef Full Text | Google Scholar

Hillier, A., Isobe, H., Shibata, K., and Berger, T. (2012b). Numerical Simulations of the Magnetic Rayleigh-taylor Instability in the Kippenhahn-Schlüter Prominence Model. Ii. Reconnection-Triggered Downflows. ApJ 756, 110. doi:10.1088/0004-637X/756/2/110

CrossRef Full Text | Google Scholar

Hillier, A., and Polito, V. (2018). Observations of the Kelvin-Helmholtz Instability Driven by Dynamic Motions in a Solar Prominence. ApJ 864, L10. doi:10.3847/2041-8213/aad9a5

CrossRef Full Text | Google Scholar

Hillier, A., Shibata, K., and Isobe, H. (2010). Evolution of the Kippenhahn-Schlüter Prominence Model Magnetic Field under Cowling Resistivity. Publ. Astron. Soc. Jpn. 62, 1231–1237. doi:10.1093/pasj/62.5.1231

CrossRef Full Text | Google Scholar

Hillier, A. S. (2016). On the Nature of the Magnetic Rayleigh-Taylor Instability in Astrophysical Plasma: the Case of Uniform Magnetic Field Strength. Mon. Not. R. Astron. Soc. 462, 2256–2265. doi:10.1093/mnras/stw1805

CrossRef Full Text | Google Scholar

Hillier, A. (2018). The Magnetic Rayleigh-Taylor Instability in Solar Prominences. Rev. Mod. Plasma Phys. 2, 1. doi:10.1007/s41614-017-0013-2

CrossRef Full Text | Google Scholar

Hoyle, F. (1960). The Origin of the Solar Nebula 1, 28.

Hunana, P., Tenerani, A., Zank, G. P., Goldstein, M. L., Webb, G. M., Khomenko, E., et al. (2019a). An Introductory Guide to Fluid Models with Anisotropic Temperatures. Part 2. Kinetic Theory, Padé Approximants and Landau Fluid Closures. J. Plasma Phys. 85, 205850603. doi:10.1017/S0022377819000850

CrossRef Full Text | Google Scholar

Hunana, P., Tenerani, A., Zank, G. P., Khomenko, E., Goldstein, M. L., Webb, G. M., et al. (2019b). An Introductory Guide to Fluid Models with Anisotropic Temperatures. Part 1. CGL Description and Collisionless Fluid Hierarchy. J. Plasma Phys. 85, 205850602. doi:10.1017/S0022377819000801

CrossRef Full Text | Google Scholar

Inutsuka, S.-I., Koyama, H., and Inoue, T. (2005). “The Role of Thermal Instability in Interstellar Medium,” in Magnetic Fields in the Universe: From Laboratory and Stars to Primordial Structures. Editors E. M. de Gouveia dal Pino, G. Lugones, and A. Lazarian (of American Institute of Physics Conference Series), 784, 318–328. doi:10.1063/1.2077195

CrossRef Full Text | Google Scholar

Ireland, R. C., Hood, A. W., and van der Linden, R. A. M. (1995). Magnetothermal Instabilities in Coronal Arcades. Sol. Phys. 160, 303–330. doi:10.1007/BF00732810

CrossRef Full Text | Google Scholar

Ireland, R. C., van der Linden, R. A. M., and Hood, A. W. (1998). The Effect of Resistivity on the Formation of Prominence Fine-Scale Structure. 179, 115–132. doi:10.1023/A:1005059010611

CrossRef Full Text | Google Scholar

Isobe, H., Miyagoshi, T., Shibata, K., and Yokoyama, T. (2005). Filamentary Structure on the Sun from the Magnetic Rayleigh-Taylor Instability. Nature 434, 478–481. doi:10.1038/nature03399

PubMed Abstract | CrossRef Full Text | Google Scholar

Jacobs, G., and Shukla, P. K. (2005). Stability of Molecular Clouds in Partially Ionized Self-Gravitating Space Plasmas. J. Plasma Phys. 71, 487–493. doi:10.1017/S0022377804003137

CrossRef Full Text | Google Scholar

Jeans, J. H. (1902). I. The Stability of a Spherical Nebula. Phil. Trans. R. Soc. Lond. A. 199, 1–53. doi:10.1098/rsta.1902.0012

CrossRef Full Text | Google Scholar

Ji, S., Oh, S. P., and McCourt, M. (2018). The Impact of Magnetic fields on thermal Instability. Monthly Notices R. Astronomical Soc. 476, 852–867. doi:10.1093/mnras/sty293

CrossRef Full Text | Google Scholar

Johansen, A., Henning, T., and Klahr, H. (2006). Dust Sedimentation and Self‐sustained Kelvin‐Helmholtz Turbulence in Protoplanetary Disk Midplanes. ApJ 643, 1219–1232. doi:10.1086/502968

CrossRef Full Text | Google Scholar

John, P. I., and Saxena, Y. C. (1975). Observation of the Farley-Buneman Instability in Laboratory Plasma. Geophys. Res. Lett. 2, 251–254. doi:10.1029/GL002i006p00251

CrossRef Full Text | Google Scholar

Johnson, J. R., Wing, S., and Delamere, P. A. (2014). Kelvin Helmholtz Instability in Planetary Magnetospheres. Space Sci. Rev. 184, 1–31. doi:10.1007/s11214-014-0085-z

CrossRef Full Text | Google Scholar

Jones, A. C., and Downes, T. P. (2012). The Kelvin-Helmholtz Instability in Weakly Ionized Plasmas - II. Multifluid Effects in Molecular Clouds. Multifluid effects Mol. clouds 420, 817–828. doi:10.1111/j.1365-2966.2011.20095.x

CrossRef Full Text | Google Scholar

Jones, A. C., and Downes, T. P. (2011). The Kelvin-Helmholtz Instability in Weakly Ionized Plasmas: Ambipolar-Dominated and Hall-Dominated Flows. Monthly Notices R. Astronomical Soc. 418, 390–400. doi:10.1111/j.1365-2966.2011.19491.x

CrossRef Full Text | Google Scholar

Julien, K., and Knobloch, E. (2010). Magnetorotational Instability: Recent Developments. Phil. Trans. R. Soc. A. 368, 1607–1633. doi:10.1098/rsta.2009.0251

PubMed Abstract | CrossRef Full Text | Google Scholar

Jun, B.-I., Jones, T. W., and Norman, M. L. (1996). Interaction of Rayleigh-Taylor Fingers and Circumstellar Cloudlets in Young Supernova Remnants. Supernova Remnants 468, L59–L63. doi:10.1086/310224

CrossRef Full Text | Google Scholar

Jun, B.-I., Norman, M. L., and Stone, J. M. (1995). A Numerical Study of Rayleigh-Taylor Instability in Magnetic Fluids. ApJ 453, 332. doi:10.1086/176393

CrossRef Full Text | Google Scholar

Kagan, D., and Wheeler, J. C. (2014). The Role of the Magnetorotational Instability in the Sun. ApJ 787, 21. doi:10.1088/0004-637X/787/1/21

CrossRef Full Text | Google Scholar

Kalra, G. L., and Talwar, S. P. (1964). Magnetogravitational Instability of Unbounded Plasma with Hall Effect. Ann. d’Astrophysique 27, 102.

Google Scholar

Kaothekar, S., and Chhajlani, R. K. (20122012). Effect of Radiative Heat-Loss Function and Finite Larmor Radius Corrections on Jeans Instability of Viscous Thermally Conducting Self-Gravitating Astrophysical Plasma. ISRN Astron. Astrophysics 2012, 1–14. doi:10.5402/2012/420938

CrossRef Full Text | Google Scholar

Kaothekar, S. (2020). Jeans Instability of Rotating Plasma with Radiative Heat-Loss Function and FLR Corrections Flowing through Porous Medium. Astrophys Space Sci. 365, 80. doi:10.1007/s10509-020-03792-8

CrossRef Full Text | Google Scholar

Kaothekar, S., Soni, G. D., Prajapati, R. P., and Chhajlani, R. K. (2016). Jeans Instability of Partially-Ionized Self-Gravitating Viscous Plasma with Hall Effect FLR Corrections and Porosity. Astrophys Space Sci. 361, 204. doi:10.1007/s10509-016-2796-y

CrossRef Full Text | Google Scholar

Karpen, J. T., Antiochos, S. K., Picone, J. M., and Dahlburg, R. B. (1989a). Nonlinear Thermal Instability in Magnetized Solar Plasmas. ApJ 338, 493. doi:10.1086/167213

CrossRef Full Text | Google Scholar

Karpen, J. T., Antiochos, S. K., Picone, J. M., and Dahlburg, R. B. (1989b). Thermal Instability in Magnetized Solar Plasmas. Wash. DC Am. Geophys. Union Geophys. Monogr. Ser. 54, 99–103. doi:10.1029/GM054p0099

CrossRef Full Text | Google Scholar

Karpen, J. T., Picone, M., and Dahlburg, R. B. (1988). Nonlinear Thermal Instability in the Solar Transition Region. ApJ 324, 590. doi:10.1086/165920

CrossRef Full Text | Google Scholar

Kelley, M. (2009). “The Earth’s Ionosphere: Plasma Physics and Electrodynamics,” in International Geophysics Series (Academic Press).

Google Scholar

Keppens, R., and Tóth, G. (1999). Nonlinear Dynamics of Kelvin-Helmholtz Unstable Magnetized Jets: Three-Dimensional Effects. Phys. Plasmas 6, 1461–1469. doi:10.1063/1.873398

CrossRef Full Text | Google Scholar

Keppens, R., Tóth, G., Westermann, R. H. J., and Goedbloed, J. P. (1999). Growth and Saturation of the Kelvin-Helmholtz Instability with Parallel and Antiparallel Magnetic fields. J. Plasma Phys. 61, 1–19. doi:10.1017/S0022377898007223

CrossRef Full Text | Google Scholar

Keppens, R., Xia, C., and Porth, O. (2015). Solar Prominences: “Double, Double… Boil and Bubble”. ApJ 806, L13. doi:10.1088/2041-8205/806/1/L13

CrossRef Full Text | Google Scholar

Keskinen, M. J. (1981). Nonlinear Stabilization of the Farley-Buneman Instability by StrongE→×B→Turbulence in a Plasma. Phys. Rev. Lett. 47, 344–348. doi:10.1103/PhysRevLett.47.344

CrossRef Full Text | Google Scholar

Khomenko, E., Collados, M., and Díaz, A. J. (2016). Observational Detection of Drift Velocity between Ionized and Neutral Species in Solar Prominences. ApJ 823, 132. doi:10.3847/0004-637X/823/2/132

CrossRef Full Text | Google Scholar

Khomenko, E., Collados, M., Díaz, A., and Vitas, N. (2014a). Fluid Description of Multi-Component Solar Partially Ionized Plasma. Phys. Plasmas 21, 092901. doi:10.1063/1.4894106

CrossRef Full Text | Google Scholar

Khomenko, E., and Collados, M. (2012). Heating of the Magnetized Solar Chromosphere by Partial Ionization Effects. ApJ 747, 87. doi:10.1088/0004-637X/747/2/87

CrossRef Full Text | Google Scholar

Khomenko, E., Díaz, A., de Vicente, A., Collados, M., and Luna, M. (2014b). Rayleigh-Taylor Instability in Prominences from Numerical Simulations Including Partial Ionization Effects. A&A 565, A45. doi:10.1051/0004-6361/201322918

CrossRef Full Text | Google Scholar

Kieokaew, R., Lavraud, B., Yang, Y., Matthaeus, W. H., Ruffolo, D., Stawarz, J. E., et al. (2021). Solar Orbiter Observations of the Kelvin-Helmholtz Instability in the Solar Wind. arXiv e-printsarXiv:2103.15489.

Google Scholar

Kippenhahn, R., and Schlüter, A. (1957). Eine Theorie der solaren Filamente. Mit 7 Textabbildungen 43, 36.

Google Scholar

Klimchuk, J. A., and Cargill, P. J. (2001). Spectroscopic Diagnostics of Nanoflare‐heated Loops. ApJ 553, 440–448. doi:10.1086/320666

CrossRef Full Text | Google Scholar

Kotake, K., Sawai, H., Yamada, S., and Sato, K. (2004). Magnetorotational Effects on Anisotropic Neutrino Emission and Convection in Core‐Collapse Supernovae. ApJ 608, 391–404. doi:10.1086/392530

CrossRef Full Text | Google Scholar

Kulkarni, A. K., and Romanova, M. M. (2008). Accretion to Magnetized Stars through the Rayleigh-Taylor Instability: Global 3D Simulations. Monthly Notices RAS 386, 673–687. doi:10.1111/j.1365-2966.2008.13094.x

CrossRef Full Text | Google Scholar

Kulsrud, R. M., Cen, R., Ostriker, J. P., and Ryu, D. (1997). The Protogalactic Origin for Cosmic Magnetic Fields. ApJ 480, 481–491. doi:10.1086/303987

CrossRef Full Text | Google Scholar

Kulsrud, R., and Pearce, W. P. (1969). The Effect of Wave-Particle Interactions on the Propagation of Cosmic Rays. ApJ 156, 445. doi:10.1086/149981

CrossRef Full Text | Google Scholar

Kumar, N., and Srivastava, K. M. (1990). Gravitational Instability of Partially-Ionized Plasma Carrying a Uniform Magnetic Field with Hall Effect. Astrophys Space Sci. 174, 211–216. doi:10.1007/BF00642507

CrossRef Full Text | Google Scholar

Kumar, V., Kumar, N., Srivastava, K. M., and Mittal, R. C. (1993). Gravitational Instability of a Rotating Partially-Ionized Plasma Carrying a Uniform Magnetic Field with Hall Effect. Astrophys Space Sci. 199, 323–331. doi:10.1007/BF00613206

CrossRef Full Text | Google Scholar

Kunz, M. W. (2008). On the Linear Stability of Weakly Ionized, Magnetized Planar Shear Flows. Monthly Notices RAS 385, 1494–1510. doi:10.1111/j.1365-2966.2008.12928.x

CrossRef Full Text | Google Scholar

Labrosse, N., Heinzel, P., Vial, J.-C., Kucera, T., Parenti, S., Gunár, S., et al. (2010). Physics of Solar Prominences: I-Spectral Diagnostics and Non-LTE Modelling. Space Sci. Rev. 151, 243–332. doi:10.1007/s11214-010-9630-6

CrossRef Full Text | Google Scholar

Langer, W. D. (1978). The Stability of Interstellar Clouds Containing Magnetic fields. ApJ 225, 95–106. doi:10.1086/156471

CrossRef Full Text | Google Scholar

Leake, J. E., DeVore, C. R., Thayer, J. P., Burns, A. G., Crowley, G., Gilbert, H. R., et al. (2014). Ionized Plasma and Neutral Gas Coupling in the Sun's Chromosphere and Earth's Ionosphere/Thermosphere. Space Sci. Rev. 184, 107–172. doi:10.1007/s11214-014-0103-1

CrossRef Full Text | Google Scholar

Leake, J. E., Lukin, V. S., Linton, M. G., and Meier, E. T. (2012). Multi-fluid Simulations of Chromospheric Magnetic Reconnection in a Weakly Ionized Reacting Plasma. ApJ 760, 109. doi:10.1088/0004-637X/760/2/109

CrossRef Full Text | Google Scholar

Lehnert, B. (1959). Plasma Physics on Cosmical and Laboratory Scale. Nuovo Cim 13, 59–110. doi:10.1007/BF02732622

CrossRef Full Text | Google Scholar

Li, D., Shen, Y., Ning, Z., Zhang, Q., and Zhou, T. (2018a). Two Kinds of Dynamic Behavior in a Quiescent Prominence Observed by the NVST. ApJ 863, 192. doi:10.3847/1538-4357/aad33f

CrossRef Full Text | Google Scholar

Li, P. S., McKee, C. F., and Klein, R. I. (2006). The Heavy‐Ion Approximation for Ambipolar Diffusion Calculations for Weakly Ionized Plasmas. ApJ 653, 1280–1291. doi:10.1086/508977

CrossRef Full Text | Google Scholar

Li, P. S., Myers, A., and McKee, C. F. (2012). AMBIPOLAR DIFFUSION HEATING IN TURBULENT SYSTEMS. ApJ 760, 33. doi:10.1088/0004-637x/760/1/33

CrossRef Full Text | Google Scholar

Li, X., Zhang, J., Yang, S., Hou, Y., and Erdélyi, R. (2018b). Observing Kelvin-Helmholtz Instability in Solar Blowout Jet. Sci. Rep. 8, 8136. doi:10.1038/s41598-018-26581-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Liberatore, S., and Bouquet, S. (2008). Analytical Modeling of Magnetic Rayleigh-Taylor Instabilities in Compressible Fluids. Phys. Fluids 20, 116101–11610119. doi:10.1063/1.3025832

CrossRef Full Text | Google Scholar

Liberatore, S., Jaouen, S., Tabakhoff, E., and Canaud, B. (2009). Compressible Magnetic Rayleigh-Taylor Instability in Stratified Plasmas: Comparison of Analytical and Numerical Results in the Linear Regime. Phys. Plasmas 16, 044502. doi:10.1063/1.3109664

CrossRef Full Text | Google Scholar

Liperovsky, V. A., Meister, C.-V., Liperovskaya, E. V., Popov, K. V., and Senchenkov, S. A. (2000). On the Generation of Modified Low-Frequency Farley-Buneman Waves in the Solar Atmosphere. Astron. Nachr. 321, 1292–1362. doi:10.1002/(SICI)1521-3994(200005)321:2<129:AID-ASNA129>3.0.COdoi:10.1002/(sici)1521-3994(200005)321:2<129:aid-asna129>3.0.co;2-2

CrossRef Full Text | Google Scholar

Litt, S. K., Smolyakov, A. I., Bains, A. S., Pokhotelov, O. A., Onishchenko, O. G., and Horton, W. (2016). Nonlinear Equation for Farley-Buneman Waves in Multispecies Plasma. Plasma Phys. Rep. 42, 400–406. doi:10.1134/S1063780X16050081

CrossRef Full Text | Google Scholar

Livescu, D. (2004). Compressibility Effects on the Rayleigh-Taylor Instability Growth between Immiscible Fluids. Phys. Fluids 16, 118–127. doi:10.1063/1.1630800

CrossRef Full Text | Google Scholar

Mackay, D. H., Karpen, J. T., Ballester, J. L., Schmieder, B., and Aulanier, G. (2010). Physics of Solar Prominences: II-Magnetic Structure and Dynamics. Space Sci. Rev. 151, 333–399. doi:10.1007/s11214-010-9628-0

CrossRef Full Text | Google Scholar

Madsen, C. A., Dimant, Y. S., Oppenheim, M. M., and Fontenla, J. M. (2014). The Multi-Species Farley-Buneman Instability in the Solar Chromosphere. ApJ 783, 128. doi:10.1088/0004-637X/783/2/128

CrossRef Full Text | Google Scholar

Malagoli, A., Bodo, G., and Rosner, R. (1996). On the Nonlinear Evolution of Magnetohydrodynamic Kelvin-Helmholtz Instabilities. ApJ 456, 708. doi:10.1086/176691

CrossRef Full Text | Google Scholar

Maneva, Y. G., Laguna, A. A., Lani, A., and Poedts, S. (2017). Multi-fluid Modeling of Magnetosonic Wave Propagation in the Solar Chromosphere: Effects of Impact Ionization and Radiative Recombination. ApJ 836, 197. doi:10.3847/1538-4357/aa5b83

CrossRef Full Text | Google Scholar

Martínez-Gómez, D., Popescu Braileanu, B., Khomenko, E., and Hunana, P. (2021). Simulations of the Biermann Battery Mechanism in Two-Fluid Partially Ionised Plasmas. A&A 650, A123. doi:10.1051/0004-6361/202039113

CrossRef Full Text | Google Scholar

Martínez-Gómez, D., Soler, R., and Terradas, J. (2017). Multi-fluid Approach to High-Frequency Waves in Plasmas. II. Small-Amplitude Regime in Partially Ionized Media. ApJ 837, 80. doi:10.3847/1538-4357/aa5eab

CrossRef Full Text | Google Scholar

Martínez-Gómez, D., Soler, R., and Terradas, J. (2016). Multi-fluid Approach to High-Frequency Waves in Plasmas. I. Small-Amplitude Regime in Fully Ionized Medium. ApJ 832, 101. doi:10.3847/0004-637X/832/2/101

CrossRef Full Text | Google Scholar

Martínez-Gómez, D., Soler, R., and Terradas, J. (2015). Onset of the Kelvin-Helmholtz Instability in Partially Ionized Magnetic Flux Tubes. A&A 578, A104. doi:10.1051/0004-6361/201525785

CrossRef Full Text | Google Scholar

Masada, Y. (2011). Impact of Magnetohydrodynamic Turbulence on thermal Wind Balance in the Sun. Monthly Notices R. Astronomical Soc. Lett. 411, L26–L30. doi:10.1111/j.1745-3933.2010.00987.x

CrossRef Full Text | Google Scholar

Masada, Y., Sano, T., and Shibata, K. (2007). The Effect of Neutrino Radiation on Magnetorotational Instability in Proto-Neutron Stars. ApJ 655, 447–457. doi:10.1086/509799

CrossRef Full Text | Google Scholar

Masson, A., and Nykyri, K. (2018). Kelvin-Helmholtz Instability: Lessons Learned and Ways Forward. Space Sci. Rev. 214, 71. doi:10.1007/s11214-018-0505-6

CrossRef Full Text | Google Scholar

Matsumoto, J., and Masada, Y. (2013). Two-dimensional Numerical Study for Rayleigh-taylor and Richtmyer-Meshkov Instabilities in Relativistic Jets. ApJ, 772, 772L1. doi:10.1088/2041-8205/772/1/L1

CrossRef Full Text | Google Scholar

Matsumoto, Y., and Hoshino, M. (2004). Onset of Turbulence Induced by a Kelvin-Helmholtz Vortex. Geophys. Res. Lett. 31, L02807. doi:10.1029/2003GL018195

CrossRef Full Text | Google Scholar

Matsumoto, Y., and Seki, K. (2010). Formation of a Broad Plasma Turbulent Layer by Forward and Inverse Energy Cascades of the Kelvin-Helmholtz Instability. J. Geophys. Res. 115, a–n. doi:10.1029/2009JA014637

CrossRef Full Text | Google Scholar

McKee, C. F., Li, P. S., and Klein, R. I. (2010). Sub-alfvénic Non-ideal Mhd Turbulence Simulations with Ambipolar Diffusion. Ii. Comparison with Observation, Clump Properties, and Scaling to Physical Units. ApJ 720, 1612–1634. doi:10.1088/0004-637x/720/2/1612

CrossRef Full Text | Google Scholar

Meerson, B. (1996). Nonlinear Dynamics of Radiative Condensations in Optically Thin Plasmas. Rev. Mod. Phys. 68, 215–257. doi:10.1103/RevModPhys.68.215

CrossRef Full Text | Google Scholar

Meier, E. T., and Shumlak, U. (2012). A General Nonlinear Fluid Model for Reacting Plasma-Neutral Mixtures. Phys. Plasmas 19, 072508. doi:10.1063/1.4736975

CrossRef Full Text | Google Scholar

Melrose, D. (1989). Instabilities in Space and Laboratory Plasmas. Cambridge University Press.

Google Scholar

Menou, K., Balbus, S. A., and Spruit, H. C. (2004). Local Axisymmetric Diffusive Stability of Weakly Magnetized, Differentially Rotating, Stratified Fluids. ApJ 607, 564–574. doi:10.1086/383463

CrossRef Full Text | Google Scholar

Meshkov, E. E. (1972). Instability of the Interface of Two Gases Accelerated by a Shock Wave. Fluid Dyn. 4, 101–104. doi:10.1007/BF01015969

CrossRef Full Text | Google Scholar

Mestel, L., and Spitzer, L. (1956). Star Formation in Magnetic Dust Clouds. Monthly Notices R. Astronomical Soc. 116, 503–514. doi:10.1093/mnras/116.5.503

CrossRef Full Text | Google Scholar

Meyer, C. D., Balsara, D. S., and Aslam, T. D. (2014). A Stabilized Runge-Kutta-Legendre Method for Explicit Super-time-stepping of Parabolic and Mixed Equations. J. Comput. Phys. 257, 594–626. doi:10.1016/j.jcp.2013.08.021

CrossRef Full Text | Google Scholar

Michikoshi, S., and Inutsuka, S. i. (2006). A Two‐Fluid Analysis of the Kelvin‐Helmholtz Instability in the Dusty Layer of a Protoplanetary Disk: A Possible Path toward Planetesimal Formation through Gravitational Instability. ApJ 641, 1131–1147. doi:10.1086/499799

CrossRef Full Text | Google Scholar

Mikhailovskii, A. B., Smolyakov, A. I., Lominadze, J. G., Churikov, A. P., Pustovitov, V. D., and Kharshiladze, O. V. (2009). Effects of Finite Heat Conductivity on Instabilities in a Rotating Plasma. Plasma Phys. Rep. 35, 658–667. doi:10.1134/S1063780X09080066

CrossRef Full Text | Google Scholar

Miura, A. (1984). Anomalous Transport by Magnetohydrodynamic Kelvin-Helmholtz Instabilities in the Solar Wind-Magnetosphere Interaction. J. Geophys. Res. 89, 801–818. doi:10.1029/JA089iA02p00801

CrossRef Full Text | Google Scholar

Miura, A., and Pritchett, P. L. (1982). Nonlocal Stability Analysis of the MHD Kelvin-Helmholtz Instability in a Compressible Plasma. J. Geophys. Res. 87, 7431–7444. doi:10.1029/JA087iA09p07431

CrossRef Full Text | Google Scholar

Moschou, S. P., Keppens, R., Xia, C., and Fang, X. (2015). Simulating Coronal Condensation Dynamics in 3D. Adv. Space Res. 56, 2738–2759. doi:10.1016/j.asr.2015.05.008

CrossRef Full Text | Google Scholar

Möstl, U. V., Temmer, M., and Veronig, A. M. (2013). The Kelvin-Helmholtz Instability at Coronal Mass Ejection Boundaries in the Solar Corona: Observations and 2.5D Mhd Simulations. ApJ 766, L12. doi:10.1088/2041-8205/766/1/L12

CrossRef Full Text | Google Scholar

Nagano, H. (1979). Effect of Finite Ion Larmor Radius on the Kelvin-Helmholtz Instability of the Magnetopause. Planet. Space Sci. 27, 881–884. doi:10.1016/0032-0633(79)90013-8

CrossRef Full Text | Google Scholar

Nakamura, T. K. M., Fujimoto, M., and Otto, A. (2008). Structure of an MHD-Scale Kelvin-Helmholtz Vortex: Two-Dimensional Two-Fluid Simulations Including Finite Electron Inertial Effects. J. Geophys. Res. 113, a–n. doi:10.1029/2007JA012803

CrossRef Full Text | Google Scholar

O'Keeffe, W., and Downes, T. P. (2014). Multifluid Simulations of the Magnetorotational Instability in Protostellar Discs. Monthly Notices R. Astronomical Soc. 441, 571–581. doi:10.1093/mnras/stu597

CrossRef Full Text | Google Scholar

O'Sullivan, S., and Downes, T. P. (2007). A Three-Dimensional Numerical Method for Modelling Weakly Ionized Plasmas. Monthly Notices R. Astronomical Soc. 376, 1648–1658. doi:10.1111/j.1365-2966.2007.11429.x

CrossRef Full Text | Google Scholar

O'Sullivan, S., and Downes, T. P. (2006). An Explicit Scheme for Multifluid Magnetohydrodynamics. Monthly Notices R. Astronomical Soc. 366, 1329–1336. doi:10.1111/j.1365-2966.2005.09898.x

CrossRef Full Text | Google Scholar

Ofman, L., and Thompson, B. J. (2011). Sdo/Aia Observation of Kelvin-Helmholtz Instability in the Solar Corona. ApJ 734, L11. doi:10.1088/2041-8205/734/1/L11

CrossRef Full Text | Google Scholar

Ogbonna, N., and Bhatia, P. K. (1984). The Rayleigh Taylor Instability of Superposed Partially-Ionized Plasmas. Astrophys Space Sci. 103, 233–240. doi:10.1007/BF00653739

CrossRef Full Text | Google Scholar

Oppenheim, M., Dimant, Y., Longley, W., and Fletcher, A. C. (2020). Newly Discovered Source of Turbulence and Heating in the Solar Chromosphere. ApJ 891, L9. doi:10.3847/2041-8213/ab75bc

CrossRef Full Text | Google Scholar

Oppenheim, M., Otani, N., and Ronchi, C. (1996). Saturation of the Farley-Buneman Instability via Nonlinear Electron E×B Drifts. J. Geophys. Res. 101, 17273–17286. doi:10.1029/96JA01403

CrossRef Full Text | Google Scholar

Oran, E. S., Mariska, J. T., and Boris, J. P. (1982). The Condensational Instability in the Solar Transition Region and corona. ApJ 254, 349–360. doi:10.1086/159739

CrossRef Full Text | Google Scholar

Otani, N. F., and Oppenheim, M. (1998). A Saturation Mechanism for the Farley-Buneman Instability. Geophys. Res. Lett. 25, 1833–1836. doi:10.1029/98GL50868

CrossRef Full Text | Google Scholar

Pandey, B. P. (2018). Can Hall Effect Trigger Kelvin-Helmholtz Instability in Sub-alfvénic Flows. Monthly Notices R. Astronomical Soc. 476, 344–353. doi:10.1093/mnras/sty201

CrossRef Full Text | Google Scholar

Pandey, B. P., and Vladimirov, S. V. (2019). Charged Grains and Kelvin-Helmholtz Instability in Molecular Clouds. Aj 157, 83. doi:10.3847/1538-3881/aafc32

CrossRef Full Text | Google Scholar

Pandey, B. P., Vranjes, J., and Vladimirov, S. V. (2012). The Stability of Weakly Ionized Collisional Dusty Plasma in the Presence of Flow. Phys. Plasmas 19, 093701. doi:10.1063/1.4750052

CrossRef Full Text | Google Scholar

Pandey, B. P., and Wardle, M. (2008). Hall Magnetohydrodynamics of Partially Ionized Plasmas. Monthly Notices RAS 385, 2269–2278. doi:10.1111/j.1365-2966.2008.12998.x

CrossRef Full Text | Google Scholar

Pandey, B. P., and Wardle, M. (2012). Magnetorotational Instability in Magnetic Diffusion Dominated Accretion Discs. Monthly Notices R. Astronomical Soc. 423, 222–235. doi:10.1111/j.1365-2966.2012.20799.x

CrossRef Full Text | Google Scholar

Parenti, S., Buchlin, E., Cargill, P. J., Galtier, S., and Vial, J. C. (2006). Modeling the Radiative Signatures of Turbulent Heating in Coronal Loops. ApJ 651, 1219–1228. doi:10.1086/507594

CrossRef Full Text | Google Scholar

Parenti, S., and Vial, J.-C. (2007). Prominence and Quiet-Sun Plasma Parameters Derived from FUV Spectral Emission. A&A 469, 1109–1115. doi:10.1051/0004-6361:20077196

CrossRef Full Text | Google Scholar

Parfrey, K. P., and Menou, K. (2007). The Origin of Solar Activity in the Tachocline. ApJ 667, L207–L210. doi:10.1086/522426

CrossRef Full Text | Google Scholar

Parker, E. N. (1953). Instability of Thermal Fields. ApJ 117, 431. doi:10.1086/145707

CrossRef Full Text | Google Scholar

Petrović, D., Vranjes, J., and Poedts, S. (2007). Analysis of the Effect of Neutral Flow on the Waves in the Solar Photosphere. A&A 461, 277–284. doi:10.1051/0004-6361:20065764

CrossRef Full Text | Google Scholar

Popescu Braileanu, B., Lukin, V. S., Khomenko, E., and de Vicente, Á. (2021a). Two-fluid Simulations of Rayleigh-Taylor Instability in a Magnetized Solar Prominence Thread. A&A 646, A93. doi:10.1051/0004-6361/202039053

CrossRef Full Text | Google Scholar

Popescu Braileanu, B., Lukin, V. S., Khomenko, E., and de Vicente, Á. (2021b). Two-fluid Simulations of Rayleigh-Taylor Instability in a Magnetized Solar Prominence Thread. A&A 650, A181. doi:10.1051/0004-6361/202140425

CrossRef Full Text | Google Scholar

Popescu Braileanu, B., Lukin, V. S., Khomenko, E., and de Vicente, Á. (2019). Two-fluid Simulations of Waves in the Solar Chromosphere. A&A 627, A25. doi:10.1051/0004-6361/201834154

CrossRef Full Text | Google Scholar

Porth, O., Komissarov, S. S., and Keppens, R. (2014). Rayleigh-Taylor Instability in Magnetohydrodynamic Simulations of the Crab Nebula. Monthly Notices R. Astronomical Soc. 443, 547–558. doi:10.1093/mnras/stu1082

CrossRef Full Text | Google Scholar

Prajapati, R. P., Pensia, R. K., Kaothekar, S., and Chhajlani, R. K. (2010). Self-gravitational Instability of Rotating Viscous Hall Plasma with Arbitrary Radiative Heat-Loss Functions and Electron Inertia. Astrophys Space Sci. 327, 139–154. doi:10.1007/s10509-010-0273-6

CrossRef Full Text | Google Scholar

Prialnik, D., Eviatar, A., and Ershkovich, A. I. (1986). The Effect of Plasma Compressibility on the Kelvin-Helmholtz Instability. J. Plasma Phys. 35, 209–218. doi:10.1017/S0022377800011284

CrossRef Full Text | Google Scholar

Rae, I. C. (1983). The MHD Kelvin-Helmholtz Instability in the Solar Photosphere, 126, 209–215.

Google Scholar

Rembiasz, T., Obergaulinger, M., Guilet, J., Cerdá-Durán, P., Aloy, M. A., and Müller, E. (2017). Magnetorotational Instability in Core-Collapse Supernovae. Acta Phys. Pol. B Proc. Suppl. 10, 361. doi:10.5506/aphyspolbsupp.10.361

CrossRef Full Text | Google Scholar

Ren, H., Cao, J., Wu, Z., and Chu, P. K. (2011). Magnetorotational Instability in a Two-Fluid Model. Plasma Phys. Control Fusion 53, 065021. doi:10.1088/0741-3335/53/6/065021

CrossRef Full Text | Google Scholar

Ren, H., Cao, J., and Wu, Z. (2012). Magnetorotational Instability in a Collisional Weakly Ionized Plasma. ApJ 754, 128. doi:10.1088/0004-637X/754/2/128

CrossRef Full Text | Google Scholar

Ribeyre, X., Tikhonchuk, V. T., and Bouquet, S. (2004). Compressible Rayleigh-Taylor Instabilities in Supernova Remnants. Phys. Fluids 16, 4661–4670. doi:10.1063/1.1810182

CrossRef Full Text | Google Scholar

Richtmyer, R. D. (1960). Taylor Instability in Shock Acceleration of Compressible Fluids. Comm. Pure Appl. Math. 13, 297–319. doi:10.1002/cpa.3160130207

CrossRef Full Text | Google Scholar

Rodgers-Lee, D., Ray, T. P., and Downes, T. P. (2016). Global Multifluid Simulations of the Magnetorotational Instability in Radially Stratified Protoplanetary Discs. Mon. Not. R. Astron. Soc. 463, 134–145. doi:10.1093/mnras/stw1980

CrossRef Full Text | Google Scholar

Rogister, A., and D'Angelo, N. (1970). Type II Irregularities in the Equatorial Electrojet. J. Geophys. Res. 75, 3879–3887. doi:10.1029/JA075i019p03879

CrossRef Full Text | Google Scholar

Rosenberg, M., and Chow, V. W. (1998). Farley-buneman Instability in a Dusty Plasma. Planet. Space Sci. 46, 103–108. doi:10.1016/S0032-0633(97)00104-9

CrossRef Full Text | Google Scholar

Ruderman, M. S., Ballai, I., Khomenko, E., and Collados, M. (2018). Rayleigh-Taylor Instabilities with Sheared Magnetic fields in Partially Ionised Plasmas. A&A 609, A23. doi:10.1051/0004-6361/201731534

CrossRef Full Text | Google Scholar

Ruderman, M. S. (2017). Compressibility Effect on the Rayleigh-Taylor Instability with Sheared Magnetic Fields. Sol. Phys. 292, 47. doi:10.1007/s11207-017-1073-8

CrossRef Full Text | Google Scholar

Ruderman, M. S., Terradas, J., and Ballester, J. L. (2014). Rayleigh-taylor Instabilities with Sheared Magnetic Fields. ApJ 785, 110. doi:10.1088/0004-637X/785/2/110

CrossRef Full Text | Google Scholar

Ryu, D., Jones, T. W., and Frank, A. (2000). The Magnetohydrodynamic Kelvin‐Helmholtz Instability: A Three‐dimensional Study of Nonlinear Evolution. ApJ 545, 475–493. doi:10.1086/317789

CrossRef Full Text | Google Scholar

Ryutova, M., Berger, T., Frank, Z., Tarbell, T., and Title, A. (2010). Observation of Plasma Instabilities in Quiescent Prominences. Sol. Phys. 267, 75–94. doi:10.1007/s11207-010-9638-9

CrossRef Full Text | Google Scholar

Ryutova, M. (2015). Physics of Magnetic Flux Tubes. Phys. Magn. Flux Tubes 417. doi:10.1007/978-3-662-45243-1

CrossRef Full Text | Google Scholar

Sano, T., and Miyama, S. M. (1999). Magnetorotational Instability in Protoplanetary Disks. I. On the Global Stability of Weakly Ionized Disks with Ohmic Dissipation. ApJ 515, 776–786. doi:10.1086/307063

CrossRef Full Text | Google Scholar

Sano, T., Miyama, S. M., Umebayashi, T., and Nakano, T. (2000). Magnetorotational Instability in Protoplanetary Disks. II. Ionization State and Unstable Regions. ApJ 543, 486–501. doi:10.1086/317075

CrossRef Full Text | Google Scholar

Sano, T., and Stone, J. M. (2002). The Effect of the Hall Term on the Nonlinear Evolution of the Magnetorotational Instability. II. Saturation Level and Critical Magnetic Reynolds Number. ApJ 577, 534–553. doi:10.1086/342172

CrossRef Full Text | Google Scholar

Schure, K. M., Kosenko, D., Kaastra, J. S., Keppens, R., and Vink, J. (2009). A New Radiative Cooling Curve Based on an Up-To-Date Plasma Emission Code. A&A 508, 751–757. doi:10.1051/0004-6361/200912495

CrossRef Full Text | Google Scholar

Sen, A. K. (1964). Effect of Compressibility on Kelvin-Helmholtz Instability in a Plasma. Phys. Fluids 7, 1293–1298. doi:10.1063/1.1711374

CrossRef Full Text | Google Scholar

Shadmehri, M., and Downes, T. P. (2007). Kelvin-Helmholtz Instability in a Weakly Ionized Layer. Astrophys Space Sci. 312, 79–84. doi:10.1007/s10509-007-9655-9

CrossRef Full Text | Google Scholar

Shadmehri, M., and Downes, T. P. (2008). The Role of Kelvin-Helmholtz Instability in Dusty and Partially Ionized Outflows. Monthly Notices R. Astronomical Soc. 387, 1318–1322. doi:10.1111/j.1365-2966.2008.13345.x

CrossRef Full Text | Google Scholar

Shadmehri, M., Yaghoobi, A., and Khajavi, M. (2013). Rayleigh-Taylor Instability in an Ionized Medium. Astrophys Space Sci. 347, 151–157. doi:10.1007/s10509-013-1485-3

CrossRef Full Text | Google Scholar

Sharma, K. C., and Sharma, S. (1985). Hall Effects on Thermal Hydromagnetic Instability of a Partially Ionized Medium. Astrophys Space Sci. 112, 391–395. doi:10.1007/BF00653521

CrossRef Full Text | Google Scholar

Sharma, R. C., and Misra, J. N. (1986). Thermal Instability of a Compressible and Partially Ionized Plasma. Z. Naturforschung Teil A 41, 729–732. doi:10.1515/zna-1986-0506

CrossRef Full Text | Google Scholar

Sharma, R. C., and Prakash, K. (1974). On Thermal-Convective Instability in a Stellar Atmosphere with Finite Larmor Radius and Hall Effects. Astrophys Space Sci. 31, 43–47. doi:10.1007/BF00642600

CrossRef Full Text | Google Scholar

Sharma, R. C. (1974a). The thermal-convective Instability in a Stellar Atmosphere with Rotation and Hall Effects. Z. Naturforschung Teil A 29, 867–869. doi:10.1515/zna-1974-0605

CrossRef Full Text | Google Scholar

Sharma, R. C. (1976). Thermal Hydromagnetic Instability of a Partially Ionized Medium. Physica B+C 81, 199–204. doi:10.1016/0378-4363(76)90259-X

CrossRef Full Text | Google Scholar

Sharma, R. C. (1974b). Thermal-convective Instability of a Stellar Atmosphere with Hall Effects. Z. für Naturforschung A 32, 223. doi:10.1515/zna-1974-0605

CrossRef Full Text | Google Scholar

Sharma, R., and Sharma, K. (1978). Thermal Instability of a Partially Ionized Plasma. Aust. J. Phys. 31, 181. doi:10.1071/PH780181

CrossRef Full Text | Google Scholar

Sharp, D. H. (1984). An Overview of Rayleigh-taylor Instability. Physica D: Nonlinear Phenomena 12, 3–18. doi:10.1016/0167-2789(84)90510-4

CrossRef Full Text | Google Scholar

Shivamoggi, B. K. (1982). A Generalised Theory of Stability of Superposed Fluids in Hydromagnetics, 84, 477–484. doi:10.1007/BF00651326

CrossRef Full Text | Google Scholar

Shivamoggi, B. K. (2012). Rayleigh-Taylor Instability of Superposed Barotropic Fluids. Z. Angew. Math. Phys. 63, 521–527. doi:10.1007/s00033-011-0179-3

CrossRef Full Text | Google Scholar

Shu, F. H., Adams, F. C., and Lizano, S. (1987). Star Formation in Molecular Clouds: Observation and Theory. Annu. Rev. Astron. Astrophys. 25, 23–81. doi:10.1146/annurev.aa.25.090187.000323

CrossRef Full Text | Google Scholar

Simon, J. B., Bai, X.-N., Armitage, P. J., Stone, J. M., and Beckwith, K. (2013a). Turbulence in the Outer Regions of Protoplanetary Disks. II. Strong Accretion Driven by a Vertical Magnetic Field. ApJ 775, 73. doi:10.1088/0004-637X/775/1/73

CrossRef Full Text | Google Scholar

Simon, J. B., Bai, X.-N., Stone, J. M., Armitage, P. J., and Beckwith, K. (2013b). Turbulence in the Outer Regions of Protoplanetary Disks. I. Weak Accretion with No Vertical Magnetic Flux. ApJ 764, 66. doi:10.1088/0004-637X/764/1/66

CrossRef Full Text | Google Scholar

Soler, R., Ballester, J. L., and Goossens, M. (2011). The Thermal Instability of Solar Prominence Threads. ApJ 731, 39. doi:10.1088/0004-637X/731/1/39

CrossRef Full Text | Google Scholar

Soler, R., Ballester, J. L., and Parenti, S. (2012a). Stability of thermal Modes in Cool Prominence Plasmas. A&A 540, A7. doi:10.1051/0004-6361/201118492

CrossRef Full Text | Google Scholar

Soler, R., Ballester, J. L., and Zaqarashvili, T. V. (2015a). Overdamped Alfvén Waves Due to Ion-Neutral Collisions in the Solar Chromosphere. A&A 573, A79. doi:10.1051/0004-6361/201423930

CrossRef Full Text | Google Scholar

Soler, R., Carbonell, M., and Ballester, J. L. (2013a). Magnetoacoustic Waves in a Partially Ionized Two-Fluid Plasma. ApJS 209, 16. doi:10.1088/0067-0049/209/1/16

CrossRef Full Text | Google Scholar

Soler, R., Carbonell, M., and Ballester, J. L. (2015b). On the Spatial Scales of Wave Heating in the Solar Chromosphere. ApJ 810, 146. doi:10.1088/0004-637X/810/2/146

CrossRef Full Text | Google Scholar

Soler, R., Carbonell, M., Ballester, J. L., and Terradas, J. (2013b). Alfvén Waves in a Partially Ionized Two-Fluid Plasma. ApJ 767, 171. doi:10.1088/0004-637X/767/2/171

CrossRef Full Text | Google Scholar

Soler, R., Díaz, A. J., Ballester, J. L., and Goossens, M. (2012b). Kelvin-Helmholtz Instability in Partially Ionized Compressible Plasmas. ApJ 749, 163. doi:10.1088/0004-637X/749/2/163

CrossRef Full Text | Google Scholar

Soler, R., Terradas, J., Oliver, R., and Ballester, J. L. (2019). Energy Transport and Heating by Torsional Alfvén Waves Propagating from the Photosphere to the Corona in the Quiet Sun. ApJ 871, 3. doi:10.3847/1538-4357/aaf64c

CrossRef Full Text | Google Scholar

Stone, J. M., and Gardiner, T. (2007). The Magnetic Rayleigh‐Taylor Instability in Three Dimensions. ApJ 671, 1726–1735. doi:10.1086/523099

CrossRef Full Text | Google Scholar

Strutt, J. W. (1882). Investigation of the Character of the Equilibrium of an Incompressible Heavy Fluid of Variable Density. Proc. Lond. Math. Soc. s1-14, 170–177. doi:10.1112/plms/s1-14.1.170

CrossRef Full Text | Google Scholar

Sudan, R. N., Akinrimisi, J., and Farley, D. T. (1973). Generation of Small-Scale Irregularities in the Equatorial Electrojet. J. Geophys. Res. 78, 240–248. doi:10.1029/JA078i001p00240

CrossRef Full Text | Google Scholar

Taylor, G. I. (1950). The Instability of Liquid Surfaces when Accelerated in a Direction Perpendicular to Their Planes. I. Proc. R. Soc. Lond. A. 201, 192–196. doi:10.1098/rspa.1950.0052

CrossRef Full Text | Google Scholar

Terradas, J., Oliver, R., and Ballester, J. L. (2012). The Role of Rayleigh-Taylor Instabilities in Filament Threads. A&A 541, A102. doi:10.1051/0004-6361/201219027

CrossRef Full Text | Google Scholar

Terradas, J., Soler, R., Luna, M., Oliver, R., and Ballester, J. L. (2015a). Morphology and Dynamics of Solar Prominences from 3D MHD Simulations. ApJ 799, 94. doi:10.1088/0004-637X/799/1/94

CrossRef Full Text | Google Scholar

Terradas, J., Soler, R., Luna, M., Oliver, R., Ballester, J. L., and Wright, A. N. (2016). Solar Prominences Embedded in Flux Ropes: Morphological Features and Dynamics from 3D MHD Simulations. ApJ 820, 125. doi:10.3847/0004-637X/820/2/125

CrossRef Full Text | Google Scholar

Terradas, J., Soler, R., Oliver, R., and Ballester, J. L. (2015b). On the Support of Neutrals against Gravity in Solar Prominences. ApJ 802, L28. doi:10.1088/2041-8205/802/2/L28

CrossRef Full Text | Google Scholar

Thomson, W. (1871). XLVI. Hydrokinetic Solutions and Observations. Lond. Edinb. Dublin Phil. Mag. J. Sci. 42, 362–377. doi:10.1080/14786447108640585

CrossRef Full Text | Google Scholar

Tóth, G., Ma, Y., and Gombosi, T. I. (2008). Hall Magnetohydrodynamics on Block-Adaptive Grids. J. Comput. Phys. 227, 6967–6984. doi:10.1016/j.jcp.2008.04.010

CrossRef Full Text | Google Scholar

van der Linden, R. A. M. (1993). Can fine-structure in Prominences Be Due to Perpendicular thermal Conduction. Geophys. Astrophysical Fluid Dyn. 69, 183–199. doi:10.1080/03091929308203579

CrossRef Full Text | Google Scholar

van der Linden, R. A. M., and Goossens, M. (1991a). The thermal Continuum in Coronal Loops: Instability Criteria and the Influence of Perpendicular thermal Conduction. Sol. Phys. 134, 247–273. doi:10.1007/BF00152647

CrossRef Full Text | Google Scholar

van der Linden, R. A. M., and Goossens, M. (1991b). Thermal Instability in Slab Geometry in the Presence of Anisotropical thermal Conduction. Sol. Phys. 131, 79–105. doi:10.1007/BF00151746

CrossRef Full Text | Google Scholar

Vandervoort, P. O. (1961). The Rayleigh-Taylor Instability in Compressible Fluids, 66, 56. doi:10.1086/108538

CrossRef Full Text | Google Scholar

Velikhov, E. P. (1959). Stability of an Ideally Conducting Liquid Flowing between Cylinders Rotating in a Magnetic Field. J. Exptl. Theoret. Phys. 36, 1398–1404.

Google Scholar

Volokitin, A. S., and Atamaniuk, B. (2010). Nonlinear Regimes of Farley-Buneman Instability. Plasma Phys. Rep. 36, 390–402. doi:10.1134/S1063780X1005003X

CrossRef Full Text | Google Scholar

von Helmholtz, H. (1868). über discontinuirliche Flüssigkeits-Bewegungen (Akademie der Wissenschaften zu Berlin).

Google Scholar

Vranjes, J. (2014). Viscosity Effects on Waves in Partially and Fully Ionized Plasma in Magnetic Field. Monthly Notices R. Astronomical Soc. 445, 1614–1624. doi:10.1093/mnras/stu1887

CrossRef Full Text | Google Scholar

Vyas, M. K., and Chhajlani, B. K. (1989). On the Gravitational Instability of an Ionized Magnetized Rotating Plasma Flowing through a Porous Medium with Other Transport Processes and the Suspended Particles. Contrib. Plasma. Phys. 29, 135–151. doi:10.1002/ctpp.2150290204

CrossRef Full Text | Google Scholar

Wang, Y.-M., and Robertson, J. A. (1985). Late Stages of the Rayleigh-Taylor Instability - A Numerical Study in the Context of Accreting Neutron Stars. ApJ 299, 85–108. doi:10.1086/163684

CrossRef Full Text | Google Scholar

Wang, Y. M., and Nepveu, M. (1983). A Numerical Study of the Nonlinear Rayleigh-Taylor Instability, with Application to Accreting X-ray Sources, 118, 267–274.

Google Scholar

Wardle, M. (1999). The Balbus-Hawley Instability in Weakly Ionized Discs. Monthly Notices R. Astronomical Soc. 307, 849–856. doi:10.1046/j.1365-8711.1999.02670.x

CrossRef Full Text | Google Scholar

Wareing, C. J., Pittard, J. M., Falle, S. A. E. G., and Van Loo, S. (2016). Magnetohydrodynamical Simulation of the Formation of Clumps and Filaments in Quiescent Diffuse Medium by thermal Instability. Mon. Not. R. Astron. Soc. 459, 1803–1818. doi:10.1093/mnras/stw581

CrossRef Full Text | Google Scholar

Waters, T., and Proga, D. (2019). Non-isobaric Thermal Instability. ApJ 875, 158. doi:10.3847/1538-4357/ab10e1

CrossRef Full Text | Google Scholar

Watson, C., Zweibel, E. G., Heitsch, F., and Churchwell, E. (2004). Kelvin‐Helmholtz Instability in a Weakly Ionized Medium. ApJ 608, 274–281. doi:10.1086/392500

CrossRef Full Text | Google Scholar

Weymann, R. (1960). Heating of Stellar Chromospheres by Shock Waves. ApJ 132, 452. doi:10.1086/146942

CrossRef Full Text | Google Scholar

Wheeler, J. C., Kagan, D., and Chatzopoulos, E. (2015). The Role of the Magnetorotational Instability in Massive Stars. ApJ 799, 85. doi:10.1088/0004-637X/799/1/85

CrossRef Full Text | Google Scholar

Whitham, G. B. (1974). “Two-timing, Variational Principles and Waves,” In Nonlinear Wave Motion. (A75-14987 04-70) Providence. 97–123.

Google Scholar

Wiechen, H. M. (2006). Simulations of Kelvin-Helmholtz Modes in Partially Ionized Dusty Plasmas Comparing Different Charge Numbers, Charge Polarities, and Masses of the Dust. Phys. Plasmas 13, 062104. doi:10.1063/1.2208309

CrossRef Full Text | Google Scholar

Xia, C., and Keppens, R. (2016). Internal Dynamics of a Twin-Layer Solar Prominence. ApJ 825, L29. doi:10.3847/2041-8205/825/2/L29

CrossRef Full Text | Google Scholar

Yang, H., Xu, Z., Lim, E.-K., Kim, S., Cho, K.-S., Kim, Y.-H., et al. (2018). Observation of the Kelvin-Helmholtz Instability in a Solar Prominence. ApJ 857, 115. doi:10.3847/1538-4357/aab789

CrossRef Full Text | Google Scholar

Young, M. A., Oppenheim, M. M., and Dimant, Y. S. (2020). The Farley‐Buneman Spectrum in 2‐D and 3‐D Particle‐in‐Cell Simulations. J. Geophys. Res. Space Phys. 125, e27326. doi:10.1029/2019JA027326

CrossRef Full Text | Google Scholar

Yuan, D., Shen, Y., Liu, Y., Li, H., Feng, X., and Keppens, R. (2019). Multilayered Kelvin-Helmholtz Instability in the Solar Corona. ApJ 884, L51. doi:10.3847/2041-8213/ab4bcd

CrossRef Full Text | Google Scholar

Zanstra, H. (1955a). On the Formation of Condensations in a Gaseous Nebula. Vistas Astron. 1, 256–268. doi:10.1016/0083-6656(55)90034-9

CrossRef Full Text | Google Scholar

Zanstra, H. (1955b). “On the Formation of Condensations in a Gaseous Nebula,” in Gas Dynamics of Cosmic Clouds, 2, 70. doi:10.1016/0083-6656(55)90034-9

CrossRef Full Text | Google Scholar

Zaqarashvili, T. V., Khodachenko, M. L., and Rucker, H. O. (2011). Magnetohydrodynamic Waves in Solar Partially Ionized Plasmas: Two-Fluid Approach. A&A 529, A82. doi:10.1051/0004-6361/201016326

CrossRef Full Text | Google Scholar

Zhelyazkov, I., Dimitrov, Z., and Bogdanova, M. (2020). Hall-magnetohydrodynamic Waves in Flowing Ideal Incompressible Solar-Wind Plasmas: Reconsidered. Astrophys Space Sci. 365, 29. doi:10.1007/s10509-020-3741-7

CrossRef Full Text | Google Scholar

Zhelyazkov, I. (2015). On Modeling the Kelvin-Helmholtz Instability in Solar Atmosphere. J. Astrophys Astron. 36, 233–254. doi:10.1007/s12036-015-9332-2

CrossRef Full Text | Google Scholar

Zhou, Y., Williams, R. J. R., Ramaprabhu, P., Groom, M., Thornber, B., Hillier, A., et al. (2021). Rayleigh-Taylor and Richtmyer-Meshkov Instabilities: A Journey through Scales. Physica D: Nonlinear Phenomena 423, 132838. doi:10.1016/j.physd.2020.132838

CrossRef Full Text | Google Scholar

Zweibel, E. G. (2015). Ambipolar Diffusion. Ambipolar Diffusion 407285, 285–309. doi:10.1007/978-3-662-44625-6_11

CrossRef Full Text | Google Scholar