Ray Tracing of MHD Rossby Waves in the Solar Tachocline: Meridional Propagation and Implications for the Solar Magnetic Activity

1 Introduction

Rossby waves are large-scale, primarily vortical, disturbances that are regarded as one of the main building blocks in the understanding of atmospheric and oceanic dynamics. These waves play an important role in different climate phenomena such as the El Niño-Southern Oscillation (McPhaden and Yu, 1999), the intraseasonal oscillation (Stechmann and Majda, 2015; Žagar and Franzke, 2015) and the Quasi-biennial Oscillation (Raphaldini et al., 2020b; Raphaldini et al., 2021). Among the most clear signal of Rossby wave propagation in the Earth’s atmosphere refers to the observed teleconnection patterns, geographically fixed regions of climate anomalies around the globe that are strongly correlated with each other (Horel and Wallace, 1981; Wallace and Gutzler, 1981; Blackmon et al., 1984; Hoskins and Ambrizzi, 1993; Boers et al., 2019).

In the recent years, Rossby waves have also been recognised as one of the main contributors to the solar magnetic activity on several timescales. While the role of Rossby waves in Solar dynamics has long been proposed on theoretical grounds (Gilman, 1969a; Gilman, 1969b), only in the last fifteen years there has been a strong resurgence in the interest of the Rossby wave role in the solar magnetic activity, specially in the solar tachocline, a thin and stratified layer that provides a favourable environment for the Rossby wave propagation. These works start fromlaying the theoretical foundations, describing the basic physical aspects of Rossby waves in the Sun, such as their fundamental frequencies and propagation properties (Zaqarashvili et al., 2007; Zaqarashvili et al., 2009), instabilities (Gilman and Dikpati, 2014; Gilman, 2015), equatorial trapping (Zaqarashvili, 2018) and nonlinear interactions (Raphaldini and Raupp, 2015; Raphaldini et al., 2019; Fedotova et al., 2021). In addition, some works have made associations between Rossby wave activity and observed features of the solar magnetic activity, such as short-medium term (Zaqarashvili et al., 2011; Dikpati et al., 2018a Dikpati et al., 2018b) and long-term (Raphaldini et al., 2019; Raphaldini et al., 2020a) periodicities. On the other hand, Zaqarashvili et al. (2010a) extended the Rossby wave propagation theory to other stars.

Even more recently, Dikpati and McIntosh (2020) compiled observational evidences from several sources suggesting that Rossby waves do play an important role in the spatio-temporal organisation of the solar magnetic activity. According to Dikpati and McIntosh (2020), short activity cycles, manifesting themselves as the occurrence of the strongest (X-class) signals in the short period spectrum (8 months–2.4 years), have been linked to retrograde propagation structures due to Rossby waves.

Regarding the role of Rossby waves in the Solar magnetic activity, an important issue that seems to be under-explored refers to their relationship with the latitudinal dependence and meridional propagation of some structures associated with the solar magnetic activity. The most obvious example of this feature is the so-called butterfly diagram, which represents the tendency of sunspots and activity regions to appear closer and closer to the equatorial region as a given solar cycle progresses (Thomas and Weiss, 2012). This historical observational record of sunspots has displayed significant correlation between the amplitude of a given solar cycle, measured by the number of sunspots, and its time-varying characteristic latitudes. More precisely, Leussu et al. (2017) have shown that the latitude of maximum sunspot appearance (the so-called H-latitude) is highly correlated with the strength of the corresponding solar cycle, whilst the latitude of minimal solar cycle activity (the so-called L-latitude) presents a weak correlation. Another phenomenon that is shown to be correlated with the strength of the solar cycle is the differential rotation profile of the Sun (Zhang et al., 2015).

While the sunspot activity shows a tendency of propagating towards the equator, other magnetic structures seem to have an opposite behaviour. For instance, crown filaments are observed to have poleward movements throughout the solar cycle in the so-called “rush to the poles” phenomena (Webb et al., 2018; Xu et al., 2021). Coronal holes, on the other hand, can exhibit both poleward and equatorward propagations (Hewins et al., 2020).

In this way, these two observed correlations mentioned above, namely 1) the one between the characteristic latitude and the strength of the Solar cycle and 2) the other between the differential rotation profile and the strength of the Solar cycle, suggest a common physical mechanism responsible for these correlations, or a relationship between both aspects of the Solar magnetic activity. A natural question that arises from the above considerations is: what is the role of MHD Rossby waves in the latitudinal dependence and meridional propagation of magnetic activity structures?

In order to answer this question, we employ the so-called asymptotic ray tracing theory. This theory has been widely used in the solar and stellar dynamics for other wave modes as a tool to investigate their internal structure through helio/stellar seismology. Lignières and Georgeot (2008) studied the propagation of acoustic waves in a self-gravitating and uniformly rotating star with a polytropic equation of state, showing the existence of chaotic trajectories in this context. Detailed studies of the ray tracing theory for inertio-gravity modes are presented in Prat et al. (2016) and Prat et al. (2018), including the effects of density stratification and differential rotation, providing the properties of the spectra and domains of propagation of these waves as a function of the rotation rate and differential rotation profile. The effect of strong magnetic fields on the inertio-gravity modes and the application of this theory to red giant stars are investigated in Loi (2020a) and Loi (2020b), who showed that, even being embedded in strong magnetic fields, some wave trajectories remain similar to the hydrodynamic case, while others exhibit a more Alfvén-like character.

We introduce in the next section the simplest model capable of reproducing the meridional propagation of MHD Rossby waves, namely the quasi geostrophic MHD equations derived by Zeitlin (2013), which consist of a straightforward generalisation of the well-known quasi-geostrophic equations of the ocean and atmosphere (Pedlosky, 2013). We linearize these equations around a background state characterised by a zonal flow and a zonal (toroidal) magnetic field, both meridionally varying functions. The meridional variation of the background zonal flow is chosen in order to realistically depict the differential rotation profile. In this set of two linear PDEs with variable coefficients, to analyse the ray tracing of MHD Rossby waves, these waves are obtained as asymptotic solutions by considering the so-called WKB (Wentzel-Kramers-Brillouin) approximation, in which the background state parameters are assumed to be slowly varying functions. In this context, the wave phases are obtained as solutions of an eikonal equation, while the wave amplitudes satisfy a transport equation. Therefore, the amplitudes of wave packages are “carried” by their corresponding group velocities, and the wave rays behave in a similar fashion to what occurs in the Snell Law of optics, in which light rays refract when the refractive index of the medium is variable.

2 Model Equations

Let us consider the simplest model supporting the existence of MHD Rossby waves, namely the quasi-geostrophic MHD equations derived by Zeitlin (2013) as a strong rotation limit of the MHD shallow-water equations (Gilman, 2000; Zaqarashvili et al., 2007). This model is described by the potential vorticity conservation and the induction equation as follows:

$\frac{\partial q}{\partial t}+\mathcal{J}\left(\psi ,q\right)={\left({\mu }_0\rho \right)}^{-1}\mathcal{J}\left(A,j\right)(\mathrm{1a})$

$\frac{\partial A}{\partial t}+\mathcal{J}\left(\psi ,A\right)=0(\mathrm{1b})$

where q = ∇²ψ + βy − Fψ is the potential vorticity, ψ the streamfunction, A the magnetic potential, j = ∇²A the magnetic current, ρ the medium density and μ₀ the magnetic permeability of the vacuum; F is the inverse of the Rossby deformation radius squared, and the latitude dependent parameter β refers to the derivative of the Coriolis parameter with respect to latitude. In this context, the spherical coordinate equations are adapted to their popular Cartesian “beta-plane” version by making use of the Mercator projection (see Appendix A2). In Eq. 1, $\mathcal{J}$ represents the Jacobian operator

$\mathcal{J}\left(f,g\right)=\frac{\partial f}{\partial x}\frac{\partial g}{\partial y}-\frac{\partial f}{\partial y}\frac{\partial g}{\partial x}(2)$

for any two differentiable functions f and g. We consider a background magnetic field in the toroidal direction, B₀(y), and a background zonal flow represented by $\bar{U}(y)$. In this way, assuming that $A=\bar{A}(y)+A^{\prime }$, and $\psi =\bar{\psi }(y)+{\psi }^{\prime }$, with $\frac{d\bar{A}(y)}{dy}=-B_0(y)$ and $\frac{d\bar{\psi }(y)}{dy}=-\bar{U}(y)$, and neglecting the terms arising from products of perturbations, the linearized version of Eq. 1 can be written as follows:

$\left(\frac{\partial }{\partial t}+\bar{U}\frac{\partial }{\partial x}\right)\left[\begin{array}{c}\hfill {\nabla }^2\psi \hfill \\ \hfill A\hfill \end{array}\right]=\left[\begin{array}{cc}\hfill {\beta }^{*}\frac{\partial }{\partial x}\hfill & \hfill \frac{B_0\left(y\right)}{{\mu }_0\rho }\frac{\partial }{\partial x}{\nabla }^2\hfill \\ \hfill B_0\left(y\right)\frac{\partial }{\partial x}\hfill & \hfill 0\hfill \end{array}\right]\left[\begin{array}{c}\hfill \psi \hfill \\ \hfill A\hfill \end{array}\right](3)$

where the superscript prime has been omitted for simplicity. In the equation above,

${\beta }^{*}=\beta +F\bar{U}-\frac{d^2\bar{U}}{d{y}^2}$

is the gradient of the background potential vorticity. Wavelike solutions of Eq. 3 are obtainable in the asymptotic limit where the spatial scale of the perturbations is assumed to be much smaller than the spatial scale of the background state, the so-called WKB approximation¹

1

A thorough reference on the WKB method for dispersive wave systems of PDEs can be found in the Chapter 5 of Majda (2003).

. In this context, the wave phases satisfy the following eikonal equation

$\frac{\partial \varphi }{\partial t}=-\omega \left(y,{\varphi }_x,{\varphi }_y\right)(4)$

where ϕ(x, y, t) represents the wave phases, and ω refers to the MHD Rossby wave dispersion relation:

$\omega {\left.\left(\vec{k},y\right)\right|}_{\vec{k}=\nabla \varphi }=\bar{U}\left(y\right)k-\frac{\left({\beta }^{*}\pm \sqrt{{\left({\beta }^{*}\right)}^2+4v_a{\left(y\right)}^2|\vec{k}{|}^4}\right)k}{2\left(|\vec{k}{|}^2+F^2\right)}(5)$

In the equation above, $\vec{k}=(k,l)$ is the vector wavenumber,

$v_a\left(y\right)=\frac{B_0\left(y\right)}{\sqrt{{\mu }_0\rho }}$

the Alfvén wave speed, and the ± sign distinguishes the fast hydrodynamic and slow magnetic branches.

On the other hand, the wave amplitudes satisfy the following transport equation

$\frac{\partial A}{\partial t}+{\nabla }_k\omega •{\nabla }_{x}A=0(6)$

$\frac{d\vec{x}}{dt}={\nabla }_k\omega ={\vec{C}}_g(7)$

where ${\vec{C}}_g=(C_{gx},C_{gy})$ represents the group velocity vector.

3 Ray Tracing for MHD Rossby Waves

By using the method of the characteristics (John, 1982), the eikonal Eq. 4 can be expressed in terms of the ray tracing equations:

$\frac{dk}{dt}=-\frac{\partial \omega }{\partial x}=0(8)$

$\begin{array}{ll}\frac{dl}{dt}=\hfill & -\frac{\partial \omega }{\partial y}=-{\bar{U}}^{\prime }k+k\hfill \\ \hfill & \times \left(\pm \frac{4{\left(k^2+l^2\right)}^2{v}_a{v}_a^{\prime }+{\beta }^{*}{\beta }^{*\prime }}{\sqrt{4{\left(k^2+l^2\right)}^2{v}_a^2+{\beta }^{*2}}}+{\beta }^{*\prime }\right)/\left(2\left(F^2+k^2+l^2\right)\right)\hfill \\ \end{array}(9)$

$\begin{array}{l}\frac{dx}{dt}=\frac{\partial \omega }{\partial k}=\bar{U}+\frac{k^2\left({\beta }^{*}\pm \sqrt{4{\left(k^2+l^2\right)}^2{v}_a^2+{\beta }^{*2}}\right)}{{\left(F^2+k^2+l^2\right)}^2}\mp \hfill \\ \hfill \frac{4k^2{v}_a^2\left(k^2+l^2\right)}{\left(F^2+k^2+l^2\right)\sqrt{4{\left(k^2+l^2\right)}^2{v}_a^2+{\beta }^{*2}}}\mp \frac{\pm {\beta }^{*}+\sqrt{4{\left(k^2+l^2\right)}^2{v}_a^2+{\beta }^{*2}}}{2\left(F^2+k^2+l^2\right)}\end{array}(10)$

$\frac{dy}{dt}=\frac{\partial \omega }{\partial l}=kl\frac{{\beta }^{*}\left(\pm {\beta }^{*}+\sqrt{4{\left(k^2+l^2\right)}^2{v}_a^2+{\beta }^{*2}}\right)\mp 4F^2{v}_a^2\left(k^2+l^2\right)}{{\left(F^2+k^2+l^2\right)}^2\sqrt{4{\left(k^2+l^2\right)}^2{v}_a^2+{\beta }^{*2}}}(11)$

The ray tracing equations above show that at any given point of the domain the trajectory of a particular wave-mode is parallel to its group velocity given by ∇_kω. Consequently, from Eq. 6, it follows that the corresponding mode amplitude (energy) will also be transported by the groups along its path. We therefore calculate the group velocity from the dispersion relation (5), and then integrate the ray tracing equations to determine the trajectory of the wave energy from an initial point. The curves that characterise the rays can then be parameterized by:

$\frac{dx}{dy}=\frac{dk}{dl}=\frac{C_{gx}}{C_{gy}}.(12)$

For the integration of the ray tracing equations above for each specified zonal wavenumber k, the meridional wavenumber l was determined by solving a bi-quadratic algebraic equation that follows from the assumption that the phase speed of the waves are much smaller than the background zonal velocity $(|\omega |\ll |\bar{U}|k)$. Details of these calculations are presented in Appendix A1.

4 Results

In this section we describe the solutions of the ray tracing Eqs 8–11 for two types of equatorially anti-symmetric toroidal magnetic fields B₀(y). The first one follows Dikpati et al. (2021) and corresponds to a narrowly banded/concentrated magnetic field profile (Figure 1, right panel); the second one (Figure 1, left panel) corresponds to a banded magnetic field profile with a slower decay with latitude, which is reminiscent of the global simulations of Passos et al. (2017). The background zonal flow utilised here is defined by $\bar{U}(y)=\mathrm{\Omega }(\theta )a$, with a corresponding to the tachocline solar radius, and Ω(θ) represents the differential rotation profile defined according to the following truncated series:

$\mathrm{\Omega }\left(\theta \right)={\mathrm{\Omega }}_0+{\mathrm{\Omega }}_2{cos}^2\theta +{\mathrm{\Omega }}_4{cos}^4\theta ,(13)$

where θ represents the latitude. The resulting meridional profile of $\bar{U}(y)$ obtained from the standard values of the coefficients given by Ω₀ = 0.0588, Ω₂ = −0.1264 and Ω₄ = −0.1591, is illustrated in Figure 2. This profile was utilised in the integrations displayed in Figures 3–5.

FIGURE 1

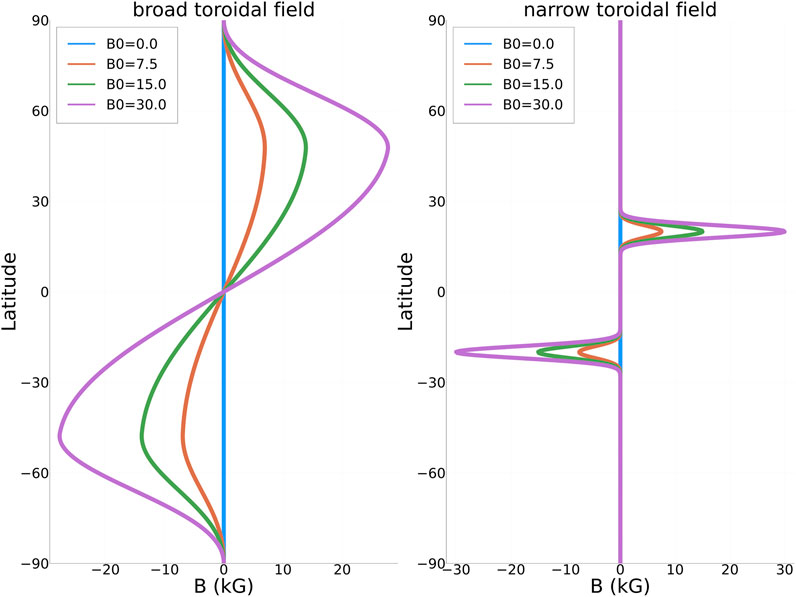
FIGURE 1. Toroidal magnetic field profiles used in this study with varying maximum field strengths of B₀ = 0G, B₀ = 7,500G, B₀ = 15,000G and B₀ = 30,000G. On the left is a slowly decaying (as a function of the latitude) Gaussian profile; on the right is a narrow profile centred at 25^o of latitude.

FIGURE 2

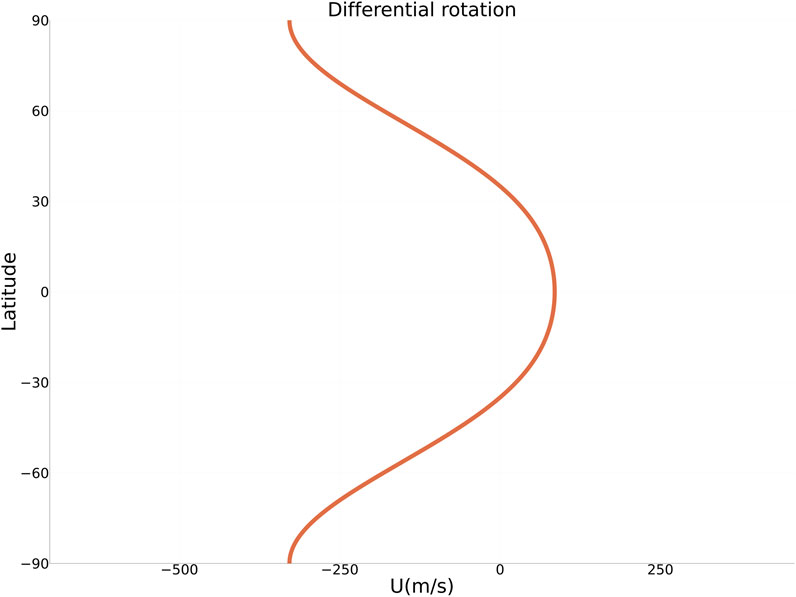
FIGURE 2. Mean zonal flow profile used in this study, mimicking the solar differential rotation profile.

FIGURE 3

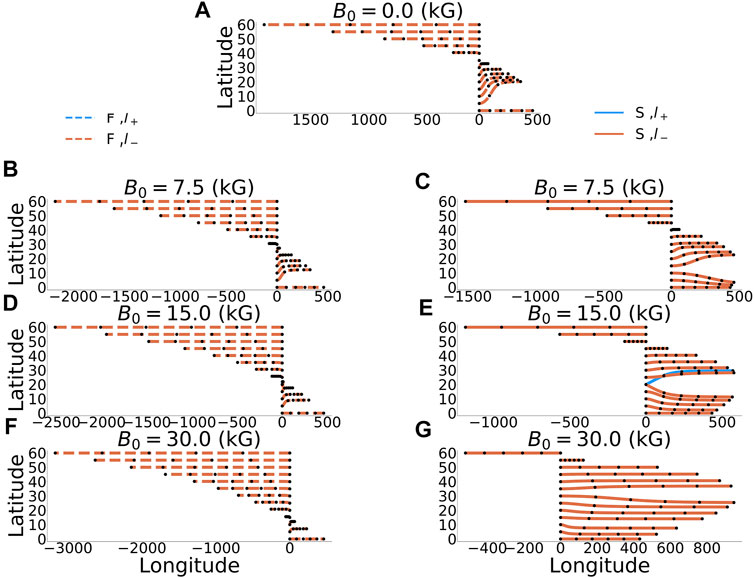
FIGURE 3. Energy trajectory (initiating at zero degrees of longitude) of the zonal wavenumber-10 wave mode embedded in the broad band toroidal magnetic field, for different initial latitudes. The figures show the trajectories for the magnetic field strengths of 0G (A), 7.5 kG (B,C), 15 kG (D,E) and 30 kG (F,G). The left panels refer to the fast hydrodynamic branch of the dispersion relation, whereas the right panels refer to the corresponding slow magnetic branch dispersion relation. For all the panels, the blue (red) curve refers to the “+” (“−”) branch of the meridional wavenumber.

Apart from the two aforementioned latitudinal structures for B₀(y), we also test the sensitivity of the solutions to the strength of the toroidal magnetic field by considering the following values for its maximum: B₀ = 0G, B₀ = 7500G, B₀ = 15000G and B₀ = 30000G. The integrations are performed for a 500-day period, with a small black circle on the curves for a 100-day window.

FIGURE 4

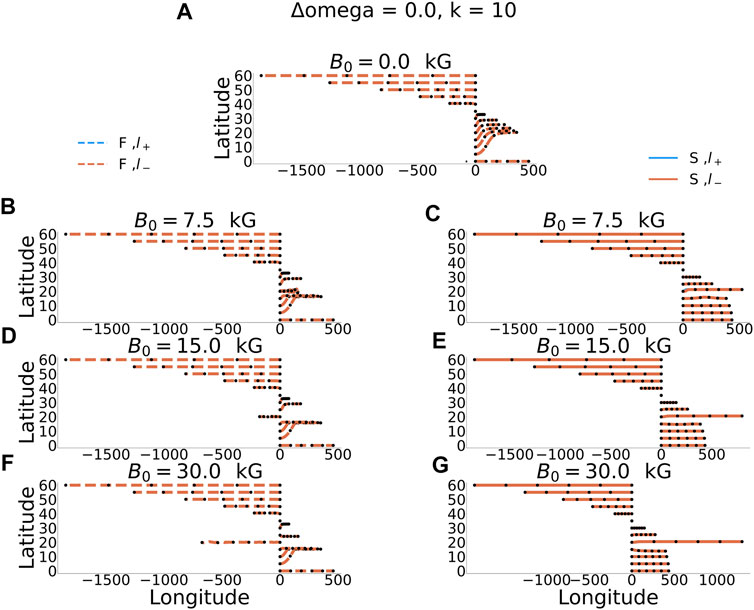
FIGURE 4. Similar to Figure 3, but for the narrow band toroidal magnetic field.

FIGURE 5

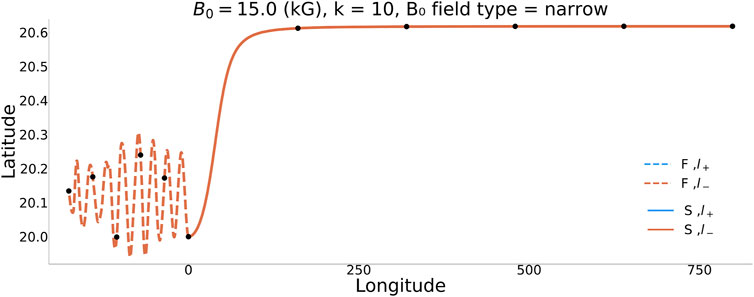
FIGURE 5. Fast hydrodynamic branch wave energy trajectory embedded in the narrow band toroidal magnetic field, for a narrow latitudinal range around the maximum of the background magnetic field.

Figure 3 displays the solution for the waves with zonal wavenumber k = 10 embedded in the broad toroidal magnetic field. For this zonal wavenumber, the wave phases are highly oscillatory such that the WKB approximation seems reasonable. One observes that, for B₀ = 0, in which only the fast hydrodynamic branch exists, there is a tendency for the wave generated near the equator to propagate towards mid-latitudes (around 30°). This tendency is reduced as the strength of the magnetic field is increased for both branches of the MHD Rossby waves. The two branches present some differences regarding the propagation speed and the latitudinal range for which the Rossby waves present prograde propagation with respect to the Carrington rotation. This difference becomes more evident for stronger magnetic fields (e.g., for B₀ = 15, 000G), for which there is an overall tendency of the fast branch to present retrograde propagation, while the slow branch exhibits a predominantly prograde propagation. Another interesting feature to be noticed from Figure 3 refers to the latitudinal location of the stationary waves that may differ between the two branches. This is the latitude where the Rossby wave propagation changes from prograde to retrograde and vice-versa. For even stronger fields (e.g., B₀ = 30000G), the difference becomes even more evident, with the latitude of the stationary waves being around 20° for the fast branch and around 60° for the slow branch. Stationary Rossby waves might be associated with the so-called active (preferential) longitudes for the Solar magnetic activity (Dikpati and McIntosh, 2020).

The solution referred to the zonal wavenumber-10 wave mode embedded in the narrowly banded toroidal magnetic field is illustrated in Figure 4. Since the toroidal magnetic field band is narrow, the region where the Rossby wave propagation is affected by the background magnetic field corresponds to a smaller latitudinal range. In particular, for mid to high latitudes where the background magnetic field is weak, the propagation of the MHD waves is very similar to that of the purely hydrodynamical waves (B₀ = 0). Unlike the broad band toroidal field case displayed in Figure 3, for the solution displayed in Figure 4, there is a very distinctive propagation in the center of the toroidal band at around 20°. This is because for a narrow enough band toroidal field, the wave modes become trapped and the background magnetic field works as a waveguide for the MHD Rossby waves. This trapping effect of the narrow band toroidal magnetic field on the MHD Rossby wave mode is more clearly noticeable in Figure 5, which shows the fast hydrodynamic branch wave energy trajectory in a narrow latitudinal range around the maximum of the background magnetic field. It is clearly noticeable from Figure 5 that, after oscillating around the initial latitude of $\approx 20°$, the corresponding wave ray is refracted toward the final latitude of $\approx 20.6°$, which refers to the latitude where the strength of the magnetic field is maximal.

The sensitivity of the Rossby wave rays to variations of the differential rotation coefficients Ω₂ and Ω₄ in Eq. 13 has also been investigated. The differences obtained for the wave trajectories were very small for perturbations up to 25% of the standard values of these coefficients (figures not shown), suggesting that either inter-cycle or intra-cycle fluctuations in the differential rotation profile probably do not significantly affect the MHD Rossby wave propagation in the solar tachocline. This is in contrast to the effects of the shape and strength of the toroidal magnetic field that, as shown by the results presented in Figures 3–5, do significantly affect the wave trajectories.

5 Discussion and Conclusions

In this study we have investigated the MHD Rossby wave propagation embedded in a background state characterised a zonal flow and a toroidal magnetic field, both meridionally varying functions. The zonal flow has been prescribed to mimic the differential rotation profile of the Sun, whilst two meridional structures have been considered for the toroidal magnetic field: a narrow band one centered at around 20° and a global structure field with maximum centered at around 50° of latitude, both having an odd symmetry about the equator. We have shown that the MHD Rossby wave trajectories are sensitive to both the meridional structure and the strength of the toroidal magnetic field.

For a global structure field, the MHD Rossby waves exhibit a significant meridional propagation, either poleward or equatorward. Moreover, the latitude where the waves exhibit an inversion from prograde to retrograde propagation with respect to Carrington rotation is shown to be highly dependent on the strength of the background toroidal magnetic field. These critical latitudes correspond to a stationary regime of the wave modes. As highlighted by Dikpati and McIntosh (2020), stationary or very slowly propagating Rossby waves might be relevant to the so-called active longitude phenomenon, since these waves no longer exhibit significant propagation for long periods. The active longitudes refer to longitudes at which persistent solar magnetic activity is observed throughout several solar rotations.

For a narrow band magnetic field, the MHD Rossby wave propagation is unaffected by the strength of the toroidal magnetic field for trajectories initiating far away from the latitude where the magnetic field is maximum. In this case, the MHD Rossby waves behave similarly to purely hydrodynamic Rossby modes. In contrast, for trajectories initiating close to the latitude of the toroidal magnetic field maximum, the fast hydrodynamic branch mode becomes trapped at this latitude, with the narrow band magnetic field working as a wave guide.

This role of the narrow band toroidal magnetic field as a waveguide for MHD Rossby waves at the solar tachocline appears to be similar to the role of the upper troposphere subtropical jet streams at the Earth atmosphere, which work as waveguides for hydrodynamic Rossby waves (Hoskins and Ambrizzi, 1993). Rossby wave disturbances in the Earth atmosphere are known to be responsible for the weather systems characterised by an alternate sequence of large-scale propagating cyclonic and anticyclonic vortices. These cyclonic (anticyclonic) vortices are associated with rainy (dry) weather conditions. In addition, for longer time-scales, forced Rossby waves are responsible for establishing the teleconnection patterns that are responsible for extreme climate events in the Earth atmosphere. An example is the one responsible for the ElNiño impact on the North America (South America) climate during the boreal (austral) winter (e.g., Horel and Wallace, 1981; Karoly, 1989).

In this scenario, an interesting analogy can be made with MHD Rossby waves in the Sun as their propagation might be responsible for the spatio-temporal organization of more localized explosive events of the solar magnetic activity. Dikpati and McIntosh (2020) discuss several aspects of this relationship between solar Rossby waves and their role in organizing solar flares and other phenomena related to the solar magnetic activity. Some of the aspects presented here such as the meridional Rossby wave propagation as well as the stationarity of MHD Rossby modes may play a role in this context.

MHD Rossby waves embedded in a realistic differential rotation profile and a large-scale toroidal magnetic field at the solar tachocline have also been studied by Zaqarashvili et al. (2010a) by using the eigenmode method, which consists of numerically solving the full eigenvalue problem. The authors found an instability of global-scale Rossby waves (zonal wavenumber 1) whose periods of the order of 155–160 days are compatible with the short-term solar oscillations of Rieger-type. A similar analysis also suggests that solar quasi-biennial oscillations could be generated by global-scale unstable Rossby modes (Zaqarashvili et al., 2010b). These studies differ from our analysis in that they focus on global-scale modes (zonal wavenumber k = 1), while we focus here on wave modes with spatial scales one order of magnitude smaller (zonal wavenumber k = 10) to be consistent with the WKB approximation.

In a recent observational analysis, Dikpati and McIntosh (2020) showed that, depending on the phase of the solar cycle, the Rossby wave signatures shift from a global scale (mainly zonal wavenumber k = 1) at the solar minimum to a smaller scale (k = $\mathcal{O}(10)$) at the solar maximum. This suggests that some type of nonlinear process might be responsible for the energy transfer between Rossby waves with these two distinct spatial scales during the evolution of the solar cycle, possibly the nonlinear interactions studied by Raphaldini and Raupp (2015) and Raphaldini et al. (2019). This kind of non-local mode interaction has also been demonstrated in the context of torsional oscillations in red giant stars (Loi and Papaloizou, 2017). Therefore, in the solar dynamics, the interaction of MHD Rossby and inertio-gravity wave modes can also play some role during the transition to the maximal phase of the solar magnetic activity. Indeed, for more realistic models of the solar dynamics, MHD inertio-gravity modes have also been obtained as linear eigenmodes (see, for instance, Zaqarashvili et al., 2009; Dhouib et al., 2021a; Dhouib et al., 2021b; Dhouib et al., 2022).

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

AT and BR conceived the work, performed the experiments and wrote most part of the manuscript; CR discussed the results and helped writing the manuscript.

Funding

The work reported here has been supported by Fundação de Amparo à Pesquisa do Estado de São Paulo (FAPESP) (grants 2015/50686-1, 2015/50122-0 and 2020/14162-6) and Coordenação de Aperfeiçoamento de Pessoal de Nível Superior—Brasil (CAPES)—Finance Code 001.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Blackmon, M. L., Lee, Y.-H., and Wallace, J. M. (1984). Horizontal Structure of 500 Mb Height Fluctuations with Long, Intermediate and Short Time Scales. J. Atmos. Sci. 41, 961–980. doi:10.1175/1520-0469(1984)041<0961:hsomhf>2.0.co;2

CrossRef Full Text | Google Scholar

Boers, N., Goswami, B., Rheinwalt, A., Bookhagen, B., Hoskins, B., and Kurths, J. (2019). Complex Networks Reveal Global Pattern of Extreme-Rainfall Teleconnections. Nature 566, 373–377. doi:10.1038/s41586-018-0872-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Dhouib, H., Mathis, S., Bugnet, L., Van Reeth, T., and Aerts, C. (2022). Detecting Deep Axisymmetric Toroidal Magnetic fields in Stars the Traditional Approximation of Rotation for Differentially Rotating Deep Spherical Shells with a General Azimutal Magnetic Field, 1–21. arXiv:2202.10026.

Google Scholar

Dhouib, H., Prat, V., Van Reeth, T., and Mathis, S. (2021a). The Traditional Approximation of Rotation for Rapidly Rotating Stars and Planets - I: The Impact of strong Deformation. Astron. Astrophysics 652, A154. doi:10.1051/0004-6361/202140615

CrossRef Full Text | Google Scholar

Dhouib, H., Prat, V., Van Reeth, T., and Mathis, S. (2021b). The Traditional Approximation of Rotation for Rapidly Rotating Stars and Planets - II: Deformation and Differential Rotation. Astron. Astrophysics 65, A122. doi:10.1051/0004-6361/202141152

CrossRef Full Text | Google Scholar

Dikpati, M., Belucz, B., Gilman, P. A., and McIntosh, S. W. (2018a). Phase Speed of Magnetized Rossby Waves that Cause Solar Seasons. ApJ 862, 159. doi:10.3847/1538-4357/aacefa

CrossRef Full Text | Google Scholar

Dikpati, M., McIntosh, S. W., Bothun, G., Cally, P. S., Ghosh, S. S., Gilman, P. A., et al. (2018b). Role of Interaction between Magnetic Rossby Waves and Tachocline Differential Rotation in Producing Solar Seasons. ApJ 853, 144. doi:10.3847/1538-4357/aaa70d

CrossRef Full Text | Google Scholar

Dikpati, M., and McIntosh, S. W. (2020). Space Weather challenge and Forecasting Implications of Rossby Waves. Space Weather 18, e2018SW002109. doi:10.1029/2018sw002109

CrossRef Full Text | Google Scholar

Dikpati, M., Norton, A. A., McIntosh, S. W., and Gilman, P. A. (2021). Dynamical Splitting of Spot-Producing Magnetic Rings in a Nonlinear Shallow-Water Model. ApJ 922, 46. doi:10.3847/1538-4357/ac1359

CrossRef Full Text | Google Scholar

Fedotova, M., Klimachkov, D., and Petrosyan, A. (2021). Variable Density Flows in Rotating Astrophysical Plasma: Linear Waves and Resonant Phenomena. Universe 7, 87. doi:10.3390/universe7040087

CrossRef Full Text | Google Scholar

Gilman, P. A. (1969a). A Rossby-Wave Dynamo for the Sun, I. Sol. Phys. 8, 316–330. doi:10.1007/bf00155379

CrossRef Full Text | Google Scholar

Gilman, P. A. (1969b). A Rossby-Wave Dynamo for the Sun, II. Sol. Phys. 9, 3–18. doi:10.1007/bf00145722

CrossRef Full Text | Google Scholar

Gilman, P. A. (2015). Effect of Toroidal fields on Baroclinic Instability in the Solar Tachocline. ApJ 801, 22. doi:10.1088/0004-637x/801/1/22

CrossRef Full Text | Google Scholar

Gilman, P. A. (2000). Magnetohydrodynamic “Shallow Water” Equations for the Solar Tachocline. ApJ 544, L79–L82. doi:10.1086/317291

CrossRef Full Text | Google Scholar

Gilman, P., and Dikpati, M. (2014). Baroclinic Instability in the Solar Tachocline. ApJ 787, 60. doi:10.1088/0004-637x/787/1/60

CrossRef Full Text | Google Scholar

Hewins, I. M., Gibson, S. E., Webb, D. F., McFadden, R. H., Kuchar, T. A., Emery, B. A., et al. (2020). The Evolution of Coronal Holes over Three Solar Cycles Using the Mcintosh Archive. Solar Phys. 295, 1–15. doi:10.1007/s11207-020-01731-y

CrossRef Full Text | Google Scholar

Horel, J. D., and Wallace, J. M. (1981). Planetary-Scale Atmospheric Phenomena Associated with the Southern Oscillation. Mon. Wea. Rev. 109, 813–829. doi:10.1175/1520-0493(1981)109<0813:psapaw>2.0.co;2

CrossRef Full Text | Google Scholar

Hoskins, B. J., and Ambrizzi, T. (1993). Rossby Wave Propagation on a Realistic Longitudinally Varying Flow. J. Atmos. Sci. 50, 1661–1671. doi:10.1175/1520-0469(1993)050<1661:rwpoar>2.0.co;2

CrossRef Full Text | Google Scholar

John, F. (1982). Partial Differential Equations. New York: Springer-Verlag.

Google Scholar

Karoly, D. J. (1989). Southern Hemisphere Circulation Features Associated with El Niño-Southern Oscillation Events. J. Clim. 2, 1239–1252. doi:10.1175/1520-0442(1989)002<1239:shcfaw>2.0.co;2

CrossRef Full Text | Google Scholar

Leussu, R., Usoskin, I. G., Senthamizh Pavai, V., Diercke, A., Arlt, R., Denker, C., et al. (2017). Wings of the Butterfly: Sunspot Groups for 1826-2015. Astron. Astrophysics 599, A131. doi:10.1051/0004-6361/201629533

CrossRef Full Text | Google Scholar

Lignières, F., and Georgeot, B. (2008). Wave Chaos in Rapidly Rotating Stars. Phys. Rev. E Stat. Nonlin Soft Matter Phys. 78, 016215. doi:10.1103/PhysRevE.78.016215

PubMed Abstract | CrossRef Full Text | Google Scholar

Loi, S. T. (2020a). Effect of a strong Magnetic Field on Gravity-Mode Period Spacings in Red Giant Stars. Monthly Notices R. Astronomical Soc. 496, 3829–3840. doi:10.1093/mnras/staa1823

CrossRef Full Text | Google Scholar

Loi, S. T. (2020b). Magneto-Gravity Wave Packet Dynamics in Strongly Magnetized Cores of Evolved Stars. Monthly Notices R. Astronomical Soc. 493, 5726–5742. doi:10.1093/mnras/staa581

CrossRef Full Text | Google Scholar

Loi, S. T., and Papaloizou, J. C. (2017). Torsional Alfvén Resonances as an Efficient Damping Mechanism for Non-Radial Oscillations in Red Giant Stars. Monthly Notices R. Astronomical Soc. 467, 3212–3225. doi:10.1093/mnras/stx281

CrossRef Full Text | Google Scholar

Majda, A. (2003). Introduction to PDEs and Waves for the Atmosphere and Ocean. Providence, United States: American Mathematical Society. doi:10.1090/cln/009

CrossRef Full Text | Google Scholar

McPhaden, M. J., and Yu, X. (1999). Equatorial Waves and the 1997-98 El Niño. Geophys. Res. Lett. 26, 2961–2964. doi:10.1029/1999gl004901

CrossRef Full Text | Google Scholar

Passos, D., Miesch, M., Guerrero, G., and Charbonneau, P. (2017). Meridional Circulation Dynamics in a Cyclic Convective Dynamo. Astron. Astrophysics 607, A120. doi:10.1051/0004-6361/201730568

CrossRef Full Text | Google Scholar

Pedlosky, J. (2013). Geophysical Fluid Dynamics. Springer Science & Business Media.

Google Scholar

Prat, V., Lignières, F., and Ballot, J. (2016). Asymptotic Theory of Gravity Modes in Rotating Stars. Astron. Astrophysics 587, A110. doi:10.1051/0004-6361/201527737

CrossRef Full Text | Google Scholar

Prat, V., Mathis, S., Augustson, K., Lignières, F., Ballot, J., Alvan, L., et al. (2018). Asymptotic Theory of Gravity Modes in Rotating Stars-Ii. Impact of General Differential Rotation. Astron. Astrophysics 615, A106. doi:10.1051/0004-6361/201832576

CrossRef Full Text | Google Scholar

Raphaldini, B., Medeiros, E., Raupp, C. F. M., and Teruya, A. S. (2020a). A New Mechanism for Maunder-Like Solar Minima: Phase Synchronization Dynamics in a Simple Nonlinear Oscillator of Magnetohydrodynamic Rossby Waves. ApJ 890, L13. doi:10.3847/2041-8213/ab71fd

CrossRef Full Text | Google Scholar

Raphaldini, B., and Raupp, C. F. M. (2015). Nonlinear Dynamics of Magnetohydrodynamic Rossby Waves and the Cyclic Nature of Solar Magnetic Activity. ApJ 799, 78. doi:10.1088/0004-637x/799/1/78

CrossRef Full Text | Google Scholar

Raphaldini, B., Teruya, A. S., Raupp, C. F. M., and Bustamante, M. D. (2019). Nonlinear Rossby Wave-Wave and Wave-Mean Flow Theory for Long-Term Solar Cycle Modulations. ApJ 887, 1. doi:10.3847/1538-4357/ab5067

CrossRef Full Text | Google Scholar

Raphaldini, B., Teruya, A. S. W., Leite da Silva Dias, P., Massaroppe, L., and Takahashi, D. Y. (2021). Stratospheric Ozone and Quasi-Biennial Oscillation (QBO) Interaction with the Tropical Troposphere on Intraseasonal and Interannual Timescales: a normal-mode Perspective. Earth Syst. Dynam. 12, 83–101. doi:10.5194/esd-12-83-2021

CrossRef Full Text | Google Scholar

Raphaldini, B., Wakate Teruya, A. S., Silva Dias, P. L., Chavez Mayta, V. R., and Takara, V. J. (2020b). Normal Mode Perspective on the 2016 QBO Disruption: Evidence for a Basic State Regime Transition. Geophys. Res. Lett. 47, e2020GL087274. doi:10.1029/2020gl087274

CrossRef Full Text | Google Scholar

Stechmann, S. N., and Majda, A. J. (2015). Identifying the Skeleton of the Madden-Julian Oscillation in Observational Data. Monthly Weather Rev. 143, 395–416. doi:10.1175/mwr-d-14-00169.1

CrossRef Full Text | Google Scholar

Thomas, J. H., and Weiss, N. O. (2012). Sunspots: Theory and Observations. New York: Springer Science & Business Media, 375.

Google Scholar

Wallace, J. M., and Gutzler, D. S. (1981). Teleconnection in the Geopotential Heigth Field during the Northern Hemisphere Winter. Monthly Weather Rev. 109, 785–812. doi:10.1175/1520-0493(1981)109<0784:titghf>2.0.co;2

CrossRef Full Text | Google Scholar

Webb, D. F., Gibson, S. E., Hewins, I. M., McFadden, R. H., Emery, B. A., Malanushenko, A., et al. (2018). Global Solar Magnetic Field Evolution over 4 Solar Cycles: Use of the Mcintosh Archive. Front. Astron. Space Sci. 5, 23. doi:10.3389/fspas.2018.00023

CrossRef Full Text | Google Scholar

Xu, Y., Banerjee, D., Chatterjee, S., Pötzi, W., Wang, Z., Ruan, X., et al. (2021). Migration of Solar Polar crown Filaments in the Past 100 Years. ApJ 909, 86. doi:10.3847/1538-4357/abdc1e

CrossRef Full Text | Google Scholar

Žagar, N., and Franzke, C. L. (2015). Systematic Decomposition of the Madden-Julian Oscillation into Balanced and Inertio-Gravity Components. Geophys. Res. Lett. 42, 6829–6835. doi:10.1002/2015GL065130

CrossRef Full Text | Google Scholar

Zaqarashvili, T. (2018). Equatorial Magnetohydrodynamic Shallow Water Waves in the Solar Tachocline. ApJ 856, 32. doi:10.3847/1538-4357/aab26f

CrossRef Full Text | Google Scholar

Zaqarashvili, T. V., Carbonell, M., Oliver, R., and Ballester, J. L. (2010a). Magnetic Rossby Waves in the Solar Tachocline and Rieger-type Periodicities. ApJ 709, 749–758. doi:10.1088/0004-637x/709/2/749

CrossRef Full Text | Google Scholar

Zaqarashvili, T. V., Carbonell, M., Oliver, R., and Ballester, J. L. (2010b). Quasi-biennial Oscillations in the Solar Tachocline Caused by Magnetic Rossby Wave Instabilities. ApJ 724, L95–L98. doi:10.1088/2041-8205/724/1/l95

CrossRef Full Text | Google Scholar

Zaqarashvili, T. V., Oliver, R., Ballester, J. L., Carbonell, M., Khodachenko, M. L., Lammer, H., et al. (2011). Rossby Waves and Polar Spots in Rapidly Rotating Stars: Implications for Stellar Wind Evolution. Astron. Astrophysics 532, A139. doi:10.1051/0004-6361/201117122

CrossRef Full Text | Google Scholar

Zaqarashvili, T. V., Oliver, R., and Ballester, J. L. (2009). Global Shallow Water Magnetohydrodynamic Waves in the Solar Tachocline. ApJ 691, L41–L44. doi:10.1088/0004-637x/691/1/l41

CrossRef Full Text | Google Scholar

Zaqarashvili, T. V., Oliver, R., Ballester, J. L., and Shergelashvili, B. M. (2007). Rossby Waves in “Shallow Water” Magnetohydrodynamics. Astron. Astrophysics 470, 815–820. doi:10.1051/0004-6361:20077382

CrossRef Full Text | Google Scholar

Zeitlin, V. (2013). Remarks on Rotating Shallow-Water Magnetohydrodynamics. Nonlin. Process. Geophys. 20, 893–898. doi:10.5194/npg-20-893-2013

CrossRef Full Text | Google Scholar

Zhang, L., Mursula, K., and Usoskin, I. (2015). Solar Surface Rotation: N-S Asymmetry and Recent Speed-Up. Astron. Astrophysics 575, 4. doi:10.1051/0004-6361/201425169

CrossRef Full Text | Google Scholar

APPENDIX A1: Stationary Wavenumber Approximation and Determination of the Meridional Wavenumber

The latitudinal dependence of the dispersion relation given by Eq. 5 suggests that one can describe the meridional wave-number of a Rossby wave locally as l = l(y). In such a case, an useful approximation that enables us to identify the propagation regions of a Rossby wave train is the so-called stationary wave-number approximation (Hoskins and Ambrizzi, 1993). This approximation is applicable for slow waves, for which the frequency of the background mean flow is much larger than that of the wave itself $(|\bar{U}k|\gg |\omega |)$. In this case, Eq. 5 now reads:

$\bar{U}\left(y\right)-\frac{{\beta }^{*}\pm \sqrt{{\beta }^{*2}+4v_a^2|\vec{k}{|}^4}}{2\left(|\vec{k}{|}^2+F^2\right)}=0,(\mathrm{A1})$

Taking the square of both sides of the equation above and making some algebraic manipulations, we get:

${\bar{U}}^2{\left(|\vec{k}{|}^2+F^2\right)}^2-\bar{U}{\beta }^{*}\left(|\vec{k}{|}^2+F^2\right)-v_a^2|\vec{k}{|}^4=0(\mathrm{A2})$

Recalling that $|\vec{k}{|}^2=k^2+l^2$, equation above is a bi-quadratic algebraic equation for l, whose roots are:

$l=\pm \sqrt{\frac{1}{2\left({\bar{U}}^2-v_a^2\right)}\left(-2F^2{U}^2-2k^2\left(U^2-v_a^2\right)+\bar{U}{\beta }^{*}+\sqrt{U\left(4F^2{v}_a^2\left(F^2\bar{U}-{\beta }^{*}\right)+\bar{U}{\beta }^{*2}\right)}\right)}(\mathrm{A3})$

The other pair of roots is spurious and has been disregarded.

APPENDIX A2: Mercartor Projection

In considering the equations of motion on the sphere in a latitude-longitude coordinate frame (θ, ϕ), one wishes to convert the equations to Cartesian form while keeping the effects of the variation of the Coriolis force and the mean flow with latitude. A simple way to do this is to make use of the Mercartor projection, which consists of considering the following transformations:

$x=a\varphi (\mathrm{A4})$

$y=\frac{a}{2}\frac{1+sin\theta }{1-sin\theta }(\mathrm{A5})$

with a representing the radius of the sphere. In this context, the derivatives become:

$\frac{\partial }{\partial x}=\frac{1}{a}\frac{\partial }{\partial \varphi }(\mathrm{A6})$

$\frac{1}{cos\theta }\frac{\partial }{\partial y}=\frac{1}{a}\frac{\partial }{\partial \theta }(\mathrm{A7})$

Equations above therefore take the form of the beta-plane equations, with the β coefficient taking into account variations of both the Coriolis parameter and the mean flow with latitude:

${\beta }^{*}=cos\theta \left(\frac{2\mathrm{\Omega }}{a}+\frac{1}{a}\frac{\partial \bar{\zeta }}{\partial \theta }\right)(\mathrm{A8})$

where

$\bar{\zeta }={\nabla }^{\perp }\bar{U}(\mathrm{A9})$