Dark matter as an effect of a minimal length

1 Introduction

Dark matter (DM) is one of the dominant components in the energy budget of the Universe. Evidence for its existence ranges from galaxy clusters, rotational curves of galaxies, and gravitational lensing all to the cosmic microwave background (CMB) (Freese, 2009; Drees and Gerbier, 2012; Arbey and Mahmoudi, 2021). However, effects related to DM have not been observed on the scale of the solar system, whereas they become significant on galactic and intergalactic scales. Nonetheless, the nature of DM remains one of the most debated problems in physics up to this day. Several proposals and speculations concerning DM have been put forward, among which are MACHOs, WIMPs, axions, sterile neutrinos, and modified Newtonian dynamics (MOND) (Freese, 2009; Drees and Gerbier, 2012; Arbey and Mahmoudi, 2021; Oks, 2021). In this work, we propose an alternative explanation for DM. Specifically, we argue that the phenomenology related to DM can be partially described in terms of quantum gravitational effects.

The development of a theory of quantum gravity (QG) is an open problem in physics. Several candidate theories have been proposed, and numerous thought experiments have shaped the expected features of such a theory. However, none could have been directly tested due to current experimental and technological limitations. For this reason, phenomenological approaches have become some of the main tools to tackle the problem of QG (Magueijo, 2006; Ali et al., 2011; Hamma and Markopoulou, 2011; Dos Santos et al., 2013; Feller and Livine, 2016; Danshita et al., 2017; Haine, 2018; van de Kamp et al., 2020) (see Addazi et al. (2022) for a recent review). Such approaches usually consider the implications of features of a full QG theory on lower energy scales, possibly accessible to current experiments and observations. Among such features, a common one is the existence of a fundamental minimal length. Such a minimal length strongly opposes the traditional Heisenberg uncertainty principle of quantum mechanics, which should be properly modified approaching the QG scale. The set of models corresponding to a modified uncertainty relation is collectively referred to as the generalized uncertainty principle (GUP) (Maggiore, 1993a; Maggiore, 1993b; Maggiore, 1994; Kempf et al., 1996; Kempf, 1997; Scardigli, 1999; Scardigli and Casadio, 2003; Ali et al., 2011; Pikovski et al., 2012; Bosso et al., 2017; Scardigli et al., 2017; Bosso, 2018; Kumar and Plenio, 2018; Gnatenko and Tkachuk, 2019; Luciano, 2021a; Bosso, 2021; Bosso and Luciano, 2021; Das and Fridman, 2021; Giardino and Salzano, 2021; Gomes, 2022). Such models are inspired from candidate theories of quantum gravity, such as string theory and loop quantum gravity, in which an effective minimal observable length appears in scattering experiments or as a structural feature of space-time. The phenomenological implications are then accounted for in terms of a minimal uncertainty in position or non-commutativity of space-time. The commutator corresponding to one of the most common GUP models can be cast as (Kempf et al., 1996; Bosso, 2021):

$\left[x_i,p_j\right]=i\hslash \left[{\delta }_{ij}+\beta \left(p^2{\delta }_{ij}+2p_i{p}_j\right)\right],(1)$

where x_i and p_j are the position and momentum operators, respectively, $\beta \equiv {\beta }_0/{(M_{P}c)}^2$, where β₀ is a dimensionless parameter, and $M_P=\sqrt{\hslash c/G}$ is the Planck mass. Such a model implies a modification of the uncertainty relation between the position and momentum, as found using the Schrödinger–Robertson relation and thus leads to a minimal uncertainty in the position. For example, in the one-dimensional case, the modified uncertainty relation reads (Kempf et al., 1996):

$\mathrm{\Delta }x\mathrm{\Delta }p\gtrsim \hslash \left[1+3\beta \mathrm{\Delta }{p}^2\right].(2)$

In this study, we propose how minimal length phenomenology can give rise to features similar to DM on galactic scales. Specifically, we deduce effects from GUP that contribute to the flatness of rotational curves. Such effects are obtained as a consequence of the modifications to the Bekenstein–Hawking entropy through the holographic principle, induced by GUP (Cai et al., 2008; Zhu et al., 2009; Awad and Ali, 2014; Giardino and Salzano, 2021; Buoninfante et al., 2022; Das et al., 2022). Therefore, we obtain corrections to the corresponding entropic force due to the presence of a minimal length. Based on Verlinde’s conjecture (Verlinde, 2011), such a modified entropic force turns out as a modified Newton’s law of gravity, thus providing a basis to study the implications of a minimal length on gravitational systems. Specifically, we require the holographic principle to hold, that is, we consider spherically symmetric surfaces of area A = 4πR² separating points in space. Such surfaces behave as the natural place to store information about particles that are inside the surfaces and that can move from one side to another. In this way, the information about the location of particles is stored in discrete bits on the surfaces. This naturally leads to the assumption that the number N_b of bits on the screens can be approximated with the number of particles N_p enclosed by the surfaces, that is, N_b ∼ N_p = N. Then, the total number N of bits of the system, which is measured by its entropy S, can be naturally assumed to be proportional to the surface area A, that is, N ∼ S ∼ A. The total energy E of the system inside the surfaces is distributed on such bits and is related to the surface temperature by the equipartition theorem (or the GUP-modified version thereof). Such energy can be written in terms of the uniformly distributed mass M inside the surface as E = Mc². It should be noticed that the aforementioned reasoning can in principle be applied to any mass distribution, as long as one defines a proper holographic screen of radius R containing the whole distribution.

It turns out that a distance dependence for the GUP parameter β₀ must be assumed to provide a reasonable mechanism to study minimal length effects on rotational curves of galaxies. Such dependence has been proposed in other works as well (see, for e.g., Ref. Ong (2018)) and suggested by the different estimations of the GUP parameter in tabletop experiments, where β₀ > 0 (Pikovski et al., 2012; Bosso et al., 2017; Scardigli et al., 2017; Kumar and Plenio, 2018; Das and Fridman, 2021), and in astrophysical/cosmological observations, where β₀ < 0 (Jizba et al., 2010; Ong, 2018; Buoninfante et al., 2019; Nenmeli et al., 2021; Das et al., 2022; Jizba et al., 2022) (see also Luciano (2021b) for a recent review).

The article is structured as follows: in Section 2, a modification to the equipartition theorem due to GUP is introduced; in Section 3, a modified Newton’s law of gravity is derived from the GUP-modified equipartition theorem and the Bekenstein–Hawking entropy; in Section 4, we summarize our results and include some final remarks.

2 GUP-modified equipartition theorem

One of the reasons to introduce DM is the flatness of galactic rotational curves, which deviate from the behavior predicted based on Kepler’s model considering only luminous matter. In particular, Kepler’s laws predict that the orbital velocities for stars outside the bulge decrease as the square root of the distance from the center, $v(R)\propto 1/\sqrt{R}$. The observation that the orbital velocities are approximately independent of the distance from the center, v(R) ∝ const., even at distances comparable with the galactic radius and beyond, suggests that either Newton’s law of gravity does not hold at such scales, or that non-visible matter, present in galaxies, affects stellar dynamics. As mentioned in Introduction, here we will consider the former, with the intent of studying the implications of a minimal length on galactic rotational curves. Specifically, following Verlinde (2011), we introduce the gravitational force F as an entropic force, which is given as:

$F\mathrm{\Delta }x=T\mathrm{\Delta }S,(3)$

where $\mathrm{\Delta }x=\eta {\lambda }_C=\eta \frac{\hslash }{mc}$ is the displacement from the source of a test particle in terms of its Compton wavelength λ_C, m is the mass of the test particle, η is the modification factor (η = 1 if no modification), T is the effective temperature at a given radius, and ΔS = 2πk_B is the minimal change in entropy, as stated by the information theory (Adami, 2004), with k_B being the Boltzmann constant. The effective temperature T can be expressed in terms of energy E of a thermodynamical system via the equipartition theorem. In our case, we assume that the mass of the system is contained within a sphere of radius R. However, when a minimal length is introduced considering the effects of GUP on statistical mechanics, the equipartition theorem presents some corrections. To see this, we first notice that the GUP-modified density of states in three spatial dimensions reads as (Das and Fridman, 2021),

$g\left(\epsilon \right)=\frac{V{\left(2m\right)}^{3/2}{\epsilon }^{1/2}}{4{\pi }^2{\hslash }^3}\left(1-\frac{75}{4}\beta m\epsilon \right),(4)$

where V is the volume of the system and ɛ is the single particle energy. Since the results in Das and Fridman, (2021) are valid up to order β, the density of states presented previously, and its consequences are understood to hold up to the same order. We anticipate that the volume V will cancel out in our considerations and does not affect the results. Furthermore, it is worth mentioning that GUP is not expected to modify the value of geometrical quantities such as volumes or areas. Since GUP is a phenomenological model of quantum mechanics including a minimal uncertainty in position, GUP only affects the precision with which particles are localized, and therefore the precision with which geometrical quantities are determined, not their actual value. Returning to the expression mentioned previously, it is worth noticing that it reduces to the standard density of states for β → 0, and that such a result is quantum in nature since it is based on the quantum energy spectrum of a particle in a box. In the classical limit ɛ − μ ≫ T, where μ is the chemical potential, and assuming no particles are added or removed from the system, μ = 0, the Bose–Einstein and Fermi–Dirac distributions reduce to

$f_{\text{BE,FD}}\left(\epsilon \right)=\frac{1}{\exp \left(\frac{\epsilon -\mu }{k_{B}T}\right)\mp 1}\approx f\left(\epsilon \right)=\exp \left(-\frac{\epsilon }{k_{B}T}\right),(5)$

where the − and the + signs refer to the Bose–Einstein and Fermi–Dirac distributions, respectively. The limit on the right hand side of Eq. 5 is the Maxwell–Boltzmann distribution.

To proceed further, we compute the number of particles in the system by considering the following ensemble average using the GUP-modified density of states from Eq. 4 and the classical limit for the particle distribution in Eq. 5. We then obtain

$\begin{array}{ll}\hfill N& ={\int }_0^{\infty }g\left(\epsilon \right)f_{\text{BE,FD}}\left(\epsilon \right)\mathrm{d}\epsilon \simeq \frac{V{\left(2m\right)}^{3/2}}{8{\pi }^{3/2}{\hslash }^3}{\left(k_{B}T\right)}^{3/2}\hfill \\ \hfill & \times \left[1-\frac{225}{8}\beta m\left(k_{B}T\right)\right],\hfill \end{array}(6)$

where the additional term with β represents the GUP correction to the number of particles in the system, given the temperature T of the system and the mass of the constituent particles m. The energy of the system is obtained in a similar manner as the number of particles in the system from Eq. 6. In this case, we find

$\begin{array}{ll}\hfill E& ={\int }_0^{\infty }\epsilon g\left(\epsilon \right)f_{\text{BE,FD}}\left(\epsilon \right)\mathrm{d}\epsilon \simeq \frac{3V{\left(2m\right)}^{3/2}}{16{\pi }^{3/2}{\hslash }^3}{\left(k_{B}T\right)}^{5/2}\hfill \\ \hfill & \times \left[1-\frac{375}{8}\beta m\left(k_{B}T\right)\right].\hfill \end{array}(7)$

The aforementioned formula represents the thermal energy of a system in three spatial dimensions. We can recast the expression for the thermal energy in a more familiar form by combining Eqs 6, 7 to obtain the GUP-modified equipartition theorem, which reads as

$E=\frac{n_s}{2}N{k}_{B}T\left[1-\frac{75}{4}\beta m\left(k_{B}T\right)\right],(8)$

in n_s-spatial dimensions. We are going to use this expression with n_s = 1, since the only relevant spatial degree of freedom in the system contributing to the entropic force is the radial one. We can then find an expression of the temperature T as a function of the energy E up to the first order in β, that is,

$T\sim \frac{2E}{k_{B}N}+\beta \frac{75m{E}^2}{k_B{N}^2}.(9)$

Since this expression is derived from a quadratic equation, two solutions in principle are allowed. However, only the solution with the minus sign is considered since it is the only one which returns the standard case as β → 0. For the case of the entropic force, the energy in Eq. 9 is not simply the thermal energy of particles in a given volume but the total energy of the system in that volume.

3 GUP-modified law of gravity

As shown in Verlinde (2011), one can derive Newton’s law of gravity as an entropic force. The same procedure is applied here, with the difference that one includes GUP corrections everywhere they apply. A similar consideration has been discussed in Sheykhi (2020), where a Tsallis entropy modification to the Bekenstein–Hawking (BH) entropy has been used to derive the modified law of gravity. Such an entropy can be modified by GUP through the holographic principle as well (Awad and Ali, 2014; Das et al., 2022). It can then be written as

$\begin{array}{ll}\hfill S& =\frac{c^3{k}_B}{8\hslash G}\left[A+\sqrt{A^2-{\beta }^{\ast }A}-\frac{{\beta }^{\ast }}{2}\right.\hfill \\ \hfill & \left.\times \ln \left(1-\frac{2}{{\beta }^{\ast }}\left(A+\sqrt{A^2-{\beta }^{\ast }A}\right)\right)\right],\hfill \end{array}(10)$

where A is the area of the horizon and β∗ = 12πℏ²β. Such a modification implies a deformation of the temperature of the system. To see this, first, we notice that the total number N of bits of information on the surface of the holographic horizon can be expressed in terms of the horizon entropy as follows (Verlinde, 2011):

$N=\frac{4S}{k_B}.(11)$

Thus, substituting Eq. 11 and Eq. 10 in Eq. 9, we get

$\begin{array}{ll}\hfill T& =\frac{2\hslash GE}{k_B{c}^{3}A}+{\beta }_0\left[\frac{6\pi {\hslash }^{3}GE}{k_B{M}_p^2{c}^5{A}^2}\left(1+\ln \left(2-\frac{M_p^2{c}^{2}A}{3\pi {\hslash }^2{\beta }_0}\right)\right)\right.\hfill \\ \hfill & \left.+\frac{75{\hslash }^2{G}^{2}m{E}^2}{k_B{M}_p^2{c}^8{A}^2}\right].\hfill \end{array}(12)$

It is worth noticing that the temperature T depends on the area A of the holographic horizon and the total energy E of the system. These quantities are related to the radius R of the horizon and the mass M contained within that radius through A = 4πR² and E = Mc², respectively. The temperature from Eq. 12, expressed in terms of R and M, and the aforementioned Δx and ΔS are substituted in Eq. 3, where the GUP-modified Compton wavelength with $\eta =1+{\beta }_0\frac{m^2}{M_p^2}$ (Carr et al., 2020) is considered. Up to leading orders in β₀, we obtain the GUP-modified law of gravity, which is

$\begin{array}{ll}\hfill F& =\frac{GmM}{R^2}+{\beta }_0\left[\frac{3{\hslash }^{2}GmM}{4M_p^2{c}^2{R}^4}\left(1+\ln \left(2-\frac{4M_p^2{c}^2{R}^2}{3{\hslash }^2{\beta }_0}\right)\right)\right.\hfill \\ \hfill & \left.+\frac{75\hslash G^2{m}^2{M}^2}{8M_p^2{c}^3{R}^4}-\frac{G{m}^{3}M}{M_p^2{R}^2}\right].\hfill \end{array}(13)$

Using the expression for the centripetal force $F=m\frac{v^2}{R}$ at radius R, we can then find the GUP-modified rotational velocity, which is

$v=\sqrt{\frac{GM}{R}+{\beta }_0\left[\frac{3{\hslash }^{2}GM}{4M_p^2{c}^2{R}^3}\left(1+\ln \left(2-\frac{4M_p^2{c}^2{R}^2}{3{\hslash }^2{\beta }_0}\right)\right)+\frac{75\hslash G^{2}m{M}^2}{8M_p^2{c}^3{R}^3}-\frac{G{m}^{2}M}{M_p^{2}R}\right]}.(14)$

The test particle, of mass m, can in principle be anything, from a subatomic particle to a large star. However, when a composite system is considered, GUP effects are reduced by the number n of constituents (Amelino-Camelia, 2013). In the present case, this amounts to replacing the modification parameter β₀ by the reduced parameter scaling with the square of the inverse number of constituents, that is, β₀ → β₀/n². It should be noted that n corresponds to the number of constituent particles of the test mass which is different from N, introduced in Eq. 6, which corresponds to the number of bits of information on the holographic screen.

The last term in Eq. 13 that dominates at galactic distances, compared to other correction terms, can be easily verified. Therefore, Eq. 13 can be rewritten as

$F\simeq \frac{G{m}_{\mathit{eff}}M}{R^2},(15)$

where we have defined an effective gravitational mass $m_{\mathit{eff}}=m\left[1-\frac{{\beta }_0}{n^2}\frac{m^2}{M_p^2}\right]$. We notice that this implies a potential GUP-induced violation of the weak equivalence principle, since m_eff ≡ m_g ≠ m ≡ m_i, where m_g is the gravitational mass and m_i is the inertial mass (see also Casadio and Scardigli, (2020)). Since in our framework β₀ < 0, we have m_g > m_i, which might partially justify the higher galaxy rotation velocities with respect to standard cosmological predictions.

From Eq. 14, the GUP-modified velocity for large distances is given as

$v\simeq \sqrt{\frac{GM}{R}\left[1-\frac{{\beta }_0}{n^2}\frac{m^2}{M_p^2}\right]}\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}{\beta }_0<0.(16)$

We point out here that other terms in Eqs 13, 14 dominate at smaller scales, where the GUP effects are significantly smaller. Furthermore, it is worth noticing that, due to the scaling of the modification parameter in Eq. 16, the mass of a star orbiting with velocity v is scaled by the number of fundamental constituents. Assuming that such constituents correspond to the elements in the plasma (mostly electrons and protons for a typical main sequence star), the quantity m/n is of the order of the proton mass regardless of the actual values of m and n. Such assumption will be considered in the following estimations.

It turns out that a distance dependence of the GUP parameter β₀ must be assumed to properly describe the flatness of rotational curves of galaxies. In fact, as can be noticed from Eq. 16, a constant GUP parameter simply shifts the orbital velocity at any given radial position by a constant factor. The assumption that the GUP parameter β₀ takes a distance dependence is compatible with the fact that similar effects are not observed at the solar system scale, at which Kepler’s laws hold, while effects usually associated with DM tend to become relevant approaching galactic and intergalactic scales. This suggests that the GUP parameter β₀ must be distance-dependent since DM effects appear to be distance-dependent. Such an assumption is also supported by Ong (2018) and the difference between estimations of the quadratic GUP parameter in tabletop experiments, where β₀ > 0 (Pikovski et al., 2012; Bosso et al., 2017; Scardigli et al., 2017; Kumar and Plenio, 2018; Das and Fridman, 2021), and in astrophysical/cosmological observations, where β₀ < 0 (Jizba et al., 2010; Ong, 2018; Buoninfante et al., 2019; Nenmeli et al., 2021; Das et al., 2022; Jizba et al., 2022). We propose different models of a distance-dependent β₀:

• Model 1: ${\beta }_0(R)=\gamma \frac{R}{R^{\ast }}$,

• Model 2: ${\beta }_0(R)=\gamma \frac{R^2}{{R^{\ast }}^2}$,

• Model 3: ${\beta }_0(R)=\gamma \ln \left(1+\frac{R}{R^{\ast }}\right)$, and

• Model 4: ${\beta }_0(R)=\gamma \frac{2}{\pi }\arctan \left(\frac{R}{R^{\ast }}\right)$,

where γ < 0 is a constant parameter and R∗ ∼ 1ly is the scale at which effects, associated with DM, become significant. We consider a toy model galaxy with the following matter distribution (Freeman, 1970):

$\rho \left(R\right)={\rho }_0{e}^{-\frac{R}{R_d}},(17)$

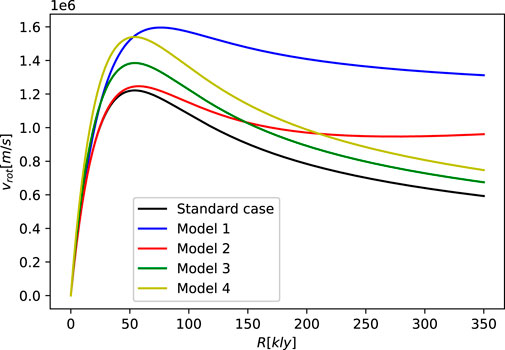
where we chose ρ₀ = 2 × 10^–19 kg/m³ for the central density and R_d = 16,000 ly for the galaxy scale parameter. We use the matter distribution from Eq. 17 to obtain the mass of the galaxy within a certain radius M(R), used in Eq. 16, to obtain Figure 1.

FIGURE 1

FIGURE 1. Galactic rotational curves for different models of R-dependence of β₀.

From Figure 1, we can see that the model which best describes the flatness of rotational curves is model 1, since the Compton correction term dominates at large distances, and the linear model 1 renders it constant. As for the natural logarithm and arc tangent models, they require a much higher peak for the rotational velocities in order to explain the flatness of the curves. Since observations of rotational curves of galaxies show no significant discrepancy from standard Newton’s theory up to about the peak of the curve, such models are not able to fit the observations. The quadratic model 2 can potentially constitute a good description for a different choice of the parameters γ and R∗. Since models 2 and 4 do not describe the DM effects satisfactorily, we are left with models 1 and 2. For these models, we can consider the two different parameters γ and R∗ as only one parameter γ/R∗ and $\gamma /{R^{\ast }}^2$ for models 1 and 2, respectively. The values for these parameters, which were used to obtain the aforementioned graphs, are γ/R∗ = −1.9, ×, 10³³ ly⁻¹ and $\gamma /{R^{\ast }}^2=-3.6\times 10^{27}\mathrm{l}{\mathrm{y}}^{-\mathrm{2}}$ for models 1 and 2, respectively. These values constitute upper bounds for such parameters, namely, |γ/R∗| ≤ 1.9 × 10³³ ly⁻¹ and $|\gamma /{R^{\ast }}^2|\le 3.6\times 10^{27}\mathrm{l}{\mathrm{y}}^{-\mathrm{2}}$, respectively.

4 Conclusion

Newton’s law of gravity can be derived as an entropic force through the holographic principle (Verlinde, 2011). In the present work, we have revised the derivation considering the influence of GUP. Specifically, we have considered the influence of GUP on the temperature T in the equipartition theorem, the Bekenstein–Hawking entropy, and the Compton wavelength. The GUP-corrected law of gravity has then been used to provide an explanation for the flatness of the rotational curves of galaxies. Specifically, alongside the proposed DM content in galaxies, we proposed that GUP effects can contribute to the observed shape of rotational curves. In the case that the GUP parameter β₀ remains constant, the rotational curves of galaxies only get magnified by a constant factor. Therefore, for GUP to effectively influence the rotational curves, we argued that the GUP parameter must be distance-dependent. This claim is directly supported by the work from Ong (2018) and indirectly by a comparison of positive bounds of quadratic GUP parameters estimated from laboratory experiments (Pikovski et al., 2012; Bosso et al., 2017; Scardigli et al., 2017; Kumar and Plenio, 2018; Das and Fridman, 2021) and negative bounds estimated from astrophysical/cosmological observations (Jizba et al., 2010; Ong, 2018; Buoninfante et al., 2019; Nenmeli et al., 2021; Das et al., 2022; Jizba et al., 2022).

We have proposed different models concerning the distance dependence for the GUP parameter β₀ and introduced a new scale parameter R∗ at which GUP effects start to contribute to the shape of the rotational curves of galaxies. Here, we note that the GUP length scale need not be of the order of the Planck length ℓ_p but can be any intermediate length scale $\sqrt{{\beta }_0}{\ell }_p$ between the electroweak and Planck scales, determined by the GUP parameter β₀. For the cases of models 1 and 2, we introduce parameters γ/R∗ and $\gamma /{R^{\ast }}^2$, respectively, since we cannot obtain bounds for γ and R∗ separately. Models 3 and 4 were found to be inadequate to explain the observed DM effects, and there would also be no possibility to combine parameters γ and R∗ in a similar fashion as for models 1 and 2.

Models 1 and 2 constrain the newly defined parameters to |γ/R∗| ≤ 1.9 × 10³³ ly⁻¹ and $|\gamma /{R^{\ast }}^2|\le 3.6\times 10^{27}\mathrm{l}{\mathrm{y}}^{-\mathrm{2}}$, respectively. However, these models can explain the flatness of rotational curves of galaxies only up to an extent. For example, we notice that for model 1 the rotational velocities would remain constant for R → ∞, while for model 2 they would diverge for R → ∞ for any values of the parameters. Furthermore, the approximations used to obtain Eqs 12, 13 break down at sufficiently large R.

The contribution of GUP effects to the shape of rotational curves of galaxies should be determined, once more information on the exact nature of particle DM and its abundance in galaxies is known. Furthermore, the feature of a distance-dependent GUP parameter, leading toward a partial explanation of galactic rotational curves, can be considered a possible additional structure of models of quantum mechanics with a minimal length having astrophysical and cosmological consequences. Finally, it is worth exploring the correspondence between our results and those presented by Ong (2018), Gnatenko and Tkachuk, (2019), and Gnatenko and Tkachuk, (2020), which still exhibit the possibility of a mass-dependent GUP parameter.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Adami, C. (2004). The Physics of information. [arXiv:quant-ph/0405005 [quant-ph]].

Google Scholar

Addazi, A., Alvarez-Muniz, J., Batista, R. A., Amelino-Camelia, G., Antonelli, V., Arzano, M., et al. (2022). Prog. Part. Nucl. Phys. 2022, 103948. [arXiv:2111.05659 [hep-ph]].

Ali, A. F., Das, S., and Vagenas, E. C. (2011). Proposal for testing quantum gravity in the lab. Phys. Rev. D. 84, 044013. [arXiv:1107.3164v2]. doi:10.1103/physrevd.84.044013

CrossRef Full Text | Google Scholar

Amelino-Camelia, G. (2013). Challenge to macroscopic probes of quantum spacetime based on noncommutative geometry. Phys. Rev. Lett. 111, 101301. [arXiv:1304.7271 [gr-qc]]. doi:10.1103/physrevlett.111.101301

PubMed Abstract | CrossRef Full Text | Google Scholar

Arbey, A., and Mahmoudi, F. (2021). Dark matter and the early universe: A review. Prog. Part. Nucl. Phys. 119, 103865. [arXiv:2104.11488 [hep-ph]]. doi:10.1016/j.ppnp.2021.103865

CrossRef Full Text | Google Scholar

Awad, A., and Ali, A. F. (2014). JHEP 06, 093. [arXiv:1404.7825 [gr-qc]].

Bosso, P., Das, S., Pikovski, I., and Vanner, M. R. (2017). Amplified transduction of Planck-scale effects using quantum optics. Phys. Rev. A 96, 023849. [arXiv:1610.06796 [gr-qc]]. doi:10.1103/physreva.96.023849

CrossRef Full Text | Google Scholar

Bosso, P., and Luciano, G. G. (2021). Generalized uncertainty principle: From the harmonic oscillator to a QFT toy model. Eur. Phys. J. C 81, 982. [arXiv:2109.15259 [hep-th]]. doi:10.1140/epjc/s10052-021-09795-1

CrossRef Full Text | Google Scholar

Bosso, P. (2021). On the quasi-position representation in theories with a minimal length. Cl. Quantum Gravity 38, 075021. arXiv:2005.12258 [gr-qc]]. doi:10.1088/1361-6382/abe758

CrossRef Full Text | Google Scholar

Bosso, P. (2018). Rigorous Hamiltonian and Lagrangian analysis of classical and quantum theories with minimal length. Phys. Rev. D. 97, 126010. [arXiv:1804.08202 [gr-qc]]. doi:10.1103/physrevd.97.126010

CrossRef Full Text | Google Scholar

Buoninfante, L., Luciano, G. G., and Petruzziello, L. (2019). Generalized uncertainty principle and corpuscular gravity. Eur. Phys. J. C 79, 663. [arXiv:1903.01382 [gr-qc]]. doi:10.1140/epjc/s10052-019-7164-y

CrossRef Full Text | Google Scholar

Buoninfante, L., Luciano, G. G., Petruzziello, L., and Scardigli, F. (2022). Bekenstein bound and uncertainty relations. Phys. Lett. B 824, 136818. [arXiv:2009.12530 [hep-th]]. doi:10.1016/j.physletb.2021.136818

CrossRef Full Text | Google Scholar

Cai, R. G., Cao, L. M., and Hu, Y. P. (2008). Corrected entropy-area relation and modified Friedmann equations. J. High. Energy Phys. 08, 090. [arXiv:0807.1232 [hep-th]]. doi:10.1088/1126-6708/2008/08/090

CrossRef Full Text | Google Scholar

Carr, B., Mentzer, H., Mureika, J., and Nicolini, P. (2020). Self-complete and GUP-modified charged and spinning black holes. Eur. Phys. J. C 80, 1166. [arXiv:2006.04892 [gr-qc]]. doi:10.1140/epjc/s10052-020-08706-0

CrossRef Full Text | Google Scholar

Casadio, R., and Scardigli, F. (2020). Generalized uncertainty principle, classical mechanics, and general relativity. Phys. Lett. B 807, 135558. [arXiv:2004.04076 [gr-qc]]. doi:10.1016/j.physletb.2020.135558

CrossRef Full Text | Google Scholar

Danshita, I., Hanada, M., and Tezuka, M. (2017). Creating and probing the Sachdev–Ye–Kitaev model with ultracold gases: Towards experimental studies of quantum gravity. Prog. Theor. Exp. Phys. 2017 (8). [arXiv:1606.02454v2]. doi:10.1093/ptep/ptx108

CrossRef Full Text | Google Scholar

Das, S., Fridman, M., Lambiase, G., and Vagenas, E. C. (2022). Baryon asymmetry from the generalized uncertainty principle. Phys. Lett. B 824, 136841. [arXiv:2107.02077 [gr-qc]]. doi:10.1016/j.physletb.2021.136841

CrossRef Full Text | Google Scholar

Das, S., and Fridman, M. (2021). Test of quantum gravity in statistical mechanics. Phys. Rev. D. 104, 026014. [arXiv:2104.04634 [gr-qc]]. doi:10.1103/physrevd.104.026014

CrossRef Full Text | Google Scholar

Dos Santos, M. M., Oniga, T., McLeman, A. S., Caldwell, M., and Wang, C. H.- T. (2013). Toward quantum gravity measurement by cold atoms. J. Plasma Phys. 79 (4), 437–442. [arXiv:1301.0494v2]. doi:10.1017/s0022377813000202

CrossRef Full Text | Google Scholar

Drees, M., and Gerbier, G. (2012). Mini-review of dark matter. [arXiv:1204.2373 [hep-ph]].

Google Scholar

Feller, A., and Livine, E. R. (2016). Ising spin network states for loop quantum gravity: A toy model for phase transitions. Cl. Quantum Grav. 33, 065005. [arXiv:1509.05297v1]. doi:10.1088/0264-9381/33/6/065005

CrossRef Full Text | Google Scholar

Freeman, K. C. (1970). On the disks of spiral and so galaxies. Astrophys. J. 160, 811. doi:10.1086/150474

CrossRef Full Text | Google Scholar

Freese, K. (2009). Review of observational evidence for dark matter in the universe and in upcoming searches for dark stars. EAS Publ. Ser. 36, 113–126. [arXiv:0812.4005 [astro-ph]]. doi:10.1051/eas/0936016

CrossRef Full Text | Google Scholar

Giardino, S., and Salzano, V. (2021). Cosmological constraints on GUP from modified Friedmann equations. Eur. Phys. J. C 81, 110. [arXiv:2006.01580 [gr-qc]]. doi:10.1140/epjc/s10052-021-08914-2

CrossRef Full Text | Google Scholar

Gnatenko, K. P., and Tkachuk, V. M. (2020). Kinetic energy properties and weak equivalence principle in a space with generalized uncertainty principle. Mod. Phys. Lett. A 35 (13), 2050096. [arXiv:1907.07057 [gr-qc]]. doi:10.1142/s0217732320500960

CrossRef Full Text | Google Scholar

Gnatenko, K. P., and Tkachuk, V. M. (2019). Macroscopic body in the Snyder space and minimal length estimation. EPL 125 (5), 50003. [arXiv:1901.10811 [physics.gen-ph]]. doi:10.1209/0295-5075/125/50003

CrossRef Full Text | Google Scholar

Gomes, A. H. (2022). A framework for nonrelativistic isotropic models based on generalized uncertainty principles. [arXiv:2202.02044 [quant-ph]].

Google Scholar

Haine, S. A. (2018). Searching for signatures of quantum gravity in quantum gases. [arXiv:1810.10202v3].

Google Scholar

Hamma, A., and Markopoulou, F. (2011). Background-independent condensed matter models for quantum gravity. New J. Phys. 13, 095006. [arXiv:1011.5754v1]. doi:10.1088/1367-2630/13/9/095006

CrossRef Full Text | Google Scholar

Jizba, P., Kleinert, H., and Scardigli, F. (2010). Uncertainty relation on a world crystal and its applications to micro black holes. Phys. Rev. D. 81, 084030. [arXiv:0912.2253 [hep-th]]. doi:10.1103/physrevd.81.084030

CrossRef Full Text | Google Scholar

Jizba, P., Lambiase, G., Luciano, G. G., and Petruzziello, L. (2022). Decoherence limit of quantum systems obeying generalized uncertainty principle: New paradigm for Tsallis thermostatistics. Phys. Rev. D. 105, L121501. [arXiv:2201.07919 [hep-th]]. doi:10.1103/PhysRevD.105.L121501

CrossRef Full Text | Google Scholar

Kempf, A. (1997). J. Phys. A 30, 2093–2102. [arXiv:hep-th/9604045 [hep-th]].

Kempf, A., Mangano, G., and Mann, R. B. (1996). Hilbert space representation of the minimal length uncertainty relation. [arXiv:9412167v3].

Google Scholar

Kumar, S. P., and Plenio, M. B. (2018). Quantum-optical tests of Planck-scale physics. [arXiv:1708.05659v2].

Google Scholar

Luciano, G. G. (2021). Tsallis statistics and generalized uncertainty principle. Eur. Phys. J. C 81, 672. doi:10.1140/epjc/s10052-021-09486-x

CrossRef Full Text | Google Scholar

Luciano, G. G. (2021). Tsallis statistics and generalized uncertainty principle. Eur. Phys. J. C 81, 672. doi:10.1140/epjc/s10052-021-09486-x

CrossRef Full Text | Google Scholar

Maggiore, M. (1993). A generalized uncertainty principle in quantum gravity. Phys. Lett. B 304, 65–69. [arXiv:hep-th/9301067]. doi:10.1016/0370-2693(93)91401-8

CrossRef Full Text | Google Scholar

Maggiore, M. (1994). Quantum groups, gravity, and the generalized uncertainty principle. Phys. Rev. D. 49, 5182–5187. [arXiv:hep-th/9305163]. doi:10.1103/physrevd.49.5182

PubMed Abstract | CrossRef Full Text | Google Scholar

Maggiore, M. (1993). The algebraic structure of the generalized uncertainty principle. Phys. Lett. B 319, 83–86. [arXiv:hep-th/9309034]. doi:10.1016/0370-2693(93)90785-g

CrossRef Full Text | Google Scholar

Magueijo, J. (2006). Phys. Rev. D. 73, 124020. [arXiv:0603073v2]. doi:10.1103/physrevd.73.124020

CrossRef Full Text

Nenmeli, V., Shankaranarayanan, S., Todorinov, V., and Das, S. (2021). Maximal momentum GUP leads to quadratic gravity. Phys. Lett. B 821, 136621. [arXiv:2106.04141 [gr-qc]]. doi:10.1016/j.physletb.2021.136621

CrossRef Full Text | Google Scholar

Oks, E. (2021). Brief review of recent advances in understanding dark matter and dark energy. New Astron. Rev. 93, 101632. [arXiv:2111.00363 [astro-ph.CO]]. doi:10.1016/j.newar.2021.101632

CrossRef Full Text | Google Scholar

Ong, Y. C. (2018). Generalized uncertainty principle, black holes, and white dwarfs: A tale of two infinities. J. Cosmol. Astropart. Phys. 09, 015. [arXiv:1804.05176 [gr-qc]]. doi:10.1088/1475-7516/2018/09/015

CrossRef Full Text | Google Scholar

Pikovski, I., Vanner, M. R., Aspelmeyer, M., Kim, M. S., and Brukner, Č. (2012). Probing Planck-scale physics with quantum optics. [arXiv:1111.1979v2].

Google Scholar

Scardigli, F., and Casadio, R. (2003). Generalized uncertainty principle, extra dimensions and holography. Cl. Quantum Gravity 20, 3915–3926. [arXiv:0307174]. doi:10.1088/0264-9381/20/18/305

CrossRef Full Text | Google Scholar

Scardigli, F. (1999). Generalized uncertainty principle in quantum gravity from micro-black hole gedanken experiment. Phys. Lett. B 452, 39–44. [arXiv:hep-th/9904025]. doi:10.1016/s0370-2693(99)00167-7

CrossRef Full Text | Google Scholar

Scardigli, F., Lambiase, G., and Vagenas, E. C. (2017). GUP parameter from quantum corrections to the Newtonian potential. Phys. Lett. B 767, 242–246. [arXiv:1611.01469]. doi:10.1016/j.physletb.2017.01.054

CrossRef Full Text | Google Scholar

Sheykhi, A. (2020). New explanation for accelerated expansion and flat galactic rotation curves. Eur. Phys. J. C 80, 25. [arXiv:1912.08693 [physics.gen-ph]]. doi:10.1140/epjc/s10052-019-7599-1

CrossRef Full Text | Google Scholar

van de Kamp, T. W., Marshman, R. J., Bose, S., and Mazumdar, A. (2020). Quantum gravity witness via entanglement of masses: Casimir screening. Phys. Rev. A 102, 062807. [arXiv:2006.06931v2]. doi:10.1103/physreva.102.062807

CrossRef Full Text | Google Scholar

Verlinde, E. P. (2011). JHEP 04, 029. [arXiv:1001.0785 [hep-th]].

Zhu, T., Ren, J. R., and Li, M. F. (2009). Influence of generalized and extended uncertainty principle on thermodynamics of FRW universe. Phys. Lett. B 674, 204–209. [arXiv:0811.0212 [hep-th]]. doi:10.1016/j.physletb.2009.03.020

CrossRef Full Text | Google Scholar