Multiscale hybrid modeling of the impact response of the Earth’s magnetotail to ionospheric O+ outflow

1 Introduction

The Earth’s magnetosphere is sustained by two major plasma sources: the solar wind and the ionosphere. While the solar wind predominantly contains hydrogen (H+) and helium ions (He++), the ionospheric sources include hydrogen, helium (He+) and oxygen (O+) ions. In particular, O+ from the ionosphere is an important source for magnetospheric plasma that plays a significant role in the magnetospheric dynamics (Kistler, 2017). Since O+ originates primarily from the ionosphere, oxygen is commonly used for studying impacts of ionospheric outflows on the magnetosphere, where O+ ions are regularly observed in the lobes, the plasma sheet and the ring current (Kistler, 2017). The O+ content in all cases is higher during geomagnetically active times, with outflow rate increasing with the general planetary activity level (Kp index) (Yau and André, 1997; Cully et al., 2003a). Ionospheric ions can be transported into the magnetosphere through two most important pathways, namely, from the nightside auroral and dayside cusp regions, which form the boundaries between open and closed magnetic field lines (e.g., Liao et al., 2010; Kistler, 2017; Toledo-Redondo et al., 2021).

Ions flowing out from the cusp (“cleft ion fountain”) are heated in this region and either carried toward the magnetopause region or convected over the polar cap at high altitudes into the tail lobes along the open magnetic field lines (Liao et al., 2015). As a result, the lobe field lines above and below the plasma sheet are filled with ionospheric ions that eventually end up in the plasma sheet or become lost in the distant tail. Heavy ions from the ionosphere, accelerated in the cusp/cleft, have been identified as a direct source for the hot plasma in the plasma sheet (Liao et al., 2010). This dayside cusp outflow is a relatively consistent feature, varying with the geomagnetic conditions and the F10.7 index, a proxy of the ionizing UV radiation from the Sun (Mouikis et al., 2010). For instance, tailward streaming O+ beams are commonly observed inside the lobes even during non-storm times (Mouikis et al., 2010). The O+ outflow increases significantly during the storm main phase and drops slightly during the recovery phase, when the convection is enhanced in the magnetotail lobes (Liao et al., 2010). Cully et al. (2003b) found that under times of enhanced convection, the “in flight” ionospheric ions preferentially supply the tail region where substorm activity is thought to originate, and that a reduction in the lobe convection, as caused, for example, by a northward turning of the interplanetary magnetic field (IMF), immediately and dramatically reduces this supply, which may have consequences for substorm triggering.

The other important transport path for ionospheric ions to the magnetotail originates in the nightside auroral region. This outflow is prone to drastic intensifications during times of high geomagnetic activity. This path transports O+ directly into the near-Earth tail plasma sheet without passing through the lobe region (Liao et al., 2010). In some cases, O+ was even found to dominate the total number density of the plasma in the tail. In particular, Kistler et al. (2016) found that the plasma sheet densities closer to the Earth, at 6 − 7R_E (R_E is the Earth radius), were characterized with the O+/H+ ratios about a factor of 10 higher than in the 15–19R_E region. Overall, in terms of mass density, the near-Earth plasma sheet is mostly dominated by the ionospheric source, owing to these O+ contributions (Toledo-Redondo et al., 2021).

At times of high solar and magnetic activity, the overall O+ fluence at the auroral latitudes increases exponentially with Kp up to $\sim 3\times 10^{26}$ ions/s, with O+ ion energies reaching up to 17 KeV (Yau and André, 1997). The nightside polar cap region, where magnetic field lines are open and connected to the IMF, may also serve as an extra source of energetic O+ ions. However, the fluences of these ions $\sim 10^{25}$ ions/s (Yau and André, 1997) are typically lower by an order of magnitude than those originating from the cusp and auroral region. Moreover, ions upflowing from the cusp and auroral oval typically reach higher energies than ions originating directly from the nightside polar cap. Overall outflow fluences of H+ and O+ from the high-latitude region can reach above 10²⁶ ions/s (Toledo-Redondo et al., 2021). These rates vary by at least one order of magnitude, increasing with stronger solar EUV and geophysical activity, especially for heavier O+ ions (Yau and André, 1997; Cully et al., 2003a).

To summarize, the outflowing ionospheric O+ is transported into the magnetosphere through the combined field-aligned (parallel) motion and magnetospheric convection. For southward IMF, magnetopause reconnection results in directing both dayside cusp and nightside auroral outflows toward the magnetotail. The cusp originating ions eventually pass over the nightside polar cap and stream into the lobes on open field lines, whereas the auroral ions may directly be injected into the magnetotail on closed field lines. In both cases, ions flowing from the high-latitude regions are also energized along their trajectories. These trajectories depend on the magnetic latitude (ML) and magnetic local time (MLT) at their initial escape surface (a sphere of radius $\ge 1R_E$). The points of entry of these ions into the magnetotail also depend on their initial energies and pitch angles (i.e., angles between the ion velocity and the magnetic field direction) at their local injection points.

The issue of ionospheric outflow acting as a possible substorm trigger was first raised by Baker et al. (1982), who argued that increased contents of large-gyroradius O+ ions during active times might help destabilize linear ion tearing mode in the thin plasma sheet because the growth rate is proportional to the ion gyroradius. Baker et al. (1982) also reported the asymmetries observed in substorm onset location, with onsets occurring preferentially on the duskside. Baker et al. (1982) related this finding to the observed asymmetries in the O+ content in the tail. Later observations, however, found no dawn-dusk asymmetry in the O+/H+ ratio at 7-8R_E, which suggests that the overall asymmetry in substorm onset location may also have some other explanation (Kistler, 2017).

Examining the ability of the ionospheric O+ ions to significantly affect the local structure and stability of the magnetotail is critical for enabling predictions of potential outflow driven substorms and reconnection regions in the tail at $\ge 20R_E$ (Artemyev et al., 2020). The effects of ionospheric outflow on sawtooth events in the magnetotail and the properties of associated substorms were investigated by Ouellette et al. (2013); Garcia et al. (2010); Brambles et al. (2010), Brambles et al. (2011), Brambles et al. (2013). Recent in situ observations by Angelopoulos et al. (2020) have also indicated that tail reconnection may be powered by intense storms at close geocentric distances $\sim 10R_E$, where magnetic reconnection is normally expected to be suppressed by the Earth’s strong dipole field. These observations also revealed a significant presence of O+ ions (up to $\sim 50\%$) in the tail, in addition to protons. What may lead to reconnection so close to Earth, however, remains an open question, together with a more general question of whether O+ may induce the triggering of reconnection in the magnetotail despite that the observations do not seem to indicate that O+ directly increases the instability of the current sheet to reconnection (Kistler, 2017).

This paper derives its interest from ample evidence suggesting that many substorms may be triggered not only by changes in the solar wind but also by the ability of the ionosphere to populate the tail lobes and the near-Earth region with heavy O+ ions, producing the associated global impact on the magnetotail, as emphasized above. The outflow impact may become especially important when the IMF turns southward, even though enhanced ion outflow delivery to the plasma sheet increases gradually due to a delay in the transport time of O+ ions from their source regions, with ions with greater parallel velocities reaching further down the tail (Moore and Horwitz, 2007; Kistler et al., 2016). In this paper, for the first time, we perform three-dimensional (3D) global hybrid simulations of the Earth’s magnetosphere with O+ outflows. For this purpose, we use a multiscale hybrid code, HYPERS, which treats all ions as kinetic particles and the electrons as a massless quasineutral fluid, as described by Omelchenko and Karimabadi (2012a), Omelchenko and Karimabadi, (2023); Omelchenko et al. (2021a). The purpose of these ion kinetic (“beyond MHD”) simulations is to demonstrate the ability of ionospheric O+ to enter and significantly modify the Earth’s magnetotail. Although the dayside magnetosphere in these simulations is not accurately resolved, it still provides a realistic global configuration for injecting O+ ions.

In Section 2, we briefly review results from the previous simulations of O+ contributions to the tail dynamics, conducted with multi-fluid MHD and local particle-in-cell (PIC) codes. In Section 3, we describe the multiscale HYPERS-Global model, which has recently become available for public use at the NASA CCMC. In Section 4, we compare results from simulations performed for two different scenarios that model the dayside cusp (“lobe”) and “auroral” O+ outflows. We also perform a baseline simulation without outflow. Finally, in Section 5, we summarize the most important points of our study and discuss implications of including ionospheric sources of plasma in the future global multiscale models of the Earth’s magnetosphere.

2 Past simulations of oxygen impact on magnetotail

Global modeling of ionospheric sources of plasma and their impact on the magnetosphere has been performed with multi-fluid magnetohydrodynamics (MHD) codes (e.g., Winglee, 2000; Garcia et al., 2010; Brambles et al., 2010; Brambles et al., 2011; Yu and Ridley, 2013a; Yu and Ridley, 2013b) (for more references see a review by Toledo-Redondo et al. (2021)). In particular, Brambles et al. (2011) used a multi-fluid MHD code to study the effects of auroral outflow on magnetotail dynamics. By combining simulations with quantitative analysis, they showed that the amount of hemispheric outflow flux rate may control the mode of magnetospheric convection. A polar wind outflow model (PWOM) was developed by Glocer et al. (2009) and applied to study the global magnetospheric dynamics and nightside reconnection during a magnetic storm (Ilie et al., 2015). More recently, Varney et al., 2016a,Varney et al., 2016b developed a two-way coupled ionosphere/polar wind model (IPWM) for different ionospheric outflow species.

Local full-electromagnetic Particle-in-Cell (PIC) simulations (e.g., Karimabadi et al., 2011; Liu et al., 2014; Tenfjord et al., 2019) and theoretical models (Zelenyi et al., 2006) have suggested that O+ ions may significantly alter the current sheet structure and properties of magnetotail reconnection. Local multi-fluid Hall-MHD simulations (Shay and Swisdak, 2004) also demonstrated that O+ slows the outflow speed and reconnection rate. Shay and Swisdak (2004), however, argue that the increased geomagnetic activity during storms may “overpower” the local reduction in the reconnection rate due to O+. At the same time, Hesse and Birn (2004) found in their full PIC simulations that the reduction in reconnection rate from O+ is not as large as expected from the simple fluid picture.

MHD simulations with test (not self-consistently modeled) outflow particles have also been performed (e.g., Peroomian et al., 2006; Moore and Horwitz, 2007). The importance of adapting MHD-particle simulations to include self-generated fields and properly assess their effects on ion motion (especially for heavy ions) was emphasized by Moore and Horwitz (2007); Peroomian et al. (2006) after they found out that global test-particle simulations of O+ ions in dynamically evolving MHD fields produced results consistent with observations of the increasing contribution of heavy ions in the near-Earth plasma sheet. MHD simulations, however, give only averaged (Maxwellian) pictures of outflow and magnetotail plasmas since they do not include important kinetic effects observed in the magnetosphere.

Peroomian et al. (2006) launched test O+ particles with an equivalent fluence of up to $\sim 10^{26}$ ions/s from the cusp region in both hemispheres from just below the inner simulation boundary with a radius of 2.5R_E. They argued that the dayside cusp outflow is 10–100 larger than the corresponding fluence of O+ ions from the nightside auroral zone, and therefore there was no need to include the latter in their simulation. This assumption, however, contradicts observations by Yau and André (1997), who measured net auroral O+ fluences up to 2 × 10²⁶ ions/s for large Kp values. An important implication of choosing the cusp source of O+ by Peroomian et al. (2006) was the generation of O+ ion streams over the nightside polar cap into the lobes, as discussed earlier. In addition, the passage of a solar wind shock and the southward turning of IMF in their simulation caused the O+ ions, injected into the lobes, to accelerate and more vigorously penetrate the plasma sheet.

Yu and Ridley (2013a), Yu and Ridley (2013b) performed multi-fluid MHD simulations to examine whether the ionospheric source of the O+ at the inner boundary with a radius of 2.5R_E may produce a significant impact on the magnetotail. In their simulation of the cusp outflow, they chose the ionospheric plasma to flow out from a wedge-shape region at the inner boundary from 65 to 85° magnetic latitude (approximately 74.5–86.8° at the ionospheric altitude when mapped down along dipole magnetic field) and from 11 to 13 magnetic local time (MLT). The simulation of the nightside auroral outflow used a wedge-shape source region at the inner boundary that extended on the nightside from 23 to 1 MLT across the midnight, and from 55 to 75° magnetic latitude (68.7–80.6° at the ionosphere altitude). Both simulations used hemispheric O+ fluences up to 2 × 10²⁶ O+ ions/sec. Similarly, Garcia et al. (2010) used O+ fluences up to 1.4 × 10²⁶ ions/s to simulate O+ ions outflowing from an isolated patch in the nightside auroral zone.

Yu and Ridley (2013b) note that the purpose of specifying such uniform and large (but still within a statistical range of observations) outflow source in their simulations aims at emphasizing the impact of O+ outflow on the magnetotail. We pursue the same goal in our hybrid simulations. Yu and Ridley (2013a) also observe that their nightside auroral outflow simulation, where O+ ions flow directly into the inner magnetosphere and plasma sheet earthward of the normal reconnection line, shows little change in the magnetotail through the entire simulation time, which implies that the mass loading in the tail produces an insignificant impact on initializing substorm onset, even though magnetic flux is constantly advected into the reconnection region.

In contrast with that simulation, the cusp outflow simulation by Yu and Ridley (2013b) indicated that the O+ ions in the tail help trigger tail reconfiguration by compressing the neutral sheet, accumulating magnetic energy in the tail, and then disrupting the tail, which was followed by another disruption. This result is consistent with results from multi-fluid simulations by Wiltberger et al. (2010), who found a second substorm in their O+ outflow model which did not occur in the no-outflow case. Yu and Ridley (2013a) finally conclude that their cusp outflow lands near the tail reconnection region and dramatically disturbs the magnetotail, while the nightside auroral outflow plasma mostly populates the near-Earth plasma sheet, “not encouraging” the release of the accumulated magnetic energy. We find these details particularly important for comparison with our hybrid simulations (see Section 4).

3 HYPERS-Global model

3.1 Hybrid equations

We model the Earth’s magnetosphere with ionospheric O+ sources using a hybrid approach to approximating the full plasma-Maxwell system of equations (see, e.g., Winske et al., 2003). This approach neglects the displacement current in Maxwell’s equations and treats ions as full-orbit kinetic species (macro-particles in our model), moving in self-consistent electric and magnetic fields. The plasma electrons are modeled as a massless quasi-neutral fluid with an adiabatic equation for scalar pressure. This approximation is described by the following set of equations, written in CGS units:

$\mathbf{E}=\frac{{\mathbf{J}}_e\times {\mathbf{B}}_{\mathit{tot}}}{e{n}_{e}c}-\frac{\mathrm{\nabla }{p}_e}{e{n}_e}+\eta \mathbf{J},{\mathbf{B}}_{\mathit{tot}}=\mathbf{B}+{\mathbf{B}}_{\mathit{ext}},(1)$

$\mathrm{\nabla }\times \mathbf{B}=\frac{4\pi }{c}\mathbf{J},\mathbf{J}={\mathbf{J}}_e+{\mathbf{J}}_i,(2)$

$\frac{\partial \mathbf{B}}{\partial t}=-c\mathrm{\nabla }\times \mathbf{E},(3)$

$e{n}_e={\rho }_i,(4)$

$p_e=n_e{T}_e\sim n_e^{\gamma }.(5)$

In Eqs. 1–5, c is the speed of light; e, T_e, n_e, J_e are the electron absolute charge, temperature, number density, and current density, respectively; p_e is the electron pressure, described by Eq. 5 with γ = 5/3; ρ_i, J_i are the total ion charge and current density, computed on the computational mesh by the PIC method; E is the electric field, found from the generalized Ohm’s Eq 1. B, B_ext, B_tot are the “self-generated” (B|_t=0 = 0), “external” (time-steady), and total magnetic fields, respectively.

This plasma approximation is implemented in a multiscale hybrid code, HYPERS (Omelchenko and Karimabadi, 2012a; Omelchenko et al., 2021a). The generalized Ohm’s law Eq. 1 includes a resistive term, where the applied plasma resistivity, η is chosen to be a function of plasma density and current (Omelchenko et al., 2021a). Applied resistivity (not to confuse with numerical resistivity) in hybrid simulations serves two purposes: 1) imitate electron inertia effects in reconnection regions, 2) enable fast magnetic field propagation (diffusion) in low-density and plasma-free regions. The latter is needed because the displacement current is excluded from the Ampere law Eq. 2 in the standard (Darwin) hybrid approximation. Failure to properly treat low-density regions in a hybrid simulation may result in producing non-physical effects (Poppe, 2019; Omelchenko et al., 2021b). In practice, the first two terms in the RHS of Eq. 1 are forced to vanish at “vacuum” cells, with n_e ≤ n_min, n_min ≃ 0.05–0.1n₀, where n₀ is the upstream solar wind electron number density.

The hybrid-PIC model, described by Eqs. 1–5 and coupled with the PIC method for ion macro-particles, provides important “beyond MHD” simulation capabilities, such as the Hall physics and ion kinetic/cyclotron motion effects. This model supports ion cyclotron, whistler, and kinetic-Alfvén wave modes that play a prominant role in regulating plasma turbulence in the Earth’s magnetosphere and impacting its global behavior. In addition, representing ion components with Lagrangian macro-particles avoids numerical diffusion that causes mesh-dependent reconnection and spatial spread of ion sources in fluid simulations (e.g., Yu and Ridley, 2013a). The HYPERS model of the magnetosphere enables using arbitrary ion species for both solar wind and ionospheric outflow. Reconnection onset and dynamics are controlled by the ion kinetics, Hall physics and parameter-dependent resistivity. Ultimately, kinetic effects should be incorporated into global models of the Earth’s magnetosphere, in order to better understand the influence of turbulent plasma dynamics on reconnection.

For presentation purposes, we use GSM coordinates everywhere in this paper. The solar wind plasma in this study consists of protons and electrons. We choose solar wind parameters close to those used in multi-fluid MHD studies by Yu and Ridley (2013a), Yu and Ridley (2013b). The solar wind is continuously injected from the leftmost x-boundary in the negative x-direction with the number density, n_SW = 3 cm⁻³ and speed, v_SW = 350 km/s. The initial electron and proton temperatures are chosen to be equal to 10 eV.

To allow for a magnetic flux barrier to build in the magnetosheath upstream of the dayside magnetopause (Samsonov et al., 2017), the initial IMF field, B_IMF = 5 nT is chosen to be directed northward everywhere. Then, at the simulation time, $t\simeq 10{\mathrm{\Omega }}_{cp}^{-1}$, where Ω_cp is the proton cyclotron frequency computed with respect to the initial IMF strength, the IMF is switched southward at the injection boundary in order to enable dayside magnetopause reconnection and promote tailward convection of lobe magnetic flux, which is also consistent with favorable physical conditions for enhanced ionospheric outflow (Winglee, 2000). The O+ outflow is initiated (see Section 4) at $t\simeq 44{\mathrm{\Omega }}_{cp}^{-1}$, just prior to the arrival of the southward IMF at the subsolar bow shock. All simulations were conducted for the time period $\simeq 600{\mathrm{\Omega }}_{cp}^{-1}$, which is long enough to observe the outflow impact on the magnetotail. The Earth’s dipole is assumed to have no tilt in this study.

3.2 Spatial scales

Normally, hybrid simulations seek to resolve spatial scales of the order of the ion inertial length, d_i and ion cyclotron radius, r_ci. Assuming the Earth’s radius, R_E ∼ 60d_i, to encompass the whole magnetosphere in a global hybrid simulation, the computational domain at minimum should include the magnetopause with a typical standoff distance, R_MP ≃ 10R_E ∼ 600d_i and the magnetotail that stretches far from the Earth to distances $\sim 100R_E\sim 6000d_i$. The CPU-intense nature of hybrid simulations currently prevents running simulations on these large scales in 3D. Therefore, in this study, we scale down the nominal magnetopause standoff distance by reducing the magnetic dipole’s strength, so that R_MP ≃ 100d_i. This numerical dipole, however, is strong enough to resolve the most essential local kinetic features of the magnetosphere (Omidi et al., 2004). Furthermore, as was demonstrated by Tóth et al. (2017), the global magnetospheric solution is not strongly sensitive to this scaling factor, with the ion inertial length dynamics of the numerical model occurring in a self-similar manner with respect to the original plasma system.

In practice, the need to accurately account for inflow and outflow boundary conditions in the presence of the Earth’s magnetic dipole requires multiplying these dimensions by a factor of 2–3. Approximating such large 3D domains with uniform meshes with cell sizes of the order of $\sim 1d_i$ is prohibitively expensive in a global hybrid model. To alleviate this problem, we cover the computational domain with a logically mapped, “stretched” Cartesian mesh (Figure 1). This mesh maintains a uniform spatial resolution of Δx = Δy = Δz = 2d_i in the central part (“patch”) of the domain, which partially covers the lobes and near-Earth tail that are of most interest to this study. This resolution is sufficient to capture the ion kinetic effects in this region. The mesh stretching pushes physical domain boundaries away from the uniform patch, making the Earth’s dipole field vanish at the inflow/outflow (x) and lateral (y and z) boundaries. This helps implement physically consistent local boundary conditions for plasma flow (Omelchenko et al., 2021a).

FIGURE 1

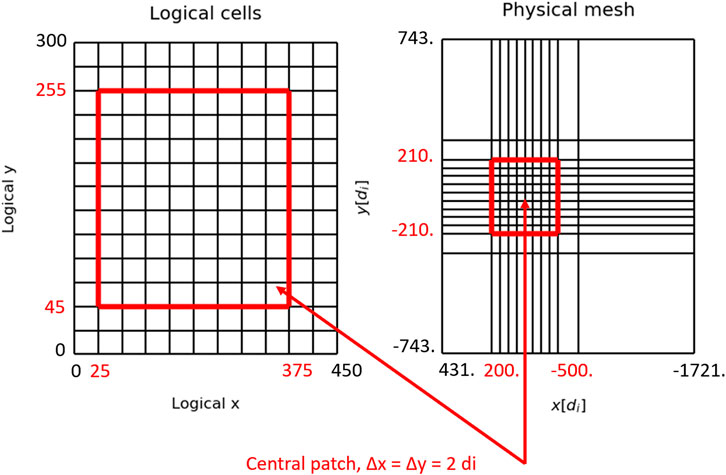
FIGURE 1. 2D (x–y) projections of logical and stretched (physical) meshes. The red color shows the boundaries of a central patch with the maximum uniform resolution of Δx = Δy = 2d_i.

For all simulations in this study, we use a logical mesh of 450 × 300 × 300 cells (see Figure 1). Initially, the uniform patch is initialized with 25 solar wind macro-particles per cell. Outside the patch in the x-direction, the number of particles at each cell is increased according to the physical cell size in this direction. Along the lateral (y and z) axes, the plasma density is initialized uniform by scaling individual weights of ion macro-particles in accordance with physical cell sizes in these directions (Omelchenko et al., 2021a).

During a simulation, each particle found in the uniform patch is dynamically split (just once) into two new particles for better resolution. To maintain the initially specified solar wind plasma, protons are continuously injected into the computational domain at the positive x-boundary with a shifted Maxwellian velocity distribution. The near-Earth environment (“inner magnetosphere”) in this study is not modeled in detail, being represented by a particle-absorbing spherical obstacle with a radius of R_obs = 65d_i = 0.65R_MP. As already mentioned, this numerical obstacle size, when scaled up to realistic magnetospheric dimensions, corresponds to the physical inner domain radius, R_obs = 6.5R_E. Finally, to account for finite ionospheric conductivity effects, we allow the Earth’s magnetic field lines to diffuse across the surface of the inner boundary by assigning a constant resistivity value to the outer shell of the obstacle.

3.3 Temporal scales

Explicit hybrid solvers need to stably integrate electromagnetic fields on the kinetic-Alfvénic and whistler timescales, in addition to the Alfvénic (“MHD”) timescales. Because of the inherent particle noise, hybrid-PIC simulations typically generate whistler mode oscillations with large wave numbers, k ∼ 1/Δ and high frequencies, ω ∼ k² ∼ 1/Δ² (Δ is the local mesh size). If not accurately resolved or resistively damped, these spurious oscillations explosively grow in time and quickly abort the simulation. Therefore, predicting optimum timesteps for computing the multiscale electromagnetic fields in hybrid simulations becomes often difficult in practice.

The problem of choosing global timesteps for the fields is further compounded by the problem of choosing proper timesteps for kinetic ions. For accuracy and stability, full-orbit particle solvers (“pushers”) typically require small timesteps, Δt_p, so that ΩΔt_p ≪ 1, where Ω is the local particle (ion) cyclotron frequency. In the Earth’s magnetosphere, where the local strength of magnetic field greatly varies in space, the need to satisfy this cyclotron constraint for all particles typically results in forcing either small timesteps for all particles or producing inaccurate trajectories for particles in strong magnetic fields. For instance, choosing particle timesteps, Ω₀Δt_p ≃ 0.05, where Ω₀ is the ion cyclotron frequency computed with respect B_IMF, may result in producing large errors in the ion cyclotron orbits and drifts for particles located closer to the inner obstacle (e.g., in the cusp or even some parts of the magnetosheath), where Ω ≥ 10Ω₀. A similar argument about timesteps can be made for non-Maxwellian particles, energized in the self-consistent electromagnetic fields in hybrid simulations. Therefore, in addition to using uniform timesteps for the fields, using the same timesteps for all particles inevitably creates another numerical bottleneck in the hybrid model.

The HYPERS code effectively overcomes this multiscale challenge by implementing an “intelligent” approach to time integration: Event-driven Multi-Agent Planning System (EMAPS), introduced by Omelchenko and Karimabadi (2006a); Omelchenko and Karimabadi (2006b); Omelchenko and Karimabadi (2007); Omelchenko and Karimabadi (2023). The time integration of cell-based fields and Lagrangian particles on a stretched mesh is performed by EMAPS in a “game of life” fashion, so that each computational quantity (cell or particle) is dynamically assigned an individual time increment, with cells being synchronized with other local cells on an “as needed” basis. In this process, EMAPS plays a role of a “simulation time operating system,” which self-adaptively predicts and corrects local time increments. This novel multiscale paradigm has enabled parallel, CPU-efficient 3D hybrid simulations of the Earth’s magnetosphere (Chen et al., 2021; Ng et al., 2021; Omelchenko et al., 2021a; Omelchenko et al., 2021b) and laboratory plasmas (Omelchenko and Karimabadi, 2012b; Omelchenko and Karimabadi, 2023).

Being restricted by the fast ion cyclotron time scales, 3D hybrid simulations of the Earth’s magnetosphere typically run for simulation periods, $t\sim 100-500{\mathrm{\Omega }}_0^{-1}$. Formally, these periods span short magnetospheric times, t < 20 min, compared to hours in global MHD simulations. For convenience of comparing results to certain observations, however, some modelers prefer to multiply these simulation times by typical hybrid model scaling factors, such as the ratio of real to numerical magnetopause distance, or the ratio of simulation to real Alfvén speed (e.g., Lin et al., 2022). This upscaling procedure serves the purpose of presenting hybrid simulation results in “magnetospheric” time. We note that although this time scaling may be useful for comparing some (macro-scale) simulation phenomena with appropriate observations, it is not appropriate for describing physical effects that result from ion-driven turbulence developing on the ion cyclotron scales. In what follows, we measure simulation time in the units of ${\mathrm{\Omega }}_{cp}^{-1}\approx 2s$.

4 Simulations and discussion

In what follows, we present simulation data from the uniform mesh patch only, in GSM coordinates, measured in solar wind proton inertial length (d_i) units. When converting these distances to distances expressed in terms of the Earth’s radius (R_E), we assume that the nominal magnetopause standoff distance (used to calculate the strength of the magnetic dipole) is 10R_E = 100d_i. All simulation quantities are normalized by their appropriate upstream values: Velocities by the Alvfén speed, V_A, temperatures (velocity squares) by $V_A^2$, number densities by n₀, Poynting vector components by $(V_A/4\pi )B_{\mathit{IMF}}^2$, and timesteps by the inverse proton cyclotron frequency, ${\mathrm{\Omega }}_{cp}^{-1}$.

To better assess the impact of different O+ outflows on the magnetotail structure, we first conducted a “baseline” simulation without outflow, where simulation parameters were chosen to ensure that no X-points appear in the tail (including its part that lies outside of the uniform patch shown) during the entire time period, Ω_cpt ∼ 600, adopted for all simulations. Results from this baseline simulation are illustrated in Figure 2. In particular, this Figure presents a regular, well-developed proton (H+) tail, shown at a late simulation time, which is also used to present results from outflow simulations. The main focus of this paper is to demonstrate how different types of O+ outflow may produce tail configurations that are considerably different compared to the baseline case. Other simulation details, e.g., those related to the temporal dynamics of the magnetotail, are left for future discussions.

FIGURE 2

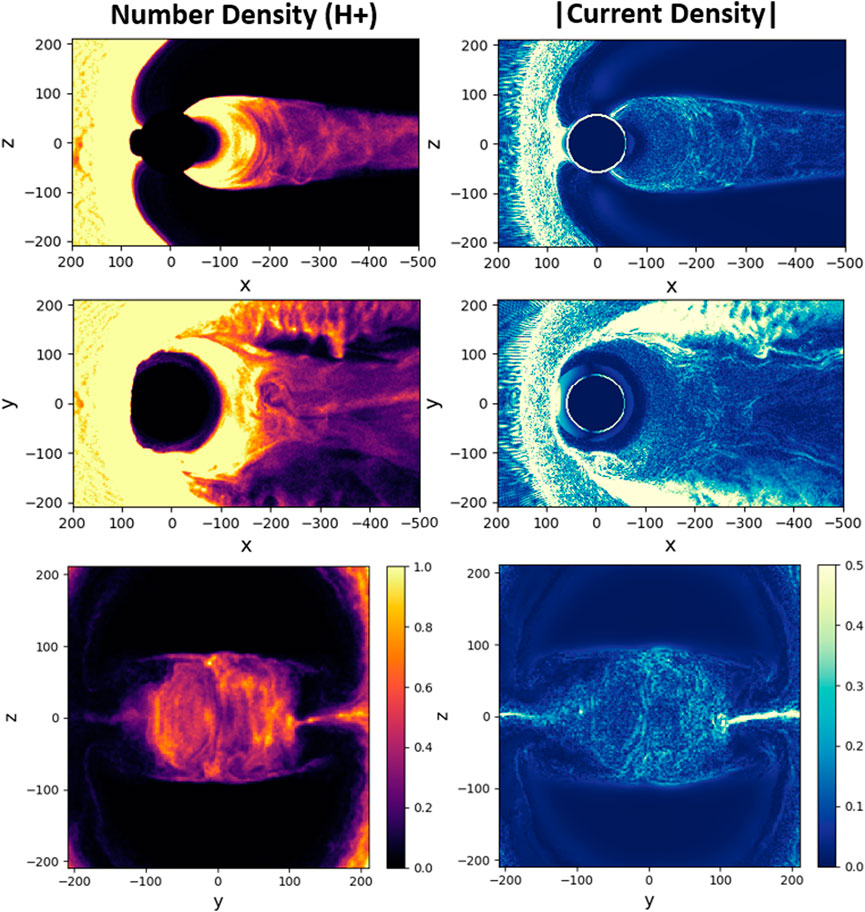
FIGURE 2. H+ number density and absolute value of net current density, |J| in three cross-sections in the baseline simulation (no outflow) at Ω_cpt = 461: x–z (y = 1d_i), x–y (z = 1d_i), and y–z (x = −199d_i).

4.1 Outflow setup

Following (Yu and Ridley, 2013a; Yu and Ridley, 2013b), we initialize nightside O+ outflows in both hemispheres inside wedge-shaped regions located between 11 p.m. and 1 a.m. magnetic local time (MLT) and within specified magnetic latitudes (ML). In these simulations, O+ ions with a parallel speed of 100 km/s and thermal speed of 35 km/s are launched along the magnetic field lines from the inner spherical surface with a radius, R = 65d_i, which approximately corresponds to R = 6.5R_E in the full-size Earth’s magnetosphere. The initial O+ energy in our simulations is consistent with observations at high altitudes (Krcelic et al., 2020) and close to O+ energy values used in the previous MHD simulations (e.g., Yu and Ridley, 2013a; Yu and Ridley, 2013b).

We consider two outflow scenarios, where O+ is injected from different nightside regions of the inner simulation boundary. In the “lobe” scenario, O+ ions are launched between 50 and 75° ML. These values respectively correspond to approximately 75 and 84° at the ionospheric altitude (R = 1R_E), when tracing ion trajectories from the inner boundary along the unperturbed Earth’s dipole lines down to the ionosphere. Physically, these injection points indirectly model the dayside cusp O+ outflow, originating from the ionospheric altitude and streaming along open field lines into the lobes, as discussed in Section 1. For this case, we perform two simulations with different total hemispheric O+ fluences: 1.9 × 10²⁶ ions/s (simulation 1) and 3.8 × 10²⁶ ions/s (simulation 2). In the other, “auroral” scenario, we launch O+ ions between 35 and 50° ML, corresponding to 71 and 75°, respectively, at the ionospheric altitude. In this case, the total hemispheric O+ fluence is approximately 2.6 × 10²⁶ ions/s.

The amount of outflow flux has been shown to be an important factor in determining the global state of the system (Zhang et al., 2020). The total O+ fluences chosen in our simulations are close to the peak O+ fluence values measured in observations (Cully et al., 2003a) and maximum fluences previously used in multi-fluid MHD studies (Garcia et al., 2010; Yu and Ridley, 2013a; Yu and Ridley, 2013b).

As mentioned in Section 3, the O+ outflow is launched approximately when the southward IMF arrives at the subsolar point of the magnetosphere. Following its onset, the streaming ionospheric O+ ions mass load the plasma sheet, increase its thermal pressure, and generate turbulent electromagnetic fields that affect the initial (proton only) magnetotail configuration. Below we discuss global responses of the magnetosphere to the lobe and auroral outflows, as defined above.

4.2 Lobe outflow

In this scenario, O+ ions are injected on the nightside of the inner obstacle surface at high latitudes and arrive at the tail by flowing along open magnetic fields. Without outflow, these lines stretch into the lobes, being void of plasma under steady solar wind/IMF conditions. Figure 3 illustrates the proton tail density and absolute value of the net plasma current density, |J| at Ω_cpt = 461 in the first simulation (the less intense outflow). Compared to the baseline case, (see Figure 2), this Figure clearly shows a significantly perturbed state of the magnetotail, with a turbulent, “wiggling” current sheet. Multiple X-points develop between $\sim 15-20R_E$ during this simulation, with eventually a dominant X-point forming near $\sim 20R_E$.

FIGURE 3

FIGURE 3. H+ number and absolute value of net current density, |J| in three cross-sections in the first lobe outflow simulation at Ω_cpt = 461: x–z (y = 1d_i), x–y (z = 1d_i), and y–z (x = −199d_i).

In this case, the current in the y − z plane demonstrates an asymmetry of the current sheet in the dawn-dusk direction, with denser currents forming on the duskside (positive y). This correlates with the presence of more energetic O+ ions in the plasma sheet on the duskside, as shown in Figure 4 (left column). The dawn-dusk asymmetry in our outflow simulations arises due to the Hall component of electric field that tends to push large-orbit O+ towards the duskside. This effect may be responsible for asymmetric reconnection signatures in observations reported by Baker et al. (1982), as discussed in Section 1. We observe this dawn-dusk asymmetry to be more pronounced in the second lobe simulation, performed with twice as many outflowing O+ ions. The results from this simulation are illustrated in Figure 5. As expected, this Figure shows a significantly more compressed H+ plasma (especially on the duskside), consistent with a larger current density observed in the sheet (not shown). The X-point in this case case develops at approximately the same distance of 20R_E.

FIGURE 4

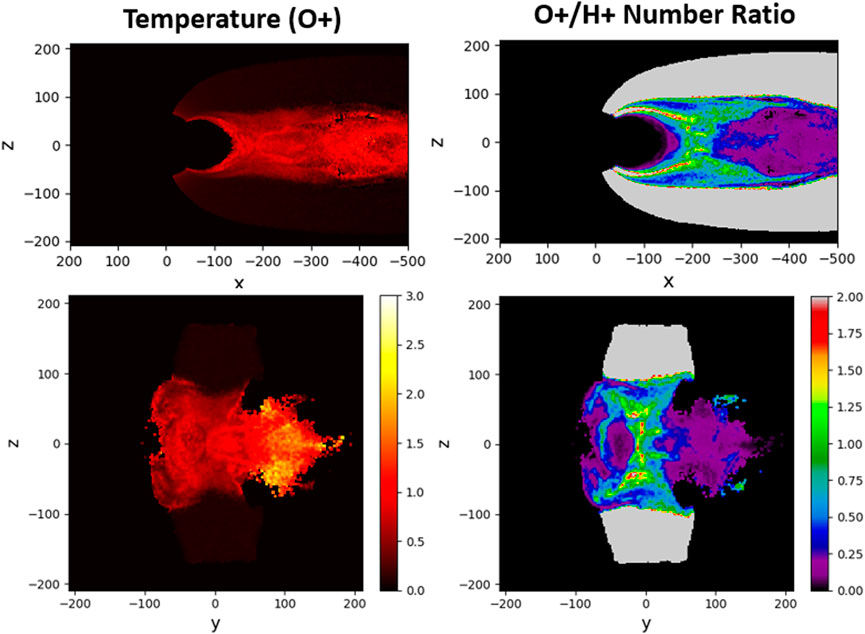
FIGURE 4. O+ temperature and O+/H+ number ratio in two cross-sections in the first lobe outflow simulation at Ω_cpt = 461: x-z (y = 1d_i) and y-z (x = −199d_i).

FIGURE 5

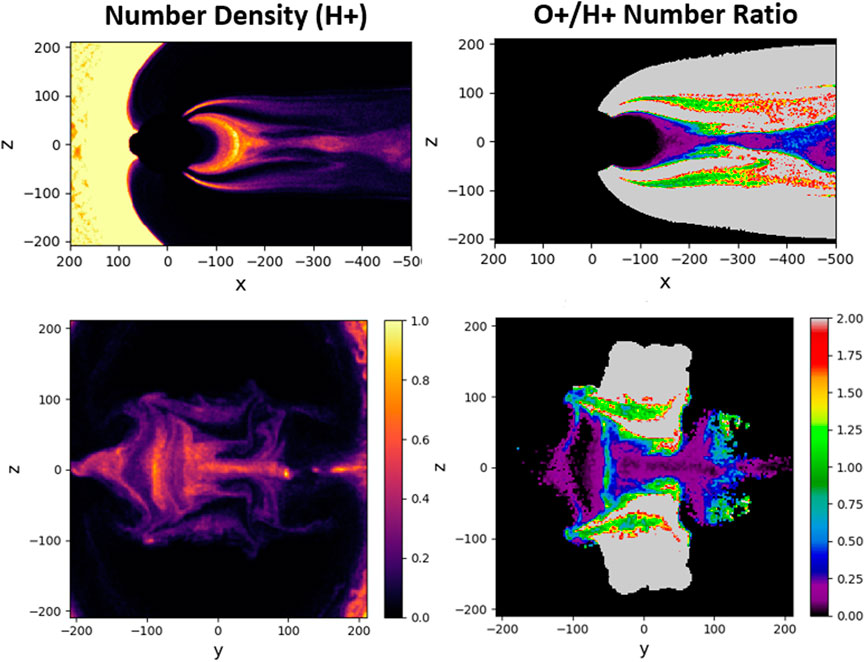
FIGURE 5. H+ number density and O+/H+ number ratio in two cross-sections in the second lobe outflow simulation at Ω_cpt = 314: x–z (y = 1d_i) and y–z (x = −199d_i).

The stronger outflow in the second lobe simulation serves the purpose of generating a faster response of the tail to the “driver” in the absence of more sophisticated details, e.g., initial amounts of O+ in the tail. This simulation demonstrates an interesting feature, shown in the right column of Figure 5, namely, the pushing of O+ ions out of the current sheet to the outer parts if the tail. This configuration, where O+ ions mostly populate the outer regions of the current sheet, correlates with a theoretical model of multilayered current sheet (Zelenyi et al., 2006). This model takes into account the contribution of non-adiabatic O+ ions as a term in the Grad–Shafranov-like system of equations, which describe the quasi-equilibrium of a multi-component (H+ and O+) tail. In this theoretical model, the bulk of the sheet current is carried by H+, while the current “wings” carried by O+.

As noted above, the hybrid model includes many physical effects not accounted for by theory or multi-fluid MHD simulations, among which ion-driven turbulence and ion energization play the most important roles. For instance, Figure 4 illustrates the transient dynamics and heating of O+ ions (left column), along with their relative population in the current sheet with respect to H+ ions (right column) in the first lobe outflow simulation. We observe that the higher temperatures of O+ ions correlate well with the regions of enhanced current density, shown in Figure 3 (right column). This property of O+ ions may serve as a useful diagnostic for future satellite observations.

Kinetic ion effects account for ion-scale plasma turbulence that plays an important role in the local and global dynamics of the dayside magnetosphere (Omelchenko et al., 2021a). Likewise, large-orbit O+ ions perturb the plasma sheet (Baker et al., 1982), enhancing the turbulent effects in the magnetotail, as evident from comparing the tail configurations with and without outflow in our simulations (see Figures 2, 3). As a result, the local inflow, redistribution, and outflow of energy in the tail plasma form a highly dynamic process, where the rate of magnetic flux conversion and concomitant energy dissipation may be enhanced or even controlled by turbulent reconnection, as previously suggested for astrophysical plasmas by Lazarian et al. (2020).

Figure 6 demonstrates an example of energy conversion in the tail near the X-point (x ∼ − 200d_i = −10R_E) due to the impact of lobe O+ ions. This Figure shows components of the “self-generated” Poynting vector, S = (c/4π)E ×B, together with the corresponding ion velocity components, where “V0” and “V1” stand for H+ and O+, respectively. At this moment, the X-point sees an influx of plasma wave energy in the x-direction (Sx panel), kinetic energy of H+ ions in the y-direction (V0y panel), and kinetic energy from O+ ions in the z-direction (V1z panel) on the sunward side of the X-point. The hydrogen V0z component is not shown in this Figure because of its insignificance compared to the oxygen V1z component at this particular moment in time. The energy flows out of the X-point in the form of wave energy in the z-direction (Sz panel) and y-direction (Sy panel), kinetic energy of H+ ions in the x-direction (V0x panel), and kinetic energy of O+ ions in the z-direction (V1z panel) on the tailward side of the X-point. The enhanced current regions also become spots of enhanced resistive dissipation of energy. Overall, the lobe outflow simulations demonstrate that field-line streaming ionospheric O+ ions are capable of creating significant disturbances in the tail upon impact by channeling their energy into the energization of tail ions and resistive (electron) dissipation.

FIGURE 6

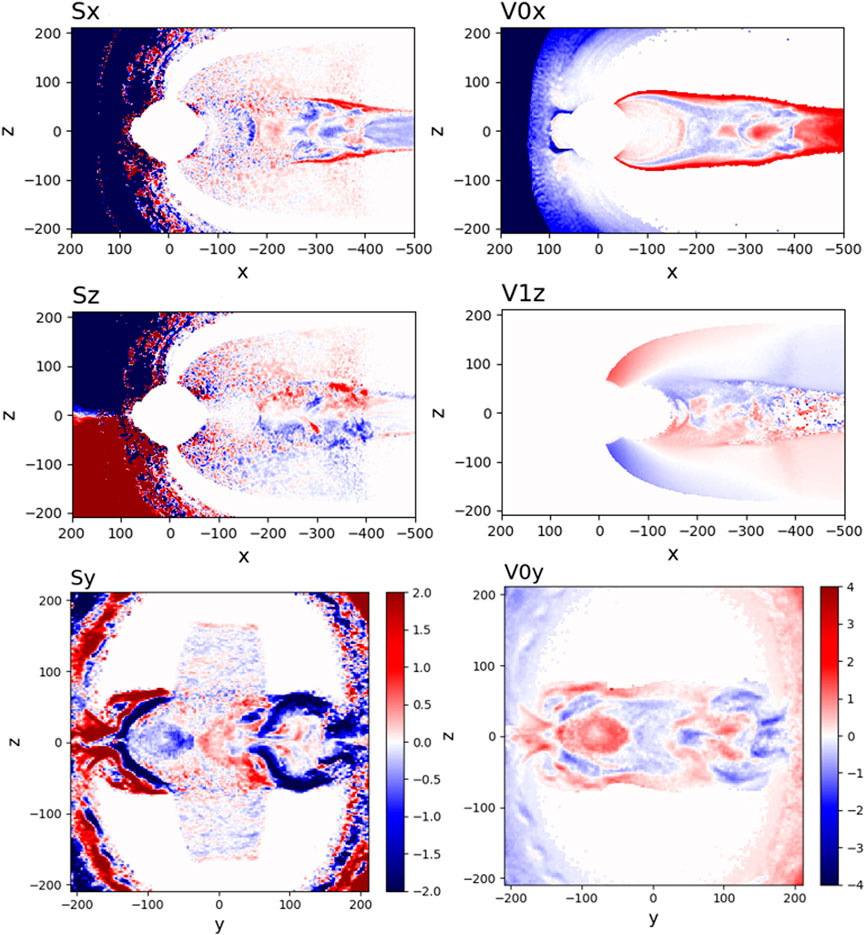
FIGURE 6. Ion velocity (V0 stands for H+ and V1 for O+) and Poynting vector (S) components in two cross-sections in the first lobe outflow simulation at Ω_cpt = 314: x–z (y = 1d_i) and y–z (x = −199d_i).

4.3 Auroral outflow

In this scenario, we inject O+ ions on the nightside of the inner obstacle surface at lower latitudes, so that they directly move into the tail plasma by following closed magnetic field lines in the inner magnetosphere. In MHD simulations of this type of outflow (Yu and Ridley, 2013a), the magnetotail appeared to be steady through the entire simulation, with the X-line staying at around the same distance $(\sim 20R_E)$, contrary to the dayside cusp (“lobe”) outflow case, where the tail was found to experience dramatic changes. Yu and Ridley (2013a) note that the mass loading in the tail in their auroral outflow case did not have a definitive role in initializing or preventing substorm onset, even though a growing amount of magnetic flux was advected into the nominal reconnection region $(\sim 20R_E)$. At the same time, their dayside cusp outflow simulation indicated that heavy O+ ions in the tail helped trigger the tail reconfiguration by compressing and disrupting the neutral sheet. Based on these results, Yu and Ridley (2013a) conclude that the degree of impact of O+ ions on the tail strongly depends on their pathways from the ionosphere into the tail.

The results from our simulation contradict their finding of the insignificant influence of auroral O+ outflow on the magnetotail. Figure 7 shows the H+ density and absolute value of net current density, |J| in the tail for this case at Ω_cpt = 461. These plots clearly indicate that the O+ outflow has dramatically affected the tail stability and resulted in inducing an X-point at x ≃ − 12RE, much closer to the Earth than the X-point distance in the lobe outflow case $(\sim 20RE)$. Moreover, the H+ tail in this (auroral) case undergoes a dramatic disruption in the near-Earth space, with H+ ions being completely flushed out by the streaming O+ ions in some parts of the tail.

FIGURE 7

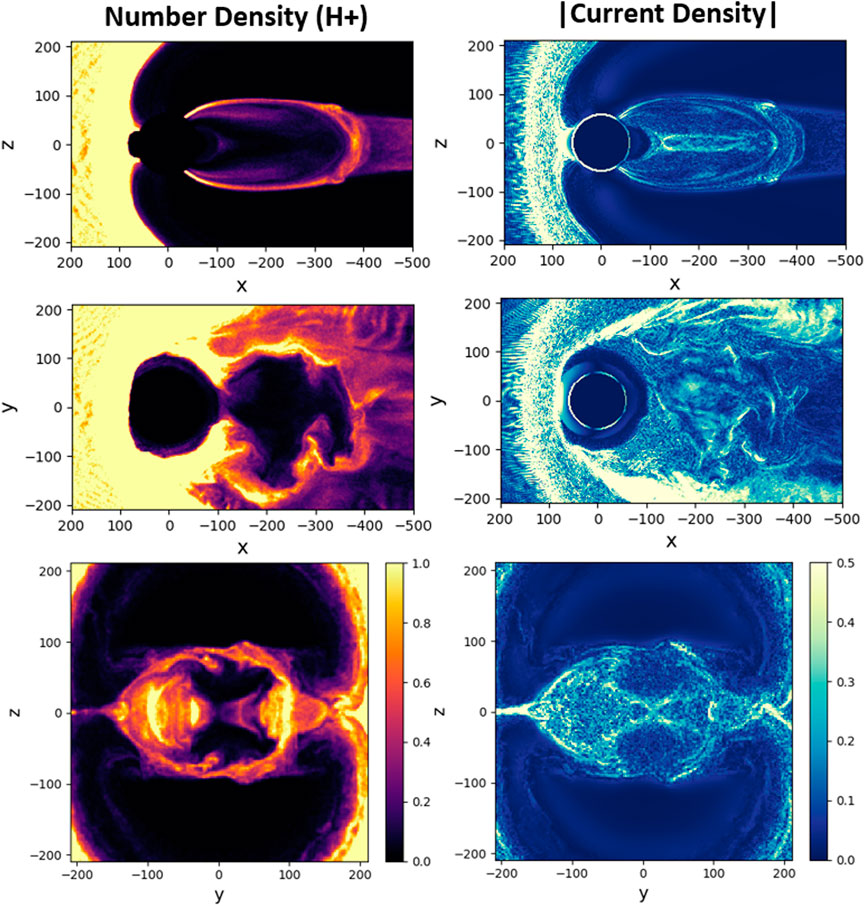
FIGURE 7. H+ number and absolute value of net current density, |J| in three cross-sections in the auroral outflow simulation at Ω_cpt = 461: x–z (y = 1d_i), x–y (z = 1d_i), and y–z (x = −119d_i).

As discussed in Section 1, the recent in situ observations by Angelopoulos et al. (2020) have suggested that magnetotail reconnection may be powered by intense storms at close geocentric distances, $\sim 10R_E$, where no reconnection is normally expected due to the Earth’s strong dipole field. The same observations found a significant percentage of O+ ions (up to $\sim 50\%$) in the tail in addition to protons. Although the upstream conditions in our simulation are different from those observed by Angelopoulos et al. (2020) during a storm, our simulation indicates that strong auroral outflows may serve as a plausible contributing factor to inducing reconnection in this region. This conclusion is also corroborated by results from multi-fluid simulations by Brambles et al. (2011), who demonstrated an X-line forming around $\sim 14R_E$ when auroral outflow was included.

Figure 8 shows temperature and density distributions of O+ ions in the auroral outflow case. By comparing the y–z density panel (O+) in this Figure with the y–z density panel (H+) in Figure 7, we conclude that plasma sheet protons are flushed away from the X-point by O+ ions. This leads to establishing a predominant population of O+ near the X-point and in the outer parts of the tail in the z-direction. This effect may also be related to the findings by Karimabadi et al. (2011), who demonstrated in their local simulations that during the non-linear stage of reconnection the initially dominating protons in the current sheet can be replaced (through a “flushing effect”) by O+ ions coming from the outer parts of the sheet.

FIGURE 8

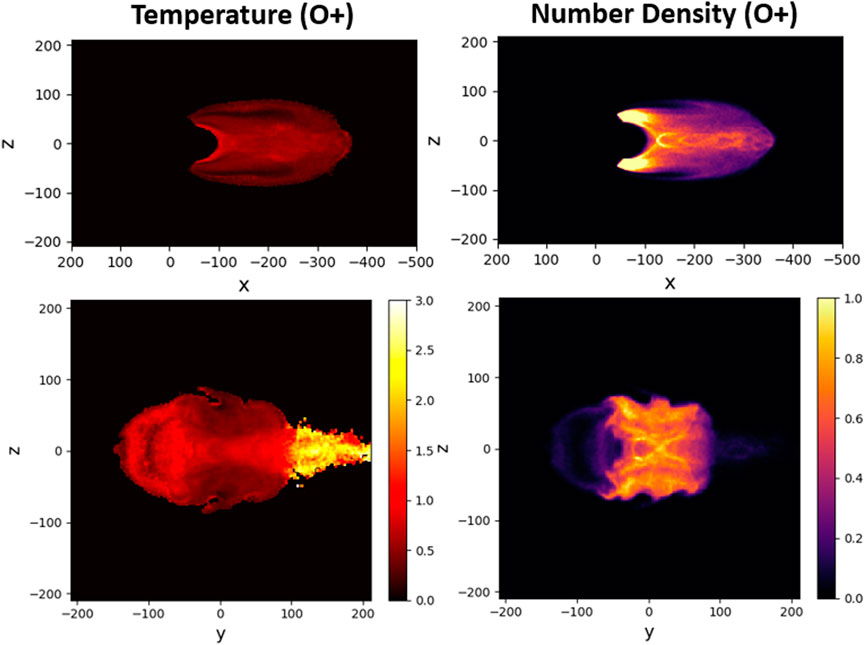
FIGURE 8. O+ temperature and number density in two cross-sections in the auroral outflow simulation at Ω_cpt = 461: x–z (y = 1d_i) and y–z (x = −119d_i).

5 Summary and conclusion

Using a multiscale, self-adaptive hybrid code, HYPERS (Omelchenko and Karimabadi, 2012a; Omelchenko et al., 2021a), we have explored possible impacts of ionospheric O+ outflow on the structure, stability, and dynamics of magnetotail for two different scenarios: “lobe” and “auroral” outflows. In these simulations, we have treated ions of both solar wind (H+) and ionospheric (O+) origin as full-orbit particles with a self-consistent PIC approach.

Our simulations account for the important kinetic (non-Maxwellian, ion cyclotron) and Hall effects that are missing from multi-fluid MHD models. The hybrid model expands the physical richness of global modeling of the Earth’s magnetosphere by adding kinetic turbulence, ion cyclotron motion, and ion energization effects on top of modeling global flow patterns that generally develop in the magnetosphere. Although this increase in physical fidelity comes at a cost of using a downsized Earth model, the physics extracted from hybrid simulations provides many important details, regularly confirmed by space observations (Omelchenko et al., 2021a) and laboratory experiments (Omelchenko and Karimabadi, 2012b; Omelchenko and Karimabadi, 2023) but not described by MHD models (Delzanno and Borovsky, 2022).

As a first step towards self-consistent kinetic modeling of ionospheric outflow in the Earth’s magnetosphere, in this paper we have chosen to explore O+ outflows. In the first (“lobe”) scenario, we have launched O+ ions from higher magnetic latitudes. Physically, this case corresponds to the dayside cusp outflow, where O+ streams along open magnetic field lines over the polar cap on the nightside into the lobes. In the second (“auroral”) scenario, we have injected O+ ions from lower magnetic latitudes into the inner magnetosphere along closed field lines. To model these outflows, we have used hemispheric outflow fluences (the total number of O+ ions injected per second) on the higher side of the spectrum of available observations, similar to those used in the previous MHD simulations.

In the case of lobe O+ ions streaming into the magnetotail, we have discovered that O+ outflow can significantly disrupt the tail structure by inducing X-points at $\sim 20R_E$ distances, which is consistent with MHD results by Yu and Ridley (2013a),Yu and Ridley (2013b). Our simulations, however, emphasize the complex internal dynamics and heating of O+ ions, which are missing from the MHD simulations. In addition, by launching a stronger lobe outflow, we have also demonstrated a multi-layer tail configuration predicted by analytical theory (Zelenyi et al., 2006).

In the case of auroral O+ outflow, our findings disagree with the results from the MHD simulations performed by Yu and Ridley (2013a) for a similar scenario (we note, however, that the numerical setups of outflows in our and their simulations are not identical). In particular, we have found that a strong auroral O+ outflow can induce an X-point in the near-Earth tail, which is consistent with storm observations by Angelopoulos et al. (2020) that also revealed substantial amounts of O+ near the reconnection site.

The multiscale outflow simulations presented in this paper have been powered by an event-driven “simulation time operating system”, EMAPS (Omelchenko and Karimabadi, 2006a; Omelchenko and Karimabadi, 2007; Omelchenko and Karimabadi, 2023). EMAPS replaces time stepping by discrete event simulation. In HYPERS, this enables asynchronous advance of both particles and electromagnetic fields on their local timescales, in accordance with their physical rates and stretched mesh geometry. EMAPS orchestrates asynchronous computation by adaptively limiting per-update increments of all variables to physically reasonable values. In global magnetospheric simulations, this approach prevents numerical instabilities, achieves superior accuracy, and produces significant computational gains, compared to similar time-stepping simulations, where choosing proper timesteps is always a “tug-of-war” battle between code performance on one side and simulation accuracy and stability on the other. To illustrate this point, in Figure 9 we provide snapshots of the cell-averaged H+ and O+ particle timesteps for the time moment used to generate Figure 3 and Figure 4. Smaller particle timesteps in Figure 9 indicate the need for the simulation to increase the local temporal resolution due to the higher local particle energies and/or stronger magnetic fields. For simplicity, we do not show here the field timesteps and timestep distributions for the whole stretched mesh that also take into account the cell size variations (Omelchenko et al., 2021a).

FIGURE 9

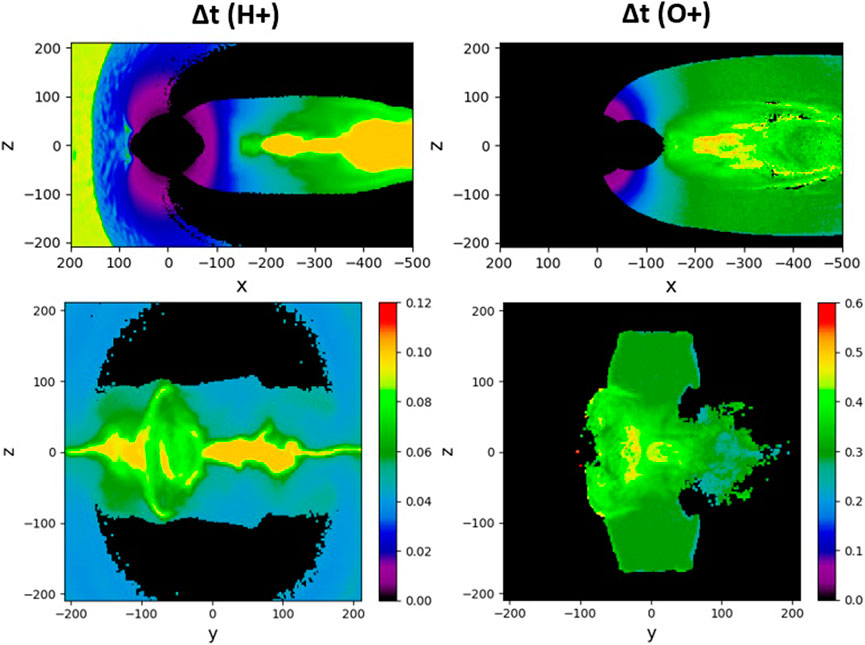
FIGURE 9. Cell-averaged H+ and O+ particle timesteps in two cross-sections in the first lobe outflow simulation at Ω_cpt = 461: x–z (y = 1d_i) and y–z (x = −199d_i).

No single computational study can answer all questions related to the observations of ionospheric O+ ions in the magnetosphere. To further explore the impact of ionospheric outflow on the magnetosphere, especially as a function of different ion sources, particle fluences, source locations, and other magnetospheric parameters, more studies need to be conducted in the future. Although there exist many different physical scenarios for exploring the effects of ionospheric ions both locally and globally, the hybrid model (kinetic ions, fluid electrons) presents a particularly useful computational venue for these studies. To improve our knowledge of the Earth’s magnetosphere, results from hybrid simulations should also be compared with properly scaled MHD and full PIC simulations. By simulating the impact of O+ outflow on the magnetotail, we have made a step in this direction.

Data availability statement

The datasets used in the current study are available from the corresponding author on reasonable request, or they can be reproduced by running the HYPERS-Global model at the NASA CCMC: https://ccmc.gsfc.nasa.gov/.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This work was supported by NASA NNH19ZDA001N-LWS, 80NSSC22K0121, 80NSSC21K1483.

Acknowledgments

Computational resources supporting this work were provided by the NASA High-End Computing (HEC) Program through the NASA Advanced Supercomputing (NAS) Division at Ames Research Center. Each simulation run took approximately 10–12 h of wallclock time on 3,600 CPU cores of the Pleiades supercomputer, depending on the type of processors used. The authors express their gratitude to the NAS personnel, and Johnny Chang in particular, for their timely help with conducting these simulations.

Conflict of interest

Author YO was employed by Trinum Research, Inc.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Angelopoulos, V., Artemyev, A., Phan, T. D., and Miyashita, Y. (2020). Near-earth magnetotail reconnection powers space storms. Nat. Phys. 16, 317–321. doi:10.1038/s41567-019-0749-4

CrossRef Full Text | Google Scholar

Artemyev, A. V., Angelopoulos, V., Runov, A., and Zhang, X. J. (2020). Ionospheric outflow during the substorm growth phase: Themis observations of oxygen ions at the plasma sheet boundary. J. Geophys. Res. Space Phys. 125, e2020JA027933. doi:10.1029/2020ja027933

PubMed Abstract | CrossRef Full Text | Google Scholar

Baker, D. N., Hones, E. W., Young, D. T., and Birn, J. (1982). The possible role of ionospheric oxygen in the initiation and development of plasma sheet instabilities. Geophys. Res. Lett. 9, 1337–1340. doi:10.1029/GL009i012p01337

CrossRef Full Text | Google Scholar

Brambles, O. J., Lotko, W., Damiano, P. A., Zhang, B., Wiltberger, M., and Lyon, J. (2010). Effects of causally driven cusp o+ outflow on the storm time magnetosphere-ionosphere system using a multifluid global simulation. J. Geophys. Res. Space Phys. 115. doi:10.1029/2010JA015469

CrossRef Full Text | Google Scholar

Brambles, O. J., Lotko, W., Zhang, B., Wiltberger, M., Lyon, J., and Strangeway, R. J. (2011). Magnetosphere sawtooth oscillations induced by ionospheric outflow. Science 332, 1183–1186. doi:10.1126/science.1202869

PubMed Abstract | CrossRef Full Text | Google Scholar

Brambles, O. J., Lotko, W., Zhang, B., Ouellette, J., Lyon, J., and Wiltberger, M. (2013). The effects of ionospheric outflow on icme and sir driven sawtooth events. J. Geophys. Res. Space Phys. 118, 6026–6041. doi:10.1002/jgra.50522

CrossRef Full Text | Google Scholar

Chen, L.-J., Ng, J., Omelchenko, Y., and Wang, S. (2021). Magnetopause reconnection and indents induced by foreshock turbulence. Geophys. Res. Lett. 48, e2021GL093029. doi:10.1029/2021GL093029

PubMed Abstract | CrossRef Full Text | Google Scholar

Cully, C. M., Donovan, E. F., Yau, A. W., and Arkos, G. G. (2003a). Akebono/suprathermal mass spectrometer observations of low-energy ion outflow: Dependence on magnetic activity and solar wind conditions. J. Geophys. Res. Space Phys. 108. doi:10.1029/2001JA009200

CrossRef Full Text | Google Scholar

Cully, C. M., Donovan, E. F., Yau, A. W., and Opgenoorth, H. J. (2003b). Supply of thermal ionospheric ions to the central plasma sheet. J. Geophys. Res. Space Phys. 108. doi:10.1029/2002JA009457

CrossRef Full Text | Google Scholar

Delzanno, G. L., and Borovsky, J. E. (2022). The need for a system science approach to global magnetospheric models. Front. Astronomy Space Sci. 9. doi:10.3389/fspas.2022.808629

CrossRef Full Text | Google Scholar

Garcia, K. S., Merkin, V. G., and Hughes, W. J. (2010). Effects of nightside o+ outflow on magnetospheric dynamics: Results of multifluid mhd modeling. J. Geophys. Res. Space Phys. 115. doi:10.1029/2010JA015730

CrossRef Full Text | Google Scholar

Glocer, A., Tóth, G., Gombosi, T., and Welling, D. (2009). Modeling ionospheric outflows and their impact on the magnetosphere, initial results. J. Geophys. Res. Space Phys. 114. doi:10.1029/2009JA014053

CrossRef Full Text | Google Scholar

Hesse, M., and Birn, J. (2004). On the cessation of magnetic reconnection. Ann. Geophys. 22, 603–612. doi:10.5194/angeo-22-603-2004

CrossRef Full Text | Google Scholar

Ilie, R., Liemohn, M. W., Toth, G., Ganushkina, N. Y., and Daldorff, L. K. (2015). Assessing the role of oxygen on ring current formation and evolution through numerical experiments. J. Geophys. Res. Space Phys. 120, 4656–4668. doi:10.1002/2015JA021157

PubMed Abstract | CrossRef Full Text | Google Scholar

Karimabadi, H., Roytershteyn, V., Mouikis, C. G., Kistler, L. M., and Daughton, W. (2011). Flushing effect in reconnection: Effects of minority species of oxygen ions. Planet. Space Sci. 59, 526–536. doi:10.1016/j.pss.2010.07.014

CrossRef Full Text | Google Scholar

Kistler, L. M., Mouikis, C. G., Spence, H. E., Menz, A. M., Skoug, R. M., Funsten, H. O., et al. (2016). The source of o+ in the storm time ring current. J. Geophys. Res. Space Phys. 121, 5333–5349. doi:10.1002/2015JA022204

CrossRef Full Text | Google Scholar

Kistler, L. M. (2017). “Ch. 6. The impact of O+ on magnetotail dynamics,” in Magnetosphere-ionosphere coupling in the solar system. Geophysical monograph. Editors C. R. Chappell, R. W. Schunk, P. M. Banks, J. L. Burch, and R. M. Thorne (John Wiley and Sons), 222, 79–89. doi:10.1002/9781119066880.ch6

CrossRef Full Text | Google Scholar

Krcelic, P., Haaland, S., Maes, L., Slapak, R., and Schillings, A. (2020). Estimating the fate of oxygen ion outflow from the high-altitude cusp. Ann. Geophys. 38, 491–505. doi:10.5194/angeo-38-491-2020

CrossRef Full Text | Google Scholar

Lazarian, A., Eyink, G. L., Jafari, A., Kowal, G., Li, H., Xu, S., et al. (2020). 3d turbulent reconnection: Theory, tests, and astrophysical implications. Phys. Plasmas 27, 012305. doi:10.1063/1.5110603

CrossRef Full Text | Google Scholar

Liao, J., Kistler, L. M., Mouikis, C. G., Klecker, B., Dandouras, I., and Zhang, J. C. (2010). Statistical study of o+ transport from the cusp to the lobes with cluster codif data. J. Geophys. Res. Space Phys. 115. doi:10.1029/2010JA015613

CrossRef Full Text | Google Scholar

Liao, J., Kistler, L. M., Mouikis, C. G., Klecker, B., and Dandouras, I. (2015). Acceleration of o+ from the cusp to the plasma sheet. J. Geophys. Res. Space Phys. 120, 1022–1034. doi:10.1002/2014JA020341

CrossRef Full Text | Google Scholar

Lin, Y., Wang, X. Y., Sibeck, D. G., Wang, C.-P., and Lee, S.-H. (2022). Global asymmetries of hot flow anomalies. Geophys. Res. Lett. 49, e2021GL096970. doi:10.1029/2021GL096970

CrossRef Full Text | Google Scholar

Liu, Y. H., Kistler, L. M., Mouikis, C. G., Roytershteyn, V., and Karimabadi, H. (2014). The scale of the magnetotail reconnecting current sheet in the presence of o+. Geophys. Res. Lett. 41, 4819–4827. doi:10.1002/2014GL060440

CrossRef Full Text | Google Scholar

Moore, T. E., and Horwitz, J. L. (2007). Stellar ablation of planetary atmospheres. Rev. Geophys. 45, RG3002. doi:10.1029/2005RG000194

CrossRef Full Text | Google Scholar

Mouikis, C. G., Kistler, L. M., Liu, Y. H., Klecker, B., Korth, A., and Dandouras, I. (2010). H+ and o+ content of the plasma sheet at 15-19 re as a function of geomagnetic and solar activity. J. Geophys. Res. Space Phys. 115. doi:10.1029/2010JA015978

CrossRef Full Text | Google Scholar

Ng, J., Chen, L.-J., and Omelchenko, Y. A. (2021). Bursty magnetic reconnection at the Earth’s magnetopause triggered by high-speed jets. Phys. Plasmas 28, 092902. doi:10.1063/5.0054394

CrossRef Full Text | Google Scholar

Omelchenko, Y., and Karimabadi, H. (2006a). Event-driven, hybrid particle-in-cell simulation: A new paradigm for multi-scale plasma modeling. J. Comput. Phys. 216, 153–178. doi:10.1016/j.jcp.2005.11.029

CrossRef Full Text | Google Scholar

Omelchenko, Y., and Karimabadi, H. (2006b). Self-adaptive time integration of flux-conservative equations with sources. J. Comput. Phys. 216, 179–194. doi:10.1016/j.jcp.2005.12.008

CrossRef Full Text | Google Scholar

Omelchenko, Y., and Karimabadi, H. (2007). A time-accurate explicit multi-scale technique for gas dynamics. J. Comput. Phys. 226, 282–300. doi:10.1016/j.jcp.2007.04.010

CrossRef Full Text | Google Scholar

Omelchenko, Y. A., and Karimabadi, H. (2012a). HYPERS: A unidimensional asynchronous framework for multiscale hybrid simulations. J. Comput. Phys. 231, 1766–1780. doi:10.1016/j.jcp.2011.11.004

CrossRef Full Text | Google Scholar

Omelchenko, Y. A., and Karimabadi, H. (2012b). Spontaneous generation of a sheared plasma rotation in a field-reversed θ-pinch discharge. Phys. Rev. Lett. 109, 065004. doi:10.1103/PhysRevLett.109.065004

PubMed Abstract | CrossRef Full Text | Google Scholar

Omelchenko, Y. A., and Karimabadi, H. (2023). “EMAPS: An intelligent agent-based technology for simulation of multiscale systems,” in Space and astrophysical plasma simulation. Editor J. Büchner (Springer), 395–428. doi:10.1007/978-3-031-11870-8

CrossRef Full Text | Google Scholar

Omelchenko, Y. A., Chen, L.-J., and Ng, J. (2021a). 3D space-time adaptive hybrid simulations of magnetosheath high-speed jets. J. Geophys. Res. Space Phys. 126, e2020JA029035. doi:10.1029/2020JA029035

CrossRef Full Text | Google Scholar

Omelchenko, Y. A., Roytershtyen, V., Chen, L.-J., Ng, J., and Hietala, H. (2021b). HYPERS simulations of solar wind interactions with the Earth’s magnetosphere and the Moon. J. Atmos. Sol.-Terr. Phys. 215, 105581. doi:10.1016/j.jastp.2021.105581

CrossRef Full Text | Google Scholar

Omidi, N., Blanco-Cano, X., Russell, C., and Karimabadi, H. (2004). Dipolar magnetospheres and their characterization as a function of magnetic moment. Adv. Space Res. 33, 1996–2003. doi:10.1016/j.asr.2003.08.041

CrossRef Full Text | Google Scholar

Ouellette, J. E., Brambles, O. J., Lyon, J. G., Lotko, W., and Rogers, B. N. (2013). Properties of outflow-driven sawtooth substorms. J. Geophys. Res. Space Phys. 118, 3223–3232. doi:10.1002/jgra.50309

CrossRef Full Text | Google Scholar

Peroomian, V., El-Alaoui, M., Abdalla, M. A., and Zelenyi, L. M. (2006). Dynamics of ionospheric o+ ions in the magnetosphere during the 24-25 september 1998 magnetic storm. J. Geophys. Res. Space Phys. 111, A12203. doi:10.1029/2006JA011790

CrossRef Full Text | Google Scholar

Poppe, A. R. (2019). Comment on ”the dominant role of energetic ions in solar wind interaction with the moon” by omidi et al. J. Geophys. Res. Space Phys. 124, 6927–6932. doi:10.1029/2019JA026692

CrossRef Full Text | Google Scholar

Samsonov, A. A., Sibeck, D. G., Dmitrieva, N. P., and Semenov, V. S. (2017). What happens before a southward imf turning reaches the magnetopause? Geophys. Res. Lett. 44, 9159–9166. doi:10.1002/2017GL075020

CrossRef Full Text | Google Scholar

Shay, M. A., and Swisdak, M. (2004). Three-species collisionless reconnection: Effect ofO+on magnetotail reconnection. Phys. Rev. Lett. 93, 175001. doi:10.1103/PhysRevLett.93.175001

PubMed Abstract | CrossRef Full Text | Google Scholar

Tenfjord, P., Hesse, M., Norgren, C., Spinnangr, S. F., and Kolstø, H. (2019). The impact of oxygen on the reconnection rate. Geophys. Res. Lett. 46, 6195–6203. doi:10.1029/2019GL082175

CrossRef Full Text | Google Scholar

Toledo-Redondo, S., André, M., Aunai, N., Chappell, C. R., Dargent, J., Fuselier, S. A., et al. (2021). Impacts of ionospheric ions on magnetic reconnection and earth’s magnetosphere dynamics. Rev. Geophys. 59. doi:10.1029/2020rg000707

CrossRef Full Text | Google Scholar

Tóth, G., Chen, Y., Gombosi, T. I., Cassak, P., Markidis, S., and Peng, I. B. (2017). Scaling the ion inertial length and its implications for modeling reconnection in global simulations. J. Geophys. Res. Space Phys. 122, 10,336–10,355. doi:10.1002/2017JA024189

CrossRef Full Text | Google Scholar

Varney, R. H., Wiltberger, M., Zhang, B., Lotko, W., and Lyon, J. (2016a). Influence of ion outflow in coupled geospace simulations: 1. Physics-based ion outflow model development and sensitivity study. J. Geophys. Res. Space Phys. 121, 9671–9687. doi:10.1002/2016JA022777

CrossRef Full Text | Google Scholar

Varney, R. H., Wiltberger, M., Zhang, B., Lotko, W., and Lyon, J. (2016b). Influence of ion outflow in coupled geospace simulations: 2. sawtooth oscillations driven by physics-based ion outflow. J. Geophys. Res. Space Phys. 121, 9688–9700. doi:10.1002/2016JA022778

CrossRef Full Text | Google Scholar

Wiltberger, M., Lotko, W., Lyon, J. G., Damiano, P., and Merkin, V. (2010). Influence of cusp o+ outflow on magnetotail dynamics in a multifluid mhd model of the magnetosphere. J. Geophys. Res. Space Phys. 115. doi:10.1029/2010JA015579

CrossRef Full Text | Google Scholar

Winglee, R. M. (2000). Mapping of ionospheric outflows into the magnetosphere for varying imf conditions. J. Atmos. Sol.-Terr. Phys. 62, 527–540. doi:10.1016/S1364-6826(00)00015-8

CrossRef Full Text | Google Scholar

Winske, D., Yin, L., Omidi, N., Karimabadi, H., and Quest, K. (2003). “Hybrid simulation codes: Past, present and future - a tutorial,” in Space plasma simulation. Lecture notes in physics. Editors J. Büchner, M. Scholer, and C. T. Dum (Berlin, Heidelberg: Springer Berlin Heidelberg), 615, 136–165. doi:10.1007/3-540-36530-3_8

CrossRef Full Text | Google Scholar

Yau, A., and André, M. (1997). Sources of ion outflow in the high latitude ionosphere. Space Sci. Rev. 80, 1–25. doi:10.1023/A:1004947203046

CrossRef Full Text | Google Scholar

Yu, Y., and Ridley, A. J. (2013a). Exploring the influence of ionospheric o+ outflow on magnetospheric dynamics: Dependence on the source location. J. Geophys. Res. Space Phys. 118, 1711–1722. doi:10.1029/2012JA018411

CrossRef Full Text | Google Scholar

Yu, Y., and Ridley, A. J. (2013b). Exploring the influence of ionospheric o+ outflow on magnetospheric dynamics: The effect of outflow intensity. J. Geophys. Res. Space Phys. 118, 5522–5531. doi:10.1002/jgra.50528

CrossRef Full Text | Google Scholar

Zelenyi, L. M., Malova, H. V., Popov, V. Y., Delcourt, D. C., Ganushkina, N. Y., and Sharma, A. S. (2006). Matreshka” model of multilayered current sheet. Geophys. Res. Lett. 33, L05105. doi:10.1029/2005GL025117

CrossRef Full Text | Google Scholar

Zhang, B., Brambles, O. J., Lotko, W., and Lyon, J. G. (2020). Is nightside outflow required to induce magnetospheric sawtooth oscillations. Geophys. Res. Lett. 47. doi:10.1029/2019GL086419

CrossRef Full Text | Google Scholar