Integral form of the beam envelope equation for electron beam propagation in vacuum and its relation to the K-V equation

The study of the beam envelope radius—a parameter characterizing the transverse size and evolution of a particle beam along its propagation path—is fundamental to the particle accelerators application and the execution of space-borne experiments employing artificial relativistic electron beams. In this paper, we investigate the propagation of electron beams in vacuum and derive an integral form of the beam envelope equation. This equation is equivalent to the simplified differential form of the Kapchinsky-Vladimirsky (K-V) equation excluding the effects of external forces and radial emittance. The integral equation is validated by the widely used ASTRA (A Space Charge Tracking Algorithm) simulation code. The effect of electron energy on beam envelope radius is uncertain and depends on whether internal force or external force dominates. When external force dominates, a decrease in electron energy results in a smaller beam envelope radius. Conversely, when internal force dominates, an increase in electron energy leads to a smaller beam envelope radius. This study is a bridge between integral form and differential form of the envelope equation, and will provide a better understanding for the K-V equation and a scientific basis for researching beam propagation technology.

Key points

• An integral form of the beam envelope equation for electron beam propagation in a vacuum is derived.

• This equation is equivalent to the simplified differential form of the K-V equation excluding the effects of external forces and radial emittance.

• The effect of electron energy on beam radius depends on whether internal or external forces dominate.

1 Introduction

An electron beam is a collection of energetic electrons, typically generated either naturally or artificially (Banks and Raitt, 1988; Winckler, 1980), which are manipulated by electromagnetic fields and directed through a vacuum or plasma (Neubert and Gilchrist, 2002a; Borovsky et al., 2020). Electron beams are found in many space environments, such as the solar wind (Arshad et al., 2014; Sun et al., 2020), magnetic reconnection outflow region (Åsnes et al., 2008), and auroras (Banks and Raitt, 1988), particularly in areas where energetic electrons are accelerated by waves. Electron beams can interact with magnetic fields and background plasma (Druyvesteyn, 1938; Mustafaev, 2001; Arshad and Mirza, 2014; Reeves et al., 2020), playing a significant role in a variety of space phenomena.

Electron beams have proven to be a powerful tool in space science research. During the 1970s and 1980s, keV electron beams were injected from balloons and sounding rockets to probe the fundamental physical processes in space physics. There experiments were used for applications such as mapping magnetic fields lines in the Earth’s magnetosphere [e.g., Hendrickson et al., 1975, 1976; Winckler et al., 1975], exciting artificial auroras, studying beam-plasma interactions [e.g., Gendrin, 1974; Cambou et al., 1978, 1980], and investigating wave generation and amplification as well as instabilities [e.g., Monson et al., 1976; Dechambre et al., 1980]. They also provided insights into spacecraft charging [e.g., Mullen et al., 1986; Sasaki et al., 1986, 1988; Banks et al., 1990], as well as military applications. From the late 1990s to the present, the development of electron accelerator technology (Szuszczewicz, 1985; Lewellen and Buechler, 2019) enabled the injection of relativistic electron beams into the space environment from spacecraft [e.g., Neubert et al., 1996; Krause, 1998, 1999; Gilchrist et al., 2001; Neubert and Gilchrist., 2002b, Neubert and Gilchrist, 2004; Miars et al., 2020; Reeves et al., 2020; Xue et al., 2023; Fang et al., 2024]. Results from these studies indicate that relativistic beams are more stable than keV beams, due to a combination of factors including the higher relativistic electron mass, lower beam densities, and reduced spacecraft charging effects.

In Earth’s auroras, magnetic reconnection generates high-energy electron beams that are accelerated and injected along magnetic field lines into regions such as the ionosphere, forming well-defined beam structures. Electron beams possess high kinetic energy and excellent directional properties, enabling them to interact with spacecraft in orbit and produce space radiation effects, such as surface charging, internal charging, and total ionizing dose effect (Zheng et al., 2019; Bodeau and Baker, 2021). These effects can lead to malfunction in spacecraft, posing significant threats to human spaceflight (Hastings, 1995; Castello et al., 2018). To mitigate or prevent the hazards associated with electron beams, scientists have investigated their generation, propagation, and interaction in the space environment through theoretical analyses and numerical simulations. It is essential for beam envelope control to understand the evolution of electron beam propagation. A critical question in the study of electron beam propagation is identifying the factors that influence the evolution of the electron beam envelope and understanding their quantitative effects.

A significant amount of pioneering work has been conducted to address this question. In 1959, Kapchinsky and Vladimirsky (K-V) made a major breakthrough in beam physics by deriving the envelope equation for a continuous beam with a uniform charge density and an elliptical cross-section (Kapchinsky and Vladimirsky, 1995). This equation accounts for the effects of the self-electric and self-magnetic fields associated with the beam’s space charge and current, as well as external forces. Comparing with the kinetic analysis of single particle, the electron beam tends to diverge owing to space charge forces between two equal-charge particles. Their work became a cornerstone in the field, with profound implications for beam analysis and design. In 1971, Sacherer expanded on this foundation by introducing the concept of root-mean-square (RMS) emittance (Sacherer, 1971). He demonstrated that the K-V equation is not limited to beams with uniform charge density, but is also valid for any charge distribution with elliptical symmetry, provided that the beam boundary and emittance are defined. For convenience, the normalized beam emittance (Lawson, 1988), which represents the product of the beam radius and divergence angle, is used in the K-V equation. The influence of internal forces associated with the beam’s space charge and current remained unclear until the concept of perveance was introduced (Chen and Davidson, 1993), providing a quantitative framework for understanding their role in the K-V equation. When electron beams are injected into plasma instead of a vacuum, the K-V equation must be modified to account for charge neutralization factor (Neubert and Gilchrist, 2002a), as plasma electrons will respond to the beam and move away from it. It is important to note that the K-V equation is a second-order differential equation, and obtaining an analytical expression for the variation of the beam envelope radius with respect to the propagation direction is challenging.

Although K-V equation is a powerful tool for studying the evolution of electron beam envelope, the integral equation is more convenient to describe the variation of the beam envelope radius with respect to the propagation direction. Some theoretical investigations into the integral equation for electron beam propagation have contributed to deriving the expression for perveance in the K-V equation. Bekefi et al. (1980) derived the integral expression for the beam radius at a distance from the source using relativistic particle dynamics. However, their integral expression did not account for the slope of the trajectory at the initial position (Bekefi et al., 1980; Vinokurov, 2001). Reiser added the initial slope to the integral expression, but he overlooked the case in which the slope of the trajectory becomes negative when the beam converges (Reiser, 2008).

Despite the progress made in these studies, further research is still needed on the integral equation governing electron beam propagation. In this paper, we examine the propagation of electron beams in a vacuum and derive an integral form of the beam envelope equation. This equation is equivalent to the simplified differential form of the K-V equation, excluding the effects of external forces and radial emittance. Additionally, we discover that the impact of electron energy on the beam envelope radius is uncertain and depends on whether internal or external forces dominate. The structure of this paper is organized as follows: Section 2 presents the derivation of the integral form of the beam envelope equation and the validation of integral equation by ASTRA simulation code. In Section 3, we provide the relationship between the integral form and the K-V equation. Finally, Section 4 offers a briefly discussion of the conclusions.

2 The electron beam envelope integral equation

This section presents the derivation of the integral form equation and benchmarks the theoretical electron beam envelope models against numerical simulations performed with ASTRA (A Space Charge Tracking Algorithm). In addition, the quantitative impact of several factors on the electron beam envelope radius is provided.

2.1 Derivation of the electron beam envelope integral equation

The following simplifying assumptions have been made in deriving the equations: (1) The electron density is assumed to be uniform within the cylindrical beam and zero outside it; (2) The transverse velocity component of the electrons is assumed to be small compared to the axial velocity, meaning the angle with the axis (slope) is small; (3) The flow is laminar, meaning all beam particles follow trajectories that do not intersect.

Based on the first assumption, the electron beam is treated as a long cylinder with a maximum radius r_b and a number density n₀. The assumption of uniform charge density results in space-charge forces that are linearly proportional to the distance from the beam’s center. This linear relationship significantly simplifies the equations of motion, making them analytically solvable. Without the assumption of uniform charge density, the charge density ρ(r) varies with radial distance r. This variation alters the calculation of the space charge force. Under the uniform charge density assumption, the radial space charge force $F_r=qE=q{E}_r=\frac{q{\rho }_{0}r}{2{ϵ}_0}$ exhibits a simple linear dependence on r. In contrast, for a Gaussian charge density distribution defined as $\rho \left(r\right)={\rho }_0{e}^{\left(-\frac{r^2}{2{\sigma }^2}\right)}$, where ${\rho }_0$ is the central charge density and is σ the standard deviation, $F_r=q{E}_r=\frac{q}{r{ϵ}_0}{\int }_0^r\rho \left(r^{\prime }\right)r^{\prime }d{r}^{\prime }$ leads to nonlinear behavior. Such nonlinear forces cause particle trajectories to deviate from simple linear oscillations, which can increase beam diffusion or emittance growth and complicate analytical solutions. However, real beams often exhibit non-uniform density distributions, such as Gaussian or parabolic distributions, which lead to nonlinear space-charge forces that the model fails to account for (Arshad et al., 2017a; Arshad 2018; Arshad and Poedts, 2020). Consequently, this limitation restricts the model’s accuracy and applicability, particularly in scenarios involving high-intensity beams, non-uniform density distributions, or dynamic conditions where nonlinear phenomena—such as emittance growth, filamentation, or instabilities—play a significant role (Arshad et al., 2017b; Arshad et al., 2022; Arshad et al., 2011). Nevertheless, the model retains practical value for how to moderate intensity beams, where space-charge effects are minimal, the uniform density assumption remains reasonably valid, and the linear approximation offers an adequate description.

As indicated by the second assumption, the velocity of the electrons in the beam, v, is primarily directed along the axial direction (i.e., v_r << v, v_θ<<v, v_z ≈ v, v_r is the radial component of velocity, v_θ is the angular component of velocity, and v_z is the axial component of velocity.). Thus, the charge density is ${\rho }_0=-\mathrm{e}{n}_0$ and the beam current $I_0=-\mathrm{e}{n}_0\mathrm{\pi }{r}_b^{2}v$, where $\mathrm{e}$ refers to the charge of the electron. The radial component of electric field is obtained using Gauss’s law (Buchholz, 1986), $\int {ϵ}_{0}E·dS=\int \rho dV$, which yields

$E_r=\frac{{\rho }_0{r}_b}{2{\mathrm{\epsilon }}_0}(1)$

$E_r=\frac{I_0}{2\mathrm{\pi }{\mathrm{\epsilon }}_0{r}_{b}v}(2)$

The azimuthal component of magnetic field is obtained using Ampère’s circuital law (Cavalleri et al., 1996), $\int B·dl={\mathrm{\mu }}_{0}I$, which gives

$B_{\theta }=\frac{{\mathrm{\mu }}_0{I}_0}{2\mathrm{\pi }{r}_b}(3)$

$E_r$ and $B_{\theta }$ refer to the electric and magnetic fields outside the beam. We now examine the motion of a beam particle in this field, using only the radial force equation (Reiser, 2008)

$\frac{d}{dt}\left(\gamma {\mathrm{m}}_0\frac{d{r}_b}{dt}\right)=-\mathrm{e}\left(E_r-v_z{B}_{\theta }\right)(4)$

where we neglect the force term $-\mathrm{e}r\frac{d\theta }{dt}{B}_z$ on the grounds that $r\frac{d\theta }{dt}$ is negligibly small, and γ is constant since there is no external acceleration. γ refers to the Lorentz factor, defined as $\gamma =\frac{1}{\sqrt{1-{\beta }^2}}$, where $\beta =\frac{v}{c}$ and c denotes the speed of light. Substituting E_r from Equations 1, 2, B_θ from Equation 3, $v_z=v=\beta c$, and the expression of I₀, Equation 4 becomes Equations 5, 6

$\frac{d^2{r}_b}{d{t}^2}=\frac{{\mathrm{e}}^2{n}_0{r}_b}{2{\mathrm{\epsilon }}_0{\mathrm{m}}_0{\gamma }^3}(5)$

$\frac{d^2{r}_b}{d{t}^2}=-\frac{\mathrm{e}{I}_0}{2\mathrm{\pi }{\mathrm{\epsilon }}_0{\mathrm{m}}_0{r}_b\beta \mathrm{c}{\gamma }^3}(6)$

Using the relationship $\frac{d^2{r}_b}{d{t}^2}=v_z\frac{d}{dz}\left(v_z\frac{d{r}_b}{dz}\right)={\left(\beta \mathrm{c}\right)}^2\frac{d^2{r}_b}{d{z}^2}$, Equation 6 becomes

$\frac{d^2{r}_b}{d{z}^2}=-\frac{\mathrm{e}{I}_0}{2\pi {\mathrm{\epsilon }}_0{\mathrm{m}}_0{r_b\beta }^3{\mathrm{c}}^3{\gamma }^3}(7)$

The perveance K, a dimensionless quantity, is defined by Chen and Davidson (1993) as Equations 8, 9

$K=-\frac{\mathrm{e}{I}_0}{2\pi {\mathrm{\epsilon }}_0{\mathrm{m}}_0{\mathrm{c}}^3{\beta }^3{\gamma }^3}(8)$

$K=\frac{2I_0}{{{\beta }^3\gamma }^3{\mathrm{I}}_{\mathrm{A}}}(9)$

where ${\mathrm{I}}_{\mathrm{A}}=\frac{4\mathrm{\pi }{\mathrm{\epsilon }}_0{\mathrm{m}}_0{\mathrm{c}}^3}{-\mathrm{e}}$ and $\beta \gamma =\sqrt{{\left(1+\frac{E}{{\mathrm{m}}_0{\mathrm{c}}^2}\right)}^2-1}$ and E is the kinetic energy. In terms of the perveance, as defined in Equation 9, Equation 7 can be expressed as

$\frac{d^2{r}_b}{d{z}^2}=\frac{K}{r_b}(10)$

It is important to note that K > 0 for electrons. Multiplying both sides of Equation 10 by $r^{\prime }=\frac{d{r}_b}{dz}$, we obtain

$r^{\prime }{r}^{″}=\frac{K}{r_b}{r}^{\prime }(11)$

By integrating Equation 11, we get

${r^{\prime }}^2-2K\ln r_b=\text{const}(12)$

Evaluating Equation 12 with the initial boundary conditions r_b = $a$ and $r^{\prime }=r_0^{\prime }$ at z = 0 where $a$ refers to initial beam radius and $r_0^{\prime }$ refers to the initial change rate of the beam radius along the z-axis, we obtain ${r^{\prime }}^2-2K\ln r_b={r_0^{\prime }}^2-2K\ln a$, or equivalently,

$\frac{d{r}_b}{dz}=\pm \sqrt{{r_0^{\prime }}^2+2K\ln \left(\frac{r_b}{a}\right)}(13)$

Next, we integrate Equation 13 by defining u = $\sqrt{\frac{{r_0^{\prime }}^2}{2K}+\ln \left(\frac{r_b}{a}\right)}$, which yields Equations 14, 15

$z=\pm {\int }_a^{r_b}\frac{d{r}_b}{\sqrt{{r_0^{\prime }}^2+2K\ln \left(\frac{r_b}{a}\right)}}(14)$

$z=\pm \frac{1}{\sqrt{2K}}{\int }_{\left|\frac{r_0^{\prime }}{2K}\right|}^{\sqrt{\frac{{r_0^{\prime }}^2}{2K}+\ln \left(\frac{r_b}{a}\right)}}\frac{1}{u}\frac{d{r}_b}{du}du(15)$

From the expression of u, we have

$\frac{d{r}_b}{du}=2auexp\left(u^2-\frac{{r_0^{\prime }}^2}{2K}\right)(16)$

Substituting Equation 16 into the Equation 15, we obtain

$z=\pm a\sqrt{\frac{2}{K}}\mathit{exp}\left(-\frac{{r_0^{\prime }}^2}{2K}\right){\int }_{\frac{\left|r_0^{\prime }\right|}{2K}}^{\sqrt{\frac{{r_0^{\prime }}^2}{2K}+\ln \left(\frac{r_b}{a}\right)}}{e}^{u^2}du(17)$

The Dawson integral is given by $F\left(w\right)=e^{-w^2}{\int }_0^w{e}^{u^2}du$. If the initial slope of the trajectory is greater than or equal to zero (i.e., $r_0^{\prime }\ge 0$), Equation 17 can be written as Equations 18, 19

$z=a\sqrt{\frac{2}{K}}\mathit{exp}\left(-\frac{{r_0^{\prime }}^2}{2K}\right){\int }_{\frac{r_0^{\prime }}{\sqrt{2K}}}^{\sqrt{\frac{{r_0^{\prime }}^2}{2K}+\ln \left(\frac{r_b}{a}\right)}}{e}^{u^2}du(18)$

$z=\sqrt{\frac{2}{K}}\left[-aF\left(\frac{\left|r_0^{\prime }\right|}{\sqrt{2K}}\right)+r_{b}F\left(\sqrt{\frac{{r_0^{\prime }}^2}{2K}+\ln \left(\frac{r_b}{a}\right)}\right)\right](19)$

using the expression for the Dawson integral. If the initial slope of the beam profile is negative ($r_0^{\prime }$ < 0), the beam radius will initially decrease until it reaches a minimum value, where $r^{\prime }$ = 0. According to Equation 13, the minimum beam radius is given by r_min = $a\exp \left(-\frac{{r_0^{\prime }}^2}{2K}\right)$. Beyond this point, the beam radius will increase again. Under the conditions that the initial slope of the trajectory is negative (i.e., $r_0^{\prime }<0$) and r_b > r_min, Equation 17 can be written as Equations 20, 21

$z=a\sqrt{\frac{2}{K}}\mathit{exp}\left(-\frac{{r_0^{\prime }}^2}{2K}\right){\int }_{-\frac{r_0^{\prime }}{\sqrt{2K}}}^{\sqrt{\frac{{r_0^{\prime }}^2}{2K}+\ln \left(\frac{r_b}{a}\right)}}{e}^{u^2}du(20)$

$z=\sqrt{\frac{2}{K}}\left[-aF\left(\frac{\left|r_0^{\prime }\right|}{\sqrt{2K}}\right)+r_{b}F\left(\sqrt{\frac{{r_0^{\prime }}^2}{2K}+\ln \left(\frac{r_b}{a}\right)}\right)\right](21)$

where F(w) represents the Dawson integral. When the initial slope of the trajectory is negative (i.e., $r_0^{\prime }<0$) and r_b < r_min, Equation 17 becomes

$z=-a\sqrt{\frac{2}{K}}\mathit{exp}\left(-\frac{{r_0^{\prime }}^2}{2K}\right){\int }_{-\frac{r_0^{\prime }}{\sqrt{2K}}}^{\sqrt{\frac{{r_0^{\prime }}^2}{2K}+\ln \left(\frac{r_b}{a}\right)}}{e}^{u^2}du(22)$

$z=-\sqrt{\frac{2}{K}}\left[-aF\left(\frac{\left|r_0^{\prime }\right|}{\sqrt{2K}}\right)+r_{b}F\left(\sqrt{\frac{{r_0^{\prime }}^2}{2K}+\ln \left(\frac{r_b}{a}\right)}\right)\right](23)$

By combining Equations 19, 21, 23, we obtain

$z=\pm \sqrt{\frac{2}{K}}\left[-aF\left(\frac{\left|r_0^{\prime }\right|}{\sqrt{2K}}\right)+r_{b}F\left(\sqrt{\frac{{r_0^{\prime }}^2}{2K}+\ln \left(\frac{r_b}{a}\right)}\right)\right](24)$

The negative sign in Equation 17 applies when $r_0^{\prime }<0$ and r_b < $a\exp \left(-\frac{{r_0^{\prime }}^2}{2K}\right)$, while the positive sign applies in all other cases. Figure 1 illustrates the variation of beam radius (r_b) as a function of propagation distance (z) under three initial conditions: $r_0^{\prime }$ > 0 (blue curve), $r_0^{\prime }$ = 0 (black curve), and $r_0^{\prime }$ < 0 (red curve) with an energy of E = 1 MeV, current I₀ = 1 mA and initial beam radius a = 0.2 m. The blue curve represents a scenario where the initial slope of trajectory is positive, resulting in a monotonic increase. A positive initial slope of trajectory ($r_0^{\prime }$ > 0) indicates that particles possess outward-directed transverse velocities. This results in beam divergence during the initial propagation phase, owing predominantly to Coulomb repulsion from space charge forces. The black curve corresponds to a zero-initial slope, leading to a steady increase without an inflection point. In this situation, the beam possesses a perfectly parallel trajectory with a uniform transverse velocity distribution. The red curve reflects a negative initial slope, showing an initial decrease followed by an upward trend. A negative initial slope of trajectory ($r_0^{\prime }$ < 0) is permissible when well-defined initial conditions are imposed, such as particles with initial velocities precisely aligned toward the beam axis.

Figure 1

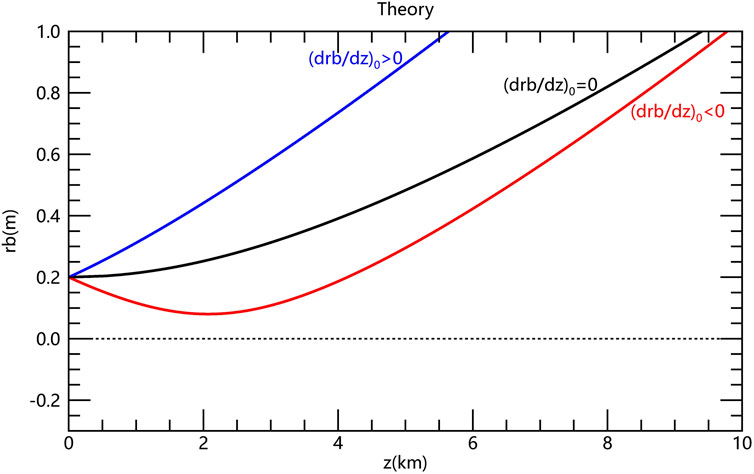0," a black line with zero slope labeled "(drb/dz)_0 = 0," and a red line with negative slope labeled "(drb/dz)_0 < 0."" id="F1" loading="lazy">

Figure 1. The theorical electron beam envelope radius as a function of propagation distance for three initial slopes of the trajectory ($r_0^{\prime }={10}^{-4},r_0^{\prime }=0\text{\hspace{0.17em}and\hspace{0.17em}} r_0^{\prime }={-10}^{-4}$) with an energy of E = 1 MeV, current I₀ = 1 mA and initial beam radius $a$ = 0.2 m.

2.2 Numerical verification of electron beam envelope equations with ASTRA

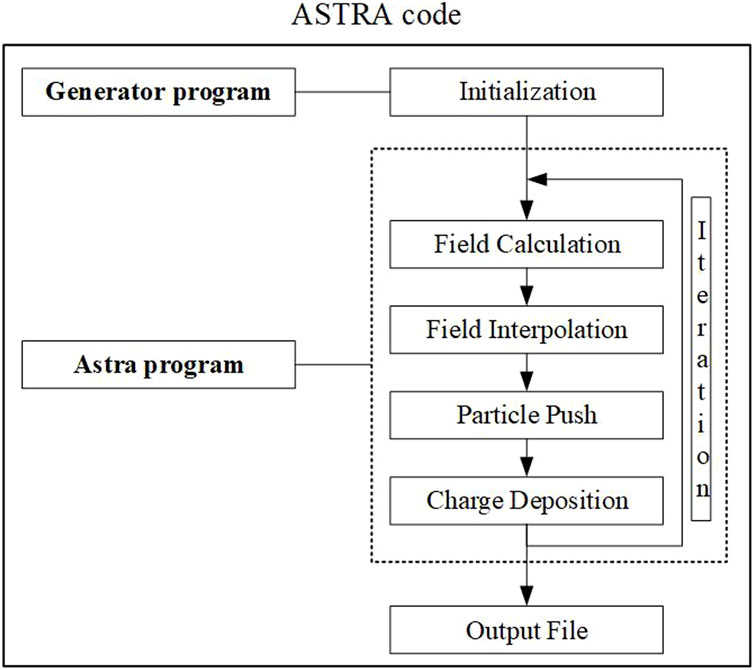
To compare and validate the theoretical electron beam envelope equations in integral form, the propagation of the electron beam is simulated using the ASTRA code (Floettmann, 2017). ASTRA, a space charge tracking algorithm developed by the German Electron Synchrotron Research Institute (DESY), employs the Particle-In-Cell (PIC) method to simulate collective self-field effects, such as space charge, in high-energy charged particle beams. The program incorporates comprehensive algorithms for generating initial particle distributions and performing particle tracking, making it a widely used tool in simulation studies of high-energy charged particles.

Figure 2 illustrates how ASTRA works. The program generator can be used to generate an initial particle distribution by specifying parameters such as the particle count, particle energy, and types of beam distributions (radial uniform/Gaussian/plateau) in the input file. The core program Astra then performs particle tracking under the influence of internally computed space-charge fields and/or external electromagnetic fields. Its computational workflow iterates through four integrated components: (1) Field Calculation, which solves the governing field equations on a discrete grid; (2) Field Interpolation, which interpolates both external and self-generated fields from the grid nodes to individual particle positions; (3) Particle Push, which integrates the equations of motion over a time step to update particle positions and momenta; and (4) Charge Deposition, which maps particle charges back onto the grid. This cycle repeats until the simulation concludes.

Figure 2

Figure 2. The flow chart of ASTRA code.

In the ASTRA program, the 1 MeV electrons are assumed to be evenly spread out across the cross-sectional area. In a uniform distribution, the maximum radius r_b is $\sqrt{2}$ times the RMS beam radius. As shown in Figure 1, the initial beam radius is 0.2 m, which corresponds to an RMS beam radius of 141.4 mm. The total charge is 5.0 pC, and the total emission time is 5 ns, resulting in a current of 1 mA. Figure 3 illustrates the simulated results of the electron beam envelope radius as a function of propagation distance for three different initial trajectory slopes, obtained using the ASTRA program. The simulations were performed with the same beam energy, current, and initial beam radius as those used in Figure 1. The theoretical results presented in Figure 1 are also superimposed as solid lines in Figure 3. The trend of the simulated results (dashed lines) by ASTRA code in Figure 3 is consistent with theoretical results (solid lines). However, the exact simulated beam radius may differ slightly from the theoretical results, as the electron distribution along the axial direction can influence the evolution of the beam envelope radius. In deriving the equations in Equations 17, the electron distribution in the axial direction is not constrained.

Figure 3

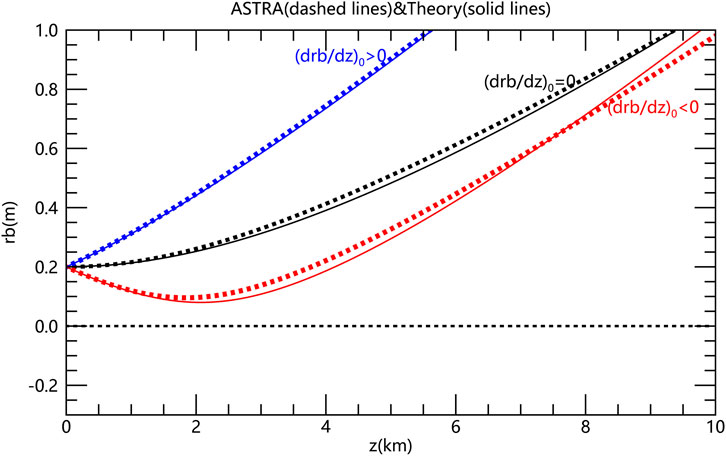
Figure 3. The electron beam envelope radius as a function of propagation distance for three initial slopes of the trajectory ($r_0^{\prime }={10}^{-4},r_0^{\prime }=0\text{\hspace{0.17em}and\hspace{0.17em}}{r}_0^{\prime }={-10}^{-4}$) with an energy of E = 1 MeV, current I₀ = 1 mA and initial beam radius $a$ = 0.2 m simulated by ASTRA code (dotted lines) and compared with theorical results (solid lines).

2.3 Results and discussion

According to Equations 17, 5, the theoretical electron beam envelope radius depends on energy, current and initial beam radius. Figure 4 presents the variation of beam radius with respect to propagation distance for three different energy levels: E = 1 MeV (black curve), E = 2 MeV (blue curve), and E = 4 MeV (red curve). These results were obtained under the following conditions: an initial current of I₀ = 1mA, an initial beam radius of $a$ = 0.2 m, and a zero-initial slope of the trajectory ($r_0^{\prime }$ = 0). As the propagation distance increases, the beam radius for the 1 MeV case expands rapidly, indicating significant beam divergence. For the 2 MeV case, the beam radius also increases, but at a slower rate compared to the 1 MeV case. In contrast, the beam radius for the 4 MeV case remains nearly constant, suggesting negligible beam expansion at this higher energy level.

Figure 4

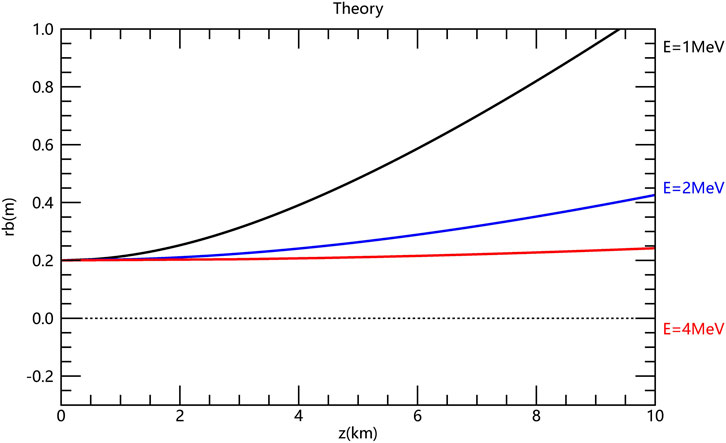
Figure 4. The theorical electron beam envelope radius as a function of propagation distance for three energies (E = 1MeV, E = 2 MeV and E = 4 MeV) with current I₀ = 1 mA, initial beam radius $a$ = 0.2 m and initial slopes of the trajectory $r_0^{\prime }=0$.

Figure 5 shows how the beam radius changes with propagation distance for three different current values: I₀ = 1 mA (black curve), I₀ = 5 mA (blue curve), and I₀ = 10 mA (red curve), while keeping the energy constant at E = 1 MeV, the initial beam radius at $a$ = 0.2 m, and the initial trajectory slope at $r_0^{\prime }$ = 0. For all current values, the beam radius increases with propagation distance. However, the rate of increase is significantly influenced by the magnitude of the current. The I₀ = 1 mA curve shows a gradual increase in beam radius, whereas higher currents lead to more rapid expansion. The I₀ = 5 mA curve displays a steeper rise, and the I₀ = 10 mA curve exhibits the most pronounced expansion.

Figure 5

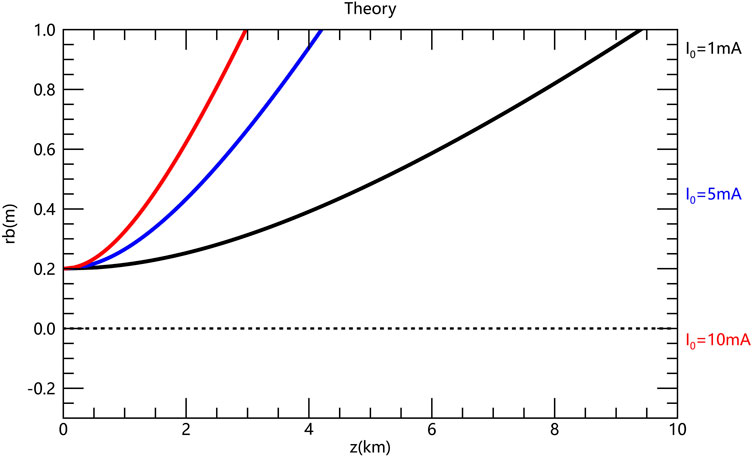
Figure 5. The theorical electron beam envelope radius as a function of propagation distance for three currents (I₀ = 1mA, I₀ = 5 mA and I₀ = 10 mA) with an energy E = 1MeV, initial beam radius $a$ = 0.2 m and initial slopes of the trajectory $r_0^{\prime }=0$.

Figure 6 illustrates the effect of varying initial beam radii on the propagation of beam radius with respect to distance. The three cases considered are: $a$ = 0.2 m (black curve), $a$ = 0.4 m (blue curve), and $a$ = 0.6 m (red curve), with the energy fixed at E = 1MeV, the current at I₀ = 1mA, and the initial slope of the trajectory set to $r_0^{\prime }$ = 0. All three curves exhibit a nonlinear increase in beam radius as the propagation distance increases with the expansion being more pronounced for smaller initial beam radii. Specifically, the case with $a$ = 0.2 m shows the most rapid expansion, as the Coulomb repulsion is stronger for smaller initial beam radii.

Figure 6

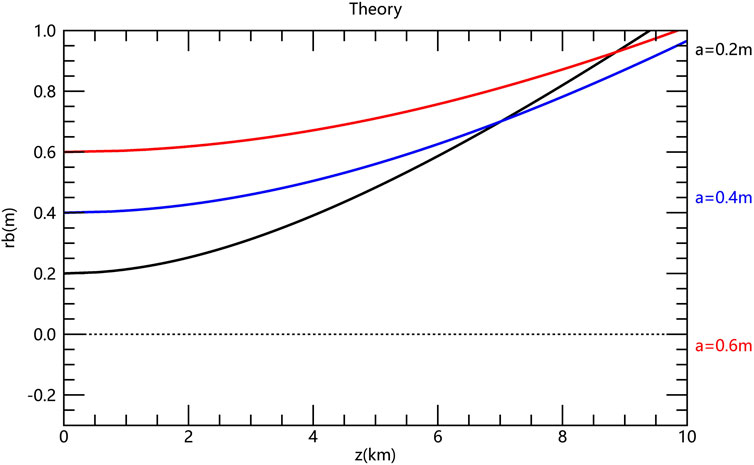
Figure 6. The theorical electron beam envelope radius as a function of propagation distance for three initial beam radii ($a$ = 0.2 m, $a$ = 0.4 m and $a$ = 0.6 m) with an energy E = 1MeV, current I₀ = 1 mA and initial slopes of the trajectory $r_0^{\prime }=0$.

3 Relationship between the integral form and K-V equation

The derivative of both sides of the Equation 24 gives

$\text{dz}=\pm \sqrt{\frac{2}{K}}\left[F\left(w\right)+r_b{F}^{\prime }\left(w\right)\frac{dw}{d{r}_b}\right]d{r}_b(25)$

where $w=\sqrt{\frac{{r_0^{\prime }}^2}{2K}+\ln \left(\frac{r_b}{a}\right)}$. The derivative of the Dawson integral is given by

$F^{\prime }\left(w\right)=1-2wF\left(w\right)(26)$

The derivative of w with respect to r_b is

$\frac{dw}{d{r}_b}=\frac{1}{2r_{b}w}(27)$

Substituting Equation 26 and Equation 27 into Equation 25 yields Equation 13. The K-V equation is expressed as

$\frac{d^2{r}_b}{d{z}^2}=-k_0^2{r}_b+\frac{K}{r_b}+\frac{{\epsilon }_r^2}{r_b^3}(28)$

where k₀ = $\frac{{\mathrm{\Omega }}_L}{V}=-\frac{eB}{2m_{0}c\left(\beta \gamma \right)}$ represents the focusing effect from the applied magnetic field, and ε_r is the radial emittance. Integrating Equation 28 gives

$\frac{d{r}_b}{dz}=\pm \sqrt{{r_0^{\prime }}^2+2K\ln \left(\frac{r_b}{a}\right)+k_0^2\left(a^2-r_b^2\right)+{\epsilon }_r^2\left(\frac{1}{a^2}-\frac{1}{r_b^2}\right)}(29)$

under the conditions of constant k₀. If the radial emittance is zero and no external force is applied, Equation 29 simplifies to Equation 13. The integral Equation 24 is equivalent to the simplified differential form of the K-V equation, excluding the effects of external forces and radial emittance. The derivative $\frac{d{r}_b}{dz}$ should be zero at the minimum of beam radius, as deducted from Equation 29. The period of electron beam between two minima of beam radius is determined by several parameters, including the initial beam radius, the initial slope of the trajectory, the magnitude of magnetic field, the current and the electron energy.

It is worth noting that electron energy is included in the expression for both k₀ and K. The combined effect of electron energy depends on whether k₀ or K dominates. When k₀ dominates, a decrease in electron energy results in a smaller beam envelope radius. Conversely, when K dominates, an increase in electron energy leads to a smaller beam envelope radius.

As shown in Figure 7, the four colored curves (purple, cyan, green, and orange) represent the results derived from the K-V equation with a current I₀ = 1 mA, an initial beam radius $a$ = 0.2 m, an initial slope $r_0^{\prime }$ = 0, radial emittanceε_r = 20 mm·mrad and a magnetic field strength of B = 2000 nT for different energy (E = 0.5 MeV, E = 1.0 MeV, E = 1.5 MeV and E = 2.0 MeV). The four colored curves display oscillatory features, with both the oscillation period and amplitude varying with energy. This oscillatory behavior is also observed in the Beam PIC simulation (Jiao et al., 2022). Electron beams with higher energy exhibit a smaller beam envelope radius during the initial half period when K dominates. However, the maximum beam envelope radius does not vary monotonically with energy. Specifically, the electron beam with an energy of 1 MeV has the smallest maximum envelope radius compared to electron beams with other energies. The black curve represents the result obtained using the simplified K-V equation with a current I₀ = 1 mA, an initial beam radius $a$ = 0.2 m but without $r_0^{\prime }$, ε_r or B. In contrast, the black curve does not display any oscillatory features and instead increases monotonically. This black curve is identical to the black curve in Figure 1, which indicates that the integral Equation 24 is equivalent to the simplified differential form of the K-V equation.

Figure 7

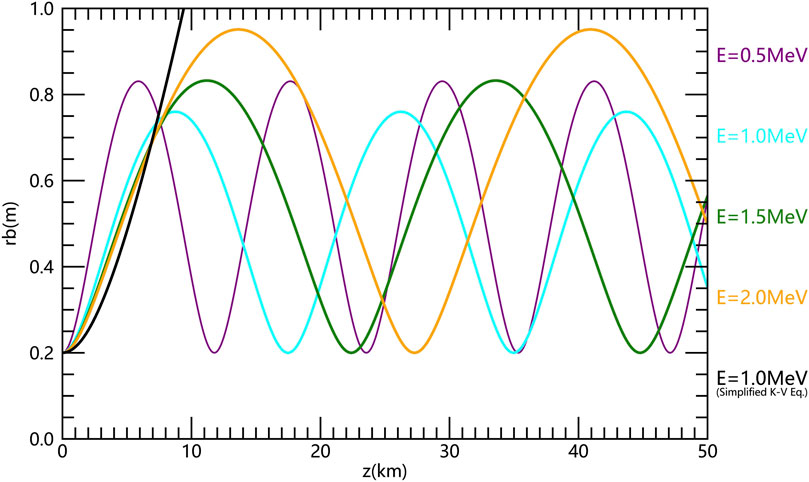
Figure 7. The electron beam envelope radius as a function of propagation distance for energies E = 0.5 MeV (purple curve), E = 1.0 MeV (cyan curve), E = 1.5 MeV (green curve) and E = 2.0 MeV (orange curve), as determined by the K-V equation. The black curve represents the result for E = 1.0MeV, guided by simplified K-V equation without $r_0^{\prime }$, k₀ or B.

4 Conclusion

This paper presents a theoretical and analytical framework for studying electron beam transport. The integral equation for the electron beam envelope in a vacuum is derived. This equation accounts for both Coulomb repulsion and self-magnetic forces. Although these two forces act in opposite directions, their combined effect causes the beam to diverge.

The radius of the electron beam envelope is determined by several factors, including the initial beam radius, the initial slope of the trajectory, the magnitude of magnetic field, the current and the electron energy. Specifically, a smaller initial radius leads to a larger beam envelope radius. If the initial slope of the trajectory is greater than or equal to zero, the electron beam will diverge. If the initial slope is negative, the beam will first converge and then diverge. The parameter k₀, which quantifies the focusing strength of the applied magnetic field, is proportional to the magnitude of the magnetic field. Thus, a stronger magnetic field causes the electron beam to converge. The perveance K, which quantifies the defocusing effect of the beam’s equilibrium self-fields, is proportional to the current. Therefore, lower current causes the electron beam to converge. The net effect of electron energy on the beam envelope radius is determined by the relative dominance of k₀ or K. If k₀ dominates, lower electron energy yields a smaller radius; whereas when K dominates, higher electron energy reduces the beam envelope radius.

This study is a bridge between integral form and differential form of the envelope equation, and will provide a better understanding for the K-V equation and a scientific basis for researching beam propagation technology. It is important to note that, in this study, we assume that the background space to be a vacuum environment, while the actual space environment typically includes background plasma. Consequently, future research will focus on the interaction between the electron beam and the background plasma, and how this interaction influences the evolution of the beam envelope radius.

Data availability statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: https://doi.org/10.6084/m9.figshare.29821676.v1.

Author contributions

CZ: Writing – review and editing, Writing – original draft. XZ: Validation, Writing – review and editing, Investigation. SF: Formal Analysis, Supervision, Writing – review and editing. HZ: Validation, Supervision, Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This work is supported by Youth Innovation Promotion Association (YIPA) of the Chinese Academy of Sciences (CAS) (E3217A031S), the National Natural Science Foundation of China (42474227), and the China Postdoctoral Science Foundation (E01Z5006).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Arshad, K. (2018). Application of kinetic theory to study twisted modes in Non-Maxwellian plasma.

Google Scholar

Arshad, K., and Mirza, A. M. (2014). Landau damping and kinetic instability in Non-Maxwellian highly electronegative multi-species plasma. Astrophysics Space Sci. 349 (2), 753–763. doi:10.1007/s10509-013-1664-2

CrossRef Full Text | Google Scholar

Arshad, K., and Poedts, S. (2020). Twisted waves in symmetric and asymmetric bi-ion kappa-distributed plasmas. Phys. Plasmas 27 (12), 122904–122917. doi:10.1063/5.0007380

CrossRef Full Text | Google Scholar

Arshad, K., Mahmood, S., and Mirza, A. M. (2011). Landau damping of ion acoustic wave in Lorentzian multi-ion plasmas. Phys. Plasmas 18 (9), 092115. doi:10.1063/1.3633237

CrossRef Full Text | Google Scholar

Arshad, K., Ehsan, Z., Khan, S. A., and Mahmood, S. (2014). Solar wind driven dust acoustic instability with lorentzian kappa distribution. Phys. Plasmas 21 (2), 023704. doi:10.1063/1.4865573

CrossRef Full Text | Google Scholar

Arshad, K., Lazar, M., Mahmood, S., Aman-ur-Rehman, A. U. R., and Poedts, S. (2017a). Kinetic study of electrostatic twisted waves instability in nonthermal dusty plasmas. Phys. Plasmas 24 (3), 033701. doi:10.1063/1.4977446

CrossRef Full Text | Google Scholar

Arshad, K., Maneva, Y. G., and Poedts, S. (2017b). Ion acoustic wave damping in a non-Maxwellian bi-ion electron plasma in the presence of dust. Phys. Plasmas 24 (9), 093708. doi:10.1063/1.4995581

CrossRef Full Text | Google Scholar

Arshad, K., Poedts, S., and Dahshan, A. (2022). Quasi-electrostatic instability in non-gyrotropic tri-ion electron plasma. Aip Adv. 12 (10), 105319. doi:10.1063/5.0014682

CrossRef Full Text | Google Scholar

Åsnes, A., Taylor, M. G. G. T., Borg, A. L., Lavraud, B., Friedel, R. W. H., Escoubet, C. P., et al. (2008). Multispacecraft observation of electron beam in reconnection region. J. Geophys. Res. Space Phys. 113 (A7). doi:10.1029/2007ja012770

CrossRef Full Text | Google Scholar

Banks, P. M., and Raitt, W. J. (1988). Observations of electron beam structure in space experiments. J. Geophys. Res. Space Phys. 93 (A6), 5811–5822. doi:10.1029/JA093iA06p05811

CrossRef Full Text | Google Scholar

Banks, P. M., Gilchrist, B. E., Neubert, T., Myers, N., Raitt, W. J., Williamson, P. R., et al. (1990). Charge-2 rocket observations of vehicle charging and charge neutralization. Adv. Space Res. 10 (7), 133–136. doi:10.1016/0273-1177(90)90286-9

CrossRef Full Text | Google Scholar

Bekefi, G., Feld, B. T., Parmentola, J., and Tsipis, K. (1980). Particle beam weapons-a technical assessment. Nature 284, 219–225. doi:10.1038/284219a0

CrossRef Full Text | Google Scholar

Bodeau, M., and Baker, D. N. (2021). Effects of space radiation on contemporary based systems II: spacecraft internal and external charging and discharging effects. Hoboken, NJ, United States: Wiley, Space Weather Effects and Applications, 13–61.

CrossRef Full Text | Google Scholar

Borovsky, J. E., Delzanno, G. L., and Henderson, M. G. (2020). A mission concept to determine the magnetospheric causes of aurora. Front. Astronomy Space Sci. 7, 595929. doi:10.3389/fspas.2020.595929

CrossRef Full Text | Google Scholar

Buchholz, D. (1986). Gauss' law and the infraparticle problem. Phys. Lett. B 174 (3), 331–334. doi:10.1016/0370-2693(86)91110-x

CrossRef Full Text | Google Scholar

Cambou, F., Lavergnat, J., Migulin, V. V., Morozov, A. I., Paton, B. E., Pellat, R., et al. (1978). ARAKS—Controlled or puzzling experiment? Nature 271, 723–726. doi:10.1038/271723a0

CrossRef Full Text | Google Scholar

Cambou, F., Reme, H., Saint-Marc, A., Lavergnat, J., Dokoukine, V. S., Zhulin, I. A., et al. (1980). General description of the ARAKS experiments. Ann. Geophys. 36, 271–284.

Google Scholar

Castello, F. L., Delzanno, G. L., Borovsky, J. E., Miars, G., Leon, O., and Gilchrist, B. E. (2018). Spacecraft-charging mitigation of a high-power electron beam emitted by a magnetospheric spacecraft: simple theoretical model for the transient of the spacecraft potential. J. Geophys. Res. Space Phys. 123 (8), 6424–6442. doi:10.1029/2017JA024926

CrossRef Full Text | Google Scholar

Cavalleri, G., Spavieri, G., and Spinelli, G. (1996). The ampere and biot-savart force laws. Eur. J. Phys. 17 (4), 205–207. doi:10.1088/0143-0807/17/4/010

CrossRef Full Text | Google Scholar

Chen, C., and Davidson, R. C. (1993). Properties of the Kapchinskij-Vladimirskij equilibrium and envelope equation for an intense charged-particle beam in a periodic focusing field.

Google Scholar

Dechambre, M., Kushnerevsky Yu, V., Lavergnat, J., Pellat, R., Pulinets, S. A., and Selegei, V. V. (1980). Waves observed by the ARAKS experiments: the whistler mode. Ann. Geophys. 36, 341–349.

Google Scholar

Druyvesteyn, M. J. (1938). The interaction between an electron beam and a plasma. Physica 5 (7), 561–567. doi:10.1016/s0031-8914(38)80003-3

CrossRef Full Text | Google Scholar

Fang, M., Liang, Z., Gong, Y., Chen, J., Zhu, G., Liu, T., et al. (2024). Study of the gyro and divergence characteristics of relativistic charged particle beam propagation in Earth’s magnetic field. Adv. High Energy Phys. 2024 (1), 5193401. doi:10.1155/2024/5193401

CrossRef Full Text | Google Scholar

Floettmann, K. (2017). ASTRA::a space charge tracking algorithm. Available online at: https://www.desy.de/∼mpyflo/.

Google Scholar

Gendrin, R. (1974). The French-Soviet ‘ARAKS’ experiment. Space Sci. Rev. 15, 905–931. doi:10.1007/BF00241068

CrossRef Full Text | Google Scholar

Gilchrist, B. E., Khazanov, G., Krause, L., and Neubert, T. (2001). “Study of relativistic electron beam propagation in the atmosphere-ionosphere-magnetosphere,”. MA: Hanscom AFB. doi:10.21236/ADA402969Tech. Rep, AFRL-VS-TR-2001-1505, Air Force Res. Lab

CrossRef Full Text | Google Scholar

Hastings, D. E. (1995). A review of plasma interactions with spacecraft in low Earth orbit. J. Geophys. Res. Space Phys. 100 (A8), 14457–14483. doi:10.1029/94JA03358

CrossRef Full Text | Google Scholar

Hendrickson, R. A., McEntire, R. W., and Winckler, J. R. (1975). Echo I: an experimental analysis of local effects and conjugate return echoes from an electron beam injected into the magnetosphere by a sounding rocket. Planet. Space Sci. 23, 1431–1444. doi:10.1016/0032-0633(75)90039-2

CrossRef Full Text | Google Scholar

Hendrickson, R. A., Winckler, J. R., and Arnoldy, R. L. (1976). Echo III: the study of electric and magnetic fields with conjugate echoes from artificial electron beams injected into the auroral zone ionosphere. Geophys. Res. Lett. 3, 409–412. doi:10.1029/GL003i007p00409

CrossRef Full Text | Google Scholar

Jiao, L., Ge, Y., Zhang, Y., Guo, Y., Feng, M., and Fu, S. (2022). Transverse confinement and periodic oscillations of electron beam structures traveling in the Earth′ s magnetic field. Chin. J. Geophys. 65 (10), 3691–3703. doi:10.6038/cjg2022Q0065

CrossRef Full Text | Google Scholar

Kapchinskij, I. M., and Vladimirskij, V. V. (1959). “Limitations of proton beam current in a strong focusing linear accelerator associated with the beam space charge,” in Proceedings of the international conference on high energy accelerators and instrumentation (CERN Scientific Information Service), 274–288.

Google Scholar

Krause, L. H. (1998). The interaction of relativistic electron beams with the near-Earth space environment. Ann Arbor, Mich: Univ. of Michigan. PhD thesis.

Google Scholar

Krause, L. H., Neubert, T., and Gilchrist, B. (1999). “Passive remote sensing of artificial relativistic electron beams in the middle atmosphere,” in Proceedings of space technology.

Google Scholar

Lawson, J. D. (1988). Physics of charged particle beams. 2nd ed. Oxford University Press.

Google Scholar

Lewellen, J. W., Buechler, C. E., Carlsten, B. E., Dale, G. E., Holloway, M. A., Patrick, D. E., et al. (2019). Space-borne electron accelerator design. Front. Astron. Space Sci. 6, 35. doi:10.3389/fspas.2019.00035

CrossRef Full Text | Google Scholar

Miars, G., Delzanno, G. L., Gilchrist, B. E., and Leon, O. (2020). New electron beam experiments in space and active spacecraft potential control. AGU Fall Meet. Abstr. 2020, SM016–SM018.

Google Scholar

Monson, S. J., Kellogg, P. J., and Cartwright, D. G. (1976). Whistler mode plasma waves observed on electron Echo 2. J. Geophys. Res. 81, 2193–2199. doi:10.1029/JA081i013p02193

CrossRef Full Text | Google Scholar

Mullen, E. G., Gussenhoven, M. S., Hardy, D. A., Aggson, T. A., Ledley, B. G., and Whipple, E. (1986). SCATHA survey of high-level spacecraft charging in sunlight. J. Geophys. Res. 91, 1474–1490. doi:10.1029/JA091iA02p01474

CrossRef Full Text | Google Scholar

Mustafaev, A. S. (2001). Dynamics of electron beams in plasmas. Tech. Phys. 46 (4), 472–483. doi:10.1134/1.1365475

CrossRef Full Text | Google Scholar

Neubert, T., and Gilchrist, B. E. (2002a). Particle simulations of relativistic electron beam injection from spacecraft. J. Geophys. Res. 107 (A8), 1167. doi:10.1029/2001JA900102

CrossRef Full Text | Google Scholar

Neubert, T., and Gilchrist, B. (2002b). 3D electromagnetic PIC simulations of relativistic electron pulse injections from spacecraft. Adv. Space. Res. 29 (9), 1385–1390. doi:10.1016/s0273-1177(02)00185-0

CrossRef Full Text | Google Scholar

Neubert, T., and Gilchrist, B. E. (2004). Relativistic electron beam injection from spacecraft: performance and applications. Adv. Space Res. 34 (11), 2409–2412. doi:10.1016/j.asr.2003.08.081

CrossRef Full Text | Google Scholar

Neubert, T., Gilchrist, B., Wilderman, S., Habash, L., and Wang, H. J. (1996). Relativistic electron beam propagation in the Earth’s atmosphere: modeling results. Geophys. Res. Lett. 23 (9), 1009–1012. doi:10.1029/96gl00247

CrossRef Full Text | Google Scholar

Reeves, G. D., Delzanno, G. L., Fernandes, P. A., Yakymenko, K., Carlsten, B. E., Lewellen, J. W., et al. (2020). The beam plasma interactions experiment: an active experiment using pulsed electron beams. Front. Astron. Space Sci. 7, 23. doi:10.3389/fspas.2020.00023

CrossRef Full Text | Google Scholar

Reiser, M. (2008). Theory and design of charged particle beams. John Wiley & Sons, 173–177.

CrossRef Full Text | Google Scholar

Sacherer, F. J. (1971). RMS envelope equations with space charge. IEEE Trans. Nucl. Sci. 18 (3), 1105–1107. doi:10.1109/tns.1971.4326293

CrossRef Full Text | Google Scholar

Sasaki, S., Kawashima, N., Kuriki, K., Yanagisawa, M., and Obayashi, T. (1986). Vehicle charging observed in SEPAC Spacelab-1 experiment. J. Spacecr. Rockets 23, 194–199. doi:10.2514/3.25801

CrossRef Full Text | Google Scholar

Sasaki, S., Oyama, K. I., Kawashima, N., Obayashi, T., Hirao, K., Raitt, W. J., et al. (1988). Tethered rocket experiment (CHARGE-2) initial results on electrodynamics. Radio Sci. 23, 975–988. doi:10.1029/RS023i006p00975

CrossRef Full Text | Google Scholar

Sun, H., Zhao, J., Liu, W., Xie, H., and Wu, D. (2020). Electron temperature anisotropy and electron beam constraints from electron kinetic instabilities in the solar wind. Astrophysical J. 902 (1), 59. doi:10.3847/1538-4357/abb3ca

CrossRef Full Text | Google Scholar

Szuszczewicz, E. P. (1985). Controlled electron beam experiments in space and supporting laboratory experiments: a review. J. Atmos. Terr. Phys. 47 (12), 1189–1210. doi:10.1016/0021-9169(85)90088-1

CrossRef Full Text | Google Scholar

Vinokurov, N. A. (2001). “Space charge,” in AIP conference proceedings (Melville, New York: American Institute of Physics), 390–404.

Google Scholar

Winckler, J. R. (1980). The application of artificial electron beams to magnetospheric research. Rev. Geophys. 18 (3), 659–682. doi:10.1029/rg018i003p00659

CrossRef Full Text | Google Scholar

Winckler, J. R., Arnoldy, R. L., and Hendrickson, R. A. (1975). Echo 2: a study of electron beams injected into the high-latitude ionosphere from a large sounding rocket. J. Geophys. Res. 80, 2083–2088. doi:10.1029/JA080i016p02083

CrossRef Full Text | Google Scholar

Xue, B., Zhao, Q., Zhang, F., Dong, Z., Hao, J., Fan, J., et al. (2023). Fast spacecraft charging induced by a high-power electron beam emission and its mitigation through a plasma contactor. J. Instrum. 18 (10), P10037. doi:10.1088/1748-0221/18/10/p10037

CrossRef Full Text | Google Scholar

Zheng, Y., Ganushkina, N. Y., Jiggens, P., Jun, I., Meier, M., Minow, J. I., et al. (2019). Space radiation and plasma effects on satellites and aviation: quantities and metrics for tracking performance of space weather environment models. Space weather. 17, 1384–1403. doi:10.1029/2018SW002042

PubMed Abstract | CrossRef Full Text | Google Scholar