Collisional excitation in reactive systems: recent advances in modeling molecular processes for astrochemistry

Collisional excitation in reactive systems plays a central role in astrochemistry. Accurate state-to-state rate coefficients are key parameter for the determination of excitation conditions of interstellar molecules with the most abundant species in space (H, He and H₂) through collisions. Unfortunately, reliable data for collisions involving interstellar reactive radicals and ions are scarce. Despite the molecular simplicity of these systems, considering the competition between nonreactive and reactive processes on equal footing remains a true theoretical and computational challenge in particular for bimolecular reactions, in addition to excitation processes in open-shell species. This minireview emphasizes recent progress in theoretical approaches for state-to-state scattering in reactive systems of astrochemical interest. We discuss the strengths and limitations of state-of-the-art quantum methods on collisions involving direct and indirect reactions; and the encouraging alternatives proposed by statistical frameworks. We highlight the impact of the computed state-to-state rate coefficients in astrophysical modeling.

1 Introduction

Molecular collisions constitute fundamental processes governing the chemical transformation of matter. Although inherently quantum by nature, they participate in the understanding of structures on astronomical scales. The astrochemical community aims to understand both the molecular composition and the physical conditions lying in the Interstellar Medium (ISM). Since the advent of radio astronomy in the 1960s, the resolution and sensitivity of ground-based and space telescopes have reached unprecedented levels of accuracy, enabling not only the detection of a large number of interstellar molecules, but also probing the chemical diversity in the gas-phase at small scale structures of interstellar sources, notably thanks to the ALMA interferometer (McGuire, 2022). More recently, JWST observations probed a rich chemistry on icy grain mantles, providing key insights into formation of molecules in star-forming regions (McClure et al., 2023).

Molecular spectra offer a window into the physical conditions of interstellar sources. On one hand, the chemical composition is inferred from the line assignment supported by computational and laboratory spectroscopy. On the other hand, line intensity is directly related to the population of molecular energy levels and hence the excitation conditions of interstellar environments. However, the microscopic mechanisms driving the molecular excitation in the ISM are complex due to its extreme density conditions ( $10^{-3}$ – $10^{12}$ cm⁻³) and prevent the distribution of the molecular populations through Local Thermodynamic Equilibrium (LTE) assumption (Roueff and Lique, 2013; Lique and Faure, 2019). Thus, radiative transfer is the common knowledge to determine the physical conditions of the source under study. Accurate modeling relies on the description of the interplay between radiative and collisional processes.

Two main cases occur during a collision between two molecules A and B in the gas-phase:

$\text{A}(v_1,j_1)+\text{B}(v_2,j_2)\to \left\{\begin{array}{cc}\text{A}(v_1^{\prime },j_1^{\prime })+\text{B}(v_2^{\prime },j_2^{\prime })\hfill & \text{inelastic}\hfill \\ \text{C}(v_3^{\prime },j_3^{\prime })+\text{D}(v_4^{\prime },j_4^{\prime })\hfill & \text{reactive}\hfill \end{array}\right.(1)$

In Equation 1, $(v,j)$ denote the vibrational quantum number and the rotational angular momentum, respectively. The first case corresponds to inelastic collisions, where internal energy is redistributed between reactants among their internal degrees of freedom $(v_1^{\prime },j_1^{\prime })$ and $(v_2^{\prime },j_2^{\prime })$ . The second case represents reactive collisions, in which the reactants are destroyed to form new products C and D in rovibrational states $(v_3^{\prime },j_3^{\prime })$ and $(v_4^{\prime },j_4^{\prime })$ , respectively. Figure 1 illustrates schematic pathways of molecular reactions. Direct reactions involve the break of the bond of one of the reactants in a short time, often requiring surmounting an activation barrier $E_a$ , which makes them less efficient at low temperatures. In contrast, indirect reactions proceed through a long-lived intermediate complex by creating bonds between reactants. ¹ In this type of reactions, exothermic and bariereless reactions do not present threshold energy and the reactive rate coefficient often decreases with increasing collision energy, due to the increasing opening of energy levels for the reactants, in opposite behavior of direct transitions (Song and Guo, 2023). These processes are usually governed by long-range interactions and concern mostly ion-molecule collisions.

Figure 1

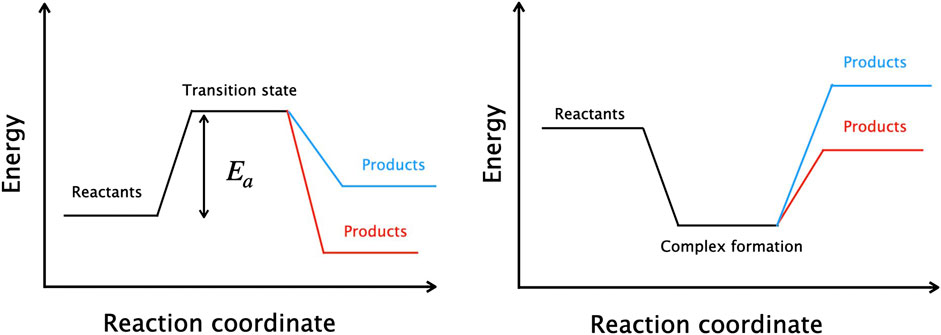
Figure 1. Schematic diagrams of direct (left) and indirect (right) reactions. Red pathways denote exothermic reactions and blue correspond to endothermic reactions.

Usually, the extreme low temperatures of interstellar objects such as molecular clouds ( $\sim$ 10–100 K) hinder direct reactions to the profit of collisional excitation (Roueff and Lique, 2013). Furthermore, exothermic and barrierless reactions still occur under such conditions and form products in excited states (Caselli and Ceccarelli, 2012). This difference of behavior in reactivity can have an impact on excitation processes. Therefore, depending on the nature of the interaction and the temperature, there can be a complex interplay between inelastic and reactive processes during a collision. This minireview focuses on collisional excitation in molecular systems presenting such competition between exctiation and reactivity, and are defined as “reactive systems”. We focus here on processes involving collisions between light species like H⁺, H and H₂ with hydrides, i.e., molecules consisting of one heavy atom and one ore more hydrogen atoms. Hydrides received considerable attention in the past decade as they are of fundamental interest in initiating the chemical evolution in both gas and solid-phases, probing conditions in diffuse and dense gas, tracing the molecular fraction of H₂ or the cosmic-ray ionization rate (Gerin et al., 2016). We will emphasize the behavior of these molecules when colliding with atomic, molecular hydrogen and protons, the main interstellar colliders.

Recent achievements in experiments like crossed-beam laser techniques or cryogenic ion traps has enabled precise measurements of rate coefficients for reactive processes (Toscano et al., 2020). Supported by theoretical investigations, these data are reported in KIDA (Wakelam et al., 2024) and UMIST (Millar et al., 2023), which are the most important reaction databases for chemical modeling. However, although experimental data take into account all processes occuring during a collision, state-to-state resolved rate coefficients tracking both, excitation and reaction, are still hardly achievable, however necessary in radiative transfer. Scattering calculations remain currently the most reliable approach to provide such collisional data. Typical study of a molecular system lies in the Born-Openheimer approximation (Born and Oppenheimer, 1927). Ab initio methods such as Configurational Interaction type (Knowles and Werner, 1988) or Coupled Clusters (Knowles et al., 1993) are currently the methods of choice for treating high dimensional reactive potential energy surface (PES), as the scattering is highly sensitive to its accuracy (Tonolo and Alessandrini, 2024; Bowman et al., 2011; Jiang et al., 2020). Collisional cross sections and rate coefficients are then derived from the $S$ -matrix obtained by solving the Schrödinger equation for the nuclear motion, with appropriated coordinate system and boundary conditions (Arthurs and Dalgarno, 1960). The competition between inelastic and reactive behavior make difficult to determine the $S$ -matrix at a state-to-state level due to the “coordinate problem”, i.e., the issue to find a common coordinate system for both reactants and products (Hu and Schatz, 2006). This problem has been carried out for atom-diatom collisions using the hyperspherical coordinates and implemented in the ABC software (Skouteris et al., 2000), but remains difficult to extend to polyatomic systems (Zhao and Guo, 2017). Of course several bimolecular reactions have been treated including diatomic or triatomic molecules in quantum state-to-state scattering, but only the reactive behavior has been discussed. We will not discuss these reactions in this minireview and refer the reader to excellent reviews about high dimensional reactive collisions (Zhang and Guo, 2016; Zhao and Guo, 2017; Song and Guo, 2023).

In this minireview, we restrict the discussion to collisional excitation in reactive systems relevant to astrochemical applications over the past decade; and available in the molecular databases EMAA (Faure et al., 2025), BASECOL (Dubernet et al., 2023) and LAMDA (Van der Tak et al., 2020). The manuscript is organized as follows: Section 2 presents the state-of-the-art methods for providing state-to-state collisional data, section 3 discusses recent work on collisions involving direct reactions, while section 4 highlights recent achievements for indirect reactions. Finally, section 5 will discuss excitation processes in open-shell molecules and the impact of the data sets in astrophysical applications.

2 Theoretical methods

State-to-state collisional cross sections characterize the probability for the reactants to transit from an initial energy state to a final one, or to react and form products (see Equation 1). Computing this observable requires the solution of the Close-Coupling equations within the Time-Independent Quantum Mechanical (TIQM) framework. This approach provides the $S$ -matrix for the reactants and products in the asymptotic region of the propagation, subject to proper boundary conditions (Arthurs and Dalgarno, 1960). TIQM method is one of the most accurate and permit the computation of the $S$ -matrix for all available quantum states at a given total energy, but restricted to low temperatures as the computational time scales as $N^3$ (with $N$ being the number of channels, representing the combination of initial and final energy levels satisfying the conservation of the total energy; Flower (2007)). At higher temperatures, Time-Dependent Quantum Mechanical (TDQM) methods based on Wave Packet (WP) propagation offer a practical alternative, which scales as $N\log N$ (Light and Carrington Jr, 2000). However, WP methods are less likely to work at low temperature due to convergence problems at low collisional energies (Honvault et al., 2011; 2012).

Both TIQM and TDQM methods are efficient for direct reactions contrary to indirect ones, which often involve a deep potential well. In the latter, calculations require large basis functions to reach convergence, especially at high angular momentum. Statistical methods are proposed as an alternative to overcome this challenge. The main assumption is that the collision proceed through a long-lived enough intermediate complex so that its formation and decay are treated as independent events. Among various approaches, the Statistical Adiabatic Channel Model (SACM; Quack and Troe (1975)) have shown satisfactory agreement with TIQM methods at low temperatures for nonreactive (Loreau et al., 2018) systems and collisions involving heavy colliders (Godard Palluet et al., 2025; Tonolo et al., 2025). For reactive systems, both SACM and Statistical Quantum Methods (SQM; Rackham et al. (2003)) were employed for indirect reactions. Comparisons with TIQM benchmarks show that statistical methods reproduce cross sections within a factor of $\sim$ 2 at low temperatures while dramatically saving computational time (González-Lezana, 2007; Konings et al., 2021). However, they are expected to fail at high temperatures, as the formation of a long-lived complex is not supposed to be the dominant mechanism in the dynamics. Quasi-Classical Trajectories (QCT) are suited to cover these ranges of temperature since quantum effects become less significant. The inelastic or reaction probability depends on the proportion of trajectories corresponding to excitation or reaction with respect to the total number of trajectories (Bai et al., 2017). Table 1 summarizes key studies from the past decade, including the methodologies applied and their accuracy with respect to the TIQM method or experiment, when clearly available from the corresponding reference.

Table 1

Table 1. Collisional studies for reactive systems of astrochemical interest.

3 Direct reactions

Unimolecular reactions are by far the most studied due to the molecular simplicity of the colliders. In case of collisional excitation in direct reactions, TIQM and TDQM can be easily applied. It is intuitive to think that activation energy should a priori inhibit reactive processes, depending on the temperature regime. For instance, in the HF + H $\to$ F + H₂ reaction, with an endothermicity of 15,000 K and a barrier $E_a$ of 20,000 K, Desrousseaux and Lique (2018) revealed that reactive and exchange channels are negligible for interstellar temperatures. Similar results were found for the HD–H ( $E_a\sim$ 5,000 K) (Zhou et al., 2021; Desrousseaux et al., 2022) and HCl–H ( $E_a\sim$ 2,500 K) (Lique, 2015a; Lique and Faure, 2017) systems for low temperatures. At higher collisional energies, reactants possess enough energy to overcome the barrier, in addition to quantum tunneling usually present for systems involving light atoms (Schreiner, 2020). Such features impact the magnitude of rate coefficients at roughly one-tenth of the reaction barrier.

Because reactive rate coefficients are often small at low temperatures, it might be tempting to facilitate scattering studies and reduce the dimensionality of the problem by omiting reactive channels. However, severe discrepancies can appear compared to full calculation especially when vibrational excitation is not negligible. Indeed, vibration has been established to strongly enhance reactivity, explained, for example, by Polanyi (1987) to the location of the barrier for atom-diatom reactions. Also, Barg et al. (1981) emphasized the decreasing of the threshold reaction energy with increasing vibration mode. For the H–H₂ (Lique, 2015b) and HD–H (Desrousseaux et al., 2022) systems, comparisons with previous studies which considered pure inelastic calculations revealed discrepancies by several orders of magnitude (Wrathmall et al., 2007; Flower and Roueff, 1999). Moreover, exchange processes were found to facilitate vibrational relaxation. Properly accounting for these effects permitted Lique (2015b) to be in good agreement with the experimental measurements of the H₂ ( $v$ = 0) + H $\to$ H₂ ( $v^{\prime }$ = 1) + H rate coefficient at room temperature (Heidner and Kasper, 1972).

Reactive systems involve sometimes radicals which are open-shell molecules, i.e., their nonzero electronic spin leads to a splitting of the energy levels into a fine structure when coupling to the rotation. Accounting simultaneously for both excitation in a complex energetic structure and reactive processes is difficult in scattering calculations. When the spin-rotation coupling is weak, one idea is closing fine structure and only consider the competition between rovibrational excitation and reactivity. This was applied to the SH⁺–H system by Zanchet et al. (2019) for the direct reaction. However, when the coupling of the electronic spin is strong, fine structure cannot be avoided. In this framework, Dagdigian (2017), Dagdigian (2022) investigated pure fine structure excitation of ( ${\text{CH}}^2\mathrm{\Pi }$ ) and ( ${\text{OH}}^2\mathrm{\Pi }$ ) by atomic hydrogen by means of a modified SQM method to account for the electronic coupling in the molecular Hamiltonian, and excluded reactive channels. Also, to propose a strategy to overcome the coordinate problem in case of bimolecular reactions, Dagdigian (2016) and Kłos et al. (2017) used the same methodology to treat the excitation of ( ${\text{CH}}^2\mathrm{\Pi }$ ) and ( ${\text{OH}}^2\mathrm{\Pi }$ ) with H₂ as nonreactive systems. These studies involve the interactions between several PESs, leading to a contribution to inelastic transitions from both direct and indirect processes. Then, neglecting the reactive channel should in principle overestimates the contribution from fine structure excitation to the cross sections.

4 Indirect reactions

For indirect reactions, calculations become more complicated due to the presence of deep potential well, requiring large basis functions in scattering calculations. Despite this challenge, TIQM approach have been successfully applied in atom-diatom reactions like H⁺–H₂ (González-Lezana and Honvault, 2017; González-Lezana et al., 2021), HD–H⁺ (Desrousseaux et al., 2021), HeH⁺–H (Desrousseaux and Lique, 2020) and CH⁺–H (Werfelli et al., 2015); however for a restricted range of temperature or basis level (see Table 1).

These systems are ideal test cases for statistical treatments. For most of the cited reactions, comparisons between TIQM and SQM methods show satisfactory statistical behavior for indirect reactions with deep well of $\sim$ 4.5 eV. Desrousseaux et al. (2021) used the HD–H⁺ system to benchmarck SACM calculations against TIQM for rotational excitation, finding an agreement within a factor of 2; and consistency with experiments on the HD + H⁺ $\to$ H₂ + D⁺ reaction (Henchman et al., 1981). Konings et al. (2021) found similar agreement between SACM and TIQM/TDQM calculations for the CH⁺–H and SH⁺–H systems for the indirect reaction. The only exception was for collisions of HeH⁺ by H, where TIQM calculations revealed that inelastic and exchange processes are not equal, characterizing a non-statistical behavior despite a well depth of about 0.8 eV.

Collisional excitation at a state-to-state level in bimolecular reactions remains a true issue due to the coordinate problem mentioned in section 1. As discussed in section 3, a possibility is reducing the dimension and treat the problem as a pure nonreactive system in the case of direct reactions. For exothermic and barrierless reactions, this aspect cannot be ignored. Pirlot Jankowiak and Lique (2025) proposed the use of SACM to investigate the rotational excitation of OH⁺(³ ${\mathrm{\Sigma }}^{-}$ ) induced by collisions with H₂. Despite the presence of a submerged barrier that should prevent a statistical behavior (Song and Guo, 2023), SACM obtained satisfactory agreement with the measurements of the OH⁺ + H₂ $\to$ H₂O⁺ + H reaction (Tran et al., 2018; Kumar et al., 2018) by a factor of 2. However, preliminary tests showed that SACM is inadequate for fine structure excitation in OH⁺ collisions, justifying the restriction of the study to rotational excitation (Pirlot Jankowiak, 2024).

5 Discussion

The inclusion of the reactive channel in the reported studies was done at the expense of interactions arising from the presence of the nuclear spin. However, the sensitivity of telescopes enables observations of hyperfine lines. Properly accounting for hyperfine excitation in scattering calculations is crucial for providing complete data set for radiative transfer modeling. Direct treatment with TIQM and TDQM approaches is computationally prohibitive, as the number of energy levels increases rapidly with the energy. Several approximations can overcome this limitation, the most accurate being recoupling techniques based on the assumption that the nuclear spin to be spectator during collision, allowing hyperfine-resolved cross sections to be reconstructed from rotational/fine-structure data (Alexander and Dagdigian, 1985). This method has been applied to the CH–H, CH–H₂ (Dagdigian, 2018), OH–H (Dagdigian, 2023) and OH–H₂ (Kłos et al., 2020) for the direct reaction. Excitation driven by a formation and decay of an intermediate complex still remains computationally excessive for recoupling approaches. Then, the $M_J$ randomization approximation (Alexander and Dagdigian, 1985) was used for the indirect processes. In this limit, the projection of the total angular momentum becomes fully randomized within the intermediate complex, leading to hyperfine transition proportional to the degeneracy of the final level. Furthermore, Infinite Order Sudden (IOS) based methods (Neufeld and Green, 1994; Faure and Lique, 2012) supposes a decoupling of orientations from the rotational motion during the collision; and was successfully applied to the HCl–H (Lique and Faure, 2017) and SH⁺–H (Lique et al., 2020) systems. These two alternatives have shown to agree with the recoupling method within a factor of 3 depending on the system and on the temperature (Faure and Lique, 2012).

It is interesting to look at the impact of the collisional data in the excitation of these molecules in the ISM. When the collisional data are absent, one common practice is to use data set involving He or H as a proxy for H₂ as a collision partner (Roueff and Lique, 2013). While this substitution can be somehow relevant for nonreactive systems at low temperature, fundamental differences arise for reactive systems from the nature of their interactions. As an example, Lique and Faure (2017) reported large differences in trend and magnitude between HCl collisions with H, He (Lanza and Lique, 2012) and H₂ (Lanza and Lique, 2014). Lique and Faure (2017) also found a substantial difference of a factor 1.5–2 in brightness temperatures for the hyperfine components of the HCl( $j$ = 1 $\to$ 0) transition at 626 GHz observed in L1157-B1 (Codella et al., 2011) when involving collisional data set for H or both H and H₂ partners. Differences are even more promounced for ion-molecule interactions. Gomez-Carrasco et al. (2014) modeled the abundance of OH⁺ in photo-dissociation regions using collisional data for the OH⁺–He system. However, the rate coefficients found for the OH⁺–H₂ system are orders of magnitude smaller, in the range of $10^{-13}$ – $10^{-12}$ cm³s^-1 below 100 K, compared to typical values of $10^{-10}$ cm³s^-1 for nonreactive systems (Pirlot Jankowiak and Lique, 2025). Such discrepancies are likely to alter significantly the populations of the OH⁺ energy levels in modeling line intensities and review the abundance of this molecule in the ISM.

Finally, the collisional data for the HD–H⁺ collisional system (González-Lezana et al., 2022) have been notably implemented in chemical network simulations for primordial chemistry of H₂ and HD in the ISM (Faure et al., 2024). Although the refine of the abundance of H₂ and HD was modest, they also checked the impact of the data for the HD–H system (Desrousseaux et al., 2022) and noticed a decreasing of the HD abundance by a factor of 3 for redshifts of $400<z<1300$ .

In this minireview, we emphasized the importance of inelastic and reactive pathways in interstellar collisions through recent advancements about collisional excitation in reactive systems of astrochemical interest. For reactions presenting a large barrier or endothermicity, reactive processes can be safely neglected up to about one-tenth of the activation barrier. However, neglecting reactive channels in case of vibrational excitation can result in large overestimations of the collisional data. In general, state-of-the-art methods can be easily applied to atom-diatom collisions especially for direct reactions. Statistical methods have proven to be efficient and reliable for treating indirect reactions. The increasing dimensionality of the systems and the complexity of open-shell molecules remain difficult for describing collisional processes at a state-to-state level, but encouraged by the use of statistical methods. Explorations based on artificial neural networks (ANN) algorithms can also offer promising perspectives to cover a more range of complex systems involving polyatomic molecules (Bossion et al., 2024).

Author contributions

PP: Writing – original draft, Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This manuscript received the support by RIKEN Special Post Doctoral Reaserchers Program.

Acknowledgements

The author acknowledges Pr. François Lique, Dr. Francesca Tonolo and Dr. Duncan Bossion for fruitful discussions and comments on the present manuscript.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alexander, M. H., and Dagdigian, P. J. (1985). Collision-induced transitions between molecular hyperfine levels: Quantum formalism, propensity rules, and experimental study of CaBr(X²Σ⁺) + Ar. J. Chem. Phys. 83, 2191–2200. doi:10.1063/1.449311

CrossRef Full Text | Google Scholar

Arthurs, A., and Dalgarno, A. (1960). The theory of scattering by a rigid rotator. Proc. R. Soc. Lond. A 256, 540–551. doi:10.1098/rspa.1960.0125

CrossRef Full Text | Google Scholar

Bai, M., Lu, D., and Li, J. (2017). Quasi-classical trajectory studies on the full-dimensional accurate potential energy surface for the OH + H₂O = H₂O + OH reaction. Phys. Chem. Chem. Phys. 19, 17718–17725. doi:10.1039/C7CP02656K

PubMed Abstract | CrossRef Full Text | Google Scholar

Barg, G.-D., Mayne, H. R., and Toennies, J. P. (1981). Quasiclassical trajectory studies of the H + H₂ reaction on an accurate potential energy surface. II. Effect of initial vibration and rotation on reactivity. J. Chem. Phys. 74, 1017–1025. doi:10.1063/1.441234

CrossRef Full Text | Google Scholar

Born, M., and Oppenheimer, R. (1927). Zur Quantentheorie Der Molekeln. Ann. Phys. 389, 457–484. doi:10.1002/andp.19273892002

CrossRef Full Text | Google Scholar

Bossion, D., Scribano, Y., Lique, F., and Parlant, G. (2018). Ro-vibrational excitation of H₂ by H extended to high temperatures. Mon. Not. R. Astron. Soc. 480, 3718–3724. doi:10.1093/mnras/sty2089

CrossRef Full Text | Google Scholar

Bossion, D., Nyman, G., and Scribano, Y. (2024). Machine learning prediction of state-to-state rate constants for astrochemistry. AIC 2, 100052. doi:10.1016/j.aichem.2024.100052

CrossRef Full Text | Google Scholar

Bowman, J. M., Czakó, G., and Fu, B. (2011). High-dimensional ab initio potential energy surfaces for reaction dynamics calculations. Phys. Chem. Chem. Phys. 13, 8094–8111. doi:10.1039/C0CP02722G

PubMed Abstract | CrossRef Full Text | Google Scholar

Caselli, P., and Ceccarelli, C. (2012). Our astrochemical heritage. Astron. Astrophys. Rev. 20, 56. doi:10.1007/s00159-012-0056-x

CrossRef Full Text | Google Scholar

Codella, C., Ceccarelli, C., Bottinelli, S., Salez, M., Viti, S., Lefloch, B., et al. (2011). First detection of hydrogen chloride toward protostellar shocks. ApJ 744, 164. doi:10.1088/0004-637X/744/2/164

CrossRef Full Text | Google Scholar

Dagdigian, P. J. (2016). Theoretical investigation of rotationally inelastic collisions of CH(X²Π) with molecular hydrogen. J. Chem. Phys. 145, 234305. doi:10.1063/1.4972142

PubMed Abstract | CrossRef Full Text | Google Scholar

Dagdigian, P. J. (2017). Theoretical investigation of rotationally inelastic collisions of CH(X²Π) with hydrogen atoms. J. Chem. Phys. 146, 224308. doi:10.1063/1.4984940

PubMed Abstract | CrossRef Full Text | Google Scholar

Dagdigian, P. J. (2018). Hyperfine excitation of CH in collisions with atomic and molecular hydrogen. Mon. Not. R. Astron. Soc. 475, 5480–5486. doi:10.1093/mnras/sty193

CrossRef Full Text | Google Scholar

Dagdigian, P. J. (2022). Theoretical investigation of rotationally inelastic collisions of OH(X²Π) with hydrogen atoms. J. Chem. Phys. 157, 104305. doi:10.1063/5.0110724

PubMed Abstract | CrossRef Full Text | Google Scholar

Dagdigian, P. J. (2023). Collisional excitation of hyperfine levels of OH by hydrogen atoms. Mon. Not. R. Astron. Soc. 518, 5976–5981. doi:10.1093/mnras/stac3458

CrossRef Full Text | Google Scholar

Desrousseaux, B., and Lique, F. (2018). The rotational excitation of HF by H. Mon. Not. R. Astron. Soc. 476, 4719–4724. doi:10.1093/mnras/sty605

CrossRef Full Text | Google Scholar

Desrousseaux, B., and Lique, F. (2020). Collisional energy transfer in the HeH⁺–H reactive system. J. Chem. Phys. 152, 074303. doi:10.1063/1.5142655

PubMed Abstract | CrossRef Full Text | Google Scholar

Desrousseaux, B., Coppola, C. M., Kazandjian, M. V., and Lique, F. (2018). Rotational excitation of HD by hydrogen revisited. J. Phys. Chem. A 122, 8390–8396. doi:10.1021/acs.jpca.8b08618

PubMed Abstract | CrossRef Full Text | Google Scholar

Desrousseaux, B., Konings, M., Loreau, J., and Lique, F. (2021). HD–H⁺ collisions: statistical and quantum state-to-state studies. Phys. Chem. Chem. Phys. 23, 19202–19208. doi:10.1039/D1CP02564C

PubMed Abstract | CrossRef Full Text | Google Scholar

Desrousseaux, B., Coppola, C. M., and Lique, F. (2022). Collisional excitation of HD by H. Mon. Not. R. Astron. Soc. 513, 900–905. doi:10.1093/mnras/stac911

CrossRef Full Text | Google Scholar

Dubernet, , Boursier, C., Denis-Alpizar, O., Ba, Y. A., Moreau, N., Zwölf, C. M., et al. (2023). BASECOL2023 scientific content. A&A 683, A40. doi:10.1051/0004-6361/202348233

CrossRef Full Text | Google Scholar

Faure, A., and Lique, F. (2012). The impact of collisional rate coefficients on molecular hyperfine selective excitation. Mon. Not. R. Astron. Soc. 425, 740–748. doi:10.1111/j.1365-2966.2012.21601.x

CrossRef Full Text | Google Scholar

Faure, A., Halvick, P., Stoecklin, T., Honvault, P., Epée Epée, M. D., Mezei, J.Zs., et al. (2017). State-to-state chemistry and rotational excitation of CH⁺ in photon-dominated regions. Mon. Not. R. Astron. Soc. 469, 612–620. doi:10.1093/mnras/stx892

PubMed Abstract | CrossRef Full Text | Google Scholar

Faure, A., Hily-Blant, P., Pineau des Forêts, G., and Flower, D. R. (2024). The chemistry and excitation of H2 and HD in the early universe. Mon. Not. R. Astron. Soc. 531, 340–354. doi:10.1093/mnras/stae994

CrossRef Full Text | Google Scholar

Faure, A., Bacmann, A., and Jacquot, R. (2025). Excitation of molecules and atoms for astrophysics (EMAA): a spectroscopic and collisional database. A&A 700, A266. doi:10.1051/0004-6361/202554403

CrossRef Full Text | Google Scholar

Federer, W., Villinger, H., Howorka, F., Lindinger, W., Tosi, P., Bassi, D., et al. (1984). Reaction of O⁺, CO⁺, and CH⁺ ions with atomic hydrogen. Phys. Rev. Lett. 52, 2084–2086. doi:10.1103/PhysRevLett.52.2084

CrossRef Full Text | Google Scholar

Flower, D. R. (2007). Molecular collisions in the interstellar medium (cambridge astrophysics series). Second edn.

Google Scholar

Flower, D. R., and Roueff, E. (1999). Rovibrational excitation of HD in collisions with atomic and molecular hydrogen. Mon. Not. R. Astron. Soc. 309, 833–835. doi:10.1046/j.1365-8711.1999.02888.x

CrossRef Full Text | Google Scholar

Gerin, M., Neufeld, D. A., and Goicoechea, J. R. (2016). Interstellar hydrides. Annu. Rev. Astron. Astrophys. 54, 181–225. doi:10.1146/annurev-astro-081915-023409

CrossRef Full Text | Google Scholar

Godard Palluet, A., Dawes, R., Quintas-Sánchez, E., Batista-Planas, A., and Lique, F. (2025). A promising statistical approach for studying the collisional excitation induced by CO: application to the CS–CO system. J. Chem. Phys. 162, 241101. doi:10.1063/5.0273126

PubMed Abstract | CrossRef Full Text | Google Scholar

Gomez-Carrasco, S., Godard, B., Lique, F., Bulut, N., Kłos, J., Roncero, O., et al. (2014). OH⁺ in astrophysical media: state-to-state formation rates, einstein coefficients and inelastic collision rates with He. ApJ 794, 33. doi:10.1088/0004-637X/794/1/33

CrossRef Full Text | Google Scholar

González-Lezana, T. (2007). Statistical quantum studies on insertion atom–diatom reactions. Int. Rev. Phys. Chem. 26, 29–91. doi:10.1080/03081070600933476

CrossRef Full Text | Google Scholar

González-Lezana, T., and Honvault, P. (2017). Rovibrational transitions of H₂ by collision with H⁺ at high temperature. Mon. Not. R. Astron. Soc. 467, 1294–1299. doi:10.1093/mnras/stx192

CrossRef Full Text | Google Scholar

González-Lezana, T., Hily-Blant, P., and Faure, A. (2021). Rate constants for the H⁺ + H₂ reaction from 5 K to 3000 K with a statistical quantum method. J. Chem. Phys. 154, 054310. doi:10.1063/5.0039629

PubMed Abstract | CrossRef Full Text | Google Scholar

González-Lezana, T., Hily-Blant, P., and Faure, A. (2022). A statistical investigation of the rate constants for the H⁺ + HD reaction at temperatures of astrophysical interest. J. Chem. Phys. 157, 214302. doi:10.1063/5.0128598

PubMed Abstract | CrossRef Full Text | Google Scholar

Heidner, R., and Kasper, J. V. (1972). An experimental rate constant for H + H₂ (ν″ = 1) → H + H₂ (ν″ = 0). Chem. Phys. Lett. 15, 179–184. doi:10.1016/0009-2614(72)80144-1

CrossRef Full Text | Google Scholar

Henchman, M. J., Adams, N. G., and Smith, D. (1981). The isotope exchange reactions H⁺ + D₂ → HD + D⁺ and D⁺ + H₂ → HD + H⁺ in the temperature range 200–300 K. J. Chem. Phys. 75, 1201–1206. doi:10.1063/1.442168

CrossRef Full Text | Google Scholar

Honvault, P., Jorfi, M., González-Lezana, T., Faure, A., and Pagani, L. (2011). Ortho-para H₂ conversion by proton exchange at low temperature: an accurate quantum mechanical study. Phys. Rev. Lett. 107, 023201. doi:10.1103/PhysRevLett.107.023201

PubMed Abstract | CrossRef Full Text | Google Scholar

Honvault, P., Jorfi, M., González-Lezana, T., Faure, A., and Pagani, L. (2012). Erratum: ortho-para H₂ conversion by proton exchange at low temperature: an accurate quantum mechanical study. Phys. Rev. Lett. 108, 109903. doi:10.1103/PhysRevLett.108.109903

CrossRef Full Text | Google Scholar

Hu, W., and Schatz, G. C. (2006). Theories of reactive scattering. J. Chem. Phys. 125, 132301. doi:10.1063/1.2213961

PubMed Abstract | CrossRef Full Text | Google Scholar

Jiang, B., Li, J., and Guo, H. (2020). High-fidelity potential energy surfaces for gas-phase and gas–surface scattering processes from machine learning. J. Phys. Chem. Lett. 11, 5120–5131. doi:10.1021/acs.jpclett.0c00989

PubMed Abstract | CrossRef Full Text | Google Scholar

Kłos, J., Ma, Q., Dagdigian, P. J., Alexander, M. H., Faure, A., and Lique, F. (2017). The excitation of OH by H2 revisited – I: fine-structure resolved rate coefficients. Mon. Not. R. Astron. Soc. 471, 4249–4255. doi:10.1093/mnras/stx1968

CrossRef Full Text | Google Scholar

Kłos, J., Dagdigian, P. J., Alexander, M. H., Faure, A., and Lique, F. (2020). The excitation of OH by H₂ revisited – II. Hyperfine resolved rate coefficients. Mon. Not. R. Astron. Soc. 493, 3491–3495. doi:10.1093/mnras/staa530

CrossRef Full Text | Google Scholar

Kłos, J., Dagdigian, P. J., and Lique, F. (2021). Collisional excitation of C+(2P) spin-orbit levels by molecular hydrogen revisited. Mon. Not. R. Astron. Soc. 501, L38–L42. doi:10.1093/mnrasl/slaa192

CrossRef Full Text | Google Scholar

Knowles, P. J., and Werner, H.-J. (1988). An efficient method for the evaluation of coupling coefficients in configuration interaction calculations. Chem. Phys. Lett. 145, 514–522. doi:10.1016/0009-2614(88)87412-8

CrossRef Full Text | Google Scholar

Knowles, P. J., Hampel, C., and Werner, H. J. (1993). Coupled cluster theory for high spin, open shell reference wave functions. J. Chem. Phys. 99, 5219–5227. doi:10.1063/1.465990

CrossRef Full Text | Google Scholar

Konings, M., Desrousseaux, B., Lique, F., and Loreau, J. (2021). Benchmarking an improved statistical adiabatic channel model for competing inelastic and reactive processes. J. Chem. Phys. 155, 104302. doi:10.1063/5.0062388

PubMed Abstract | CrossRef Full Text | Google Scholar

Kumar, S. S., Grussie, F., Suleimanov, Y. V., Guo, H., and Kreckel, H. (2018). Low temperature rates for key steps of interstellar gas-phase water Formation. Sci. Adv. 4, eaar3417. doi:10.1126/sciadv.aar3417

PubMed Abstract | CrossRef Full Text | Google Scholar

Kumaran, S. S., Lim, K. P., and Michael, J. V. (1994). Thermal rate constants for the Cl + H₂ and Cl + D₂ reactions between 296 and 3000 K. J. Chem. Phys. 101, 9487–9498. doi:10.1063/1.468486

CrossRef Full Text | Google Scholar

Lanza, M., and Lique, F. (2012). Collisional excitation of interstellar HCl by He. Mon. Not. R. Astron. Soc. 424, 1261–1267. doi:10.1111/j.1365-2966.2012.21304.x

CrossRef Full Text | Google Scholar

Lanza, M., and Lique, F. (2014). Hyperfine excitation of linear molecules by Para- and Ortho-H₂: application to the HCl–H₂ system. J. Chem. Phys. 141, 164321. doi:10.1063/1.4898855

PubMed Abstract | CrossRef Full Text | Google Scholar

Light, J. C., and Carrington, Jr., T. (2000). Discrete-variable representations and their utilization. Adv. Chem. Phys., 263–310. doi:10.1002/9780470141731.ch4

CrossRef Full Text | Google Scholar

Lique, F. (2015a). Communication: rotational excitation of HCl by H: rigid rotor vs. reactive approaches. J. Chem. Phys. 142, 241102. doi:10.1063/1.4922987

PubMed Abstract | CrossRef Full Text | Google Scholar

Lique, F. (2015b). Revisited study of the ro-vibrational excitation of H₂ by H: towards a revision of the cooling of astrophysical media. Mon. Not. R. Astron. Soc. 453, 810–818. doi:10.1093/mnras/stv1683

CrossRef Full Text | Google Scholar

Lique, F., and Faure, A. (2012). Communication: the rotational excitation of D₂ by H: on the importance of the reactive channels. J. Chem. Phys. 136, 031101. doi:10.1063/1.3678310

PubMed Abstract | CrossRef Full Text | Google Scholar

Lique, F., and Faure, A. (2017). Collisional excitation and dissociation of HCl by H. Mon. Not. R. Astron. Soc. 472, 738–743. doi:10.1093/mnras/stx2025

CrossRef Full Text | Google Scholar

Lique, F., and Faure, A. (2019). Gas-phase chemistry in space: from elementary particles to complex organic molecules. London: The Institute of Physics. doi:10.1088/2514-3433/aae1b5

CrossRef Full Text | Google Scholar

Lique, F., Honvault, P., and Faure, A. (2012). Ortho–Para-H₂ conversion by hydrogen exchange: Comparison of theory and experiment. J. Chem. Phys. 137, 154303. doi:10.1063/1.4758791

PubMed Abstract | CrossRef Full Text | Google Scholar

Lique, F., Zanchet, A., Bulut, N., Goicoechea, J. R., and Roncero, O. (2020). Hyperfine excitation of SH⁺ by H. A&A 638. Astron. Astrophys. 638, A72. doi:10.1051/0004-6361/202038041

CrossRef Full Text | Google Scholar

Loreau, J., Lique, F., and Faure, A. (2018). An efficient statistical method to compute molecular collisional rate coefficients. ApJL 853, 5. doi:10.3847/2041-8213/aaa5fe

CrossRef Full Text | Google Scholar

McClure, M. K., Rocha, W. R. M., Pontoppidan, K. M., Crouzet, N., Chu, L. E. U., Dartois, E., et al. (2023). An ice age JWST inventory of dense molecular cloud ices. Nat. Astron 7, 431–443. doi:10.1038/s41550-022-01875-w

CrossRef Full Text | Google Scholar

McGuire, B. A. (2022). 2021 census of interstellar, circumstellar, extragalactic, protoplanetary disk, and exoplanetary molecules. ApJS 259, 30. doi:10.3847/1538-4365/ac2a48

CrossRef Full Text | Google Scholar

Millar, T. J., Walsh, C., Van de Sande, M., and Markwick, A. J. (2023). The UMIST database for astrochemistry 2022. A&A 682, A109. doi:10.1051/0004-6361/202346908

CrossRef Full Text | Google Scholar

Neufeld, D. A., and Green, S. (1994). Excitation of interstellar hydrogen chloride. ApJ 432, 158–166. doi:10.1086/174557

CrossRef Full Text | Google Scholar

Pirlot Jankowiak, P. (2024). Collisional excitation of radicals of astrophysical interest. France: Université de Rennes. Thesis. Available online at: https://theses.hal.science/tel-05039944v1.

Google Scholar

Pirlot Jankowiak, P., and Lique, F. (2025). Collisional energy transfer in the highly reactive OH⁺–H₂ system. Phys. Rev. Lett. 134, 253002. doi:10.1103/hpcb-q7wh

PubMed Abstract | CrossRef Full Text | Google Scholar

Plasil, R., Mehner, T., Dohnal, P., Kotrik, T., Glosik, J., and Gerlich, D. (2011). Reactions of cold trapped CH⁺ ions with slow H atoms. ApJ 737, 60. doi:10.1088/0004-637X/737/2/60

CrossRef Full Text | Google Scholar

Polanyi, J. C. (1987). Some concepts in reaction dynamics. Science 236, 680–690. doi:10.1126/science.236.4802.680

PubMed Abstract | CrossRef Full Text | Google Scholar

Quack, M., and Troe, J. (1975). Complex formation in reactive and inelastic scattering: statistical adiabatic channel model of unimolecular processes III. Berichte Bunsenges. für Phys. Chem. 79, 170–183. doi:10.1002/bbpc.19750790211

CrossRef Full Text | Google Scholar

Rackham, E. J., Gonzalez-Lezana, T., and Manolopoulos, D. E. (2003). A rigorous test of the statistical model for atom–diatom insertion reactions. J. Chem. Phys. 119, 12895–12907. doi:10.1063/1.1628218

CrossRef Full Text | Google Scholar

Roueff, E., and Lique, F. (2013). Molecular excitation in the interstellar medium: recent advances in collisional, radiative, and chemical processes. Chem. Rev. 113, 8906–8938. doi:10.1021/cr400145a

PubMed Abstract | CrossRef Full Text | Google Scholar

Schreiner, P. R. (2020). Quantum mechanical tunneling is essential to understanding chemical reactivity. Trends Chem. 2, 980–989. doi:10.1016/j.trechm.2020.08.006

CrossRef Full Text | Google Scholar

Schulz, W. R., and Le Roy, D. J. (1965). Kinetics of the reaction H + p-H₂=o-H₂ + H. J. Chem. Phys. 42, 3869–3873. doi:10.1063/1.1695853

CrossRef Full Text | Google Scholar

Skouteris, D., Castillo, J. F., and Manolopoulos, D. E. (2000). ABC: a quantum reactive scattering program. Comput. Phys. Comm. 133, 128–135. doi:10.1016/S0010-4655(00)00167-3

CrossRef Full Text | Google Scholar

Song, H., and Guo, H. (2023). Theoretical insights into the dynamics of gas-phase bimolecular reactions with submerged barriers. ACS Phys. Chem. Au 3, 406–418. doi:10.1021/acsphyschemau.3c00009

PubMed Abstract | CrossRef Full Text | Google Scholar

Tonolo, F., and Alessandrini, S. (2024). Ab initio calculations for astrochemistry. Mem. S. A. It. 95, 77.

Google Scholar

Tonolo, F., Quintas-Sánchez, E., Batista-Planas, A., Dawes, R., and Lique, F. (2025). Collisional excitation of HCN by CO to refine the modeling of cometary comae. J. Phys. Chem. A 129, 9583–9590. doi:10.1021/acs.jpca.5c05448

PubMed Abstract | CrossRef Full Text | Google Scholar

Toscano, J., Lewandowski, H. J., and Heazlewood, B. R. (2020). Cold and controlled chemical reaction dynamics. Phys. Chem. Chem. Phys. 22, 9180–9194. doi:10.1039/D0CP00931H

PubMed Abstract | CrossRef Full Text | Google Scholar

Tran, T. D., Rednyk, S., Kovalenko, A., Roučka, Š., Dohnal, P., Plašil, R., et al. (2018). Formation of H₂O⁺ and H₃O⁺ cations in reactions of OH⁺ and H₂O⁺ with H₂: experimental studies of the reaction rate coefficients from T = 15 to 300K. ApJ 854, 25. doi:10.3847/1538-4357/aaa0d8

CrossRef Full Text | Google Scholar

Van der Tak, F. F. S., Lique, F., Faure, A., Black, J. H., and van Dishoeck, E. F. (2020). The leiden atomic and molecular database (LAMDA): current status, recent updates, and future plans. Atoms 8, 15. doi:10.3390/atoms8020015

CrossRef Full Text | Google Scholar

Wakelam, V., Gratier, P., Loison, J.-C., Hickson, K. M., Penguen, J., and Mechineau, A. (2024). The 2024 KIDA network for interstellar chemistry. A&A 689, A63. doi:10.1051/0004-6361/202450606

CrossRef Full Text | Google Scholar

Werfelli, G., Halvick, P., Honvault, P., Kerkeni, B., and Stoecklin, T. (2015). Low temperature rate coefficients of the H + CH⁺ → C⁺ + H₂ reaction: new potential energy surface and time-independent quantum scattering. J. Chem. Phys. 143, 114304. doi:10.1063/1.4931103

PubMed Abstract | CrossRef Full Text | Google Scholar

Wrathmall, S. A., Gusdorf, A., and Flower, D. R. (2007). The excitation of molecular hydrogen by atomic hydrogen in astrophysical media. Mon. Not. R. Astron. Soc. 382, 133–138. doi:10.1111/j.1365-2966.2007.12420.x

CrossRef Full Text | Google Scholar

Zanchet, A., Agúndez, M., Herrero, V. J., Aguado, A., and Roncero, O. (2013). Sulfur chemistry in the interstellar medium: the effect of vibrational excitation of H₂ in the reaction S⁺ + H₂ → SH⁺ + H. AJ 146, 125. doi:10.1088/0004-6256/146/5/125

CrossRef Full Text | Google Scholar

Zanchet, A., Lique, F., Roncero, O., Goicoechea, J. R., and Bulut, N. (2019). Formation of interstellar SH⁺ from vibrationally excited H₂: Quantum study of S⁺ + H₂ → SH⁺ + H reaction and inelastic collision. A&A 626, A103. doi:10.1051/0004-6361/201935471

CrossRef Full Text | Google Scholar

Zhang, H., and Guo, H. (2016). Recent advances in quantum dynamics of bimolecular reactions. Annu. Rev. Phys. Chem. 67, 135–158. doi:10.1146/annurev-physchem-040215-112016

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, B., and Guo, H. (2017). State-to-state quantum reactive scattering in four-atom systems. WIREs Comput. Mol. Sci. 7, e1301. doi:10.1002/wcms.1301

CrossRef Full Text | Google Scholar

Zhou, B., Yang, B., Balakrishnan, N., Kendrick, B. K., Chen, M., and Stancil, P. C. (2021). Inelastic, exchange, and reactive processes in rovibrationally excited collisions of HD with H. Mon. Not. R. Astron. Soc. 507, 6012–6019. doi:10.1093/mnras/stab2381

CrossRef Full Text | Google Scholar