- 1 Laboratory of Experimental Psychology, University of Leuven, Leuven, Belgium
- 2 Laboratory of Biological Psychology, University of Leuven, Leuven, Belgium
Visual object recognition is remarkably accurate and robust, yet its neurophysiological underpinnings are poorly understood. Single cells in brain regions thought to underlie object recognition code for many stimulus aspects, which poses a limit on their invariance. Combining the responses of multiple non-invariant neurons via weighted linear summation offers an optimal decoding strategy, which may be able to achieve invariant object recognition. However, because object identification is essentially parameter optimization in this model, the characteristics of the identification task trained to perform are critically important. If this task does not require invariance, a neural population-code is inherently more selective but less tolerant than the single-neurons constituting the population. Nevertheless, tolerance can be learned – provided that it is trained for – at the cost of selectivity. We argue that this model is an interesting null-hypothesis to compare behavioral results with and conclude that it may explain several experimental findings.
Neural Representations Underlying Visual Object Recognition
Any visual system, biological or artificial, challenged to recognize real-world objects, must satisfy two fundamental and seemingly opposing goals. First, due to the overwhelming number of objects, and the even larger number of geometrically possible object shapes, correct identification requires a high degree of selectivity. Second, due to the equally overwhelming number of different retinal images any given object can produce – reflecting variations in object and/or viewer position, light configuration and scene context – object identification requires a high degree of tolerance for such changes. In everyday life, the human visual system achieves remarkably accurate and robust object recognition. As illustrated in Figure 1 , this cannot be understood from the information present in the retinal image alone, but implies that the brain makes use of knowledge about image formation and geometrical transformations in determining object identity.
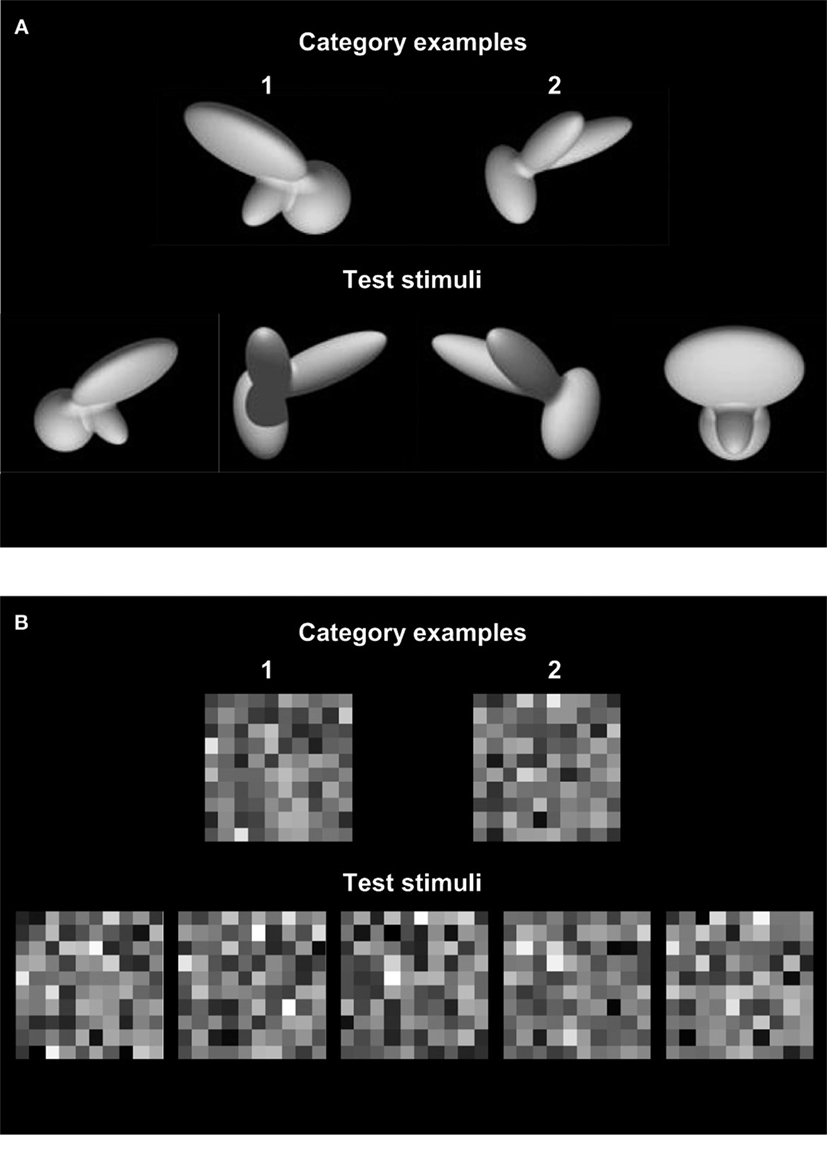
Figure 1. Examples of invariant and non-invariant object recognition. (A) Single exemplars of two categories (‘1’ and ‘2’; stimuli taken from Zoccolan et al., 2009 ) are shown in the upper row. When asked to classify unknown instances of these new visual objects (bottom row), human observers solve this problem effortlessly and “see” that the right answer is ‘1, 2, 2, 1’. This is remarkable, given that an ideal observer having access to all available image information, but lacking knowledge of image formation and geometrical transformations, cannot perform this task correctly. Such an ideal observer bases classification on a pixel-by-pixel comparison (Green and Swets, 1966 ) and judges the test stimuli depicted in the bottom row to belong to category ‘2, 2, 1, 1’, respectively. (B) The tolerance for irrelevant variations in object appearance that is achieved by the human visual system is limited to “natural” irrelevant dimensions such as position, light and context. Although the task portrayed here is much simpler from a computational perspective and trivially easy for the ideal observer, most readers will find it very hard to ignore the irrelevant variations, i.e., weak random perturbations of the exact luminance levels of the category exemplars, and see that the patterns in the lower row belong to category ‘1, 1, 2, 1, 2’, respectively.
At present, it is not known which brain computations underlie invariant object recognition . Moreover, the inability to fully reproduce such invariance in artificial vision systems is illustrative of the computational difficulty and complexity associated with object identification (Pinto et al., 2008 ); thus, it is not surprising that much of the research into the neural representations underlying object recognition is dedicated to understanding its computational underpinnings. Over the last decades, evidence suggesting that the response characteristics of neurons in the higher areas of the primate ventral visual stream – more specifically, inferior temporal cortex (IT) – play a crucial role has cumulated (Peissig and Tarr, 2007 ). The traditional view on neurons in these regions emphasizes their selectivity for relatively complex stimulus dimensions and tolerance for various image transformations, which contrasts with neurons in more upstream regions, such as primary visual cortex (V1). The prime example is sensitivity for stimulus position. Due to their small receptive field size, V1-neurons tend to be very sensitive to manipulations of stimulus position, while the larger receptive fields encountered in IT-neurons allow these to be less sensitive for variations in stimulus position. Computationally, position-invariant neurons with complex stimulus preferences could result from applying a max-operator to afferent subunits tuned to generic features at different locations (Riesenhuber and Poggio, 1999 ); thus, behavioral invariance for certain image transformations may reflect invariance at single cell level (Serre et al., 2007 ).
However, this view on IT-neurons is too simplified and somewhat misleading. For instance, IT-neurons are characterized by a wide variety of receptive field sizes (Op de Beeck and Vogels, 2000 ). Consequently, there is also a wide variety in the degree of tolerance for stimulus translations achieved by these neurons. The same argument applies to transformations affecting object size and viewpoint (Ito et al., 1995 ) – although the degree of tolerance differs across these dimensions. Furthermore, it has recently been shown that selectivity and tolerance for several types of transformations trade-off in IT-neurons (Zoccolan et al., 2007 ); thus, the ideal of high selectivity and high tolerance is not a prototypical characteristic of single cell responses in IT. Hence, invariant object recognition as illustrated in Figure 1 does not seem to reflect invariant neural object representations in the top level of the ventral object vision or “what” pathway.
Neural Population-Codes May Underlie Behavioral Invariance
Traditional views on the relation between behavioral performance and single cell characteristics emphasize the importance of each neuron in signaling the presence or absence of a particular feature in the visual stimulus (Barlow, 1972 ). In contrast, more recent approaches have explored how the combined responses of multiple neurons may underlie psychophysical sensitivity (Pouget et al., 2000 ; Jazayeri and Movshon, 2006 ). Population-coding models have been applied successfully to explain a variety of behavioral results in simple perceptual tasks as contrast discrimination (Goris et al., 2009 ), motion discrimination (Britten et al., 1992 ) and the tilt after-effect in orientation perception (Jin et al., 2005 ). For object recognition, the information conveyed in the population-response of a pool of IT-neurons may be crucial to represent objects (Logothetis and Pauls, 1995 ; Perrett et al., 1998 ).
Recent attempts to explain how invariant object recognition arises, despite the lack of invariance at single-cell level, have made use of linear classification methods to read-out the population activity of IT-neurons. Hung et al. (2005) recorded responses of single IT-neurons while monkeys viewed a set of object images at multiple retinal positions and sizes. During training, the read-out network was exposed to exactly one position and size. Intriguingly, when tested, network classification performance was only mildly affected by variations in position and size, seemingly suggesting that pooling responses of non-invariant IT-neurons results in invariant behavior. While tempting to interpret these findings as showing that a neural population-code is inherently more robust than the single-neurons constituting the population, this conclusion is likely to be wrong. The reason is the following: although a fairly small population of IT-neurons may convey sufficient information to allow invariant object recognition in a low-dimensional stimulus space, it is not clear how invariant behavior can emerge without being trained for, as was the case in the aforementioned study.
To see this, it may be helpful to think of identification as probability density estimation (Green and Swets, 1966 ) and to realize that training in the context of linear classification methods refers to parameter estimation or, more specifically, optimizing the weights of a linear function (Jäkel et al., 2009 ) known as the decision template. Formally, the challenge to recognize previously unseen instances of a visual object category, using the IT-population response, is identical to the typical problem faced in machine-learning, i.e., to build a model from a finite training set that generalizes the properties characterizing the training stimuli to new stimuli. It is well-known that the training data must be representative of the distribution of the test data for a classifier to generalize well (Duda et al., 2001 ). For non-invariant IT-neurons, this condition is not met in the experiment of Hung et al. (2005) .
This is illustrated in more detail in Figure 2 for a linear classifier operating on neural responses in a 2-D stimulus space. The decision templates shown in the bottom row of Figure 2 clarify why a linear classifier, not optimized for variation on irrelevant dimensions such as retinal position or size, will not be able to correctly categorize stimuli that are severely different from the training stimuli in their task-irrelevant aspects: responses to such stimuli are simply ignored by the classifier (Figure 2 C). So, why then did Hung et al. (2005) find invariant performance with a classifier that was not trained, i.e., not optimized for variation on any irrelevant dimension? This finding was most likely due to the fact that the variations on the irrelevant dimensions tested by Hung et al. (2005) were relatively small – 4° position displacement and size scale doubling – and most likely within the limited range where single IT-neurons display approximately invariant behavior. Furthermore, this variation led to a small, but significant, drop in classification performance; thus, it is premature to conclude that this study demonstrates that invariant object recognition emerges spontaneously at the population level when single neurons only show limited invariance.
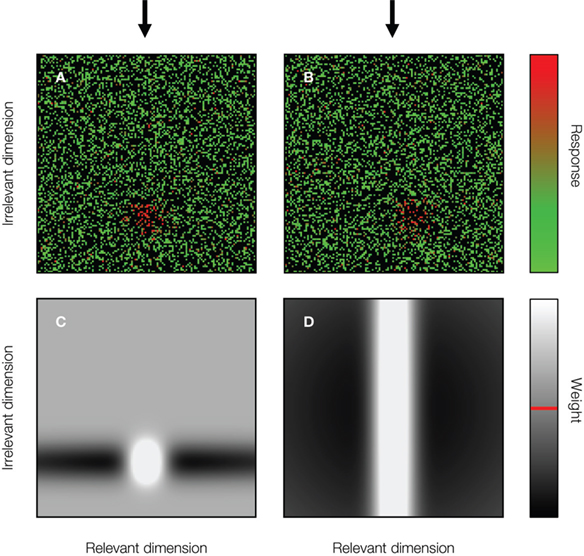
Figure 2. Identification is weight optimization. To classify each stimulus in an identification task (explained in detail in Figure 3 A), an optimal linear classifier bases its decision on the (thresholded) weighted sum of responses (Green and Swets, 1966 ). Neurons tuned to the target location are weighted positively while neurons tuned to the non-target locations are weighted negatively (the red line in the lower legend indicates the grey level matching zero). Non-informative neurons are ignored (i.e., they receive a weight equal to zero). (A) Responses of a pool of simulated IT-neurons to a 2-D stimulus. Each neuron’s response is plotted at the neuron’s preferred stimulus location. Only one of the stimulus dimensions is relevant for the identification task. The target location on the relevant dimension is indicated by the black arrow. The stimulus shown to the neural network is at the target location. (B) Same as (A) for a stimulus at a non-target location. The stimulus location on the irrelevant dimension has not changed. (C) The normalized decision template of a classifier optimized for identification at one specific location on the irrelevant dimension. Neurons tuned to stimulus locations remote from the target and distracter stimuli are not informative, and thus do not contribute to the decision. (D) The normalized decision template of a classifier optimized for identification at all possible locations on the irrelevant dimension.
Lessons Learned from Simulations
The simulations performed by Goris and Op de Beeck (2009) are a case-study of the typical machine-learning problem and investigated in more detail how selectivity and tolerance of a linear classifier trained to identify a 2-D target stimulus depend on several single-cell and population characteristics. Simulations have the benefit over real data that they allow much more systematic and controlled manipulations of the neural code in a fully-understood environment. To approximate realistic circumstances, simulated neurons were characterized by several biologically inspired constraints, i.e., response variability, dependent or correlated tuning , inter-unit variability and correlated noise. All these characteristics are adopted in the simulations discussed in this paper and illustrated in more detail in Figure 3 .
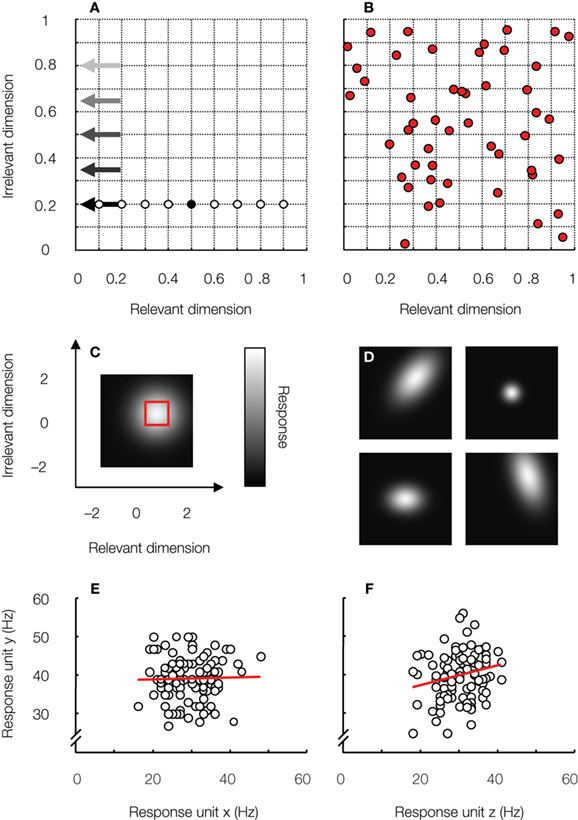
Figure 3. Task and network characteristics studied in the simulations. (A) Design of the identification experiment. A linear classifier was trained to discriminate a 2-D target stimulus (black symbol) from a 2-D distracter – randomly selected from a set of eight distracters (white symbols) on each trial – using the responses of a simulated pool of IT-neurons as input. After training, classification performance of the network was tested in five identification tasks, each characterized by the test stimuli’s location on the irrelevant dimension (indicated by the arrows; lighter arrow colors correspond to a larger test-training difference on the irrelevant dimension). (B) Preferred stimulus location was sampled randomly from a bivariate uniform distribution – red square in (C) – for each unit in the network. The distribution of preferred stimulus locations is shown for one particular network. (C) Each network unit is characterized by a 2-D Gaussian-shaped tuning function. This unit is broadly tuned to both stimulus dimensions. Tuning width and dependence was manipulated in the simulations. (D) Some example unit tuning functions. (E) To mimic neural noise, unit responses varied across stimulus presentations. Responses of one unit to 100 stimulus presentations are plotted as a function of the responses of another unit to the same stimuli. These units share no noise. In the nervous system, responses of cortical neurons are typically weakly correlated (Zohary et al., 1994 ), as shown in (F). This characteristic was shown to impair tolerance by Goris and Op de Beeck (2009) . For further details on the methods, the reader is referred to this paper.
The simulations essentially showed that the classifier averages out effects of inter-unit variability. Consequently, the hypothetical “average” neuron determines network behavior to a large degree. Given that IT-neurons code for many stimulus aspects and are only moderately invariant, it is most interesting to consider networks that have, on average, similar tuning widths for the relevant and irrelevant stimulus dimension. One example of such tuning function is shown in Figure 3 C (this particular tuning function is the average tuning function of the networks used in the simulations in this paper).
Not surprisingly, for these “circularly tuned” networks, selectivity decreases with increasing tuning width, while tolerance increases. This observation mimics the trade-off between selectivity and tolerance at single-cell level (Zoccolan et al., 2007 ) and can be understood from the decision templates shown in Figure 2 . Smaller circular tuning functions allow better identification performance at the trained location on the irrelevant dimension, but also lead to a weighting profile that is sharper, and thus deviates more from the flat profile needed to achieve invariant behavior. As is well-known in machine learning, the same fundamental trade-off implies that selectivity grows with pool size, but tolerance decreases (the more complex the classifier – complexity refers here to the number of units –, the more data are needed to avoid over-fitting and obtain good generalization). Thus, on the most challenging identification tests, larger pools are outperformed by smaller pools. This is illustrated in Figure 4 . Average performance in the identification task is shown for three pool sizes at two locations on the irrelevant dimension. When the test stimuli’s location on the irrelevant dimension is identical to the training situation, larger pools perform better in discriminating the target from distracter stimuli. Changing the test stimuli’s location on the irrelevant dimension leads to a drop in performance for all networks. However, performance is most impaired for the larger pools, both in absolute and relative terms.
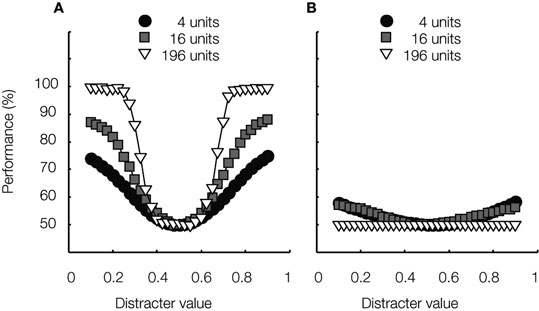
Figure 4. The effect of pool size on classification performance. The average networks’ tuning function is shown in Figure 3 C. Networks were further characterized by noisy neurons, inter-neuron variability in the 2-D tuning functions, and correlated noise. (A) Average classification performance is plotted as a function of distracter value for three different pool sizes, consisting of 4, 16 and 196 units, respectively. The test stimuli’s location on the irrelevant dimension was identical to the training situation. Thus, these data express the selectivity of the considered networks. The smooth shape of the curves shows that the classifier can interpolate between stimuli encountered during training. (B) Same as (A) for the maximal test-training difference illustrated in Figure 3 A; thus, these data express the tolerance of the considered networks. The large difference with the data shown in (A) shows that the classifier cannot extrapolate from stimuli encountered during training. Similar results were shown in Goris and Op de Beeck (2009) .
The performance curves in Figure 4 A have no obvious peaks at the exact location of the training stimuli (Figure 3 A), but are very smooth in shape. This shows that the classifier can interpolate between the distracters encountered during training. Nevertheless, the drop in performance seen in Figure 4 B clearly illustrates that the classifier fails to extrapolate from the training stimuli. All these results support the hypothesis that for the “circularly tuned” networks considered in our simulations, invariant object recognition does not appear spontaneously when responses of non-invariant neurons are pooled; thus, a neural population-code is not inherently more robust than the single neurons constituting the population. Quite the contrary, the average single-neuron selectivity provides an upper bound for the degree of network tolerance.
However, results like these should not be taken to imply that invariant object recognition cannot be achieved by a linear classifier. Invariant classification is possible, provided that the classifier is trained for variation on the irrelevant dimension(s). This is illustrated in Figure 5 . Networks having exactly the same characteristics as those shown in Figure 4 were trained to perform target identification at all five locations on the irrelevant dimension shown in Figure 3 . All other aspects of the training and test procedure were held constant.
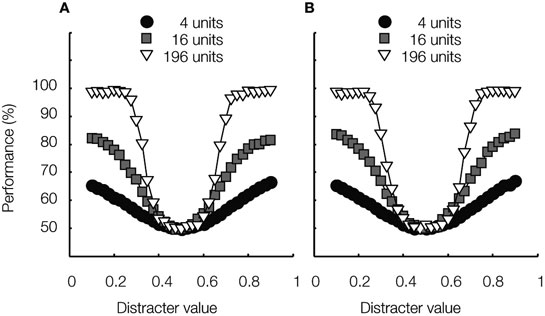
Figure 5. Learned invariance. Average classification performance is plotted as a function of distracter value for three different network sizes, consisting of 4, 16 and 196 units, respectively. These networks were trained to perform identification at all five locations on the irrelevant dimension. (A) The test stimuli’s location on the irrelevant dimension is indicated by the black arrow in Figure 3 A. (B) The test stimuli’s location on the irrelevant dimension is indicated by the lightest arrow in Figure 3 A. These results were not part of the simulations in Goris and Op de Beeck (2009) .
As can be seen in Figure 5 , average classification performance is now approximately identical for both identification tests; thus, invariance can be learned by a linear read-out mechanism, but requires experience with variation on the irrelevant task aspects. Note that the networks’ neurons’ rank-order stimulus preference is often not preserved due to the effects of correlated tuning – see examples in Figure 3 D. It has been suggested that this property is crucial to support invariant object-recognition (Vogels and Orban, 1996 ; Li et al., 2009 ). On average, however, tuning for both stimulus dimensions is not correlated and the average level of correlated tuning in the pool of neurons underlying a perceptual decision may be more important than idiosyncratic tuning properties of single neurons (Goris and Op de Beeck, 2009 ).
Finally, note that for the two smaller network sizes, performance is somewhat impaired relative to the non-invariant classifier shown in Figure 4 A. This difference shows that, for difficult tasks, tolerance can be learned at the cost of selectivity.
A Valuable Null-Hypothesis for Behavioral Tests?
The linear classifier used in our simulations describes only one of many possible ways to read-out neural activity; thus, it is by no means guaranteed that decoding in the real nervous system is fully captured by this simple model. Indeed, the brain is no tabula rasa in which a new task is learned without reference to prior experience. Shortcuts based on previously established learning and wiring may increase the efficiency and speed of reading out object representations in an invariant manner. Moreover, receptive field properties of IT-neurons are only crudely captured by our circularly tuned networks; and in real neurons, these properties may even change due to recent visual experience (Li and DiCarlo, 2008 ). Nevertheless, we argue here that the model considered in our simulations is an interesting null-hypothesis to compare behavioral data with. First, the formal problem faced by the visual system and the linear classifier is the same: both need to learn from data (Jäkel et al., 2009 ). Second, despite its simplicity, the linear classifier optimally combines the available information to perform the task it is trained for. There is a wealth of literature demonstrating the usefulness of the ideal observer framework in studying perceptual systems (Geisler, 2003 ). Third, this kind of read-out model is neurophysiologically plausible, and thus a sensible model for a biological system (Jazayeri and Movshon, 2006 ). Finally, identifying and quantifying when and how behavioral data deviate from ideal stimulus-limited performance may provide insight in the ways the brain uses knowledge about object constancy in the world when determining object identity.
Data-sets suitable for testing this null-hypothesis directly require estimates of both the response characteristics of neurons underlying an object recognition task that requires generalization, as well as behavioral performance measurements in that task. One readily available example in the literature is the work performed by Logothetis et al. (1994 , 1995 ) on view-dependent object recognition in monkeys. In other cases, without explicit knowledge of the response characteristics of neurons underlying particular behavioral tasks, we are limited to a qualitative assessment in comparing psychophysical data and model performance.
Nevertheless, several observations are in line with the proposed null-hypothesis. First, there are some illustrative behavioral analogues to the effects described here. We are experts in recognizing faces and letters. Despite the fact that these stimuli are “overlearned”, we are not tolerant for rotations (McKone, 2009 ) – try reading upside down! Given that a non-invariant system in the limit may achieve a higher degree of selectivity than an invariant system (Figures 4 and 5 ) it may be advantageous to sacrifice tolerance for some specific dimensions (such as orientation) for some special classes of stimuli.
Second, in a recent review paper, Kravitz et al. (2008) concluded that even translations as small as 0.5° affect object recognition to a certain degree; thus, object recognition is not completely position-independent – contrary to popular wisdom. Moreover, all behavioral paradigms discussed in their review, i.e., priming, training, matching and adaptation, show a largely monotonic decrease in the amount of transfer with translation size. This finding is in line with the proposed null-hypothesis, as model classification performance decreases monotonically with test-training difference (Goris and Op de Beeck, 2009 ).
Third, it is worth mentioning that two recent studies have investigated to what degree rats form an appropriate animal model for invariant object recognition (Minini and Jeffery, 2006 ; Zoccolan et al., 2009 ). Intriguingly, the studies reach opposite conclusions. Minini and Jeffery (2006) found rats to be poor shape-perceivers that do not rely on invariant shape processing at all, but instead use low-level image cues to solve shape discrimination tasks. Zoccolan et al. (2009) , on the other hand, demonstrated that rats do possess some form of invariant visual object recognition as they can successfully discriminate between previously unseen transformations of learned objects (some examples are shown in Figure 1 ) and even extrapolate to unseen variation dimensions (i.e., novel lighting conditions). Consistent with the model presented here, the crucial difference between both studies is to be found in the training protocol. Indeed, rats trained to discriminate between two stimuli that do not vary on task-irrelevant aspects do not generalize to unseen stimulus instances (Minini and Jeffery, 2006 ). However, when rats are trained to discriminate target objects despite variation in object size and viewpoint, they are able to generalize to new combinations of previously encountered variations on the irrelevant dimensions (Zoccolan et al., 2009 ). Generalization is not perfect though, but decreases with distance to the closest stimulus seen during training. As mentioned earlier, such finding is also in line with the null-hypothesis, as model performance decreases with test-training difference (Goris and Op de Beeck, 2009 ).
These three examples provide interesting tests for our null-hypothesis, but they do not yet allow a test of quantitative predictions because there are no data on the response characteristics of the neurons that are relevant in these tasks. Further experiments will be necessary to find out whether or not invariance in behavior can be predicted quantitatively from two factors: required invariance during training, and the average degree of invariance of single neurons. Such tests might further support our conclusion that optimal read-out of a population of non-invariant IT-neurons may explain several aspects of (the lack of) invariance in visual object recognition.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We wish to thank G. Kreiman, D. Zoccolan and J. Wagemans for valuable comments. This research was supported by a post-doctoral fellowship from the Fund for Scientific Research (FWO) of Flanders (Robbe L. T. Goris), and the Human Frontier Science Program (CDA 0040/2008).
Key Concepts
Invariant object recognition: The ability to correctly classify visual objects in their previously learned object-name category, despite variations in object appearance due to object-identity preserving transformations, such as changes in object and viewer position, illumination conditions, and occlusion by other objects.
Population-coding: A neural information coding strategy, whereby information is presented in populations of cells rather than in single cells.
Linear classification: Classifying stimuli into different response categories based on the thresholded weighted sum of extracted stimulus features. In the applications discussed in this paper (simulated) IT-neurons operate as feature detectors.
Probability density estimation: Estimating the probability density or likelihood that an observed event, such as a multi-dimensional population response, is a sample from a specific distribution, e.g., the distribution of multi-dimensional responses to the target stimulus.
Correlated tuning: A multidimensional tuning-function, wherein the preferences along one of the dimensions change with the value on the other dimension(s).
Interpolate: Here, interpolation refers to generalizing what is learned about two different exemplars of a given category to other exemplars that are weighted combinations of both exemplars, with all weights having values between zero and one.
Extrapolate: Here, extrapolation refers to generalizing what is learned about different exemplars of a given category to other, more extreme, exemplars that were not encountered during training.
Rank-order stimulus preference: A neuron’s stimulus preference derived from the order of the magnitude of the stimulus responses – rather than from the absolute magnitude. Changing the stimulus value along one dimension might rescale the entire tuning function on another dimension, and thus the absolute stimulus responses, without affecting the rank-order.
References
Barlow, H. B. (1972). Single units and sensation: a neuron doctrine for perceptual psychology? Perception 1, 371–394.
Britten, K. H., Shadlen, M. N., Newsome, W. T., and Movshon, J. A. (1992). The analysis of visual motion: a comparison of neuronal and psychophysical performance. J. Neurosci. 12, 4745–4765.
Duda, R. O., Hart, P. E., and Stork, D. G. (2001). Pattern Classification. New York, John Wiley & Sons, Inc.
Geisler, W. S. (2003). Ideal observer analysis. In The Visual Neurosciences, L. Chalupa and J. Werner, eds (Boston, MIT press), pp. 825–837.
Goris, R. L. T., and Op de Beeck, H. P. (2009). Neural representations that support invariant object recognition. Front. Comput. Neurosci. 3, 1–16. doi:10.3389/neuro.10.003.2009.
Goris, R. L. T., Wichmann, F. A., and Henning, G. B. (2009). A neurophysiologically plausible population code model for human contrast discrimination. J. Vis. 9, 1–22.
Green, D. M., and Swets, J. A. (1966). Signal Detection Theory and Psychophysics. New York, John Wiley & Sons, Inc.
Hung, C. P., Kreiman, G., Poggio, T., and DiCarlo, J. J. (2005). Fast readout of object identity from macaque inferior temporal cortex. Science 310, 863–866.
Ito, M., Tamura, H., Fujita, I., and Tanaka, K. (1995). Size and position invariance of neuronal responses in monkey inferotemporal cortex. J. Neurophysiol. 73, 218–226.
Jäkel, F., Schölkopf, B., and Wichmann, F. A. (2009). Does cognitive science need kernels? Trends Cogn. Sci. 13, 381–388.
Jazayeri, M., and Movshon, J. A. (2006). Optimal representation of sensory information by neural populations. Nat. Neurosci. 9, 690–696.
Jin, D. Z., Dragoi, V., Sur, M., and Seung, H. S. (2005). Tilt aftereffect and adaptation-induced changes in orientation tuning in visual cortex. J. Neurophysiol. 94, 4038–4050.
Kravitz, D. J., Vinson, L. D., and Baker, C. I. (2008). How position dependent is visual object recognition? Trends Cogn. Sci. 12, 114–122.
Li, N., Cox, D. D., Zoccolan, D., and DiCarlo, J. J. (2009). What response properties do individual neurons need to underlie position and clutter “invariant” object recognition? J. Neurophysiol. 102, 360–376.
Li, N., and DiCarlo, J. J. (2008). Unsupervised natural experience rapidly alters invariant object representation in visual cortex. Science 321, 1502–1507.
Logothetis, N. K., and Pauls, J. (1995). Psychophysical and physiological evidence for viewer-centered object representations in the primate. Cereb. Cortex 5, 270–288.
Logothetis, N. K., Pauls, J., Bülthoff, H. H., and Poggio, T. (1994). View-dependent object recognition by monkeys. Curr. Biol. 4, 401–414.
Logothetis, N. K., Pauls, J., and Poggio, T. (1995). Shape representation in the inferior temporal cortex of monkeys. Curr. Biol. 5, 552–563.
McKone, E. (2009). Holistic processing for faces operates over a wide range of sizes but is strongest at identification rather than conversational distances. Vision. Res. 49, 268–283.
Minini, L., and Jeffery, K. J. (2006). Do rats use shape to solve “shape discriminations”? Learn. Mem. 13, 287–297.
Op de Beeck, H. P., and Vogels, R. (2000). Spatial sensitivity of macaque inferior temporal neurons. J. Comp. Neurol. 426, 505–518.
Peissig, J. J., and Tarr, M. J. (2007). Visual object recognition: do we know more now than we did 20 years ago? Annu. Rev. Psychol. 58, 75–96.
Perrett, D. I., Oram, M. W., and Ashbridge, E. (1998). Evidence accumulation in cell populations responsive to faces: an account of generalisation of recognition without mental transformations. Cognition 67, 111–145.
Pinto, N., Cox, D. D., and DiCarlo, J. J. (2008). Why is real-world visual object recognition hard? PLoS Comput. Biol. 4, e27.
Pouget, A., Dayan, P., and Zemel, R. (2000). Information processing with population codes. Nat. Rev. Neurosci. 1, 125–132.
Riesenhuber, M., and Poggio, T. (1999). Hierarchical models of object recognition in cortex. Nat. Neurosci. 2, 1019–1025.
Serre, T., Oliva, A., and Poggio, T. (2007). A feedforward architecture accounts for rapid categorization. Proc. Natl. Acad. Sci. U.S.A. 104, 6424–6429.
Vogels, R., and Orban, G. A. (1996). Coding of stimulus invariances by inferior temporal neurons. Prog. Brain Res. 112, 195–211.
Zoccolan, D., Kouh, M., Poggio, T., and DiCarlo, J. J. (2007). Trade-off between object selectivity and tolerance in monkey inferotemporal cortex. J. Neurosci. 27, 12292–12307.
Zoccolan, D., Oertelt, N., DiCarlo, J. J., and Cox, D. D. (2009). A rodent model for the study of invariant visual object recognition. Proc. Natl. Acad. Sci. U.S.A. 106, 8748–8753.
Keywords: object recognition, inferior temporal cortex, population coding, invariance, training
Citation: Front. Neurosci. (2010) 4:1. doi: 10.3389/neuro.01.012.2010
Received: 08 October 2009;
Paper pending published: 14 December 2009;
Accepted: 17 December 2009;
Published online: 15 May 2010
Edited by:
Hava T. Siegelmann, University of Massachusetts Amherst, USAReviewed by:
Michel Vidal-Naquet, RIKEN Brain Science Institute, JapanYasser Roudi, Nordic Institute for Theoretical Physics, Sweden
Copyright: © 2010 Goris and Op de Beeck. This is an open-access publication subject to an exclusive license agreement between the authors and the Frontiers Research Foundation, which permits unrestricted use, distribution, and reproduction in any medium, provided the original authors and source are credited.
*Correspondence: Hans P. Op de Beeck is Associate Professor at the University of Leuven (K.U. Leuven), Belgium. After obtaining his Ph.D. at the K.U. Leuven in 2003, he worked as a Post-doctoral Research Fellow in the labs of Nancy Kanwisher and James DiCarlo at the Massachusetts Institute of Technology. His research focuses on how humans and other animals perceive and learn about their visual environment. These studies involve the help of many fantastic colleagues and students, and a wide variety of methods, including psychophysics, brain imaging, invasive electrophysiological recordings, and computational modeling.aGFucy5vcGRlYmVlY2tAcHN5Lmt1bGV1dmVuLmJl

