Statistical learning and mathematics knowledge: the case of arithmetic principles

Introduction

Implicit learning of patterns and regularities, known as statistical learning, is a core attribute of human cognition (Saffran et al., 1996; Fiser and Aslin, 2002; Krogh et al., 2013; Schapiro and Turk-Browne, 2015). Characterized as automatic, associative, and non-conscious, statistical learning is considered distinct from intentional, explicit learning (Gebauer and Mackintosh, 2007; Arciuli and Simpson, 2011). Statistical learning is believed to play a role in the acquisition of various kinds of knowledge from social understanding (Ruffman et al., 2012) to the components of language (Erickson and Thiessen, 2015). To our knowledge, however, there has been no previous investigation of whether statistical learning is related to the acquisition of numerical knowledge, despite the prominence of patterns and regularities in the number system and operations. In the present study, we examined whether individual differences in statistical learning are related to children's ability to solve arithmetic problems.

Statistical learning and arithmetic

Statistical learning is well-established as a fundamental mechanism underlying learning and development throughout the lifespan (c.f. Krogh et al., 2013). It contributes to learning regularities across a wide range of domains of cognition, including visual and auditory perception, social cognition, face recognition, and syntax acquisition (Ruffman et al., 2012; Kidd and Arciuli, 2016). Most recently, it has been implicated in the acquisition of reading skills, including the regularities between letters and sounds in word reading and spelling across languages (Treiman and Kessler, 2022). Arciuli and Simpson (2012) found that individual differences in kindergartners' statistical learning predicted their scores on the reading subset of the Wide Range Achievement Test, even after age and attention had been taken into account. Thus, statistical learning has been found to be an important mechanism for learning not only simple artificial patterns over just a few minutes in the lab but also complex real-world relations underlying academic knowledge typically considered to be acquired via slow, explicit processes.

Akin to reading, mathematics operations are founded upon patterns and regularities (Collins and Laski, 2015; Rittle-Johnson et al., 2019). These regularities exist at multiple levels such as the repetition of the digits 1–9 in each decade of the count sequence, the successor principle relating count words to quantities (e.g., each successive number in the count string represents an increase in quantity of exactly one), the correspondence between place-value notation and base-10 structure, and arithmetic principles that dictate consistent properties of operations (e.g., if a + b = c then b + a = c). The ability to deduce rules and structure, as indicated by patterning knowledge, has been found to be related to both procedural and conceptual mathematics knowledge from preschool through college (MacKay and De Smedt, 2019; Wijns et al., 2021; Borriello et al., 2023). Given that statistical learning is responsible for implicit learning of patterns, it may be the most proximal process accounting for the relation between individual differences in pattern knowledge and mathematics outcomes.

Arithmetic, like other aspects of mathematics, involves understanding regular relations among numbers and between operations, generally referred to as arithmetic principles (Gilmore, 2006). Two fundamental arithmetic principles are commutativity and inversion. The commutativity principle describes regularities in the relations between the addends and the sum of addition problems: the order of the operands does not influence the outcome. The inversion principle describes regularities in the relations between addition and subtraction: the inverse operation will result in the same value with no net change (i.e., if c–a = b, then a + b = c). Individual differences in the extent to which children demonstrate knowledge of these principles have implications for both concurrent and future problem-solving (Steinberg, 1985; Christensen and Cooper, 1991; Canobi et al., 1998). For example, Canobi et al. (1998) designed a study in which children's conceptual understanding was measured by the ability to spontaneously use arithmetic principles in problem solving and to recognize and explain them when prompted. They found that 6–8-year-olds who recognize commutativity-based relations between consecutive problems solve problems more quickly and accurately than those who demonstrated relatively poor conceptual understanding. Detecting these regularities in arithmetic may facilitate arithmetic learning by leading to a reduction in the number of addition/subtraction combinations children need to learn because automatizing the response to one problem can generate the response to a related one (Ginsburg, 1989).

While arithmetic principles are often explicitly taught, there is evidence that children may also incidentally deduce them from experience (e.g., Prather and Alibali, 2011). For instance, Baroody and Gannon (1984) noted that a small proportion of kindergartners who participated in their study discovered commutativity in the absence of explicit instruction over the course of solving problems across three sessions. Similarly, although preschoolers are unlikely to have been explicitly taught the inverse relation between addition and subtraction, they seem to deduce it from experience; 3- and 4-year-olds solve inversion problems more accurately than standard ones when the problems involve sets of objects (Sherman and Bisanz, 2007; Canobi and Bethune, 2008). At the same time, even after exposure to explicit instruction of inversion during kindergarten, not all children demonstrate knowledge of regularity when solving symbolic problems. Rather, the number of children who demonstrate knowledge of the inversion principle on symbolic problems increases between the ages of 5 and 7-years, suggesting there are differences in children's ability to detect the regularity even with explicit instruction (Bryant et al., 1999; Canobi, 2005). These individual differences may be accounted for, in part, by children's statistical learning capacity.

The extent to which individual differences in using arithmetic principles in problem solving are related to statistical learning capacity may vary as a function of children's experience/familiarity with particular types of problems. When children have a greater level of experience, they are more likely to have developed procedural strategies for solving the problem or to have automatized fact retrieval. These factors might affect the relation between statistical learning and arithmetic problem solving.

Consider a situation where a child is provided with a problem that has a solution (e.g., 6 + 3 = 9) and then asked to solve a second related problem (e.g., 3 + 6 =?). Depending on the child's experience/skill with the problem type, using statistical learning to arrive at a response may affect accuracy, latency, both, or neither. If a child has already automatized the sum of 3 + 6, there is no reason to expect they would solve this problem more accurately or quickly when it is preceded by 6 + 3, even if they recognize the similarity between the problems. In this scenario, statistical learning capacity is unlikely to be related to either accuracy or latency. A second possible scenario involves a child who has not yet automatized the sum but has some familiarity with a counting strategy. If the child can execute this strategy correctly with a high level of consistency, then detecting the commutativity regularity is unlikely to increase accuracy, but it may lead to a shorter response time because it would provide a short-cut strategy. In other words, statistical learning capacity is likely to be related to latency but not accuracy. If, however, a child is less able to execute the strategy accurately, then detecting the principle relation between the two problems may be more likely to lead to an accurate response. In this case, statistical learning capacity is likely to be related to accuracy, while its relation to response time is less clear. Finally, a third scenario is possible when a child has such limited experience with a problem type that it may constrain the very ability to recognize arithmetic principles due to a lack of knowledge about where to direct their attention. In this case, statistical learning is unlikely to be related to either accuracy or latency of problem solving.

In summary, there is reason to believe that individual differences in statistical learning are related to children's proficiency in solving arithmetic problems (captured in both accuracy and response time) and that this relation may vary with level of experience, but no research has tested these hypotheses empirically.

Statistical learning and executive control

Statistical learning is one of several domain-general cognitive processes that contribute to learning. As such, it is important to consider how it is related to other key cognitive processes and whether it interacts with them in predicting learning. Previous studies with infants and adults suggest that statistical learning aids decision-making, action predictions, and memory by creating a mental framework of the environment based on existing regularities (Sherman et al., 2020). To date, the issue has primarily been investigated in the context of language learning. Several studies indicate that statistical learning tasks tap an ability that is not correlated with non-verbal intelligence, working memory, and rapid naming (Conway et al., 2010; Siegelman and Frost, 2015; Kidd and Arciuli, 2016). The findings are less consistent with respect to executive control processes (Ma and Yu, 2015; Park et al., 2020). Bulgarelli and Weiss (2016) found no relation between inhibitory control and statistical learning in a study of artificial language learning with adults. In contrast, Deocampo and Conway (2016) found that statistical learning was not only correlated with attention, conflict response, and inhibition but also mediated their relation to language learning among 7–12 year-olds. The mixed findings in the domain of language learning may be due to age differences across the studies. Examining this issue in the context of mathematics may provide new insights.

The present study

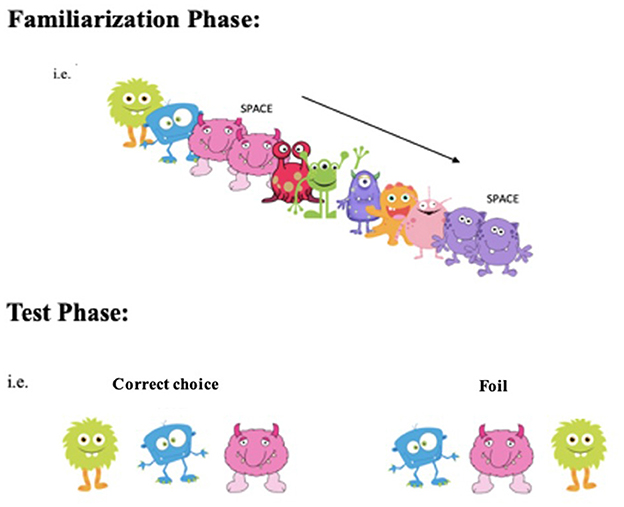
The central goal of the present paper was to examine the association between statistical learning and first graders' arithmetic principle knowledge. Statistical learning was measured using one of the most common visual statistical learning tasks—the embedded triplet paradigm (Arciuli and Simpson, 2011). Children are shown a series of novel cartoon figures presented in triplets; then asked in the second phase of the paradigm to determine which of two triplets (a previously seen triplet or a foil triplet) they had previously seen. Arithmetic principle knowledge was measured using a task adapted from previous studies (e.g., Baroody et al., 1983; Canobi, 2009). Children were shown pairs of three term equations where the first equation in each pair had the answer displayed and was either related via a principle (i.e., commutativity or inversion) or not to the second equation. Children who were able to notice the regularity between the principle pairs (e.g., same addends but in a different order) would have an advantage in that they could rely on the answer of the first equation to solve the second (e.g., if 7 + 2 + 4 = 13 then 2 + 7 + 4 = 13; if 7–4–2 = 1 then 7–4–1 = 2). Using three term equations helped to ensure implicit pattern recognition was driving the response. Because three term equations are not familiar to first graders, they would be unable to rely on automatic fact retrieval and would be motivated to apply a short-cut to decrease the difficulty of these equations.

This design allowed us to test predictions about the relation between statistical learning and arithmetic principle knowledge. We reasoned that if children responded more accurately and/or quickly on related than on unrelated pairs of problems, it could be inferred that they noticed and used the regularity between the pairs to arrive at their response. We expected that children with greater statistical learning capacity for identifying and extracting regularities would be more likely to notice the relation between the pairs of problems, as reflected in the accuracy/latency of their responses. Further, we tested the extent to which individual differences in statistical learning predicted children's use of arithmetic principles above and beyond executive control processes. In particular, we included a measure of inhibitory control and cognitive flexibility. Deocampo and Conway (2016) found that statistical learning is correlated with conflict response and inhibition among 7–12 year-olds; whereas, working memory has not been found to be correlated with statistical learning (Conway et al., 2010).

A second goal was to examine whether the level of experience with arithmetic problems influences the association between statistical learning capacity and use of arithmetic principles. We expected there would be an interaction between children's baseline knowledge (as it reflects their prior experience) and their statistical learning capacity in solving the principle pairs. Further, as students receive instruction on addition prior to subtraction, arithmetic operation can also serve as a proxy for the level of experience. Thus, we included addition items, with which first graders were likely to have had greater experience, as well as subtraction items, for which they were likely to be in the earlier learning phase, and expected a different pattern of results for these two operations.

Most first graders possess procedural strategies for carrying out addition, which would enable them to accurately solve the problems regardless of whether they notice the regularity. However, those who do notice the principle and use it to shortcut the procedure should respond more quickly. Thus, we hypothesized that on addition problems, statistical learning would be most closely related with latency, as opposed to accuracy. With respect to subtraction items, we did not have specific hypothesis but conducted exploratory analyses. Because children were likely to have less experience with subtraction, we did not expect them to be highly accurate with this operation. It is possible that noticing and taking an advantage of the regularity may facilitate generating accurate responses, but it is also possible that at least some level of experience is needed to know where to direct one's attention to identify regularities (Casco et al., 1998; Deocampo and Conway, 2016). Given this uncertainty with respect to accuracy, we also did not have specific predictions with respect to latency on subtraction items.

Method

Participants

Participants included 54 first graders (55.6% female; M = 6.67 years, SD = 0.56; 5.7–7.6) from primarily high-income families (76% of parents had received a bachelor's degree or higher). Based on parental reports, 54% of participating children were White, 17% Black or African American, 2% Hispanic, 4% Asian or Asian American, and 23% multiracial. Children were recruited from three different schools in the Greater Boston area. Children completed the tasks individually with an experimenter in a quiet room in schools. Based on a sensitivity power analysis of the paired t-test using G^*Power (Version 3.1; Faul et al., 2007), the smallest effect size that can be observed given a sample size of 54, p-value of 0.05, and 80% power is d = 0.39.

Researchers received approval to conduct this study from their university's Institutional Review Board (Protocol #: 22.092.01). Both written parental consent and verbal child assent were obtained for each participant.

Procedure and measures

Children were tested individually by an experimenter in the Spring of the school year. Based on the scope and sequence of the first-grade curriculum and the Common Core Mathematics Standards, by the time of testing, children had been exposed to arithmetic instruction focused on addition, subtraction, and different strategies for solving problems within 20. These strategies include using fingers to count-all or count-on and retrieval of facts. During the testing session, children completed an executive control task, arithmetic principle task, and visual statistical learning task, in that order. All of the measures were administered on a computer using OpenSesame, Version 3.312.

Statistical learning

Statistical learning was assessed using a modified version of an established measure of visual statistical learning, with good internal consistency (Cronbach's α = 0.83) and split-half reliability (Guttman's λ = 0.72) (Fiser and Aslin, 2002; Brady and Oliva, 2008; Arciuli and Simpson, 2011; Arnon, 2020). The stimuli included 12 unique alien characters grouped arbitrarily into four base triplets (ABC, DEF, GHI, JKL, where each letter represents a different alien). A base triplet was always presented in the same order. For example, for the base triplet ABC, whenever stimulus A appeared on a screen, it was always followed by B, which was then followed by C.

The procedure began with two rounds of practice to ensure children knew how to respond in the familiarization phase. In the first round, one triplet was presented with the last alien appearing twice; all four characters appeared simultaneously on the computer screen. Children were told that whenever they see an alien appearing twice in a row, they should say “same.” In the second round, three triplets were presented similarly to the first round (with the last character repeated) so that children could practice the procedure again.

The practice was followed by the familiarization phase, in which children learned the order of the aliens in the base triplets that would be used on test trials. These base triplets were unique from the triplets that had been presented as practice trials. Aliens were displayed on the screen one at a time, with a blank screen appearing between each successive alien for 500 msec. Each of the four base triplets was shown 24 times in a random order. For six of these 24 instances, the third alien in the triplet was repeated twice in a row (e.g., ABCC-GHI); children were told to say “same” whenever they saw an alien appearing twice in a row. These trials helped ensure that children paid attention to the familiarization phase.

Finally, the test phase was conducted, where each of the 30 total trials included two versions of a base triplet–one that children had seen during familiarization and one they had not seen before (e.g., ABC or ACB). The children were prompted to identify which of the two versions of the base triplet had appeared during familiarization (Figure 1). The correct choice and the foil were randomly arranged across trials so that in half the trials, the correct base triplet appeared on the left, and in the other half, it appeared on the right. The outcome measure was the percentage of correctly identified triplets in the test phase, with 50% being chance performance.

Figure 1

Figure 1. Example of the statistical learning task.

Executive control

Children's inhibitory control and cognitive flexibility were measured with the Shape School task (Espy, 1997). The task included four conditions that were presented in a fixed order: baseline, inhibition, cognitive flexibility, and inhibition + flexibility. For each condition, the children saw 15 “shape figures” (i.e., circles or squares with cartoon faces) arranged in a 5 × 3 array on a computer screen. In each array, there was an equal number of red, blue, and green shape figures.

In the baseline condition, the cartoon faces were emotionally neutral. The child's task was to name the color of each figure as quickly as possible. In the inhibition condition, the figures were presented with one of two facial expressions–happy or sad. Children were instructed only to name the color of the figures with happy faces; this required children to name the color of nine figures and inhibit their impulse to name the color of the other six. In the cognitive flexibility condition, all shape figures had neutral faces but varied in whether they had a hat on. Children's task was to name, as quickly as possible, the shape of the figures with hats and to name the color of the figures without hats. Finally, children were presented with the inhibition + cognitive flexibility condition, where the figures varied both in facial expression (happy/sad) and in whether they had hats. Children's task was to name an attribute (either color or shape depending on the presence of hat) for only happy-faced figures. In all conditions, children received practice with feedback before proceeding to the test trials.

As soon as the children completed their verbal response, the experimenter pressed a button to automatically code response time and manually code accuracy. For each condition, the number of stimuli named correctly and the total time needed to name all stimuli were used to calculate an efficiency score: Efficiency score = (number correct–the number of errors) / total time (sec). A higher efficiency score indicates greater cognitive inhibition and flexibility. The Shape School task demonstrated adequate reliability in prior research with preschoolers (Espy et al., 2006): baseline (α = 0.56), inhibition (α = 0.71), cognitive flexibility (α = 0.80), and inhibition + flexibility (α = 0.74). The reliability for this task in the current sample also showed adequate reliability: baseline (α = 0.62), inhibition (α = 0.73), cognitive flexibility (α = 0.82), and inhibition + flexibility (α = 0.77).

Arithmetic principle task

The arithmetic principle task included problems with totals within 20: addition problems with three addends and subtraction problems with a minuend and two subtrahends. The task involved four blocks of problems presented in a fixed order: small addition problems, large addition problems, small subtraction problems, and large subtraction problems. The small problems included addends or subtrahends within five, whereas the large problems included addends or subtrahends <5.

The problems were grouped into either baseline pairs or principle pairs. For the 12 baseline pairs, the two problems were not related via any arithmetic principles, so the accuracy and latency of solving the second problem were not expected to be influenced by solving the first. For the 12 principle pairs, the two problems were related via the commutativity principle for addition (e.g., 7 + 2 + 4 = 13 followed by 2 + 7 + 4 = ___) or via the inversion principle for subtraction (e.g., 12–6–4 = 2 followed by 12–6–2 = ___). Because the problems were related via a principle, the first problem was expected to prime the solution to the second. A total of 24 pairs of problems were given on the arithmetic task.

Children were first presented with a block of small addition problems that included four baseline and four principle pairs; the pairs were presented in a different random order for each child. Then, they were given a block of large addition problems, which included four principle pairs and no baseline pairs to avoid fatigue. The two addition blocks were followed by the small and large subtraction problems with the same structure. Problems comprising each pair were presented successively on a computer screen one at a time. The first problem in each pair included the answer. Children were given as much time as they wanted to look at the problem and confirm the answer by typing it on the keypad. Then, the first problem disappeared; children were shown the second problem of the pair and asked to type the answer. As children entered the numerical response to the problems using the external keypad, they could see it on the computer screen and were allowed to change their answer up to the point they hit the “enter” button. Response time for each problem was calculated automatically by OpenSesame as the duration between the presentation of the problem and when children hit “enter.”

Performance on the small baseline problems provided a measure of children's arithmetic skill, while performance on the principle problems provided a measure of children's ability to recognize and use the arithmetic principles. A difference in accuracy or latency between the baseline and principle small problems would suggest that children were able to notice the relation between the pairs in the principle condition. A difference in accuracy or latency between the small principle problems and large principle problems would suggest that the ability to detect the regularity varied by problem difficulty. To ensure that the latency measure did not include noise from guessing, it was calculated only for correct responses. The arithmetic tasks showed adequate reliability: for addition, baseline (α = 0.67) and principle (α = 0.88); for subtraction, baseline (α = 0.66) and principle (α = 0.87).

Results

Absolute level of performance on each of the key measures

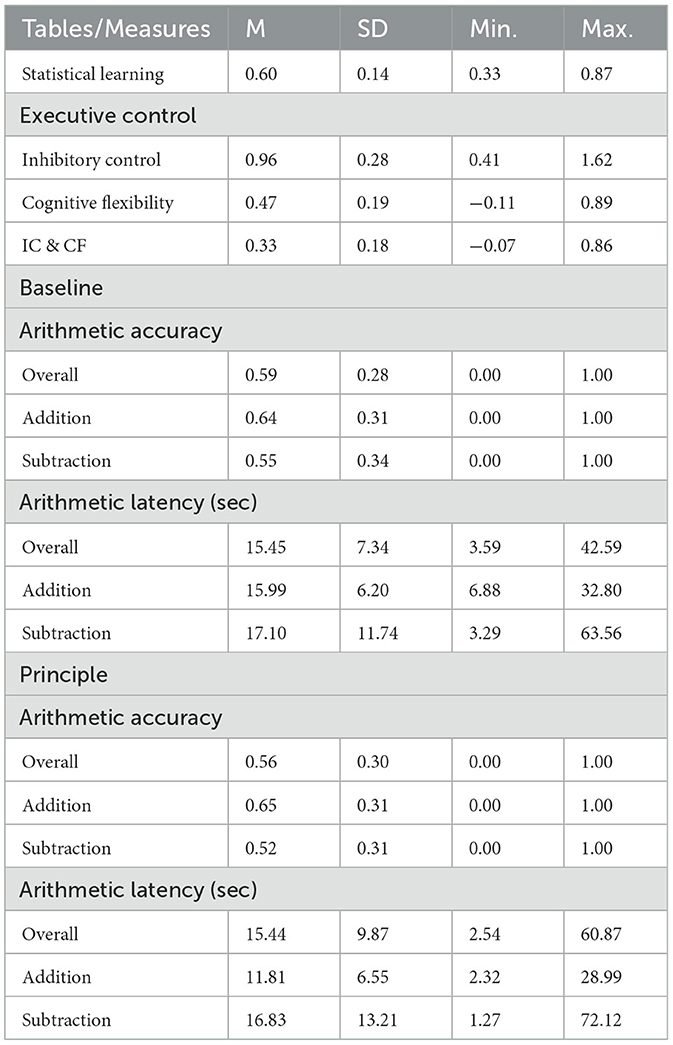
Children's performance on the statistical learning, executive control, and arithmetic principle tasks are reported in Table 1. All measures showed sufficient variance, and there were no floor or ceiling effects. For the statistical learning task, we compared children's performance to the chance level. A binomial test indicated that the average accuracy on this task was above chance (M = 0.60 SD = 0.14, p < 0.001). The percentage of individual children performing above chance was 66.7%. For the executive control task, we compared children's performance across conditions. A repeated measures ANOVA using Shape School condition as the within-subject factor and the efficiency score as the dependent factor found a main effect of condition [F_(1.76,93.28) = 180.99, p < 0.001, ${\eta }_p^2$ = 0.77]. Post hoc analyses with a Bonferroni adjustment indicated that children's efficiency scores were lower in the inhibitory control + cognitive flexibility condition (M = 0.33, SD = 0.18) than in the cognitive flexibility condition (M = 0.47, SD = 0.18), which in turn were lower than in the inhibition condition (M = 0.96, SD = 0.28), all p's < . 05. These results are consistent with previous findings in terms of both the mean efficiency scores and the pattern across conditions (Espy et al., 2006).

Table 1

Table 1. Descriptive statistics, N = 54.

For the arithmetic principle task, we first examined children's performance on small problems, which varied as a function of operation (addition vs. subtraction) and problem type (baseline vs. principle). A 2 (operation) X 2 (problem type) repeated measures ANOVA using arithmetic accuracy as the dependent variable found a main effect of operation; children were more accurate [F_(1,53) = 10.26, p < 0.01, ${\eta }_p^2$ = 0.16] at solving addition than subtraction problems across both types of problems. No effect was found for problem type; children's accuracy was comparable on baseline and principle problems [F_(1,53) = 0.19, p = 0.67, ${\eta }_p^2$ = 0.003].

A parallel repeated measures ANOVA was conducted using arithmetic latency as the dependent variable, except that this analysis examined response time only on correct responses. The results indicated main effects of both operation and problem type: children were faster [F_(1,39) = 9.47, p < 0.01, ${\eta }_p^2$ = 0.20] at solving addition than subtraction problems and were faster at solving principle than baseline problems, M = 11.81 s vs. M = 15.81 s, respectively [F_(1,39) = 8.90, p < 0.01, ${\eta }_p^2$ = 0.19]. In addition, the results found a significant interaction between operation and problem type for children's arithmetic latency [F_(1,39) = 4.95, p < 0.05, ${\eta }_p^2$ = 0.11]. That is, children were faster at solving small principle addition problems than subtraction ones.

Next, we compared children's performance on small and large problems. Because all baseline problems used small terms, this analysis included only the principle problems. A 2 (operation) × 2 (problem size) repeated measures ANOVA using arithmetic accuracy as the dependent variable found a main effect of operation; children were more accurate [F_(1,53) = 5.17, p < 0.05, ${\eta }_p^2$ = 0.09] at solving addition than subtraction problems. No effect was found for problem size; children's accuracy was comparable on the small and large principle problems [F_(1,53) = 2.42, p = 0.13, ${\eta }_p^2$ = 0.04]. A parallel repeated measures ANOVA using arithmetic latency (on correct responses only) as the dependent variable found main effects of both operation and problem size: children were faster [F_(1,36) = 11.27, p < 0.01, ${\eta }_p^2$ = 0.24] at solving addition than subtraction problems and also faster at solving small principle problems than large ones, M = 13.59 s vs. M = 16.33 s, respectively [F_(1,36) = 6.05, p < 0.05, ${\eta }_p^2$ = 0.14].

Correlational analyses

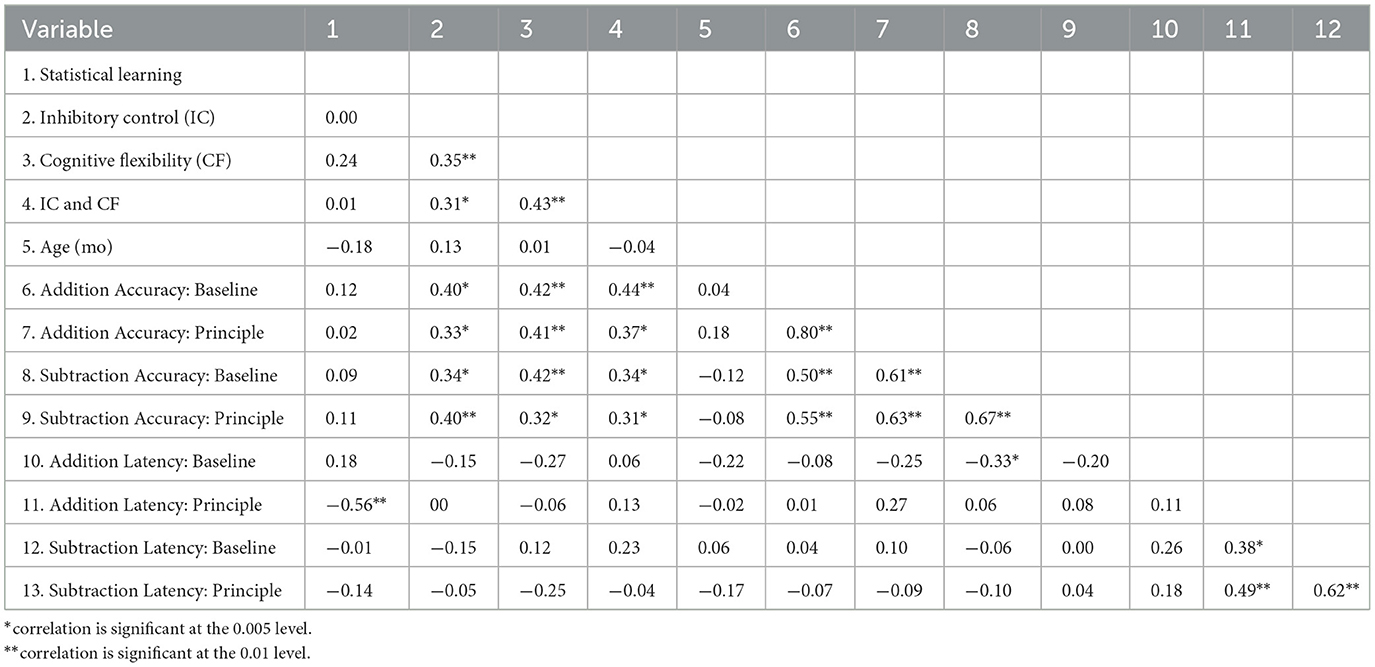
Table 2 shows a full correlation matrix. Here, we focus on the correlation analyses that were central to the research questions.

Table 2

Table 2. Pearson correlation matrix (N = 54).

Statistical learning and executive control

Individual differences in statistical learning were not correlated with any of the measures of executive control: inhibitory control [r₍₅₂₎ = 0.00 p = 0.99], cognitive flexibility [r₍₅₂₎ = 0.24, p = 0.08], and both processes combined [r₍₅₂₎ = 0.01, p = 0.93].

Executive control and arithmetic

Individual differences in each measure of executive control – inhibitory control, cognitive flexibility, and inhibitory control + cognitive flexibility - were correlated with each other (p's < 0.05). Further, each measure was positively correlated with children's overall arithmetic accuracy. This association held when looking at accuracy separately for each operation (addition and subtraction) and for each kind of problem type (baseline and principle; small and large problems), all p's < 0.05. In contrast, there were no correlations between individual differences in executive control and children's arithmetic latency for either operation and for different problem types (p's > 0.10).

Statistical learning and arithmetic

Statistical learning was related to overall latency on principle problems [r₍₅₂₎ = −0.29, p = 0.04], but not to overall accuracy on principle problems [r₍₅₂₎ = 0.24, p = 0.08]. Statistical learning was not related to latency on baseline problems or accuracy on any kind of problem (baseline and principle; small and large).

To examine the influence of level of experience on the relation between statistical learning and arithmetic, we conducted correlational analyses of the relations to statistical learning for addition and subtraction as well as for small and large principle problems separately. For addition, statistical learning was negatively related to latency on both the small and large principle problems [r₍₄₄₎ = −0.53, p < 0.01 and r₍₃₉₎ = −0.53, p < 0.01, respectively]: children with greater statistical learning capacity solved addition principle problems faster than their peers with less statistical learning capacity. For subtraction, statistical learning was not correlated with accuracy or latency on both the small and large principle problems (all p's > 0.10). In sum, children's capacity for statistical learning was related to arithmetic proficiency, but only on addition problems.

Regression analyses

To further examine the relation between statistical learning and arithmetic for each operation and the size of the problem, we conducted regression analyses to determine whether statistical learning accounted for individual differences in solving principle problems above and beyond executive control. We also tested for a moderating effect of level of experience, as measured by children's baseline performance, on the relation between statistical learning and children's accuracy and latency. Regression models that were run separately for small and large principle problems (with accuracy and latency as outcome variables) showed the same pattern of findings. Thus, we ran the subsequent regression models combining small and large principle problems.

Statistical learning as a predictor of addition accuracy and latency

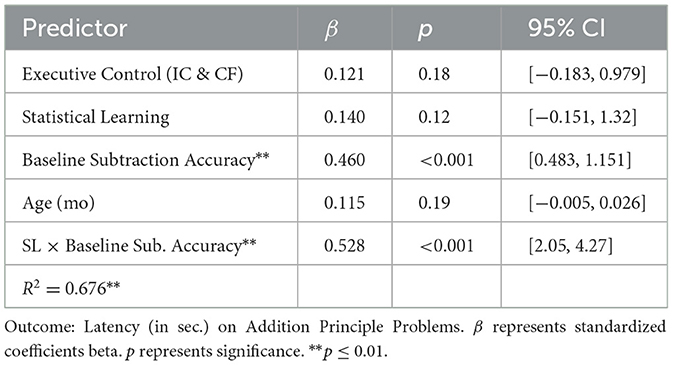
Together statistical learning, baseline addition accuracy, executive control, and age accounted for 84% of the variance in first graders' accuracy on the addition principle problems [F_(5,48) = 55.82, p < 0.05]. Children's baseline addition accuracy positively predicted accuracy on principle problems (β = 0.71, p < 0.05), but statistical learning was not a significant predictor (p = 0.41). Executive function and age were also not significant (p = 0.66 and p = 0.80, respectively).

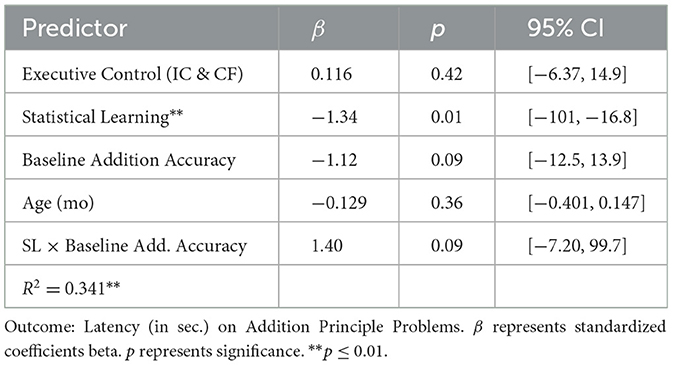
A parallel regression analysis was conducted for statistical learning as a predictor of children's latency on addition principle problems. Together statistical learning, baseline addition accuracy, executive control, and age accounted for 34% of the variance in first graders' latency on the addition principle problems [F_(5,42) = 4.35, p < 0.01]. Specifically, statistical learning negatively predicted children's addition latency on the principle problems, β = −1.34, p < 0.01, above and beyond the measure of baseline addition accuracy, executive function, and age, which were not predictive (p = 0.09, p = 0.42, and p = 0.36). There was no interaction between statistical learning and baseline addition, p = 0.09 as illustrated in Table 3.

Table 3

Table 3. Predictors of latency on principle addition problems.

Statistical learning as a predictor of subtraction accuracy and latency

Statistical learning, baseline subtraction accuracy, executive control, and age accounted for 68% of the variance in first graders' accuracy on the subtraction principle problems [F_(5,48) = 20.07, p < 0.01]. Executive function and age were not significant in predicting children's subtraction accuracy on principle problems (p = 0.18 and p = 0.19). As shown in Table 4, the model indicated a main effect of baseline subtraction accuracy and a moderating effect of baseline subtraction accuracy on the relation between statistical learning and children's principle problem subtraction accuracy. There was a significant interaction between children's baseline subtraction accuracy and statistical learning on their subtraction accuracy on the principle problems, β = 0.53, p < 0.01. This interaction is illustrated in Figure 2. The interaction was probed by testing the conditional effects of statistical learning at three levels of children's baseline subtraction accuracy, one standard deviation below the mean, at the mean, and one standard deviation above the mean. As shown in Figure 2, the strength of the relation between statistical learning and subtraction accuracy on the principle problems was strongest among the children with the highest level of baseline subtraction accuracy (R² = 0.12).

Table 4

Table 4. Predictors of accuracy on principle subtraction problems.

Figure 2

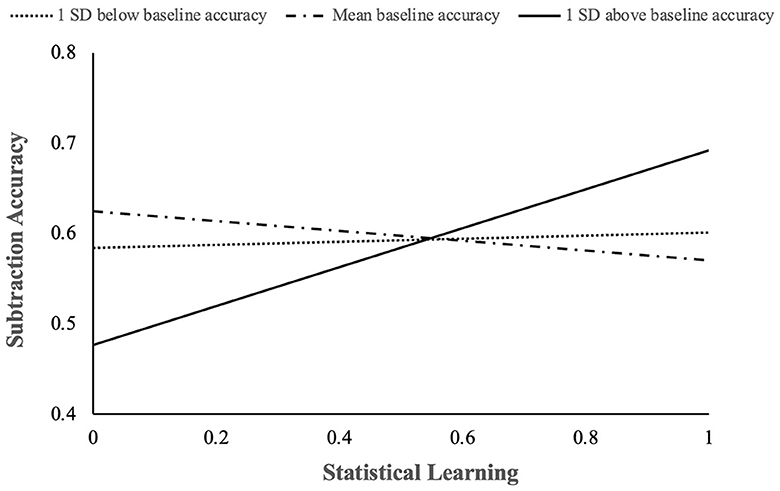
Figure 2. Interaction between baseline knowledge and statistical learning on accuracy of principle subtraction problems.

Statistical learning, baseline subtraction accuracy, executive control, and age accounted for only 7% of the variance in first graders' latency on the subtraction principle problems [F_(5,44) = 0.70, p = 0.63]. The lack-of-fit of the regression model was expected as the correlation between the predictors and the outcome was low (p's > 0.10).

Discussion

Previous studies have shown that various domain-general (verbal and visuospatial working memory, inhibition, and cognitive shifting) and domain-specific (e.g., numerical magnitude representations) cognitive capacities are involved in developing arithmetic knowledge (Siegler and Araya, 2005; Cragg et al., 2017; Wong, 2023). The current study adds to the understanding of the processes underlying arithmetic learning by examining the extent to which individual differences in statistical learning capacity predict children's ability to notice and use arithmetic principles. First graders were shown pairs of three term equations where the first equation in each pair had the answer displayed and was either related to the second equation via a principle (i.e., commutativity or inversion) or unrelated to the second equation. Findings support the hypothesis that statistical learning is involved in arithmetic learning and that its involvement depends, in part, upon the level of experience with arithmetic.

Statistical learning and arithmetic

The present results provide evidence of the involvement of statistical learning in arithmetic development. Statistical learning predicted latency for addition only: children with greater statistical learning capacity responded more quickly to addition problems that were part of a principle pair than to unrelated problems, even after accounting for baseline performance, executive control, and age. For subtraction, statistical learning predicted accuracy only among those children with high levels of baseline knowledge. Previous research indicates that children can incidentally deduce arithmetic principles from experience (e.g., Prather and Alibali, 2011). Combined with this previous research, the current findings raise the possibility that statistical learning may be an underlying mechanism by which children extrapolate regularities in mathematics.

While further work is needed to test this possibility, we believe it is consistent with recent work pointing to a relation between patterning skill and numeracy knowledge (Kidd et al., 2013; Rittle-Johnson et al., 2017; Burgoyne et al., 2019; MacKay and De Smedt, 2019). Children who do better on patterning tasks also have greater numeracy knowledge. For instance, children in first- and second-grade who were better able to complete growing patterns (e.g., “5, 7, 9, 11,?”) were also better at calculating number facts, controlling for a broad range of cognitive skills (MacKay and De Smedt, 2019). Some evidence also supports a causal relation between patterning ability and arithmetic. For example, Lüken and Kampmann (2018) found that first-graders randomly selected to receive instruction on patterning were more accurate at solving arithmetic problems after 5-months than children who received business-as-usual instruction. These findings related to patterning provide convergent evidence that an individual's propensity to notice patterns is important for mathematics learning. Both repeating pattern knowledge and statistical learning involve noticing co-occurrences and using that information to make predictions, however, statistical learning can be considered the more proximal process of the two. Statistical learning is an implicit process, available as early as infancy; while patterning knowledge, is explicit and emerges over childhood. In fact, measures of repeating pattern knowledge require children to not only notice the pattern but also to articulate how they arrived at their selection (e.g., Borriello et al., 2023). Thus, it seems conceivable that an individual's statistical learning capacity partly accounts for the relation between individual differences in pattern knowledge and mathematics outcomes.

Statistical learning for different levels of experience

We hypothesized that the relation between statistical learning capacity and the use of arithmetic principles to solve related problems would vary by the level of experience/skill with particular problem types. In this study, arithmetic operation served as a proxy for experience – first graders typically have more experience with and greater accuracy on addition than subtraction problems. We found that the statistical learning was related to latency for addition, but not subtraction. On subtraction problems, baseline knowledge moderated the relation between children's statistical learning capacity and their accuracy on principle problems. Specifically, among children who scored above the mean on baseline subtraction problems, those with greater statistical learning capacity were more accurate on subtraction principle problems than those with less statistical learning capacity. In contrast, there was no relation between accuracy and statistical learning capacity for those who demonstrated less prior knowledge of subtraction. Thus, it may be that a certain level of experience is necessary to be able to use statistical learning to identify regularities.

There are at least three potential explanations for the moderating effect of experience. Prior experience with a problem type may guide children's attention to relevant patterns, facilitating the use of statistical learning (Casco et al., 1998; Deocampo and Conway, 2016). Alternatively, a lack of experience in solving particular problems may tax cognitive resources, thereby limiting the functioning of statistical learning (Kirschner, 2002). Finally, it may be that children adaptively choose among different strategies based on the trade-offs between accuracy and speed (Siegler, 1998).

The pattern of findings related to children's latency and accuracy provides evidence for this third possibility – an adaptive choice between statistical learning and other problem solving approaches. Because first graders have more experience using procedural strategies with addition than subtraction, we predicted this would enable them to solve addition problems with relatively high accuracy regardless of whether they notice the regularity. Yet, those who do notice the principle and use it to shortcut the procedure are likely to respond more quickly. Consistent with this idea, statistical learning predicted children's latency on principle addition problems but not their accuracy.

Limitation and future directions

The present study offers initial evidence of the relation between statistical learning and children's math knowledge, specifically the ability to detect and use arithmetic principles. The results add to the growing body of work suggesting statistical learning is involved in academic knowledge, typically thought to be acquired primarily through explicit processes. As with recent results implicating statistical learning in the acquisition of reading skills (Arciuli and Simpson, 2012; Treiman and Kessler, 2022), these findings suggest statistical learning may influence the ease with which children notice the patterns and regularities in arithmetic.

Yet, further work is needed to establish the reliability and strength of the association. The current study included a small number of trials and inferred arithmetic principle knowledge via speed and accuracy rather than requiring explicit explanations. To obtain a more complete characterization of the role of statistical learning in children's arithmetic principle understanding, future studies could include a greater number of trials and additional tasks that tap different dimensions of arithmetic principle knowledge, such as explicit recognition and use of procedural short-cuts (Prather, 2012; Robinson et al., 2017). In addition, the current study did not control for cognitive factors, such as working memory or patterning skills, that have been shown to predict math knowledge. For example, to detect the regularity across a pair of principle problems, one must keep the numbers from the first problem in working memory and compare them to the second problem to notice that the addends are the same despite being in a different order. Several studies indicate that statistical learning tasks tap an ability not correlated with working memory (Conway et al., 2010). Thus, if statistical learning is found to predict arithmetic principle knowledge above and beyond working memory, it would provide stronger evidence for its influence in extracting regularities in mathematics tasks. While including a baseline measure of math performance partly addresses the omitted variable concern, future studies may benefit from including additional measures to better understand the complex relations between different types of predictors and math knowledge.

It would also be worthwhile for future studies to examine the association between individuals' statistical learning capacity and their knowledge of other aspects of mathematics. Various other early math concepts involve statistical regularities – such as the repetition of the digits 1–9 in each decade of the count sequence, the successor principle relating count words to quantities (e.g., each successive number in the count string represents an increase in quantity of exactly one), the correspondence between place-value notation and base-10 structure. Finding an association between statistical learning and knowledge across various math concepts would help establish the generality of the relation between statistical learning and mathematics knowledge.

While the present work does not allow for any causal claims, the pattern of findings is consistent with the possibility that statistical learning may serve as a mechanism underlying the acquisition of mathematics knowledge. There are several potential ways that future studies could test this possibility. One might explore whether statistical learning mediates the effect of instruction of patterning or arithmetic principles on improvement in those skills. Another might be comparing learning in situations where the regularities are more or less apparent. For example, the regularities across problems could be varied systematically (e.g., a practice set of problems with 100% involving commutativity vs. 75% vs. 50%). A finding of better learning, when regularities are more apparent, would point to the involvement of statistical learning. Together, these kinds of studies would extend the current work and provide a basis for models that include statistical learning as a key process in mathematical knowledge acquisition.

Data availability statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found at: https://doi.org/10.23668/psycharchives.14078.

Ethics statement

The studies involving humans were approved by the Institutional Review Board of Boston College (Protocol #: 22.092.01). The studies were conducted in accordance with the local legislation and institutional requirements. Written informed consent for participation in this study was provided by the participants' legal guardians/next of kin.

Author contributions

HC: Writing—original draft, Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Software, Writing—review & editing. MV: Funding acquisition, Writing—review & editing, Supervision. EL: Conceptualization, Funding acquisition, Methodology, Project administration, Writing—original draft, Writing—review & editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. Research reported in this publication was supported by the grant from the Institute of Education of Sciences under the reward number R305A200315 (principle investigator: MV; co-investigators: EL and Beth Casey). The content is solely the responsibility of the authors and does not necessarily represent the official view of the Institute of Education Sciences.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Arciuli, J., and Simpson, I. C. (2011). Statistical learning in typically developing children: the role of age and speed of stimulus presentation. Dev. Sci. 14, 464–473. doi: 10.1111/j.1467-7687.2009.00937.x

PubMed Abstract | Crossref Full Text | Google Scholar

Arciuli, J., and Simpson, I. C. (2012). Statistical learning is related to reading ability in children and adults. Cognit. Sci. 36, 286–304. doi: 10.1111/j.1551-6709.2011.01200.x

PubMed Abstract | Crossref Full Text | Google Scholar

Arnon, I. (2020). Do current statistical learning tasks capture stable individual differences in children? An investigation of task reliability across modality. Behav. Res. Methods 52, 68–81. doi: 10.3758/s13428-019-01205-5

PubMed Abstract | Crossref Full Text | Google Scholar

Baroody, A. J., and Gannon, K. E. (1984). The development of the commutativity principle and economical addition strategies. Cognit. Instr. 1, 321–339. doi: 10.1207/s1532690xci0103_3

Crossref Full Text | Google Scholar

Baroody, A. J., Ginsburg, H. P., and Waxman, B. (1983). Children's use of mathematical structure. J. Res. Mathematics Educ. 14, 156–168. doi: 10.2307/748379

Crossref Full Text | Google Scholar

Borriello, G. A., Grenell, A., Vest, N. A., Moore, K., and Fyfe, E. R. (2023). Links between repeating and growing pattern knowledge and math outcomes in children and adults. Child Dev. 94, e103–e118. doi: 10.1111/cdev.13882

PubMed Abstract | Crossref Full Text | Google Scholar

Brady, T. F., and Oliva, A. (2008). Statistical learning using real-world scenes: extracting categorical regularities without conscious intent. Psychol. Sci. 19, 678–685. doi: 10.1111/j.1467-9280.2008.02142.x

PubMed Abstract | Crossref Full Text | Google Scholar

Bryant, P., Christie, C., and Rendu, A. (1999). Children's understanding of the relation between addition and subtraction: Inversion, identity, and decomposition. J. Exp. Child Psychol. 74, 194–212. doi: 10.1006/jecp.1999.2517

PubMed Abstract | Crossref Full Text | Google Scholar

Bulgarelli, F., and Weiss, D. J. (2016). Anchors aweigh: the impact of overlearning on entrenchment effects in statistical learning. J. Exp. Psychol. Learn. Memory Cognit. 42:1621. doi: 10.1037/xlm0000263

PubMed Abstract | Crossref Full Text | Google Scholar

Burgoyne, K., Malone, S., Lervag, A., and Hulme, C. (2019). Pattern understanding is a predictor of early reading and arithmetic skills. Early Childhood Res. Q. 49, 69–80. doi: 10.1016/j.ecresq.2019.06.006

Crossref Full Text | Google Scholar

Canobi, K. H. (2005). Children's profiles of addition and subtraction understanding. J. Exp. Child Psychol. 92, 220–246. doi: 10.1016/j.jecp.2005.06.001

PubMed Abstract | Crossref Full Text | Google Scholar

Canobi, K. H. (2009). Concept–procedure interactions in children's addition and subtraction. J. Exp. Child Psychol. 102, 131–149. doi: 10.1016/j.jecp.2008.07.008

PubMed Abstract | Crossref Full Text | Google Scholar

Canobi, K. H., and Bethune, N. E. (2008). Number words in young children's conceptual and procedural knowledge of addition, subtraction and inversion. Cognition 108, 675–686. doi: 10.1016/j.cognition.2008.05.011

PubMed Abstract | Crossref Full Text | Google Scholar

Canobi, K. H., Reeve, R. A., and Pattison, P. E. (1998). The role of conceptual understanding in children's addition problem solving. Dev. Psychol. 34:882. doi: 10.1037/0012-1649.34.5.882

PubMed Abstract | Crossref Full Text | Google Scholar

Casco, C., Tressoldi, P. E., and Dellantonio, A. (1998). Visual selective attention and reading efficiency are related in children. Cortex 34, 531–546. doi: 10.1016/S0010-9452(08)70512-4

PubMed Abstract | Crossref Full Text | Google Scholar

Christensen, C. A., and Cooper, T. J. (1991). The effectiveness of instruction in cognitive strategies in developing proficiency in single-digit addition. Cognit. Instr. 8, 363–271. doi: 10.1207/s1532690xci0804_6

PubMed Abstract | Crossref Full Text | Google Scholar

Collins, M. A., and Laski, E. V. (2015). Preschoolers' strategies for solving visual pattern tasks. Early Childhood Res. Q. 32, 204–214. doi: 10.1016/j.ecresq.2015.04.004

Crossref Full Text | Google Scholar

Conway, C. M., Bauernschmidt, A., Huang, S. S., and Pisoni, D. B. (2010). Implicit statistical learning in language processing: Word predictability is the key. Cognition 114, 356–371. doi: 10.1016/j.cognition.2009.10.009

PubMed Abstract | Crossref Full Text | Google Scholar

Cragg, L., Keeble, S., Richardson, S., Roome, H. E., and Gilmore, C. (2017). Direct and indirect influences of executive functions on mathematics achievement. Cognition 162, 12–26. doi: 10.1016/j.cognition.2017.01.014

PubMed Abstract | Crossref Full Text | Google Scholar

Deocampo, J., and Conway, C. (2016). A Developmental Shift in the Relationship Between Sequential Learning, Executive Function, and Language Ability as Revealed by Event-Related Potentials. Berkeley, CA: CogSci.

Google Scholar

Erickson, L. C., and Thiessen, E. D. (2015). Statistical learning of language: theory, validity, and predictions of a statistical learning account of language acquisition. Dev. Rev. 37, 66–108. doi: 10.1016/j.dr.2015.05.002

PubMed Abstract | Crossref Full Text | Google Scholar

Espy, K. A. (1997). The shape school: assessing executive function in preschool children. Dev. Neuropsychol. 13, 495–499. doi: 10.1080/87565649709540690

Crossref Full Text | Google Scholar

Espy, K. A., Bull, R., Martin, J., and Stroup, W. (2006). Measuring the development of executive control with the shape school. Psychol. Assess. 18:373. doi: 10.1037/1040-3590.18.4.373

PubMed Abstract | Crossref Full Text | Google Scholar

Faul, F., Erdfelder, E., Lang, A. G., and Buchner, A. (2007). G^* Power 3: a flexible statistical power analysis program for the social, behavioral, and biomedical sciences. Behav. Res. Methods 39, 175–191. doi: 10.3758/BF03193146

PubMed Abstract | Crossref Full Text | Google Scholar

Fiser, J., and Aslin, R. N. (2002). Statistical learning of higher-order temporal structure from visual shape sequences. J. Exp. Psychol. Learn Mem. Cognit. 28:458. doi: 10.1037//0278-7393.28.3.458

PubMed Abstract | Crossref Full Text | Google Scholar

Gebauer, G. F., and Mackintosh, N. J. (2007). Psychometric intelligence dissociates implicit and explicit learning. J. Exp. Psychol. Learn. Mem. Cognit. 33:34. doi: 10.1037/0278-7393.33.1.34

PubMed Abstract | Crossref Full Text | Google Scholar

Gilmore, C. K. (2006). Investigating children's understanding of inversion using the missing number paradigm. Cognit. Dev. 21, 301–316. doi: 10.1016/j.cogdev.2006.03.007

Crossref Full Text | Google Scholar

Ginsburg, H. (1989). Children's Arithmetic: How They Learn It and How You Teach It. Pro-ed.

PubMed Abstract | Google Scholar

Kidd, E., and Arciuli, J. (2016). Individual differences in statistical learning predict children's comprehension of syntax. Child Dev. 87, 184–193. doi: 10.1111/cdev.12461

PubMed Abstract | Crossref Full Text | Google Scholar

Kidd, J. K., Carlson, A. G., Gadzichowski, K. M., Boyer, C. E., Gallington, D. A., Pasnak, R., et al. (2013). Effects of patterning instruction on the academic achievement of 1st-grade children. J. Res. Childhood Educ. 27, 224–238. doi: 10.1080/02568543.2013.766664

PubMed Abstract | Crossref Full Text | Google Scholar

Kirschner, P. A. (2002). Cognitive load theory: implications of cognitive load theory on the design of learning. Learn. Instr. 12, 1–10. doi: 10.1016/S0959-4752(01)00014-7

Crossref Full Text | Google Scholar

Krogh, L., Vlach, H. A., and Johnson, S. P. (2013). Statistical learning across development: Flexible yet constrained. Frontiers in Psychology 3, 598. doi: 10.3389/fpsyg.2012.00598

PubMed Abstract | Crossref Full Text | Google Scholar

Lüken, M. M., and Kampmann, R. (2018). The influence of fostering children's patterning abilities on their arithmetic skills in grade 1. Contemp. Res. Persp. Early Childhood Mathematics Educ. 22, 55–66. doi: 10.1007/978-3-319-73432-3_4

Crossref Full Text | Google Scholar

Ma, N., and Yu, A. J. (2015). Statistical learning and adaptive decision-making underlie human response time variability in inhibitory control. Front. Psychol. 6:1046. doi: 10.3389/fpsyg.2015.01046

PubMed Abstract | Crossref Full Text | Google Scholar

MacKay, K. J., and De Smedt, B. (2019). Patterning counts: individual differences in children's calculation are uniquely predicted by sequence patterning. J. Exp. Child Psychol. 177, 152–165. doi: 10.1016/j.jecp.2018.07.016

PubMed Abstract | Crossref Full Text | Google Scholar

Park, J., Yoon, H. D., Yoo, T., Shin, M., and Jeon, H. A. (2020). Potential and efficiency of statistical learning closely intertwined with individuals' executive functions: a mathematical modeling study. Sci. Rep. 10:18843. doi: 10.1038/s41598-020-75157-8

PubMed Abstract | Crossref Full Text | Google Scholar

Prather, R., and Alibali, M. W. (2011). Children's acquisition of arithmetic principles: the role of experience. J. Cognit. Dev. 12, 332–354. doi: 10.1080/15248372.2010.542214

Crossref Full Text | Google Scholar

Prather, R. W. (2012). Implicit learning of arithmetic regularities is facilitated by proximal contrast. PLoS ONE 7:e48868. doi: 10.1371/journal.pone.0048868

PubMed Abstract | Crossref Full Text | Google Scholar

Rittle-Johnson, B., Fyfe, E. R., Hofer, K. G., and Farran, D. C. (2017). Early math trajectories: low-income children's mathematics knowledge from ages 4 to 11. Child Dev. 88, 1727–1742. doi: 10.1111/cdev.12662

PubMed Abstract | Crossref Full Text | Google Scholar

Rittle-Johnson, B., Zippert, E. L., and Boice, K. L. (2019). The roles of patterning and spatial skills in early mathematics development. Early Childhood Res. Q. 46, 166–178. doi: 10.1016/j.ecresq.2018.03.006

Crossref Full Text | Google Scholar

Robinson, K. M., Dubé, A. K., and Beatch, J. A. (2017). Children's understanding of additive concepts. J. Exp. Child Psychol. 156, 16–28. doi: 10.1016/j.jecp.2016.11.009

PubMed Abstract | Crossref Full Text | Google Scholar

Ruffman, T., Taumoepeau, M., and Perkins, C. (2012). Statistical learning as a basis for social understanding in children. Br. J. Dev. Psychol. 30, 87–104. doi: 10.1111/j.2044-835X.2011.02045.x

PubMed Abstract | Crossref Full Text | Google Scholar

Saffran, J. R., Aslin, R. N., and Newport, E. L. (1996). Statistical learning by 8-month-old infants. Science 274, 1926–1928. doi: 10.1126/science.274.5294.1926

PubMed Abstract | Crossref Full Text | Google Scholar

Schapiro, A., and Turk-Browne, N. (2015). Statistical learning. Brain Mapping 3, 501–506. doi: 10.1016/B978-0-12-397025-1.00276-1

Crossref Full Text | Google Scholar

Sherman, B. E., Graves, K. N., and Turk-Browne, N. B. (2020). The prevalence and importance of statistical learning in human cognition and behavior. Curr. Opin. Behav. Sci. 32, 15–20. doi: 10.1016/j.cobeha.2020.01.015

PubMed Abstract | Crossref Full Text | Google Scholar

Sherman, J., and Bisanz, J. (2007). Evidence for use of mathematical inversion by three-year-old children. J. Cognit. Dev. 8, 333–344. doi: 10.1080/15248370701446798

Crossref Full Text | Google Scholar

Siegelman, N., and Frost, R. (2015). Statistical learning as an individual ability: theoretical perspectives and empirical evidence. J. Memory Lang. 81, 105–120. doi: 10.1016/j.jml.2015.02.001

PubMed Abstract | Crossref Full Text | Google Scholar

Siegler, R., and Araya, R. (2005). A computational model of conscious and unconscious strategy discovery. Adv. Child Dev. Behav. 33, 1–42. doi: 10.1016/S0065-2407(05)80003-5

PubMed Abstract | Crossref Full Text | Google Scholar

Siegler, R. S. (1998). Emerging Minds: The Process of Change in Children's Thinking. New York, NY: Oxford University Press.

Google Scholar

Steinberg, R. M. (1985). Instruction on derived facts strategies in addition and subtraction. J. Res. Mathematics Educ. 16, 337–355. doi: 10.2307/749356

Crossref Full Text | Google Scholar

Treiman, R., and Kessler, B. (2022). Statistical learning in word reading and spelling across languages and writing systems. Sci. Stu. Reading 26, 139–149. doi: 10.1080/10888438.2021.1920951

Crossref Full Text | Google Scholar

Wijns, N., Verschaffel, L., Smedt, D., and Torbeyns, B. (2021). Associations between repeating patterning, growing patterning, and numerical ability: a longitudinal panel study in 4-to 6-year olds. Child Dev. 92, 1354–1368. doi: 10.1111/cdev.13490

PubMed Abstract | Crossref Full Text | Google Scholar

Wong, T. T. Y. (2023). Cognitive predictors of children's arithmetic principle understanding. J. Exp. Child Psychol. 227:105579. doi: 10.1016/j.jecp.2022.105579

PubMed Abstract | Crossref Full Text | Google Scholar