Viscoelastic Networks: Forming Cells and Tissues

Introduction

The viscoelastic or material properties of cells and tissues are key regulators of cell and tissue growth, motion, and homeostasis [1–5]. Viscoelasticity allows living systems to preserve a basic architecture due to their solid-like characteristics, but also at the same time to dynamically reorganize in different shapes and patterns due to their viscous-like characteristics [4, 6–8]. Cellular-scale viscoelasticity influences several single-cell functions such a shape, division, and motility, and it is predominantly determined by the physical properties of the underlying cytoskeletal networks [8]. Tissue-scale viscoelasticity was shown to be important in collective morphogenetic processes such as tissue folding, spreading, wound healing and migration, and it is mainly determined by the interplay of cell-cell and/or cell-extracellular space interactions [2, 4, 5]. Advances in biophysical tools measuring viscoelasticity [4, 9, 10] have revealed an essential and physiologically relevant link between material properties and morphogenesis [11–13], opening the challenge to now understand how emergent viscoelasticity is regulated by, and in turn, regulates the mechanochemistry of living systems.

A material is viscoelastic if it displays both viscous and elastic behavior [14]. Our knowledge of viscoelasticity mainly comes from material sciences, where certain physical parameters are well-defined for non-living materials such as glasses, rubbers, metals and polymers [14, 15]. Viscoelasticity of such materials is evaluated from the degree of deformation upon constant force application and release, an experimental procedure called creep and recovery test (Figure 1A). Solid-like objects deform shortly and reversibly under constant force, whereas fluid-like objects irreversibly increase their deformation as long as a force is exerted. Viscoelastic materials exhibit characteristics of both solids and fluids: at short time scales they deform elastically and, at long timescales, they behave as viscous fluids. On the theoretical level, viscoelasticity was independently modelled by Maxwell and Kelvin in the 19th century [14]. Both models abstract a viscoelastic system as a composite structure containing an elastic spring connected to a dashpot containing a viscous fluid (Figure 1B). The difference between Maxwell’s and Kelvin’s approaches comes from the disposition of the system: In Maxwell’s model, the dashpot and the spring are connected in series, whereas in Kelvin’s model, the two components are connected in parallel. As a result, when force is applied on the system, in the former, the deformation of the spring will drag the dashpot, describing the deformation of a viscoelastic fluid; whereas when force is applied in the latter, the dashpot response is restricted by the deformation of the spring, describing thus the deformation of a viscoelastic solid [16]. Although biological materials display characteristics of viscoelastic materials, due to their heterogeneous composition and dynamic nature, fitting such models and frameworks from material science, is conceptually and technically still difficult [16, 17]. For instance, during experimental measurements of cell and tissue viscoelasticity, typically an external force is applied to the system such as via a micropipette, or a magnetic field [13, 18, 19] for a certain time window, during which its deformation is monitored (Figure 1C’). From such measurements, parameters such as elastic modulus, viscosity, and yield stress can be extrapolated (Box 1) [16, 20, 21]. However, whether such measurements are relevant to the time window of morphogenesis still needs to be addressed, since such measurements show how a tissue deforms when applying an exogenous force for a certain time. How these features compare to the magnitude and duration of the endogenously exerted forces is still unclear [9, 22, 23]. In addition, during such experimental measurements, the applied force typically triggers a large deformation of the material (nonlinear regime). In contrast however, most theoretical frameworks predicting viscoelasticity upon deformation, are based on forces triggering infinitesimal deformations (linear regime) [24]. Last, similar to the viscoelasticity of non-living materials, viscoelasticity of cells and tissues is a property arising from their underlying structure, defined by the way macromolecules and cells interact [1, 8, 15, 25–29]. Several theoretical frameworks have for long been used in non-living materials to link the microscopic structure to the macroscopic viscoelastic properties (Box 1), showing that viscoelasticity may behave as an emergent property [27–32], in the same way, e.g., temperature arises non-trivially from microscopic particle motion in statistical mechanics [14]. How macroscopic viscoelasticity can be predicted by the interactions of the microscopic constituents of living cells and tissues is an open question at the interface of statistical and soft matter physics with molecular and cell biology, and the main topic of this review.

BOX 1 | Terminology.

Affine deformation: Deformation of a body in which the macroscopic strain is translated uniformly to all microscopic parts of the material.

Bulk modulus: Denoted by K, describes the material’s response to isotropic hydrostatic pressure.

Cell contact network: A network where the nodes are cells and links represent active contacts between neighbouring cells.

Contour length: In a polymer chain, the contour length, l_c, is the distance between the two extremes of the filament if the polymer is fully unfolded.

Critical point: Magnitude of the control parameter that triggers a phase transition. At the critical point, a discontinuity on some macroscopic observable is expected, and specific statistical patterns, such as power-laws, often largely independent of system’s details, are observed. Formally, the functional dependence of the order parameter on the control parameter shows a singularity in some of its derivatives at the critical point.

Cytoskeleton: A network of biopolymer fibres that extends throughout a cell. It is the main determinant of the material response of the cell under deformations and stress.

ECM network: The extracellular matrix (ECM) is a non-cellular component providing the material backbone for the cellular constituents. Beyond its structural character, it plays a key, active role in morphogenesis, differentiation and homeostasis.

Elastic modulus: Also known as Young’s modulus, E, quantifies the strain response to uniaxial stress in the direction of this stress in the linear regime.

Enthalpic elasticity: In a polymer network where $l_p/l_c\gg 1$ filaments are considered stiff, and deformation comes from the stretching or compression of them. The main energetic costs come from changes of the enthalpy of the system. Systems in the enthalpic regime show in general small deformations under stress.

Entropic elasticity: In a polymer network where $l_p/l_c\ll 1$ filaments are rugged and fluctuate due to thermal agitation. In these systems, the elastic response against deformation is due to the unfolding of these filaments towards the axis of the stress. This unfolding results in a decrease of the entropy of the system. The materials in these regimes are usually elastic and deformations can be in general big, and recover the initial configurations when the stress is released

Interstitial fluid: space between the cells of a nonconfluent tissue.

Isostatic point: A system is at the isostatic point when the degrees of freedom of its constituents are absorbed by the constraints imposed by the structure in a non-redundant way. In the theory of rigidity, the isostatic point is marked by the critical value of connectivity in which the system becomes rigid, e.g., the lowest value of connectivity that leaves no degrees of freedom within the internal constituents of the system.

Jamming: Divergence of the viscosity of a material with increasing particle density

Micro/macro mapping: The mapping between microscopic dynamics, often containing a great number of degrees of freedom to a single, often scalar microscopic observable. The most common example is the microscopic motion of particles in a gas giving rise to the macroscopic observable of temperature.

Network rigidity: A topological concept where a network structure (or part of it) made of nodes and connecting links is considered to be generically rigid if no independent (geometric) movement of the nodes is possible without stretching/compressing a link.

Percolation: A network is in the percolating regime if a significant part of its nodes define a connected cluster, that is, for any pair of nodes of this cluster, there is a path that connects them. In a random network, the emergence of the percolating cluster is an abrupt event, and has all the properties of a high order phase transition as described in statistical mechanics. Many different classes of percolation transitions can be defined, depending on the attributes one expects to observe in the emerging cluster when the average connectivity increases.

Persistence length: In a polymer chain, the persistence length, $l_p$, quantifies the length scale at which significant bending fluctuations occur. Formally, it is the length at which the polymer chain appears straight in the presence of Brownian forces.

Phase transition: Macroscopic change in the properties of a system (order parameter) when a parameter crosses a certain critical value (control parameter), also called critical point.

Rigidity percolation: A high order phase transition triggered by increasing the average number of links per node in a network, leading to the sudden emergence of a rigid region that spans almost the whole network, the Giant Rigid Cluster (GRC). The term rigidity percolation comes from the fact that almost any two nodes of the graph are connected through a path that is entirely inside the same rigid cluster.

Shear modulus: Denoted by G, quantifies the material's response to shear stress.

Strain: Denoted by $\gamma$, quantifies the deformation of a body. It quantifies relative displacements of parts of the body other than the ones that can be attributed to rigid body motions.

Strain softening response: Non-linear response of many biological materials consisting on the decrease of the stiffness along the increase of strain.

Strain stiffening response: Non-linear response of many biological materials consisting on the increase of the stiffness along the increase of strain.

Vertex models: Tissue models represented by tilling of the space (in general, over 2D surfaces) in which the energetic contributions come from geometric considerations on the cell shape and cell-cell contact regions (vertices).

Viscosity: Denoted by $\text{η}$, quantifies the material’s flow at a given velocity upon stress

T1 transition: Relative movement of cells in a tissue occurring when an edge between two cells shrinks to a point and a new edge arises between two neighbouring cells. The outcome of this process is a net change of neighbouring cells and, in consequence, a relative movement, with respect to the other cells, of at least one cell within the tissue.

FIGURE 1

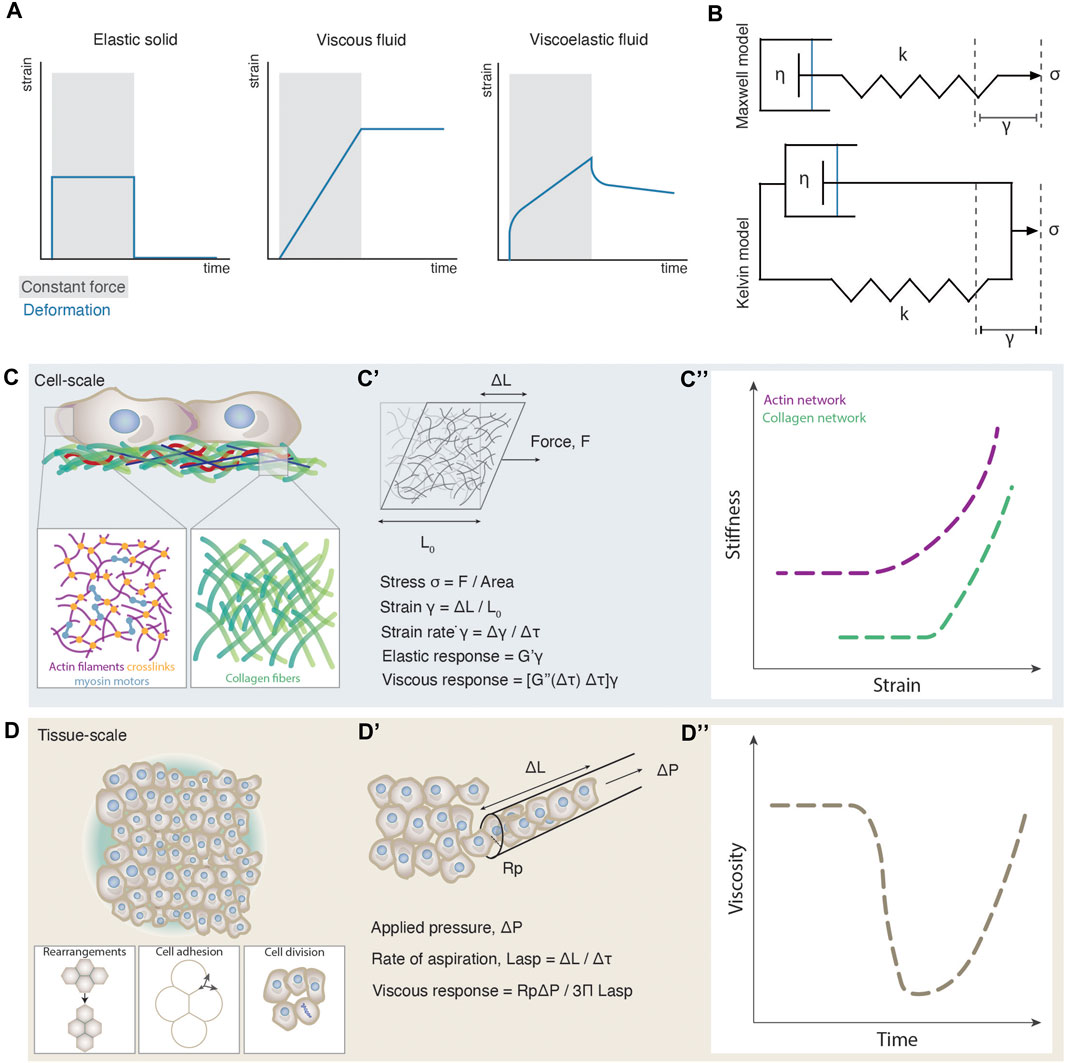
FIGURE 1. Emergence of cell and tissue viscoelasticity. (A) Strain plots as a function of time for different materials during constant force application (grey shaded box) and release. (B) Schematic illustrations of the Maxwell and Kelvin viscoelastic models. In the Maxwell model (top) the spring and dashpot are connected in series and account for the behaviour of viscoelastic fluid materials. In the Kelvin model (bottom) the spring and dashpot are connected in parallel and account for the behaviour of viscoelastic solid materials. Stress σ is applied along the axis of the spring triggering a strain γ. k is the spring constant and η is the viscosity of the fluid. (C) Cellular-scale viscoelasticity is defined by the cytoskeletal network and extracellular matrix. The close ups illustrate an exemplary composition of an actin and collagen network. (C’) Schematic illustration of an experimentally induced deformation of a cytoskeletal network and a paradigm of how viscoelastic properties can be computed from such experiments. (C”) Stiffness-strain plots of actin and collagen networks exhibiting a non-linear increase of their elastic modulus, or a stress-stiffening response. The plot was adapted from [71, 141]. (D) Tissue-scale viscoelasticity is determined by several cellular processes such as cell rearrangements, cell-cell adhesion and cell division. (D’) Schematic illustration of an experimentally induced deformation of an embryonic tissue using micropipette aspiration and a paradigm of how viscoelastic properties can be computed from such experiments. (D”) Plot of the nonlinear decrease of tissue viscosity as observed during zebrafish morphogenesis. $F$, Force; σ, stress; γ, strain; $G\text{'}$, elastic modulus; $G\text{'}\text{'}$, viscous modulus; $\Delta P$, applied pressure; $\Delta L$, deformation length; $R_p$, pipette radius.

An intriguing empirical observation is that the material properties of the microscale components of cell and tissue viscoelasticity, such as the cytoskeletal elements and the cells, respectively, usually do not match the macroscale material properties of cells and tissues [15, 29, 33]. Macroscopic viscoelasticity frequently exhibits nonlinear changes that are not observed at the microscopic level. Such examples have been experimentally detected such as the strain-stiffening response of the cytoskeleton networks [26, 30, 34], phase transitions in the energetic costs of cell movements [12] or abrupt changes in tissue viscosity [13] (Box 1, Figures 1C”,D”). In the above cases, the mechanical resilience of the individual microscopic components to forces falls short in explaining the macroscopic viscoelastic changes, and thus probing the pattern of interactions between the components instead, is key.

Such nonlinear phenomena set a number of challenges to the theoretical understanding of cell and tissue dynamics. Theoretical analyses of cell and tissue material properties are typically addressed from the biopolymer or cell level, respectively. In the first theoretical approach, the microscopic basis is the mechanical properties of the biopolymer filaments building the cytoskeleton [35] and the macroscopic viscoelastic features are derived from the network geometry and local topology of the filaments [26]. Nonlinear phenomena such as strain-stiffening of cytoskeletal networks have been probed with such models. In the second theoretical approach, the microscopic basis is the tiling patterns of the constituents, such as the cells forming a tissue. In such modeling frameworks, mainly represented by the vertex models (Box 1) [25, 36, 37], rheological properties such as rigidity and fluidity are inferred from the energetic costs for cells to independently move through the tissue [27, 28, 38–41]. This viewpoint comes from the fundamental observation that material deformation can only take place through cell-cell rearrangements. Nonlinear phenomena such as jamming transitions (Box 1) have been predicted with such frameworks [27, 28, 40–42]. A third theoretical approach that is not as frequently applied in active viscoelastic systems, but has been used so far to probe material properties across scales, is network theory [29, 31, 43, 44]. In this framework, the starting point is the topology of the network, e.g., how the system’s constituents are connected between them. Of particular relevance for these approaches is the concept of percolation (Box 1). Percolation refers to a wide range of phenomena where a sudden shift in the macroscopic properties of a system made of microscopic, interacting units, is observed when a certain threshold of connectivity at the microscopic scale is overcome [45]. In material sciences, percolation transitions underlie many sudden, qualitative changes in the behavior/response of the material, including, among other, shifts in rigidity and force transmission properties [46–54]. A paradigmatic example of the role of percolation theory in explaining material properties is found in the exploration of the emergence of cracks when the material is under stress. In this context, the length and width of cracks emerging in the material increase dramatically when the system approaches the critical point of rigidity percolation [55, 56] (Box 1). Several forms of percolation theory have been applied to cytoskeletal networks, fiber networks and, recently, to “cellular” networks - tissues - to map material properties [29, 31, 43, 44]. As is the case with inanimate materials, the structure of interactions at the microscopic level --and the potential nonlinear shifts arising from small changes in them-- are supposed to underlie and, ultimately, explain, the emergence of macroscopic material properties like viscoelasticity.

In this review we summarize and discuss experimental and theoretical work probing cell and tissue viscoelasticity as an emergent property. We will first introduce experimental findings on how viscoelasticity emerges in cytoskeletal networks, extracellular matrix fiber networks and tissues. We will then summarize and classify theoretical frameworks supporting such experimental findings that address cell and tissue material properties. Finally, we will discuss the potential of applying network theory to predict viscoelasticity, and speculate how such an approach could impact our biophysical understanding of the material properties of living systems and their morphogenesis.

Viscoelasticity as an Emergent Property: Experimental Observations

Cellular Viscoelasticity

Changes in cellular-scale viscoelasticity are key for cell physiology [57]. Both the cytosol and cytoskeleton contribute to cellular-scale viscoelasticity, with cytoplasmic viscosity dominating processes of macromolecular movement [58] and cytoskeletal viscoelasticity influencing cell morphology, motility and division [8, 57]. Given that experimental work suggests that the cytoskeleton is the major determinant of cellular viscoelasticity [59, 60], we focus here on its viscoelastic properties. The cytoskeleton is the underlying biopolymer scaffold of living cells, and its viscoelasticity offers a balance between dynamic reorganization and maintenance of the cell body. Cytoskeletal viscoelasticity is a complex phenomenon, since it arises from the mechanical properties and interactions of at least three different biopolymers: actin, microtubules and intermediate filaments. These fiber structures further self-organize into filaments and heterogeneous networks through mechanisms of entanglement, branching, crosslinking and bundling (Figure 1C) [61–64]. Such mechanisms involve several types of linkers, such as cross-linking/bundling proteins a-actinin and fascin, and motor proteins like myosin and kinesin [65]. In general, the mechanical properties of the cytoskeleton depend on the physical properties of the individual filaments, the pattern of linkages between the filaments, and the geometry of the filament arrangement [66, 67]. Although cell viscoelasticity is a result of the heterogeneous mechanical properties of all cytoskeletal elements together, our understanding of this process comes mostly from studying each type of element separately (for extensive reviews see [1, 3, 8]).

At the single-filament level, each cytoskeletal biopolymer displays different physical properties, assessed by the ratio of its persistence length ($l_p$) over its contour length ($l_c$) (Box 1). When $l_c$ > $l_p$, the polymers are flexible, and this is the case for the intermediate filaments, which display the shortest $l_p$ (from 200 nm to ∼1 μm) and are the softest among the cytoskeletal elements [68, 69]. Actin filaments have a higher $l_p$ (from 3 to 17 μm) and are semiflexible and microtubules exhibit the highest $l_p$ (>1 mm) and are stiff polymers [70]. Already at the single filament level, semiflexible polymers such as actin and vimentin, display a nonlinear increase of their shear modulus at different strain amplitudes [71] (Box 1). This nonlinear force-extension relationship becomes more apparent at the network level, where new material properties emerge that are absent at the single filament level. Cytoskeletal elements build networks via various forms of filament interactions that influence the viscoelastic behavior of the whole network. For example, transient and non-covalent interactions with crosslinks turn the network into a viscoelastic material, whereas covalent interactions turn the network into an elastic material [3]. Experimental measurements of reconstituted cytoskeletal networks (Figure 1C’) revealed nonlinear force-extension relationships such as stress-stiffening in the presence of tensile load (Figure 1C”) but also stress-softening in the presence of compressive load [5, 30, 33, 62, 71, 72] (Box 1). Actin and intermediate filament networks are highly strain-sensitive, with 10–100 times stiffening appearing at very low strains [71, 73]. Experimental work suggests that depending on the density and interactions in the network e.g. dense vs sparse, the macroscopic material properties change following a well-defined phase diagram [30]. Gardel and colleagues have shown that the addition of crosslinkers results in the formation of rigid solid networks, with elastic modulus several orders of magnitude greater [30]. Even when using flexible crosslinkers like filamin, the network displays nonlinear increases of the elastic modulus when increasing strain, reaching values that match the elastic moduli of cells [34]. Similarly, addition of molecular motors to reconstituted actin networks, such as myosin II, leads to a sharp increase of the elastic modulus [74, 75]. Microtubules on the other hand, and also weakly cross linked actin networks, decrease their modulus as the applied stress is increasing displaying a stress-softening response [30, 76–78]. In conclusion, experimental work shows a very rich collection of nonlinear macroscopic viscoelastic behaviors of the cytoskeleton that represent a challenge for theoretical understanding at the microscopic level.

Extracellular Matrix Viscoelasticity

Besides the emergence of material properties in intracellular cytoskeletal networks, similar behaviors are observed in networks of the extracellular matrix (ECM), the non-cellular material backbone spanning cells and tissues. ECM viscoelasticity is fundamental in cell migration, tissue morphogenesis, organ development, and cancer progression [5, 79, 80]. The ECM is a heterogeneous network composed by several biopolymer filaments, such as fibronectin, laminin, and collagen, that exhibit various persistence lengths. This can range from the 4–8 nm persistence length $l_p$ of flexible hyaluronan biopolymers to a few millimeters’ persistence length $l_p$ of stiff collagen fibers [81, 82]. Given that the ECM is composed of various proteins, enzymes and polysaccharides, probing its viscoelasticity becomes highly complex. Due to its covalent nature of crosslinking, in contrast to the cytoskeletal networks, the ECM is considered an elastic-like network [83]. Collagen networks also display a strain-stiffening response that is in this case emerging from the network level and specifically its connectivity [73, 84, 85] (Figures 1C, C’’). In this case, the nonlinear behaviour emerges for strain of only 10% increase where stiffness increases by 100x before network rupture [44] (Figure 1C’’).

Tissue Viscoelasticity

Similarly, tissue-scale viscoelasticity has been recently experimentally measured to undergo nonlinear changes [11–13, 86–89] resembling phase transitions [90–92]. Direct measurements of viscoelastic features such as yield stress and viscosity have been performed in embryonic tissues and spatial and/or temporal drastic changes have been observed [12, 13]. In the case of the early zebrafish blastoderm, for example, tissue viscosity was found to abruptly drop by more than an order of magnitude within a few minutes at the onset of morphogenesis [13] (Figures 1D’, D’’). In addition, comparison of the yield stress between two neighboring tissues along the zebrafish body axis, the presomitic mesoderm and the progenitor zone, has revealed the presence of solid-like and fluid-like tissues, respectively [12]. However, does cell viscoelasticity scale in such cases with tissue viscoelasticity? Although --to our knowledge-- no simultaneous analysis has been performed yet on measuring both cell and tissue scale viscoelasticity under different conditions to quantitatively assess their relationship, several lines of evidence point at the hypothesis that tissue-scale viscoelasticity critically depends on the interaction patterns between cells. Along these lines, it was reported that inhibition of myosin cytoskeletal motors in zebrafish, that is expected to decrease cell-scale viscoelasticity, had no effect on tissue viscosity [29]. Similarly, pharmacological treatments of the zebrafish tailbud with blebbistatin (a pharmacological myosin II inhibitor), which lowers cytoskeletal elasticity, had surprisingly inverse results on the tissue-scale material properties, where the tissue yield stress in treated embryos it is almost double than the control embryos [12]. In contrast, changes in cell rearrangements, cell-cell adhesion, contractility and cell division rates were shown to trigger changes in the tissue scale material properties (Figure 1D) [11–13, 86–88, 93]. This agrees with extensive theoretical work inferring tissue material phase transitions based on certain cell parameters such as cell motility and adhesion [27, 28, 32, 41], and quantitatively linking tissue rigidity to cell-cell connectivity and adhesion [29], but not directly to the rigidity of individual cells.

Overall, experimental measurements of several viscoelastic characteristics in cells and tissues have revealed nonlinear changes at the macroscale, e.g., viscosity, yield-stress, elastic modulus that do not trivially match similar changes at the microscale, e.g., individual cell and filaments material properties, strongly supporting that viscoelasticity of living systems is an emergent property.

Viscoelasticity as an Emergent Property: Theoretical Models

Several theoretical frameworks have been developed to establish a micro-macro link that can explain cell and tissue viscoelasticity. Numerous models exist in describing complex viscoelastic behaviors in chemical polymers where we recommend to the reader for a more specialized relevant literature [94–96]. Here however, we will summarize experimentally-based models belonging to three categories, based on the abstraction used to represent the biological system: In cytoskeleton networks, the building blocks are the biopolymer filaments and their mechanical properties, in vertex models, the geometrical properties of individual cells tilling the tissue and finally, in the topological models, the local topological arrangements of e.g., cell-cell contacts.

Modeling Viscoelasticity in Cytoskeleton Networks

The theoretical modeling of filament networks must account for the particular rheological phenomena these systems show, such as the strain stiffening response, stiffening tunability, and recoverable network fluidization [8, 15, 26, 30, 33, 71, 77, 97–99]. These models consider, at the microscopic level, filament properties like stiffness or length, and the local geometric and topological patterns of cross-linking, which project to the macroscopic level as material properties. Given these parameters, qualitative shifts in the response of the network are expected while increasing the density of filaments: First, beyond a certain threshold of density, the phenomenon of geometric percolation is observed, usually referred to simply as percolation, purely based on the network topology (Box 1). At higher filament density, another qualitative shift in the properties of the network is observed, when the stiffness percolation threshold is overcome (Figure 2A). Beyond this filament density threshold, any stress applied at any point of the network will propagate throughout the whole system, meaning that the Young modulus, $E$, transits from $E=0$ to $E>0$ [26, 100]. Stiffness percolation is related to rigidity percolation (Box 1), where stresses are no longer absorbed locally, but rather globally. Rigidity percolation, however, only refers to the topological structure [48, 101], whereas, in the case of filament networks, further parameters are considered, as discussed below.

FIGURE 2

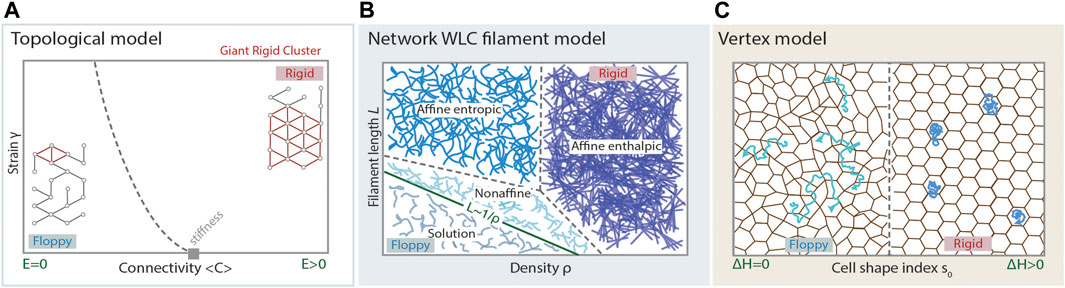
FIGURE 2. Modelling cell and tissue viscoelasticity. (A) Phase diagram of the regimes arising in a topological model for rigidity, such as stiffness percolation, predicting a floppy to rigid transition at a critical point of average connectivity of the underlying network (grey rectangle). A random network displaying average connectivity below the isostatic point (critical point), has a small Giant Rigid Cluster (red) and the whole network is floppy, displaying Young’s modulus $E=0$. The same network, exhibiting connectivity above the critical point forms a big Giant Rigid Cluster making the whole network rigid, hence displaying $E>0$. Figure adapted from [31, 138]. (B) Phase diagram of the network of WLC filaments’ model showing strain-stiffening response of semiflexible biopolymer networks. At low density and low filament length, the network is in solution and in a floppy regime. The solid line indicates the rigidity percolation transition where the network gains stability above a critical density and length, and can be approximated by $L\sim 1/\mathit{\varrho }$. At intermediate density but longer lengths, the network displays an affine elastic deformation due to the entropic stretching of the filaments. At higher density the network displays an affine elastic deformation dominated by the enthalpic stretching and bending of the network and is in a rigid regime. Figure adapted from [26]. (C) Phase diagram of a vertex model predicting a floppy to rigid phase transition in simulated confluent tissues. Below a critical point of a cell shape index $s_0$ (defined by cell-cell adhesion and cell contractility) cells are free to move and display high mean squared displacement (long cell trajectories) and the tissue is fluid-like, thanks that the increase of energy due to cell-cell rearrangements $\Delta H=0$. Above the critical point cells acquire a hexagonal shape and display caged limited motion (short cell trajectories), and cell-cell rearrangements have a positive energy penalty $\Delta H>0$. Figure adapted from [27, 28].

A well accepted model describing the phase space of filament viscoelasticity defined by the parameters of filament density and individual filament properties is the Worm-like Chain (WLC) model [15, 102]. In the WCL model, biopolymers are considered as elastic rods or fibers with finite resistance to bending. Geometrically, such fibers are depicted by an inextensible curve with an energy penalty for bending. Let $r\left(s,t\right)$ denote the path the curve takes in space (and time), parameterized by $s$, the arc length along the curve and $\chi$ the bending modulus. The functional accounting for the energy costs of fiber deformation will be given by:

$H=\frac{\chi }{2}{\displaystyle {\int }_0^{l_c}{\left|\frac{d^{2}r}{d{s}^2}\right|}^{2}ds}$

The second derivative accounts for the local curvature of the filament. The bending modulus $\chi$ has units of energy times length. The above energy function is penalizing any increase of the filament curvature and $\chi$ gives us the scale of such energy penalties. Thermal fluctuations play an important role here, due to the microscopic size of the filaments. As it is standard in statistical mechanics [103], non-zero temperature regimes imply the presence of stochastic, brownian fluctuations whose scale is $k_{B}T$, where $T$ is the room temperature and $k_B$ is the Boltzmann constant. Knowing the scale of the local stochasticity due to temperature enables the definition of a characteristic length for the system, as:

$l_p=\frac{\chi }{k_{B}T}$

which corresponds to the persistence length $l_p$(Box 1). Together with the contour length $l_c$ (Box 1), the filaments are classified according to their stiffness as flexible, semi-flexible and stiff. If $l_p/l_c\ll 1$, the filament is flexible and thermal agitation can induce traverse fluctuations. In this regime, entropic elasticity (Box 1) dominates the dynamics, such as during cytoskeleton stretching [30, 71, 75, 104]. In the case where $l_p/l_c\gg 1$ , filaments are considered stiff and no fluctuations induced by thermal agitation are allowed. In this regime, enthalpic elasticity (Box 1) dominates the deformations of the filament, such as during cytoskeleton bending or buckling observed in branched actin networks in the cell lamellipodia [77, 105]. Finally, when $l_p/l_c\approx 1$, filaments are considered semi-flexible and transverse undulations due to thermal fluctuations are possible, although attenuated. Whereas both the flexible and rigid regime show linear response to strain, the response in the semiflexible regime is nonlinear. To characterize the phase space, we observe that the system can transit between different regimes by changing the filament density $\rho$ (proportional to $1/l_c$) and filament length $L$ playing the role of $l_p$ (proportional to the chain’s molecular weight). Taking these two parameters as the coordinates of a phase diagram, one can identify four regimes: Affine entropic, affine enthalpic, non-affine, solution [15, 26, 33] (Figure 2B, Box 1). In this phase diagram, the phase transition from a fluid regime to a rigid regime is found at the border between the solution and the non-affine regime (Figure 2B), whose functional shape can be approximated as:

$L\sim {\rho }^{-1}$

Experimental work on reconstituted F-actin networks, revealed that linear and nonlinear strain-stress relationships can be explained by entropic and enthalpic models, respectively. In the absence of crosslinkers, actin networks generally form weak elastic gels mimicking the elastic nature of the filaments [106, 107]. At the entropic regime, elasticity comes from the resistance of each polymer/filament against stretching [33, 107]. At the enthalpic regime, while increasing strain, filaments first bend, reorganize along the direction of shear strain and the network deformation arises from the enthalpic stretching of the aligned filaments [108–110]. Further work showed that by decreasing the concentration of cross-linkers the network transits from affine to non-affine [74, 75]. In conclusion, the modeling of biopolymer networks within this framework has proven powerful enough to account for the special viscoelastic properties of these systems.

Modeling Viscoelasticity in Tissues

Cell-Based and Energy Minimization in Vertex models

When modelling tissue viscoelasticity, the fundamental units, cells, are considered to exhibit certain properties [25, 111–117] (Box 1) arising from the cell cytoskeleton [118]. Parameters, such as departure from an ideal cell shape and active fluctuations condense the material response of the cell and its effect to the tissue architecture under stress. There are several abstractions, depending on where the emphasis is placed concerning the energetic cost of the tissue deformations or configurations. Here, we will briefly mention Cellular Potts models and Centroid models, and focus more on the Vertex models (Box 1) which provide a widely applicable framework to the understanding of biological tissue properties.

Cellular Potts models idealize the tissue architecture as a mesh in which each point can be in several states and, accordingly, can represent a part of the cell, a contact point, or a free space. Each state of the mesh point has a particular contribution to the overall energy of the system, and may depend critically on the state of its neighbors [116]. Cellular Potts models may be considered within the much broader family of network models. In turn, centroid models base the analysis on the assumption that cells can be represented by their centroid position within the geometry of the tissue. Energetic contributions are based on geometrical considerations between centroids, such as distance between them [117, 119, 120]. The source of energetic contributions can be considered somehow complementary or even opposed [120] to the one considered in vertex models and the energetic costs associated with different configurations can be associated with material properties of the modeled tissue.

Vertex models have recently received a lot of attention due to their potential in describing a wide range of tissue properties [25, 27, 36, 111–115, 117–119, 121–123]. Moreover, the accurate study of their mathematical properties revealed a plethora of interesting physical properties [27, 28], such as second order rigidity [121], that could play a relevant role in the modeling of biological tissues. Importantly, these properties may imply an interesting departure from the framework proposed by inanimate material science, and proposes a theoretical framework that extends to biological materials. In principle, vertex models have been postulated to model confluent tissues, with recent approaches extending the framework to non-confluent tissues [32]. The essential problem vertex models try to answer is: what are the energetic costs for cell migration within a tissue? In that framework, fluid states are those by which the movement of cells can happen at almost no cost, and rigid states will correspond to those states by which moving a cell - in particular, performing a T1 transition - implies a positive energy penalty, to be paid either in the form of external work or by the cells themselves (Figure 2C). Arguably, the response to an external stress will be, at least partially, driven by the possibility of cell rearrangements which, in turn, depend on the ease of movements of cells within the tissue. The energetic contributions that configure the overall energy of the tissue come from the resistance against compression and the departure from some preferred shape in cells which, in most cases, is introduced as the preferred relation perimeter/area in 2D projections [27, 113, 121, 122]. Having N cells, the functional accounting for the energy of the (2D) system reads:

$H={\displaystyle {\sum }_j^N{K}_{Aj}{\left(A_j-A_{0j}\right)}^2+K_{Pj}{\left(P_j-P_{0j}\right)}^2}(1)$

where $A_j$ and $A_{0j}$ are the actual and preferred areas of cell $j$; $P_j$ and $P_{0j}$ are the actual and preferred perimeter of cell $j$. $K_{Aj}$ and $K_{Pj}$ are the area and perimeter moduli, respectively. The first term models volume incompressibility and the second term models the active contractility of the actomyosin subcellular cortex. As shown, the underlying complex properties of the filament network which are themselves the outcome of a multidimensional problem have been absorbed by the scalar parameters $K_{Aj}$ and $K_{Pj}$. The above equation can be non-dimensionalized in length if we divide it by $\sqrt{A_0}$, resulting in an effective shape index $s_0$:

$s_0=\frac{P_0}{\sqrt{A_0}}$

$s_0$ will act as the control parameter in the different phase transitions between the material regimes of the tissue (Figure 2C). The study of the energetic costs of motility within the tissue is performed through the analysis of the energy barriers arising when a T1 transition occurs (Box 1). The energy barrier corresponding to a T1 transition can, in consequence, be computed as the energy difference, based on Eq. 1, associated to the reduction of the length of an edge to 0 [124, 125]:

$\Delta H=H\left(l\right)-H\left(0\right)$

If a T1 transition can be performed at no energy cost, the tissue is in a fluid configuration. Otherwise, the tissue is considered rigid. Remarkably, one can observe a well-defined phase transition from $\Delta H=0$to $\Delta H>0$ as a function of $s_0$. In particular, for values $s_0<3.81$, the energy imbalance is no longer zero, meaning that T1 transitions happen at a finite energy cost. Interestingly, in disordered systems, the shear modulus vanishes at $s_0<3.81$ [25, 27]. Given the composition of tissues, any deformation must involve rearrangement of cells and, therefore T1 transitions. Consistently, one would expect that the shear modulus goes hand in hand with the energy barriers. Remarkably, this is not the case, and for values $3.71<s_0<3.81$, the tissue has zero linear response but non-zero high-order response [121]. In consequence, this phenomenon has been called “second order rigidity” and the material regime has been named “soft solid” regime [126]. In spite of the numerical evidence that the emergence in the linear regime of the shear modulus coincides with the emergence of theoretical energy barriers in disordered systems, it is currently still unclear what is the theoretical background that could explain the emergence of viscoelastic properties from the theoretical framework of vertex models. Finally, an extension of this vertex model has been developed for non-confluent tissues where stochastic fluctuations in cell surface tensions, density and cell rearrangements control rigid-to-fluid transitions [32]. This contribution detaches the framework of vertex models from the structural constraints that confluency imposes, hence broadening their application in biological tissues.

Topological Models Based on Cell Contact Networks

The presence of interstitial fluid (Box 1) in non-confluent tissues, such as embryonic tissues and tumors [12, 13, 127], opens the possibility to apply even simpler theoretical frameworks to study their viscoelasticity [29]. The reason is that abandoning confluence liberates the system from a lot of implicit constraints at the structural level. Within non-confluent tissues, the range of potential structural patterns increases enormously and topological models can exploit this potential heterogeneity. Here we discuss how topological models can be connected to the rheological properties of non-confluent tissues.

Topological models consider only the structural pattern of connections as the source of the material properties of the tissues. When the system is abstracted at the topological level, its structure is represented by a network defined by nodes and connections among them (Figure 2A). It is important to stress that, at first approximation, no other component, such as link properties or geometric embedding, is considered. The topological analysis, therefore, distills the structure of the system at the level of microscopic minimal components and combinatorial relations among them. In that sense, the basic observables of these models are, for example, the number of links connecting a given node to other nodes of the network, or the existence of paths, within the graph, between a given pair of them. In general, the approximation of a random network, in which the number of connections per node fluctuates stochastically according to some general constraint, quite accurately describes the behavior of real systems --given a suitable choice of constraints [92, 128–131]. For example, in the case that a network is representing the contacts of cells in epithelial (2D) tissues, it must belong to the class of planar networks, namely, those networks that can be extended in a 2D surface without displaying any link overlap [131]. In spite of the apparent simplicity of the approach, the study of networks at the topological level displays a wide range of non-linear phenomena, such as phase transitions or self-organized criticality [92, 129–131]. Particularly relevant is the phenomenon of percolation [91, 92, 128, 129], briefly mentioned in previous sections (Box 1). We will focus on the emergence of the so-called rigid cluster percolation (Box 1), due to its important implications in cells and tissue material properties.

Rigid cluster percolation is based on generic rigidity theory. Given a graph of $N$ nodes and $N_L$ links, a graph is rigid if none of its nodes can be moved independently without constraining or stretching a link (Figure 3A). Despite that the informal definition provided above for rigidity percolation appeals to material deformations e.g., stretching, compressing links, it turns out that the identification of rigid regions in a graph is a purely topological problem: it relies on the identification of actual degrees of freedom remaining in the network through application of the pebble game algorithm [47] based on a theorem considering only the topology of the network [101] (see Figure 3A). A natural question arises: what are the conditions leading to rigidity in a network? The answer is based on Maxwell’s constraint counting [48, 132], where very large networks made of $N$ nodes and $N_L$ links are considered, the links acting as pairwise constraints, limiting the possibilities of independent motion of the nodes connected by the link. For simplicity, a random triangular lattice is considered (e.g., networks in Figure 2A) where the probability that a link exists is $p_e$. If $p_e=1$, all the links are present and the average connectivity $\langle c\rangle$, the average number of links per node, is $\langle c_M\rangle =6$ --recall we are considering very large networks where the boundary effects are negligible. In consequence, the number of links of this network will be fairly approximated by:

$N_L=\frac{p_e}{2}N\langle c_M\rangle (2)$

A network will be rigid if the constraints absorb all the degrees of freedom for the motion of nodes (Figure 3A). Considering a triangular lattice embedded in a 2D plane, each node has, a priori, $d=2$ degrees of freedom (position x and y). The number of degrees of freedom remaining in the network or Floppy modes,$F$, will be approximated by:

$F=dN-N_L$

Note that here we consider that all links are responsible for an independent constraint. We must notice that this is an important simplification [51, 132] of the problem, but has proven useful in terms of both simplicity and predictive power. Starting from $p_e=0$, the number of floppy modes is expected to decrease as long as $p_e$ grows. The key question is to identify the $p_e$ by which $F=0$ and, thus, the whole network is expected to be rigid. This is known as the isostatic point (Box 1) and, using the expression for $E$ found in Eq. 2, and setting $F=0$, we obtain:

$dN=\frac{p_e}{2}N\langle c_M\rangle$

that lead us to:

$p_e=\frac{2d}{\langle c_M\rangle }=\frac{2}{3}(3)$

which, in terms of average network connectivity, implies $\langle c\rangle =4$. That is, if the probability of link existence is $p_e>\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$3$}\right.$, one expects the network to be rigid, and no independent movements could, in principle, be performed without imposing work over the system. Nevertheless, the emergence of rigidity is a much more complex phenomenon. In the case that $p_e<\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$3$}\right.$, for example, there are constraints already acting in the system, so one would expect to see rigid regions within the network. At the same time, the probabilistic nature of the reasoning for finding the isostatic point may induce one to think that some regions of the network may remain floppy even for $p_e>\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$3$}\right.$ The answer is that, in very large systems, the relative size of rigid regions at $p_e<\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$3$}\right.$, is negligible and that, for $p_e>\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$3$}\right.$ one observes the emergence of the giant rigid cluster (GRC) spanning almost all the network (Figure 2A). The emergence of the GRC is abrupt and has all the features of high order phase transitions. Therefore, the isostatic point $p_e=\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$3$}\right.$ is the critical point of a phase transition called generic rigidity percolation, or simply, rigidity percolation [47, 51].

FIGURE 3

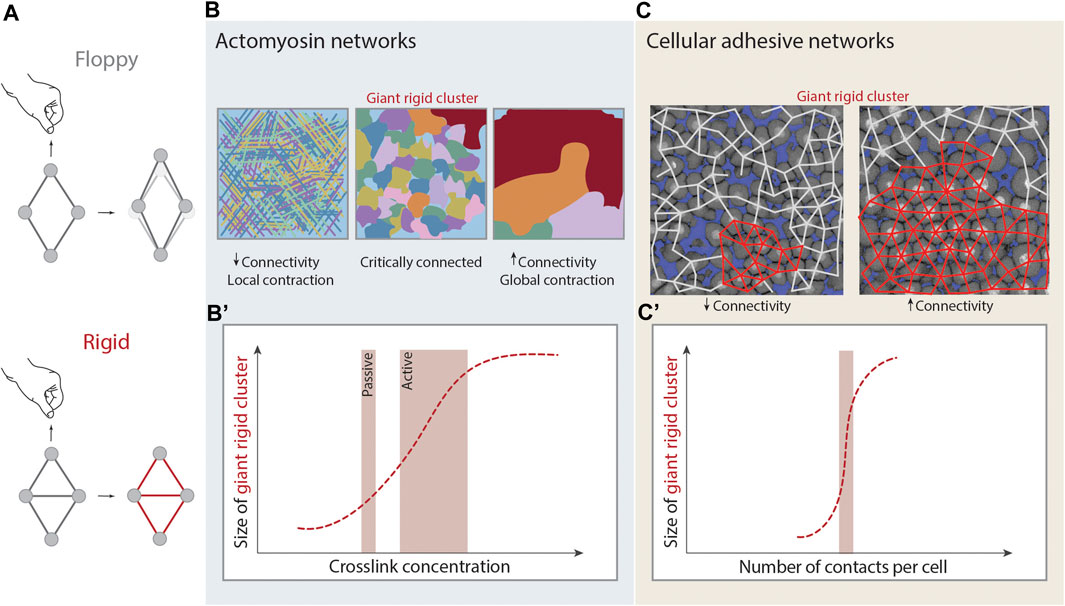
FIGURE 3. Rigidity percolation in living systems. (A) Schematic illustration of rigidity. A rhombus cluster of four nodes and four links deforms in the presence of a deformation force. Just by the addition of one link that absorbs the remaining degrees of freedom of the central nodes, under the same deformation force it does not deform and it is considered rigid. (B,B’) Rigidity percolation transition in actomyosin crosslinked networks. (B) At low connectivity (left) or low crosslinker concentration the network is mostly disconnected and displays local contractions. At intermediate connectivity (middle) and intermediate crosslinker concentration the network is critically connected. At higher connectivity (right) and high crosslinker concentration the network is fully connected, the Giant Rigid Cluster (GRC, red) emerges and the network displays global contractions and signs of fracture. (B’) Plot of the size of the GRC as a function of crosslinker concentration and thus average connectivity. Depending on the absence or presence of contractility the system can be considered as passive or active respectively, and this changes the transition point. Figure adapted from [43]. (C,C’) Rigidity percolation transition in cellular networks - tissues - of the zebrafish embryonic blastoderm. (C) At low average connectivity (∼3.5 contacts per cell) the GRC (red) is small and the blastoderm is fluidized whereas at higher connectivity (>4 contacts per cell) the GRC is big, occupies almost the whole network and the tissue displays experimentally high viscosity. (C’) Plot of the size of the GRC as a function of cell connectivity. Note that the GRC is emerging sharply at the critical point of connectivity (2/3 of maximum potential connectivity). Figure adapted from [29].

In order to connect rigidity and topology with the material properties, the mechanics of the links, considered as springs, should also be considered. In that context, $p_e<\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$3$}\right.$ (subcritical regime) implies that one can perform a differential deformation over the network at no cost. On the contrary, if $p_e>\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$3$}\right.$, any deformation implies an energetic cost in the form of external work performed over the network, as some spring will have to be unavoidably stretched or compressed. Therefore, in the case of very large systems, the first natural consequence of the emergence of the rigid cluster is that the Young modulus $E$ will be $E=0$ in the subcritical regime and $E>0$ in the supercritical regime. In consequence, the topological phase transition that results into the emergence of the GRC projects into the material properties, implying a qualitative shift in the material response of the system under deformations. How does it project specifically into the viscoelastic behavior of the network? To understand that, a minimal ingredient of viscoelastic behavior should be introduced within the springs. This is performed by considering that each spring may update its rest length at random [29, 133]. Specifically, in the simplest approach, the spring updates its rest length at random at every time unit step with probability $p=\frac{1}{\tau }$. Formally, if at time $t$ the rest length is $l\left(t\right)$ and the actual length, due to some external stress, is $l\left(t\right)+\Delta l\left(t\right)$, then:

$p\left(l\left(t+1\right)\to l\left(t\right)+\Delta l\left(t\right)\right)=\frac{1}{\tau }$

In Box 2 we show how the microscopic dynamics of energy dissipation gives rise to macroscopic viscosity. In particular, if $E$ is the Young modulus of the network, each link has the same spring constant $k$, and all such springs update their rest length at random with probability $p=\frac{1}{\tau }$ at every time step, one is led to:

$\frac{d\gamma }{dt}=\frac{1}{E}\left(\frac{d\sigma }{dt}+\frac{\sigma }{\tau }\right)(4)$

where γ, is the strain and σ, the applied stress (Figure 1B). Eq. 4 is a constitutive equation for a Maxwellian viscoelastic material [14] (Figure 1B). The above equation enables us to identify:

$\eta =E\tau (5)$

as the viscosity of the system. What is relevant here is that we have a direct relation between the Young’s modulus of the system, $E$, and the viscosity of the material, $\eta$, up to a constant that is the average lifetime of springs: The faster the update of the spring rest length is, the more fluid the behavior of the material will be. On the contrary, in the limit of no updating, the material is only elastic. Moreover, it is established above that the emergence of a finite Young’s modulus depends critically on the rigidity regime of the network. In conclusion, non-zero viscosity will emerge as the consequence of the emergence of the GRC, at least at the linear level. The phase transition observed for the emergence of the rigid cluster must therefore leave a footprint in the viscoelastic behavior of the network at the critical point.

BOX 2 | Viscosity of a network of springs.

We sketch here, in a very simplified way, the connection between viscoelasticity and the topological property of generic rigidity. We present a version of the Maxwell’s model for viscoelasticity (see Figure 1B), where the particularity comes from the conceptualization of the dashpot, whose role is absorbed by a stochastic resetting of the rest-lengths of the springs forming a network that, in turn, models the structure of the material. This modelization enables the linking of Maxwell’s network rigidity to Maxwell’s theory of viscoelasticity.Let us consider a network of springs, each with elastic constant k. Each spring updates its rest length at random with probability $p=1/\tau$ at every time step. If, at time t the rest length is $l\left(t\right)$ and the actual length, due to some external stress, is $l\left(t\right)+\Delta \left(t\right)$, with probability $p=1/\tau$ , the rest length at time $t+1$ will be updated as:

$l\left(t+1\right)\to l\left(t\right)+\Delta l\left(t\right).$

The whole network has Young’s modulus E. We consider a random lattice arranged in a rectangular form, in a way that the bottom layer is attached to the ground and the upper layer receives the stress $\sigma \left(t\right)$ uniformly —is pulled up. To study the strain $\gamma \left(t\right)$, the elastic contribution, ${\gamma }_e\left(t\right)$ and the contribution of the energy dissipation due to rest-length resetting, ${\gamma }_u\left(t\right)$ must be considered. The overall strain will thus read:

$\gamma \left(t\right)={\gamma }_e\left(t\right)+{\gamma }_u\left(t\right).$

We first consider the elastic component, e.g.:

${\gamma }_e\left(t\right)=\frac{\sigma \left(t\right)}{E}.$

To compute ${\gamma }_u\left(t\right)$, we observe that, in a mean-field approximation, a fraction of $1/\tau$ of springs of the network will update their rest length per time step. Since the elastic deformation for the applied stress is ${\gamma }_e\left(t\right)$, the equation for ${\gamma }_u\left(t\right)$ is:

$\delta {\gamma }_u\left(t\right)\approx \frac{{\gamma }_e\left(t\right)}{\tau }.$

Using the expression for ${\gamma }_e\left(t\right)$, and applying the continuous approximation, this leads to:

$\frac{d{\gamma }_u}{dt}=\frac{\sigma }{\tau E}.$

Considering the two contributions, the overall strain evolves according to the following equation:

$\frac{d\gamma }{dt}=\frac{1}{E}\left(\frac{d\sigma }{dt}+\frac{\sigma }{t}\right),$

Which is a constitutive equation for a Maxwellian viscoelastic material [14]. The above equation enables us to identify the viscosity as:

$\eta =E\tau .$

In consequence, qualitative changes in the Young’s modulus of the network will project into qualitative changes in the viscoelastic behaviour of the system. If $k=0$, as it happens in spring networks whose connectivity is in the rigidity subcritical regime, one expects that, at the linear level, $\eta =0$. On the contrary, if the network is in the supercritical rigidity regime, $k>0$ and, in consequence, $\eta >0$.To grasp the physical role of τ, we consider the simple scenario where we perform an instantaneous, small deformation over the network by pushing the upper layer a distance d, under the assumption that $k>0$. In this case, the constitutive equation can be rewritten as:

$\frac{d\sigma }{dt}+\frac{\sigma }{t}=0,$

since the strain is 0. The solution of the above equation is given by $\sigma \left(t\right)={\sigma }_0{e}^{-t/\tau }$, that is a dissipation of energy in as system with characteristic scale $\tau$.

The above framework is able to bridge, in spite of its simplicity, microscopic topological patterns to macro-structural properties [47, 51], without a priori reference to the mechanical properties of the constituents. These patterns, in turn, can be formally mapped to macroscopic material observables, such as viscoelasticity, hence demonstrating a potentially widely applicable framework to quantitatively link microscopic interactions to macroscopic viscoelasticity across scales.

Rigidity Percolation Probing Viscoelasticity Across Scales

Recent experimental work indicates that analysis at the purely topological level has the potential to indeed probe viscoelastic properties across scales. These models have been applied to several forms of biological networks, such as the cytoskeleton, ECM and cellular networks–tissues, to probe their material properties [29, 31, 44].

In the case of the cytoskeleton, both experimental and theoretical studies have shown that network connectivity is an essential parameter for cytoskeletal network mechanics [26]. If the actomyosin cytoskeleton is considered as a passive system, then rigidity percolation can predict the elastic modulus of the system based solely on its connectivity. In fact, a phase transition is proposed to occur in such networks, where mechanical rigidity emerges at the isostatic point --see Eq. 3 [31] (Figures 3B,B’). Such a framework can be expanded to active systems, where network connectivity together with motor activity can be further used as parameters to predict the contractile behavior of the actin cytoskeleton. Experiments on actin gels, where connectivity is regulated by the density of fascin crosslinkers and the motor activity by the density of myosin, showed characteristics of a rigidity percolation transition [43]. Briefly, weakly crosslinked networks (low connectivity) showed local contractions, medially crosslinked networks (higher connectivity) formed distinct contractile clusters within the network with a certain rigid cluster size distribution and, strongly crosslinked networks (highest connectivity) exhibited global network contraction associated with network fracture [43] (Figure 3B). The authors further propose that the motors have the ability to reduce connectivity via forcing the crosslinkers to unbind, in order to avoid network fracture and thus the interplay of motor activity and crosslinking drives active gels to a critically connected state that can balance between local and global contractions [43].

Rigidity properties of ECM networks and, in particular, type I collagen fiber networks, have also been well-described by rigidity percolation theory [134]. Studies combining experiments and theory suggest that the shear modulus of collagen fibers shows a strong correlation with the collagen volume fraction, and that these networks display connectivity near the percolation threshold [134–138]. Further experimental work however, has revealed that collagen networks with connectivity slightly below the isostatic threshold, can also become rigid in the presence of large deformation instead, thus in such cases passive rigidity percolation may not be sufficient to explain ECM rigidity [44, 85]. In particular, increasing shear deformation in sub-isostatic networks leads to nonlinear increase of the elastic modulus of such networks along different connectivity values, an observation highlighting the possibility of incorporating the active nature of such systems when applying rigidity percolation theory [139].

Recently, the concept of rigidity percolation has been applied in non-confluent embryonic tissues to map tissue rigidity/viscosity (Box 2). Although tissues do not form physically crosslinked networks as the cytoskeleton or ECM, they can be approached as “cellular networks”, where the nodes are the cells and the connecting links the adherens-junctions (Figure 3C) [140]. This theory was applied to the zebrafish blastoderm which undergoes an abrupt and dramatic loss in viscosity at the onset of morphogenesis [13, 29]. These changes in blastoderm viscosity were probed via rigidity percolation analysis over cell contact networks of the blastoderm. The size of the GRC was analyzed as a function of connectivity, and it was found that the GRC size correlates with the experimentally observed changes in tissue viscosity [29] (Figure 3C). The emergence and disappearance of the GRC around the critical point matched the empirical observations where embryos whose cell contact network displays an average connectivity below the critical point, display a small GRC and are fluidized, whereas embryos whose network displays an average connectivity above the critical point display a big GRC and are rigid (Figure 3C). This work further traced hallmarks of phase transitions, such as the diverge of macroscopic observables and its critical exponents at criticality, showing that rigidity percolation theory can be applied in embryonic tissues in vivo to link macroscopic tissue rigidity to the microscopic cell connectivity of these tissues [13, 29].

Discussion and Outlook

Living cells and tissues behave like viscoelastic materials [20, 141], a long-standing observation that has only recently been linked to cell and tissue physiology [2–5]. Spatiotemporal regulation of viscoelasticity has been shown to influence essential biological processes, such as cell motility, proliferation, wound healing and the morphogenetic processes of body axis elongation and tissue spreading during embryonic development [11–13, 86, 88, 142–144]. Tracing the microscopic regulators of viscoelasticity is, however, a challenging task: typically, the mechanical properties of these microscopic building blocks do not match trivially the emerging viscoelastic behavior of cells and tissues at the macroscopic scale. Among many examples, we find the nonlinear increase of the elastic modulus of cytoskeletal and fiber networks in response to strain, or abrupt drastic changes in tissue viscosity without associated mechanical changes at the cellular level [12, 29, 30, 33]. Given that the mechanical properties of tissues are regulated at the microscopic level, e.g., from the properties of the microscopic building blocks and their interactions, quantitatively bridging the microscale to macroscale is fundamental in order to understand the emergence of viscoelasticity [145]. Several theoretical approaches shed light on the biological mechanisms by which viscoelasticity can emerge in a system. However, the application of such theories is still far from comprehensive, given several challenges --such as the active, non-equilibrium nature of living systems.

At the cellular scale, the viscoelasticity of networked biopolymer filaments forming the cytoskeleton and ECM is most frequently modeled based on the mechanics, geometric alignment and local topology of the biopolymer fibers. It is worth mentioning that most of the research activity was performed in networks composed of actin or microtubules or intermediate filaments. In fact, biopolymer networks show a much wider heterogeneity, since the cytoskeleton is a dynamic mixture of all the cytoskeletal elements, interacting with each other, and these interactions were shown to affect their mechanical properties. Percolating networks of actin and vimentin for example, display synergistic effects in the elastic modulus, which becomes much greater than the sum of the elastic moduli of the two networks alone [146]. Another synergistic effect on actin and IFs networks is the recently reported phenomenon of super-elasticity, observed during epithelial morphogenesis [147]. Similarly, actin and MTs composite networks were shown to exhibit reinforcement against compression and mechanical enhancement [148–150], and a similar phenomenon was also observed when compressing composite ECM networks of collagen and hyaluronan [151, 152]. Future experimental and theoretical work on composite networks is expected to provide a more complete understanding of cell and ECM viscoelasticity.

At the tissue scale, the vertex models are widely used to represent tissue viscoelasticity and have the special advantage of collapsing the emergence of macroscopic properties on a single cellular parameter, such as cell shape, and its associated scalar parameters, such as compressibility or departure from preferred area/perimeter [27, 28]. Since, in a tilling of cells, deformation can only arise through cell-cell rearrangements, vertex models mostly focus the analysis on the study of the energy penalties associated with these cell-cell rearrangements. Such rearrangements can for example be induced by differences in cell-cell adhesion and cortical tension or active tension fluctuations [27, 28, 32, 125]. It is implicitly postulated that the results at that level of abstraction will project into the material properties of the system. Even though numerical approaches are coherent with the predictions of the models, a direct bridge between micro and macro scales in tissue viscoelasticity has yet to be clearly described. The recent application of rigidity percolation in tissues however, provides a quantitative link between the topological patterns of cell-cell contacts and tissue rigidity regime (quantified by the size of the GRC). In the case of the zebrafish blastoderm, the topological approach of rigidity percolation was sufficient to capture the floppy and rigid regimes of the tissue by one single (microscopic) measurable parameter, the average number of cell-cell contacts in different cell types and, as a result, match the observed (macroscopic) changes in viscoelasticity [29]. Cell connectivity was further shown to be defined by the biophysics of cell-cell contacts and specifically the cell-cell interfacial tension at the contact. In this biological context, experimental testing of the phase transition parameters revealed that changes in connectivity and cell-cell adhesion were driven by cell division, and not by cell rearrangements, cell shape or active tension fluctuations [29]. Since cell-cell adhesion is key in tissue rigidity theoretical frameworks so far, we speculate that some parameters may be common, such as cell-cell adhesion strength [29, 32, 118, 123], and some others may be context-specific such as cell division and rearrangements. Future experimental work has the potential to disentangle the physiological role of several cellular parameters in rigidity transitions.

In all of the above models, incorporating detailed dynamic analyses of the microscopic parameters that can account for local heterogeneities, such as in adhesion strength (between the cells and with their environment), shape differences or heterogeneous motility patterns, will increase their potential to model absolute viscosity values and provide a more accurate and representative image of tissue viscoelasticity. A key challenge is the choice of the viscoelastic model relevant to the biological system. Here, we have extensively described how Maxwell viscoelasticity has the potential to be linked to Maxwell rigidity. However, other biological systems may be better described with different models. For example, the Kelvin model was recently used to describe the phenomenon of arrested coalescence in multicellular aggregates from the adherent and contractile protrusion interactions between the cells [153]. In addition, both Maxwell and Kelvin viscoelastic models can describe different viscoelastic regimes during density/packing dependent collective cell migration [154]. Another important challenge is to understand if and how the timescale of a biological process taking place at the microscale is relevant to the timescale of a biological process taking place at the macroscale when bridging scales in viscoelasticity. For example, how macromolecular motion within the cytoskeleton (milliseconds to seconds) influences cell shape changes driven by the mechanics of the cytoskeleton (seconds to minutes), or how cellular motion within a tissue (minutes) influences tissue-scale fluidization (minutes) and spreading (hours)? Several theoretical and experimental frameworks should be developed do bridge scales in time and space [142, 155].

Disentangling the connection between microscale behavior and emerging, macroscopic properties is not a novel goal: it has been the long-sought target of statistical mechanics in order to connect thermodynamics to a solid microscopic basis [156]. Moving towards a broader conception of statistical mechanics encompassing the living phenomena requires the introduction of the microscopic role of the biological building blocks - which are far more complex than gas particles, for example. Nevertheless, establishing the critical point in the microscopic dynamics of the building blocks that would trigger a macroscopic phase transition would create a rich toolbox for biology, regardless of the theoretical approach being used. Phase diagrams or morphospaces, accounting for what is possible in the relations between tissue organization and material properties, can be defined that will allow further exploration for the different regimes the system can occupy and their grounding. In the case of the zebrafish blastoderm, for example, it was experimentally possible to position the system in the vicinity of criticality. Hallmarks of criticality, such as divergence of macroscopic observables with associated power laws, were determined experimentally in the living embryo, showing that tissue morphogenesis in vertebrates may start close to a critical point of a rigidity transition. This indicates that embryonic tissues may be at optimal fitness [157] since they are able to easily switch between rigid and floppy regimes by slightly changing their connectivity at almost zero energetic cost [29]. Through this lens, one can explore fundamental questions concerning morphogenesis. How do local heterogeneities in the microscopic parameters influence the emergence of macroscopic viscoelasticity? How do noisy biological systems [158–160] guarantee stability during development when they are poised at criticality?

Networked systems and criticality have been for long used to understand an extremely rich palette of macroscopic phenomena occurring in the natural world [92, 131, 161, 162], that now include the viscoelastic characteristics of biological systems, from the nanometer scale of the cytoskeleton to the micrometer scale of tissues and embryos. Such observations indicate that an efficient organizing strategy of complex biological systems may be to behave as networked systems close to criticality.

Author Contributions

BC-M and NP designed, drafted, revised and finalised the work.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank Preeti Sahu and Edouard Hannezo for critical discussion on the topic and Anna Erzberger and Gautam Dey for feedback on the manuscript.

References

1. Huber F, Schnauß J, Rönicke S, Rauch P, Müller K, Fütterer C. Emergent Complexity of the Cytoskeleton: from Single Filaments to Tissue. Adv Phys (2013) 62(1):1–112. doi:10.1080/00018732.2013.771509

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Barriga EH, Mayor R. Adjustable Viscoelasticity Allows for Efficient Collective Cell Migration. Semin Cell Dev Biol (2019) 93:55–68. doi:10.1016/j.semcdb.2018.05.027

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Burla F, Mulla Y, Vos BE, Aufderhorst-Roberts A, Koenderink GH. From Mechanical Resilience to Active Material Properties in Biopolymer Networks. Nat Rev Phys (2019) 1(4):249–63. doi:10.1038/s42254-019-0036-4

CrossRef Full Text | Google Scholar

4. Petridou NI, Heisenberg CP. Tissue Rheology in Embryonic Organization. EMBO J (2019) 38(20):e102497. doi:10.15252/embj.2019102497

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Chaudhuri O, Cooper-White J, Janmey PA, Mooney DJ, Shenoy VB. Effects of Extracellular Matrix Viscoelasticity on Cellular Behaviour. Nature (2020) 584(7822):535–46. doi:10.1038/s41586-020-2612-2

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Lecuit T, Lenne P-F, Munro E. Force Generation, Transmission, and Integration during Cell and Tissue Morphogenesis. Annu Rev Cell Dev Biol (2011) 27:157–84. doi:10.1146/annurev-cellbio-100109-104027

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Clément R, Dehapiot B, Collinet C, Lecuit T, Lenne P-F. Viscoelastic Dissipation Stabilizes Cell Shape Changes during Tissue Morphogenesis. Curr Biol (2017) 27(20):3132–42.e3134. doi:10.1016/j.cub.2017.09.005

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Pegoraro AF, Janmey P, Weitz DA. Mechanical Properties of the Cytoskeleton and Cells. Cold Spring Harb Perspect Biol (2017) 9(11):a022038. doi:10.1101/cshperspect.a022038

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Campàs O. A Toolbox to Explore the Mechanics of Living Embryonic Tissues. Semin Cell Dev Biol (2016) 55:119–30. doi:10.1016/j.semcdb.2016.03.011

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Gómez-González M, Latorre E, Arroyo M, Trepat X. Measuring Mechanical Stress in Living Tissues. Nat Rev Phys (2020) 2(6):300–17. doi:10.1038/s42254-020-0184-6

CrossRef Full Text | Google Scholar

11. Barriga EH, Franze K, Charras G, Mayor R. Tissue Stiffening Coordinates Morphogenesis by Triggering Collective Cell Migration In Vivo. Nature (2018) 554(7693):523–7. doi:10.1038/nature25742

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Mongera A, Rowghanian P, Gustafson HJ, Shelton E, Kealhofer DA, Carn EK. A Fluid-To-Solid Jamming Transition Underlies Vertebrate Body axis Elongation. Nature (2018) 561(7723):401–5. doi:10.1038/s41586-018-0479-2

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Petridou NI, Grigolon S, Salbreux G, Hannezo E, Heisenberg C-P. Fluidization-mediated Tissue Spreading by Mitotic Cell Rounding and Non-canonical Wnt Signalling. Nat Cell Biol (2019) 21(2):169–78. doi:10.1038/s41556-018-0247-4

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Findley WN, Lai JS, Onaran K. Creep and Relaxation of Nonlinear Viscoelastic Materials. Amsterdam: Elsevier (1989).

15. Broedersz CP, MacKintosh FC. Modeling Semiflexible Polymer Networks. Rev Mod Phys (2014) 86(3):995–1036. doi:10.1103/RevModPhys.86.995

CrossRef Full Text | Google Scholar

16. Özkaya N, Nordin M. Mechanical Properties of Biological Tissues. Editor Nordin M. In: Fundamentals of Biomechanics. New York: Springer (1999).

Google Scholar

17. Gutierrez-Lemini D. Engineering Viscoelasticity. New York: Springer (2014). doi:10.1007/978-1-4614-8139-3

CrossRef Full Text

18. Serwane F, Mongera A, Rowghanian P, Kealhofer DA, Lucio AA, Hockenbery ZM. In Vivo quantification of Spatially Varying Mechanical Properties in Developing Tissues. Nat Methods (2017) 14(2):181–6. doi:10.1038/nmeth.4101

PubMed Abstract | CrossRef Full Text | Google Scholar

19. D'Angelo A, Dierkes K, Carolis C, Salbreux G, Solon J. In Vivo Force Application Reveals a Fast Tissue Softening and External Friction Increase during Early Embryogenesis. Curr Biol (2019) 29(9):1564–71.e6. doi:10.1016/j.cub.2019.04.010

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Forgacs G, Foty RA, Shafrir Y, Steinberg MS. Viscoelastic Properties of Living Embryonic Tissues: a Quantitative Study. Biophysical J (1998) 74(5):2227–34. doi:10.1016/S0006-3495(98)77932-9

CrossRef Full Text | Google Scholar

21. Bonn D, Denn MM, Berthier L, Divoux T, Manneville S. Yield Stress Materials in Soft Condensed Matter. Rev Mod Phys (2017) 89(3):035005. doi:10.1103/RevModPhys.89.035005

CrossRef Full Text | Google Scholar

22. Davidson LA. Embryo Mechanics. Curr Top Dev Biol (2011) 95:215–41. doi:10.1016/b978-0-12-385065-2.00007-4

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Mongera A, Pochitaloff M, Gustafson HJ, Stooke-Vaughan GA, Rowghanian P, Campàs O. Mechanics of the Cellular Microenvironment as Perceived by Cells <em>In Vivo</em&gt. bioRxiv (2021). 2021.2001.2004.425259. doi:10.1101/2021.01.04.425259

CrossRef Full Text | Google Scholar

24. Kollmannsberger P, Fabry B. Linear and Nonlinear Rheology of Living Cells. Annu Rev Mater Res (2011) 41(1):75–97. doi:10.1146/annurev-matsci-062910-100351

CrossRef Full Text | Google Scholar

25. Farhadifar R, Röper J-C, Aigouy B, Eaton S, Jülicher F. The Influence of Cell Mechanics, Cell-Cell Interactions, and Proliferation on Epithelial Packing. Curr Biol (2007) 17(24):2095–104. doi:10.1016/j.cub.2007.11.049

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Pritchard RH, Shery Huang YY, Terentjev EM. Mechanics of Biological Networks: from the Cell Cytoskeleton to Connective Tissue. Soft Matter (2014) 10(12):1864–84. doi:10.1039/C3SM52769G

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Bi D, Lopez JH, Schwarz JM, Manning ML. A Density-independent Rigidity Transition in Biological Tissues. Nat Phys (2015) 11(12):1074–9. doi:10.1038/nphys3471

CrossRef Full Text | Google Scholar

28. Bi D, Yang X, Marchetti MC, Manning ML. Motility-driven Glass and Jamming Transitions in Biological Tissues. Phys Rev X (2016) 6(2). doi:10.1103/PhysRevX.6.021011

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Petridou NI, Corominas-Murtra B, Heisenberg C-P, Hannezo E. Rigidity Percolation Uncovers a Structural Basis for Embryonic Tissue Phase Transitions. Cell (2021) 184(7):1914–28.e19. doi:10.1016/j.cell.2021.02.017

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Gardel ML, Shin JH, MacKintosh FC, Mahadevan L, Matsudaira P, Weitz DA. Elastic Behavior of Cross-Linked and Bundled Actin Networks. Science (2004) 304(5675):1301–5. doi:10.1126/science.1095087

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Alvarado J, Sheinman M, Sharma A, MacKintosh FC, Koenderink GH. Force Percolation of Contractile Active Gels. Soft Matter (2017) 13(34):5624–44. doi:10.1039/c7sm00834a

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Kim S, Pochitaloff M, Stooke-Vaughan GA, Campàs O. Embryonic Tissues as Active Foams. Nat Phys (2021). doi:10.1038/s41567-021-01215-1

CrossRef Full Text | Google Scholar

33. MacKintosh FC, Käs J, Janmey PA. Elasticity of Semiflexible Biopolymer Networks. Phys Rev Lett (1995) 75(24):4425–8. doi:10.1103/PhysRevLett.75.4425

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Gardel ML, Nakamura F, Hartwig JH, Crocker JC, Stossel TP, Weitz DA. Prestressed F-Actin Networks Cross-Linked by Hinged Filamins Replicate Mechanical Properties of Cells. Proc Natl Acad Sci (2006) 103(6):1762–7. doi:10.1073/pnas.0504777103

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Wen Q, Janmey PA. Polymer Physics of the Cytoskeleton. Curr Opin Solid State Mater Sci (2011) 15(5):177–82. doi:10.1016/j.cossms.2011.05.002

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Fletcher AG, Osterfield M, Baker RE, Shvartsman SY. Vertex Models of Epithelial Morphogenesis. Biophysical J (2014) 106(11):2291–304. doi:10.1016/j.bpj.2013.11.4498

CrossRef Full Text | Google Scholar

37. Alt S, Ganguly P, Salbreux G. Vertex Models: from Cell Mechanics to Tissue Morphogenesis. Phil Trans R Soc B (2017) 372:20150520. doi:10.1098/rstb.2015.0520

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Angelini TE, Hannezo E, Trepat X, Marquez M, Fredberg JJ, Weitz DA. Glass-like Dynamics of Collective Cell Migration. Proc Natl Acad Sci (2011) 108(12):4714–9. doi:10.1073/pnas.1010059108

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Sadati M, Taheri Qazvini N, Krishnan R, Park CY, Fredberg JJ. Collective Migration and Cell Jamming. Differentiation (2013) 86(3):121–5. doi:10.1016/j.diff.2013.02.005

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Park J-A, Kim JH, Bi D, Mitchel JA, Qazvini NT, Tantisira K. Unjamming and Cell Shape in the Asthmatic Airway Epithelium. Nat Mater (2015) 14(10):1040–8. doi:10.1038/nmat4357

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Merkel M, Manning ML. A Geometrically Controlled Rigidity Transition in a Model for Confluent 3D Tissues. New J Phys (2018) 20(2):022002. doi:10.1088/1367-2630/aaaa13

CrossRef Full Text | Google Scholar

42. Atia L, Bi D, Sharma Y, Mitchel JA, Gweon B, A. Koehler S. Geometric Constraints during Epithelial Jamming. Nat Phys (2018) 14:613–20. doi:10.1038/s41567-018-0089-9

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Alvarado J, Sheinman M, Sharma A, MacKintosh FC, Koenderink GH. Molecular Motors Robustly Drive Active Gels to a Critically Connected State. Nat Phys (2013) 9(9):591–7. doi:10.1038/nphys2715

CrossRef Full Text | Google Scholar

44. Sharma A, Licup AJ, Jansen KA, Rens R, Sheinman M, Koenderink GH. Strain-controlled Criticality Governs the Nonlinear Mechanics of Fibre Networks. Nat Phys (2016) 12(6):584–7. doi:10.1038/nphys3628

CrossRef Full Text | Google Scholar

45. Hunt A, Ewing R, Ghanbarian B. Percolation Theory: Topology and Structure. Cham: Springer (2014). doi:10.1007/978-3-319-03771-4

CrossRef Full Text

46. Thorpe MF. Continuous Deformations in Random Networks. J Non-Crystalline Sol (1983) 57(3):355–70. doi:10.1016/0022-3093(83)90424-6

CrossRef Full Text | Google Scholar

47. Jacobs DJ, Thorpe MF. Generic Rigidity Percolation: The Pebble Game. Phys Rev Lett (1995) 75(22):4051–4. doi:10.1103/PhysRevLett.75.4051

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Jacobs DJ, Thorpe MF. Generic Rigidity Percolation in Two Dimensions. Phys Rev E (1996) 53(4):3682–93. doi:10.1103/PhysRevE.53.3682

CrossRef Full Text | Google Scholar

49. Alexander S. Amorphous Solids: Their Structure, Lattice Dynamics and Elasticity. Phys Rep (1998) 296(2):65–236. doi:10.1016/S0370-1573(97)00069-0

CrossRef Full Text | Google Scholar

50. Thorpe MF, Jacobs DJ, Chubynsky MV, Phillips JC. Self-organization in Network Glasses. J Non-Crystalline Sol (2000) 266-269:859–66. doi:10.1016/S0022-3093(99)00856-X

CrossRef Full Text | Google Scholar

51. Chubynsky MV, Thorpe MF. Algorithms for Three-Dimensional Rigidity Analysis and a First-Order Percolation Transition. Phys Rev E (2007) 76(4). doi:10.1103/PhysRevE.76.041135

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Wyart M, Liang H, Kabla A, Mahadevan L. Elasticity of Floppy and Stiff Random Networks. Phys Rev Lett (2008) 101(21):215501. doi:10.1103/PhysRevLett.101.215501

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Broedersz CP, Depken M, Yao NY, Pollak MR, Weitz DA, MacKintosh FC. Cross-link-governed Dynamics of Biopolymer Networks. Phys Rev Lett (2010) 105(23):238101. doi:10.1103/PhysRevLett.105.238101

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Tighe BP. Relaxations and Rheology Near Jamming. Phys Rev Lett (2011) 107(15):158303. doi:10.1103/PhysRevLett.107.158303

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Driscoll MM, Chen BG-g., Beuman TH, Ulrich S, Nagel SR, Vitelli V. The Role of Rigidity in Controlling Material Failure. Proc Natl Acad Sci USA (2016) 113(39):10813–7. doi:10.1073/pnas.1501169113

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Bouzid M, Del Gado E. Network Topology in Soft Gels: Hardening and Softening Materials. Langmuir (2018) 34(3):773–81. doi:10.1021/acs.langmuir.7b02944

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Fletcher DA, Mullins RD. Cell Mechanics and the Cytoskeleton. Nature (2010) 463(7280):485–92. doi:10.1038/nature08908

PubMed Abstract | CrossRef Full Text | Google Scholar

58. Shamipour S, Caballero-Mancebo S, Heisenberg C-P. Cytoplasm's Got Moves. Dev Cell (2021) 56(2):213–26. doi:10.1016/j.devcel.2020.12.002

PubMed Abstract | CrossRef Full Text | Google Scholar

59. Trickey WR, Vail TP, Guilak F. The Role of the Cytoskeleton in the Viscoelastic Properties of Human Articular Chondrocytes. J Orthop Res (2004) 22(1):131–9. doi:10.1016/s0736-0266(03)00150-510.1016/s0736-0266(03)0150-5

PubMed Abstract | CrossRef Full Text | Google Scholar

60. Bonakdar N, Gerum R, Kuhn M, Spörrer M, Lippert A, Schneider W. Mechanical Plasticity of Cells. Nat Mater (2016) 15(10):1090–4. doi:10.1038/nmat4689

PubMed Abstract | CrossRef Full Text | Google Scholar

61. de Gennes PG. Reptation of a Polymer Chain in the Presence of Fixed Obstacles. J Chem Phys (1971) 55(2):572–9. doi:10.1063/1.1675789

CrossRef Full Text | Google Scholar

62. Lin Y-C, Broedersz CP, Rowat AC, Wedig T, Herrmann H, MacKintosh FC. Divalent Cations Crosslink Vimentin Intermediate Filament Tail Domains to Regulate Network Mechanics. J Mol Biol (2010) 399(4):637–44. doi:10.1016/j.jmb.2010.04.054

PubMed Abstract | CrossRef Full Text | Google Scholar

63. Blanchoin L, Boujemaa-Paterski R, Sykes C, Plastino J. Actin Dynamics, Architecture, and Mechanics in Cell Motility. Physiol Rev (2014) 94(1):235–63. doi:10.1152/physrev.00018.2013

PubMed Abstract | CrossRef Full Text | Google Scholar

64. Basnet N, Nedozralova H, Crevenna AH, Bodakuntla S, Schlichthaerle T, Taschner M. Direct Induction of Microtubule Branching by Microtubule Nucleation Factor SSNA1. Nat Cell Biol (2018) 20(10):1172–80. doi:10.1038/s41556-018-0199-8

PubMed Abstract | CrossRef Full Text | Google Scholar

65. Lieleg O, Claessens MMAE, Bausch AR. Structure and Dynamics of Cross-Linked Actin Networks. Soft Matter (2010) 6(2):218–25. doi:10.1039/B912163N

CrossRef Full Text | Google Scholar

66. Fabry B, Maksym GN, Butler JP, Glogauer M, Navajas D, Fredberg JJ. Scaling the Microrheology of Living Cells. Phys Rev Lett (2001) 87(14):148102. doi:10.1103/PhysRevLett.87.148102

PubMed Abstract | CrossRef Full Text | Google Scholar

67. Chen DTN, Wen Q, Janmey PA, Crocker JC, Yodh AG. Rheology of Soft Materials. Annu Rev Condens Matter Phys (2010) 1(1):301–22. doi:10.1146/annurev-conmatphys-070909-104120

CrossRef Full Text | Google Scholar

68. Schopferer M, Bär H, Hochstein B, Sharma S, Mücke N, Herrmann H. Desmin and Vimentin Intermediate Filament Networks: Their Viscoelastic Properties Investigated by Mechanical Rheometry. J Mol Biol (2009) 388(1):133–43. doi:10.1016/j.jmb.2009.03.005

PubMed Abstract | CrossRef Full Text | Google Scholar

69. Beck R, Deek J, Choi MC, Ikawa T, Watanabe O, Frey E. Unconventional Salt Trend from Soft to Stiff in Single Neurofilament Biopolymers. Langmuir (2010) 26(24):18595–9. doi:10.1021/la103655x

PubMed Abstract | CrossRef Full Text | Google Scholar

70. Gittes F, Mickey B, Nettleton J, Howard J. Flexural Rigidity of Microtubules and Actin Filaments Measured from thermal Fluctuations in Shape. J Cell Biol (1993) 120(4):923–34. doi:10.1083/jcb.120.4.923

PubMed Abstract | CrossRef Full Text | Google Scholar

71. Storm C, Pastore JJ, MacKintosh FC, Lubensky TC, Janmey PA. Nonlinear Elasticity in Biological Gels. Nature (2005) 435(7039):191–4. doi:10.1038/nature03521

PubMed Abstract | CrossRef Full Text | Google Scholar

72. van Oosten ASG, Vahabi M, Licup AJ, Sharma A, Galie PA, MacKintosh FC. Uncoupling Shear and Uniaxial Elastic Moduli of Semiflexible Biopolymer Networks: Compression-Softening and Stretch-Stiffening. Sci Rep (2016) 6(1):19270. doi:10.1038/srep19270

PubMed Abstract | CrossRef Full Text | Google Scholar

73. Wen Q, Janmey PA. Effects of Non-linearity on Cell-ECM Interactions. Exp Cell Res (2013) 319(16):2481–9. doi:10.1016/j.yexcr.2013.05.017

PubMed Abstract | CrossRef Full Text | Google Scholar

74. Mizuno D, Tardin C, Schmidt CF, MacKintosh FC. Nonequilibrium Mechanics of Active Cytoskeletal Networks. Science (2007) 315(5810):370–3. doi:10.1126/science.1134404

PubMed Abstract | CrossRef Full Text | Google Scholar

75. Koenderink GH, Dogic Z, Nakamura F, Bendix PM, MacKintosh FC, Hartwig JH. An Active Biopolymer Network Controlled by Molecular Motors. Proc Natl Acad Sci (2009) 106(36):15192–7. doi:10.1073/pnas.0903974106

PubMed Abstract | CrossRef Full Text | Google Scholar

76. Xu S, W. Reinhardt H. Crack Extension Resistance and Fracture Properties of Quasi-Brittle Softening Materials like Concrete Based on the Complete Process of Fracture. Int J Fracture (1998) 92(1):71–99. doi:10.1023/A:1007553012684

CrossRef Full Text | Google Scholar

77. Chaudhuri O, Parekh SH, Fletcher DA. Reversible Stress Softening of Actin Networks. Nature (2007) 445(7125):295–8. doi:10.1038/nature05459

PubMed Abstract | CrossRef Full Text | Google Scholar

78. Lin Y-C, Koenderink GH, MacKintosh FC, Weitz DA. Viscoelastic Properties of Microtubule Networks. Macromolecules (2007) 40(21):7714–20. doi:10.1021/ma070862l

CrossRef Full Text | Google Scholar

79. Rozario T, Dzamba B, Weber GF, Davidson LA, DeSimone DW. The Physical State of Fibronectin Matrix Differentially Regulates Morphogenetic Movements In Vivo. Dev Biol (2009) 327(2):386–98. doi:10.1016/j.ydbio.2008.12.025

PubMed Abstract | CrossRef Full Text | Google Scholar

80. Rozario T, DeSimone DW. The Extracellular Matrix in Development and Morphogenesis: a Dynamic View. Dev Biol (2010) 341(1):126–40. doi:10.1016/j.ydbio.2009.10.026

PubMed Abstract | CrossRef Full Text | Google Scholar

81. Licup AJ, Münster S, Sharma A, Sheinman M, Jawerth LM, Fabry B. Stress Controls the Mechanics of Collagen Networks. Proc Natl Acad Sci USA (2015) 112(31):9573–8. doi:10.1073/pnas.1504258112

PubMed Abstract | CrossRef Full Text | Google Scholar

82. Berezney JP, Saleh OA. Electrostatic Effects on the Conformation and Elasticity of Hyaluronic Acid, a Moderately Flexible Polyelectrolyte. Macromolecules (2017) 50(3):1085–9. doi:10.1021/acs.macromol.6b02166

CrossRef Full Text | Google Scholar

83. Muiznieks LD, Keeley FW. Molecular Assembly and Mechanical Properties of the Extracellular Matrix: A Fibrous Protein Perspective. Biochim Biophys Acta (Bba) - Mol Basis Dis (2013) 1832(7):866–75. doi:10.1016/j.bbadis.2012.11.022

CrossRef Full Text | Google Scholar

84. Han YL, Ronceray P, Xu G, Malandrino A, Kamm RD, Lenz M. Cell Contraction Induces Long-Ranged Stress Stiffening in the Extracellular Matrix. Proc Natl Acad Sci USA (2018) 115(16):4075–80. doi:10.1073/pnas.1722619115

PubMed Abstract | CrossRef Full Text | Google Scholar

85. Jansen KA, Licup AJ, Sharma A, Rens R, MacKintosh FC, Koenderink GH. The Role of Network Architecture in Collagen Mechanics. Biophysical J (2018) 114(11):2665–78. doi:10.1016/j.bpj.2018.04.043

PubMed Abstract | CrossRef Full Text | Google Scholar

86. Iyer KV, Piscitello-Gómez R, Paijmans J, Jülicher F, Eaton S. Epithelial Viscoelasticity Is Regulated by Mechanosensitive E-Cadherin Turnover. Curr Biol (2019) 29(4):578–91.e575. doi:10.1016/j.cub.2019.01.021

PubMed Abstract | CrossRef Full Text | Google Scholar

87. Khalilgharibi N, Fouchard J, Asadipour N, Barrientos R, Duda M, Bonfanti A. Stress Relaxation in Epithelial Monolayers Is Controlled by the Actomyosin Cortex. Nat Phys (2019) 15(8):839–47. doi:10.1038/s41567-019-0516-6

PubMed Abstract | CrossRef Full Text | Google Scholar

88. Tetley RJ, Staddon MF, Heller D, Hoppe A, Banerjee S, Mao Y. Tissue Fluidity Promotes Epithelial Wound Healing. Nat Phys (2019) 15(11):1195–203. doi:10.1038/s41567-019-0618-1

PubMed Abstract | CrossRef Full Text | Google Scholar

89. Cavanaugh KE, Staddon MF, Banerjee S, Gardel ML. Adaptive Viscoelasticity of Epithelial Cell Junctions: from Models to Methods. Curr Opin Genet Dev (2020) 63:86–94. doi:10.1016/j.gde.2020.05.018

PubMed Abstract | CrossRef Full Text | Google Scholar

90. Stanley HE. Introduction to Phase Transitions and Critical Phenomena. New York: Oxford University Press (1971).

91. Domb C, Green MS. Phase Transitions and Critical Phenomena. London: Academic Press (1972).

92. Solé R. Phase Transitions. Princeton, NJ: Princeton University Press (2011). doi:10.1515/9781400838929

CrossRef Full Text

93. Jain A, Ulman V, Mukherjee A, Prakash M, Cuenca MB, Pimpale LG. Regionalized Tissue Fluidization Is Required for Epithelial gap Closure during Insect Gastrulation. Nat Commun (2020) 11(1):5604. doi:10.1038/s41467-020-19356-x

PubMed Abstract | CrossRef Full Text | Google Scholar

94. Rubinstein M, Colby RH, Dobrynin AV, Joanny J-F. Elastic Modulus and Equilibrium Swelling of Polyelectrolyte Gels. Macromolecules (1996) 29(1):398–406. doi:10.1021/ma9511917

CrossRef Full Text | Google Scholar

95. Gurtovenko AA, Gotlib YY. Dynamics of Inhomogeneous Cross-Linked Polymers Consisting of Domains of Different Sizes. J Chem Phys (2001) 115(14):6785–93. doi:10.1063/1.1401819

CrossRef Full Text | Google Scholar

96. Müller P. Critical Behaviour of the Rouse Model for Gelling Polymers. J Phys A: Math Gen (2003) 36(42):10443–50. doi:10.1088/0305-4470/36/42/002

CrossRef Full Text | Google Scholar

97. Janmey PA, McCormick ME, Rammensee S, Leight JL, Georges PC, MacKintosh FC. Negative normal Stress in Semiflexible Biopolymer Gels. Nat Mater (2007) 6(1):48–51. doi:10.1038/nmat1810

PubMed Abstract | CrossRef Full Text | Google Scholar

98. Lieleg O, Bausch AR. Cross-Linker Unbinding and Self-Similarity in Bundled Cytoskeletal Networks. Phys Rev Lett (2007) 99(15):158105. doi:10.1103/PhysRevLett.99.158105

PubMed Abstract | CrossRef Full Text | Google Scholar

99. Trepat X, Deng L, An SS, Navajas D, Tschumperlin DJ, Gerthoffer WT. Universal Physical Responses to Stretch in the Living Cell. Nature (2007) 447(7144):592–5. doi:10.1038/nature05824

PubMed Abstract | CrossRef Full Text | Google Scholar

100. Zaccone A, Scossa-Romano E. Approximate Analytical Description of the Nonaffine Response of Amorphous Solids. Phys Rev B (2011) 83(18):184205. doi:10.1103/PhysRevB.83.184205

CrossRef Full Text | Google Scholar

101. Laman G. On Graphs and Rigidity of Plane Skeletal Structures. J Eng Math (1970) 4(4):331–40. doi:10.1007/BF01534980

CrossRef Full Text | Google Scholar

102. Kratky O, Porod G. Röntgenuntersuchung Gelöster Fadenmoleküle. Recl Trav Chim Pays-bas (1949) 68(12):1106–22. doi:10.1002/recl.19490681203

CrossRef Full Text | Google Scholar

103. Pathria RK, Beale PD. Statistical Mechanics. Oxford: Oxford University Press (2002).

104. Tharmann R, Claessens MMAE, Bausch AR. Viscoelasticity of Isotropically Cross-Linked Actin Networks. Phys Rev Lett (2007) 98(8):088103. doi:10.1103/PhysRevLett.98.088103

PubMed Abstract | CrossRef Full Text | Google Scholar

105. Wagner B, Tharmann R, Haase I, Fischer M, Bausch AR. Cytoskeletal Polymer Networks: The Molecular Structure of Cross-Linkers Determines Macroscopic Properties. Proc Natl Acad Sci (2006) 103(38):13974–8. doi:10.1073/pnas.0510190103

PubMed Abstract | CrossRef Full Text | Google Scholar

106. Janmey PA, Peetermans J, Zaner KS, Stossel TP, Tanaka T. Structure and Mobility of Actin Filaments as Measured by Quasielastic Light Scattering, Viscometry, and Electron Microscopy. J Biol Chem (1986) 261(18):8357–62. doi:10.1016/s0021-9258(19)83920-0

PubMed Abstract | CrossRef Full Text | Google Scholar

107. Hinner B, Tempel M, Sackmann E, Kroy K, Frey E. Entanglement, Elasticity, and Viscous Relaxation of Actin Solutions. Phys Rev Lett (1998) 81(12):2614–7. doi:10.1103/PhysRevLett.81.2614

CrossRef Full Text | Google Scholar

108. Onck PR, Koeman T, van Dillen T, van der Giessen E. Alternative Explanation of Stiffening in Cross-Linked Semiflexible Networks. Phys Rev Lett (2005) 95(17):178102. doi:10.1103/PhysRevLett.95.178102

PubMed Abstract | CrossRef Full Text | Google Scholar

109. van Dillen T, Onck PR, Van der Giessen E. Models for Stiffening in Cross-Linked Biopolymer Networks: A Comparative Study. J Mech Phys Sol (2008) 56(6):2240–64. doi:10.1016/j.jmps.2008.01.007

CrossRef Full Text | Google Scholar

110. Žagar G, Onck PR, Van der Giessen E. Elasticity of Rigidly Cross-Linked Networks of Athermal Filaments. Macromolecules (2011) 44(17):7026–33. doi:10.1021/ma201257v

CrossRef Full Text | Google Scholar

111. Nagai T, Honda H. A Dynamic Cell Model for the Formation of Epithelial Tissues. Philosophical Mag B (2001) 81(7):699–719. doi:10.1080/13642810108205772

CrossRef Full Text | Google Scholar

112. Hilgenfeldt S, Erisken S, Carthew RW. Physical Modeling of Cell Geometric Order in an Epithelial Tissue. Proc Natl Acad Sci (2008) 105(3):907–11. doi:10.1073/pnas.0711077105

PubMed Abstract | CrossRef Full Text | Google Scholar

113. Staple DB, Farhadifar R, Röper J-C, Aigouy B, Eaton S, Jülicher F. Mechanics and Remodelling of Cell Packings in Epithelia. Eur Phys J E (2010) 33(2):117–27. doi:10.1140/epje/i2010-10677-0

PubMed Abstract | CrossRef Full Text | Google Scholar

114. Chiou KK, Hufnagel L, Shraiman BI. Mechanical Stress Inference for Two Dimensional Cell Arrays. PLoS Comput Biol (2012) 8(5):e1002512. doi:10.1371/journal.pcbi.1002512

PubMed Abstract | CrossRef Full Text | Google Scholar

115. Wang G, Manning ML, Amack JD. Regional Cell Shape Changes Control Form and Function of Kupffer's Vesicle in the Zebrafish Embryo. Dev Biol (2012) 370(1):52–62. doi:10.1016/j.ydbio.2012.07.019

PubMed Abstract | CrossRef Full Text | Google Scholar

116. Vroomans RMA, Hogeweg P, ten Tusscher KHWJ. Segment-Specific Adhesion as a Driver of Convergent Extension. PLoS Comput Biol (2015) 11(2):e1004092. doi:10.1371/journal.pcbi.1004092

PubMed Abstract | CrossRef Full Text | Google Scholar

117. Marin-Riera M, Brun-Usan M, Zimm R, Välikangas T, Salazar-Ciudad I. Computational Modeling of Development by Epithelia, Mesenchyme and Their Interactions: a Unified Model. Bioinformatics (2016) 32(2):219–25. doi:10.1093/bioinformatics/btv527

PubMed Abstract | CrossRef Full Text | Google Scholar

118. Manning ML, Foty RA, Steinberg MS, Schoetz E-M. Coaction of Intercellular Adhesion and Cortical Tension Specifies Tissue Surface Tension. Proc Natl Acad Sci USA (2010) 107(28):12517–22. doi:10.1073/pnas.1003743107

PubMed Abstract | CrossRef Full Text | Google Scholar

119. Delile J, Herrmann M, Peyriéras N, Doursat R. A Cell-Based Computational Model of Early Embryogenesis Coupling Mechanical Behaviour and Gene Regulation. Nat Commun (2017) 8(1):13929. doi:10.1038/ncomms13929

PubMed Abstract | CrossRef Full Text | Google Scholar

120. Sharpe J. Computer Modeling in Developmental Biology: Growing Today, Essential Tomorrow. Development (2017) 144(23):4214–25. doi:10.1242/dev.151274

PubMed Abstract | CrossRef Full Text | Google Scholar

121. Sahu P, Sussman DM, Rübsam M, Mertz AF, Horsley V, Dufresne ER. Small-scale Demixing in Confluent Biological Tissues. Soft Matter (2020) 16(13):3325–37. doi:10.1039/C9SM01084J

PubMed Abstract | CrossRef Full Text | Google Scholar

122. Wang X, Merkel M, Sutter LB, Erdemci-Tandogan G, Manning ML, Kasza KE. Anisotropy Links Cell Shapes to Tissue Flow during Convergent Extension. Proc Natl Acad Sci USA (2020) 117(24):13541–51. doi:10.1073/pnas.1916418117

PubMed Abstract | CrossRef Full Text | Google Scholar

123. Lawson-Keister E, Manning ML. Jamming and Arrest of Cell Motion in Biological Tissues arXiv (2021).

Google Scholar

124. Weaire DL, Hutzler S. The Physics of Foams. Oxford: Oxford University Press (1999).

125. Bi D, Lopez JH, Schwarz JM, Manning ML. Energy Barriers and Cell Migration in Densely Packed Tissues. Soft Matter (2014) 10(12):1885–90. doi:10.1039/C3SM52893F

PubMed Abstract | CrossRef Full Text | Google Scholar

126. Moshe M, Bowick MJ, Marchetti MC. Geometric Frustration and Solid-Solid Transitions in Model 2D Tissue. Phys Rev Lett (2018) 120(26):268105. doi:10.1103/PhysRevLett.120.268105

PubMed Abstract | CrossRef Full Text | Google Scholar

127. Douezan S, Guevorkian K, Naouar R, Dufour S, Cuvelier D, Brochard-Wyart F. Spreading Dynamics and Wetting Transition of Cellular Aggregates. Proc Natl Acad Sci (2011) 108(18):7315–20. doi:10.1073/pnas.1018057108

PubMed Abstract | CrossRef Full Text | Google Scholar

128. Bollobas B. Modern Graph Theory. US: Springer (1998). doi:10.1007/978-1-4612-0619-4

CrossRef Full Text

129. Newman MEJ, Strogatz SH, Watts DJ. Random Graphs with Arbitrary Degree Distributions and Their Applications. Phys Rev E (2001) 64(2):026118. doi:10.1103/PhysRevE.64.026118

PubMed Abstract | CrossRef Full Text | Google Scholar

130. Dorogovtsev SN, Mendes JFF. Evolution of Networks: From Biological Nets to the Internet and WWW. Oxford: Oxford University Press (2003). doi:10.1093/acprof:oso/9780198515906.001.0001

CrossRef Full Text

131. Newman M. Networks: An Introduction. Oxford: Oxford University Press (2010). doi:10.1093/acprof:oso/9780199206650.001.0001

CrossRef Full Text

132. Maxwell JC. I.-On Reciprocal Figures, Frames, and Diagrams of Forces. Trans R Soc Edinb (1870) 26(1):1–40. doi:10.1017/S0080456800026351

CrossRef Full Text | Google Scholar

133. Muñoz JJ, Albo S. Physiology-based Model of Cell Viscoelasticity. Phys Rev E (2013) 88(1):012708. doi:10.1103/PhysRevE.88.012708

CrossRef Full Text | Google Scholar

134. Silverberg JL, Barrett AR, Das M, Petersen PB, Bonassar LJ, Cohen I. Structure-Function Relations and Rigidity Percolation in the Shear Properties of Articular Cartilage. Biophysical J (2014) 107(7):1721–30. doi:10.1016/j.bpj.2014.08.011

CrossRef Full Text | Google Scholar

135. Poole AR, Pidoux I, Rosenberg L. Role of Proteoglycans in Endochondral Ossification: Immunofluorescent Localization of Link Protein and Proteoglycan Monomer in Bovine Fetal Epiphyseal Growth Plate. J Cell Biol (1982) 92(2):249–60. doi:10.1083/jcb.92.2.249

PubMed Abstract | CrossRef Full Text | Google Scholar

136. Forgacs G, Newman SA, Hinner B, Maier CW, Sackmann E. Assembly of Collagen Matrices as a Phase Transition Revealed by Structural and Rheologic Studies. Biophysical J (2003) 84(2 Pt 1):1272–80. doi:10.1016/s0006-3495(03)74942-x

CrossRef Full Text | Google Scholar

137. Yadavalli VK, Svintradze DV, Pidaparti RM. Nanoscale Measurements of the Assembly of Collagen to Fibrils. Int J Biol Macromolecules (2010) 46(4):458–64. doi:10.1016/j.ijbiomac.2010.02.012

CrossRef Full Text | Google Scholar

138. Shivers JL, Arzash S, Sharma A, MacKintosh FC. Scaling Theory for Mechanical Critical Behavior in Fiber Networks. Phys Rev Lett (2019) 122(18):188003. doi:10.1103/PhysRevLett.122.188003

PubMed Abstract | CrossRef Full Text | Google Scholar

139. Iravani A, Thambyah A, Burrowes KS. A Viscoelastic Two-Dimensional Network Model of the Lung Extracellular Matrix. Biomech Model Mechanobiol (2020) 19(6):2241–53. doi:10.1007/s10237-020-01336-1

PubMed Abstract | CrossRef Full Text | Google Scholar

140. Pinheiro D, Bellaïche Y. Mechanical Force-Driven Adherens Junction Remodeling and Epithelial Dynamics. Dev Cell (2018) 47(1):3–19. doi:10.1016/j.devcel.2018.09.014

PubMed Abstract | CrossRef Full Text | Google Scholar

141. Kasza KE, Rowat AC, Liu J, Angelini TE, Brangwynne CP, Koenderink GH. The Cell as a Material. Curr Opin Cell Biol (2007) 19(1):101–7. doi:10.1016/j.ceb.2006.12.002

PubMed Abstract | CrossRef Full Text | Google Scholar

142. Ranft J, Basan M, Elgeti J, Joanny J-F, Prost J, Jülicher F. Fluidization of Tissues by Cell Division and Apoptosis. Proc Natl Acad Sci (2010) 107(49):20863–8. doi:10.1073/pnas.1011086107

PubMed Abstract | CrossRef Full Text | Google Scholar

143. Saadaoui M, Rocancourt D, Roussel J, Corson F, Gros J. A Tensile Ring Drives Tissue Flows to Shape the Gastrulating Amniote Embryo. Science (2020) 367(6476):453–8. doi:10.1126/science.aaw1965

PubMed Abstract | CrossRef Full Text | Google Scholar

144. Zhu M, Tao H, Samani M, Luo M, Wang X, Hopyan S. Spatial Mapping of Tissue Properties In Vivo Reveals a 3D Stiffness Gradient in the Mouse Limb Bud. Proc Natl Acad Sci USA (2020) 117(9):4781–91. doi:10.1073/pnas.1912656117

PubMed Abstract | CrossRef Full Text | Google Scholar

145. Barber DL, Trepat X. Editorial Overview: Cell Dynamics: Integrating Cell Dynamics across Scales. Curr Opin Cell Biol (2020) 66:130–2. doi:10.1016/j.ceb.2020.06.003

PubMed Abstract | CrossRef Full Text | Google Scholar

146. van Doorn JM, Lageschaar L, Sprakel J, van der Gucht J. Criticality and Mechanical Enhancement in Composite Fiber Networks. Phys Rev E (2017) 95(4):042503. doi:10.1103/PhysRevE.95.042503

PubMed Abstract | CrossRef Full Text | Google Scholar

147. Latorre E, Kale S, Casares L, Gómez-González M, Uroz M, Valon L. Active Superelasticity in Three-Dimensional Epithelia of Controlled Shape. Nature (2018) 563(7730):203–8. doi:10.1038/s41586-018-0671-4

PubMed Abstract | CrossRef Full Text | Google Scholar

148. Brangwynne CP, MacKintosh FC, Kumar S, Geisse NA, Talbot J, Mahadevan L. Microtubules Can bear Enhanced Compressive Loads in Living Cells Because of Lateral Reinforcement. J Cell Biol (2006) 173(5):733–41. doi:10.1083/jcb.200601060

PubMed Abstract | CrossRef Full Text | Google Scholar

149. Das M, MacKintosh FC. Poisson's Ratio in Composite Elastic Media with Rigid Rods. Phys Rev Lett (2010) 105(13):138102. doi:10.1103/PhysRevLett.105.138102

PubMed Abstract | CrossRef Full Text | Google Scholar

150. Huisman EM, Heussinger C, Storm C, Barkema GT. Semiflexible Filamentous Composites. Phys Rev Lett (2010) 105(11):118101. doi:10.1103/PhysRevLett.105.118101

PubMed Abstract | CrossRef Full Text | Google Scholar

151. Lai VK, Nedrelow DS, Lake SP, Kim B, Weiss EM, Tranquillo RT. Swelling of Collagen-Hyaluronic Acid Co-gels: An In Vitro Residual Stress Model. Ann Biomed Eng (2016) 44(10):2984–93. doi:10.1007/s10439-016-1636-0

PubMed Abstract | CrossRef Full Text | Google Scholar

152. Burla F, Tauber J, Dussi S, van der Gucht J, Koenderink GH. Stress Management in Composite Biopolymer Networks. Nat Phys (2019) 15(6):549–53. doi:10.1038/s41567-019-0443-6

CrossRef Full Text | Google Scholar

153. Oriola D, Marin-Riera M, Aalderink G, Anlas K, Gritti N, Sharpe J (2020). Arrested Coalescence of Multicellular Aggregates. arXiv.2012.01455.

Google Scholar

154. Pajic-Lijakovic I, Milivojevic M. Viscoelasticity and Cell Jamming State Transition. bioRxiv (2021) 436195, 2021. 2021.2003.2019. doi:10.1101/2021.03.19.436195

CrossRef Full Text | Google Scholar

155. Pajic-Lijakovic I, Milivojevic M. Multiscale Nature of Cell Rearrangement Caused by Collective Cell Migration. Eur Biophys J (2021) 50(1):1–14. doi:10.1007/s00249-021-01496-7

PubMed Abstract | CrossRef Full Text | Google Scholar

156. Sklar L. Physics and Chance: Philosophical Issues in the Foundations of Statistical Mechanics. Cambridge: Cambridge University Press (1993). doi:10.1017/cbo9780511624933

CrossRef Full Text

157. Hidalgo J, Grilli J, Suweis S, Muñoz MA, Banavar JR, Maritan A. Information-based Fitness and the Emergence of Criticality in Living Systems. Proc Natl Acad Sci (2014) 111(28):10095–100. doi:10.1073/pnas.1319166111

PubMed Abstract | CrossRef Full Text | Google Scholar

158. Arias AM, Hayward P. Filtering Transcriptional Noise during Development: Concepts and Mechanisms. Nat Rev Genet (2006) 7(1):34–44. doi:10.1038/nrg1750

PubMed Abstract | CrossRef Full Text | Google Scholar

159. Mateus AM, Gorfinkiel N, Arias AM. Origin and Function of Fluctuations in Cell Behaviour and the Emergence of Patterns. Semin Cell Dev Biol (2009) 20(7):877–84. doi:10.1016/j.semcdb.2009.07.009

PubMed Abstract | CrossRef Full Text | Google Scholar

160. Garcia-Ojalvo J, Martinez Arias A. Towards a Statistical Mechanics of Cell Fate Decisions. Curr Opin Genet Dev (2012) 22(6):619–26. doi:10.1016/j.gde.2012.10.004

PubMed Abstract | CrossRef Full Text | Google Scholar

161. Newman M, Barabasi A-L, Watts DJ. The Structure and Dynamics of Networks. Princeton: Princeton University Press (2006).

162. Muñoz MA. Colloquium: Criticality and Dynamical Scaling in Living Systems. Rev Mod Phys (2018) 90(3):031001. doi:10.1103/RevModPhys.90.031001

CrossRef Full Text | Google Scholar