Mathematical Modeling and Computational Predictions in Oncoimmunology

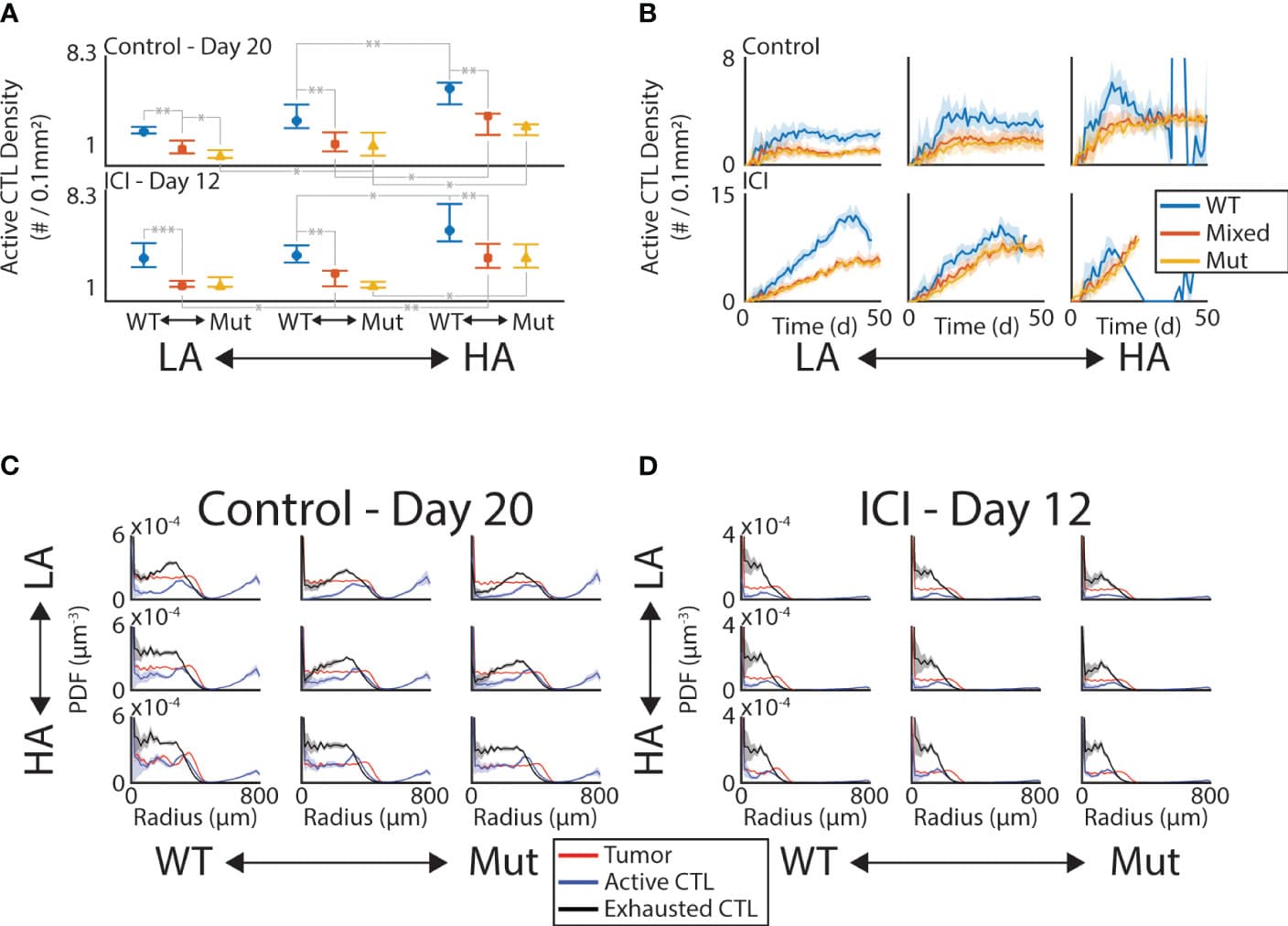
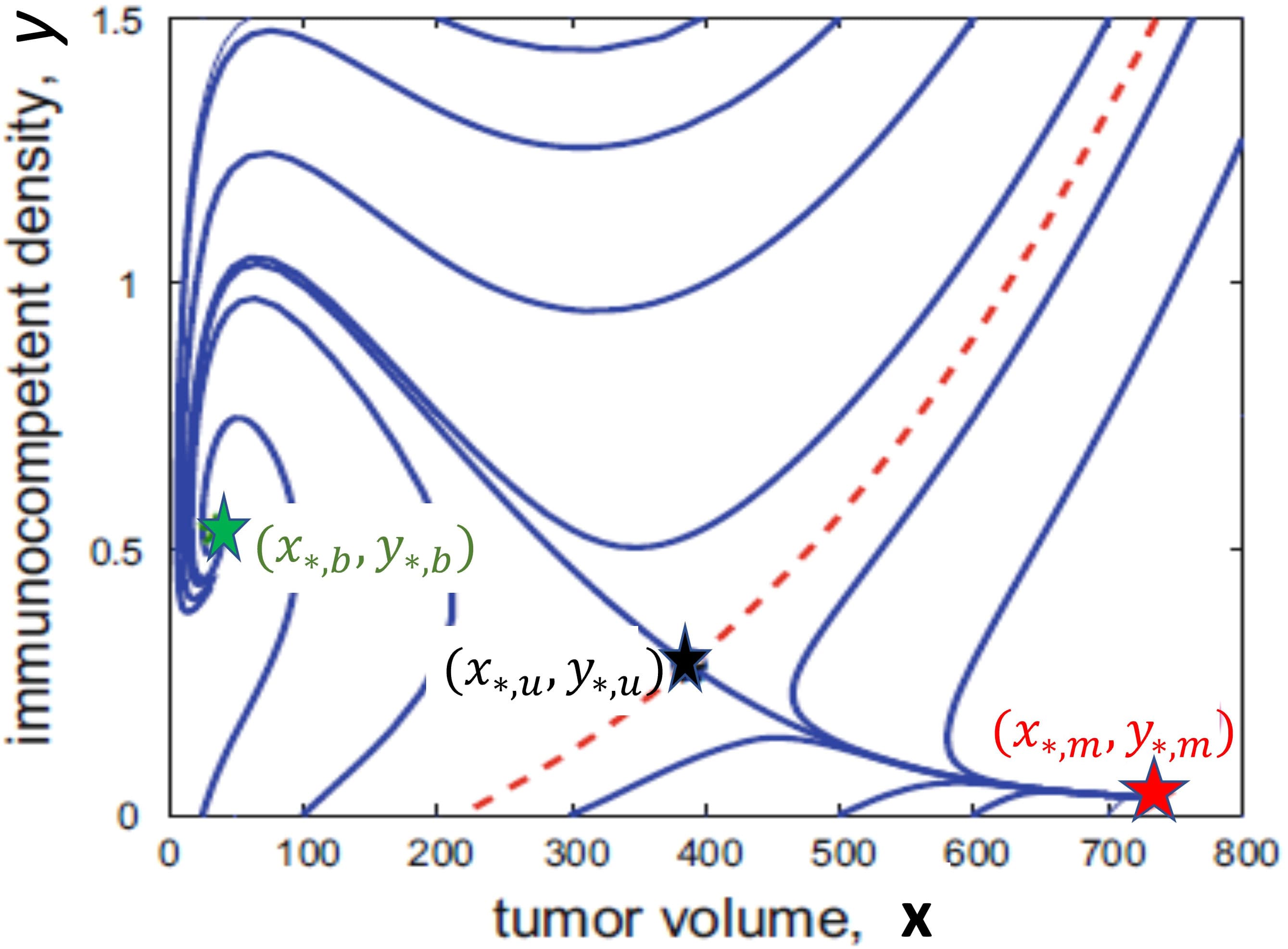
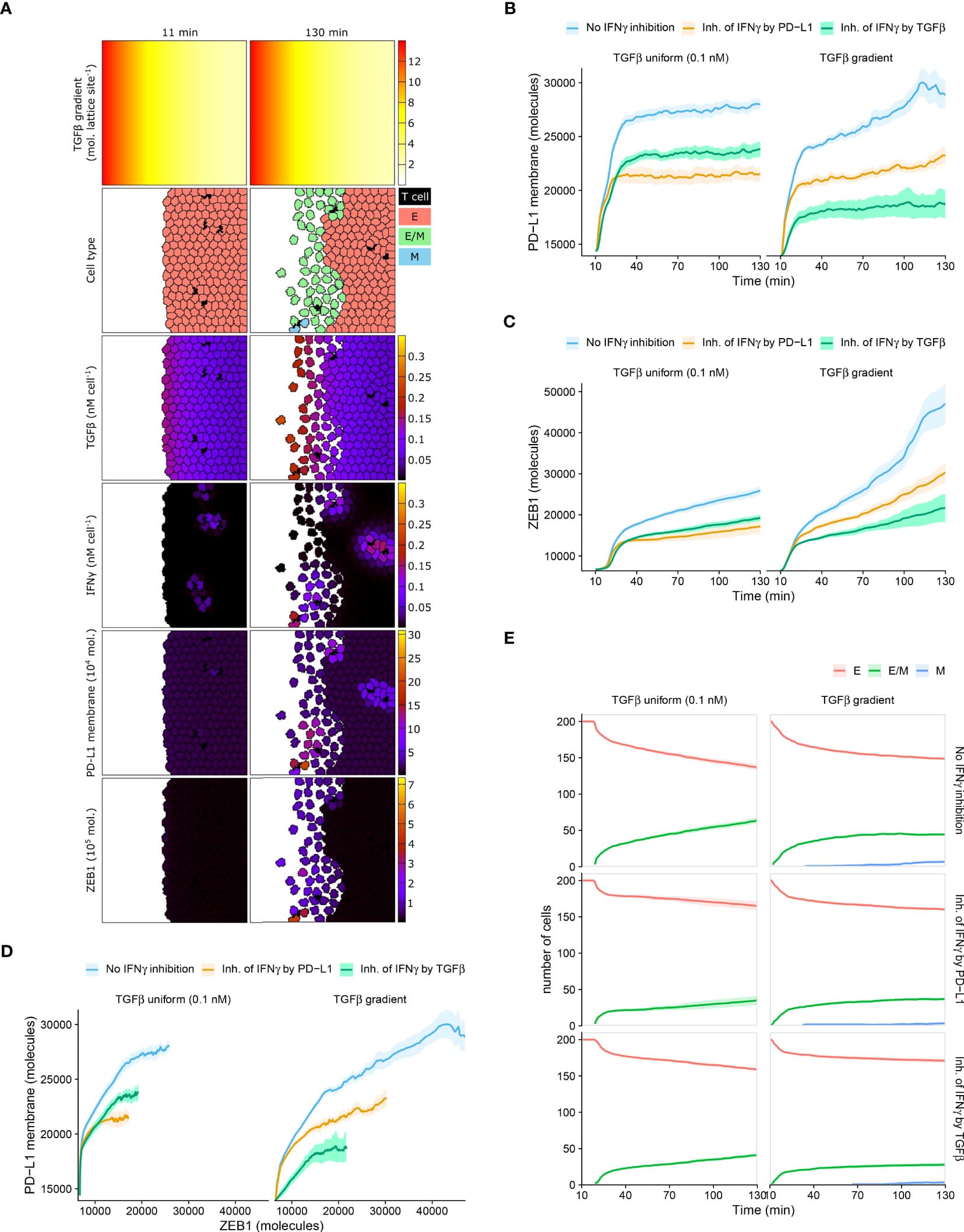
Introduction: Cancer combination treatments involving immunotherapies with targeted radiation therapy are at the forefront of treating cancers. However, dosing and scheduling of these therapies pose a challenge. Mathematical models provide a unique way of optimizing these therapies.

Methods: Using a preclinical model of multiple myeloma as an example, we demonstrate the capability of a mathematical model to combine these therapies to achieve maximum response, defined as delay in tumor growth. Data from mice studies with targeted radionuclide therapy (TRT) and chimeric antigen receptor (CAR)-T cell monotherapies and combinations with different intervals between them was used to calibrate mathematical model parameters. The dependence of progression-free survival (PFS), overall survival (OS), and the time to minimum tumor burden on dosing and scheduling was evaluated. Different dosing and scheduling schemes were evaluated to maximize the PFS and optimize timings of TRT and CAR-T cell therapies.

Results: Therapy intervals that were too close or too far apart are shown to be detrimental to the therapeutic efficacy, as TRT too close to CAR-T cell therapy results in radiation related CAR-T cell killing while the therapies being too far apart result in tumor regrowth, negatively impacting tumor control and survival. We show that splitting a dose of TRT or CAR-T cells when administered in combination is advantageous only if the first therapy delivered can produce a significant benefit as a monotherapy.

Discussion: Mathematical models are crucial tools for optimizing the delivery of cancer combination therapy regimens with application along the lines of achieving cure, maximizing survival or minimizing toxicity.