- 1Faculty of Built Environment, University of New South Wales, Sydney, NSW, Australia
- 2Faculty of Engineering and Information Technologies, School of Civil Engineering, University of Sydney, Sydney, NSW, Australia
A key decision in the design of urban lighting is the location of the luminaries that are used to illuminate the specified region. The decision needs to account for coverage requirements identified in certain areas, based on safety considerations and nature of work activity, along with ensuring the cost effectiveness of the installation pattern adopted. In this work, a novel approach is presented via a multi-objective mathematical optimization model that results in a sustainable layout of light poles in urban region. A maximal coverage objective, with implicit demand cover, is formulated as a measure of the social requirement in urban lighting, which models security and safety associated with night-time lighting of the urban region. At the same time, the economical aspect of the layout is considered via minimizing the installation cost of the lighting layout. A realistic case example is then solved using the ϵ-constraint method. A Pareto optimal front for the case considered is constructed and analyzed.
Introduction
Light pollution is a considerable issue that is facing a significant number of cities around the world (Meier et al., 2014). This is mainly attributed to the changes in the life styles of people, induced by higher urbanization rates, leading to increased night-time activity (Talbot, 2007; Shaw, 2014).
The use of public lighting in cities is crucial to enhance the quality of life for humans (Brandi and Geissmar, 2007). Sufficient outdoor night time lighting is associated with increased security (Loomis et al., 2002), safety (Johansson et al., 2011) and economic development of the underlying urban region (Brons et al., 2008). Road lighting has been linked to increased driver and pedestrian safety (Wanvik, 2009; Stoker et al., 2015). Lighting is also often used for decorative purposes to promote a touristic vibe and attract more people, hence leading to enhanced night-time economy (Heath, 1997; Guo et al., 2011). Retailers use lighting to provide signage, and architects adopt it to enhance certain architectural features of a building during night-time (Rea, 2000). With all the advantages and benefits that night-time lighting offers to an urban setting, there are collateral effects that also need to be accounted for. These negative impacts are a result of light pollution, creating a nuisance due to excessive lighting that falls outside its designated zone (Bennie et al., 2014). Poorly designed night-time lighting arrangements can create discomfort glare, where an instinctive desire to look away from the direction of the light source results, or disability glare, where the inter-reflection of light within the eyeball reduces the ability of humans to distinguish between the task and glare source (Narisada and Schreuder, 2004). Serious medical conditions, including diseases such as breast cancer (Touitou et al., 2017) have also been associated with excessive exposure to night-time light pollution. Impacts of light pollutions are not only restricted to affecting human behavior, as wildlife can also be intensely influenced (Truscott et al., 2017). For instance, the available literature reveals the detrimental effect of night-time lighting on bird species (Ouyang et al., 2017).
Intelligent light systems or energy efficient lighting, such as the use of LED (Beatley, 2007; Cellucci et al., 2015; Villa et al., 2017) have been reported as a sustainable measure that minimizes energy consumption along with total economic costs associated with urban area lighting (Khatavkar et al., 2017; Mahoor et al., 2017). When considering the arrangement of light-poles in urban regions that illuminate the area under consideration, it is necessary that public and private interests are balanced out.
On closer inspection, it becomes evident that in many urban areas, the use of night-time lighting is excessive, leading to wasteful lighting that contributes to the light pollution issues faced (Maithili et al., 2017). The wasteful light also results in excessive energy consumption and thus reflects negatively on the environment (Galvão et al., 2015). Therefore, a sustainable solution is needed to help ensure an adequate level of lighting that minimizes the intrusiveness associated with lighting, while at the same time avoiding the over dimming of cities during night-time which can lead to economical downfalls along with safety concerns (Brands et al., 2015). To achieve this, this paper proposes a novel approach that is based on a mathematical optimization model for optimizing the arrangement of urban lighting. In particular, the proposed model addresses the social aspect of urban lighting arrangements through the sustained coverage of areas, hence ensuring security and safety requirements at night-time are satisfied. In addition, the economic aspect is also accounted for via minimizing the installation cost associated with the lighting layout arrangement.
Background
Prior to discussing the literature on optimizing the lighting layout, a couple of “light-specific” terms are defined. Luminance, which is measured in candela per square meter, describes the amount of lighting that is reflected off a given surface. Illuminance on the other hand describes the measurement of the amount of light that falls onto a given surface; it is measured in lux (Schreuder, 2008).
Even though several studies exist in the literature that examine the optimization of lighting operations, very few focus on a sustainable lighting layout in urban regions that strikes a balance between the economic, social and environmental objectives of sustainability, simultaneously. Genetic algorithms were deployed to optimize the design of office lighting in order to maximize energy efficiency while satisfying visual requirements for workers (Cassol et al., 2011). Lighting installation that balanced luminance, illuminance and glare was also proposed through an optimization approach (Yoshizawa and Kanematsu, 2010). Sport field lighting was optimized by ensuring a lighting arrangement associated with a uniform light distribution that satisfied the illuminance requirements (Corcione and Fontana, 2003). A multi-objective approach that optimizes the installation of lighting, taking into account user preferences, was presented by Villa and Labayrade (2013). There is however not much focus on optimizing the layout of lighting in urban regions such that sustainability pillars, including social, environmental or economical aspects are simultaneously considered.
To fill in the gap, this paper presents a novel approach that is based on a mathematical optimization model for solving the urban light location problem (ULLP) proposed in this study. The novelty of this research lies in the integration of 2 important sustainability criteria which are highly relevant in the planning of the lighting requirements in an urban region, namely safety, through sufficient lighting coverage of the zone, and the economic cost involved, through minimizing installation costs. The importance of adequate lighting in terms of deterring crime and reducing crime rates in cities has been reported in Arvate et al. (2017), Doleac and Sanders (2015), and Xu et al. (2018). In addition, a balance needs to be achieved between the lighting arrangement utilized to maximize the areas that are lit, and the cost of the installation procedure involved in order to stay within a reasonable monetary budget constraining the local planning authorities. As a result, another novelty in the proposed approach is the use of a multi-objective mathematical optimization model which relies on an integrated location-coverage problem in order to achieve an optimized solution that results in a trade-off between the considered criteria. The use of the model allows for optimizing the arrangement of urban lighting in a sustainable fashion. Both objectives formulated will be shown to be conflicting with the simultaneous optimization of both functions leading to a Pareto front from which sustainable solutions can be obtained.
This paper is organized as follows: in the next section, the notion of multi-objective optimization is presented. The problem description is then provided, along with the framework proposed for solving the ULLP. A binary integer programming (BIP) model proposed for the ULLP is then formulated. The paper then describes the applications of the model on a realistic case example where the problem is solved via a mono and multi-objective approach. Insights and concluding remarks are presented at the end.
Multi-Objective Optimisation
Applications of multi-objective optimization are wide and varied in the built environment (Wang et al., 2005; Asadi et al., 2012; Fesanghary et al., 2012; Hammad et al., 2015, 2016,a,b) and urban design fields (Bowerman et al., 1995; Hammad et al., 2017a,b, 2018). As opposed to single/mono objective optimization, multi-objective optimization involves more than one objective function being optimized. As a result, instead of searching for a single solution that minimizes all functions, the concept of Pareto optimality (Censor, 1977) is adopted. In particular, Pareto optimality relies on establishing a trade-off between all considered objectives. Formally, the concept of Pareto optimality can be stated as follows:
Assuming a minimization problem, a solution of a multi-objective optimization problem, z* is Pareto optimal if there does not exist another feasible solution such that and for at least one index m∈O, where O is the set of objective functions solved in the multi-objective problem.
The concept of Pareto optimality is adopted in this paper in order to solve the proposed multi-objective ULLP. A description of the ULLP is provided next.
Problem Description
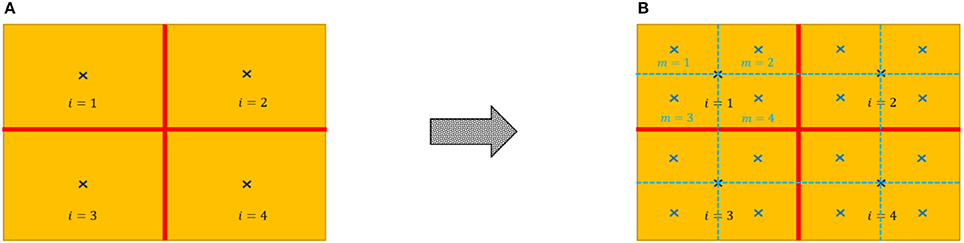
The ULLP can be described as follows. Assume that the urban region being considered is a planar area, which can be divided into zones, Figure 1A, to accommodate differing lighting requirements across the region. The main goal is to establish an optimal lighting layout across the planar area such that 2 objectives are considered: the first objective is to maximize the coverage of the lighting arrangement to ensure that the safety and security of the area during night-time is maximized. The second objective function deals with the cost of the lighting installation. In order to define the locations of the lighting poles to be placed in the region, a discretized version of the planar region is presented. In particular, a discretization procedure is proposed where the delineated area under consideration is divided into a grid based structure to outline the demand requirements for each zone within the urban region. Many examples of real-world location problems can be represented through a grid-based system (Noor-E-Alam et al., 2012). In the literature, these are referred to as grid-based location problems (Noor-E-Alam and Doucette, 2015).
Figure 1 displays the discretization procedure. Once the urban space is divided into a number of zones, where each zone is then represented by its centroid, i (Figure 1A), each zone is then further split into a number of grids, m (Figure 1B). In Figure 1B, only the girds belonging to Zone 1 (i = 1) are labeled for illustrative purposes. The number of grids needs to be determined via a trade-off between solution accuracy and computation expense; the greater the number of grids, the higher the accuracy of the solution, however, the more computation times that is needed to arrive at a solution. This is particularly important to consider since the ULLP examined is likely to be NP-hard due to the use of integer variables (Floudas, 1995; Daskin, 2011).
A number of assumptions are made: first, the lighting requirement of each zone is represented via a number positioned at the centroid of that zone. Second, in order to service a particular zone, the light pole installed needs to be placed within the grid division of that zone. Any light pole placed outside the zone does not contribute toward the coverage requirement of that respective zone. Third, the light poles are placed at the centroid of the girds. Fourth, for each grid, m, a heterogeneous distribution of light is assumed, modeled as a gradient of values, measured in lumens, rather than discrete points. As a result, the relationship of light demand is assumed such that each cell of the grid modeled can be represented by a single light value; an inter-relation between all values of neighboring cells is assumed. The computation of lighting supply at each grid is performed as a pre-processing step as will be explained later. In the next section, the framework utilized to solve the proposed ULLP is further expanded on.
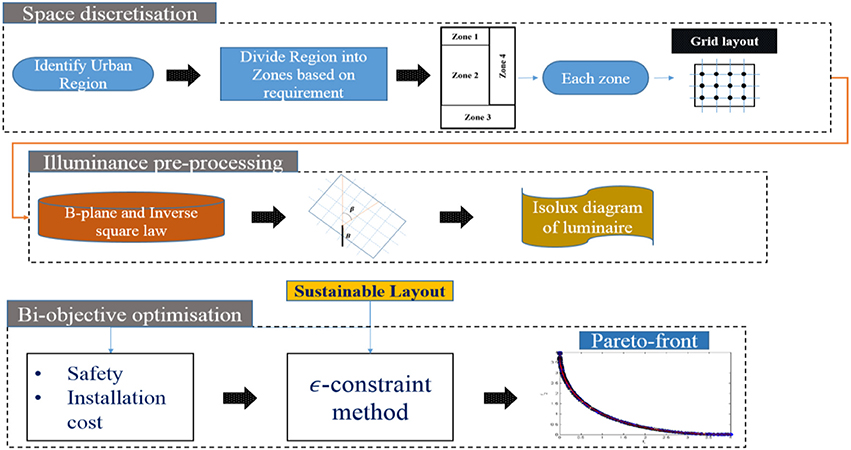
Framework
A framework is outlined in order to describe the process that is followed when solving the ULLP. The first component of the framework, labeled, Space discretization, has been explained via Figure 1 above. The division of the urban planar region into zones is necessary since each zone can have a separate lighting requirement depending on the nature of activities taking place within that zone. Security requirements for each zone is thus specific to that zone and hence the lighting coverage in that zone needs to be considered accordingly. The decision maker needs to decide on the trade-off between solution accuracy, in terms of the exact location of the lighting pole, and the computation effort required to yield a solution, in order to determine the grid spacing.
The second component of the framework, labeled Illumination pre-processing, computes the requirements of the illuminance level at each grid point of the discretized zone, due to placing the light-pole at the centroid of the grids. The computation of the illuminance levels is conducted in line with the requirements enlisted by the International Commission on Illumination (CIE, 2000). In order to reduce computational effort of the optimization problem, a pre-computation step is proposed to pre-process the supply of light that is generated by each positioned lighting pole. The following subsection explains the calculation procedure.
Pre-Computation of Supply of Light
The supply of light due to a pole placed on a grid within the urban zone will largely depend on the characteristics of the lighting fixture to be placed (i.e., lumen output from all luminaires within the light fixture, maintenance factors of the luminaires and atmospheric loss factors). Each lighting fixture is modeled as a source with a specific coverage; the coverage area is calculated based on the distribution of light. In order to model the distribution of light from a single source, an inverse relationship between the brightness of the light and the distance from the light source is utilized (Simons and Bean, 2008). To satisfy the demand requirements for a particular area, it is assumed that the coverage can be accumulated through provisions of requirements from a number of light sources. Each light source will therefore be responsible for the provision of a specified level of coverage to the zones requiring the lighting.
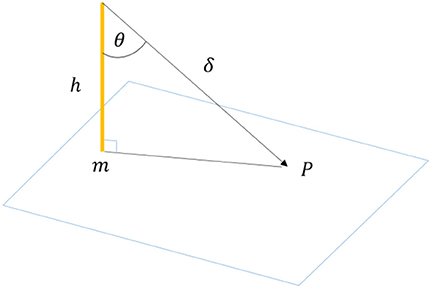
The light supply is calculated based on the lumen method (Rea, 2000). The set of light poles to be positioned is denoted as l ∈ L. Let Eml denote the illuminance in lx due to light pole l that is placed at grid point m, let δ denote the distance of the point illuminated from the source, m∈G, let θ denote the angle of the light from the normal, let h denote the perpendicular distance from the source to the plane and let denote the proportion of lamp flux reaching a specific area due to light source l; this is obtained from the I-tables/isolux diagram for the luminaire, l∈L being considered. The I-tables specify the luminous intensity in candela per 100 lamp lumens based on the B-planes of reference (CIE, 2011). Such I-tables can be obtained from manufacturers of luminaires.
Figure 3 is produced to denote some of the major parameters involved in the calculation of the light supply, measured as illuminance. Illuminance is based on the inverse square law which states that as the mounting height of the luminaire is doubled, the illumination level decreases to a quarter of the original value. Equation (1), which is derived based on the inverse square law, is used to pre-compute the illuminance level produced at the centroid of each zone due to light pole l placed at each of the grid points m∈G. This is then used to identify the percentage of coverage required in each zone, as specified by the light pole l.
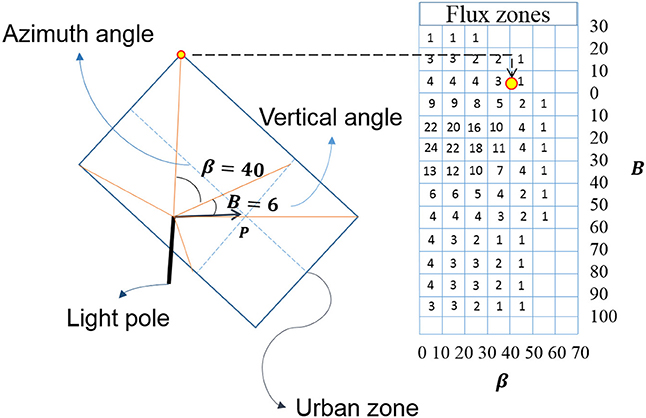
An example to demonstrate the calculation of the illuminance level based on the B-plane and the use of I-tables is given in Figure 4. Within the B-plane, the vertical angle is detonated as B while the azimuth angle is denoted as β. Once both of these angles for a single post have been determined, they are plotted on the isolux table shown in Figure 4 to obtain a measure of the level of illuminance at the point of interest P.
Mathematical Model
In this section, the set notation and formulations for the BIP mathematical optimization model proposed to solve the ULLP are described.
Set Notation
Sets:
i ∈ I: Urban zones that require certain level of lighting
m ∈ M: Set of grid cells that divide the urban region
l ∈ L: Light pole type to be installed.
k ∈ K: Set of all coverage levels, in ascending order of coverage (i.e., 60, 70, 80% etc.)
k ∈ Ri: Set of permitted coverage at zone i ∈ I
m ∈τ ikl: Set of grid points within urban region i ∈ I that produce a coverage level k∈Rifor light pole typel ∈ L, as determined from the pre-processing step of illuminance using the B-Plane
Parameters:
: Number of light poles l∈Lthat will produce a cover ofk∈K, as determined from the pre-processing step of illuminance using the B-Plane
ri: Critical level of providing coverage for region i ∈ I
Variables:
yik ∈ {0, 1}: Binary variable which equals 1 if urban area i ∈ I is covered at levelk ∈ K, and 0 otherwise.
zml ∈ {0, 1}: Binary variable which equals 1 if grid cellm ∈ M, contains light polel ∈ L, and 0 otherwise.
Objective Functions
Two objective functions are formulated in the model. The first objective function, Equation (2), assesses the coverage at each zone. In particular, it is formulated as a proxy to the level of safety and security of the zone. Equation (2) is maximized since maximizing the coverage through increasing the illumination levels results in less security threats (robbery, assault etc.) as demonstrated in previous literature (Bromley et al., 2000). The level of coverage, k, at each zone is desired to be maximized, since it is assumed that the maximum level of illuminance will create the highest level of safety during night-time.
The second objective function seeks to minimize the total cost of installation associated with the placement of the light poles. Different zones will have different installation requirements and hence the cost function,cml, across the zones of the urban region will differ.
Constraints
A number of constraints are defined in the ULLP in order to delineate the feasible region of the problem. The first constraint formulated, Equation (4) requires each zone to be covered up to a certain coverage level. Since each zone will have different lighting requirements, the set Ri is constructed and deployed in Equation (4) to ensure an appropriate selection of a level of coverage that suits the respective zone lighting requirement.
The second constraint, Equation (5), states that each grid cell within a defined zone can contain a maximum of 1 light pole.
The third constraint, Equation (6), specifies that if region i ∈ I is covered at levelk ∈ K, then there needs to be a minimum number of light poles located on grids m∈τikl that can achieve the level of coverage k ∈ K at regioni ∈ I. As previously stated, the set τikl is determined from the pre-processing step of illuminance, through calculating the light level while changing the location of the pole across all girds of the zone, utilizing the concept of the B-Plane in Figure 4. It is important to note that Equation (6) is formulated to allow for implicit coverage (Murray et al., 2010), where the lighting supplied to a zone, can be achieved through the accumulated coverage associated with several light poles located within that zone.
The set of constraints, Equations (7, 8) define the domain of the integer variables
Solution Approach
The ϵ-Constraint Approach
The ϵ-constraint approach is adopted to solve the multi-objective optimization problem. In its simplest form, the model reformulates the set of objective functions given so that one is optimized whilst the rest are executed as constraints (Chankong and Haimes, 2008). Since in this paper only 2 objective functions are considered, the transformation of the multi-objective objective model into a single objective problem is as shown below:
The coverage objective function is represented byf1(x)while the installation cost objective is defined byf2(x), where xis a vector of decision variables belonging to the set of feasible solutionsX, and is the optimum solution of the installation cost objective function, satisfying all k constraints, gu(x), specified for the two models (Ehrgott and Ruzika, 2008; Mavrotas, 2009). Each objective function is initially solved in a lexicographic fashion to obtain a payoff-off matrix, within which non-dominated solutions on the Pareto front are located. This payoff matrix is used to define the right hand side (RHS) of the objective function passed as a constraint. As a result, after obtaining the extreme points for each respective objective function on the Pareto frontier, the imposed restriction onf2(x) is relaxed gradually, where the parameter ε is incremented gradually.
Case Study
In order to demonstrate the applicability of the proposed model, a realistic case example is considered. An urban area composed of 9 regions, and located 70 km south-west from the City of Wollongong in New South Wales, Australia, is proposed to be a commercial and touristic hub. The divisions of the 9 regions is displayed in Figure 5.
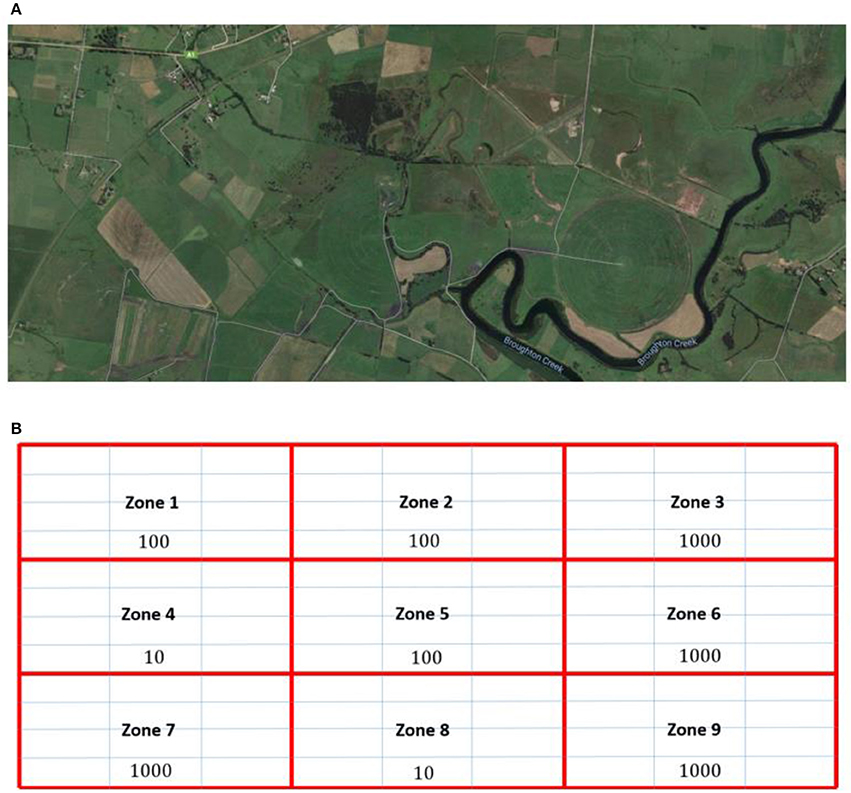
Figure 5. (A) Case example considered; and (B) The distribution of zones and the gird cell discretization for the case study examined. Number in each zone indicate the relative importance of lighting in the zone, with 10 being the least important and 1,000 being the most important.
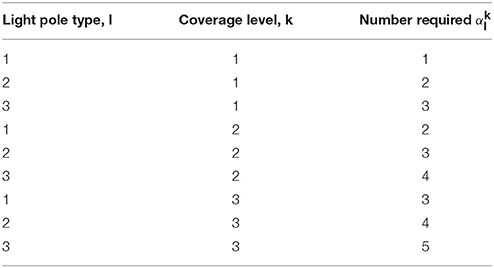
Three levels of coverage are considered for the lighting namely 1 (60% coverage), 2 (80% coverage) and 3 (100% coverage). Three types of light poles are assumed. The number of each light pole type required to produce the specified level of coverage is given in Table 1. Table 2 displays the lighting requirment in each zone.
In order to construct the set Ri, the importance of lighting for each zone is specifed as shown in Figure 5 (10 the lowest, meaning that low coverage is required, and 1000 the highest, meaning that high lighting coverage is necessary at the zone).
The case example of Figure 5 is solved through 2 approaches: in the 1st approach, the problem is solved by focusing only on a single objective function, namely the coverage objective function, Equation (2). The second approach involves introducing the light installation cost and solving the problem as a multi-objetive optimisation problem through the ϵ-constraint method.
Mono-Obejctive Maximal Coverage
Solving the problem where only coverage maximization is formulated as an objective function, with no limit on the number of light poles that can be used, and having the requirement of ensuring coverage to all areas of the urban region, results in a distribution as is displayed in Figure 6. The distribution is one which is uniform, with all zones being supplied at the maximum level of lighting, 150 lx. Installation costs associated with the maximal coverage distribution is $1,140,505. The use of a maximal coverage problem without introducing a limit on wasted lighting through economic cost consideration therefore results in an expensive layout of light-poles.

Figure 6. Distribution of lighting around the urban region where maximal coverage is ensured, with black indicating 150 lx of lighting in the zones of the region.
In terms of security, the impact of the distribution shown in Figure 6 is that since all regions within the urban area are lit at the brightest level, it is expected that crime rates will be lower at night-time, based on the correlation that is evident in the literature between reduced crime rates and well-lit areas in cities (Xu et al., 2018). Economically, the solution presented in Figure 6 is not viable since the solution procedure that yielded the distribution depicted does not account for budget concerns; this will be a major factor for urban planners and local councils when it comes to deciding on street lighting.
The problem is re-solved, where this time a limit of 9 light poles is placed through introducing the following constraint to the model, Equation (9):
The resulting distribution of lighting is shown in Figure 7. As can be noticed, light poles are installed only in zones where the relative importance of lighting associated with the zone is set at a high level, namely zones 3, 6, 7, and 9. Most zones are left without lighting, since only a limited number of light poles are available. The relative importance of each zone in terms of lighting requirement will typically be based on the specifications for safety and work activity (i.e., a shopping district), as determined by the governing local authority.
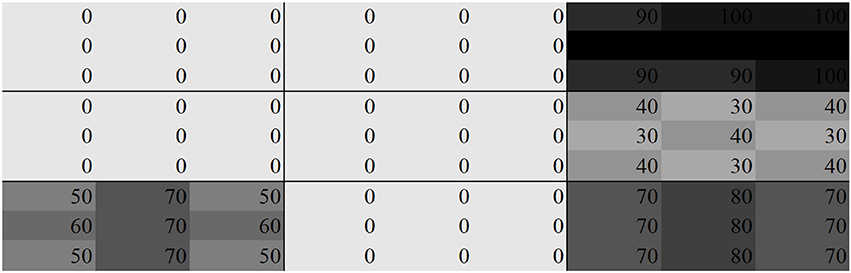
Figure 7. Distribution of illuminance around the urban region where a limit is placed on number of lighting.
Multi-Objective Results
The Pareto optimal front yielded through solving the problem via the ϵ-constraint method is shown in Figure 8. It is important to note that when solving the multi-objective ULLP, no limit is placed on the number of light poles that can be utlised. A clear trade-off between light coverage and light installation is evident; at the maximum level of total light flux in the region, 700 lx, the assessed light installation of the region is given as about $1,156,383 (Point A), whereas for a lower level of permited light flux, 400 lx, the cost associated is given as $413,842 (Point B).
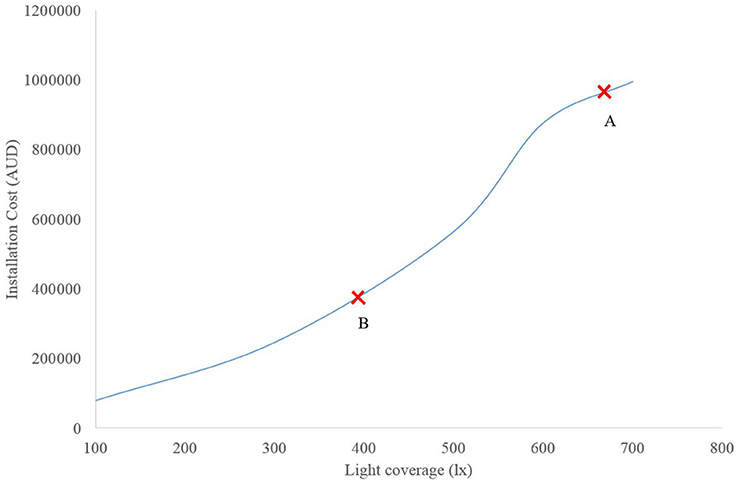
Figure 8. Pareto Optimal front. Point A is one where cost installation is less emphasized, compared to Point B.
One of the Pareto optimal solutions is presented in Figure 9, (see Point A on Figure 8). The model positions light poles that produce the required coverage level at each zone. Compared to Figure 7, the distribution is lower throughout the region since the coverage is only set at the required level in each zone of the urban region; this is due to the economic cost objective function which prevents the model from utilizing the maximum level of lighting at each zone. As a result, solving the 2 conflicting objective functions simultaneously results in a light pole configuration where demand is satisfied while minimizing the waste due to oversupply in the zones of the urban region.
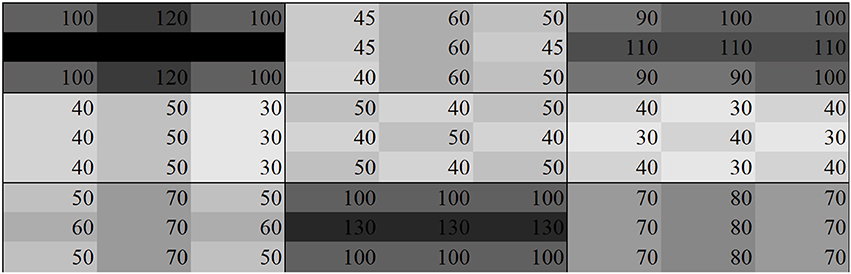
Figure 9. Distribution of illuminance based on maximized coverage levels around the zones, with little emphasis on light installation cost, Point A.
In Figure 10, the distribution that results is due to the increased influence of the light installation cost, through increasing the RHS of the ϵ-constraint function (See Point B in Figure 8).
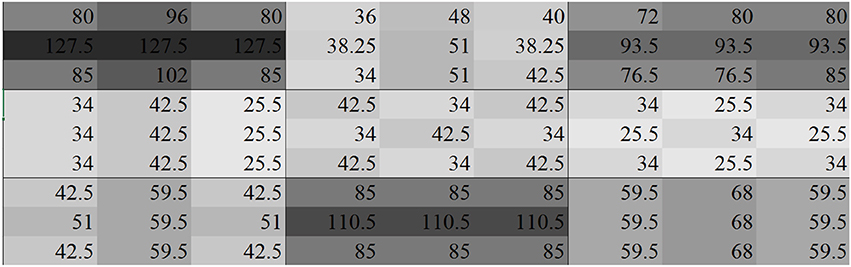
Figure 10. Distribution of illuminance based on maximized coverage levels around the zones, with greater influence of light installation cost on solution produced, Point B.
Compared to Figure 9, the overall illumination levels in each of the urban regions is now less. Even though the minimum level of coverage is satisfied in each zone, the brightness levels associated with each zone have dropped by around 15%. Given that the influence of installation cost of lighting has increased, less lighting is utilized, and so the coverage levels in each zone consequently drops.
Results of Figures 9, 10 are associated with an optimization model which is more economically viable since it considers the cost of locating the light poles. As such, the associated model can be adopted by governing authorities in order to align with budget requirements placed for lighting installation within the urban region.
Insights
A number of insights can be yielded from the proposed optimization model. First, the fact that social measures of lighting distribution around an urban region (i.e., increased security and safety due to well-lit regions) is an important consideration to account for when deciding on an installation pattern for lighting in urban regions, can be achieved through formulating the problem as an implicit coverage one. The coverage of each zone of the urban region is assumed as accumulative, with multiple lighting poles providing the required level of illumination specified for the given zones. Second, as the optimization results of Figures 6–10 revealed, when solving the ULLP, a multi-objective approach leads to a sustainable light distribution where wasted lighting is reduced, especially when increasing the influence of the installation cost on the optimization model. This is mainly due to the conflicting nature of the two objective functions modeled in this problem. Third, the average wasted light that is saved through utilizing a multi-objective approach was assessed to be on average 79% (Figure 6 vs. Figure 10) highlighting the importance of accounting for installation costs when solving the ULLP. Even though the installation objective is a pure economic cost function, solving the installation cost in conjunction with the coverage objective yields a sustainable solution that minimizes the wasted level of light supplied to the region, while ensuring that the illuminance level of the zones is kept at a sufficient level to maintain the safety of the area. This leads to the notion that the sustainability of lighting installation can be achieved through proper utilization of economic measures that ultimately lead to savings in social and environmental cost, in terms of excessive light pollution and wasted energy respectively.
Conclusion
This paper presented a mathematical optimization model for the sustainable location of light poles in urban regions. The model is based on a multi-objective approach, where coverage of the region under consideration is maximized in an attempt to satisfy security requirements, while the cost associated with installation of the lighting poles is minimized. Demand of the region is assumed as a priori input, and the supply of lighting is based on the luminaries utilized, which is calculated via a pre-processing step through use of the inverse square law and isolux diagrams obtained from luminaire manufacturers. The urban space is discretized into zones, with zones further divided into girds. Integer variables are then introduced to highlight where the light poles will be positioned in the urban space. The ϵ-constraitnt approach was adopted to yield the Pareto front. A clear trade-off between coverage and installation cost was highlighted. In addition, the use of a limit on the number of poles leads to a limited number of lights being installed in locations where the requirement for lighting is assessed to be critical. A distinction between solutions obtained using single vs. multiple optimization objective was also observed, with the introduction of the installation cost objective yielding an economic saving of 79% on average.
The proposed method finds applicability in many urban design related fields, including, street lighting, retail lighting and park lighting. The limitation of this work lies in the implicit modeling of light pollution, through accounting for social and environmental measures via only a single objective function that acts as a proxy (i.e., coverage objective function). Even though this yields a sustainable solution, as was demonstrated in this work, a further extension of this work can involve the formulation of a multi-objective optimization problem with additional objective functions that explicitly measure energy wasted and light pollution at each respective urban zone modeled. This can then be contrasted with the multi-objective approach introduced in this paper.
Author Contributions
AH performed the work involved in developing and implementing the optimization framework. AA contributed to problem definition and supervised the work conducted leading to the paper.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The reviewer, BH, declared a shared affiliation, with no collaboration, with one of the authors, AA, to the handling Editor.
References
Arvate, P., Falsete, F. O., Ribeiro, F. G., and Souza, A. P. (2017). Lighting and homicides: evaluating the effect of an electrification policy in rural brazil on violent crime reduction. J. Quant. Criminol. 1–32. doi: 10.1007/s10940-017-9365-6
Asadi, E., da Silva, M. G., Antunes, C. H., and Dias, L. (2012). Multi-objective optimization for building retrofit strategies: A model and an application. Energy Build. 44, 81–87. doi: 10.1016/j.enbuild.2011.10.016
Beatley, T. (2007). Envisioning solar cities: urban futures powered by sustainable energy. J. Urban Technol. 14, 31–46. doi: 10.1080/10630730701531682
Bennie, J., Davies, T. W., Duffy, J. P., Inger, R., and Gaston, K. J. (2014). Contrasting trends in light pollution across Europe based on satellite observed night time lights. Sci. Rep. 4:3789. doi: 10.1038/srep03789
Bowerman, R., Hall, B., and Calamai, P. (1995). A multi-objective optimization approach to urban school bus routing: Formulation and solution method. Transp. Res. Part Policy Pract. 29, 107–123. doi: 10.1016/0965-8564(94)E0006-U
Brandi, U., and Geissmar, C. (2007). Light for Cities: Lighting Design for Urban Spaces, a Handbook. Basel: Springer Science & Business Media.
Brands, J., Schwanen, T., and van Aalst, I. (2015). Fear of crime and affective ambiguities in the night-time economy. Urban Stud. 52, 439–455. doi: 10.1177/0042098013505652
Bromley, R., Thomas, C., and Millie, A. (2000). Exploring safety concerns in the night-time city: revitalising the evening economy. Town Plan. Rev. 71:71. doi: 10.3828/tpr.71.1.rnk3336381678247
Brons, J., Bullough, J., and Rea, M. (2008). Outdoor site-lighting performance: a comprehensive and quantitative framework for assessing light pollution. Light. Res. Technol. 40, 201–224. doi: 10.1177/1477153508094059
Cassol, F., Schneider, P. S., França, F. H. R., and Silva Neto, A. J. (2011). Multi-objective optimization as a new approach to illumination design of interior spaces. Build. Environ. 46, 331–338. doi: 10.1016/j.buildenv.2010.07.028
Cellucci, L., Burattini, C., Drakou, D., Gugliermetti, F., Bisegna, F., Vollaro, A., et al. (2015). Urban lighting project for a small town: Comparing citizens and authority benefits. Sustainability 7, 14230–14244. doi: 10.3390/su71014230
Chankong, V., and Haimes, Y. Y. (2008). Multiobjective Decision Making: Theory and Methodology. New York, NY; North Holland.
CIE (2011). International Lighting Vocabulary (No. CIES 017). Paris: Commission Internationale de l'Éclairage.
Corcione, M., and Fontana, L. (2003). Optimal design of outdoor lighting systems by genetic algorithms. Light. Res. Technol. 35, 261–277. doi: 10.1191/1365782803li068oa
Daskin, M. S. (2011). Network and Discrete Location: Models, Algorithms, and Applications. New Jersey: John Wiley & Sons.
Doleac, J. L., and Sanders, N. J. (2015). Under the cover of darkness: how ambient light influences criminal activity. Rev. Econ. Stat. 97, 1093–1103. doi: 10.1162/REST_a_00547
Ehrgott, M., and Ruzika, S. (2008). Improved e-constraint method for multiobjective programming. J. Optim. Theory Appl. 138, 375–396. doi: 10.1007/s10957-008-9394-2
Fesanghary, M., Asadi, S., and Geem, Z. W. (2012). Design of low-emission and energy-efficient residential buildings using a multi-objective optimization algorithm. Build. Environ. 49, 245–250. doi: 10.1016/j.buildenv.2011.09.030
Floudas, C. A. (1995). Nonlinear and Mixed-Integer Optimization: Fundamentals and Applications: Fundamentals and Applications. Oxford: Oxford University Press.
Galvão, J. R., Moreira, L. M., Ascenso, R. M. T., and Leitão, S. A. (2015). “Energy systems models for efficiency towards Smart Cities,” in: IEEE EUROCON 2015-International Conference on Computer as a Tool (EUROCON) (Lisbon), 1–6.
Guo, Q., Lin, M., Meng, J., and Zhao, J. (2011). The development of urban night tourism based on the nightscape lighting projects–a Case Study of Guangzhou. Energy Procedia 2010 5, 477–481. doi: 10.1016/j.egypro.2011.03.083
Hammad, A., Akbarnezhad, A., and Rey, D. (2016). “A Multi-Objective Mixed Integer Programming Model for Minimising Obtrusive Effects and Installation Costs of Night-time Lighting on Construction Sites,” in International Symposium on Automation and Robotics in Construction (Auburn, AL).
Hammad, A., Akbarnezhad, A., Rey, D., and Waller, S. (2015). A computational method for estimating travel frequencies in site layout planning. J. Constr. Eng. Manag. 142. doi: 10.1061/(ASCE)CO.1943-7862.0001086
Hammad, A. W. A., Akbarnezhad, A., and Rey, D. (2016a). A multi-objective mixed integer nonlinear programming model for construction site layout planning to minimise noise pollution and transport costs. Autom. Constr. 61, 73–85. doi: 10.1016/j.autcon.2015.10.010
Hammad, A. W. A., Akbarnezhad, A., and Rey, D. (2017a). Bilevel mixed-integer linear programming model for solving the single airport location problem. J. Comput. Civ. Eng. 31:6017001. doi: 10.1061/(ASCE)CP.1943-5487.0000697
Hammad, A. W. A., Akbarnezhad, A., and Rey, D. (2017b). Sustainable urban facility location: minimising noise pollution and network congestion. Transp. Res. E Logist. Transp. Rev. 107, 38–59. doi: 10.1016/j.tre.2017.09.005
Hammad, A. W., Akbarnezhad, A., and Rey, D. (2016b). “Accounting for noise pollution in planning of smart cities,” in Smart Cities as a Solution for Reducing Urban Waste and Pollution, ed Goh Bee Hua (IGI Global), 149–196.
Hammad, A. W. A., Rey, D., and Akbarnezhad, A. (2018). “A bi-level mixed integer programming model to solve the multi-servicing facility location problem, minimising negative impacts due to an existing semi-obnoxious facility,” in Data and Decision Sciences in Action, Lecture Notes in Management and Industrial Engineering. (Cham: Springer), 381–395.
Heath, T. (1997). The twenty-four hour city concept—A review of initiatives in British cities. J. Urban Des. 2, 193–204.
Johansson, M., Rosén, M., and Küller, R. (2011). Individual factors influencing the assessment of the outdoor lighting of an urban footpath. Light. Res. Technol. 43, 31–43. doi: 10.1177/1477153510370757
Khatavkar, N., Naik, A. A., and Kadam, B. (2017). “Energy efficient street light controller for smart cities,” in 2017 International Conference on Microelectronic Devices, Circuits and Systems (ICMDCS) (Vellore), 1–6.
Loomis, D., Marshall, S. W., Wolf, S. H., Runyan, C. W., and Butts, J. D. (2002). Effectiveness of safety measures recommended for prevention of workplace homicide. JAMA 287, 1011–1017. doi: 10.1001/jama.287.8.1011
Mahoor, M., Salmasi, F. R., and Najafabadi, T. A. (2017). A hierarchical smart street lighting system with brute-force energy optimization. IEEE Sens. J. 17, 2871–2879. doi: 10.1109/JSEN.2017.2684240
Maithili, P., Sharmitha, D., Vigneshwaran, R., Jeganath, R., and Suresh, M. (2017). “Energy efficient and eco-friendly street lighting,” in 2017 International Conference on Innovations in Green Energy and Healthcare Technologies (IGEHT) (Coimbatore), 1–5. doi: 10.1109/IGEHT.2017.8094067
Mavrotas, G. (2009). Effective implementation of the ε-constraint method in Multi-Objective Mathematical Programming problems. Appl. Math. Comput. 213, 455–465. doi: 10.1016/j.amc.2009.03.037
Meier, J., Hasenöhrl, U., Krause, K., and Pottharst, M. (2014). Urban Lighting, Light Pollution and Society. New York, NY: Routledge.
Murray, A. T., Tong, D., and Kim, K. (2010). Enhancing classic coverage location models. Int. Reg. Sci. Rev. 33, 115–133. doi: 10.1177/0160017609340149
Narisada, K., and Schreuder, D. (2004). Light Pollution Handbook. Groningen: Springer Science & Business Media.
Noor-E-Alam, M., and Doucette, J. (2015). Solving large-scale fixed cost integer linear programming models for grid-based location problems with heuristic techniques. Eng. Optim. 47, 1085–1106. doi: 10.1080/0305215X.2014.947973
Noor-E-Alam, M., Mah, A., and Doucette, J. (2012). Integer linear programming models for grid-based light post location problem. Eur. J. Oper. Res. 222, 17–30. doi: 10.1016/j.ejor.2012.04.032
Ouyang, J. Q., Jong, M., Grunsven, R. H. A., Matson Kevin, D., Haussmann Mark, F., Meerlo, P., et al. (2017). Restless roosts: Light pollution affects behavior, sleep, and physiology in a free-living songbird. Glob. Change Biol. 23, 4987–4994. doi: 10.1111/gcb.13756
Rea, M. S. (2000). The IESNA Lighting Handbook: Reference & Application. New York, NY: Illuminating Engineering Society of North America.
Schreuder, D. (2008). Outdoor Lighting: Physics, Vision and Perception. Leidschendam: Springer Science & Business Media.
Shaw, R. (2014). Beyond night-time economy: affective atmospheres of the urban night. Geoforum 51, 87–95. doi: 10.1016/j.geoforum.2013.10.005
Simons, R. H., and Bean, A. R. (2008). Lighting Engineering : Applied Calculations. Jordan Hill: Taylor and Francis.
Stoker, P., Garfinkel-Castro, A., Khayesi, M., Odero, W., Mwangi, M. N., Peden, M., et al. (2015). Pedestrian safety and the built environment: a review of the risk factors. J. Plan. Lit. 30, 377–392. doi: 10.1177/0885412215595438
Talbot, D. (2007). Regulating the Night: Race, Culture and Exclusion in the Making of the Night-time Economy. London: Routledge.
Touitou, Y., Reinberg, A., and Touitou, D. (2017). Association between light at night, melatonin secretion, sleep deprivation, and the internal clock: Health impacts and mechanisms of circadian disruption. Life Sci. 173, 94–106. doi: 10.1016/j.lfs.2017.02.008
Truscott, Z., Booth, D. T., and Limpus, C. J. (2017). The effect of on-shore light pollution on sea-turtle hatchlings commencing their off-shore swim. Wildl. Res. 44, 127–134. doi: 10.1071/WR16143
Villa, C., Bremond, R., and Saint-Jacques, E. (2017). Assessment of pedestrian discomfort glare from urban LED lighting, assessment of pedestrian discomfort glare from urban LED lighting. Light. Res. Technol. 49, 147–172. doi: 10.1177/1477153516673402
Villa, C., and Labayrade, R. (2013). Multi-objective optimisation of lighting installations taking into account user preferences–a pilot study. Light. Res. Technol. 45, 176–196. doi: 10.1177/1477153511435629
Wang, W., Zmeureanu, R., and Rivard, H. (2005). Applying multi-objective genetic algorithms in green building design optimization. Build. Environ. 40, 1512–1525. doi: 10.1016/j.buildenv.2004.11.017
Wanvik, P. O. (2009). Effects of road lighting: An analysis based on Dutch accident statistics 1987–2006. Accid. Anal. Prev. 41, 123–128. doi: 10.1016/j.aap.2008.10.003
Keywords: binary integer programming, location theory, sustainable urban lighting, multi-objective optimization, urban lighting, sustainable lighting layout
Citation: Hammad AWA and Akbarnezhad A (2018) Sustainable Lighting Layout in Urban Areas: Maximizing Implicit Coverage and Minimizing Installation Cost. Front. Built Environ. 4:42. doi: 10.3389/fbuil.2018.00042
Received: 21 April 2018; Accepted: 23 July 2018;
Published: 10 August 2018.
Edited by:
Onuegbu Ugwu, Federal University, Ndufu-Alike, NigeriaReviewed by:
Bao-Jie He, University of New South Wales, AustraliaAli Behnood, Purdue University, United States
Copyright © 2018 Hammad and Akbarnezhad. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ahmed W. A. Hammad, a.hammad@unsw.edu.au
 Ahmed W. A. Hammad
Ahmed W. A. Hammad Ali Akbarnezhad
Ali Akbarnezhad