- 1Institute for Advanced Biosciences, Keio University, Tsuruoka, Japan
- 2Systems Biology Program, Graduate School of Media and Governance, Keio University, Fujisawa, Japan
Living systems have the ability to adapt and self-organize when challenged with drastic environmental changes. The remarkable characteristic of plasticity and collectivity allow them to evolve and survive over billions of years in a rather unpredictable manner. Observing and studying the dynamic complexity have influenced many scientists across diverse disciplines to believe that living systems operate far from equilibrium and, hence, the second law of thermodynamics and ergodicity breaks down (Stuart, 1995; Prigogine, 1997). Therefore, it may not be feasible to develop simple deterministic models to interpret complex living systems' behavior.
Briefly, the second law of thermodynamics states that entropy in systems that are in equilibrium will increase over time or space. In other words, order will decrease in a thermodynamically equilibrium system where there is no exchange of matter or energy. Living systems, which constantly exchange matter and energy to the surroundings, can be considered to exist far from equilibrium to achieve biological order (Stuart, 1995). One appropriate example is the ability of bacteria to exchange pheromone during environmental threats, such as during antibiotic treatment, to form biofilms which are highly organized structures resistant to the therapeutic intervention (Chatterjee et al., 2013). The biofilm example demonstrates that the cooperative behavior of organisms can be very different to the individual response. Thus, using ergodic principle or predictive deterministic approaches to understand cellular behaviors can be questionable, and this issue has been debated from time to time.
Most biological experimentations of mammalian cells are performed in vitro, where cells from living tissues are removed from their physiological neighbors and regrown in minimum media that will support the morphology, survival, and growth of the cells. The number of cells used in different experiments, although variable, are usually several order of magnitudes lower than that in actual tissues or organs. Under such far from realistic laboratory conditions, are in vitro cells able to display emergent behaviors?
Remarkably, genome-wide oscillatory behaviors have been observed in continuously cultured laboratory yeast, and the mammalian circadian clocks have been reproduced in a plate (Klevecz et al., 2004; Sato et al., 2006). Although fascinating, the collective behaviors were achieved for limited periods under carefully controlled experimental conditions, such as the rate of aeration and agitation of fermenters, etc. Outside the specified range, the synchronization of cells fade. In a more recent effort, cultured, and self-assembling engineered human cardiac tissue created rhythmic heart beat that was highly similar to the human heart (Turnbull et al., 2014). Therefore, from these examples, it becomes conceivable that during in vitro laboratory experimentations, complex non-linear and self-organizing behaviors can still be achieved if the technical and environmental conditions are carefully and tightly managed to mimic the actual reality, considering the exchange of key matter between the surroundings.
Today, in the name of systems biology approaches, we have seen numerous works that have employed theoretical models to interpret and predict cellular responses. It is surprising to note that despite the complexity of living systems, numerous deterministic models have been rather successfully used to understand both linear and non-linear responses (Selvarajoo, 2014). A vast majority of cellular models are based on ordinary differential equations, mass-action kinetics, Michaelis–Menten kinetics or Boolean logics. In most circumstances, if not all, the investigations considered “closed” system modular approach, where the models did not include continuous exchange of materials between the internal and external environments and, hence, chemical and thermal equilibrium have been assumed. That is, the approaches often adopted well-mixed, homogenous and isothermal environment where each reaction in the cellular network is connected through first-order, higher-order mass-action, enzyme kinetic equations, or simply Boolean logics, depending on the knowledge gained for individual reaction.
Despite the simplicity, these models, combined with experimental verifications, have progressed our understanding of several complex mechanisms controlling cell processes. For example, the elucidation of distinct feedback mechanisms in epidermal- and nerve- growth factor signaling utilizing the same MAP kinases module (Santos et al., 2007), and the identification of key target for enhancement of apoptosis in cancers (Piras et al., 2011; Hayashi et al., 2015). In several other studies, even without the need to know graded response, simple binary (ON/OFF) state approaches utilizing discrete Boolean network modeling have produced insightful results in understanding diseases processes (Benenson et al., 2004; Zhang et al., 2008; Schlatter et al., 2009). More recently, even immune cell divisions based on main and co-stimuli have induced responses that can be shown to be linear functions of their signaling components (Hawkins et al., 2013; Marchingo et al., 2014). So, if deterministic and rule-based models can be applied successfully using in vitro dataset, does it indicate that ergodic hypothesis could hold in 2-D plated cell cultures? That is, under the conditions where simple models work, are cells experiencing thermodynamic equilibrium?
Here, it is noteworthy to give some examples from our research on analyzing in vitro large scale time-series gene expressions dataset of mammalian innate and adaptive immune cell types to distinct environmental stimulations (Tsuchiya et al., 2009; Selvarajoo and Giuliani, 2012; Simeoni et al., 2015). Using simple statistical approaches of Pearson/Spearman correlations, Shannon entropy, Mutual Information and noise (squared coefficient of variation), in summary, we found that these metrics changed from an initial value at stimulation to achieve stable values at later times. More precisely, we noticed the levels of transcriptome-wide expression disorder increased after appropriate immune stimulation, and eventually reached asymptotic values. (This can be analogous to a tiny drop of ink added to water will show increasing disorder in color, and eventually stabilizes). In another recent study (Piras et al., 2014), on tracking transcriptome-wide variability in mammalian developmental cells, we also observed the increase in gene expressions disorder across the developmental process, reaching stable values at later stages (Figure 1). The observations from these in vitro studies indicate that cultured cells with fixed stimulation and condition may be reaching a state that is indicative of pseudo equilibrium.
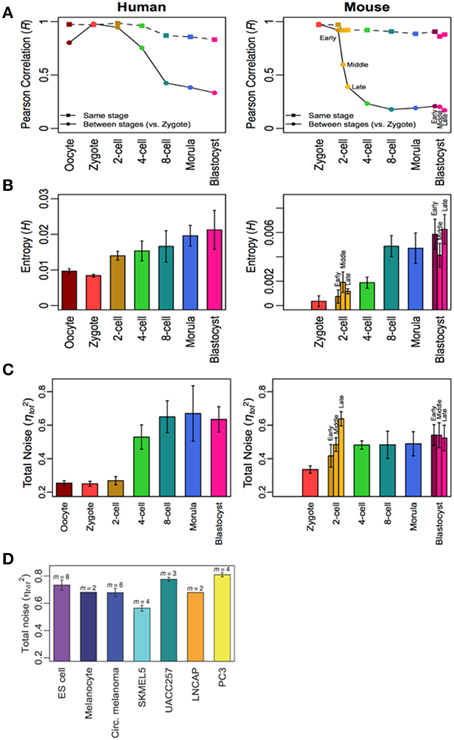
Figure 1. Increasing transcriptome-wide disorder for human and mouse development cells. (A) Pearson correlation, (B) Shannon entropy, and (C) noise from oocyte to blastocysts indicate increasing disorder which stabilizes, and is similar to other differentiated and cancer cells (D). Figure adapted from Piras et al. (2014).
On a different note, we monitored the transcriptome-wide expression variability from single cells to cell population in increasing ensemble sizes across six mammalian cell types (Piras and Selvarajoo, 2015). We observed that while increasing cell ensemble size, transcriptome-wide noise reduced approximately following the law of large numbers. Furthermore, the entire gene expressions of cell populations (and only the highly expressed portion of single cells) followed the central limit theorem. More simply, unlike single cells, which are probably more vulnerable to stochastic noise (Elowitz et al., 2002; Selvarajoo, 2012), cell populations showed reduced transcriptome-wide noise. It is, therefore, conceivable that deterministic rules can be utilized and modeled for the stable population-wide average response. However, for single cell responses stochastic modeling have been shown to be most appropriate, consider the investigations on bistable cell fates in bacteria (Dubnau and Losick, 2006). Nevertheless, both single cell stochastic and population-wide deterministic modeling based on in vitro data exclude or disregard the exchange of matter between other diverse cell types or the natural environment. This is especially important for multicellular organisms, where information is constantly exchanged within the entire system.
To summarize, it has been debated for a long time whether living systems can be mathematically conceptualized using simple theories as they possess very complex dynamic and emergent behaviors, and many times display unpredictable outcomes. Interestingly, certain self-organizing and non-ergodic behaviors have been observed even in laboratory conditions. In the case of an oscillating system, we can set up experiments and define conditions to mimic in vivo-like response of molecular dynamics. Whereas, in other situations, it may be very difficult to define experimental conditions that consider far from thermodynamic equilibrium phenomenon observed in self-organizing in vivo systems. Under such conditions, simple statistical techniques on large-scale time series omics dataset can be used to monitor multi-dimensional entropy and variability that could provide hints into the global state of the system (Piras et al., 2014). Notably, we have highlighted that tracking the global responses of living cells, in vitro, have shown a general increase in entropy and variability from initial values, which stabilize at higher levels at later time points. Under such stabilizing entropy condition, it is our opinion that deterministic models can continue to play vital roles for in vitro studies. Nevertheless, for in vivo systems, the rules for self-organization require further investigations (Stuart, 1995), especially for multi-cellular organisms considering the exchange of matter between different cell types. Knowing this will allow us to better predict the emergent properties of the “real” living systems.
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The author acknowledges the research fund of Tsuruoka City, Yamagata Prefecture and the JSPS Grants-in-Aid for Scientific Research FX132008K3.
References
Benenson, Y., Gil, B., Ben-Dor, U., Adar, R., and Shapiro, E. (2004). An autonomous molecular computer for logical control of gene expression. Nature 429, 423–429. doi: 10.1038/nature02551
Chatterjee, A., Cook, L. C., Shu, C. C., Chen, Y., Manias, D. A., Ramkrishna, D., et al. (2013). Antagonistic self-sensing and mate-sensing signaling controls antibiotic-resistance transfer. Proc. Natl. Acad. Sci. U.S.A. 110, 7086–7090. doi: 10.1073/pnas.1212256110
Dubnau, D., and Losick, R. (2006). Bistability in bacteria. Mol. Microbiol. 61, 564–572. doi: 10.1111/j.1365-2958.2006.05249.x
Elowitz, M. B., Levine, A. J., Siggia, E. D., and Swain, P. S. (2002). Stochastic gene expression in a single cell. Science 297, 1183–1186. doi: 10.1126/science.1070919
Hawkins, E. D., Turner, M. L., Wellard, C. J., Zhou, J. H., Dowling, M. R., and Hodgkin, P. D. (2013). Quantal and graded stimulation of B lymphocytes as alternative strategies for regulating adaptive immune responses. Nat. Commun. 4:2406. doi: 10.1038/ncomms3406
Hayashi, K., Tabata, S., Piras, V., Tomita, M., and Selvarajoo, K. (2015). Systems Biology Strategy Reveals PKCδ is Key for Sensitizing TRAIL-Resistant Human Fibrosarcoma. Front Immunol. 5:659. doi: 10.3389/fimmu.2014.00659
Klevecz, R. R., Bolen, J., Forrest, G., and Murray, D. B. (2004). A genomewide oscillation in transcription gates DNA replication and cell cycle. Proc. Natl. Acad. Sci. U.S.A. 101, 1200–1205. doi: 10.1073/pnas.0306490101
Marchingo, J. M., Kan, A., Sutherland, R. M., Duffy, K. R., Wellard, C. J., Belz, G. T., et al. (2014). T cell signaling. Antigen affinity, costimulation, and cytokine inputs sum linearly to amplify T cell expansion. Science 346, 1123–1127. doi: 10.1126/science.1260044
Piras, V., Hayashi, K., Tomita, M., and Selvarajoo, K. (2011). Enhancing apoptosis in TRAIL-resistant cancer cells using fundamental response rules. Sci. Rep. 1:144. doi: 10.1038/srep00144
Piras, V., and Selvarajoo, K. (2015). The reduction of gene expression variability from single cells to populations follows simple statistical laws. Genomics 105, 137–144. doi: 10.1016/j.ygeno.2014.12.007
Piras, V., Tomita, M., and Selvarajoo, K. (2014). Transcriptome-wide variability in single embryonic development cells. Sci. Rep. 4:7137. doi: 10.1038/srep07137
Santos, S. D., Verveer, P. J., and Bastiaens, P. I. (2007). Growth factor-induced MAPK network topology shapes Erk response determining PC-12 cell fate. Nat. Cell Biol. 9, 324–330. doi: 10.1038/ncb1543
Sato, T. K., Yamada, R. G., Ukai, H., Baggs, J. E., Miraglia, L. J., Kobayashi, T. J., et al. (2006). Feedback repression is required for mammalian circadian clock function. Nat. Genet. 38, 312–319. doi: 10.1038/ng1745
Schlatter, R., Schmich, K., Avalos Vizcarra, I., Scheurich, P., Sauter, T., Borner, C., et al. (2009). ON/OFF and beyond–a boolean model of apoptosis. PLoS Comput. Biol. 5:e1000595. doi: 10.1371/journal.pcbi.1000595
Selvarajoo, K., and Giuliani, A. (2012). Finding self-organization from the dynamic gene expressions of innate immune responses. Front. Physiol. 3:192. doi: 10.3389/fphys.2012.00192
Selvarajoo, K. (2012). Understanding multimodal biological decisions from single cell and population dynamics. Wiley Interdiscip. Rev. Syst. Biol. Med. 4, 385–399. doi: 10.1002/wsbm.1175
Selvarajoo, K. (2014). Parameter-less approaches for interpreting dynamic cellular response. J. Biol. Eng. 8:23. doi: 10.1186/1754-1611-8-23
Simeoni, O., Piras, V., Tomita, M., and Selvarajoo, K. (2015). Tracking global gene expression responses in T cell differentiation. Gene 569, 259–266. doi: 10.1016/j.gene.2015.05.061
Stuart, K. (1995). At Home in the Universe: The Search for Laws of Self-Organization and Complexity. New York, NY: Oxford University Press.
Tsuchiya, M., Piras, V., Choi, S., Akira, S., Tomita, M., Giuliani, A., et al. (2009). Emergent genome-wide control in wildtype and genetically mutated lipopolysaccarides-stimulated macrophages. PLoS ONE 4:e4905. doi: 10.1371/journal.pone.0004905
Turnbull, I. C., Karakikes, I., Serrao, G. W., Backeris, P., Lee, J. J., Xie, C., et al. (2014). Advancing functional engineered cardiac tissues toward a preclinical model of human myocardium. FASEB J. 28, 644–654. doi: 10.1096/fj.13-228007
Keywords: self-organization, entropy, cell dynamics, thermodynamics, computational biology
Citation: Selvarajoo K (2015) Can the second law of thermodynamics hold in cell cultures? Front. Genet. 6:262. doi: 10.3389/fgene.2015.00262
Received: 09 April 2015; Accepted: 24 July 2015;
Published: 07 August 2015.
Edited by:
Rongling Wu, Pennsylvania State University, USAReviewed by:
Yunqian Guo, Beijing Forestry University, ChinaCopyright © 2015 Selvarajoo. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Kumar Selvarajoo,a3VtYXJAdHRjay5rZWlvLmFjLmpw
 Kumar Selvarajoo
Kumar Selvarajoo