- 1 Department of Psychiatry and Behavioral Sciences, University of Louisville, Louisville, KY, USA
- 2 Department of Bioengineering, University of Louisville, Louisville, KY, USA
Development, aging, and evolution offer different time scales regarding possible anatomical transformations of the brain. This article expands on the perspective that the cerebral cortex exhibits a modular architecture with invariant properties in regards to these time scales. These properties arise from morphometric relations of the ontogenetic minicolumn as expressed in Noether’s first theorem, i.e., that for each continuous symmetry there is a conserved quantity. Whenever minicolumnar symmetry is disturbed by either developmental or aging processes the principle of least action limits the scope of morphometric alterations. Alternatively, local and global divergences from these laws apply to acquired processes when the system is no longer isolated from its environment. The underlying precepts to these physical laws can be expressed in terms of mathematical equations that are conservative of quantity. Invariant properties of the brain include the rotational symmetry of minicolumns, a scaling proportion or “even expansion” between pyramidal cells and core minicolumnar size, and the translation of neuronal elements from the main axis of the minicolumn. It is our belief that a significant portion of the architectural complexity of the cerebral cortex, its response to injury, and its evolutionary transformation, can all be captured by a small set of basic physical laws dictated by the symmetry of minicolumns. The putative preservations of parameters related to the symmetry of the minicolumn suggest that the development and final organization of the cortex follows a deterministic process.
Introduction
It is increasingly clear that the symmetry group of nature is the deepest thing that we can understand about nature today. (Feynman and Weinberg, 1987, p. 73)
The numerical values that nature has assigned to the fundamental constants […] may be mysterious, but they are crucially relevant to the structure of the universe that we perceive. As more and more physical systems, from nuclei to galaxies, have become better understood, scientists have begun to realize that many characteristics of these systems are remarkably sensitive to the precise values of the fundamental constants. (Davies, 1982, p. vii)
As genetic variations accumulate through sexual reproduction successive generations provide the substrate for evolutionary change. The possible number of combinations for the segregation of homologous genes during meiosis is 223. Although the total number of permutations is great, it pales in comparison to the architectural complexity of the brain: an organ with 1010 neurons each one making 104 connections with a variety of cells that exhibit any 1 of 50 or so different neurotransmitters. Furthermore, the total number of glial cells exceeds that of neurons by 2–10 times depending on location. It is therefore of interest that despite the genetic drive toward evolutionary variability the final outcome of brain development is an organ that exhibits a fairly uniform shape and parcelation scheme, be it in cytoarchitecture, myeloarchitecture, pigmentoarchitecture, or chemoarchitecture. This overpowering sense of constancy has been variously expressed in the literature, e.g., “In spite of the enormous variations in cortical surface area, and in the sulci and gyri, the basic cortical circuitry is similar. The laminar allocation of cells connecting to the thalamus, spinal cord, or intracortical areas is remarkably conserved among all mammals studied” (Molnár et al., 2006). This cytoarchitectural commonality may stem from the fact that gliophilic migration and its engendered structure (i.e., the minicolumn) is a conserved motif readily evidenced in all mammalian species thus far studied (Gressens and Evrard, 1993; Buxhoeveden and Casanova, 2005).
The preservation of brain parameters across countless individuals bears analogy to the many examples of convergent evolutionary themes in the history of species (Carroll, 2001; Willmer, 2003). Accordingly, the last common ancestor between octopuses and humans lived well over half a billion years ago (Ramachandran, 2011). Yet, when observing similarities between the eyes of vertebrates and octopuses it is easily concluded that some type of design rule for eyes should exist (Striedter, 2007). This has led numerous scientists to suggest that the course of evolution has been channeled according to undisclosed developmental and/or physical constraints (Amundson, 1994). The putative existence of these constraints therefore stands as the null hypothesis to the adaptationist paradigm (i.e., arguments in favor of the power of natural selection in shaping the brain toward its evolutionary optimum; Gould and Lewontin, 1979; Antonovics and Van Tienderen, 1991). However, as animals randomly generate genetic variations that become adaptations of particular populations, the less need the environment has to act through natural selection. In the end, there would be no need for natural selection at all. Kirschner and Gerhart have expressed this reservation as follows: “Widespread conservation must reflect some limit on the organism’s freedom to generate viable variation in all directions under the impact of mutation” (Kirschner and Gerhart, 2005, p. 68).
Even if mutations are random at the genetic level they are channeled through developmental mechanisms that favor certain phenotypes (Striedter, 2007). This means that adaptations are not optimal by design; rather, they represent compromises between costs and benefits. It is now readily accepted that Neo-Darwinian competition is only one of several principles molding evolution. Neo-Darwinism (sometimes called the Modern Synthesis) is the merger of Darwin’s theory of evolution and genetics. It postulates that gene mutations and other rearrangements underlie the variations needed for natural selection to occur. Besides Neo-Darwinism, the endosymbiotic theory that formulated the interdependence and cooperative existence of microorganisms is another principle of evolution (Margulis, 1970). The expressed reservations are important because they emphasize developmental constrains on the ability of natural selection to dictate evolutionary change.
The emphasis of this article will be on how laws of physics, defined by symmetry operations, may help explain various aspects of brain growth and organization. More specifically, these laws provide a reasonable explanation to some cases of convergent evolution without invoking the necessity of adaptation to similar environments. In evolutionary terms these laws (contrary to the organisms that they apply to) imply descent without modifications. In effect, these measurable properties of the isolated brain do not change as the organ itself evolves. Ultimately we aim to prove that some of the complexity ingrained within the cerebral cortex can be defined in terms of “laws of conservation.”
A review of the literature indicates that scaling rules, explaining brain size as a function of neuronal cell number or size, differ among species (e.g., rodents vs. primates; Herculano-Houzel et al., 2006, 2007). Evolutionary and developmental constraints imposed by cellular elements seem undercut by their flailing generalizability. It therefore seems possible that constraints are a property of modules rather than their individual cellular elements. In the next section we summarize some of the basic knowledge available in the scientific literature regarding the anatomical basis of cortical modularity. For a historical review on the physiology of the minicolumn see Trippe and Casanova (2005) and for a review of cortical organization from the perspective of systems theory see Casanova (2010).
Cortical Organization and Minicolumns
The isocortex is an autopoietic (Gk. αυτóς, self + ποίησɩς, production; Maturana and Varela, 1973) system composed of canonical circuits where the flow of information maintains the stability of the system. In other words, the “modular architectonics may be seen as a pattern resulting from the dynamics of self-organization rather than being completely laid down in the genome” (Arbib and Érdi, 2000). The genesis of this system resides in the recursive migration of cells along a radial glial cell scaffolding. The end result is a receptive scenario to Hebbian reciprocity: the close apposition of neurons along a columnar arrangement propitiates their interconnectivity. In effect, as precursors of pyramidal neurons migrate during corticogenesis they are connected to each other by gap junctions (Peinado et al., 1993). It is thus unsurprising that axonal density studies suggest that the majority of cortical projections are local (intracolumnar) in nature (Douglas and Martin, 1998). Recent studies using enhanced green fluorescent protein (EGFP)-expressing retroviruses and multiple electrode whole-cell recordings clearly illustrate the propensity for developing connections among sister cells (i.e., stemming from the same mother cell) rather than with neighboring non-siblings. The authors of one such labeling study concluded, “These results indicate that specific microcircuits develop preferentially within ontogenetic radial clones of excitatory neurons in the developing neocortex and contribute to the emergence of functional columnar microarchitecture in the mature cortex” (Yu et al., 2009). In analogous fashion evidence obtained with two-photon imaging of calcium fluxes in cat and rodent visual cortex show that orientation-response fields are comprised of columns 1–2 cells wide with organization and response properties capable of differentiating between areas V1 and V2 (Ohki et al., 2005). The anatomical counterparts to these experiments comes from computerized image analysis using a step-wise algorithm involving region growing and recursive line tracing suggesting that minicolumns in supragranular layers are one cell wide (Casanova et al., 2009a). The staggered arrangements of cells in infragranular layers provide for wider minicolumnar cores.
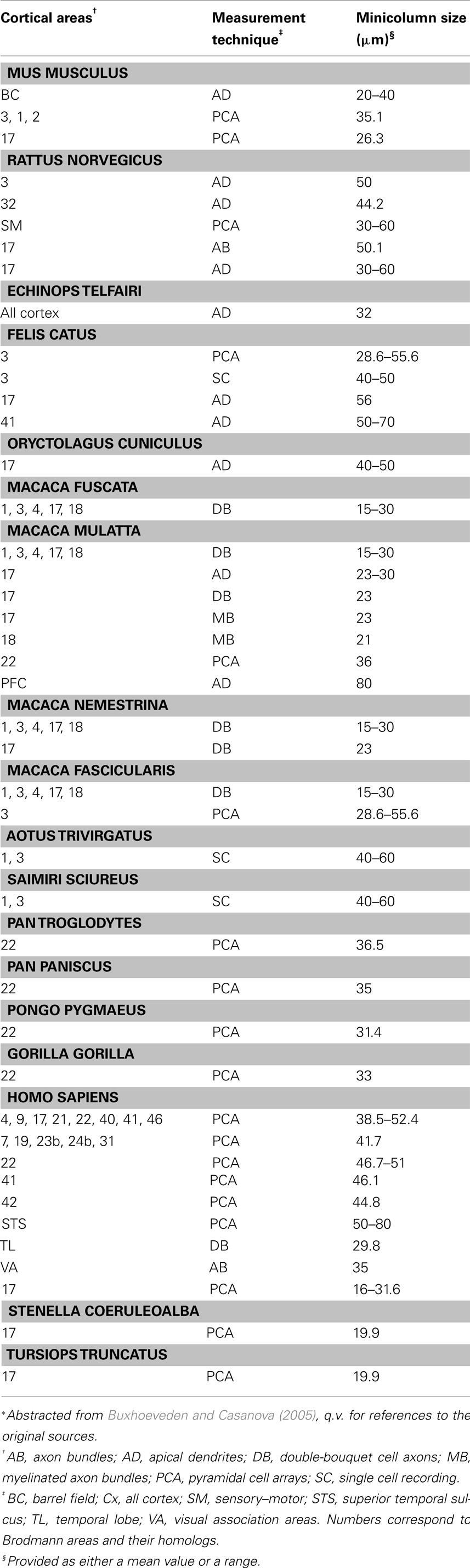
The mammalian iso-/neocortex is remarkable for the periodic spacing of stereotypical, radially oriented cellular features that are common to all of its distinct cytoarchitectural areas. Chords of pyramidal cells spanning multiple neocortical layers were first observed by the pioneering neuroanatomists of the late Nineteenth Century (DeFelipe, 2005). Von Economo and Koskinas (1925) devoted one section of their book on the cytoarchitectonics of the human cortex to the anatomical motif provided by the vertical arrangements of cells. Since the anatomical motif represented the direction of the white matter fibers of the cortex, the so-called Radii, they named the structure “radial arrangements.” Later investigators identified columns of Nissl-stained pyramidal cells distributed with a tangential periodicity of between 30 and 80 μm according to neocortical area and species (Table 1). Peters et al. (1991) showed that the apical dendrites of pyramidal neurons form bundles aligned with the cell-column radial axis and oriented towards the pial surface. As demonstrated in visual and temporal cortex of rodents and monkeys, these apical dendritic bundles are tangentially spaced at regular intervals in register with the cell columns giving rise to them (Peters and Sethares, 1991, 1996; del Río and DeFelipe, 1997). Likewise, in double-labeled rat visual cortex, myelinated axon bundles extending perpendicularly through the cortical plate into white matter were shown to have tangential spacing comparable to that of apical dendritic bundles in the same area (Lohmann and Köppen, 1995). More recently, our group used a novel recursive trace line method in serial sections to demonstrate a high degree of positive correlation between width estimates for pyramidal cell arrays and myelinated bundles (Casanova et al., 2008).
Various species of inhibitory interneurons, classified according to morphology, calcium-binding protein, and neuropeptide content, are located in a pericolumnar zone termed peripheral neuropil space. This zone, or minicolumnar compartment, contains collateral processes, synapses, glia, and other supporting elements. These GABAergic interneurons vary with layer, area, and observed species (DeFelipe, 2005). Double-bouquet interneurons are a characteristic cell-type of primate neocortex. Subsets of this cell class are typically immunoreactive for the calcium-binding proteins calbindin or calretinin and the neuropeptide somatostatin and feature axon bundles, or “horsetails,” which extend from each cell body through several layers of peripheral neuropil. The “horsetails” of double-bouquet interneurons are spaced at regular intervals and have shown one-to-one alignment with myelinated axon bundles in both monkey visual cortex and human temporal cortex (DeFelipe et al., 1990; Peters and Sethares, 1997; Ballesteros Yáñez et al., 2005). Accordingly, double-bouquet neurons may represent an adaptation of this radial motif in primate neocortex which provides enhanced inhibitory modulation and isolation of fluxes of excitatory activity through vertical chains of pyramidal neurons (DeFelipe, 2005).
Recent studies have used various biased and unbiased quantitative methods to assess the spatial organization of minicolumns and their components. These methods employ parameters related to mean cell spacing, verticality, component compartment, and overall minicolumnar width, gray level index (proportion of neocortical image area covered by Nissl-stained cell bodies), and cellular compactness (Schlaug et al., 1995; Buldyrev et al., 2000; Buxhoeveden et al., 2000; Skoglund et al., 2004; Vercelli et al., 2004; Casanova et al., 2007). Results obtained with such methods show that measures of center-to-center spacing and other parameters provide redundant and complementary information regarding overall minicolumnar measurements (Casanova, 2008). Morphometric relations between component compartments are transitive and are conserved during fetal and postnatal development and in neuropathological conditions (Buldyrev et al., 2000; Casanova et al., 2007).
The juxtaposition of these cellular features at regular intervals suggests that together they contribute to a canonical cortical microcircuit. Termed the cortical cell minicolumn by Mountcastle (1978, 1997), this putative microcircuit incorporates radially arranged pyramidal neurons linked by re-iterative translaminar connections extending through all cortical layers, whose activity is modulated by inhibitory interneurons in the minicolumn’s peripheral neuropil. The minicolumn constitutes a radial histogenetic domain easily defined by studies of fate maps of different brain fields (Medina, 2007). The existence of such radial divisions makes them the natural unit for comparing cortical homologies (Casanova et al., 2009b).
The minicolumn has been proposed to serve as the elemental functional module of neocortex (Mountcastle, 1997; Buxhoeveden and Casanova, 2002; DeFelipe, 2005). According to this model, each minicolumn implements a stereotypical information-processing operation which is executed in parallel arrays throughout the neocortex. This common minicolumnar algorithm is modified by specific patterns of cell morphology and transcortical, subcortical, and local connections to suit the specific requirements of each neocortical area (Creutzfeldt, 1977). Minicolumnar variability, prominent in humans as compared to other species, is most salient within the peripheral neuropil space (Casanova et al., 2009b). These differences in minicolumnar morphology among species may be directly related to various interneuron subtypes located within the peripheral space of minicolumns (Casanova et al., 2009b; Raghanti et al., 2010). Together, these findings support the hypothesis that variations in component features and measures may be imposed upon a stereotypical and stable modular microstructure of the neocortex (Casanova, 2008).
Circuits resulting from the stereotypical positioning of neuroblasts along the radial glial scaffolding should work in similar and parallel fashion. Minicolumns are in this way analogous to logic gates (e.g., NOR) in the sense that varying combinations of these elements provide for higher-level functions (Casanova et al., 2003). Alternatively, different properties of a canonical circuit can manifest non-linear behaviors. According to neurophysiological data modeling these circuits within a hierarchical organization leads to neural representations capable of object recognition (Kouh and Poggio, 2008). The existence of a canonical circuit provides the basis for symmetry operations discussed in the following section (for a review on the canonical circuit see Douglas and Martin, 2004).
Symmetry of the Minicolumn
Minicolumns are the result of germinal cell proliferation within the ventricular zone early in gestation. A series of symmetrical divisions define the total number of minicolumns. A later series of asymmetrical divisions provides for progenitor and daughter cells that will eventually become neurons. Following the asymmetric cell division daughter cells migrate along a glial/stem cell scaffolding in a process often denoted as radial migration. The layer to which a neuron will migrate is largely defined by when it is born. Layers of the cortex are thus formed in an inside-out fashion, the exception being the first layer which always remains as the superficial marginal zone. A tangential mode of migration which is independent of glial processes provides for the cortical placement of a significant portion of inhibitory neurons. The cortex is therefore primarily formed by a recursive process that embeds cell after cell within a hierarchical structure. Without this recursive process there is no “discrete infinity.” This is Nature’s way of making unbound diversity or “infinite use of finite means” (Humboldt, 1999, p. 91) by taking discrete elements from a finite set and combining them to provide larger units having a more diverse structure than their individual constituents (Studdert-Kennedy and Goldstein, 2003). The end result of the recursive positioning of cells is a multistep optimization process similar to the one observed in dynamic programming. Recursion is therefore a way of providing an optimal solution to cortical architecture while working with a suboptimal structure (Linden, 2007).
A cursory microscopic examination of the minicolumn during cortical embryogenesis suggests their isotropy in space, i.e., identical in all directions. Our laboratory found this to be true for minicolumns of the striate cortex when probed in the sagittal, coronal, and transverse planes (Figure 1). This rotational symmetry (an isometry preserving orientation) indicates that there are no preferred minicolumnar orientations in regards to these reference planes. The symmetry is such that rotation of the coordinate system used to describe the phenomena, by any amount, does not affect the laws of nature/physics governing the system. In the present article we hypothesize that these minicolumnar parameters which are “unchanged in value by an arbitrary continuous deformation is (are) a fortiori unchanged in value by the passage of time” (Finkelstein and Misner, 1959). In our biological system time is defined in terms of brain development, aging, and evolution (encephalization).
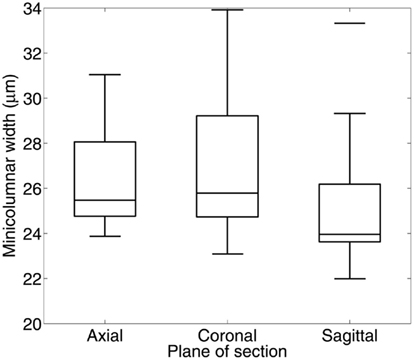
Figure 1. Box plots of minicolumar width measurements in Brodmann area 17 (human). Width was estimated using a single section of Nissl-stained tissue cut along one of the three principal axes. Materials for this study included 8 brains cut in the transverse plane (4 male, 4 female, age 40–72 years), 15 brains cut in the coronal plane (10 male, 5 female, age 1–94 years), and 11 brains cut in the sagittal plane (5 male, 6 female, age 4–87 years). Minicolumnar width was estimated using computerized image analysis of micrographs of these regions of interest (Casanova and Switala, 2005). There was one possible outlier at 33.3 μm in the sagittal plane. There is no significant dependence of width estimates on the plane of section (F2,8 = 1.05; p = 0.410).
The cortex, or more specifically its neuropil space (the space between neuronal bodies including, among others, axons, dendrites, and glial cell processes), is a homogenous space that acts in a permissive way to conserve the geometry of the minicolumn. This property of the neuropil is seen in all brain regions that we have examined following a continuum from brain development to advanced aging (Figure 2). The permissive nature of the neuropil applies when examining either fragments or whole lengths of minicolumns. The significance of the finding is that we can perform transformative operations to the space coordinates of minicolumns (e.g., rotation, vide supra) and the final result(s) will be independent on the amount of translation, rotation, or combination of both. The minicolumn therefore conforms to Feynman’s definition of symmetry which states that an object is symmetrical if it looks the same after applying a particular operation (Feynman et al., 1963).
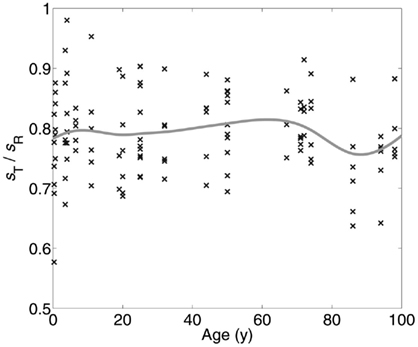
Figure 2. Little change is seen in minicolumnar structure among 19 persons with a range of ages at death from 4 months to 98 years. The neuropil distribution is derived from the empirical “linear contact distribution,” the distribution of distances from points within the neuropil to the nearest Nissl-stained object, measured along a line with fixed orientation (Casanova et al., 2007). Taking the orientation parallel to the minicolumar axis, the median of the distribution is termed the radial neuropil space sR, while the same measurement in the orthogonal direction (parallel to the laminar boundaries) provides the tangential neuropol space sT. Mean sT/sR (solid curve) was estimated with a smoothing spline over measurements (points) from up to 6 cortical areas in each of 19 individual brains. The ratio of tangential neuropil space sT to radial neuropil space sR remains nearly constant at approximately 0.8 throughout the human lifespan.
Similar arguments apply to the translation of pyramidal cells around the central axis of the cell minicolumn. The central axis is an imaginary line through the minicolumn that serves as a reference point when making measurements of symmetry. Although early in development pyramidal cells lay in a rectilinear pattern, development, and aging disturb their placement making their unitary composition less noticeable. Still, the vectorial sum of discrete or contiguous pyramidal cell translations around the central axis of the minicolumn is zero regardless of brain parcelation or age (Figure 3). The resultant arrangement therefore links symmetry in space (i.e., translation of cells in different brain regions) with time (i.e., aging).
Figure 3. We identified the minicolumns in each of 192 micrographs (the same material as was used for Figure 5, excluding individuals on the autistic spectrum) using a line tracing method that groups cells into minicolumns by finding the shortest cell-to-cell paths from one end of the layer to the next (Casanova et al., 2009a). Using the clusters so identified, cell dispersions about the minicolumnar axes were compared to a chi-square distribution with one degree of freedom, which is what one would expect if the neurons were located at random positions in space under a symmetric distribution. The mean displacement of neurons from the minicolumnar axis was very nearly zero, consistent with symmetry; however, the empirical distribution of C2 was far from chi-square distributed (Kuiper V = 0.932; p < 0.0001). Examination of a q–q plot confirmed that observed C2 were smaller and under-dispersed relative to the expected χ2. We suspect this is due to the bias inherent in image processing – as opposed to stereology – and that accurate localization of both neurons and the minicolumnar axis in three-dimensional space is necessary for a proper test of the symmetry hypothesis.
The final transformation discussed in this article is the preservation of the relative size of pyramidal cells as related to minicolumnar width (Figure 4). Resizing (also called dilation or even expansion) is a conversion whereby objects or systems become bigger or smaller while leaving unaltered the content and relationship of its component elements. In the case of the minicolumn the validity of such a geometric transformation lends credence to O. D. Creutzfeldt’s early proposal of a canonical circuit patent throughout the cortex (Creutzfeldt, 1977). This scalar relationship is obvious and expected to those who examine the microscopy of the cortex. Thus, V1 (BA 17) is the prototype of granular cortex and exhibits the smallest minicolumnar widths reported for any given isocortical area (Buxhoeveden and Casanova, 2002, 2005). By way of contrast the largest neurons in the cortex (Betz cells) are found in the motor cortex, site of the widest minicolumns thus far reported (Buxhoeveden and Casanova, 2002, 2005).
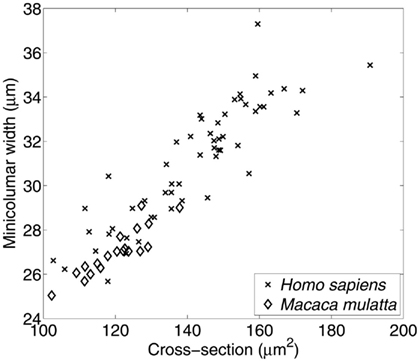
Figure 4. Relationship between average size of minicolums and pyramidal cells. Material included 55 micrographs of Nissl-stained human tissue comprising Brodmann areas 4, 9, 17, 21, 22, and 40; and 19 micrographs of area 17 in the macaque. The average cross-section of pyramidal cell somata is positively correlated with the minicolumnar width estimated from the same set of micrographs. Minicolumnar width was estimated using our established methodology (Casanova and Switala, 2005), while the average neuronal cross-sectional area was estimated using the Boolean model (Casanova et al., 2006). The high degree of linear correlation (r = 0.913; p < 0.0001) is evident.
During evolution the cortex has grown by adding supernumerary minicolumns but the relative number of cells has been preserved. In primates, a recent study showed a linear relationship between structure size and number of neurons (Herculano-Houzel et al., 2007). Among the six primate species analyzed in the study neuronal size and density did not vary significantly with brain size. Another comparative anatomy study in primates found that despite major changes in minicolumnar width across species, core spaces remained the same (Casanova et al., 2009b). The core compartment of the minicolumn is composed of pyramidal cells and their projections. These basic constitutive elements of the minicolumn’s core appear to be to some extent irreducible (Casanova and Tillquist, 2008). Variability is inherent in the peripheral neuropil space which is comprised of non-pyramidal cellular elements derived from assorted sources (Casanova et al., 2009b).
A conservation law is the statement that there exists a measurable quantity that does not change when subject to a specified physical process. Such a physical measure is called a conserved quantity. The fact that minicolumns exhibit scalar properties relating pyramidal cell size and minicolumnar core size, rotational symmetry, and conservation of translational movements helps to conceptually organize the cytoarchitecture of the isocortex. In an isolated system (i.e., one where the brain does not directly exchange energy or matter with its surroundings), broken symmetry is a pre-requisite of directionality wherein changes always display greater entropy. In essence, more entropy requires that the result of different operations have less symmetry than their predecessors. With passage of time processes that require greater entropy seemingly diminish the hegemony of the minicolumn in cortical organization. One could say that the significance of the minicolumn in modern studies diminishes as the module seemingly loses its rectilinear orientation; however, its influence on cortical organization remains tangible as proven by the existence of laws of conservation.
Pathology
Early during gestation minicolumnar structures are readily noticeable by their rectilinear arrangement. Later on, with aging, pyramidal cell translation, and neuropil growth make the patency of these modular structures less apparent. Still, as long as the system (i.e., brain) is isolated, the putative existence of laws of conservation requires the preservation of certain invariant quantities. In physics, as well as in biological systems, an isolated system is one separated from its environment so as to prevent the direct transfer of energy and/or matter between them. Developmental conditions tend to unfold within isolated systems. In contrast, traumas, abscesses, and metastases provide venues for direct interactions between the brain and its external environment. Once the system is perturbed by environmental exigencies these laws of conservation are “broken” and so-called conserved parameters or invariants no longer apply. In this regard “broken” is a technical term used in physics to denote how a given action on a system perturbs its initial symmetry.
Conserved quantities apply, despite broken symmetry, only when systems are isolated. Thus, an acquired process such as an infarct may affect the amount of pyramidal cell translation around the central axis of a minicolumn within the ischemic and penumbra regions. The spatial malformation may be propitiated by infiltration of hematogenous species (e.g., neutrophils), astrocytic proliferation, and neovascularization (Ferrer et al., 2008). Acquired processes therefore bring to center stage the role of supporting cells or glia which in the normal brain outnumber neurons 10–50 to 1, depending on brain region (Vinters and Kleinschmidt-DeMasters, 2008). Otherwise, developmental conditions unfold within an isolated system and any subsequent neuropathological findings should conform to constraints imposed by laws of conservation.
Autism as an Example
Autism is traditionally regarded as a neurodevelopmental condition that manifests itself behaviorally within the first 3 years of a person’s life. Postmortem studies have shown that minicolumnar width in these patients is significantly diminished specially in their peripheral neuropil compartment (Casanova et al., 2002, 2006). Other studies have shown that the cell soma of cortical and subcortical neurons in both typical and syndromic autism is reduced (Bauman and Kemper, 1985, 1994; Raymond et al., 1995; Casanova et al., 2006; Van Kooten et al., 2008; Wegiel et al., 2010). Small neurons invariably suggest the presence of neuropathology. According to the literature, small neurons provide a variety of phenotypes spanning developmental arrest, a stage leading to cell death, aposklesis, or abiotrophy (i.e., cell withering associated with neurodegeneration; Gowers, 1902; Moran and Graeber, 2008), and, in some cases, a type of non-apoptotic dark cell degeneration.
We hypothesize that the smaller cell soma in the brains of autistic patients are not the result of a neuropathological processes but a necessity imposed by laws of conservation in order to make the system work most efficiently. Results from our group (Figure 5) indicate that smaller pyramidal cell size in autism is related to the “even expansion” of minicolumns. Smaller cells in this sense are not an advantage or a disadvantage, but simply a fact that “…evolution couldn’t readily build us [our brains] in any other way” (Marcus, 2008, p. 154; see below). This finding has important implications in regards to defining difference in brain connectivity that may be particular to the condition.
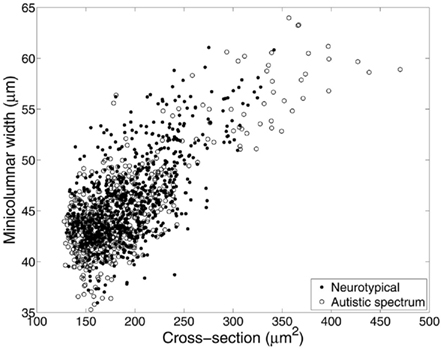
Figure 5. Relationship between average size of minicolumns and pyramidal cells, revisited. Material included 270 micrographs of Nissl-stained human tissue from up to 16 cortical areas in each of 8 brain donors with autistic spectrum disorder and 10 neurotypical comparison clients. In this instance, mean pyramidal cell cross-section was calculated directly from the segmented neurons used to identify minicolumns. Correcting for the effects of diagnosis, cortical area, and lamina (II–VI), minicolumnar width varies strongly with mean cell cross-section (F1,1187 = 2417; p < 0.0001).
Individual size of cells may not decrease with increasing brain size because this parameter is defined by the cell’s connections. According to Vinters and Kleinschmidt-DeMasters (2008), “The volume of the neuronal soma parallels the length of the axon for which it is responsible: the longer the axon, the larger the cell body must be” (p. 2). This correlation is an exigency of the increased metabolic requirements and organelle machinery necessary to sustain a longer axon. It is therefore unsurprising that the main diameter of fibers across longer commissural connections (i.e., corpus callosum) is essentially constant across species (Doty, 2007). This shift in cell/minicolumnar size has biased brain connectivity so that larger brains are most efficient at developing an “intrahemispheric modus operandi” (Doty, 2007, p. 282). Hemispheric specialization thus reflects a solution to the struggle between metabolic exigencies and connectivity (Ringo et al., 1994).
A decrease in size of pyramidal neurons would likely constrain formation of longer-range, metabolically expensive projections biasing the network toward establishment of local connections. Increased numbers of smaller minicolumns, as seen in autistic patients, would complement this trend. As numbers of modules increase, the number of potential connections required to maintain a constant degree of connectivity among them increases geometrically providing for deficiencies based on limitations in space, signal timing, and metabolic constraints (Casanova, 2004). Optimization of network path length would require a relative increase in short-range connections with selective retention of longer-range transcortical projections linking distributed networks (Hofman, 2001).
Reductions of pyramidal neuron size corresponding to smaller minicolumns have implications for information-processing within a network and for the clinical features of autism. As metabolic limits preferentially constrain the activity of smaller cells, cortical adaptations emerge featuring locally linked modules with limited information-processing operations. These are distributed within large decentralized networks in which metabolic demands on any cell or module are limited. Such operations, subserved by minicolumns or small networks of minicolumns, increase efficiency by preferentially processing transient changes in focal input and integrating information with neighboring modules, thus limiting activity of individual modules. Decreases in field size of small neuron collaterals would bias cortical organization toward smaller, more integrated minicolumnar networks, providing the basis for increased discriminatory capacity. This sparse distributed coding architecture (Laughlin, 2004) is especially salient in visual cortex in which discontinuities are extracted from arrays of focal inputs processed in parallel (Weliky et al., 2003). Pathology, as in autism, in which cortical development is biased toward analogous connectivity among smaller minicolumns may be expected to give rise to a hyperspecific pattern of cortical information-processing (McClelland, 2000) related to the increased discriminative perceptual abilities and impaired ability to integrate information among perceptual, executive, and other cognitive domains (Baron-Cohen, 2004). The resultant “hyperconnectivity” underlies the intense world syndrome hypothesis of autism (Markram et al., 2007) based on the valproic acid animal model of autism (Rinaldi et al., 2008).
Concluding Remarks
Noether’s theorem is based on the unchangeability, or invariance, of the laws of physics. The theorem states that for each continuous symmetry there is a conserved quantity (Lederman and Hill, 2004). These invariants, or conserved properties, are the same regardless of the perspective from which they are examined (different reference planes). In this article we have studied how architectonic relations among select minicolumnar elements (i.e., pyramidal cells) are conserved under spatial and temporal variation. Specifically, minicolumns are observed to exhibit translational (across the central axis of the minicolumn) and rotational (displacement in different planes of section) symmetry, transitive symmetry with respect to geometric scaling of morphometric relations in different cortical areas, and temporal symmetry of morphometric relations during cortical development and maturation (Casanova et al., 2007). Maintenance of continuous symmetry with these operations is a defining characteristic of physical systems in which conservation laws can be derived from the stochastic activity of its elements (Noether, 1971).
The authors spouse symmetry as a devise or technique to better describe changes in cortical organization. The work presented shows that despite changes accrued to time, there is preservation (or conservation) of parameters related to the symmetry of the minicolumn. In this regard measurements of symmetry for the cell minicolumn serve as a pattern classification scheme, suggest the existence of mathematical ways of describing modular interactions, and simplify understanding the integrative function of multiple anatomical elements of the cortex. The existence of such conserved quantities generalizes known physical tenets to biological systems.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
Funding for this work was provided by the National Institutes of Health, grant numbers R01 MH-086784 and R01 HD-065279.
References
Amundson, R. (1994). Two concepts of constraint: adaptationism and the challenge from developmental biology. Philos. Sci. 61, 556–578.
Antonovics, J., and Van Tienderen, P. H. (1991). Ontoecogenophyloconstraints? The chaos of constraint terminology. Trends Ecol. Evol. 6, 166–168.
Arbib, M. A., and Érdi, P. (2000). Précis of neural organization: structure, function, and dynamics. Behav. Brain Sci. 23, 513–571.
Ballesteros Yáñez, I., Muñoz, A., Contreras, J., Gonzalez, J., Rodriguez-Veiga, E., and Defelipe, J. (2005). Double bouquet cell in the human cerebral cortex and a comparison with other mammals. J. Comp. Neurol. 486, 344–360.
Baron-Cohen, S. (2004). The cognitive neuroscience of autism. J. Neurol. Neurosurg. Psychiatry 75, 945–948.
Bauman, M. L., and Kemper, T. L. (1985). Histoanatomic observations of the brain in early infantile autism. Neurology 35, 866–874.
Bauman, M. L., and Kemper, T. L. (1994). “Neuroanatomic observations of the brain in autism,” in The Neurobiology of Autism, eds M. L. Bauman and T. L. Kemper (Baltimore: Johns Hopkins University Press), 119–145.
Buldyrev, S. V., Cruz, L. R. C., Gomez-Isla, T., Gomez-Tortosa, E., Havlin, S., Le, R., Stanley, H. E., Urbanc, B., and Hyman, B. T. (2000). Description of microcolumnar ensembles in association cortex and their disruption in Alzheimer and Lewy body dementias. Proc. Natl. Acad. Sci. U.S.A. 97, 5039–5043.
Buxhoeveden, D. P., and Casanova, M. F. (2002). The minicolumn hypothesis in neuroscience. Brain 125, 935–951.
Buxhoeveden, D. P., and Casanova, M. F. (2005). “The cell column in comparative anatomy,” in Neocortical Modularity and The Cell Minicoumn, ed. M. F. Casanova (New York: Nova Biomedical), 93–116.
Buxhoeveden, D. P., Switala, A. E., Roy, E., and Casanova, M. F. (2000). Quantitative analysis of cell columns in the cerebral cortex. J. Neurosci. Methods 97, 7–17.
Carroll, S. B. (2001). Chance and necessity: the evolution of morphological complexity and diversity. Nature 409, 1102–1109.
Casanova, M. F. (2004). Intracortical circuitry: one of psychiatry’s missing assumptions. Eur. Arch. Psychiatry Clin. Neurosci. 254, 148–151.
Casanova, M. F. (2008). “The significance of minicolumnar size variability in autism: a perspective from comparative anatomy,” in Autism: Current Theories and Evidence, ed. A. W. Zimmerman (Totowa, NJ: Humana Press), 349–360.
Casanova, M. F. (2010). Cortical organization: anatomical findings based on systems theory. Transl. Neurosci. 1, 62–71.
Casanova, M. F., Buxhoeveden, D. P., and Gomez, J. (2003). Disruption in the inhibitory architecture of the cell minicolumn: implications for autism. Neuroscientist 9, 496–507.
Casanova, M. F., Buxhoeveden, D. P., Switala, A. E., and Roy, E. (2002). Minicolumnar pathology in autism. Neurology 58, 428–432.
Casanova, M. F., El-Baz, A. S., Vanbogaert, E., Narahari, P., and Trippe, J. (2009a). Minicolumnar width: comparison between supragranular and infragranular layers. J. Neurosci. Methods 184, 19–24.
Casanova, M. F., Trippe, J., Tillquist, C., and Switala, A. E. (2009b). Morphometric variability of minicolumns in the striate cortex of Homo sapiens, Macaca mulatta, and Pan troglodytes. J. Anat. 214, 226–234.
Casanova, M. F., Konkachbaev, A. I., Switala, A. E., and Elmaghraby, A. S. (2008). Recursive trace line method for detecting myelinated bundles: a comparison study with pyramidal cell arrays. J. Neurosci. Methods 168, 367–372.
Casanova, M. F., and Switala, A. E. (2005). “Minicolumnar morphometry: computerized image analysis,” in Neocortical Modularity and The Cell Minicolumn, ed. M. F. Casanova (New York: Nova Biomedical), 161–179.
Casanova, M. F., and Tillquist, C. (2008). Encephalization, emergent properties, and psychiatry: a minicolumnar perspective. Neuroscientist 14, 101–118.
Casanova, M. F., Trippe, J., and Switala, A. E. (2007). A temporal continuity to the vertical organization of the human neocortex. Cereb. Cortex 17, 130–137.
Casanova, M. F., Van Kooten, I. A. J., Switala, A. E., Van Engeland, H., Heinsen, H., Steinbusch, H. W. M., Hof, P. R., Trippe, J., Stone, J., and Schmitz, C. (2006). Minicolumnar abnormalities in autism. Acta Neuropathol. 112, 287–303.
Creutzfeldt, O. D. (1977). Generality of the functional structure of the neocortex. Naturwissenschaften 64, 507–517.
DeFelipe, J. (2005). “Reflections on the structure of the cortical minicolumn,” in Neocortical Modularity and The Cell Minicolumn, ed. M. F. Casanova (New York: Nova Biomedical), 57–92.
DeFelipe, J., Hendry, S. H. C., Hashikawa, T., Molinari, M., and Jones, E. G. (1990). A microcolumnar structure of monkey cerebral cortex revealed by immunocytochemical studies of double bouquet cell axons. Neuroscience 37, 655–673.
del Río, M. R., and DeFelipe, J. (1997). Double bouquet cell axons in the human temporal neocortex: relationship to bundles of myelinated axons and colocalization of calretinin and calbindin D-28k immunoreactivities. J. Chem. Neuroanat. 13, 243–251.
Doty, R. W. (2007). “Cortical commisural connections in primates,” in Evolution of Nervous Systems: A Comprehensive Reference, Vol. 4, Primates, eds J. H. Kaas, and L. A. Krubitzer (Amsterdam: Elsevier), 277–289.
Douglas, R. J., and Martin, K. A. C. (1998). “Neocortex,” in The Synaptic Organization of the Brain, 4th Edn, ed. G. M. Shepherd (New York: Oxford University Press), 459–509.
Douglas, R. J., and Martin, K. A. C. (2004). Neuronal circuits of the neocortex. Annu. Rev. Neurosci. 27, 419–451.
Ferrer, I., Kaste, M., and Kalimo, H. (2008). “Vascular diseases,” in Greenfield’s Neuropathology, 8th Edn, eds S. Love, D. N. Louis, and D. W. Ellison (London: Hodder Arnold), 121–240.
Feynman, R. P., Leighton, R. B., and Sands, M. (1963). The Feynman Lectures on Physics. Reading, MA: Addison-Wesley.
Feynman, R. P., and Weinberg, S. (1987). Elementary Particles and the Laws of Physics: The 1986 Dirac Memorial Lectures. Cambridge: Cambridge University Press.
Gould, S. J., and Lewontin, R. C. (1979). The spandrels of San Marco and the Panglossian paradigm: a critique of the adaptationist programme. Proc. R. Soc. Lond. B Biol. Sci. 205, 581–598.
Gressens, P., and Evrard, P. (1993). The glial fascicle: an ontogenic and phylogenic unit guiding, supplying and distributing mammalian cortical neurons. Brain Res. Dev. Brain Res. 76, 272–277.
Herculano-Houzel, S., Collins, C. E., Wong, P., and Kaas, J. H. (2007). Cellular scaling rules for primate brains. Proc. Natl. Acad. Sci. U.S.A. 104, 3562–3567.
Herculano-Houzel, S., Mota, B., and Lent, R. (2006). Cellular scaling rules for rodent brains. Proc. Natl. Acad. Sci. U.S.A. 103, 12138–12143.
Hofman, M. A. (2001). “Brain evolution in hominoids: are we at the end of the road?” in Evolutionary Anatomy of the Primate Cerebral Cortex, eds D. Falk and K. R. Gibson (Cambridge: Cambridge University Press), 113–127.
Humboldt, W. (1999). On Language: On the Diversity of Human Language Construction and its Influence on the Mental Development of the Human Species. New York: Cambridge University Press.
Kirschner, M. W., and Gerhart, J. C. (2005). The Plausibility of Life, Resolving Darwin’s Dilemma. New Haven, CT: Yale University Press.
Kouh, M., and Poggio, T. (2008). A canonical neural circuit for cortical nonlinear operations. Neural Comput. 20, 1427–1451.
Laughlin, S. B. (2004). “The implications of metabolic energy requirements for the representation of information in neurons,” in The Cognitive Neurosciences, 3rd Edn, ed. M. S. Gazzaniga (Cambridge: MIT Press), 187–196.
Lederman, L. M., and Hill, C. T. (2004). Symmetry and the Beautiful Universe. Amherst, NY: Prometheus Books.
Lohmann, H., and Köppen, H.-J. (1995). Postnatal development of pyramidal dendritic and axonal bundles in the visual cortex of the rat. J. Hirnforsch. 36, 101–111.
Margulis, L. (1970). Origin of Eukaryotic Cells: Evidence and Research Implications for a Theory of the Origin and Evolution of Microbial, Plant, and Animal Cells on the Precambrian Earth. New Haven, CT: Yale University Press.
Markram, H., Rinaldi, T., and Markran, K. (2007). The intense world syndrome – an alternative hypothesis for autism. Front. Neurosci. 1:1. doi:10.3389/neuro.01/1.1.006.2007
Maturana, H. R., and Varela, F. J. (1973). De máquinas y seres vivos: una teoría sobre la organización biológia. Santiago: Editorial Universitaria.
McClelland, J. L. (2000). The basis of hyperspecificity in autism: a preliminary suggestion based on the properties of neural nets. J. Autism Dev. Disord. 30, 497–502.
Medina, L. (2007). “Field homologies,” in Evolution of Nervous Systems: A Comprehensive Reference, Vol. 1: Theories, Development, Invertebrates, eds G. F. Striedter and J. L. R. Rubenstein (Amsterdam: Elsevier Academic Press), 73–87.
Molnár, Z., Tavare, A., and Cheung, A. F. P. (2006). “The origin of neocortex: lessons from comparative embryology,” in Evolution of Nervous Systems, Vol. 3: Mammals, eds J. H. Kaas and L. A. Krubitzer (London: Academic Press), 13–26.
Moran, L. B., and Graeber, M. B. (2008). Towards a pathway definition of Parkinson’s disease: a complex disorder with links to cancer, diabetes and inflammation. Neurogenetics 9, 1–13.
Ohki, K., Chung, S., Ch’ng, Y. H., Kara, P., and Reid, R. C. (2005). Functional imaging with cellular resolution reveals precise micro-architecture in visual cortex. Nature 433, 597–603.
Peinado, A., Yuste, R., and Katz, L. C. (1993). Extensive dye coupling between rat neocortical neurons during the period of circuit formation. Neuron 10, 103–114.
Peters, A., Palay, S. L., and Webster, H. F. (1991). The Fine Structure of the Nervous System: Neurons and Their Supporting Cells, 3rd Edn. New York: Oxford University Press.
Peters, A., and Sethares, C. (1991). Organization of pyramidal neurons in area 17 of monkey visual cortex. J. Comp. Neurol. 306, 1–23.
Peters, A., and Sethares, C. (1996). Myelinated axons and the pyramidal cell modules in monkey primary visual cortex. J. Comp. Neurol. 365, 232–255.
Peters, A., and Sethares, C. (1997). The organization of double bouquet cells in monkey striate cortex. J. Neurocytol. 26, 779–797.
Raghanti, M. A., Spocter, M. A., Butti, C., Hof, P. R., and Sherwood, C. C. (2010). A comparative perspective on minicolumns and inhibitory GABAergic interneurons in the neocortex. Front. Neuroanat. 4:3. doi:10.3389/neuro.05.003.2010
Ramachandran, V. S. (2011). The Tell-Tale Brain: A Neuroscientist’s Quest for What Makes Us Human. New York: W. W. Norton.
Raymond, G. V., Bauman, M. L., and Kemper, T. L. (1995). Hippocampus in autism: a Golgi analysis. Acta Neuropathol. 91, 117–119.
Rinaldi, T., Perrodin, C., and Markram, H. (2008). Hyper-connectivity and hyper-plasticity in the medial prefrontal cortex in the valproic acid animal model of autism. Front. Neural Circuits 2:4 doi:10.3389/neuro.04.004.2008
Ringo, J. L., Doty, R. W., Demeter, S., and Simard, P. Y. (1994). Time is of the essence: a conjecture that hemispheric specialization arises from interhemispheric conduction delay. Cereb. Cortex 4, 331–343.
Schlaug, G., Schleicher, A., and Zilles, K. (1995). Quantitative analysis of the columnar arrangement of neurons in the human cingulate cortex. J. Comp. Neurol. 351, 441–452.
Skoglund, T. S., Pascher, R., and Berthold, C.-H. (2004). Aspects of the organization of neurons and dendritic bundles in primary somatosensory cortex of the rat. Neurosci. Res. 50, 189–198.
Striedter, G. F. (2007). “A history of ideas in evolutionary neuroscience,” in Evolution of Nervous Systems: A Comprehensive Reference, Vol. 1: Theories, Development, Invertebrates, eds G. F. Striedter and J. L. R. Rubenstein (Amsterdam: Elsevier Academic Press), 1–5.
Studdert-Kennedy, M., and Goldstein, L. (2003). “Launching language: the gestural origin of discrete infinity,” in Language Evolution, eds M. Christiansen and S. Kirby (Oxford: Oxford University Press), 235–254.
Trippe, J., and Casanova, M. F. (2005). “Vernon B. Mountcastle: scientific achievements,” in Neocortical Modularity and the Cell Minicolumn, ed. M. F. Casanova (New York: Nova Biomedical), 15–32.
Van Kooten, I. A. J., Palmen, S. J. M. C., Von Cappeln, P., Steinbusch, H. W. M., Korr, H., Heinsen, H., Hof, P. R., Van Engeland, H., and Schmitz, C. (2008). Neurons in the fusiform gyrus are fewer and smaller in autism. Brain 131, 987–999.
Vercelli, A. E., Garbossa, D., Curtetti, R., and Innocenti, G. M. (2004). Somatodendritic minicolumns of output neurons in the rat visual cortex. Eur. J. Neurosci. 20, 495–502.
Vinters, H. V., and Kleinschmidt-DeMasters, B. K. (2008). “General pathology of the central nervous system,” in Greenfield’s Neuropathology, eds S. Love, D. N. Louis, and D. W. Ellison (London: Hodder Arnold), 1–62.
Von Economo, C., and Koskinas, G. N. (1925). Die Cytoarchitektonik der Hirnrinde des erwachsenen Menschen. Wien: Springer.
Wegiel, J., Kuchna, I., Nowicki, K., Imaki, H., Wegiel, J., Marchi, E., Ma, S. Y., Chauhan, A., Chauhan, V., Wierzba Bobrowicz, T., De Leon, M., Saint Louis, L. A., Cohen, I. L., London, E., Brown, W. T., and Wisniewski, T. (2010). The neuropathology of autism: defects of neurogenesis and neuronal migration, and dysplastic changes. Acta Neuropathol. 119, 755–770.
Weliky, M., Fiser, M., Hunt, R. H., and Wagner, D. N. (2003). Coding of natural scenes in primary visual cortex. Neuron 37, 703–718.
Willmer, P. (2003). “Convergence and homoplasy in the evolution of organismal form,” in Origination of Organismal Form, eds G. B. Müller and S. A. Newman (Cambridge, MA: MIT Press), 33–49.
Keywords: cerebral cortex, neocortex, minicolumns, symmetry
Citation: Casanova MF, El-Baz A and Switala A (2011) Laws of conservation as related to brain growth, aging, and evolution: symmetry of the minicolumn. Front. Neuroanat. 5:66. doi: 10.3389/fnana.2011.00066
Received: 05 October 2011;
Accepted: 08 December 2011;
Published online: 26 December 2011.
Edited by:
Patrick R. Hof, Mount Sinai School of Medicine, USAReviewed by:
Efrain Azmitia, New York University, USAChristoph Schmitz, Ludwig-Maximilians-University of Munich, Germany
Copyright: © 2011 Casanova, El-Baz and Switala. This is an open-access article distributed under the terms of the Creative Commons Attribution Non Commercial License, which permits non-commercial use, distribution, and reproduction in other forums, provided the original authors and source are credited.
*Correspondence: Manuel F. Casanova, University of Louisville, 500 S Preston Street Building 55A Ste 217, Louisville, KY 40292, USA e-mail:bTBjYXNhMDJAbG91aXN2aWxsZS5lZHU=

 Ayman El-Baz2 and Andrew Switala1
Ayman El-Baz2 and Andrew Switala1