- 1 Institute of Clinical Neuroanatomy, Goethe-University, Frankfurt am Main, Germany
- 2 Ernst Strüngmann Institute in Cooperation with Max Planck Society, Max-Planck Institute, Frankfurt am Main, Germany
Much is known about the computation in individual neurons in the cortical column. Also, the selective connectivity between many cortical neuron types has been studied in great detail. However, due to the complexity of this microcircuitry its functional role within the cortical column remains a mystery. Some of the wiring behavior between neurons can be interpreted directly from their particular dendritic and axonal shapes. Here, I describe the dendritic density field (DDF) as one key element that remains to be better understood. I sketch an approach to relate DDFs in general to their underlying potential connectivity schemes. As an example, I show how the characteristic shape of a cortical pyramidal cell appears as a direct consequence of connecting inputs arranged in two separate parallel layers.
The laws of time, space, and material conservation, which must be considered the final cause of all variations in the shape of neurons, should in our view be immediately obvious to anyone thinking about or trying to verify them, and ought to constitute the final proof of our axopetal polarity theory. All that remains is to substantiate the influence of these laws on the conformation of particular neurons.
Cortical circuits are modular and subdivide functionally into cortical columns (Mountcastle, 1957; Hubel and Wiesel, 1962). While it remains controversial as to how stringent this organizational principle is (Horton and Adams, 2005) and the advantages for such an organization remain largely unknown (Malach, 1994), the importance of understanding the columnar organization of the cortex is undisputed. In order to understand the computation occurring in the single column, the principles underlying its local circuitry need to be fully understood. Physiological analyses (e.g., through multiple simultaneous recordings) in combination with anatomical characterizations of the individual neurons involved were successful in unraveling many details of local cortical connectivity (e.g., Szentágothai, 1975; Douglas and Martin, 2004; Lübke and Feldmeyer, 2007). Anatomically, evidence exists that neurons send out their dendrites to allow potential connections (points of anatomical proximity; Stepanyants and Chklovskii, 2005) to the axons of all neurons of their particular target neuron types within their column (Lübke et al., 2003; Douglas and Martin, 2004; Kalisman et al., 2005). To which degree neurons in the cortical column form such an anatomical substrate which allows for all combinations of functional connections remains the subject of debate (e.g., DeFelipe et al., 2002; Shepherd et al., 2005). Whether anatomical connections target specific individual cells probably depends on the neuron type (Stepanyants et al., 2004). Functionally then, only subsets of the anatomical potential connections are in use and highly non-random features have been observed in the corresponding functional connectivity map (Song et al., 2005). Selecting functional synapses among anatomical potential connection sites may happen through spine rearrangement, a rewiring which does not require reshaping entire dendritic branches (e.g., Stepanyants et al., 2002; Chklovskii et al., 2004).
Are dendrites and axons then ideally matched to anatomically maximize connections to their potential connection partners? Theoretical predictions from optimality criteria are indeed in line with this idea (Wen et al., 2009). For dendrites and axons, wiring principles and branching patterns are certainly intertwined (Chklovskii, 2004; Cuntz et al., 2007; Wen and Chklovskii, 2008; Budd et al., 2010). Moreover, branching patterns can actually be predicted based predominantly on wiring principles (Cuntz et al., 2010). Simulation approaches such as these deepen our insights by testing whether the theoretical predictions are valid under realistic conditions. In order to simulate anatomical connections between neurons, model assumptions for both dendrite and axon morphologies are required. One approach is to estimate synaptic connectivity based on anatomical neuron models obtained from neuron reconstructions (Lübke et al., 2003; Douglas and Martin, 2004; Fares and Stepanyants, 2009) or by simulating the mechanisms of dendrite and axon growth (Koene et al., 2009; van Pelt et al., 2010). The second approach is to predict dendrite and axon morphologies according to the optimal implementation of a particular connectivity scheme and compare the results with biological data. In the following, I will briefly describe the method of morphological modeling (Cuntz et al., 2008, 2010) which follows this second strategy. From there I will make a direct link between a specific connectivity pattern and the corresponding dendritic tree. In the process I will show how the dendritic density field (DDF) can be estimated on the basis of this link.
The Dendritic Density Field and Morphological Modeling
We have shown previously that by extending the minimum spanning tree (MST) algorithm it is possible to connect a set of point targets which are distributed in space to satisfy biological optimization costs of dendritic trees (Cuntz et al., 2007). The required cost function is composed of two individual costs (Figure 1A): the total amount of wiring (cable length cost) and the cost of signal conduction (path length cost: the sum of the length of all paths along the tree from any target point to the root) corresponding well with costs originally proposed by Ramón y Cajal (1909). When a set of target points is adequately selected, any dendritic tree morphology can be reproduced after connecting the target points to a tree using the MST algorithm. This approach represents a method of morphological modeling useful for generating realistic synthetic dendritic trees (Cuntz et al., 2010). The sketch in Figure 1B shows a synthetic starburst amacrine cell which was generated by distributing target points stochastically according to a geometrical arrangement of densities. Target points are then connected to a tree structure whilst observing the wiring costs mentioned above. This simple procedure highlights the usefulness of a DDF, here representing the density of target points per area, to describe a dendrite’s morphology. The DDF and the one parameter balancing the two costs for wiring mentioned above are thereby sufficient to describe the dendrite type. In fact, we have previously shown that for fly interneurons the spanning field is the most informative element for classifying dendritic trees into their respective cell types (Cuntz et al., 2008). In some cases, DDFs can be obtained directly from reconstructions of real neurons. By superimposing their soma locations and rotating them such that they lie symmetrically around the y-axis and then scaling their width, height, and depth, a set of reconstructions of dentate gyrus granule cell (data from Rihn and Claiborne, 1990) dendrites are brought into a common context. An appropriate approximation of the DDF is then obtained directly from the density of branch and termination points from the reconstructions (Figure 1C). When apical and basal dendrites are considered separately, the DDFs of pyramidal cells can be calculated in a similar way (L5 PCs, Figure 1D; data from Wang et al., 2002).
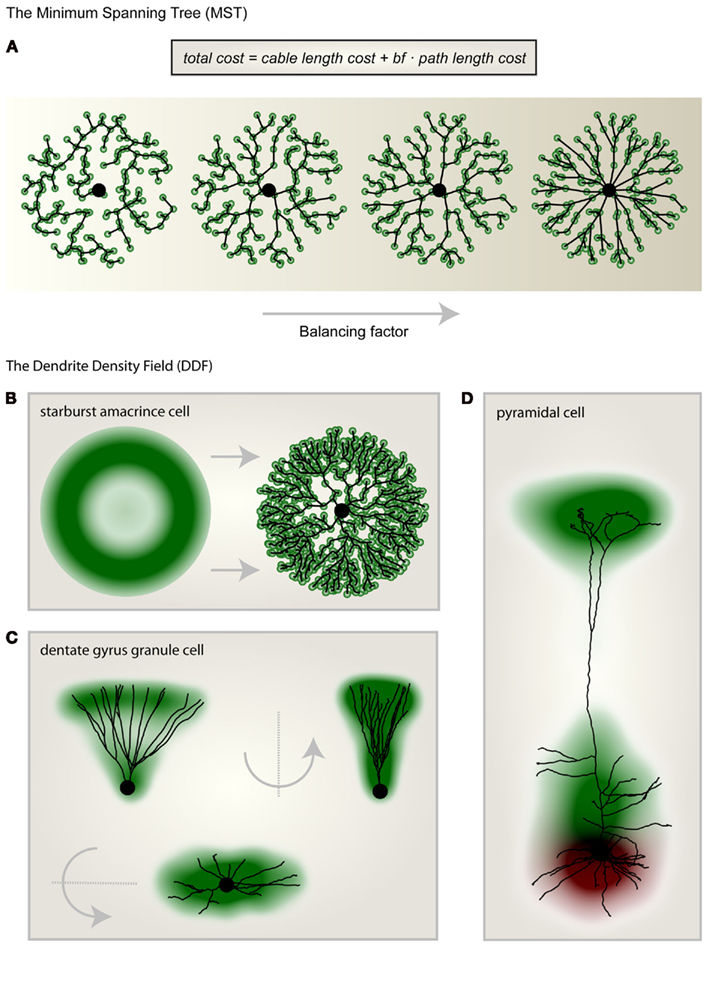
Figure 1. Morphological modeling and the dendritic density field (DDF). (A) From left to right the same set of unconnected target points (green) were connected to a starting point (large black dot) according to the minimum spanning tree (MST) algorithm with increasing balancing factor bf between the two wiring costs: total cable length and sum of all paths. (B) Geometric description of the DDF of a starburst amacrine cell (left). By randomly selecting target points according to the DDF and subsequently connecting them using the MST algorithm (right) to a starting node (large black dot), a synthetic starburst amacrine cell dendrite can be generated. (C) The DDF obtained directly from reconstructions of dentate gyrus granule cells with its characteristic cone-like shape. A representative real morphology is shown. (D) Separate DDFs for L5 cortical pyramidal cell basal trees (red) and apical trees (green). One representative real morphology is shown. Parts of the figure were adapted from Cuntz et al. (2010).
Predicting the Dendritic Density Field from Input Axon Configurations
While the dendrites of starburst amacrine cells, dentate gyrus granule cells, and many other neurons exhibit complex DDFs, some simpler ones such as pyramidal cell basal dendrites observe basic principles which can be characterized by studying the statistical moments of their density distributions (Snider et al., 2010). Stevens and colleagues have shown that the cable density distributions in dendrites roughly follow separate Gaussian distributions for each dimension in space which are cut off at 2 standard deviation. What determines this particular density profile? In synthetic dendrites generated using the MST, homogenously distributed carrier points lead to a homogeneous cable density. The MST alone can therefore not be responsible for the observed Gaussian cable density distribution. Intuitively, the shape of a DDF should be determined by the set of axons which are a dendrite’s potential, i.e., anatomical connection partners. This simple intuition can provide direct explanations for basic features of DDFs.
When input target points were distributed along one dimension, the MST was simply a straight line connecting these points (Figure 2A). When these target points were extended to parallel lines as in Figure 2B, and the MST was set to connect to each axon once, the resulting synthetic dendrite was not changed. Out of cable and conduction time minimization, a straight and direct connection remained ideal. When more axons were added and noise was introduced to their trajectories (Figure 2C), the MST dendrite started to branch out. In a similar but more realistic setting, a dendrite connecting to a set of parallel axons traversing space was flat according to the MST (Figure 2D). A flat dendrite which lies perpendicular to a set of parallel axons was shown to be the overall ideal geometrical arrangement given Cajal’s wiring costs (Wen and Chklovskii, 2008). It is therefore not surprising that the MST approach reproduces this intuition. Such a planar dendritic structure can be observed in cerebellar Purkinje cells for example which reach out to the molecular layer to collect their parallel fiber inputs. These being arranged entirely in parallel the dendrite must grow in a planar way perpendicular to the parallel fibers to connect to them most efficiently.
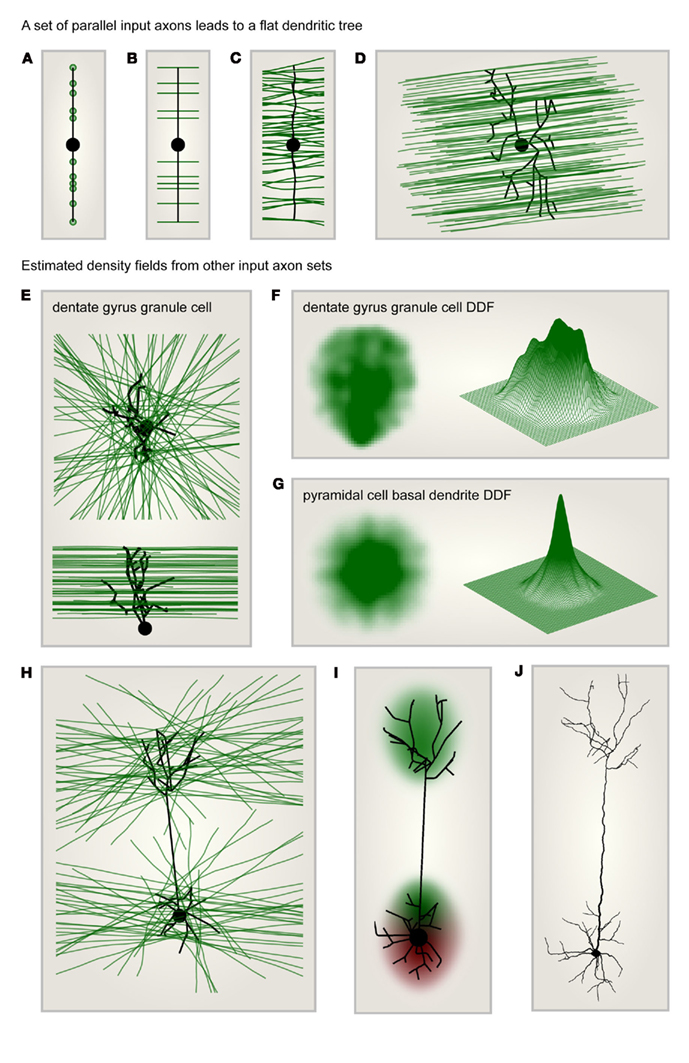
Figure 2. Dendritic density field (DDF) estimation directly from input axon distributions. (A) Target points (green) lying on one line are connected to a starting node (large black dot) using the MST algorithm. This leads to a dendrite consisting of a single line. (B) Same as in (A) but targets are parallel lines (axons, green) rather than points. The optimal dendrite connecting to these axons is the same as in (A). (C) Same as in (B) but the number of target axons is increased and the axon trajectories are slightly jittered: the MST is slightly jittered and a few branch points appear. (D) Synthetic dendrite (black) connecting a starting point (large black dot) in 3D space to a set of parallel axons (green): the resulting MST is flat. (E) Target axons (green) are arranged in parallel planes but are of isotropic orientation within these planes. The axons are connected using MST (black tree) to a starting point (large black dot) located below the layer of axons. Top: view from the top; bottom: view from the side. The result is a typical dentate gyrus granule cell morphology. (F) DDF of 50 synthetic granule cells grown as in (E); compare with Figure 1C. Left: side view of density profile; right: mesh representation of the same density distribution. (G) Same as in (F) but the starting point was moved to the center of the layer to reproduce the characteristic shape of the basal tree of a cortical pyramidal cell. (H) Same as in (E) but the MST connects to axons located in two parallel layers. The starting point is located in the middle of the lower layer. The result is a characteristic pyramidal cell shape. (I) DDF of 100 synthetic pyramidal cells grown as in (H); compare with Figure 1D. (J) One such synthetic pyramidal cell where diameter values were mapped onto the dendritic segments and spatial jitter was added along the dendrite.
Most neural systems however are not entirely optimized for the connection between only one set of axons and one dendrite type. Axon distributions are therefore more complex. In order to illustrate the potential of this constructive approach, I demonstrate in the following how a few sample input axon sets would impact on the resulting MST dendrites and therefore on their average DDF. The first case scenario that I chose exhibits a set of axons which were located in parallel neighboring planes forming a neuronal layer. Within their respective planes, the axons were isotropically oriented and the starting point, the root of the dendrite, was positioned below the layer of axons. Only the axons passing in close vicinity with a cutoff at half of the thickness of the layer were considered (Figure 2E). In such a configuration the distribution of axons was homogeneous. However, the resulting MST dendrite grew a shape reminiscent of dentate gyrus granule cell dendrites and exhibited an inhomogeneous DDF (Figure 2F). When the starting point was moved to the center of the axonal layer, this resulted in an isotropic DDF similar to a pyramidal cell basal dendritic density profile (Figure 2G). It is possible that such a DDF follows similar features as the dendritic cable densities measured previously (Snider et al., 2010; Teeter and Stevens, 2011). Note that the precise relation between density of topological points in a dendrite and dendrite cable density has yet to be studied in detail. In any case, it will be possible to find the type of arrangement of input axons which generally reproduces their measures, thereby unveiling general principles of axon arrangements and connectivity patterns. To finish, I would like to suggest a last sample configuration in which two separate layers of axons similar to the one previously described were both connected to a single starting point located in the middle of the lower of the two layers (Figure 2H). Under these conditions, the natural shape of a pyramidal cell, including its apical dendrite and its two separate DDFs (Figure 2I) were a natural consequence. When biological jitter and diameter values were mapped onto the corresponding tree structure (as in Cuntz et al., 2010), this resulted in a biologically realistic pyramidal cell (Figure 2J).
Outlook
I have shown that morphological models can provide more than just anatomical profiles for realistic neural network simulations. They can also be a tool to understand how dendrite morphology comes about and a tool to test our knowledge about the local connectivity in the brain. This short exercise provides once more evidence that the major determinant for a dendrite’s morphology is its role in the connectivity. It is well known that morphology particularly in cortical pyramidal cells plays a role for the intrinsic computation that a single neuron performs on its inputs (Vetter et al., 2001; Polsky et al., 2004; Sjöström and Häusser, 2006; Branco et al., 2010). The role of morphology on single neuron computation, and vice versa, can also be studied using morphological modeling. In the morphological model, neuronal computation is affected in various ways. The main morphological parameter which impacts neuronal computation is the balancing factor bf between the two wiring costs (Figure 1A). We have previously shown that a large bf promotes a higher electrotonic compartmentalization of the resulting synthetic dendritic tree (Cuntz et al., 2010). This adds to the natural increase in conduction time speeds which is favored with increasing bf to the detriment of wiring economy. Secondly, dendritic diameters play a role in dendritic signal integration. We have previously attributed diameter tapering to synaptic democracy. However, only electron microscopy reconstructions (e.g., Kubota et al., 2011) will resolve the precise role of diameter distributions on the electrotonic properties of a dendrite. Lastly, to implement a given computation, the single neuron can select a subset out of a large variety of possible ion channel combinations which may be adapted to suit the underlying morphological template (Prinz et al., 2003). Interestingly, the toy model of a pyramidal cell presented here does not build on any functional differences between the two layers that it connects. The location of the starting point alone determines which of the layers will yield an apical dendrite and which one a basal dendrite. This dendrite root corresponds to the summation point of the input signals but more importantly it is the coordinate from which the axon, the output of the neuron, exits the cell. The fact that the location of the exiting axon determines the neuron’s shape was at the center of Cajal’s axopetal polarity theory. In the cortex, most long-range axons project toward the white matter away from the pial surface. We would therefore predict a stereotypic polarity of pyramidal cell morphology: Basal dendrites of pyramidal cells should be on the inside closer to the white matter, whereas the apical dendrites should be on the pial side. This indeed is the case. At the example of the pyramidal cell dendrite I showed that it is possible to predict both their DDF and their precise branching structure by making assumptions about the input axon distribution. In this way it might for example be possible to link regionalized specializations in pyramidal cell dendrite shape (Elston, 2003) with differences in local connectivity. To summarize, I have shown that the DDF is a promising attribute of dendrite shape which enables direct conclusions on the arrangement of a neuron’s axonal inputs.
Methods
The methods presented here have been discussed in depth in previous reports (Cuntz et al., 2007, 2008, 2010, 2011) and the corresponding code is available at www.treestoolbox.org.
Extension to the MST Algorithm
The original MST algorithm was implemented as an iterative process which connects unconnected target points one at a time to an existing tree structure following the wiring costs mentioned in the text (Figure 1A; see Cuntz et al., 2007). The algorithm was adapted to allow labeling of groups of target points. When a target point is connected to the tree, the remaining target points in the same group become unavailable for the algorithm in the further process. Target input axons were then implemented as labeled groups of target points distributed in close intervals along the trajectory of the respective axons. This was tested in Figures 2B–D on simple parallel axon trajectories including a slight spatial jitter in Figure 2C (50 axons) and 2D (100 axons). The resulting MST dendrite grown to connect a set of parallel axons was flat in all cases (Figure 2D).
Granule Cell Morphological Model
For the dentate gyrus granule cell model in Figures 2E,F, the set of axons was generated by randomly selecting X and Y coordinates and a random angle for each axon within a 1.5-mm × 1.5-mm plane and drawing straight lines with these coordinates. Three hundred axons were generated in this way and a random Z-value between 0 and 250 μm was associated to each axon. The starting point for the dendrite was located 25 μm below the axonal layer and in the center of the XY plane. Only axons passing in 125 μm of the center of the axonal layer were selected resulting on average in a set of around 60 axons. Target points were distributed every 50 μm along the axons. The resulting synthetic granule cells had an average of 20 branch points.
Pyramidal Cell Morphological Model
For the pyramidal cell basal dendrite in Figure 2G, the procedure for Figures 2E,F was reproduced after moving the starting point to the center of the axonal layer. For the complete pyramidal cell model in Figure 2H–J, two layers similar to the granule cell axonal layer from Figures 2E,F were generated with 200 axons each. Around 30–40 axons were selected by the same 125 μm sharp cutoff criterion. The starting point for the dendrite was located in the center of the lower axonal layer.
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
I am grateful to Alexander Borst, Alexandre Mathy, and Arnd Roth for their helpful discussions and comments on the manuscript.
References
Branco, T., Clark, B. A., and Häusser, M. (2010). Dendritic discrimination of temporal input sequences in cortical neurons. Science 329, 1671–1675.
Budd, J. M. L., Kovács, K., Ferecskó, A. S., Buzás, P., Eysel, U. T., and Kisvárday, Z. F. (2010). Neocortical axon arbors trade-off material and conduction delay conservation. PLoS Comput. Biol. 6, e1000711.
Chklovskii, D. B. (2004). Synaptic connectivity and neuronal morphology: two sides of the same coin. Neuron 43, 609–617.
Chklovskii, D. B., Mel, B. W., and Svoboda, K. (2004). Cortical rewiring and information storage. Nature 431, 782–788.
Cuntz, H., Borst, A., and Segev, I. (2007). Optimization principles of dendritic structure. Theor. Biol. Med. Model. 4, 21.
Cuntz, H., Forstner, F., Borst, A., and Häusser, M. (2010). One rule to grow them all: a general theory of neuronal branching and its practical application. PLoS Comput. Biol. 6, e1000877.
Cuntz, H., Forstner, F., Borst, A., and Häusser, M. (2011). The TREES toolbox probing the basis of axonal and dendritic branching. Neuroinformatics 9, 91–96.
Cuntz, H., Forstner, F., Haag, J., and Borst, A. (2008). The morphological identity of insect dendrites. PLoS Comput. Biol. 4, e1000251.
DeFelipe, J., Elston, G. N., Fujita, I., Fuster, J., Harrison, K. H., Hof, P. R., Kawaguchi, Y., Martin, K. A., Rockland, K. S., Thomson, A. M., Wang, S. S., White, E. L., and Yuste, R. (2002). Neocortical circuits: evolutionary aspects and specificity versus non-specificity of synaptic connections. Remarks, main conclusions and general comments and discussion. J. Neurocytol. 31, 387–416.
Douglas, R. J., and Martin, K. A. C. (2004). Neuronal circuits of the neocortex. Annu. Rev. Neurosci. 27, 419–451.
Elston, G. N. (2003). Cortex, cognition and the cell: new insights into the pyramidal neuron and prefrontal function. Cereb. Cortex 13, 1124–1138.
Fares, T., and Stepanyants, A. (2009). Cooperative synapse formation in the neocortex. Proc. Natl. Acad. Sci. U.S.A. 106, 16463–16468.
Horton, J. C., and Adams, D. L. (2005). The cortical column: a structure without a function. Philos. Trans. R. Soc. Lond. B Biol. Sci. 360, 837–862.
Hubel, D. H., and Wiesel, T. N. (1962). Receptive fields, binocular interaction and functional architecture in the cat’s visual cortex. J. Pysiol. 160, 106–154.
Kalisman, N., Silberberg, G., and Markram, H. (2005). The neocortical microcircuit as a tabula rasa. Proc. Natl. Acad. Sci. U.S.A. 102, 880–885.
Koene, R. A., Tijms, B., vanHees, P., Postma, F., deRidder, A., Ramakers, G. J. A., van Pelt, J., and van Ooyen, A. (2009). NETMORPH: a framework for the stochastic generation of large scale neuronal networks with realistic neuron morphologies. Neuroinformatics 7, 195–210.
Kubota, Y., Karube, F., Nomura, M., Gulledge, A. T., Mochizuki, A., Schertel, A., and Kawaguchi, Y. (2011). Conserved properties of dendritic trees in four cortical interneuron subtypes. Sci. Rep. 1, 89.
Lübke, J., and Feldmeyer, D. (2007). Excitatory signal flow and connectivity in a cortical column: focus on barrel cortex. Brain Struct. Funct. 212, 3–17.
Lübke, J., Roth, A., Feldmeyer, D., and Sakmann, B. (2003). Morphometric analysis of the columnar innervation domain of neurons connecting layer 4 and layer 2/3 of juvenile rat barrel cortex. Cereb. Cortex 13, 1051–1063.
Malach, R. (1994). Cortical columns as devices for maximizing neuronal diversity. Trends Neurosci. 17, 101–104.
Mountcastle, V. B. (1957). Modality and topographic properties of single neurons of cat’s somatic sensory cortex. J. Neurophysiol. 20, 408–434.
Polsky, A., Mel, B. W., and Schiller, J. (2004). Computational subunits in thin dendrites of pyramidal cells. Nat. Neurosci. 7, 621–627.
Prinz, A. A., Billimoria, C. P., and Marder, E. (2003). Alternative to hand-tuning conductance-based models: construction and analysis of databases of model neurons. J. Neurophysiol. 90, 3998–4015.
Ramón y Cajal, S. (1909). Histologie du système nerveux de l’homme et des vertébrés. Paris: Maloine. [Quote: from engl. translation by Swanson N. and Swanson L. W. (1995). Histology of the nervous system of man and vertebrates. Oxford University Press. Vol. 1, Chap. 5, p. 116].
Rihn, L. L., and Claiborne, B. J. (1990). Dendritic growth and regression in rat dentate granule cells during late postnatal development. Brain Res. Dev. Brain Res. 54, 115–124.
Shepherd, G. M. G., Stepanyants, A., Bureau, I., Chklovskii, D. B., and Svoboda, K. (2005). Geometric and functional organization of cortical circuits. Nat. Neurosci. 8, 782–790.
Sjöström, P. J., and Häusser, M. (2006). A cooperative switch determines the sign of synaptic plasticity in distal dendrites of neocortical pyramidal neurons. Neuron 51, 227–238.
Snider, J., Pillai, A., and Stevens, C. F. (2010). A universal property of axonal and dendritic arbors. Neuron 66, 45–56.
Song, S., Sjöström, P. J., Reigl, M., Nelson, S., and Chklovskii, D. B. (2005). Highly nonrandom features of synaptic connectivity in local cortical circuits. PLoS Biol. 3, e68.
Stepanyants, A., and Chklovskii, D. B. (2005). Neurogeometry and potential synaptic connectivity. Trends Neurosci. 28, 387–394.
Stepanyants, A., Hof, P. R., and Chklovskii, D. B. (2002). Geometry and structural plasticity of synaptic connectivity. Neuron 34, 175–288.
Stepanyants, A., Tamás, G., and Chklovskii, D. B. (2004). Class-specific features of neuronal wiring. Neuron 43, 251–259.
Szentágothai, J. (1975). The “module-concept” in cerebral cortex architecture. Brain Res. 95, 475–496.
Teeter, C. M., and Stevens, C. F. (2011). A general principle of neural arbor branch density. Curr. Biol. 21, 2105–2108.
van Pelt, J., Carnell, A., de Ridder, S., Mansvelder, H. D., and van Ooyen, A. (2010). An algorithm for finding candidate synaptic sites in computer generated networks of neurons with realistic morphologies. Front. Comput. Neurosci. 4:148.
Vetter, P., Roth, A., and Häusser, M. (2001). Propagation of action potentials in dendrites depends on dendritic morphology. J. Neurophysiol. 85, 926–937.
Wang, Y., Gupta, A., Toledo-Rodriguez, M., Wu, C. Z., and Markram, H. (2002). Anatomical, physiological, molecular and circuit properties of nest basket cells in the developing somatosensory cortex. Cereb. Cortex 12, 395–410.
Wen, Q., and Chklovskii, D. B. (2008). A cost-benefit analysis of neuronal morphology. J. Neurophysiol. 99, 2620–2328.
Keywords: modeling, dendrite, axon, pyramidal cell, Ramón y Cajal
Citation: Cuntz H (2012) The dendritic density field of a cortical pyramidal cell. Front. Neuroanat. 6:2. doi: 10.3389/fnana.2012.00002
Received: 29 September 2011; Accepted: 11 January 2012;
Published online: 01 February 2012.
Edited by:
Julian Budd, University of Sussex, UKReviewed by:
Armen Stepanyants, Northeastern University, USAGuy Elston, International Brain Research Organization, Switzerland
Copyright: © 2012 Cuntz. This is an open-access article distributed under the terms of the Creative Commons Attribution Non Commercial License, which permits non-commercial use, distribution, and reproduction in other forums, provided the original authors and source are credited.
*Correspondence: Hermann Cuntz, Institute of Clinical Neuroanatomy, Goethe-University, Theodor-Stern-Kai 7, D-60590 Frankfurt am Main, Germany. e-mail:aGVybWFubi5uZXVyb0BnbWFpbC5jb20=
