- 1 Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ, USA
- 2 Department of Zoology, Tel Aviv University, Tel Aviv, Israel
- 3 Department of Mathematics, Program in Applied and Computational Mathematics, Princeton University, Princeton, NJ, USA
- 4 Department of Kinesiology, University of Maryland, College Park, MD, USA
Animals’ ability to demonstrate both stereotyped and adaptive locomotor behavior is largely dependent on the interplay between centrally generated motor patterns and the sensory inputs that shape them. We utilized a combined experimental and theoretical approach to investigate the relative importance of CPG interconnections vs. intersegmental afferents in the cockroach: an animal that is renowned for rapid and stable locomotion. We simultaneously recorded coxal levator and depressor motor neurons (MN) in the thoracic ganglia of Periplaneta americana, while sensory feedback was completely blocked or allowed only from one intact stepping leg. In the absence of sensory feedback, we observed a coordination pattern with consistent phase relationship that shares similarities with a double-tripod gait, suggesting central, feedforward control. This intersegmental coordination pattern was then reinforced in the presence of sensory feedback from a single stepping leg. Specifically, we report on transient stabilization of phase differences between activity recorded in the middle and hind thoracic MN following individual front-leg steps, suggesting a role for afferent phasic information in the coordination of motor circuits at the different hemiganglia. Data were further analyzed using stochastic models of coupled oscillators and maximum likelihood techniques to estimate underlying physiological parameters, such as uncoupled endogenous frequencies of hemisegmental oscillators and coupling strengths and directions. We found that descending ipsilateral coupling is stronger than ascending coupling, while left–right coupling in both the meso- and meta-thoracic ganglia appear to be symmetrical. We discuss these results in comparison with recent findings in stick insects that share similar neural and body architectures, and argue that the two species may exemplify opposite extremes of a fast–slow locomotion continuum, mediated through different intersegment coordination strategies.
Introduction
In order to coordinate body segments and limbs for movement, animals rely on both central mechanisms and sensory inputs (Skinner and Mulloney, 1998; Friesen and Cang, 2001; Yu and Friesen, 2004; Borgmann et al., 2009; Zill and Keller, 2009; Puhl and Mesce, 2010). The former includes endogenously rhythmic and centrally coupled central pattern generator neural networks (CPGs) that generate alternating activity in antagonistic motor neurons (MNs). In contrast, afferent-based control depends on local sensory inputs to coordinate motion through feedback loops. Each of these control strategies has limitations and benefits, and it has been shown that they are used to a different degree in different animals moving through environments with different properties. Specifically, evidence from swimmers and undulatory crawlers indicate that central coupling, inherent to the rhythm-generating circuitry, is primarily responsible for intersegmental coordination (Hill et al., 2003 and refs. within), while legged locomotion studies suggest that local feedback plays a significant role in coordinating limbs: in insects (Ritzmann and Büschges, 2007; Borgmann et al., 2009), cats (Bouyer and Rossignol, 2003; Pearson, 2004), and humans (Yang and Gorassini, 2006). In particular, detailed studies of intersegmental coordination in the stick insect have shown that MNs innervating specific leg muscles of different legs are at most weakly coupled, and that local proprioceptive feedback is essential for functional walking gaits (Büschges, 2005; Borgmann et al., 2009). This is in accordance with theoretical predictions suggesting that when animals navigate slowly through a complex environment, where great flexibility and precision are required, motor activity is likely to be modulated by neural reflexes and sensory information (Koditschek et al., 2004; Holmes et al., 2006). In contrast, the need for sensory input, relatively slow neural processing, and subsequent muscular activation make feedback-based coordination unlikely in cockroaches, especially when running fast over rough terrain. Indeed, these insects are known for their remarkably stable, yet rapidly adaptable, locomotion that has been crucial for their evolutionary success; they have also motivated mathematical models of multi-legged locomotion and biologically inspired robotics.
In this paper we attempt to shed light on the neural mechanisms underlying inter-limb coordination in cockroaches: mechanisms which are as yet poorly understood, despite their relevance to our understanding of adaptive control in animals and machines. Specifically, we studied functional coordination among homologous MNs innervating different cockroach legs, when sensory feedback was completely blocked or allowed only from one intact stepping leg. These experiments allowed us to investigate how local movement-induced sensory inputs affect the activity of the different segmental CPGs. A key innovation is our use of a stochastic model of coupled phase oscillators that approximates the activity of motor circuits innervating different pairs of legs in the absence of sensory feedback. This model, described in detail in Kiemel and Cohen (1998), was used to estimate physiological properties such as natural bursting frequencies of, and functional coupling among, different hemiganglia. Both strongly coupled oscillators that differ substantially in endogenous frequencies and weakly coupled oscillators with similar frequencies can exhibit similar phase differences. Hence, the parameter estimation method was extended to utilize cycle-to-cycle variations and intersegmental delays in the data sequences to determine the impact of one oscillator on the other.
Materials and Methods
Neurophysiological Procedures
Experiments were conducted on adult female cockroaches (Periplaneta americana) obtained from our colony at Tel Aviv University. Since cockroaches are largely nocturnal, the colony was kept under a 12L:12D (light:dark) cycle, and all experiments were performed during the 12-h dark periods, when cockroaches are most active. Animals were briefly anesthetized in CO2 and fixed dorsal side up on a Sylgard plate (Sylgard 182 silicon Elastomer, Dow Corning Corp. Midland, MI, USA). An insect pin staple was gently pressed against the cockroach neck to decrease hemolymph loss during surgery. We performed experiments on animals whose brains had been removed, leaving their subesophageal ganglia (SEG) intact, to minimize descending influences while maintaining normal leg coordination during walking (Ridgel and Ritzmann, 2005). This was done by opening a small flap in the dorsal cuticle between the compound eyes and then cutting the circumesophageal connectives and the connectives to the antennae and eyes to surgically remove the brain. The staple pin was then slowly removed to allow gradual recovery of the hemolymph flow to the head, and the cuticular flap was sealed back by hemolymph coagulation.
After brain removal, animals were subjected to a second anesthesia in CO2 and fixed ventral side up to allow electrode implementation. All legs, except a specific stepping leg in the experiments presented in Sections “Influence of single Front-Leg Stepping” and “Movement-Induced Entrainment of Activity in Neighboring Hemiganglia,” were amputated either at the thorax–coxa joints or at the coxa–femur joints, to allow access to their motor nerves. The coxa of the hind and middle legs that were to be recorded from were rotated to expose their dorsal surfaces (following Pearson and Iles, 1970) and fixed to the thorax with a drop of wax. The soft cuticle connecting the dorsal coxal rim to the abdomen was removed, fat tissue and trachea were carefully cleared, and the coxal depressor muscles were moved laterally to expose nerves 6Br4 and 5r1 (Pearson and Iles, 1970) containing depressor and levator coxal MNs. This enabled bipolar 0.003 mm silver-wire hook electrodes, fixed to the overlying cuticle, to be manipulated under the nerves 6Br4 and 5r1. The nerves were lifted clear of the hemolymph to give good signal-to-noise ratios and were coated with petroleum jelly to prevent drying. To ensure that the hemiganglia that were to be recorded from were completely deafferented, we crushed the recorded nerves distally from the recording sites and cut all other nerves close to the ganglia.
After electrode fixation and implantation, animals were left for an hour to recover and then carefully rotated dorsal side up and suspended by their pronotum above a treadmill, to allow practically normal stepping with their single intact leg. Sequences of stepping movements on the lightweight, low-friction treadmill were recorded by a DC motor attached to the treadmill, serving as a tachometer for treadmill velocity. Analog voltage transmitted from the extracellular recordings and the DC motor were sampled, played back in real time and recorded at 10 kHz using a 4-channel differential amplifier (Model 1700 A-M Systems), an A-D board (Digidata 1200, Axon instruments), and Axoscope software (Axon instruments).
Data Analysis
Burst detection
Recorded data were first analyzed by means of routine spike (action potential) detection. Burst locations for a given spike sequence were determined by calculating a spike density function and locating local maxima. The spike density function was obtained by convoluting spike counts in time bins of t = 100 ms with a smooth Gaussian kernel (with σ = t/2). Each such maximum represents the center of activity of a burst and characterizes its location in time.
Evaluating physiological parameters from recorded data using maximum likelihood estimation
The sequences of burst times recorded from coxal MNs of the different hemiganglia were analyzed by fitting parameters of a stochastic model of two coupled phase oscillators [previously described by Kiemel and Cohen (1998) and Kiemel et al. (2003)], using a maximum likelihood estimation (MLE) method. This stochastic phase model (SPM) method was used to estimate the functional coupling strength and direction between pairs of oscillators. We focused on motor patterns recorded from pairs of hemiganglia; estimating right–left, contralateral, coupling within the meso- or meta-thoracic ganglia (R2–L2 or R3–L3), and ipsilateral connections between the meso- and meta-thoracic ganglia (R2–R3 and L2–L3).
Stochastic phase models provide a simple and plausible description of coupled neural oscillators at the level of burst outputs. They contain the three basic factors that determine the phase relationship between the oscillators: the coupling between them, the difference in their intrinsic frequencies, and sources of intrinsic (stochastic) variation. In the deterministic case, theoretical results show that phase models are good approximations of a general class of weakly coupled oscillators having similar uncoupled frequencies (e.g., Neu, 1979; Rand and Holmes, 1980; Ermentrout and Kopell, 1984). Thus, SPMs are natural candidates to describe weakly coupled oscillators influenced by noise. Kiemel et al. (2003) tested this idea by applying the SPM method to simulated data from two different models: coupled connectionist oscillators and coupled intrinsically bursting cells. In both cases, not only did the method perform well when coupling was weak, it also gave useful results for stronger coupling.
Following Kiemel and Cohen (1998), the SPM method is based on the following model:
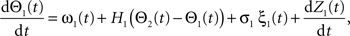
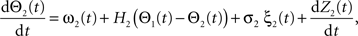
where the stochastic variables Θ1 and Θ2 are the absolute phases of the oscillators (e.g., corresponding to the state of R2–L2 or R2–R3 in each bursting cycle). These capture the timing of bursts in that Θj(t) (j = 1 or 2) passes through 0 (mod 1) at every burst center (plus some random measurement error). The functions ω1(t) and ω2(t) are the mean values at time t of the (slowly varying) uncoupled frequencies of the oscillators. As for lamprey data (Kiemel and Cohen, 1998; Kiemel et al., 2003), we found it adequate to model ωj(t) as a quadratic function of time:
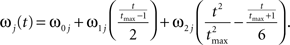
(We chose this specific form of ωj(t) so that ω0j and ω1j are the mean and net change, respectively, of ωj(t) over the trial of length tmax).
The functions H1 and H2 describe bidirectional coupling between the oscillators. Each has the form 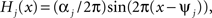 where αj is the coupling strength and ψj is the preferred phase, i.e., the stable relative phase Θk − Θj between the oscillators when noise and coupling in the other direction are absent and the frequencies ω1 and ω2 are equal.
where αj is the coupling strength and ψj is the preferred phase, i.e., the stable relative phase Θk − Θj between the oscillators when noise and coupling in the other direction are absent and the frequencies ω1 and ω2 are equal.
Noise in the absolute phase dynamics comes in two forms: continuous diffusion (white noise) and discontinuous jumps. The former was modeled by independent white-noise processes ξ1(t) and ξ2(t) with noise levels σ1 and σ2. The discontinuous jumps were modeled by independent compound Poisson processes Z1(t) and Z2(t) with rates ρ1 and ρ2 and jump sizes uniformly distributed on [−½, ½]. Diffusion modeled continuous changes in the instantaneous frequencies of the oscillators, whereas discontinuous jumps accounted for the possibility of more abrupt changes. Thus far, the model contains 14 parameters; four further ones, 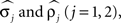 were used to describe measurement errors, that is, deviations of Θj(t) from zero when a burst time occurs (see Kiemel and Cohen, 1998 for details).
were used to describe measurement errors, that is, deviations of Θj(t) from zero when a burst time occurs (see Kiemel and Cohen, 1998 for details).
Parameters were estimated using MLE (Harvey, 1990). Initial parameter values were chosen to describe two weakly coupled oscillators. Specifically, values for parameters 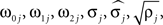
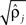 were based separately on each sequence of bursts j = 1, 2. We estimated
were based separately on each sequence of bursts j = 1, 2. We estimated 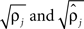 rather than
rather than 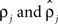 to insure that
to insure that 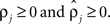 Initial coupling strengths were small (αj = 0.01), and initial preferred phases ψj were arbitrarily set to 0. Then, for any set of parameter values, the log of the likelihood P of the recorded data, given the parameter values, was computed as described in Kiemel and Cohen (1998).
Initial coupling strengths were small (αj = 0.01), and initial preferred phases ψj were arbitrarily set to 0. Then, for any set of parameter values, the log of the likelihood P of the recorded data, given the parameter values, was computed as described in Kiemel and Cohen (1998).
Parameters were adjusted to maximize the log-likelihood of the probability function using a quasi-Newton method. Let λ ∈ ℛ18 be the vector consisting of the 18 parameters defined above, and λ* denote values of the best fit, asymptotic 95% confidence intervals of the best fitting parameters were computed using the Hessian matrix A, where Alm = ∂2 (logP)/∂λl ∂λm at λ = λ* (Harvey, 1990; see Kiemel and Cohen, 1998 for further details).
We defined coupling strengths in terms of the stochastic averages of the slopes of the coupling functions Hj. As a simplification, we approximated the slowly varying mean frequencies ωj(t) by their values ωj,mid = ωj (tmax/2) at the midpoint of the trial. The uni-directional average absolute coupling strengths were defined as 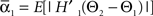 and
and 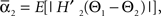 where “E” stands for “expected value,” and averaging was done over the equilibrium distribution of relative phases predicted by the fitted SPM (Kiemel and Cohen, 1998). The total absolute coupling strength was defined as
where “E” stands for “expected value,” and averaging was done over the equilibrium distribution of relative phases predicted by the fitted SPM (Kiemel and Cohen, 1998). The total absolute coupling strength was defined as 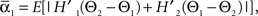 which we transformed by
which we transformed by 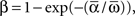 where
where 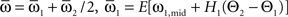 and
and 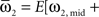
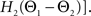 For phase-locked bursting, β is roughly the fraction of a relative-phase perturbation that is, on average, corrected after one cycle period; β ranges between β = 0 for no coupling and β = 1 for infinite-strength coupling. We described coupling asymmetry by the parameter
For phase-locked bursting, β is roughly the fraction of a relative-phase perturbation that is, on average, corrected after one cycle period; β ranges between β = 0 for no coupling and β = 1 for infinite-strength coupling. We described coupling asymmetry by the parameter 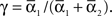 In particular, for the case of R2–R3 or L2–L3, γ is the ascending strength fraction, so that pure descending coupling corresponds to γ = 0 and pure ascending coupling to γ = 1.
In particular, for the case of R2–R3 or L2–L3, γ is the ascending strength fraction, so that pure descending coupling corresponds to γ = 0 and pure ascending coupling to γ = 1.
Calculation of confidence region for coupling strengths
In the final part of the analysis, we used likelihood-ratio tests to construct an asymptotic 95% confidence region for the coupling strength pair αH = (α1, α2). Specifically, to test whether a given αH is different from the maximum likelihood estimate α* mentioned above, we fitted the model with the restriction α = αH and compared the log-likelihood FH for the restricted model to the log-likelihood F* for the unrestricted model. Using standard asymptotic MLE theory (Harvey, 1990), we considered αH to be statistically different from α* if 2(F* − FH) was greater than the critical value of a χ2 distribution with ν = 2 degrees of freedom (the number of fixed parameters in the restricted model) at significance level 0.05. Then, the set of all αH, not significantly different from α*, form an asymptotic 95% confidence region.
Results
Motor Patterns Recorded from Deafferented Preparations
Recordings from nerves that contain the axons of MNs innervating the leg muscles in fully deafferented preparations revealed weak tonic spontaneous activity. In order to estimate intersegmental coupling among the different leg motor circuits, we tried to non-specifically increase the level of activity and elicit fictive locomotor patterns in leg MNs, in the absence of sensory feedback from walking legs, using neuromodulators (such as Octopamine, IBMX, and Pilocarpine). Among these, the muscarinic agonist pilocarpine, which is known to activate arthropod CPGs (Büschges et al., 1995), produced prolonged episodes of rhythmic bursting activity in thoracic leg MNs when applied to the thoracic cavity at a concentration of 1 × 10−4 M. The concentration of Pilocarpine was chosen to be the one that induced reliable bursting activity in most preparations. This concentration is in the range of the concentrations reported to induce rhythmic bursts in locusts (Ryckebusch and Laurent, 1993), crayfish (Chrachri and Clarac, 1987), and stick insects (Büschges et al., 1995). Lower concentrations (5 × 10−5 M) induced only a slight increase in tonic activity while higher concentrations (10−3 M and higher) often generated rapid, but not rhythmic, firing of the MNs.
The bursting episodes comprised alternating activity in antagonistic coxal depressor and levator MN groups, related to the stance and swing phases of a single stepping leg respectively (Figure 1A). Cycle periods occupied a broad range (mean bursting frequency 1.295 ± 1.16 Hz, n = 9), varying substantially between preparations and over long time scales within a single preparation (average coefficient of variation in a single preparation 0.301 ± 0.093). In several of our recordings we were able to positively identify specific units described by Pearson and Bergman (1969) and Pearson and Iles (1970, 1971). These include common inhibitory units (smaller spikes co-occurring in 6Br4 and 5r1 ), the slow depressor motor axon (larger units in 5r1, referred to as Ds in Pearson and Iles, 1970, 1971) and axons 5 and 6 that typically fire together in bursts of activity that are strongly reciprocal to the activity of Ds (Figure 1A). However, due to the nature of the preparation, this was not always possible, nor was it required for our model fitting. Hence we limited our physiological analysis to the level of the temporal characteristics of the rhythmic (multi unit) bursts.
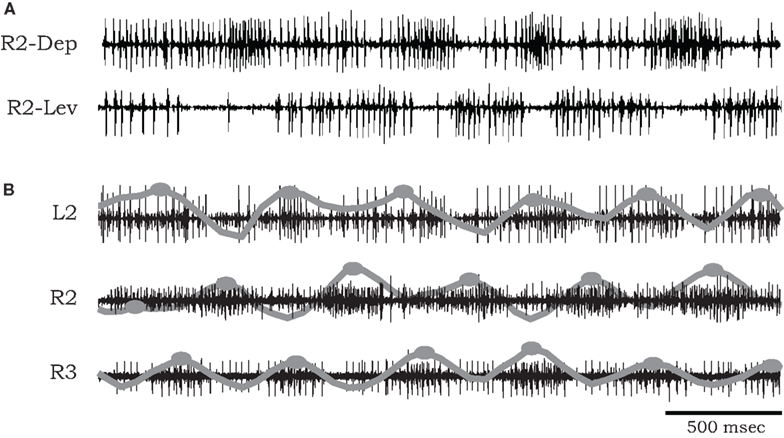
Figure 1. (A) Simultaneous extracellular recordings showing alternation of burst activity in antagonistic coxal depressor and levator motoneurons of the mesothoracic ganglia of a cockroach after application of pilocarpine. (B) Simultaneous recordings from coxal depressor MNs in R2, L2, and R3 in the presence of pilocarpine. Raw data are overlaid by local spike densities (gray lines) and burst centers used for phase difference analysis are marked by gray dots.
Phase relationships of motor activity among the different thoracic segments varied with time. On average, however, pilocarpine-activated MNs of neighboring contra- and ipsilateral hemiganglia tended to fire out of phase with similar characteristics to the cockroach’s predominant double-tripod gait. Specifically, segmental depressor burst activity alternated with contralateral depressor bursts and with depressor bursts in adjacent ipsilateral segments. Figure 1B shows an example of such a recording obtained from depressor MNs at the right and left sides of the mesothoracic ganglion (R2 and L2) and from the right side of the meta-thoracic ganglion (R3). Raw data are overlaid by the smoothed local spike densities (gray lines) used to locate burst peaks (gray dots). The corresponding phase differences between burst peaks of homologous (depressor and levator) coxal MNs innervating different legs (R2–L2, R2–R3, and R2–L3) are summarized in Figure 2. Each histogram shows the distribution of phase differences between a different pair of MNs, obtained from sequences of 50 burst cycles from each preparation (n = 5 preparations for R2–L2 and R2–R3 each and n = 4 for R2–L3, encompassing all the preparations that displayed bursting activity in at least two hemisegments simultaneously). Despite a relatively high degree of variability in phase relations, these experiments suggest the existence of central intersegmental coupling and a possibility of coordinated gaits in the absence of sensory feedback.
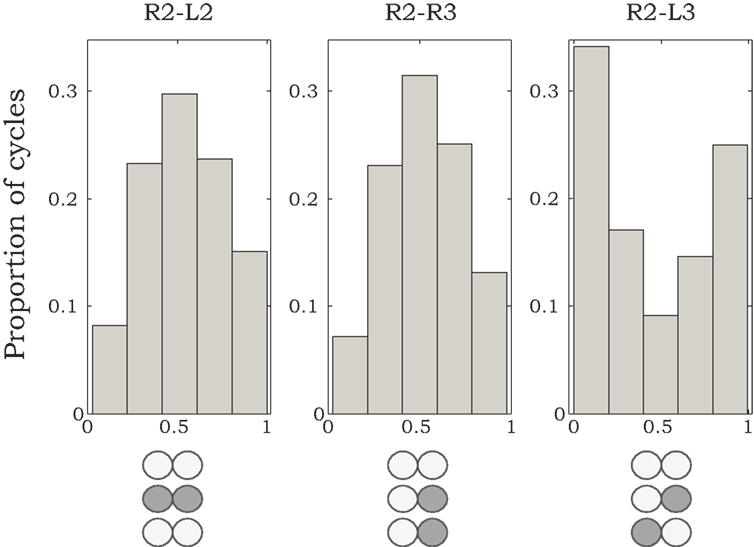
Figure 2. Histograms of phase differences in burst activity recorded from coxal MNs of R2–L2, R2–R3, and R2–L3. We analyzed data from nine animals, from which we could record burst activity from R2–L2 and R2–R3 in five preparations, and from R2–L3 in four preparations. Sequences of 50 burst cycles were taken for each preparation. Histogram areas are normalized to 1.
Influence of Single Front-Leg Stepping
Semi-intact preparations and simultaneous recordings from homologous MNs in different segments allowed us to test the influence of sensory feedback on neighboring motor units and intersegmental coordination. As demonstrated in Figure 3, we recorded coxal levator MNs activity in the mesothoracic ganglia of preparations with a single front or hind leg spontaneously stepping on a low-friction treadmill. To characterize phase delays between stepping and MN activity at the other segments, we averaged the spiking activity after each step of front (Figure 3A) or hind (Figure 3B) leg, using the beginning of stance (detected by the start of each treadmill acceleration) as the reference time. A characteristic time delay between a front-leg step and activity of the contralateral levator MN in the adjacent segment was 0.2 s (Figure 3A3), 0.18 s shorter than the average delay from steps of the contralateral adjacent hind leg (Figure 3B3).
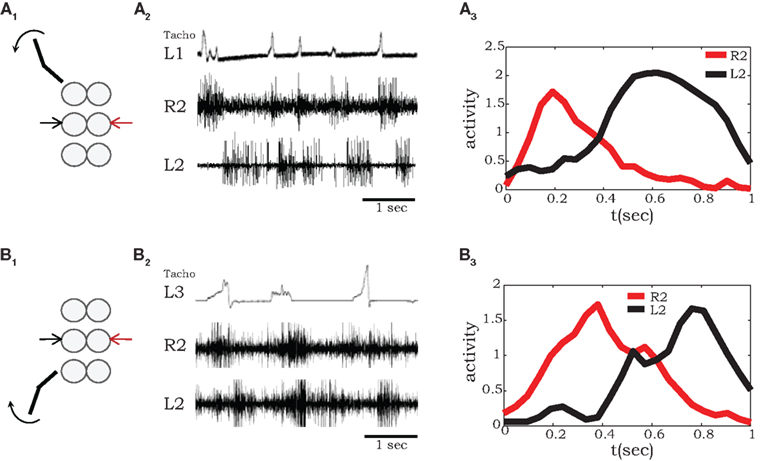
Figure 3. A single stepping leg elicits out-of-phase burst activity in neighboring ganglia. (A1,2) Simultaneous extracellular recordings from mesothoracic coxal levator MNs on both sides of the mesothoracic ganglion during single front-leg (L1) stepping (monitored by tachometer in the top panel). (A3) Shows averaged rectified activity in contralateral (red) and ipsilateral (black) levator MNs in the adjacent segment (R2 and L2) calculated from 16 sequential front-leg steps. Similarly, (B1,2) shows recordings from mesothoracic coxal levator MNs in a preparation with a single intact stepping hind leg (L3), while (B3) show the corresponding averaged spiking activity in contralateral (red) and ipsilateral (black) levator MNs of the mesothoracic ganglion (R2 and R3), calculated from 12 sequential hind leg steps.
Our results obtained with a single intact stepping front-leg are in accordance with those previously reported for stick insect locomotion (Ludwar et al., 2005; Borgmann et al., 2007, 2009). In both preparations, phasic information from the stepping leg passes caudally and entrains activity patterns in leg MNs of the mesothoracic ganglia (Figure 3A). However, unlike in stick insects, in the cockroach this entrainment maintained the anti-phase relationships among the motor circuits in neighboring hemiganglia, resulting in a coordination pattern that approximates a functional walking gait.
Movement-Induced Entrainment of Activity in Neighboring Hemiganglia
As noted above, in the absence of all leg sensory feedback, pilocarpine-activated bursts exhibited large cycle-to-cycle variability, both in burst frequency and phase relationship (Figure 2). However, as illustrated in Figure 4, in the presence of a stepping front-leg we observed transient stabilization of the phase differences between activities in the middle and hind thoracic MNs after each individual step of the single leg. Phase differences were calculated between burst centers estimated from levator MNs at the right sides of the meso- and meta-thoracic segments (R2 and R3, Figure 4A). Typical phase differences are plotted against time in Figure 4B, demonstrating reduced variability for several burst cycles following each step. Such transient entrainment was seen in four different experiments in which animals voluntarily stepped with an intact leg and in which simultaneous recordings were obtained from homologous MNs at the other segments. Phase difference histograms, plotted in Figure 4C, were calculated by partitioning these data (overall 18 stepping events of the four different animals) into discrete groups of bursts: the bursts occurring in the first three cycles after each step, bursts in the following three cycles, and bursts in the next three cycles. These clearly show the decay of entrainment. The relatively narrow distribution of phase relationships immediately after each step suggests movement-induced inter-leg sensory interactions and/or movement-induced neuromodulation of central coordination pathways. Hence, each step provides global feedback to modulate the overall motor program.
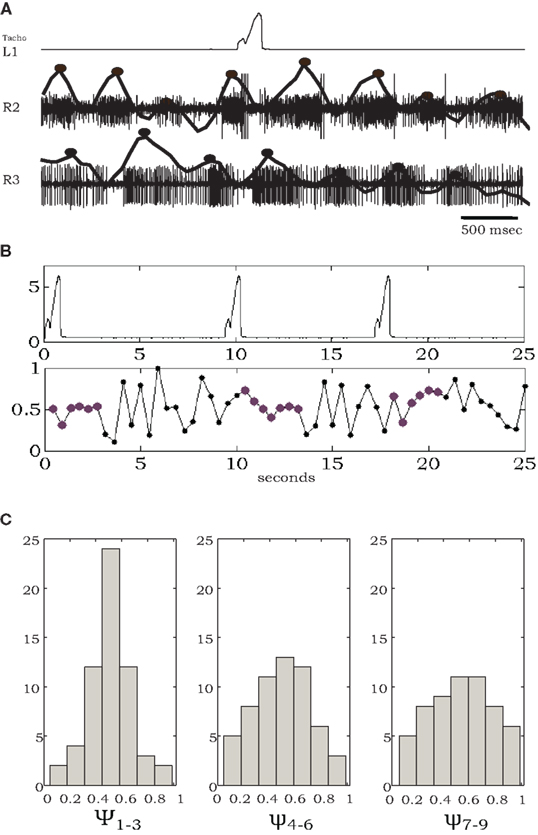
Figure 4. Individual steps entrain pilocarpine-activated bursts of leg MNs. (A) Simultaneous recordings of one front-leg step (tachometer, top) and extracellular activity of coxal levator MNs in R2 and R3, with spike density functions and estimated burst centers superimposed (solid lines and black dots). (B) A longer record showing multiple steps and corresponding phase differences between MN bursts in R2 and R3; note tighter phase-locking for several cycles after each individual step. (C) Histograms of phase differences, obtained from four experiments, each containing 4–5 steps, and the following nine burst cycles divided into the first, second, and third sets of three cycles after each step (see text for details). The relatively narrow distribution around phase 0.5 in ψ1–3 broadens in ψ4–6 and ψ7–9 as time elapsed after each step increases.
Estimated Values of Central Coupling Among Motor Circuits that Innervate Different Legs
We used the generic stochastic phase oscillator model, introduced above, to estimate natural bursting frequencies of the motor circuits in hemiganglia innervating the different legs and the directional coupling among them. As we have noted, in the absence of sensory feedback from walking legs, phase relationships between MNs in different hemiganglia show high variability with time. To estimate the underlying parameters, we simulated the motor units and searched for the parameter sets (λ) that best fit the recorded sequences. We estimated parameters separately for each pair of simultaneously recorded spike sequences in deafferented preparations: either two sides of a single segment to test contralateral coupling within a segment (R2–L2 and R3–L3, n = 4 preparations), or a pair of ipsilateral hemiganglia (R2–R3, n = 3) to test ipsilateral connections between meso- and meta-thoracic ganglia.
Figures 5A1,A2 respectively, show an example of the burst activity recorded simultaneously from levator MNs in R2 and L2 and the corresponding spike trains produced by simulating the SPM with parameters that best fit this data set. For demonstration purposes, we transformed the phases Θ1 and Θ2 of the simulated oscillators to spike trains clumped around burst centers (black dots) occurring when the corresponding phase Θj = 0. Following Kiemel and Cohen (1998), we defined burst widths b and firing rates f1 within and f0 between bursts so that the spike train of oscillator j at time t is given by fj(Θj(t)), where fj is a square wave function: fj(Θ) = f1j if −bj/2 < Θ < bj/2, otherwise fj(Θ) = f0j. To best match the experimental recordings, we set b1,2 = 0.4, f01 = 60 Hz, f02 = 80 Hz, f11 = 5 Hz, f12 = 15 Hz.
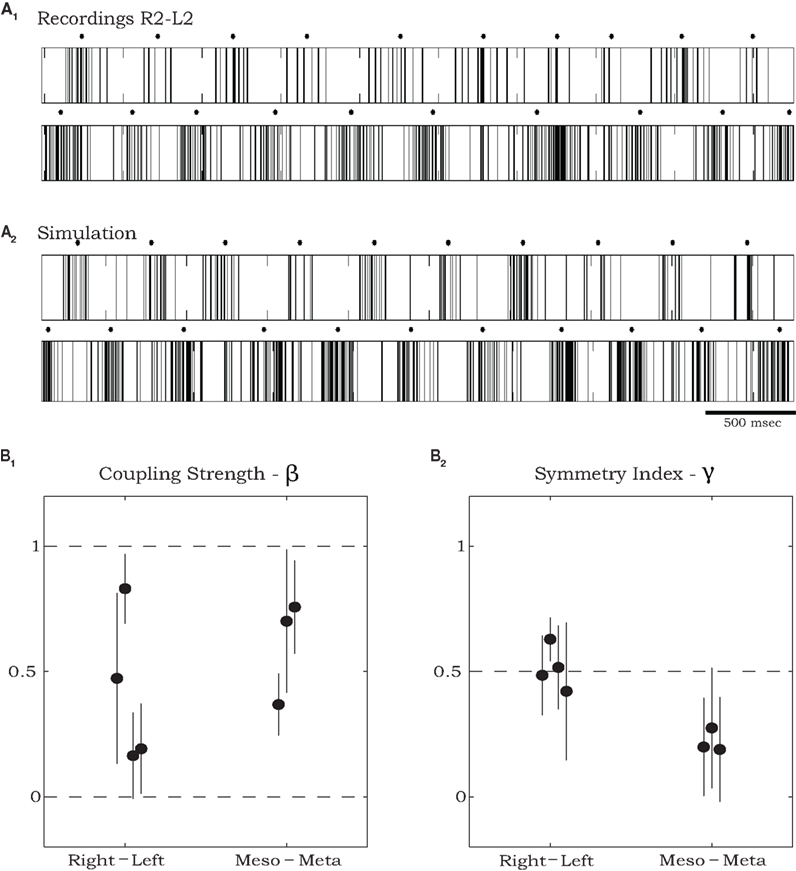
Figure 5. Estimating parameters of recorded sequences using simulations of the stochastic phase model. (A) An example of spike train recordings from R2 and L2 (A1), and corresponding spike trains of a simulated model (A2) with parameters that best fit the data shown in (A1). Black dots in (A1) and (A2) mark burst centers. Model parameters were: ω01 = 1.025 Hz, ω02 = 1.146 Hz, ω11 = −0.152 Hz, ω12 = 0.252 Hz, ω21 = 0.408 Hz, ω22 = 0.871 Hz, σ1 = 0.024 s−0.5, σ2 = 0.092 s−0.5, ρ1 = 0.129 s−1, ρ2 = 0.668 s−1, ψ1 = 0.376, ψ2 = 0.197, α1 = 0.730 s−1, α2 = 0.655 s−1 (see text for further details of spike train generation). (B) Estimated total coupling strength β (B1) and symmetry index γ (B2) for rhythmic burst sequences recorded from coxal MNs in deafferented cockroaches. Points on the left of each panel show values that best fit pairs of contralateral MNs (two from R2–L2 and two from R3–L3) and points on the right show values that best fit pairs of ipsilateral MNs in R2 and R3. Error bars denote asymptotic 95% confidence intervals. For the ipsilateral groups, the symmetry index indicates significantly stronger descending than ascending coupling strengths (γ < 0.5, p < 0.01 using t-test).
In the example shown in Figure 5A average burst frequencies, ω0, were 1.025 and 1.146 Hz for the left and right oscillators respectively. Overall the difference in estimated frequencies between each pair of oscillators, averaged over all our experiments, was 15.6%. In three of seven preparations, the fitting procedure suggested that oscillator frequencies ωj remained approximately constant throughout the records of >50 burst cycles (ω1j = ω2j ≈ 0: see the frequency expression in Evaluating Physiological Parameters from Recorded Data Using Maximum Likelihood Estimation). For the other four preparations, quadratic variations allowed by ω1j, ω2j ≠ 0 provided superior fits. Estimated values of total coupling strengths and symmetry indices (see Materials and Methods), along with their asymptotic 95% confidence intervals, are plotted in Figure 5B. Estimated values of total coupling strengths, β, normalized to range between 0 and 1, indicate significant coupling (higher than zero) between each pair of motor units recorded in the deafferented preparations. The estimated coupling strength values did not exhibit a significant difference between overall contralateral and ipsilateral coupling (Figure 5B1). However, values of the symmetry index γ = α1/(α1 + α2) indicate that while contralateral coupling is most likely to be symmetric (γ ≈ 0.5), ipsilateral coupling is not; in particular, descending connections are significantly stronger than ascending ones in all tested preparations (γ < 0.5).
Since we are primarily interested in estimating coupling strengths among the CPGs of the different legs, we maximized the likelihood of the data with coupling strengths (α1, α2) fixed at values between 0 and 1 while the remaining parameters 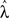 ∈ ℜ16 were allowed to vary. Maps of maximum log-likelihoods for different potential coupling strengths between R2–L2 (contralateral) and R2–R3 (ipsilateral) are plotted in Figure 6. While each map exhibits a unique maximum (corresponding to the coupling strengths predicted by λ*, cf. Figure 5B) they indicate a clear qualitative difference between the two cases. Boundaries of asymptotic 95% confidence regions were calculated using a likelihood-ratio test (see Materials and Methods). As can be seen, the area of good fit for the R2–R3 pair is characterized by descending strengths that are higher than ascending ones, while the area for the R2–L2 pair is more symmetric around its maximum, with equal left–right and right–left coupling strengths, in agreement with expected bilateral symmetry.
∈ ℜ16 were allowed to vary. Maps of maximum log-likelihoods for different potential coupling strengths between R2–L2 (contralateral) and R2–R3 (ipsilateral) are plotted in Figure 6. While each map exhibits a unique maximum (corresponding to the coupling strengths predicted by λ*, cf. Figure 5B) they indicate a clear qualitative difference between the two cases. Boundaries of asymptotic 95% confidence regions were calculated using a likelihood-ratio test (see Materials and Methods). As can be seen, the area of good fit for the R2–R3 pair is characterized by descending strengths that are higher than ascending ones, while the area for the R2–L2 pair is more symmetric around its maximum, with equal left–right and right–left coupling strengths, in agreement with expected bilateral symmetry.
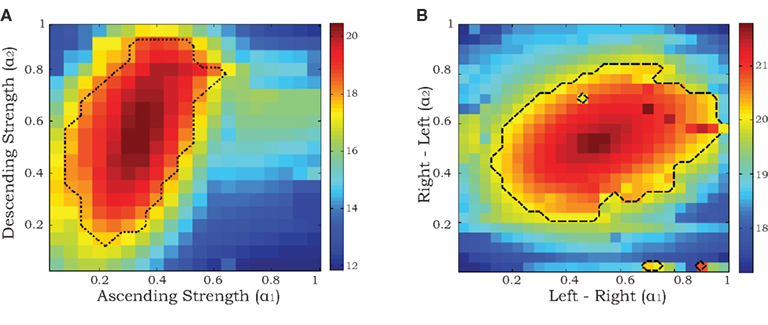
Figure 6. Maximum log-likelihoods for the data from recorded pairs of motor units (ipsilateral R2–R3 in A and contralateral R2–L2 in B) for the stochastic phase model with fixed values of coupling strengths α1 and α2 ranging from 0 to 1. The dashed curves denote the boundaries of asymptotic 95% confidence regions based on likelihood-ratio tests (see Materials and Methods).
The oscillator model we used is a stochastic version of the reduced phase models of lamprey and cockroach CPGs presented by Cohen et al. (1982, 1992), cf. Varkonyi et al. (2008), and Ghigliazza and Holmes (2004), which have been incorporated into neuromechanical models of swimming and insect running (Holmes et al., 2006; McMillen et al., 2008; Proctor et al., 2010). We anticipate that the parameter values estimated above and from similar experiments can be used to further improve such models.
Discussion
An animal’s ability to demonstrate stereotyped, consistent, or stable locomotor behavior that can, nonetheless, show large context-dependent variability and rich behavioral plasticity, is largely dependent on the interplay between centrally generated motor patterns and the sensory inputs that shape them. Oscillator coupling and intersegmental neuronal inputs have an important functional role in shaping the temporal characteristics of the rhythmic motor output and in stabilizing it.
In this study we investigated the relative importance of intersegmental afferent signals vs. central CPG interconnections for the coordination of cockroach locomotion. Using phase difference histograms and MLE, we find that, in the absence of sensory feedback, there is a consistent intersegmental coordination pattern that shares similarities with a double-tripod gait, the predominant stepping pattern in cockroaches (Delcomyn, 1971; Pearson and Iles, 1973). Sensory input from an individual stepping leg further reinforces the central coupling, resulting in a more functional (less variable) motor pattern, similar to the one exhibited in walking (Delcomyn, 1987).
Evidence that Central CPG Coupling Might Mediate Inter-Leg Coordination in Cockroaches
Despite the growing interest in understanding the mechanisms of animal locomotion control and coordination for the development of bio-inspired robotics, little is yet known about the neural basis of intersegmental coordination in legged animals. Previous work in the stick insect has shown that cycle-by-cycle coupling of intersegmental CPGs is seldom observed in deafferented ganglia (Büschges et al., 1995; Ludwar et al., 2005), suggesting that central mechanisms play at most a minor role in inter-leg coordination. This is also supported by evidence that selectively activated prothoracic CPGs do not drive the other segmental CPGs (Ludwar et al., 2005), and that movement-induced sensory feedback from an active (walking) front CPG can entrain activated ipsilateral middle- and hind leg walking CPGs to burst in phase with the front one (with front-leg movements), an activity pattern never seen in vivo (Borgmann et al., 2007, 2009).
As in the studies by Borgmann et al. (2007, 2009), our current observations in cockroaches show that single front-leg steps were always accompanied by a general activation of leg MNs in the neighboring hemiganglia (Figure 3). As suggested by Borgmann et al. (2007), such a general activation could result either from a change in the behavioral state of the whole locomotor system, or from a direct influence of the stepping front-leg on the neighboring segments. Although our current observations cannot exclude either of these mechanisms, they show that in cockroaches, in contrast to stick insects, such an excitatory drive to leg MNs suffices to create coordinated activity patterns with functional phasing. This, in turn, could enhance internal coupling among individual leg CPGs. Since similar, albeit weaker, phase relationships were also observed in entirely deafferented cockroach preparations following pilocarpine application, we suggest that both mechanisms provide excitatory modulation to activate the cockroach locomotor system. This excitation reinforces the coupling among the thoracic CPGs to coordinate leg movement in normal locomotion. Fitting a stochastic oscillator model and using a maximum likelihood method, we found that coupling strengths in the deafferented preparations were significantly greater than zero in all tested preparations.
We note that in the current study we have not attempted to fully characterize the elicited motor pattern in the presence of Pilocarpine, but only to investigate the existence of central coupling. A further analysis of the onset of bursts in levator and depressor MNs of the different legs when these are discharged at different rates would be required to characterize how similar they are to those exhibited during walking at different speeds – metachronal waves vs. tripod gait in slow and fast walking respectively (Delcomyn, 1971).
Movement-Induced Entrainment of the Walking CPGs
For controlling motor behavior, CPGs must act in a highly coordinated and self-regulated mode in order to demonstrate flexible modulation without losing their essential stability. The plasticity needed to generate continuously adjusting behavior is thus achieved via the endogenous capacity to show very large variations in output. In the lamprey spinal cord, a common model for the study of mechanisms of locomotory behavior, Ayali et al. (2007) demonstrated that the motor output of single unit oscillators in this complex system is characterized by high variability. This is, however, restricted by morphological and functional constraints (including descending, intersegmental, and sensory inputs) in the intact animal. Similarly, in the deafferented cockroach preparation, we always observed high variability in phase relationships among the different pairs of hemisegmental oscillators (Figures 1 and 2), even when frequency differences were relatively small (phases were entrained, but not locked).
We remark that the stochastic model chosen for the analysis employs pairs of oscillators with bidirectional interactions rather than hexapedal architecture with six oscillators such as that investigated by Ghigliazza and Holmes (2004). This was done to limit the number of fitting parameters, and because we were only able to record simultaneously from two or three hemisegments. The stochastic model produces phase relationships and spike patterns similar to those observed experimentally, and coupling strengths are found to be relatively weak (5–10% of uncoupled frequencies), as required by phase reduction and averaging theory (Ermentrout and Kopell, 1984), on which the model is based.
Sensory feedback is thought to be instrumental in central rhythm-generating networks: regulating phase relationships and adjusting movements during ongoing behavior (e.g., Pearson, 1995). We studied the effect of sensory feedback from single steps of one intact front-leg and showed a temporary stabilization of the burst phases in the two caudal hemiganglia. Specifically, tighter coupling between CPGs in the other thoracic segments lasted for several burst cycles after each step, reinforcing the central generated pattern in the actual movement.
To date, it is unknown whether inter-leg sensory interactions can be activated during stepping or whether such movement-induced entrainment is mediated through the neuromodulation of central coordination pathways following the behavioral input. The latter is supported by behavioral observations in stick insects demonstrating that strength and efficacy of inter-leg coupling depend on the specific behavioral context (Dürr, 2005). As mentioned above, the cockroach and stick insect exemplify opposite extremes of a fast–slow locomotion continuum and, furthermore, commonly reside in very different environments. The result may be that while these two insects share similar neural and body architectures, they may greatly differ in the degree to which their control and coordination of locomotion depends on sensory feedback (respectively approaching the extremes of a feedforward–feedback continuum). Integrating previous and new experimental observations of the two preparations with mathematical models such as those presented here and in Daun-Gruhn (2010) will aid in defining a common framework of intersegmental control strategies.
Rostro-Caudal Asymmetry in Intersegmental Coupling
Evidence for asymmetries in coupling between segmental oscillators has been previously suggested in the lamprey spinal cord. For example, when phasic movement stimuli were applied to the caudal or rostral ends of a spinal cord preparation over a range of frequencies, entrainment of the CPG was obtained over a greater range when movement was applied to the caudal rather than to the rostral end (McClellan and Sigvardt, 1988; Cohen et al., 1992). In addition, physiological and computer modeling results suggest that longitudinal coupling among lamprey segmental CPGs consists of ipsilateral excitatory connections that are stronger in the descending than the ascending direction (Hagevik and McClellan, 1994). Ayali et al. (2007) findings also suggest endogenous functional rostral–caudal asymmetry in the lamprey spinal cord. Such asymmetry could result from anatomical and physiological differences between rostral and caudal segments, either in segmental CPGs or at the level of proprioception (Tytell and Cohen, 2008). Although this has not yet been directly tested in lampreys, in Xenopus embryos a clear rostro-caudal longitudinal gradient in MNs and synaptic properties has been observed (Tunstall and Roberts, 1994).
Most legged locomotion involves a higher degree of segment specialization than the above, and hence greater longitudinal asymmetry is likely in connections among segmental oscillators. Currently, the neural basis of intersegmental coordination in walking CPGs is largely unknown (Ritzmann et al., 2004; Büschges and Gruhn, 2007). Behavioral experiments in stick insects testing the influence of perturbations of stepping movements of one leg on itself and on other legs have identified distinct rules that can establish inter-leg coordination, specifying the directions of such influences (Cruse, 1990; Dürr et al., 2004). Our estimated coupling parameters are consistent with these behavioral rules and provide estimates for the weights of the directional influence specified by Cruse (1990) and Dürr et al. (2004). Specifically, contralateral weights were observed to be similar, while descending influences were found to be stronger than ascending ones. This is in accord with the ipsilateral asymmetry among segmental CPGs observed by Hagevik and McClellan (1994), and with the indications of front-leg dominance that can be drawn from Borgmann et al. (2009).
This study contributes to our understanding of the neural basis of intersegmental coordination in cockroach locomotion. While our findings clearly show the instrumental role of central coupling they also suggest sensory modulation. Future studies are needed to further identify the intricate intersegmental connections, as well as fully elucidate the mechanisms by which different sensory pathways participate in the control of cockroach locomotion.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We thank A. Büschges and A. Borgmann for providing much useful help, advice and equipment for planning and establishing the experimental setup, and J. Proctor and T. David for ongoing discussion and contributions. This work was partially supported by the National Science Foundation under EF-0425878 (Frontiers in Biological Research), PHS grant MH62196 (Cognitive and Neural Mechanisms of Conflict and Control, Silvio M. Conte Center), and Princeton University under the J. Insley Blair Pyne Fund.
References
Ayali, A., Fuchs, E., Hulata, E., and Ben Jacob, E. (2007). The function of inter segmental connections in determining temporal characteristics of the spinal cord rhythmic output. Neuroscience 147, 236–246.
Borgmann, A., Hooper, S. L., and Büschges, A. (2009). Sensory feedback induced by front-leg stepping entrains the activity of central pattern generators in caudal segments of the stick insect walking system. J. Neurosci. 29, 2972–2983.
Borgmann, A., Scharstein, H., and Büschges, A. (2007). Intersegmental coordination: influence of a single walking leg on the neighboring segments in the stick insect walking system. J. Neurophysiol. 98, 1685–1696.
Bouyer, L. J. G., and Rossignol, S. (2003). Contribution of cutaneous inputs from the hindpaw to the control of locomotion. I. Intact cats. J. Neurophysiol. 90, 3625–3639.
Büschges, A. (2005). Sensory control and organization of neural networks mediating coordination of multisegmental organs for locomotion. J. Neurophysiol. 93, 1127–1135.
Büschges, A., and Gruhn, M. (2007). Mechanosensory feedback in walking: from joint control to locomotory patterns. Adv. Insect Physiol. 34, 194–234.
Büschges, A., Schmitz, J., and Bassler, U. (1995). Rhythmic patterns in the thoracic nerve cord of the stick insect induced by pilocarpine. J. Exp. Biol. 198, 435–456.
Chrachri, A., and Clarac, F. (1987). Induction of rhythmic activity in motoneurons of crayfish thoracic ganglia by cholinergic agonists. Neurosci. Lett. 77, 49–54.
Cohen, A. H., Ermentrout, G. B., Kiemel, T., Kopell, N., Sigvardt, K. A., and Williams, T. L. (1992). Modelling of intersegmental coordination in the lamprey central pattern generator for locomotion. Trends Neurosci. 15, 434–438.
Cohen, A. H., Holmes, P., and Rand, R. (1982). The nature of coupling between segmental oscillators of the lamprey spinal generator for locomotion: a model. J. Math. Biol. 13, 345–369.
Cruse, H. (1990). What mechanisms coordinate leg movement in walking arthropods? Trends Neurosci. 13, 15–21.
Daun-Gruhn, S. (2010). A mathematical modeling study of inter-segmental coordination during stick insect walking. J. Comp. Neurosci. doi: 10.1007/s10827-010-0254–253. [Epub ahead of print].
Delcomyn, F. (1971). The locomotion of the cockroach Periplaneta americana. J. Exp. Biol. 54, 443–452.
Delcomyn, F. (1987). Motor activity during searching and walking movements of cockroach legs. J. Exp. Biol. 133, 111–120.
Dürr, V. (2005). Context-dependent changes in strength and efficacy of leg coordination mechanisms. J. Exp. Biol. 208, 2253–2267.
Dürr, V., Schmitz, J., and Cruse, H. (2004). Behaviour-based modelling of hexapod locomotion: linking biology and technical application. Arthropod Struct. Dev. 33, 237–250.
Ermentrout, G. B., and Kopell, N. (1984). Frequency plateaus in a chain of weakly coupled oscillators, I. SIAM J. Math. Anal. 15, 215–237.
Friesen, W. O., and Cang, J. (2001). Sensory and central mechanisms control intersegmental coordination. Curr. Opin. Neurobiol. 11, 678–683.
Ghigliazza, R. M., and Holmes, P. (2004). A minimal model of a central pattern generator and motoneurons for insect locomotion. SIAM J. Appl. Dyn. Syst. 3, 671–700.
Hagevik, A., and McClellan, A. D. (1994). Coupling of spinal locomotor networks in larval lamprey revealed by receptor blockers for inhibitory amino acids: neurophysiology and computer modeling. J. Neurophysiol. 72, 1810–1829.
Hill, A. V., Masino, M. A., and Calabrese, R. L. (2003). Intersegmental coordination of rhythmic motor patterns. J. Neurophysiol. 90, 531–538.
Holmes, P., Full, R. J., Koditschek, D. E., and Guckenheimer, J. (2006). The dynamics of legged locomotion: models, analyses and challenges. SIAM Rev. 48, 207.
Kiemel, T., and Cohen, A. H. (1998). Estimation of coupling strength in regenerated lamprey spinal cords based on a stochastic phase model. J. Comp. Neurosci. 5, 267–284.
Kiemel, T., Gormley, K. M., Guan, L., Williams, T. L., and Cohen, A. H. (2003). Estimating the strength and direction of functional coupling in the lamprey spinal cord. J. Comp. Neurosci. 15, 233–245.
Koditschek, D. E., Full, R. J., and Buehler, M. (2004). Mechanical aspects of legged locomotion control. Arthropod Struct. Dev. 33, 251–257.
Ludwar, B. C., Göritz, M. L., and Schmidt, J. (2005). Intersegmental coordination of walking movements in stick insects. J. Neurophysiol. 93, 1255–1265.
McClellan, A. D., and Sigvardt, K. (1988). Features of entrainment of spinal pattern generators for locomotor activity in the lamprey. J. Neurosci. 8, 133–145.
McMillen, T., Williams, T. L., and Holmes, P. (2008). Nonlinear muscles, passive viscoelasticity and body taper conspire to create neuro-mechanical phase lags in anguilliform swimmers. PLoS Comput. Biol. 4, e1000157. doi: 10.1371/journal.pcbi.1000157
Pearson, K. G. (2004). Generating the walking gait: role of sensory feedback. Prog. Brain Res. 143, 123–129.
Pearson, K. G., and Bergman, S. J. (1969). Common inhibitory motoneurones in insects. J. Exp. Biol. 50, 445–471.
Pearson, K. G., and Iles, J. F. (1970). Discharge patterns of coxal levator and depressor motoneurons of the cockroach, Periplaneta Americana. J. Exp. Biol. 52, 139–165.
Pearson, K. G., and Iles, J. F. (1971). Innervation of coxal depressor muscles in the cockroach, Periplaneta Americana. J. Exp. Biol. 54, 215–232.
Pearson, K. G., and Iles, J. F. (1973). Nervous mechanisms underlying intersegmental co-ordination of leg movements during walking in the cockroach. J. Exp. Biol. 58, 725–744.
Proctor, J., Kukillaya, R., and Holmes, P. (2010). A phase-reduced neuro-mechanical model for insect locomotion: feedforward stability and proprioceptive feedback. Philos. Trans. R. Soc. Lond. A 368, 5087–5104.
Puhl, J. G., and Mesce, K. A. (2010). Keeping it together: mechanisms of intersegmental coordination for a flexible locomotor behavior. J. Neurosci. 30, 2373–2383.
Rand, R. H., and Holmes, P. J. (1980). Bifurcation of periodic motions in two weakly coupled van der Pol oscillators. Int. J. Non Linear Mech. 15, 387–399.
Ridgel, A. L., and Ritzmann, R. E. (2005). Effects of neck and circumoesophageal connective lesions on posture and locomotion in the cockroach. J. Comp. Physiol. A Neuroethol. Sens. Neural Behav. Physiol. 191, 559–573.
Ritzmann, R. E., and Büschges, A. (2007). Adaptive motor behavior in insects. Curr. Opin. Neurobiol. 17, 629–636.
Ritzmann, R. E., Gorb, S. N., and Quinn, R. D. (eds). (2004). Arthropod locomotion systems: from biological materials and systems to robotics. Arthropod Struct. Dev. 33, 183–185. (special issue).
Ryckebusch, S., and Laurent, G. (1993). Rhythmic patterns evoked in locust leg motor neurons by the muscarinic agonist pilocarpine J. Neurophysiol. 69, 1583–1595.
Skinner, F. K., and Mulloney, B. (1998). Intersegmental coordination in invertebrates and vertebrates. Curr. Opin. Neurobiol. 8, 725–732.
Tunstall, M. J., and Roberts, A. (1994). A longitudinal gradient of synaptic drive in the spinal cord of Xenopus embryos and its role in co-ordination of swimming. J. Physiol. 474, 393–405.
Tytell, E. D., and Cohen, A. H. (2008). Rostral versus caudal differences in mechanical entrainment of the lamprey central pattern generator for locomotion. J. Neurophysiol. 99, 2408–2419.
Varkonyi, P., Holmes, P., Keimel, T., Hoffman, K., and Cohen, A. H. (2008). On the derivation and tuning of phase oscillator models for lamprey central pattern generators. J. Comput. Neurosci. 25, 245–261.
Yang, J. F., and Gorassini, M. (2006). Spinal and brain control of human walking: implications for retraining of walking. Neuroscientist 12, 379–389.
Yu, X., and Friesen, W. O. (2004). Entrainment of leech swimming activity by the ventral stretch receptor. J. Comp. Physiol. A 190, 939–949.
Keywords: cockroach, locomotion, intersegmental coordination, central pattern generator, rostral–caudal asymmetry, maximum likelihood estimation
Citation: Fuchs E, Holmes P, Kiemel T and Ayali A (2011) Intersegmental coordination of cockroach locomotion: adaptive control of centrally coupled pattern generator circuits. Front. Neural Circuits 4:125. doi: 10.3389/fncir.2010.00125
Received: 19 October 2010;
Paper pending published: 08 December 2010;
Accepted: 28 December 2010;
Published online: 20 January 2011
Edited by:
Aravinthan Samuel, Harvard, USACopyright: © 2011 Fuchs, Holmes, Kiemel and Ayali. This is an open-access article subject to an exclusive license agreement between the authors and Frontiers Media SA, which permits unrestricted use, distribution, and reproduction in any medium, provided the original authors and source are credited.
*Correspondence: Einat Fuchs, Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA. e-mail:ZWluYXRAcHJpbmNldG9uLmVkdQ==



