- Division of Child Neurology, The University of Texas Southwestern Medical Center, Dallas, TX, United States
The past 25 years have seen a strong increase in the number of publications related to criticality in different areas of neuroscience. The potential of criticality to explain various brain properties, including optimal information processing, has made it an increasingly exciting area of investigation for neuroscientists. Recent reviews on this topic, sometimes termed brain criticality, make brief mention of clinical applications of these findings to several neurological disorders such as epilepsy, neurodegenerative disease, and neonatal hypoxia. Other clinicallyrelevant domains – including anesthesia, sleep medicine, developmental-behavioral pediatrics, and psychiatry – are seldom discussed in review papers of brain criticality. Thorough assessments of these application areas and their relevance for clinicians have also yet to be published. In this scoping review, studies of brain criticality involving human data of all ages are evaluated for their current and future clinical relevance. To make the results of these studies understandable to a more clinical audience, a review of the key concepts behind criticality (e.g., phase transitions, long-range temporal correlation, self-organized criticality, power laws, branching processes) precedes the discussion of human clinical studies. Open questions and forthcoming areas of investigation are also considered.
Introduction
The brain criticality hypothesis suggests that neural networks and thus, many aspects of brain activity self-organize into a critical state (Wilting and Priesemann, 2019). Critical states are unique configurations of physical systems that have been a central focus of statistical physics for more than a century. Criticality, which is a synonymous term for “critical phenomena” or “critical states,” marks the transition between ordered and disordered states. The theory of critical phenomena has found applications in many scientific fields, including neuroscience and clinical neurology (Sornette, 2004; Cocchi et al., 2017). In the neurosciences, criticality is appealing because theory and modeling suggest that neural networks at criticality exhibit optimal processing and computing properties (Beggs, 2008; Shew and Plenz, 2013). These properties include information transmission, information storage, dynamic range, metastable states, and computational power (Maass et al., 2002; Bertschinger and Natschläger, 2004; Latham and Nirenberg, 2004; Haldeman and Beggs, 2005; Kinouchi and Copelli, 2006; Tanaka et al., 2009; Boedecker et al., 2012; Shriki et al., 2013; Gautam et al., 2015; Shriki and Yellin, 2016; Hoffmann and Payton, 2018). The term “brain criticality” is used in this review as a catch-all term for the various manifestations of critical phenomena in human neuroscience.
This scoping review of the brain criticality literature will start with a section that reviews the physics-based ideas behind brain criticality, including a discussion of the Ising model. It will then review the brain criticality literature in each of seven domains (i.e., anesthesia, epilepsy, neurodegeneration, neurodevelopment, cognition, sleep medicine, and psychiatry), focusing on the clinical applications. This review should serve as an entry-point for clinicians and translational researchers interested in using this conceptual framework and its associated tools to advance patient care. Understandably, it is not possible to summarize nearly a century of developments in statistical physics − not to mention 30 years of applications of these physical concepts to neuroscience−in a single review paper. An excellent introductory paper for newcomers to criticality is Beggs and Timme, 2012. References are available for those interested in diving into the technical details of critical phenomena (Nishimori and Ortiz, 2011; Tomko et al., 2018), including two books on criticality in neural dynamics (Plenz and Niebur, 2014; Tomen et al., 2019). In this section, criticality is introduced from the perspective of phase transitions and is illustrated using the two-dimensional Ising model (see Figure 1). This is followed by a discussion of the various characteristics of critical phenomena and a brief discussion of self-organized criticality.
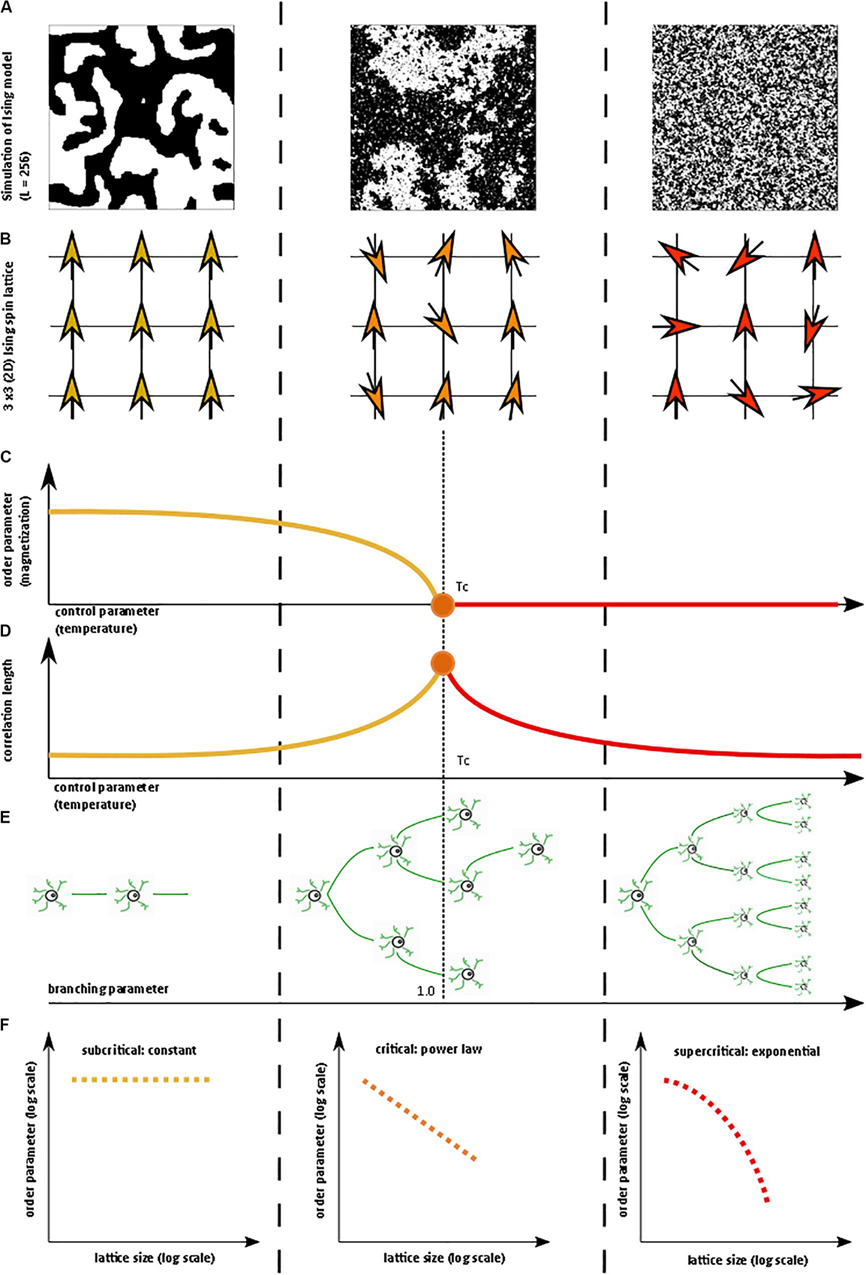
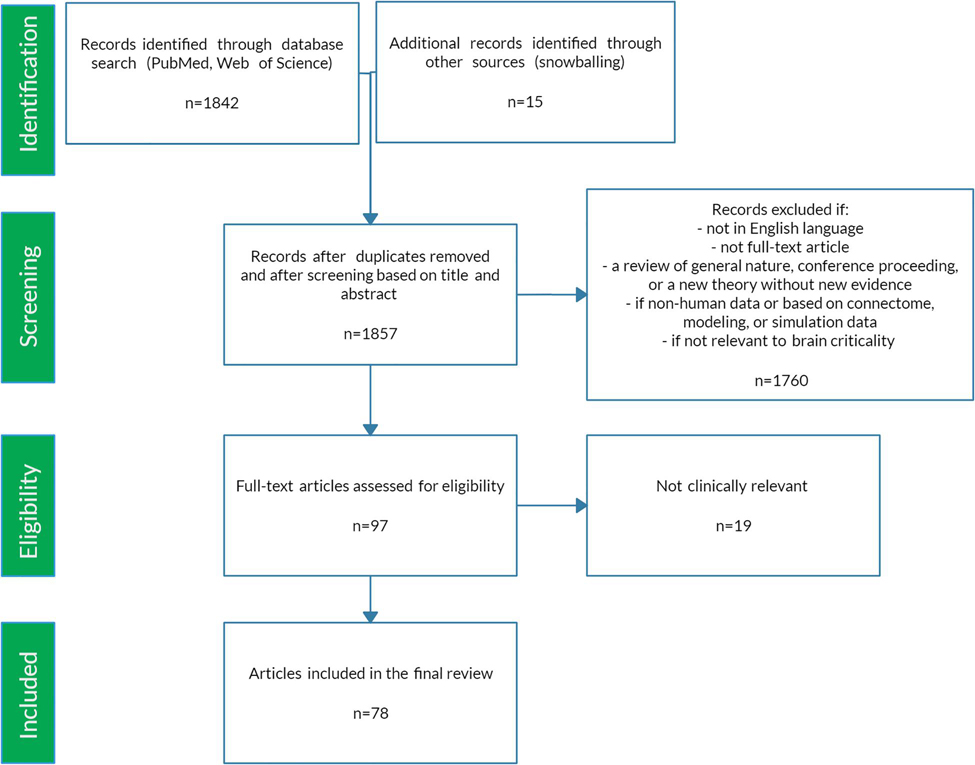
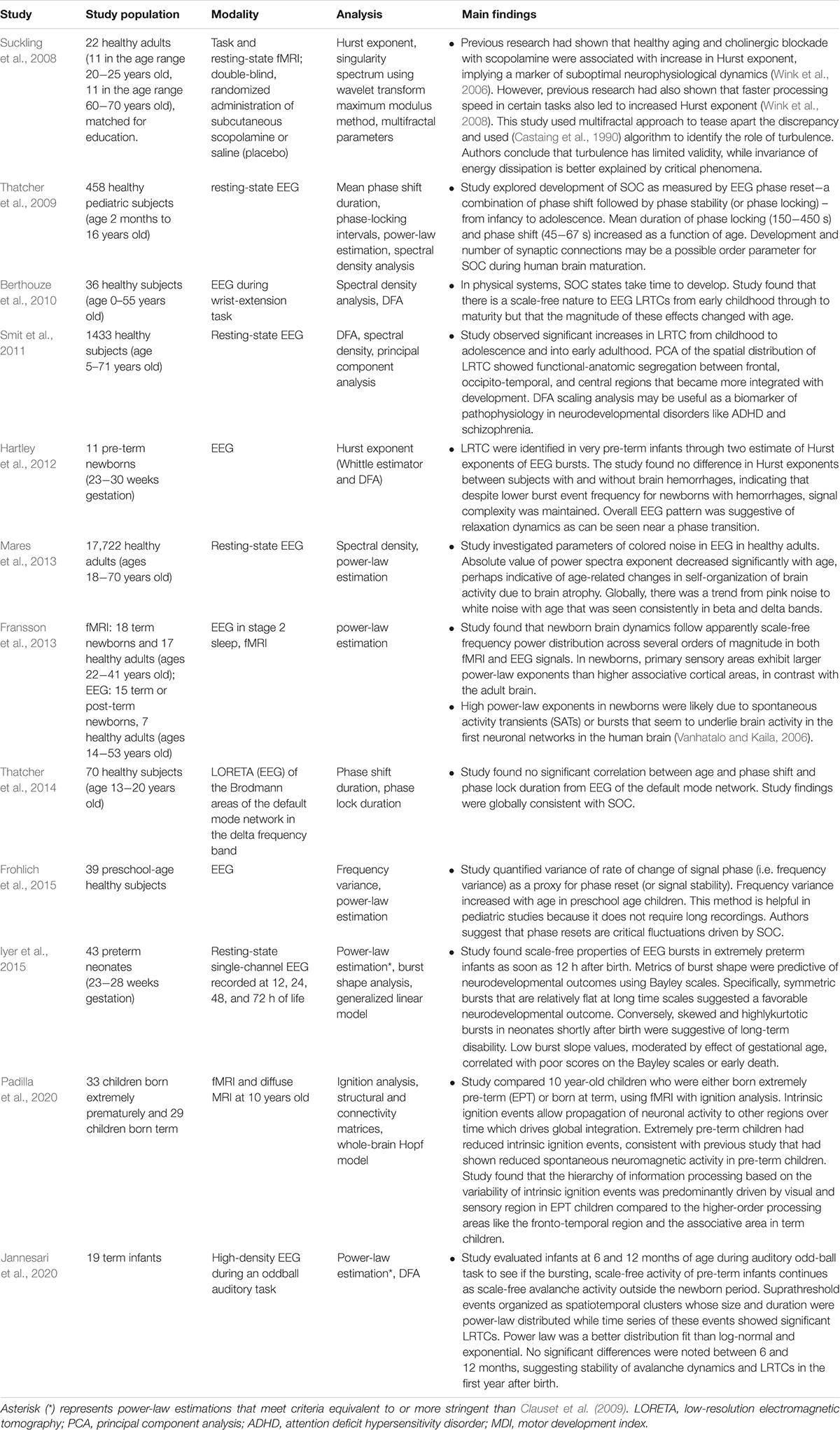
Figure 1. Illustration of critical phase transition using the two-dimensional (2D) Ising model. For more information on the Ising model, see Nishimori and Ortiz (2011), Beggs and Timme (2012). (A) Simulation of 2D Ising model with length = 256 in subcritical, critical, and super-critical states as temperature increases from left to right. Black and white areas represent magnetization domains with differing spins. Simulations were generated using open-source code from Matt Bierbaum (mattbierbaum.github.io/ising.js) using the Metropolis algorithm. (B) Illustration of 2D Ising spin lattice to show differing spin states during phase transition. Image adapted with permission from Beggs and Timme (2012). The organized spins in the subcritical state give way to random spin arrangements in the supercritical state, passing through an intermediate critical state with a complex arrangement of spins. (C) The order parameter of the system decreases smoothly as the control parameter increases, until it abruptly changes at the critical temperature (Tc or the Curie temperature). (D) The correlation length is maximized at the critical point. (E) A branching parameter of 1 allows an aggregate one-to-one transmission of neural signals. Branching parameter greater than 1 leads to supercritical, run-away neuronal excitation. Branching parameter less than 1 leads to subcritical dying-off of the neuronal transmission. (F) At the critical point, observables of the system, including the order parameter, obey a power-law or scale-free distribution, seen as a straight-line on a log-log plot. The order parameter remains constant in the subcritical case, while it drops off exponentially in the supercritical state.
Criticality and Associated Concepts
In statistical physics, criticality refers to the behavior that is seen when a physical system undergoes a specific kind of phase transition. Typically, a macroscopic property of the system called the order parameter changes as a function of an underlying feature called the control parameter. In the example of a vapor-to-water phase transition, the order parameter is the macroscopic appearance reflective of the phase’s entropy (i.e., water or vapor), and the control parameter is the temperature (Hesse and Gross, 2014). Generally, gradual changes in the control parameter lead to similarly gradual changes in the order parameter. However, at specific points, the order parameter changes abruptly. On a plot of the order parameter on the y-axis and the control parameter on the x-axis (i.e., a phase diagram), there is either a jump (i.e., a discontinuity) or a sharp corner (i.e., a non-differentiable point) at the transition point of a phase transition. If the change in the order parameter is a jump, the phase transition is known as first-order or discontinuous. If the change in the order parameter is a sharp corner, the phase transition is known as second-order or continuous. The second-order phase transition allows a system to be at the exact transition point at the interface between two very different states, with usually one state being more disordered than the other. The system is said to be “at criticality” or in the critical state (Nishimori and Ortiz, 2011; Hesse and Gross, 2014). The phase in which the control parameter is below the critical value is called the subcritical phase, while the phase in which the control parameter is above the critical value is called the supercritical phase. It is important to note that the theory of phase transitions usually involves systems at the thermodynamic limit, i.e. infinitelylarge volume. When not at the thermodynamic limit, phase transitions occur over a parameter range called a Griffiths phase rather than at a single critical point and are sometimes referred to as quasi-critical states (Moretti and Munoz, 2013). Quasi-critical states obey many of the properties of a critical system but are not entirely critical.
These concepts can be illustrated with the help of the two-dimensional Ising model, which is a classic example of a critical transition in ferromagnetism (Beggs and Timme, 2012). The Ising model consists of a lattice in a piece of iron, with each site of the lattice corresponding to a dipole moment (i.e., an up or down spin) (Figure 1B). Each dipole moment operates like a bar magnet and can influence its nearest neighbors to align in the same direction. At a low temperature, nearest-neighbor effects will dominate the system. At a fixed temperature below the critical temperature, a cluster of aligned spins will get larger and larger, and, with time, will take over the entire lattice to make a uniform dipole moment (Figure 1A). Thus, at this low temperature, the piece of iron will behave like a magnet because the spins will align throughout the lattice to yield a strong net magnetization (i.e., order parameter). However, as temperature (i.e., control parameter) increases, the energy from heat begins to jostle the spins. Past a critical temperature called the Curie temperature (Tc), the disordered spins from the added heat will overwhelm the ordering effect of the nearest-neighbor interaction, leading to a loss of the magnetization (Figures 1A–C). Heat, therefore, takes the system from a subcritical, magnetic phase through a critical phase transition and on to a supercritical, non-magnetic and disordered phase. At the critical temperature, a critical phase emerges where order and disorder are evenly matched (Nishimori and Ortiz, 2011; Beggs and Timme, 2012). The correlation length (i.e., how far a single spin change can propagate through the system) is maximized in this phase (Figure 1D), and in the infinitely large system, goes to infinity at the critical point. The order parameter (i.e., magnetization)−along with other observables like magnetization domain size and magnetic susceptibility−become power-law distributed with unique power-law exponents (Figure 1F). Power laws refer to a probability density function of the form of p(x) = Cx−α for some x > x_o and with αcorresponding to the power-law exponent. Power laws exhibit scale invariance and are therefore called scale-free. A function f(x) is scale invariant if f(cx)∝f(x), where α signifies “proportional to.” In other words, scaling the argument of the function is equivalent to a proportional scaling of the function itself. In the case of the power-law, f(cx) = (cx)−α = c−α x−α =c−α f(x) ∝f(x). Moreover, because log(f(x)) = log∝(x−α) = −αlog(x), a log-log plot of a power-law distributed dataset should produce a straight line with slope −α. Caveats on using this log-log plot technique to extract the power-law exponent are addressed in a subsequent section.
The Ising model can lead to very complex behavior patterns and has been used to model neural networks (Fraiman et al., 2009; Beggs and Timme, 2012; Deco et al., 2012; Marinazzo et al., 2013; Stramaglia et al., 2017). The Ising model and several other well-characterized models have led to a better understanding of how critical systems behave. Nevertheless, critical systems remain difficult to identify because the relevant order and control parameters may not always be readily available for experimentation, making it difficult to construct a complete phase diagram. In the absence of a complete phase diagram, one can use several known markers of criticality, as follows:
Branching Parameter
A branching parameter σ, in the setting of brain criticality, is the ratio of downstream activated neurons to upstream activated neurons (Harris, 1963). In other words, as in Figure 1E, a branching parameter of 1 means that every activated neuron on average fires or activates one other downstream neuron (Hobbs et al., 2010). Branching parameter less than 1 indicates a subcritical phase that evolves with time to a quiescent, inactive state. On the other hand, a branching parameter greater than 1 indicates a supercritical phase of increasing activity. Of course, branching parameters are variable and dynamic. Caution is needed in the interpretation of the branching parameter, however, because a branching parameter of 1 can also be observed in certain supercritical states (Hesse and Gross, 2014).
Long-Range Temporal Correlation, Critical Slowing, and Flickering
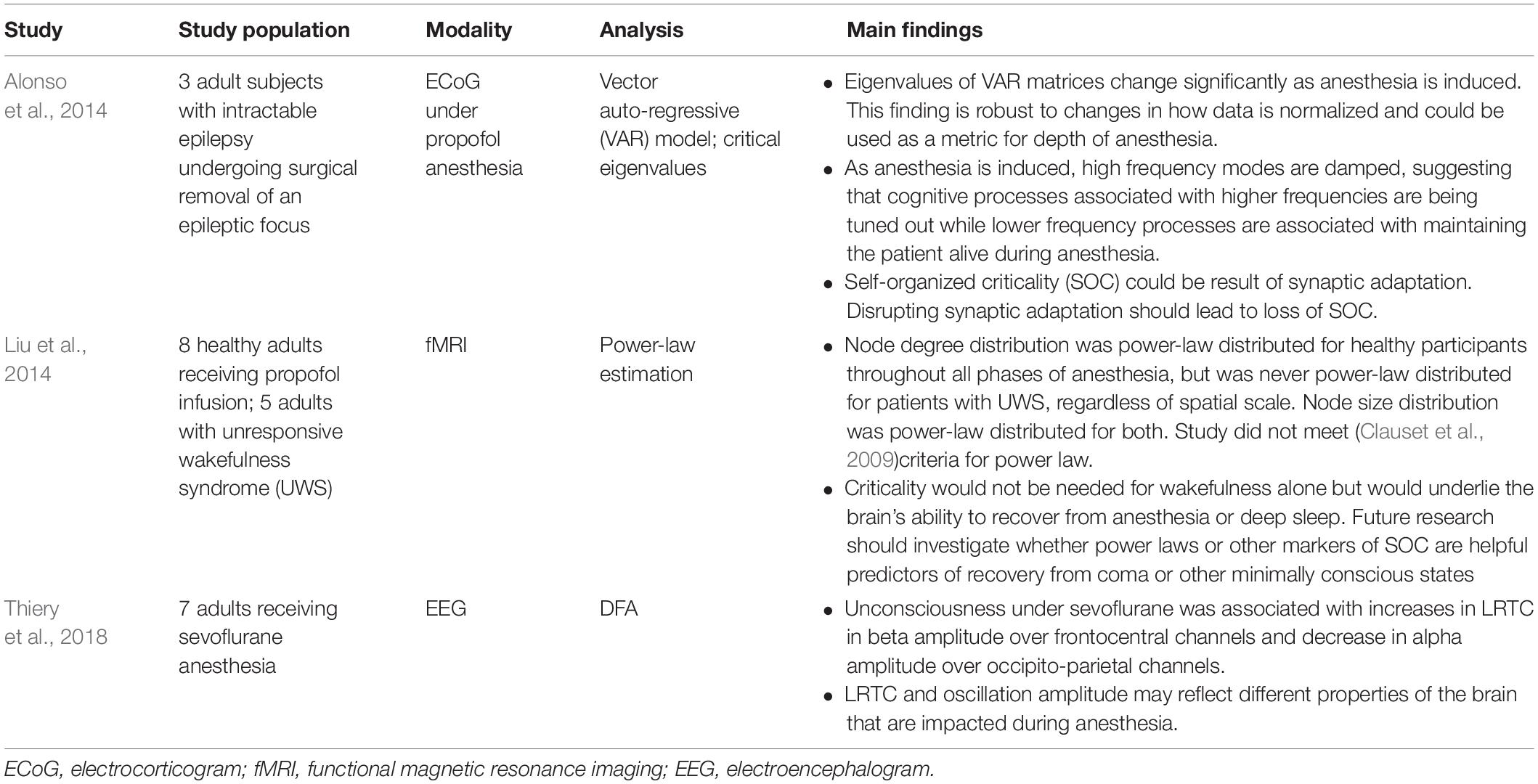
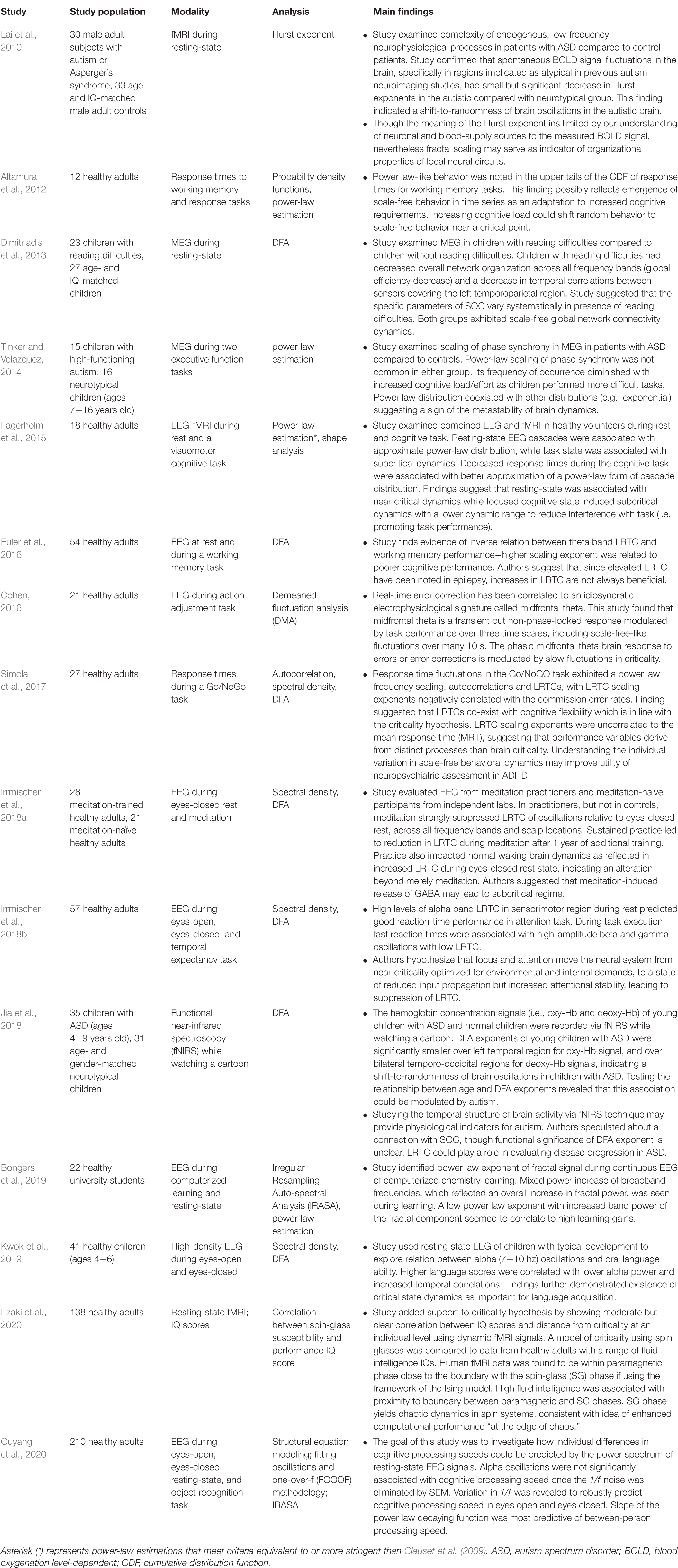
In critical systems, the response of the system to external stimuli – called the dynamic range or dynamic correlation – is maximized. Small perturbations of the system at criticality lead to geometric (rather than exponential) returns to the steady-state (Hesse and Gross, 2014), leading to long-range temporal correlation (LRTC or long-memory). One can measure LRTC in multiple ways. Popular methods include the Hurst exponent (through various estimators) and detrended fluctuation analysis (DFA) (Peng et al., 1995a, b; Simonsen et al., 1998; Hardstone et al., 2012). DFA produces a scaling exponent over a defined time period (see Figure 2 for an illustration of DFA). If that scaling exponent is between 0.5 and 1, with a good fit (see Figure 2), one can conclude that the time series exhibits LRTC over that time period.
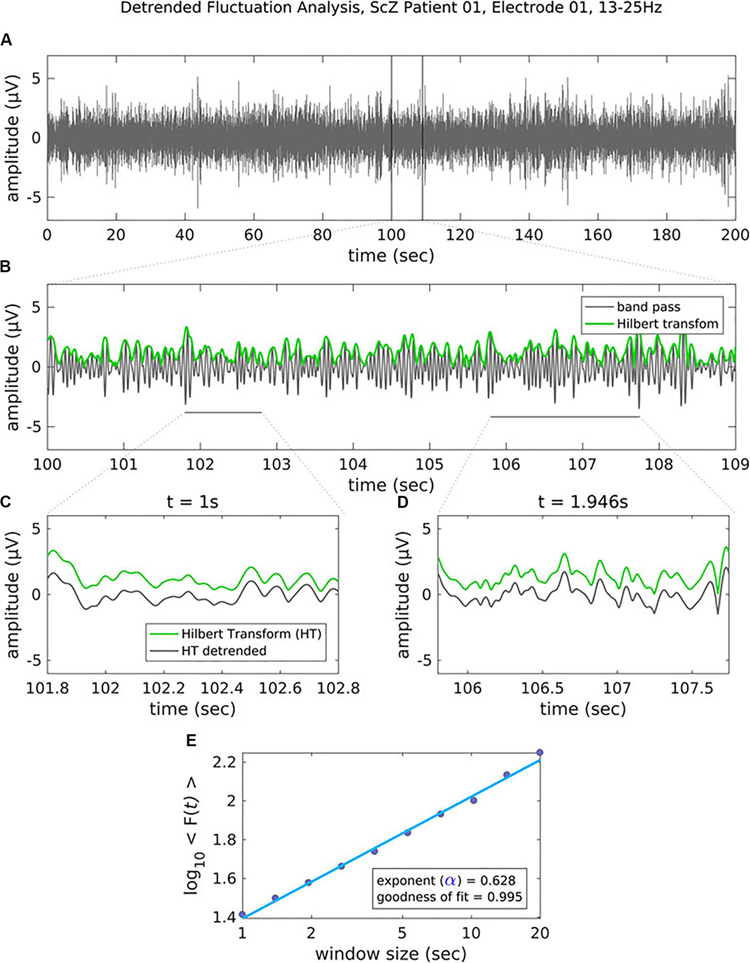
Figure 2. Figure legend taken from Moran et al. (2019) and reproduced with permission. This figure depicts the steps of the detrended fluctuation analysis (DFA). (A) 200 s EEG recording that has been band-pass filtered (13–25 Hz, channel 01 = Cz) in a patient with schizophrenia. (B) A close-up view (9 s) of the band-pass filtered EEG along with the amplitude envelope derived from the Hilbert transformation (in green), which is used for estimating the scaling exponent. (C–D) Two examples of the amplitude envelope with two window sizes. In the left graph, no detrending (i.e., removal of the trend line) has been applied whereas in the right graph, detrending has been applied. For each time window size, the fluctuation of the detrended signal is calculated as the mean standard deviation over all identical sized segments (E) The DFA scaling exponent is given by the slope of the log-log plot between fluctuation F and window size. A DFA scaling exponent between 0.5 and 1 indicates the presence of LRTC – in this case, the correlation extends up to 20 s. In this example, the DFA scaling exponent for the beta-band-oscillations in this channel is α = 0.628. It is common to report the R2 value of the linear regression of the log-log plot as a goodness-of-fit score.
This geometric rate of return to steady-state is also called critical slowing down (Scheffer et al., 2009; Van De Leemput et al., 2014). More generally, at the critical point, the dynamic correlation of the system diverges such that avalanches (i.e., network activity) occur at all scales of the system (Hesse and Gross, 2014). Another phenomenon seen at the critical transition is called flickering, which emerges when noise allows a system to migrate back-and-forth between two attractor basins (Wang et al., 2012). This phenomenon is not to be confused with flicker noise or 1/f noise, which is discussed next.
The Emergence of Power-Law (1/f) Noise and Power-Law Observables
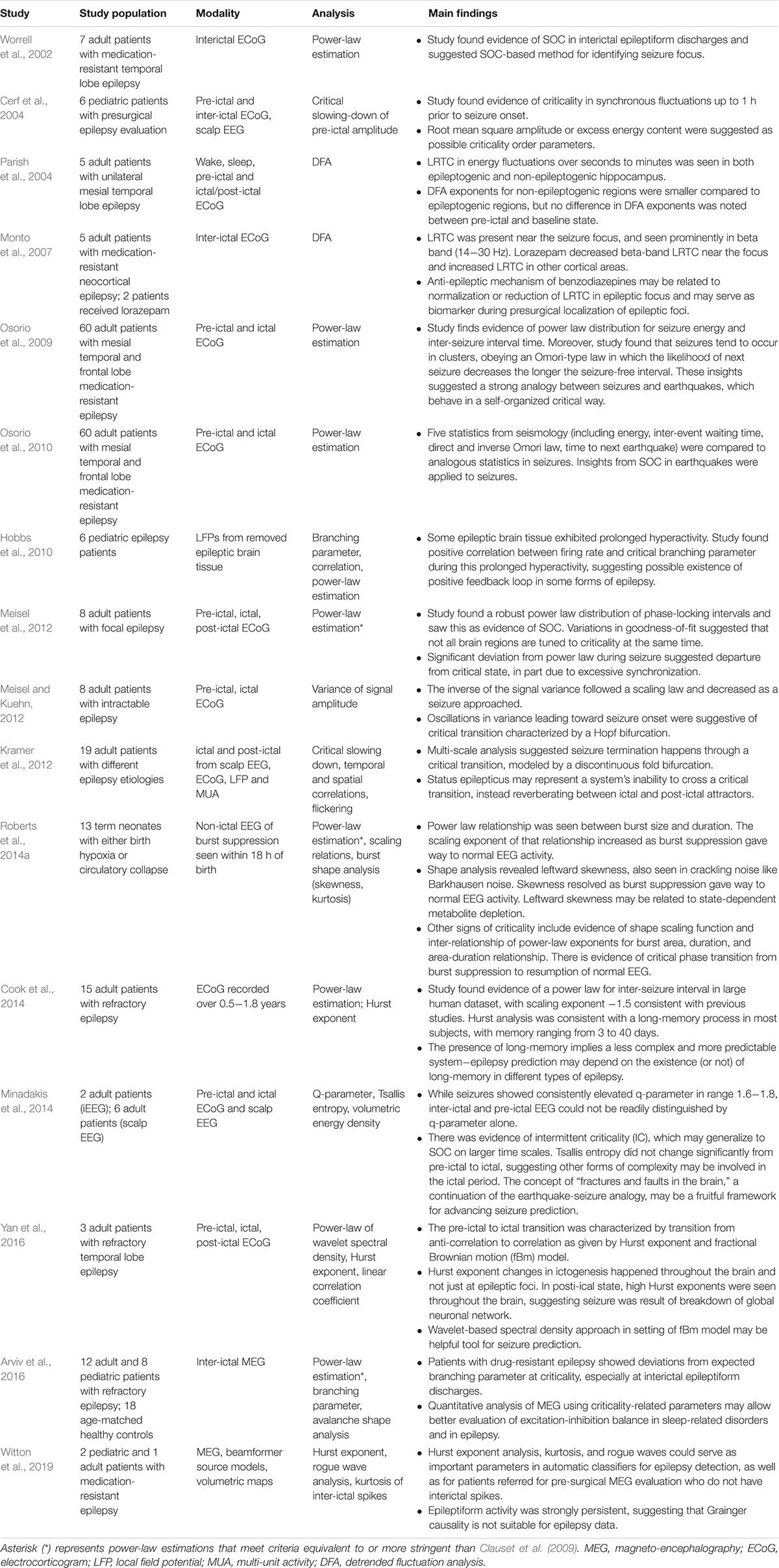
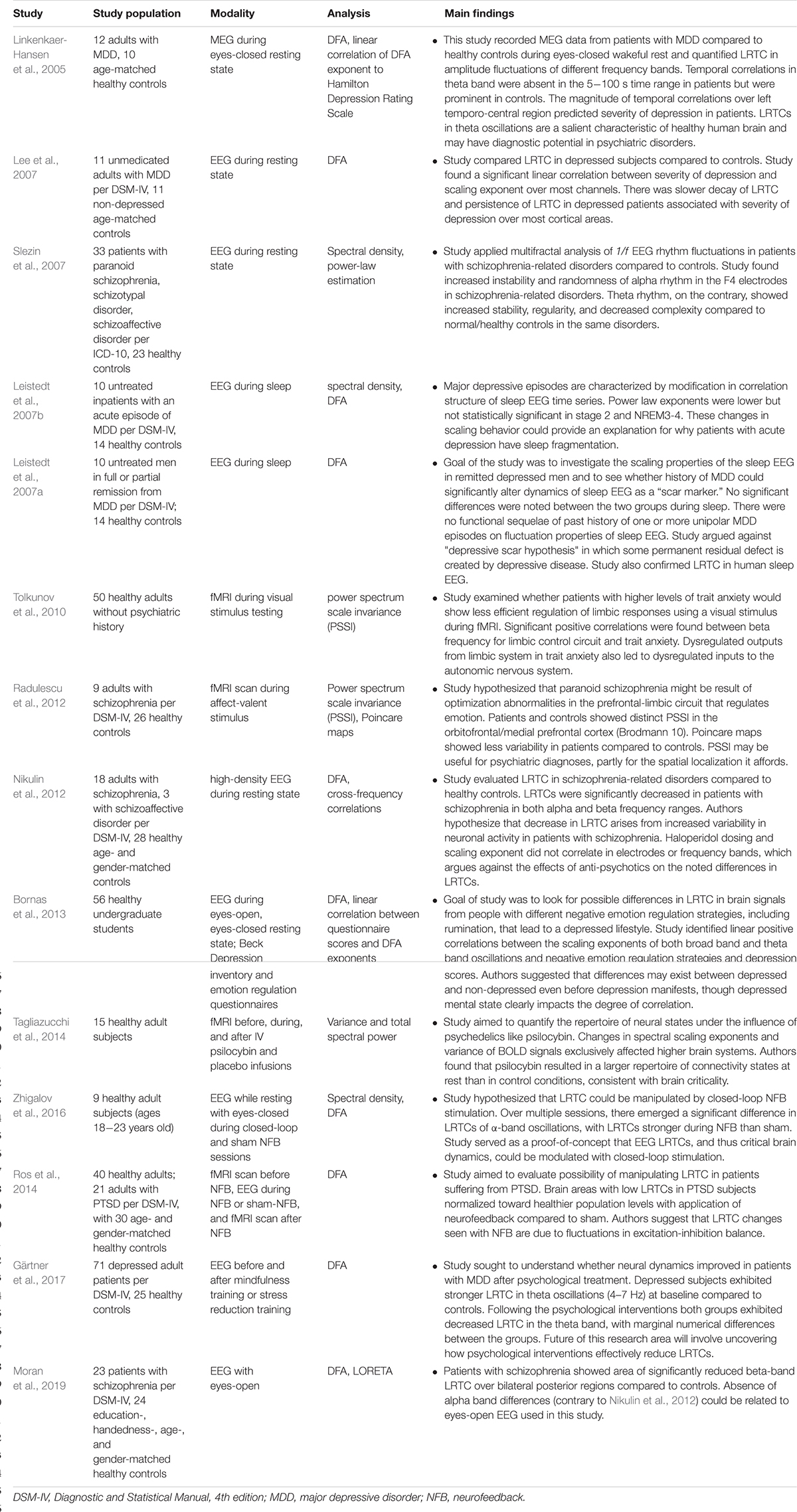
Critical systems, when perturbed by weak inputs, will exhibit superposed geometric responses to the inputs, which yields 1/f noise, also called pink noise, power-law noise, or flicker noise (see Figure 3C). Many authors employ these terms synonymously with long-range dependence or long-memory, as these are identical phenomena. The term 1/f noise refers to the phenomenon in which the power spectrum S(f) of a time series obeys a power law of the formS(f) = αf−β. Historically, the cases of β = 0,β = 1,β = 2 are referred to as “white” noise, “pink” noise, and “brown” noise, respectively (Li et al., 2005). The range 0.5 < β < 1.5 is commonly accepted as 1/f noise. While all critical systems should exhibit 1/f noise, not all 1/f noise is indicative of criticality (Bédard et al., 2006; Hesse and Gross, 2014).
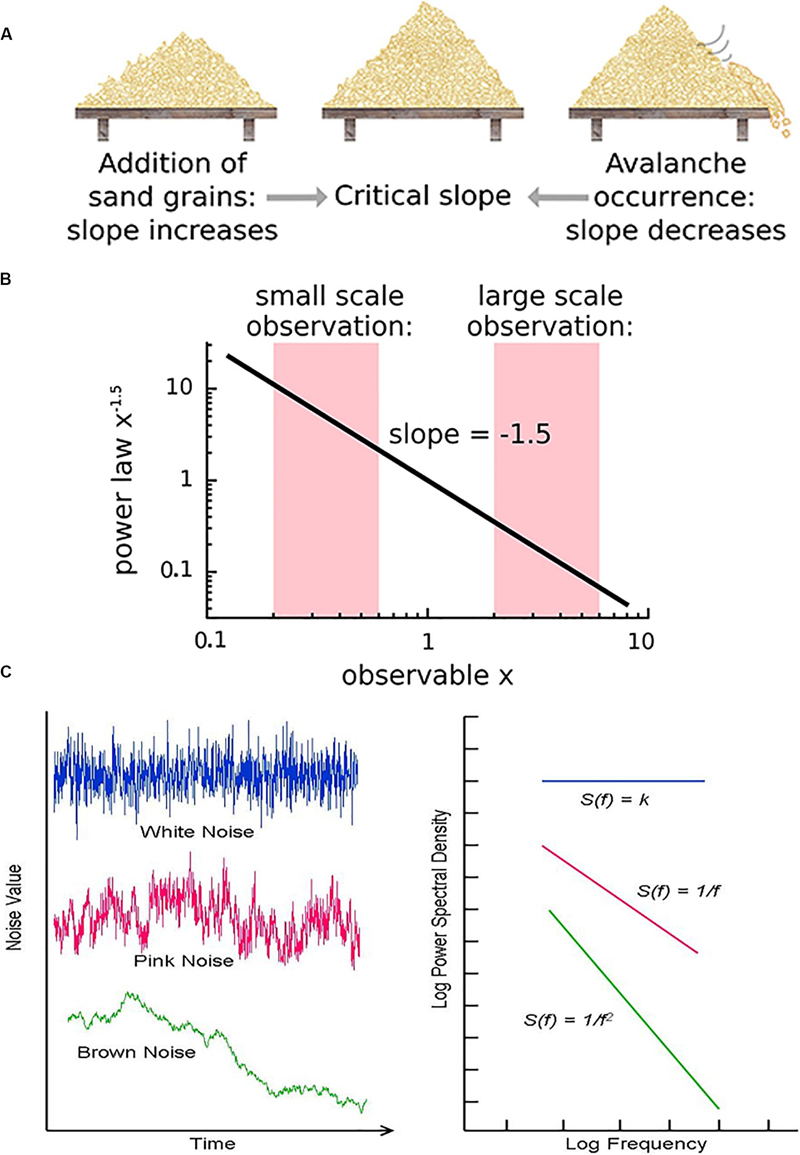
Figure 3. (A) The sandpile model is a classic model of self-organized criticality (SOC), derived as a though experiment (Bak et al., 1988) and proven later with rice piles (Frette et al., 1996). Sand is dropped continuously at a fixed rate onto a flat surface. A sandpile forms. As the sand is added, the slope of the pile increases and avalanches of sand grains begin to occur. If the slope exceeds a “critical slope,” small and large avalanches will decrease the slope back closer to the critical slope. (B) At the critical slope, the distribution of avalanche sizes (i.e., number of sand grains) is power-law distributed. On a log-log plot, the slope of a power-law-distributed variable gives the power-law exponent. Most avalanches are small but a non-negligible number are quite large, up to nearly the size of the entire system. (A,B) reused with permission from Hesse and Gross (2014). (C) Neurophysiologic measurements such as voltage from an EEG recording can be displayed as time series that exhibit characteristic spectral densities S(f). (C) Figure reused with permission from Scholarpedia and E. Izhikevich. Plot of different color-coded time series (left) and a log-log plot of their respective spectral densities (right). In Gaussian “white” noise, each frequency has equal energy, leading to a constant spectral density. “Pink” noise, which is characteristic of SOC but arises in many other settings, has a spectral density given by 1/f, thus the name “1/f noise.” “Brown” noise refers to Brownian or random motion, whose spectral density is typically given by 1/f2.
As mentioned earlier, multiple observables will follow a power-law distribution when in a critical state. However, power laws are necessary but not sufficient to prove the existence of criticality – many other processes can generate a power-law distribution. For more on this topic, see the following references (Mitzenmacher, 2004; Newman, 2005; Touboul and Destexhe, 2010). Demonstrating the existence of a power law is not straightforward. As a rule, power laws take the form of Y = Cx−α for some x > xo. For many years, it was common practice to plot y against x (from the previous formula) in log-log coordinates – if a straight line emerged, the slope of that line was interpreted as the power-law exponent α (see Figure 3B). This approach led to many false claims of power-laws since many other finite datasets (e.g., from a log-normal distribution) can also approximate a straight line on a log-log plot. Since Clauset et al. (2009) and subsequent work, researchers have had access to more sophisticated statistical methodology to argue that their variable obeys a power law, as opposed to other heavy-tailed distributions. While definitions vary, heavy-tail distributions are probability distributions whose tails are “heavier” than the exponential distribution, of which the Gaussian is a sub-type. Examples include the Fisher-Tippett (double-exponential) distribution, the log-normal distribution, the Weibull distribution, among many others. An exhaustive review of several heavy-tailed distributions and their role in neuroscience can be found in Roberts et al. (2015). In this review, publications that claim a power-law distribution based on current practices are contrasted with publications that rely on the previously accepted “log-log approach.”
Relationship of Power-Law Exponents to Each Other
In systems at criticality, many observable variables (e.g., correlation, size distribution) obey power laws. The different exponents of these power laws are inter-related. The details of these mathematical relationships are beyond the scope of this review but represent a fascinating topic in their own right. To give but one example, avalanche size distribution with power exponent α and avalanche lifetime distribution with power exponent β should be related to avalanche lifetime γ by the following equation: . This relationship has been experimentally validated in individual neurons (Beggs and Timme, 2012; Friedman et al., 2012).
Scaling Function
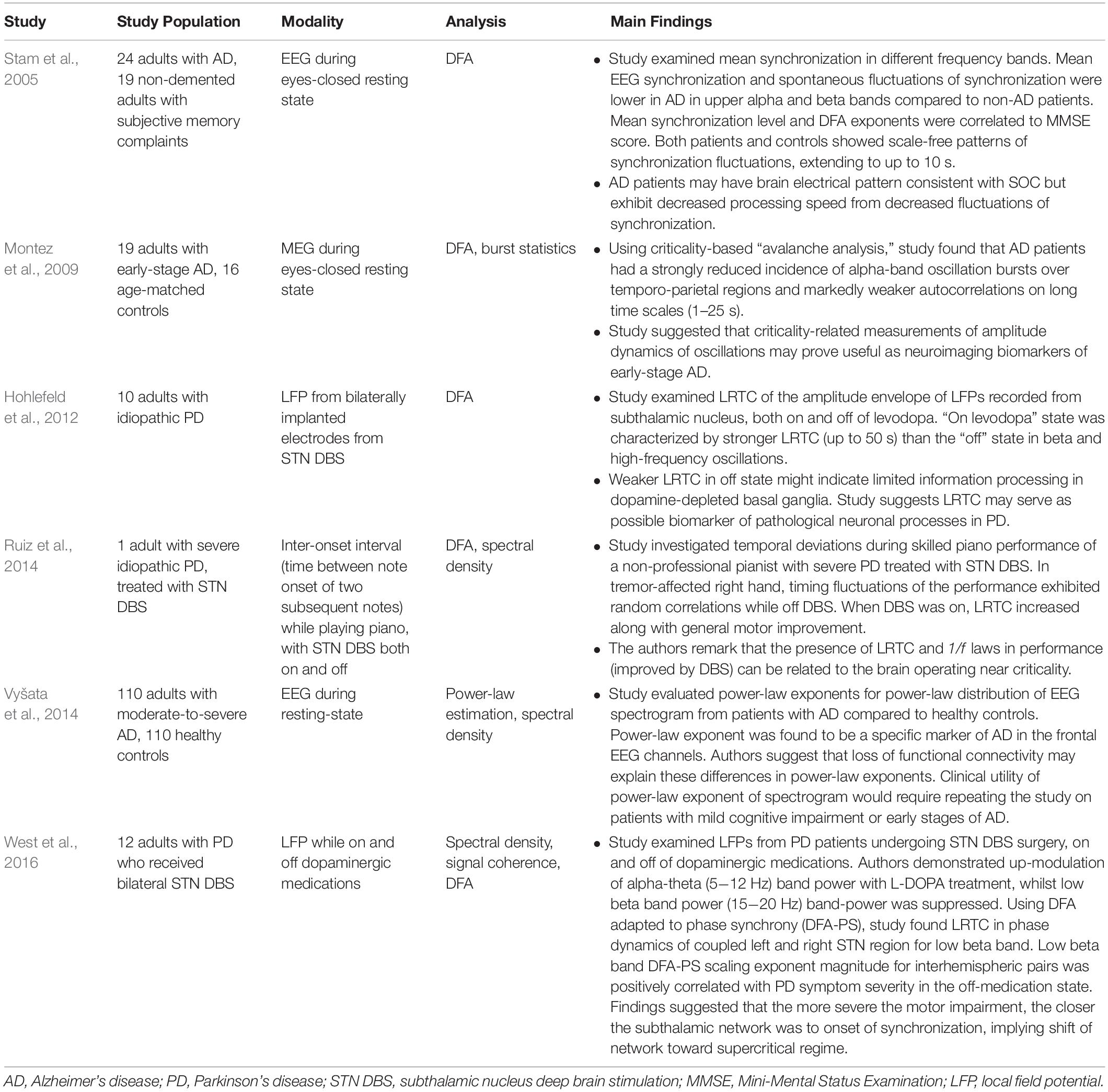
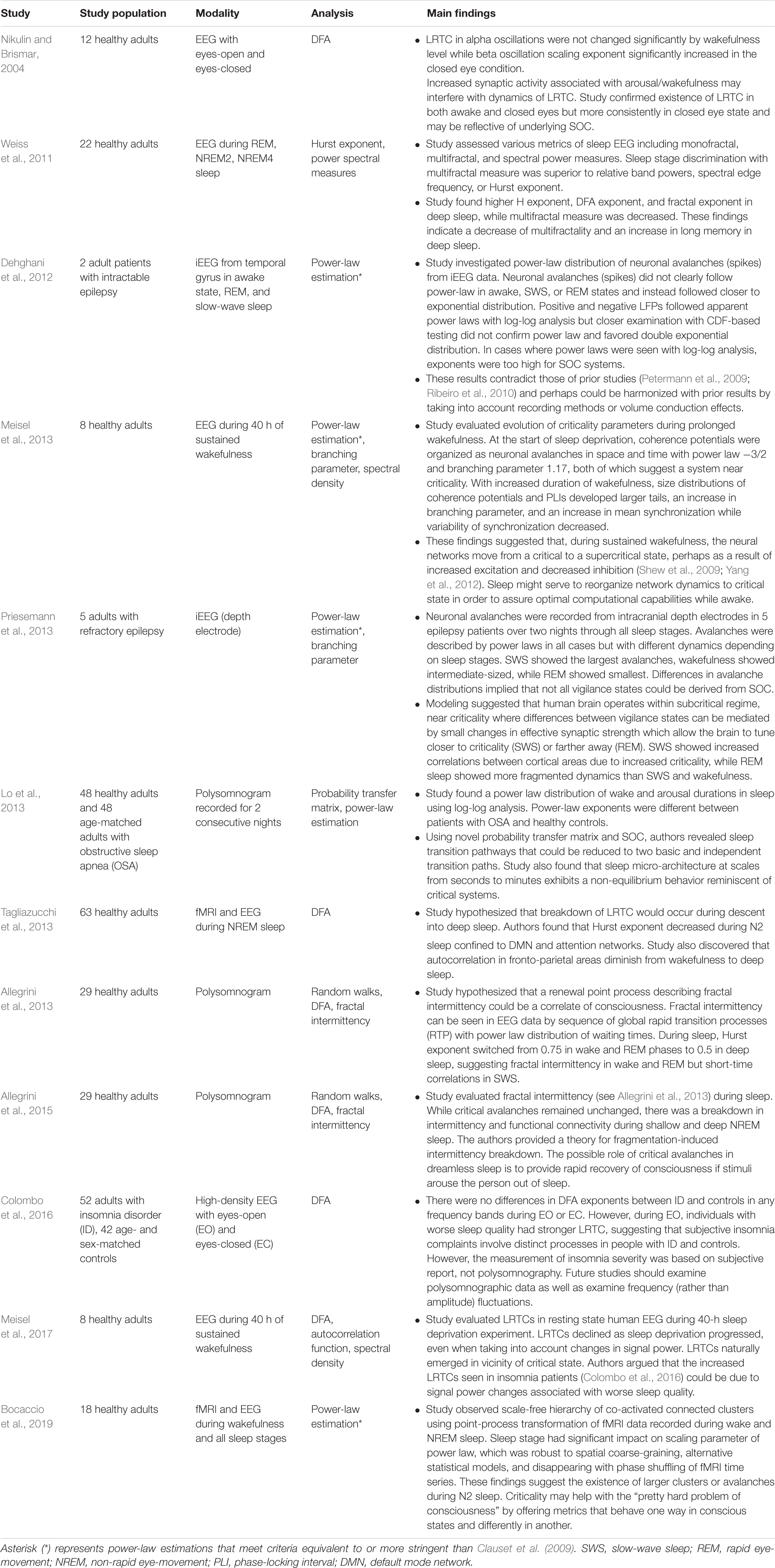
Because of the self-similar or fractal nature of the avalanches of activity in critical systems, the “shape” of avalanche activity is also expected to behave as a fractal (see Figures 4A–G). Therefore, all cascades of activity at criticality ought to be re-scalable to a unique shape, as a function of time (or duration) and power exponents (see Figure 4H). This phenomenon of critical systems allows a “data collapse” or “shape collapse” of all activity onto a single unique shape (Friedman et al., 2012). In some neural avalanches, this shape takes the form of an inverted parabola (Beggs and Timme, 2012). This kind of shape collapse has been observed in many critical systems (Perković et al., 1995; Mehta et al., 2006; Papanikolaou et al., 2011).
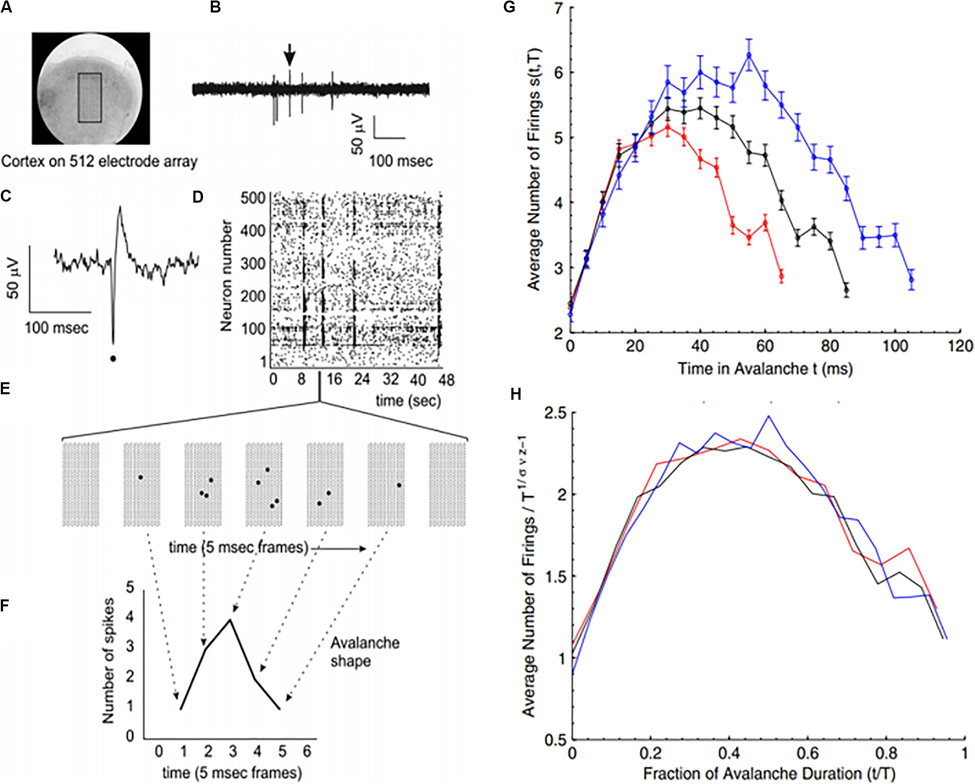
Figure 4. Avalanches recorded from neural tissue. (A) Micrograph of a cortical slice on an electrode array, represented by a black rectangle. (B) Electrical potential recorded from an electrode. Arrow points to a spike from an individual neuron. The spike is expanded in panel (C) and marked by a black dot. (D) Raster plot of spike times (dots) from multiple neurons over time. (E) Expanding the view of the raster plot reveals an avalanche. Each frame represents the electrode array during a single 5 ms period. Black dots are spikes detected on the array. An avalanche is made up of consecutively active frames, beginning and ending with inactive frames. (F) Plotting the number of spikes in each frame versus time produces an avalanche shape. (G) Avalanche shapes are produced by averaging the temporal profiles of all avalanches of a particular duration from an experimental dataset close to criticality. Different colors here represent different durations. (H) The collapses are plotted by rescaling the horizontal and vertical axes. The tight overlap after rescaling is indicative of criticality. Images reproduced with permission Beggs and Timme (2012) and Friedman et al. (2012).
There are various theories as to how physical systems can bring themselves to criticality. In the case of the brain, one of the popular theories is called self-organized criticality or SOC for short (Bak et al., 1987; Christensen et al., 1992; Hesse and Gross, 2014). It is also referred to as self-organized quasi-criticality (Bonachela and Muñoz, 2009) since, as mentioned earlier, true criticality occurs only in infinitelysized systems. Introduced initially by Bak et al. (1987), the idea of SOC is that the control parameter is constantly being adjusted to the critical value by a decentralized feedback mechanism. In other words, the control parameter spontaneously decreases when the system is in a supercritical phase and increases when in a subcritical phase. The use of the term “control parameter” is maintained, even if the parameter is not being controlled externally but rather by the system itself (Hesse and Gross, 2014). Figure 3A illustrates one of the earliest models of SOC, called the sandpile model (Bak et al., 1988; Frette et al., 1996). Imagine that sand is accumulating at a certain rate on a flat surface. As the sandpile rises, the slope of the sandpile increases. At a critical point, the distribution of sand-pile avalanche sizes (i.e., a few grains of sand or the entire pile) obeys a power-law. With a power-law or scale-free distribution, avalanches of all scales can occur, but most avalanches will be small with a few being very large (Figure 3B). As sand continues to be added at the same rate, larger avalanches take place and the slope decreases back to the “critical slope.” The criticality in this system is therefore self-organized and the control parameter does not have to be tuned externally, as it does for example in the Ising model.
The internal “tuning” of SOC models for the brain is reminiscent of the concept of homeostatic plasticity. Homeostatic plasticity refers to the capacity of neurons to regulate their excitability based on network activity (Turrigiano and Nelson, 2004). Criticality seems to be connected to homeostatic plasticity though the exact details remain unclear. A recent experiment, however, has cast some light on this question. Rat cortical networks exhibiting criticality in controlled circadian conditions lost their network criticality when deprived of visual inputs. However, signs of criticality resumed in under 48 h with neuronal firing rates being maximally inhibited. This finding suggests that homeostatic regulation of inhibition plays an important role in generating criticality (Ma et al., 2019).
Article Selection
The preceding review was conducted to set the stage for a scoping review of the literature (Colquhoun et al., 2014) using PRISMA-ScR methodology (Moher et al., 2009). A scoping review format was chosen since the nature of this literature is large, heterogeneous, and not amenable to a more precise systematic review. See Figure 5 for a schematic of the article selection process. PubMed and Web of Science databases were searched from their inception until March 2020. The search terms were: “criticality anesthesia,” “criticality brain,” “criticality epilepsy,” “criticality neural,” “criticality neurology,” “criticality seizure,” and “criticality sleep.” A snowball approach identified additional studies that were not captured by the search terms. The reviewer screened titles and abstracts for English language original articles with full-text availability. The following manuscripts were excluded: (1) reviews of a general nature, conference proceedings, and publications offering new theories but without empirical evidence, (2) papers based on non-human data, on connectome data, or mainly on modeling or simulation, (3) duplicates and studies not relevant to brain criticality. The remaining articles were then evaluated for eligibility based on clinical relevance. Ultimately, seventy-eight studies met study criteria for the scoping review. These articles were then analyzed according to seven major categories: anesthesia, epilepsy, neurodegeneration, neurodevelopment, cognition, psychiatry, and sleep medicine. Figure 6 summarizes the changes in LRTC along a subcriticality–supercriticality spectrum that are thought to occur in disease states belonging to these seven clinical categories.
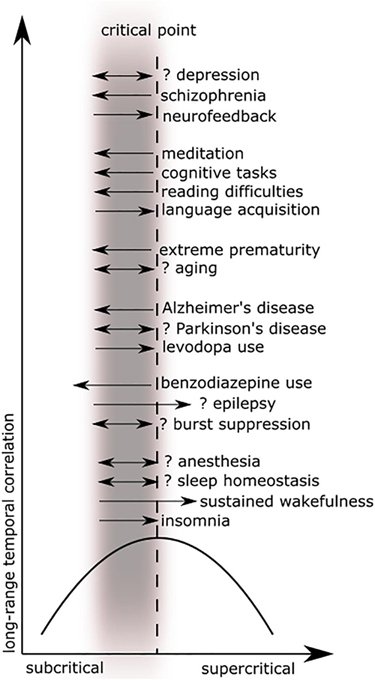
Figure 6. These plots illustrate long-range temporal correlation (LRTC) in different clinical areas as a function of criticality. Figure adapted from Colombo et al. (2016) with permission. The black parabolic curve represents the dynamics of long-range temporal correlation from the subcritical state, reaching a theoretical maximum at the critical point, and decreasing in a supercritical state. The gray blurred rectangle represents the physiological range of brain dynamics, which is thought to be near or below the critical point. Black arrows (excluding the x- and y-axes) represent deviations toward subcriticality (to the left) or toward supercriticality (to the right) with associated decreases in correlation along the black parabolic curve. Double arrows imply that evidence for both increases and decreases (or absence) in LRTC have been reported in that disease process. See the relevant tables for further detail.
Clinical Applications of Brain Criticality
Anesthesia
The literature on criticality in anesthesia is limited but has already shown signs of significant clinical promise. From this small body of research, one can extract two areas of clinical relevance: markers for the depth of anesthesia and predictors of recovery from a persistent comatose state. This literature harmonizes well overall with that of sleep medicine (see Sleep Medicine below).
Three studies have reported on criticality-based markers of the anesthesia depth (see Table 1). An electrocorticogram (ECoG) study of patients undergoing anesthesia for surgical removal of epileptic foci showed that the critical eigenvalues of matrices obtained from a vector auto-regressive (VAR) model could potentially serve as a marker of the depth of anesthesia (Alonso et al., 2014). A scalp electroencephalogram (EEG) study of patients under anesthesia found that LRTC, in combination with oscillation amplitude, could help differentiate between consciousness and anesthesia-induced unconsciousness (Thiery et al., 2018). The authors found that, under anesthesia, LRTC increases in the beta frequency range in frontocentral channels. This increase may reflect decreased neuronal excitability, leading to signal persistence and a resulting limitation on cognitive processes (He, 2014; Thiery et al., 2018). The results of this study contradict a previous study that had found a decrease in LRTC during anesthesia (Krzemiński et al., 2017). However, the contradiction may be secondary to significant differences between the experiments. Thiery et al. (2018) examined human subjects undergoing light anesthesia with sevoflurane, while Krzemiński et al. (2017) examined macaques undergoing deep anesthesia with different anesthetic agents. These differences suggest that future research should focus on identifying criticality-based metrics (e.g., power-law estimation, VAR eigenvalues, LRTC) that are specific to each anesthetic agent at different depths of anesthesia.
Another area of ongoing research is the use of criticality signatures to distinguish persistent coma from other forms of unconsciousness, including deep sleep and anesthesia-induced unconsciousness. A function magnetic resonance imaging (fMRI) study compared both blood oxygen level-dependent (BOLD) signals and brain networks between patients undergoing anesthesia and patients in unresponsive wakefulness syndrome (UWS or persistent coma) (Liu et al., 2014). While the node size in these brain networks was power-law distributed in both patient groups, the node degree distribution (i.e., the number of connections between nodes in the brain network) was only power-law distributed in the healthy patients undergoing anesthesia. The authors offer a helpful analogy from the world of airports and air traffic control. In patients under anesthesia, both the airport size and the air traffic follow a power-law distribution. But in patients with UWS, the airport size remains power-law distributed while the air traffic loses its power-law distribution. This loss may reflect changes in underlying neuronal network topology that give UWS such a poor prognosis. However, more research in this area is required since the node degree distribution in this study does not meet the power-law criteria of Clauset et al. (2009) and, therefore, may follow a different distribution. In fact, another study found an exponentially truncated power law for both patients groups (anesthetized and UWS patients), which suggests the absence of a distinctive signature for the UWS group (Achard et al., 2012). Significant technical differences between Liu et al. (2014) and Achard et al. (2012) make a direct comparison difficult. Nevertheless, these studies raise the possibility that SOC underlies the brain’s ability to rebound quickly from anesthesia or deep sleep, but not from UWS or other major brain insults. Future research in this area will benefit intensivists and neurologists looking for prognostic markers of irreversible brain damage.
Epilepsy
Epilepsy, a disorder characterized by multiple seizures and affecting 1% of the world’s population, represents a significant clinical challenge (Fiest et al., 2017). There is a robust body of work examining the applications of critical phenomena to epilepsy, as summarized in Table 2. From this literature, the following four topics emerge as clinically relevant areas of ongoing research: seizure prediction, seizure localization, seizure characterization, and quantitative analysis of seizure genesis and termination.
Seizure prediction is an important goal in epileptology (Mormann et al., 2007). Efficient seizure prediction, even if only by a few seconds to minutes, may allow patients enough time to administer anti-epileptic medications before seizure onset, either by themselves or through automated implanted devices (Cook et al., 2013). To this end, several studies have identified criticality-based signatures that may help predict the onset of a seizure. For example, critical systems near a phase transition will exhibit signs of “critical slowing.” A combined EEG and ECoG study of children with epilepsy found evidence of such critical slowing in synchronous fluctuations up to 1 h before seizure onset (Cerf et al., 2004). Other studies have taken advantage of an uncanny similarity between seizures and earthquakes. Seizures, like earthquakes, exhibit several properties that are characteristic of SOC (Bak and Tang, 1989; Bak et al., 2002). For example, both seizures and earthquakes cluster temporally, such that the likelihood of the next seizure or earthquake decreases the longer the seizure-free or earthquake-free interval (Omori, 1895; Sornette and Sornette, 1989; Osorio et al., 2009, 2010). Studies have identified other SOC properties in seizures. These include a power-law distribution of inter-seizure intervals (Osorio et al., 2009, 2010; Cook et al., 2014) and of time intervals between non-ictal epileptiform discharges, including burst suppression in neonatal hypoxia (Worrell et al., 2002; Roberts et al., 2014a). By better characterizing these properties, one could hope to identify parameters that can help predict a future seizure−much the same way that seismologists would like to predict the next earthquake (Meisel and Loddenkemper, 2019).
The predictability of these seizures may be related to increased temporal correlation or long memory. A study of long-term ECoG recordings found that epileptiform discharges and seizures in some patients were consistent with long-memory processes, with signal correlations going as far back as 40 days before seizure onset (Cook et al., 2014). Long memory suggests a decrease in signal complexity and, thus, more predictability. These studies open up the possibility of using LRTC and other correlation measures to predict impending seizures. While there is no gold-standard approach for seizure prediction at this time, the brain criticality framework offers new insights that will hopefully produce several candidates for effective seizure prediction. Some of these candidates include excess energy content of EEG signals (Cerf et al., 2004), heavy-tailed distributions of inter-ictal discharges (Osorio et al., 2010), signal variance (Meisel and Kuehn, 2012), Hurst exponent analysis (Cook et al., 2014; Yan et al., 2016), q-parameter, and volumetric energy density from Tsallis non-extensive statistical mechanics (Minadakis et al., 2014).
The surgical removal of epileptic foci for treating refractory epilepsy requires adequate localization of the source of epileptiform discharges (Mu et al., 2014). Localizing the epileptic focus remains a challenging part of this process. Epileptic foci exhibit many critical features, like power-law distributions and LRTC, that are useful for localization. In an ECoG study of patients with temporal lobe epilepsy, the epileptic foci produced a power-law-like behavior of seizure energy and inter-seizure intervals (Worrell et al., 2002). An ECoG study of epileptic patients found that both non-epileptic and epileptic foci in the hippocampus exhibited LRTC (Parish et al., 2004). However, the epileptic foci had larger scaling exponents compared to the non-epileptic foci. Another ECoG study found a similar result, namely stronger LRTC near the seizure focus (Monto et al., 2007). More recently, a magnetoencephalography (MEG) study found that the Hurst exponent – a metric of LRTC – improved the detection of seizure foci (Witton et al., 2019). These studies globally suggest that observables of critical phenomena, like power-law regimes and increased correlation, can improve seizure localization techniques.
The lens of criticality is also casting new light on the characteristics and dynamics of seizures themselves. Several publications have argued that seizures and inter-ictal epileptiform discharges, including burst suppression, represent a critical phenomenon that is power-law distributed (Worrell et al., 2002; Cerf et al., 2004; Osorio et al., 2009, 2010; Roberts et al., 2014a). If this is correct and the reported power-law exponents for seizure energy are between 2 and 3 (as many are), then it follows that, at least mathematically, seizures ought to have a finite mean (energy, size, duration) but infinite (energy, size, duration) variance. Some have argued that this may account for status epilepticus, the phenomenon of prolonged seizures lasting hours to days. The theoretically infinite variance of seizure energy would lead to prolonged seizures that would ultimately resolve because of the finite metabolic supply available to neurons (Osorio et al., 2010; Roberts et al., 2014b). Moreover, if seizures represent a power-law distributed critical phenomenon, they cannot be described by their mean values, since, in a scale-free distribution, there is no “typical” value or mean. Thus, there may be no point in reporting mean seizure duration or energy in clinical publications. Rather, in future clinical and epidemiological studies, it may be more pertinent to report power-law exponents, which best characterize this distribution (Osorio et al., 2009).
However, other publications have argued that the normal brain at rest is in a critical state. Therefore, seizures and interictal epileptiform activity should represent a departure from criticality. This departure from criticality perhaps arises from synchronization effects and characteristic scales present in seizures that become dominant, thus diminishing the scale-free distribution (Osorio et al., 2009; Meisel et al., 2012; Arviv et al., 2016). This departure from a scale-free distribution has been confirmed visually with a “knee,” “shoulder,” or “bump” – different words for the same anomalous deviation−in the log-log plot of several probability density functions, including that of seizure energy (Osorio et al., 2009), phase-locking intervals (Meisel et al., 2012), neuronal avalanche size (Arviv et al., 2016) and burst area in burst suppression (Roberts et al., 2014a). The evidence suggesting that the resting brain is in a critical state is strong (Kitzbichler et al., 2009; He, 2011; Tagliazucchi et al., 2012; Daffertshofer et al., 2018), even if some of that evidence (Kitzbichler et al., 2009; Meisel et al., 2012) has been challenged (Botcharova et al., 2012). Seizures would logically seem to represent a departure from the resting state of the brain and thus from a critical state. How then can one reconcile this with all the evidence suggesting that seizures behave like a critical phenomenon?
Perhaps one way to reconcile this information is to look more closely at the types of variables (Milton, 2012). In cases that have identified power-laws in the resting brain (with departures during seizures), the variables studied were usually neuronal avalanche size and duration, in what could be called an “avalanche approach.” On the other hand, studies that found power-law behaviors of seizures took more of an “earthquake approach” in which the variables were usually seizure energy and inter-seizure interval (Worrell et al., 2002; Osorio et al., 2009). Since different properties, or “laminar phases,” are being examined in each case, it may not be reasonable to compare their power-law exponents (Milton, 2012).
Moreover, the range of power-law exponents found in both the avalanche and earthquake approaches is broad and overlapping. The exponents encompass the range of –3/2, which is expected for avalanche size in SOC, up to −5/3, characteristic in turbulent dynamical systems (Milton, 2012). This broad range may result from particular experimental conditions (including digitization rates of instruments). But this range may also reflect the reality that neurons, unlike earthquakes and sand-piles, learn and adapt (Bonachela et al., 2010). The existence of characteristic scales (“bumps”) on log-log plots, which perturb the expected scale-free distribution, may also be due to characteristic scales from rare neurological events such as dragon-kings (Pisarenko and Sornette, 2012; Sachs et al., 2012). Finally, since many control parameters may be involved in governing these systems, the possibility of “double criticality” whereby critical regimes coexist with different order and control parameters may also be at work in this apparent disagreement (Hesse and Gross, 2014). Resolving this disagreement on both theoretical and experimental grounds will be an important area of future research.
Brain criticality also offers insights into seizure initiation. Epileptic foci removed from pediatric epilepsy patients exhibited neuronal hyperactivity, whose increased firing rate correlated with an increased branching parameter (Hobbs et al., 2010). This finding suggests that in some epileptic syndromes, a positive feedback loop between firing rate and branching parameter may be responsible for generating seizures as a super-critical state. An ECoG study found oscillations in signal variance in the lead-up to a seizure (Meisel and Kuehn, 2012). These pre-ictal oscillations were suggestive of a critical transition, characterized mathematically by a Hopf bifurcation. Despite the small number of studies in this area, research on seizure generation using criticality is promising.
Several studies suggest that seizure termination may also involve a critical transition. In one study by Kramer et al. (2012) the brain’s inability to complete a critical transition results in status epilepticus, in which the brain dynamics constantly reverberate between the ictal and post-ictal state (i.e., attractor), without ever crossing the threshold that effectively ends a seizure. In a study of neonates with birth hypoxia, researchers found evidence of a critical phase transition in the shift from burst suppression to the resumption of normal EEG patterns (Roberts et al., 2014a). The role of benzodiazepines in seizure termination may also be related to criticality. In a small ECoG study of patients with epilepsy, study authors found that a decrease in LRTC in the ictal focus accompanied the clinical resolution of a seizure after benzodiazepine administration (Monto et al., 2007). These studies all suggest that criticality plays a role in seizure termination.
Neurodegeneration
A small number of studies (see Table 3) have examined the role of critical phenomena in neurodegenerative diseases, like Alzheimer’s disease (AD) and Parkinson’s disease (PD). These studies reveal new insights about the pathophysiology of these diseases and suggest novel markers for disease monitoring.
Cognition requires production and subsequent decay of synchronization in neural networks (Breakspear and Terry, 2002). Moreover, in healthy adults, spontaneous fluctuations in synchronization are known to follow a power-law distribution, suggestive of an underlying SOC state (Stam and de Bruin, 2004). Does AD represent a departure from critical dynamics? Is synchronization perhaps a control parameter given its importance in cognition? To begin to answer these questions, researchers compared various measures of synchronization on EEG between patients with AD and non-demented patients with subjective memory problems (Stam et al., 2005). While both cohorts maintained a scale-free distribution of spontaneous fluctuations of synchronization, the mean synchronization and its fluctuations were both decreased in the upper alpha and beta frequency range in the AD patients compared to the non-demented patients. This finding is consistent with the view that AD patients maintain a SOC state but with decreased ability to generate and destroy synchronized neural networks. The authors go on to speculate that perhaps synchronization loss in the upper alpha and beta band is one of the first quantifiable changes in AD since it is statistically different from non-demented patients who report memory impairment. Moreover, the mean synchronization level and the DFA exponent of synchronization fluctuations were both correlated to the Mini-Mental State Examination (MMSE) score. Synchronization-based metrics may, therefore, prove helpful for diagnosis and monitoring of early-onset AD.
Other metrics inspired by brain criticality show promise for the diagnostic evaluation of early-onset AD. A MEG study discovered a decreased incidence of alpha-frequency oscillation bursts and weaker auto-correlations in patients with early-onset AD compared to controls (Montez et al., 2009). Its authors concluded that oscillation amplitude dynamics may be beneficial for early-onset AD detection. Operating from the framework of SOC, a large, resting-state EEG study of patients with moderate-to-severe AD compared to healthy controls also identified a possible marker for early AD detection (Vyšata et al., 2014). The power-law exponents for spectral densities (per brain region) were compared between AD and healthy patients. A statistically significant difference in the power-law exponent in the frontal and pre-frontal lobes was noted. This result is perhaps not so surprising given that frontal lobe atrophy typically accompanies AD dementia. Interestingly, the most highlyspecific and predictive area of the brain for AD in this study was the temporal region (Vyšata et al., 2014). Future studies using this approach and focusing on the temporal region may be able to validate this power-law approach as a diagnostic metric in patients with early manifestations of AD. To this point, a recent fMRI-connectome study showed that a combination of criticality-based metrics can help distinguish neurotypical adults from those with mild cognitive impairment or AD (Jiang et al., 2018).
Parkinson’s disease (PD) may be a case of how deviation from a critical state in crucial motor circuits leads to motor symptoms like tremors, bradykinesia, and rigidity. Researchers have identified LRTC from the subthalamic nuclei (STN) of patients with PD undergoing deep brain stimulation (DBS) (Hohlefeld et al., 2012). These correlations increased with the administration of levodopa, one of the common medications for treating PD. In a rat model of PD, LRTC also increased following administration of apomorphine (Cruz et al., 2009), which suggests that restoration of LRTC may be related to symptomatic improvement in PD. A study of PD patients who underwent DBS surgery found LRTC in the dynamics of the bilateral STN, both on and off medications (West et al., 2016). Using an adaptation of DFA to study synchronization called DFA-PS (Botcharova et al., 2015), the authors found that the DFA-PS exponent was positively correlated with motor symptom severity when patients were not receiving dopaminergic medications. Therefore, these authors suggested that patients with more severe motor symptoms are closer to the onset of pathological synchronization, which may reduce effective information transfer in these important neural circuits (Hanslmayr et al., 2012; West et al., 2016). In this regard, PD may represent a situation of departure from a critical state toward perhaps a hyper-synchronized supercritical state.
Obtaining recordings from deep brain structures like the basal ganglia is not usually possible outside of DBS. Since DBS is not the first-line therapy for PD, it seems unlikely that LRTC will develop into a helpful marker of PD onset and progression. Gait analysis and related behavioral metrics, on the other hand, may offer a more convenient way to follow the clinical evolution of PD. Healthy human gait is characterized by 1/f noise, which is known to be a feature of SOC systems (Hausdorff, 2009). This 1/f noise disappears in PD but resumes with non-invasive auditory rhythmic stimulation (Hove et al., 2012). In a unique study, a single patient with idiopathic PD and right-handed tremor, who happened to be an accomplished pianist, received DBS and was subsequently asked to perform works of piano both with and without active DBS (Ruiz et al., 2014). Without DBS, correlations in the inter-onset interval (i.e., the time between note onset of subsequent piano notes) were random. But with active DBS, long-range correlations of inter-onset interval emerged, along with general motor improvement of the affected right hand on the Unified Parkinson’s Disease Rating Scale (UPDRS) - III scale. The authors suspected that DBS provides a similar stimulus to the non-invasive rhythmic stimulation of Hove et al.’s (2012) experiment, which restores the 1/f noise of gait, presumably by restoring a critical state in the motor basal ganglia circuit (Ruiz et al., 2014). Future research should focus on establishing whether restoration of 1/f noise is necessary for motor improvement in PD and whether gait-based metrics can serve a clinical purpose in either diagnosing or monitoring PD.
Neurodevelopment
The brain criticality hypothesis also applies to the newborn brain that matures and ages across an average human lifespan. As it grows, the brain’s electrical signature undergoes changes that are helpful markers of typical development. Research in this area has taken shape around two central themes (see Table 4). The first is the study of brain oscillations in premature infants or infants with birth asphyxia (hypoxemic-ischemic encephalopathy or HIE). The other is the study of brain oscillations in children, adolescents, and adults to characterize the electrical patterns that correlate with structural and anatomic changes of aging.
If the mature human brain exhibits signs of criticality, it seems reasonable to ask whether those signs are also present in the term or pre-term neonate. Studying burst activity on the EEG of pre-term infants, Hartley et al. identified LRTC and dynamics that were suggestive of a phase transition (Hartley et al., 2012). Despite several infants having intracranial hemorrhages, the Hurst exponents describing the LRTC were similar for infants with and without bleeding. This finding suggested that the brain maintains temporal complexity despite this vascular insult. Another EEG study showed that power-law exponents of electrical bursts were predictive of neurodevelopmental sequelae in term infants with HIE (Roberts et al., 2014a). This fascinating discovery led to a similar EEG study in extremely preterm infants, searching for criticality-based metrics that could predict long-term sequelae. A careful analysis of several parameters from shape analysis led to the identification of the slope of burst shape, among other parameters, that could serve as a sensitive and specific predictor of neurocognitive and motor sequelae in this unique population (Wikstro et al., 2015). In sum, shape analysis and power-law exponents predict clinical outcomes in preterm and term infants, respectively. Regardless of hemorrhage status, the brains of preterm infants exhibit LRTC. These findings suggest that criticality plays a vital role in the dynamics of the preterm and term infant brain.
How criticality or near-criticality emerges and evolves in the infant’s brain through adolescence into adulthood is another crucial area of investigation. Jannesari et al. (2020) studied term infants at 6 and 12 months of life using high-density EEG to see if scale-free brain activity that was already known to exist at birth (Fransson et al., 2013) continued in the first year of life (Jannesari et al., 2020). At both 6 and 12 months, the EEG organized spatiotemporally according to a power-law with significant LRTC. The authors found no significant differences between the 6- and 12-month data, suggesting a degree of stability in neuronal avalanche dynamics after the newborn period. But while there do not seem to be significant differences in LRTC and power-law distributions during the first year of life in term babies, a significant difference does exist between pre-term babies and term babies, even a decade after birth. Using functional and diffusion MRI, researchers examined the brain dynamics of 10-year-old children, roughly half of whom were born extremely premature, and the other half at term (Padilla et al., 2020). Extremely premature (EP) children generated fewer electrical events (i.e., decreased ignition) compared to the term children – suggesting decreased global integration from decreased firing to other important brain regions over time (Deco et al., 2017). EP children also exhibited abnormal hierarchical organization, which autistic children are also known to exhibit (Parr et al., 2018), further linking prematurity and autism (Padilla et al., 2017). EP children’s brain dynamics showed decreased synchrony and sub-criticality compared to term children, mainly in brain areas with rich-club architecture (Ball et al., 2014). This difference in synchronization perhaps occurs due to abnormal development of white matter in EP children (Uhlhaas et al., 2010). Yet, whereas extreme prematurity seems to predispose to some degree of sub-critical brain dynamics, it seems from other studies that term infants go on to exhibit similar power-law-like brain dynamics as adults. In an EEG-fMRI study, newborn brain dynamics followed scale-free power (frequency) distributions across several orders of magnitude, with larger power-law exponents in primary sensory areas compared to associative cortical areas (Fransson et al., 2013). In contrast, power-law exponents for adult brain dynamics were highest in associative cortices. While both adults and term infants exhibit scale-free dynamics, the increased exponents in different brain areas suggest that development and aging control, to some degree, the cartography of near-criticality in the brain.
As for aging, the development of criticality and its suspected decay with age have been the subjects of several studies (see Table 4). Phase reset (PR), a combination of phase-shift followed by phase-locking of EEG signals, is a powerful marker of SOC used in many age-based studies of criticality. In a study of PR in close to 460 subjects in the age range of 2 months to 16 years old, PR followed a 1/f distribution, with a longer mean duration of both phase-shift and phase-locking as a function of age (Thatcher et al., 2009). The presence of this distribution argues in favor of scale-invariant fluctuations in PR, consistent with SOC (Thatcher et al., 2009, 2014). In a study of pre-school children, EEG frequency variance, a proxy for PR, was also power-law distributed and increased with age (Frohlich et al., 2015). Like PR, frequency variance may reflect critical fluctuations driven by SOC.
LRTC has also been found to correlate with aging. A study of about 1430 subjects from ages 5 to 71 revealed significant increases in LRTC from childhood through adolescence into early adulthood (about age 25), after which LRTC stabilized (Smit et al., 2011). Scale-free modulations of resting-state oscillations, therefore, seem to reflect brain maturation. Moreover, principal component analysis (PCA) showed progressive integration of segregated functional-anatomic brain regions with age – consistent with increased spatial correlation from critical dynamics. In a smaller study of subjects ages 0 to 55, EEG LRTC was present from early childhood into adulthood but with magnitudes that changed differently depending on age, EEG electrode, and frequency band (Berthouze et al., 2010). For example, LRTC magnitude increased with age in the beta band in central and parietal electrodes but decreased with age in the theta frequency range. But temporal correlation is not the only observable that appears to decrease with age in some frequency bands. A study of resting-state EEG in nearly 18,000 individuals ages 18 to 70 found a decrease in the power-law exponent of spectral density with age (Vyšata et al., 2014). The authors theorized that brain atrophy with age might lead to loss of neuronal connections (Morrison and Hof, 1997), which would shift the neural networks away from their scale-free topology (Barabási and Albert, 1999) and thus away from power-law dynamics.
While there may be some appearance of contradiction in these results (i.e., increased LRTC in one frequency range versus another with aging), there is precedent for contradictory results finding resolution when the right tool is applied. For example, both healthy aging and anticholinergic medications increase the Hurst exponent (Wink et al., 2006). Yet, faster processing speeds, which are not characteristic of aging, also lead to increases in the Hurst exponent (Wink et al., 2008). Suckling et al. (2008) reconciled these results with the introduction of a multi-fractal approach and demonstrated that criticality offered a better explanation than turbulence for these brain dynamics. This example highlights how the right methodology and tools can help make sense of disparate results. Methodological developments, like the index of functional criticality (Jiang et al., 2019), will hopefully generate more useful clinical results in this area. The applications of criticality to aging and geriatric medicine are still in their infancy but deserve more emphasis in a society with an increasingly elderly population.
Cognition, Attention, Learning, and Autism
In computational and theoretical models, criticality optimizes certain features of learning, including optimal information capacity and transmission (Shew et al., 2011; Shew and Plenz, 2013; Del Papa et al., 2017). Important aspects of human learning, including cognition and attention, have been analyzed through the lens of criticality (see Table 5). Studies on attention-deficit hypersensitivity disorder (ADHD) and autism, in which features of neurotypical cognition and attention are disrupted, are few in number but appear promising.
In the area of cognition, researchers have wondered whether criticality plays a role in the brain’s response to increasing cognitive loads. In a study of healthy adults undergoing working memory and response tasks, Altamura et al. (2012) found power-law-like behavior in the upper tails of the cumulative distribution of response times. One possible interpretation of this result is the emergence of scale-free behavior in response to increased cognitive loads. In other words, increased cognitive load shifts random behavior toward scale-free behavior near a critical point. Another study of healthy adults undergoing a cognitive task also showed a power-law scaling of response time fluctuations (Simola et al., 2017). Furthermore, Simola et al. (2017) found autocorrelations and LRTC of response time fluctuations, with the LRTC scaling exponents correlating negatively with error rates and positively with executive function testing scores. As the authors pointed out, LRTC can originate in the setting of criticality but also exist in systems with a slow decay of memory. The negative correlation of LRTC scaling exponent with error rates suggests increased cognitive flexibility, which is more consistent with criticality than with a system that operates with slowlydecaying memory. Without criticality, LRTC would decrease cognitive flexibility because long-memory would not allow reconfigurations. Patients with ADHD are known to show increased response time variability in these kinds of tasks. However, in this study, the LRTC scaling exponents were not correlated to response time variability or mean response time, implying that another brain process may be involved in ADHD. Studies of behavioral dynamics (e.g., response times on tasks) in ADHD patients compared to neurotypical patients may grant further insights into the role of scale-free, critical dynamics in ADHD.
But while the behavioral response (i.e., response times) to increased cognitive load may be power-law-like, studies of the electrical brain response to increased cognitive load show more mixed results. A MEG study of neurotypical children and children with high-functioning autism undergoing executive function tasks demonstrated a decrease in power-law scaling of phase synchrony as cognitive tasks became more difficult, i.e., increased cognitive load (Tinker and Velazquez, 2014). Power-law distributions were uncommon in this study in both autistic and neurotypical children and were more likely to co-exist with other distributions (e.g., exponential). These results suggest that metastable, rather than purely critical, dynamics are at play in the brain’s response to increased cognitive loads (Bressler and Kelso, 2001; Deco and Jirsa, 2012). Along similar lines, an EEG study of healthy adults during a working memory task found an inverse correlation between LRTC in the theta frequency range and memory performance (Euler et al., 2016). This result is perhaps the opposite of what one might have predicted from work that had found indications of criticality in behavioral dynamics (Altamura et al., 2012; Simola et al., 2017).
But not all brain studies of human cognition have argued against the existence of critical dynamics. An EEG study of 210 neurotypical adults undergoing an object recognition task showed that variation in 1/f noise was a robust predictor of cognitive processing speed (Ouyang et al., 2020). Moreover, the power-law exponent of the 1/f noise was most predictive of person-to-person processing speeds. While there are many non-critical sources of 1/f noise, this study harmonizes well with the theoretical literature on criticality’s optimization of information transmission. In an EEG study of healthy adults undergoing an action adjustment task, midfrontal theta – an electrical signature known to correlate with real-time error correction (Cavanagh and Frank, 2014) – displayed scale-free-like fluctuations over durations of up to tens of seconds (Cohen, 2016). The author suggested that fluctuations may modulate the midfrontal theta brain response to errors at a critical point (Cohen, 2016). In summary, evidence from both brain dynamics and behavioral dynamics points to some aspects of criticality in human cognition (Altamura et al., 2012; Cohen, 2016; Simola et al., 2017; Ouyang et al., 2020) while other studies do not (Tinker and Velazquez, 2014; Euler et al., 2016).
Studies of human attention have centered on the roles of criticality in meditation and its possible applications to ADHD, as mentioned earlier. There are many forms of meditation, and a commonly practiced form, called focused attention (FA) meditation, helps its practitioners improve their ability to focus (e.g., on their breath, on their bodily sensations). An EEG study of FA meditation-trained subjects compared to meditation-naïve subjects found that FA meditation in practitioners led to strong suppression of LRTC in oscillations across all frequency bands and electrodes, compared to the eyes-closed state (Irrmischer et al., 2018a). Meditation-naïve subjects did not show this suppression of LRTC. A year’s worth of meditation practice led to more permanent changes since FA meditation practitioners had increased LRTC during eyes-closed rest state when they underwent EEG a year later. The authors hypothesized that meditation-related release of GABA might be contributing to excess inhibition and a subcritical regime as seen by decreased DFA exponent (i.e., LRTC suppression). In a similar EEG study of healthy subjects, high levels of alpha frequency LRTC in the sensorimotor region of the brain during rest predicted strong reaction-time performance in an attention task (Irrmischer et al., 2018b). During the execution of the task, on the other hand, suppressed LRTC in beta and gamma frequencies was associated with fast reaction-time performance. This study complements the results obtained in an earlier EEG-fMRI study of healthy adults during a visuomotor task and at rest. It found that the resting-state is associated with near-critical dynamics, while focused cognitive tasks induce subcritical dynamics that may reduce interference with the task at hand (Fagerholm et al., 2015). The upshot of these three studies is that focused attention – whether meditation-related (Irrmischer et al., 2018a) or visual attention (Fagerholm et al., 2015; Irrmischer et al., 2018b) – is associated with a reduction in criticality fluctuations. Generalized human attention at rest, on the other hand, balances a certain degree of focus with the ability to respond quickly to both internal and external stimuli. That balance should theoretically be optimal near criticality.
A handful of studies have examined the role of criticality in human learning, both in children and in adults. A MEG study of children with reading difficulties showed decreased temporal correlations in the left temporoparietal region compared to age and IQ matched children without reading difficulties (Dimitriadis et al., 2013). While this study examined subjects at rest instead of in a reading activity, its results dovetail well with previous studies that showed aberrant cortical activation in left posterior and temporal regions in children with severe reading difficulty during a reading assignment (Hoeft et al., 2007; Cao et al., 2008). Both groups of children exhibited scale-free global network connectivity, suggesting that local, rather than global, decreases in LRTC may be involved in reading difficulties and dyslexia. A high-density EEG study of neurotypical children found that lower alpha frequency power and increased LRTC correlated positively with language scores (Kwok et al., 2019). This study confirmed the findings of Dimitriadis et al. (2013) that critical state dynamics are important for language acquisition.
A recent resting-state fMRI study of neurotypical adults with a range of IQ scores found that high fluid intelligence is associated with proximity to a critical phase transition in a spin-glass model (Ezaki et al., 2020). This finding was consistent with previous work suggesting near-criticality as perhaps optimal for learning (Gisiger et al., 2014). From an EEG study of healthy university students learning organic chemistry, it is also known that a lower power-law exponent of the fractal component of EEG signals correlates with higher learning gains during a computerized learning task under EEG (Bongers et al., 2019). While this latter study makes no claims regarding criticality, one can infer that the scale-free behavior of neurons matters for the acquisition of complex new knowledge.
Only a few studies have examined the role of criticality-related markers in autism. A resting-state fMRI study of adult males with autism spectrum disorders, including high-functioning autism, detected a small but significant decrease in the Hurst exponent compared to controls in brain regions implicated in autism by previous neuroimaging studies (Lai et al., 2010). This decrease in the Hurst exponent indicates a shift toward randomness of fluctuations in blood oxygen level-dependent (BOLD) signals in the brain impacted by autism. Though the interpretation of the Hurst exponent in BOLD signals is challenging because of the unclear roles of blood supply and neural circuits among many others, the use of fractal scaling can serve as a barometer of underlying coordination and organization of neural circuits. In this study, the shift toward randomness in BOLD signals may indicate decreased coordination of small-scale circuits, to the disadvantage of larger brain circuitry. This hypothesis harmonizes well with one of many prevailing theories about the origins of autism, namely the local overconnectivity theory (Belmonte et al., 2004; Baron-Cohen and Belmonte, 2005). A more recent study of children with autism spectrum disorders (ASD) used functional near-infrared spectroscopy (fNIRS) to compare LRTC with age and gender-matched neurotypical children (Jia et al., 2018). Consistent with the findings of Lai et al. (2010) this study found that DFA exponents (i.e., LRTC scaling exponents) were significantly smaller over the left temporal region for the oxy-hemoglobin (oxy-Hb) signal in children with ASD compared to controls. DFA exponents were also significantly smaller over both temporo-occipital regions for deoxy-hemoglobin (deoxy-Hb) signals in children with ASD compared to controls. DFA exponents correlated well with age in neurotypical children, consistent with findings discussed previously (Smit et al., 2011). However, DFA exponents of oxy-Hb in the left temporal region correlated negatively with autism symptom severity on a parental questionnaire. This result dovetails nicely with a previouslyidentified negative correlation between cerebral blood flow to the left superior temporal gyrus and Autism Diagnostic Interview-Revised scores (Meresse et al., 2005). While the authors of this fNIRS study suspect that autism may represent a departure from SOC, it seems further neuroimaging studies using criticality-based approaches will be needed before one can safely reach that conclusion.
Psychiatry
Researchers have turned to criticality-based tools to improve their understanding of common psychiatric conditions like depression, schizophrenia, anxiety, post-traumatic stress disorder (PTSD) (see Table 6). Insights from criticality theory have also helped describe the psychological effects of neurofeedback and psychedelics.
Studies of major depressive disorder (MDD) or unipolar depression have mostly relied on the search for temporal correlations (LRTC) using DFA. A small MEG study of patients with MDD and healthy controls found absent LRTC in the theta frequency band in patients with MDD compared to controls (Linkenkaer-Hansen et al., 2005). The study authors suggested that abnormal temporal structure of theta oscillations could reflect an underlying defect in limbic-cortical networks identified in anatomic-functional studies of MDD. Another small EEG study of patients with MDD and healthy controls did not reproduce this finding of absent theta LRTC (Lee et al., 2007). Instead, the study authors found that increased LRTC scaling exponents (i.e., slower decay of LRTC) correlated positively with the severity of depression over most EEG channels. This finding led the authors to speculate that rumination and psychomotor retardation – typical features of MDD – may be responsible for this persistence of LRTC.
Other studies have examined whether depression leads to alterations in LRTC during sleep. A small sleep EEG study of patients with untreated, acute episodes of MDD found a decrease in LRTC scaling exponents in NREM2, NREM3, and NREM4 compared to healthy controls (Leistedt et al., 2007b). However, this decrease was not statistically significant. A similar study by the same research team, this time with patients in remission from MDD, found no differences in LRTC through the stages of sleep (Leistedt et al., 2007a). In addition to demonstrating the existence of LRTC during sleep (see Sleep Medicine section for more details), these results argue against the “depressive scar” hypothesis, according to which depression leads to permanent residual defects.
Researchers have also taken an interest in negative emotional regulation as a precursor for MDD. A large EEG study of non-depressed undergraduate students found a positive linear correlation between LRTC scaling exponents of theta and broad-band frequencies and negative emotional regulation on various questionnaires (Bornas et al., 2013). Their research suggested that negative emotional control may anticipate full-blown MDD by several years. While this study broadly agreed with the findings of Lee et al. (2007), it disagreed with Linkenkaer-Hansen et al.’s (2005) conclusions with regards to the magnitude of scaling exponents with worsening rumination. A more recent, large EEG study found that, at baseline, patients with MDD have higher LRTC scaling exponents in the theta frequency range than healthy controls (Gärtner et al., 2017). After intervention with either mindfulness training or stress reduction training, both groups experienced a reduction in the strength of LRTC. This latter result suggests a new approach for examining the physiological mechanism by which psychotherapeutic interventions improve depressive symptoms. Given the inconsistencies in findings, more extensive studies will help clarify the nature of the LRTC in the various frequency bands and the multiple stages of depression (acute, treated, etc…). Future studies could assess whether LRTC changes significantly after initiation of first-line pharmacological intervention for MDD. Other criticality-based metrics could be useful to characterize the nature of brain dynamics in MDD as either sub-critical or, less likely, super-critical.
Criticality-based studies of schizophrenia are few but have opened up new horizons. An EEG study of around 30 patients with schizophrenia and schizoaffective disorders used a fractal analysis of 1/f EEG rhythm fluctuations to try to distinguish the brain dynamics of schizophrenia from that of healthy controls (Slezin et al., 2007). A frontal electrode (F4) exhibited increased instability and randomness in the alpha band for patients with schizophrenia and schizoaffective disorders. The theta band, on the other hand, exhibited increased stability and decreased complexity in patients with schizophrenia compared to healthy controls. A subsequent fMRI study of patients with schizophrenia compared to healthy controls (Radulescu et al., 2012) also identified decreased complexity of brain dynamics, but different from that of Slezin et al’s. (2007)study. In Radulescu et al’s. (2012) study, a sophisticated analysis pipeline, including power spectrum scale invariance (PSSI) and Poincare maps (a measure of signal variance), found that signals coming from Brodmann area 10 (BA10) exhibited lower power-law exponents in schizophrenic patients than in healthy controls. In other words, schizophrenic patients displayed white (Gaussian or random) noise in this brain region, compared to pink (1/f) noise in healthy patients. This finding is consistent with previous research documenting the role of BA10 in executive function, working memory, and emotion regulation (Radulescu et al., 2012). This transition from pink noise to white noise in schizophrenia suggests, from the perspective of criticality, a loss of responsiveness to stimuli.
While the studies mentioned above took a fractal and power-law approach to signal analysis, others have taken the route of studying LRTC in schizophrenia. Their results complement and refine those obtained using fractal approaches. A high-density EEG study of LRTC in adults with schizophrenia and schizoaffective disorders found strong attenuation of LRTC scaling exponents in alpha and beta frequency bands in patients compared to healthy controls (Nikulin et al., 2012). While Slezin et al. (2007) did not study the beta frequency range, they did observe increased complexity in the alpha range, which is globally consistent with the findings in this study. These attenuated scaling exponents indicate decreased temporal correlation and a decrease in temporal precision of neuronal firing compared to healthy subjects. This interpretation fits well with at least two theories for the origins of schizophrenia, namely that of excessive neuronal noise and variability (Rolls et al., 2008) and the “disconnection hypothesis” of dysfunctional relationships between neural networks (Friston et al., 2016). A follow-up study found similar results (Moran et al., 2019). In this high-density EEG and standardized low-resolution brain electromagnetic tomography (sLORETA) study of patients with schizophrenia compared to healthy controls, there was a significant reduction in LRTC in the beta-band over the bilateral posterior regions in patients compared to healthy controls. This study found no differences in the alpha frequency between patients and controls. However, the study authors suggested that the eyes-open state of their study (compared to the eyes-closed, resting state of Nikulin et al., 2012) may have eliminated an underlying difference in that frequency range. More importantly, both studies confirm the importance of LRTC as markers of network instability in schizophrenia.
A much smaller number of studies have examined the role of neurofeedback (NFB) as a treatment modality for psychiatric disorders. A small study of healthy adults randomized to either closed-loop NFB or sham NFB found that, after three sessions, LRTC in the alpha frequency band was stronger in the NFB group compared to the sham (Zhigalov et al., 2016). This difference was statistically significant and did not involve any statistically significant topographical changes in alpha power. The study provided proof-of-concept that closed-loop NFB can restore critical brain dynamics by altering the excitation-inhibition balance in psychiatric disorders with decreased LRTC. A larger EEG and fMRI study of healthy patients confirmed this improvement in LRTC after closed-loop NFB compared to sham. The study also involved a population of patients with PTSD, whose LRTC improved with closed-loop NFB (Ros et al., 2014). The study authors speculated that NFB leads to stronger excitation with an associated increase in temporal correlation and symptomatic improvement. While it is unclear whether NFB can help in disorders characterized by super-criticality (e.g., seizures), NFB has already shown benefit in several disorders characterized to some degree by sub-criticality, including schizophrenia (Surmeli et al., 2012) and major depression (Escolano et al., 2014).
A few criticality-based studies have taken an interest in the role of psychedelics in treating mental illnesses. Researchers have focused on psilocybin, the active ingredient in “magic mushrooms,” and lysergic acid diethylamine (LSD). In an fMRI study of healthy patients receiving psilocybin versus a placebo, study authors found an increased variance in BOLD signals in the hippocampi of psychedelic recipients (Tagliazucchi et al., 2014). The increased variance implies increased synchronization, consistent with a super-critical state of brain dynamics. This super-critical state could account for the hyper-associative cognition characteristic of psychedelics (Carhart-Harris et al., 2014; Carhart-Harris, 2018). While this review limits itself to non-connectomic data, the works of Atasoy et al. (2017, 2018) deserve mention here. Using a unique connectome-harmonic decomposition approach, her research team has found in several studies that infusions of psychedelics “push” brain dynamics out of baseline sub-criticality toward criticality (Atasoy et al., 2017, 2018). More and more studies are finding that psychedelics are helpful adjuncts to psychotherapy (Atasoy et al., 2017). A psychedelic-induced transition out of a sub-critical disorder like depression and closer to criticality may account for this benefit.
Sleep Medicine
Sleep medicine deals with human sleep and its associated disorders, including insomnia, sleep apnea, and narcolepsy. There are multiple stages of sleep, including rapid eye movement (REM), non-rapid eye movement (NREM), which is further divided into light sleep (NREM1 and NREM2) and deep sleep (NREM3 and NREM4). A typical night’s sleep runs through several cycles of each of these sleep stages. The brain criticality literature centers on two key areas of sleep medicine – characterization of sleep stages and the physiology of sleeping disorders.
Researchers have tried improving the classification of sleep stages with the help of criticality-based metrics. The results of these studies seem, for now, largely inconsistent. An EEG study of healthy patients found LRTC in brain oscillations in both the open-eye and closed-eye states (Nikulin and Brismar, 2004). LRTC was more consistent, however, in the closed-eye state, with a significant difference in the scaling exponent between closed and open eye conditions in the beta frequency range. Building on this initial result for LRTC, an EEG study of healthy patients examined the ability of various fractal and spectral metrics to distinguish REM, NREM2, and NREM4 (Weiss et al., 2011). The authors found that the multifractal metric was superior to other metrics for sleep stage classification. From wakefulness to deep sleep, multifractality decreased while monofractality (e.g., the Hurst exponent) increased. The loss of multifractality and disruptions in the 1/f noise in the deep sleep stages suggested that sleep-specific brain rhythms (e.g., sleep spindles) disrupt the day-time self-similarity. Previous studies had shown an increase, not a decrease, in multifractality in deepening sleep (Ma et al., 2006). These differing results suggest that additional studies of multifractality are needed.
The increase in mono-fractality that accompanied deep sleep in the study by Weiss et al. (2011) suggested increased long-memory (LRTC) in sleep, similar to the increase in scaling exponent noted in the closed eye state by Nikulin and Brismar (2004). Subsequent studies, however, have produced results that seem to contradict these findings. Using EEG-fMRI data from healthy adults in NREM sleep, Tagliazucchi et al. (2013) found that a breakdown in LRTC happened as patients moved into the deeper sleep stages. Specifically, the Hurst exponent decreased in the default-mode network (DMN) and attention centers of the brain during NREM2 (Tagliazucchi et al., 2013). Two studies of polysomnogram data from a different cohort of healthy adults found a similar result (Allegrini et al., 2013, 2015). The monofractal metric (i.e., the Hurst exponent) decreased from ∼0.75 during wakefulness and REM, to ∼0.5 in NREM3 and NREM4. Recall that a Hurst exponent of 0.5 indicates random, white noise, while 0.75 suggests a moderate amount of positive correlation. This finding suggested the existence of a breakdown in LRTC when entering deep sleep. Complicating matters further is that studies showing decreases in LRTC during sleep did not control for changes in signal power that naturally occur during sleep (Meisel et al., 2017). More studies on the existence and changes of LRTC during sleep, taking into account fluctuations in signal power, are needed if these are to become useful in sleep stage classification or in understanding sleep microarchitecture.
There are also conflicting results in the literature when it comes to power-law distributions of various observables during sleep. In an EEG study, researchers noted that subjects in normal states of wakefulness exhibited a power-law distribution of coherence potentials and phase-locking intervals (PLI)(Meisel et al., 2013). Also, their EEG signals produced a branching parameter near one, which suggests a system at or near criticality (Yang et al., 2012; Meisel et al., 2013). As patients were kept awake longer and deprived of sleep, the distributions of coherence potentials and PLIs developed larger tails along with an increase in the branching parameter, a decrease in the variability of synchronization, and an increase in mean synchronization – all suggestive of a supercritical state. The authors suggested that prolonged wakefulness leads to a supercritical state through excess excitability of neurons (Shew et al., 2009), as is also thought to occur in epilepsy. Meisel et al. (2013) proposed that, during restorative sleep, a decrease in synaptic strength should lead to a shift away from super-criticality, back toward a critical regime. This view is in line with a similar theory that sleep is designed to restore brain dynamics to a slightly subcritical or near-critical regime to avoid the risk of run-away excitation in a supercritical state (Pearlmutter and Houghton, 2009, 2013).
An ECoG study of patients during sleep revealed power-law distributions of neuronal avalanches in local field potentials (LFPs), but with different exponents depending on the sleep stage (Priesemann et al., 2013). After making adjustments for the fact that LFP amplitude naturally increases from wakefulness to deep sleep, the study authors found that slow-wave sleep (SWS or NREM3) displayed large avalanches. Wakefulness and REM sleep, on the other hand, displayed intermediate and small avalanches, respectively. Because the study found a branching parameter less than one during wakefulness, the authors concluded that the awake human brain at rest is in a subcritical state rather than in a critical state as had been previously argued (Meisel et al., 2013). The authors suggest that brain dynamics shift closer to criticality during SWS and then back into sub-criticality during REM sleep (Priesemann et al., 2013). Their data and additional computational modeling found that small changes in effective synaptic strength could tune the brain closer to a critical state during SWS or closer to a subcritical state with fragmented dynamics during REM. Of note, this study did not find power-law distributions under the more stringent criteria of Clauset et al. (2009). Moreover, a small study of power-law distributions of cortical spikes and LFPs under awake, SWS, and REM sleep conditions could not confirm a power-law distribution of those brain signals using the Clauset et al. (2009) criteria (Dehghani et al., 2012).
While the study of Dehghani et al. (2012) casts doubt on these power-law findings, a recent study of EEG-fMRI data in healthy patients during sleep suggests that critical dynamics may be involved nonetheless (Bocaccio et al., 2019). A power-law distribution of co-activated connected clusters (voxel groups) from fMRI data during sleep was confirmed using the Clauset et al. (2009) criteria. As in Priesemann et al. (2013), this study found larger neuronal avalanches in NREM compared to REM or wakefulness. Moreover, each particular sleep stage impacted the power-law exponent significantly – a result that was independent of spatial coarse-graining of the fMRI data and which could not be accounted for by the presence of evoked neural bistabilities (e.g., K complexes).
All in all, while there are discrepancies in the results obtained from studies in this area, one can be optimistic about the role of criticality-based metrics in refining the understanding of sleep stages and their classification. Research into the role of LRTC (with adjustments made for signal power during sleep), branching parameters, power-law distributions of various metrics (coherence potential, PLI, LFP), mean synchronization, and other criticality parameters should lead to robust classifiers of sleep stages.
The conceptual framework of criticality is also helping researchers better understand various sleep pathologies (Iyer, 2018). Many animal and computational models show that critical dynamics play a central role in sleep stage transitions (Comte et al., 2006; Wang et al., 2019; Lombardi et al., 2020). Human studies are also beginning to capture this essential role by studying various sleep disorders. In the previouslymentioned EEG study of sleep deprivation (Meisel et al., 2013), there was a progressive decline in markers of criticality and an increase in markers of supercriticality as the sleep deprivation worsened. This finding supports the idea that sleep restores healthy brain function by bringing dynamics back toward criticality. This study was followed up by an evaluation of LRTC in the same cohort under similar conditions of sleep deprivation (Meisel et al., 2017). After controlling for signal amplitude changes, LRTC strength declined as sleep deprivation progressed, consistent with the view that sleep restores brain criticality.
In contrast with forced sleep deprivation, insomnia disorder (ID) leads to chronic sleep deprivation despite the patient’s attempts to fall asleep. In a study of patients with ID, there were no statistically significant differences in the LRTC during eyes-open and eyes-closed testing between patients and their age and sex-matched controls (Colombo et al., 2016). However, patients who subjectively reported lower quality sleep had increased LRTC during the eyes-open state. The study authors suggested that an increased excitation-inhibition ratio during wakefulness may translate into similar excitation during sleep, leading to lower sleep quality. Similar processes seem to be at work in obstructive sleep apnea (OSA), one of the most common sleep disorders. A polysomnogram study of patients with OSA and healthy controls found a power-law distribution of wakefulness durations during sleep in both groups (Lo et al., 2013). But the study did find a statistically significant difference between the power-law exponents. This finding reinforces the prospect that power-law exponents, perhaps in combination with other established metrics like the apnea-hypopnea index, could prove to be a helpful marker of diagnosis and monitoring of OSA. In the future, a study of LRTC in patients with OSA and ID compared to healthy patients in sleep could help determine whether the prevalent theory of sleep as a safety margin from supercriticality is correct. More broadly, the theory of brain criticality is likely to offer a different but complementary perspective on many sleep disorders (including narcolepsy, restless legs syndrome, and circadian disorders). See Table 7 for a summary of findings from the sleep-related criticality literature.
Conclusion
This scoping review surveyed the brain criticality literature, focusing on seven major domains of clinical application. Wherever possible, an effort was made to emphasize areas of future research for those interested in pursuing a “critical approach” to these clinical questions. In this concluding section, controversies that continue to be problematic for the field of brain criticality as a whole are addressed.
Brain criticality is both an established area of neuroscience research and yet remains controversial in several regards (Wilting and Priesemann, 2019).
1. Diverse and inconsistent uses of the terms “critical” and “criticality” have led to confusion. In this review, criticality has mostly referred to avalanche dynamics that behave at the limit between stability and instability. But other variants of criticality exist (Wilting and Priesemann, 2019). These include criticality between ordered and chaotic phases called the “edge of chaos” (Boedecker et al., 2012), criticality between synchrony and asynchrony (Botcharova et al., 2014), and multiple paradigms for the time-evolution of a critical phase transition as in extended criticality, intermittent criticality, and self-organized criticality (Saleur et al., 1996; Huang et al., 1998; Sammis and Smith, 1999; Bowman and Sammis, 2004). These forms of dynamical criticality are also distinct from statistical criticality (Mora and Bialek, 2011; Tkačik et al., 2013). How these all inter-connect is a topic of ongoing research. Rigorously defining these states and enforcing a more consistent vocabulary would allow for better study comparison.
2. Proving the existence of a control parameter has been difficult. Candidates have included synchronization, excitation-inhibition balance, and synaptic conductance (Beggs and Timme, 2012). Feedback processes between these properties may make it difficult to prove that they behave as genuine control parameters in isolation.
3. Many of the publications that lay the groundwork for brain criticality did not have the benefit of a reliable statistical framework for verifying a power-law distribution. While publications since Clauset et al. (2009) have mostly implemented strong statistical testing of power laws, many of the initial papers and even some more recent publications suffer from this deficit. Establishing a standard pipeline of statistical analysis for common datasets (e.g., EEG, MEG, LFP) – a kind of statistical “best practices”−will eliminate a source of confusion and help clarify the clinical situations in which power-law regimes do and do not exist. Moreover, arguing for a mechanism that generates a power-law – whether criticality or another mechanism−may be as important as the discovery of the power-law distribution itself (Stumpf and Porter, 2012).
4. In many publications, the objects of study are defined differently from one paper to the next. Such is the case, for example, with neuronal avalanches (Wilting and Priesemann, 2019) and seizure energy (Worrell et al., 2002; Osorio et al., 2009). While flexibility in definitions may help with making discoveries or adjusting for specific experimental situations, frequent changes in definition make it difficult to compare results, which slows down the progress of the field as a whole.
5. A common strategy, especially since the invention of DFA, is to look for LRTC as an indication of criticality. However, recent research suggests there may be different types of LRTC at play in these various systems and not distinguishing them carefully may be leading to false conclusions about criticality. For example, the discovery of crucial events in the area of turbulence led to the identification of “crucial event LRTC” or CELRTC (Bohara et al., 2018; Culbreth et al., 2019). CELRTC emerges in critical systems, specifically self-organized temporal criticality (SOTC) and is based on a slowly-decaying, non-stationary correlation function (Mahmoodi et al., 2017). CELRTC is distinct from Hurst exponent LRTC (HLRTC) which is based on a slowlydecaying but stationary correlation function, and which may not be indicative of underlying criticality. Future papers relying on detection of LRTC should incorporate this methodology in order to clarify the origin of the long-range correlation.
6. DFA was introduced for the study of non-stationary datasets. Yet there is evidence that this approach may not be adequate for that purpose (Bryce and Sprague, 2012). The introduction of a finite-size effect by DFA, leading to artifact, may have led to spurious results in many publications mentioned in this review. Future research should clarify the relevance of DFA-based methods for the purpose of LRTC detection.
Despite these challenges and controversies, there is also room for optimism. There has been rapid growth in the number of new articles published in this area. In fact, approximately two-thirds of the clinical articles discussed in this review were published in the last 8 years. The range of tools and concepts available from statistical physics and complexity science with which to tackle these problems is staggeringly broad and continually expanding. Determining how these tools and concepts inter-relate and in which research situation to use them should be an ongoing focus of research. Insights from other sciences−including geophysics, finance, applied physics, and signal processing, where these ideas are also commonly circulated – will undoubtedly shape the future of this already multidisciplinary field.
The future of criticality in the clinical arena will depend in large part on the formation of multidisciplinary teams in which physicists, mathematicians, data scientists, and clinicians collaborate to better answer a clinical question through the lens of criticality. While none of the applications mentioned in this review has yet to become mainstream or routine, it is conceivable that, under the broad umbrella of quantitative analysis of EEG, MEG, and fMRI, several of these techniques may transition to the bedside if they prove helpful in the diagnosis, prognosis, or treatment of diseases. In addition to more detailed studies in the clinical areas mentioned in this review, one can expect the next decade to see innovative studies, anchored in criticality, in areas like addiction medicine, stroke, neuro-immunology, traumatic brain injury, and headache medicine.
There are inevitable hurdles when concepts from one field (i.e., statistical physics) are translated into another (i.e., biomedicine). Still, there can be no doubt that these hurdles are worthwhile if they open up new horizons for both the understanding and the treatment of brain-related diseases.
Author Contributions
VZ evaluated the literature and wrote the manuscript.
Funding
This study was supported by the Department of Pediatrics at the University of Texas Southwestern, which funded open access publication fees. No other funding was received for this research.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The author would like to thank Lina Chalak, MD and Jeffrey McKinney, MD, Ph.D. for proposing the idea of this review. The author would also like to thank Mario Altamura, Ph.D. for kindly sending his manuscript as well as Didier Sornette, Ph.D., Gregory Worrell, MD, Ph.D., Luca Cocchi, Ph.D., John Beggs, Ph.D., Paolo Grigolini, Ph.D., and Michele Colombo, Ph.D. for sharing their insights.
References
Achard, S., Delon-Martin, C., Vértes, P. E., Renard, F., Schenck, M., Schneider, F., et al. (2012). Hubs of brain functional networks are radically reorganized in comatose patients. Proc. Natl. Acad. Sci. U.S.A.109, 20608–20613. doi: 10.1073/pnas.1208933109
Allegrini, P., Paradisi, P., Menicucci, D., Laurino, M., Bedini, R., Piarulli, A., et al. (2013). Sleep unconsciousness and breakdown of serial critical intermittency: new vistas on the global workspace. Chaos Solit. Fract.55, 32–43. doi: 10.1016/j.chaos.2013.05.019
Allegrini, P., Paradisi, P., Menicucci, D., Laurino, M., Piarulli, A., and Gemignani, A. (2015). Self-organized dynamical complexity in human wakefulness and sleep: different critical brain-activity feedback for conscious and unconscious states. Phys. Rev. E Stat. Nonlinear Soft Matt. Phys.92:032808. doi: 10.1103/PhysRevE.92.032808
Alonso, L. M., Proekt, A., Schwartz, T. H., Pryor, K. O., Cecchi, G. A., and Magnasco, M. O. (2014). Dynamical criticality during induction of anesthesia in human ECoG recordings. Front. Neural Circuits.8:20. doi: 10.3389/fncir.2014.00020
Altamura, M., Elvevag, B., Campi, G., De Salvia, M., Marasco, D., Ricci, A., et al. (2012). Toward scale-free like behavior under increasing cognitive load. Complexity18, 38–43. doi: 10.1002/cplx.21407
Arviv, O., Medvedovsky, M., Sheintuch, L., Goldstein, A., and Shriki, O. (2016). Deviations from critical dynamics in interictal epileptiform activity. J. Neurosci.36, 12276–12292. doi: 10.1523/JNEUROSCI.0809-16.2016
Atasoy, S., Roseman, L., Kaelen, M., Kringelbach, M. L., Deco, G., and Carhart-Harris, R. L. (2017). Connectome-harmonic decomposition of human brain activity reveals dynamical repertoire re-organization under LSD. Sci. Rep.7:17661. doi: 10.1038/s41598-017-17546-0
Atasoy, S., Vohryzek, J., Deco, G., Carhart-Harris, R. L., and Kringelbach, M. L. (2018). Common neural signatures of psychedelics: frequency-specific energy changes and repertoire expansion revealed using connectome-harmonic decomposition. Prog. Brain Res.242, 97–120. doi: 10.1016/bs.pbr.2018.08.009
Bak, P., Christensen, K., Danon, L., and Scanlon, T. (2002). Unified scaling law for earthquakes. Phys. Rev. Lett.99, 2509–2513. doi: 10.1103/PhysRevLett.88.178501
Bak, P., and Tang, C. (1989). Earthquakes as a self-organized critical phenomenon. J. Geophys. Res.94, 15635–15637. doi: 10.1029/jb094ib11p15635
Bak, P., Tang, C., and Wiesenfeld, K. (1987). Self-organized criticality: an explanation of the 1/f noise. Phys. Rev. Lett.59, 381–384. doi: 10.1103/PhysRevLett.59.381
Bak, P., Tang, C., and Wiesenfeld, K. (1988). Self-organized criticality. Phys. Rev. A38, 364–374. doi: 10.1103/PhysRevA.38.364
Ball, G., Aljabar, P., Zebari, S., Tusor, N., Arichi, T., Merchant, N., et al. (2014). Rich-club organization of the newborn human brain. Proc. Natl. Acad. Sci. U.S.A.111, 7456–7461. doi: 10.1073/pnas.1324118111
Barabási, A. L., and Albert, R. (1999). Emergence of scaling in random networks. Science286, 509–512. doi: 10.1126/science.286.5439.509
Baron-Cohen, S., and Belmonte, M. K. (2005). AUTISM: a window onto the development of the social and the analytic brain. Annu. Rev. Neurosci.28, 109–126. doi: 10.1146/annurev.neuro.27.070203.144137
Bédard, C., Kröger, H., and Destexhe, A. (2006). Does the 1/f frequency scaling of brain signals reflect self-organized critical states?Phys. Rev. Lett.97:118102. doi: 10.1103/PhysRevLett.97.118102
Beggs, J. M. (2008). The criticality hypothesis: how local cortical networks might optimize information processing. Philos. Trans. A Math. Phys. Eng. Sci.366, 329–343. doi: 10.1098/rsta.2007.2092
Beggs, J. M., and Timme, N. (2012). Being critical of criticality in the brain. Front. Physiol.3:163. doi: 10.3389/fphys.2012.00163
Belmonte, M. K., Allen, G., Beckel-Mitchener, A., Boulanger, L. M., Carper, R. A., and Webb, S. J. (2004). Autism and abnormal development of brain connectivity. J. Neurosci.24, 9228–9231. doi: 10.1523/JNEUROSCI.3340-04.2004
Berthouze, L., James, L. M., and Farmer, S. F. (2010). Human EEG shows long-range temporal correlations of oscillation amplitude in Theta, Alpha and Beta bands across a wide age range. Clin. Neurophysiol.121, 1187–1197. doi: 10.1016/j.clinph.2010.02.163
Bertschinger, N., and Natschläger, T. (2004). Real-time computation at the edge of chaos in recurrent neural networks. Neural Comput.16, 1413–1436. doi: 10.1162/089976604323057443
Bocaccio, H., Pallavicini, C., Castro, M. N., Sanchez, S. M., De Pino, G., Laufs, H., et al. (2019). The avalanche-like behaviour of large-scale haemodynamic activity from wakefulness to deep sleep. J. R. Soc. Interface16:20190262. doi: 10.1098/rsif.2019.0262
Boedecker, J., Obst, O., Lizier, J. T., Mayer, N. M., and Asada, M. (2012). Information processing in echo state networks at the edge of chaos. Theory Biosci.131, 205–213. doi: 10.1007/s12064-011-0146-8
Bohara, G., West, B. J., and Grigolini, P. (2018). Bridging waves and crucial events in the dynamics of the brain. Front. Physiol.9:1174. doi: 10.3389/fphys.2018.01174
Bonachela, J. A., De Franciscis, S., Torres, J. J., and Muoz, M. A. (2010). Self-organization without conservation: are neuronal avalanches generically critical? J. Stat. Mech. Theory Exp. 2010. doi: 10.1088/1742-5468/2010/02/P02015
Bonachela, J. A., and Muñoz, M. A. (2009). Self-organization without conservation: true or just apparent scale-invariance?J. Stat. Mech. Theory Exp. 2009. doi: 10.1088/1742-5468/2009/09/P09009
Bongers, A., Flynn, A. B., and Northoff, G. (2019). Is learning scale-free? Chemistry learning increases EEG fractal power and changes the power law exponent. Neurosci. Res. doi: 10.1016/j.neures.2019.10.011 [Epub ahead of print]
Bornas, X., Noguera, M., Balle, M., Morillas-Romero, A., Aguayo-Siquier, B., Tortella-Feliu, M., et al. (2013). Long-range temporal correlations in resting EEG: its associations with depression-related emotion regulation strategies. J. Psychophysiol.27, 60–66. doi: 10.1027/0269-8803/a000087
Botcharova, M., Berthouze, L., Brookes, M. J., Barnes, G. R., and Farmer, S. F. (2015). Resting state MEG oscillations show long-range temporal correlations of phase synchrony that break down during finger movement. Front. Physiol.6:183. doi: 10.3389/fphys.2015.00183
Botcharova, M., Farmer, S. F., and Berthouze, L. (2012). Power-law distribution of phase-locking intervals does not imply critical interaction. Phys. Rev. E. Stat. Nonlin. Soft Matter Phys.86:51920. doi: 10.1103/PhysRevE.86.051920
Botcharova, M., Farmer, S. F., and Berthouze, L. (2014). Markers of criticality in phase synchronization. Front. Syst. Neurosci.8:176. doi: 10.3389/fnsys.2014.00176
Bowman, D. D., and Sammis, C. G. (2004). Intermittent criticality and the Gutenberg-Richter distribution. Pure Appl. Geophys.161, 1945–1956. doi: 10.1007/s00024-004-2541-z
Breakspear, M., and Terry, J. R. (2002). Detection and description of non-linear interdependence in normal multichannel human EEG data. Clin. Neurophysiol.113, 735–753. doi: 10.1016/S1388-2457(02)00051-2
Bressler, S. L., and Kelso, J. A. S. (2001). Cortical coordination dynamics and cognition. Trends Cogn. Sci.5, 26–36. doi: 10.1016/S1364-6613(00)01564-3
Bryce, R. M., and Sprague, K. B. (2012). Revisiting detrended fluctuation analysis. Sci. Rep.2:345. doi: 10.1038/srep00315
Cao, F., Bitan, T., and Booth, J. R. (2008). Effective brain connectivity in children with reading difficulties during phonological processing. Brain Lang.107, 91–101. doi: 10.1016/j.bandl.2007.12.009
Carhart-Harris, R. L. (2018). The entropic brain – revisited. Neuropharmacology142, 167–178. doi: 10.1016/j.neuropharm.2018.03.010
Carhart-Harris, R. L., Leech, R., Hellyer, P. J., Shanahan, M., Feilding, A., Tagliazucchi, E., et al. (2014). The entropic brain: a theory of conscious states informed by neuroimaging research with psychedelic drugs. Front. Hum. Neurosci.8:20. doi: 10.3389/fnhum.2014.00020
Castaing, B., Gagne, Y., and Hopfinger, E. J. (1990). Velocity probability density functions of high Reynolds number turbulence. Phys. D Nonlinear Phenom.46, 177–200. doi: 10.1016/0167-2789(90)90035-N
Cavanagh, J. F., and Frank, M. J. (2014). Frontal theta as a mechanism for cognitive control. Trends Cogn. Sci.18, 414–421. doi: 10.1016/j.tics.2014.04.012
Cerf, R., El Ouasdad, E. H., and Kahane, P. (2004). Criticality and synchrony of fluctuations in rhythmical brain activity: pretransitional effects in epileptic patients. Biol. Cybern.90, 239–255. doi: 10.1007/s00422-004-0463-9
Christensen, K., Olami, Z., and Bak, P. (1992). Deterministic 1/f noise in nonconserative models of self-organized criticality. Phys. Rev. Lett.68, 2417–2420. doi: 10.1103/PhysRevLett.68.2417
Clauset, A., and Shalizi, C. R. and Newman, M. E. J (2009). Power-law distributions in empirical data. SIAM Rev.51, 661–703. doi: 10.1137/070710111
Cocchi, L., Gollo, L. L., Zalesky, A., and Breakspear, M. (2017). Criticality in the brain: a synthesis of neurobiology, models and cognition. Prog. Neurobiol.158, 132–152. doi: 10.1016/j.pneurobio.2017.07.002
Cohen, M. X. (2016). Midfrontal theta tracks action monitoring over multiple interactive time scales. Neuroimage141, 262–272. doi: 10.1016/j.neuroimage.2016.07.054
Colombo, M. A., Wei, Y., Ramautar, J. R., Linkenkaer-Hansen, K., Tagliazucchi, E., and Van Someren, E. J. W. (2016). More severe insomnia complaints in people with stronger long-range temporal correlations in wake resting-state EEG. Front. Physiol.7:576. doi: 10.3389/fphys.2016.00576
Colquhoun, H. L., Levac, D., O’Brien, K. K., Straus, S., Tricco, A. C., Perrier, L., et al. (2014). Scoping reviews: time for clarity in definition, methods, and reporting. J. Clin. Epidemiol.67, 1291–1294. doi: 10.1016/j.jclinepi.2014.03.013
Comte, J. C., Ravassard, P., and Salin, P. A. (2006). Sleep dynamics: a self-organized critical system. Phys. Rev. E73:056127. doi: 10.1103/PhysRevE.73.056127
Cook, M. J., O’Brien, T. J., Berkovic, S. F., Murphy, M., Morokoff, A., Fabinyi, G., et al. (2013). Prediction of seizure likelihood with a long-term, implanted seizure advisory system in patients with drug-resistant epilepsy: a first-in-man study. Lancet Neurol.12, 563–571. doi: 10.1016/S1474-4422(13)70075-9
Cook, M. J., Varsavsky, A., Himes, D., Leyde, K., Berkovic, S. F., O’Brien, T., et al. (2014). The dynamics of the epileptic brain reveal long-memory processes. Front. Neurol.5:217. doi: 10.3389/fneur.2014.00217
Cruz, A. V., Mallet, N., Magill, P. J., Brown, P., and Averbeck, B. B. (2009). Effects of dopamine depletion on network entropy in the external globus pallidus. J. Neurophysiol.102, 1092–1102. doi: 10.1152/jn.00344.2009
Culbreth, G., West, B. J., and Grigolini, P. (2019). Entropic approach to the detection of crucial events. Entropy21, 1–20. doi: 10.3390/e21020178
Daffertshofer, A., Ton, R., Kringelbach, M. L., Woolrich, M., and Deco, G. (2018). Distinct criticality of phase and amplitude dynamics in the resting brain. Neuroimage180, 442–447. doi: 10.1016/j.neuroimage.2018.03.002
Deco, G., and Jirsa, V. K. (2012). Ongoing cortical activity at rest: criticality, multistability, and ghost attractors. J. Neurosci.32, 3366–3375. doi: 10.1523/JNEUROSCI.2523-11.2012
Deco, G., Kringelbach, M. L., Jirsa, V. K., and Ritter, P. (2017). The dynamics of resting fluctuations in the brain: Metastability and its dynamical cortical core. Sci. Rep.7:3095. doi: 10.1038/s41598-017-03073-5
Deco, G., Senden, M., and Jirsa, V. (2012). How anatomy shapes dynamics: a semi-analytical study of the brain at rest by a simple spin model. Front. Comput. Neurosci.6:68. doi: 10.3389/fncom.2012.00068
Dehghani, N., Hatsopoulos, N. G., Haga, Z. D., Parker, R. A., Greger, B., Halgren, E., et al. (2012). Avalanche analysis from multielectrode ensemble recordings in cat, monkey, and human cerebral cortex during wakefulness and sleep. Front. Physiol.3:302. doi: 10.3389/fphys.2012.00302
Del Papa, B., Priesemann, V., and Triesch, J. (2017). Criticality meets learning: criticality signatures in a self-organizing recurrent neural network. PLoS One12:e0178683. doi: 10.1371/journal.pone.0178683
Dimitriadis, S. I., Laskaris, N. A., Simos, P. G., Micheloyannis, S., Fletcher, J. M., Rezaie, R., et al. (2013). Altered temporal correlations in resting-state connectivity fluctuations in children with reading difficulties detected via MEG. Neuroimage83, 307–317. doi: 10.1016/j.neuroimage.2013.06.036
Escolano, C., Navarro-Gil, M., Garcia-Campayo, J., Congedo, M., De Ridder, D., and Minguez, J. (2014). A controlled study on the cognitive effect of alpha neurofeedback training in patients with major depressive disorder. Front. Behav. Neurosci.8:296. doi: 10.3389/fnbeh.2014.00296
Euler, M. J., Wiltshire, T. J., Niermeyer, M. A., and Butner, J. E. (2016). Working memory performance inversely predicts spontaneous delta and theta-band scaling relations. Brain Res.1637, 22–33. doi: 10.1016/j.brainres.2016.02.008
Ezaki, T., Fonseca Dos Reis, E., Watanabe, T., Sakaki, M., and Masuda, N. (2020). Closer to critical resting-state neural dynamics in individuals with higher fluid intelligence. Commun. Biol.3:52. doi: 10.1038/s42003-020-0774-y
Fagerholm, E. D., Lorenz, R., Scott, G., Dinov, M., Hellyer, P. J., Mirzaei, N., et al. (2015). Cascades and cognitive state: focused attention incurs subcritical dynamics. J. Neurosci.35, 4626–4634. doi: 10.1523/JNEUROSCI.3694-14.2015
Fiest, K. M., Sauro, K. M., Wiebe, S., Patten, S. B., Kwon, C. S., Dykeman, J., et al. (2017). Prevalence and incidence of epilepsy. Neurology88, 296–303. doi: 10.1212/WNL.0000000000003509
Fraiman, D., Balenzuela, P., Foss, J., and Chialvo, D. R. (2009). Ising-like dynamics in large-scale functional brain networks. Phys. Rev. E Stat. Nonlinear, Soft Matt. Phys.79(Pt 1):061922. doi: 10.1103/PhysRevE.79.061922
Fransson, P., Metsäranta, M., Blennow, M., Åden, U., Lagercrantz, H., and Vanhatalo, S. (2013). Early development of spatial patterns of power-law frequency scaling in fMRI resting-state and EEG data in the newborn brain. Cereb. Cortex23, 638–646. doi: 10.1093/cercor/bhs047
Frette, V., Christensen, K., Malthe-Sørenssen, A., Feder, J., Jøssang, T., and Meakin, P. (1996). Avalanche dynamics in a pile of rice. Nature379, 49–52. doi: 10.1038/379049a0
Friedman, N., Ito, S., Brinkman, B. A. W., Shimono, M., Deville, R. E. L., Dahmen, K. A., et al. (2012). Universal critical dynamics in high resolution neuronal avalanche data. Phys. Rev. Lett.108:208102. doi: 10.1103/PhysRevLett.108.208102
Friston, K., Brown, H. R., Siemerkus, J., and Stephan, K. E. (2016). The dysconnection hypothesis (2016). Schizophr. Res.176, 83–94. doi: 10.1016/j.schres.2016.07.014
Frohlich, J., Irimia, A., and Jeste, S. S. (2015). Trajectory of frequency stability in typical development. Brain Imaging Behav.9, 5–18. doi: 10.1007/s11682-014-9339-3
Gärtner, M., Irrmischer, M., Winnebeck, E., Fissler, M., Huntenburg, J. M., Schroeter, T. A., et al. (2017). Aberrant long-range temporal correlations in depression are attenuated after psychological treatment. Front. Hum. Neurosci.11:340. doi: 10.3389/fnhum.2017.00340
Gautam, S. H., Hoang, T. T., McClanahan, K., Grady, S. K., and Shew, W. L. (2015). Maximizing sensory dynamic range by tuning the cortical state to criticality. PLoS Comput. Biol.11:e1004576. doi: 10.1371/journal.pcbi.1004576
Gisiger, T., Linkenkaer-Hansen, K., Nikouline, V. V., Palva, J. M., Ilmoniemi, R. J., Worrell, G. A., et al. (2014). Spike avalanches in vivo suggest a driven, slightly subcritical brain state. Front. Syst. Neurosci.9:108. doi: 10.3389/fnsys.2014.00108
Haldeman, C., and Beggs, J. M. (2005). Critical branching captures activity in living neural networks and maximizes the number of metastable states. Phys. Rev. Lett.94:058101. doi: 10.1103/PhysRevLett.94.058101
Hanslmayr, S., Staudigl, T., and Fellner, M. C. (2012). Oscillatory power decreases and long-term memory: the information via desynchronization hypothesis. Front. Hum. Neurosci.6:74. doi: 10.3389/fnhum.2012.00074
Hardstone, R., Poil, S., Schiavone, G., Jansen, R., Nikulin, V. V., Mansvelder, H. D., et al. (2012). Detrended fluctuation analysis?: a scale-free view on neuronal oscillations. Front. Physiol.3:450. doi: 10.3389/fphys.2012.00450
Hartley, C., Berthouze, L., Mathieson, S. R., Boylan, G. B., Rennie, J. M., and Farmer, S. F. (2012). Long-range temporal correlations in the EEG bursts of human preterm babies. PLoS One7:e0031543. doi: 10.1371/journal.pone.0031543
Hausdorff, J. M. (2009). Gait dynamics in Parkinson’s disease: common and distinct behavior among stride length, gait variability, and fractal-like scaling. Chaos19:026113. doi: 10.1063/1.3147408
He, B. J. (2011). Scale-free properties of the functional magnetic resonance imaging signal during rest and task. J. Neurosci.31, 13786–13795. doi: 10.1523/JNEUROSCI.2111-11.2011
He, B. J. (2014). Scale-free brain activity: past, present, and future. Trends Cogn. Sci.18, 480–487. doi: 10.1016/j.tics.2014.04.003
Hesse, J., and Gross, T. (2014). Self-organized criticality as a fundamental property of neural systems. Front. Syst. Neurosci.8:166. doi: 10.3389/fnsys.2014.00166
Hobbs, J. P., Smith, J. L., and Beggs, J. M. (2010). Aberrant neuronal avalanches in cortical tissue removed from juvenile epilepsy patients. J. Clin. Neurophysiol.27, 380–386. doi: 10.1097/WNP.0b013e3181fdf8d3
Hoeft, F., Meyler, A., Hernandez, A., Juel, C., Taylor-Hill, H., Martindale, J. L., et al. (2007). Functional and morphometric brain dissociation between dyslexia and reading ability. Proc. Natl. Acad. Sci. U.S.A.104, 4234–4239. doi: 10.1073/pnas.0609399104
Hoffmann, H., and Payton, D. W. (2018). Optimization by self-organized criticality. Sci. Rep.8:2358. doi: 10.1038/s41598-018-20275-7
Hohlefeld, F. U., Huebl, J., Huchzermeyer, C., Schneider, G.-H., Schoenecker, T., Kuehn, A. A., et al. (2012). Long-range temporal correlations in the subthalamic nucleus of patients with Parkinson’s disease. Eur. J. Neurosci.36, 2812–2821. doi: 10.1111/j.1460-9568.2012.08198.x
Hove, M. J., Suzuki, K., Uchitomi, H., Orimo, S., and Miyake, Y. (2012). Interactive rhythmic auditory stimulation reinstates natural 1/f timing in gait of parkinson’s patients. PLoS One7:e32600. doi: 10.1371/journal.pone.0032600
Huang, Y., Saleur, H., Sammis, C., and Sornette, D. (1998). Precursors, aftershocks, criticality and self-organized criticality. Europhys. Lett.41, 43–48. doi: 10.1209/epl/i1998-00113-x
Irrmischer, M., Houtman, S. J., Mansvelder, H. D., Tremmel, M., Ott, U., and Linkenkaer-Hansen, K. (2018a). Controlling the temporal structure of brain oscillations by focused attention meditation. Hum. Brain Mapp.39, 1825–1838. doi: 10.1002/hbm.23971
Irrmischer, M., Poil, S.-S., Mansvelder, H. D., Intra, F. S., and Linkenkaer-Hansen, K. (2018b). Strong long-range temporal correlations of beta/gamma oscillations are associated with poor sustained visual attention performance. Eur. J. Neurosci.48, 2674–2683. doi: 10.1111/ejn.13672
Iyer, K. K. (2018). Sleep, wake, and critical brain states: corollaries from brain dynamics. Front. Neurosci.12:948. doi: 10.3389/fnins.2018.00948
Iyer, K. K., Roberts, J. A., Hellström-Westas, L., Wikström, S., Hansen Pupp, I., Ley, D., et al. (2015). Cortical burst dynamics predict clinical outcome early in extremely preterm infants. Brain138(Pt 8), 2206–2218. doi: 10.1093/brain/awv129
Jannesari, M., Saeedi, A., Zare, M., Ortiz-Mantilla, S., Plenz, D., and Benasich, A. A. (2020). Stability of neuronal avalanches and long-range temporal correlations during the first year of life in human infants. Brain Struct. Funct.225, 1169–1183. doi: 10.1007/s00429-019-02014-4
Jia, H., Li, Y., and Yu, D. (2018). Attenuation of long-range temporal correlations of neuronal oscillations in young children with autism spectrum disorder. NeuroImage Clin.20, 424–432. doi: 10.1016/j.nicl.2018.08.012
Jiang, L., Qiao, K., Sui, D., Zhang, Z., and Dong, H. (2019). Functional criticality in the human brain?: physiological, behavioral and neurodevelopmental correlates. PLoS One14:e0213690. doi: 10.1371/journal.pone.0213690
Jiang, L., Sui, D., Qiao, K., Dong, H.-M., Chen, L., and Han, Y. (2018). Impaired functional criticality of human brain during Alzheimer’s disease progression. Sci. Rep.8:1324. doi: 10.1038/s41598-018-19674-7
Kinouchi, O., and Copelli, M. (2006). Optimal dynamical range of excitable networks at criticality. Nat. Phys.2, 348–351. doi: 10.1038/nphys289
Kitzbichler, M. G., Smith, M. L., Christensen, S. R., and Bullmore, E. (2009). Broadband criticality of human brain network synchronization. PLoS Comput. Biol.5:e1000314. doi: 10.1371/journal.pcbi.1000314
Kramer, M. A., Truccolo, W., Eden, U. T., Lepage, K. Q., Hochberg, L. R., Eskandar, E. N., et al. (2012). Human seizures self-terminate across spatial scales via a critical transition. Proc. Natl. Acad. Sci. U.S.A.109, 21116–21121. doi: 10.1073/pnas.1210047110
Krzemiński, D., Kamiński, M., Marchewka, A., and Bola, M. (2017). Breakdown of long-range temporal correlations in brain oscillations during general anesthesia. Neuroimage159, 146–158. doi: 10.1016/j.neuroimage.2017.07.047
Kwok, E. Y. L., Cardy, O., Allman, B., Allen, P., and Herrmann, B. (2019). Dynamics of spontaneous alpha activity correlate with language ability in young children. Behav. Brain Res.359, 56–65. doi: 10.1101/679670
Lai, M. C., Lombardo, M. V., Chakrabarti, B., Sadek, S. A., Pasco, G., Wheelwright, S. J., et al. (2010). A shift to randomness of brain oscillations in people with autism. Biol. Psychiatry68, 1092–1099. doi: 10.1016/j.biopsych.2010.06.027
Latham, P. E., and Nirenberg, S. (2004). Computing and stability in cortical networks. Neural Comput.16, 1385–1412. doi: 10.1162/089976604323057434
Lee, J. S., Yang, B. H., Lee, J. H., Choi, J. H., Choi, I. G., and Kim, S. B. (2007). Detrended fluctuation analysis of resting EEG in depressed outpatients and healthy controls. Clin. Neurophysiol.118, 2489–2496. doi: 10.1016/j.clinph.2007.08.001
Leistedt, S., Dumont, M., Coumans, N., Lanquart, J. P., Jurysta, F., and Linkowski, P. (2007a). The modifications of the long-range temporal correlations of the sleep EEG due to major depressive episode disappear with the status of remission. Neuroscience148, 782–793. doi: 10.1016/j.neuroscience.2007.06.032
Leistedt, S., Dumont, M., Lanquart, J. P., Jurysta, F., and Linkowski, P. (2007b). Characterization of the sleep EEG in acutely depressed men using detrended fluctuation analysis. Clin. Neurophysiol.118, 940–950. doi: 10.1016/j.clinph.2007.01.003
Li, X., Polygiannakis, J., Kapiris, P., Peratzakis, A., Eftaxias, K., and Yao, X. (2005). Fractal spectral analysis of pre-epileptic seizures in terms of criticality. J. Neural Eng.2, 11–16. doi: 10.1088/1741-2560/2/2/002
Linkenkaer-Hansen, K., Monto, S., Rytsälä, H., Suominen, K., Isometsä, E., and Kähkönen, S. (2005). Breakdown of long-range temporal correlations in theta oscillations in patients with major depressive disorder. J. Neurosci.25, 10131–10137. doi: 10.1523/JNEUROSCI.3244-05.2005
Liu, X., Ward, B. D., Binder, J. R., Li, S.-J., and Hudetz, A. G. (2014). Scale-free functional connectivity of the brain is maintained in anesthetized healthy participants but not in patients with unresponsive wakefulness syndrome. PLoS One9:e92182. doi: 10.1371/journal.pone.0092182
Lo, C. C., Bartsch, R. P., and Ivanov, P. C. (2013). Asymmetry and basic pathways in sleep-stage transitions. Europhys. Lett.102:10008. doi: 10.1209/0295-5075/102/10008
Lombardi, F., Gómez-Extremera, M., Bernaola-Galván, P., Vetrivelan, R., Saper, C. B., Scammell, T. E., et al. (2020). Critical dynamics and coupling in bursts of cortical rhythms indicate non-homeostatic mechanism for sleep-stage transitions and dual role of VLPO neurons in both sleep and wake. J. Neurosci.40, 171–190. doi: 10.1523/JNEUROSCI.1278-19.2019
Ma, Q., Ning, X., Wang, J., and Bian, C. (2006). A new measure to characterize multifractality of sleep electroencephalogram. Chinese Sci. Bull.51, 3259–3264. doi: 10.1007/s11434-006-2213-y
Ma, Z., Turrigiano, G. G., Wessel, R., and Hengen, K. B. (2019). Cortical circuit dynamics are homeostatically tuned to criticality in vivo. Neuron104, 655–664.e4. doi: 10.1016/j.neuron.2019.08.031
Maass, W., Natschläger, T., and Markram, H. (2002). Real-time computing without stable states: a new framework for neural computation based on perturbations. Neural Comput.14, 2531–2560. doi: 10.1162/089976602760407955
Mahmoodi, K., West, B. J., and Grigolini, P. (2017). Self-organizing complex networks: individual versus global rules. Front. Physiol.8:478. doi: 10.3389/fphys.2017.00478
Mares, J., Vysata, O., Prochazka, A., and Valis, M. (2013). Age-dependent complex noise fluctuations in the brain. Physiol. Meas.34, 1269–1279. doi: 10.1088/0967-3334/34/10/1269
Marinazzo, D., Pellicoro, M., Wu, G.-R., Angelini, L., Cortes, J., and Stramaglia, S. (2013). Information transfer of an Ising model on a brain network. BMC Neurosci.14(Suppl. 1):376. doi: 10.1186/1471-2202-14-s1-p376
Mehta, A. P., Dahmen, K. A., and Ben-Zion, Y. (2006). Universal mean moment rate profiles of earthquake ruptures. Phys. Rev. E Stat. Nonlinear, Soft Matter Phys.73(Pt 2):056104. doi: 10.1103/PhysRevE.73.056104
Meisel, C., Bailey, K., Achermann, P., and Plenz, D. (2017). Decline of long-range temporal correlations in the human brain during sustained wakefulness. Sci. Rep.7, 1–11. doi: 10.1038/s41598-017-12140-w
Meisel, C., and Kuehn, C. (2012). Scaling effects and spatio-temporal multilevel dynamics in epileptic seizures. PLoS One7:e30371. doi: 10.1371/journal.pone.0030371
Meisel, C., and Loddenkemper, T. (2019). Seizure prediction and intervention. Neuropharmacology172:107898. doi: 10.1016/j.neuropharm.2019.107898
Meisel, C., Olbrich, E., Shriki, O., and Achermann, P. (2013). Fading signatures of critical brain dynamics during sustained wakefulness in humans. J. Neurosci.33, 17363–17372. doi: 10.1523/JNEUROSCI.1516-13.2013
Meisel, C., Storch, A., Hallmeyer-Elgner, S., Bullmore, E., and Gross, T. (2012). Failure of adaptive self-organized criticality during epileptic seizure attacks. PLoS Comput. Biol.8:e1002312. doi: 10.1371/journal.pcbi.1002312
Meresse, I. G., Zilbovicius, M., Boddaert, N., Robel, L., Philippe, A., Sfaello, I., et al. (2005). Autism severity and temporal lobe functional abnormalities. Ann. Neurol.58, 466–469. doi: 10.1002/ana.20597
Milton, J. G. (2012). Neuronal avalanches, epileptic quakes and other transient forms of neurodynamics. Eur. J. Neurosci.36, 2156–2163. doi: 10.1111/j.1460-9568.2012.08102.x
Minadakis, G., Ventouras, E., Gatzonis, S. D., Siatouni, A., Tsekou, H., Kalatzis, I., et al. (2014). Dynamics of regional brain activity in epilepsy: a cross-disciplinary study on both intracranial and scalp-recorded epileptic seizures. J. Neural Eng.11:026012. doi: 10.1088/1741-2560/11/2/026012
Mitzenmacher, M. (2004). A brief history of generative models for power law and lognormal distributions. Internet Math.1, 226–251. doi: 10.1080/15427951.2004.10129088
Moher, D., Liberati, A., Tetzlaff, J., Altman, D. G., Altman, D., Antes, G., et al. (2009). Preferred reporting items for systematic reviews and meta-analyses: the PRISMA statement. PLoS Med.6:e1000097. doi: 10.1371/journal.pmed.1000097
Montez, T., Poil, S. S., Jones, B. F., Manshanden, I., Verbunt, J. P. A., Van Dijk, B. W., et al. (2009). Altered temporal correlations in parietal alpha and prefrontal theta oscillations in early-stage Alzheimer disease. Proc. Natl. Acad. Sci. U.S.A.106, 1614–1619. doi: 10.1073/pnas.0811699106
Monto, S., Vanhatalo, S., Holmes, M. D., and Palva, J. M. (2007). Epileptogenic neocortical networks are revealed by abnormal temporal dynamics in seizure-free subdural EEG. Cereb. Cortex17, 1386–1393. doi: 10.1093/cercor/bhl049
Mora, T., and Bialek, W. (2011). Are biological systems poised at criticality?J. Stat. Phys.144, 268–302. doi: 10.1007/s10955-011-0229-4
Moran, J. K., Michail, G., Heinz, A., Keil, J., and Senkowski, D. (2019). Long-range temporal correlations in resting state beta oscillations are reduced in schizophrenia. Front. Psychiatry10:517. doi: 10.3389/fpsyt.2019.00517
Moretti, P., and Munoz, M. A. (2013). Griffiths phases and the stretching of criticality in brain networks. Nat. Commun.4:2521. doi: 10.1038/ncomms3521
Mormann, F., Andrzejak, R. G., Elger, C. E., and Lehnertz, K. (2007). Seizure prediction: the long and winding road. Brain.130(Pt 2), 314–333. doi: 10.1093/brain/awl241
Morrison, J. H., and Hof, P. R. (1997). Life and death of neurons in the aging brain. Science278, 412–419. doi: 10.1126/science.278.5337.412
Mu, J., Rampp, S., Carrette, E., Roessler, K., Sommer, B., Schmitt, F. C., et al. (2014). Clinical relevance of source location in frontal lobe epilepsy and prediction of postoperative long-term outcome. Seizure23, 553–559. doi: 10.1016/j.seizure.2014.04.006
Newman, M. E. J. (2005). Power laws, pareto distributions and Zipf’s law. Contemp. Phys.46, 323–351. doi: 10.1080/00107510500052444
Nikulin, V. V., and Brismar, T. (2004). Long-range temporal correlations in alpha and beta oscillations: effect of arousal level and test-retest reliability. Clin. Neurophysiol.115, 1896–1908. doi: 10.1016/j.clinph.2004.03.019
Nikulin, V. V., Jönsson, E. G., and Brismar, T. (2012). Attenuation of long-range temporal correlations in the amplitude dynamics of alpha and beta neuronal oscillations in patients with schizophrenia. Neuroimage61, 162–169. doi: 10.1016/j.neuroimage.2012.03.008
Nishimori, H., and Ortiz, G. (2011). Elements of Phase Transitions and Critical Phenomena. Oxford: Oxford University Press, doi: 10.1093/acprof:oso/9780199577224.001.0001
Osorio, I., Frei, M. G., Sornette, D., and Milton, J. (2009). Pharmaco-resistant seizures: self-triggering capacity, scale-free properties and predictability?Eur. J. Neurosci.30, 1554–1558. doi: 10.1111/j.1460-9568.2009.06923.x
Osorio, I., Frei, M. G., Sornette, D., Milton, J., and Lai, Y. C. (2010). Epileptic seizures: quakes of the brain?Phys. Rev. E Stat. Nonlinear, Soft Matter Phys.82:021919. doi: 10.1103/PhysRevE.82.021919
Ouyang, G., Hildebrandt, A., Schmitz, F., and Herrmann, C. S. (2020). Decomposing alpha and 1/f brain activities reveals their differential associations with cognitive processing speed. Neuroimage205:116304. doi: 10.1016/j.neuroimage.2019.116304
Padilla, N., Eklöf, E., Mårtensson, G. E., Bölte, S., Lagercrantz, H., and Ådén, U. (2017). Poor brain growth in extremely preterm neonates long before the onset of autism spectrum disorder symptoms. Cereb. Cortex27, 1245–1252. doi: 10.1093/cercor/bhv300
Padilla, N., Saenger, V. M., Van Hartevelt, T. J., Fernandes, H. M., Lennartsson, F., Andersson, J. L. R., et al. (2020). Breakdown of whole-brain dynamics in preterm-born children. Cereb. Cortex30, 1159–1170. doi: 10.1093/cercor/bhz156
Papanikolaou, S., Bohn, F., Sommer, R. L., Durin, G., Zapperi, S., and Sethna, J. P. (2011). Universality beyond power laws and the average avalanche shape. Nat. Phys.7, 316–320. doi: 10.1038/nphys1884
Parish, L. M., Worrell, G. A., Cranstoun, S. D., Stead, S. M., Pennell, P., and Litt, B. (2004). Long-range temporal correlations in epileptogenic and non-epileptogenic human hippocampus. Neuroscience 125, 1069–1076. doi: 10.1016/j.neuroscience.2004.03.002
Parr, T., Rees, G., and Friston, K. J. (2018). Computational neuropsychology and bayesian inference. Front. Hum. Neurosci.12:61. doi: 10.3389/fnhum.2018.00061
Pearlmutter, B. A., and Houghton, C. J. (2009). A new hypothesis for sleep: tuning for criticality. Neural Comput.21, 1622–1641. doi: 10.1162/neco.2009.05-08-787
Pearlmutter, B. A., and Houghton, C. J. (2013). Dreams, mnemonics, and tuning for criticality. Behav. Brain Sci.36, 625–659. doi: 10.1017/S0140525X13001404
Peng, C. K., Buldyrev, S. V., Goldberger, A. L., Havlin, S., Mantegna, R. N., Simons, M., et al. (1995a). Statistical properties of DNA sequences. Phys. A Stat. Mech. its Appl.221, 180–192. doi: 10.1016/0378-4371(95)00247-5
Peng, C. K., Havlin, S., Stanley, H. E., and Goldberger, A. L. (1995b). Quantification of scaling exponents and crossover phenomena in nonstationary heartbeat time series. Chaos5, 82–87. doi: 10.1063/1.166141
Perković, O., Dahmen, K., and Sethna, J. P. (1995). Avalanches, Barkhausen noise, and plain old criticality. Phys. Rev. Lett.75, 4528–4531. doi: 10.1103/PhysRevLett.75.4528
Petermann, T., Thiagarajan, T. C., Lebedev, M. A., Nicolelis, M. A. L., Chialvo, D. R., and Plenz, D. (2009). Spontaneous cortical activity in awake monkeys composed of neuronal avalanches. Proc. Natl. Acad. Sci. U.S.A.106, 15921–15926. doi: 10.1073/pnas.0904089106
Pisarenko, V. F., and Sornette, D. (2012). Robust statistical tests of Dragon-Kings beyond power law distributions. Eur. Phys. J. Spec. Top.205, 95–115. doi: 10.1140/epjst/e2012-01564-8
Plenz, D., and Niebur, E. (2014). Criticality in Neural Systems. Hoboken, NJ: Wiley, doi: 10.1002/9783527651009
Priesemann, V., Valderrama, M., Wibral, M., and Le Van Quyen, M. (2013). Neuronal avalanches differ from wakefulness to deep sleep–evidence from intracranial depth recordings in humans. PLoS Comput. Biol.9:e1002985. doi: 10.1371/journal.pcbi.1002985
Radulescu, A. R., Rubin, D., Strey, H. H., and Mujica-Parodi, L. R. (2012). Power spectrum scale invariance identifies prefrontal dysregulation in paranoid schizophrenia. Hum. Brain Mapp.33, 1582–1593. doi: 10.1002/hbm.21309
Ribeiro, T. L., Copelli, M., Caixeta, F., Belchior, H., Chialvo, D. R., Nicolelis, M. A. L., et al. (2010). Spike avalanches exhibit universal dynamics across the sleep-wake cycle. PLoS One5:e0014129. doi: 10.1371/journal.pone.0014129
Roberts, J. A., Boonstra, T. W., and Breakspear, M. (2015). The heavy tail of the human brain. Curr. Opin. Neurobiol.31, 164–172. doi: 10.1016/j.conb.2014.10.014
Roberts, J. A., Iyer, K. K., Finnigan, S., Vanhatalo, S., and Breakspear, M. (2014a). Scale-free bursting in human cortex following hypoxia at birth. J. Neurosci.34, 6557–6572. doi: 10.1523/jneurosci.4701-13.2014
Roberts, J. A., Iyer, K. K., Vanhatalo, S., and Breakspear, M. (2014b). Critical role for resource constraints in neural models. Front. Syst. Neurosci.8:154. doi: 10.3389/fnsys.2014.00154
Rolls, E. T., Loh, M., Deco, G., and Winterer, G. (2008). Computational models of schizophrenia and dopamine modulation in the prefrontal cortex. Nat. Rev. Neurosci.9, 696–709. doi: 10.1038/nrn2462
Ros, T. J., Baars, B., Lanius, R. A., and Vuilleumier, P. (2014). Tuning pathological brain oscillations with neurofeedback: a systems neuroscience framework. Front. Hum. Neurosci.8:1008. doi: 10.3389/fnhum.2014.01008
Ruiz, M. H., Bin Hong, S., Hennig, H., Altenmueller, E., and Kuehn, A. A. (2014). Long-range correlation properties in timing of skilled piano performance: the influence of auditory feedback and deep brain stimulation. Front. Psychol.5:1030. doi: 10.3389/fpsyg.2014.01030
Sachs, M. K., Yoder, M. R., Turcotte, D. L., Rundle, J. B., and Malamud, B. D. (2012). Black swans, power laws, and dragon-kings: earthquakes, volcanic eruptions, landslides, wildfires, floods, and SOC models. Eur. Phys. J. Spec. Top.205, 167–182. doi: 10.1140/epjst/e2012-01569-3
Saleur, H., Sammis, C. G., and Sornette, D. (1996). Discrete scale invariance, complex fractal dimensions, and log-periodic fluctuations in seismicity. J. Geophys. Res. Solid Earth.101, 17661–17677. doi: 10.1029/96jb00876
Sammis, C. G., and Smith, S. W. (1999). Seismic cycles and the evolution of stress correlation in cellular automaton models of finite fault networks. Pure Appl. Geophys.155, 307–334. doi: 10.1007/s000240050267
Scheffer, M., Bascompte, J., Brock, W. A., Brovkin, V., Carpenter, S. R., Dakos, V., et al. (2009). Early-warning signals for critical transitions. Nature461, 53–59. doi: 10.1038/nature08227
Shew, W. L., and Plenz, D. (2013). The functional benefits of criticality in the cortex. Neuroscientist19, 88–100. doi: 10.1177/1073858412445487
Shew, W. L., Yang, H., Petermann, T., Roy, R., and Plenz, D. (2009). Neuronal avalanches imply maximum dynamic range in cortical networks at criticality. J. Neurosci.29, 15595–15600. doi: 10.1523/JNEUROSCI.3864-09.2009
Shew, W. L., Yang, H., Yu, S., Roy, R., and Plenz, D. (2011). Information capacity and transmission are maximized in balanced cortical networks with neuronal avalanches. J. Neurosci.31, 55–63. doi: 10.1523/JNEUROSCI.4637-10.2011
Shriki, O., Alstott, J., Carver, F., Holroyd, T., Henson, R. N. A., Smith, M. L., et al. (2013). Neuronal avalanches in the resting MEG of the human brain. J. Neurosci.33, 7079–7090. doi: 10.1523/JNEUROSCI.4286-12.2013
Shriki, O., and Yellin, D. (2016). Optimal information representation and criticality in an adaptive sensory recurrent neuronal network. PLoS Comput. Biol.12:e1004698. doi: 10.1371/journal.pcbi.1004698
Simola, J., Zhigalov, A., Morales-Munoz, I., Palva, J. M., and Palva, S. (2017). Critical dynamics of endogenous fluctuations predict cognitive flexibility in the Go/NoGo task. Sci. Rep.7:2909. doi: 10.1038/s41598-017-02750-9
Simonsen, I., Hansen, A., and Nes, O. M. (1998). Determination of the Hurst exponent by use of wavelet transforms. Phys. Rev. E Stat. Physics, Plasmas, Fluids, Relat. Interdiscip. Top.58:2779. doi: 10.1103/PhysRevE.58.2779
Slezin, V. B., Korsakova, E. A., Dytjatkovsky, M. A., Schultz, E. A., Arystova, T. A., and Siivola, J. R. (2007). Multifractal analysis as an aid in the diagnostics of mental disorders. Nord. J. Psychiatry61, 339–342. doi: 10.1080/08039480701643175
Smit, D. J. A., de Geus, E. J. C., van de Nieuwenhuijzen, M. E., van Beijsterveldt, C. E. M., van Baal, G. C. M., Mansvelder, H. D., et al. (2011). Scale-free modulation of resting-state neuronal oscillations reflects prolonged brain maturation in humans. J. Neurosci.31, 13128–13136. doi: 10.1523/JNEUROSCI.1678-11.2011
Sornette, A., and Sornette, D. (1989). Self-organized criticality and earthquakes. Europhys. Lett.9:197. doi: 10.1209/0295-5075/9/3/002
Stam, C. J., and de Bruin, E. A. (2004). Scale-free dynamics of global functional connectivity in the human brain. Hum. Brain Mapp.22, 97–109. doi: 10.1002/hbm.20016
Stam, C. J., Montez, T., Jones, B. F., Rombouts, S. A. R. B., van der Made, Y., Pijnenburg, Y. A. L., et al. (2005). Disturbed fluctuations of resting state EEG synchronization in Alzheimer’s disease. Clin. Neurophysiol.116, 708–715. doi: 10.1016/j.clinph.2004.09.022
Stramaglia, S., Pellicoro, M., Angelini, L., Amico, E., Aerts, H., Cortés, J. M., et al. (2017). Ising model with conserved magnetization on the human connectome: implications on the relation structure-function in wakefulness and anesthesia. Chaos.27:047407. doi: 10.1063/1.4978999
Stumpf, M. P. H., and Porter, M. A. (2012). Critical truths about power laws. Science335, 665–666. doi: 10.1126/science.1216142
Suckling, J., Wink, A. M., Bernard, F. A., Barnes, A., and Bullmore, E. (2008). Endogenous multifractal brain dynamics are modulated by age, cholinergic blockade and cognitive performance. J. Neurosci. Methods174, 292–300. doi: 10.1016/j.jneumeth.2008.06.037
Surmeli, T., Ertem, A., Eralp, E., and Kos, I. H. (2012). Schizophrenia and the efficacy of qEEG-guided neurofeedback treatment: a clinical case series. Clin. EEG Neurosci.43, 133–144. doi: 10.1177/1550059411429531
Tagliazucchi, E., Balenzuela, P., Fraiman, D., and Chialvo, D. R. (2012). Criticality in large-scale brain FMRI dynamics unveiled by a novel point process analysis. Front. Physiol.3:15. doi: 10.3389/fphys.2012.00015
Tagliazucchi, E., Carhart-Harris, R., Leech, R., Nutt, D., and Chialvo, D. R. (2014). Enhanced repertoire of brain dynamical states during the psychedelic experience. Hum. Brain Mapp.35, 5442–5456. doi: 10.1002/hbm.22562
Tagliazucchi, E., von Wegner, F., Morzelewski, A., Brodbeck, V., Jahnke, K., and Laufs, H. (2013). Breakdown of long-range temporal dependence in default mode and attention networks during deep sleep. Proc. Natl. Acad. Sci. U.S.A.110, 15419–15424. doi: 10.1073/pnas.1312848110
Tanaka, T., Kaneko, T., and Aoyagi, T. (2009). Recurrent infomax generates cell assemblies, neuronal avalanches, and simple cell-like selectivity. Neural Comput.21, 1038–1067. doi: 10.1162/neco.2008.03-08-727
Thatcher, R. W., North, D. M., and Biver, C. J. (2009). Self-organized criticality and the development of EEG phase reset. Hum. Brain Mapp.30, 553–574. doi: 10.1002/hbm.20524
Thatcher, R. W., North, D. M., and Biver, C. J. (2014). LORETA EEG phase reset of the default mode network. Front. Hum. Neurosci.8:529. doi: 10.3389/fnhum.2014.00529
Thiery, T., Lajnef, T., Combrisson, E., Dehgan, A., Rainville, P., Mashour, G. A., et al. (2018). Long-range temporal correlations in the brain distinguish conscious wakefulness from induced unconsciousness. Neuroimage179, 30–39. doi: 10.1016/j.neuroimage.2018.05.069
Tinker, J., and Velazquez, J. L. P. (2014). Power law scaling in synchronization of brain signals depends on cognitive load. Front. Syst. Neurosci.8:73. doi: 10.3389/fnsys.2014.00073
Tkačik, G., Marre, O., Mora, T., Amodei, D., Berry, M. J., and Bialek, W. (2013). The simplest maximum entropy model for collective behavior in a neural network. J. Stat. Mech. Theory Exp. 2013. doi: 10.1088/1742-5468/2013/03/P03011
Tolkunov, D., Rubin, D., and Mujica-Parodi, L. R. (2010). Power spectrum scale invariance quantifies limbic dysregulation in trait anxious adults using fMRI: adapting methods optimized for characterizing autonomic dysregulation to neural dynamic time series. Neuroimage 50, 72–80. doi: 10.1016/j.neuroimage.2009.12.021
Tomen, N., Ernst, U. A., and Herrmann, J. M. (2019). The Functional Role of Critical Dynamics in Neural Systems. Berlin: Springer International Publishing.
Tomko, G. J., Crapper, D. R., Wilson, K. G., Madison, D. V., Nicoll, R. A., Sauer, T., et al. (2018). The theory of critical phenomena: an introduction to the renormalization group. Neuron.46:671. doi: 10.1101/107185
Touboul, J., and Destexhe, A. (2010). Can power-law scaling and neuronal avalanches arise from stochastic dynamics?PLoS One5:e8982. doi: 10.1371/journal.pone.0008982
Turrigiano, G. G., and Nelson, S. B. (2004). Homeostatic plasticity in the developing nervous system. Nat. Rev. Neurosci.5, 97–107. doi: 10.1038/nrn1327
Uhlhaas, P. J., Roux, F., Rodriguez, E., Rotarska-Jagiela, A., and Singer, W. (2010). Neural synchrony and the development of cortical networks. Trends Cogn. Sci.14, 72–80. doi: 10.1016/j.tics.2009.12.002
Van De Leemput, I. A., Wichers, M., Cramer, A. O. J., Borsboom, D., Tuerlinckx, F., Kuppens, P., et al. (2014). Critical slowing down as early warning for the onset and termination of depression. Proc. Natl. Acad. Sci. U.S.A.111, 87–92. doi: 10.1073/pnas.1312114110
Vanhatalo, S., and Kaila, K. (2006). Development of neonatal EEG activity: from phenomenology to physiology. Semin. Fetal Neonatal Med.11, 471–478. doi: 10.1016/j.siny.2006.07.008
Vyšata, O., Procházka, A., Mareš, J., Rusina, R., Pazdera, L., Vališ, M., et al. (2014). Change in the characteristics of EEG color noise in alzheimer’s disease. Clin. EEG Neurosci.45, 147–151. doi: 10.1177/1550059413491558
Wang, J. W. J. L., Lombardi, F., Zhang, X., Anaclet, C., and Ivanov, P. C. (2019). Non-equilibrium critical dynamics of bursts in Θ and δ rhythms as fundamental characteristic of sleep and wake micro-architecture. PLoS Comput. Biol.15:e1007268. doi: 10.1371/journal.pcbi.1007268
Wang, R., Dearing, J. A., Langdon, P. G., Zhang, E., Yang, X., Dakos, V., et al. (2012). Flickering gives early warning signals of a critical transition to a eutrophic lake state. Nature492, 419–422. doi: 10.1038/nature11655
Weiss, B., Clemens, Z., Bodizs, R., and Halasz, P. (2011). Comparison of fractal and power spectral EEG features: effects of topography and sleep stages. BRAIN Res. Bull.84, 359–375. doi: 10.1016/j.brainresbull.2010.12.005
West, T., Farmer, S., Berthouze, L., Jha, A., Beudel, M., Foltynie, T., et al. (2016). The parkinsonian subthalamic network: measures of power, linear, and non-linear synchronization and their relationship to L-DOPA treatment and OFF state motor severity. Front. Hum. Neurosci.10:517. doi: 10.3389/fnhum.2016.00517
Wikstro, S., Iyer, K. K., Roberts, J. A., Hellstro, L., Pupp, I. H., Ley, D., et al. (2015). Cortical burst dynamics predict clinical outcome early in extremely preterm infants. Brain138(Pt 8), 2206–2218. doi: 10.1093/awv147
Wilting, J., and Priesemann, V. (2019). 25 years of criticality in neuroscience - established results, open controversies, novel concepts. Curr. Opin. Neurobiol.58, 105–111. doi: 10.1016/j.conb.2019.08.002
Wink, A. M., Bernard, F., Salvador, R., Bullmore, E., and Suckling, J. (2006). Age and cholinergic effects on hemodynamics and functional coherence of human hippocampus. Neurobiol. Aging.27, 1395–1404. doi: 10.1016/j.neurobiolaging.2005.08.011
Wink, A. M., Bullmore, E., Barnes, A., Bernard, F., and Suckling, J. (2008). Monofractal and multifractal dynamics of low frequency endogenous brain oscillations in functional MRI. Hum. Brain Mapp.29, 791–801. doi: 10.1002/hbm.20593
Witton, C., Sergeyev, S. V., Turitsyna, E. G., Furlong, P. L., Seri, S., Brookes, M., et al. (2019). Rogue bioelectrical waves in the brain: the Hurst exponent as a potential measure for presurgical mapping in epilepsy. J. Neural Eng.16:56019. doi: 10.1088/1741-2552/ab225e
Worrell, G. A., Cranstoun, S. D., Echauz, J., and Litt, B. (2002). Evidence for self-organized criticality in human epileptic hippocampus. Neuroreport13, 2017–2021. doi: 10.1097/00001756-200211150-00005
Yan, J., Wang, Y., Ouyang, G., Yu, T., Li, Y., Sik, A., et al. (2016). Analysis of electrocorticogram in epilepsy patients in terms of criticality. Nonlinear Dyn.83, 1909–1917. doi: 10.1007/s11071-015-2455-9
Yang, H., Shew, W. L., Roy, R., and Plenz, D. (2012). Maximal variability of phase synchrony in cortical networks with neuronal avalanches. J. Neurosci.32, 1061–1072. doi: 10.1523/JNEUROSCI.2771-11.2012
Keywords: criticality, brain, long-range temporal correlation, neurodevelopment, neurodegeneration, sleep, epilepsy, anesthesia
Citation: Zimmern V (2020) Why Brain Criticality Is Clinically Relevant: A Scoping Review. Front. Neural Circuits 14:54. doi: 10.3389/fncir.2020.00054
Received: 24 May 2020; Accepted: 23 July 2020;
Published: 26 August 2020.
Edited by:
Ioanna Sandvig, Norwegian University of Science and Technology, NorwayReviewed by:
Adriano Barra, University of Salento, ItalyStephen M. Johnson, University of Wisconsin-Madison, United States
Copyright © 2020 Zimmern. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Vincent Zimmern, dmluY2VudC56aW1tZXJuQHV0c291dGh3ZXN0ZXJuLmVkdQ==
 Vincent Zimmern
Vincent Zimmern