- 1Cancer Research UK Cambridge Institute and Department of Biochemistry, University of Cambridge, Cambridge, UK
- 2Commissariat à l’Energie Atomique, Institut d’Imagerie Biomédicale, Molecular Imaging Research Center, Fontenay-Aux-Roses, France
- 3Centre de Résonance Magnétique des Systèmes Biologiques, UMR 5536, Université Bordeaux Segalen - Centre National de la Recherche Scientifique, Bordeaux, France
13C nuclear magnetic resonance (NMR) spectroscopy is the method of choice for studying brain metabolism. Indeed, the most convincing data obtained to decipher metabolic exchanges between neurons and astrocytes have been obtained using this technique, thus illustrating its power. It may be difficult for non-specialists, however, to grasp the full implication of data presented in articles written by spectroscopists. The aim of the review is, therefore, to provide a fundamental understanding of this topic to facilitate the non-specialists in their reading of this literature. In the first part of this review, we present the metabolic fate of 13C-labeled substrates in the brain in a detailed way, including an overview of some general neurochemical principles. We also address and compare the various spectroscopic strategies that can be used to study brain metabolism. Then, we provide an overview of the 13C NMR experiments performed to analyze both intracellular and intercellular metabolic fluxes. More particularly, the role of lactate as a potential energy substrate for neurons is discussed in the light of 13C NMR data. Finally, new perspectives and applications offered by 13C hyperpolarization are described.
Introduction
The brain is metabolically the most energy-consuming organ. Adequate brain physiology depends on the unceasing supply of proper amounts of oxygen and plasma glucose (Glc). Consequently, limitations in the delivery of these two cerebral substrates cause most physiopathological states (Nicholls, 2007; Okada and Lipton, 2007).
Classical approaches to study cerebral metabolism, both in physiological and in physiopathological conditions, required the use of optical methods or radioactive isotopes and the isolation and purification of the enzymes or transport systems involved to study the corresponding in vitro kinetics (Bachelard, 1989; Clark and Lai, 1989; Sokoloff, 1989). This reductionist approach provided essential information on the operation of the central nervous system (CNS), despite the limitations brought by the small amounts of the involved proteins present in cerebral tissues and by the fact that its utilization was circumscribed to postmortem biopsies or cerebral extracts.
The remarkable advance during the past decades of powerful tools for investigating the human brain has had a tremendous impact on our ability to investigate and understand brain function. Autoradiography and positron emission tomography (PET) methods have been developed based on the measurement of regional Glc consumption, after the administration of 2-deoxyglucose, either labeled with 14C or with 18F, respectively (Sokoloff, 1981; Wienhard, 2002; Herholz and Heiss, 2004). These methodologies can be used to determine the regional accumulation of 2-(14C or 18F)-deoxyglucose-6-phosphate, virtually unmetabolizable analogs of glucose-6-phosphate, using autoradiography or PET. Autoradiography provides ex vivo images of the regional accumulation of radioactive 2-deoxyglucose-6-phosphate (or other radioactive substrates such as acetate and butyrate, among others), as reflected in photographic plates obtained from sections of fixed brain tissue. PET produces in vivo, possibly dynamic, images of the regional uptake of 2-(18F)-deoxyglucose (FDG, or other positron emitters) in different brain sections, as resolved tomographically by a coronal arrangement of positron selective gamma cameras. Both approaches allow the determination of cerebral metabolic rates for Glc transport and phosphorylation (CMRglc) in different cerebral regions after appropriate modeling of the underlying tracer kinetics (Price, 2003). However, these radioactive approaches are limited in resolution and chemical specificity, making it not possible to investigate the downstream metabolism of Glc after the first glycolytic enzymatic step. Similarly, functional magnetic resonance imaging (fMRI) indirectly allowed the investigation of the hemodynamic and blood oxygenation changes associated with sensory or motor stimulation (Heeger and Ress, 2002). Despite their importance, FDG uptake or fMRI provided no information on the pathways and metabolic interactions underlying the cerebral activation process. This implies that further advances in this area would involve necessarily the use of additional methodologies. From this perspective, genome cloning and sequencing techniques, as well as the important development of novel nuclear magnetic resonance (NMR) approaches have overcome many of the limitations of the traditional strategies, as explained below. In particular, sequencing of the human and mouse genomes has provided a broad understanding of the different isoforms of enzymes and transporters present in the brain, without the need to isolate and purify the corresponding proteins (International Human Genome Sequencing Consortium, 2001; Mouse Genome Sequencing Consortium, 2002). These genomic methods, however, do not allow the investigation of the function and in vivo performance of the genes sequenced or cloned. It is in this respect that NMR technologies have become more helpful, providing the quantitative assessment of transport steps, metabolic fluxes and cellular compartmentalization of glycolysis, pyruvate (Pyr) oxidation, and tricarboxylic acid (TCA) cycle, among other pathways, in a plethora of neural systems ranging from primary cell cultures to the intact rodent or human brain (Gruetter et al., 2003; Shulman et al., 2004; Rodrigues and Cerdán, 2005).
Pioneering NMR approaches to cerebral energetics begun with the application of 31P NMR (Moore et al., 1999). These 31P NMR spectra from rodent, cat, dog, or human brain – depicted resonances from adenosine triphosphate (ATP), phosphocreatine (PCr), inorganic phosphate (Pi), phosphomonoesters (PME, mainly phosphorylethanolamine), and phosphodiesters (PDE, glycerophosphorylcholine; Hilberman et al., 1984; Komatsumoto et al., 1987; Nioka et al., 1991). With this technique it was possible to follow non-invasively the rates of PCr breakdown and recovery after hypoxic and ischemic episodes.
Nowadays, the most extended NMR approach to explore brain in the clinic is 1H NMR spectroscopy (Burtscher and Holtas, 2001). 1H NMR spectra from human or rodent brain show resonances from the methyl group of N-acetyl-aspartic acid (NAA), the methyl groups of creatine (Cr) and PCr, the trimethylammonium groups of choline (Cho) containing compounds and the myo-inositol (Ins), glutamate (Glu), glutamine (Gln), and γ-aminobutyric acid (GABA) resonances, among others. Ins and NAA are thought to represent the glial and neuronal contributions to the observed voxel, respectively. Remarkably, lactate (Lac) becomes evidently observable under hypoxic or ischemic conditions, providing a proof of augmented net glycolytic flux under these conditions. However, 1H NMR spectroscopy has the limitation of poor signal dispersion, compared to other commonly used spin nuclei, with the consequent severe overlap problems.
13C NMR approaches constitute probably the most elaborated, chemically specific, tool to follow the metabolic fate of 13C-labeled substrates in the brain, both in vivo and in vitro (de Graaf et al., 2003b; Gruetter et al., 2003; Garcia-Espinosa et al., 2004; Rodrigues et al., 2009). Since the first 13C NMR spectroscopy study of a living organism, describing the metabolism of [1-13C]Glc by an eukaryotic cell system (Eakin et al., 1972), this approach developed into a powerful method for metabolic research with cells, perfused organs, in vivo animals and humans (Morris and Bachelard, 2003). It enabled measuring metabolic processes as they occur in their intracellular environment. Furthermore, it continues to provide unique information, not accessible from previously used approaches.
13C NMR spectroscopy allows detecting resonances from 13C, the only stable isotope of carbon having a magnetic moment. The natural abundance (NA) for 13C is approximately 1.1% of the total carbon and its magnetogyric ratio is approximately one-fourth of that of the proton. These two circumstances make 13C NMR spectroscopy a relatively insensitive technique (Friebolin, 1991). The sensitivity can be improved noticeably by using 13C-enriched substrates. The combination of 13C NMR spectroscopy detection and substrates selectively enriched in 13C in specific carbon positions has made it possible to follow in vitro and in vivo the activity of a large variety of metabolic pathways. These include glycolysis and the pentose phosphate pathway, glycogen synthesis and degradation, gluconeogenesis, the TCA cycle, ketogenesis, ureogenesis, and the Glu–Gln/GABA cycle in brain, among others (Cerdan and Seelig, 1990; Kunnecke, 1995; Morris and Bachelard, 2003; Rodrigues et al., 2007). The 13C NMR approach also enables to investigate the activities of the neuronal and glial TCA cycles in vitro and in vivo, providing direct insight into cerebral metabolic compartmentalization (Cerdan et al., 2009).
The design of 13C NMR experiments with selectively 13C-enriched substrates is similar to the classical radiolabeling experiments using 14C. An important difference is that 13C precursors are administered in substrate amounts, while 14C substrates are used in tracer amounts. Despite this, 13C NMR presents important advantages over methodologies using 14C: (i) the metabolism of the 13C-labeled substrate can be followed in real-time, in situ and non-invasively (Szyperski, 1998; Morris and Bachelard, 2003); (ii) even if tissue extracts are prepared, the detection of 13C in the different carbon resonances of a specific metabolite does not require separation and carbon by carbon degradation, a prerequisite in the experiments with radioactive 14C (Dobbins and Malloy, 2003); and (iii) when two or more 13C atoms occupy contiguous positions in the same metabolite molecule it will give rise to isotope effects, called homonuclear spin-coupling, that lead to the appearance of multiplets (instead of single resonances). The analysis by 13C NMR of these homonuclear spin-coupling patterns represents an enormous gain in the information obtained as compared to the classical radioactive 14C experiments (Dobbins and Malloy, 2003). As a counterpart to these advantages, 13C NMR is significantly less sensitive than other conventional metabolic techniques like radioactive counting, mass spectrometry, and fluorimetric or spectrophotometric methods.
Investigation of metabolic pathways using 13C NMR spectroscopy is comprised of three main tasks: (i) the infusion of a 13C-labeled substrate; (ii) the detection of 13C-labeled metabolites following substrate consumption; and (iii) the metabolic modeling of measured 13C enrichments to quantitatively derive metabolic fluxes. In general, these three tasks are closely interconnected. Each of them imposes constraints on the two others, and all three must be designed depending on metabolic pathways that are to be investigated. The choice of the substrate (such as Glc, acetate, Pyr, among others) will allow more or less specific feeding of a specific cell type (such as neurons and astrocytes). This will, in-turn, impose the choice of modeling for these cells, and may drive the NMR methodological choices to measure 13C labeling for cell-specific metabolites (such as Glu, Gln, GABA, among others). Alternatively, the ability of 13C spectroscopy methods to resolve certain peaks on NMR spectra may lead to the refinement of metabolic models, while the inability to resolve peaks may impose the choice of a labeled substrate whose consumption does not lead to the formation of species with spectral overlap.
Due to the connection between biological questions and methodological issues, a good understanding of the practical implementation of 13C experiments, with associated caveats and pitfalls, is a prerequisite to any investigation and discussion of metabolism based on 13C studies. In this review, we will initially provide a simple picture of brain energy metabolism, with a level of details commensurable with NMR accessible information, and explain how 13C nuclei from different substrates flow through metabolic pathways. Then, spectroscopic acquisition techniques will be reviewed, with associated advantages, drawbacks, and technical difficulties. The basis of metabolic modeling to derive quantitative flux values will be then explained. Finally, we will address two different models of neuroglial coupling : the astrocyte–neuron lactate shuttle (ANLS) model (Pellerin and Magistretti, 1994; Pellerin et al., 2007) and the redox switch/redox coupling hypothesis (Cerdan et al., 2006; Ramirez et al., 2007).
The Journey of Carbon: Metabolic Fates of Labeled Substrates
Fuels for the Brain
The quasi-universal energy molecule of living systems is ATP, which is predominantly synthesized during aerobic cellular respiration (Gjedde, 2007). A central mechanism of aerobic cellular respiration is the TCA cycle, where fuel molecules undergo complete oxidation, ultimately leading to ATP synthesis through oxidative phosphorylation in mitochondrial cristae. When these fuel molecules are labeled with 13C and continuously infused, their degradation in the TCA cycle will lead to the progressive incorporation of 13C into metabolic intermediates and by-products (Rodrigues and Cerdán, 2007). The journey of 13C nuclei is summarized in Figure 1.
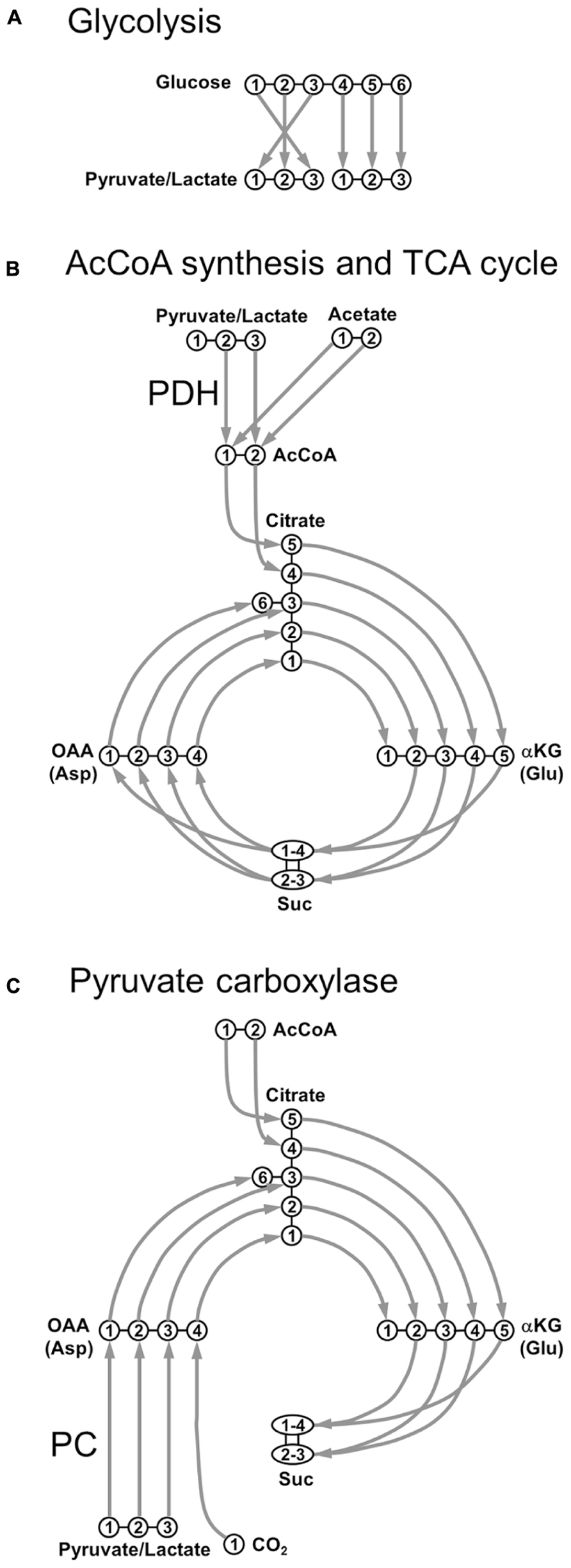
FIGURE 1. Transfer of individual 13C nuclei during the main steps of oxidative metabolism. (A) Glycolysis; (B) acetyl-CoA synthesis through pyruvate dehydrogenase (PDH) and TCA cycle; (C) pyruvate carboxylase (PC). AcCoA, acetyl-CoA; αKG, α-ketoglutarate; Asp, aspartate; Glu, glutamate; OAA, oxaloacetate; Suc, succinate.
Under physiological conditions, the main cerebral substrate is Glc. After crossing the blood–brain barrier (BBB), a Glc molecule originates two Pyr molecules through glycolysis (Figure 1A). Pyr can be reduced to Lac by the lactate dehydrogenase (LDH, fast exchange) with the following reversible reaction:
Lactate dehydrogenase is a tetramer composed of different combinations of two subunits, H (isolated from heart) and M (from muscle): H4 (LDH1), H3M (LDH2), H2M2 (LDH3), HM3 (LDH4), and M4 (LDH5). LDH1 is mostly neuronal and its kinetic properties promote the formation of Pyr (Bittar et al., 1996). Conversely, LDH5 is primarily astrocytic and its kinetic characteristics favor mainly Lac formation. Pyr is also transported into mitochondria and decarboxylated to acetyl-CoA (AcCoA) via the oxidative pathway (pyruvate dehydrogenase, PDH), as shown in Figure 1B. AcCoA enters TCA cycle by irreversibly condensating with oxaloacetate (OAA) to form citrate, which is subsequently converted to α-ketoglutarate (αKG) via isocitrate. αKG is then degraded into succinate (Suc) via succinyl-CoA, where scrambling occurs between C1 and C4 positions, and between C2 and C3 positions, due to the symmetry of the Suc molecule. Suc is then oxidized to fumarate, with flavin adenine dinucleotide (FADH2) used as the hydrogen acceptor. The next step is the hydration of fumarate to form malate, and the cycle becoming complete with the oxidation of malate to OAA (Figure 1B). Pyr, or even Lac, can be directly supplied to the brain as fuels for TCA cycle. An alternative fuel is acetate, which can be directly converted to AcCoA. This was primarily suggested to happen in astrocytes (Waniewski and Martin, 1998). It was proposed that the main reason acetate is a relatively poor substrate for neurons was due to transporter affinity. This study was based on poor uptake of acetate by synaptosomal fractions compared to astrocytes, not measuring the uptake of acetate by neurons in this work. Further studies revealed that metabolism of acetate is tightly controlled at the enzyme level, via changes in the acetylation status of AcCoA and is not regulated by restriction of uptake (Rae et al., 2012).
In addition to PDH, Pyr may also enter the TCA cycle via the anaplerotic pathway, after its carboxylation to OAA, through the pyruvate carboxylase (PC), as depicted in Figure 1C. In contrast to PDH metabolism, which preserves the source of carbon skeletons in TCA cycle, OAA is synthesized de novo by PC. The total number of carbon skeletons in the TCA cycle is therefore increased, consequently requiring a net efflux before a turn has been completed. This anaplerotic pathway is mainly glial, due to the specific astrocytic localization of PC (Shank et al., 1985; Sonnewald and Rae, 2010).
Labeling of NMR-Visible Amino Acids
Nuclear magnetic resonance detection threshold is typically in the millimolar (mM) range, which is above the typical concentration of most TCA cycle intermediates, including αKG and OAA. However, these intermediates are in fast exchange with amino acids, which exist in concentrations that are above the detection threshold, making 13C-labeling measurements possible. In particular, αKG is in fast exchange with Glu through aspartate aminotransferase, with identical labeling patterns for the keto acid and the amino acid pools. In neurons, neuronal OAA (OAAn) is in exchange with a pool of Asp, with identical labeling patterns as well.
Exploring Figure 1, it is relatively easy to track 13C labeling along metabolic pathways from labeled substrates to amino acids. For example, following [1-13C]Glc or [1,6-13C2]Glc infusions, generation of [3-13C]pyruvate is observed, which via PDH leads to the labeling of αKG and Glu at the C4 position during the first turn of the TCA cycle. During the second turn of the TCA cycle, 13C label is then transferred to Glu C2 and Glu C3. Note that comparing to [1,6-13C2]Glc, the use of [1-13C]Glc as precursor will lead to a 50%-dilution in the 13C enrichment of Pyr at the end of the glycolysis.
Neurotransmission and Metabolic Interactions Between Neurons and Astrocytes
The TCA cycle plays a central role in brain metabolism because sugars, fatty acids, and amino acids are oxidized in this pathway. This metabolic route provides numerous intermediates for cerebral biosynthetic pathways, including the neurotransmitters Glu and GABA. In the case of brain cell compartmentalization, two different TCA cycles may be considered as functioning in parallel: an astrocytic and a neuronal cycle. The existence of these two cycles, with different kinetics, was firstly demonstrated in the 1960s. When 14C-labeled Glu was administered to rats, brain radioactivity was mainly found in the form of Gln (Berl et al., 1961), showing that there is an exchange between Glu and Gln. In addition, the specific activity recovered was higher for Gln than for Glu. Therefore, a pool of Glu exists in the brain that is not exchanged. The use of 15N-labeled ammonium confirmed the existence of two pools of Glu (Berl et al., 1962), originating the concept that there are two different Glu compartments: a “small” compartment where the Glu–Gln conversion is fast, and a “large” compartment in which the renewal of Glu is much slower. Subsequently, it was shown that glutamine synthetase (GS), an enzyme responsible for the synthesis of Gln, was found mainly in astrocytes (Norenberg and Martinez-Hernandez, 1979). On the other hand, the enzyme responsible for its conversion to Glu, glutaminase, was found mainly in the neurons (Patel et al., 1982). Thereafter, the two compartments were assigned to the two cell types: neurons representing the “large” compartment and astrocytes the “small” one. One of the main consequences of the metabolic compartmentation concept is that there is a Glu–Gln cycle between neurons and astrocytes (cf. Figure 2B). In this intercellular metabolic exchange, Gln is synthesized by astrocytes and then transferred to the neuronal compartment, where it is converted to Glu. The Glu, a major neuronal signaling molecule, is released by the neurons into the synaptic cleft during neuronal activity, and then taken up by astrocytes, where it is transformed back into Gln (Badar-Goffer et al., 1990; Cerdan et al., 1990; Shank et al., 1993; Lapidot and Gopher, 1994). This exchange has been widely studied (Schousboe and Hertz, 1981; Waniewski and Martin, 1986; Erecinska and Silver, 1990), including in vivo using 13C NMR spectroscopy (for review, see Rothman et al., 2011), and various Glu transporters have been found on astrocytes (Erecinska and Silver, 1990; Flott and Seifert, 1991; Danbolt, 2001; Huang and Bergles, 2004).
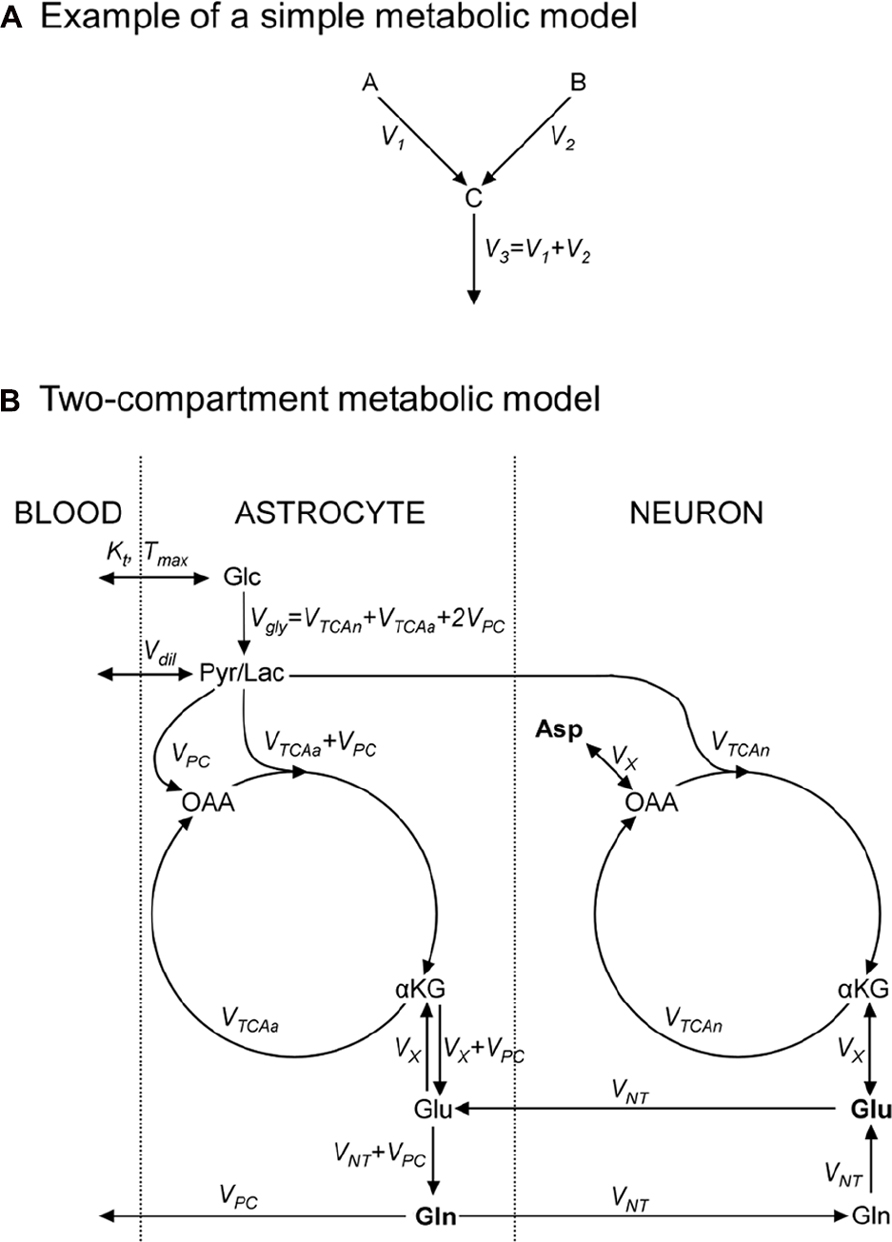
FIGURE 2. Metabolic models consist in an ensemble of metabolic pools, connected by metabolic fluxes respecting the steady-state condition for metabolic pools. (A) Example of a simple metabolic model used to illustrate how to write 13C-labeling equations; metabolic pools A and B yield C at rates V1 and V2, respectively; (B) a “classical” two-compartment metabolic model (see main text for model’s description). αKG, α-ketoglutarate; Asp, aspartate; Glc, glucose; Gln, glutamine; Glu, glutamate; Lac, lactate; OAA, oxaloacetate; Pyr, pyruvate; Suc, succinate.
The metabolic relationship between neurons and astrocytes appears, however, to be much more complex than the existence of a simple Glu–Gln cycle. Indeed, it is possible to show that the uptake of Gln by neurons does not offset the continuous loss of Glu (Hertz, 1979). Therefore, the neurons must use other metabolites that are precursors of the synthesis of Glu, as the components of the TCA cycle, and must therefore be equipped with an enzymatic route to allow their net synthesis from Glc. As briefly addressed above, this synthesis occurs mainly through the PC activity (Voet and Voet, 1990). However, it turns out that this enzymatic activity is present only in astrocytes (Yu et al., 1983; Shank et al., 1985), imposing a necessary anaplerotic transfer of carbons from astrocytes to neurons to replenish the neuronal pools of oxidized TCA intermediates.
In GABAergic neurons, Glu is converted to GABA by glutamate decarboxylase, which is subsequently released in the synaptic cleft. Most GABA molecules are recaptured by neurons, but a small fraction is also recaptured by astrocytes and incorporated into the glial TCA cycle.
Additional pathways exist that may impact the 13C labeling of NMR-visible metabolites such as Pyr recycling, the transfer of Lac from astrocytes to neurons and the alanine–lactate shuttle between neurons and astrocytes (Waagepetersen et al., 2000; Zwingmann and Leibfritz, 2003).
13C NMR spectroscopy acquisition techniques
The ability to detect 13C enrichment in brain amino acids is governed by two parameters: sensitivity and spectral resolution. High signal-to-noise ratio (SNR) means that metabolites can potentially be quantified with lower concentrations or enrichments, in smaller volumes, or in shorter periods. Good spectral resolution means that more resonances (corresponding to more metabolites or more specific positions) can be individually quantified, resulting in a higher chemical specificity. SNR and spectral resolution increase linearly with the magnetic field, although technical challenges become significant in vivo (shorter T2 relaxation times, increased energy deposition in tissues, higher demand on radiofrequency (RF) pulse bandwidth, and poor homogeneity of the RF field). Essentially, two main approaches can be distinguished for 13C detection, each trading one of these parameters against the others: direct 13C detection and indirect 13C detection.
Direct 13C Detection: Chemical Specificity
13C NMR resonances of brain metabolites span a very broad chemical shift range (~250 ppm), in which conveys the ability to resolve virtually all carbon positions in the detectable metabolites. In particular, direct 13C spectroscopy allows simultaneously resolving Glu and Gln at C2, C3, and C4 positions, as well as Asp and GABA at positions C2 and C3, even in vivo (Gruetter et al., 2003; Henry et al., 2003a). The carboxylic carbons are, in all cases, more difficult to observe because of their long T1s and significant saturation effects.
Beyond the information about positional enrichment, direct 13C spectroscopy allows quantifying isotopomers (i.e., individual molecules labeled at different atomic positions), since it is sensitive to a constant value – called scalar J coupling – that is different for each 13C neighborhood type. Indeed, the scalar J coupling will result in the splitting of singlet resonances, corresponding to a given enriched position, into multiplets for 13C nuclei coupled with neighboring 13C. This additional information about isotopomers allows one to resolve the activity of different metabolic pathways, as discussed below.
One-bond heteronuclear coupling between 13C and 1H may compromise spectral resolution and SNR, since it results in the splitting of 13C resonances in doublets or multiplets (J ~ 130 Hz), with reduced peak heights. Therefore, it is generally desirable to perform heteronuclear decoupling during 13C acquisition. This is achieved by the application of a RF train at 1H frequency, resulting in the effective suppression of the effects of 1H–13C coupling on 13C spectra. Besides technical difficulties associated with the necessity to control two RF chains and to prevent noise injection from the 1H transmission chain into the 13C acquisition chain, decoupling may become problematic for in vivo application at high field due to the large power deposition in tissues (de Graaf, 2005). It has, however, been shown that detection without decoupling could be achieved in the human brain at 9.4 T with acceptable accuracy (concentration uncertainty was 35–90% higher; Deelchand et al., 2006).
The main disadvantage of direct 13C spectroscopy is its low sensitivity, derived from the low gyromagnetic ratio of 13C. Three different strategies, namely nuclear Overhauser effect (nOe), pulsed polarization transfer (PPT), and cross-polarization (CP; Ernst et al., 1987) have been proposed to transfer polarization (or magnetization) from neighboring 1H to 13C, both in liquids and in vivo. This implies an increase in the 13C polarization, ultimately resulting in higher SNR. Like heteronuclear decoupling, these strategies require two transmission channels at 1H and 13C frequencies.
Nuclear Overhauser effect relies on direct (through-space) dipolar coupling between spins, and refers to the transfer of polarization from 1H to 13C due to cross-relaxation. This is achieved when RF irradiation is performed at the 1H frequency while longitudinal relaxation occurs, which drives the 13C thermodynamic equilibrium polarization to a higher value. Assuming that 13C relaxation is entirely due to dipolar interaction with 1H, nOe increases 13C polarization up to a factor 1 + 0.5 × γI/γS = 3, where γI and γS are 1H and 13C gyromagnetic ratios. Excitation is thus performed both in the 1H and 13C frequencies, while detection is obtained only in the 13C channel.
Cross-polarization and PPT rely on indirect (through-bond) scalar coupling between spins (J-coupling), the excitation being initially performed for 1H. Then, under the combined effect of J-coupling and RF perturbation, polarization is driven to an observable 13C state with amplitude corresponding to γI instead of γS, as would result from direct 13C excitation. Ideal CPT and PPT therefore yield up to a γI/γS = 4-fold gain in SNR. For CPT, this is optimally achieved after RF irradiation of 1H and 13C frequencies during a 1/J delay, when the Hartmann–Hahn condition is met (γI B1I = γS B1S; Hartmann and Hahn, 1962) and high B1 amplitudes are used. On the other hand, PPT only requires short RF perturbations (simultaneous 90° pulse at both frequencies at time 1/2J after initial excitation). It is therefore particularly interesting for in vivo applications due to the limited power deposition, while CPT can yield slightly larger SNR gains. An important feature for the in vivo application is that the localization can be fully achieved at the 1H frequency before transferring polarization, resulting in better localization accuracy compared to the direct 13C localization, due to the narrower 1H chemical shift range.
In practice, gains in SNR are significantly smaller than predicted under ideal conditions and vary between different resonances, complicating the quantification process. SNR gains up to 3.5 have been reported in the human brain at 3 T, combining nOe and CPT (Klomp et al., 2006).
Indirect 13C Detection: High Sensitivity
As an alternative to detecting 13C signal directly, an efficient way to increase these measurements sensitivity is to detect 1H bound to 13C. SNR gains result mostly from the increased signal voltage, which is proportional to the higher 1H thermal equilibrium magnetization – by a factor (γI/γS)2 – and to the higher precession frequency – by a factor γI/γS – compared to 13C. At the same time, state-of-the-art coils yield noise voltage increasing roughly linearly with the frequency, i.e., as γI/γS. Therefore, a (γI/γS)2 ~ 16-fold increase in SNR can be expected when going from direct detection (without polarization transfer) to indirect detection.
Indirect detection is usually based on a proton-observed carbon-edited (POCE) strategy, requiring two transmission channels at 1H and 13C frequencies. The strategy is based on a standard 1H spectroscopy sequence with an additional 180° pulse at 13C frequency, being ON or OFF every other scan (Rothman et al., 1985). When the 13C pulse is ON, satellite resonances due to coupling between 1H and 13C nuclei are of opposite sign when compared with the OFF case, while resonances corresponding to 1H bound to 12C nuclei are unaffected. Therefore, subtracting odd from even scans will result in the cancellation of signal from 1H bound to 12C, while signal from 1H bound to 13C will build up.
Heteronuclear decoupling is generally performed by the application of a RF train at 13C frequency during the 1H acquisition. This is complicated by the large chemical shift range of 13C, which imposes a requirement for ultra-broadband decoupling (resulting in high-power deposition) if all resonances on the 1H spectra have to be decoupled. Decoupling is performed to increase SNR but also to improve spectral resolution, which is critical when observing 1H resonances. Indeed, the 1H chemical shift range only spans ~3 ppm for the aliphatic portion which covers the metabolites’ resonances of interest. It is generally accepted that resolution of Glu and Gln C4 becomes possible only for B0 > 3 T, while resolving Glu and Gln C3 remains problematic even at much higher field (Pfeuffer et al., 1999). Indirect detection of GABA and Asp labeling remains problematic and has only been reported at B0 = 7 T or above in the rodent brain (Pfeuffer et al., 1999; de Graaf et al., 2003a; Yang et al., 2005; van Eijsden et al., 2010). Therefore, the loss of chemical specificity associated with indirect detection is acceptable mostly for in vivo applications where sensitivity is critical, especially when performing a dynamic measurement: collecting multiple spectra during 13C-labeled substrate infusion. Indirect 13C spectroscopy in vivo was extensively reviewed by de Graaf et al. (2003b).
An alternative method has been recently proposed for in vivo applications, which presents the unique characteristic of requiring no 13C RF pulse-chain. The method is based on the subtraction of 1H spectra collected during the 13C infusion from a baseline spectra acquired prior to infusion (Boumezbeur et al., 2004). Using this approach, C4 and C3 positions could be resolved for the total “Glu + Gln” pool at 3 T. Note that the technique demands extremely stable acquisition (including shimming and coil sensitivity) over the entire experiment.
Note On Spectral Quantification
Analysis of 13C spectra has long been performed by simple peak integration, which is possible due to the limited spectral overlap on direct 13C spectra. More recently, spectral quantification based on prior knowledge has been introduced, using for example the LCModel software (Provencher, 1993). In this approach, individual spectra of labeled molecules (obtained by experimental measurement or numerical simulation) are linearly combined to fit experimental data. This allows accurate quantification despite partial overlap, which becomes particularly interesting to discriminate different isotopomers around a given resonance, being possible to perform it even in vivo, where lines are broader (Henry et al., 2003a). Although still uncommon in direct 13C spectroscopy, prior knowledge spectral fitting is now routinely implemented in indirect 13C spectroscopy, due to unavoidable overlap on 1H spectra.
Absolute quantification, i.e., the determination of metabolite concentration and enrichment (in mM and %13C), as required for dynamic metabolic modeling (see below), is generally easier using indirect spectroscopy, due to the presence of internal references of known concentration, such as unlabeled Cr or water. With direct spectroscopy, absolute quantification can be complicated by the different polarization transfer efficiency for the different resonances, and for in vivo experiments by the absence of a suitable internal 13C reference of known concentration.
Metabolic Modeling
Examination of 13C enrichment can yield qualitative information about metabolite compartmentalization and the existence and relative importance of metabolic pathways. When seeking quantitative information, one must turn to metabolic modeling, whose basic principle is to mathematically express 13C labeling of detected metabolites as a function of the metabolic fluxes underlying the labeling process.
Writing Equations: Mass Conservation and Label Incorporation
As an exercise, we should consider two metabolite pools, A and B, yielding a third pool, C, at rates V1 and V2 (in μmol/g/min), respectively, and C being then consumed at rate V3 (Figure 2A). A usual assumption is that the size of pool C remains constant:
This imposes that the total influx in the pool is equal to the total efflux from the pool, V3 = V1 + V2. We should also assume that 13C nuclei, at position i in A and j in B, both enter the C pool at position k. We use Ai*, Bj*, and Ck* to denote molecules labeled at these positions. 13C mass conservation imposes that the increase in the Ck* pool size is equal to the amount of 13C entering the pool minus what exits the pool at each instant:
A metabolic model typically consists in several equations of the previous type, describing label transfer from infused substrates to metabolic intermediates and, ultimately, to detected metabolites. To favor an efficient solution, the number of differential equations describing the model should be minimized. Equations describing low-concentration intermediates can generally be omitted since their enrichment mimics that of the immediately preceding high-concentration metabolite. Except at steady-state, these systems of differential equations can generally not be solved analytically and require numerical computing to determine what flux values yield the best fit to experimental data.
Temporal Resolution: Steady-State Versus Dynamic Modeling
To illustrate the impact of temporal resolution on a model, we can assume constant, but different, fractional enrichments for A and B ([Ai*]/[A] = FEA, [Bj*]/[B] = FEB). A common procedure in acquiring these data is to wait a period of time after the start of the 13C infusion, ensuring that isotopic steady-state has been reached for [Ck*]. In this case, Eq. 2 immediately yields, with FEC = [Ck*](t = ∞/[C]:
The ratio V1 to V2 can therefore be determined from known values of FEA, FEB, and FEC. In general, metabolic models at steady-state only yield flux ratios, not absolute values.
In contrast, we can also explore how dynamic modeling (i.e., using data collected at different time points) carries richer information. We solve Eq. 2 assuming fractional enrichment (also called specific enrichment) for A and B going instantaneously from 13C NA = 1.1% to FEA and FEB at t > 0:
It appears that the enrichment curve will again carry information about the ratio V1/V2 from long-time enrichment, and independently V1 + V2 from the exponential rise (provided [C] is known). This means that the absolute values of V1 and V2 (in μmol/g/min) can now be determined. The ability to assess absolute flux values and, potentially, for a number of fluxes greater than the number of equations is a unique feature of dynamic modeling. However, absolute quantification of concentrations is required.
Feeding Dynamic Models: Substrate Entry Into the Brain
Dynamic metabolic modeling is complicated by the need to estimate the temporal evolution of substrate’s intracellular concentration and the enrichment as an entry function. Since, in general, these parameters cannot be directly measured, they are calculated from plasma concentrations and enrichments by modeling transport through the BBB. Transport of Glc and monocarboxylic acids through the BBB is a bidirectional process and is best modeled by reversible Michaelis–Menten transport equations (Simpson et al., 2007). Kinetic parameters have been estimated in the mammalian brain for Glc (Gruetter et al., 1998), acetate (Deelchand et al., 2009), and Lac (Boumezbeur et al., 2010). Blood sampling throughout the infusion is required to determine plasmatic concentration and enrichment of the investigated substrate. However, it has been shown for Glc that, provided the infusion protocol yields “reasonably” stable plasmatic fractional enrichment, blood sampling, as well as Michaelis–Menten kinetics, can be omitted. Cerebral Pyr/Lac fractional enrichment can be directly fitted as an additional unknown parameter (Valette et al., 2009).
Toward Dynamic Modeling of Isotopomers
For a given set of metabolic pathways, dynamic modeling of isotopomer time courses should, in theory, allow the derivation of metabolic fluxes with the highest achievable reliability, due to the higher information content (provided SNR is high enough). In practice, this has been performed in a very limited number of studies (e.g., Haberg et al., 1998; Serres et al., 2007), and never in vivo. Isotopomer modeling is regularly performed in vitro and ex vivo at steady-state (see Wiechert, 2001 for a review). Conversely, in vivo modeling in the brain has been almost exclusively performed using dynamic positional enrichments (for review of this, see de Graaf et al., 2003b; Gruetter et al., 2003; Henry et al., 2006; Rothman et al., 2011). As far as we know, isotopomer modeling has not been successfully achieved in the brain in vivo, although it can theoretically yield flux values with unparalleled accuracy (Shestov et al., 2012). This is probably due to the difficulty of measuring 13C spectra fine structure in vivo, especially with a high-temporal resolution to perform dynamic modeling. However, it has been shown that using high-field NMR systems allowed the dynamic detection of 13C isotopomers in the rat brain during an infusion of [1,6-13C2]Glc (Henry et al., 2003b) and double infusion of [1,2-13C2]acetate and [1,6-13C2]Glc (Deelchand et al., 2009). Recent modeling of these data suggests that current metabolic models are incomplete to account for the dynamics of all isotopomer time-curves (Jeffrey et al., 2013), appealing for new refined models.
Single- or Two-Compartment Model
A detailed description of models found in the literature is beyond the scope of this review. We will only briefly present the main metabolic pathways and assumptions in two popular models. The first one is the single-compartment model, which allows the measurement of TCA cycle flux (VTCA) following infusion of [1-13C]Glc or [1,6-13C2]Glc. The Pyr/Lac pool is in exchange with the blood pool at the rate Vdil, leading to label dilution (Figure 2B). Measuring Glu C4 and C3 is required to derive both the VTCA and the rate of exchange (VX) between αKG and Glu. Some early works proposed that VX was much higher than VTCA (Mason et al., 1992), allowing VTCA estimation from Glu C4 only. There is still some controversy about the value of VX, and modeling of Glu C3 and C4 should be considered safer if no assumption is done on VX (Henry et al., 2006). An Asp pool can be added to the model, in exchange with OAA at the same rate VX, to ensure nitrogen mass balance through the malate–aspartate shuttle. In this model, the Glu–Gln cycle is usually modeled by a simple exchange between both pools at a rate usually set to ~0.5 × VTCA. Since most Glu is neuronal, this model essentially reflects neuronal VTCA. Extensive review of this model for in vivo applications was provided by Henry et al. (2003a).
An increasingly popular model (including in vivo) is the so-called two-compartment model, where neurons and astrocytes are explicitly considered (Figure 2B). Infusion of various substrates ([1-13C]Glc, [1,6-13C2]Glc, [2-13C]Glc, [1,2-13C2]acetate) may be performed to calculate simultaneously neuronal TCA cycle, glial PDH and PC fluxes, and the glutamatergic neurotransmission flux VNT (Glu–Gln cycle). A net efflux of Gln in the blood is generally considered to remove extra carbon skeletons added by PC. Robustness of the model requires the measurement of Glu and Gln at position C4 and C3, and measurement of Asp C2 and C3 may help stabilize the model (Gruetter et al., 2001). Isotopomer modeling may significantly improve model’s reliability.
Some publications have sought to refine single-compartment or two-compartment models by including conversion of Glu to GABA and its reentry into TCA cycle, which is associated with GABAergic neurotransmission (Lapidot and Gopher, 1994; Patel et al., 2005; van Eijsden et al., 2010; Duarte and Gruetter, 2013).
Assessing a Model’s Reliability
When performing modeling, the quality and amount of measured 13C enrichments should be high enough for the problem to be well determined (i.e., estimated flux values should be close to the real values), and standard deviation on fluxes, as well as covariance between fluxes should be low. A method of choice to explore model’s reliability is Monte Carlo simulations. Enrichments are simulated for to-be-infused substrates and to-be-measured metabolites, using the metabolic model and given flux values. Noise is then added to yield SNR comparable to experimental SNR, and noised enrichments are fitted using the model. This procedure is repeated hundreds of times to derive mean and standard deviation for the estimated fluxes. The degree of confidence one can have in flux values can therefore be assessed for a given metabolic model and given experimental conditions. It allowed showing that estimation of VTCA and VX from the Glu C4 time-course only is very uncertain (Henry et al., 2006), and that the glutamatergic neurotransmission VNT may not be reliable when only [1-13C]Glc or [1,6-13C2]Glc infusion is performed (Shestov et al., 2007).
Metabolic Cooperation Between Neurons and Astrocytes Studied by NMR Spectroscopy
Astrocyte–Neuron Lactate Shuttle Hypothesis: Following Lactate Production and Consumption by the Brain
Since the astrocytes are located between blood vessels and neurons, the question arises whether the astrocytes play the role of intermediary in the flow of substrates from blood to neurons. Indeed, Glc can reach neurons (i) directly, by diffusing from the capillaries through the intercellular space using the Glc transporters present in each of these cells (GLUT-1 and GLUT-3; Vannucci et al., 1997); or (ii) through the astrocytes, since astrocytic end-feet continuously cover blood vessel walls (Mathiisen et al., 2010). In this latter option, Glc that enters the astrocytic end-feet can be metabolized and the product can be subsequently transferred to the neurons and used as a substrate. A growing body of evidence supports this latter hypothesis and indicates that the astrocytic metabolic supply for neurons could be Lac (Dringen et al., 1993; Pellerin and Magistretti, 1994; Larrabee, 1995; Poitry-Yamate et al., 1995; Waagepetersen et al., 1998). Indeed, it has been shown that the presence of Lac in a Glc-free medium maintains synaptic activity in brain slices (Schurr et al., 1988). In addition, Lac has a protective effect and allows better recovery of neurons after hypoxia (Schurr et al., 1997). Although Lac has relatively low permeability at the BBB, different isoforms of monocarboxylate transporters have been localized on endothelial cells (MCT1; Leino et al., 1999), astrocytes (MCT1), and neurons (MCT2; Bröer et al., 1997, 1999). Moreover, the isoenzymes of LDH, LDH1 and LDH5, have been found in different cellular locations (Bittar et al., 1996), supporting the hypothesis of astrocytic Lac utilization by neurons.
The traditional metabolic coupling theory (ANLSH for the astrocyte–neuron lactate shuttle hypothesis), firstly proposed by Pellerin and Magistretti in the mid-1990s (Pellerin and Magistretti, 1994), describes that neurotransmitter Glu released to the synaptic cleft, following an action potential, is recaptured predominantly by the high-affinity Glu transporters of surrounding astrocytes in the neuropil (Figure 3). Three Na+ atoms are co-transported with each Glu molecule to the astrocytic cytosol and metabolized into Gln by GS. The Na+ atoms are extruded from the cytosol through the Na+/K+ ATPase, at the expense of one ATP molecule, and GS consumes one additional ATP molecule. These two ATP molecules were originally proposed to be compensated for by the degradation of one Glc molecule in the astrocyte through the glycolytic pathway. Gln is then extruded to the extracellular space, being recaptured by the neurons to regenerate Glu. Therefore, in this particular process, we assist in the consumption of one Glc molecule from plasma, with the subsequent generation of two molecules of astrocytic Lac. These Lac molecules are exported to the neurons to become their main metabolic fuel. Thus, Gln production appears to be stoichiometrically coupled to Glc uptake (1:1 stoichiometry), glycolysis occurring mainly in the astrocytes while Pyr oxidation remaining as a predominantly neuronal process. These findings fit well with early 13C NMR results, which determined the cerebral Gln cycle and the TCA cycle fluxes from a minimal mathematical model. This model assumed that [4-13C]Glu and [4-13C]Gln turnover curves reflected the neuronal TCA cycle and the Gln cycle fluxes, respectively (Sibson et al., 1998). Later, Rothman et al. (2003) proposed Gln as the major precursor of cerebral Glu and the Gln cycle was found to be stoichiometrically coupled to Glc uptake, accounting for 60–80% of the energy derived from Glc metabolism.
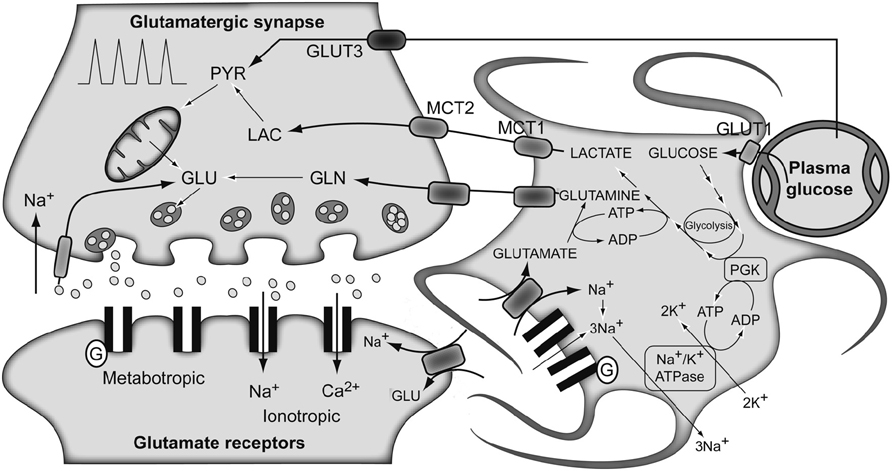
FIGURE 3. The traditional metabolic coupling hypothesis between neurons and astrocytes during glutamatergic neurotransmission. Glutamate released to the synaptic cleft during glutamatergic neurotransmission is co-transported with Na+ to the astrocytes. Astrocytic Na+ is exchanged by extracellular K+ through the Na+/K+ ATPase, consuming one ATP molecule. Astrocytic glutamate produces glutamine through glutamine synthetase, consuming one additional ATP molecule. Lactate produced exclusively in astrocytic glycolysis to support these energy demands, is extruded to the extracellular medium, taken up by the surrounding neurons and oxidized as their main metabolic fuel. Note the apparent stoichiometric coupling between glutamate–glutamine cycling and glucose uptake as well as the exclusive glycolytic or oxidative metabolisms in astrocytes and neurons, respectively. Gln, glutamine; Glu, glutamate; GLUT 1 and GLUT 3, glucose transporters 1 and 3; Lac, lactate; MCT1 and MCT2, monocarboxylate transporters 1 and 2; PGK, phosphoglycerate kinase; Pyr, pyruvate. Adapted with permission from Tsacopoulos and Magistretti (1996).
Importantly, a thorough examination of the earlier evidences led several authors to challenge the traditional approach proposed by the ANLSH (Chih et al., 2001; Dienel and Hertz, 2001; Chih and Roberts, 2003; Dienel and Cruz, 2003). In response to these criticisms, Pellerin and Magistretti (2003) presented a revised version of their proposal. The main differences are that this newer proposal does not exclude the activation of glycolysis and production of Lac in active neurons. Additionally, it does not require a direct coupling between astrocytic Lac release and neuronal Lac oxidation, proposing that Lac from both active astrocytes and neurons is released into the extracellular space. This Lac is eventually used by neurons (at rest or during activity). The current version of the ANLSH has been also critically reviewed (Hertz, 2004).
In the context of this review, it is important to remark that both 1H (Prichard, 1991; Prichard et al., 1991; Merboldt et al., 1992; Sappey-Marinier et al., 1992) and 13C NMR spectroscopy studies have been used to explore the ANLSH/metabolic coupling theory by monitoring and comparing the fate of 13C-glucose and 13C-lactate metabolism in neurons (Sonnewald et al., 1991; Schousboe et al., 1997; Bouzier-Sore et al., 2003), astrocytes (Alves et al., 1995), rat brain (Bouzier et al., 2000; Hassel and Brathe, 2000; Serres et al., 2004; Sampol et al., 2013) and human brain (Boumezbeur et al., 2010).
The Redox Switch/Redox Coupling Hypothesis
Several other convincing evidences have accumulated since the above explained interpretations of metabolic neuroglial coupling during glutamatergic neurotransmission, with relevant consequences. These new pieces of evidence showed that: (i) an important portion of the energy used to synthesize Gln is derived from the astroglial TCA cycle (Garcia-Espinosa et al., 2003); (ii) up to 40% of cerebral Glu is derived from alternative sources to Gln (Garcia-Espinosa et al., 2003); (iii) Gln cycling may not present a 1:1 stoichiometry with Glc uptake (Gruetter et al., 2001; McKenna, 2007); (iv) different kinetic pools of Lac, Pyr, Gln, Glu, and GABA exist both in astrocytes and in neurons (Cruz et al., 2001; Zwingmann et al., 2001; Rodrigues et al., 2005; Cerdan et al., 2009). All the previous described findings indicate that the coupling mechanisms between neuronal and glial metabolisms are more complex than previously envisioned.
Figure 4 shows the conception of metabolic coupling between neurons and astrocytic during glutamatergic neurotransmission proposed by Cerdan and colleagues (Cerdan et al., 2006; Ramirez et al., 2007). This hypothesis is based on the existence of transcellular coupling of oxidative and non-oxidative metabolisms in both neurons and astrocytes through the exchange of monocarboxylate reducing equivalents and on the operation of intracellular redox switches. So, after presynaptic Glu release, astrocytes incorporate Glu and three Na+ ions, being the latter removed subsequently through the plasma membrane Na+/K+ ATPase. The energetic cost of this process implies reduced astrocytic ATP/ADP concentrations, stimulating astroglial glycolysis and TCA cycle. Both astrocytic metabolic pathways contribute the energy required by GS, with a major contribution of the oxidative metabolism. However, the energy demands during glutamatergic neurotransmission eventually exceed the reduced capacity of the astrocytic TCA cycle, what could result in a net activation of the glycolytic flux and a net production of astrocytic Lac, which is rapidly extruded to the extracellular space. The resulting extracellular Lac is taken up by neurons with a consequent reduction of the cytosolic redox state to a point where neuronal glycolysis could be inhibited at the glyceraldehyde 3-phosphate dehydrogenase step. An opposite flux of Pyr, from neurons to astrocytes, is proposed to connect and balance the redox state in both neurons and glial cells. Under these conditions, extracellular Lac is predominantly consumed by neuronal oxidation until its extracellular concentration reaches the pre-activation levels, preparing the stage for a new glutamatergic event.
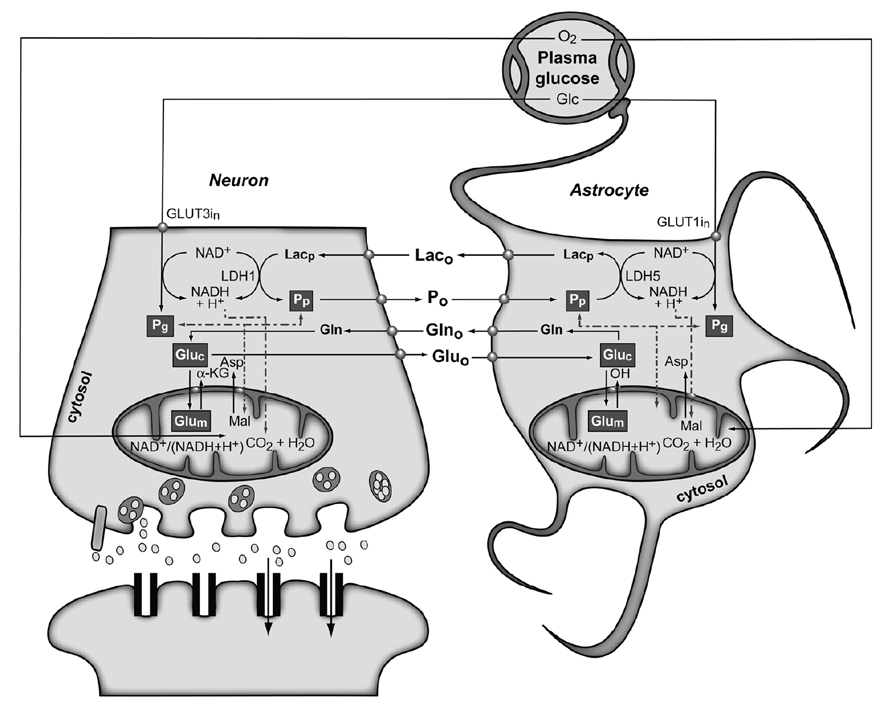
FIGURE 4. The subcellular compartmentation of pyruvate and glutamate and the redox switch/redox coupling hypothesis. Two pools of pyruvate exist in neurons and astrocytes derived from extracellular monocarboxylates (Pp) or glucose (Pg). A lactate/pyruvate redox shuttle is able to transfer continuously lactate from astrocytes to neurons, taking advantage of the kinetics of plasma membrane transporters and lactate dehydrogenase isoenzymes. High cytosolic lactate concentration inhibits neuronal glycolysis at the glyceraldehyde-3-phosphate dehydrogenase step by competition with cytosolic NAD+, favoring the oxidation of extracellular Lac. Neuronal pyruvate is transferred back to the astrocyte to close the transcellular exchange of reducing equivalents. Two α-ketoglutarate/glutamate pools exist in neurons and astrocytes, associated probably to cytosolic and mitochondrial compartments. Exchange of α-ketoglutarate/glutamate between mitochondria and cytosol appears to be slow in the H3 glutamate hydrogen exchange timescale and dependent of the cytosolic and mitochondrial NAD(P)+/NAD(P)H ratios, as determined by the malate–aspartate shuttle. Both glycolysis and oxidative astrocytic metabolism contribute the energy for glutamine production in the astrocytes, indicating that this coupling involves both transcellular and intracellular redox coupling mechanisms that allow the simultaneous operation of glycolysis and oxidation in astrocytes. Asp, aspartate; Glc, glucose; Gln, glutamine; Glu, glutamate; GLUT1 and GLUT3, glutamate transporters 1 and 3; α-KG, α-ketoglutarate; Lac, lactate; LDH1 and LDH5, lactate dehydrogenase 1 and 5; Mal, malate. Reproduced with permission from Rodrigues et al. (2012).
This redox switch/redox coupling hypothesis integrates basically the described experimental findings, both obtained in vivo and in vitro. More specifically, it includes: (i) the simultaneous operation of both astrocytic and neuronal glycolysis and TCA cycles during neuronal activation; (ii) the fact that both astrocytes and neurons may potentially use Glc or Lac as complementary, or even alternative, substrates; this depends on the extracellular redox state and availability; (iii) the stoichiometric or non-stoichiometric coupling of the Glu cycle and Glc uptake; (iv) the intracellular compartmentalization of cytosolic monocarboxylates; and, finally, (v) the intracellular Glu compartmentalization also both in neurons and astrocytes (Cruz et al., 2005; Dienel and Hertz, 2005). The transcellular redox switch/redox coupling proposal mimics the intracellular coupling mechanisms existing between cytosolic glycolysis and the TCA cycle which involves the transfer of reducing equivalents through the inner mitochondrial membrane. During transcellular redox coupling, however, reducing equivalents are reversibly exchanged between neurons and astrocytes in the form of Lac and Pyr (Arco and Satrustegui, 2005; McKenna et al., 2006).
Perspective: Hyperpolarized 13C NMR Approaches
As explained before, one of the most limiting features of NMR is its lack of sensitivity. Therefore, magnetic resonance imaging (MRI) has relied primarily on imaging of water protons. This results from the fact that the SNR ratio of the NMR signal is proportional to the equilibrium polarization between the two proton spin states under thermal equilibrium conditions in an external magnetic field (B0), as well as the proton concentration. Clinical imaging applications have until now been restricted to 1H MRI because the existence of a high concentration of protons in biological tissue is able to counterbalance the inherent low sensitivity. Unfortunately, MR sensitivity of 13C is too low to allow conventional 13C MRI due to the vestigial in vivo abundance of this nucleus and its lower magnetogyric ratio.
Although it is possible to improve the sensitivity using MRI systems at high B0 and extremely low temperatures, a maximum polarization (and corresponding SNR) increase (~103), obtained by cooling down the sample to liquid He temperature at a field strength of 20 T, would not be sufficient for clinical 13C MRI applications. Alternatively, it is possible to improve the sensitivity by transferring polarization from an electron or nuclear spin that has a higher polarization, creating a non-equilibrium distribution of nuclear spins called the hyperpolarized state (Månsson et al., 2006). In this state, the polarization of spins can be increased by a factor of ~105 compared with that in the thermal equilibrium state and independently of the B0 value, leading to a corresponding gain in signal strength for MRI. This allows imaging of nuclei other than protons, namely 13C, and their molecular distribution in vivo can be visualized in a clinically relevant time window (Ardenkjær-Larsen et al., 2003).
The hyperpolarized state is created by an external device followed by rapid administration of the agent to the subject to be imaged. However, the lifetime of the hyperpolarized state is limited by the T1 relaxation time which depends on the chemical structure and environment of the hyperpolarized compound. In the case of 13C, it can range from a few seconds to several minutes, depending on the functional groups where the 13C nucleus is present.
Both parahydrogen-induced polarization (PHIP) and dynamic nuclear polarization (DNP) techniques have been able to hyperpolarize a wide range of organic 13C-labeled substances. As the polarization of electrons is much higher than the 13C nuclear polarization, due to the much larger gyromagnetic ratio of the electron, the DNP approach implies transferring polarization from hyperpolarized electron spins in a solid to the coupled 13C nuclear spins in a doping substance (~3 T and ~1 K; Månsson et al., 2006). Microwave irradiation near the electron resonance frequency transfers the polarization from the unpaired electrons to the 13C nuclei. After reaching an appropriate polarization, the solid is rapidly dissolved and injected with small polarization losses (Ardenkjær-Larsen et al., 2003).
An interesting use of 13C-labeled endogenous compounds is metabolic imaging. Chemical shift imaging (CSI) has been traditionally used to image the cerebral distribution of metabolites from 13C-labeled substances, such as Glc (van der Zijden et al., 2008). However, without using hyperpolarization techniques, such images can only be obtained using long scan times (minutes). Using the previously described hyperpolarization approaches, images of the metabolic processes can be generated in a significant faster time scale (seconds). Endogenous compounds selectively labeled with 13C have been hyperpolarized by the DNP technique, extending substantially the applications of cerebral metabolic imaging. Basically, enzymatic processes can be non-invasively quantified and imaged in vivo using these hyperpolarized 13C-labeled metabolites. The metabolic fate of [1-13C]Pyr in images of tumor-bearing animals injected with hyperpolarized labeled Pyr has been followed using the DNP approach, and allowed mapping the metabolic pattern of labeled Pyr, as well as of Lac and alanine. It was confirmed that gliomas abundantly transform Pyr into Lac through anaerobic glycolysis. Using this strategy, it was shown that exchange of hyperpolarized 13C label between Pyr and Lac could be imaged in tumors (Day et al., 2011). This flux was decreased in tumors receiving treatment undergoing drug-induced cell death. Using the same substrate, fast dynamic spiral CSI and transport modeling were combined to better characterize the bolus, transport, and metabolic effects, separating the metabolites in the cerebral blood volume from the metabolites in the brain tissue. This allowed developing a repeatable non-invasive measurement of regional BBB transport kinetics and regional cerebral Lac levels (Hurd et al., 2010). A novel non-invasive method for imaging tissue pH in vivo was also demonstrated (Gallagher et al., 2008). It was shown that interstitial tumor pH can be imaged in vivo from the ratio of the signal intensities of hyperpolarized bicarbonate (H13CO3-) and 13CO2, after the intravenous injection of hyperpolarized H13CO3-. Additionally, other neurochemical pathways have been exploited using this approach. Conversion of 13C-labeled acetate to 2-oxoglutarate, a key biomolecule connecting metabolism to neuronal activity, was recently shown using the DNP approach, reporting a direct in vivo observation of a TCA cycle intermediate in intact brain (Mishkovsky et al., 2012). The cerebral distribution and metabolism of hyperpolarized 2-keto[1-13C]isocaproate (KIC) has also been described in the normal rat using MR (Butt et al., 2012). Hyperpolarized KIC is metabolized to [1-13C]leucine by branched chain amino acid transaminase, having this enzyme an important role in nitrogen shuttling and glutamate metabolism in the brain. Another group was able to show how sodium 1-13C acetylenedicarboxylate, which after hydrogenation by PASADENA (Parahydrogen and Synthesis Allows Dramatically Enhanced Nuclear Alignment), becomes 13C sodium succinate. Fast in vivo imaging demonstrated that, following carotid arterial injection, the hyperpolarized 13C-succinate appeared in the head and cerebral circulation of normal and tumor-bearing rats (Bhattacharya et al., 2007). Even more recently, the injection of hyperpolarized [U-2H,U-13C]Glc allowed real-time imaging of the glycolytic flux in two non-cerebral murine tumor models in vivo, due to the clear detection of labeled Lac (Rodrigues et al., in press). Low levels of dihydroxyacetone phosphate, 6-phosphogluconate and bicarbonate were also observed, with the latter two synthesized by the pentose phosphate pathway activity. The possible use of labeled Glc in cerebral studies could open a very important avenue in neurochemistry, mainly because of the possibility to investigate a completely new metabolic timeframe with this approach. Therefore, the application of 13C metabolic imaging using hyperpolarized 13C-labeled substrates to neurochemistry is an open field of research.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
Tiago B. Rodrigues was in receipt of an Intra-European Marie Curie (FP7-PEOPLE-2009-IEF, Imaging Lymphoma) and a Long-Term EMBO (EMBO-ALT-1145-2009) fellowships. Anne-Karine Bouzier-Sore is supported by a public grant from the French “Agence Nationale de la Recherche” within the context of the Investments for the Future Program, referenced ANR-10-LABX-57 and named TRAIL. The authors would like to thank Dr. Mikko I. Kettunen and Dr. Alan J. Wright for the critical reading of the manuscript.
Abbreviations
AcCoA, acetyl-CoA; αKG, α-ketoglutarate; ANLS, astrocyte–neuron lactate shuttle; Asp, aspartate; ATP, adenosine triphosphate; B0, external magnetic field; BBB, blood–brain barrier; Cho, choline; CMRglc, cerebral metabolic rates for glucose; CNS, central nervous system; CP, cross-polarization; Cr, creatine; CSI, chemical shift imaging; DNP, dynamic nuclear polarization; FDG, 2-(18F)-deoxyglucose-6-phosphate; fMRI, functional magnetic resonance imaging; GABA, γ-aminobutyric acid, Glc, glucose; Gln, glutamine; Glu, glutamate; GLUT, glucose transporter; GS, glutamine synthetase; Ins, myo-inositol; KIC, 2-ketoisocaproate; Lac, lactate; LDH, lactate dehydrogenase; Mal, malate; MCT, monocarboxylate transporter; MRI, magnetic resonance imaging; NAA, N-acetyl-aspartic acid; NMR, nuclear magnetic resonance; nOe, nuclear Overhauser effect; OAA, oxaloacetate; OAAn, neuronal OAA; PC, pyruvate carboxylase; PCr, phosphocreatine; PDE, phosphodiesters; PDH, pyruvate dehydrogenase; PET, positron emission tomography; PGK, phosphoglycerate kinase; PHIP, parahydrogen-induced polarization; Pi, inorganic phosphate; PME, phosphomonoesters; POCE, proton-observed carbon-edited; PPT, pulsed polarization transfer; Pyr, pyruvate; RF, radiofrequency; SNR, signal-to-noise ratio; Suc, succinate; TCA, tricarboxylic acid; VNT, glutamatergic neurotransmission flux; VTCA, TCA cycle flux; VX, rate of exchange between α-ketoglutarate and glutamate.
References
Alves, P. M., Mckenna, M. C., and Sonnewald, U. (1995). Lactate metabolism in mouse brain astrocytes studied by [13C]NMR spectroscopy. Neuroreport 6, 2201–2204. doi: 10.1097/00001756-199511000-00024
Arco, A. D., and Satrustegui, J. (2005). New mitochondrial carriers: an overview. Cell. Mol. Life Sci. 62, 2204–2227. doi: 10.1007/s00018-005-5197-x
Ardenkjær-Larsen, J. H., Fridlund, B., Gram, A., Hansson, G., Hansson, L., Lerche, M. H., et al. (2003). Increase in signal-to-noise ratio of >10,000 times in liquid-state NMR. Proc. Natl. Acad. Sci. U.S.A. 100, 10158–10163. doi: 10.1073/pnas.1733835100
Bachelard, H. S. (1989). “Measurement of carbohydrates and their derivatives in neuronal tissues,” in Carbohydrates and Energy Metabolism, eds A. A. Boulton, G. B. Baker, and R. F. Butterworth (Clifton, NJ: Humana Press), 133–154.
Berl, S., Lajtha, A., and Waelsch, H. (1961). Amino acid and protein metabolism. VI. Cerebral compartments of glutamic acid metabolism. J. Neurochem. 7, 186–197. doi: 10.1111/j.1471-4159.1961.tb13503.x
Berl, S., Takagaki, G., Clarke, D. D., and Waelsch, H. (1962). Metabolic compartments in vivo. Ammonia and glutamic acid metabolism in brain and liver. J. Biol. Chem. 237, 2562–2569.
Bhattacharya, P., Chekmenev, E. Y., Perman, W. H., Harris, K. C., Lin, A. P., Norton, V. A., et al. (2007). Towards hyperpolarized 13C-succinate imaging of brain cancer. J. Magn. Reson. 186, 150–155. doi: 10.1016/j.jmr.2007.01.017
Bittar, P. G., Charnay, Y., Pellerin, L., Bouras, C., and Magistretti, P. J. (1996). Selective distribution of lactate dehydrogenase isoenzymes in neurons and astrocytes of human brain. J. Cereb. Blood Flow Metab. 16, 1079–1089. doi: 10.1097/00004647-199611000-00001
Boumezbeur, F., Besret, L., Valette, J., Vaufrey, F., Henry, P. G., Slavov, V., et al. (2004). NMR measurement of brain oxidative metabolism in monkeys using 13C-labeled glucose without a 13C radiofrequency channel. Magn. Reson. 52, 33–40. doi: 10.1002/mrm.20129
Boumezbeur, F., Petersen, K. F., Cline, G. W., Mason, G. F., Behar, K. L., Shulman, G. I., et al. (2010). The contribution of blood lactate to brain energy metabolism in humans measured by dynamic 13C nuclear magnetic resonance spectroscopy. J. Neurosci. 30, 13983–13991. doi: 10.1523/JNEUROSCI.2040-10.2010
Bouzier, A. K., Thiaudiere, E., Biran, M., Rouland, R., Canioni, P., and Merle, M. (2000). The metabolism of [3-(13)C]lactate in the rat brain is specific of a pyruvate carboxylase-deprived compartment. J. Neurochem. 75, 480–486. doi: 10.1046/j.1471-4159.2000.0750480.x
Bouzier-Sore, A. K., Voisin, P., Canioni, P., Magistretti, P. J., and Pellerin, L. (2003). Lactate is a preferential oxidative energy substrate over glucose for neurons in culture. J. Cereb. Blood Flow Metab. 23, 1298–1306. doi: 10.1097/01.WCB.0000091761.61714.25
Bröer, S., Bröer, A., Schneider, H. P., Stegen, C., Halestrap, A. P., and Deitmer, J. W. (1999). Characterization of the high-affinity monocarboxylate transporter MCT2 in Xenopus laevis oocytes. Biochem. J. 341, 529–535.doi: 10.1042/0264-6021:3410529
Bröer, S., Rahman, B., Pellegri, G., Pellerin, L., Martin, J. L., Verleysdonk, S., et al. (1997). Comparison of lactate transport in astroglial cells and monocarboxylate transporter 1 (MCT 1) expressing Xenopus laevis oocytes. Expression of two different monocarboxylate transporters in astroglial cells and neurons. J. Biol. Chem. 272, 30096–30102. doi: 10.1074/jbc.272.48.30096
Burtscher, I. M., and Holtas, S. (2001). Proton MR spectroscopy in clinical routine. J. Magn. Reson. Imaging 13, 560–567. doi: 10.1002/jmri.1079
Butt, S. A., Søgaard, L. V., Magnusson, P. O., Lauritzen, M. H., Laustsen, C., Åkeson, P., et al. (2012). Imaging cerebral 2-ketoisocaproate metabolism with hyperpolarized (13)C magnetic resonance spectroscopic imaging. J. Cereb. Blood Flow Metab. 32, 1508–1514. doi: 10.1038/jcbfm.2012.34
Cerdan, S., Kunnecke, B., and Seelig, J. (1990). Cerebral metabolism of [1,2-13C2]acetate as detected by in vivo and in vitro 13C NMR. J. Biol. Chem. 265, 12916–12926.
Cerdan, S., Rodrigues, T. B., Sierra, A., Benito, M., Fonseca, L. L., Fonseca, C. P., et al. (2006). The redox switch/redox coupling hypothesis. Neurochem. Int. 48, 523–530. doi: 10.1016/j.neuint.2005.12.036
Cerdan, S., and Seelig, J. (1990). NMR studies of metabolism. Annu. Rev. Biophys. Biophys. Chem. 19, 43–67. doi: 10.1146/annurev.bb.19.060190.000355
Cerdan, S., Sierra, A., Fonseca, L. L., Ballesteros, P., and Rodrigues, T. B. (2009). The turnover of the H3 deuterons from (2-13C) glutamate and (2-13C) glutamine reveals subcellular trafficking in the brain of partially deuterated rats. J. Neurochem. 109(Suppl. 1), 63–72. doi: 10.1111/j.1471-4159.2009.05962.x
Chih, C.-P., Lipton, P., and Roberts, E. L. Jr. (2001). Do active cerebral neurons really use lactate rather than glucose? Trends Neurosci. 24, 573–578. doi: 10.1016/S0166-2236(00)01920-2
Chih, C. P., and Roberts, E. L. Jr. (2003). Energy substrates for neurons during neural activity: a critical review of the astrocyte–neuron lactate shuttle hypothesis. J. Cereb. Blood Flow Metab. 23, 1263–1281. doi: 10.1097/01.WCB.0000081369.51727.6F
Clark, J. B., and Lai, J. C. K. (1989). “Glycolytic, tricarboxylic acid cycle and related enzymes in brain,” in Carbohydrates and Energy Metabolism, eds A. A. Boulton, G. B. Baker, and R. F. Butterworth (Clifton, NJ: Humana Press), 233–281.
Cruz, F., Villalba, M., Garcia-Espinosa, M. A., Ballesteros, P., Bogonez, E., Satrustegui, J., et al. (2001). Intracellular compartmentation of pyruvate in primary cultures of cortical neurons as detected by (13)C NMR spectroscopy with multiple (13)C labels. J. Neurosci. Res. 66, 771–781. doi: 10.1002/jnr.10048
Cruz, N. F., Lasater, A., Zielke, H. R., and Dienel, G. A. (2005). Activation of astrocytes in brain of conscious rats during acoustic stimulation: acetate utilization in working brain. J. Neurochem. 92, 934–947. doi: 10.1111/j.1471-4159.2004.02935.x
Danbolt, N. C. (2001). Glutamate uptake. Prog. Neurobiol. 65, 1–105. doi: 10.1016/S0301-0082(00)00067-8
Day, S. E., Kettunen, M. I., Cherukuri, M. K., Mitchell, J. B., Lizak, M. J., Morris, H. D., et al. (2011). Detecting response of rat C6 glioma tumors to radiotherapy using hyperpolarized [1-13C]pyruvate and 13C magnetic resonance spectroscopic imaging. Magn. Reson. Med. 65, 557–563.doi: 10.1002/mrm.22698
Deelchand, D. K., Shestov, A. A., Koski, D. M., Ugurbil, K., and Henry, P. G. (2009). Acetate transport and utilization in the rat brain. J. Neurochem. 109(Suppl. 1), 46–54. doi: 10.1111/j.1471-4159.2009.05895.x
Deelchand, D. K., Ugurbil, K., and Henry, P. G. (2006). Investigating brain metabolism at high fields using localized 13C NMR spectroscopy without 1H decoupling. Magn. Reson. Med. 55, 279–286. doi: 10.1002/mrm.20756
de Graaf, R. A. (2005). Theoretical and experimental evaluation of broadband decoupling techniques for in vivo nuclear magnetic resonance spectroscopy. Magn. Reson. Med. 53, 1297–1306. doi: 10.1002/mrm.20507
de Graaf, R. A., Brown, P. B., Mason, G. F., Rothman, D. L., and Behar, K. L. (2003a). Detection of [1,6-13C2]-glucose metabolism in rat brain by in vivo 1H-[13C]-NMR spectroscopy. Magn. Reson. Med. 49, 37–46. doi: 10.1002/mrm.10348
de Graaf, R. A., Mason, G. F., Patel, A. B., Behar, K. L., and Rothman, D. L. (2003b). In vivo 1H-[13C]-NMR spectroscopy of cerebral metabolism. NMR Biomed. 16, 339–357. doi: 10.1002/nbm.847
Dienel, G. A., and Cruz, N. F. (2003). Neighborly interactions of metabolically-activated astrocytes in vivo. Neurochem. Int. 43, 339–354. doi: 10.1016/S0197-0186(03)00021-4
Dienel, G. A., and Hertz, L. (2001). Glucose and lactate metabolism during brain activation. J. Neurosci. Res. 66, 824–838. doi: 10.1002/jnr.10079
Dienel, G. A., and Hertz, L. (2005). Astrocytic contributions to bioenergetics of cerebral ischemia. Glia 50, 362–388. doi: 10.1002/glia.20157
Dobbins, R. L., and Malloy, C. R. (2003). Measuring in-vivo metabolism using nuclear magnetic resonance. Curr. Opin. Clin. Nutr. Metab. Care 6, 501–509. doi: 10.1097/00075197-200309000-00003
Dringen, R., Gebhardt, R., and Hamprecht, B. (1993). Glycogen in astrocytes: possible function as lactate supply for neighboring cells. Brain Res. 623, 208–214. doi: 10.1016/0006-8993(93)91429-V
Duarte, J. M., and Gruetter, R. (2013). Glutamatergic and GABAergic energy metabolism measured in the rat brain by 13C NMR spectroscopy at 14.1 T. J. Neurochem. 126, 579–590. doi: 10.1111/jnc.12333
Eakin, R. T., Morgan, L. O., Gregg, C. T., and Matwiyoff, N. A. (1972). Carbon-13 nuclear magnetic resonance spectroscopy of living cells and their metabolism of a specifically labeled 13C substrate. FEBS Lett. 28, 259–264. doi: 10.1016/0014-5793(72)80726-9
Erecinska, M., and Silver, I. A. (1990). Metabolism and role of glutamate in mammalian brain. Prog. Neurobiol. 35, 245–296. doi: 10.1016/0301-0082(90)90013-7
Ernst, R. R., Bodenhausen, G., and Wokaun, A. (1987). Principles of Nuclear Magnetic Resonance in One and Two Dimensions. Oxford: Clarendon Press/Oxford University Press.
Flott, B., and Seifert, W. (1991). Characterization of glutamate uptake systems in astrocyte primary cultures from rat brain. Glia 4, 293–304. doi: 10.1002/glia.440040307
Gallagher, F. A., Kettunen, M. I., Day, S. E., Hu, D. E., Ardenkjær-Larsen, J. H., Zandt, R., et al. (2008). Magnetic resonance imaging of pH in vivo using hyperpolarized 13C-labelled bicarbonate. Nature 453, 940–943. doi: 10.1038/nature07017
Garcia-Espinosa, M. A., Garcia-Martin, M. L., and Cerdan, S. (2003). Role of glial metabolism in diabetic encephalopathy as detected by high resolution 13C NMR. NMR Biomed. 16, 440–449. doi: 10.1002/nbm.843
Garcia-Espinosa, M. A., Rodrigues, T. B., Sierra, A., Benito, M., Fonseca, C., Gray, H. L., et al. (2004). Cerebral glucose metabolism and the glutamine cycle as detected by in vivo and in vitro 13C NMR spectroscopy. Neurochem. Int. 45, 297–303. doi: 10.1016/j.neuint.2003.08.014
Gjedde, A. (2007). “Coupling of brain function to metabolism: evaluation of energy requirements,” in Handbook of Neurochemistry and Molecular Neurobiology, eds A. Lajtha, G. Gibson, and G. Dienel (New York: Springer), 343–400.
Gruetter, R., Adriany, G., Choi, I. Y., Henry, P. G., Lei, H., and Oz, G. (2003). Localized in vivo 13C NMR spectroscopy of the brain. NMR Biomed. 16, 313–338. doi: 10.1002/nbm.841
Gruetter, R., Seaquist, E. R., and Ugurbil, K. (2001). A mathematical model of compartmentalized neurotransmitter metabolism in the human brain. Am. J. Physiol. Endocrinol. Metab. 281, E100–E112.
Gruetter, R., Ugurbil, K., and Seaquist, E. R. (1998). Steady-state cerebral glucose concentrations and transport in the human brain. J. Neurochem. 70, 397–408. doi: 10.1046/j.1471-4159.1998.70010397.x
Haberg, A., Qu, H., Haraldseth, O., Unsgard, G., and Sonnewald, U. (1998). In vivo injection of [1-13C]glucose and [1,2-13C]acetate combined with ex vivo 13C nuclear magnetic resonance spectroscopy: a novel approach to the study of middle cerebral artery occlusion in the rat. J. Cereb. Blood Flow Metab. 18, 1223–1232. doi: 10.1097/00004647-199811000-00008
Hartmann, S. R., and Hahn, E. L. (1962). Nuclear double resonance in the rotating frame. Phys. Rev. 128, 2042–2053. doi: 10.1103/PhysRev.128.2042
Hassel, B., and Bråthe, A. (2000). Cerebral metabolism of lactate in vivo: evidence for neuronal pyruvate carboxylation. J. Cereb. Blood Flow Metab. 20, 327–336. doi: 10.1097/00004647-200002000-00014
Heeger, D. J., and Ress, D. (2002). What does fMRI tell us about neuronal activity. Nat. Rev. Neurosci. 3, 142–151. doi: 10.1038/nrn730
Henry, P. G., Adriany, G., Deelchand, D., Gruetter, R., Marjanska, M., Oz, G., et al. (2006). In vivo 13C NMR spectroscopy and metabolic modeling in the brain: a practical perspective. Magn. Reson. Imaging 24, 527–539. doi: 10.1016/j.mri.2006.01.003
Henry, P. G., Oz, G., Provencher, S., and Gruetter, R. (2003a). Toward dynamic isotopomer analysis in the rat brain in vivo: automatic quantitation of 13C NMR spectra using LCModel. NMR Biomed. 16, 400–412. doi: 10.1002/nbm.840
Henry, P. G., Tkac, I., and Gruetter, R. (2003b). 1H-localized broadband 13C NMR spectroscopy of the rat brain in vivo at 9.4 T. Magn. Reson. Med. 50, 684–692. doi: 10.1002/mrm.10601
Herholz, K., and Heiss, W. D. (2004). Positron emission tomography in clinical neurology. Mol. Imaging Biol. 6, 239–269. doi: 10.1016/j.mibio.2004.05.002
Hertz, L. (1979). Functional interactions between neurons and astrocytes. I. Turnover and metabolism of putative amino acid transmitters. Prog. Neurobiol. 13, 277–323. doi: 10.1016/0301-0082(79)90018-2
Hertz, L. (2004). The astrocyte–neuron lactate shuttle: a challenge of a challenge. J. Cereb. Blood Flow Metab. 24, 1241–1248. doi: 10.1097/00004647-200411000-00008
Hilberman, M., Subramanian, V. H., Haselgrove, J., Cone, J. B., Egan, J. W., Gyulai, L., et al. (1984). In vivo time-resolved brain phosphorus nuclear magnetic resonance. J. Cereb. Blood Flow Metab. 4, 334–342. doi: 10.1038/jcbfm.1984.50
Huang, Y. H., and Bergles, D. E. (2004). Glutamate transporters bring competition to the synapse. Curr. Opin. Neurobiol. 14, 346–352. doi: 10.1016/j.conb.2004.05.007
Hurd, R. E., Yen, Y. F., Tropp, J., Pfefferbaum, A., Spielman, D. M., and Mayer, D. (2010). Cerebral dynamics and metabolism of hyperpolarized [1-(13)C]pyruvate using time-resolved MR spectroscopic imaging. J. Cereb. Blood Flow Metab. 30, 1734–1741. doi: 10.1038/jcbfm.2010.93
International Human Genome Sequencing Consortium. (2001). Initial sequencing and analysis of the human genome. Nature 409, 860–921. doi: 10.1038/35057062
Jeffrey, F. M., Marin-Valencia, I., Good, L. B., Shestov, A. A., Henry, P. G., Pascual, J. M., et al. (2013). Modeling of brain metabolism and pyruvate compartmentation using 13C NMR in vivo: caution required. J. Cereb. Blood Flow Metab. 33, 1160–1167. doi: 10.1038/jcbfm.2013.67
Klomp, D. W., Renema, W. K., Van Der Graaf, M., De Galan, B. E., Kentgens, A. P., and Heerschap, A. (2006). Sensitivity-enhanced 13C MR spectroscopy of the human brain at 3 Tesla. Magn. Reson. Med. 55, 271–278. doi: 10.1002/mrm.20745
Komatsumoto, S., Nioka, S., Greenberg, J. H., Yoshizaki, K., Subramanian, V. H., Chance, B., et al. (1987). Cerebral energy metabolism measured in vivo by 31P-NMR in middle cerebral artery occlusion in the cat – relation to severity of stroke. J. Cereb. Blood Flow Metab. 7, 557–562. doi: 10.1038/jcbfm.1987.105
Kunnecke, B. (1995). “Application of 13C NMR spectroscopy to metabolic studies on animals,” in Carbon-13 NMR Spectroscopy of Biological Systems, ed. N. Beckman (New York: Academic Press, Inc.), 159–267.
Lapidot, A., and Gopher, A. (1994). Cerebral metabolic compartmentation. Estimation of glucose flux via pyruvate carboxylase/pyruvate dehydrogenase by 13C NMR isotopomer analysis of D-[U-13C]glucose metabolites. J. Biol. Chem. 269, 27198–27208.
Larrabee, M. G. (1995). Lactate metabolism and its effects on glucose metabolism in an excised neural tissue. J. Neurochem. 64, 1734–1741. doi: 10.1046/j.1471-4159.1995.64041734.x
Leino, R. L., Gerhart, D. Z., and Drewes, L. R. (1999). Monocarboxylate transporter (MCT1) abundance in brains of suckling and adult rats: a quantitative electron microscopic immunogold study. Brain Res. Dev. Brain Res. 113, 47–54. doi: 10.1016/S0165-3806(98)00188-6
Månsson, S., Johansson, E., Magnusson, P., Chai, C.-M., Hansson, G., Petersson, J. S., et al. (2006). 13C imaging – a new diagnostic platform. Eur. Radiol. 16, 57–67. doi: 10.1007/s00330-005-2806-x
Mason, G. F., Rothman, D. L., Behar, K. L., and Shulman, R. G. (1992). NMR determination of the TCA cycle rate and alpha-ketoglutarate/glutamate exchange rate in rat brain. J. Cereb. Blood Flow Metab. 12, 434–447. doi: 10.1038/jcbfm.1992.61
Mathiisen, T. M., Lehre, K. P., Danbolt, N. C., and Ottersen, O. P. (2010). The perivascular astroglial sheath provides a complete covering of the brain microvessels: an electron microscopic 3D reconstruction. Glia 58, 1094–1103. doi: 10.1002/glia.20990
McKenna, M. C. (2007). The glutamate–glutamine cycle is not stoichiometric: fates of glutamate in brain. J. Neurosci. Res. 85, 3347–3358. doi: 10.1002/jnr.21444
McKenna, M. C., Waagepetersen, H. S., Schousboe, A., and Sonnewald, U. (2006). Neuronal and astrocytic shuttle mechanisms for cytosolic-mitochondrial transfer of reducing equivalents: current evidence and pharmacological tools. Biochem. Pharmacol. 71, 399–407. doi: 10.1016/j.bcp.2005.10.011
Merboldt, K. D., Bruhn, H., Hanicke, W., Michaelis, T., and Frahm, J. (1992). Decrease of glucose in the human visual cortex during photic stimulation. Magn. Reson. Med. 25, 187–194. doi: 10.1002/mrm.1910250119
Mishkovsky, M., Comment, A., and Gruetter, R. (2012). In vivo detection of brain Krebs cycle intermediate by hyperpolarized magnetic resonance. J. Cereb. Blood Flow Metab. 32, 2108–2113. doi: 10.1038/jcbfm.2012.136
Moore, C. M., Frederick, B. B., and Renshaw, P. F. (1999). Brain biochemistry using magnetic resonance spectroscopy: relevance to psychiatric illness in the elderly. J. Geriatr. Psychiatry Neurol. 12, 107–117. doi: 10.1177/089198879901200304
Morris, P., and Bachelard, H. (2003). Reflections on the application of C-13-MRS to research on brain metabolism. NMR Biomed. 16, 303–312. doi: 10.1002/nbm.844
Mouse Genome Sequencing Consortium. (2002). Initial sequencing and comparative analysis of the mouse genome. Nature 420, 520–562. doi: 10.1038/nature01262
Nicholls, D. (2007). “Bioenergetics,” in Brain Energetics. Integration of Molecular and Cellular Processes, 3rd Edn, eds A. Lajhta, G. Gibson, and G. Dienel (New York: Springer), 3–16.
Nioka, S., Zaman, A., Yoshioka, H., Masumura, M., Miyake, H., Lockard, S., et al. (1991). 31P magnetic resonance spectroscopy study of cerebral metabolism in developing dog brain and its relationship to neuronal function. Dev. Neurosci. 13, 61–68. doi: 10.1159/000112142
Norenberg, M. D., and Martinez-Hernandez, A. (1979). Fine structural localization of glutamine synthetase in astrocytes of rat brain. Brain Res. 161, 303–310. doi: 10.1016/0006-8993(79)90071-4
Okada, Y., and Lipton, P. (2007). “Glucose, oxidative energy metabolism, and neural function in brain slices – glycolysis plays a key role in neural activity,” in Brain Energetics. Integration of Molecular and Cellular Processes, 3rd Edn, eds A. Lajhta, G. Gibson, and G. Dienel (New York: Springer), 17–39.
Patel, A. B., De Graaf, R. A., Mason, G. F., Rothman, D. L., Shulman, R. G., and Behar, K. L. (2005). The contribution of GABA to glutamate/glutamine cycling and energy metabolism in the rat cortex in vivo. Proc. Natl. Acad. Sci. U.S.A. 102, 5588–5593. doi: 10.1073/pnas.0501703102
Patel, A. J., Hunt, A., Gordon, R. D., and Balazs, R. (1982). The activities in different neural cell types of certain enzymes associated with the metabolic compartmentation glutamate. Brain Res. 256, 3–11.
Pellerin, L., Bouzier-Sore, A. K., Aubert, A., Serres, S., Merle, M., Costalat, R., et al. (2007). Activity-dependent regulation of energy metabolism by astrocytes: an update. Glia 55, 1251–1262. doi: 10.1002/glia.20528
Pellerin, L., and Magistretti, P. J. (1994). Glutamate uptake into astrocytes stimulates aerobic glycolysis: a mechanism coupling neuronal activity to glucose utilization. Proc. Natl. Acad. Sci. U.S.A. 91, 10625–10629. doi: 10.1073/pnas.91.22.10625
Pellerin, L., and Magistretti, P. J. (2003). Food for thought: challenging the dogmas. J. Cereb. Blood Flow Metab. 23, 1282–1286. doi: 10.1097/01.WCB.0000096064.12129.3D
Pfeuffer, J., Tkac, I., Choi, I. Y., Merkle, H., Ugurbil, K., Garwood, M., et al. (1999). Localized in vivo 1H NMR detection of neurotransmitter labeling in rat brain during infusion of [1-13C] D-glucose. Magn. Reson. Med. 41, 1077–1083. doi: 10.1002/(SICI)1522-2594(199906)41:6<1077::AID-MRM1>3.0.CO;2-#
Poitry-Yamate, C. L., Poitry, S., and Tsacopoulos, M. (1995). Lactate released by Muller glial cells is metabolized by photoreceptors from mammalian retina. J. Neurosci. 15, 5179–5191.
Price, J. C. (2003). Principles of tracer kinetic analysis. Neuroimaging Clin. N. Am. 13, 689–704. doi: 10.1016/S1052-5149(03)00107-2
Prichard, J., Rothman, D., Novotny, E., Petroff, O., Kuwabara, T., Avison, M., et al. (1991). Lactate rise detected by 1H NMR in human visual cortex during physiologic stimulation. Proc. Natl. Acad. Sci. U.S.A. 88, 5829–5831. doi: 10.1073/pnas.88.13.5829
Prichard, J. W. (1991). What the clinician can learn from MRS lactate measurements. NMR Biomed. 4, 99–102. doi: 10.1002/nbm.1940040212
Provencher, S. W. (1993). Estimation of metabolite concentrations from localized in vivo proton NMR spectra. Magn. Reson. Med. 30, 672–679. doi: 10.1002/mrm.1910300604
Rae, C., Fekete, A., Kashem, M., Nasrallah, F., and Bröer, S. (2012). Metabolism, compartmentation, transport and production of acetate in the cortical brain tissue slice. Neurochem. Res. 37, 2541–2553. doi: 10.1007/s11064-012-0847-5
Ramirez, B. G., Rodrigues, T. B., Violante, I. R., Cruz, F., Fonseca, L. L., Ballesteros, P., et al. (2007). Kinetic properties of the redox switch/redox coupling mechanism as determined in primary cultures of cortical neurons and astrocytes from rat brain. J. Neurosci. Res. 85, 3244–3253. doi: 10.1002/jnr.21386
Rodrigues, T. B., and Cerdán, S. (2005). 13C MRS: an outstanding tool for metabolic studies. Concepts Magn. Reson. Part A 27A, 1–16. doi: 10.1002/cmr.a.20039
Rodrigues, T. B., and Cerdán, S. (2007). “The cerebral tricarboxylic acid cycles,” in Handbook of Neurochemistry and Molecular Neurobiology, eds A. Lajtha, G. Gibson, and G. Dienel (New York: Springer), 63–91.
Rodrigues, T. B., Granado, N., Ortiz, O., Cerdan, S., and Moratalla, R. (2007). Metabolic interactions between glutamatergic and dopaminergic neurotransmitter systems are mediated through D(1) dopamine receptors. J. Neurosci. Res. 85, 3284–3293. doi: 10.1002/jnr.21302
Rodrigues, T. B., Gray, H. L., Benito, M., Garrido, S., Sierra, A., Geraldes, C. F., et al. (2005). Futile cycling of lactate through the plasma membrane of C6 glioma cells as detected by (13C, 2H) NMR. J. Neurosci. Res. 79, 119–127. doi: 10.1002/jnr.20308
Rodrigues, T. B., Lopez-Larrubia, P., and Cerdan, S. (2009). Redox dependence and compartmentation of [13C]pyruvate in the brain of deuterated rats bearing implanted C6 gliomas. J. Neurochem. 109(Suppl. 1), 237–245. doi: 10.1111/j.1471-4159.2009.05935.x
Rodrigues, T. B., Serrao, E. M., Kennedy, B. W. C., Hu, D. E., Kettunen, M. I., and Brindle, K. M. (in press). Magnetic resonance imaging of tumor glycolysis using hyperpolarized 13C-labeled glucose. Nat. Med. doi: 10.1038/nm.3416
Rodrigues, T. B., Sierra, A., Ballesteros, P., and Cerdán, S. (2012). “Pyruvate transport and metabolism in the central nervous system,” in Neural Metabolism In Vivo, eds I.-Y. Choi and R. Gruetter (Berlin: Springer), 715–753.
Rothman, D. L., Behar, K. L., Hetherington, H. P., Den Hollander, J. A., Bendall, M. R., Petroff, O. A., et al. (1985). 1H-observe/13C-decouple spectroscopic measurements of lactate and glutamate in the rat brain in vivo. Proc. Natl. Acad. Sci. U.S.A. 82, 1633–1637. doi: 10.1073/pnas.82.6.1633
Rothman, D. L., Behar, K. L., Hyder, F., and Shulman, R. G. (2003). In vivo NMR studies of the glutamate neurotransmitter flux and neuroenergetics: implications for brain function. Annu. Rev. Physiol. 65, 401–427. doi: 10.1146/annurev.physiol.65.092101.142131
Rothman, D. L., De Feyter, H. M., De Graaf, R. A., Mason, G. F., and Behar, K. L. (2011). 13C MRS studies of neuroenergetics and neurotransmitter cycling in humans. NMR Biomed. 24, 943–957. doi: 10.1002/nbm.1772
Sampol, D., Ostrofet, E., Jobin, M. L., Raffard, G., Sanchez, S., Bouchaud, V., et al. (2013). Glucose and lactate metabolism in the awake and stimulated rat: a (13)C-NMR study. Front. Neuroenergetics 5:5. doi: 10.3389/fnene.2013.00005
Sappey-Marinier, D., Calabrese, G., Fein, G., Hugg, J. W., Biggins, C., and Weiner, M. W. (1992). Effect of photic stimulation on human visual cortex lactate and phosphates using 1H and 31P magnetic resonance spectroscopy. J. Cereb. Blood Flow Metab. 12, 584–592. doi: 10.1038/jcbfm.1992.82
Schousboe, A., and Hertz, L. (1981). Role of astroglial cells in glutamate homeostasis. Adv. Biochem. Psychopharmacol. 27, 103–113. doi: 10.1007/BF03033975
Schousboe, A., Westergaard, N., Waagepetersen, H. S., Larsson, O. M., Bakken, I. J., and Sonnewald, U. (1997). Trafficking between glia and neurons of TCA cycle intermediates and related metabolites. Glia 21, 99–105. doi: 10.1002/(SICI)1098-1136(199709)21:1<99::AID-GLIA11>3.0.CO;2-W
Schurr, A., Dong, W. Q., Reid, K. H., West, C. A., and Rigor, B. M. (1988). Lactic acidosis and recovery of neuronal function following cerebral hypoxia in vitro. Brain Res. 438, 311–314. doi: 10.1016/0006-8993(88)91354-6
Schurr, A., Payne, R. S., Miller, J. J., and Rigor, B. M. (1997). Brain lactate, not glucose, fuels the recovery of synaptic function from hypoxia upon reoxygenation: an in vitro study. Brain Res. 744, 105–111. doi: 10.1016/S0006-8993(96)01106-7
Serres, S., Bezancon, E., Franconi, J. M., and Merle, M. (2004). Ex vivo analysis of lactate and glucose metabolism in the rat brain under different states of depressed activity. J. Biol. Chem. 279, 47881–47889. doi: 10.1074/jbc.M409429200
Serres, S., Bezancon, E., Franconi, J. M., and Merle, M. (2007). Brain pyruvate recycling and peripheral metabolism: an NMR analysis ex vivo of acetate and glucose metabolism in the rat. J. Neurochem. 101, 1428–1440. doi: 10.1111/j.1471-4159.2006.04442.x
Shank, R. P., Bennett, G. S., Freytag, S. O., and Campbell, G. L. (1985). Pyruvate carboxylase: an astrocyte-specific enzyme implicated in the replenishment of amino acid neurotransmitter pools. Brain Res. 329, 364–367. doi: 10.1016/0006-8993(85)90552-9
Shank, R. P., Leo, G. C., and Zielke, H. R. (1993). Cerebral metabolic compartmentation as revealed by nuclear magnetic resonance analysis of D-[1-13C]glucose metabolism. J. Neurochem. 61, 315–323. doi: 10.1111/j.1471-4159.1993.tb03570.x
Shestov, A. A., Valette, J., Deelchand, D. K., Ugurbil, K., and Henry, P. G. (2012). Metabolic modeling of dynamic brain 13C NMR multiplet data: concepts and simulations with a two-compartment neuronal-glial model. Neurochem. Res. 37, 2388–2401. doi: 10.1007/s11064-012-0782-5
Shestov, A. A., Valette, J., Ugurbil, K., and Henry, P. G. (2007). On the reliability of 13C metabolic modeling with two-compartment neuronal-glial models. J. Neurosci. Res. 85, 3294–3303. doi: 10.1002/jnr.21269
Shulman, R. G., Rothman, D. L., Behar, K. L., and Hyder, F. (2004). Energetic basis of brain activity: implications for neuroimaging. Trends Neurosci. 27, 489–495. doi: 10.1016/j.tins.2004.06.005
Sibson, N. R., Dhankhar, A., Mason, G. F., Rothman, D. L., Behar, K. L., and Shulman, R. G. (1998). Stoichiometric coupling of brain glucose metabolism and glutamatergic neuronal activity. Proc. Natl. Acad. Sci. U.S.A. 95, 316–321. doi: 10.1073/pnas.95.1.316
Simpson, I. A., Carruthers, A., and Vannucci, S. J. (2007). Supply and demand in cerebral energy metabolism: the role of nutrient transporters. J. Cereb. Blood Flow Metab. 27, 1766–1791. doi: 10.1038/sj.jcbfm.9600521
Sokoloff, L. (1981). Localization of functional activity in the central nervous system by measurement of glucose utilization with radioactive deoxyglucose. J. Cereb. Blood Flow Metab. 1, 7–36. doi: 10.1038/jcbfm.1981.4
Sokoloff, L. (1989). “Circulation and energy metabolism of the brain,” in Basic Neurochemistry, eds G. Siegel, B. Agranoff, R. W. Albers, and P. Molinoff (New York: Raven Press), 565–590.
Sonnewald, U., and Rae, C. (2010). Pyruvate carboxylation in different model systems studied by 13C MRS. Neurochem. Res. 35, 1916–1921. doi: 10.1007/s11064-010-0257-5
Sonnewald, U., Westergaard, N., Krane, J., Unsgard, G., Petersen, S. B., and Schousboe, A. (1991). First direct demonstration of preferential release of citrate from astrocytes using [13C]NMR spectroscopy of cultured neurons and astrocytes. Neurosci. Lett. 128, 235–239. doi: 10.1016/0304-3940(91)90268-X
Szyperski, T. (1998). 13C-NMR, MS and metabolic flux balancing in biotechnology research. Q. Rev. Biophys. 31, 41–106. doi: 10.1017/S0033583598003412
Tsacopoulos, M., and Magistretti, P. J. (1996). Metabolic coupling between glia and neurons. J. Neurosci. 16, 877–885.
Valette, J., Boumezbeur, F., Hantraye, P., and Lebon, V. (2009). Simplified 13C metabolic modeling for simplified measurements of cerebral TCA cycle rate in vivo. Magn. Reson. Med. 62, 1641–1645. doi: 10.1002/mrm.22160
van der Zijden, J. P., Van Eijsden, P., De Graaf, R. A., and Dijkhuizen, R. M. (2008). 1H/13C MR spectroscopic imaging of regionally specific metabolic alterations after experimental stroke. Brain 131, 2209–2219. doi: 10.1093/brain/awn139
van Eijsden, P., Behar, K. L., Mason, G. F., Braun, K. P., and De Graaf, R. A. (2010). In vivo neurochemical profiling of rat brain by 1H-[13C] NMR spectroscopy: cerebral energetics and glutamatergic/GABAergic neurotransmission. J. Neurochem. 112, 24–33. doi: 10.1111/j.1471-4159.2009.06428.x
Vannucci, S. J., Maher, F., and Simpson, I. A. (1997). Glucose transporter proteins in brain: delivery of glucose to neurons and glia. Glia 21, 2–21. doi: 10.1002/(SICI)1098-1136(199709)21:1<2::AID-GLIA2>3.0.CO;2-C
Voet, D., and Voet, J. G. (1990). “Regulation of the citric acid cycle,” in Biochemistry (Hoboken: John Wiley), 522–527.
Waagepetersen, H. S., Bakken, I. J., Larsson, O. M., Sonnewald, U., and Schousboe, A. (1998). Comparison of lactate and glucose metabolism in cultured neocortical neurons and astrocytes using 13C-NMR spectroscopy. Dev. Neurosci. 20, 310–320. doi: 10.1159/000017326
Waagepetersen, H. S., Sonnewald, U., Larsson, O. M., and Schousboe, A. (2000). A possible role of alanine for ammonia transfer between astrocytes and glutamatergic neurons. J. Neurochem. 75, 471–479. doi: 10.1046/j.1471-4159.2000.0750471.x
Waniewski, R. A., and Martin, D. L. (1986). Exogenous glutamate is metabolized to glutamine and exported by rat primary astrocyte cultures. J. Neurochem. 47, 304–313. doi: 10.1111/j.1471-4159.1986.tb02863.x
Waniewski, R. A., and Martin, D. L. (1998). Preferential utilization of acetate by astrocytes is attributable to transport. J. Neurosci. 18, 5225–5233.
Wiechert, W. (2001). 13C metabolic flux analysis. Metab. Eng. 3, 195–206. doi: 10.1006/mben.2001.0187
Wienhard, K. (2002). Measurement of glucose consumption using [(18)F]fluorodeoxyglucose. Methods 27, 218–225. doi: 10.1016/S1046-2023(02)00077-4
Yang, J., Li, C. Q., and Shen, J. (2005). In vivo detection of cortical GABA turnover from intravenously infused [1-13C]D-glucose. Magn. Reson. Med. 53, 1258–1267. doi: 10.1002/mrm.20473
Yu, A. C., Drejer, J., Hertz, L., and Schousboe, A. (1983). Pyruvate carboxylase activity in primary cultures of astrocytes and neurons. J. Neurochem. 41, 1484–1487. doi: 10.1111/j.1471-4159.1983.tb00849.x
Zwingmann, C., and Leibfritz, D. (2003). Regulation of glial metabolism studied by 13C-NMR. NMR Biomed. 16, 370–399. doi: 10.1002/nbm.850
Keywords: 13C NMR spectroscopy, brain metabolism, neuron, astrocyte, neuroglial coupling, metabolic modeling, hyperpolarized NMR
Citation: Rodrigues TB, Valette J and Bouzier-Sore A-K (2013) 13C NMR spectroscopy applications to brain energy metabolism. Front. Neuroenergetics 5:9. doi: 10.3389/fnene.2013.00009
Received: 31 July 2013; Accepted: 15 November 2013;
Published online: 09 December 2013.
Edited by:
Sebastian Cerdan, Instituto de Investigaciones Biomedicas Alberto Sols, SpainReviewed by:
Sebastian Cerdan, Instituto de Investigaciones Biomedicas Alberto Sols, SpainUrsula Sonnewald, Norwegian University of Science and Technology, Norway
Copyright © 2013 Rodrigues, Valette and Bouzier-Sore. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Tiago B. Rodrigues, Cancer Research UK Cambridge Institute and Department of Biochemistry, University of Cambridge, Robinson Way, Cambridge CB2 0RE, UK e-mail:dGlhZ28ucm9kcmlndWVzQGNydWsuY2FtLmFjLnVr
 Tiago B. Rodrigues
Tiago B. Rodrigues Julien Valette
Julien Valette Anne-Karine Bouzier-Sore
Anne-Karine Bouzier-Sore