1
Department of Electronics, Computer Science and Systems, University of Bologna, Bologna, Italy
2
Department of Neurobiology and Anatomy, Wake Forest University School of Medicine, Winston-Salem, NC, USA
Neurons in the cat superior colliculus (SC) integrate information from different senses to enhance their responses to cross-modal stimuli. These multisensory SC neurons receive multiple converging unisensory inputs from many sources; those received from association cortex are critical for the manifestation of multisensory integration. The mechanisms underlying this characteristic property of SC neurons are not completely understood, but can be clarified with the use of mathematical models and computer simulations. Thus the objective of the current effort was to present a plausible model that can explain the main physiological features of multisensory integration based on the current neurological literature regarding the influences received by SC from cortical and subcortical sources. The model assumes the presence of competitive mechanisms between inputs, nonlinearities in NMDA receptor responses, and provides a priori synaptic weights to mimic the normal responses of SC neurons. As a result, it provides a basis for understanding the dependence of multisensory enhancement on an intact association cortex, and simulates the changes in the SC response that occur during NMDA receptor blockade. Finally, it makes testable predictions about why significant response differences are obtained in multisensory SC neurons when they are confronted with pairs of cross-modal and within-modal stimuli. By postulating plausible biological mechanisms to complement those that are already known, the model provides a basis for understanding how SC neurons are capable of engaging in this remarkable process.
Superior colliculus (SC) neurons integrate inputs they receive from multiple sensory modalities, thereby enhancing and speeding their responses to spatiotemporally coincident cross-modal stimuli (Rowland et al., 2007b
; Stein and Stanford, 2008
). This increases the reliability and accuracy of SC-mediated behavioral responses (Stein et al., 1989
; Gingras et al., 2009
). Because each sense operates independently and transduces a different form of energy, multisensory integration yields more informative products than can be obtained from any single sense (Ernst and Banks, 2002
). The SC is particularly interesting because it receives converging, topographically-aligned unisensory inputs from many subcortical and cortical areas (Edwards et al., 1979
), but inputs from association cortex (AES and rLS in the cat) are requisite for the development (Jiang et al., 2007
), maintenance (Wallace and Stein, 1994
; Jiang et al., 2001
, 2002
; Jiang and Stein, 2003
; Alvarado et al., 2007a
), and expression (Wilkinson et al., 1996
; Jiang et al., 2002
, 2007
) of multisensory integration. When these cortices are inoperative, multisensory SC neurons retain the ability to respond to multiple sensory modalities but lose the ability to integrate their signals. Unfortunately, our understanding of this highly adaptive capacity is limited by our ignorance of the specific biological mechanisms by which it operates.
In an effort to reproduce the observed physiology, multiple models have been proposed to describe multisensory integration in the SC (Anastasio and Patton, 2003
; Patton and Anastasio, 2003
; Knill and Pouget, 2004
; Rowland et al., 2007a
; Ma and Pouget, 2008
; Magosso et al., 2008
; Martin et al., 2009
; Ursino et al., 2009
). While it is commonly assumed that excitatory inputs from different senses converge directly on individual SC neurons, different models suggest different mechanisms by which converging inputs (especially inputs from cortex) alter other signals (Anastasio and Patton, 2003
; Patton and Anastasio, 2003
). Some suggest that integration observed at the single neuron is an emergent property of the SC network itself (Knill and Pouget, 2004
; Ma and Pouget, 2008
; Magosso et al., 2008
; Ursino et al., 2009
). Here we present a model that incorporates both perspectives, while also emphasizing the importance of the cortico-SC projection. The model is informed by the most recent anatomical and physiological data supporting the fundamental hypothesis according to which the activity of the SC is almost completely controlled by cortical areas AES/rLS. It reflects non-AES/rLS inputs only when these areas are inactive. In the model, cortical inputs from different senses facilitate one another, while other non-cortical inputs compete through a winner-take-all (WTA) mechanism. The proposal is consistent with empirical findings that: multisensory integration is not an innate feature of this circuit, its postnatal development is protracted, and it adapts to the statistics of the animal’s experience with cross-modal events. In other words, the cortex “knows” that certain cross-modal cues belong to common events and imposes this knowledge on the SC so that they are integrated. Other cross-modal inputs compete in driving SC-mediated responses.
General Model Structure
We provide a brief introduction to the essential model structure before describing its equations and parameters in explicit detail. Figure 1
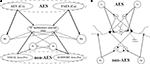
provides a scheme of the model architecture.
Figure 1. The general structure of the network (A) and its physiological counterpart (B). The four projection areas (AES and non-AES) make excitatory connections (arrows) with the SC and with interneurons. The interneurons work in concert to provide two competitive mechanisms based on their inhibitory synapses (dots). Ha and Hv = interneurons receiving auditory (a) or visual (v) input from cortex; Ia, Iv = interneurons receiving auditory and visual inputs from non-AES areas.
Neuron model
The output (“activation”) of each unit in the network is a continuous variable that changes according to both its own internal time constant and its changing inputs. As such, each unit should be interpreted as representing the collective activity of an ensemble of similar neurons on a given trial, whose responses will be compared to a single neuron’s activity averaged over multiple trials in evaluating the model performance. During the simulation the network engages attractor dynamics and settles into a steady state, with the “response magnitude” of each unit to a simulated stimulus corresponding to its output at this time (Magosso et al., 2008
; Ursino et al., 2009
, for more details).
Input neurons
The inputs to the cat SC are simplified and represented as arrays of 100 units grouped into four sensory regions: visual inputs from AES (subregion AEV), auditory inputs from AES (subregion FAES), all non-AES visual inputs (“ascending” visual inputs), and all non-AES auditory inputs (“ascending” auditory inputs). Each input unit is sensitive to restricted but overlapping regions of space, which are topographically organized, so that a simulated stimulus will activate a restricted population of adjacent units. Units within each region exchange connections with one another that, for the sake of simplicity, may be excitatory or inhibitory. Excitatory connections are made with nearby units and inhibitory connections with more distant units.
SC interneurons
The model SC contains four different populations of inhibitory interneurons, each receiving input from a single unit within a specific input region (i.e., there are four separate arrays of 100 interneurons). The inhibitory interneurons receiving input from AES (Hv, Ha in Figure 1
) effectively eliminate the influence of non-AES excitatory inputs when they are active. The inhibitory interneurons receiving input from non-AES sources (Iv, Ia) project to and inhibit one another. This means that, in the absence of AES input, stimulation of more than one non-AES sensory region will invoke a competition so that the stronger input will overwhelm the weaker (i.e., a WTA competition).
SC multisensory neurons
The SC multisensory neurons are modelled as an array of 100 topographically-organized units. Each SC neuron receives weighted input from the four input regions and from one of the members of each of the interneuron populations described above. Inputs derived from the sensory afferent populations are aligned topographically, so that a given SC neuron receives inputs from units in different sensory regions that are sensitive to the same region of space. SC neurons also exchange lateral connections that are locally excitatory but inhibitory at greater distances.
Mathematical Description
Notational conventions
The model contains four sensory input arrays, four arrays of SC interneurons, and a single array of SC multisensory neurons. Each of these nine different arrays are referenced as follows:
Ca (cortical auditory): auditory AES (FAES) neurons:
Cv (cortical visual): visual AES (AEV) neurons;
Na: non-FAES auditory neurons;
Nv: non-AEV visual neurons;
Hv: inhibitory interneurons which receive input from AEV;
Ha: inhibitory interneurons which receive input from FAES;
Ia: inhibitory interneurons which receive input from the non-FAES auditory region;
Iv: inhibitory interneurons which receive input from the non-AEV;
Sm (superior colliculus multisensory): multisensory neurons in the SC.
Single neurons are referenced with superscripts indicating their array and subscripts that indicate their position within that array (i.e., indicating their spatial position/sensitivity). u(t) and z(t) are used to represent the net input and output of a given neuron at time t, respectively. Thus, zih(t) represents the output of a unit receiving net input uih(t) at location i within array h at time t.
Each excitatory connection linking two neurons in different regions, both at the same position i, is denoted 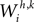 , where the first superscript (h) represents the receiving region and the second superscript (k) the projecting region. Inhibitory connections adopt the same convention but are denoted by a capital K instead of W. The lateral (excitatory or inhibitory) connections linking two neurons in the same region (but with different spatial position) are denoted
, where the first superscript (h) represents the receiving region and the second superscript (k) the projecting region. Inhibitory connections adopt the same convention but are denoted by a capital K instead of W. The lateral (excitatory or inhibitory) connections linking two neurons in the same region (but with different spatial position) are denoted 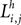 , where h is the region and the subscripts i and j represent the position of the target and projecting unit, respectively.
, where h is the region and the subscripts i and j represent the position of the target and projecting unit, respectively.
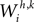 , where the first superscript (h) represents the receiving region and the second superscript (k) the projecting region. Inhibitory connections adopt the same convention but are denoted by a capital K instead of W. The lateral (excitatory or inhibitory) connections linking two neurons in the same region (but with different spatial position) are denoted
, where the first superscript (h) represents the receiving region and the second superscript (k) the projecting region. Inhibitory connections adopt the same convention but are denoted by a capital K instead of W. The lateral (excitatory or inhibitory) connections linking two neurons in the same region (but with different spatial position) are denoted 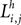 , where h is the region and the subscripts i and j represent the position of the target and projecting unit, respectively.
, where h is the region and the subscripts i and j represent the position of the target and projecting unit, respectively.Unit model
The output of each unit in the network at each simulated moment in time is computed with a first-order dynamics of its input, which is transformed by a sigmoidal function. Specifically, for a unit i in region s with time constant τs receiving net input uis(t) at a moment in time t, its output is determined by the following differential equation (Eq. 1):
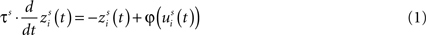
where φ(us(t)) is a sigmoidal function with parameters ϑs (the central point) and ps, which sets the slope at the central point (Eq. 2):

Thus, in this model, unit activity is limited to the range (0 1) as a convention (i.e., all neuronal activities are normalized to a maximum of 1). All units are initialized to an output of zero. The response of the unit for comparison to empirical data is taken as its output when the network reaches steady state in response to an external stimulus (see below).
Unisensory input regions
For simplicity, each unisensory input area is represented by an array of 100 units that receive input from external stimuli as well as from intrinsic lateral connections. External stimuli generate inputs that are functions of space (x) and time (t) to which a particular input area s is sensitive: Is(x,t). The receptive field of a generic unit i in an input area s is defined by a Gaussian function of space having a default maximum amplitude  , center xi, and standard deviation σis:
, center xi, and standard deviation σis:
 , center xi, and standard deviation σis:
, center xi, and standard deviation σis:
As a consequence of Eq. 3, a stimulus presented at a particular position xi maximally excites unit i but can also excite adjacent units. The input an external stimulus provides to a generic unit i in input area s, ris(t), is determined by summing the products of the receptive field and the input stimulus for each spatial location:

Unisensory input units within an area s also receive input through intrinsic lateral connections. The net lateral input,  , is defined by the sum of the products of the weights of the lateral connections and the output of the projecting units for each location:
, is defined by the sum of the products of the weights of the lateral connections and the output of the projecting units for each location:
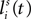 , is defined by the sum of the products of the weights of the lateral connections and the output of the projecting units for each location:
, is defined by the sum of the products of the weights of the lateral connections and the output of the projecting units for each location:
Lateral connections are symmetric and their weights (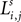 ) are defined by a “Mexican hat” function derived by subtracting an inhibitory Gaussian function (max amplitude =
) are defined by a “Mexican hat” function derived by subtracting an inhibitory Gaussian function (max amplitude = 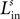 , std =
, std = 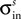 ) from an excitatory one (max amplitude =
) from an excitatory one (max amplitude = 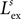 , std =
, std = 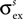 ):
):
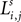 ) are defined by a “Mexican hat” function derived by subtracting an inhibitory Gaussian function (max amplitude =
) are defined by a “Mexican hat” function derived by subtracting an inhibitory Gaussian function (max amplitude = 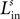 , std =
, std = 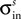 ) from an excitatory one (max amplitude =
) from an excitatory one (max amplitude = 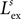 , std =
, std = 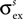 ):
):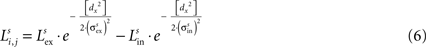
In this equation, dx represents the distance between the projecting and target units. Units at the extreme ends of a linear array potentially might not receive the same number of connections as other units (e.g., there are no units to the “left” of i = 1), which can produce undesired border effects. To avoid this complication, the array is imagined as having a circular structure so that each unit within an area receives the same number of lateral connections:
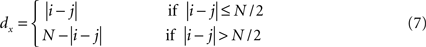
The net input received by a unit at position i in a unisensory input area s, uis(t), is the sum of the inputs from the external stimulus (Eq. 4) and the intrinsic connections (Eq. 5):

The output of these units in each unisensory input area is determined by Eqs 1, 2 and 8 where s is either Ca, Cv, Na, or Nv.
Interneuron populations
The four interneuron populations, each an array of 100 topographically-organized units, receive input from specific sensory input sources and send projections to the SC multisensory neurons and (in some cases) each other. Interneurons that receive input from AES areas have net inputs defined by the product of the activity of the topographically-aligned AES unit and the weight of the connection:

Interneurons that receive input from non-AES areas also receive inhibitory input from each other. Their inputs are computed as follows (K denoting an inhibitory connection):
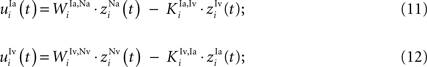
The output of these units is determined by these input equations and Eqs 1 and 2 where s is Ha, Hv, Ia, and Iv, respectively.
SC multisensory units
SC multisensory units receive three types of inputs: weighted excitatory inputs from unisensory input areas (Ca, Cv, Na, Nv), inhibitory inputs from interneuron populations (Ha, Hv, Ia, Iv), and inputs from other SC multisensory neurons via intrinsic lateral connections. The different sensory inputs converging on an SC neuron are assumed to be in spatial register with one another (Meredith and Stein, 1996
; Kadunce et al., 2001
), and here we assume that the inhibitory interneurons have a matching spatial topography.
The direct excitatory inputs from AES are not subject to inhibition and their net inputs are computed as the product of the synaptic weight and the output of the upstream unisensory neuron:

The non-AES inputs are subject to a multiplicative (“shunting”) inhibition (as is the case in GABAa-mediated inhibition, see Koch, 1998
) from all of the interneuron populations with matching location, producing more complicated input equations:
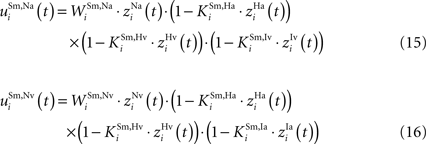
Finally, each SC multisensory neuron also receives lateral input from other SC neurons:

For the sake of simplicity, we assume these connections can be either excitatory or inhibitory, with strengths conforming to a Mexican hat disposition, as in the unisensory input areas (see Eqs 5 and 6 above, where s = Sm).
The net input to a multisensory unit i is computed as the sum of all of these inputs:
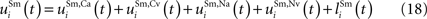
Its output is computed from this input using Eqs 1 and 2 where s = Sm.
Fixed Parameters
The values of all model parameters for the majority of the simulations are shown in Table 1
. To avoid limiting the model to a description of just one particular neuron or experiment, and to enhance its usefulness to the general audience, we fixed some of these parameters for simplicity and (as described in the Results) adjusted others to describe their influence on the unisensory and multisensory response properties of the model. For the most part, the parameters describing the input/output transformations of the units themselves (i.e., in Eqs 1 and 2) are fixed for different populations, while the strengths of connections between different populations and the properties of the external stimulus are varied experimentally.
Table 1. Parameter values.
Fixed unit properties
The time constant (a few milliseconds) is fixed for all units and is consistent with those normally used in deterministic mean-field equations (Ben-Yishai et al., 1995
) and the time constants of SC neurons measured in vivo (Grantyn and Lux, 1988
). For the units in the input areas and the SC multisensory units, the central abscissa of neurons, ϑs, is selected to produce a small amount of baseline activity (i.e., without any external stimulus), and the slope of the sigmoidal relationships, pS, is assigned so that there is a smooth transition from silence to saturation in response to different input magnitudes. For interneuron units, the slope and the central abscissa of the sigmoidal relationships have been assigned so that there is a fast transition from silence to saturation in response to inputs coming from unisensory input areas, but little baseline activity in the absence of any external stimulation. This allows the implementation of a strong competitive mechanism even in the presence of a moderate stimulation. The standard deviation of the visual receptive fields of input units (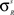 , s = Cv, Nv) has been selected to be approximately 10° in diameter and the standard deviation for the auditory receptive fields (
, s = Cv, Nv) has been selected to be approximately 10° in diameter and the standard deviation for the auditory receptive fields (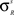 , s = Ca, Na) is selected to be approximately 15° in diameter.
, s = Ca, Na) is selected to be approximately 15° in diameter. 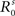 (s = Cv, Nv, Ca, Na) is set to 1 to fix a scale for the external input.
(s = Cv, Nv, Ca, Na) is set to 1 to fix a scale for the external input.
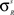 , s = Cv, Nv) has been selected to be approximately 10° in diameter and the standard deviation for the auditory receptive fields (
, s = Cv, Nv) has been selected to be approximately 10° in diameter and the standard deviation for the auditory receptive fields (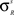 , s = Ca, Na) is selected to be approximately 15° in diameter.
, s = Ca, Na) is selected to be approximately 15° in diameter. 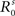 (s = Cv, Nv, Ca, Na) is set to 1 to fix a scale for the external input.
(s = Cv, Nv, Ca, Na) is set to 1 to fix a scale for the external input.Lateral interactions within unisensory input areas
Extant data suggest that the simultaneous presentation of a stimulus in the best area of the SC neuron’s unisensory receptive field with another within-modal stimulus outside the receptive field can suppress the response by as much as 40% (Kadunce et al., 1997
). Furthermore, we found it necessary to set the inhibition strength of these connections sufficiently high to suppress uncontrolled propagation of excitation to the overall area. Finally, an arbitrary decision was made to restrict the parameters of these lateral connections so that the presence of an external stimulus produced an activation bubble of neurons which is approximately equal to the size of the input receptive field. These constraints fixed the values of 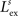
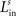 ,
, 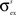 and
and 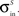 .
.
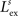
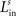 ,
, 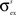 and
and 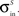 .
.Lateral interactions between SC multisensory neurons
Extant data suggest that two cross-modal stimuli placed within overlapping regions of their respective receptive fields produce enhanced responses (Stein and Meredith, 1993
), while two within-modal stimuli in the same configuration yield no enhancement or even a marginal suppression at the boundary (Alvarado et al., 2007a
,b
). Furthermore, two cross-modal or within-modal stimuli placed far apart (i.e., one inside, another outside the receptive field) cause significant suppression (Kadunce et al., 1997
, 2001
). These observations were used to fix the values of 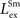
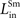 ,
, 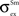 and
and 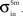 .
.
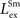
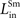 ,
, 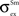 and
and 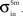 .
.Connections between non-AES inputs and SC multisensory neurons
The parameters of direct connections from the unisensory non-AES input areas to the SC multisensory neurons (i.e., 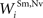 and
and 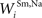 ) were fixed relative to the strengths of the AES-derived connections (see below) so that unisensory responses were 50% depressed when AES was deactivated, as recently reported in (Alvarado et al., 2007a
,b
).
) were fixed relative to the strengths of the AES-derived connections (see below) so that unisensory responses were 50% depressed when AES was deactivated, as recently reported in (Alvarado et al., 2007a
,b
).
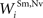 and
and 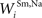 ) were fixed relative to the strengths of the AES-derived connections (see below) so that unisensory responses were 50% depressed when AES was deactivated, as recently reported in (Alvarado et al., 2007a
,b
).
) were fixed relative to the strengths of the AES-derived connections (see below) so that unisensory responses were 50% depressed when AES was deactivated, as recently reported in (Alvarado et al., 2007a
,b
).Connections with and between interneuron units
Connections from unisensory input areas to their topographically-aligned interneuron units (i.e., 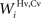 ,
, 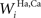 ,
, 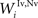 , and
, and 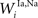 ) were selected so that even moderate levels of activity would drive near-maximum activity in their target interneuron populations. Furthermore, the inhibitory influence of these interneuron populations stimulated by unisensory input areas was set to a maximum value (i.e.,
) were selected so that even moderate levels of activity would drive near-maximum activity in their target interneuron populations. Furthermore, the inhibitory influence of these interneuron populations stimulated by unisensory input areas was set to a maximum value (i.e., 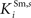 = 1 for s = Hv, Ha, Iv, Ia, see Eqs 15 and 16). Inhibitory connections between interneurons stimulated by non-AES inputs (
= 1 for s = Hv, Ha, Iv, Ia, see Eqs 15 and 16). Inhibitory connections between interneurons stimulated by non-AES inputs (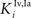 and
and 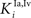 ) were balanced to implement a WTA competition between the two at a given location i in the non-AES route so that, during cortical deactivation, the stronger non-AES unisensory input would overwhelm the weaker and its influence would be seen in the output of the multisensory SC neuron (see Eqs 11 and 12).
) were balanced to implement a WTA competition between the two at a given location i in the non-AES route so that, during cortical deactivation, the stronger non-AES unisensory input would overwhelm the weaker and its influence would be seen in the output of the multisensory SC neuron (see Eqs 11 and 12).
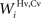 ,
, 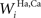 ,
, 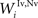 , and
, and 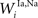 ) were selected so that even moderate levels of activity would drive near-maximum activity in their target interneuron populations. Furthermore, the inhibitory influence of these interneuron populations stimulated by unisensory input areas was set to a maximum value (i.e.,
) were selected so that even moderate levels of activity would drive near-maximum activity in their target interneuron populations. Furthermore, the inhibitory influence of these interneuron populations stimulated by unisensory input areas was set to a maximum value (i.e., 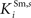 = 1 for s = Hv, Ha, Iv, Ia, see Eqs 15 and 16). Inhibitory connections between interneurons stimulated by non-AES inputs (
= 1 for s = Hv, Ha, Iv, Ia, see Eqs 15 and 16). Inhibitory connections between interneurons stimulated by non-AES inputs (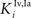 and
and 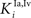 ) were balanced to implement a WTA competition between the two at a given location i in the non-AES route so that, during cortical deactivation, the stronger non-AES unisensory input would overwhelm the weaker and its influence would be seen in the output of the multisensory SC neuron (see Eqs 11 and 12).
) were balanced to implement a WTA competition between the two at a given location i in the non-AES route so that, during cortical deactivation, the stronger non-AES unisensory input would overwhelm the weaker and its influence would be seen in the output of the multisensory SC neuron (see Eqs 11 and 12).After fixing many of the model parameters based on some of the available physiological data in order to codify the model’s essential structure (see above), we now evaluate how the model reproduces other physiological data by adjusting the few remaining free parameters (e.g., stimulus efficacy and the strength of the connections between AES inputs and the SC, i.e., 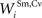 and
and 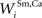 ).
).
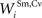 and
and 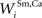 ).
).The Operation of the Intact Model
Dynamic range
An initial set of simulations was performed to verify that the model would replicate the normal behavior of a typical SC neuron in response to different simulated modality-specific and cross-modal stimuli having different efficacies and spatial configurations. In each case the results of the model simulations were compared to those obtained from physiological recordings of individual SC neurons. The first test compared the output of a model neuron to one described in detail by (Perrault et al., 2003
), in which visual and auditory stimuli were presented either individually or simultaneously at the same location in space. For this particular neuron, the visual stimulus evoked a stronger response, and so we assigned a slightly higher value to 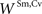 than
than 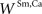 . In this experiment, the efficacy of each modality-specific stimulus was systematically manipulated to explore the response magnitudes evoked by each stimulus or stimulus complex (i.e., the “dynamic range”). The empirical observation was that, as the efficacy of the individual modality-specific stimuli increased, the multisensory response evoked by their combination was larger. However, measured proportionately, the enhancement evoked by their combination was largest when the individual modalities were weakest, otherwise known as the “principle of inverse effectiveness” (Meredith and Stein, 1986a
; Stein and Meredith, 1993
; Wallace et al., 1998
; Perrault et al., 2003
, 2005
; Stanford et al., 2005
; Stein et al., 2009
). These observations are common among SC neurons.
. In this experiment, the efficacy of each modality-specific stimulus was systematically manipulated to explore the response magnitudes evoked by each stimulus or stimulus complex (i.e., the “dynamic range”). The empirical observation was that, as the efficacy of the individual modality-specific stimuli increased, the multisensory response evoked by their combination was larger. However, measured proportionately, the enhancement evoked by their combination was largest when the individual modalities were weakest, otherwise known as the “principle of inverse effectiveness” (Meredith and Stein, 1986a
; Stein and Meredith, 1993
; Wallace et al., 1998
; Perrault et al., 2003
, 2005
; Stanford et al., 2005
; Stein et al., 2009
). These observations are common among SC neurons.
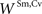 than
than 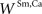 . In this experiment, the efficacy of each modality-specific stimulus was systematically manipulated to explore the response magnitudes evoked by each stimulus or stimulus complex (i.e., the “dynamic range”). The empirical observation was that, as the efficacy of the individual modality-specific stimuli increased, the multisensory response evoked by their combination was larger. However, measured proportionately, the enhancement evoked by their combination was largest when the individual modalities were weakest, otherwise known as the “principle of inverse effectiveness” (Meredith and Stein, 1986a
; Stein and Meredith, 1993
; Wallace et al., 1998
; Perrault et al., 2003
, 2005
; Stanford et al., 2005
; Stein et al., 2009
). These observations are common among SC neurons.
. In this experiment, the efficacy of each modality-specific stimulus was systematically manipulated to explore the response magnitudes evoked by each stimulus or stimulus complex (i.e., the “dynamic range”). The empirical observation was that, as the efficacy of the individual modality-specific stimuli increased, the multisensory response evoked by their combination was larger. However, measured proportionately, the enhancement evoked by their combination was largest when the individual modalities were weakest, otherwise known as the “principle of inverse effectiveness” (Meredith and Stein, 1986a
; Stein and Meredith, 1993
; Wallace et al., 1998
; Perrault et al., 2003
, 2005
; Stanford et al., 2005
; Stein et al., 2009
). These observations are common among SC neurons.As illustrated in Figure 2
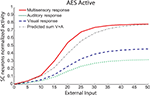
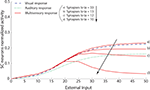
, the model robustly accounts for each result and produces responses very similar to those reported in the empirical literature: (a) the model produces the same pattern of multisensory enhancement; (b) multisensory responses evidence a greater dynamic range than unisensory responses (i.e., a single stimulus cannot lead the SC neuron to saturation) (c) the model transitions from a superadditive computation to an additive computation at higher levels of stimulus effectiveness, and (d) the model reproduces inverse effectiveness. Enhancement in the model is related to the presence of the sigmoidal relationship in SC neurons and the presence of two simultaneous inputs from different sensory modalities that interact synergistically. A small modality-specific input cannot be strong enough to produce a significant response in the sigmoidal function of the SC neuron, but if it is coupled with another weak stimulus, this combination could produce an appreciable result in the sigmoidal curve. This cannot be replicated by two within-modal stimuli because a saturation occurs within the unisensory input layers when two stimuli use the same channel. It should be noted that the “tail” of the response (i.e., at the very lowest levels of effectiveness) is unlikely to represent a statistically significant response from the perspective of the physiologist.
Figure 2. Behavior of the intact network – Dynamic Ranges (DRs). The figure shows the activity of SC neurons in response to different inputs in the case of the intact model (i.e., with AES active and all the membrane receptors working). In all simulations the activity was assessed by stimulating the model with auditory (dotted line), visual (dashed line) and multisensory (solid line) inputs at various intensities. The stimuli were presented in the center of the RF of the observed SC neuron. Note that the model shows a response to a cross-modal stimulation greater than the predicted sum of the two modality-specific responses.
Spatial configuration
Results from physiological experiments have shown that SC multisensory integration is highly dependent on the spatial configuration of the stimuli. Response enhancement is elicited when the cross-modal stimuli are within their respective receptive fields, which overlap one another in space and, thus, the stimuli are in close spatial correspondence. However, within the region of overlap, response magnitude is generally the same regardless of small shifts in spatial displacement (Kadunce et al., 2001
). Multisensory enhancement is not a consequence of simple stimulus “redundancy,” as equivalent results are not obtained when two within-modal stimuli are placed within a receptive field. In the latter case there is marginal or no response enhancement (Alvarado et al., 2008
). Nevertheless, when either a cross-modal or a within-modal stimulus pair is arranged so that one stimulus is within its receptive field and the other is outside its receptive field (so that the stimuli are spatially disparate), there is either no response enhancement or response depression. This spatial principle of SC multisensory integration has been repeatedly demonstrated both physiologically (Meredith and Stein, 1986b
, 1996
; Stein et al., 1993
; Stein and Wallace, 1996
; Wallace et al., 1996
, 1998
; Kadunce et al., 1997
) and behaviorally (Stein et al., 1989
; Wilkinson et al., 1996
; Jiang et al., 2002
; Burnett et al., 2004
).
We conducted simulations in which single or multiple auditory (Figure 3
A) or visual (Figure 3
B) stimuli were presented alone or together in different spatial configurations, and found similar results. In each example, the auditory or visual stimulus was placed in the center of the receptive field. To this stimulus we added another (within- or cross-modal stimulus) at different spatial disparities (sometimes inside, sometimes outside the receptive field). All stimuli were sufficiently robust to evoke strong responses. When cross-modal stimuli were in spatial register (i.e., at 0°) there was substantial (100–150%) response enhancement (compare solid and dotted lines in Figure 3
). When the cross-modal stimuli were spatially-displaced, but still within the overlapping receptive fields, the magnitude of the response enhancement was generally the same. However, when the second stimulus, regardless of modality, was located far outside its receptive field and clearly disparate from the first, it significantly depressed the SC response. Conversely, when two high intensity within-modal stimuli were in spatial register, the response did not change from that obtained by the presentation of a single stimulus (compare dashed and dotted lines in Figure 3
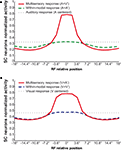
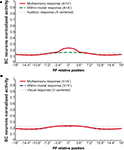
). If the two within-modal stimuli are extremely weak (i.e., the output of the unisensory neurons lies at the very bottom portion of the sigmoidal relationship) one can actually observe some within-modal enhancement, but this remains subadditive. Moreover, results demonstrate that if two stimuli are moved away, enhancement progressively decreases with the distance, until it is converted into a depressed response when one of the two stimuli is outside the RF of the SC neuron. The model explains that the absence of within-modal enhancement is due to the fact that the saturation of unisensory input neurons precludes higher responses. Multiple within-modal stimuli compete with one another within the respective modality-specific input regions for access to the cortico-collicular input channel. On the other hand, lateral inhibitory synapses within the SC are responsible for the cross-modal depression and they, coupled with their counterparts in the unisensory input areas, account for within-modal depression.
Figure 3. Behavior of the intact network – Integration as a function of the position of two stimuli. The figures show the response of the intact network to paired stimuli in different spatial configurations. Simulations are made by stimulating the model with an auditory (A) or a visual (B) stimulus at the center of the RF of the observed SC neuron. The response elicited by this unimodal stimulus (dotted thin lines) is then compared with those produced by coupling either a second stimulus of the same sensory modality (dashed thick lines) or a stimulus of different sensory modality (solid lines) in different positions. The x axis displays the relative position of the second stimulus relative to the center of the RF. x = 0° means that both stimuli are at the center of the RF; increasing x means that the position of the second stimulus is increasingly farther from the RF. Results show: multisensory enhancement in the case of cross-modal stimulation inside the RF irrespective of the position of the two stimuli; no unisensory enhancement within the RF; multisensory and unisensory inhibition in the case of two stimuli far in space.
These observations demonstrate that the model functions quite well in the intact condition. It behaves in the same way as does the biological circuit when dealing with multiple stimuli of different modalities, different spatial configurations and different levels of effectiveness. However, an effective way of testing the functional viability of the model is to examine its reaction to critical conditions and compare it to those of the actual biological circuit. Perhaps the best such condition is the deactivation of AES.
The Operation of the Model Under Simulated Deactivation of AES
Recent evidence suggests that not all inputs to the SC neuron factor equally in determining the multisensory response. Indeed, empirical data reveal that the deactivation of AES eliminates multisensory integration in SC neurons, but does not eliminate their unisensory responses (Wallace and Stein, 1994
; Jiang et al., 2001
; Alvarado et al., 2007a
, 2009
), although recent evidence suggests there is a reduction in their magnitude (Alvarado et al., 2007a
). The same essential observation is made when individual subregions of AES are deactivated (e.g., AEV or FAES, see (Alvarado et al., 2009
)). However, when individual subregions of AES are deactivated, only the responses that are sensitive to inputs from that region are affected (Alvarado et al., 2009
). In the present case, deactivation was simulated by assigning a value of 0 to the appropriate input areas, be they derived from the simulated regions AEV, FAES, or both. This effectively silences the AES-derived input to both multisensory SC neurons and to the inhibitory interneurons.
Dynamic range
When a modality-specific input (e.g., auditory) is simulated in the model during cortical deactivation, a response is generated in the SC target neuron because its matching non-AES input is still active and no longer subject to AES-induced suppression. When the entire AES is deactivated, the unisensory responses are smaller (Figure 4
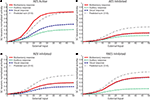
B), with saturation at about 0.1–0.2 (10–20%) of the maximum activity, a finding that parallels the physiology. Also, and more importantly, multisensory enhancement to spatially concordant cross-modal stimuli is lost throughout the dynamic range: the multisensory response is not significantly greater than the response to the more effective of the two component stimuli.
Figure 4. Behavior of the network as function of AES cortex. These figures compare the activity of SC neurons in response to different inputs with AES active (A) or inhibited, fully (B) or only partially [AEV inhibited (C), FAES inhibited (D)]. In all simulations, the activity was assessed by stimulating the model with auditory (dotted line), visual (dashed line) and multisensory (solid line) inputs at various intensities. If the AES is totally inhibited (B), the SC shows no multisensory integration, the unisensory responses are reduced by about 50% and the response to two cross-modal stimuli looks like the stronger unisensory one. If just the AEV is inhibited (C), the SC presents a normal response to an auditory stimulation, but the response to a unimodal visual stimulation is reduced by about 50% compared to that produced when AEV is active. The multisensory response looks like the stronger one (in this case the auditory one). In (D) FAES is inhibited: the SC response to a visual stimulus is unaffected whereas the response to an auditory stimulus is depressed compared with the intact case; multisensory stimulation elicits a response similar to the visual one. The stimuli were presented in the center of the RF of the observed SC neuron. Note the loss of multisensory integration when AES is deactivated even partially. Multisensory integration capability needs both AES subregions active.
When only AEV (Figure 4
C) or FAES (Figure 4
D) was deactivated, the effects on the SC target neuron were modality-specific: deactivation of AEV affected its visual responses but not its auditory responses and the reverse occurred with deactivation of FAES. However, even subregional deactivation eliminated multisensory enhancement. Conceptually, one might describe this result as indicating a “synergy” between the unisensory inputs derived from the subregions of AES (Alvarado et al., 2009
). In the present model this synergy is an emergent property of the circuit. In the complete absence of AES, the influence of non-AES inputs is exposed. Because modality-specific non-AES inputs contact inhibitory interneurons that suppress the influence of other modalities, cross-modal stimuli generate signals that inhibit one another, reaching a stalemate response that represents no enhancement. Thus, in the complete absence of AES, the competition results in a multisensory response no better than the response to one of the component stimuli. However, when either AES subregion is intact, it suppresses the influence of all non-AES inputs through the interneuron population. Thus, when a cross-modal stimulus is presented, one sees only the influence of the stimulus that corresponds to the non-deactivated modality.
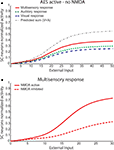
It must be noted that there is always variability in the electrophysiological observations both within and across neurons, and the model can account for those as well. A slightly different behaviour can be obtained assuming a weaker competition. Figure 5
shows results of a sensitivity analysis, in which weaker competition is simulated by progressively reducing the strength of the inhibitory synapses between the interneurons in the non-AES pathways (i.e., parameters 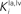 and
and 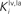 in Eqs 11 and 12) during total cortical deactivation. In the case of strong competition, the SC response to cross-modal stimuli resembles the response to the stronger modality-specific stimulus. Conversely, assuming weak competition, both interneurons Ia and Iv display non-zero activity and inhibit the excitation from the ascending path of the different sensory modality. As a consequence, the SC response to cross-modal stimulation becomes even smaller than the stronger individual unisensory response. This apparently paradoxical result, which is a consequence of the competition in the ascending routes, has been observed empirically (see Figure 9 in Jiang et al., 2001
).
in Eqs 11 and 12) during total cortical deactivation. In the case of strong competition, the SC response to cross-modal stimuli resembles the response to the stronger modality-specific stimulus. Conversely, assuming weak competition, both interneurons Ia and Iv display non-zero activity and inhibit the excitation from the ascending path of the different sensory modality. As a consequence, the SC response to cross-modal stimulation becomes even smaller than the stronger individual unisensory response. This apparently paradoxical result, which is a consequence of the competition in the ascending routes, has been observed empirically (see Figure 9 in Jiang et al., 2001
).
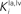 and
and 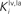 in Eqs 11 and 12) during total cortical deactivation. In the case of strong competition, the SC response to cross-modal stimuli resembles the response to the stronger modality-specific stimulus. Conversely, assuming weak competition, both interneurons Ia and Iv display non-zero activity and inhibit the excitation from the ascending path of the different sensory modality. As a consequence, the SC response to cross-modal stimulation becomes even smaller than the stronger individual unisensory response. This apparently paradoxical result, which is a consequence of the competition in the ascending routes, has been observed empirically (see Figure 9 in Jiang et al., 2001
).
in Eqs 11 and 12) during total cortical deactivation. In the case of strong competition, the SC response to cross-modal stimuli resembles the response to the stronger modality-specific stimulus. Conversely, assuming weak competition, both interneurons Ia and Iv display non-zero activity and inhibit the excitation from the ascending path of the different sensory modality. As a consequence, the SC response to cross-modal stimulation becomes even smaller than the stronger individual unisensory response. This apparently paradoxical result, which is a consequence of the competition in the ascending routes, has been observed empirically (see Figure 9 in Jiang et al., 2001
).Figure 5. Sensitivity analysis of the strength of inhibitory competition in the ascending path. The figure shows the activity of SC neurons (continuous lines) in response to different cross-modal inputs during total AES deactivation (the same case as in Figure 4
B) and assuming a different strength for the inhibitory synapses between the interneurons in the ascending path (i.e., parameters 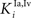 and
and 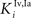 in Eqs 11 and 12). The responses to unimodal (auditory or visual) stimulation are also shown for comparison (dotted and dashed lines, respectively). In the case of strong competition (
in Eqs 11 and 12). The responses to unimodal (auditory or visual) stimulation are also shown for comparison (dotted and dashed lines, respectively). In the case of strong competition (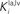 and
and 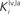 greater than 15), the SC response to cross-modal stimuli resembles the response to the stronger unisensory stimulus. Conversely, assuming weak competition (
greater than 15), the SC response to cross-modal stimuli resembles the response to the stronger unisensory stimulus. Conversely, assuming weak competition (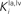 and
and 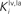 smaller than 12–13) the SC response to cross-modal stimulation becomes smaller than the stronger individual unisensory response.
smaller than 12–13) the SC response to cross-modal stimulation becomes smaller than the stronger individual unisensory response.
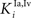 and
and 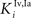 in Eqs 11 and 12). The responses to unimodal (auditory or visual) stimulation are also shown for comparison (dotted and dashed lines, respectively). In the case of strong competition (
in Eqs 11 and 12). The responses to unimodal (auditory or visual) stimulation are also shown for comparison (dotted and dashed lines, respectively). In the case of strong competition (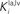 and
and 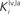 greater than 15), the SC response to cross-modal stimuli resembles the response to the stronger unisensory stimulus. Conversely, assuming weak competition (
greater than 15), the SC response to cross-modal stimuli resembles the response to the stronger unisensory stimulus. Conversely, assuming weak competition (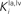 and
and 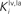 smaller than 12–13) the SC response to cross-modal stimulation becomes smaller than the stronger individual unisensory response.
smaller than 12–13) the SC response to cross-modal stimulation becomes smaller than the stronger individual unisensory response.Spatial configuration
Observations that AES deactivation in the model leads to the prohibition of SC multisensory enhancement prompted additional simulated experiments to investigate whether other multisensory interactions, specifically those leading to depression, would be similarly affected. The empirical results in this case are less clear-cut, but the general observation is that in most cases the deactivation of AES yielded a slight reduction in the amount of depression that was induced when spatially disparate cross-modal stimuli were presented (Jiang et al., 2002
).
Figure 6
shows the response of the model to two simulated stimuli at different spatial disparities (using the same design as in Figure 3
) after deactivation of AES. The enhanced response to spatiotemporally concordant stimuli was lost, as expected (see also Figure 4
), and the overall response was much weaker than in the intact condition. Although cross-modal and within-modal depression were still evident when the stimuli were spatially disparate, cross-modal depression was weaker than in the intact condition. This weak inhibition is due to the presence of lateral inhibition within the SC area. Since SC neurons are weakly activated by non-AES inputs, the competition between them is weakened.
Figure 6. The effect of AES on integration. The same simulations as in Figure 3
performed after inactivation of AES. Results show: (1) a reduction in the SC response both to a unisensory and to a multisensory stimulation; (2) the loss of multisensory enhancement in case of cross-modal stimulation inside the RF: the response of the network looks like the one elicited by the strongest unisensory input; (3) a slight inhibition in case of two stimuli of the same or different sensory modality far in space.
Effect of NMDA Deactivation
One common idea on multisensory integration is that it depends on the temporal coincidence of stimuli from different senses. A component of biological circuits popularly conceptualized as engaged in coincidence detection is the NMDA receptor, which acts as a type of biological AND-gate. There are experimental results that suggest that SC multisensory integration depends on the functional integrity of NMDA receptors, as responses to cross-modal stimuli are reduced during the application of the NMDA receptor antagonist AP5 (Binns and Salt, 1996
). Moreover, responses to visual stimuli are greatly reduced, whereas inconsistent results are reported for responses to auditory stimuli. These results suggest that NMDA receptors play a greater role in the transmission of visual than auditory information in the SC. These observations were incorporated in the model by assuming that deactivation of NMDA receptors greatly reduces the strength of all AEV-SC synapses (see Table 1
) but does not significantly affect FAES-SC synapses. This aspect of the model is purely speculative at present, although it works in reproducing experimental data. This issue deserves a detailed analysis in the laboratory.
The impact of this manipulation is similar to deactivating AEV, and the results of simulations where stimulus intensity has been varied are shown in Figure 7
A. By comparing these results with those in Figure 2
it is apparent that the cross-modal and visual responses are strongly reduced, but the auditory response is only moderately degraded. The reduction of the strength of the synapses from AEV produces a similar effect as deactivating it. Also of note is that the relationship between neuronal activity and stimulus intensity changes from the non-linear one in the intact condition, to a quite linear one after NMDA deactivation (see Figure 7
B). These results agree fairly well with the physiological results reported by (Binns and Salt, 1996
) (see also Rowland et al., 2007a
).
Figure 7. Behavior of the network with NMDA receptors deactivated. The upper panel shows the activity of SC neurons after deactivation of NMDA receptors, in the same simulations as in Figure 2
. Deactivation of NMDA receptors causes a 43% decrease in the unimodal response to visual stimuli, whereas it barely influences the auditory response (−7%). The multisensory response is also significantly reduced, and is lower than the sum of unisensory responses at every input intensity (subadditivity). The lower panel compares the multimodal responses in the intact case and after NMDA deactivation. It is worth noting that the characteristic becomes quite linear after deactivation.
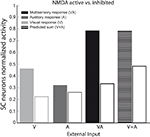
A more direct comparison between model and physiological results is provided in Figure 8
, where the model results are shown for input intensity level close to saturation of the unisensory neurons. The simulated visual response reduction was 43.4% (45 ± 9% in Binns and Salt, 1996
); the auditory response reduction was 6.7% (−4 ± 21% in Binns and Salt, 1996
); the multisensory response reduction was 62.6% (59 ± 7% in Binns and Salt, 1996
); and the sum of the single modality responses was reduced by 27.9% (26 ± 10% in Binns and Salt, 1996
).
Figure 8. Unisensory and multisensory responses with NMDA receptors active or inhibited. Activity was assessed by presenting to the network auditory (dark-grey bars), visual (light-grey bars) and multisensory (black bars) inputs (with a high level of intensity, / = 50), at the center of the RF both with NMDA receptors active (filled bars) and inhibited (empty bars). It is worth noting that the visual response is more affected (50%) by the NMDA inhibition than the auditory one, and the cross-modal response is reduced more than the sum of the unimodal stimuli.
Sensitivity Analysis
To gain a deeper understanding on model behavior, we preformed a sensitivity analysis on some parameter changes. In particular we analyzed (i) the WTA mechanism; (ii) the role of lateral inhibition in the SC and in unisensory areas; iii) the key role played by interneurons. Results can be summarized as follows:
WTA mechanism
The analysis was performed by varying the intensity of the two ascending inputs and the relative strength of the inhibitory synapses linking the interneurons Ia and Iv. Results show that in case of strong competition (as with the basal values reported in Table 1
), only the higher input survives and there is no enhancement. When the competition is weak, both ascending inputs survive and inhibit one another, producing a depressed response. In general, the mechanism is quite robust and works even in the presence of a small unbalance between the two inputs.
Lateral synapses
With the basal value of parameters (Table 1
), lateral inhibition in the SC plays a greater role than lateral inhibition in unisensory areas, for what concerns both cross-modal and within-modal suppression. However, by changing the strength of lateral synapses, different situations can be mimicked (for instance, if stronger lateral inhibition is used in unisensory areas but weaker lateral inhibition in the SC area, one can observe within-modal suppression without cross-modal suppression, as experimentally found in some SC neurons, Kadunce et al., 1997
).
Inhibitory interneurons
The mechanisms realized by means of interneuron populations are robust despite moderate small variations in their parameters. Conversely, if the inputs to inhibitory interneurons Ia and Iv are dramatically reduced the SC exhibits enhancement even in case of AES deactivation. Moreover, if the afferents to interneurons Hv and Ha are dramatically reduced, the model exhibits cross-modal enhancement even in case of subregional AES deactivation (only AEV or only FAES). Both results are clearly in contrast with experimental evidences, emphasizing the critical role played by all inhibitory connections to reproduce the correct behaviour of the SC.
The present network model is able to account for and provide a mechanistic explanation for the major physiological observations pertaining to SC multisensory integration (see review of Stein and Stanford, 2008
). This includes multisensory enhancement and suppression, inverse effectiveness, the effects of selective cortical deactivation, NMDA blockade, and the differing responses and underlying computations that characterize responses to pairs of spatially disparate cross-modal and within-modal stimuli. This was achieved by including a limited number of biologically realistic mechanisms, some of which are known to be in place in this circuit and others of which require physiological verification.
The proposed model presents a new perspective on multisensory integration in the SC. Some extant models have assumed that multisensory integration reflects a synergistic amplification of cross-modal signals at the level of the single neuron (Rowland et al., 2007a
), while others assume that integration is an emergent property based on network dynamics (Patton and Anastasio, 2003
; Magosso et al., 2008
; Ursino et al., 2009
). The former do not incorporate the fact that the individual SC neuron is embedded in a network in which there is the potential for interactions between units that can affect responses, while the latter do not incorporate the fact that different circuit components do not appear to play equal roles in multisensory integration. The present model joins this discussion by merging these two perspectives in an architecture in which multisensory integration is an emergent network property only when certain components of the circuit are engaged.
The basic hypothetical assumption of the model is that in the cat the operation of the SC is, under normal circumstances, almost entirely controlled by the sensory inputs derived from AES and rLS. One of the most important mechanisms included in the model is that of nonlinearity. All neurons exhibit a non-linear characteristic, with lower threshold and upper saturation. Another essential feature of the model is the presence of two competitive mechanisms that are expressed via separate sets of interneurons. One of these mechanisms is initiated by descending inputs from AES that can inhibit the non-AES (“ascending”) inputs, and is necessary to simulate the loss of multisensory enhancement occurring after deactivation of a single AES subregion (e.g., AEV or FAES, see Alvarado et al., 2009
). The second mechanism assumes a strong competition between the two ascending sources, so that the dominant ascending input causes the near complete inhibition of the other in a “Winner Take All” dynamic (WTA). Although empirical support for two competitive mechanisms via two different sets of interneurons is still needed, inhibitory interneurons are common in the SC and have recently been shown to be involved in the AES projection to multisensory neurons (Fuentes-Santamaria et al., 2008
, 2009
). A parallel involving non-AES inputs remains to be determined, but the arrangement predicted by the model is reasonable as it provides the substrate for a competition that would reflect the physiological effects of AES deactivation: loss of multisensory integration and a multisensory response that becomes similar to that evoked by the dominant modality-specific stimulus (Wallace and Stein, 1994
; Jiang et al., 2001
; Alvarado et al., 2007a
, 2009
). WTA dynamics in the ascending path is also hypothetical at present. A more sophisticated “sensory fusion strategy,” able to exploit the presence of cross-modal inputs in spatiotemporal register, may be implemented only in the descending path after incorporating the experience with such correlated sensory input (Stein and Stanford, 2008
).
Actually, although some model assumptions (such as the arrangement of inhibitory synapses, the presence of both additive and shunting inhibition, and the effect of NMDA deactivation) are hypothetical, they are already in common use in neural networks. It is remarkable that this is one of the functions of a model – to bring together what is known and help generate new hypotheses to guide future empirical studies (in this case physiological studies at both extracellular and intracellular levels, and anatomical studies documenting the underlying circuitry).
Despite the successes of the model, it should be understood that in addition to the simplifications and assumptions noted above, the role of rLS in this process was ignored. This was justified by the observation that many SC neurons depend solely on AES, and in others AES appears to be the more important mediator of SC multisensory integration (Jiang et al., 2001
). Given the model’s operational effectiveness, it may be that a parallel rLS-SC circuit exists that can work independent of, or in concert with, the proposed AES-SC circuit. The presence of parallel circuits that have the potential to expand to substitute for one another during early life would be in keeping with physiological observations. Unlike the deleterious effects of disrupting the integrity of either rLS or AES in adults, ablating them individually early in life has no obvious effects on the maturation of SC multisensory integration. Only their combined loss precludes the maturation of this capacity (Jiang et al., 2007
).
A previous model developed by (Rowland et al., 2007a
) also leans heavily on the roles of AES and interneurons. It assumes that multisensory SC neurons receive both direct ascending and descending AES inputs, as well as indirect projections from each of these sources via inhibitory interneurons. A fundamental difference between the two models, however, is that in the (Rowland et al., 2007a
) model converging inputs descending from different sensory subdivisions of AES preferentially target the same electrotonic compartment of the SC target neuron, whereas the two ascending inputs preferentially target different compartments. Since in this model each compartment exerts a squaring function, the descending inputs exhibit a synergistic interaction. This choice allows the different role of descending and ascending inputs to be simulated using a single population of interneurons, whereas the present model assumes two interneuron populations with different inhibitory roles. The advantage of the present strategy is that it can account for the AES deactivation-induced reduction in the unisensory responses of multisensory SC neurons. In addition, assuming a chain of neurons with receptive fields at different positions interacting via lateral synapses (the Mexican hat formation), rather than a single neuron, allows the model to account for response depression with spatially disparate cross-modal (and even within-modal) stimuli. Furthermore, the synaptic configurations in the model are also likely to be highly sensitive to early sensory experience and can serve as the foundation for how these experiences alter the circuit essential for the emergence and maintenance of multisensory integration (Wallace and Stein, 1997
; 2000
, 2001
; Stein, 2005
).
Additional model predictions pertain to the nature of its internal inhibitory dynamics. Inhibitory interactions that lead to multisensory depression are likely to depend on lateral inhibition, a feature expressed in the model via a Mexican hat disposition for synapses within afferent sources of inputs as well as within the SC itself. This assumption can explain the initiation of suppression when cross-modal or within-modal paired stimuli are spatially disparate (Meredith and Stein, 1996
; Kadunce et al., 1997
). Although such an arrangement is well documented in cortex (Rolls and Treves, 1998
), it is less well documented in subcortical structures. Nevertheless, a consequence of this assumption is the model’s prediction that spatially disparate cross-modal and within-modal stimuli would produce response depression even after AES deactivation (see Figure 6
). Although this prediction still requires validation, some support for it already exists. (Jiang and Stein, 2003
) showed that deactivation of AES and rLS severely compromised, but did not eliminate multisensory depression from the population of SC neurons, and only minor effects were noted on unisensory responses (within-modal suppression was not examined). The authors speculated that “… there are several afferent sources that mediate multisensory depression in SC neurons.”
NMDA receptors are thought to play a substantial role in SC multisensory integration (Stein and Meredith, 1993
; Binns and Salt, 1996
; Rowland et al., 2007a
), and potentially do so via a preferential effect on the visual channel (Binns and Salt, 1996
). The effect of instantiating this in the present model was a reduction in synaptic strength of AEV-SC inputs during NMDA blockade that proved effective in simulating the percentage changes in SC responses to modality-specific and cross-modal stimulation, as well as the non-linear to linear shift in the multisensory responses. However, the specificity of the presumptive NMDA influence (one afferent source from one sensory modality) requires empirical validation.
A limitation of the present model is that it does not account for the temporal aspects of multisensory enhancement. More particularly, model dynamics is very rapid: this signifies that two stimuli must occur in very close temporal proximity to interact and induce enhancement or suppressive effects. Conversely, data in the literature suggest the existence of a wider temporal window (about 200 ms) to have multisensory integration (Meredith et al., 1987
; Maruff et al., 1999
; Holmes and Spence, 2005
). In order to improve this aspect, model needs more sophisticated dynamics able to sustain the input for a longer period before its decay.
In conclusion, the incorporation of additional biophysical elements into this model represents a substantial advancement that provides a new appreciation of the complexity of the implementation of multisensory integration in this circuit. The longevity and ultimate utility of this model rely on several aspects. First, the model described here shows the ability to summarily describe, within a unique theoretical structure, the massive physiological observations on SC neurons; thus it may be of value to physiologists to help interpretation of unisensory and multisensory response properties of SC neurons. Second, the model can be manipulated to understand additional properties of this circuit that are already known. For example, the model described here assumes a particular pattern of connectivity between specific populations of neurons and interneurons; however how this architecture may come into being as a consequence of normal maturation and development have yet to be explored. This can be the focus of future research. Moreover, the present model can make testable predictions that can help guide future experiments in order to validate, reject, or modify the main hypotheses. For example, one fundamental assumption of the model is the pivotal role of AES-initiated inhibitory mechanisms in suppressing other tectopetal sensory inputs. A second pivotal hypothesis is the ability of the stronger of these non-AES tectopetal inputs to suppress the weaker of them when AES is rendered non-functional. The role of these inhibitory effects can be tested in an experiment that combined SC infusion of a GABA antagonistic, AES deactivation and SC recording during cross-modal stimulation. The model predicts that under these circumstances, AES deactivation would not preclude SC multisensory integration as is normally the case (Wallace and Stein, 1994
; Jiang et al., 2001
) because the intrinsic SC inhibition that normally block it under these circumstances has been removed. Furthermore, in cases in which only one of the unisensory AES tectopetal input is deactivated (either AEV or FAES) SC multisensory integration would not be eliminated as is normally the case (Alvarado et al., 2009
), because the active AES cortex cannot inhibit all non-AES tectopetal inputs as would be required to preclude multisensory integration.
The authors declare that the research was conducted in absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The research described was supported in part by NIH grants EY016716 (BES) and NS036916 (BES), and a grant from the Wallace Research Foundation (BES).
Fuentes-Santamaria, V., Alvarado, J. C., McHaffie, J. G., and Stein, B. E. (2009). Axon morphologies and convergence patterns of projections from different sensory-specific cortices of the anterior ectosylvian sulcus onto multisensory neurons in the cat superior colliculus. Cereb. Cortex 19, 2902–2915.