- 1 Department of Psychology, University of Oldenburg, Oldenburg, Germany
- 2 Jacobs University Bremen, Bremen, Germany
The spatiotemporal window of integration has become a widely accepted concept in multisensory research: crossmodal information falling within this window is highly likely to be integrated, whereas information falling outside is not. Here we further probe this concept in a reaction time context with redundant crossmodal targets. An infinitely large time window would lead to mandatory integration, a zero-width time window would rule out integration entirely. Making explicit assumptions about the arrival time difference between peripheral sensory processing times triggered by a crossmodal stimulus set, we derive a decision rule that determines an optimal window width as a function of (i) the prior odds in favor of a common multisensory source, (ii) the likelihood of arrival time differences, and (iii) the payoff for making correct or wrong decisions; moreover, we suggest a detailed experimental setup to test the theory. Our approach is in line with the well-established framework for modeling multisensory integration as (nearly) optimal decision making, but none of those studies, to our knowledge, has considered reaction time as observable variable. The theory can easily be extended to reaction times collected under the focused attention paradigm. Possible variants of the theory to account for judgments of crossmodal simultaneity are discussed. Finally, neural underpinnings of the theory in terms of oscillatory responses in primary sensory cortices are hypothesized.
Introduction
Visual–auditory integration manifests itself in different ways, e.g., as an increase of the mean number of impulses of a multisensory neuron relative to unimodal stimulation (Stein and Meredith, 1993 ), acceleration of manual or saccadic reaction time (RT, Diederich and Colonius, 1987 ; Frens et al., 1995 ), effective audiovisual speech integration (van Wassenhove et al., 2007 ), or in improved, or degraded, judgment of temporal order or subjective simultaneity of a bimodal stimulus pair (cf. Zampini et al., 2003 ). Within the multisensory research community, the concept of a temporal window of integration has been well-described over 20 years ago (Meredith et al., 1987 ; Stein and Meredith, 1993 ) and has enjoyed popularity as an important determinant of the dynamics of crossmodal integration both at the neural and behavioral levels of observation (e.g., Lewald et al., 2001 ; Meredith, 2002 ; Lewald and Guski, 2003 ; Spence and Squire, 2003 ; Colonius and Diederich, 2004a ; Wallace et al., 2004 ; Bell et al., 2005 , 2006 ; Navarra et al., 2005 ; Romei et al., 2007 ; Rowland and Stein, 2007 ; Rowland et al., 2007 ; van Wassenhove et al., 2007 ; Musacchia and Schroeder, 2009 ; Powers III et al., 2009 ; Royal et al., 2009 ). On a descriptive level, the time-window hypothesis holds that information from different sensory modalities must not be too far apart in time so that integration into a multisensory perceptual unit may occur. In particular, when a sensory event simultaneously produces both sound and light, we usually do not notice any temporal disparity between the two sensory inputs (within a distance of up to 20–26 m), even though the sound arrives with a delay, a phenomenon sometimes referred to as “temporal ventriloquism” (cf. Morein-Zamir et al., 2003 ; Recanzone, 2003 ; Lewald and Guski, 2004 ). In the area of audiovisual speech perception, it has been observed that auditory speech has to lag behind matching visual speech, i.e., lip movements, by more than 250 ms for the asynchrony to be perceived (Dixon and Spitz, 1980 ; Conrey and Pisoni, 2006 ; van Wassenhove et al., 2007 ). In cat and other animals, a temporal window of integration has been observed in multisensory convergence sites, such as the superior colliculus (SC): enhanced spike responses of multisensory neurons occur when periods of unimodal peak activity overlap within a certain time range (King and Palmer, 1985 ; Meredith et al., 1987 ). In orienting responses to a visual–auditory stimulus complex, acceleration of saccadic RTs has been observed under a multitude of experimental settings within a time window of 150–250 ms (e.g., Frens et al., 1995 ; Corneil et al., 2002 ; Diederich and Colonius, 2004 , 2008a ,b ; Colonius et al., 2009 ; Van Wanrooij et al., 2009 ).
While the ubiquity of the notion of a temporal window is evident, estimates of the range differ widely, ranging from 40 to 600 ms, sometimes even up to 1,500 ms, depending on context. Given that these estimates arise from rather different experimental paradigms, i.e., judgments of temporal order or simultaneity, simple manual or saccadic RT, single-cell recordings, these differences may not be all that surprising. Nevertheless, this observation casts some doubt on the notion of time window proper: Is it simply a metaphor, or does it constitute a unifying concept underlying multisensory integration dynamics?
In this paper, we address this question by considering “time window of integration” from a decision-theoretic point of view. It has been recognized that integrating crossmodal information implies a decision about whether or not two (or more) sensory cues originate from the same event, i.e., have a common cause (Stein and Meredith, 1993 ; Koerding et al., 2007 ). Several research groups have suggested that multisensory integration follows rules based on optimal Bayesian inference procedures, more or less closely (Ernst, 2005 , for a review). Here we extend this approach by determining a temporal window of optimal width: An infinitely large time window will lead to mandatory integration, a zero-width time window will rule out integration entirely. From a decision-making point of view, however, neither case is likely to be optimal in the long run. In a noisy, complex, and potentially hostile environment exhibiting multiple sources of sensory stimulation, the issue of whether or not two given stimuli of different modality arise from a common source may be critical for an organism. For example, in a predator–prey situation, when the potential prey perceives a sudden movement in the dark, it may be vital to recognize whether this is caused by a predator or a harmless wind gust. If the visual information is accompanied by some vocalization from a similar direction, it may be adequate to respond to the potential threat by assuming that the visual and auditory information are caused by the same source, i.e., to perform multisensory integration leading to a speeded escape reaction. On the other hand, in such a rich dynamic environment it may also be disadvantageous, e.g., leading to a depletion of resources, or even hazardous, to routinely combine information associated with sensory events which – in reality – may be entirely independent and unrelated to each other.
Towards an Optimal Time Window of Integration
First, we introduce the basic decision situation for determining a time window of integration. The main part of this paper is a proposal for deriving an optimal estimate of time-window width. We conclude with an illustration of the approach to the time-window-of-integration (TWIN) model introduced in Colonius and Diederich (2004a) and describe an experiment to be conducted to test the viability of this proposal.
The Basic Decision Situation
The basic decision situation just described can be presented in a simplified and schematic manner by the following Table 1 (“payoff matrix”). It defines the gain (or cost) function U associated with the states of nature (C) and the action (I) of audiovisual integration:Variable C indicates whether visual and auditory stimulus information are generated by a common source (C = 1), i.e., an audiovisual event, or by two separate sources (C = 2), i.e., auditory and visual stimuli are unrelated to each other. Variable I indicates whether or not integration occurs (I = 1 or I = 0, respectively). The values U11 and U20 correspond to correct decisions and will in general be assumed to be positive numbers, while U21 and U10, corresponding to incorrect decisions, will be negative. The organism’s task is to balance these costs and benefits of multisensory integration by an appropriate optimizing strategy (cf. Koerding et al., 2007 ).
We assume that a priori probabilities for the events {C = i}i=1,2 exist, with P(C = 1) = 1 − P(C = 2). In general, an optimal strategy may involve many different aspects of the empirical situation, like spatial and temporal contiguity, or more abstract aspects, like semantic relatedness of the information from different modalities (cf. van Attefeldt et al., 2007 ). For example, Sato et al. (2007) take into account both spatial and temporal conditions simulating performance in an audiovisual localization task. Although a more general formulation of our approach is possible, here we limit the analysis to temporal information alone because this suffices for the application of our decision-theoretic setup in the context of the TWIN model (see Application to TWIN Model Framework). In other words, the only perceptual evidence utilized by the organism is the temporal disparity between the “arrival times” of the unimodal signals (to be defined below), sometimes supplemented by information about the identity of the first-terminating modality. Thus, computation of the optimal time window will be based on the prior probability of a common cause and the likelihood of temporal disparities between the unimodal signals. Note that our approach does not claim existence of a high-level decision-making entity contemplating different action alternatives. We only assume that an organism’s behavior can be assessed as being consistent – or not – with an optimal strategy for the time window width.
Redundant Targets: An Experimental Paradigm for Crossmodal Interaction
For concreteness, we outline an experimental paradigm where crossmodal interaction is typically observed. In the redundant target paradigm (sometimes referred to as redundant signals or divided-attention paradigm), stimuli from different modalities are presented simultaneously or with a certain interstimulus interval (ISI), and participants are instructed to respond by pressing a response button as soon as a stimulus is detected, or by a saccadic eye movement away from the fixation point toward the stimulus detected first. Obviously, from the RT measured in a single experimental trial one cannot tell whether or not multisensory integration has occurred in that instance. However, evaluating average response times under invariant experimental conditions permits conclusions about the existence and direction of crossmodal effects. For example, the time to respond in the crossmodal condition is typically faster than in either of the unimodal conditions (e.g., Diederich and Colonius, 1987 , 2008a ,b ; Frens et al., 1995 ).
Introducing the Likelihood Function
For each stimulus presented in a given modality, we introduce a non-negative random variable representing the peripheral processing time (“arrival time,” for short), that is, the time it takes to transmit the stimulus information through a modality-specific sensory channel up to the first site where crossmodal interaction may occur.
Let A, V denote the auditory and visual arrival time, respectively. For the redundant target task, the absolute difference in arrival times, T = |V − A|, is again a non-negative random variable assumed to represent the empirical evidence available to the decision mechanism. For a realization t of T, we define the likelihood function f(t|C), where f denotes the probability mass function or, if it exists, the density function of T given C. The distribution of T will generally depend on the specific ISI value in the experiment but there is no need to make that explicit for now. Using Bayes’ rule, we immediately have the posterior probability of a common cause given the occurrence of an arrival time difference t,
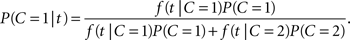
Introducing the likelihood ratio
L(t) = f(t|C = 1)/f(t|C = 2),
implies a well-known identity (e.g., Green and Swets, 1974 ),

between the posterior odds in favor of a common event after evidence t has occurred (left-hand side), and the likelihood ratio times the prior odds in favor of a common event (right-hand side).
Decision Rule: Maximize the Expected Value of U
On each trial, in order to maximize the expected value E[U] of function U in the payoff matrix (Table 1 ), the decision-making mechanism should choose that action alternative (to integrate or not) which contributes, on the average, more to E[U] than the other action alternative (Egan, 1975 ). Given the available empirical evidence, i.e., the specific value t of random arrival time difference T, and assuming knowledge of the prior probability and the likelihood ratio, the expected payoff when integration is performed is
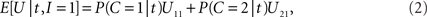
while the expected payoff for not integrating is
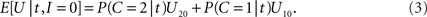
Thus, integration should be performed if and only if E[U|t,I = 1] > E[U|t,I = 0] holds; using the right-hand terms in Eqs 2 and 3 in this inequality gives, after some rearrangement, the following decision rule:

integrate, otherwise do not integrate.”
Using Eq. 1 to replace the posterior odds, the decision rule may be written in terms of the likelihood ratio of the observation t:
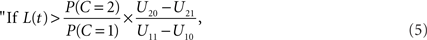
integrate, otherwise do not integrate.”
The Optimal Time Window of Integration
The decision rule just derived implicitly defines a time window of integration that is optimal in the sense of maximizing E[U]: it is simply the set of all values of arrival time differences t satisfying the inequality in the decision rule (Eq. 5).
This set of numbers does not necessarily have the intuitive form of a “window”, i.e., of an interval of the reals. However, if L(t) is a strictly decreasing function, the decision rule can by written equivalently as
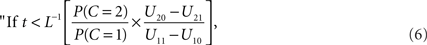
integrate, otherwise do not integrate.”
Setting
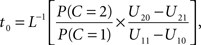
the optimal window is defined by all arrival time differences shorter than t0. Note that, since L−1 is strictly decreasing, increasing the prior probability P(C = 1) for a common cause will make the optimal window larger, as expected.
The window size t0 also depends on the U-values in the payoff matrix as follows. Keeping the (negative) values U21 and U10 fixed, an increase in U11, (the gain of integrating when there is a common cause) will decrease the ratio of U-differences occurring in the decision rule and leads to an increase of optimal window width; on the other hand, an increase in U20 (the gain of not integrating when there is no common cause) will increase the ratio of U-differences leading to a narrowing of the window. Both effects are to be expected, and a symmetric argument holds for the remaining values U21 and U10.
An exact value of t0 can only be determined for explicit values of P(C = 1), the payoff matrix entries, and the likelihood ratio function. A plausible scenario for a decreasing likelihood ratio, illustrated in the example below, is to assume that f(t|C = 1) has a maximum at t = 0 and then decreases, i.e., higher arrival time differences become less likely under a common cause, whereas f(t|C = 2) is constant across all t values that may occur in a trial.
Example: Exponential-Uniform Likelihood Functions
For a common source, we assume an exponential law likelihood,
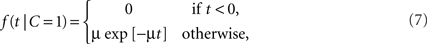
where μ > 0. Thus, the likelihood for a zero arrival time difference is largest (equal to μ) and decreases exponentially. For two separate sources, we assume a uniform law,
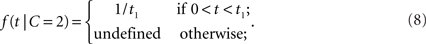
Thus, within the observation interval (0, t1), any arrival time difference occurs with the same likelihood. For 0 ≤ t < t1, the likelihood ratio becomes
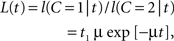
which is a function monotonically decreasing in t. To simplify matters, we set
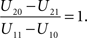
Thus, according to the optimal decision rule, audiovisual integration should be performed if and only if
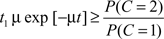
or, equivalently,

Figure 1 illustrates the optimal time window width as a function of the prior probability P(C = 1) and the exponential parameter μ. Increasing prior probability of a common cause implies that the optimal window width increases as well; moreover, for a fixed and not too small prior probability, this optimal width decreases as the likelihood for a zero arrival time difference (μ) becomes larger. The value of t0 will be positive for 1/(1 + t1μ) < P(C = 1) ≤ 1. Moreover, window width will be 0 for P(C = 1) = 1/(1 + t1μ). Thus, in this example and, in fact, whenever the likelihood ratio converges to a non-zero value for t → 0, the prediction is that the window will disappear for a small enough value of the prior, thereby providing a possibly strong model test. (Note that the crossing of the curves is merely an artifact of having to set the observation interval to a finite value.)
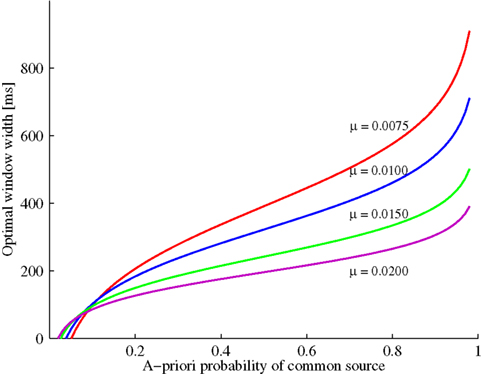
Figure 1. Example (see Example: Exponential-Uniform Likelihood Functions) with exponential-uniform likelihood functions: Optimal window width increases as a function of the a priori probability of a common event. The increase becomes less steep by increasing the likelihood of an arrival time difference of zero (μ).
Application to Twin Model Framework
We demonstrate the proposed approach within the framework of the TWIN model for saccadic RTs (Colonius and Diederich, 2004a ).
The model postulates that a crossmodal stimulus triggers a race mechanism in the very early, peripheral sensory pathways which is then followed by a compound stage of converging subprocesses that comprise neural integration of the input and preparation of a response. Note that this second stage is defined by default: it includes all subsequent, possibly temporally overlapping, processes that are not part of the peripheral processes in the first stage. The central assumption of the model concerns the temporal configuration needed for multisensory integration to occur: Multisensory integration occurs only if the peripheral processes of the first stage all terminate within a given temporal interval, the “time window of integration” (TWIN assumption). Thus, the window acts as a filter determining whether afferent information delivered from different sensory organs is registered close enough in time to trigger multisensory integration. Passing the filter is necessary but not sufficient for crossmodal interaction to occur, the reason being that the amount of interaction may also depend on many other aspects of the stimulus set, like spatial configuration of the stimuli. The amount of crossmodal interaction manifests itself in an increase or decrease of second stage processing time.
Thus, the basic tenet of the TWIN framework is the priority of temporal proximity over any other type of proximity, rather than assuming a joint spatiotemporal window of integration. Although this two-stage assumption clearly oversimplifies matters, it affords quite a number of experimentally testable predictions, many of which have found empirical support in recent studies (cf. Diederich and Colonius, 2007a ,b , 2008a ,b ). It is also important to keep in mind that the two-stage TWIN assumption is not a precondition for applying the optimal time window decision strategy developed in the previous section.
For the redundant target paradigm and a visual–auditory stimulus complex, first stage processing time S1 is defined as
S1 = min(V, A),
with V and A denoting the peripheral visual and auditory arrival times, respectively. According to the TWIN assumption,
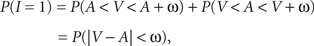
where non-negative constant ω denotes the width of the time window of integration and, as before, I = 1 is the event that multisensory integration occurs. Given the prior probability and (strictly decreasing) likelihood functions, it is now straightforward to implement the optimal decision rule derived above by setting ω equal to the value of t0 as defined in the expression following In Eq. 6.
The computation of the probability of multisensory integration and the definition of first-stage processing time in the crossmodal condition vary somewhat depending on the experimental paradigm (cf., Diederich and Colonius, 2008a ). The TWIN framework makes a number of experimentally testable predictions without having to specify probability distributions for the random variables in the first stage, V and A (cf. Diederich and Colonius, 2007a ,b , 2008a ,b ). However, in order to fit TWIN to observed mean (saccadic) RTs, some probability distributions must be postulated and their parameters estimated. Reasonably good fits have been obtained assuming exponential distributions for these variables (Diederich and Colonius, 2007a ,b , 2008a ,b ). The width of the time window, ω, is another numerical parameter that can be estimated from the data. For example, Diederich et al. (2008) found window width to differ between young and old age groups. Thus, it seems feasible in principle to perform an experiment probing whether subjects are in fact able to adapt their window width to changing environmental conditions in an optimal manner.
A Suggested Empirical Validation
The first goal of an empirical validation of the proposed approach is to show that an appropriate experimental manipulation has an effect on RT that is consistent with the hypothesis of a time window of integration changing its width according to the optimal decision rule derived above. Having demonstrated such a consistency, however, does not prove that the optimal time window is in fact determined by employing the computational principles laid out in Section “Towards an Optimal Time Window of Integration” (for an extended discussion of conceiving Bayesian decision theory as a process model, see Maloney and Mamassian, 2009 ).
We assume that, in a reduced laboratory situation with simple visual and auditory stimuli, spatial contiguity is the main determinant of perceiving visual and auditory information as a common crossmodal event, given a small enough arrival time difference. This premise is supported by the observation that facilitation of (saccadic) RT is maximal when visual and auditory stimuli appear at the same position in space and that it decreases, or even turns into inhibition, when spatial distance increases (Frens et al., 1995 ; Corneil and Munoz, 1996 ; Colonius and Arndt, 2001 ; Whitchurch and Takahashi, 2006 ). Obviously, this scheme would not work in a (localization) task where a joint spatiotemporal window would be most plausible.
This suggests using a simple setup with one visual and one auditory stimulus appearing at a horizontal position to the left or right of the fixation point. The stimuli either appear at the same position (ipsilateral condition, for common event) or at opposite positions (contralateral condition, for separate events). Variables that can be controlled for within an experimental block, or across multiple blocks, are the ISI between visual and auditory stimulus and the frequency of ipsilateral vs. contralateral presentations, randomized with respect to laterality. According to the proposed decision rule, there are three factors by which one can manipulate the optimal window width: (i) the prior odds in favor of a common event, (ii) the likelihood ratio, and (iii) the payoff matrix. We consider each in turn.
Prior Odds
In this setup, a common event, C = 1, corresponds to the visual and auditory stimulus being presented ipsilaterally, left or right of fixation point. Thus, prior odds in favor of a common event are easily manipulated by changing the relative frequency of ipsilateral vs. contralateral presentations. Keeping all other conditions in the setup invariant, the prediction is that, e.g., prior odds of 4:1 in favor of a common event within a session should lead to a wider window of integration, entailing faster mean RTs, than prior odds not favoring either type of event. If, however, the odds for a common event are approaching 0, it may be difficult to find evidence that integration is getting ruled out entirely.
Likelihood Ratio
Arrival time differences are non-observable entities. Nevertheless, one can indirectly manipulate their distribution by changing the ISI: large ISI values should generate, on average, large arrival time differences and this will have a discernable effect as long as the variability of the arrival times is not too large. In the above example of exponential-uniform likelihood functions (see Example: Exponential-Uniform Likelihood Functions) for the arrival time differences, the likelihood ratio L(t) in favor of integration was large for small values of arrival time difference t and decreased with increasing t. One possible manipulation would be to reverse this relation by more frequently presenting ipsilateral stimuli with large ISIs. The non-trivial prediction is that increasing the likelihood for large arrival time differences will lead to a larger window of integration and, thereby, to faster reactions. This prediction has in fact been confirmed in Navarra et al. (2005) , albeit for a temporal order judgment (TOJ) task. Monitoring asynchronous audiovisual speech participants required a longer interval between the auditory and visual stimuli in order to perceive their temporal order correctly, suggesting a widening of the temporal window for audiovisual integration, presumably as a consequence of increasing the likelihood for non-zero arrival time differences under a common cause (for TOJ tasks, see Discussion).
Payoff Matrix
Increasing the gains for integrating visual and auditory information when they derive from a common event, and/or decreasing the costs when they don’t, should lead to a larger window of integration and, thus, to shorter average RTs. This can be achieved in the above setting through appropriate instruction, using different response deadlines and reward settings.
An important caveat in planning and evaluating empirical validation of the time window hypothesis concerns the plasticity of its width. It is not yet clear how much stimulus exposition is needed to establish, e.g., the prior probability of a common event, and how quickly changes in the experimental conditions will affect the setting of the time window width. We are not aware of any relevant findings in the realm of RTs, but recent results on the perception of audiovisual simultaneity suggest a high degree of flexibility in multisensory temporal processing (Vroomen et al., 2004 ; Keetels and Vroomen, 2007 ; Powers III et al., 2009 ; Roseboom et al., 2009 ).
Discussion
The spatiotemporal window of integration has become a widely accepted concept in multisensory research: crossmodal information falling within this window is (highly likely to be) integrated, whereas information falling outside is not (e.g., Meredith et al., 1987 ; Meredith, 2002 ; Colonius and Diederich, 2004a ; Powers III et al., 2009 ). The aim of this paper was to further probe this idea in a RT setting. Making explicit assumptions about the arrival time difference between peripheral sensory processing times triggered by a crossmodal stimulus set, we derive a decision rule that determines an optimal window width as a function of (i) the prior odds in favor of a common multisensory source, (ii) the likelihood of arrival time differences, and (iii) the payoff for making correct or wrong decisions. Thus, our approach is in line with the – by now – well-established framework for modeling multisensory integration as (nearly) optimal decision making (e.g., Anastasio et al., 2000 ; Ernst and Banks, 2002 ; Hillis et al., 2002 ; Battaglia et al., 2003 ; Alais and Burr, 2004 ; Colonius and Diederich, 2004b ; Wallace et al., 2004 ; Shams et al., 2005 ; Roach et al., 2006 ; Sato et al., 2007 ; Beierholm et al., 2008 ; Ma and Pouget, 2008 ; Di Luca et al., 2009 ). However, to our knowledge, none of these studies has considered RT as observable variable.
The line of investigation suggested here is not limited to the redundant targets paradigm but can easily be extended to the focused attention paradigm where subjects are instructed to only respond to stimuli from a target modality and to ignore stimuli from another, non-target modality (Corneil et al., 2002 ; Hairston et al., 2003 ; Diederich and Colonius, 2008a ; Van Wanrooij et al., 2009 ). In this case, arrival time differences can take on either positive or negative values depending on which modality is registered first, and the likelihood function must be defined both at the left and right side of the zero point of simultaneity. A straightforward and computationally simple extension of the exponential-uniform example is to replace the exponential by a – possibly asymmetric – Laplace distribution (e.g., Kotz, et al., 2001 ).
The notion of a time window as considered here must be distinguished from an apparently closely related concept, the “time window of simultaneity.” The latter refers to the maximum time interval between two stimuli that leads to a subject’s judgment of perceiving the two stimuli as “simultaneous” or, in the case of TOJs, i.e., “stimulus x occurs before stimulus y”, an appropriate definition in terms of threshold is available. Although direct estimates of the time window of simultaneity derived from such judgments tasks with stimuli from different modalities often come close to those observed in comparable RT experiments (e.g., Burr et al., 2009 ; Roseboom et al., 2009 ), it has been argued that, since very different demands are placed on the observer by judgments of simultaneity (or temporal order) compared to the RT task, the underlying mechanisms may also be substantially different (cf. Sternberg and Knoll, 1973 ; for discussions, see Tappe et al., 1994 ; Neumann and Niepel, 2004 ). For example, in the saccadic RT task participants are encouraged to respond as quickly as possible after a stimulus has been presented but are also asked to avoid anticipatory responses or false alarms. In the judgment tasks, no such time pressure exists and false alarms may not even be definable. Nevertheless, it has recently been shown by Miller and Schwarz (2006) that one can account for dissociations of RT and TOJ by a common quantitative model assuming different, possibly optimal criterion settings. Therefore, we hypothesize that an extension of our decision-theoretic approach to describe an optimal time window of simultaneity for stimuli from different modalities should be feasible, and this issue certainly requires further scrutiny.
Results on the neural underpinnings of the time window of integration are, as yet, rather scarce. A promising direction has been taken by Rowland and colleagues (Rowland et al., 2007 ; Rowland and Stein, 2008 ). The classic way of assessing multisensory response enhancement by the change in the mean number of impulses over the entire duration of the response (of a single neuron) is a useful overall measure, but it is insensitive to the timing of the multisensory interactions. Therefore, they developed methods to obtain, and compare, the temporal profile of the response to uni- and crossmodal stimulation. For multisensory neurons in the deep layers of SC, they found that the minimum multisensory response latency was shorter than the minimum unisensory response latency. This initial response enhancement (IRE), in the first 40 ms of the response, was typically superadditive and may have a more or less direct effect on reaction speed observed in behavioral experiments. What remains to be shown, however, is whether IRE generalizes to a situation where the unimodal inputs do not arrive at the neuron very close in time and, more generally, how these properties at the individual neuron level can be combined – under possible cortical influences – to generate the time window behavior observed in behavioral experiments.
Given the growing support of the hypothesis that coherence of oscillatory responses at the level of primary sensory cortices may play a crucial role in multisensory processing (Lakatos et al., 2007 ; Senkowski et al., 2008 ; Chandrasekaran and Ghazanfar, 2009 ), a hypothetical relation between window width and oscillatory activity has recently been derived by Lakatos, Schroeder, and colleagues from certain rules about neuronal oscillations (see Schroeder et al., 2008 , pp. 107–108 for a more complete description): (1) neuronal oscillations reflect synchronized fluctuation of a local neuronal ensemble between high and low excitability states, i.e., “ideal” and “worst” phases for stimulus processing; (2) “if two stimuli occur with a reasonably predictable lag, the first stimulus can reset an oscillation to its ideal phase and thus enhance the response to the second stimulus” (Schroeder et al., 2008 ); in particular, attended stimuli in one sensory modality may reset the phase of ongoing oscillations in primary cortices not only within that modality but also within another modality (see Lakatos et al., 2009 ); (3) oscillatory phase modulates subsequent stimulus processing: “…after reset, inputs that arrive within the ideal (high-excitability) phase evoke amplified responses, whereas the responses to inputs that arrive slightly later during the worst phase are suppressed” (Lakatos et al., 2009 ); (4) oscillations exist at different frequencies, from below 1 Hz to over 200 Hz and tend to be phase-amplitude coupled in a hierarchical fashion (Lakatos et al., 2005 ). To summarize, if one can identify the phase an oscillations is reset to by, say a visual stimulus, and its frequency, then one can in principle predict when a temporal window of high excitability (or low excitability) will occur (cf. Schroeder et al., 2008 , p. 427). The different oscillation frequencies in lower and higher cortical structures may in fact contribute to the multitude of different window widths that have been observed in behavioral studies. Although the behavioral consequences of these oscillatory mechanism and their relation to optimal decision-making principles remain speculative at this point, these neurophysiological findings are intriguing and suggest a variety of experimental studies of crossmodal behavior.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This research is supported by grant SFB/TR31 (Project B4) from Deutsche Forschungsgemeinschaft (DFG) to Hans Colonius and by a grant from NOWETAS Foundation to Hans Colonius and Adele Diederich. We thank the reviewers for very helpful comments and suggestions.
References
Alais, D., and Burr, D. (2004). The ventriloquist effect results from near-optimal bimodal integration. Curr. Biol. 14, 257–262.
Anastasio, T. J., Patton, P. E., and Belkacem-Boussaid, K. (2000). Using Bayes’ rule to model multisensory enhancement in the superior colliculus. Neural Comput. 12, 1165–1187.
Battaglia, P. W., Jacobs, R. A., and Aslin, R. N. (2003). Bayesian integration of visual and auditory signals for spatial localization. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 20, 1391–1397.
Beierholm, U., Koerding, K., Shams, L., and Ma, W. J. (2008). Comparing Bayesian models for multisensory cue combination without mandatory integration. Adv. Neural Inf. Process. Syst. 20, 81–88.
Bell, A. H., Meredith, A., Van Opstal, A. J., and Munoz, D. P. (2005). Crossmodal integration in the primate superior colliculus underlying the preparation and initiation of saccadic eye movements. J. Neurophysiol. 93, 3659–3673.
Bell, A. H., Meredith, A., Van Opstal, A. J., and Munoz, D. P. (2006). Stimulus intensity modifies saccadic reaction time and visual response latency in the superior colliculus. Exp. Brain Res. 174, 53–59.
Burr, D., Silva, O., Cicchini, G. M., Banks, M., and Morrone, M. C. (2009). Temporal mechanisms of multimodal binding. Proc. R. Soc. Lond., B, Biol. Sci. 276, 1761–1769.
Chandrasekaran, C., and Ghazanfar, A. A. (2009). Different neural frequency bands integrate faces and voices differently in the superior temporal sulcus. J. Neurophysiol. 101, 773–788.
Colonius. H., and Arndt, P. (2001). A two-stage model for visual–auditory interaction in saccadic latencies. Percept. Psychophys. 63, 126–147.
Colonius, H., and Diederich, A. (2004a). Multisensory interaction in saccadic reaction time: a time-window-of-integration model. J. Cogn. Neurosci. 16, 1000–1009
Colonius, H., and Diederich, A. (2004b). Why aren’t all deep superior colliculus neurons multisensory? A Bayes’ Ratio Analysis. Cogn. Affect. Behav. Neurosci. 4, 344–353.
Colonius, H., Diederich, A., and Steenken, R. (2009). Time-window-of-integration (TWIN) model for saccadic reaction time: effect of auditory masker level on visual–auditory spatial interaction in elevation. Brain Topogr. 21, 177–184.
Conrey, B., and Pisoni, D. B. (2006). Auditory–visual speech perception and synchrony detection for speech and nonspeech signals. J. Acoust. Soc. Am. 119, 4065–4073.
Corneil, B. D., and Munoz, D. P. (1996). The influence of auditory and visual distractors on human orienting gaze shifts. J. Neurosci. 16, 8193–8207.
Corneil, B. D., Van Wanrooij, M., Munoz, D. P., and Van Opstal, A. J. (2002). Auditory–visual interactions subserving goal-directed saccades in a complex scene. J. Neurophysiol. 88, 438–454.
Diederich, A., and Colonius, H. (1987). Intersensory facilitation in the motor component? A reaction time analysis. Psychol. Res. 49, 23–29.
Diederich, A., and Colonius, H. (2004). “Modeling the time course of multisensory interaction in manual and saccadic responses,” in Handbook of Multisensory Processes, eds G. Calvert, C. Spence and B. E. Stein (Cambridge, MA: MIT Press), 395–408.
Diederich, A., and Colonius, H. (2007a). Why two “distractors” are better then one: modeling the effect on non-target auditory and tactile stimuli on visual saccadic reaction time. Exp. Brain Res. 179, 43–54.
Diederich, A., and Colonius, H. (2007b). Modeling spatial effects in visual-tactile saccadic reaction time. Percept. Psychophys. 69, 56–67.
Diederich, A., and Colonius, H. (2008a). Crossmodal interaction in saccadic reaction time: separating multisensory from warning effects in the time window of integration model. Exp. Brain Res. 186, 1–22.
Diederich, A., and Colonius, H. (2008b). When a high-intensity “distractor” is better then a low-intensity one: modeling the effect of an auditory or tactile nontarget stimulus on visual saccadic reaction time. Brain Res. 1242, 219–230.
Diederich, A., Colonius, H., and Schomburg, A. (2008). Assessing age-related multisensory enhancement with the time-window-of-integration model. Neuropsychologia 46, 2556–2562.
Di Luca, M., Machulla, T. K., and Ernst, M. O. (2009). Recalibration of multisensory simultaneity: cross-modal transfer coincides with a change in perceptual latency. J. Vision 9, 1–16.
Dixon, N. F., and Spitz, L. (1980). The detection of auditory visual desynchrony. Perception 9, 719–721.
Ernst, M. O. (2005). “A Bayesian view on multimodal cue integration,” in Human Body Perception From the Inside Out, eds G. Knoblich, I. Thornton, M. Grosjean and M. Shiffrar (New York, NY: Oxford University Press), 105–131.
Ernst, M. O., and Banks, M. S. (2002). Humans integrate visual and haptic information in a statistically optimal fashion. Nature 415, 429–433.
Frens, M. A., Van Opstal, A. J., and Van der Willigen, R. F. (1995). Spatial and temporal factors determine auditory–visual interactions in human saccadic eye movements. Percept. Psychophys. 57, 802–816.
Green, D. M., and Swets, J. A. (1974). Signal Detection Theory and Psychophysics.Oxford: Robert E. Krieger.
Hairston, W. D., Wallace, M. T., Vaughan, J. W., Stein, B. E., Norris, J. L., and Schirillo, J. A. (2003). Visual localization ability influences cross-modal bias. J. Cogn. Neurosci. 15, 20–29.
Hillis, J. M., Ernst, M. O., Banks, M. S., and Landy, M. S. (2002). Combining sensory information: mandatory fusion within, but not between, senses. Science 298, 1627–1630.
Keetels, M., and Vroomen, J. (2007). No effect of auditory–visual spatial disparity on temporal recalibration. Exp. Brain Res. 182, 559–65.
King, A. J., and Palmer, A. R. (1985). Integration of visual and auditory information in bimodal neurones in the guinea-pig superior colliculus. Exp. Brain Res. 60, 492–500.
Koerding, K. P., Beierholm, U., Ma, W. J., Quartz, S., Tenenbaum, J. B., and Shams, L. (2007). Causal inference in multisensory perception. PLoS ONE 2, e943. doi:10.1371/journal.pone.0000943.
Kotz, S., Kozubowski, T. J., and Podgórski, K. (2001). The Laplace Distribution and Generalizations. A Revisit with Applications to Communications, Economics, Engineering, and Finance. Boston: Birkhäuser.
Lakatos, P., Chen, C.M., O’Connell, M. N., Mills, A., and Schroeder, C. E. (2007). Neuronal oscillations and multisensory interaction in primary auditory cortex. Neuron 53, 279–292.
Lakatos, P., O’Connell, M. N., Barczak, A., Mills, A., Javitt, D. C., and Schroeder, C. E. (2009). The leading sense: supramodal control of neurophysiological context by attention. Neuron 64, 419–430.
Lakatos, P., Shah, A. S., Knuth, K. H., Ulbert, I., Karmos, G., and Schroeder, C. E. (2005). An oscillatory hierarchy controlling neuronal excitability and stimulus processing in the auditory cortex. J. Neurophysiol. 94, 1904–1911.
Lewald, J., Ehrenstein, W. H., and Guski, R. (2001). Spatio-temporal constraints for auditory–visual integration. Behav. Brain Res. 121, 69–79.
Lewald, J., and Guski, R. (2003). Cross-modal perceptual integration of spatially and temporally disparate auditory and visual stimuli. Brain Res. Cogn. Brain Res. 16, 468–478.
Lewald, J., and Guski, R. (2004). Auditory–visual temporal integration as a function of distance: no compensation for sound-transmission time in human perception. Neurosci. Lett. 357, 119–122.
Ma, W. J., and Pouget, A. (2008). Linking neurons to behavior in multisensory perception: a computational review. Brain Res. 1242, 4–12.
Maloney, L. T., and Mamassian, P. (2009). Bayesian decision theory as a model of human visual perception: testing Bayesian transfer. Vis. Neurosci. 26, 147–155.
Meredith. M. A. (2002). On the neuronal basis for multisensory convergence: a brief overview. Brain Res. Cogn. Brain Res. 14, 31–40.
Meredith, M. A., Nemitz, J. W., and Stein, B. E. (1987). Determinants of multisensory integration in superior colliculus neurons. I. Temporal factors. J. Neurosci. 7, 3215–3229.
Miller, J., and Schwarz, W. (2006). Dissociations between reaction times and temporal order judgments: a diffusion model approach. J. Exp. Psychol. Hum. Percept. Perform. 32, 394–412.
Morein-Zamir, S., Soto-Faraco, S., and Kingstone, A. (2003). Auditory capture of vision: examining temporal ventriloquism. Brain Res. Cogn. Brain Res. 17, 154–163.
Musacchia, G., and Schroeder, C. E. (2009). Neuronal mechanisms, response dynamics and perceptual functions of multisensory interactions in auditory cortex. Hear. Res. 258, 72–79.
Navarra, J., Vatakis, A., Zampini, M., Soto-Faraco, S., Humphreys, W., and Spence, C. (2005). Exposure to asynchronous audiovisual speech extends the temporal window for audiovisual integration. Brain Res. Cogn. Brain Res. 25, 499–507
Neumann, O., and Niepel, M. (2004). “Timing of perception and perception of time,” in Psychophysics Beyond Sensation: Laws and Invariants of Human Cognition, eds C. Kaernbach, E. Schroeger and H. Mueller, (Mahwah, NJ: Erlbaum), 245–269.
Powers A. R., III, Hillock, A. R., and Wallace, M. T. (2009). Perceptual training narrows the temporal window of multisensory binding. J. Neurosci. 29, 12265–12274.
Recanzone, G. H. (2003). Auditory influences on visual temporal rate perception. J. Neurophysiol. 89, 1078–1093.
Roach, N. W., Heron, J., and McGraw, P. V. (2006). Resolving multisensory conflict: a strategy for balancing the costs and benefits of audio–visual integration. Proc. R. Soc. Lond., B, Biol. Sci. 273, 2159–2168.
Romei, V., Murray, M. M., Merabet, L. B., and Thut, G. (2007). Occipital transcranial magnetic stimulation has opposing effects on visual and auditory stimulus detection: implications for multisensory interactions. J. Neurosci. 7, 11465–11472.
Roseboom, W., Nishida, S., and Arnold, D. H. (2009). The sliding window of audio–visual simultaneity. J. Vision 9, 1–8.
Rowland, B. A., and Stein, B. E. (2007). Multisensory integration produces an initial response enhancement. Front. Integr. Neurosci. 1, 1–8.
Rowland, B. A., and Stein, B. E. (2008). Temporal profiles of response enhancement in multisensory integration. Front. Neurosci. 2, 218–224.
Rowland, B. A., Quessy, S., Stanford, T. R., and Stein, B. E. (2007). Multisensory integration shortens physiological response latencies. J. Neurosci. 27, 5879–5884.
Royal, D. W., Carriere, B. N., and Wallace, M. T. (2009). Spatiotemporal architecture of cortical receptive fields and its impact on multisensory interactions. Exp. Brain Res. 198, 127–136.
Sato, Y., Toyoizumi, T., and Aihara, K. (2007). Bayesian inference explains perception of unity and ventriloquism aftereffect: identification of common sources of audiovisual stimuli. Neural. Comput. 19, 3335–3355.
Schroeder, C. E., Lakatos, P., Kajikawa, Y., Partan, S., and Puce, A. (2008). Neuronal oscillations and visual amplification of speech. Trends Cogn. Sci. 12, 106–113.
Senkowski, D., Schneider, T. R., Foxe, J. J., and Engel, A. K. (2008). Crossmodal binding through neural coherence: implications for multisensory processing. Trends Neurosci. 31, 401–409.
Shams, L., Ma, W. J., and Beierholm, U. (2005). Sound-induced flash illusion as an optimal percept. Neuroreport 16, 1923–1927.
Spence, C., and Squire, S. (2003). Multisensory integration: maintaining the perception of synchrony. Curr. Biol. 13, R519–R521.
Sternberg, S., and Knoll, R. L. (1973). “The perception of temporal order: fundamental issues and a general model,” in Attention and Performance, Vol. IV, ed. S. Kornblum (New York: Academic Press), 629–685.
Tappe, T., Niepel, M., and Neumann, O. (1994). A dissociation between reaction time to sinusoidal gratings and temporal-order judgment. Perception 23, 335–347.
van Attefeldt, N. M., Formisano, E., Blomert, L., and Goebel, R. (2007). The effect of temporal asynchrony on the multisensory integration of letters and speech sounds. Cereb. Cortex 17, 962–974.
Van Wanrooij, M. M., Bell, A. H., Munoz, D. P., and Van Opstal, A. J. (2009). The effect of spatial–temporal audiovisual disparities on saccades in a complex scene. Exp. Brain Res. 198, 425–437.
van Wassenhove, V., Grant, K. W., and Poeppel, D. (2007). Temporal window of integration in auditory–visual speech perception. Neuropsychologia 45, 598–607.
Vroomen, J., Keetels, M., de Gelder, B., and Bertelson, P. (2004). Recalibration of temporal order perception by exposure to audio–visual asynchrony. Brain Res. Cogn. Brain Res. 22, 32–35.
Wallace, M. T., Roberson, G. E., Hairston, W. D., Stein, B. E., Vaughan, J. W., and Schirillo, J. A. (2004). Unifying multisensory signals across time and space. Exp. Brain Res. 158, 252–258.
Whitchurch, E. A., and Takahashi, T. T. (2006). Combined auditory and visual stimuli facilitate head saccades in the barn owl (Tyto alba). J. Neurophysiol. 96, 730–745.
Keywords: multisensory integration, time window of integration, optimal decision rule, saccadic reaction time, TWIN model, Bayesian estimation
Citation: Colonius H and Diederich A (2010) The optimal time window of visual–auditory integration: a reaction time analysis. Front. Integr. Neurosci. 4:11. doi: 10.3389/fnint.2010.00011
Received: 04 January 2010;
Paper pending published: 01 March 2010;
Accepted: 02 April 2010;
Published online: 11 May 2010
Edited by:
Mark T. Wallace, Vanderbilt University, USAReviewed by:
Benjamin A. Rowland, Wake Forest University, USAUlrik R. Beierholm, UCL, UK
Copyright: © 2010 Colonius and Diederich. This is an open-access article subject to an exclusive license agreement between the authors and the Frontiers Research Foundation, which permits unrestricted use, distribution, and reproduction in any medium, provided the original authors and source are credited.
*Correspondence: Hans Colonius, Department of Psychology, University of Oldenburg, P.o. Box 2503, D-26111 Oldenburg, Germany. e-mail:aGFucy5jb2xvbml1c0B1bmktb2xkZW5idXJnLmRl


