Ten dollars today is more attractive than the same amount of money tomorrow and is consistent with the well known proverb, “a bird in the hand is worth two in the bush.” We all know that the value of a reward is discounted over time. How the value discounts over time and what is the rationale for such discounting, however, is less clear. Classical economic theory has assumed an exponential form of discounting which has been repeatedly shown insufficient for explaining the data(Frederick and Loewenstein, 2002). Hyperbolic discounting, with a faster discount rate in the beginning than in the distant future, is found to fit the data better empirically. Consequently, it is of great interest to understand why people and other animals discount future rewards hyperbolically.
In the past, a number of explanations have been offered. Not surprisingly these explanations can be categorized into either value-based models or time-based models. In value-based models, hyperbolic discounting emerges when discount rates are assumed to be stochastic (Farmer and Geanakoplos, 2009), or there is uncertainty of the risk that the future reward will not be realized (Sozou, 1998), or there is uncertainty of the timing of the realization (Dasgupta and Maskin, 2005). In time-based models, hyperbolic discounting can be shown to result from the perceptual distortion of time (Takahashi, 2005; Kim and Zauberman, 2009). Recently, Ray and Bossaerts (2011) offered another time-based explanation beginning with the crucial observation that subjective or psychological time is different from objective or physical time. They argued that the discounting function is indeed exponential with respect to the subject’s internal clock, but it appears to be hyperbolic to observers who use objective time – the measurement of which isn’t dependent upon biological systems and their inherent variability. Specifically, they made three assumptions:
1 Increment of psychological time is stochastic and auto-correlated (i.e., the internal clock is positive quadrant dependent).
2 Increment of psychological time is stationary.
3 Value discounting over psychological time is exponential.
Ray and Bossaerts performed both analytical proof and numeric simulation. When the auto-correlation of psychological time increments is reduced to 0, the discounting function becomes the classical exponential form; when the auto-correlation is non zero (e.g., 0.3), the discounting function becomes hyperbolic. Thus, hyperbolic discounting naturally emerges when psychological time advances in a self-correlated way – i.e., if the current increment is large, it’s likely that the next increment is also large.
This explanation is quite interesting and unlike other subjective time-based models (e.g., Takahashi, 2005; Kim and Zauberman, 2009) in which psychological time is a concave function of physical time, the psychological time in this model is actually synchronized with the physical time on average. This is an important property because experiments have shown that while we have uncertainty in estimating time intervals, the average of our estimates is actually quite accurate (Church et al., 1994; Rakitin et al., 1998; Buhusi and Meck, 2005).
On the other hand, the representation of psychological time in this model does not follow the scalar property (or Weber’s law) of timing and time perception, which has been demonstrated in numerous studies – including those involving optimal foraging (see Gibbon et al., 1984, 1997; Bateson, 2003 for reviews). The scalar property of interval timing means that the coefficient of variation of time estimates is a constant, thereby producing timescale invariance (Gibbon, 1977). Based on numeric simulation, the coefficient of variation in the Ray and Bossaerts (2011) model is decreasing over time.
Here we demonstrate that hyperbolic discounting can be shown to result from the scalar property of time perception alone, without the assumption of internal exponential discounting over time. In a nutshell, Weber’s law states that the incremental amount of change required for a stimulus to be perceptually differentiated or noticeable is proportional to the current stimulus magnitude. Time perception is well known to abide by Weber’s law across a wide range of durations (Buhusi and Meck, 2005; Grondin, 2010 – but see Lewis and Miall, 2009). We reason that if the change in duration is not noticeable, then the change of the corresponding reward value should not be noticeable either. Otherwise people can detect the difference of time based on the difference of value.
Let’s assume that both the perception of value and time follow Weber’s law with Weber fractions a and b, respectively. Imagine that a subject perceives the value of reward is V at time t. As time advances, the perceived value decreases. Consider a delay τ in time where the subject just perceives a noticeable change in time. With the scalar property of time perception, we have
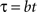
The delay also causes the perceived value to decrease. As the delay τ is a barely noticeable change, the change of value V, denoted as Δ, should also be barely noticeable (see Figure 1). That is:
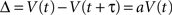
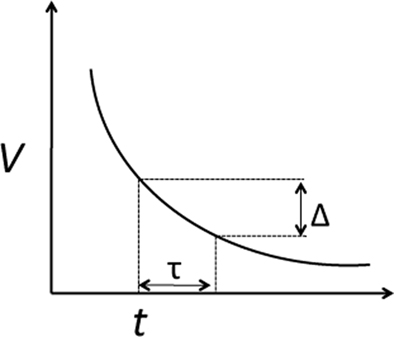
Figure 1. A “just noticeable” change in time will result in a “just noticeable” change in the corresponding value.
Combining the two equations together we get:
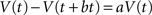
We want to find an explicit form of V(t) satisfying the above condition. One solution is:
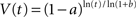
This discounting function is hyperbolic, as the discount rate, |dV/dt/V|, is a decreasing function of t. This model has two advantages: (1) the free parameters, a and b, have psychological meaning and can be independently measured – see Meck, 2006; (2) the model does not assume any form of discounting to start with. However, it should be emphasized that the assumptions made in this model, i.e., Weber’s law in time and value perception, are only valid within certain time ranges. Particularly, in the sub-second range, time perception typically does not always follow Weber’s law so clearly (see Gibbon, 1977; Grondin, 2010).
Acknowledgments
We thank Professor Warren Meck for his thoughtful comments and thorough revisions.
References
Bateson, M. (2003). “Interval timing and optimal foraging,” in Functional and Neural Mechanisms of Interval Timing, ed. W. H. Meck (Boca-Raton, FL: CRC Press), 113–141.
Buhusi, C. V., and Meck, W. H. (2005). What makes us tick? Functional and neural mechanisms of interval timing. Nat. Rev. Neurosci. 6, 755–765.
Church, R. M., Meck, W. H., and Gibbon, J. (1994). Application of scalar timing theory to individual trials. J. Exp. Psychol. Anim. Behav. Process. 20, 135–155.
Dasgupta, P., and Maskin, E. (2005). Uncertainty and hyperbolic discounting. Am. Econ. Rev. 95, 1290–1299.
Farmer, J. D., and Geanakoplos, J. (2009). Hyperbolic Discounting is Rational: Valuing the Far Future with Uncertain Discount Rates. Cowles Foundation Discussion Paper No. 1719. Available at http://ssrn.com/abstract=1448811
Frederick, S., and Loewenstein, G. (2002). Time discounting and time preference: a critical review. J. Econ. Lit. 40, 351–401.
Gibbon, J. (1977). Scalar expectancy theory and Weber’s law in animal timing. Psychol. Rev. 84, 279–325.
Gibbon, J., Church, R. M., and Meck, W. H. (1984). Scalar timing in memory. Ann. N. Y. Acad. Sci. 423, 52–77.
Gibbon, J., Malapani, C., Dale, C. L., and Gallistel, C. R. (1997). Toward a neurobiology of temporal cognition: advances and challenges. Curr. Opin. Neurobiol. 7, 170–184.
Grondin, S. (2010). Timing and time perception: A review of recent behavioral and neuroscience findings and theoretical directions. Atten. Percept. Psychophys. 72, 561–582.
Kim, B. K., and Zauberman, G. (2009). Perception of anticipatory time in temporal discounting. J. Neurosci. Psychol. Econ. 2, 91–101.
Lewis, P. A., and Miall, R. C. (2009). The precision of temporal judgement: milliseconds, many minutes, and beyond. Philos. Trans. R. Soc. Lond. B Biol. Sci. 364, 1897–1905.
Meck, W. H. (2006). Neuroanatomical localization of an internal clock: A functional link between mesolimbic, nigrostriatal, and mesocortical dopaminergic systems. Brain Res. 1109, 93–107.
Rakitin, B. C., Gibbon, J., Penney, T. B., Malapani, C., Hinton, S. C., and Meck, W. H. (1998). Scalar expectancy theory and peak-interval timing in humans. J. Exp. Psychol. Anim. Behav. Process. 24, 15–33.
Ray, D., and Bossaerts, P. (2011). Positive temporal dependence of the biological clock implies hyperbolic discounting. Front. Neurosci. 5:2. doi: 10.3389/fnins.2011.00002
Sozou, P. D. (1998). On hyperbolic discounting and uncertain hazard rates. Proc. R. Soc. Lond. B Biol. Sci. 265, 2015–2020.
Citation: Cui X (2011) Hyperbolic discounting emerges from the scalar property of interval timing. Front. Integr. Neurosci. 5:24. doi: 10.3389/fnint.2011.00024
Received: 16 May 2011; Accepted: 21 May 2011;
Published online: 06 June 2011.
Copyright: © 2011 Cui. This is an open-access article subject to a non-exclusive license between the authors and Frontiers Media SA, which permits use, distribution and reproduction in other forums, provided the original authors and source are credited and other Frontiers conditions are complied with.
*Correspondence:Y3VpeHVAc3RhbmZvcmQuZWR1
