- 1 Department of Physics and Astronomy, College of Charleston, Charleston, SC, USA
- 2 Department of Neurosciences, Medical University of South Carolina, Charleston, SC, USA
In most species, the capability of perceiving and using the passage of time in the seconds-to-minutes range (interval timing) is not only accurate but also scalar: errors in time estimation are linearly related to the estimated duration. The ubiquity of scalar timing extends over behavioral, lesion, and pharmacological manipulations. For example, in mammals, dopaminergic drugs induce an immediate, scalar change in the perceived time (clock pattern), whereas cholinergic drugs induce a gradual, scalar change in perceived time (memory pattern). How do these properties emerge from unreliable, noisy neurons firing in the milliseconds range? Neurobiological information relative to the brain circuits involved in interval timing provide support for an striatal beat frequency (SBF) model, in which time is coded by the coincidental activation of striatal spiny neurons by cortical neural oscillators. While biologically plausible, the impracticality of perfect oscillators, or their lack thereof, questions this mechanism in a brain with noisy neurons. We explored the computational mechanisms required for the clock and memory patterns in an SBF model with biophysically realistic and noisy Morris–Lecar neurons (SBF–ML). Under the assumption that dopaminergic drugs modulate the firing frequency of cortical oscillators, and that cholinergic drugs modulate the memory representation of the criterion time, we show that our SBF–ML model can reproduce the pharmacological clock and memory patterns observed in the literature. Numerical results also indicate that parameter variability (noise) – which is ubiquitous in the form of small fluctuations in the intrinsic frequencies of neural oscillators within and between trials, and in the errors in recording/retrieving stored information related to criterion time – seems to be critical for the time-scale invariance of the clock and memory patterns.
Introduction
The capability of perceiving and using the passage of time in the seconds-to-minutes range (interval timing) is essential for survival and adaptation, and its impairment leads to severe cognitive and motor dysfunctions (Gallistel, 1990; Buhusi and Meck, 2005; Meck et al., 2008). Considerable progress has been made in recent years toward elucidating the neural bases of time perception in the seconds-to-minutes range (Mauk and Buonomano, 2004; Buhusi and Meck, 2005, 2009; Meck et al., 2008). Recent studies point toward the cortico-striatal circuits as being critical for interval timing both, in animals (Matell and Meck, 2000; Matell et al., 2003; Meck, 2006) and humans (Coull et al., 2004, 2011; Stevens et al., 2007). Other experiments pointed toward an important role of the parietal lobe in timing behavior (Harrington et al., 1998; Schubotz et al., 2000; Onoe et al., 2001; Rao et al., 2001). In particular, Leon and Shadlen (2003) found evidences of a correlation between the judgment of time and cell-level neural activity in the lateral intraparietal area of the posterior parietal cortex of monkey (Leon and Shadlen, 2003). As Matell and Meck (2004); Leon and Shadlen (2003) and others highlighted, it is likely that the interval timing uses multiple mechanisms and time is represented in many structures in the brain. Moreover, severe deficiencies in reproducing temporal intervals were found in various neuropsychiatric disorders, such as Parkinson’s (Harrington and Haaland, 1991; Malapani et al., 1998, 2002).
In most species interval timing is not only accurate but also time-scale invariant, or simply scalar, in that the errors in time estimation are linearly related to the estimated duration (Gibbon, 1977; Gibbon et al., 1984). In other words, interval timing is increasingly less precise as the interval being timed lengthens (Figure 1A). When timing a 30-s interval (left panel of Figure 1A), responses are distributed with a quasi–Gaussian distribution around the 30-s target duration. On the other hand, when timing a 90-s interval (right panel of Figure 1A), responses are distributed with a quasi–Gaussian distribution around the 90-s target duration. The scalar property is evident in that normalizing the response functions by the target duration and by the maximum response rate yields superimposition of response functions (middle panel of Figure 1A). The time-scalar invariance property of interval timing is ubiquitous in many species from invertebrates such as bees (Boisvert and Sherry, 2006), to many vertebrates, such as fish (Talton et al., 1999), birds (Cheng and Westwood, 1993), and mammals such as rats (Dews, 1962), mice (Buhusi et al., 2009) and humans (Rakitin et al., 1998). Scalar timing is particular to timing in the seconds-to-minutes range, but not to circadian timing, which is far more accurate than interval timing, but whose variance increases very little with the mean of the interval (Gibbon, 1977; Hinton and Meck, 1997).
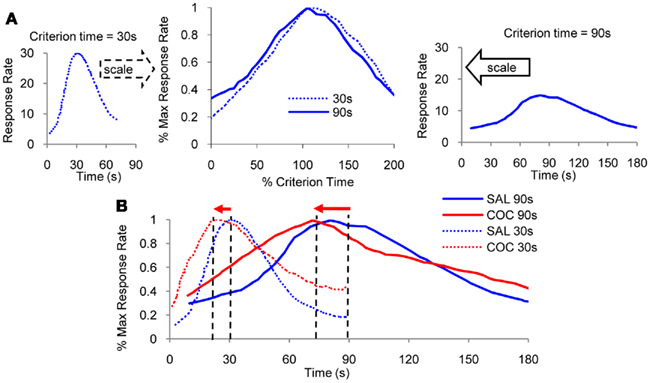
Figure 1. Scalar property. (A) Mean lever-press response rate in peak-interval experiments with rats trained with a criterion time of 30 s (left panel), respectively, 90 s (right panel; re-drawn from Matell et al., 2004). When normalized by maximum response rate and by the criterion duration on the horizontal scale, response functions for the two criteria overlap (middle panel). (B) Administration of indirect dopamine agonist cocaine results in an immediate, scalar (proportional) leftward shift in response functions.
The ubiquity of scalar timing extends over behavioral, lesion (Meck et al., 1987), and pharmacological manipulations of interval timing (Buhusi and Meck, 2010). For example, acute administration of cocaine results in a characteristic leftward shift of response functions (Figure 1B), consistent with the speeding up of an internal clock (Matell et al., 2004). Most interestingly, at the same dose, cocaine speeds up timing of a 90-s interval three times more than when timing a 30-s interval (Figure 1B), suggesting that the effect of the drug is proportional – scalar – to the timed interval. Moreover, when normalized in both amplitude and time as in Figure 1A, the response functions under cocaine (Figure 1B) superimpose, indicative of the scalar property.
In mammals, manipulations involving dopaminergic (DA) drugs such as cocaine induce a particular pattern of response – clock pattern – that is characterized by several features exemplified by the data presented in Figure 2A (Meck, 1996). Figure 2A shows the clock pattern obtained during seven sessions of administration of DA agonists (red dots) or antagonists (black squares), followed by seven sessions off-drug, in two groups of rats trained to time a criterion duration of either a 20-s (lower pattern), or 40s (upper pattern). First, DA drugs produce an immediate, scalar change in the perceived time when administered either systemically (Maricq et al., 1981; Maricq and Church, 1983; Meck, 1983, 1996; Matell and Meck, 1997; Matell et al., 2004), or directly into the anterior portion of the striatum (Neil and Herndon Jr., 1978); the pattern is often taken to be suggestive of a change in the speed of an internal clock, and thus is known as a “clock pattern” (Meck, 1996). For example, an immediate, scalar (proportional), leftward shift in perceived time (responding earlier in time than under control conditions) is evident following systemic DA agonist administration, e.g., methamphetamine or cocaine (black squares in Figure 2A, upper pattern for a 40-s criterion, lower pattern for a 20-s criterion). Similarly, an immediate, proportional, rightward shift in perceived time (responding later in time than under control conditions) occurs following systemic administration of DA antagonist, e.g., haloperidol (red circles in Figure 2A). Second, as shown in Figure 1B, the magnitude of the shift in the temporal response scales with the timed duration, and the response functions on- and off-drug overlap when normalized in amplitude and duration (Figure 1B). Third, upon chronic administration of DA drugs, the timing functions recalibrate, i.e., they shift back to the values prior to drug administration, an effect often interpreted as a relearning of the clock value associated with a particular duration (left side of the Figure 2A). Fourth, upon discontinuing the drug regimen, the timing functions rebound (in a scalar manner) in the opposite direction from the initial effects of the drug (Meck, 1983; right-side of Figure 2A). This rebound effect is a signature of the clock pattern. Finally, the magnitude of the shift in the temporal response scales roughly linearly with the dose (Meck, 1996; Matell and Meck, 1997; Meck et al., 2011), suggesting a tight relationship between synaptic dopamine levels and clock-speed.
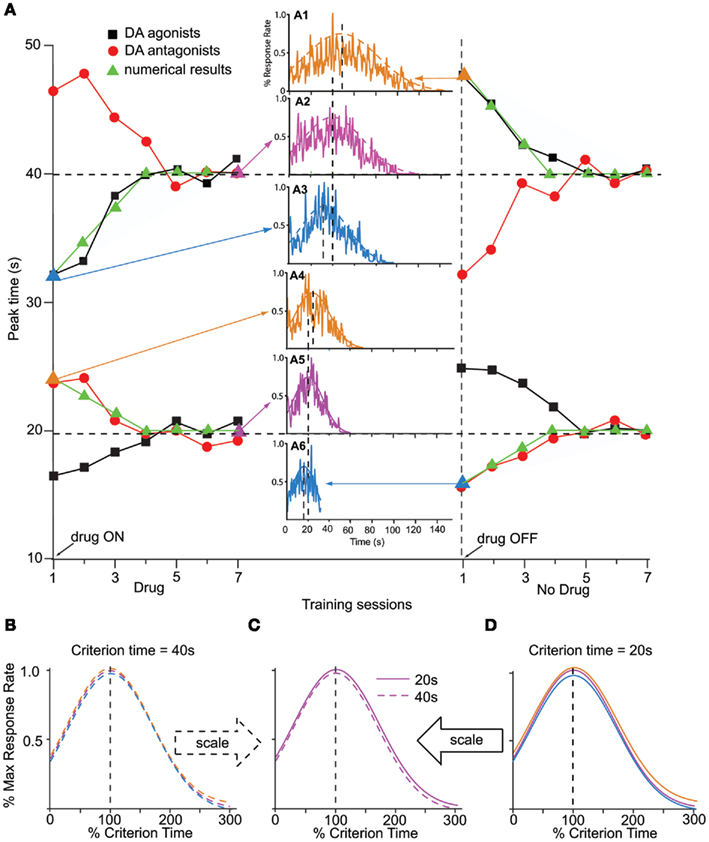
Figure 2. Clock pattern. (A) The clock pattern of dopaminergic (DA) drugs (re-drawn from Meck, 1996): two groups of rats were trained off-drug to time a criterion time of either 40 s (upper pattern) or 20 s (lower pattern); they were then administered either DA agonists or antagonists for seven sessions, followed by seven session off-drug. The first administration of DA drugs results in an immediate, dose-dependent shift in timing, leftward (faster timing) for DA agonists (solid squares, methamphetamine), and rightward (slower timing) for DA antagonists (solid circles, haloperidol). Under continuous training with the pre-drug criterion time and despite continuing the drug administration, the timing functions recalibrate to the pre-drug criterion time. Upon discontinuing the drug, timing functions immediately rebound in the opposite direction, then gradually recalibrate to the pre-drug criterion time (Meck, 1996). Solid triangles indicate numerical simulations with the SBF–ML model. The insets indicate the response function generated by the SBF–ML model throughout the clock pattern (indicated by arrows, and by a triangle symbol of the color of the inset). Insets: A1: immediate rebound from T = 40 to T** = 48 s upon discontinuing methamphetamine; A2: recalibration under methamphetamine; A3: immediate shift under methamphetamine from T = 40 to T* = 32 s; A4: immediate shift under haloperidol from T = 20 to T*= 24 s; A5: recalibration under haloperidol; A6: immediate rebound upon discontinuing haloperidol. The dashed (A1–3), respectively, continuous (A4–6) smooth lines represent Gaussian fits. (B). The Gaussian fits (dashed smooth lines) in (A1–3) are given by Gauss (48, 31 s), Gauss (40, 27 s), respectively, Gauss (32, 21 s). Timing functions at different points of the clock pattern for T = 40 s are time-scale invariant. (C). Timing functions from the 20-s clock pattern and 40-s clock pattern are time-scale invariant. (D). The Gaussian fits (continuous smooth lines) in (A4–6) are given by Gauss (24, 16 s), Gauss (20, 13 s), respectively, Gauss (16, 11 s). Timing functions at different points of the clock pattern for T = 20 s are time-scale invariant. Colors match the insets. All Gaussian fits of numerical simulations gave COD > 0.9 and p < 0.0001.
On the other hand, pharmacological manipulations (Meck, 1983, 1996; Meck and Church, 1987a,b) and lesions (Meck et al., 1987) aimed at the cholinergic (ACh) systems produce gradual, scalar (proportional) effects on the memory storage, as shown in data from Figure 3A. Figure 3A shows the memory pattern obtained during seven sessions of administration of ACh agonists (red dots) or antagonists (black squares), followed by seven sessions off-drug, in two groups of rats trained to time a criterion duration of either a 20-s (lower pattern) or 40-s (upper pattern): first, administration of ACh drugs produced a gradual (rather than immediate), scalar temporal shift (Meck, 1996); ACh lesions produce permanent effects (Malapani and Fairhurst, 2002). Second, chronic administration amplifies (rather than recalibrates) the temporal shift (left side of Figure 3A). Third, upon discontinuing the drug administration, the timing functions gradually return to the original criterion time (Figure 3A, right-side). Finally, the magnitude of the shift in the temporal response scales with the timed duration (Meck, 1996), twice as large for the 40-s group (upper pattern in Figure 3A) than for the 20-s group (lower pattern in Figure 3A). The memory pattern is consistent with alterations of the internal representation of the memorized criterion time (Meck, 1996).
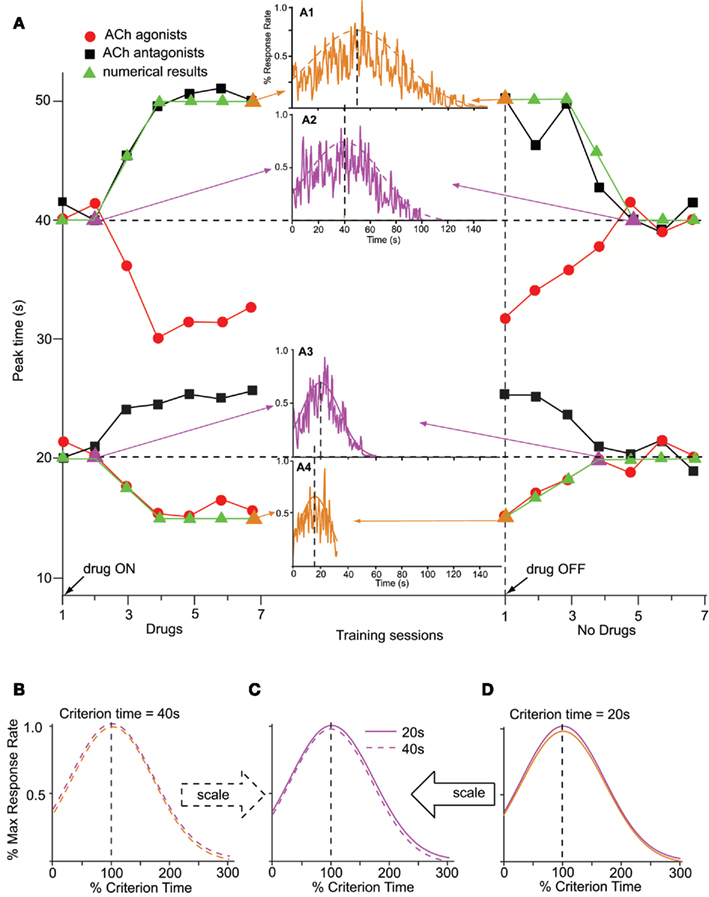
Figure 3. Memory pattern. (A) The memory pattern of cholinergic (ACh) drugs (re-drawn from Meck, 1996): two groups of rats were trained off-drug to time a criterion time of either 40 s (upper pattern) or 20 s (lower pattern); they were then administered either ACh agonists or antagonists for seven sessions, followed by seven session off-drug. The first administration of ACh drugs results in a minimal effect; repeated ACh drug administration results in a gradual, dose-dependent shift in timing, leftward for ACh agonists (solid circles, physostigmine), and rightward for ACh antagonists (solid squares, atropine). Upon discontinuing the drug, timing functions gradually recalibrate to the initial criterion time (Meck, 1996). Solid triangles indicate numerical simulations obtained with the SBF–ML model. The insets indicate the output function generated by the SBF–ML model with biophysically realistic ML neurons throughout the memory pattern (indicated by arrows, and by a triangle symbol of the color of the inset). Insets: A1: gradual shift from T = 40 to T* = 50 s under atropine; A2: gradual recalibration upon discontinuing atropine; A3: gradual recalibration upon discontinuing physostigmine; A4: gradual recalibration under physostigmine. The dashed (A1,2), respectively, continuous (A3,4) smooth lines represent Gaussian fits. (B). The Gaussian fits (dashed smooth lines) in (A1,2) are given by Gauss (50, 33 s), respectively, Gauss (40, 27 s). Timing functions at different points of the memory pattern for T = 40 s are time-scale invariant. (C). Timing functions from the 20-s memory pattern and 40-s memory pattern are time-scale invariant. (D). The Gaussian fits (continuous smooth lines) in (A3,4) are given by Gauss (20, 13 s), respectively, Gauss (15, 10 s). Timing functions at different points of the memory pattern for T = 20 s are time-scale invariant. Colors match the insets. All Gaussian fits of numerical simulations gave COD > 0.9 and p < 0.0001.
How do the pharmacological properties of timing in the seconds-to-minutes range, including the scalar effect of dopaminergic (DA) and cholinergic (ACh) drugs, emerge from unreliable, noisy neurons firing in the milliseconds range? A response to these questions was recently proposed by a neurobiologically inspired computational model of interval timing: the striatal beat frequency (SBF) model (Matell and Meck, 2000, 2004; Buhusi and Meck, 2005; Figure 4). The model is based on the idea that striatal spiny neurons integrate the activity of massive ensembles of cortical oscillators to produce coincidental beats that have periods spanning a much wider range of durations than the intrinsic periods of the cortical oscillators (Miall, 1989; Matell and Meck, 2004; Buhusi and Meck, 2005). Our implementation of the SBF–Morris–Lecar (ML) model closely follows Matell and Meck (2004) with three main changes: (1) we replaced the sine wave mathematical abstraction of oscillators with biophysically realistic and noisy ML (Morris and Lecar, 1981; Rinzel and Ermentrout, 1998) model neurons, and (2) we implemented neuromodulatory circuits that mimic the DA and ACh systems, and (3) we implemented the equivalent of trials and sessions, to address the effect of experimental DA, ACh, and lesion manipulations (Figure 4). Our SBF–ML implementation contains a time-base provided by a large number of neural oscillators presumably localized in the frontal cortex (FC; Matell et al., 2003). Following Matell and Meck (2004) review of the neuroanatomical foundations of the SBF model, among many other firing patterns observed in FC, the synchronized cortical oscillations in the 8- to 13-Hz range (alpha) could serve as pacemakers for temporal accumulation (Anliker, 1963). Furthermore, Rizzuto et al. (2003) have shown that alpha range oscillations in humans reset upon occurrence of to-be-remembered or probe stimuli, suggesting that the phase of these rhythms may be of importance in interval timing. The set of synaptic weights between neural oscillators in the FC and the spiny neurons in the striatum, which is the input to the basal ganglia (BG), represent a (long-term) memory buffer. Learning of the criteria times also depends on nucleus basalis magnocellularis (Meck et al., 1987), FC (Olton et al., 1988), and the hippocampus (Meck et al., 1987; Olton et al., 1988). A coincidence detector was implemented to mimic the spiny neurons in the striatum, which integrate a very large number of different inputs, and responds selectively to particular reinforced patterns (Houk, 1995; Houk et al., 1995; Beiser and Houk, 1998). As opposed to the existing implementations of the SBF model (Miall, 1989; Matell and Meck, 2004; Buhusi and Meck, 2005), a neuromodulatory circuit that mimics “a start gun” in regard to the effect of DA projections from substantia nigra pars compacta (SNc), a neuromodulatory circuit that models the DA projections from the ventral tegmental area (VTA) to the FC, and a cholinergic system which modulates the BG activity were also implemented in our SBF–ML model (Figure 4).
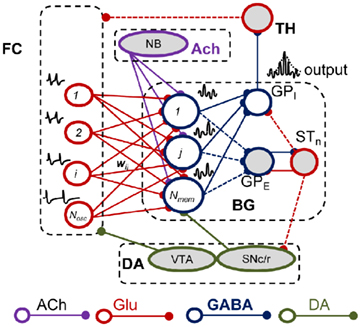
Figure 4. The striatal beat frequency model. Schematic representation of the neurobiological structures involved in interval timing in the SBF model. Dashed lines signify couplings that are not implemented in our SBF version. Frontal oscillators are implemented as biophysically realistic ML neurons. ACh, acetylcholine; FC, frontal cortex; BG, basal ganglia; DA, dopamine; Glu, glutamate; GPE, globus pallidus external; GPI, globus pallidus internal; STn, subthalamic nucleus; SNc/r, substantia nigra pars compacta/reticulata; TH, thalamus; VTA, ventral tegmental area.
While “biologically plausible,” the impracticality (or lack thereof) of perfect oscillators questions the robustness of an SBF model in a brain with real, noisy neurons, particularly after pharmacological manipulations. Here we explore the neural mechanisms required for clock (Figure 2), and memory (Figure 3) patterns in an SBF–ML model. First, we checked numerically that, in the limit of a very large number of neural oscillators and in the presence of noise, the output of an SBF–ML model is Gaussian-like (Figure 5). Second, under the assumption that DA drugs modulate the firing frequency of cortical oscillators, and that ACh drugs modulate the memory representation of the criterion time, we show that the SBF–ML model reproduces the pharmacological clock (Figure 2), and memory (Figure 3) patterns observed in the literature. Third, our numerical results support the conjecture (Matell and Meck, 2004) that parameter variability (noise) – which is ubiquitous in the form of small fluctuations in the intrinsic frequencies of the neural oscillators within and between trails, and in the errors in recording/retrieving stored information related to criterion time – is critical for the time-scale invariance of the clock and memory patterns of interval timing.
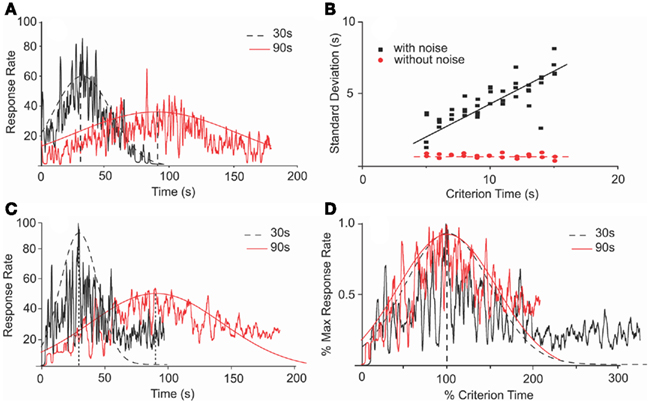
Figure 5. Scalar property in an SBF–ML model is dependent on noise. (A) Numerical simulations of an SBF–ML model with Gaussian variability of the criterion time and between-trial variability in frequencies of cortical neurons generated response functions (jagged traces) with Gaussian-like envelopes (smooth curves). The dashed (continuous) envelope corresponds to 30 s (90 s) criterion time. (B) In the presence of noise, the variance of output function is proportional with the criterion time, thus indicating time-scale invariance (filled squares). The coefficient of correlation for the linear regression (continuous line) was r = 0.9 with a p-value less than 0.001. In the absence of the noise, the variance of the output function is constant (filled circles), thus violating the time-scale invariance. The coefficient of correlation for the linear regression (dashed line) was r = 0.98 with a p-value less than 0.0001. (C) Numerical simulations of an SBF–ML model with normally distributed variability for both the criterion time and both within- and between-trials variability in frequencies generate response functions (jagged traces) with Gaussian-like envelopes (smooth curves). The only noticeable difference when adding within-trial frequency variability is the occurrence of the skewness in the response rate at late times. A similar skewness was observed in the behavioral data (see Figure 1) (D) The Gaussian envelopes for the case of criterion time variability (A) are given by Gauss (30, 21 s), respectively, Gauss (90, 60 s). They overlap when normalized in amplitude and in time.
Materials and Methods
Numerical Simulations Assume Biophysically Realistic Morris–Lecar Neurons.
Since action potential recordings from real neurons are never phase oscillators, i.e., sine waves, we departed from cortical phase oscillators (Matell and Meck, 2004) and we instead implemented biophysically realistic ML cortical neurons (Morris and Lecar, 1981; Rinzel and Ermentrout, 1998). The membrane potential of the ML model neuron is given by CmV′ = Ibias − ICa − IK − IL, where Cm is the membrane capacitance, prime denotes the derivative of the membrane potential V, Ibias is a constant bias current required to bring the model to the excitability threshold, ICa = gCam(V − ECa) is the calcium current that involves the conductance gCa, the fraction m of calcium channels open at a given V, and the reversal potential ECa for calcium channels, IK = gKn(V − EK) is the potassium current that involves the conductance gK, the fraction n of channels open at a given V, and the reversal potential EK for potassium channels, IL = gL(V − EL) is a leak current that only involves a conductance gL and a reversal potential EL. (Morris and Lecar, 1981; Rinzel and Ermentrout, 1998).
The SBF–ML Model
Briefly, a set of Nosc = 600 neural oscillators with uniformly distributed intrinsic frequencies fi was assumed to activate through synaptic weights wij(t) a set of Nmem = 1000 spiny neurons at time t (Figure 4; our choice of Nosc and Nmem was due to limitations on simulation duration, about 5 days on an HP Blade computer). The membrane potential of neural oscillators was normalized from [−80, +40 mV] to [−1,1] by a linear transformation that preserves the shape of the action potential (Rinzel and Ermentrout, 1998). The modeled experimental setting included both reinforced and non-reinforced trials. At the onset of each trial, the oscillators were reset (0 phase), then neurons were set to fire with frequencies fi, set during each trial, but variable from trial to trial. During reinforced trials, upon delivery of the reinforcement at criterion time T, a linear combination of oscillators’ membrane potential in the current trial at the criterion time T was stored in long-term memory as criterion pattern wij(T) (Matell and Meck, 2004). During non-reinforced (test) trials, spiny neurons were assumed to act as coincidence detectors by computing the projection (dot product) of the running weights wij(t) stored in the working memory onto the retrieved reference weights wij(T) stored in the long-term memory:
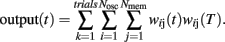
We assumed that both the storage and retrieval of the criterion time [stored as criterion pattern wij(T)] to and from long-term memory is affected by random biological noise, modeled as follows: criterion time variability was modeled by randomly distributing the criterion time T according to a normal density probability function pdfT with 0.4T variance. This assumption accounts for the randomness in learned sample times (reinforced times) and in response time; e.g., in a peak-interval procedure (Gibbon et al., 1984) animals are reinforced for the first response after a criterion time, but since the animal’s response is random, the reinforced time is random, though close in time to the criterion. Therefore, sample times stored in memory were assumed to be distributed around T. Additional randomness was included in our SBF–ML implementation by a Gaussian noise added to the intrinsic frequencies fi of the neural oscillators within and between trails. The within-trial variability in frequencies fi accounts for the randomness in response (e.g., for the first response reinforced), while the between-trial variability accounts for the observed differences in response between-trials (Church et al., 1994; Swearingen and Buhusi, 2010). Another reason to differentiate between within- and between-trial variability in frequencies fi has to do with our focus on pharmacological manipulations, which experimentally are conducted in on- and off-drug sessions. Because we assumed that DA drugs change the frequencies fi, this implies differences in coding and decoding of criterion time in on- and off-drug sessions (trials). This in turn implies variations in both the encoding and the recall of the criterion time due to the current (on- or off-drug) frequencies fi.
The Clock Pattern of Dopaminergic Drugs
We assumed that phasic release of dopamine from VTA to FC modulates the firing rate of FC neural oscillators, and that DA drugs affect the frequency of the cortical oscillators, 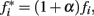 where α accounts for the action of the drug and its magnitude is dose-dependent, with 0 < α < 1 for dopamine agonists, such as methamphetamine or cocaine, and −1 < α < 0 for dopamine antagonists, such as haloperidol. Simulations in Figure 2 were carried out with an SBF–ML model using Nosc = 600 biophysically realistic ML cortical neurons firing in the range [8, 12] Hz, using Nmem = 1000 memory samples, with a drug dose effect α = ± 0.25.
where α accounts for the action of the drug and its magnitude is dose-dependent, with 0 < α < 1 for dopamine agonists, such as methamphetamine or cocaine, and −1 < α < 0 for dopamine antagonists, such as haloperidol. Simulations in Figure 2 were carried out with an SBF–ML model using Nosc = 600 biophysically realistic ML cortical neurons firing in the range [8, 12] Hz, using Nmem = 1000 memory samples, with a drug dose effect α = ± 0.25.
Relearning of the Criterion Time On-Drug, and Off-Drug
Meck (1996) suggested that the recalibration of the clock pattern may be due to relearning of the criterion time T under the drug. Numerically, we assumed that the criterion time is stored in long-term memory as a distribution of Nmem = 1000 samples, and that in each session, a fraction (25%) of the weights wij(T) are updated, by storing the new pattern of the FC oscillators (off-drug or on-drug) upon delivery of reinforcement at criterion time T. We ran four sessions of 250 trials off-drug to acquire the distribution wij(T) with the off-drug frequency set fi which vary from trial to trial. For each trial, a sample wij(T) was computed as a linear combination of the membrane potential at the criterion time T (Matell and Meck, 2004). During drug sessions, a fraction (25%) of the weights wij(T) originally stored off-drug, are replaced with new running weights w(T*), stored on-drug, such that gradually the weights w stored in the reference (long-term) memory are characteristic of the on-drug state. Similarly, when discontinuing the drug, we assumed that the criterion time, stored in long-term memory as a distribution of w(T*) samples, stored on-drug, is replaced with a fraction (25%) during each off-drug session, such that with sufficient training, the weights w stored in the reference (long-term) memory will be characteristic of the off-drug state.
The Memory Pattern of Cholinergic Drugs
Our numerical implementation assumes that administration of ACh drugs alters the re-coding of the criterion time in long-term memory (Meck, 1996; Matell and Meck, 2004). Briefly, we assumed that criterion time T is coded in long-term memory as a distribution of Nmem = 1000 samples w(T), and that ACh drugs alter the process involved in memorizing this distribution, with about 25% samples learned in each session. The new samples are assumed to represent an altered, on-drug representation of the criterion time, T* = k*T, where the multiplicative coefficient k* is both drug and dose-dependent (Gibbon et al., 1984; Meck, 1996). At the beginning of the drug administration, only a small subpopulation of the memory samples is affected; with continuing training on-drug, these altered samples make up the majority of the memory samples and lead to a progressive shift of the peak output to T*. For simulations presented in Figure 3 we assumed k* = 1.25 for ACh antagonist atropine, and k* = 0.75 for ACh agonist physostigmine.
Statistical Analyses
Throughout this paper, the Origin package (OriginLab Co., Northampton, MA, USA) was used to perform data fits to smooth analytic curves, and to compare the degree of superposition between curves. The degree of superposition of curves was indexed by a coefficient of determination (COD) and the probability (p) to obtain a certain COD value by chance was estimated. Briefly, the COD measures the proportion of the total variation in the dependent variable that is explained by the regression equation (fit function), with 0 < COD < 1 (Brockwell and Davis, 1991; Resnick, 2006). The correlation described by the COD is usually considered “good” if the COD > 0.7 (Nagelkerke, 1991; Cameron and Windmeijer, 1997; Anderson et al., 2009). If the regression curve is linear, then the COD reduces to the correlation coefficient (r).
Results
The SBF–ML Exhibits Time-Scale Invariance
Previous studies indicated that in the absence of biological noise, an SBF model with cortical phase oscillators (sine waves) does not exhibit time-scale invariance (Matell and Meck, 2004). We found a similar behavior of our implementation of the SBF–ML model. In the presence of normally distributed variability in the criterion time, and between-trial variability in the frequencies of cortical neurons, the output functions were Gaussian-like (Figure 5A) and exhibited more variance when increasing the criterion duration T (filled squares in Figure 5B). On the other hand, in the absence of biological noise the SBF–ML model produces an output function whose envelope is almost Gaussian but violates the scalar property (filled circles in Figure 5B). Moreover, when adding normally distributed within-trial frequency variability on top of the existing between-trial frequency variability, and variability in criterion time, the output functions were still Gaussian-like with SD proportional to the criterion time (Figure 5C). Moreover, in the presence of these three sources of variability (Figure 5C) the output function has a long tail that does not decrease to zero as fast as the smooth Gaussian fit. Such a skewed and long-tailed Gaussian-like output function was observed in behavioral experiments (see Figure 1). When normalized in amplitude and over time, the envelopes of the response functions from Figure 5C overlap (Figure 5D). These findings support the conjecture made by Matell and Meck (2004) that in an SBF model at least one source of variability is required in order to observe time-scale invariance. Therefore, biological noise – which is ubiquitous in the form of small fluctuations of the intrinsic within- and between-trial frequencies of the neural oscillators, errors in recording/retrieving stored information related to criterion time – seems to be a rather critical component of this feature of the SBF–ML model. However, considering the focus of our paper on pharmacological manipulations, for numerical efficiency reasons and without reducing the generality of our results, in the following analyzes we only used two sources of variability (noise) when numerically integrating the equations of the SBF–ML model: normally distributed variability in the criterion time, and between-trial variability in the frequencies of cortical neurons.
The Clock Pattern of Dopaminergic Drugs in the SBF–ML Model
Immediate shift upon changes in drug state
The clock effect of DA drugs can be easily understood as an interplay between the storage and retrieval of the criterion time representation wij(T) on- and off-drug. A change in drug state induced an immediate change in oscillator frequencies from the off-drug frequencies f to the on-drug frequencies f*, respectively, from the on-drug frequencies f* to the off-drug frequencies f. In our numerical implementation of the SBF–ML, the neural oscillators fire off-drug in the frequency range [fmin, fmax] and that the criterion time T is represented off-drug as a set of synaptic weights wij(T). The DA drugs alter the frequency of the cortical oscillators to 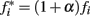 such that the on-drug frequency range changes to
such that the on-drug frequency range changes to 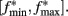 As a result, the projection (coincidence detection) of the vector of the current on-drug weights
As a result, the projection (coincidence detection) of the vector of the current on-drug weights 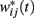 to the vector of reference off-drug weights wij(T) peaks at a time T* that differs from T.
to the vector of reference off-drug weights wij(T) peaks at a time T* that differs from T.
Numerical simulations indicate that our implementation of the SBF–ML model shows the major features of the clock pattern effect: immediate, scalar shift in timing, and recalibration on-drug, followed by an immediate, scalar rebound, and recalibration off-drug (solid triangles in Figure 2A). Simulations carried with α > 0 for dopamine agonists, indicate an immediate, leftward shift of the response function to T* < T (inset A3 in Figure 2A), in agreement with experimental data for DA agonists methamphetamine, and cocaine (Meck, 1996; Buhusi and Meck, 2002; Matell et al., 2004). On the other hand, for α < 0 we replicated numerically an immediate rightward shift due to a slow down of cortical oscillators during retrieval T* > T (inset A4 in Figure 2A), in agreement with experimental observation of the effect of DA antagonist haloperidol (Meck, 1996; Buhusi and Meck, 2005).
Recalibration upon chronic drug administration
According to the clock pattern (Meck, 1996), chronic drug administration results in a gradual recalibration, such that the response time on-drug gradually approaches the response time off-drug drug, an effect which is not due to receptor desensitization, but rather attributed to relearning of the criterion time using the drug-altered cortical frequencies (Meck, 1996). In our implementation, the repeated drug administration results in the criterion time T – which is represented in memory by a distribution of learned patterns wij(T) – to be gradually re-written with new samples of reinforced duration, samples which are computed using drug-altered oscillator frequencies. We found that our SBF–ML model exhibits recalibration of the criterion time T* back to T under repeated methamphetamine administration (α > 0, inset A2 of Figure 2A) as well as under repeated haloperidol administration (α < 0, inset A5 of Figure 2A). A similar recalibration occurs after the drug is discontinued, when the model re-learns the weights wij(T) for the criterion T off-drug (see right-side of Figure 2A). Interestingly, the rates of the two recalibration processes (Figure 2A) to the original criterion time T are not necessarily identical since the presence of the drugs may also significantly change the rate at which the memory is overwritten. In order to match pharmacological data from (Meck, 1996; Buhusi and Meck, 2002; Matell et al., 2004), we set the overwrite rate at 25% samples per session (Figure 2A).
Immediate rebound in the opposite direction, upon discontinuing the drug
In the SBF–ML model, discontinuing the drug results in a scalar rebound of the response in the opposite direction, due to the sudden change from on-drug cortical frequencies f* to the off-drug cortical frequencies f = (1 − β)f*. For example, an immediate leftward shift from T = 40 s (inset A2 in Figure 2A) to T* = 32 s (inset A3 in Figure 2A) under methamphetamine is followed by relearning of the criterion on-drug; discontinuing the drug results in an immediate rightward displacement to T** = 48 s (inset A1 in Figure 2A), followed again by a slow recalibration back to the original criterion time T = 40 s due to relearning of the criterion time with the new cortical frequencies.
Time-scale invariance of the clock-speed effect
For our implementation of the SBF–ML model, the preservation of time-scale invariance throughout the clock pattern is shown in the lower panels of Figure 2. For example, the amplitude of the immediate shift in response time at the transition between the off-drug to the on-drug state, and the amplitude of the immediate, opposite rebound at the transition between the on-drug to the off-drug state, are proportional to the criterion interval T (see Figure 2B for T = 40 s and Figure 2D for T = 20 s). Moreover, the variance in the response rate (width of response/output function), throughout the pharmacological manipulation remains proportional to the current response time, either off-drug T, or off-drug T* (Figures 2B and 2D). For the 40-s criterion, Figure 2B indicates that the envelopes of response functions in the insets A1, A2, and A3 of Figure 2A superimpose when renormalized in amplitude and time. Similarly, for the 20 s criterion time, Figure 2D indicates that the envelopes of response functions in the insets A4, A5, and A6 of Figure 2A superimpose when normalized in amplitude and time. Finally, the scalar property is preserved also between different criterion times: Figure 2C indicates that the envelopes of the response functions from inset A2 of Figure 2A (T** = 40 s recalibrated under methamphetamine) and inset A5 of Figure 2A (T** = 20 s recalibrated under haloperidol) superimposed when normalized in amplitude and in time.
The Memory Pattern of Cholinergic Drugs in the SBF–ML Model
Previous research indicates that the administration of ACh agonist physostigmine results in a gradual, dose-dependent leftward shift of the response (solid circles in Figure 3A; Meck, 1996). Similarly, administration of ACh blocker atropine leads to a gradual and dose-dependent rightward shift of the psychophysical functions (solid squares in Figure 3A; Meck, 1996). Moreover, the magnitudes of the temporal shifts observed are dose-dependent and proportional to the intervals being timed (Meck, 1996). To address this issue, it was proposed that training under the influence of the ACh drug produces a gradually re-learning of an altered criterion time T* = k*T (Gibbon et al., 1984; Meck, 1996; Buhusi and Meck, 2010).
In the SBF–ML model, the dynamics of memory pattern (Figure 3A) is significantly different from that of the clock pattern (Figure 2A): while the clock pattern takes effect as soon as the frequencies of neural oscillators are changed by the drug, thus producing an immediate temporal shift because of the sudden mismatch in cortical frequencies during storage, and retrieval, the memory pattern is determined by a gradual alteration of representation of the criterion time in the long-term memory that affects a growing number of memorized sample weights. Relearning the criterion under the ACh drug eventually overwrites the entire long-term memory with the altered representation k*T of the criterion time T. This induces a gradual change in the content of the long-term memory that leads to an increasing mismatch between the contents of the working and the long-term memory (Figure 3A).
In our numerical implementation, for ACh agonist atropine, we assumed k* = 1.25 in order to match the pharmacological data from Meck (1996). As shown in Figure 3A (solid triangles), the gradual change in memory samples under atropine gradually shifts the peak of the output function from the initial value, T = 20 s (inset A3 in Figure 3A), to the altered value T* = k*T = 15 s (inset A4 in Figure 3A). A similar shift takes place for ACh antagonists, say from T = 40 s (inset A2 in Figure 3A) to T* = 50 s (inset A1 in Figure 3A). Most importantly, both the amplitude of the gradual shift on-drug and the amplitude of the recalibration when the ACh drug is discontinued are proportional to the criterion interval T (Figure 3A). Moreover, the variance (width) of the response remains scalar, i.e., proportional to the current peak time, either off-drug, T, or on-drug, T* (Figure 3B for T = 40 s and Figure 3D for T = 20 s). For the 40-s criterion time, Figure 3B indicates that the envelopes of response functions in the insets A1 and A2 of Figure 3A superimpose when normalized in amplitude and time. Similarly, for the 20-s criterion, Figure 3D indicates that the envelopes of response functions in the insets A3 and A4 of Figure 3A superimpose when normalized in amplitude and time. Finally, the scalar property is preserved also between different criterion times: Figure 3C indicates that the envelopes of the response functions from inset A2 of Figure 3A (T = 40 s, dashed line) and inset A3 of Figure 3A (T = 20 s, solid line) superimposed when normalized in amplitude and time.
Discussion
In mammals, DA drugs induce an immediate, scalar change in the perceived time (clock pattern, Figure 2), whereas ACh drugs induce a gradual change in perceived time (memory pattern, Figure 3). To explain these patterns, we assumed that DA drugs induce a sudden change in the speed of an internal clock, while ACh drugs induce a gradual change in the memory of the criterion duration (Gibbon et al., 1984; Meck, 1996). Most importantly, both the clock and memory patterns are scalar, i.e., the drug effects are proportional to the criterion duration (Gibbon et al., 1984; Meck, 1996).
Current neurobiological data supports a SBF model, in which time is coded by the coincidental activation of striatal spiny neurons by cortical neural oscillators (Matell and Meck, 2000, 2004; Buhusi and Meck, 2005). While generally biologically plausible, the impracticality of perfect oscillators (or the lack thereof), questions the robustness of such a mechanisms in a brain with real, noisy neurons, particularly after pharmacological manipulations. Here we explored the neural mechanisms required for the time-scale invariance of the clock (Figure 2) and memory (Figure 3) patterns produced by the SBF–ML model (Figure 4). To our knowledge, this is the first time the SBF-type model was used to match pharmacological data, and the first time it is implemented using biophysically realistic neurons instead of simple sine waves. This combination of features opens the possibility of calibrating the timing network by adjusting conductances and half-activation voltages for specific ionic channels to mimic the effect of different drugs at channel-level.
Under the assumption that the biological noise is ubiquitous in the form of, e.g., variability of frequency within- and between-trails, variability in memory storage, and retrieval, etc., numerical simulations indicated that the SBF–ML model shows the scalar property, i.e., errors in time estimation are linearly related to the estimated duration (filled squares in Figure 5B). Interestingly, simply replacing crisp cortical phase oscillators with crisp cortical ML neurons did not produce scalar effects (filled circles in Figure 5B). It was only when at least one source of variability (noise) was introduced that the scalar property was evident. This result supports and extends the conjecture of Matell and Meck (2004) by which the SBF model requires at least one source of variance (noise) to address time-scale invariance.
Computational models of interval timing vary largely with respect to the hypothesized mechanisms by which temporal processing is explained, and by which time-scale invariance, or drug effects are explained. The putative mechanisms of timing rely on pacemaker/accumulator processes (Gibbon, 1977; Gibbon et al., 1984), sequences of behaviors (Killeen and Fetterman, 1988), pure sine oscillators (Church and Broadbent, 1990; Matell and Meck, 2000, 2004), memory traces (Grossberg and Schmajuk, 1989; Grossberg and Merrill, 1992; Machado, 1997; Buhusi and Schmajuk, 1999; Staddon and Higa, 1999), or cell and network-level models (Leon and Shadlen, 2003; Simen et al., 2011). For example, both neurometric functions from single neurons and ensemble of neurons successfully paralleled the psychometric functions for the to-be-timed intervals shorter than 1 s (Leon and Shadlen, 2003). Reutimann et al. (2004) also considered interacting populations that are subject to neuronal adaptation and synaptic plasticity based on the general principle of firing rate modulation in single-cell. Balancing LTP and LTD mechanisms are thought to modulate the firing rate of neural populations with the net effect that the adaptation leads to a linear decay of the firing rate in time. Therefore, the linear relationship between time and the number of clock ticks of the pacemaker–accumulator model in the scalar expectancy theory of interval timing (Gibbon, 1977) was successfully translated into a linearly decaying firing rate model that maps time and variable firing rate. As Matell and Meck (2004) stated, it may be that the brain uses both (relatively) stable neural oscillators in an SBF-based paradigm and a variable firing rate paradigm for interval timing.
Dopaminergic drugs modulation of the firing frequency of cortical oscillators led in our numerical simulations of the SBF–ML model to clock patterns (Meck, 1996): immediate change in timing (inset A3 of Figure 2A) and gradual re-calibration under the drug (inset A2 of Figure 2A), immediate re-bound in the opposite direction (inset A1 of Figure 2A) and gradual re-calibration upon discontinuing the drug, and scalar (proportional) effects (Figures 2B–D). ACh drugs modulation of the representation wij(T) of the criterion time in the long-term memory led in our numerical simulations of the SBF–ML model to memory patterns (Meck, 1996): gradual change in timing on-drug (inset A1 of Figure 3A), gradual re-calibration upon discontinuing the drug (inset A3 of Figure 3A), and scalar (proportional) effects (Figures 3B–D). Our interpretation of the clock and memory patterns within the SBF model is in accord with the interpretation of drug effect in the scalar expectancy theory (SET; Gibbon, 1977; Gibbon et al., 1984). As in SET, our numerical simulations assume that DA drugs alter the time-base of the model, and that ACh drugs alter memory processes. In recognition of this legacy, our description of the ACh memory effects continue to use the (rather famous) k* factor (Gibbon et al., 1984; Meck, 1996).
In summary, numerical simulations with the SBF–ML model successfully reproduced the clock (Figure 2) and memory (Figure 3) effects reported in the literature (Meck, 1996), including their scalar effects (Gibbon, 1977; Gibbon et al., 1984; Meck, 1996), previously addressed only by a few established behavioral models in the field, such as SET (Gibbon, 1977; Gibbon et al., 1984), and STM (Grossberg and Schmajuk, 1989). Together with previous studies (Matell and Meck, 2000, 2004; Buhusi and Meck, 2005), the current results establish the SBF model as a neurobiologically realistic model of interval timing capable of explaining a large range of phenomena, from behavior, to lesions, and pharmacology, with the potential to provide insight into the neurobiological bases on interval timing.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This research was supported the National Science Foundation CAREER award IOS 1054914 to Sorinel A. Oprisan. Catalin V. Buhusi was supported by the National Institutes of Health grants MH65561 and MH73057. We are also indebted to Warren H. Meck and Matthew S. Matell for helpful discussions about the SBF model, and to Joshua Swearingen for helpful comment on an early version of the manuscript.
References
Anderson, D. R., Sweeney, D. J., and Williams, T. A. (2009). Essentials of Statistics for Business and Economics. Mason, OH: Thomson Higher Education.
Anliker, J. (1963). Variations in alpha voltage of the electroencephalogram and time perception. Science 140, 1307–1309.
Beiser, D. G., and Houk, J. C. (1998). Model of cortical-basal ganglionic processing: encoding the serial order of sensory events. Clin. Neurophysiol. 79, 3168–3188.
Boisvert, M. J. M. J., and Sherry, D. F. D. F. (2006). Interval timing by an invertebrate, the bumble bee Bombus impatiens. Curr. biol. 16, 1636–1640.
Brockwell, P. J., and Davis, R. A. (1991). Time Series: Theory and Models, 2nd Edn. New York: Springer.
Buhusi, C. V., Aziz, D., Winslow, D., Carter, R. E., Swearingen, J. E., and Buhusi, M. C. (2009). Interval timing accuracy and scalar timing in C57BL/6 mice. Behav. Neurosci. 123, 1102–1113.
Buhusi, C. V., and Meck, W. H. (2002). Differential effects of methamphetamine and haloperidol on the control of an internal clock. Behav. Neurosci. 116, 291–297.
Buhusi, C. V., and Meck, W. H. (2005). What makes us tick? Functional and neural mechanisms of interval timing. Nat. Rev. Neurosci. 6, 755–765.
Buhusi, C. V., and Meck, W. H. (2009). Relative time sharing: new findings and an extension of the resource allocation model of temporal processing. Philos. Trans. R. Soc. Lond. B Biol. Sci. 364, 1875–1885.
Buhusi, C. V., and Meck, W. H. (2010). “Timing behavior,” in Encyclopedia of Psychopharmacology, ed. I. P. Stolerman (Berlin: Springer), 1319–1323.
Buhusi, C. V., and Schmajuk, N. A. (1999). Timing in simple conditioning and occasion setting: a neural network approach. Behav. Process. 45, 33–57.
Cameron, A. C., and Windmeijer, F. A. G. (1997). An R-squared measure of goodness of fit for some common nonlinear regression models. J. Econom. 77, 329–342.
Cheng, K., and Westwood, R. (1993). Analysis of single trials in pigeons’ timing performance. J. Exp. Psychol. Anim. Behav. Process. 19, 56–67.
Church, R. M., and Broadbent, H. A. (1990). Alternative representations of time, number, and rate. Cognition 37, 55–81.
Church, R. M., Meck, W. H., and Gibbon, J. (1994). Application of scalar timing theory to individual trials. J. Exp. Psychol. Anim. Behav. Process. 20, 135–155.
Coull, J. T., Cheng, R. K., and Meck, W. H. (2011). Neuroanatomical and neurochemical substrates of timing. Neuropsychopharmacology 36, 3–25.
Coull, J. T., Vidal, F., Nazarian, B., and Macar, F. (2004). Functional anatomy of the attentional modulation of time estimation. Science 303, 1506–1508.
Dews, P. B. (1962). The effect of multiple S delta periods on responding on a fixed-interval schedule. J. Exp. Anal. Behav. 5, 369–374.
Gibbon, J. (1977). Scalar expectancy theory and Weber’s law in animal timing. Psychol. Rev. 84, 279–325.
Gibbon, J., Church, R. M., and Meck, W. H. (1984). Scalar timing in memory. Ann. N. Y. Acad. Sci. 423, 52–77.
Grossberg, S., and Merrill, J. W. (1992). A neural network model of adaptively timed reinforcement learning and hippocampal dynamics. Brain Res. Cogn. Brain Res. 1, 3–38.
Grossberg, S., and Schmajuk, N. A. (1989). Neural dynamics of adaptive timing and temporal discrimination during associative learning. Neural Netw. 2, 79–102.
Harrington, D. L., and Haaland, K. Y. (1991). Sequencing in Parkinson’s disease. Abnormalities in programming and controlling movement. Brain Res. 114, 99–115.
Harrington, D. L., Haaland, K. Y., and Knight, R. T. (1998). Cortical networks underlying mechanisms of time perception. J. Neurosci. 18, 1085–1095.
Hinton, S. C., and Meck, W. H. (1997). The ‘internal clocks’ of circadian and interval timing. Endeavour 21, 3–8.
Houk, J. C. (1995). “Information processing in modular circuits linking basal ganglia and cerebral cortex,” in Models of Information Processing in the Basal Ganglia, eds J. C. Houk, J. L. Davis, and D. G. Beiser (Cambridge: MIT Press), 3–10.
Houk, J. C., Davis, J. L., and Beiser, D. G. (1995). Computational Neuroscience, Models of Information Processing in the Basal Ganglia. Cambridge: MIT Press.
Killeen, P. R., and Fetterman, J. G. (1988). A behavioral theory of timing. Psychol. Rev. 95, 274–295.
Leon, M. I., and Shadlen, M. N. (2003). Representation of time by neurons in the posterior parietal cortex of the macaque. Neuron 38, 317–327.
Malapani, C., Deweer, B., and Gibbon, J. (2002). Separating storage from retrieval dysfunction of temporal memory in Parkinson’s disease. J. Cogn. Neurosci. 14, 311–322.
Malapani, C., and Fairhurst, S. (2002). Scalar timing in animals and humans. Learn. Motiv. 33, 156–176.
Malapani, C., Rakitin, B., Levy, R., Meck, W. H., Deweer, B., Dubois, B., and Gibbon, J. (1998). Coupled temporal memories in Parkinson’s disease: a dopamine-related dysfunction. J. Cogn. Neurosci. 10, 316–331.
Maricq, A. V., and Church, R. M. (1983). The differential effects of haloperidol and methamphetamine on time estimation in the rat. Psychopharmacology (Berl.) 79, 10–15.
Maricq, A. V., Roberts, S., and Church, R. M. (1981). Methamphetamine and time estimation. J. Exp. Psychol. Anim. Behav. Process. 7, 18–30.
Matell, M. S., King, G. R., and Meck, W. H. (2004). Differential modulation of clock speed by the administration of intermittent versus continuous cocaine. Behav. Neurosci. 118, 150–156.
Matell, M. S., and Meck, W. H. (1997). A comparison of the tri-peak and peak-interval procedure in rats: equivalency of the clock speed enhancing effect of methamphetamine on interval timing. Abst. Soc. Neurosci. 23, 1315–1316.
Matell, M. S., and Meck, W. H. (2000). Neuropsychological mechanisms of interval timing behavior. Bioessays 22, 94–103.
Matell, M. S., and Meck, W. H. (2004). Cortico-striatal circuits and interval timing: coincidence detection of oscillatory processes. Cogn. Brain Res. 21, 139–170.
Matell, M. S., Meck, W. H., and Nicolelis, M. A. (2003). Interval timing and the encoding of signal duration by ensembles of cortical and striatal neurons. Behav. Neurosci. 117, 760–773.
Mauk, M. D., and Buonomano, D. V. (2004). The neural basis of temporal processing. Annu. Rev. Neurosci. 27, 307–340.
Meck, W. H. (1983). Selective adjustment of the speed of internal clock and memory processes. J. Exp. Psychol. Anim. Behav. Process. 171–201.
Meck, W. H. (2006). Neuroanatomical localization of an internal clock: a functional link between mesolimbic, nigrostriatal, and mesocortical dopaminergic systems. Brain Res. 1109, 93–107.
Meck, W. H., Cheng, R.-K., Macdonald, C. J., Gainetdinov, R. R., Caron, M. G., and Çevik, M. N. Ö. (2011). Gene-dose dependent effects of methamphetamine on interval timing in dopamine-transporter knockout mice. Neuropharmacology doi: 10.1016/j.neuropharm.2011.01.042. [Epub ahead of print].
Meck, W. H., and Church, R. M. (1987a). Cholinergic modulation of the content of temporal memory. Behav. Neurosci. 101, 457–464.
Meck, W. H., and Church, R. M. (1987b). Nutrients that modify the speed of internal clock and memory storage processes. Behav. Neurosci. 101, 465–475.
Meck, W. H., Church, R. M., Wenk, G. L., and Olton, D. S. (1987). Nucleus basalis magnocellularis and medial septal area lesions differentially impair temporal memory. J. Neurosci. 7, 3505–3511.
Meck, W. H., Penney, T. B., and Pouthas, V. (2008). Cortico-striatal representation of time in animals and humans. Curr. Opin. Neurobiol. 18, 145–152.
Miall, R. C. (1989). The storage of time intervals using oscillating neurons. Neural Comput. 1, 359–371.
Morris, C., and Lecar, H. (1981). Voltage oscillations in the barnacle giant muscle fiber. Biophys. J. 35, 193–213.
Nagelkerke, N. (1991). A note on a general definition of the coefficient of determination. Biometrika 78, 691–692.
Neil, D. B., and Herndon, J. D. Jr. (1978). Anatomical specificity within rat striatum for the dopaminergic modulation of DRL responding and activity. Brain Res. 153, 529–538.
Olton, D. S., Wenk, G. L., Church, R. M., and Meck, W. H. (1988). Attention and the frontal cortex as examined by simultaneous temporal processing. Neuropsychologia 26, 307–318.
Onoe, H., Komori, M., Onoe, K., Takechi, H., Tsukada, H., and Watanabe, Y. (2001). Cortical networks recruited for time perception: a monkey positron emission tomography (PET) study. Neuroimage 13, 37–45.
Rakitin, B. C., Gibbon, J., Penney, T. B., Malapani, C., Hinton, S. C., and Meck, W. H. (1998). Scalar expectancy theory and peak-interval timing in humans. J. Exp. Psychol. Anim. Behav. Process. 24, 15–33.
Rao, S. M., Mayer, A. R., and Harrington, D. L. (2001). The evolution of brain activation during temporal processing. Nat. Neurosci. 4, 317–323.
Resnick, S. I. (2006). Heavy-Tail Phenomena: Probabilistic and Statistical Modeling. New York: Springer.
Reutimann, J., Yakovlev, V., Fusi, S., and Senn, W. (2004). Climbing neuronal activity as an event-based cortical representation of time. J. Neurosci. 24, 3295–3303.
Rinzel, J., and Ermentrout, B. (1998). “Analysis of neural excitability and oscillations,” in Methods of Neuronal Modeling, eds C. Koch, and I. Segev (Cambridge, MA: MIT Press), 135–169.
Rizzuto, D. S., Madsen, J. R., Bromfield, E. B., Schulze-Bonhage, A., Seelig, D., Aschenbrenner-Scheibe, R., and Kahana, M. J. (2003). Reset of human neocortical oscillations during a working memory task. Proc. Natl. Acad. Sci. U.S.A. 100, 7931–7936.
Schubotz, R. I., Friederici, A. D., and Yves Von Cramon, D. (2000). Time perception and motor timing: a common cortical and subcortical basis revealed by fMRI. Neuroimage 11, 1–12.
Simen, P., Balci, F., Desouza, L., Cohen, J. D., and Holmes, P. (2011). A model of interval timing by neural integration. J. Neurosci. 31, 9238–9253.
Staddon, J. E., and Higa, J. J. (1999). Time and memory: towards a pacemaker-free theory of interval timing. J. Exp. Anal. Behav. 71, 215–251.
Stevens, M. C., Kiehl, K. A., Pearlson, G., and Calhoun, V. D. (2007). Functional neural circuits for mental timekeeping. Hum. Brain Mapp. 28, 394–408.
Swearingen, J. E., and Buhusi, C. V. (2010). The pattern of responding in the peak-interval procedure with gaps: an individual-trials analysis. J. Exp. Psychol. Anim. Behav. Process. 36, 443–455.
Keywords: interval timing, striatal beat frequency, computer simulations, dopamine, acetylcholine, neural noise, noise
Citation: Oprisan SA and Buhusi CV (2011) Modeling pharmacological clock and memory patterns of interval timing in a striatal beat-frequency model with realistic, noisy neurons. Front. Integr. Neurosci. 5:52. doi: 10.3389/fnint.2011.00052
Received: 30 June 2011; Paper pending published: 18 July 2011;
Accepted: 24 August 2011; Published online: 23 September 2011.
Edited by:
Warren H. Meck, Duke University, USAReviewed by:
Adrian Rodriguez-Contreras, City College of New York, USAEric Shea-Brown, University of Washington, USA
Christopher MacDonald, Boston University, USA
Copyright: © 2011 Oprisan and Buhusi. This is an open-access article subject to a non-exclusive license between the authors and Frontiers Media SA, which permits use, distribution and reproduction in other forums, provided the original authors and source are credited and other Frontiers conditions are complied with.
*Correspondence: Catalin V. Buhusi, Department of Neurosciences, Medical University of South Carolina, 173 Ashley Avenue, 403 Basic Science Building, Charleston, SC 29425, USA. e-mail:YnVodXNpQG11c2MuZWR1

