- Languages, Culture, Media and Identities Research Unit, University of Luxembourg, Luxembourg
With two experiments it was examined whether one or two clocks operate the timing of two intervals presented simultaneously. The target interval always preceded the distracter interval, and was longer than it. Thus, the distracter was completely embedded within the target interval. The participants used the method of temporal production. The stimuli to be judged differed in modality which allowed for testing the hypothesis of modality-specific internal clocks that operate in parallel and independent from one another when two stimuli were presented at the same time. The main results of this study were as follows. First, production times of the target interval increased proportionally with production times of the distracter interval. Second, the auditory distracter interval was on average produced in less time than the visual distracter interval. Third, a target interval that was accompanied by an auditory distracter interval was on average produced in less time than a target interval that was accompanied by a visual distracter interval. The results obtained support the hypothesis of multiple clocks being involved in the timing of different intervals presented simultaneously.
Introduction
Decision making involves the selection of at least two options which may differ regarding any attribute that is salient to the decision maker. Temporal decision making is a special case of choices made between alternatives differing in duration (Klapproth, 2008). Examples of temporal decision making in real live are numerous and ubiquitous, be it the judgment of the duration of a boring situation (often accompanied by the hope of an early ending of that situation) or the estimation of cooking time in order to prevent a meal from getting burnt. Several models have been proposed to explain and predict human and non-human temporal judgments. Most of these models rely on assumptions concerning an internal clock that in some aspects resembles a physical clock. For example, both the physical clock and the “mental” clock emit “pulses” at a regular pace (like the finger or the digits of a clock), both do in some way record the elapsed time by either storing the emitted pulses (mental clock) or adding seconds to the next minute (physical clock), and both need some form of energy (current in case of a physical clock and attention in case of a mental clock) to make them work. Moreover, as with the physical clock, the mental clock is prone to errors (although to a much larger degree). The latter attribute has provoked a lot of research since errors in judgments of time seem to obey some principles. One principle asserts that estimates of real duration are, on average, accurate, that is, if a subject makes several estimates of a given duration, then the mean time measured by the mental clock corresponds to the time measured by the physical clock. A second principle is a form of Weber’s Law which means that SDs of temporal judgments grow proportionally with the mean of time estimations.
Most prominent theories that explain regularities in human and non-human temporal judgments with reference to mental clocks are the scalar-timing theory (Gibbon et al., 1984; Gibbon, 1991) and modifications of it. The scalar-timing theory posits three stages of processing temporal information that are involved in temporal judgments: a clock, consisting of a pacemaker which generates pulses at a regular pace (with random error), which are recorded and added by an accumulator; a memory which stores pulses transferred from the accumulator for a longer while; and a comparison process through which a judgment is made by relating the to be judged duration to a reference duration stored in memory. Modifications of scalar-timing theory (or of its information-processing model) have altered the decision rule as to which sameness or differences of durations are examined (e.g., Wearden, 1992), have added attention as a factor that is supposed to affect temporal judgments (e.g., Block and Zakay, 1996), or have proposed the clock to be sensitive to physiological or physical properties (like, for example, stimulus modality, cf. Penney et al., 1998; Wearden et al., 1998).
One model that is able to explain variations in attention and clock speed is the attentional-gate model proposed by Block and Zakay (1996) and Zakay and Block(1996, 1998). Like the scalar-timing model, the attentional-gate model is composed of a pacemaker that emits pulses at a constant rate, a cognitive counter, and a decision-making stage. An additional component is the attentional-gate. The attentional-gate is assumed to explain the influence of a person’s attentional resource allocation to timing. The more attention is allocated to the timing process, the wider (metaphorically speaking) is the gate, thus allowing more pulses to be counted within a given period of time. Conversely, limiting attention for the timing of events will result in fewer pulses counted. Limitation of attention may be achieved by dividing attentional resources between attending to external events and attending to time (Zakay and Block, 1997). How accuracy in timing declines when processing demands are increased has often been investigated by the use of so-called dual-task procedures. In timing experiments, examples of tasks that were executed in order to distract attention from the timing were card sorting (Hicks et al., 1976), memory scanning (Fortin and Rousseau, 1998), or listening to music (Brown et al., 1992).
Models of temporal decision making have initially been developed to describe and explain judgments of single durations, that is, durations of stimuli that occur in succession rather than in parallel. However, we know from everyday life and from a growing body of research that humans and even non-human animals are able to estimate the durations of more than one stimulus simultaneously (cf. Curtis and Rule, 1977; Rule et al., 1983; Meck and Church, 1984; Rule and Curtis, 1985; Brown and West, 1990; van Rijn and Taatgen, 2008).
Most authors who aimed at explaining effects of simultaneous timing referred to limited attentional resources. If a timing device necessitates attention to be operated, timing of two intervals simultaneously might lead to a conflict in sharing attentional resources in order to monitor these intervals. Sharing attention means that less attention is devoted to the timing of either interval, resulting in judgmental biases compared to single-stimulus timing. According to the attentional-gate model (e.g., Block and Zakay, 1996), withdrawing attention from a timing task will result in less accurate temporal judgments. However, their model might allow for more precise predictions on how simultaneous timing will alter temporal judgments. The model predicts that if attention is distracted from the main timing task, fewer pulses will be accumulated during a certain period of time which will result in a shortening of perceived time. However, with temporal productions, the opposite pattern is likely to occur. Because perceived time is shortened, more time will be needed to accumulate the number of pulses that defines the mental equivalent of that duration. In other words, when people are required to produce a time interval and are to fulfill another task in parallel, time productions should become longer, compared to people who are engaged in the time-production task only (see for example, Hemmes et al., 2004; Brown and Merchant, 2007). This should also be true when two timing tasks are conducted concurrently. That is, if attention is divided between both timing tasks, each task will be provided with fewer attentional resources, resulting in longer time productions, than if it would be done solely.
Concerning the internal clock in simultaneous timing, some authors suggest the existence of one central pacemaker but different counters, each for every signal to be timed (e.g., Church, 1984; van Rijn and Taatgen, 2008). If one clock operates the timing of two parallel events, simultaneous timing has to be converted into sequential timing. This might be done by dividing the stream of stimuli into segments that are defined by stimulus onsets and offsets. For example, suppose the duration of two stimuli has to be judged, and both stimuli overlap to a certain degree. The first stimulus to be judged starts at t1, and while the stimulus is being presented, the second stimulus occurs at t2. Suppose further that the second stimulus is completely embedded within the first one. That is, presentation of the second stimulus will end at t3, and finally the first stimulus will end at t4. When judging the duration of both stimuli, one can divide the duration of the stimuli into three segments, which are the segment t1t2, the segment t2t3, and the segment t3t4. The duration of the first stimulus can then be judged by adding all segments, whereas the duration of the second stimulus might be judged by judging the segment t2t3.
Others propose that timing different intervals simultaneously necessitates multiple independent clocks which generate pulses that are switched into multiple accumulators. First hints referring to the existence of multiple clocks come from studies where rats were trained on a peak procedure in which three levers were individually associated with different durations initiated by the onset of a single signal (Matell et al., 2004, 2006; Buhusi and Meck, 2009). The responses of the rats showed that they were able to time the durations quite independently from each other, suggesting the use of independent clocks rather than a single clock.
If each of both concurrent stimuli is timed by a separate and independent pacemaker, judging both durations might be affected by different pacemaker speeds. Pacemaker speed has been discussed to be governed by stimulus modality (Penney et al., 1998; Wearden et al., 1998), referring to the fact that intervals marked by auditory signals are judged – on average – as being longer in duration than intervals marked by visual signals when both intervals are in fact the same (e.g., Goldstone and Goldfarb, 1964; Goldstone, 1968; Goldstone and Lhamon, 1974; Sebel and Wilsoncroft, 1983; Stubbs et al., 1984). According to the attentional-gate model, auditory stimulation increases the frequency of the pacemaker, resulting in a larger number of pulses being accumulated within a given time period. Thus, compared to time intervals presented by visual signals of equal length, time intervals presented by auditory signals should be judged as being longer in duration.
In this study, the method of temporal production was used to examine effects of concurrent timing on timing performance. In temporal production, participants are presented with a stimulus, and their task is to stop its presentation after a pre-specified time has elapsed. Usually, mean time productions vary linearly, and approximately accurately, with the time the participants are asked to produce, with more variance in judgments the longer the time produced is (Wearden and McShane, 1988; Wearden, 2003). In simultaneous temporal production, two (or more) durations have to be produced in parallel. This is achieved when the stimuli which have to be terminated overlap in part or in total. In the experiments of this study, the target interval was accompanied by a distracter interval, which was always shorter than the target interval and completely embedded within it.
Temporal productions have frequently been used for eliciting temporal judgments, especially within the dual-task paradigm in order to show interference effects between the timing task and the distracter task (e.g., Fortin and Breton, 1995; Hemmes et al., 2004; Brown and Merchant, 2007). However, when individual temporal productions are transformed into relative frequencies, distributions of these frequencies tend to be slightly skewed, although the fit to the normal distribution has been shown to be generally good (Wearden and McShane, 1988).
Two hypotheses were tested with this study, each pertinent to a single possible source of variance in simultaneous temporal judgments. First, it was hypothesized that if attentional resources needed to judge stimulus duration are limited and must be divided in case of the timing of two concurrent stimuli, temporal judgments in simultaneous timing should be altered in relation to the overlap of the two durations. During overlap, fewer pulses would be accumulated within a time period for each interval to be judged than if only a single interval has to be estimated. Therefore, it would take more time to reach the critical number of pulses that reflect the time to be produced. Accordingly, production times of the target interval should vary as a function of production times of the distracter interval: the longer the distracter interval is produced, the longer should be the production times of the target interval.
The second hypothesis was concerned with the question of whether one or two clocks are needed if two durations have to be judged concurrently. If the stimuli presented in different modalities would be timed by different and independent clocks, one would expect modality-dependent effects on clock speed to occur. More precisely, if one stimulus is presented within the visual modality and the other stimulus is presented within the auditory modality, the speed of the clock timing the visual interval should be lower than the speed of the clock timing the auditory interval (cf. Penney et al., 1998; Wearden et al., 1998). Hence, in case of two independent clocks, productions of the distracter interval should be shorter in the VIS–AUD condition than in the VIS–VIS condition (and shorter in the AUD–AUD condition than in the AUD–VIS condition) since clock speed in the auditory modality is assumed to be higher than in the visual modality. Moreover, if mean productions of the distracter interval presented within the visual modality are longer than mean productions of the distracter interval presented within the auditory modality, the duration of the overlap of the target interval and the distracter interval should be longer in the VIS–VIS condition than in the VIS–AUD condition (and accordingly longer in the AUD–VIS condition than in the AUD–AUD condition). The longer the overlap, the longer should be the production time for the target interval. Hence, mean productions of the target interval should be longer in the VIS–VIS condition than in the VIS–AUD condition, and longer in the AUD–VIS condition than in the AUD–AUD condition. Figure 1 illustrates the hypotheses stated above.
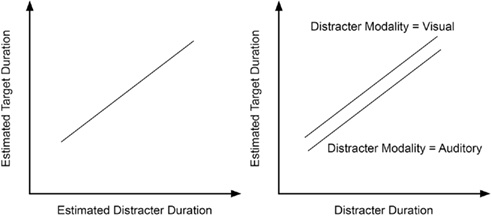
Figure 1. Illustration of the hypotheses of this study. Left panel: Illustration of Hypothesis 1 which states that estimated target duration grows proportionally with estimated distracter duration; right panel: Illustration of Hypothesis 2 which asserts that estimated target duration grows proportionally with the announced distracter duration, but is longer in case of a visual distracter stimulus than in case of an auditory distracter stimulus.
Materials and Methods
In both experiments, the participants had to simultaneously produce two time intervals which had different onsets. The target interval was the longer of both intervals, and the durations chosen for the target interval were 9, 10, or 11 s. The second interval, the distracter interval, was shorter than the target interval and was always embedded within the target interval. The conditions realized differed regarding the modality of the target interval and of the distracter interval. In Experiment 1, the target interval was presented visually, and the distracter was either presented auditorily or visually. In Experiment 2, the distracter was again either auditory or visual, but the target interval was presented auditorily. Thus, four conditions were realized in total. In Experiment 1, the conditions were VIS–VIS and VIS–AUD, and in Experiment 2 the conditions were AUD–AUD and AUD–VIS.
In this study, control trials in which participants judged only a single duration were omitted. The major reason for this decision was that comparisons between single-stimulus timing and simultaneous timing might be confounded with an effect of the mere presentation of a second stimulus. Suppose that in simultaneous timing the target duration is produced longer than the same duration in single-stimulus timing. This effect might be due to the attention that is distracted from timing the target duration in order to judge the distracter duration in parallel. However, detecting the distracter stimulus might also capture attention, irrespectively of its duration (cf. Ivry and Hazeltine, 1995). Hence, variance in judging the target interval in simultaneous timing could be an effect of both the concurrent timing of the distracter stimulus and attending to its mere presentation. In this study, duration-independent variance due to the mere presentation of the distracter stimulus was kept constant by comparing conditions only differing in duration of the distracter stimulus. Therefore, the hypotheses according to effects of the production of the distracter duration on the production of the target duration were tested by varying the production times of the distracter duration.
Participants
With Experiment 1, temporal judgments of 40 participants (22 women, 18 men) were examined. Mean age of all participants was 30.3 years (SD = 4.6). In Experiment 2, 21 women and 19 men participated. Mean age of all participants was 29.7 years (SD = 7.2). The participants were randomly assigned to the conditions. The participants attended voluntarily and gave their consent for participation in the experiments.
Stimuli and Apparatus
The target stimulus in Experiment 1 was a white square (3 cm × 3 cm) presented on a dark background on the left side of the computer monitor screen. In Experiment 2, the target stimulus was a sine tone of 300 Hz, presented via headphones. The distracter intervals were presented either visually or auditorily. The visual distracter stimulus was the same as the target stimulus, but presented on the right side of the screen. The auditory distracter stimulus was a 500-Hz sine tone, presented via headphones.
All visual experimental events (including the instructions) were presented on a 15″ computer screen (50 Hz refresh rate), and were controlled by the software “Experimental Run Time System” [ERTS], version 3.00, from BeriSoft, Frankfurt, Germany, running on a Pentium-II-Computer. The software allows for precise timing of stimuli and responses in the milliseconds range. The distance between the participants and the screen was about 70 cm.
In both experiments, white digits were presented on dark background to the participants on the monitor prior to onset of the target and distracter durations on each trial. These digits announced the durations (in seconds) to be produced. The digits were either “9,” “10,” or “11” for the target duration (presented on the left side of the screen), and “2,” “4,” or “6” for the distracter duration (presented on the right side of the screen).
Procedure
The participants were tested individually in a moderately illuminated and quiet room. After each participant took her/his seat in front of the monitor, she/he was informed about the purpose of the experiment. Then, the participant received instructions presented on the computer screen.
Both the target interval and the distracter interval to be produced were symbolized as digits presented at the beginning of each trial. The digit on the left side represented the target duration, the digit on the right side the duration of the distracter. Presentation of the digits was aborted by the participant’s key press.
Two seconds after abortion of the presentation of the digits, the production task started in Experiment 1 with a white square presented on the left side of the monitor, and in Experiment 2 with the presentation of a 300-Hz sine tone. Presentation of the target stimulus indicated the participants to begin with the production of the target interval. After a randomly chosen inter-onset interval (IOI), the stimulus indicating the beginning of the production of the distracter interval started, which was either a second square appearing on the right side of the monitor (Condition VIS–VIS and Condition AUD–VIS), or a tone presented via headphones (Condition AUD–AUD and Condition VIS–AUD). The production times of the target intervals were announced to be 9, 10, or 11 s, the production times of the distracter interval were announced to be 2, 4, or 6 s.
After the time had elapsed that was judged to be the same as previously announced, the participants pressed the ALT key for the target interval and the ALT-R key for the distracter interval. By pressing either key, the respective stimulus disappeared. After that, a new trial began following an inter-trial interval of 3 s.
The participants were instructed to conduct the production task by the following instruction (here an example of the VIS–VIS condition is used; the original instructions were given in German). In order to prevent the participants from using a simple arithmetic as a strategy for timing the simultaneous stimuli, they were encouraged not to count when producing the durations.
You will now be presented with two digits that will appear on the computer monitor screen. One digit will appear on the left side of the screen, and one will appear on the right side of the screen. These digits represent the durations (in seconds) you will have to produce then. By pressing the space bar, the digits will disappear. Please keep the digits in mind.
After disappearance of the digits, a white square will be presented on the left side of the screen. Please wait for the time that was previously indicated by the left digit until you have to press the ALT key to terminate the appearance of the left square.
While the left square is being presented, a second square will occur on the right sight of the screen. Please wait for the time that was previously indicated by the right digit until you have to press the ALT-R key to terminate the appearance of the right square.
Please do not count when judging the durations.
Each participant judged every possible combination of the target duration and the distracter duration three times, resulting in a total of 27 trials per participant. The onset of both durations was temporally displaced, with the onset of the distracter duration occurring later than the onset of the target duration. The IOI was chosen randomly, with a minimum IOI = 1.5 s and a maximum IOI = 2.5 s (mean IOI = 2.0 s).
Results
Experiment 1
A first step toward the analyses of the data obtained was to inspect the frequency distributions of the temporal productions in order to evaluate their appropriateness for being entered into parametric analyses. Therefore, frequencies of times produced were grouped into bins of 0.50 s width, and histograms were plotted. A Gaussian curve was fitted to the frequency distributions, with the same mean and the same SD as the frequency distribution. Figure 2 shows the distributions for both the target durations (upper panel) and the distracter durations (lower panel).
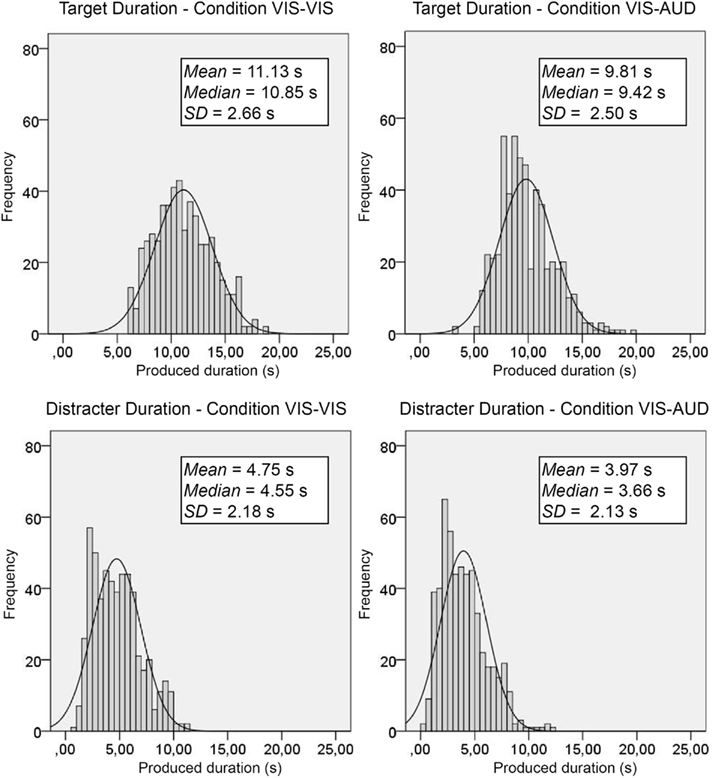
Figure 2. Histograms for times produced in Experiment 1. Upper panel: Frequency distributions for the target durations. Lower panel: Frequency distributions for the distracter durations. Each distribution is accompanied with a Gaussian curve with the same mean and the same SD as the frequency distribution. Additionally, the means, the medians, and the SDs of the frequency distributions are depicted in the figure.
As can be seen, the distributions were unimodal and slightly shifted to the left, which is also indicated by a mean being somewhat larger than the median value. However, Kolmogorov–Smirnov tests conducted for each distribution to test for deviances from normality yielded significant deviations in most cases (almost all p-values were smaller than p = 0.01). Therefore, square-root transformations of raw production times were conducted, which yielded values that were better described by a normal distribution that the raw values. In fact, only one out of four p-values were smaller than p = 0.05, the remaining three p-values were larger than p = 0.10.
With Experiment 1 the hypothesis was tested that the duration needed for producing the target interval should be linearly related to the productions of the distracter interval. This hypothesis was tested by regression analysis, with the square root of the temporal productions of the target time as criterion, and the square root of the temporal productions of the distracter time as predictor. Figure 3 shows the scatter plots obtained from Experiment 1 wherein the square root of the production times of the target interval (plotted on the ordinate) are related to the square root of the production times of the distracter interval (plotted on the abscissa). It is clearly visible that a linear relationship well describes the connection between both durations. Regression analyses yielded a slope of B1 = 0.39 and an intercept of B0 = 2.50 for Condition VIS–VIS, and a slope of B1 = 0.38 and an intercept of B0 = 2.37 for Condition VIS–AUD. Both linear trends were highly significant (p < 0.001).
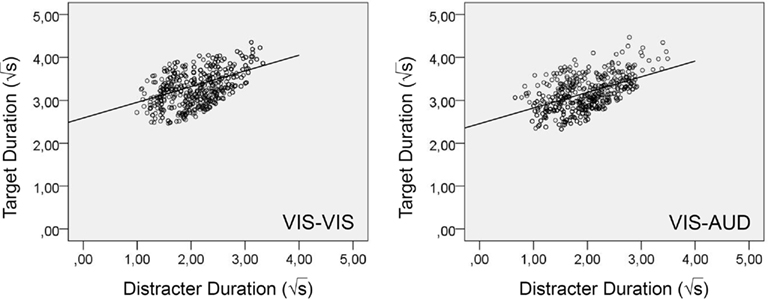
Figure 3. Scatter plots showing the relationship between the square root of the production times of the distracter interval (abscissa) and the square root of the production times of the target interval (ordinate) obtained from Experiment 1. Left panel: Data obtained from Condition VIS–VIS; Right panel: Data obtained from Condition VIS–AUD. The straight line indicates the least-square regression line.
Moreover, Experiment 1 aimed at answering the question of how many clocks were involved in the production of two intervals in parallel. If one clock would be sufficient, one would expect that temporal productions of the target interval should not differ between both conditions. However, if one clock would operate the timing of the target interval and another clock would operate the timing of the distracter interval, each clock should be triggered by stimulus modality. For the bimodal condition, this would mean that the (auditory) distracter interval was timed by a clock that was assumed to be “faster” than the clock timing the (visual) target interval. If this were true, two consequences should follow. The first consequence is related to the production time of the distracter intervals. If clock speed was altered due to stimulus modality, then the auditory distracter interval should on average be produced in less time than the visual distracter interval because the “auditory” clock is supposed to emit pulses at a faster rate than the “visual” clock.
As a second consequence, the mean production times of the target interval should be shorter in Condition VIS–AUD than in Condition VIS–VIS due to a shorter overlap of the target and the distracter duration.
To test the second hypothesis, regression analysis was run, with the square root of estimated target time as the criterion, and both the square root of the announced distracter duration and distracter modality as predictors. If the hypothesis holds, regression analysis should reveal a linear trend, a positive regression weight for distracter duration (since the longer the distracter was announced to be produced, the longer should the target be produced), and a negative regression weight for modality (since target productions should be shorter with an auditory than with a visual distracter). Indeed, regression analysis confirmed the hypothesis. Estimated target time was a function of both distracter time (B1 = 0.08, p = 0.004) and distracter modality (B2 = −0.20, p < 0.001), with an intercept of B0 = 3.36, p < 0.001. The linear trend was shown to be significant, F(2, 1075) = 40.36, p < 0.001. Figure 4 displays temporal productions of the target interval, estimated by regression analysis.
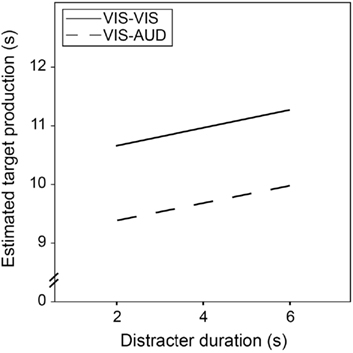
Figure 4. Temporal productions of the target interval in Experiment 2, estimated by linear regression analysis. The straight line indicates estimations of temporal productions in case the distracter stimulus was presented visually, the interrupted line indicates temporal productions in case the distracter stimulus was presented auditorily. Note that temporal estimates and distracter times were displayed as untransformed values to yield better comprehensibility.
Experiment 2
Analyses of results of Experiment 2 were the same as those conducted in Experiment 1. First, the frequency distributions of the production times were plotted (see Figure 5). As in Experiment 1, the distributions were in part skewed. Kolmogorov–Smirnov tests yielded significant deviations in most cases (almost all p-values were smaller than p = 0.01). After square-root transformation, Kolmogorov–Smirnov tests identified only in one case a slight deviation from normality (p = 0.02), the remaining three p-values were larger than p = 0.25.
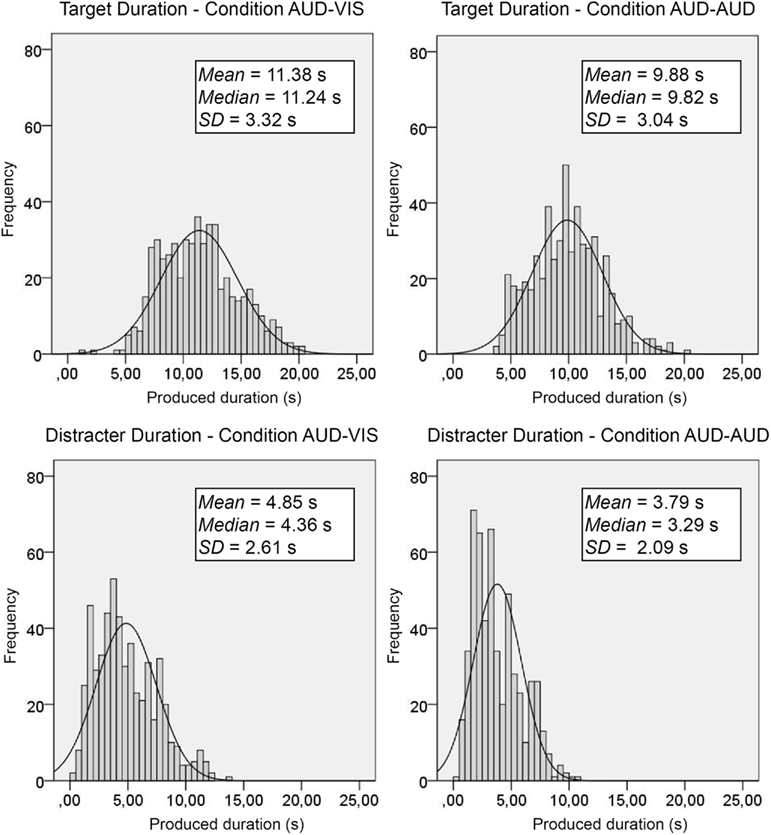
Figure 5. Histograms for times produced in Experiment 2. Upper panel: Frequency distributions for the target durations. Lower panel: Frequency distributions for the distracter durations. Each distribution is accompanied with a Gaussian curve with the same mean and the same SD as the frequency distribution. Additionally, the means, the medians, and the SDs of the frequency distributions are depicted in the figure.
Second, scatter plots were obtained with the transformed estimates (Figure 6) which show the square root of the production times of the target interval (plotted on the ordinate) related to the square root of the production times of the distracter interval (plotted on the abscissa).
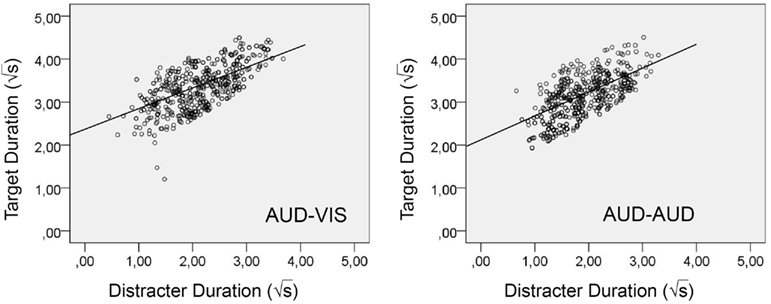
Figure 6. Scatter plots showing the relationship between the square root of the production times of the distracter interval (abscissa) and the square root of the production times of the target interval (ordinate) obtained from Experiment 2. Left panel: Data obtained from Condition AUD–AUD; right panel: Data obtained from Condition AUD–VIS. The straight line indicates the least-square regression line.
Both inspection of the scatter plots and regression analyses show a clear linear relationship between production times of the target interval and production times of the distracter interval, indicating again a proportional effect of the duration of the distracter interval on the duration of the target interval. Regression analyses yielded a slope of B1 = 0.53 and an intercept of B0 = 2.21 for Condition AUD–VIS, and a slope of B1 = 0.61 and an intercept of B0 = 1.97 for Condition AUD–AUD. Both linear trends were again highly significant (p < 0.001).
To examine whether stimulus modality affected the production times of both the distracter stimuli and the target stimuli, regression analysis was run, with the square root of estimated target time as the criterion, and the square root of the announced distracter duration and distracter modality as predictors. Again, regression analysis confirmed the hypothesis. Estimated target time was a function of both the distracter time (B1 = 0.18, p < 0.001) and distracter modality (B2 = −0.23, p < 0.001), with an intercept of B0 = 3.23, p < 0.001. The linear trend was significant, F(2, 1077) = 42.69, p < 0.001. Figure 7 displays temporal productions of the target interval, estimated by regression analysis.
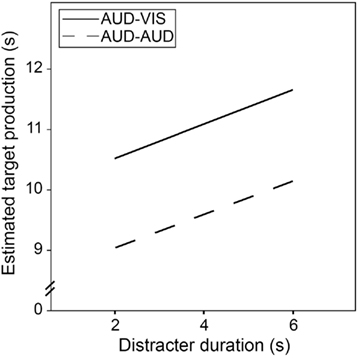
Figure 7. Temporal productions of the target interval in Experiment 2, estimated by linear regression analysis. The straight line indicates estimations of temporal productions in case the distracter stimulus was presented visually, the interrupted line indicates temporal productions in case the distracter stimulus was presented auditorily. Note that temporal estimates and distracter times were displayed as untransformed values to yield better comprehensibility.
Discussion
With this study, it was examined whether one or two clocks operate the timing of two intervals which were presented simultaneously. The target interval always preceded the distracter interval, and was longer than it. Thus, the distracter interval was completely embedded within the target interval. The participants used the method of temporal production, that is, they monitored the duration of both stimuli and pressed a button when they judged a match between a criterion which was announced prior to stimulus presentation, and the actual stimulus duration. The stimuli to be judged differed in modality which allowed for testing the hypothesis of modality-specific internal clocks that operate in parallel and independent from one another when two stimuli were presented at the same time.
The distributions of the production times of this study resembled those obtained in previous studies (e.g., Wearden and McShane, 1988). The distributions were slightly skewed, with more productions made at intervals shorter than the mean than made at intervals longer than the mean. Since skewness of data might affect estimates of parametric statistical analyses, production times were square-root transformed. Transformation of the data actually yielded a better fit to normality than did untransformed data. The following discussion of the results is done with regard to the transformed data, although it might be generalized to untransformed data as well.
The main results of this study were as follows. First, production times of the target interval varied proportionally with production times of the distracter interval. On average, productions of the target interval increased with increasing productions of the distracter interval. This result corresponds to predictions made by the attentional-gate model proposed by Block and Zakay (1996) which assumes that – due to limited attentional resources – doing two tasks in parallel will affect performance on either task. Moreover, a linear relationship between production of the target and production of the distracter points to a constant amount of attention per time unit that misses in temporal judgment when the duration of two stimuli has to be judged concurrently. This result is furthermore in contradiction to the assumption of a single clock that operates the timing of two stimuli presented in parallel by dividing both durations into a succession of segments.
It may be argued that prolongation of the distracter duration occurred in part due to a tendency of the participants not to end the production of the target interval before production of the distracter interval had been finished because the participants knew that one interval (the target) was always longer than the other (the distracter). However, it should be noted that there was no explicit requirement given in the instructions to wait with finishing the production of the target interval until production of the distracter interval had been done. Moreover, as the IOI between the presentation of the target stimulus and the presentation of the distracter stimulus randomly varied, the participants were not able to infer that production of the distracter interval should always be embedded within production of the target interval. Moreover, inspection of the scatter plots might suggest that producing a short distracter resulted in a shortening of the target production. Shortening in this sense means that a short distracter would lead to a target that is produced in less time than when no distracter is presented. If this were true, a contradiction to Zakay’s and Block’s attentional-gate model would have been found since this model assumes always a prolongation of the target production if a distracter duration is to be judged in parallel. The reason for the assumed prolongation is that according to the model doing two tasks in parallel leaves fewer attentional resources for the single task so that each single task has to be done with attentional deficits. Hence, if less attention is devoted to timing, longer instead of shorter temporal productions should result. However, if a shortening effect in the sense described above was actually present in this study it could hardly be detected because there was no condition realized wherein only one duration was to be judged.
Second, if one clock would operate the timing of the target interval and another clock would operate the timing of the distracter interval, it was expected that each clock should be triggered by stimulus modality separately. For the bimodal conditions realized in this study, this would mean that the distracter interval was timed by a clock that was assumed to be either “faster” than the clock timing the target interval, if the target was a light and the distracter was a sound, or “slowed down,” if the target was a sound and the distracter was a light. According to this hypothesis, two findings were expected. First, if clock speed was altered due to stimulus modality, then the auditory distracter interval should on average be produced in less time than the visual distracter interval because the “auditory” clock is supposed to emit pulses at a faster rate than the “visual” clock (Penney et al., 1998; Wearden et al., 1998) Second, the produced duration of the target stimulus should be shorter when accompanied by an auditorily presented distracter than when accompanied by a visually presented distracter.
The actual outcomes matched the expected ones. As regression analyses have shown, target durations were produced in less time when distracter stimuli were presented auditorily rather than visually. Moreover, production times of the target interval grew proportionally with the announced duration of the distracter stimulus.
This study brought evidence in favor of a timing device in humans that is able to estimate two durations in parallel by the use of separate and independent clocks. Timing, however, appeared to be affected by limited attention since it was found that temporal estimates of one stimulus varied proportionally with temporal estimates of the second stimulus. The attentional-gate model offers a straightforward explanation of this proportional effect. It assumes a gate that allows pulses emitted by the pacemaker to be stored and accumulated in a counter if attention is devoted to the timing task. If, however, attention is detached from the timing task, fewer pulses are accumulated. This assumption can easily be adapted to simultaneous timing. Whenever two timing tasks have to be executed in parallel, attention has to be divided between both timing tasks, therefore less attention is devoted to the timing of a stimulus in simultaneous timing, compared to timing single durations.
A quantitative modeling of simultaneous timing may be achieved when the slopes and the intercepts obtained in this study, and differences of slopes and intercepts between the conditions realized, are analyzed and interpreted. The slope reflects the impact of the duration produced for the distracter stimulus on the duration produced for the target stimulus. The larger the slope, the larger was the impact of the distracter duration on the target duration. If the distracter duration would have had no effect on the target duration, a slope of (or near to) zero would be expected. The intercept represents an estimate of the target duration, if one would assume that there was no effect of the distracter on the target. It is an additive constant that best predicts the nominal average value for the target duration (which actually was 10 s). The value of the slope points to the amount of prolongation of the target duration. For example, in Condition VIS–VIS of Experiment 1, mean slope was 0.39. This value means that the square root of the production of the target time increased by 0.39 times the square root of the production of the distracter time. If the production time for the distracter was, for example, 4 s, the additional time the square root of the target was produced was on average √4 × 0.39 s. Inserting the values into the regression equation obtained will, of course, easily yield the untransformed production times.
With respect to the attentional-gate model, the slope may be interpreted as the amount to which attention was detached from the timing of the target interval. If the slope would be zero, attention would be fully devoted to the target interval. On the contrary, if the slope would be one, all attention would be withdrawn from the timing of the target interval, since producing 1 s of the distracter would result in an additional 1 s of the target. Hence, in case of a slope that equals one, timing both the distracter and the target could be well described by the stop mode suggested by Meck and Church (1983). In the stop mode, participants behave as if they retain the pulses accumulated prior to the distracter, and proceed with the timing of the target after producing the distracter had been finished.
One might speculate about the reason why the slopes obtained from Experiment 1 were smaller than those obtained from Experiment 2. A possible explanation refers to differences in clock speed that have been assumed for the visually and auditorily displayed target intervals, and the role attention might play in timing. There is some evidence that information being active in working memory is processed serially instead of simultaneously (e.g., Sternberg, 1966; Schneider and Shiffrin, 1977). For example, in a dual-count task in which subjects were required to keep two running counts in working memory, they switched between these counts in order to update both running counts (Garavan, 1998). If attention is necessary for counting the pulses that are emitted by the pacemaker, one can assume analogously that attention has to be switched from one counter to the other counter in order to keep the counts in working memory, in case of two counters being involved in timing. Consequently, since switching needs some time, the pace with which attention switches between both counters should have an effect on the outcome of the timing process. Suppose that switching from one counter to the other counter takes the same time than to emit one pulse from the pacemaker. In this case, attention would only capture every second pulse, thus doubling the “normal” production time would result. In case the attentional switch is twice as fast as the pacemaker rate, every pulse will be monitored, and counted. In Experiment 1, the target stimulus was visual, whereas in Experiment 2 it was auditory. If a clock timing an auditory stimulus is faster than a clock timing a visual one, more pulses would be left during the attentional switch in the auditory modality than in the visual modality. Accordingly, the slope would be larger in audition than in vision.
The results obtained are in line with the hypothesis of multiple clocks timing different overlapping stimuli. Nonetheless it is unknown whether there exist components of the clock that might be shared when judging time intervals in parallel. For example, it seems plausible that only one reference memory is needed two judge more than one interval simultaneously. Further research should address this issue. Moreover, within this study only simultaneous temporal judgments were realized. This experimental design did not allow for comparisons between simultaneous and single time productions. With respect to a possible shortening of target productions when being accompanied with short distracter durations, it might be worth to extend this design by including direct comparisons between single and parallel temporal productions.
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This research paper was financially supported by the Fonds National de la Recherche Luxembourg. (Grant number: FNR/11/AM4/67).
References
Block, R. A., and Zakay, D. (1996). “Models of psychological time revisited,” in Time and Mind, ed. H. Helfrich (Göttingen: Hogrefe & Huber Publishers), 171–195.
Brown, S. W., and Merchant, S. M. (2007). Processing resources in timing and sequencing tasks. Percept. Psychophys. 69, 439–449.
Brown, S. W., Stubbs, D. A., and West, A. N. (1992). “Attention, multiple timing, and psychophysical scaling of temporal judgments,” in Time, Action, and Cognition, eds F. Macar, V. Pouthas, and W. J. Friedman (Dordrecht: Kluwer Academic Publishers), 129–140.
Brown, S. W., and West, A. N. (1990). Multiple timing and the allocation of attention. Acta Psychol. (Amst.) 75, 103–121.
Buhusi, C. V., and Meck, W. H. (2009). Relativity theory and time perception: single or multiple clocks? PLoS ONE 4, 1–6. doi: 10.1371/journal.pone.0006268
Church, R. M. (1984). “Properties of the internal clock,” in Timing and Time Perception. Annals of the New York Academy of Sciences, Vol. 423, eds J. Gibbon, and L. Allan (New York: New York Academy of Sciences), 566–582.
Curtis, D. W., and Rule, S. J. (1977). Judgment of duration relations: simultaneous and sequential presentation. Percept. Psychophys. 22, 578–584.
Fortin, C., and Breton, R. (1995). Temporal interval production and processing in working memory. Percept. Psychophys. 57, 203–215.
Fortin, C., and Rousseau, R. (1998). Interference from short-term memory processing on encoding and reproducing brief durations. Psychol. Res. 61, 269–276.
Gibbon, J., Church, R. M., and Meck, W. H. (1984). “Scalar timing in memory,” in Timing and Time Perception. Annals of the New York Academy of Sciences, Vol. 423, eds J. Gibbon, and L. Allan (New York: New York Academy of Sciences), 52–77.
Goldstone, S. (1968). Production and reproduction of duration: intersensory comparisons. Percept. Mot. Skills 26, 755–760.
Goldstone, S., and Goldfarb, J. L. (1964). Auditory and visual time judgment. J. Gen. Psychol. 70, 369–387.
Goldstone, S., and Lhamon, W. T. (1974). Studies of auditory-visual differences in human time judgment: 1. Sounds are judged longer than lights. Percept. Motor Skills 39, 63–82.
Hemmes, N. S., Brown, B. L., and Kladopoulos, C. N. (2004). Time perception with and without a concurrent nontemporal task. Percept. Psychophys. 66, 328–341.
Hicks, R. E., Miller, G. W., and Kinsbourne, M. (1976). Prospective and retrospective judgments of time as a function of amount of information processed. Am. J. Psychol. 89, 719–730.
Ivry, R. B., and Hazeltine, R. E. (1995). Perception and production of temporal intervals across a range of durations: evidence for a common timing mechanism. J. Exp. Psychol. Hum. Percept. Perform. 21, 3–18.
Klapproth, F. (2008). Time and decision making in humans. Cogn. Affect. Behav. Neurosci. 8, 509–524.
Matell, M. S., Bateson, M., and Meck, W. H. (2006). Single-trial analyses demonstrate that increases in clock speed contribute to the methamphetamine-induced horizontal shifts in peak-interval timing functions. Psychopharmacology (Berl.) 188, 201–212.
Matell, M. S., King, G. R., and Meck, W. H. (2004). Differential modulation of clock speed by the administration of intermittent versus continuous cocaine. Behav. Neurosci. 118, 150–156.
Meck, W. H., and Church, R. M. (1983). A mode control model of counting and timing processes. J. Exp. Psychol. Anim. Behav. Process. 9, 320–334.
Meck, W. H., and Church, R. M. (1984). Simultaneous temporal processing. J. Exp. Psychol. Anim. Behav. Process. 10, 1–29.
Penney, T. B., Allan, L. G., Meck, W. H., and Gibbon, J. (1998). “Memory mixing in duration bisection,” in Timing of Behavior: Neural, Computational, and Psychological Perspectives, eds D. A. Rosenbaum, and C. E. Collyer (Cambridge, MA: MIT Press), 165–193.
Rule, S. J., and Curtis, D. W. (1985). Ordinal properties of perceived average duration: simultaneous and sequential presentations. J. Exp. Psychol. Hum. Percept. Perform. 11, 509–516.
Rule, S. J., Mahon, M. L., and Curtis, D. W. (1983). Composition rule for perceived duration of simultaneous events. Percept. Psychophys. 34, 569–572.
Schneider, W., and Shiffrin, R. M. (1977). Controlled and automatic human information processing: I. Detection, search, and attention. Psychol. Rev. 84, 1–66.
Sebel, A. J., and Wilsoncroft, W. E. (1983). Auditory and visual differences in time perception. Percept. Mot. Skills 57, 295–300.
Stubbs, D. A., Dreyfus, L. R., and Fetterman, J. G. (1984). “The perception of temporal events,” in Timing and Time Perception. Annals of the New York Academy of Sciences, Vol. 423, eds J. Gibbon, and L. Allan (New York: New York Academy of Sciences), 30–42.
van Rijn, H., and Taatgen, N. A. (2008). Timing of multiple overlapping intervals: how many clocks do we have? Acta Psychol. (Amst.) 129, 365–375.
Wearden, J. H. (1992). Temporal generalization in humans. J. Exp. Psychol. Anim. Behav. Process. 18, 134–144.
Wearden, J. H. (2003). “Applying the scalar timing model to human time psychology: progress and challenges,” in Time and Mind I: Information Processing Perspectives, ed. H. Helfrich (Göttingen: Hogrefe & Huber Publishers), 21–39.
Wearden, J. H., Edwards, H., Fakhri, M., and Percival, A. (1998). Why “sounds are judged longer than lights”: application of a model of the internal clock in humans. Q. J. Exp. Psychol. 51B, 97–120.
Wearden, J. H., and McShane, B. (1988). Interval production as an analogue of the peak procedure: evidence for similarity of human and animal timing processes. Q. J. Exp. Psychol. 40B, 363–375.
Zakay, D., and Block, R. A. (1996). “The role of attention in time estimation processes,” in Time, Internal Clocks and Movement, eds M. A. Pastor, and J. Artieda (Amsterdam: Elsevier), 143–164.
Keywords: simultaneous timing, temporal judgment, temporal decision making, modality, dual-clock hypothesis, multiple timers
Citation: Klapproth F (2011) Temporal decision making in simultaneous timing. Front. Integr. Neurosci. 5:71. doi: 10.3389/fnint.2011.00071
Received: 15 June 2011; Paper pending published: 30 June 2011;
Accepted: 08 October 2011; Published online: 28 October 2011.
Edited by:
Warren H. Meck, Duke University, USAReviewed by:
Catalin V. Buhusi, Medical University of South Carolina, USAClaudette Fortin, Université Laval, Canada
Copyright: © 2011 Klapproth. This is an open-access article subject to a non-exclusive license between the authors and Frontiers Media SA, which permits use, distribution and reproduction in other forums, provided the original authors and source are credited and other Frontiers conditions are complied with.
*Correspondence: Florian Klapproth, Languages, Culture, Media and Identities Research Unit, University of Luxembourg, Building III, Office 007, Route de Diekirch, L-7201Walferdange, Luxembourg. e-mail:Zmxvcmlhbi5rbGFwcHJvdGhAdW5pLmx1
