- 1Department of Psychology, University of Illinois at Chicago, Chicago, IL, USA
- 2Laboratory of Integrative Neuroscience, University of Illinois at Chicago, Chicago, IL, USA
- 3Department of Psychology and Neuroscience, Duke University, Durham, NC, USA
- 4Center for Cognitive Neuroscience, Duke University, Durham, NC, USA
- 5Duke Institute for Brain Sciences, Duke University, Durham, NC, USA
- 6Department of Neurobiology, Duke University Medical Center, Durham, NC, USA
Humans and animals appear to share a similar representation of number as an analog magnitude on an internal, subjective scale. Neurological and neurophysiological data suggest that posterior parietal cortex (PPC) is a critical component of the circuits that form the basis of numerical abilities in humans. Patients with parietal lesions are impaired in their ability to access the deep meaning of numbers. Acalculiac patients with inferior parietal damage often have difficulty performing arithmetic (2 + 4?) or number bisection (what is between 3 and 5?) tasks, but are able to recite multiplication tables and read or write numerals. Functional imaging studies of neurologically intact humans performing subtraction, number comparison, and non-verbal magnitude comparison tasks show activity in areas within the intraparietal sulcus (IPS). Taken together, clinical cases and imaging studies support a critical role for parietal cortex in the mental manipulation of numerical quantities. Further, responses of single PPC neurons in non-human primates are sensitive to the numerosity of visual stimuli independent of low-level stimulus qualities. When monkeys are trained to make explicit judgments about the numerical value of such stimuli, PPC neurons encode their cardinal numerical value; without such training PPC neurons appear to encode numerical magnitude in an analog fashion. Here we suggest that the spatial and integrative properties of PPC neurons contribute to their critical role in numerical cognition.
Humans possess a deep understanding of the meaning of numbers, and the practical use of this abstract ability is ubiquitous. We rely on numerical information in a myriad of daily tasks ranging from the simplicity of purchasing a cup of coffee to the complexity of developing financial instruments like mortgage-backed securities—irrespective of the wisdom of doing so. Complex quantitative behaviors are not limited to humans. Even the apparently simple behavior of a bee collecting pollen from a flower involves the computation and comparison of relative rates of return from various patches of flowers (Couvillon and Bitterman, 1985; Montague et al., 1995; Shapiro et al., 2001). A wealth of research suggests that humans share with animals a representation of number as an analog magnitude on an internal, subjective, scaled “number line” that is less precise with increasing magnitude (Platt and Johnson, 1971; Whalen et al., 1999).
However, there are several considerations that may constrain the instantiation of such a numerical scaling in neural circuits. For example, it remains hotly debated whether small numbers (one-two-three) are represented in a qualitatively different manner than larger estimated numerosities (Hyde, 2011). Moreover, the neural signatures of numerical judgments must be compatible with the manner in which an analog magnitude system estimates quantity. Ultimately, the representation of quantity must be stripped of the continuous properties of that which is quantified, e.g., “six” has the same meaning whether it describes six drops of water or six beluga whales. Psychophysical measurements provide limits as to the properties that must be accounted for by the neural systems that represent quantity. One concept of such a number line could be more literal, akin to an orderly spatial map of quantity in the brain (Dehaene et al., 1993; Gut et al., 2012). Here, we take a broader view that the properties of numerical cognition evident from behavior emerge from the response properties of neurons in parieto-frontal circuitry, in which posterior parietal cortex (PPC) plays a crucial role.
Psychophysics of Numerical Discrimination
Psychophysical data suggest that number is represented as a point on an analog mental number line. For example, rats or humans asked to produce n responses or estimate n events do so with less precision as n increases (Platt and Johnson, 1971; Whalen et al., 1999). In addition, the variability of responses increases proportionally with n such that the coefficient of variation (CV, the ratio of the standard deviation to the mean) is constant as n increases. Indeed, members of the Piraha tribe of Amazonia, whose numerical language is limited to “one-two-many,” show a similar pattern of behavior in which both the number and variability of numerical estimates increase with n, with a constant CV (Gordon, 2004). The similarity between animals and humans, even those using innumerate language, suggests a common underlying system for numerical estimation.
Hallmarks of numerical comparison are the distance and magnitude effects. Humans reporting the larger of two numbers do so faster and more accurately as the distance between them increases. And, when the distance between two numbers is fixed, accuracy and speed decrease as the overall magnitude of the two numbers increases (Moyer and Landauer, 1967). Thus, subjects more accurately and quickly discriminate 2 vs. 9 than 6 vs. 7 (distance effect) or 32 vs. 39 (magnitude effect). Distance and magnitude effects are also found in the accuracy and reaction times of monkeys and pigeons ordering pairs of numerosities (Brannon and Terrace, 1998, 2000; Nieder and Miller, 2004a; Scarf et al., 2011). Figure 1 shows the similar ratio-dependence in the accuracy and speed of monkeys and humans reporting which of a pair of numerosity stimuli contains more (or fewer) elements (Cantlon and Brannon, 2006). These behavioral findings endorse the idea that the internal representation by the mental number line has greater variability with increasing quantity. Such a number line could be logarithmically compressed or linear with scalar variability (Brannon et al., 2001; Dehaene, 2001).
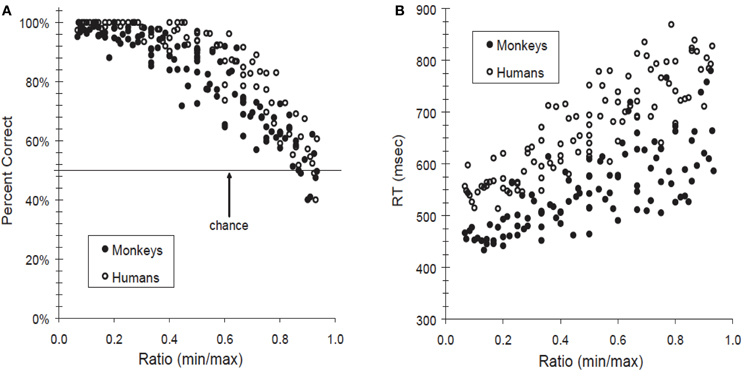
Figure 1. Humans' and monkeys' judgments of relative numerosity (more/fewer) depend on the ratio difference between the two stimuli. When judging arrays of dots that differ in quantity, accuracy increased (A) and response time decreased (B) as their ratio deviated from 1. For example, discrimination performance for 2 vs. 10 (ratio = 0.2) was faster and more accurate than for 9 vs. 10 (ratio = 0.9). From Cantlon and Brannon (2006).
Performance of simple approximate arithmetic tasks suggests that these operations are carried out using an analog representation of quantity. Participants who cannot rely on the rote memorization of basic mathematical operations (such as 2 + 3 = 5) nevertheless demonstrate the ability to perform simple calculations. Pre-schoolers accurately report whether the sum of two arrays of dots contains a larger number than a comparison array (Barth et al., 2006) and monkeys can choose a visual array that matches the sum of two sample arrays (Cantlon and Brannon, 2007). Even pigeons can discriminate the result of a subtraction operation from a constant value (Brannon et al., 2001; Dehaene, 2001). The Munduruku tribe of Amazonia, which lacks language for quantities greater than five, can estimate the results of approximate addition and subtraction, as well as compare quantitative stimuli well beyond their range of numerical literacy (Pica et al., 2004). Further, in these studies, accuracy for mathematical operations depended on the ratio of quantities compared. These findings suggest that mathematical operations are computed over a representation of quantity that is either linear with scaled variability or logarithmically compressed.
A critical prediction of Weber's law is that the ratio of two numbers determines their discriminability, regardless of their actual magnitude. Several lines of evidence using tests of non-symbolic numerical processing suggest number is innately represented on a compressed analog scale that supports ratio-dependence in discriminations. Human infants have been shown to discriminate large numbers, provided they differ by a ratio of 2:1, e.g., 8 vs. 4 or 16 vs. 8 (Xu and Spelke, 2000; Lipton and Spelke, 2003; Wood and Spelke, 2005). Adult human discrimination of non-symbolic visual arrays has also been shown to depend on the ratio of values compared, rather than their absolute magnitude (Piazza et al., 2004, 2007). A potential advantage of compressed scaling is the ability to process a wide range of quantities, just as the visual or auditory systems can process stimuli differing over orders of magnitude.
In studies of non-verbal subjects, such as animals and human infants, the confounding relationship between number and other stimulus attributes makes it difficult to demonstrate the capacity to represent number per se. For example, choices based on simultaneously presented stimuli that differ in number could be determined on the basis of such features as total surface area or density whereas the discrimination of sequentially presented stimuli, or production of a series of n responses, could be controlled by duration (of individual elements or the entire series) rather than number. More generally, number, space, and time all show similar properties of discriminability that follow Weber's law (Walsh, 2003), thus it is difficult to disentangle judgments based solely on numerosity apart from spatial and temporal magnitudes. Although animals are able to use number, it is possible that they do so only as last resort (Davis and Perusse, 1988). This proposition seems unlikely since both humans and animals performing tasks that do not oblige them to represent number do so (Meck and Church, 1983; Roberts and Mitchell, 1994; Brannon and Terrace, 1998; Roitman et al., 2007a; Jordan et al., 2008). Number thus appears to be spontaneously encoded, even when it is redundant with other cues.
Neurobiology of Numerical Representation
Neurological and neurophysiological data indicate that parietal cortex is a critical component of the circuits that form the basis of numerical abilities in humans. Patients with parietal lesions are impaired in their ability to access the deep meaning of numbers. Acalculiac patients with inferior parietal damage often have difficulty performing arithmetic (2 + 4?) or number bisection (what is between 3 and 5?) tasks, but are able to recite multiplication tables and read or write numerals (Dehaene and Cohen, 1991, 1997; Cohen and Dehaene, 1994). Gerstmann syndrome, which is characterized by the tetrad of acalculia, left-right disorientation, finger agnosia, and agraphia, is found in patients with inferior parietal damage (Gerstmann, 1940; Roeltgen et al., 1983; Benton, 1992). The progress of Gerstmann syndrome onset in Alzheimer's disease patients suggest that the degeneration underlying these four cognitive impairments share anatomical proximity in the parietal lobe (Wingard et al., 2002). Further, Turner's syndrome, an X-linked chromosomal disorder in humans, is marked by both structural abnormalities of the intraparietal sulcus (IPS) and abnormal development of numerical representation (Molko et al., 2003).
Complementary data from fMRI studies of neurologically intact humans performing subtraction (Simon et al., 2002), number comparison (Pinel et al., 2001), and non-verbal magnitude comparison (Fias et al., 2003) tasks show activity in the IPS. Taken together, clinical cases and imaging studies support a critical role for parietal cortex in the mental manipulation of numerical quantities. More specifically, Simon et al. (2002) suggest that the functional organization of human parietal lobe resembles that found in monkeys (Rizzolatti et al., 1998), and propose that correlates of numerical processing in primates may be found in areas along the IPS.
Studies of the role of parietal cortex in non-symbolic numerical representation in humans have produced conflicting data. Imaging studies have consistently reported the activation of parietal cortex in the processing of symbolic number, i.e., number words or Arabic numerals (Dehaene and Cohen, 1997; Pinel et al., 2001; Simon et al., 2002). To test whether representation of number in parietal cortex extends to non-symbolic stimuli, Piazza et al. (2004) employed an fMRI adaptation paradigm. In that study, human participants passively viewed visual arrays of n elements. As subjects habituated to a standard number (16 or 32), deviant values, ranging from half to double the value of the standard, were presented infrequently. Although participants were not explicitly required to discriminate the visual stimuli in any way, recovery of the BOLD signal along right and left IPS was proportional to the ratio of the standard and deviant stimuli (Figure 2). The same regions did not respond to changes in the shape of the elements. Further, adaptation to repeated numerosities and recovery in response to a deviant numerical value did not depend on whether non-symbolic (arrays of dots) or symbolic (Arabic numerals) stimuli were used (Piazza et al., 2007). Thus, brain activation by deviant numerical stimuli followed Weber's law. Subsequent studies not only replicated the adaptation of regions along the IPS to non-symbolic visual stimuli, but extended these findings to proportions (Jacob and Nieder, 2009). Subjects habituated to arrays of elements in which 50% (of totals ranging from 4 to 32) were colored blue and the rest were red. Infrequent probes with deviant stimuli composed of 60–90% red items drove recovery of the BOLD signal, with greater recovery as the distance between habituation and deviant proportion increased. Thus, regions along the IPS not only appear to encode estimates of whole numbers, but proportions as well.
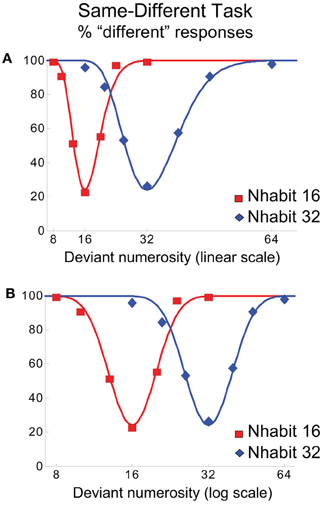
Figure 2. Areas along the horizontal intraparietal sulcus showed activation in response to a change in the numerosity of sequentially presented visual stimuli. The level of activation was proportional to the magnitude in the change of numerosity from a habituated standard value (16 or 32). The discriminability of probe values relative to the standard is compressed on a linear scale (A), and symmetrical on a logarithmic scale (B), consistent with Weber's law. Reprinted with permission from Piazza et al. (2004).
Counter to the suggestion that dedicated circuitry in parietal cortex is responsible for processing symbolic and non-symbolic quantity, Shuman and Kanwisher (2004) did not find adaptation of parietal responses to repeated presentations of non-symbolic numerical stimuli. Although they found greater IPS activation for difficult non-symbolic numerical comparisons, similar patterns of activation were observed for difficult color comparisons, suggesting that activation of this region is not limited specifically to the number domain. Ongoing research using electrophysiological methods (described below) similarly suggests that broader functions of parietal cortex support numerical cognition.
The earliest findings of a neural representation of number in animals also suggested a role for parietal cortex. Neurons in parietal cortex in anesthetized cats responded to the nth stimulus in a series, regardless of modality or inter-stimulus interval (Thompson et al., 1970). In monkeys, parietal neurons in area 5 were shown to respond to repetition number in a sequence of arm movements (Sawamura et al., 2002). These neurons had somatosensory receptive fields, but approximately one-third of the neurons studied had activity that was also modulated in relation to the position of the movement in a sequence. When inactivated, monkeys were impaired in completing the number of required repetitions of movements accurately, suggesting that these neurons were required to track the number of movements completed (Sawamura et al., 2010). Although the majority of studies related to neural encoding of quantity focus on regions within parietal cortex that process visual and oculomotor function, the work of Sawamura and colleagues shows similar encoding of quantity in circuits that process somatosensory information in arm movements.
The strongest evidence for neural correlates of numerical quantity has been found in the activity of single neurons in PPC of macaque monkeys judging visual stimuli varying in numerosity. PPC has been implicated in higher order sensorimotor processing and while not primarily sensory or motor in function, receives inputs from multiple sensory modalities and influences movement planning. There are several characteristics of PPC neurons that have implications for our interpretation of how quantity may be encoded at the level of single neurons. The areas along the IPS are considered to be part of the dorsal visual pathway carrying information about the location and movement of objects, and guiding eye or hand movements toward those objects in space (Ungerleider and Mishkin, 1982). The ventral intraparietal area (VIP), located in the fundus of the IPS, is situated to process visual and somatosensory information via inputs from the middle temporal (MT) and medial superior temporal (MST) visual areas, and from somatosensory areas 5 and 7 of the superior parietal lobule (Seltzer and Pandya, 1986; Ungerleider and Desimone, 1986; Boussaoud et al., 1990; Duhamel et al., 1998). Neurons in the lateral intraparietal area (LIP), in the lateral bank of the IPS, also receive inputs from visual motion areas MT and MST, but are driven by auditory stimuli as well (Felleman and Van Essen, 1991; Mazzoni et al., 1996b; Mullette-Gillman et al., 2005). Area LIP is interconnected with areas involved in the generation of saccadic eye movements, such as the superior colliculus and frontal eye field (Baizer et al., 1991). Anterior to LIP along the lateral bank of the IPS is the anterior intraparietal area (AIP), which responds to both visual stimuli and grasping movements of the hand (Jeannerod et al., 1995; Sakata et al., 1995). Intraparietal neurons are thus ideally situated to organize perception of multimodal stimuli toward appropriate behavioral responses.
A defining trait of neurons along the IPS is their spatially selective response fields (RF). These neurons respond to stimuli presented in Colby et al. (1996) and/or movements directed toward (Barash et al., 1991; Mazzoni et al., 1996a) a restricted area of space, typically in the contralateral hemi-field. The spatial selectivity of parietal neurons is modulated by a variety of task parameters, such as the salience of visual stimuli (Colby and Goldberg, 1999), motor planning (Snyder et al., 1997), decision-making (Shadlen and Newsome, 2001), categorization (Freedman and Assad, 2006), reward expectation (Platt and Glimcher, 1999; Sugrue et al., 2004), social expectations (Klein et al., 2008), and elapsed time (Leon and Shadlen, 2003). In addition, responses of parietal neurons can be affected by non-spatial information such as shape and color (Sereno and Maunsell, 1998; Toth and Assad, 2002), as well as information located outside of the classical RF (Freedman and Assad, 2009).
Neurons in PPC were first shown to encode the cardinal value, e.g., “4,” of visible objects in monkeys performing a delayed-match-to-sample task (Nieder and Miller, 2004b). On each trial, a sample stimulus containing 1–5 elements was presented, followed by a delay period in which no stimuli were visible. After the delay, a test stimulus containing either the same number of elements or a set that differed by one element was presented. The locations of the elements were randomized around a central fixation point, and monkeys reported when the test stimulus matched the sample by releasing a lever. Thus, the spatial configuration of the stimuli was not matched to the RFs of neurons studied, and the motor response did not have a spatial component such as a reach or eye movement to a particular target. The area, circumference, arrangement, density, and shape of the items in the numerosity stimuli were systematically varied to ensure that number alone was the basis for a match. Consistent with standard magnitude effects on numerical performance, behavioral response accuracy declined as the number of items in the sample increased. In an additional set of behavioral experiments where the sample and test stimuli differed by more than one element, performance improved as the difference between the sample and test stimuli increased (Merten and Nieder, 2009). The performance of monkeys in this task thus demonstrated distance and magnitude effects like those seen in Brannon and Terrace (1998, 2000).
While monkeys performed the delayed-match-to-numerosity task, the activity of randomly selected neurons in prefrontal and PPC was measured. For approximately one-third of neurons in prefrontal cortex (PFC), ~20% of neurons in the fundus of the VIP, and ~10% of neurons in the lateral bank of the intraparietal sulcus (LIP), activity measured during the presentation of the sample stimulus or the delay period was maximal for one quantity and declined as distance from that quantity increased. “Tuning” curves for numerosity were broader as numerosity increased from 1 to 5, suggesting a possible correlate of numerical distance and magnitude effects (Nieder et al., 2002; Nieder and Miller, 2003). Figure 3 shows an example of a single neuron with tuned for the preferred value of “3.” For numerosities up to 30, individual PFC neurons preferred a particular value, with tuning curves better fit by logarithmic rather than linear scaling (Nieder and Merten, 2007). The onset of numerical discrimination by parietal neurons preceded that of prefrontal neurons by ~30 ms, suggesting that quantity is initially encoded in PPC then passed to PFC for task-related processing (Dehaene, 2002; Nieder and Miller, 2004a).
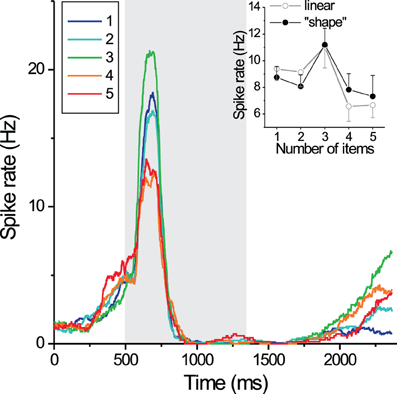
Figure 3. Single neurons in posterior parietal cortex and prefrontal cortex (shown) respond most strongly for a “preferred” numerosity. In this example, firing rate was most elevated for arrays of “3” in a delayed-match-to-numerosity task, and declined with numerical distance from 3. Reprinted with permission from Nieder et al. (2002).
In addition to coding the quantity of elements in simultaneously presented numerical arrays, VIP neurons show similar preferences for a preferred ordinal position in a numerical sequence, i.e., respond best to the second stimulus, regardless of whether the number of elements in the sequence is 1, 2, 3, or 4 (Nieder et al., 2006). The tuning for preferred sequence position resembles that for preferred numerosity, in that different sets of neurons represent each of the possible ordinal positions. In fact, in VIP a larger proportion of neurons (~22%) were selective for sequential quantity than were selective for simultaneous quantity (~12%). The two populations did not overlap—that is—single neurons did not exhibit an abstract preference for “3,” regardless of whether presented simultaneously or sequentially during the sample viewing period. During the delay period, when subjects are presumably holding an abstract representation of quantity in working memory, neurons representation of quantity did not depend on the format of presentation. Overall, the findings suggest coding for ordinal position as well as cardinal value in VIP that potentially drives representation of cardinal value in PFC.
In the explicit delayed-match-to-numerosity task, it is possible that factors other than number modulated neural responses. The majority of number-selective neurons in PFC and PPC preferred the quantity “1” (Nieder et al., 2002; Nieder and Miller, 2004b). Behavioral studies also showed that monkeys' accuracy was highest when the sample value was 1 (Nieder and Miller, 2004a). An alternative explanation for the over-representation of the value 1 by neurons may be that the responses also convey information about reward expectations. It is possible that monkeys were more certain of achieving rewards when the sample value was 1, and this certainty is reflected in the discharge of some neurons categorized as preferring 1 (Leon and Shadlen, 1999). In this task, monkeys have extensive experience with a limited range of numerosities, and potentially treat cardinal number as other stimulus categories (Freedman et al., 2002; Freedman and Assad, 2006).
Extensive experience with categorization of visual stimuli as governed by task demands may contribute to the generation of different patterns of neural responses. In the non-symbolic numerical stimuli contain cardinal values of stimulus elements (e.g., 1, 2, 3, etc.), thus while we hypothesize that these values correspond to values drawn from a continuous representation of quantity, the stimuli themselves are inherently categorical. When monkeys were tasked with the discrimination of the continuous variable of line length, neurons in VIP exhibited tuning for one preferred line length from four possibilities, similar to tuning for cardinal value in numerosity tasks (Tudusciuc and Nieder, 2009). Thus, the delayed-match-to-sample task requires subjects to categorize even continuous stimulus characteristics, and the patterns of neural activity observed may be a product of experience and/or task demands. Indeed, when tested on comparisons of relative magnitude (“greater than” or “less than” a sample) PFC neurons did not show selective responses at the time the monkeys viewed the sample stimulus. Only when the monkeys were told which comparison rule to perform did task-related modulation emerge (Bongard and Nieder, 2010). Although monkeys viewed the same numerical arrays as those used in the delayed-match-to-numerosity task, the neural responses were qualitatively different. Rather than peaking for one cardinal value, most neurons represented the mathematical rule (“greater than,” “less than”), suggesting that they carry higher-level cognitive signals, rather than performing a basic calculation of quantity. It is not known whether PPC neurons likewise might encode a rule for quantitative comparisons while monkeys perform this task, or if they maintain a representation of magnitude/cardinal value for such comparisons.
Given the human literature supporting a strong role for PPC in numerical cognition, it is perhaps surprising that a greater proportion of neurons in VIP and LIP were not driven by numerical stimuli in the previous studies. Several models of how to calculate numerosity from a set of elements include the process of accumulation as a critical step (Meck and Church, 1983; Dehaene and Changeux, 1993; Verguts and Fias, 2004). Neurons in LIP have been proposed to integrate information with respect to their RFs. Monkeys discriminating the direction of motion of a random-dot stimulus behave as though they integrate the amount of information in the stimulus (measured as percent coherence) across the viewing duration (Gold and Shadlen, 2000, 2002). While monkeys view the motion stimulus outside of the RF, neurons in LIP show time- and motion coherence-dependent increases in activity that reach a common level when a decision to shift gaze into the RF is reached (Roitman and Shadlen, 2002). That is, when an eye movement is used to report the direction of visual motion, the activity of single LIP neurons increases with the amount of evidence favoring the eye movement toward its RF. Here, the integration of information is toward the initiation of a motor response. While related to the amount of information contained in the motion stimulus, the activity does not report the strength or direction of the motion in the manner of a sensory MT neuron (Britten et al., 1992). The pattern of activity exhibited by LIP neurons has been modeled as the accumulation of sensory information from visual area MT toward a “threshold,” at which time a binary decision is complete and the eye movement initiated (Mazurek et al., 2003).
The notion that LIP neurons would estimate the number of stimuli within their spatially selective RFs by the computation of integration was directly tested using an implicit numerical discrimination task similar to that used to map numerical processing of the IPS in humans (Piazza et al., 2004). Here, monkeys passively viewed arrays of dots with different numerosities ranging from 2 to 32 located within the RF of each LIP neuron studied (Roitman et al., 2007b). In each block of trials, a standard numerosity (e.g., “8”) was presented on half of the trials, while on the remaining half a deviant numerosity (2, 4, 16, or 32) was displayed. Although monkeys were required only to maintain fixation on a central point while the stimulus was displayed, presentation of a deviant stimulus predicted that the monkey would receive a larger reward for completing a gaze shift to a target in the opposite hemi-field from the RF when the fixation point was extinguished. Other stimulus variables (size, color, area, density) were controlled to not systematically vary with number.
When visual arrays were presented within the RFs of LIP neurons, and monkeys were not trained to explicitly discriminate numerosity, the majority of LIP neurons recorded (54%) had activity that was significantly modulated by the number of elements in the visual array. Neurons responded in a graded manner, either increasing or decreasing activity as the number of elements increased (Figure 4). Responses did not depend on other stimulus characteristics, or whether the numerosity served as standard or deviant in a given block of trials. The neurons with increasing responses resemble what would be expected by the integration of the number of elements within the RF. Similar monotonically increasing responses have also been observed in parietal neurons encoding the rate of a mechanical vibration applied to the fingertips (Hernandez et al., 2000, 2002). Neurons with responses that decreased with increasing numerosity may reflect the operation of other processes. In the random-dot motion discrimination, for example, LIP neurons show a time-and coherence-dependent reduction in activity when evidence favors a saccade away from the RF (Roitman and Shadlen, 2002; Mazurek et al., 2003). Multiple stimuli within a RF lead to competitive interactions and a reduction in activity in superior colliculus neurons, which are strongly interconnected with LIP (Li and Basso, 2005), in a process akin to divisive normalization (Carandini and Heeger, 2011).
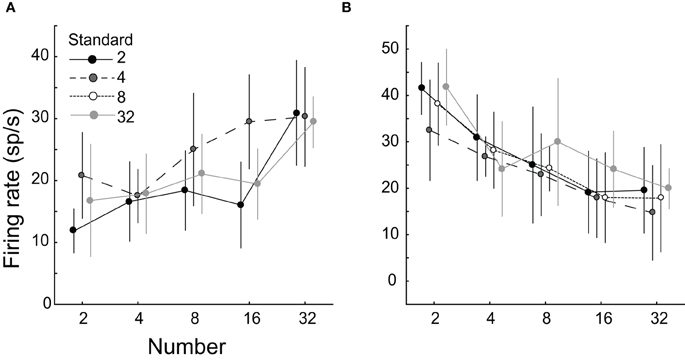
Figure 4. Single neurons in the lateral parietal area (LIP) respond in a graded manner to numerosity. Arrays containing 4–32 elements were presented within the response fields of LIP neurons in an implicit task, while the subjects prepared to shift their gaze away from the array. Neuronal firing rate either increased (A) or decreased (B) with larger numerosities. From Roitman et al. (2007b).
Positive and negative profiles of graded responses are sufficient to support the basic characteristics of numerical judgments. In numerical bisection tasks, participants tend to treat the geometric mean of large and small anchor values as the subjective midpoint, e.g., 4 as the midpoint between 2 and 8 (Meck and Church, 1983; Jordan and Brannon, 2006). That the subjective midpoint falls at the geometric, rather than arithmetic, mean provides further evidence that mental estimations are based on ratio differences between numbers. Numerical bisection judgments also show superposition—regardless of the range of anchors tested (2 vs. 8, 3 vs. 12, 4 vs. 16) the probability that an intermediate value is judged as “large” depends its ratio to the “large” value. Bisection points at the geometric mean and superposing judgments can be predicted over a range of anchor values based on a calculation of the difference between the responses of positive and negative neurons reported in LIP (Pearson et al., 2010). Because the “ideal” performance of a pair of neurons with monotonic responses (one increasing and one decreasing) produce judgments with sensitivity greater than that exhibited behaviorally, the model matches behavior by pooling noisy neurons, much as that needed by computational comparisons of neuronal and psychophysical sensitivity in visual area MT (Shadlen et al., 1996). The graded response profiles of LIP neurons can, therefore, support numerical judgments consistent with Weber's law and without explicit representation of cardinal numerical value. This type of coding scheme of number has adaptive value as it can represent a wide range of values, without having to represent every possible number explicitly. To date, there are not data to address the maximum non-symbolic quantity that can be encoded with a graded coding scheme or the extent to which this value depends on experience/task-demands. For example, responses in LIP could increase to some maximum firing rate, which could correspond to the maximal numerosity the circuitry could represent. Alternatively, neural responses may adapt in order to encode multiple ranges of numerosities, such that when asked to discriminate values ranging from 1 to 5, the numerosity “5” elicits maximal responses, but when asked to discriminate values ranging from 2 to 64, scaling is compressed such that “64” elicits a maximal response, with less precision at intermediate values. The range over which such scaling might occur, and the adaptations single neurons might display have not yet been explicitly tested.
Thus, the measurements of single neuron responses to date yield two patterns of numerosity encoding-graded responses in LIP and peaked tuning curves for cardinal value in VIP and PFC. Models of numerical processing that ultimately represent cardinal number utilize an accumulation stage to sum the number of stimuli before converting this accumulated value to numerosity (Dehaene and Changeux, 1993; Verguts and Fias, 2004). These findings are consistent with models in which the representation of numerosity in VIP is derived from LIP inputs, and are then subsequently communicated to PFC to use as a categorical decision rule. Recent modeling has shown that units detecting the numerosity of visual stimuli emerge from a network learning to represent visual arrays (Stoianov and Zorzi, 2012). These numerosity detectors showed spatial selectivity like neurons in LIP, and encoded numerosity on a compressed analog scale. It is possible that differences in task demands and experience lead to the different patterns of responses in parietal cortex. In the implicit numerical discrimination task used by Roitman et al., monkeys were never required to employ the information about quantity to explicitly guide behavior. Behavioral data suggest that monkeys do attend to the numerosity of the stimulus, as saccade response times decreased with increasing differences of the deviant value from the standard, although there was no explicit report of cardinal value. In addition, stimuli in the implicit numerical discrimination task were tailored to the spatial properties of neurons, while those in the delayed-match-to-numerosity used by Nieder and colleagues were not.
The degree to which numerical sensitivity in parietal cortex depends on the spatial properties of the task performed remains unclear. Recent work has challenged the classical view of PPC physiological responses solely guiding sensorimotor transformations to guide spatial behavior. Neurons in LIP, originally thought to be involved in visual attention or oculomotor intention, have been shown to respond to stimuli outside of the RF. In monkeys reporting the category of the direction of a random-dot motion stimulus, LIP neurons also discriminated category identity, even when the stimuli were presented outside of the RF and the behavioral response was the (non-spatial) release of a lever (Freedman and Assad, 2009). Similarly, neurons in LIP report the decision about the direction of a random-dot motion stimulus (right vs. left) in the absence of an available choice target for motor planning (Bennur and Gold, 2011). This flexibility of PPC responses beyond the confines of spatially restricted RF is considerably greater than previously considered.
Behavioral evidence from human, infant, and animal studies suggest that numerosity is represented in a common, non-verbal format in which larger quantities are represented with less precision, resulting in judgments that follow Weber's law. Patients with PPC damage show deficits consistent with the notion that this region is necessary to support the estimation of quantity and understanding of the deep meaning of numbers. Converging findings from human imaging studies and non-human primate electrophysiological recordings support the idea that neurons within PPC respond to quantity with both graded responses that represent magnitude and tuning to identify cardinal value. While it has not been shown that the spatial arrangement of favors a more literal embodiment of a “number line,” the physiological response profiles can functionally encode numerosity in a manner that can begin to account for the psychophysics of numerical judgments. Future investigations of the neural bases of numerical cognition should address a number of issues. Do these patterns of responses denote separate analog magnitude estimation and cardinal value systems? Is the representation of cardinal value derived from graded estimates of magnitude? To what extent are these representations innate, or do they depend on explicit training and experience? How do they form the basis for such simple computations as addition or division? The answers to these questions will undoubtedly shed light not only on the role of PPC in numerical cognition, but also its related abstract cognitive functions.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Baizer, J. S., Ungerleider, L. G., and Desimone, R. (1991). Organization of visual inputs to the inferior temporal and posterior parietal cortex in macaques. J. Neurosci. 11, 168–190.
Barash, S., Bracewell, R. M., Fogassi, L., Gnadt, J. W., and Andersen, R. A. (1991). Saccade-related activity in the lateral intraparietal area. II. Spatial properties. J. Neurophysiol. 66, 1109–1124.
Barth, H., La Mont, K., Lipton, J., Dehaene, S., Kanwisher, N., and Spelke, E. (2006). Non-symbolic arithmetic in adults and young children. Cognition 98, 199–222.
Bennur, S., and Gold, J. I. (2011). Distinct representations of a perceptual decision and the associated oculomotor plan in the monkey lateral intraparietal area. J. Neurosci. 31, 913–921.
Bongard, S., and Nieder, A. (2010). Basic mathematical rules are encoded by primate prefrontal cortex neurons. Proc. Natl. Acad. Sci. U.S.A. 107, 2277–2282.
Boussaoud, D., Ungerleider, L. G., and Desimone, R. (1990). Pathways for motion analysis: cortical connections of the medial superior temporal and fundus of the superior temporal visual areas in the macaque. J. Comp. Neurol. 296, 462–495.
Brannon, E. M., and Terrace, H. S. (1998). Ordering of the numerosities 1 to 9 by monkeys. Science 282, 746–749.
Brannon, E. M., and Terrace, H. S. (2000). Representation of the numerosities 1-9 by rhesus macaques (Macaca mulatta). J. Exp. Psychol. Anim. Behav. Process. 26, 31–49.
Brannon, E. M., Wusthoff, C. J., Gallistel, C. R., and Gibbon, J. (2001). Numerical subtraction in the pigeon: evidence for a linear subjective number scale. Psychol. Sci. 12, 238–243.
Britten, K. H., Shadlen, M. N., Newsome, W. T., and Movshon, J. A. (1992). The analysis of visual motion: a comparison of neuronal and psychophysical performance. J. Neurosci. 12, 4745–4765.
Cantlon, J. F., and Brannon, E. M. (2006). Shared system for ordering small and large numbers in monkeys and humans. Psychol. Sci. 17, 401–406.
Cantlon, J. F., and Brannon, E. M. (2007). How much does number matter to a monkey (Macaca mulatta)? J. Exp. Psychol. Anim. Behav. Process. 33, 32–41.
Carandini, M., and Heeger, D. J. (2011). Normalization as a canonical neural computation. Nat. Rev. Neurosci. 13, 51–62.
Cohen, L., and Dehaene, S. (1994). Amnesia for arithmetic facts: a single case study. Brain Lang. 47, 214–232.
Colby, C. L., Duhamel, J. R., and Goldberg, M. E. (1996). Visual, presaccadic, and cognitive activation of single neurons in monkey lateral intraparietal area. J. Neurophysiol. 76, 2841–2852.
Colby, C. L., and Goldberg, M. E. (1999). Space and attention in parietal cortex. Annu. Rev. Neurosci. 22, 319–349.
Couvillon, P. A., and Bitterman, M. E. (1985). Analysis of choice in honeybees. Anim. Learn. Behav. 13, 246–252.
Davis, H., and Perusse, R. (1988). Numerical competence: from backwater to mainstream of comparative psychology. Behav. Brain Sci. 11, 602–615.
Dehaene, S. (2001). Subtracting pigeons: logarithmic or linear? Psychol. Sci. 12, 244–246. discussion 247.
Dehaene, S., Bossini, S., and Giraux, P. (1993). The mental representation of parity and number magnitude. J. Exp. Psychol. Gen. 122, 371–396.
Dehaene, S., and Changeux, J.-P. (1993). Development of elementary numerical abilities: a neuronal model. J. Cogn. Neurosci. 5, 390–407.
Dehaene, S., and Cohen, L. (1991). Two mental calculation systems: a case study of severe acalculia with preserved approximation. Neuropsychologia 29, 1045–1054.
Dehaene, S., and Cohen, L. (1997). Cerebral pathways for calculation: double dissociation between rote verbal and quantitative knowledge of arithmetic. Cortex 33, 219–250.
Duhamel, J. R., Colby, C. L., and Goldberg, M. E. (1998). Ventral intraparietal area of the macaque: congruent visual and somatic response properties. J. Neurophysiol. 79, 126–136.
Felleman, D. J., and Van Essen, D. C. (1991). Distributed hierarchical processing in the primate cerebral cortex. Cereb. Cortex 1, 1–47.
Fias, W., Lammertyn, J., Reynvoet, B., Dupont, P., and Orban, G. A. (2003). Parietal representation of symbolic and nonsymbolic magnitude. J. Cogn. Neurosci. 15, 47–56.
Freedman, D. J., and Assad, J. A. (2006). Experience-dependent representation of visual categories in parietal cortex. Nature 443, 85–88.
Freedman, D. J., and Assad, J. A. (2009). Distinct encoding of spatial and nonspatial visual information in parietal cortex. J. Neurosci. 29, 5671–5680.
Freedman, D. J., Riesenhuber, M., Poggio, T., and Miller, E. K. (2002). Visual categorization and the primate prefrontal cortex: neurophysiology and behavior. J. Neurophysiol. 88, 929–941.
Gerstmann, J. (1940). Syndrome of finger agnosia, disorientation of right and left, agraphia and acalculia. Arch. Neurol. Psychiatry 44, 398–408.
Gold, J. I., and Shadlen, M. N. (2000). Representation of a perceptual decision in developing oculomotor commands. Nature 404, 390–394.
Gold, J. I., and Shadlen, M. N. (2002). Banburismus and the brain: decoding the relationship between sensory stimuli, decisions, and reward. Neuron 36, 299–308.
Gut, M., Szumska, I., Wasilewska, M., and Jaskowski, P. (2012). Are low and high number magnitudes processed differently while resolving the conflict evoked by the SNARC effect? Int. J. Psychophysiol. doi: 10.1016/j.ijpsycho.2012.02.007. [Epub ahead of print].
Hernandez, A., Zainos, A., and Romo, R. (2000). Neuronal correlates of sensory discrimination in the somatosensory cortex. Proc. Natl. Acad. Sci. U.S.A. 97, 6191–6196.
Hernandez, A., Zainos, A., and Romo, R. (2002). Temporal evolution of a decision-making process in medial premotor cortex. Neuron 33, 959–972.
Hyde, D. C. (2011). Two systems of non-symbolic numerical cognition. Front. Hum. Neurosci. 5:150. doi: 10.3389/fnhum.2011.00150
Jacob, S. N., and Nieder, A. (2009). Tuning to non-symbolic proportions in the human frontoparietal cortex. Eur. J. Neurosci. 30, 1432–1442.
Jeannerod, M., Arbib, M. A., Rizzolatti, G., and Sakata, H. (1995). Grasping objects: the cortical mechanisms of visuomotor transformation. Trends Neurosci. 18, 314–320.
Jordan, K. E., and Brannon, E. M. (2006). Weber's Law influences numerical representations in rhesus macaques (Macaca mulatta). Anim. Cogn. 9, 159–172.
Jordan, K. E., Maclean, E. L., and Brannon, E. M. (2008). Monkeys match and tally quantities across senses. Cognition 108, 617–625.
Klein, J. T., Deaner, R. O., and Platt, M. L. (2008). Neural correlates of social target value in macaque parietal cortex. Curr. Biol. 18, 419–424.
Leon, M. I., and Shadlen, M. N. (1999). Effect of expected reward magnitude on the response of neurons in the dorsolateral prefrontal cortex of the macaque. Neuron 24, 415–425.
Leon, M. I., and Shadlen, M. N. (2003). Representation of time by neurons in the posterior parietal cortex of the macaque. Neuron 38, 317–327.
Li, X., and Basso, M. A. (2005). Competitive stimulus interactions within single response fields of superior colliculus neurons. J. Neurosci. 25, 11357–11373.
Lipton, J. S., and Spelke, E. (2003). Origins of number sense: large-number discrimination in human infants. Psychol. Sci. 14, 396–401.
Mazurek, M. E., Roitman, J. D., Ditterich, J., and Shadlen, M. N. (2003). A role for neural integrators in perceptual decision making. Cereb. Cortex 13, 1257–1269.
Mazzoni, P., Bracewell, R. M., Barash, S., and Andersen, R. A. (1996a). Motor intention activity in the macaque's lateral intraparietal area. I. Dissociation of motor plan from sensory memory. J. Neurophysiol. 76, 1439–1456.
Mazzoni, P., Bracewell, R. M., Barash, S., and Andersen, R. A. (1996b). Spatially tuned auditory responses in area LIP of macaques performing delayed memory saccades to acoustic targets. J. Neurophysiol. 75, 1233–1241.
Meck, W. H., and Church, R. M. (1983). A mode control model of counting and timing processes. J. Exp. Psychol. Anim. Behav. Process. 9, 320–334.
Merten, K., and Nieder, A. (2009). Compressed scaling of abstract numerosity representations in adult humans and monkeys. J. Cogn. Neurosci. 21, 333–346.
Molko, N., Cachia, A., Riviere, D., Mangin, J. F., Bruandet, M., Le Bihan, D., Cohen, L., and Dehaene, S. (2003). Functional and structural alterations of the intraparietal sulcus in a developmental dyscalculia of genetic origin. Neuron 40, 847–858.
Montague, P. R., Dayan, P., Person, C., and Sejnowski, T. J. (1995). Bee foraging in uncertain environments using predictive hebbian learning. Nature 377, 725–728.
Moyer, R. S., and Landauer, T. K. (1967). Time required for judgements of numerical inequality. Nature 215, 1519–1520.
Mullette-Gillman, O. A., Cohen, Y. E., and Groh, J. M. (2005). Eye-centered, head-centered, and complex coding of visual and auditory targets in the intraparietal sulcus. J. Neurophysiol. 94, 2331–2352.
Nieder, A., Diester, I., and Tudusciuc, O. (2006). Temporal and spatial enumeration processes in the primate parietal cortex. Science 313, 1431–1435.
Nieder, A., Freedman, D. J., and Miller, E. K. (2002). Representation of the quantity of visual items in the primate prefrontal cortex. Science 297, 1708–1711.
Nieder, A., and Miller, E. K. (2003). Coding of cognitive magnitude. Compressed scaling of numerical information in the primate prefrontal cortex. Neuron 37, 149–157.
Nieder, A., and Miller, E. K. (2004a). Analog numerical representations in rhesus monkeys: evidence for parallel processing. J. Cogn. Neurosci. 16, 889–901.
Nieder, A., and Miller, E. K. (2004b). A parieto-frontal network for visual numerical information in the monkey. Proc. Natl. Acad. Sci. U.S.A. 101, 7457–7462.
Nieder, A., and Merten, K. (2007). A labeled-line code for small and large numerosities in the monkey prefrontal cortex. J. Neurosci. 27, 5986–5993.
Pearson, J., Roitman, J. D., Brannon, E. M., Platt, M. L., and Raghavachari, S. (2010). A physiologically-inspired model of numerical classification based on graded stimulus coding. Front. Behav. Neurosci. 4:1. doi: 10.3389/neuro.08.001.2010
Piazza, M., Izard, V., Pinel, P., Le Bihan, D., and Dehaene, S. (2004). Tuning curves for approximate numerosity in the human intraparietal sulcus. Neuron 44, 547–555.
Piazza, M., Pinel, P., Le Bihan, D., and Dehaene, S. (2007). A magnitude code common to numerosities and number symbols in human intraparietal cortex. Neuron 53, 293–305.
Pica, P., Lemer, C., Izard, V., and Dehaene, S. (2004). Exact and approximate arithmetic in an Amazonian indigene group. Science 306, 499–503.
Pinel, P., Dehaene, S., Riviere, D., and LeBihan, D. (2001). Modulation of parietal activation by semantic distance in a number comparison task. Neuroimage 14, 1013–1026.
Platt, J. R., and Johnson, D. M. (1971). Localization of position within a homogeneous behavior chain: effects of error contingencies. Learn. Motiv. 2, 386–414.
Platt, M. L., and Glimcher, P. W. (1999). Neural correlates of decision variables in parietal cortex. Nature 400, 233–238.
Rizzolatti, G., Luppino, G., and Matelli, M. (1998). The organization of the cortical motor system: new concepts. Electroencephalogr. Clin. Neurophysiol. 106, 283–296.
Roberts, W. A., and Mitchell, S. (1994). Can a pigeon simultaneously process temporal and numerical information? J. Exp. Psychol. Anim. Behav. Process. 20, 66–78.
Roeltgen, D. P., Sevush, S., and Heilman, K. M. (1983). Pure Gerstmann's syndrome from a focal lesion. Arch. Neurol. 40, 46–47.
Roitman, J. D., Brannon, E. M., Andrews, J. R., and Platt, M. L. (2007a). Nonverbal representation of time and number in adults. Acta Psychol. (Amst.) 124, 296–318.
Roitman, J. D., Brannon, E. M., and Platt, M. L. (2007b). Monotonic coding of numerosity in macaque lateral intraparietal area. PLoS Biol. 5:e208. doi: 10.1371/journal.pbio.0050208
Roitman, J. D., and Shadlen, M. N. (2002). Response of neurons in the lateral intraparietal area during a combined visual discrimination reaction time task. J. Neurosci. 22, 9475–9489.
Sakata, H., Taira, M., Murata, A., and Mine, S. (1995). Neural mechanisms of visual guidance of hand action in the parietal cortex of the monkey. Cereb. Cortex 5, 429–438.
Sawamura, H., Shima, K., and Tanji, J. (2002). Numerical representation for action in the parietal cortex of the monkey. Nature 415, 918–922.
Sawamura, H., Shima, K., and Tanji, J. (2010). Deficits in action selection based on numerical information after inactivation of the posterior parietal cortex in monkeys. J. Neurophysiol. 104, 902–910.
Scarf, D., Hayne, H., and Colombo, M. (2011). Pigeons on par with primates in numerical competence. Science 334, 1664.
Seltzer, B., and Pandya, D. N. (1986). Posterior parietal projections to the intraparietal sulcus of the rhesus monkey. Exp. Brain Res. 62, 459–469.
Sereno, A. B., and Maunsell, J. H. (1998). Shape selectivity in primate lateral intraparietal cortex. Nature 395, 500–503.
Shadlen, M. N., Britten, K. H., Newsome, W. T., and Movshon, J. A. (1996). A computational analysis of the relationship between neuronal and behavioral responses to visual motion. J. Neurosci. 16, 1486–1510.
Shadlen, M. N., and Newsome, W. T. (2001). Neural basis of a perceptual decision in the parietal cortex (area LIP) of the rhesus monkey. J. Neurophysiol. 86, 1916–1936.
Shapiro, M. S., Couvillon, P. A., and Bitterman, M. E. (2001). Quantitative tests of an associative theory of risk-sensitivity in honeybees. J. Exp. Biol. 204, 565–573.
Shuman, M., and Kanwisher, N. (2004). Numerical magnitude in the human parietal lobe: tests of representational generality and domain specificity. Neuron 44, 557–569.
Simon, O., Mangin, J. F., Cohen, L., Le Bihan, D., and Dehaene, S. (2002). Topographical layout of hand, eye, calculation, and language-related areas in the human parietal lobe. Neuron 33, 475–487.
Snyder, L. H., Batista, A. P., and Andersen, R. A. (1997). Coding of intention in the posterior parietal cortex. Nature 386, 167–170.
Stoianov, I., and Zorzi, M. (2012). Emergence of a ‘visual number sense’ in hierarchical generative models. Nat. Neurosci. 15, 194–196.
Sugrue, L. P., Corrado, G. S., and Newsome, W. T. (2004). Matching behavior and the representation of value in the parietal cortex. Science 304, 1782–1787.
Thompson, R. F., Mayers, K. S., Robertson, R. T., and Patterson, C. J. (1970). Number coding in association cortex of the cat. Science 168, 271–273.
Toth, L. J., and Assad, J. A. (2002). Dynamic coding of behaviourally relevant stimuli in parietal cortex. Nature 415, 165–168.
Tudusciuc, O., and Nieder, A. (2009). Contributions of primate prefrontal and posterior parietal cortices to length and numerosity representation. J. Neurophysiol. 101, 2984–2994.
Ungerleider, L. G., and Desimone, R. (1986). Cortical connections of visual area MT in the macaque. J. Comp. Neurol. 248, 190–222.
Ungerleider, L. G., and Mishkin, M. (1982). Two Cortical Visual Systems. Cambridge, MA: The MIT Press.
Verguts, T., and Fias, W. (2004). Representation of number in animals and humans: a neural model. J. Cogn. Neurosci. 16, 1493–1504.
Walsh, V. (2003). A theory of magnitude: common cortical metrics of time, space and quantity. Trends Cogn. Sci. 7, 483–488.
Whalen, J., Gelman, I. I., and Gallistel, C. R. (1999). Non-verbal counting in humans: the psychophysics of number representation. Psychol. Sci. 10, 130–137.
Wingard, E. M., Barrett, A. M., Crucian, G. P., Doty, L., and Heilman, K. M. (2002). The Gerstmann syndrome in Alzheimer's disease. J. Neurol. Neurosurg. Psychiatry 72, 403–405.
Wood, J. N., and Spelke, E. (2005). Infants' enumeration of actions: numerical discrimination and its signature limits. Dev. Sci. 8, 173–181.
Keywords: posterior parietal cortex, number, human, animal cognition, electrophysiology, psychophysics
Citation: Roitman JD, Brannon EM and Platt ML (2012) Representation of numerosity in posterior parietal cortex. Front. Integr. Neurosci. 6:25. doi: 10.3389/fnint.2012.00025
Received: 17 January 2012; Accepted: 12 May 2012;
Published online: 31 May 2012.
Edited by:
Christos Constantinidis, Wake Forest University, USAReviewed by:
Andreas Nieder, University of Tübingen, GermanyHugo Merchant, Universidad Nacional Autónoma de México, México
Copyright: © 2012 Roitman, Brannon and Platt. This is an open-access article distributed under the terms of the Creative Commons Attribution Non Commercial License, which permits non-commercial use, distribution, and reproduction in other forums, provided the original authors and source are credited.
*Correspondence: Michael L. Platt, Department of Neurobiology, Center for Cognitive Neuroscience, Duke Institute for Brain Sciences, Duke University, Rm. B243F LSRC Building, Durham, NC 27708, USA. e-mail:cGxhdHRAbmV1cm8uZHVrZS5lZHU=


