Diffusion tensor imaging detects early cerebral cortex abnormalities in neuronal architecture induced by bilateral neonatal enucleation: an experimental model in the ferret

Introduction

Diffusion tensor imaging (DTI) studies have shown that in several neurological disorders, affected individuals possess white matter (WM) that is characterized by abnormally low fractional anisotropy (FA) in water diffusion (see reviews by Lim and Helpern, 2002; White et al., 2008). In WM of mature normal individuals, water diffusion is anisotropic because it is preferentially hindered or otherwise obstructed in directions perpendicular to an axonal fiber tract, but less so in directions parallel to the tract. The degree of anisotropy in water diffusion is commonly quantified in terms of FA (Basser and Pierpaoli, 1996), which ranges from 0 (isotropic diffusion) to 1 (maximally anisotropic diffusion). Several reports have shown that behavioral and/or sensory impairment correlates with a reduction in WM FA, and suggest that this reduction is a manifestation of abnormal axonal organization within the tract, or abnormal myelin structure. Although DTI provides a unique approach for studying the biological basis of neurological disorders, the abnormalities in WM identified using this strategy likely reflect an endpoint of disease because plasticity in the CNS typically decreases after critical/sensitive periods (Katz and Crowley, 2002; Olavarria and Hiroi, 2003; Innocenti and Price, 2005; Fields, 2008).

A potential way to extend the DTI approach to the developing brain is to monitor changes in water diffusion anisotropy within the cerebral cortex at the time in which neurons undergo morphological differentiation. In the immature cerebral cortex, water diffusion is highly anisotropic due to the influence of a different set of cellular structures (e.g., apical dendrites, undifferentiated dendrites, and axons) than those that influence water diffusion within WM at maturity (e.g., myelinated axons). Apical dendrites of pyramidal neurons are aligned perpendicular to the pial surface, and these selectively impose restrictions in directions parallel to the pial surface (Neil et al., 1998; McKinstry et al., 2002). However, as the brain matures, diffusion within cortex becomes increasingly restricted in all directions, causing fractional anisotropy of water diffusion to become progressively smaller, although still measurable in the mature brain (McNab et al., 2009). Immediately after pyramidal neurons of the isocortex migrate from germinal zones to the cortical plate, the neuropil, consisting primarily of neuronal and glial processes and the associated extracellular space, begins to differentiate (Rakic, 1995). Dendrites and axons begin as simple elongated structures, oriented perpendicular to the pial surface, and then gain structural complexity as they arborize to form interconnected, functional neural circuits (Conel, 1939). It has previously been proposed that the reduction in FA associated with development of the cerebral cortex arises from morphological differentiation of the neuropil (McKinstry et al., 2002). This idea is supported by the fact that the age-related decreases in cerebral cortical FA coincide with developmental changes in neuropil morphology. Indeed, the progressive reduction of cortical diffusion anisotropy with age has been quantified for several mammalian species (see Leigland and Kroenke, 2010 for review), and in each case the period of cortical diffusion anisotropy loss occurs immediately following the genesis and subsequent migration of pyramidal neurons from ventricular/subventricular zones to the cortical plate (Kroenke et al., 2009). In addition, the neuropil represents 70–80% of the cortical volume fraction (Miller and Potempa, 1990; Granger et al., 1995), which is significantly greater than the volume fraction of other elements such as glial and neuron cell somas (3.6% and 22%, respectively, Miller and Potempa, 1990).

It has been established that certain neurodevelopmental disorders are associated with abnormal morphological differentiation of the cerebral cortical neuropil (e.g., Rett syndrome, Armstrong et al., 1995) and fetal alcohol spectrum disorder (Davies and Smith, 1981). Determining whether neurological disorders affecting development of the cortical neuropil lead to measurable changes in cortical FA would be of significant value because it would provide a means of detecting and monitoring the deleterious effects of pathological insults on cortical development, as well as allow for therapeutic interventions while the brain is still plastic. Here we describe an animal model designed to explore the potential of DTI techniques for detecting abnormal morphological development of the cerebral cortex.

Ferrets are recognized as an ideal model system for studies of brain development (Jackson and Hickey, 1985), and they have been utilized in numerous studies of visual system plasticity (see review by Katz and Crowley, 2002). We chose blindness induced by early enucleation as an experimental perturbation because there is a vast literature indicating that blindness induced by neonatal enucleation or other forms of visual deprivation can alter intracortical cellular morphology, as well as the patterns of cortico–cortical connectivity in visual areas. For example, in humans, early blindness has been shown to be associated with reductions in visual WM FA at adulthood (Shimony et al., 2006). Golgi studies of animals that have been dark-reared (Coleman and Riesen, 1968; Borges and Berry, 1978), stripe-reared (Tieman and Hirsch, 1982), or binocularly enucleated (Ryugo et al., 1975; Heumann and Rabinowicz, 1982) have documented effects on several aspects of dendritic development in the isocortex, including abnormalities in dendritic fields of pyramidal cells, and reductions in the number of dendritic spines. Moreover, neonatal enucleation induces massive changes in the distribution and topography of the interhemispheric connections through the corpus callosum (Berman, 1991; Olavarria and Li, 1995; Zufferey et al., 1999; Olavarria and Hiroi, 2003; Innocenti and Price, 2005; Olavarria and Safaeian, 2006). At the cellular level, enucleation increases the length of callosal axon branches and total length of arbors, without major effects on the number of branch tips (Olavarria et al., 2008), and reduces the proportion of multiple synaptic boutons in the visual callosal projection (Sorensen et al., 2003).

Due to the widespread distribution of callosal connections in the brain, the overall cortical area affected by enucleation can be readily estimated by determining which regions contain abnormal callosal patterns. In turn, this greatly facilitates the identification of areas to be analyzed with DTI methods. To test whether DTI methods are capable of detecting abnormal neuropil development, we compared measurements of FA in visual cortex of control and enucleated ferrets at P31, a stage in which neuronal morphological differentiation is still underway. We further asked whether changes in the organization of dendrites induced by enucleation are linked to abnormal changes in cortical FA. To address this question, we examined the effect of enucleation on dendrite morphology in Golgi-stained sections, and correlated the changes observed with abnormal changes in cortical FA. Our data indicate that enucleation causes morphological changes in the visual system that can be detected with DTI methods at early stages of cerebral cortical development. Moreover, our Golgi data suggest that abnormalities in the development of dendrites may underlie, at least in part, the abnormal changes in cortical FA that we observed in visual cortex of enucleated ferrets at early developmental stages.

Materials and Methods

Animal Handling and Procedures

Animal care

Our study is based on data obtained from a total of 10 ferrets (Mustela putorius furo) purchased from Marshall Bioresources (North Rose, NY, USA) and delivered to the Oregon Health & Science University (OHSU) Department of Comparative Medicine on postnatal day 5 (P5). This study, and all procedures involved, were approved by the OHSU and University of Washington Institutional Animal Care and Use Committees, and were carried out in accordance with the NIH “Guide for the Care and Use of Laboratory Animals” (NIH publication no. 86-23, revised 1987).

Enucleations

Ferrets were binocularly enucleated on postnatal day 7 (BEP7). Animals were placed under 2% isoflurane anesthesia, and arterial pulse oxygenation, pulse rate, respiration rate, and core body temperature were monitored throughout surgical in vivo procedures. Under aseptic conditions, slits were cut in both eyelids, the eyes were removed with iridectomy scissors, and the eyelids sutured closed. Topical bupivacaine was administered intra-operatively in the orbital cavity immediately after removing the eyes. After full recovery from anesthesia, animals were returned to their mothers.

Tracer injections

Anatomical tracer injections were performed on six animals (three controls and three animals binocularly enucleated on P7, BEP7) at adulthood (P120 or older). Animals were placed under 2% isoflurane anesthesia, intubated, and arterial pulse oxygenation, pulse rate, respiration rate, end-tidal pCO₂, and core body temperature were monitored throughout surgical procedures. A 1 cm × 2 cm craniotomy was performed over the occipital and parietal lobes using a hand-held bone drill. Multiple 0.01–0.02 μl injections of the anatomical tracer horseradish peroxidase (HRP, 20% in saline), separated by 200–300 μm, were administered through glass micropipettes (50–100 μm tip diameter) 600–800 μm below the dura throughout the exposed cortex of one hemisphere. Following injections, the bone chip was replaced and the muscle and skin layers were sutured closed.

Histological Analyses

Tissue collection

After a survival period of 2 days, animals were injected with 0.5 mL euthasol (i.p.) and previously described fixation procedures to unfold and flatten the cortical mantle were followed (Olavarria and Van Sluyters, 1985). Heparinized phosphate-buffered saline (PBS) was injected into the left cardiac ventricle until the fluid of the right atria was clear. Phosphate-buffered paraformaldehyde (2% for brains to undergo cortical unfolding and flattening, 4% for remaining brains, pH 7.4) was perfused through the left ventricle for 8 min. Brains were removed from the skull and those fixed in 2% paraformaldehyde were placed in PBS at 4°C, and brains fixed with 4% paraformaldehyde were post-fixed for 24 h (in 4% paraformaldehyde), and then transferred to PBS and allowed to equilibrate for at least 48 h prior to DTI experiments.

Callosal connectivity pattern

The hemisphere contralateral to tracer injections was unfolded and flattened according to procedures described previously (Olavarria and Van Sluyters, 1985, 1995). The patterns of retrogradely labeled somas and anterogradely labeled axon terminals in the contralateral hemisphere were revealed with standard HRP protocols (Olavarria et al., 1987) in histological sections (70-μm thick) cut tangentially to the cortical surface. The surface area occupied by callosal connections was calculated from thresholded versions of the patterns reconstructed using Adobe Photoshop CS2. The same parameters for image analysis were applied to all control and BE animals. Differences in the percent of area occupied by callosal connections were analyzed statistically using t-tests with the level of significance set at 0.05.

Golgi staining

Four animals (two controls and two BEP7) euthanized on P31 were used for Golgi staining and analysis following DTI experiments. Golgi staining was performed using the Rapid GolgiStain kit (FD NeuroTechnologies, Inc., Ellicott City, MD, USA). Tissue samples were frozen in Tissue Tek OCT (optimal cutting temperature) compound (Ted Pella, Inc., Redding, CA, USA) using a dry-ice slurry, 150-μm thick coronal slices were cut using a rotary microtome. Right hemispheres from two animals (herein termed Cntrl-1 and BEP7-1) were sectioned in the coronal plane, and hemispheres from the remaining two animals (Cntrl-2, left and BEP7-2, right) were sectioned in the axial plane. The left hemisphere of Cntrl-2 was analyzed here because the right hemisphere of this animal was used in a prior study (Kroenke et al., 2009, see below). Tissue sections were directly mounted onto Gelatin subbed slides and left to dry and then coverslipped. Photographic montages of entire coronal sections taken from Cntrl-1 and BEP7-1 were prepared from light microscope images captured at 2.5× magnification (e.g., see Figure 2B). Subsequent steps in the analyses of Golgi-stained tissue were performed using images captured at 10× magnification.

Quantification of orientation distributions of neuronal processes

Each of the 10× images was stored to disk as a 512 pixel × 512 pixel tif image (each pixel represents a 3 × 3 μm area), and a series of initial image processing operations were performed using ImageJ software (http://rsbweb.nih.gov/ij/). First, binarized images of Golgi-stained neurons and neuronal processes were generated by applying a threshold operation to each 10× image. These images were stored to disk and denoted “somas + processes”. Second, neuronal processes were removed from the binary images by applying an erosion operation, followed by a dilation operation. The resulting images were stored to disk and denoted “somas”. Third, difference images were constructed between the “somas + processes” and “somas” images to generate binary images of only neuronal processes. Last, a skeletonization operation was applied to the images of neuronal processes, and the output of this operation was stored to disk and denoted “skeletons”.

Binary 2D skeletons representing the set of neuronal process were then approximated as a set of linear segments. To accomplish this, skeleton images were imported into the Matlab programming environment (The MathWorks, Boston, MA, USA) for further processing using a series of custom-built image processing macros. First, the length (e.g., the number of connected non-zero pixels) of each fragment of the skeletonized image was determined, and fragments of less than 10 pixels were removed from subsequent analysis (by setting the pixel values to 0). Second, a region within the cerebral cortex was identified within each image. This operation prevented contamination of Golgi-stained white matter. In addition, this operation enabled the analysis to be focused on cortical areas that have minimal curvature, thus minimizing the effect that macroscopic structure of the cerebral cortex may have on the orientation of cortical axons and dendrites (e.g., see Figure 4). Third, each skeleton fragment within the identified cerebral cortical region of interest was approximated using the equation for a line. Last, the set of slope parameters were converted to polar angles, θ, ranging from 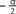to 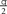, using the relation θ = tan⁻¹(slope).

To facilitate comparisons between sets of axon and dendrite orientations derived from the various images of Golgi-stained tissue, the orientation distribution was modeled using the von Mises-type axial distribution (Fisher, 1993)

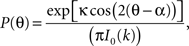
in which I₀(k) is the modified Bessel function of order zero, and P(θ) is the observed distribution of angles θ in a region of interest. The factor of 2 in the cos argument differs from the expression given by Fisher (1993) because the distribution considered herein is undirected rather than directed (see Mardia et al., 1979). Such modeling is standard in the analysis of circular data; the von Mises parameters that provide quantitative characterizations of the mean and width of a set of angles are the mean angle, α, and the concentration parameter, κ, respectively. The parameter κ can be interpreted as the precision of the mean direction, and is somewhat analogous to the inverse of the standard deviation of a Gaussian distribution of linear data; larger κ reflects less variability in the set of angles comprising the distribution (a larger standard deviation in a Gaussian distribution corresponds to more variability). A maximum likelihood approach for estimating parameters in the von Mises distribution was implemented in Matlab using the property that the distribution of 2θ follows the standard (unimodal) von Mises distribution with parameters κ and 2α.

Orientation distributions were measured for a total of 14 (seven control/BEP7 pairs) of cortical locations, including five in coronal sections from cases Cntrl-1 and BEP7-1, and two in axial sections from cases Cntrl-2 and BEP7-2 (see Figure 5). For the control cortical locations, a mean ± standard deviation of 216 ± 80 linear segments representing neuronal processes were used to estimate κ; and for the BEP7 locations, the number of line segments was 202 ± 153. Analysis of simulated data was performed to confirm accuracy of the procedure for estimating κ, and to ensure that bias in numerical procedures used to estimate κ is negligible for the sample sizes used. To estimate 95% confidence intervals for each of the 14 κ estimates, a bootstrap procedure (Fisher, 1993), using the “bootstrp” Matlab function, was utilized. For a cortical location with N line elements, this involved estimating the von Mises distribution parameters 1000 times, each time using a random sampling of the N values of θ. The 95% confidence interval for κ is estimated to range from the 26th to the 975th smallest κ value. A pair of κ values was interpreted to be significantly different if their associated 95% confidence intervals did not overlap.

Diffusion Tensor Imaging and Cortical Surface Calculations

Post mortem DTI procedures

Diffusion tensor imaging was performed on the same P31 brains analyzed by Golgi. Each brain was sectioned along the midline prior to DTI measurements. For all cases except one control brain (Cntrl-2), the right hemisphere was analyzed. For the animal in which the left hemisphere was characterized, it’s right hemisphere was included in a previously published study (brain P31b in Kroenke et al., 2009), and no differences between the left and right hemispheres for this animal were observed (data not shown). A 2-cm diameter single-turn solenoidal coil was utilized for radiofrequency transmission and reception. Experiments were performed using a 11.7 T magnet interfaced with a 9-cm inner diameter magnetic field gradient coil (Bruker, Rheinstetten, Germany). A Stejskal–Tanner multi-slice spin-echo pulse sequence with parameters δ = 12 ms, δ = 21 ms, and G = 27.3 G/cm (resulting in b = 2.7 ms/μm²) was used to perform DTI measurements. Diffusion anisotropy measurements were made using a 25-direction, icosahedral sampling scheme (Batchelor et al., 2003). Other pulse sequence settings were TR > 5 s, TE = 42 ms, and image resolution was isotropic voxels of dimensions (0.25 mm)³. Fractional anisotropy was calculated from diffusion-weighted images following standard procedures (Basser and Pierpaoli, 1996). To facilitate FA comparisons between animals at corresponding coronal planes, FA parameter maps for each hemisphere were registered to one another using the FMRIB non-linear registration tool (FNIRT) (Smith et al., 2006; Klein et al., 2009).

Cortical diffusion anisotropy

For each right hemisphere, surface models were constructed of inner (white matter to subplate or layer VI) and outer (layer I to the pial surface) boundaries of the cortex (olfactory bulbs were omitted at the lateral olfactory tract in all analyses) using the CARET software package (Van Essen et al., 2001). Previously described procedures (Kroenke et al., 2009) were followed to project cortical FA values onto cortical surface models, and to register surfaces to a common atlas.

Results

The distribution of labeled cell bodies and axon terminals was charted in flattened contralateral hemispheres of control (N = 3) and BEP7 (N = 3) adult ferrets following injection of HRP into the visual cortex of one hemisphere (Figure 1). Previous physiological studies have mapped the locations of visual areas relative to anatomical landmarks such as gyri and sulci (see green shaded areas in Figures 1A,B) (Manger et al., 2002, 2004). Figure 1D illustrates the overall callosal pattern demonstrated following multiple HRP injections into the contralateral visual cortex of a control animal, while Figure 1F shows the callosal pattern from a BEP7 ferret. In normal animals, the callosal pattern consists of a series of densely HRP-labeled bands and patches within extrastriate cortex, outlined in green on the flattened cortex (Figure 1C). These patterns were compared across animals by using several landmarks as reference, including the series of red dots that were drawn along the crown of the suprasylvian and ectosylvian gyri, and along the dorsal/caudal edge of the occipital lobe (Figure 1). Similar arrangement of labeled and unlabeled areas was observed in all three control ferrets studied, providing evidence that the callosal pattern in normal animals is consistent from animal to animal. Moreover, callosal labeling at the 17/18 border of the hemisphere contralateral to injection was sparse in all three control animals studied in spite of the fact that, in the injected hemisphere, the region of the 17/18 border was densely infiltrated with HRP, as confirmed by inspection of the cortex and thalamus in the injected hemisphere (data not shown). The approximate location of the representation of the horizontal meridian is shown as a blue line in Figure 1. In adult BEP7 ferrets the visual callosal pattern is more irregular and occupies a significantly greater cortical area compared to controls. As illustrated in Figures 1F,G, the callosal pattern in BEP7 ferrets consists of smaller patches of labeled cells and axon terminations compared to controls, and these patches often occupy regions that are relatively free of callosal labeling in control animals. This is particularly striking throughout visual areas 18, 19, and 21 (Figures 1F,G). Comparison of thresholded renderings (Figures 1E,G) of the patterns in Figure 1D,F reveals that the percent area occupied by callosal connections is significantly (p < 0.05) greater in BEP7 than control ferrets (Figure 1H).

FIGURE 1

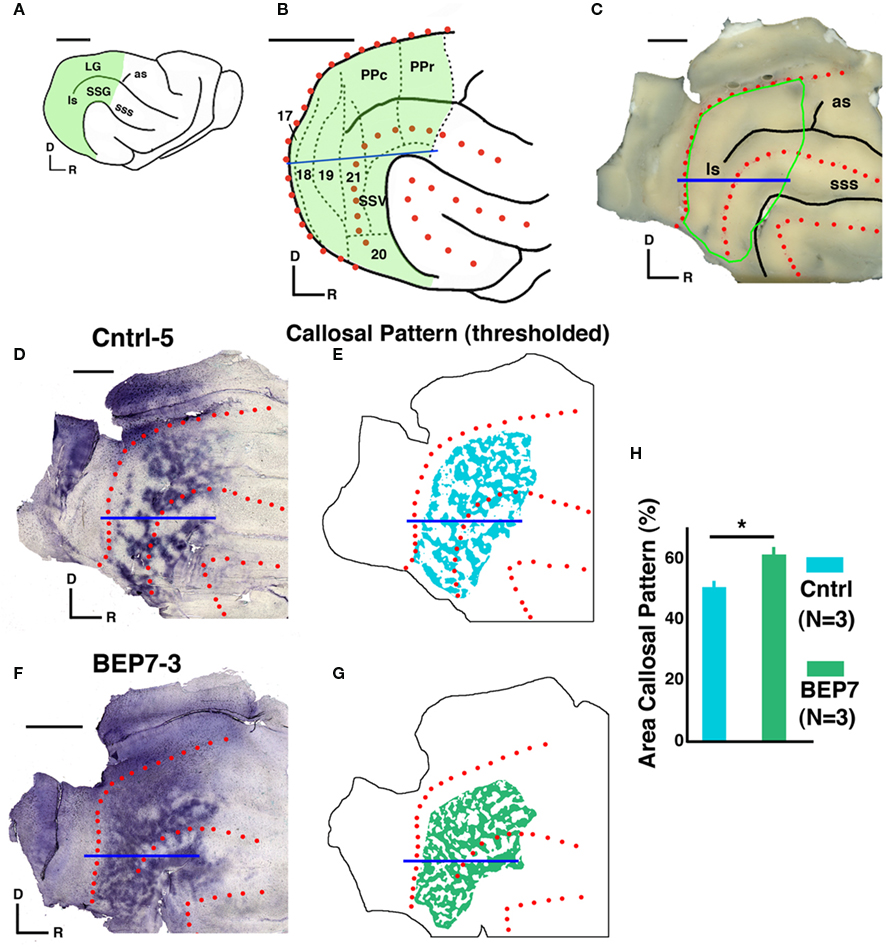
Figure 1. Effect of bilateral enucleation on postnatal day 7 (BEP7) on the distribution of interhemispheric visual callosal connections in the ferret. The distribution of callosal connections in one hemisphere of adult BEP7 and control ferrets were studied following multiple intracortical injections of the tracer HRP in the contralateral hemisphere. Green areas in (A) and (B) include regions of visual cortex analyzed. Approximate locations of visual areas described in previous reports are indicated in (B); the blue line marks the representation of the horizontal meridian. Red dots indicate the crown of the suprasylvian and ectosylvian and gyri, and the dorsal/caudal edge of the occipital lobe, which were marked directly on the brains before flattening. (C) Flattened brain before sectioning, area outlined by green line contains visual areas analyzed. Labeled callosal connections (labeled somas and axon terminations) appear as dark areas in (D) and (F); and as colored areas in the thresholded versions (E, G). The percent area occupied by callosal connections was significantly (p < 0.05) greater in BEP7 ferrets than in Control ferrets (H). LG, lateral gyrus; PPc, posterior parietal caudal area; PPr, posterior parietal rostral area; SSG, suprasylvian gyrus; SSV, suprasylvian visual areas; as, ansate sulcus; ls, lateral sulcus, sss; suprasylvian sulcus. Scale = 5 mm.

Abnormalities in the callosal pattern induced by neonatal enucleation have been shown in other species to be present at early stages of development (Olavarria and Safaeian, 2006; Olavarria et al., 2008). Therefore, the abnormal distribution of labeling in mature BEP7 ferrets suggests that DTI measurements of cortical FA may provide a strategy for detecting developmental abnormalities early in life by characterizing morphological differentiation of cerebral cortical neurons. Figure 2A shows a coronal view of DTI data obtained from a P31 BEP7 animal (case BEP7-1), following tissue fixation. The grayscale underlay in Figure 2A is a diffusion-weighted image, and the overlaying red line segments indicate principal eigenvector orientations for each voxel, which are parallel to the direction of least restricted diffusion. The length of each primary eigenvector displayed in Figure 2A is scaled by FA so that longer line segments overlap voxels with larger FA. Subsequent to acquiring DTI data, the tissue was stained using the rapid Golgi method, and sectioned in the coronal plane. Figure 2B is a montage of images acquired at 2.5× magnification from a section taken at a rostrocaudal level corresponding to that for Figure 2A (this level of the brain is indicated by the segmented line in the inset). Figures 2C,D illustrate the close similarity between the orientations of water diffusion tensor primary eigenvectors (Figures 2A,C) and apical dendrites (Figure 2D). The rectangle in Figure 2C indicates the size and approximate location of the region shown in Figure 2D. The square in Figure 2D illustrates the size of a single DTI voxel. As indicated in Figure 2D, the P31 cerebral cortex contains incompletely differentiated pyramidal neurons with dendritic arbors that consist primarily of apical dendrites not yet ramified with oblique collaterals. Basal dendritic arbors are nascent at this developmental stage. As a result, cortical diffusion anisotropy at P31 is significant (Kroenke et al., 2009) and exhibits a radial orientation (Figures 2A,C).

FIGURE 2

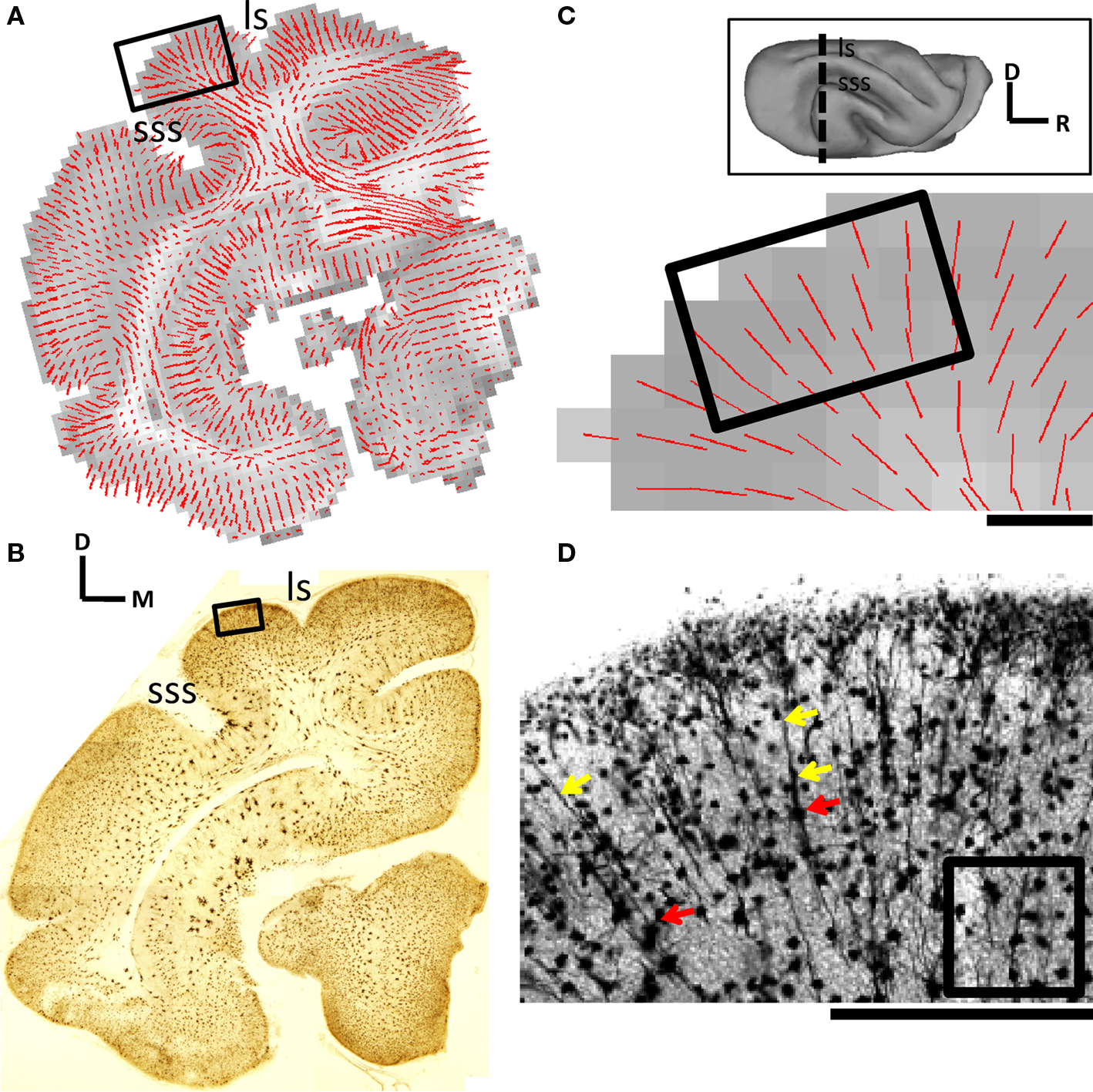
Figure 2. Anisotropy in water diffusion within the developing cerebral cortex is oriented parallel to apical dendrites of pyramidal neurons. Corresponding coronal views of DTI data (A) and Golgi-stained tissue (B) obtained from brain BEP7-1. The rostrocaudal level of the coronal plane is represented by the dashed line in the inset. (C,D) Close-up views of the region of the suprasylvian gyrus indicated by the rectangles in A and B, respectively. Diffusion tensor primary eigenvector (C) and apical dendrites (D) are both oriented perpendicular to the pial surface. In (D), yellow arrows indicate two apical dendrites, and red arrows indicate the associated cell bodies. The approximate size of the field in (D) is shown as a rectangle in (C). The size of an individual DTI voxel is illustrated as a square in (D). Abbreviations are as in Figure 1. Scale bars = 0.5 mm in panels (C) and (D).

To examine whether potential morphological differences between neurons of BEP7 and control animals can be detected through cortical diffusion anisotropy measurements at P31, cortical FA was compared between two BEP7 animals and two control animals, as shown in Figure 3. Figure 3A shows coronal views of FA parameter maps obtained at a rostrocaudal level (white segmented line in Figure 3B) running through visual cortical areas that are sensitive to visual deprivation (cf. Figure 1). Light colored regions, indicative of higher FA (gray-tone scale), occupy larger areas in the two BEP7 ferrets as compared to control ferrets, suggesting that cortical FA in the two BEP7 animals is increased relative to control at this position. To characterize diffusion anisotropy throughout the entire cerebral cortex, cortical FA was projected onto surface models of cerebral cortices for each of the four hemispheres. FA values are encoded by the yellow/high, red/low colormap shown in Figure 3. A surface region of interest (ROI) corresponding approximately to the green shading in Figures 1A,B was drawn, and its boundary is indicated by black dots in Figure 3, while the blue dots indicate the approximate representation of the horizontal meridian of the visual field. A rostrally located control area is also identified, outlined by blue-green dots (Figure 3B). Increased cortical diffusion anisotropy in visual areas of BEP7 animals is evident in the more extensive yellow pattern in the BEP7 brain compared to control. This difference is quantified for all four animals in Figure 3C. Increased cortical FA is observed within visual cortical areas (Figure 3C), but not within the rostral control area (Figure 3D), of BEP7 animals. The difference in mean values of cortical FA distributions between BEP7 and control animals was 0.07 in visual areas, but only 0.01 in the rostrally located non-visual area.

FIGURE 3

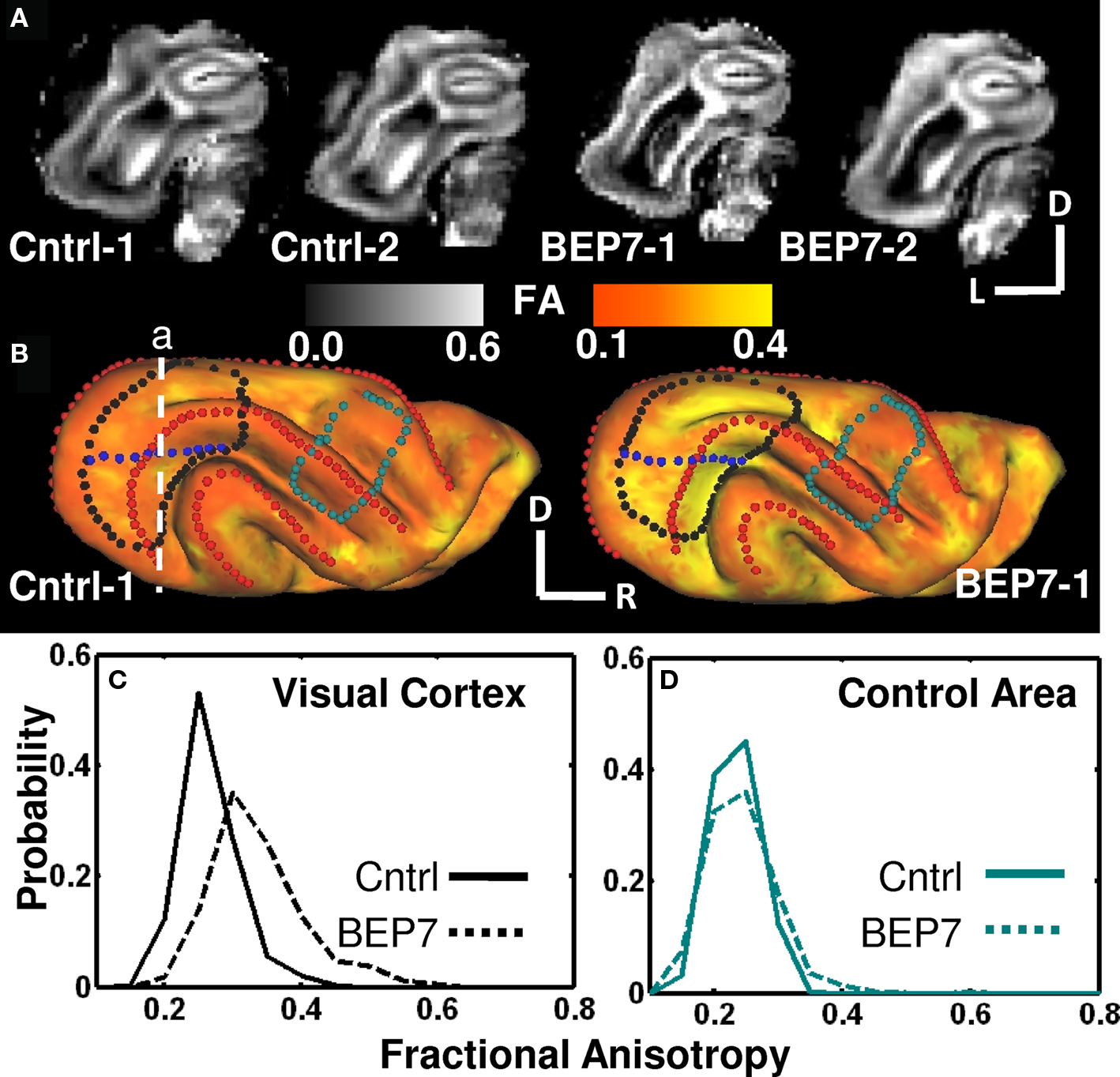
Figure 3. Post mortem DTI measurements of two BEP7 hemispheres show increased visual cortical FA relative to two control hemispheres at P31. Coronal views of FA parameter maps are shown in (A) for two control animals (left) and two BEP7 animals (right) according to the gray color scale. In (B), cortical FA is presented on cortical surface models for animals Cntrl-1 and BEP7-1, according to the red/yellow color scale. In A and B, increased FA is evident in visual areas of BEP7 animals compared to controls. Blue dots in (B) indicate the approximate location of the representation of the horizontal meridian (see Figure 1 for comparison). Red dots indicate crown of gyri, as in Figure 1. Histograms reflecting data from all four animals are shown in (C) for visual cortex [encircled by black dots in (B)] and a rostrally located control area in (D) [encircled by blue-green dots in (B)].

The cortical FA pattern evident in Figure 3 suggests that the neuropil of BEP7 animals is less differentiated in the extrastriate visual cortex of P31 animals than in controls. This was further investigated by comparing Golgi-stained tissue from BEP7 animals to corresponding data from control animals. Figure 4 illustrates the method used to quantify differentiation of the cerebral cortex, as reflected in the differential distribution of neuronal process orientations measured in Golgi-stained tissue. Figure 4A shows a region of the extrastriate visual cortex in Cntrl-1 visualized at 10× magnification (Region 3 in Figure 5, described below). The Figure 4B underlay is a skeleton image of neuronal processes, with skeleton elements of less than 10 image pixels in length removed. For a region of cerebral cortex within the Figure 4B field, the set of skeleton elements are approximated as lines, which are overlaid on the skeletonized image in Figure 4B and the original image in Figure 4C (red lines). Figure 4D shows an image/overlay obtained from a similar location within extrastriate visual cortex of BEP7-1. To characterize the orientation distribution of line segments within a region of cerebral cortex, the slope of each line segment is converted to an angle, θ, and the distribution in the set of angles is characterized by the von Mises mean α and concentration κ parameters. As shown in Figure 4E, the set of neuronal processes in the control animal (black) is distributed over a broader range than for the BEP7 animal (red), and hence the concentration parameter calculated from this data is smaller for the control (κ = 1.41) than for the BEP7 animal (κ = 2.08). To assess whether the difference in κ values achieved statistical significance, 95% confidence intervals in κ were determined using a bootstrap procedure. Figure 4F shows the distributions of κ values obtained from 1000 random samples from the Cntrl-1 (black) and BEP7-1 (red) polar angles. The means of the distributions are the values of κ used for the solid lines in Figure 4E, and as can be observed in the Figure 4F histograms, the 95% confidence ranges for the Cntrl-1 and BEP7-1 estimates of κ do not overlap, and therefore the BEP7-1 distribution is considered to be significantly more concentrated than Cntrl-1 for location 3 in Figure 5 (see below).

FIGURE 4

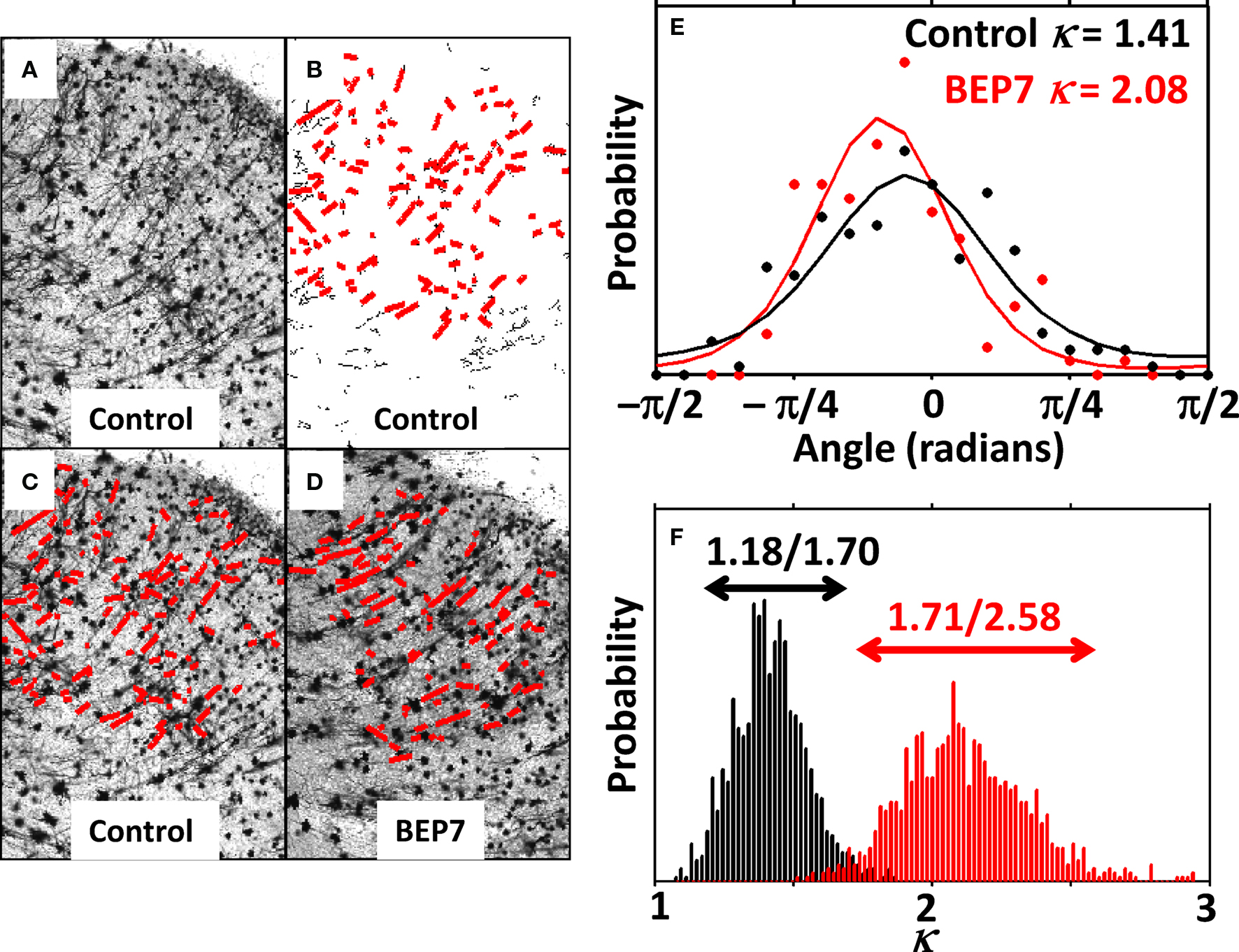
Figure 4. Characterization of the distributions of neuronal process orientations. Golgi-stained tissue visualized at 10× magnification from the Cntrl-1 hemisphere is shown in (A). Line segments (red) representing neuronal processes throughout a region of the cerebral cortex (corresponding to location 3 in Figure 5) are overlaid on the skeletonized image and original image in (B) and (C), respectively. Line segments derived from the corresponding location in BEP7-1 are overlaid on the Golgi image in (D). The polar angle for each line segment was determined as described in the text, and in (E), histograms representing the distribution of polar angles are shown for the Cntrl-1 (black data points) and BEP7-1 (red data points) Golgi fields. Solid lines in (E) represent the results of approximating the data points as a von Mises distribution. To estimate 95% confidence intervals κ, a bootstrap procedure was used in which κ was determined 1000 times from randomly sampled subsets of the measured polar angles for each field. Histograms, with associated 95% confidence regions, of the resulting κ values are shown in (F) for the set of angles derived from Cntrl-1 (black) and BEP7-1 (red).

FIGURE 5

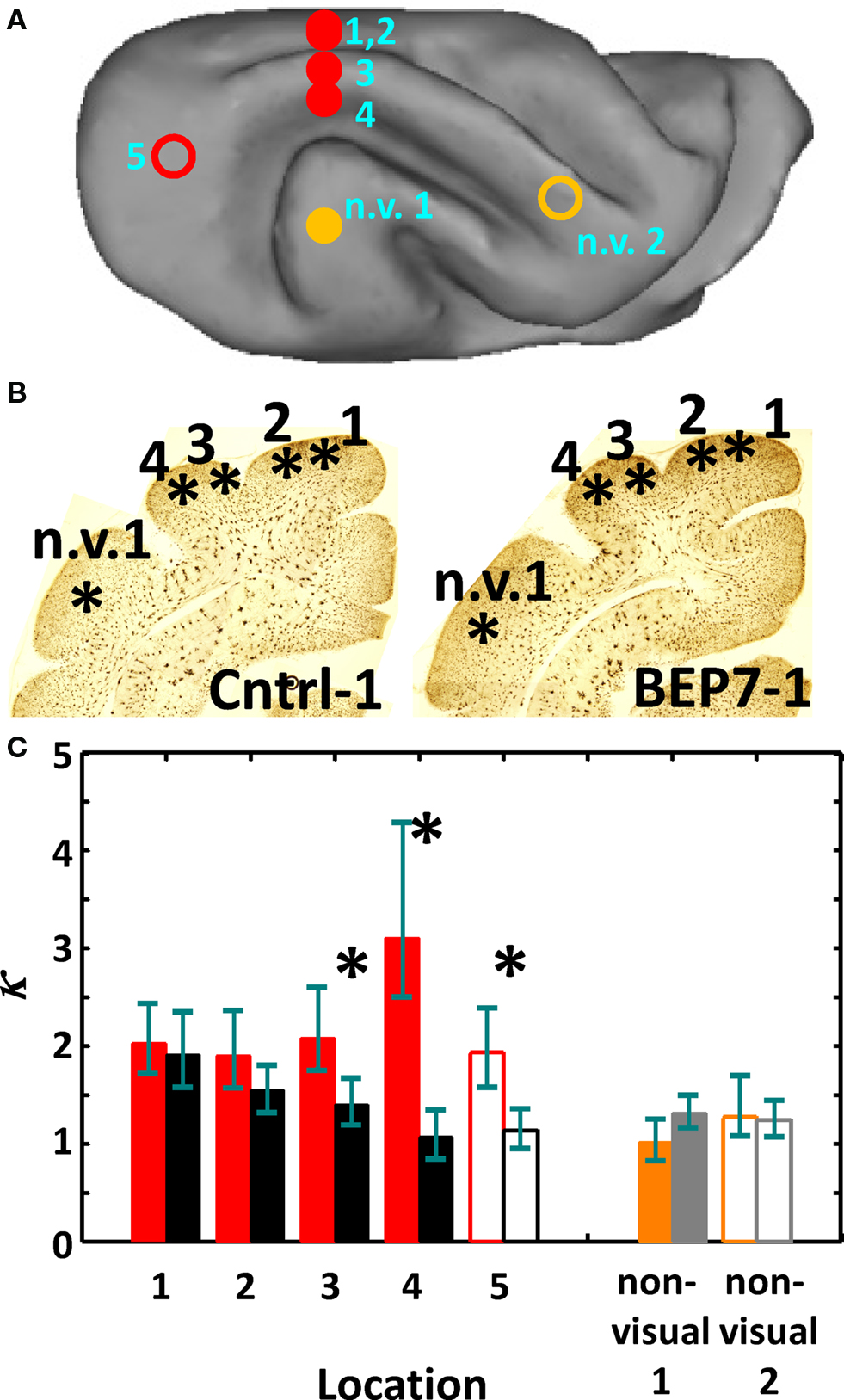
Figure 5. Comparison of the distributions of orientations of neuronal processes in visual and non-visual areas of BEP7 and control ferrets at P31. The value of the parameter κ decreases as the distribution of orientations broadens (less concentrated). In (A), filled circles represent locations of regions analyzed in coronal sections of Cntrl-1 and BEP7-1, with red indicating visual cortical areas, and orange a non-visual area. Open circles represent locations of regions analyzed in axial sections of Cntrl-2 and BEP7-2, with red and orange indicating visual and non-visual areas, respectively. (B) Cortical locations 1–4 and non-visual area 1 are shown in montages of Golgi sections (C) Concentration parameters, κ, of von Mises distributions associated with the sets of neuronal process orientations are shown for case BEP7-1 (visual locations, red filled bars; non-visual location, filled orange bar) and case Cntrl-1 (visual locations, black filled bars; non-visual location, filled gray bar), and case BEP7-2 (visual location, red open bar; non-visual location, open orange bar) and case Cntrl-2 (visual location, black open bar; non-visual location, open gray bar). Error bars represent 95% confidence intervals for κ. For visual locations indicated with asterisks, 95% confidence intervals for BEP7 and control regions do not overlap.

Figure 5 summarizes measurements of the orientation distribution widths (expressed as κ values) of neuronal processes obtained from five visual cortical locations and two non-visual locations. The position of each cortical location is indicated on the Figure 5A surface model. Five locations were analyzed within coronal slices obtained from corresponding positions in cases Cntrl-1 and BEP7-1 (filled bars in Figure 5C; black/gray indicates data from Cntrl-1 for visual/non-visual locations, respectively; red/orange indicates data from BEP7-1 for visual/non-visual locations, respectively). The five locations obtained from coronal sections are illustrated on the montage images in Figure 5B. In addition, two locations were analyzed within axial slices obtained from corresponding positions in cases Cntrl-2 and BEP7-2 (open bars in Figure 5C; black/gray indicates data from Cntrl-2 for visual/non-visual locations, respectively; red/orange indicates data from BEP7-2 for visual/non-visual locations, respectively). Concentration parameters reflecting the distribution of neuronal process orientations, with associated 95% confidence regions, are given for BEP7 brains (red/orange) and control animals (black/gray) in Figure 5C. For all visual regions analyzed, κ is larger in BEP7 subjects than in controls. In three of these, the difference is sufficient to separate 95% confidence intervals (asterisks, Figure 5C). In contrast, neuronal process orientation κ measured within one non-visual cortical region is slightly lower within BEP7-1 than for Cntrl-1, and the non-visual region characterized in BEP7-2 and Cntrl-2 exhibits nearly identical κ values. For both non-visual regions, there is a large amount of overlap in the 95% confidence intervals for κ. These findings indicate that in the visual cortex, neuronal process arborizations are less elaborate in the BEP7 brain than in the control.

Discussion

We found that bilateral enucleation at P7 induces marked changes in the overall distribution of callosal connections in visual cortex. Cortical areas affected by these structural changes were associated with increases in cerebral cortical FA measured at P31. At the cellular level we observed that neuronal process arbors were less differentiated in Golgi-stained visual neurons from BEP7 animals on postnatal day 31 compared to age-matched controls. These results suggest that DTI measurements at early developmental stages are capable of detecting abnormalities in neuropil development induced by neonatal enucleation.

In agreement with previous studies in the rat (Cusick and Lund, 1982; Olavarria et al., 1987; Olavarria and Li, 1995; Olavarria and Hiroi, 2003; Olavarria and Safaeian, 2006), the cat (Innocenti and Frost, 1980; Berman, 1991; Olavarria, 1995; Olavarria and Van Sluyters, 1995), and the macaque (Dehay et al., 1989), neonatal enucleation in the ferret leads to abnormal development of callosal connections. Within visual cortex, we found that the area occupied by callosal connections in enucleated ferrets was significantly larger than in control ferrets. Based on previous physiological subdivisions of ferret visual cortex (Manger et al., 2002, 2004), our data indicate that regions showing abnormal patterns of callosal connectivity encompassed many visual areas, including areas 18, 19, and 21.

In BEP7 animals, cortical visual areas exhibiting differences in callosal connectivity at adulthood were spatially correlated with regions exhibiting altered cortical FA at P31. Water diffusion anisotropy in these visual areas was larger than controls in BEP7 animals at P31, while no differences in FA were found between BEP7 animals and controls in a more rostrally located non-visual area. This provides further evidence that binocular enucleation perturbs the normal development of visual cortex, and supports the notion that DTI is capable of detecting changes in connectivity associated with binocular enucleation at early stages of brain development. It is important to note that, in addition to the abnormalities induced on callosal connections, enucleation at P7 in the ferret likely affects several other visual connection systems, including thalamocortical and ipsilateral cortico–cortical projections (Berman, 1991; Ankaoua and Malach, 1993; Ruthazer and Stryker, 1996; Toldi et al., 1996; Karlen et al., 2006). It is therefore possible that the effect on FA within cerebral cortical gray matter we observed over much of visual cortex of BEP7 ferrets reflects the effect of enucleation in multiple pathways that either terminate or originate in visual cortex.

In order to directly examine the cellular-level determinants of the differences between control and BEP7 animals observed by DTI, a procedure was developed to quantitatively characterize orientation distributions of neuronal processes within Golgi-stained cerebral cortical tissue. For a subset of cortical locations, Golgi-stained neurons in visual cortex of BEP7 ferrets were found to possess less differentiated neuronal processes on postnatal day 31, and among these, radially oriented apical dendrites appear to be a dominant structure. Control animals were found to have more obliquely oriented collaterals of apical dendrites and basilar dendrites, contributing to a more complex and less organized neuropil than BEP7 animals. Although it is possible that the effect of binocular enucleation on cortical FA is mediated by cellular elements not detectable by Golgi staining, the findings reported here are consistent with a study in the rat (Olavarria et al., 2008), which showed that bilateral enucleation increased the length of axon branches and arbors without changing the number of branches, as well as a study in the mouse (Heumann and Rabinowicz, 1982) that showed a reduction in the number of spines on apical dendrites of pyramids in bilaterally enucleated animals. The possibility that enucleation delays the development of radial glial elements into astrocytes is unlikely because studies in other species have shown that enucleation does not affect the timing of other developmental milestones, such as the formation of topographically organized cortico–cortical projections (Olavarria et al., 1987; Olavarria and Safaeian, 2006). Together, these results suggest that bilateral enucleation affects the differentiation of axonal and dendritic arbors in visual cortex.

Our approach builds upon previous comparisons between DTI and immunohistochemical studies related to cerebral cortical microarchitecture in the neonatal rat brain (Sizonenko et al., 2007), in which cortical FA was compared to indices reflecting the quantity of neuronal and glial fibers oriented approximately parallel to apical dendrites. Since radial glial cells have differentiated into astrocytes by P21 (Voigt, 1989), it is unlikely that they contribute significantly to cortical FA at the age we performed our analysis (P31). Therefore, Golgi-staining procedures were used here to estimate the orientation distribution of neuronal processes. Leergaard et al. (2010) have conducted an analysis similar to the approach presented here, in which diffusion MRI data were subsequently quantitatively validated with histological measurements. However, in the study by Leergaard and co-workers, white matter fibers in mature rat brain were compared to myelin-stained histological images. Though the purpose of the experiments presented herein differ from those of Leergaard et al., their study demonstrates the utility of performing morphological analysis of tissue to validate DTI measurements.

While our data provide evidence that neonatal bilateral enucleation induces alterations of neuronal processes that can be detected by DTI at early stages of development, a number of issues remain that must be addressed in future studies. First, the developmental trajectory of the difference between normal and bilaterally enucleated ferrets must be measured by examining brains at postnatal ages other than P31, and sample sizes for DTI and Golgi data must be increased. Such extensions of the approach described here will enable robust delineation of the cortical areas affected by enucleation, and identification of the developmental stage in which DTI is most sensitive for detecting abnormal morphological development of cerebral cortical neurons. Second, DTI methods characterize the three-dimensional properties of water diffusion, whereas the Golgi analysis employed herein was restricted to two dimensions. For the results presented here, care was taken to analyze sections at locations where gyri are approximately orthogonal to the section plane. However to address this issue more generally, work is currently underway in our laboratories to extend the analysis of Golgi data to a three-dimensional approach utilizing confocal microscopic data acquisition. Last, while DTI has sufficient sensitivity to detect changes in neuronal morphology using post-mortem tissue, it is possible that this sensitivity may be lost in an in vivo setting. Future studies involving DTI measurements of live ferrets and incorporating rapid image acquisition techniques such as echo-planar imaging will be needed to address this issue.

The data presented here indicate that the developmental trajectory produced by neonatal binocular enucleation in the ferret is an ideal experimental model for investigating the sensitivity of DTI for detecting abnormalities in neuronal architecture. Specifically, the system described here is amenable for systematically investigating water diffusion anisotropy patterns within the cerebral cortex associated with early stages of development. Such studies will be useful for understanding the morphological factors underlying the DTI findings in human studies of developmental disorders of the CNS. By avoiding potential confounds related to in utero manipulations or preterm birth, the use of newborn ferrets greatly facilitates DTI analysis of changes in diffusion anisotropy at stages of brain development that in primate species occur before birth. The strategy outlined here will thus potentially provide a means for using DTI to identify abnormalities early in brain development, thereby enabling therapeutic intervention before reduction of brain plasticity occurs.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

Financial support from National Institutes of Health grants R01NS070022 (Christopher D. Kroenke and Jaime F. Olavarria), P51RR000163 (Christopher D. Kroenke), and a grant from the Foundation for Alcohol Research (Christopher D. Kroenke). Sune N. Jespersen acknowledges financial support from The Danish National Research Foundation (CFIN), and Korning’s fund. Lindsey A. Leigland was partially supported by T32AA007468. High-field MRI instrumentation used in this work was purchased with support from the W.M. Keck Foundation.

References

Ankaoua, D., and Malach, R. (1993). Evidence for plasticity of intrinsic horizontal connections in area 17 of the rat. Isr. J. Med. Sci. 29, 555–569.

Pubmed Abstract | Pubmed Full Text

Armstrong, D., Dunn, J. K., Antalffy, B., and Trivedi, R. (1995). Selective dendritic alterations in the cortex of Rett syndrome. J. Neuropathol. Exp. Neurol. 54, 195–201.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Basser, P. J., and Pierpaoli, C. (1996). Microstructural and physiological features of tissues elucidated by quantitative-diffusion-tensor MRI. J. Magn. Reson. B 111, 209–219.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Batchelor, P. G., Atkinson, D., Hill, D. L., Calamante, F., and Connelly, A. (2003). Anisotropic noise propagation in diffusion tensor MRI sampling schemes. Magn. Reson. Med. 49, 1143–1151.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Berman, N. (1991). Alterations of visual cortical connections in cats following early removal of retinal input. Brain Res. Dev. Brain Res. 63, 163–180.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Borges, S., and Berry, M. (1978). The effects of dark rearing on the development of the visual cortex of the rat. J. Comp. Neurol. 180, 277–300.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Coleman, P. D., and Riesen, A. H. (1968). Evironmental effects on cortical dendritic fields. I. Rearing in the dark. J. Anat. 102(Pt 3), 363–374.

Pubmed Abstract | Pubmed Full Text

Conel, J. L. (1939). The Postnatal Development of the Human Cerebral Cortex. Cambridge, MA: Harvard University Press.

Cusick, C. G., and Lund, R. D. (1982). Modification of visual callosal projections in rats. J. Comp. Neurol. 212, 385–398.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Davies, D. L., and Smith, D. E. (1981). A Golgi study of mouse hippocampal CA1 pyramidal neurons following perinatal ethanol exposure. Neurosci. Lett. 26, 49–54.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Dehay, C., Horsburgh, G., Berland, M., Killackey, H., and Kennedy, H. (1989). Maturation and connectivity of the visual cortex in monkey is altered by prenatal removal of retinal input. Nature 337, 265–267.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Fields, R. D. (2008). White matter in learning, cognition and psychiatric disorders. Trends Neurosci. 31, 361–370.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Fisher, N. I. (1993). Statistical Analysis of Circular Data. Cambridge, UK: Cambridge University Press, 277 p.

Granger, B., Tekaia, F., Le Sourd, A. M., Rakic, P., and Bourgeois, J. P. (1995). Tempo of neurogenesis and synaptogenesis in the primate cingulate mesocortex: comparison with the neocortex. J. Comp. Neurol. 360, 363–376.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Heumann, D., and Rabinowicz, T. (1982). Postnatal development of the visual cortex of the mouse after enucleation at birth. Exp. Brain Res. 46, 99–106.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Innocenti, G. M., and Frost, D. O. (1980). The postnatal development of visual callosal connections in the absence of visual experience or of the eyes. Exp. Brain Res. 39, 365–375.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Innocenti, G. M., and Price, D. J. (2005). Exuberance in the development of cortical networks. Nat. Rev. Neurosci. 6, 955–965.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Jackson, C. A., and Hickey, T. L. (1985). Use of ferrets in studies of the visual system. Lab. Anim. Sci. 35, 211–215.

Pubmed Abstract | Pubmed Full Text

Karlen, S. J., Kahn, D. M., and Krubitzer, L. (2006). Early blindness results in abnormal corticocortical and thalamocortical connections. Neuroscience 142, 843–858.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Katz, L. C., and Crowley, J. C. (2002). Development of cortical circuits: lessons from ocular dominance columns. Nat. Rev. Neurosci. 3, 34–42.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Klein, A., Andersson, J., Ardekani, B. A., Ashburner, J., Avants, B., Chiang, M. C., Christensen, G. E., Collins, D. L., Gee, J., Hellier, P., Song, J. H., Jenkinson, M., Lepage, C., Rueckert, D., Thompson, P., Vercauteren, T., Woods, R. P., Mann, J. J., and Parsey, R. V. (2009). Evaluation of 14 nonlinear deformation algorithms applied to human brain MRI registration. NeuroImage 46, 786–802.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kroenke, C. D., Taber, E. N., Leigland, L. A., Knutsen, A. K., and Bayly, P. V. (2009). Regional patterns of cerebral cortical differentiation determined by diffusion tensor MRI. Cereb Cortex 19, 2916–2929.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Leergaard, T. B., White, N. S., de Crespigny, A., Bolstad, I., D’Arceuil, H., Bjaalie, J. G., and Dale, A. M. (2010). Quantitative histological validation of diffusion MRI fiber orientation distributions in the rat brain. PloS One 5(1), e8595. doi: 10.1371/journal.pone.0008595.

CrossRef Full Text

Leigland, L. A., and Kroenke, C. D. (2010). “A comparative analysis of cellular morphological differentiation within the cerebral cortex using diffusion tensor imaging (Chapter 13),” in Neuromethods: Animal Models of Behavioral Analysis, Vol. 50, ed J. Raber (Berlin: Springer).

Lim, K. O., and Helpern, J. A. (2002). Neuropsychiatric applications of DTI – a review. NMR Biomed. 15, 587–593.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Manger, P. R., Kiper, D., Masiello, I., Murillo, L., Tettoni, L., Hunyadi, Z., and Innocenti, G. M. (2002). The representation of the visual field in three extrastriate areas of the ferret (Mustela putorius) and the relationship of retinotopy and field boundaries to callosal connectivity. Cereb Cortex 12, 423–437.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Manger, P. R., Nakamura, H., Valentiniene, S., and Innocenti, G. M. (2004). Visual areas in the lateral temporal cortex of the ferret (Mustela putorius). Cereb. Cortex 14, 676–689.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Mardia, K. V., Kent, J. T., and Bibby, J. M. (1979). Multivariate Analysis (Probability and Mathematical Statistics). London: Academic Press, 518 p.

McKinstry, R. C., Mathur, A., Miller, J. H., Ozcan, A., Snyder, A. Z., Schefft, G. L., Almli, C. R., Shiran, S. I., Conturo, T. E., and Neil, J. J. (2002). Radial organization of developing preterm human cerebral cortex revealed by non-invasive water diffusion anisotropy MRI. Cereb Cortex 12, 1237–1243.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

McNab, J. A., Jbabdi, S., Deoni, S. C., Douaud, G., Behrens, T. E., and Miller, K. L. (2009). High resolution diffusion-weighted imaging in fixed human brain using diffusion-weighted steady state free precession. NeuroImage 46, 775–785.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Miller, M. W., and Potempa, G. (1990). Numbers of neurons and glia in mature rat somatosensory cortex: effects of prenatal exposure to ethanol. J. Comp. Neurol. 293, 92–102.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Neil, J. J., Shiran, S. I., McKinstry, R. C., Schefft, G. L., Snyder, A. Z., Almli, C. R., Akbudak, E., Aronovitz, J. A., Miller, J. P., Lee, B. C., and Conturo, T. E. (1998). Normal brain in human newborns: apparent diffusion coefficient and diffusion anisotropy measured by using diffusion tensor MR imaging. Radiology 209, 57–66.

Pubmed Abstract | Pubmed Full Text

Olavarria, J., Malach, R., and Van Sluyters, R. C. (1987). Development of visual callosal connections in neonatally enucleated rats. J. Comp. Neurol. 260, 321–348.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Olavarria, J., and Van Sluyters, R. C. (1985). Unfolding and flattening the cortex of gyrencephalic brains. J. Neurosci. Methods 15, 191–202.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Olavarria, J. F. (1995). The effect of visual deprivation on the number of callosal cells in the cat is less pronounced in extrastriate cortex than in the 17/18 border region. Neurosci. Lett. 195, 147–150.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Olavarria, J. F., and Hiroi, R. (2003). Retinal influences specify cortico-cortical maps by postnatal day six in rats and mice. J. Comp. Neurol. 459, 156–172.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Olavarria, J. F., Laing, R., Hiroi, R., and Lasiene, J. (2008). Topography and axon arbor architecture in the visual callosal pathway: effects of deafferentation and blockade of N-methyl-D-aspartate receptors. Biol. Res. 41, 413–424.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Olavarria, J. F., and Li, C. P. (1995). Effects of neonatal enucleation on the organization of callosal linkages in striate cortex of the rat. J. Comp. Neurol. 361, 138–151.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Olavarria, J. F., and Safaeian, P. (2006). Development of callosal topography in visual cortex of normal and enucleated rats. J. Comp. Neurol. 496, 495–512.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Olavarria, J. F., and Van Sluyters, R. C. (1995). Overall pattern of callosal connections in visual cortex of normal and enucleated cats. J. Comp. Neurol. 363, 161–176.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Rakic, P. (1995). A small step for the cell, a giant leap for mankind: a hypothesis of neocortical expansion during evolution. Trends Neurosci. 18, 383–388.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Ruthazer, E. S., and Stryker, M. P. (1996). The role of activity in the development of long-range horizontal connections in area 17 of the ferret. J. Neurosci. 16, 7253–7269.

Pubmed Abstract | Pubmed Full Text

Ryugo, R., Ryugo, D. K., and Killackey, H. P. (1975). Differential effect of enucleation on two populations of layer V pyramidal cells. Brain Res. 88, 554–559.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Shimony, J. S., Burton, H., Epstein, A. A., McLaren, D. G., Sun, S. W., and Snyder, A. Z. (2006). Diffusion tensor imaging reveals white matter reorganization in early blind humans. Cereb Cortex 16, 1653–1661.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Sizonenko, S. V., Camm, E. J., Garbow, J. R., Maier, S. E., Inder, T. E., Williams, C. E., Neil, J. J., and Huppi, P. S. (2007). Developmental changes and injury induced disruption of the radial organization of the cortex in the immature rat brain revealed by in vivo diffusion tensor MRI. Cereb Cortex 17, 2609–2617.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Smith, S. M., Jenkinson, M., Johansen-Berg, H., Rueckert, D., Nichols, T. E., Mackay, C. E., Watkins, K. E., Ciccarelli, O., Cader, M. Z., Matthews, P. M., and Behrens, T. E. (2006). Tract-based spatial statistics: voxelwise analysis of multi-subject diffusion data. NeuroImage 31, 1487–1505.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Sorensen, S. A., Jones, T. A., and Olavarria, J. F. (2003). Neonatal enucleation reduces the proportion of callosal boutons forming multiple synaptic contacts in rat striate cortex. Neurosci. Lett. 351, 17–20.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Tieman, S. B., and Hirsch, H. V. (1982). Exposure to lines of only one orientation modifies dendritic morphology of cells in the visual cortex of the cat. J. Comp. Neurol. 211, 353–362.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Toldi, J., Feher, O., and Wolff, J. R. (1996). Neuronal plasticity induced by neonatal monocular (and binocular) enucleation. Prog. Neurobiol. 48, 191–218.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Van Essen, D. C., Drury, H. A., Dickson, J., Harwell, J., Hanlon, D., and Anderson, C. H. (2001). An integrated software suite for surface-based analyses of cerebral cortex. J. Am. Med. Inform. Assoc. 8, 443–459.

Pubmed Abstract | Pubmed Full Text

Voigt, T. (1989). Development of glial cells in the cerebral wall of ferrets: direct tracing of their transformation from radial glia into astrocytes. J. Comp. Neurol. 289, 74–88.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

White, T., Nelson, M., and Lim, K. O. (2008). Diffusion tensor imaging in psychiatric disorders. Top. Magn. Reson. Imaging 19, 97–109.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Zufferey, P. D., Jin, F., Nakamura, H., Tettoni, L., and Innocenti, G. M. (1999). The role of pattern vision in the development of cortico-cortical connections. Eur. J. Neurosci. 11, 2669–2688.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text