- 1 The Mind Research Network, Albuquerque, NM, USA
- 2 Department of Electrical and Computer Engineering, University of New Mexico, Albuquerque, NM, USA
- 3 Olin Neuropsychiatry Research Center, Hartford, CT, USA
- 4 Department of Psychiatry, Yale University, New Haven, CT, USA
The functional architecture of the human brain has been extensively described in terms of complex networks characterized by efficient small-world features. Recent functional magnetic resonance imaging (fMRI) studies have found altered small-world topological properties of brain functional networks in patients with schizophrenia (SZ) during the resting state. However, little is known about the small-world properties of brain networks in the context of a task. In this study, we investigated the topological properties of human brain functional networks derived from fMRI during an auditory oddball (AOD) task. Data were obtained from 20 healthy controls and 20 SZ; A left and a right task-related network which consisted of the top activated voxels in temporal lobe of each hemisphere were analyzed separately. All voxels were detected by group independent component analysis. Connectivity of the left and right task-related networks were estimated by partial correlation analysis and thresholded to construct a set of undirected graphs. The small-worldness values were decreased in both hemispheres in SZ. In addition, SZ showed longer shortest path length and lower global efficiency only in the left task-related networks. These results suggested small-world attributes are altered during the AOD task-related networks in SZ which provided further evidences for brain dysfunction of connectivity in SZ.
Introduction
Small-world networks (Watts and Strogatz, 1998) characterized by a high level of clustering and a short node-to-node distance, are of special interest in statistical physics of complex network studies (Newman, 2003). Many real systems including social, biological, and technological networks display small-world features which may reflect an optimal architecture for information processing (Strogatz, 2001). Recently, graph theoretical analysis methods have been successfully translated to examine neuroimaging data (Reijneveld et al., 2007; Stam and Reijneveld, 2007; Bassett and Bullmore, 2009; Bullmore and Sporns, 2009; Guye et al., 2010; Rubinov and Sporns, 2010). Some studies using brain mapping techniques such as electroencephalography (EEG), magnetoencephalography (MEG), magnetic resonance imaging (MRI), and diffusion tensor imaging (DTI) have consistently demonstrated that human brain anatomical and functional networks also have small-world properties (Sporns and Zwi, 2004; Stam, 2004; Eguiluz et al., 2005; Salvador et al., 2005; Achard et al., 2006; Bassett and Bullmore, 2006; Bassett et al., 2006; Humphries et al., 2006; Ferri et al., 2007; He et al., 2007; Ioannides, 2007; Reijneveld et al., 2007; Stam and Reijneveld, 2007; Dosenbach et al., 2008; Smit et al., 2008; Valencia et al., 2008; van den Heuvel et al., 2008; Yu et al., 2008; Bullmore and Sporns, 2009; Gomez Portillo and Gleiser, 2009; Robinson et al., 2009; Wang et al., 2009a; Guye et al., 2010; Palva et al., 2010; Rubinov and Sporns, 2010; Sanabria-Diaz et al., 2010; Vaessen et al., 2010) which may indicate the brain generates and integrates information with high efficiency (Achard and Bullmore, 2007). Further studies suggested that patients with brain disorders such as Alzheimer’s disease (AD), autism attention deficit/hyperactivity disorder (ADHD), epilepsy, especially schizophrenia often present abnormalities in brain networks properties (Micheloyannis et al., 2006; Ponten et al., 2007; Stam et al., 2007; Bassett et al., 2008; Bassett and Bullmore, 2009; He et al., 2009; Wang et al., 2009b; Liao et al., 2010). For example, in EEG studies, De Vico Fallani et al. (2010), found the structure of network altered radically in patients with schizophrenia (SZ); Pachou et al. (2008) discovered decreased small-world architecture in SZ; Micheloyannis et al. (2006) even reported disrupted small-world properties of brain networks in different bands. In functional magnetic resonance imaging (fMRI) studies, Liu et al. (2008) revealed small-world properties including clustering coefficient, shortest path length, global efficiency, local efficiency, and small-worldness are significantly disrupted in SZ; Zalesky et al. (2010) identified a expansive disconnected subnetwork in a group with schizophrenia using network-based statistic (NBS) method; Lynall et al. (2010) showed reduced clustering and small-worldness in schizophrenic group. Bassett et al. (2009) even found performance in people with schizophrenia was strongly associated with nodal cost efficiency of network in frontal regions during a working memory task based on MEG data. However, graph theoretical studies based on fMRI data acquired from SZ and healthy controls (HCs) underlying cognitive tasks are sparse (Wang et al., 2010b).
Schizophrenia is a chronic, disabling, and one of the most mysterious, costliest mental disorder which impairs multiple cognitive domains including memory, attention, and executive function (Calhoun et al., 2009a; Danielyan and Nasrallah, 2009; Javitt, 2009; van Os and Kapur, 2009; Hugdahl and Calhoun, 2010). Previous neuroimaging studies have found both structural and functional abnormalities in temporal lobe brain regions for SZ (Iritani, 2007; Calhoun et al., 2009a; Palmer et al., 2009). One of the most robust functional abnormalities in SZ is a different “oddball response” compared with HCs, reported for both event-related potential (ERP) and fMRI data. For example, reduced P300 amplitude in SZ is usually found in ERP studies during auditory oddball tasks (Bramon et al., 2004; O’Donnell et al., 2004; Doege et al., 2009). Aberrant activations in auditory cortex for SZ are often reported in fMRI studies during auditory oddball tasks (Pearlson, 1997; Calhoun et al., 2006; Sui et al., 2009). However, it is not clear if there are altered properties of auditory oddball task-related small-world networks in auditory cortex. The present study was designed to address this issue.
Disturbed brain asymmetry is another important determinant for schizophrenic pathophysiology (Ribolsi et al., 2009). Disturbances in hemispheric lateralization are widely reported in SZ, including electrophysiological (Gruzelier et al., 1999), structural (Schlaepfer et al., 1994), and functional (Pearlson et al., 1996; Ross and Pearlson, 1996; Li et al., 2009) domains. The default mode network (DMN) also shows lateral differences during auditory oddball tasks (Swanson et al., in press). As both hemispheres involve auditory cortex, it is natural to inquire whether both auditory cortices show altered network properties in SZ during an auditory oddball task.
In this study, group independent component analysis (ICA) was used to detect the strongest auditory oddball task-related component. A left and a right task-related network were constructed by using the top 95 task-related voxels in the left auditory cortex and the top 95 task-related voxels in the right auditory cortex respectively. Some previous small-world brain network studies (Liu et al., 2008; Wang et al., 2009b; Liao et al., 2010) parcellated brain images into 90 anatomical regions of interest using the anatomical automatic labeling (AAL) template (Tzourio-Mazoyer et al., 2002). Because temporal lobe was one of the regions most implicated in previous work in SZ we hypothesized that there would be group difference in the local small-world network properties (Calhoun et al., 2004; Micheloyannis et al., 2006; Liu et al., 2009; Palmer et al., 2009; Zhang et al., 2009). In addition, because previous work suggested temporal lobe changes in both structure and function may be lateralized, we assessed small-world network properties separately for left and right temporal lobe. To determine if the information processing pattern was different between HCs and SZ in a strongly task-related brain region which consisted of temporally coherent voxels within the temporal lobe (Calhoun et al., 2008a) during an auditory oddball detection (AOD) task, we used 95 voxels from each hemisphere and assessed their small-world network properties. All voxels were selected from the most task-related component based on the Z-maps from the group ICA results. Properties of the left and the right task-related networks including clustering coefficient, shortest path length, local efficiency, global efficiency, and the small-worldness as a function of threshold or degree (defined below) were computed from the partial correlation matrices. Two-sample t-tests were used to detect any possible group difference. Since most graph studies based on fMRI data found less clustering coefficient, less local efficiency, less global efficiency, longer path length, and less small-worldness in SZ (Liu et al., 2008; Bullmore and Sporns, 2009; Lynall et al., 2010), we predicted the patients group in the present study would show the same trend in these metrics.
Materials and Methods
Participants
Subjects consisted of 20 (four females) HCs and 20 (three females) SZ. All of them gave written, informed, IRB-approved consent at Hartford Hospital and were compensated for their participation. Schizophrenia was diagnosed according to the DSM-IV TR criteria on the basis of a structured clinical interview (First et al., 1995). administered by a research nurse and by review of the medical records. All patients had chronic schizophrenia [PANSS: positive score 16 ± 6 (SD); negative score 16 ± 5 (SD)] and all were taking medication (including the atypical antipsychotic medications aripiprazole, clozapine, risperidone, quetiapine, and olanzapine, first-generation antipsychotics including fluphenazine, and miscellaneous mood-stabilizing, hypnotic, and anti-cholinergic medications including zolpidem, zaleplon, lorazepam, benztropine, divalproex, trazodone, clonazepam). Patients were on average about 7 years older (but not significantly, P = 0.085) than controls (SZ: mean age 36.7, range 19–59; HCs: mean age 29.9, range 18–56). All participants except two patients were right-handed. Exclusion criteria included auditory or visual impairment, mental retardation (full scale IQ < 70), traumatic brain injury with loss of consciousness greater than 15 min, and presence or history of any central nervous system (CNS) neurological illness. Participants were also excluded if they met criteria for alcohol or drug dependence within the past 6 months or showed a positive urine toxicology screen (screening was for cocaine, opioids including methadone, cannabis, amphetamine, barbiturates, PCP, propoxyphene, and benzodiazepines) on the day of scanning. All participants were able to perform the AOD task successfully during practice prior to the scanning session. Healthy participants were free of any DSM-IV TR Axis I disorder or psychotropic medication.
Experimental Design
All participants were scanned during an AOD task. The AOD consisted of detecting an infrequent sound within a series of regular and different sounds. The task consisted of two runs of auditory stimuli presented to each participant by a computer stimulus presentation system via insert earphones embedded within 30-dB sound attenuating MR compatible headphones. The standard stimulus was a 500-Hz tone, the target stimulus was a 1000-Hz tone, and the novel stimuli consisted of non-repeating random digital noises (e.g., tone sweeps, whistles). The target and novel stimuli each occurred with a probability of 0.10; the standard stimuli occurred with a probability of 0.80. The stimulus duration was 200 ms with a 1000-, 1500-, or 2000-ms inter-stimulus interval randomly chosen with equal probability. All stimuli were presented at 80 dB above the standard threshold of hearing. All participants reported that they could hear the stimuli and discriminate them from the background scanner noise. Prior to entry into the scanning room, each participant performed a practice block of 10 trials to ensure understanding of the instructions. The participants were instructed to respond as quickly and accurately as possible with their right index finger every time they heard the target stimulus and not to respond to the non-target stimuli or the novel stimuli. An MRI compatible fiber-optic response device (Lightwave Medical, Vancouver, BC, USA) was used to acquire behavioral responses. The stimulus paradigm data acquisition techniques and previously found stimulus-related activation were described more fully elsewhere (Kiehl et al., 2005).
Healthy controls had a success average of 99.8% and an average total reaction time of 397 ms for performing the AOD task, while SZ had a 98.3% success rate average, with an average total reaction time of 462 ms. Two-sample t-tests indicated only reaction time had significant group difference (for success rate, t = 1.874, P = 0.069; for reaction time, t = −2.524, P = 0.008). Both patients and controls were able to perform the task well.
Image Acquisition
Scans were acquired at the Olin Neuropsychiatry Research Center at the Institute of Living/Hartford Hospital on a Siemens Allegra 3T dedicated head scanner equipped with 40 mT/m gradients and a standard quadrature head coil. The functional scans were acquired transaxially using gradient-echo echo-planar-imaging with the following parameters: repeat time (TR) 1.50 s, echo time (TE) 27 ms, field of view 24 cm, acquisition matrix 64 × 64, flip angle 70°, voxel size 3.75 mm × 3.75 mm × 4 mm, slice thickness 4 mm, gap 1 mm, 29 slices, ascending acquisition. Six “dummy” scans were acquired at the beginning to allow for longitudinal equilibrium, after which the paradigm was automatically triggered to start by the scanner. The AOD consisted of two 8-min runs.
Preprocessing
Functional magnetic resonance imaging data were preprocessed using the SPM51 software package. Data were motion corrected using INRIalign – a motion correction algorithm unbiased by local signal changes (Freire et al., 2002), spatially normalized into the standard Montreal Neurological Institute (MNI) space using a symmetric template (Stevens et al., 2005), and spatially smoothed with a 10 mm × 10 mm × 10 mm full width at half-maximum Gaussian kernel. Following spatial normalization, the data (originally acquired at 3.75 mm × 3.75 mm × 4 mm) were resliced to 3 mm × 3 mm × 3 mm, resulting in 53 × 63 × 46 voxels. Group spatial ICA (Calhoun et al., 2009b) was used to decompose all the data into components using the GIFT software2 as follows. Dimension estimation, to determine the number of components, was performed using the minimum description length criteria, modified to account for spatial correlation (Li et al., 2007). Using this approach, the data were estimated to have 19 components. A more complete explanation of the ICA algorithm and its theoretical constructs, as well as choosing the appropriate number of components, can be found elsewhere (Bell and Sejnowski, 1995; Calhoun et al., 2001; Stevens et al., 2007). Once the estimate of the number of components was determined, we applied ICA to the data using group ICA (Calhoun et al., 2001, 2009b) as follows. Data from HCs or SZ were concatenated and the aggregate data set reduced to 19 temporal dimensions using principal component analysis (PCA), followed by an independent component estimation using the infomax algorithm (Bell and Sejnowski, 1995). Group ICA was performed separately on HCs and SZ. A temporal multiple regression of the ICA time courses and an SPM5 general linear model (GLM) design matrix coded for the target stimuli was performed. This resulted in a set of beta weights for each regressor associated with a particular subject and component. The resulting beta weights represent the degree to which the component was associated with the AOD task (i.e., a high beta weight represents a large task-related modulation of component for a given regressor; White et al., 2010). One sample t-tests of beta values for each component were performed to define task-related components (Calhoun et al., 2008b). The most task-related component for HCs (P < 0.0001, t = 11.81, df = 19) and the most task-related component for SZ (P < 0.0001, t = 8.80, df = 19) were averaged into one Z-map (McKeown et al., 1998; Calhoun et al., 2001).
Voxels Selection
All voxels were sorted from high to low according to their Z-scores and the top 95 voxels (most task-related) in the left and right temporal lobe constituted a left and a right task-related network (we call it task-related because the nodes of network are task-related voxels) respectively. MNI coordinates of the left 95 voxels: X mean −57, range: (−66)–(−45); Y mean −21, range: (−33)–(−12); Z mean 12, range 3–21. MNI coordinates of the right 95 voxels: X mean 60, range 48–69; Y mean −12, range (−24)–9; Z mean 9, range (−3)–18.
Estimation of the Partial Correlations
Partial correlation could be used as a measure of connectivity between a given pair of voxels by attenuating the contribution of other sources of covariance (Hampson et al., 2002; Marrelec et al., 2006). In this case, following a previous study (Liu et al., 2008), we used partial correlation to reduce indirect dependencies by other voxels, and built undirected graphs respectively in the left and the right network. Given a set of N random variables, the partial correlation matrix is a symmetric matrix, where each off-diagonal element is the correlation coefficient between a pair of variables after filtering out the contributions of all other variables included in the dataset. In the present study, therefore, the partial correlation between any pair of voxels filters out the effects of the other 93 voxels (Salvador et al., 2005).
The first step was to estimate the sample covariance matrix S from the data matrix Y = (xi), i = 1,…,95, of observations for each individual. Here xi was the time series of each ith voxel. If we introduce X = (xj, xk) to denote the observations in the jth and kth voxels, Z = Y\X denotes the other 93 time series matrices. Each component of S contains the sample covariance value between two voxels (say j and k). If the covariance matrix of [X, Z] was

in which S11 was the covariance matrix of X, S12 was the covariance matrix of X and Z and S22 was the covariance matrix of Z, then the partial correlation matrix of X, controlling for Z, could be defined formally as a normalized version of the covariance matrix,

Finally, a Fisher’s r-to-z transformation (Fisher, 1914, 1921; Liu et al., 2008) was used on the partial correlation matrix in order to induce normality on the partial correlation coefficients.
Graph Theoretical Analysis
An N × N (N = 95 in the present study) binary graph brain network, G, consisting of nodes (brain voxels) and undirected edges (connectivity) between nodes, could be constructed by applying a correlation threshold T (Fisher’s r-to-z) to the partial correlation coefficients:

That was, if the absolute z(i, j) (Fisher r-to-z of the partial correlation coefficient) of a pair of voxels, i and j, exceeds a given threshold T, an edge was said to exist; otherwise it did not exist. We defined the subgraph Gi as the set of nodes that were the direct neighbors of the ith node, i.e., directly connected to the ith node with an edge. The degree of each node, Ki, i = 1,2,…,95, was defined as the number of nodes in the subgraph Gi. The degree of connectivity, Knet, of a graph was the average of the degrees of all the nodes in the graph:

which was a measure to evaluate the degree of sparsity (or density, cost) of a network.
The clustering coefficient of a node was the ratio of the number of existing connections to the number of all possible connections in the subgraph Gi:

where Ei was the number of edges in the subgraph Gi (Watts and Strogatz, 1998; Strogatz, 2001). The clustering coefficient of a network was the average of the clustering coefficients of all nodes:

where Cnet was a measure of the extent of the local density or cliquishness of the network.
The mean shortest path length of a node was:

in which min{Li,j} was the shortest path length between the ith node and the jth node, and the path length was the number of edges included in the path connecting two nodes. The mean shortest path length of a network was the average of the shortest path lengths between the nodes:

Lnet was a measure of the extent of average connectivity of the network.
Eglobal, a measure of the global efficiency of parallel information transfer in the network, was defined by the inverse of the harmonic mean of the minimum path length between each pair of nodes (Latora and Marchiori, 2001, 2003; Achard and Bullmore, 2007):

The local efficiency of the ith node could be calculated:

In fact, since the ith node was not an element of the subgraph Gi, the local efficiency could also be understood as a measure of the fault tolerance of the network, indicating how well each subgraph exchanges information when the index node was eliminated (Achard and Bullmore, 2007). In addition, based on its definition, it was a measure of the global efficiency of the subgraph Gi. The mean local efficiency of a graph,

was the mean of all the local efficiencies of the nodes in the graph.
Small-Worldness
Compared with random networks, small-world networks have similar path lengths but higher clustering coefficients, that is γ = Cnet/Crandom > 1, λ = Lnet/Lrandom ≈1 (Watts and Strogatz, 1998). These two conditions can also be summarized into a scalar quantitative measurement, small-worldness, σ = γ/λ, which is typically >1 for small-world networks (Achard et al., 2006; Humphries et al., 2006; He et al., 2007). To examine the small-world properties, the values of Cnet and Lnet of the functional brain network need to be compared with those of random networks. As suggested by Stam et al. (2007), statistical comparisons should generally be performed between networks that have equal (or at least similar) degree sequences. Whereas theoretical random networks have Gaussian degree distributions that may differ from the degree distribution of the brain networks that we discovered in this study. To obtain a better control for the functional brain networks, following previous studies (Liu et al., 2008; Liao et al., 2010), we generated 100 random networks for each degree K and threshold T of each individual network by a Markov-chain algorithm (Maslov and Sneppen, 2002; Milo et al., 2002; Sporns and Zwi, 2004). In the original network, if node i1 was connected to j1 and i2 was connected to j2, for the corresponding randomized matrices, we removed the edges between i1j1, and i2j2 but added new edges between i1j2, and i2j1. That means two pairs of vertices (i1, j1) and (i2, j2) in the existing network were selected where 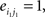
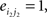
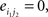 and
and 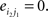 The corresponding randomized matrices would be created with
The corresponding randomized matrices would be created with 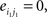
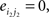
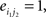 and
and 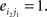 The matrices were randomly permuted which assured that the random matrices had the same degree distribution as the original matrix. This procedure was repeated until the topological structure of the original matrix was randomized (Achard et al., 2006). Finally, we averaged across all 100 generated random networks to obtain a mean Crandom and a mean Lrandom for each degree K and threshold T.
The matrices were randomly permuted which assured that the random matrices had the same degree distribution as the original matrix. This procedure was repeated until the topological structure of the original matrix was randomized (Achard et al., 2006). Finally, we averaged across all 100 generated random networks to obtain a mean Crandom and a mean Lrandom for each degree K and threshold T.
Statistical Analysis and Small-World Regime
Statistical comparisons of Cnet, Lnet, Eglobal, Elocal, γ, λ, and σ between the two groups were performed for the left and the right task-related networks separately. Following the approach of Liu, et al. (2008), a two-sample two-tailed t-test was performed to detect possible group difference for each value over a range of T or K. False discovery rate (FDR) correction (Benjamini and Hochberg, 1995) was used for multiple comparisons.
In the present study, we investigated the topological properties of the left and right task-related network as a function of T and K, following the studies by Liao et al. (2010), Stam et al. (2007), and Liu et al. (2008). All matrices were thresholded using a single, conservative threshold chosen to construct a sparse graph with mean degree Knet ≥ 2logN ≈ 9.1. (1) The maximum threshold (T) was selected also to assure that each network was fully connected with N = 95 nodes. This allowed us to compare the topological properties between the two groups in a way that was relatively independent of the size of the network. (2) The minimum threshold was selected to ensure that the brain networks have a lower global efficiency and a larger local efficiency compared to random networks with relatively the same distribution of the degree of connectivity (Achard and Bullmore, 2007). We selected the threshold range, Tmin ≤ T ≤ Tmax by intersecting the upper criteria. In both left and right network, we selected the small-world regime as 0.086 ≤ T ≤ 0.110 and repeated the full analysis for each value of T with increments of 0.002, corresponding to the degree of connectivity threshold 9.5 ≤ K ≤ 17.5 (cost range: 0.101–0.186) and did analysis with steps of 0.5.
Results
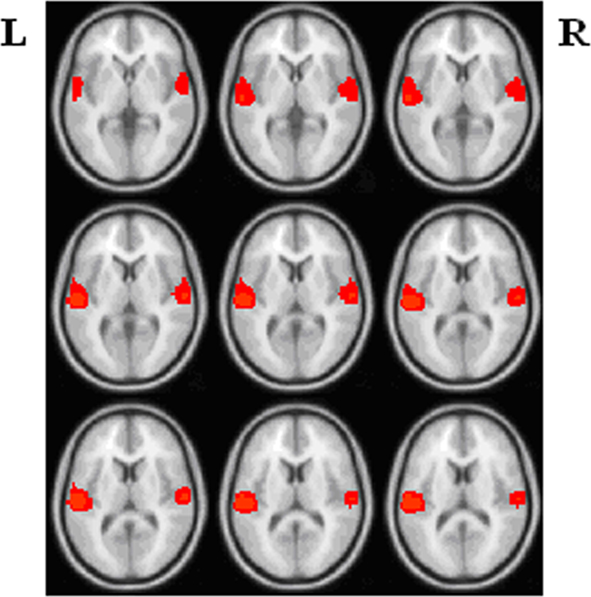
In line with prior findings (Calhoun et al., 2008a,b), group ICA results indicated the most task-related component for HCs and the most task-related component for SZ involving both left and right temporal lobe. Figure 1 displays schematic location of top 95 task-related voxels in both hemispheres selected based on the average of the most task-related component for HCs and the most task-related component for SZ. Figure 2 shows mean absolute Fisher’s z-score matrices of partial correlation results for both left and right 95 voxels. Figure A3 shows the histogram for absolute partial correlation (Fisher’s z) values of one subject in the left task-related network.
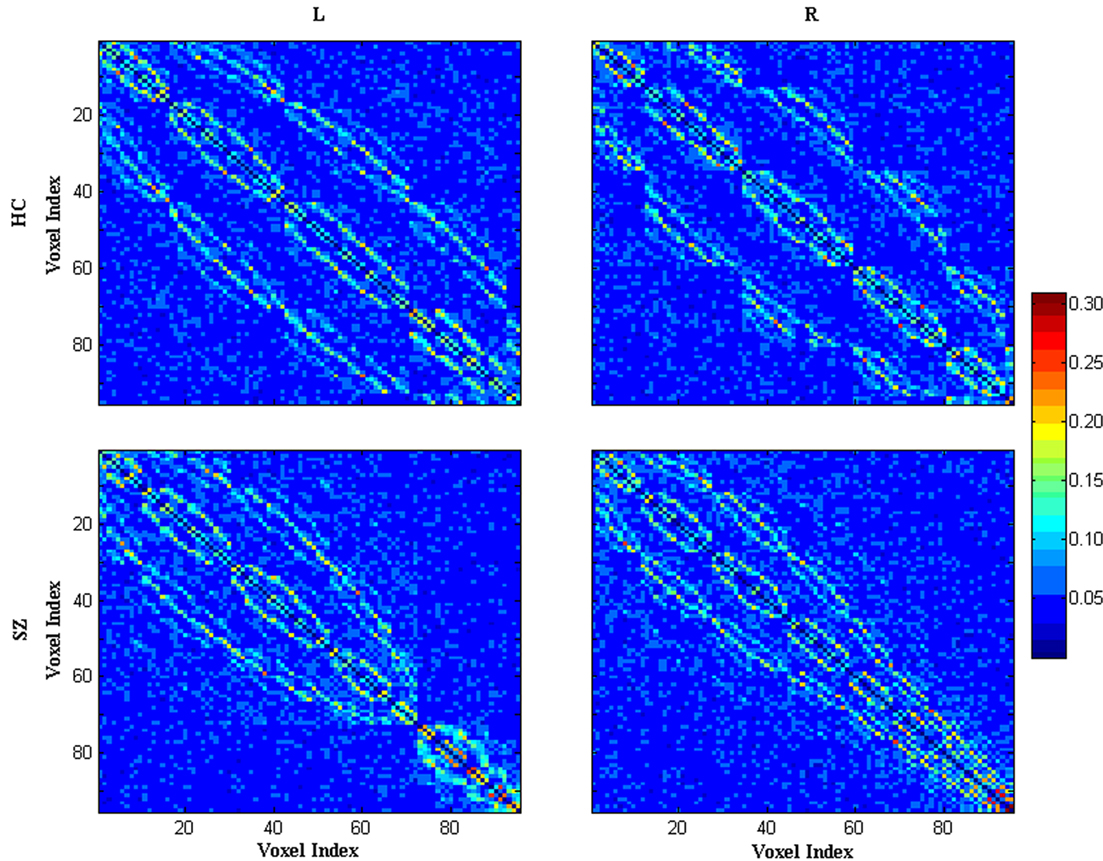
Figure 2. Mean absolute z-score matrices for HCs and SZ. Each figure shows a 95 × 95 square matrix, where each entry indicates the mean strength of the connectivity between each pair of voxels. For comparison, z values corresponding to P = 0.05 are 0.0975 (uncorrected) and 0.118 (FDR corrected). 3D spatial organization of 95 voxels were transformed into 1D alignment organized by slice (z-coordinate). The diagonal running from the upper left to the lower right is intentionally set to zero (L: the left task-related network; R: the right task-related network).
When looking at the topological indices as a function of threshold T, in both left and right task-related networks, the higher threshold resulted in a lower clustering coefficient, lower local efficiency, lower global efficiency, lower degree, and higher shortest path length because more and more edges were being lost with an increase in the threshold. Two-sample t-tests (FDR correction for multiple comparisons) indicated only shortest path length had significant group differences in the left task-related networks. As shown in Figure 3A, SZ had higher shortest path length at higher threshold points (0.098–0.110). Effect size (Cohen, 1988; Hartung et al., 2008) of shortest path length at threshold 0.104 was 0.9619. No group difference was found in the right task-related networks.
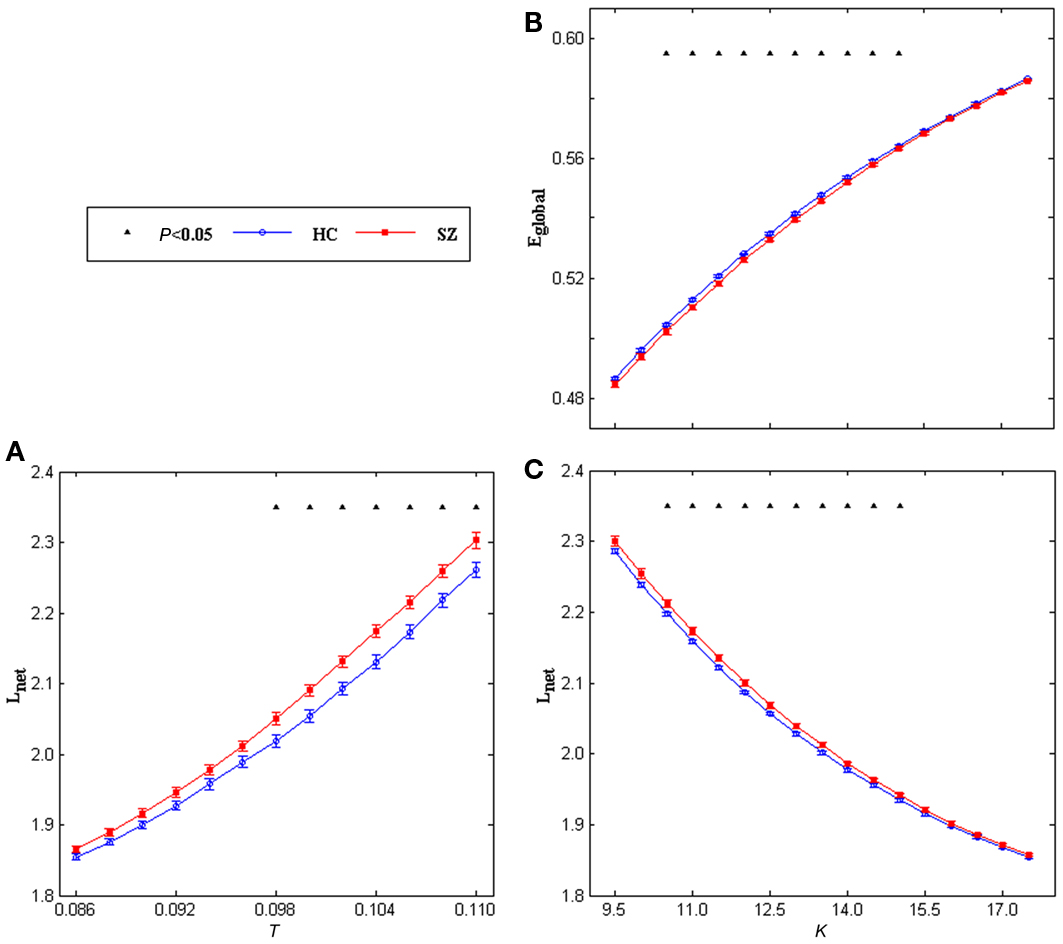
Figure 3. Mean shortest path length of the left task-related networks for HCs (blue circles) and SZ (red squares) as a function of threshold T (A), mean global efficiency (B) and shortest path length (C) of the left task-related networks for HCs (blue circles) and SZ (red squares) as a function of degree K. Error bars correspond to SEM (across 20 subjects of each group). Black triangles indicate where the group difference is significant (t-test, df = 38, 0.026 < P < 0.05, FDR correction for multiple comparisons).
For the topological indices as a function of degree K, with an increase in the degree, the global efficiency, local efficiency, clustering coefficient increased whereas shortest path length decreased in both left and right task-related networks. Significant group differences (two-sample t-tests, FDR correction for multiple comparisons) were only found in the left hemisphere. As shown in Figures 3B,C, SZ showed lower global efficiency and higher shortest path length at most K values (10.5–15.0). Effect size (Cohen, 1988; Hartung et al., 2008) of global efficiency at degree point K = 13.0 is −0.91, effect size of shortest path length at degree point K = 13.0 is 0.91. Figure 4 displays original distributions of global efficiency and shortest path length across subjects of the two groups at that degree point.
Figure 4. An example scatter plot of original distributions of global efficiency (Eglobal) andshortest path length (Lnet) across subjects for HCs (blue circles) and SZ (red circles) at degree point K = 13. 0 (in the left task-related network). The inverse relationship evident between Eglobal and Lnet is consistent with the fact the two variables are inversely correlated by definition.
The small-world attribute was evident in both left and right networks for both groups: γ was significantly greater than 1 while λ was near 1 over the whole range of T or K. Significant group differences were found in both left and right hemisphere networks. γ values and σ values were significantly decreased in SZ at all T and K values in the left network (Figure 5) and at most T and K values in the right network (Figure 6). See Figures A1,A2 for example graph (in form of nodes and edges) of networks.
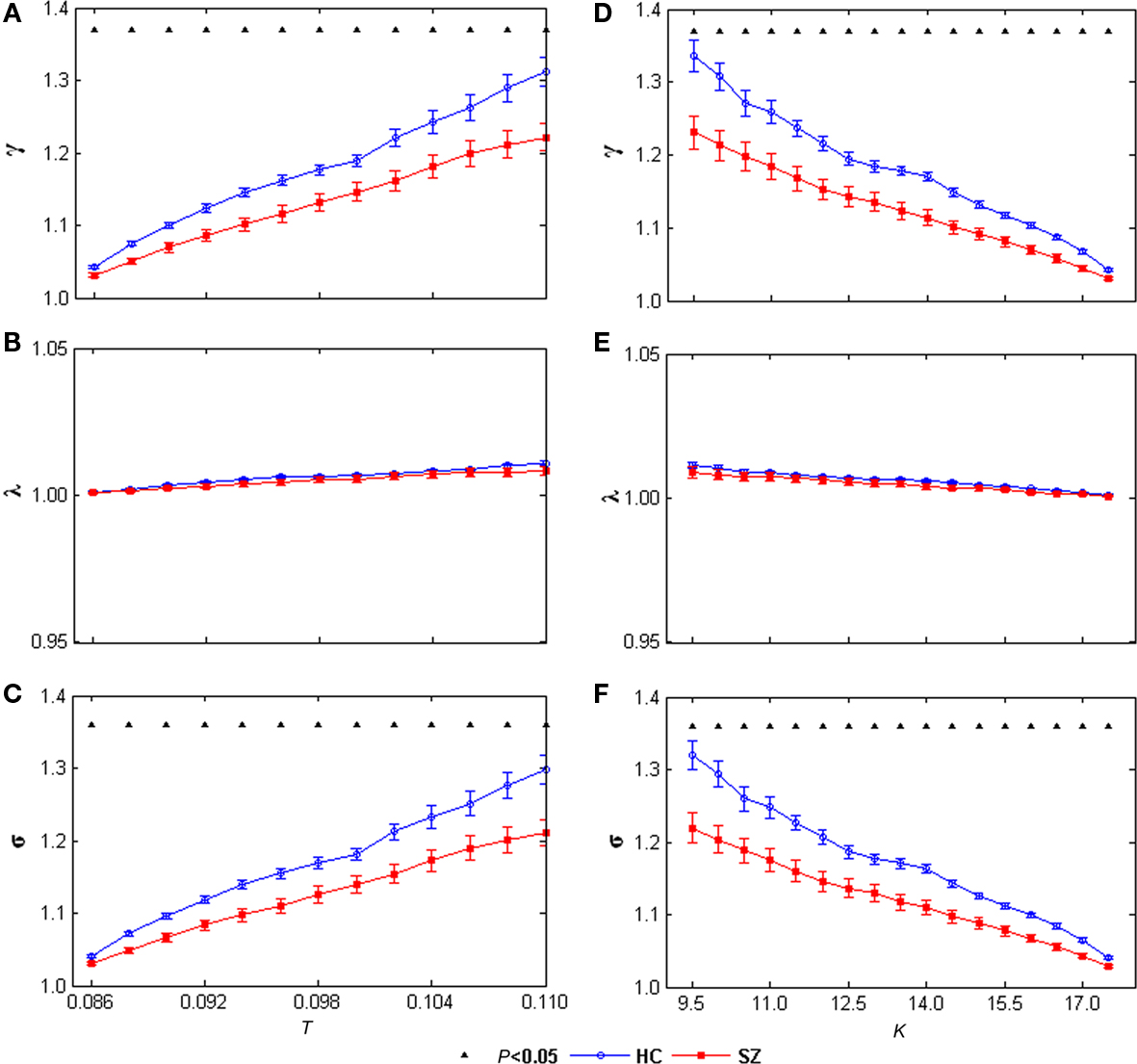
Figure 5. γ (A), λ (B), and σ (C) of the left task-related networks for HCs (blue circles) and SZ (red squares) as a function of thereshold T. γ (D), λ (E), and σ (F) of the left task-related networks for HCs (blue circles) and SZ (red squares) as a function of degree K. Error bars correspond to SEM (across 20 subjects of each group), Black triangles indicate where the group difference is significant (t-test, df = 38, P < 0.05, FDR correction for multiple comparisons).
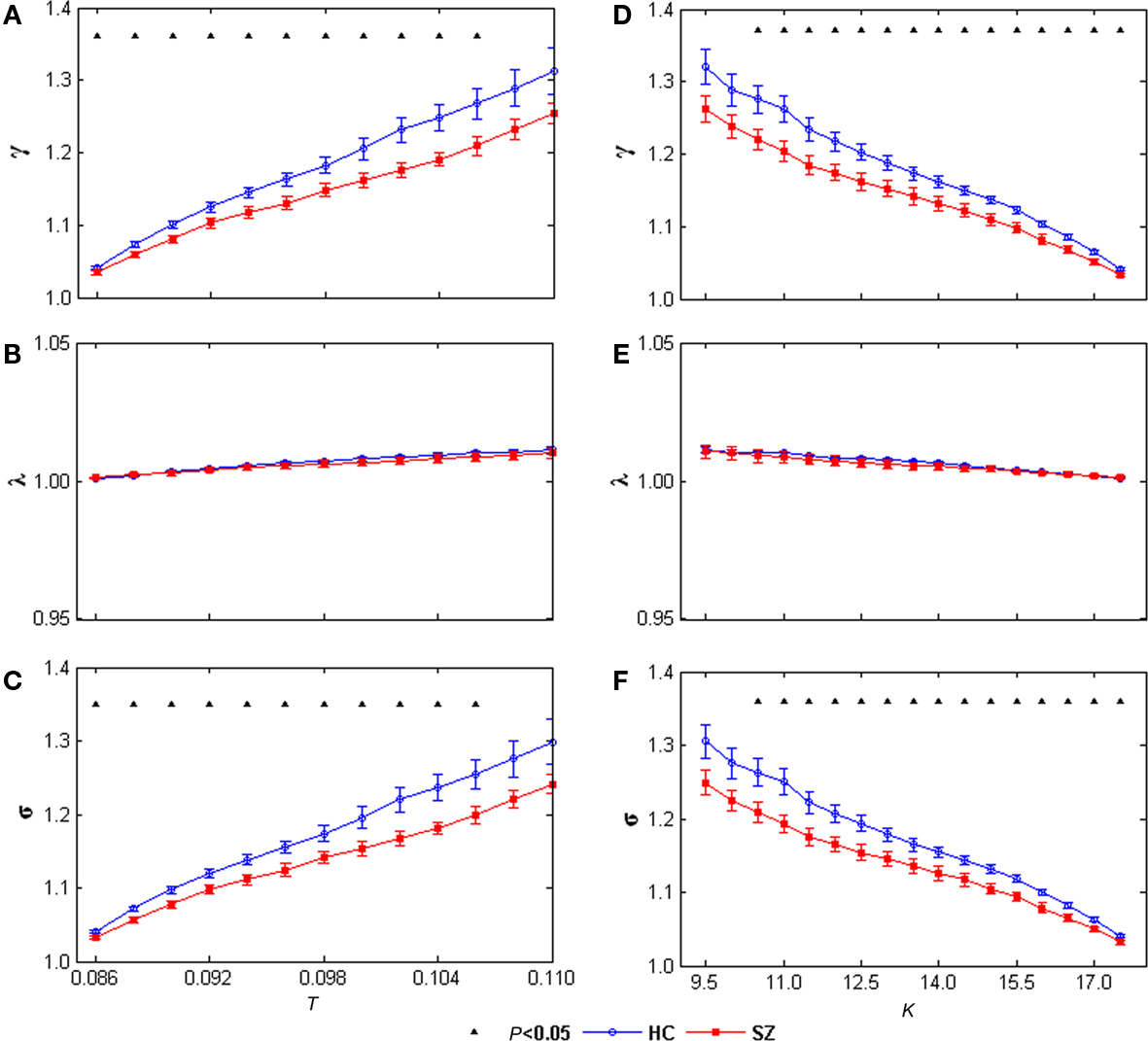
Figure 6. γ(A), λ (B), and σ (C) of the right task-related networks for HCs (blue circles) and SZ (red squares) as a function of threshold T. γ (D), λ (E), and σ (F) of the right task-related networks for HCs (blue circles) and SZ (red squares) as a function of degree K. Error bars correspond to SEM (across 20 subjects of each group), Black triangles indicate where the group difference is significant (t-test, df = 38, P < 0.05, FDR correction for multiple comparisons).
Two-sample t-tests were performed to compare strength (Lynall et al., 2010) of connectivity between HCs and SZ. There was no group difference (the left task-related network: t = 0.897, P = 0.375; the right task-related network: t = −0.117, P = 0.907). Two-sample Kolmogorov–Smirnov tests indicated the distribution of connectivity strengths was similar in the two groups (the left task-related network: P = 0.497, the right task-related network: P = 0.275). Associations between network properties and clinical symptom severity (PANSS scale) were explored using Pearson’s correlation coefficient. We found no significant result. Pearson’s correlation coefficient was also used to evaluate associations between network properties and task performance, no significant result was found either.
Discussion
In this fMRI study, topological properties of an AOD task-related networks as a function of threshold and degree were examined for both HCs and SZ. First, group ICA was performed to detect task-related networks in left and right hemisphere, both of which consisted of top 95 activated voxels during an AOD task. Then partial correlation matrix of the network was used to generate binary adjacency matrix. Both left and right task-related networks showed “small-world” pattern in the selected range of threshold and degree in HCs and SZ which provided further support for the presence of small-world features in complex brain networks (Sporns and Zwi, 2004; Stam and Reijneveld, 2007). However, SZ showed some different small-world characteristics. In the left task-related network, when examining topological properties as a function of threshold, SZ showed longer shortest path length; when looking at the topological properties as a function of degree, SZ had lower global efficiency, and longer shortest path length. Moreover, SZ showed lower γ and small-worldness σ when looking at them as a function of threshold or degree. In the right task-related network, only γ and small-worldness σ had significant group difference. SZ had lower value when looking at γ and σ as a function of threshold or degree. Our results suggest that during this AOD task, in the task-related networks consisting of activated voxels, SZ have different functional connectivity pattern from HCs. This finding is consistent with prior studies (Friston, 2005; Honey et al., 2005) which reported functional disconnectivity in SZ and provides further evidence for brain dysfunction associated with this disease. The structure of the absolute connection matrix for the left and right task-related network for HCs and SZ can be directly compared by visual inspection in Figure 2.
A short average path length and high global efficiency in graph system is of significance in minimizing noise, shortening signaling delay and increasing synchrony (Kaiser and Hilgetag, 2004). In a network of Hodgkin–Huxley neurons, (Lago-Fernandez et al., 2000) showed the structural and functional robustness of neural systems increases when path lengths are shorter. Short path lengths have also been demonstrated to promote effective interactions both between and across different cortical regions (Bassett and Bullmore, 2006; Achard and Bullmore, 2007). Consistent with previous studies (Micheloyannis et al., 2006; Bassett et al., 2008; Liu et al., 2008), SZ showed lower global efficiency at most K values and longer path length at some T values and most K values. That group differences were significant only for the left hemisphere, may indicate information interactions between interconnected task-related voxels were slower and less efficient in the left hemisphere in SZ during the AOD task.
Clustering coefficient and local efficiency of a graph system assess efficiency of communication between the first neighbors of a node when it is removed (Latora and Marchiori, 2001). Brain networks with high clustering and high local efficiency are robust in local information processing even if some neurons are inefficient or damaged (Zhao et al., 2008). Lower clustering coefficient and lower local efficiency imply relatively sparse local connectedness of brain functional networks (Micheloyannis et al., 2006). Although previous studies (Bassett et al., 2008; Liu et al., 2008; Lynall et al., 2010) reported reduced clustering coefficient and local efficiency in SZ, no significant group difference were found for the two measures in this study. That may suggest information processing efficiencies are equal robust in local in the networks consisted of task-related voxels for HCs and SZ during this AOD task.
Most interestingly, that γ and small-worldness σ values were decreased at the same threshold T or degree K in SZ in both hemispheres suggests that the task-related networks in both left and right hemispheres for SZ are closer to the random networks that have equal degree sequences. These group differences imply that the small-world AOD task-related networks are altered in SZ. That some significant group differences (including shortest path length and global efficiency) are restricted to the left hemisphere is compatible with previous contributions reporting predominantly left hemisphere abnormalities in SZ (Ross and Pearlson, 1996; Ribolsi et al., 2009).
Overall, we built “equi-threshold” networks using threshold T and “equi-sparse” networks using degree K. Similar results were found in the two separated ways might be due to the average partial correlation (connectivity strength) and the distribution of it showed no significant difference between the two groups.
However, several limitations should be concerned for this study. The first consideration is medication of patients may possibly influence the results. The types of medications used to treat SZ are complex, therefore, we are unable to perform a treatment similar to van Dellen et al. (2009) which divided temporal lobe epilepsy patients into two groups. But in further studies we may perform an analysis in first-episode, never medicated patients before and after antipsychotic treatment as Lui et al. (2010). Secondly, undirected, unweighted networks are built in the present study like most previous researches (Liu et al., 2008; Bullmore and Sporns, 2009; Lynall et al., 2010). Further studies may perform a weighted network analysis which could supply more information (van den Heuvel and Hulshoff Pol, 2010; Wang et al., 2010a). The third issue is smooth during preprocessing. It has been pointed out that spatial smoothing could introduce artificial correlations between voxels by previous voxel-based network analysis studies in which graphs were built based on correlation matrices (van den Heuvel et al., 2008; Hayasaka and Laurienti, 2010). However, Partial correlation in this study would remove the local correlation (including that caused by smoothing) but preserve the unique voxel variance. Further studies are required to determine the full impact of smoothing on correlation and partial correlation including its relationship to the variability from subject to subject. Moreover, two hemispheres were compared separately in this study. The two left handed patients might bias the results. Further studies are necessary to assess any relationship between handedness and lateralization of network effects during AOD tasks. One more concern is the limitation to perform group comparisons in standard space. As SZ consistently show decreased brain volume (Meyer-Lindenberg, 2010), voxels in patients may not correspond anatomically to controls. Future studies in native space are needed to confirm the findings of this study.
To our knowledge, this is the first fMRI study to examine the topological properties of AOD task-related small-world networks in HCs and SZ, using ICA and graph theoretical analysis methods. SZ showed longer path length and lower global efficiency in the left task-related network, suggests altered robustness of global information processing in SZ. In addition, γ and small-worldness σ values were decreased in SZ in both hemispheres, indicating the task-related networks of SZ are closer to random networks having equal degree sequences. Taken together, these results suggest altered properties of AOD task-related networks in SZ, which helps advance our understanding of the underlying pathophysiology of the disorder from functional brain architecture.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgment
This work was supported by NIH grant RO1 EB000840 (PI: Calhoun).
Footnotes
References
Achard, S., and Bullmore, E. (2007). Efficiency and cost of economical brain functional networks. PLoS Comput. Biol. 3, e17. doi: 10.1371/journal.pcbi.0030017
Achard, S., Salvador, R., Whitcher, B., Suckling, J., and Bullmore, E. (2006). A resilient, low-frequency, small-world human brain functional network with highly connected association cortical hubs. J. Neurosci. 26, 63–72.
Bassett, D. S., and Bullmore, E. T. (2009). Human brain networks in health and disease. Curr. Opin. Neurol. 22, 340–347.
Bassett, D. S., Bullmore, E., Verchinski, B. A., Mattay, V. S., Weinberger, D. R., and Meyer-Lindenberg, A. (2008). Hierarchical organization of human cortical networks in health and schizophrenia. J. Neurosci. 28, 9239–9248.
Bassett, D. S., Bullmore, E. T., Meyer-Lindenberg, A., Apud, J. A., Weinberger, D. R., and Coppola, R. (2009). Cognitive fitness of cost-efficient brain functional networks. Proc. Natl. Acad. Sci. U.S.A. 106, 11747–11752.
Bassett, D. S., Meyer-Lindenberg, A., Achard, S., Duke, T., and Bullmore, E. (2006). Adaptive reconfiguration of fractal small-world human brain functional networks. Proc. Natl. Acad. Sci. U.S.A. 103, 19518–19523.
Bell, A. J., and Sejnowski, T. J. (1995). An information maximisation approach to blind separation and blind deconvolution. Neural. Comput. 7, 1129–1159.
Benjamini, Y., and Hochberg, Y. (1995). Controlling the false discovery rate: a practical and powerful approach to multiple testing. J. R. Stat. Soc. Series B 57, 289–300.
Bramon, E., Rabe-Hesketh, S., Sham, P., Murray, R. M., and Frangou, S. (2004). Meta-analysis of the P300 and P50 waveforms in schizophrenia. Schizophr. Res. 70, 315–329.
Bullmore, E., and Sporns, O. (2009). Complex brain networks: graph theoretical analysis of structural and functional systems. Nat. Rev. Neurosci. 10, 186–198.
Calhoun, V. D., Adali, T., Giuliani, N. R., Pekar, J. J., Kiehl, K. A., and Pearlson, G. D. (2006). Method for multimodal analysis of independent source differences in schizophrenia: combining gray matter structural and auditory oddball functional data. Hum. Brain Mapp. 27, 47–62.
Calhoun, V. D., Adali, T., Pearlson, G. D., and Pekar, J. J. (2001). A method for making group inferences from functional MRI data using independent component analysis. Hum. Brain Mapp. 14, 140–151.
Calhoun, V. D., Eichele, T., and Pearlson, G. (2009a). Functional brain networks in schizophrenia: a review. Front. Hum. Neurosci. 3, 17.
Calhoun, V. D., Liu, J., and Adali, T. (2009b). A review of group ICA for fMRI data and ICA for joint inference of imaging, genetic, and ERP data. Neuroimage 45, 163–172.
Calhoun, V. D., Kiehl, K. A., Liddle, P. F., and Pearlson, G. D. (2004). Aberrant localization of synchronous hemodynamic activity in auditory cortex reliably characterizes schizophrenia. Biol. Psychiatry 55, 842–849.
Calhoun, V. D., Kiehl, K. A., and Pearlson, G. D. (2008a). Modulation of temporally coherent brain networks estimated using ICA at rest and during cognitive tasks. Hum. Brain Mapp. 29, 828–838.
Calhoun, V. D., Maciejewski, P. K., Pearlson, G. D., and Kiehl, K. A. (2008b). Temporal lobe and “default” hemodynamic brain modes discriminate between schizophrenia and bipolar disorder. Hum. Brain Mapp. 29, 1265–1275.
Cohen, J. (1988). Statistical Power Analysis for the Behavioral Sciences, 2nd Edn. Hillsdale, New Jersey: Lawrence Erlbaum Associates.
Danielyan, A., and Nasrallah, H. A. (2009). Neurological disorders in schizophrenia. Psychiatr. Clin. North Am. 32, 719–757.
De Vico Fallani, F., Maglione, A., Babiloni, F., Mattia, D., Astolfi, L., Vecchiato, G., De Rinaldis, A., Salinari, S., Pachou, E., and Micheloyannis, S. (2010). Cortical network analysis in patients affected by schizophrenia. Brain Topogr. 23, 214–220.
Doege, K., Bates, A. T., White, T. P., Das, D., Boks, M. P., and Liddle, P. F. (2009). Reduced event-related low frequency EEG activity in schizophrenia during an auditory oddball task. Psychophysiology 46, 566–577.
Dosenbach, N. U., Fair, D. A., Cohen, A. L., Schlaggar, B. L., and Petersen, S. E. (2008). A dual-networks architecture of top-down control. Trends Cogn. Sci. (Regul. Ed.) 12, 99–105.
Eguiluz, V. M., Chialvo, D. R., Cecchi, G. A., Baliki, M., and Apkarian, A. V. (2005). Scale-free brain functional networks. Phys. Rev. Lett. 94, 018102.
Ferri, R., Rundo, F., Bruni, O., Terzano, M. G., and Stam, C. J. (2007). Small-world network organization of functional connectivity of EEG slow-wave activity during sleep. Clin. Neurophysiol. 118, 449–456.
First, M. B., Spitzer, R. L., Gibbon, M., and Williams, J. B. W. (1995). Structured Clinical Interview for DSM-IV Axis I Disorders – Patient Edition (SCID-I/P, Version 2.0). New York: New York State Psychiatry Institute.
Fisher, R. A. (1914). Frequency distribution of the values of the correlation coefficient in samples from an indefinitely large population. Biometrika 10, 507–521.
Fisher, R. A. (1921). On the ‘probable error’ of a coefficient of correlation deduced from a small sample. Metron 1, 3–32.
Freire, L., Roche, A., and Mangin, J. F. (2002). What is the best similarity measure for motion correction in fMRI time series? IEEE Trans. Med. Imaging 21, 470–484.
Friston, K. (2005). Disconnection and cognitive dysmetria in schizophrenia. Am. J. Psychiatry 162, 429–432.
Gomez Portillo, I. J., and Gleiser, P. M. (2009). An adaptive complex network model for brain functional networks. PLoS ONE 4, e6863. doi: 10.1371/journal.pone.0006863
Gruzelier, J., Wilson, L., and Richardson, A. (1999). Cognitive asymmetry patterns in schizophrenia: retest reliability and modification with recovery. Int. J. Psychophysiol. 34, 323–331.
Guye, M., Bettus, G., Bartolomei, F., and Cozzone, P. J. (2010). Graph theoretical analysis of structural and functional connectivity MRI in normal and pathological brain networks. MAGMA 23, 409–421.
Hampson, M., Peterson, B. S., Skudlarski, P., Gatenby, J. C., and Gore, J. C. (2002). Detection of functional connectivity using temporal correlations in MR images. Hum. Brain Mapp. 15, 247–262.
Hartung, J., Knapp, G., and Sinha, B. K. (2008). Statistical Meta-Analysis with Application. Hoboken, NJ: Wiley.
Hayasaka, S., and Laurienti, P. J. (2010). Comparison of characteristics between region- and voxel-based network analyses in resting-state fMRI data. Neuroimage 50, 499–508.
He, Y., Chen, Z., Gong, G., and Evans, A. (2009). Neuronal networks in Alzheimer’s disease. Neuroscientist. 15, 333–350.
He, Y., Chen, Z. J., and Evans, A. C. (2007). Small-world anatomical networks in the human brain revealed by cortical thickness from MRI. Cereb. Cortex 17, 2407–2419.
Honey, G. D., Pomarol-Clotet, E., Corlett, P. R., Honey, R. A., McKenna, P. J., Bullmore, E. T., and Fletcher, P. C. (2005). Functional dysconnectivity in schizophrenia associated with attentional modulation of motor function. Brain 128, 2597–2611.
Hugdahl, K., and Calhoun, V. D. (2010). An update on neurocognitive impairment in schizophrenia and depression. Front. Hum. Neurosci. 4:4. doi:10.3389/neuro.09.004.2010
Humphries, M. D., Gurney, K., and Prescott, T. J. (2006). The brainstem reticular formation is a small-world, not scale-free, network. Proc. Biol. Sci. 273, 503–511.
Javitt, D. C. (2009). When doors of perception close: bottom-up models of disrupted cognition in schizophrenia. Annu. Rev. Clin. Psychol. 5, 249–275.
Kaiser, M., and Hilgetag, C. C. (2004). Modelling the development of cortical systems networks. Neurocomputing 58–60, 297–302.
Kiehl, K. A., Stevens, M. C., Laurens, K. R., Pearlson, G., Calhoun, V. D., and Liddle, P. F. (2005). An adaptive reflexive processing model of neurocognitive function: supporting evidence from a large scale (n = 100) fMRI study of an auditory oddball task. Neuroimage 25, 899–915.
Lago-Fernandez, L. F., Huerta, R., Corbacho, F., and Siguenza, J. A. (2000). Fast response and temporal coherent oscillations in small-world networks. Phys. Rev. Lett. 84, 2758–2761.
Latora, V., and Marchiori, M. (2001). Efficient behavior of small-world networks. Phys. Rev. Lett. 87, 198701.
Latora, V., and Marchiori, M. (2003). Economic small-world behavior in weighted networks. Eur. Phys. J. B. 32, 249–263.
Li, X., Branch, C. A., and DeLisi, L. E. (2009). Language pathway abnormalities in schizophrenia: a review of fMRI and other imaging studies. Curr. Opin. Psychiatry 22, 131–139.
Li, Y., Adali, T., and Calhoun, V. D. (2007). Estimating the number of independent components for fMRI data. Hum. Brain Mapp. 28, 1251–1266.
Liao, W., Zhang, Z., Pan, Z., Mantini, D., Ding, J., Duan, X., Luo, C., Lu, G., and Chen, H. (2010). Altered functional connectivity and small-world in mesial temporal lobe epilepsy. PLoS ONE 5, e8525. doi: 10.1371/journal.pone.0008525
Liu, J., Liang, J., Qin, W., Tian, J., Yuan, K., Bai, L., Zhang, Y., Wang, W., Wang, Y., Li, Q., Zhao, L., Lu, L., von Deneen, K. M., Liu, Y., and Gold, M. S. (2009). Dysfunctional connectivity patterns in chronic heroin users: an fMRI study. Neurosci. Lett. 460, 72–77.
Liu, Y., Liang, M., Zhou, Y., He, Y., Hao, Y., Song, M., Yu, C., Liu, H., Liu, Z., and Jiang, T. (2008). Disrupted small-world networks in schizophrenia. Brain 131, 945–961.
Lui, S., Li, T., Deng, W., Jiang, L., Wu, Q., Tang, H., Yue, Q., Huang, X., Chan, R. C., Collier, D. A., Meda, S. A., Pearlson, G., Mechelli, A., Sweeney, J. A., and Gong, Q. (2010). Short-term effects of antipsychotic treatment on cerebral function in drug-naive first-episode schizophrenia revealed by “resting state” functional magnetic resonance imaging. Arch. Gen. Psychiatry 67, 783–792.
Lynall, M. E., Bassett, D. S., Kerwin, R., McKenna, P. J., Kitzbichler, M., Muller, U., and Bullmore, E. (2010). Functional connectivity and brain networks in schizophrenia. J. Neurosci. 30, 9477–9487.
Marrelec, G., Krainik, A., Duffau, H., Pelegrini-Issac, M., Lehericy, S., Doyon, J., and Benali, H. (2006). Partial correlation for functional brain interactivity investigation in functional MRI. Neuroimage 32, 228–237.
Maslov, S., and Sneppen, K. (2002). Specificity and stability in topology of protein networks. Science 296, 910–913.
McKeown, M. J., Jung, T. P., Makeig, S., Brown, G., Kindermann, S. S., Lee, T. W., and Sejnowski, T. J. (1998). Spatially independent activity patterns in functional MRI data during the stroop color-naming task. Proc. Natl. Acad. Sci. U.S.A. 95, 803–810.
Meyer-Lindenberg, A. (2010). From maps to mechanisms through neuroimaging of schizophrenia. Nature 468, 194–202.
Micheloyannis, S., Pachou, E., Stam, C. J., Breakspear, M., Bitsios, P., Vourkas, M., Erimaki, S., and Zervakis, M. (2006). Small-world networks and disturbed functional connectivity in schizophrenia. Schizophr. Res. 87, 60–66.
Milo, R., Shen-Orr, S., Itzkovitz, S., Kashtan, N., Chklovskii, D., and Alon, U. (2002). Network motifs: simple building blocks of complex networks. Science 298, 824–827.
O’Donnell, B. F., Vohs, J. L., Hetrick, W. P., Carroll, C. A., and Shekhar, A. (2004). Auditory event-related potential abnormalities in bipolar disorder and schizophrenia. Int. J. Psychophysiol. 53, 45–55.
Pachou, E., Vourkas, M., Simos, P., Smit, D., Stam, C. J., Tsirka, V., and Micheloyannis, S. (2008). Working memory in schizophrenia: an EEG study using power spectrum and coherence analysis to estimate cortical activation and network behavior. Brain Topogr. 21, 128–137.
Palmer, B. W., Dawes, S. E., and Heaton, R. K. (2009). What do we know about neuropsychological aspects of schizophrenia? Neuropsychol. Rev. 19, 365–384.
Palva, S., Monto, S., and Palva, J. M. (2010). Graph properties of synchronized cortical networks during visual working memory maintenance. Neuroimage 49, 3257–3268.
Pearlson, G. D. (1997). Superior temporal gyrus and planum temporale in schizophrenia: a selective review. Prog. Neuropsychopharmacol. Biol. Psychiatry 21, 1203–1229.
Pearlson, G. D., Petty, R. G., Ross, C. A., and Tien, A. Y. (1996). Schizophrenia: a disease of heteromodal association cortex? Neuropsychopharmacology 14, 1–17.
Ponten, S. C., Bartolomei, F., and Stam, C. J. (2007). Small-world networks and epilepsy: graph theoretical analysis of intracerebrally recorded mesial temporal lobe seizures. Clin. Neurophysiol. 118, 918–927.
Reijneveld, J. C., Ponten, S. C., Berendse, H. W., and Stam, C. J. (2007). The application of graph theoretical analysis to complex networks in the brain. Clin. Neurophysiol. 118, 2317–2331.
Ribolsi, M., Koch, G., Magni, V., Di Lorenzo, G., Rubino, I. A., Siracusano, A., and Centonze, D. (2009). Abnormal brain lateralization and connectivity in schizophrenia. Rev. Neurosci. 20, 61–70.
Robinson, P. A., Henderson, J. A., Matar, E., Riley, P., and Gray, R. T. (2009). Dynamical reconnection and stability constraints on cortical network architecture. Phys. Rev. Lett. 103, 108104.
Ross, C. A., and Pearlson, G. D. (1996). Schizophrenia, the heteromodal association neocortex and development: potential for a neurogenetic approach. Trends Neurosci. 19, 171–176.
Rubinov, M., and Sporns, O. (2010). Complex network measures of brain connectivity: uses and interpretations. Neuroimage 52, 1059–1069.
Salvador, R., Suckling, J., Coleman, M. R., Pickard, J. D., Menon, D., and Bullmore, E. (2005). Neurophysiological architecture of functional magnetic resonance images of human brain. Cereb. Cortex 15, 1332–1342.
Sanabria-Diaz, G., Melie-Garcia, L., Iturria-Medina, Y., Aleman-Gomez, Y., Hernandez-Gonzalez, G., Valdes-Urrutia, L., Galan, L., and Valdes-Sosa, P. (2010). Surface area and cortical thickness descriptors reveal different attributes of the structural human brain networks. Neuroimage 50, 1497–1510.
Schlaepfer, T. E., Harris, G. J., Tien, A. Y., Peng, L. W., Lee, S., Federman, E. B., Chase, G. A., Barta, P. E., and Pearlson, G. D. (1994). Decreased regional cortical gray matter volume in schizophrenia. Am. J. Psychiatry 151, 842–848.
Smit, D. J., Stam, C. J., Posthuma, D., Boomsma, D. I., and de Geus, E. J. (2008). Heritability of “small-world” networks in the brain: a graph theoretical analysis of resting-state EEG functional connectivity. Hum. Brain Mapp. 29, 1368–1378.
Sporns, O., and Zwi, J. D. (2004). The small world of the cerebral cortex. Neuroinformatics 2, 145–162.
Stam, C. J. (2004). Functional connectivity patterns of human magnetoencephalographic recordings: a ‘small-world’ network? Neurosci. Lett. 355, 25–28.
Stam, C. J., Jones, B. F., Nolte, G., Breakspear, M., and Scheltens, P. (2007). Small-world networks and functional connectivity in Alzheimer’s disease. Cereb. Cortex 17, 92–99.
Stam, C. J., and Reijneveld, J. C. (2007). Graph theoretical analysis of complex networks in the brain. Nonlinear Biomed. Phys. 1, 3.
Stevens, M., Calhoun, V. D., and Kiehl, K. A. (2005). Hemispheric differences in hemodynamics elicited by auditory oddball stimuli. Neuroimage 26, 782–792.
Stevens, M., Kiehl, K. A., Pearlson, G. D., and Calhoun, V. D. (2007). Functional neural circuits for mental timekeeping. Hum. Brain Mapp. 28, 394–408.
Sui, J., Adali, T., Pearlson, G. D., and Calhoun, V. D. (2009). An ICA-based method for the identification of optimal FMRI features and components using combined group-discriminative techniques. Neuroimage 46, 73–86.
Swanson, N., Eichele, T., Pearlson, G., Kiehl, K., Yu, Q., and Calhoun, V. D. (in press). Lateral differences in the default mode network in healthy controls and patients with schizophrenia. Hum. Brain Mapp. doi: 10.1002/hbm.21055
Tzourio-Mazoyer, N., Landeau, B., Papathanassiou, D., Crivello, F., Etard, O., Delcroix, N., Mazoyer, B., and Joliot, M. (2002). Automated anatomical labeling of activations in SPM using a macroscopic anatomical parcellation of the MNI MRI single-subject brain. Neuroimage 15, 273–289.
Vaessen, M. J., Hofman, P. A., Tijssen, H. N., Aldenkamp, A. P., Jansen, J. F., and Backes, W. H. (2010). The effect and reproducibility of different clinical DTI gradient sets on small world brain connectivity measures. Neuroimage 51, 1106–1116.
Valencia, M., Martinerie, J., Dupont, S., and Chavez, M. (2008). Dynamic small-world behavior in functional brain networks unveiled by an event-related networks approach. Phys. Rev. E. Stat. Nonlin. Soft Matter Phys. 77, 050905.
van Dellen, E., Douw, L., Baayen, J. C., Heimans, J. J., Ponten, S. C., Vandertop, W. P., Velis, D. N., Stam, C. J., and Reijneveld, J. C. (2009). Long-term effects of temporal lobe epilepsy on local neural networks: a graph theoretical analysis of corticography recordings. PLoS ONE 4, e8081. doi: 10.1371/journal.pone.0008081
van den Heuvel, M. P., and Hulshoff Pol, H. E. (2010). Exploring the brain network: a review on resting-state fMRI functional connectivity. Eur. Neuropsychopharmacol. 20, 519–534.
van den Heuvel, M. P., Stam, C. J., Boersma, M., and Hulshoff Pol, H. E. (2008). Small-world and scale-free organization of voxel-based resting-state functional connectivity in the human brain. Neuroimage 43, 528–539.
Wang, H., Douw, L., Hernandez, J. M., Reijneveld, J. C., Stam, C. J., and Van Mieghem, P. (2010a). Effect of tumor resection on the characteristics of functional brain networks. Phys. Rev. E. Stat. Nonlin. Soft Matter Phys. 82, 021924.
Wang, L., Metzak, P. D., Honer, W. G., and Woodward, T. S. (2010b). Impaired efficiency of functional networks underlying episodic memory-for-context in schizophrenia. J. Neurosci. 30, 13171–13179.
Wang, J., Wang, L., Zang, Y., Yang, H., Tang, H., Gong, Q., Chen, Z., Zhu, C., and He, Y. (2009a). Parcellation-dependent small-world brain functional networks: a resting-state fMRI study. Hum. Brain Mapp. 30, 1511–1523.
Wang, L., Zhu, C., He, Y., Zang, Y., Cao, Q., Zhang, H., Zhong, Q., and Wang, Y. (2009b). Altered small-world brain functional networks in children with attention-deficit/hyperactivity disorder. Hum. Brain Mapp. 30, 638–649.
Watts, D. J., and Strogatz, S. H. (1998). Collective dynamics of ‘small-world’ networks. Nature 393, 440–442.
White, T., Schmidt, M., Kim, D. I., and Calhoun, V. D. (2010). Disrupted functional brain connectivity during verbal working memory in children and adolescents with schizophrenia. Cereb. Cortex. doi: 10.1093/cercor/bhq114
Yu, S., Huang, D., Singer, W., and Nikolic, D. (2008). A small world of neuronal synchrony. Cereb. Cortex 18, 2891–2901.
Zalesky, A., Fornito, A., and Bullmore, E. T. (2010). Network-based statistic: identifying differences in brain networks. Neuroimage 53, 1197–1207.
Zhang, Z., Lu, G., Zhong, Y., Tan, Q., Yang, Z., Liao, W., Chen, Z., Shi, J., and Liu, Y. (2009). Impaired attention network in temporal lobe epilepsy: a resting FMRI study. Neurosci. Lett. 458, 97–101.
Keywords: small-world, fMRI, schizophrenia, auditory oddball, ICA, network
Citation: Yu Q, Sui J, Rachakonda S, He H, Pearlson G and Calhoun VD (2011) Altered small-world brain networks in temporal lobe in patients with schizophrenia performing an auditory oddball task. Front. Syst. Neurosci. 5:7. doi: 10.3389/fnsys.2011.00007
Received: 24 June 2010;
Accepted: 24 January 2011;
Published online: 08 February 2011.
Edited by:
Jonathan B. Fritz, University of Maryland, USAReviewed by:
Danielle S. Bassett, University of California Santa Barbara, USAJaap C. Reijneveld, VU University Medical Center, Netherlands
Danko Nikolic, Max Planck Institute for Brain Research, Germany
Copyright: © 2011 Yu, Sui, Rachakonda, He, Pearlson and Calhoun. This is an open-access article subject to an exclusive license agreement between the authors and Frontiers Media SA, which permits unrestricted use, distribution, and reproduction in any medium, provided the original authors and source are credited.
*Correspondence: Qingbao Yu, The Mind Research Network, 1101 Yale Boulevard NE, Albuquerque, NM 87106, USA. e-mail:cXl1QG1ybi5vcmc=