Striatal fast-spiking interneurons: from firing patterns to postsynaptic impact

1 Introduction

Striatal fast-spiking (FS) interneurons provide strong inhibitory input to medium-sized spiny (MS) projection neurons (Koós and Tepper, 1999; Tepper et al., 2004, 2008; Mallet et al., 2005; Gustafson et al., 2006). The proximal location of FS-to-MS synapses enables FS neurons to influence MS activity – either by delaying or by totally suppressing spike generation in MS cells (Tepper et al., 2004, 2008). Despite their small number in the striatum (∼1%; Kita et al., 1990; Luk and Sadikot, 2001), FS interneurons are therefore able to shape the output of the striatum to the downstream nuclei of the basal ganglia.

The discharge of striatal FS neurons in awake, behaving animals is characterized by irregular fluctuations of the instantaneous firing rate with numerous high-frequency bursts, single spikes, and periods of silence (Berke et al., 2004; Berke, 2008; Gage et al., 2010). It is currently not known if and to which extent FS firing variability is determined by the input that these neurons receive under natural conditions. An additional source of the firing variability could originate from intrinsic cellular mechanisms that underlie the irregular, random bursting (“stuttering”) in FS neurons. Stuttering spike behavior is characterized by a variable number of spikes per burst and a variable interburst interval (Figure 1B). Since stuttering discharge has only been reported in vitro in response to somatic step currents (Kawaguchi, 1993; Gupta et al., 2000; Koós and Tepper, 2002; Bracci et al., 2003; Tepper et al., 2004; La Camera et al., 2006; Druckmann et al., 2007; Taverna et al., 2007), we in this study systematically investigated the effect of fluctuating and steady input on FS firing patterns in a model and in vitro. Indeed, we observed random stuttering only in response to steady input. In this regime, however, our model predicts a significant amount of spike synchronization among electrically coupled FS cells, which is in contrast to the lack of synchronized spiking among striatal FS interneurons in vivo (Berke, 2008). Conversely, when driven by fluctuating input, FS model neurons showed reliable spike timing and no spike synchronization. Therefore, these results suggest that in the awake, behaving animal, neighboring striatal FS interneurons are not in the stuttering regime simultaneously and that the high in vivo FS firing variability is more likely determined by the input fluctuations.

FIGURE 1

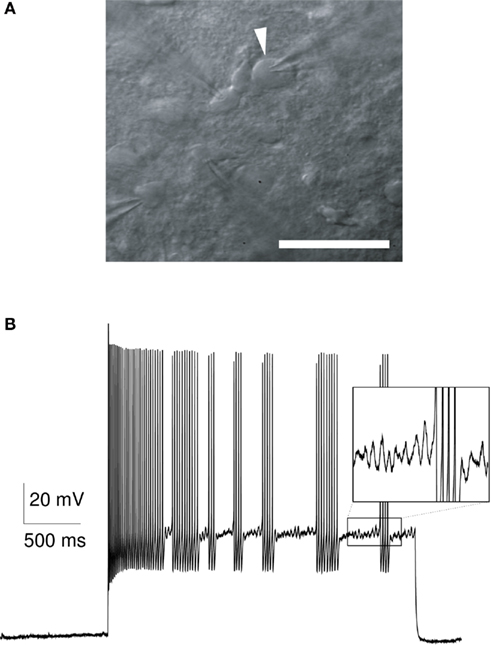
Figure 1. (A) Infrared microscopy image of a striatal FS interneuron (arrowhead) in a patch-clamp experiment (scale bar, 50 μm). (B) Experimental response of a striatal fast-spiking neuron (rat, P15) to a 2-s long somatic current injection (600 pA). This FS neuron shows a typical stuttering response with a variable number of action potentials in each burst, and a variable length of the interburst interval. The subthreshold membrane potential during the interburst intervals is characterized by oscillatory fluctuations in the range of 40–50 Hz (inset).

High firing rates of striatal FS interneurons in vivo (Berke, 2008, 2011) and the synaptic depression in FS-to-MS synapses (Plenz and Kitai, 1998; Koós et al., 2004; Gittis et al., 2010; Planert et al., 2010) cause changes in FS firing patterns to affect the synaptic strength of these synapses. This will ultimately modify the impact that FS cells have over MS firing, and thus, over striatal output. We therefore investigated how in vivo firing patterns in striatal FS interneurons influence the amplitude distribution of PSPs in MS cells. Our FS-to-MS synapse model predicted that these synapses are strongly depressed over extended periods of time. Despite the lack of general FS spike synchronization in vivo, this result suggests that the combined inhibition mediated by multiple presynaptic FS cells might be required to effectively shape the activity of MS projection neurons.

2 Materials and Methods

2.1 The Neuron Model

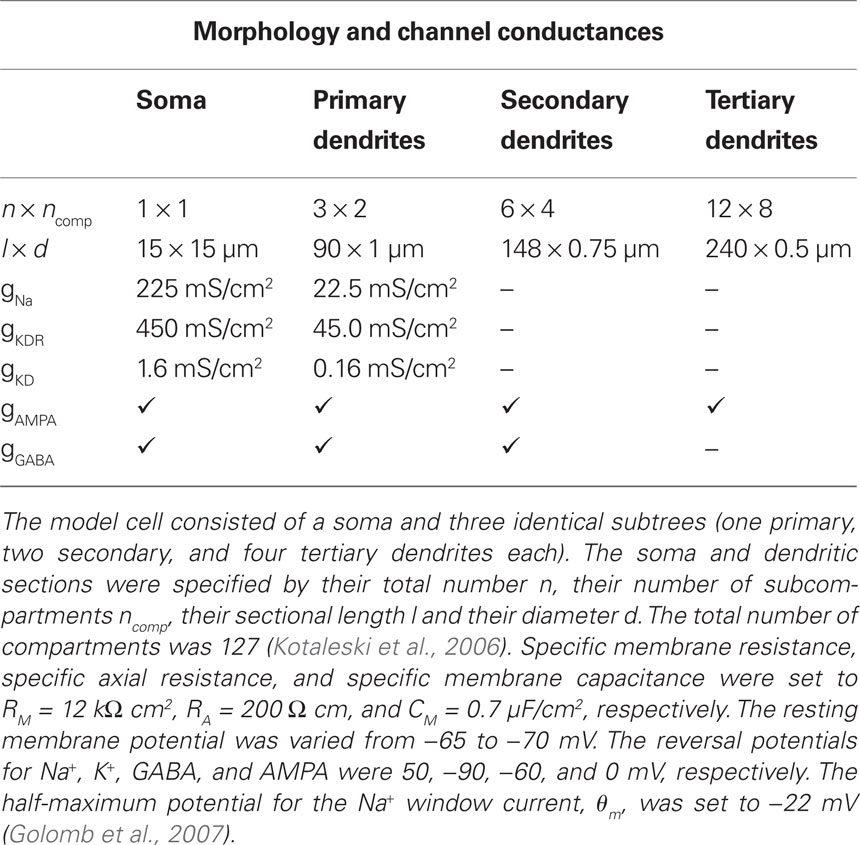
Parvalbumin-positive FS interneurons have been characterized by their immunochemical, morphological, and electrophysiological properties in both striatum (Kawaguchi, 1993, 1997; Taverna et al., 2007) and cortex (Kawaguchi and Kubota, 1997; Markram et al., 2004). Despite some striking differences in the organization of the cortical and striatal microcircuits, in which they are embedded, these neurons show many similarities in both areas, including a similar electrophysiological signature (see references above), a common developmental origin (Marín et al., 2000) and the coupling via gap junctions (Galarreta and Hestrin, 1999; Koós and Tepper, 1999; Beierlein et al., 2000; Amitai et al., 2002; Fukuda, 2009). Therefore, to model the stuttering in striatal FS interneurons, we used the channel descriptions of a previously published cortical one-compartment model (Golomb et al., 2007). This model contained the following voltage-dependent ionic channels, which have also been reported to be expressed in the rat striatum (Lenz et al., 1994; Weiser et al., 1994; Chung et al., 2000; Kotaleski et al., 2006): a fast Na⁺ window current (I_Na), a fast delayed rectifier K⁺ current (I_Kdr), and a slowly inactivating (d-type) K⁺ current (I_Kd). The d-type current has been shown to delay spike initiation (Goldberg et al., 2008), which is also observed in many striatal FS interneurons (Plenz and Kitai, 1998). With a small Na⁺ window current and a sufficiently large d-type K⁺ current, the model was able to generate the typical subthreshold oscillations (40–50 Hz) and stuttering episodes in response to somatic current injections as observed in striatal FS interneurons (Figure 1). In the current study, the half-maximum potential for the sodium current was θ_m = −22 mV and the d-type conductance was g_KD = 1.6 mS/cm² (Table 1, see also Golomb et al., 2007). Some experiments were also performed with a model neuron that produced tonic discharge (θ_m = −28 mV, g_KD = 0.39 mS/cm², see Figures A2 and A3 in Appendix). To induce oscillatory fluctuations in the subthreshold membrane potential during the interburst episodes, a Gaussian white noise current with zero mean and 15 pA SD (0.1 ms time step) was applied to the model neuron (Golomb et al., 2007).

TABLE 1

Table 1. Parameters for the FS model neuron.

In order to model distal synaptic input and dendritic gap junctions, we extended the original one-compartment model of Golomb et al. (2007) by a dendritic tree consisting of three identical subtrees (cf. Kotaleski et al., 2006). Each subtree comprised one primary, two secondary, and four tertiary dendrites (i.e., each of the primary and secondary dendrites branched into two daughter arms). To allow for the same high firing rates as in the original one-compartment model, we increased the active conductances by a factor of 2 in the morphologically extended model, and in addition assumed active primary dendrites. Detailed model cell parameters are shown in Table 1.

We used a single FS model neuron for the simulation of the responses to fluctuating input, and a pair of FS model cells for the study of electrical coupling in these neurons. To be able to use parallel computing for the simulation of the FS cell pair, we implemented the FS model in Parallel Genesis (Bower and Beeman, 1998) with a fixed step size of 10 μs. The model implementation can be obtained from http://senselab.med.yale.edu/modeldb/showmodel.asp?model=140254

2.2 Synaptic Input and Electrical Coupling in the Model

The FS neuron model included α-amino-3-hydroxyl-5-methyl-4-isoxazole-propionate (AMPA) and fast γ-aminobutyric acid (GABA) synapses. Some tests were performed with additional N-methyl-d-aspartate (NMDA) synapses (not shown). The presented results did not depend on the presence or absence of NMDA synapses. All synapses received independent input in the form of random Poisson spike trains. AMPA synapses were distributed over all 127 compartments (Kotaleski et al., 2006). If NMDA synapses were present, they were located in the same compartments and received the same input as the AMPA synapses. GABA synapses were located more proximally, resulting in a total number of 31 inhibitory synapses (Table 1). In vitro measurements of spontaneous activity have shown that FS neurons receive a similar ratio between inhibitory and excitatory currents during an up-state (Blackwell et al., 2003). Therefore, to compensate for the smaller number of inhibitory synapses, the activation rate per GABA synapse was approximately threefold higher than for AMPA synapses. This was equivalent to using three GABA synapses per proximal compartment and activating them at the same rate as AMPA since we used the non-saturating synapse model synchan in Genesis. The time constants of the double-exponential function, which described the evolution of the synaptic conductances in this model, were τ₁ = 0.7, τ₂ = 2 ms for AMPA, τ₁ = 1.3, τ₂ = 4 ms for GABA, and τ₁ = 3.6, τ₂ = 116 ms for NMDA synapses, respectively (Hjorth et al., 2009).

Gap junctions between two FS neurons were modeled as conductive elements between the soma, the outer proximal dendrites, or the outer secondary dendrites. The conductance of a single gap junction was set to 0.5 nS, a value within the range of gap junction conductances in cortical FS neurons (Galarreta and Hestrin, 2002). A single soma-somatic gap junction resulted in a coupling coefficient of ∼11% in our model, which was within the range of coupling coefficients reported in the striatum (Galarreta and Hestrin, 2001; Koós et al., 2004). In order to obtain the same coefficient for the dendro-dendritic coupling, we increased the number of gap junctions on the primary and secondary dendrites to two and three, respectively.

2.3 Modeling of the FS-to-MS Synaptic Dynamics

For the FS-to-MS connections we used data from rat that was recently published by Planert et al. (2010). In short, synaptic connections were identified and characterized by stimulation of a presynaptic FS cell with a train (10, 20, or 40 Hz) of 8 strong and brief current pulses (0.5–2 nA, 3 ms), followed by a so-called recovery test pulse approximately 550 ms after the end of the train, all reliably eliciting action potentials (APs). Postsynaptic neurons were held near −80 mV to ensure strongly depolarizing responses to GABAergic input. For the analysis of synaptic properties, average postsynaptic traces over multiple repetitions were examined for the existence of synaptic responses (Planert et al., 2010).

The depressing synapse was modeled using a scheme described by Markram et al. (1998), where the synapse is assumed to have a limited amount of resources which are slowly restored over time (see also Tsodyks et al., 1998). The amplitude of a postsynaptic potential, PSP_n, in response to the nth AP in a spike train is a product of the fraction of available resources, R_n, and a facilitating utilization factor, u_n, scaled by the absolute synaptic efficacy, A_se:

The utilization factor is increased by each AP and decays back toward U in the time between APs:

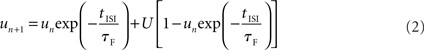
with u₁ =U. t_ISI denotes the time between the nth and (n + 1)th AP. Each AP utilizes the fraction u_n from the synaptic resources, R_n, which then recovers to a value of 1 at a rate of τ_D:

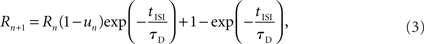
with R₁ = 1. The parameters U, τ_D, and τ_F were fitted to the experimental traces using a two-step process. First, the amplitudes were extracted by fitting an exponential decay to the previous response and subtracting it from the new response. The second step in the parameter fitting performed a grid search (range 0–5 s for τ_D,F and 0–1 for U). The error was defined as the weighted sum of the absolute values of the amplitude difference at each peak between the reference trace and the modeled trace. The initial response and the recovery test response (RTR) were weighted five times stronger, and the second response was weighted by two. This was done to prevent the first set of inputs from dominating over the RTR. The parameters were fitted to a train of spikes at 20 Hz and verified for some synapses at 10 and 40 Hz (see Figure A1 in Appendix).

2.4 Slice Preparation and Experimental Recordings

All animal experiments were carried out according to the guidelines of the Stockholm municipal committee for animal experiments. Slices (300 μm thick) were obtained from rats on postnatal days 14 to 23, cut in ice-cold extracellular solution, kept at 35°C for 30 minutes, and then moved to room temperature before the recording. Whole-cell patch recordings were obtained at a temperature of 35 ± 0.5°C. Neurons were visualized using IR-DIC microscopy (Zeiss FS Axioskop, Oberkochen, Germany) as shown in Figure 1A. Recorded neurons were selected visually in cortex and striatum. In the striatum, neighboring cells with lateral somatic distances less than 100 μm were recorded simultaneously. MS neurons and fast-spiking interneurons were classified according to their typical membrane properties. The extracellular solution (both for cutting and recording) contained (in mM) 125 NaCl, 25 glucose, 25 NaHCO₃, 2.5 KCl, 2 CaCl₂, 1.25 NaH₂PO₄, 1 MgCl₂. Recordings were amplified using Axoclamp 2B or Multiclamp 700B amplifiers (Molecular Devices, CA, USA), filtered at 2 kHz, digitized (5–20 kHz) using ITC-18 (Instrutech, Port Washington, NY, USA), and acquired using Igor Pro (Wavemetrics, Lake Oswego, OR, USA). Patch pipettes were pulled with a Flamming/Brown micropipette puller P-97 (Sutter Instruments, Novato, CA, USA) and had an initial resistance of 5–10 MΩ, containing (in mM) 10 HEPES, 0.3 GTP-Na, and 10 Na₂-phosphocreatine. The intracellular solution furthermore contained either 110 K-gluconate, 10 KCl, and 4 ATP-Mg, or 110 K-gluconate, 10 KCl, 4 ATP-Na₂, and 4 MgCl₂, or 105 K-gluconate, 30 KCl, and 4 ATP-Mg. Chloride concentrations were increased for some connectivity experiments, as increasing internal chloride increases absolute synaptic current amplitudes. We did not observe differences in parameters describing the synaptic dynamics (not shown). All striatal FS responses reported in Figure 3 were recorded with the last mentioned concentrations. In a subset of neurons, 0.2–0.5% biocytin was added. Liquid junction potential was not corrected for. Recordings were performed in current-clamp mode, with access resistance compensated throughout the experiments. Data was discarded when access resistance exceeded 35 MΩ.

2.5 Stimulation Protocol (Generation of Fluctuating Current Input)

We investigated the spiking pattern of the model neuron and of stuttering striatal and cortical (layer 2/3 and 5) FS cells in response to fluctuating versus steady input. Current input with varying degree of fluctuations was generated as follows. We used the FS model neuron to simulate somatic, subthreshold membrane potential fluctuations in response to random synaptic input (f_AMPA = 760, f_GABA = 560 Hz, firing rate was ∼11 Hz). To avoid the influence of any suprathreshold activity, the model neuron was prevented from firing by removing the active sodium conductance. The resulting membrane potential was used as a measure of the synaptic input fluctuations, and a current proportional to the membrane potential was used for subsequent somatic injection (the time course of the fastest fluctuations in the resulting trace matched therefore the membrane time constant of the model neuron, which was ∼8 ms). The scaling of the current was chosen such that the firing rate in the model (now with sodium conductance) matched the synaptically driven case. In most cases, generated current traces induced the same spikes as the synaptic input had done originally (not shown). This indicates that somatic current injection was able to mimic to a high degree the synaptic input of dendritic origin in the FS model. Next, we determined the amount of steady current injection that resulted in the same firing rate as in the case of synaptic input (10–12 Hz). We denote this input by q_DC = 1 (fraction of steady current equal to unity, no synaptic input). Conversely, we denote the current trace that was entirely derived from the synaptic activation by q_DC = 0 (fraction of steady current equal to zero). To control the amount of input fluctuations, we varied the level of steady input, q_DC, between zero and one. The firing rate of the model neuron was held constant by reducing the synaptic AMPA and GABA conductances accordingly.

2.6 In vivo Recordings

Samples (>12 min duration) of awake in vivo rat FS spike trains were taken from a previously described data set (Berke et al., 2004; Berke, 2008). Interspike intervals (ISIs) smaller than 1.5 ms (<0.8%) were excluded from the analysis.

2.7 Data Analysis

Correlation analysis

Sub- and suprathreshold synchronization and spike train similarity was measured by Pearson’s correlation coefficient

where t denotes the time lag between the two zero-mean vectors of data samples, x_i and y_i (i = 1,…,n+t). For a time lag t = 0 and for identical vectors x_i and y_i, the correlation, C(0), is equal to unity. Since we were interested in millisecond synchronization, the bin size for the suprathreshold activity was 1 or 2 ms. Synchronization was either shown as a function of time lag or reported as a single number, the latter referring to the correlation value at time lag zero.

Measurement of stuttering onset

The time of stuttering onset was measured as the time of the first spike peak in the first stuttering episode for each model neuron. The onset time difference for a pair of FS neurons was defined as the absolute value of the time difference of stuttering onset in the two neurons. To avoid stimulus-driven correlation in the stuttering discharge of two neurons, the begin of step current input was randomly shifted by ±25 ms for each cell.

Measurement of the phase lag of the subthreshold oscillations

The phase lag of the subthreshold oscillations between two FS model neurons was defined as the phase difference for frequencies 40–48 Hz, i.e., for frequencies for which the power spectrum showed a peak (see Figure A5 in Appendix). The phase difference was mapped from 0 − 2π (0–360°) to 0 − π by mirroring the phase angles in the polar coordinate system along the horizontal axis. This is equivalent to using the absolute value if the phase difference would have been defined in the range ±π.

Measurement of spike clustering

For the analysis of clustered spikes in the model and in vitro, we used the minimal interspike interval, ISI_min, for each individual trace and considered two spikes to be member of the same spike group if their ISI was less than 2 ISI_min. To exclude the possibility that ISI_min was affected by ISI outliers, which were sometimes observed for short, strong depolarizations in the case of fluctuating input, ISI_min was obtained by using the second percentile of the ISIs. However, the results did not depend on this particular choice, i.e., similar results were obtained when using the smallest ISI or the first percentile. ISI_min varied between individual FS neurons and was also dependent on the stimulus strength; for the striatal FS cells it was 14.7 ± 8.8 ms (mean ± SD, average over various input scalings, n = 450 traces). The shortest ISI for each cell was 3–5 ms (second percentile). Clusters were defined as groups with 3 or more spikes. For the simulated traces in the stuttering and the tonically firing FS model neuron, we also used the coefficient of variation of the ISI, CV_ISI, as an indicator for spike clustering (see Figures A2 and A3 in Appendix).

Spike shuffling

For an in vivo spike train with mean firing frequency, f, we obtained shuffled, Poisson-distributed ISIs from an exponential distribution with rate parameter λ = 1/f, and uniformly distributed ISIs from a continuous uniform distribution on the interval (0, 2/f). To account for the refractory period, random numbers were discarded and repeatedly drawn if an ISI was shorter than 1.5 ms. The resulting spike trains had the same spike rate, f, as the original in vivo trace.

Statistical analysis

Values are expressed as mean ± SD if not noted otherwise. For the regression analysis between sub- and suprathreshold activity we used the F-test, for the multiple comparison between control and electrical coupling the one-way ANOVA test (significance level 0.01), and for comparison of the mean percentage of clustered spikes the unequal variance t-test. Data was analyzed in Matlab (Mathworks, MA, USA) and R¹ and visualized with Gnuplot².

3 Results

3.1 Stuttering Discharge Requires Steady Depolarization

Many fast-spiking (FS) interneurons show random stuttering in response to somatic current steps (Figure 1B). However, the response to such an artificial step current can only reveal specific features of the electrophysiological signature of neuronal cells (see, e.g., Mainen and Sejnowski, 1995). Two hallmarks of the stuttering in FS interneurons are the clustered spiking and the stochastic nature of firing discharge (Englitz et al., 2008). To study if these features contribute to FS firing under more physiological conditions, we investigated the influence of input fluctuations on the spike activity in FS interneurons. This was first done in a morphologically extended version of the one-compartment model by Golomb et al. (2007), which allowed the conductance-based modeling of proximal and distal synaptic input (Table 1).

In the FS model, stuttering in response to somatic step currents could be observed over a wide range of firing frequencies, where both the spike rate and the average length of the stuttering episodes increased with larger input amplitudes (Figure 2A, firing rates ranged from 1 to 45 Hz from left to right). The amplitude of the somatic current step also had an influence on the subthreshold membrane potential, V_m. In the model, V_m was about −46 mV when the first spikes were elicited (i.e., 19 mV above the resting potential, left panel in Figure 2A) and depolarized by an additional 2 mV at firing rates > 40 Hz (Figure 2A, right panel). When the FS model was activated by synaptic AMPA input, the spike discharge was characterized by many single spikes and spike doublets, without showing the characteristic stuttering behavior (Figure 2B, increasing synaptic input frequency from left to right). Interestingly, even though V_m depolarized with increasing input frequency, it remained far below −46 mV, which was the subthreshold membrane potential above which stuttering was readily observed for step current injections (Figure 2A). At a firing rate of 25 Hz, for example, the subthreshold V_m was −54 mV (Figure 2B, right panel). To study the effect of the input type on the subthreshold depolarization and on the stuttering discharge in more detail, we systematically varied the fraction of steady input, q_DC. For each level of q_DC, the firing rate of the FS model was held constant by simultaneously reducing the synaptic conductances (see Section 2). Thus, larger values of q_DC resulted in smaller input fluctuations at the same FS spike rate. Figure 2C shows the responses of the FS model for two levels of q_DC. To obtain the same firing rate (∼12 Hz) for q_DC = 0.4 and 0.8, the synaptic conductances were reduced to 50 and 14% compared to q_DC = 0, respectively. The synaptic input train in Figure 2C is the same as in the middle trace of Figure 2B (f_AMPA = 760, f_GABA = 560 Hz, only synaptic amplitudes were reduced). This can be seen in the spike signature, which is hardly affected by the reduction of the synaptic conductances at q_DC = 0.4, despite the fact that the subthreshold V_m depolarized from −56 mV (synaptic input only, q_DC = 0) to −52 mV (q_DC = 0.4). At q_DC = 0.8, however, the spike signature changed to more stuttering-like firing (V_m = −47 mV, right panel in Figure 2C). In summary, increasing levels of q_DC led to a linear depolarization of the subthreshold V_m and an abrupt (non-linear) change from more regular firing to stuttering discharge at the same firing rate (Figure 2D).

FIGURE 2

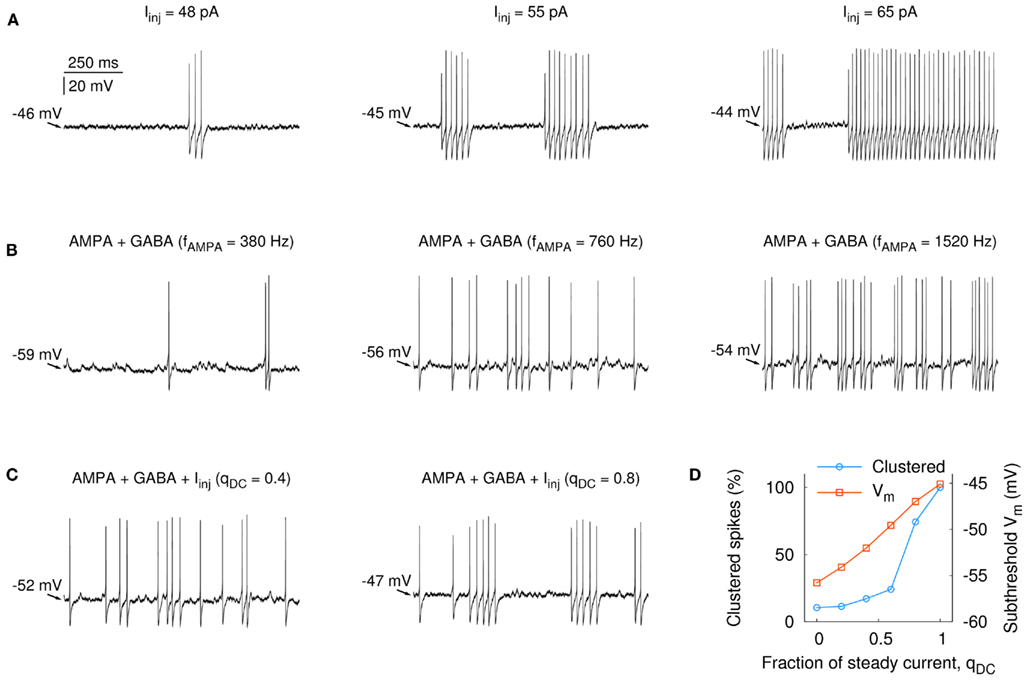
Figure 2. Fast-spiking firing discharge and subthreshold membrane potential in the model neuron in response to increasing step current injections and synaptic input frequency, as well as systematic combinations of the two. Firing patterns covary with the amount of subthreshold depolarization. (A) Somatically applied current injection was able to induce stuttering over a wide range of firing frequencies (1–45 Hz, from left to right). The subthreshold V_m varied between −46 and −44 mV (the resting potential for this cell was −65 mV). (B) Increasing frequency of AMPA and GABA synaptic input (from left to right: f_AMPA = 380, 760, and 1520 Hz, f_GABA = 280, 560, and 1120 Hz) led to an increase of the average subthreshold membrane potential (indicated by the arrows). (C) Relation between q_DC, subthreshold V_m, and the firing pattern. The neuron received in addition to AMPA and GABA synaptic input (f_AMPA = 760, f_GABA = 560 Hz) a somatically applied current step. The amplitude of the current step was scaled and the synaptic input was adjusted such that the output frequency of the neuron was 12 ± 1 Hz. Left: I_inj = 22 pA (q_DC = 0.4); right: I_inj = 44 pA (q_DC = 0.8). (D) A gradual increase of q_DC resulted in a linear depolarization of the subthreshold V_m from −53 to −45 mV. The percentage of clustered spikes increased strongly for I_inj > 33 pA (q_DC > 0.6), reflecting the stuttering behavior of the cell in response to more steady input.

The opening of synaptic channels decreases the input resistance of a neuron. Was the smaller amount of subthreshold depolarization a result of the synaptic activation alone (the GABA synapses had a reversal potential of −60 mV), or was it also attributable to the input fluctuations? To answer this question, we created traces of fluctuating current that resembled somatic potential fluctuations in the case of synaptic input. The current traces were derived from the model for different amounts of q_DC (see Section 2). This allowed us to study the response of the model neuron by an entirely current-driven approach, that is, without the activation of synaptic conductances. Furthermore, the current traces enabled us to measure the response of striatal FS interneurons to changing levels of input fluctuations in whole-cell patch-clamp recordings in vitro. The traces in Figure 3A show the resulting discharge for the model and a striatal FS cell for different levels of steady input, q_DC. As for the case with synaptic conductances (Figures 2C,D), V_m increased in a linear manner, and with decreasing input fluctuations the firing pattern changed from regular spiking to stuttering discharge with a high percentage of clustered spikes (Figures 3B,C; black traces: n = 5 striatal neurons, firing rate ranged from 2.2 to 64 Hz; red trace: model neuron). The mean percentage of clustered spikes was significantly different between fluctuating and steady input (4.7 and 82.9%, respectively; p = 0.0002, n = 5 striatal FS neurons, unequal variance t-test, right panel in Figure 3C). These results indicate that steady input leads to a more depolarized subthreshold membrane potential and induces stuttering discharge in FS interneurons (compare Figures A2 and A3 in Appendix for a tonically firing FS model).

FIGURE 3

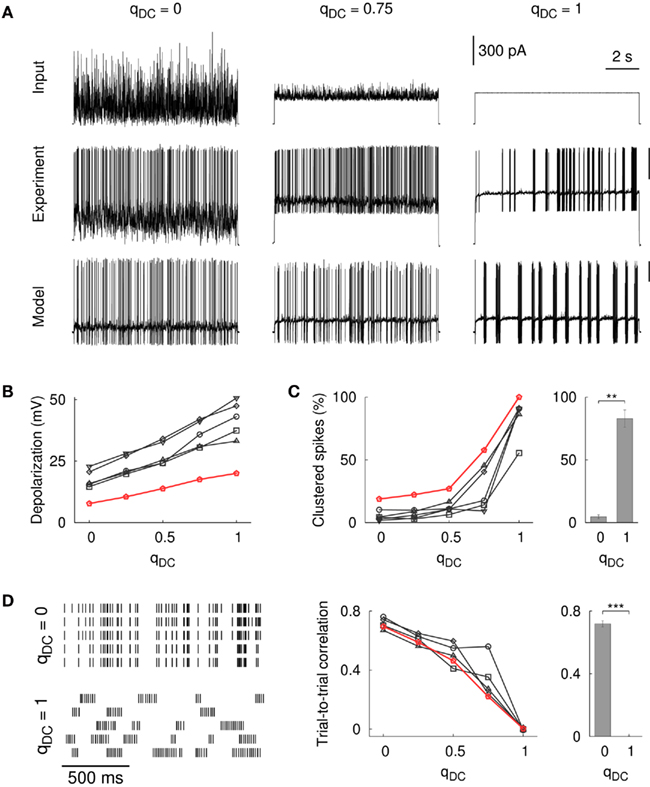
Figure 3. Influence of input fluctuations on FS firing patterns in the model and in vitro. (A) The spike pattern of the model neuron and of a striatal FS neuron following a somatically applied current injection with varying degree of fluctuations. Responses are shown for q_DC = 0, 0.75, and 1.0 (from left to right). The scale bars for the voltage traces correspond to 30 mV. The scale bar for the current traces corresponds to the in vitro experiment. (B) Depolarization of the subthreshold membrane potential (measured from the resting baseline). The membrane potential depolarized continuously as the input fluctuations diminish, that is, with increasing levels of steady input (black lines: n = 5 striatal FS neurons, red line: model cell). Two random input traces and different scalings were tested (450 traces in total, firing rate ranged from 2.2 to 64.4 Hz, the average firing rate was 18.9 ± 11.5 Hz). (C) Steady current input resulted in stuttering seen as an increase in the percentage of clustered spikes. The number of clustered spikes was significantly different between fluctuating and steady input [n = 5 striatal FS cells, t(4.4) = −11.0, p = 0.0002, unequal variance t-test]. (D) Left: example rastergram for a striatal FS neuron that repeatedly receives the same input (5 trials). Spike trains were more reliable for FS cells that were not in the stuttering regime (q_DC = 0). Variability was high for stuttering cells (q_DC = 1) resulting in zero trial-to-trial correlation [t(3) = 0.11, p = 0.92, one-sample t-test]. Middle: trial-to-trial correlation as a function of q_DC (black lines: n = 5 striatal FS neurons, red line: model cell). Right: The difference between q_DC = 0 and q_DC = 1 was statistically significant [n = 5 striatal FS neurons, t(3.2) = 34.7, p < 10⁻⁴, unequal variance t-test]. The bin size for the spike detection was 2 ms.

Importantly, the responses to steady input (q_DC = 1) in the model and in vitro showed a large variability between trials, whereas spike trains in response to fluctuating input (q_DC = 0) were more repeatable from trial to trial (cf. Mainen and Sejnowski, 1995). For striatal FS neurons, this can be seen in the elevated trial-to-trial correlation for q_DC = 0 compared to q_DC = 1 (Figure 3D, p < 10⁻⁵, n = 4 cells, unequal variance t-test, bin size 2 ms). The trial-to-trial correlation at q_DC = 1 was not significantly different from zero (p = 0.92, one-sample t-test) as was the trial-to-trial correlation for shuffled traces (random permutation of 2 ms bins, not shown). Taken together, these results show that the amount of input fluctuations strongly influences the firing pattern and the spike time reliability in striatal FS interneurons.

3.2 Spike Synchrony in Electrically Coupled FS Interneurons

Fast-spiking interneurons in the striatum are coupled by gap junctions (Kita et al., 1990; Galarreta and Hestrin, 2001; Fukuda, 2009) and electrical connections between these neurons have been confirmed in vitro (Koós and Tepper, 1999). In cortical FS cells, such electrical coupling contributes to synchronized spiking (Gibson et al., 2005; Mancilla et al., 2007). However, in awake, behaving animals, neighboring FS cells in the striatum do not show any sign of broadly synchronized firing (Berke, 2008). The lack of spike synchrony among striatal FS cells in vivo might give an indication of the input regime in which these cells operate, i.e., fluctuating versus steady input (Hjorth et al., 2009). We therefore used the stuttering FS model neuron to explore how the amount of input fluctuations influences the spike synchronization in a pair of electrically connected cells.

In the model, electrical coupling through gap junctions had a strong ability to synchronize periods of stuttering activity in neurons that received steady current input. Figure 4A shows an example of two unconnected FS neurons (upper traces) and the same pair of cells electrically coupled at the distal part of the primary dendrites (lower traces, ∼11% steady-state coupling). Although the cross-correlation, which measures the spike synchronization between the two neurons, decreased substantially with increasing distance between the location of the gap junctions and the soma (Figure 4B), the time difference of stuttering onset in both cells was in the majority of cell pairs smaller than 50 ms for proximal coupling (i.e., soma and primary dendrites, Figure 4C). In the model, proximal electrical coupling was also able to synchronize subthreshold oscillations in the connected FS neurons, although this effect was not very strong (Figures A4 and A5 in Appendix). Importantly, the fast entrainment of spiking activity in two connected neurons did not require a small phase lag between the preceding subthreshold oscillations, which is apparent in the missing correlation between the phase lag of the subthreshold oscillations and the time difference of the stuttering onset in both cells (Figure 4C). Furthermore, proximal coupling via gap junctions did not significantly change the number of spikes per burst but it resulted in a delayed stuttering discharge after stimulus onset (Figure 4D). The reason for this firing delay, which was only seen for proximal coupling, is most likely the shunting of charge across the gap junctions.

FIGURE 4

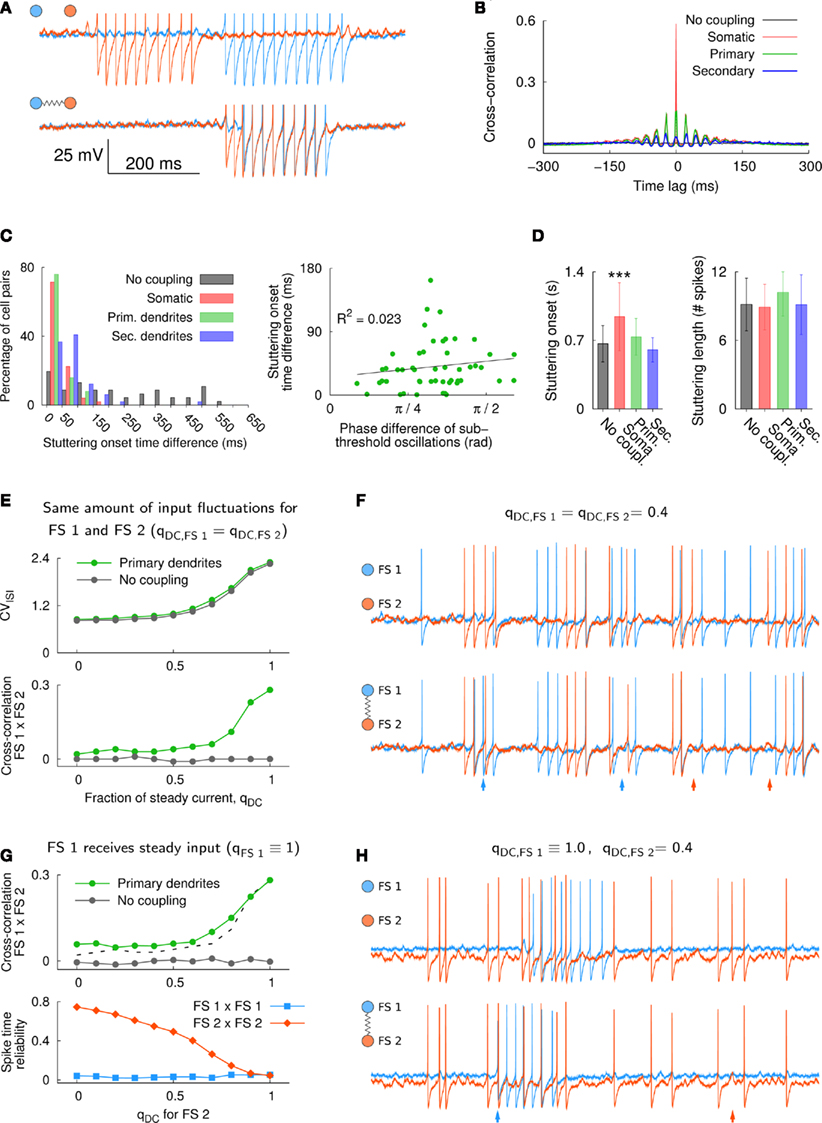
Figure 4. Synchronization of suprathreshold spiking activity in the neuron model. (A) Section of the voltage traces for a pair of uncoupled and electrically coupled FS cells (upper and lower traces, respectively). Each neuron received the same steady somatic input and only electrical coupling was added to the primary dendrites (2 × 0.5 nS total). The onset of the somatic current step input was random for each neuron (onset at 50 ± 25 ms). Spikes were truncated at −30 mV for better visualization. (B) Average cross-correlogram of spiking activity in the two neurons (n = 10; somatic current injection 74 pA, 60 s duration; bin size 1 ms). (C) Absolute onset time difference of the first stuttering episode in the two neurons (n = 49, left panel). The bars between 0 and 50 ms, for example, indicate the percentage of cell pairs with a time difference in the range 0–50 ms. There was no significant relation between the phase difference of the subthreshold oscillations and the stuttering onset time difference for electrically coupled FS neurons [right panel, R² = 0.023, F(1,98) = 1.106, p = 0.298, n = 50; gap junctions located at primary dendrites, see also Figures A4 and A5 in Appendix]. (D) The average delay of the first stuttering episode after stimulus onset increased significantly in somatically coupled neurons, i.e., from 665 ms under the control condition without electrical coupling to 942 ms for somatically coupled neurons [n = 49; one-way ANOVA, F(3,192) = 20.65, p < 10⁻⁶, Tukey–Kramer multiple comparison]. Electrical coupling did not have a strong effect on the average stuttering length, which was measured as the average number of action potentials within the first burst and ranged from 8.9 to 10.2 spikes for all conditions. The comparison of the average stuttering lengths gave a p-value of 0.024 (n = 49; one-way ANOVA, F(3,192) = 3.23]. Error bars denote the SD. (E) CV_ISI (upper panel) and spike synchronization as measured by the cross-correlation at time lag zero (lower panel, bin size 2 ms) for two FS model neurons that received the same amount of input fluctuations. The spike synchronization was almost absent in electrically coupled neurons that received fluctuating (synaptic) input and it increased in a similar manner as the CV_ISI for increasing levels of steady input, q_DC. (F) The traces show an example for q_DC = 0.4. The two neurons received the following input: f_AMPA = 1900, f_GABA = 1400 Hz, g_AMPA = g_GABA = 200 pA, somatic current injection I_inj = 22 pA; upper traces: uncoupled, lower traces: gap junctions at the distal part of the primary dendrites (2 × 0.5 nS total). (G) Spike synchronization (upper panel, bin size 2 ms) and spike time reliability (lower panel) in two FS model neurons that received different levels of q_DC. High spike synchronization between the FS model neurons required steady input in both neurons [the cross-correlation from (E) is plotted as a dashed line for comparison]. Electrical coupling did not affect the spike signature in FS 2 if it received fluctuating input, which can be seen by the high spike time reliability at q_DC = 0. However, in the stuttering cell, FS 1, the temporal spike occurrence was dramatically altered by electrical coupling (low spike time reliability). (H) Example traces for two neurons that received different levels of steady input (q_DC = 1 and 0.4 for FS 1 and FS 2, respectively).

In the case of steady current injection, a small number of spikes in one FS neuron was sufficient to induce a stuttering episode in an electrically connected cell (Figures 4A,C). We next analyzed the spike synchronization in two electrically connected FS cells over a wide range of input fluctuations, i.e., from q_DC = 0 to 1 (Figure 4E). The voltage traces in Figure 4F show an example of two cells that were not in the stuttering regime. The neurons received a small amount of somatic current input (q_DC = 0.4) and in addition AMPA and GABA synaptic input. Although gap junctions at the primary dendrites were able to induce and suppress single APs in connected neurons (Figure 4F, arrows), spike synchronization as measured by the cross-correlation between FS 1 and FS 2 was low (Figure 4E). With increasing levels of q_DC, FS firing tended to be more clustered and more variable (increasing CV_ISI, upper panel in Figure 4E, see also Figure A2 in Appendix), and spike correlation between the two connected cells increased (lower panel in Figure 4E). To test if this spike synchronization required steady input in both FS model neurons, we repeated the simulation with one of the FS cells, FS 1, being permanently in the stuttering regime, and by varying q_DC for FS 2 only (Figures 4G,H). Figure 4H shows an example of two model cells that receive different levels of q_DC as it can be seen in the different levels of V_m and different firing patterns in the two cells. While the stuttering cell, FS 1, showed strong changes in the spike signature (i.e., low values of spike time reliability) as a result of electrical coupling, the neighboring neuron, FS 2, showed a high spike time reliability when driven by fluctuating input (Figure 4G, lower panel), thus, resulting in little spike synchronization among the two cells (Figure 4G, upper panel). Therefore, stuttering in a single FS model neuron was not sufficient to broadly induce synchronized spikes in electrically connected neighbor cells. These results and the lack of spike synchrony in vivo (Berke, 2008) suggest that in awake, behaving animals, striatal FS cells are not in the stuttering regime simultaneously.

3.3 FS Firing Patterns Influence the Distribution of Postsynaptic Potentials in Medium Spiny Neurons

The discharge of striatal FS neurons in awake, behaving animals is characterized by large fluctuations of the instantaneous firing rate with numerous high-frequency bursts, single spikes, and periods of silence (Berke et al., 2004; Berke, 2008). Given the strong depressive component in the dynamics of striatal FS-to-MS synapses (Plenz and Kitai, 1998; Koós et al., 2004; Gittis et al., 2010; Planert et al., 2010), differences in the firing patterns of FS interneurons might affect the influence on the postsynaptic MS cells (cf. Abbott et al., 1997). We used the firing patterns of three FS neurons from the prior in vivo studies by Berke et al. (2004) and Berke (2008), and simulated the resulting train of synaptic potentials in postsynaptic MS neurons. The measurement of the FS-to-MS synaptic parameters was done in vitro (Planert et al., 2010). Figure 5A shows an example of the averaged postsynaptic MS response to a train of presynaptic FS spikes in vitro (8 spikes plus one test pulse). From these averaged responses we extracted the PSPs and used their amplitude values for the parameter fitting in the FS-to-MS model synapse (see Section 2). The model synapse was able to replicate the PSP amplitudes for different FS firing frequencies (Figure A1 in Appendix). Figure 5B shows the normalized PSP amplitude for a typical FS-to-MS synapse as a function of spike number for different ISIs (1.5–20 ms). A fully recovered synapse responded with a sequence of decreasing PSP amplitudes to the first few spikes independent of input frequency. Differences in the PSP amplitudes and their steady-state values became, however, evident for larger numbers of APs. Lower spike frequencies allowed more synaptic recovery between the arrival of spikes, resulting in larger steady-state amplitudes (compare, e.g., ISI = 6 and 20 ms in Figure 5B). Full recovery of the synaptic resources required longer firing pauses. Figure 5C shows the normalized values of recovered PSP amplitudes as a function of pause duration, which is measured from the end of a preceding spike train that caused a steady-state depression of the synapse (same synapse as in Figure 5B, in black). The time course for the synaptic recovery, τ_F, ranged from 230 ms to almost 5 s (1.03 ± 1.34 s, n = 11 synapses from rat). Thus, depressing FS-to-MS synapses particularly emphasize the onset of FS firing after prolonged pauses. Taken together, these results suggest that differences in the FS firing pattern have an influence on the amount of synaptic depression and/or recovery and therefore on PSP amplitudes. We determined the distribution of PSP amplitudes in the FS-to-MS synapse model in response to FS firing patterns that were recorded in vivo and compared it to PSP distributions that resulted from random, shuffled spike activity.

FIGURE 5

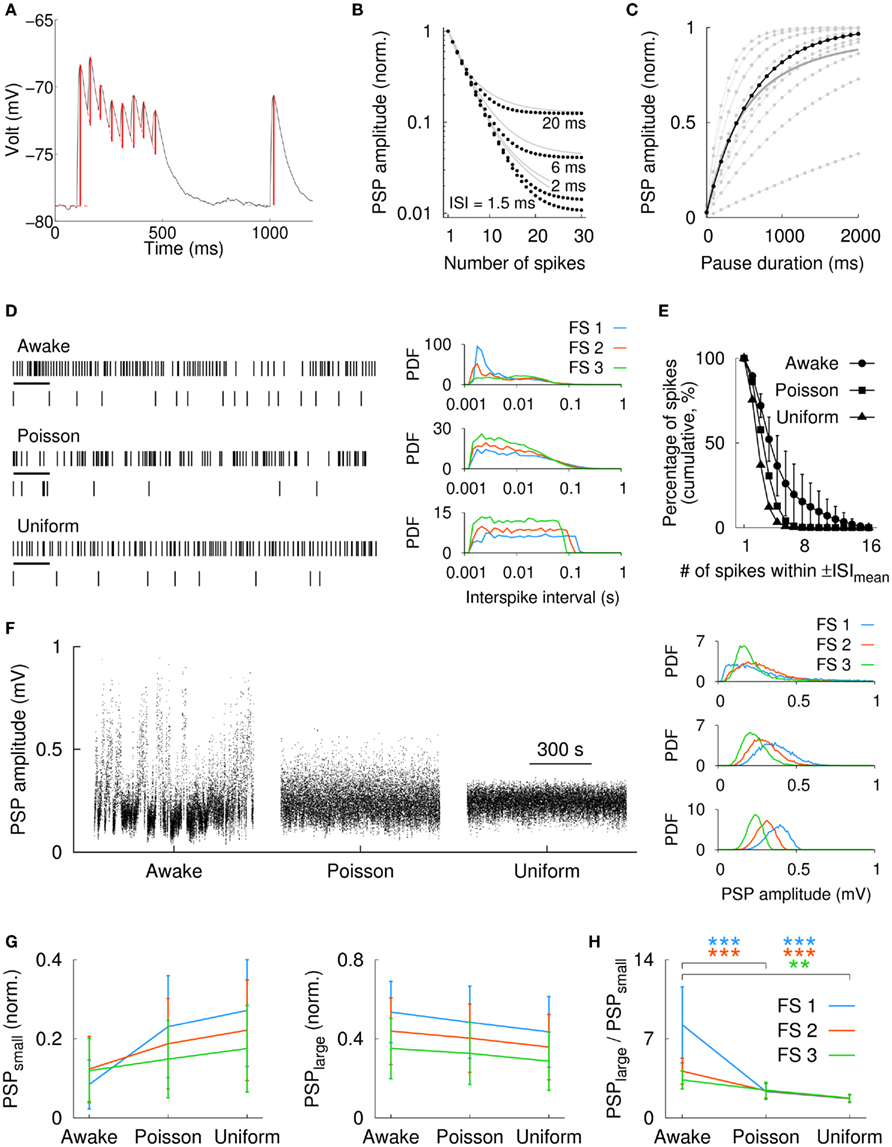
Figure 5. Influence of natural FS firing discharge on the PSP distribution in MS neurons. (A) Averaged experimental postsynaptic response of an FS-to-MS connection. Synaptic activation amplitudes (red vertical lines) for the model fitting were extracted by subtracting the baseline or the residual of the exponential decay of preceding PSPs. (B) Simulated synaptic depression in a typical FS-to-MS synapse (black dots) for synthetic spike traces at different frequencies (gray lines: average over n = 11 synapses, rat). A cluster of 4 spikes resulted in more than 50% depression. (C) Recovery from synaptic depression for the same synapse (black) as a function of time. Gray/dots: individual synapses, gray/solid: average over all synapses (n = 11). (D) Left: spike raster of an extracellularly recorded striatal FS cell in an awake, behaving rat, and for two modes of shuffling (Poisson distributed and uniformly distributed). Shown is a 5-s long fragment of a 760-s recording. In addition, a more detailed view of 500 ms length (corresponding to the black horizontal bars in the upper traces) is shown below each raster. Right: probability density functions (PDFs) of the interspike intervals in three FS cells for the awake and spike shuffled data (same vertical order as in the left panel). Firing rates were 12 Hz (FS 1), 17 Hz (FS 2), and 23 Hz (FS 3). The awake spike raster in the left panel corresponds to FS 3. (E) Average in vivo spike clustering in the FS cells (n = 3) for the awake condition and for the two modes of spike shuffling. In the awake data, more than 10% of all spikes were part of spike clusters with 9 or more spikes (cluster duration was defined as ±ISI_mean). (F) Left: distribution of the simulated postsynaptic potentials for a typical FS-to-MS synapse in response to the spike train of FS 3. For the original spike train (awake), the distribution of PSPs covered the widest range, i.e., from very small (depressed synapse) to almost maximum (fully recovered; maximum possible PSP for this synapse was ∼1 mV). Right: PDFs of the simulated PSPs for the same synapse and the spike trains in all three FS cells [same vertical order as in (D)]. (G) Average value of the 25% smallest (PSP_small, left panel) and largest (PSP_large, right panel) PSPs for all three FS cells. (H) The rank of the ratio PSP_large/PSP_small was for the awake data always larger than for the corresponding Poisson or uniformly distributed spike times (n = 11 synapses). Statistical significance: **p < 0.001, ***p < 0.0001 (Kruskal–Wallis test with Tukey–Kramer multiple comparison).

The upper rastergram in Figure 5D shows a 5-s long section and a 500-ms detail (black bar) from an extracellular in vivo recording in a freely moving rat (“awake”). This “awake” spike activity was used to derive Poisson distributed and uniformly distributed spike rasters with the same average spike rate. Figure 5D (right panel) shows the ISI distributions in three FS cells for the in vivo and the corresponding shuffled spike trains. The graph in Figure 5E visualizes the clustering of spikes; it shows the percentage of spikes that contain at least a given number of APs within a period of ±ISI_mean ms around each spike. Here, we analyzed the clustering in terms of the mean interspike interval, ISI_mean, which was more comparable to the time constant of synaptic depression than ISI_min was (see above). ISI_mean ranged from 43 to 82 ms for the three neurons. In the awake spike train, more than 10% of the spikes were organized in groups of at least nine spikes (Figure 5E). For Poisson and uniformly shuffled spike trains, the percentage of spikes that were member of large spike clusters was comparatively smaller (Figure 5E). High-frequency clusters and intermittent firing pauses in the in vivo spike train furthermore resulted in a wide range of simulated PSP amplitudes. Figure 5F shows the PSP amplitude distribution for the model of a typical FS-to-MS synapse for in vivo as well as Poisson and uniformly shuffled spike activity (from left to right). The PSP distributions for the in vivo input and the shuffled data for this synapse are shown in the right panels of Figure 5F for the three FS cells (same vertical order as in Figure 5D). The relative large number of extended spike cluster in the awake data, as it can be seen in Figure 5E, resulted in a reduction of the small PSP amplitudes as shown in Figure 5G for all three FS cells (left panel, n = 11 synapses). Here, PSP_small was defined as the average normalized amplitude of the 25% smallest PSPs. Importantly, pauses in the awake FS activity allowed also for the recovery of synaptic amplitudes as evident from the average normalized amplitude of the 25% largest PSPs, PSP_large, which was largest for the awake data (Figure 5G, right panel). Consequently, the ratio PSP_large/PSP_small was largest for the awake spike train, and shuffling of the data as described above destroyed the structure of the in vivo firing and resulted in a smaller range of observed PSP amplitudes (Figure 5H). Therefore, these results suggest that FS-to-MS synapses utilize a large fraction of their possible amplitude spectrum in response to in vivo-like input, i.e., from strongly depressed to entirely recovered.

4 Discussion

4.1 Modeling of FS Firing

Fast-spiking interneurons can be characterized electrophysiologically by their firing discharge in response to somatic current steps (Markram et al., 2004; Taverna et al., 2007). Based on the model of a cortical FS neuron, it was suggested that the size of the Na⁺ window current influences minimal firing rate and firing patterns (Golomb et al., 2007). In the present study, we used a morphologically extended version of the FS model by Golomb et al. (2007) with a small Na⁺ window current, which together with “intrinsic” (white) noise induced the characteristic stuttering behavior and subthreshold oscillations observed in many FS cells of the cortex and the striatum. Indeed, although the precise origin of the stuttering discharge is not known, intrinsic stochastic mechanisms are the most likely source for the irregular bursting in these cells (Englitz et al., 2008).

The FS model parameters in the present study were not additionally adjusted to match the FS cell properties recorded in vitro. Consequently, the FS model showed some differences compared to the in vitro measurements, that is, the model had a stronger afterhyperpolarization (Golomb et al., 2007) and a longer minimal ISI. While the strong afterhyperpolarization was not a critical issue for the present study, the larger ISI in the model cell (∼10 ms compared to less than 4 ms in vitro and in vivo) prevented the use of simulated spike trains for the depressing synapse model because synaptic depression was strongly dependent on the ISI. However, instead of adjusting the model parameters in order to achieve a shorter minimal ISI, we used spike trains from striatal FS interneurons recorded in vivo (Berke et al., 2004; Berke, 2008) for the simulation of the postsynaptic FS-to-MS response. Importantly, despite the above differences, the model captured and predicted key features of striatal and cortical FS interneurons in vitro (Figure 3 and Figure A6 in Appendix, respectively). For increasing levels of steady input, both the model and in vitro measurements showed: (i) a linear rise of the subthreshold V_m, (ii) a non-linear onset of stuttering discharge, and (iii) an increase of the trial-to-trial variability. Therefore, the broad agreement between the model and the measurements in vitro provides strong support for the validity of the results from the simulation of electrically coupled FS cells (see below).

4.2 FS Firing and the Influence of Steady and Fluctuating Input

In the present study, we investigated the influence of steady and fluctuating input on FS firing. As shown previously, steady input resulted in random stuttering activity in the model (Golomb et al., 2007) as well as in vitro (Kawaguchi, 1993; Markram et al., 2004), while the response to fluctuating (synaptic) input was characterized by reliable spiking (Mainen and Sejnowski, 1995; Schneidman et al., 1998) without showing the characteristic stuttering discharge (La Camera et al., 2006). The profound difference in the spike reliability for different input was also reflected in the amount of spike synchronization among electrically coupled FS cells in the model. Although the steady-state coupling in electrically connected FS neurons is not sufficient to induce APs in neighboring FS cells in the striatum (Koós and Tepper, 1999) and in the model, our simulations indicate that spikes are easily synchronized when the neurons receive suprathreshold, steady input. This finding is consistent with previous reports from in vitro and modeling studies in the striatum (Tepper et al., 2004; Hjorth et al., 2009) and the cortex (Galarreta and Hestrin, 1999; Nomura et al., 2003; Mancilla et al., 2007; Zahid and Skinner, 2009). In contrast, spike synchronization was drastically reduced when the FS cells received fluctuating input (see Hjorth et al., 2009, who showed a similar behavior in a model of tonically firing FS cells).

In our experiments, additional (steady) depolarization was achieved by somatic current injection. In the striatum, similar effects might result from the excitatory effects of various neuromodulators, such as serotonin (Blomeley and Bracci, 2009), acetylcholine (Koós and Tepper, 2002), and dopamine (Bracci et al., 2002) – many of them showing task-related regulation (see, e.g., Hyland et al., 2002). Membrane depolarization can also be induced by the metabotropic glutamate receptor mGluR1 (Bonsi et al., 2007) or by NMDA receptor mediated currents, although a recent study reports a lack of NMDA receptor mediated synaptic currents (Gittis et al., 2010). Thus, whether the reported amounts of depolarization occur in vivo and if they would be sufficient for FS neurons to enter the stuttering regime at least transiently is not known. Our modeling results for a pair of electrically connected FS cells and the lack of evident spike synchronization in vivo (Berke, 2008) rather suggest that in awake, behaving animals neighboring FS interneurons are not in the stuttering regime simultaneously. Therefore, the FS firing variability in vivo with short periods of high firing (reminiscent of stuttering) is likely to represent temporally precise activity, which is driven by the fluctuations in the input (Softky and Koch, 1993; van Vreeswijk and Sompolinsky, 1996). Importantly, inhibitory connections between striatal FS neurons can not fully explain the lack of in vivo spike synchronization since only about half of the pairs of FS cells are connected (Gittis et al., 2010). It should be noted, however, that although gap junction coupling between striatal FS interneurons has been demonstrated in electrophysiological recordings in vitro (Tepper et al., 2004) and immunohistochemical stainings (Fukuda, 2009), another possible explanation for the absence of spike synchronization might be the lack of functional electrical coupling in vivo. Indeed, gap junctions have been shown to be regulated by various factors (Harris, 2001; Urschel et al., 2006; Gonzlez-Nieto et al., 2008) and in vivo patch-clamp recordings, in which subthreshold activity can be recorded, would allow the investigation of this question directly.

4.3 FS Firing Variability is Translated into Variability of Postsynaptic Responses in MS Projection Neurons

Fast-spiking interneurons of the striatum form symmetrical synapses on MS projection neurons. Similar to cortical FS to principal neuron connections (Galarreta and Hestrin, 1998), these synapses show depressing dynamics in vitro (Plenz and Kitai, 1998; Gittis et al., 2010; Planert et al., 2010). The in vivo FS discharge in behaving rats is characterized by numerous large clusters of high-frequency spikes, which resulted in strong depression in the synapse model. Importantly, pauses in the FS firing allowed for the recovery of synaptic resources. Together this suggests that striatal FS-to-MS synapses might operate over a wide range of PSP amplitudes in which the depressive nature of the synapses contributes to the variability of PSP sizes. However, if synaptic depression in FS-to-MS connections is dominating the synaptic dynamics also in vivo is currently not known. In fact, recent evidence from cortical neurons suggests that synaptic depression observed in vitro can be diminished by ongoing activity in vivo (Reig et al., 2006; Reig and Sanchez-Vives, 2007). Nevertheless, the impact of FS synapses on postsynaptic MS neurons also depends on the timing of the PSPs, which directly reflects the firing variability observed in FS cells. Striatal FS neurons receive excitatory afferents from cortex and thalamus, and inhibitory input along the pallidostriatal pathway and from intrastriatal sources (as well as various modulatory projections, see above; Wilson, 2004). These inputs are most likely the main source for the observed firing variability in the FS cells.

Striatal FS neurons have been shown to prevent or delay spiking in postsynaptic MS cells (Koós and Tepper, 1999). However, our results indicate that FS cells in vivo communicate via substantially depressed synapses over extended periods of time. The summative effect of several converging FS cells (Tepper et al., 2004) as well as temporal summation might compensate for the depletion in individual synapses. In order to study the combined effect of all presynaptic FS cells onto a single MS neuron, knowledge about the spike times in the presynaptic FS population would be required. Similarly, to predict how postsynaptic currents (which are proportional to our PSPs in the current-clamp measurements) influence an MS neuron in vivo requires knowledge about the membrane potential of the MS cell, since these neurons are known to show strong inward rectification (Kawaguchi, 1993). These points were not addressed in this study and could be a question for future research.

4.4 Conclusion

Our results indicate that FS firing variability observed in vivo is most likely due to the input that these neurons receive, and that this variability is translated into variability of the postsynaptic responses in MS projection neurons. The fact that the FS-to-MS synapse model showed substantial depression over extended periods of time in response to natural FS firing patterns might indicate the importance of cooperative effects of multiple presynaptic FS interneurons and the precise orchestration of their activity in shaping the activity of the MS projection neuron.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

Andreas Klaus, Henrike Planert, J. J. Johannes Hjorth, Gilad Silberberg and Jeanette Hellgren Kotaleski are grateful for support from the Swedish Research Council and the Parkinson’s Foundation. Andreas Klaus was in addition supported by the NIH–Karolinska Institute joint PhD program. Henrike Planert and Gilad Silberberg received additional support from the European Commission Coordination Action ENINET (contract number LSHM-CT-2005-19063), the Human Frontier Science Program, and the European Union Seventh Framework Programme (Cortex and Select and Act). Joshua D. Berke is grateful for support from the Tourette Syndrome Association, the Whitehall Foundation, and the US National Institute on Drug Abuse.

Footnotes

1. ^http://www.r-project.org/
2. ^http://gnuplot.info

References

Abbott, L. F., Varela, J. A., Sen, K., and Nelson, S. B. (1997). Synaptic depression and cortical gain control. Science 275, 221–224.

CrossRef Full Text

Amitai, Y., Gibson, J., Beierlein, M., Patrick, S., Ho, A., Connors, B., and Golomb, D. (2002). The spatial dimensions of electrically coupled networks of interneurons in the neocortex. J. Neurosci. 22, 4142.

Pubmed Abstract | Pubmed Full Text

Beierlein, M., Gibson, J., and Connors, B. (2000). A network of electrically coupled interneurons drives synchronized inhibition in neocortex. Nat. Neurosci. 3, 904–910.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Berke, J. (2008). Uncoordinated firing rate changes of striatal fast-spiking interneurons during behavioral task performance. J. Neurosci. 28, 10075.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Berke, J. (2011). Functional properties of striatal fast-spiking interneurons. Front. Syst. Neurosci. 5:45.

Berke, J., Okatan, M., Skurski, J., and Eichenbaum, H. (2004). Oscillatory entrainment of striatal neurons in freely moving rats. Neuron 43, 883–896.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Blackwell, K., Czubayko, U., and Plenz, D. (2003). Quantitative estimate of synaptic inputs to striatal neurons during up and down states in vitro. J. Neurosci. 23, 9123–9132.

Pubmed Abstract | Pubmed Full Text

Blomeley, C. P., and Bracci, E. (2009). Serotonin excites fast-spiking interneurons in the striatum. Eur. J. Neurosci. 29, 1604–1614.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Bonsi, P., Sciamanna, G., Mitrano, D. A., Cuomo, D., Bernardi, G., Platania, P., Smith, Y., and Pisani, A. (2007). Functional and ultrastructural analysis of group I mGluR in striatal fast-spiking interneurons. Eur. J. Neurosci. 25, 1319–1331.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Bower, J., and Beeman, D. (1998). The Book of GENESIS: Exploring Realistic Neural Models with the GEneral NEural SImulation System. New York, NY: Springer-Verlag.

Bracci, E., Centonze, D., Bernardi, G., and Calabresi, P. (2002). Dopamine excites fast-Spiking interneurons in the striatum. J. Neurophysiol. 87, 2190–2194.

Pubmed Abstract | Pubmed Full Text

Bracci, E., Centonze, D., Bernardi, G., and Calabresi, P. (2003). Voltage-dependent membrane potential oscillations of rat striatal fast-spiking interneurons. J. Physiol. (Lond.) 549, 121–130.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Chung, Y., Shin, C., Kim, M., and Cha, C. (2000). Immunohistochemical study on the distribution of six members of the Kv1 channel subunits in the rat basal ganglia. Brain Res. 875, 164–170.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Druckmann, S., Banitt, Y., Gidon, A., Schürmann, F., Markram, H., and Segev, I. (2007). A novel multiple objective optimization framework for constraining conductance-based neuron models by experimental data. Front. Neurosci. 1:7–18.

CrossRef Full Text

Englitz, B., Stiefel, K. M., and Sejnowski, T. J. (2008). Irregular firing of isolated cortical interneurons in vitro driven by intrinsic stochastic mechanisms. Neural Comput. 20, 44–64.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Fukuda, T. (2009). Network architecture of gap junction-coupled neuronal linkage in the striatum. J. Neurosci. 29, 1235–1243.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Gage, G. J., Stoetzner, C. R., Wiltschko, A. B., and Berke, J. D. (2010). Selective activation of striatal fast-Spiking interneurons during choice execution. Neuron 67, 466–479.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Galarreta, M., and Hestrin, S. (1998). Frequency-dependent synaptic depression and the balance of excitation and inhibition in the neocortex. Nat. Neurosci. 1, 587–594.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Galarreta, M., and Hestrin, S. (1999). A network of fast-spiking cells in the neocortex connected by electrical synapses. Nature 402, 72–75.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Galarreta, M., and Hestrin, S. (2001). Electrical synapses between GABA-releasing interneurons. Nat. Rev. Neurosci. 2, 425–433.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Galarreta, M., and Hestrin, S. (2002). Electrical and chemical synapses among parvalbumin fast-spiking GABAergic interneurons in adult mouse neocortex. Proc. Natl. Acad. Sci. U.S.A. 99, 12438–12443.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Gibson, J. R., Beierlein, M., and Connors, B. W. (2005). Functional properties of electrical synapses between inhibitory interneurons of neocortical layer 4. J. Neurophysiol. 93, 467–480.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Gittis, A. H., Nelson, A. B., Thwin, M. T., Palop, J. J., and Kreitzer, A. C. (2010). Distinct roles of GABAergic interneurons in the regulation of striatal output pathways. J. Neurosci. 30, 2223–2234.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Goldberg, E., Clark, B., Zagha, E., Nahmani, M., Erisir, A., and B, R. (2008). K+ channels at the axon initial segment dampen near-threshold excitability of neocortical fast-spiking GABAergic interneurons. Neuron 58, 387–400.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Golomb, D., Donner, K., Shacham, L., Shlosberg, D., Amitai, Y., and Hansel, D. (2007). Mechanisms of firing patterns in fast-spiking cortical interneurons. PLoS Comput. Biol. 3, e156.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Gonzlez-Nieto, D., Gmez-Hernndez, J. M., Larrosa, B., Gutirrez, C., Muoz, M. D., Fasciani, I., O’Brien, J., Zappal, A., Cicirata, F., and Barrio, L. C. (2008). Regulation of neuronal connexin-36 channels by pH. Proc. Natl. Acad. Sci. 105, 17169–17174.

CrossRef Full Text

Gupta, A., Wang, Y., and Markram, H. (2000). Organizing principles for a diversity of GABAergic interneurons and synapses in the neocortex. Science 287, 273.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Gustafson, N., Gireesh-Dharmaraj, E., Czubayko, U., Blackwell, K., and Plenz, D. (2006). A comparative voltage and current-clamp analysis of feedback and feedforward synaptic transmission in the striatal microcircuit in vitro. J. Neurophysiol. 95, 737–752.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Harris, A. L. (2001). Emerging issues of connexin channels: biophysics fills the gap. Q. Rev. Biophys. 34, 325–472.

Pubmed Abstract | Pubmed Full Text

Hjorth, J., Blackwell, K., and Hellgren Kotaleski, J. (2009). Gap junctions between striatal fast-spiking interneurons regulate spiking activity and synchronisation as a function of cortical activity. J. Neurosci. 29, 5276–5286.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hyland, B., Reynolds, J., Hay, J., Perk, C., and Miller, R. (2002). Firing modes of midbrain dopamine cells in the freely moving rat. Neuroscience 114, 475–492.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kawaguchi, Y. (1993). Physiological, morphological, and histochemical characterization of three classes of interneurons in rat neostriatum. J. Neurosci. 13, 4908–4923.

Pubmed Abstract | Pubmed Full Text

Kawaguchi, Y. (1997). Neostriatal cell subtypes and their functional roles. Neurosci. Res. 27, 1–8.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kawaguchi, Y., and Kubota, Y. (1997). GABAergic cell subtypes and their synaptic connections in rat frontal cortex. Cereb. Cortex 7, 476–486.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kita, H., Kosaka, T., and Heizmann, C. (1990). Parvalbumin-immunoreactive neurons in the rat neostriatum: a light and electron microscopic study. Brain Res. 536, 1–15.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Koós, T., and Tepper, J. (1999). Inhibitory control of neostriatal projection neurons by GABAergic interneurons. Nat. Neurosci. 2, 467–472.

CrossRef Full Text

Koós, T., Tepper, J., and Wilson, C. (2004). Comparison of IPSCs evoked by spiny and fast-spiking neurons in the neostriatum. J. Neurosci. 24, 7916–7922.

CrossRef Full Text

Koós, T., and Tepper, J. M. (2002). Dual cholinergic control of fast-spiking interneurons in the neostriatum. J. Neurosci. 22, 529–535.

Kotaleski, J., Plenz, D., and Blackwell, K. (2006). Using potassium currents to solve signal-to-noise problems in inhibitory feedforward networks of the striatum. J. Neurophysiol. 95, 331–341.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

La Camera, G., Rauch, A., Thurbon, D., Lüscher, H., Senn, W., and Fusi, S. (2006). Multiple time scales of temporal response in pyramidal and fast spiking cortical neurons. J. Neurophysiol. 96, 3448–3464.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Lenz, S., Perney, T., Qin, Y., Robbins, E., and Chesselet, M. (1994). GABA-ergic interneurons of the striatum express the shaw-like potassium channel Kv3.1. Synapse 18, 55–66.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Luk, K. C., and Sadikot, A. F. (2001). GABA promotes survival but not proliferation of parvalbumin-immunoreactive interneurons in rodent neostriatum: an in vivo study with stereology. Neuroscience 104, 93–103.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Mainen, Z., and Sejnowski, T. (1995). Reliability of spike timing in neocortical neurons. Science 268, 1503–1506.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Mallet, N., Le Moine, C., Charpier, S., and Gonon, F. (2005). Feedforward inhibition of projection neurons by fast-spiking GABA interneurons in the rat striatum in vivo. J. Neurosci. 25, 3857–3869.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Mancilla, J., Lewis, T., Pinto, D., Rinzel, J., and Connors, B. (2007). Synchronization of electrically coupled pairs of inhibitory interneurons in neocortex. J. Neurosci. 27, 2058.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Marín, O., Anderson, S. A., and Rubenstein, J. L. R. (2000). Origin and molecular specification of striatal interneurons. J. Neurosci. 20, 6063–6076.

Markram, H., Toledo-Rodriguez, M., Wang, Y., Gupta, A., Silberberg, G., and Wu, C. (2004). Interneurons of the neocortical inhibitory system. Nat. Rev. Neurosci. 5, 793–807.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Markram, H., Wang, Y., and Tsodyks, M. (1998). Differential signaling via the same axon of neocortical pyramidal neurons. Proc. Natl. Acad. Sci. U.S.A. 95, 5323–5328.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Nomura, M., Fukai, T., and Aoyagi, T. (2003). Synchrony of fast-spiking interneurons interconnected by GABAergic and electrical synapses. Neural. Comput. 15, 2179–2198.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Planert, H., Szydlowski, S. N., Hjorth, J. J. J., Grillner, S., and Silberberg, G. (2010). Dynamics of synaptic transmission between fast-spiking interneurons and striatal projection neurons of the direct and indirect pathways. J. Neurosci. 30, 3499–3507.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Plenz, D., and Kitai, S. T. (1998). Up and down states in striatal medium spiny neurons simultaneously recorded with spontaneous activity in fast-spiking interneurons studied in cortex-striatum-substantia nigra organotypic cultures. J. Neurosci. 18, 266–283.

Pubmed Abstract | Pubmed Full Text

Reig, R., Gallego, R., Nowak, L. G., and Sanchez-Vives, M. V. (2006). Impact of cortical network activity on short-term synaptic depression. Cereb. Cortex 16, 688–695.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Reig, R., and Sanchez-Vives, M. V. (2007). Synaptic transmission and plasticity in an active cortical network. PLoS ONE 2, e670.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Schneidman, E., Freedman, B., and Segev, I. (1998). Ion channel stochasticity may be critical in determining the reliability and precision of spike timing. Neural. Comput. 10, 1679–1703.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Softky, W., and Koch, C. (1993). The highly irregular firing of cortical cells is inconsistent with temporal integration of random EPSPs. J. Neurosci. 13, 334–350.

Pubmed Abstract | Pubmed Full Text

Taverna, S., Canciani, B., and Pennartz, C. (2007). Membrane properties and synaptic connectivity of fast-spiking interneurons in rat ventral striatum. Brain Res. 1152, 49–56.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Tepper, J., Koós, T., and Wilson, C. (2004). GABAergic microcircuits in the neostriatum. Trends Neurosci. 27, 662–669.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Tepper, J., Wilson, C., and Koós, T. (2008). Feedforward and feedback inhibition in neostriatal GABAergic spiny neurons. Brain Res. Rev. 58, 272–281.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Tsodyks, M., Pawelzik, K., and Markram, H. (1998). Neural networks with dynamic synapses. Neural Comput. 10, 821–835.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Urschel, S., Hher, T., Schubert, T., Alev, C., Shl, G., Wrsdrfer, P., Asahara, T., Dermietzel, R., Weiler, R., and Willecke, K. (2006). Protein kinase a-mediated phosphorylation of connexin36 in mouse retina results in decreased gap junctional communication between AII amacrine cells. J. Biol. Chem. 281, 33163–33171.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

van Vreeswijk, C., and Sompolinsky, H. (1996). Chaos in neuronal networks with balanced excitatory and inhibitory activity. Science 274, 1724–1726.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Weiser, M., Vega-Saenz de Miera, E., Kentros, C., Moreno, H., Franzen, L., Hillman, D., Baker, H., and B, R. (1994). Differential expression of shaw-related K⁺ channels in the rat central nervous system. J. Neurosci.14, 949–972.

Pubmed Abstract | Pubmed Full Text

Wilson, C. (2004). “Basal Ganglia,” in The synaptic organization of the brain, 5th Edn, Chapter 9, ed. G. Shepherd (New York: Oxford University Press), 361–413.

Zahid, T., and Skinner, F. K. (2009). Predicting synchronous and asynchronous network groupings of hippocampal interneurons coupled with dendritic gap junctions. Brain Res. 1262, 115–129.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text