Empirical and theoretical aspects of generation and transfer of information in a neuromagnetic source network

1. Introduction

Recently, significant progress has been made showing that cognitive operations result from the generation and transformation of cooperative modes of neural activity (Bressler, 1995, 2002; McIntosh, 1999). Specifically, the progress in this field was based on the principle that emphasizes the integrative capacity of the brain in terms of ensembles of coupled neural systems (Nunez, 1995; Jirsa and McIntosh, 2007). In turn, we have witnessed advances both in the modeling endeavors to explore brain integration and the collection of empirical evidence in support for this integration.

From the theoretical point of view, the neural ensembles can be represented by single oscillators (Haken, 1996). Further, different neural ensembles can be coupled with long-range connections, forming a large-scale network of coupled oscillators. Due to the separation of sources in the space and limited transmission speeds, communication between brain regions may include time delays. Thus, the coupling between two nodes in a brain network can be characterized by the connection strength, directionality, and time delay. In turn, time delays in coupling can influence the dynamical properties of coupled oscillatory models (Niebur et al., 1991). Encouraging results were obtained in modeling the resting state network dynamics wherein time delays play a crucial role in generation of the realistic fluctuations in brain signals (Ghosh et al., 2008; Deco et al., 2009).

At the same time, from the perspective of empirical analysis, recently developed non-linear tools were able to characterize variability of local brain dynamics and interaction effects of distributed brain activity (see Stam, 2005 for a review). Information-theoretic techniques provide a model-free non-linear approach to address both issues (Pereda et al., 2005; Vakorin et al., 2011).

First, such techniques can be used to characterize the variability in brain signals as a consequence of more complicated neural processing. A typical application includes a comparative analysis of different groups, for example, in brain development (McIntosh et al., 2008) or clinical versus normal populations (Stam, 2005), or different conditions within the same groups (Lippé et al., 2009). Traditionally, the analysis is performed at the level of electroencephalographic (EEG) or magnetoencephalographic (MEG) scalp measurements that do not directly represent localized brain regions in the vicinity of one electrode due to volume conduction (Nunez and Shrinivasan, 2005). The translation to source space would be a logical extension, and it has been recently shown that entropy-based techniques are sensitive enough to discriminate the variability of neural activity within a network of sources (Mišić et al., 2010; Vakorin et al., 2010b).

Second, a number of studies have explored methods of assessing linear and non-linear interactions between dynamics of neuronal sources, reconstructed using beamformers (Hadjipapas et al., 2005; Vakorin et al., 2010b; Wibral et al., 2011). Analyses of asymmetries in non-linear interdependency between different brain areas, both in normal and clinical populations, may provide an insight upon processing and integration of information in a neuronal network. The time course of one process may predict the time course of another process better than the other way around. This enhancement in predictive power can characterize the coupling between these two processes (Blinowska et al., 2004; Hlavackova-Schindler et al., 2007). This idea was originally proposed by Granger (1969), who used autoregressive models to describe the interaction between the processes as well as the time courses of the processes themselves. A non-linear extension of the framework of predicting a future of one system from the past and present of another one is based on estimating the information transfer, using information-theoretic tools. Two measures can be used, namely transfer entropy (Schreiber, 2000) or conditional mutual information (Palus et al., 2001), which are essentially equivalent to each other under certain conditions (Palus and Vejmelka, 2007). Transfer entropy has been applied in both EEG (Chavez et al., 2003; Vakorin et al., 2010a) and MEG data (Vicente et al., 2011; Wibral et al., 2011), as well in functional magnetic resonance imaging (Hinrichs et al., 2006).

Differences in signal variability among brain areas constituting an activated network as a reaction to a cognitive or perceptual task, can be indicative of how that task is being processed in the brain (Mišić et al., 2010; Vakorin et al., 2010b). In this study, we explored empirical aspects of the relations between complexity of individual sources constituting a network and the exchange of information between them. The analysis was performed under the assumption that the neuronal ensembles activated in performing the task can be represented by non-linear dynamic systems interacting with each other.

The first part of this study presents a data-driven pipeline for non-linear analysis of neuromagnetic sources reconstructed from human MEG data collected in reaction to face recognition task. Specifically, we first computed the asymmetries in mutual interdependencies between the original MEG sources using the conditional mutual information as a measure of information transfer. We then estimated variability of the MEG sources using the measure of sample entropy. Sample entropy was designed in essence as an approximation to the Kolmogorov entropy (Richman and Moorman, 2000), which can be interpreted as the mean rate of information generated by a dynamic system (Kolmogorov, 1959). Sample entropy can be used to infer the presence of non-linear effects. In practice, however, sample entropy is sensitive not only to non-linear deterministic effects but also to the linear stochastic effects such as, for example, auto-correlation. A number of studies indicate that the information averaged over a larger time horizon can reflect non-linear determinism with higher confidence (Govindan et al., 2007; Kaffashi et al., 2008). Multi-scale entropy represents an approach when sample entropy is estimated at different time scales (Costa et al., 2002). In this study, we explored how the differences in variability of the source dynamics, estimated at fine and coarse time scales, can be explained, in a statistical sense, by an asymmetry in the amount of information transferred from one source to another. In the second part of this study, using synthetic data based on a model of coupled non-linear oscillators with time delay in coupling, we demonstrated how the effects found in the MEG data, may arise from time delayed interactions.

2. Methods

2.1. Participants

Twenty-two healthy adults (20–41 years, mean = 25.7 year, 9 female) took part in the study. None of the participants wore any metallic implants or had metal in their dental work and all reported normal or corrected-to-normal vision. Experiments were performed with the informed consent of each individual and with the approval of the Research Ethics Board at the Hospital for Sick Children.

2.2. Stimuli and Task

Participants performed a one-back task in which they judged whether the currently viewed stimulus was the same as the previous one. The stimulus set comprised 240 grayscale photographs of unfamiliar faces of young adults (2.4° × 3° visual angle) with neutral expressions. All faces were without glasses, earrings, jewelry, or other paraphernalia. Male and female faces were equiprobable. In each block of trials, one-third of the faces immediately repeated. Thus, there were 120 new faces that either did or did not repeat on the subsequent trial (N1 and N2, 60 trials each), as well as 60 repeated faces (R) per block (180 faces in total). Upright faces were presented in one block and inverted faces in the other, with the order of the two blocks counterbalanced across participants. For more information on stimulus control please see Taylor et al. (2008). The tasks will be coded as invN1, invN2, invR, upN1, upN2, and upR.

2.3. MEG Signal Acquisition

The MEG was acquired in a magnetically shielded room at the Hospital for Sick Children. Head position relative to the MEG sensor array was determined at the start and end of each block using three localization coils that were placed at the nasion and bilateral preauricular points prior to acquisition. Motion tolerance was set to 0.5 cm. Surface magnetic fields were recorded using a 151-channel whole-head CTF system (MEG International Services, Ltd., Coquitlam, BC) at a rate of 625 Hz, with a band pass of DC-100 Hz. Data were epoched into [−100 1500] ms segments time-locked to stimulus onset. Structural Magnetic Resonance Imaging (MRI) data were also acquired for each participant. Following the MEG recording session, the three localization coils were replaced by MRI-visible markers and 3D SPGR (T1-weighted) anatomical images were acquired using a 1.5-T Signa Advantage system (GE Medical Systems, Milwaukee, WI).

2.4. Extraction of Neuromagnetic Sources

Individual anatomical MR images were warped into a common Talairach space using a non-linear transform in SPM2. Latencies of interest were chosen from the group average event-related fields (ERFs). Source analysis was performed using event-related beamforming (ERB; Robinson and Vrba, 1999; Sekihara et al., 2001; Cheyne et al., 2007), a 3D spatial filtering technique which is used to estimate instantaneous source power at desired locations in the brain. To model the forward solution for the beamformer, multiple sphere models were fit to the inner skull surface of each participant’s MRI using BrainSuite software (Shattuck and Leahy, 2002). Activity at each target source was estimated as a weighted sum of the surface field measurements. Weight parameters and the orientation of the source dipole were optimized in the least squares sense, such that the average power originating from all other locations was maximally attenuated without any change to the power of the forward solution associated with the target source. The weights were then used to compute single-trial time series for each source.

Two prominent peaks sensitive to facial orientation were observed at 100 ms and 150 ms following stimulus onset (Figure 1A) and were localized bilaterally to the primary visual cortex (Figure 1B, sources 1 and 2) and bilaterally to fusiform gyrus (Figure 1B, sources 3 and 4), respectively. A third, less prominent peak was observed at 220 ms (Figure 1C) and was most affected by the memory manipulation (i.e., it differed most between the first presentation of a face and its repeat). To avoid any confounding interaction between the effects of face inversion and working memory, the N2-R difference waves were computed and localized separately for Upright and Inverted faces (Figure 1D, sources 5 and 6, respectively). Both were localized to the anterior cingulate cortex. Thus, neuromagnetic activity was extracted from all six source locations, in all six conditions. For the purpose of this paper, the sources were coded as follows: (1) VIS_L; (2) VIS_R; (3) FUS_L; (4) FUS_R; (5) ACC_UP; (6) ACC_INV.

FIGURE 1

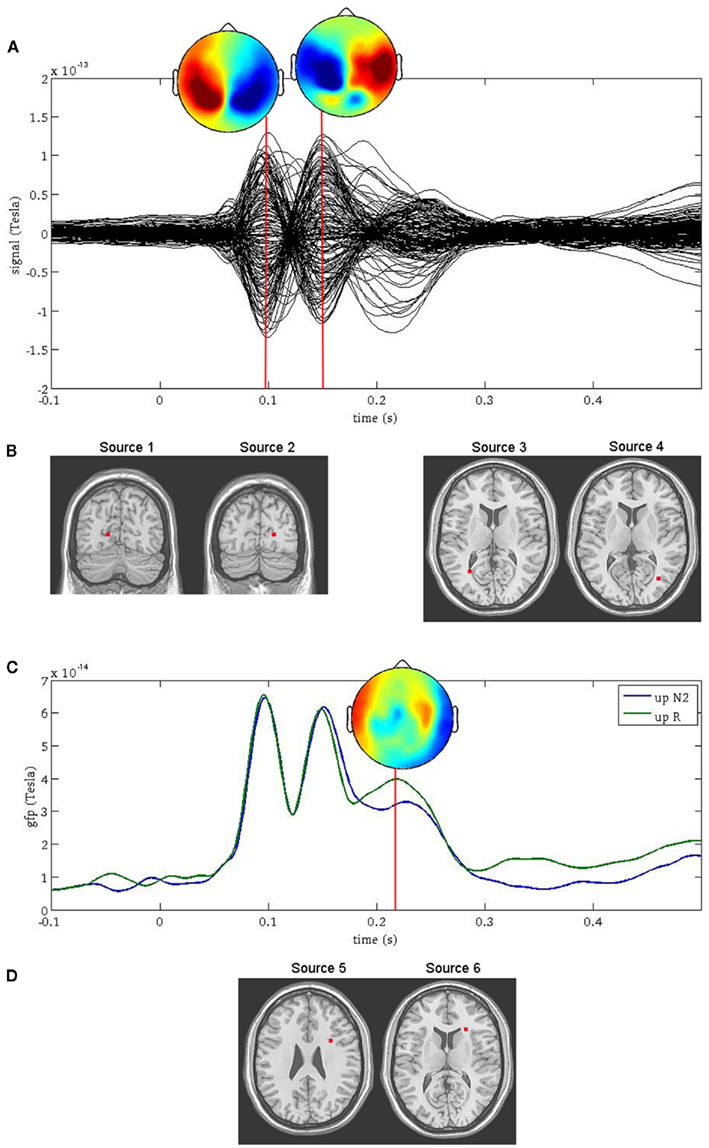
Figure 1. Source reconstruction using ERB. The first two peaks in the surface fields (A) were directly localized to the left and right primary visual cortex [sources 1 and 2, (B) left] and the left and right occipito-temporal cortex [sources 3 and 4, (B) right]. The third peak [sources 5 and 6, (D)] was not localized directly from the surface field ERFs, but rather at the latency at which the difference in global field power (GFP) was greatest between the N2 and R conditions (C).

2.5. Information Generated by a System

Many complex biophysiological phenomena are due to non-linear effects. Recently there has been an increasing interest in studying complex neural networks in the brain, specifically by applying concepts and time series analysis techniques derived from non-linear dynamics (see Stam, 2005 for a comprehensive review on non-linear dynamical analysis of EEG/MEG). Various statistics quantifying signal variability based on the presence of non-linear deterministic effects, were developed to compare and distinguish time series. Among others, sample entropy was developed as a measure of signal regularity (Richman and Moorman, 2000). The sample entropy was proposed as a refined version of approximate entropy (Pincus, 1991), compensating for self-matches in the signal patterns. In turn, approximate entropy was devised as an attempt to estimate Kolmogorov entropy (Grassberger and Procaccia, 1983), the rate of information generated by a dynamic system, from noisy and short time series of clinical data.

One approach to non-linear analysis consists of reconstructing the underlying dynamical systems underlying EEG or MEG time series through time delay embedding. Specifically, let x_t denote the delay vectors, describing recent history of the observed process x_t:

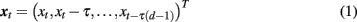
where d is embedding dimension, and τ is embedding delay measured in multiples of the sampling interval.

For estimating sample entropy of time series x_t, two multi-dimensional representations of x_t are used, as defined by two sets of embedding parameters: {d, τ} and {d + 1, τ}. Typically, the values of the time embedding delay τ are kept equal to 1, measured in data points of a given time series for which sample entropy is to be estimated. Sample entropy can be estimated in terms of the average natural logarithm of conditional probability that two delay vectors (points in a multi-dimensional state-space), which are close in the d-dimensional space (meaning that the distance between them is less than the scale length r), will remain close in the (d + 1)-dimensional space. A greater likelihood of remaining close results in smaller values for the sample entropy statistic, indicating fewer irregularities. Conversely, higher values are associated with the signals having more variability and less regular patterns in their representations.

Specifically, let 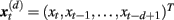represent d-dimensional (N − m − 1) delay vectors reconstructed from a time series x_t of length N. The function 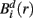is defined as 1/(N − d − 1) multiplied by the number of state vectors 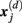located within r of :

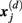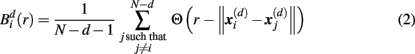
where j goes from 1 to N − d, and ||·|| stands for the maximum norm distance between two state vectors. Then, averaging across (N − d) vectors, we have

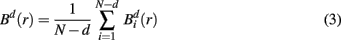
Similarly, the equivalent of 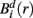in a (d + 1)-dimensional representation of the original time series x(t), the function 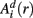, is given by 1/(N − d − 1) times the number of state vectors 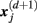located within r of :

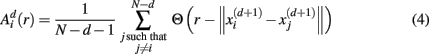
which can be averaged across (M − n) points as

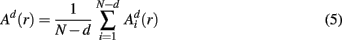
Sample entropy is defined as

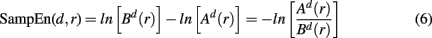
Multi-scale entropy (MSE) was proposed to estimate sample entropy of finite time series at different time scales (Costa et al., 2002). First, multiple coarse-grained time series are constructed from the original signal. This is performed by averaging the data points from the original time series within non-overlapping windows of increasing length. Specifically, the amplitude of the coarse-grained time series y^(θ)(t) at time scale θ is calculated according to

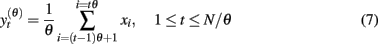
wherein the fluctuations at scales smaller than θ are eliminated. The window length, measured in data points, represents the scale factor, þeta = 1, 2, 3,…. Note that þeta = 1 represents the original time series, whereas relatively large θ produces a smooth signal, containing basically low frequency components of the original signal. To obtained the MSE curve, sample entropy is computed for each coarse-grained time series.

2.6. Information Transfer

A number of studies have used information-theoretic tools to characterize coupled systems (see Pereda et al., 2005 for a comprehensive review). Within this approach, predictive information transfer is a key concept used to define asymmetries in mutual interdependence (Palus et al., 2001; Lizier and Prokopenko, 2010). Information transfer I_k(x → y) is defined as the conditional mutual information I(x_t, y_{t + k}| y_t) between the past and present of one system, x_t, and a future of another system, y_{t + k}, provided that information about the past and present of the second system, y_t is excluded (Palus et al., 2001). The subindex k is used to designate dependence of the conditional mutual information I( x_t, y_{t + k}| y_t) on the latency k, which typically is measured in units of data points. Thus, I( x_t, y_{t + k}| y_t) can be considered as a function of the latency between the past and present of the first system and the future of the second one.

The measure I(x_t, y_{t + k}|y_t) can be expressed in terms of individual H(·) and joint entropies H(·,·) and H(·,·,·) as follows:

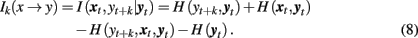
In a similar way, we can define the transfer of information from the past and present of the second system, y_t, to the future of the first one, x_{t + k}:

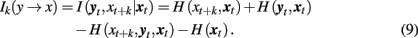
I(x_t, y_{t + k}|y_t) or I(y_t, x_{t + k}|x_t) are closely related to the statistic termed transfer entropy, a measure of the deviation from the independence property for coupled systems evolving in time (Schreiber, 2000). It can be shown that under proper conditions the transfer entropy is equivalent to the conditional mutual information (Palus and Vejmelka, 2007): I_k(x → y) = T_k(x → y).

Net transfer entropy or information transfer, ΔT(x → y) = T_k(x → y) − T_k(y → x), can be used to infer the directionality of the dominant transfer of information between coupled systems. Positive ΔT(x → y) would imply that the system x_t has a higher predictive power to explain the time course of the system y_t, than vice verse.

In estimating transfer entropy, the key issue is estimation of the entropies themselves. The straightforward approach is to divide the state-space into bins, i = 1, 2, 3,…, of some size δ and calculate the entropy of the multi-dimensional dynamics through constructing a multi-dimensional histogram, estimating probabilities of being in the ith bin. This study took another approach, as proposed by Prichard and Theiler (1995) and tested using linear and linear models (Chavez et al., 2003; Gourévitch et al., 2007). Specifically, individual and joint entropies H(x) are approximated by estimating the corresponding correlation integral C_q(x, r) computed as

where

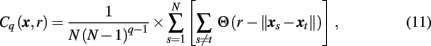
N is the number of data points, and Θ is the Heaviside function. Specifically, the correlation integral C_q(x, r) is a function of a scale parameter r, which in general, can be related to the bin size δ, and the integral order q. The second order (q = 2) correlation integral, as used in this study, is interpreted as the likelihood that the distance between two randomly chosen delay vectors (points in the multi-dimensional state-space) is smaller than r.

3. Analysis

3.1. Pipeline of the Analysis

The dynamics of the networks consisting of six sources were identified for 22 participants in 6 conditions, as described in the Section 1. To determine the optimal embedding parameters for reconstructing the delay vector from the observed time series, we applied the information criterion proposed by Small and Tse (2004). For most of the time series, with a few exceptions, the embedding window was estimated to be equal to 2, which implies the embedding dimension d = 2 (a two-dimensional system) and the embedding delay τ = 1. For each subject and condition, sample entropy was computed for the scales 1–20 for all of the single trials. The information rate produced by a system underlying the observed signal was computed by averaging the sample entropy statistic across the trials, as well as over some range of scale factors. Specifically, the information rate at fine time scales was estimated by averaging the first five scale factors, whereas the information rate of coarse-grained time series was computed by averaging the time scales 16–20. Thus, for a network of six sources, each source was associated with two values: information rate at fine and coarse time scales. For the purpose of this study, we use the terms variability, sample entropy and information rate interchangeably.

For the same networks, transfer entropy was computed as a function of the latency between the past of dynamics of one source and a future of the dynamics of another source (k = 1, 2,…,50), for all possible pairs of the sources (30 connections in total) and for all single trials. Following Palus et al., 2001, the transfer entropy was averaged across the latency k with the idea to decrease the variability of estimated statistics and to increase the robustness of the results. Note that as the MEG epochs were relatively short, the transfer entropy was computed only at time scale þeta = 1, which corresponds to the original time series. For each trial and pathway, the information transfer was estimated in both directions: I_k(x → y) and I_k(y → x), as described in Section 6. The net information transfer was computed as the difference between two amounts of transfer entropy, averaged across trials. Thus, for a network of six sources, each pathway between two sources was associated with a value of the net information transfer, reflecting the asymmetry in the predictive power between the source activity.

3.2. MEG Data

In Figure 2, the relations between asymmetry in mutual interdependence and variability are shown across subjects, separately for all the conditions. Specifically, the figure shows the net information transfer between two sources as a function of difference in sample entropy computed at fine (Figure 2A) and coarse (Figure 2B) time scales, separately for each condition. Each point is associated with one subject and a pair of sources. Correlations between the two variables are given at the top of corresponding plots. In all the cases, the correlations are relatively strong (on the order of 0.5–0.8), statistically significant with p-values less than 0.001. Positive correlations in Figure 2A imply that a system with higher variability can better predict the behavior of a system with lower variability, than the other way around. Conversely, negative correlations observed in Figure 2B support the conclusion that at coarse time scales more information is transferred from sources with lower variability to sources with higher variability, than vice versa.

FIGURE 2

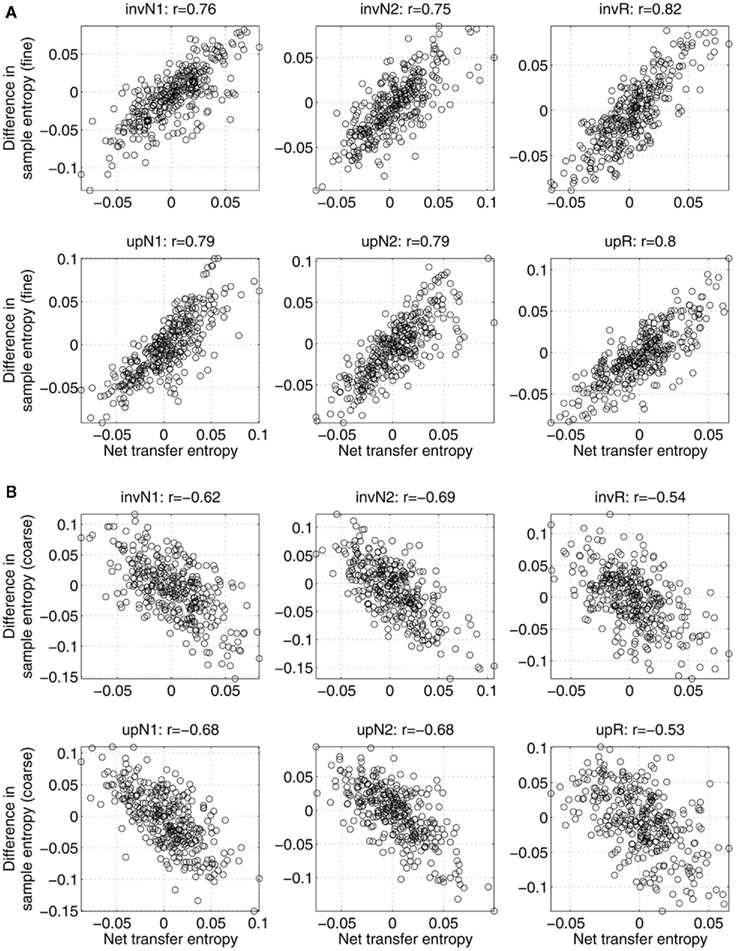
Figure 2. Net information transfer between sources within the same network versus the difference in sample entropy, computed (A) at fine time scales; (B) at coarse time scales. Each point is associated with one subject (22 in total) and one connection (out of 30 possible pathways between 6 sources). The top of each plot shows the correlation value r between the two measures (significant for all the conditions with p-values less than 0.001). A positive correlation implies that the net information is transferred from a source with higher sample entropy to a source with lower sample entropy. Negative correlations imply that more information is transferred toward a system with a higher sample entropy.

In addition to the relations between information transfer and complexity, it may be important to explore the connectivity maps of the networks based on neuromagnetic sources, in the context of the latencies between the peaks of the event-related fields (ERF). Figure 3 illustrates the measures of transfer entropy for a pair of sources, shown as functions of the latency k between the future of one signal and the past of the other signal. Figure 4 shows the reconstructed connectivity patterns masked by the bootstrap ratio maps, computed separately for six conditions. The significance of the couplings was estimating by bootstrapping the subjects (selection with replacement). The bootstrap ratio threshold of 3.0, which corresponds roughly to a 95% confidence interval, was used to define the connections which were robust across the subjects.

FIGURE 3

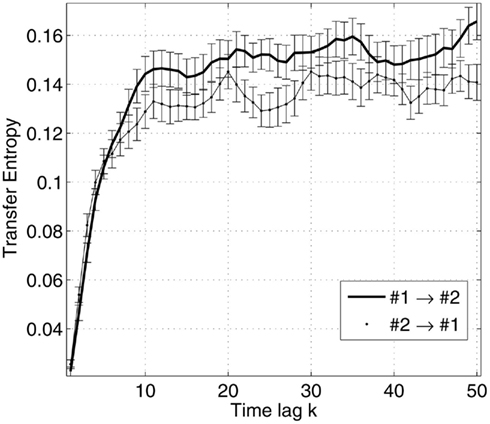
Figure 3. Transfer entropy as a function of the time lag between the future of one signal and the past of the other signal, illustrated for a pair of sources. The sources are taken from the same network for a given subject and condition. The errorbars are specified by the mean and standard error of the estimated measures across trials.

FIGURE 4

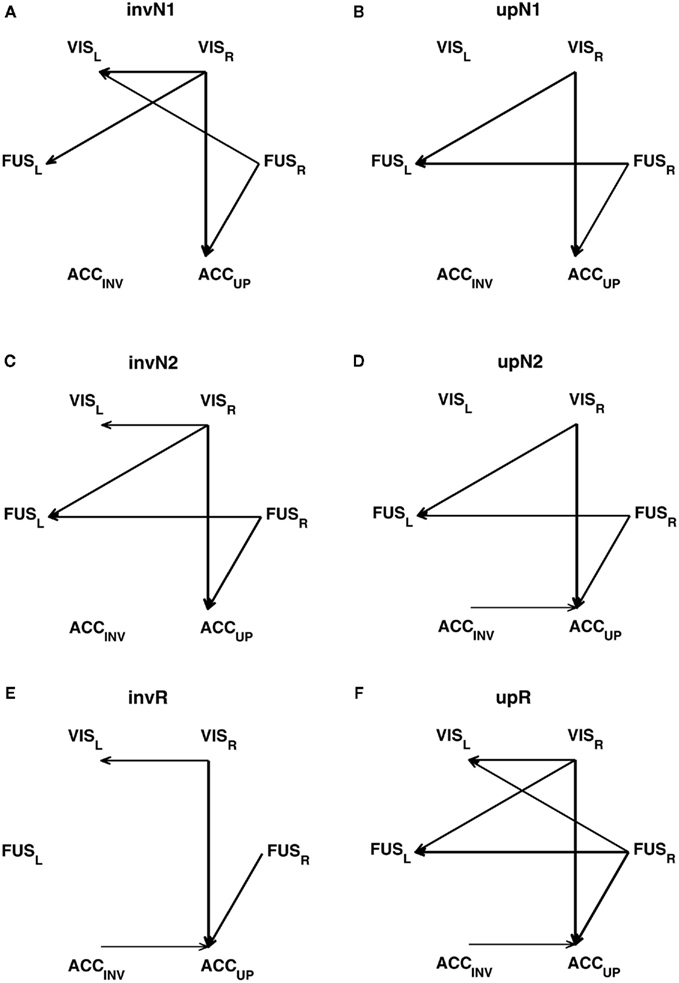
Figure 4. Net information transfer, robustly expressed across the participants in six conditions: (A) invN1; (B) upN1; (C) invN2; (D) upN2; (E) invR; (F) upR. The robustness is estimated by bootstrapping, selecting the participants with replacement. The net transfer information maps are masked by the bootstrap maps, using the bootstrap ratio threshold of 3.0, corresponding roughly to a 95% confidence interval. The arrow’s width is related to the bootstrap ratio value associated with a given connection.

Connections can essentially be divided into two groups. One group represents the connections between the brain regions with the asymmetry in predictive power leading from right to left. Those are VIS_R → VIS_L, FUS_R → FUS_L, and FUR_R → VIS_L. The other group unites the connections with the net information transfer directed from the sources with smaller latencies in the peaks of ERF to those with larger latencies, such as VIS_R → FUS_L, VIS_R → ACC_UP, or FUR_R → ACC_UP.

3.3. Synthetic Data

In the previous section, we considered some empirical aspects of the interplay between sample entropy (information rate) and transfer entropy (information transfer) in the pairwise relations between the neuromagnetic sources. In the following section, we propose that such an interplay might be explained by coupling parameters, such as time delays or coupling strength, characterizing coupled non-linear dynamic systems. Our objective would be to demonstrate the same pattern of relationships between variability computed at different time scales and asymmetry in mutual interdependence between the original time series, using a simple computational model of interacting sources. Specifically, we will consider a model of coupled oscillators with time delay in coupling. We will show that such a model has a potential to explain the peculiarities we observed in Figure 2. The model we simulate is based on unidirectionally coupled chaotic Rössler oscillators.

Hadjipapas et al. (2009) used coupled Rössler systems to study collective dynamics in oscillatory networks as a simple case of periodic systems perturbed by a noise that has a deterministic rather than stochastic nature. Such systems represent a relatively simple non-linear system able to generate self-sustained non-periodic oscillations. In turn, oscillatory behavior and rhythms of the brain have been extensively studied as a plausible mechanism for neuronal synchronization (Varela et al., 2001). Under this context, the coupled Rössler oscillators can be viewed as a prototypical example of oscillatory networks.

Explicitly, the model reads

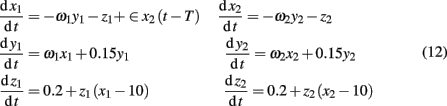
where ω₁ = ω₂ = 0.99 are the natural frequencies of the oscillators, ∈ is the coupling strength, and T denotes the delay in coupling. In the model, the dynamics of the first system determined by a behavior of three variables (x₁, y₁, z₁) is the response driven by the second system based on a behavior of (x₂, y₂, z₂). Further analysis is based on an assumption that only the dynamics of the variables x₁(t) and x₂(t) can be observed. Our specific goal is threefold: (i) to reconstruct the directionality of coupling between x₁(t) and x₂(t), (ii) to analyze the complexity of these signals, and (iii) explore relations between the complexity and causal information.

Numerical solutions of Eqs. (12) were obtained using the dde23 Matlab function (the Mathworks, Natick, MA) with a subsequent resampling of the time series with a fixed step 0.1. The dynamics were solved on the interval [0, 600], subsequently discarding the interval [0, 300] to avoid transitory effects. Thus, each time series had 3000 data points.

For a given pair of parameters, ∈ and T, the signals were generated 20 times. Analyses of sample entropy and transfer entropy were performed similarly to the pipeline for the analysis of the MEG data, as described in Section 1. The only difference was that for synthetic data, we had a network consisting of two systems, and realizations of the model as an equivalent to trials. Transfer entropy between the two systems was computed for all the realizations, as functions of the past of system #1 and the future of system #2. The latency varied from 1 to 100 data points, which corresponded to the interval [0, 10]s. To obtain a value of the net information transfer, the difference between two amounts of transfer entropy was averaged across realizations and latency range. For the same data, sample entropy was computed as a function of scale factors 1–20. As in the MEG data analysis, the variability at fine time scales was estimated by averaging the sample entropy values across the first five scale factors, whereas the variability of coarse-grained time series was computed by averaging the sample entropy across the time scales 16–20.

First, we considered the influence of the time delay, T, varied on the interval [1, 20], with the coupling parameter ∈ fixed. The effects of its variability on complexity and information exchange are shown in Figure 5. The figure shows net transfer entropy (Figure 5A), differences in sample entropy at fine (Figure 5B) and coarse time scales (Figure 5D) as functions of the time delay T. Note that, when we deal with real data, such relations cannot be observed as typically the true values of T are not known (see, however, Prokhorov and Ponomarenko, 2005; Silchenko et al., 2010; Vicente et al., 2011 for the attempts in recovering time delays in coupling). What we can observe is the correlations between the net transfer entropy and the differences in sample entropy shown in Figures 5C,E. The results revealed the presence of a relatively strong and robust linear correlation between the two statistics, similar to what we saw for MEG data in Figure 2A. However, the correlation observed in Figure 5E is close to zero and statistically insignificant, contrary to Figure 2B.

FIGURE 5

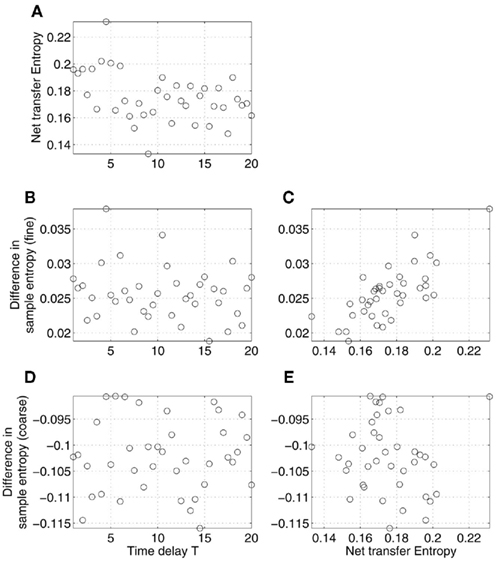
Figure 5. Effects of time delay in coupling on the relations between differences in sample entropy between coupled Rössler’s oscillators and net information transfer between them. Specifically, net transfer entropy (A) and differences in sample entropy computed at fine (B) and coarse (D) time scales are plotted as functions of the time delay T in coupling. Sample entropy and transfer entropy were estimated based on the time series x₁ and x₂, generated according to the model (12) for the different values of the parameter T with a contant ∈. Only the relations illustrated in (C,E) can be observed in the MEG data analysis (Figure 2). Specifically, (C) (correlation r = 0.73, p-value < 0.0001) corresponds to Figure 2A, whereas (E) (correlation r = −0.08, statistically not different from 0) corresponds to Figure 2B.

Similar to the time delay, the coupling parameter ∈ turned out to be able to explain, to some degree, the results in Figure 2. As expected, the net transfer entropy was found to be a monotonically increasing function of the coupling strength ∈, as shown in Figure 6A. Also, the difference in coarse-grained sample entropy was, at first approximation, a linear function of ∈, as shown in Figure 6D. In turn, this led to the negative correlation between the complexity difference and net transfer entropy for all the values of the coupling parameter, as plotted in Figure 6E, in a good accordance with the results observed in Figure 2B. The influence of ∈ on the fine-grained sample entropy was ambiguous, as shown in Figures 6B,C. It is worth noting that Figures 2A,B are consistent with Figures 6C,E, respectively, only for a weak coupling.

FIGURE 6

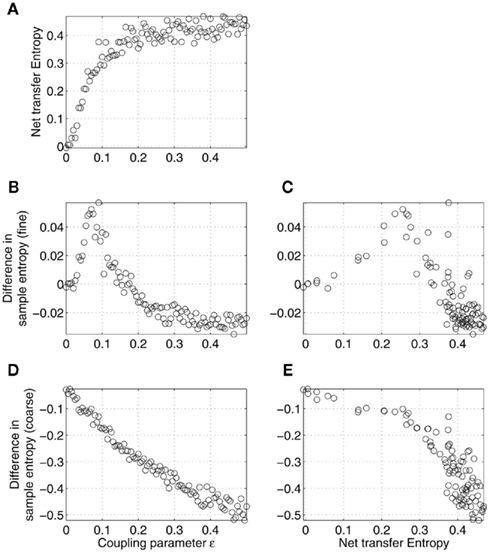
Figure 6. Effects of the strength of coupling (parameter ∈) on the relations between differences in sample entropy between coupled Rössler’s oscillators and net information transfer between them. Specifically, net transfer entropy (A) and differences in sample entropy estimated at fine (B) and coarse (D) time scales are given as functions of the coupling strength ∈. Complexity and transfer entropy were estimated based on the signals x₁ and x₂, according to the model (12) for the different values of the parameter ∈ with a fixed T. As in Figure 5, only the relations illustrated in (C,E) can be observed in the MEG data analysis (Figure 2). Note that Figures 2A,B are consistent with (C,E), respectively, only for relatively weak couplings, with ∈ < 0.08 (B).

4. Conclusion and Discussion

In this paper, we examined relations between signal variability and asymmetry in mutual interdependencies between activated neuromagnetic sources. Variability was quantified based on sample entropy (Richman and Moorman, 2000), which is ultimately interpreted as the average rate of information generated by a dynamic system (Grassberger and Procaccia, 1983; Pincus, 1995). Using the concept of multi-scale entropy (Costa et al., 2002), we examined variability at fine and coarse resolutions of the same time series. Interdependencies between source dynamics was estimated using conditional mutual information between the past and present of one signal and the future of another signal, provided that the knowledge about the past and present of the second signal is excluded (Palus et al., 2001). The asymmetry in information transfer represent the differences in predictive power between sources, i.e., to predict the activity of each other.

The analyses of signal variability and information transfer were performed under an assumptions that neuronal ensembles involved in performing a task can be described by coupled non-linear dynamic systems (Haken, 1996). Noise can be present at different levels of the non-linear models describing the observed time series. For the purpose of this study, we differentiate three types of noise-like activity. First, there is internal noise, which is an inherent component of a model, and is a part of the input entering the non-linear deterministic system. Second, we distinguish the variability in the signal generated by non-linear dynamic system. Finally, observational noise can be mixed with the output of the system.

This study focuses on exploring the variability in non-linear dynamics and describes this variability in its relations to the transfer of information in functional networks. Typically, there is the assumption that one observes non-linear systems in different states, and the goal is to describe these differences. Although different, two initial conditions would not be differentiated with certain experimental precision. However, they may evolve into distinguishable states after some finite time. Thus, one could say that a system that is sensitive to initial conditions produces information (Eckmann and Ruelle, 1985).

Sample entropy, which was used as a measure of variability, is closely related to the mean rate of information generated by a dynamic system underlying the observed signals. In practice, however, both linear stochastic and non-linear deterministic effects can contribute to the measure of sample entropy. A number of studies indicate that averaging the information rate over a larger time horizon allows one to alleviate linear effects, in particular, those associated with observational noise, and to focus on the signal variability due to the underlying non-linear determinism (Govindan et al., 2007; Kaffashi et al., 2008). Down-sampling of the original time series, as used in the multi-scale entropy approach, can be viewed as a way to extend the period over which the information generated by a system is averaged.

The first part of our analysis was based on the dynamics of neuromagnetic sources reconstructed from MEG data collected during a face recognition task. In the second part, we extended our empirical findings with an analysis of synthetic data based on the dynamics of coupled non-linear oscillators with time delay in coupling. We found that relations between sample entropy of the activity of neuromagnetic sources and the net information transfer between them depends on time scales at which the sample entropy is computed. Specifically, we found that more information is transferred from a source with a higher sample entropy at coarse time scales, but with a lower sample entropy at fine time scales.

Under certain conditions, analysis of the synthetic data offered a potential explanation our empirical findings. Specifically, a study of the system of two coupled oscillators with time delay in coupling revealed the same relations between the difference in sample entropy and asymmetry in information transfer. In particular, we found that the interplay between sample entropy-based on fine-grained signals and information transfer can be explained, in a statistical sense, by the variability in the time delay in coupling. On the contrary, correlations between information transfer and sample entropy computed at coarse time scales were insignificant. In addition, we found that the variability in the coupling strength can contribute to the observed relations between the sample entropy-based on the coarse-grained signals and the information transfer. Taking into account that the coarse scales would better reflect non-linear effects, these results indicate that the variability of the signals due to non-linear determinism become more diversified as a result of the propagation of information in the network. In other words, propagation of information in a network may be described as accumulation of complexity (variability) of the brain signals. Similar results were found in (Mišić et al., 2011), who showed that the variability of a region’s activity systematically varied according to its topological role in functional networks. Specifically, the rate at which information was generated was largely predicted by graph-theoretic measures characterizing the importance of a given node in a functional network, such as the node centrality or efficiency of information transfer.

It would be worth discussing the differences between an analysis of transfer entropy, as performed in this study, and an analysis of causal relationships between the source activity. Lizier and Prokopenko (2010) suggested to distinguish information transfer and causal effects. Information transfer is defined as the conditional mutual information, representing the averaged information contained in the future of one process about the past of another process, but not in the past of the first process itself. In contrast, causal effect can be viewed as information flow quantifying the deviation of one process from causal independence on another process, given a set of variables that may affect these two processes of interest. Along a similar line of reasoning, Valdes-Sosa et al. (2011) differentiate predictive capacity between temporally distinct events and the effects of controlled intervention on the target process. Observing activity at a network node may potentially indicate its effects at remote nodes. However, identification of a physical influence upon a node at a given network assumes that any other physical influence that this node receives should be excluded.

Under this context, it should be emphasized that this study focuses on predictive information transfer, rather than on information flow. Using bivariate variant of information transfer, compared to the multivariate version, imposes a few limitations. First, it is impossible to distinguish between direct and indirect connections (Gourévitch et al., 2007). Specifically, confounding effects of indirect connections on estimation of transfer entropy were considered in Vakorin et al. (2009). Second, bivariate estimates of directionality in case of mutually interdependent sources may produce spurious results (Blinowska et al., 2004). With regards to this study, it should be noted that the issue associated with common sources is less of a problem in MEG than in EEG, as neuromagnetic signals do not suffer from volume conduction (Hämäläinen et al., 1993). However, in general, choosing an optimal set of variables constituting a network to analyze in a multivariate way remains an open issue. For example, it was shown that information-theoretic measures (transfer entropy), which in general does not require a model of interactions between nodes of a network, in contrast to autoregressive models, remain sensitive to model misspecification, wherein excluding a node from the analysis or adding a node affects the estimation of transfer entropy and robustness of the results (Vakorin et al., 2009).

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This research was supported by research grants from the J. S. McDonnell Foundation to Dr. Anthony R. McIntosh. We thank Dr. Margot J. Taylor for sharing the MEG data. Also, we would like to thank Maria Tassopoulos and Tanya Brown for their assistance in preparing this manuscript.

References

Blinowska, K. J., Kus, R., and Kaminski, M. (2004). Granger causality and information flow in multivariate processes. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 70, 050902.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Bressler, S. L. (1995). Large-scale cortical networks and cognition. Brain Res. Brain Res. Rev. 20, 288–304.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Bressler, S. L. (2002). Understanding cognition through large-scale cortical networks. Curr. Dir. Psychol. Sci. 11, 58–61.

CrossRef Full Text

Chavez, M., Martinerie, J., and Le Van Quyen, M. (2003). Statistical assessment of nonlinear causality: application to epileptic EEG signals. J. Neurosci. Methods 124, 113–128.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Cheyne, D., Bostan, A. C., Gaetz, W., and Pang, E. W. (2007). Event-related beamforming: a robust method for presurgical functional mapping using MEG. Clin. Neurophysiol. 118, 1691–1704.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Costa, M., Goldberger, A. L., and Peng, C. K. (2002). Multiscale entropy analysis of physiologic time series. Phys. Rev. Lett. 89, 062102.

CrossRef Full Text

Deco, G., Jirsa, V., McIntosh, A. R., Sporns, O., and Ktter, R. (2009). Key role of coupling, delay, and noise in resting brain fluctuations. Proc. Natl. Acad. Sci. U.S.A. 106, 10302–10307.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Eckmann, J.-P., and Ruelle, D. (1985). Ergodic theory of chaos and strange attractors. Rev. Mod. Phys. 57, 617–656.

CrossRef Full Text

Ghosh, A., Rho, Y., McIntosh, A. R., Ktter, R., and Jirsa, V. (2008). Cortical network dynamics with time delays reveals functional connectivity in the resting brain. Cogn. Neurodyn. 2, 115–120.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Gourévitch, B., Le Bouquin-Jeannès, R., and Faucon, G. (2007). Linear and nonlinear causality between signals: methods, examples and neurophysiological applications. Biol. Cybern. 95, 349–369.

CrossRef Full Text

Govindan, R. B., Wilson, J. D., Eswaran, H., Lowery, C. L., and Preißl, H. (2007). Revisiting sample entropy analysis. Physica A 376, 158164.

CrossRef Full Text

Granger, C. W. J. (1969). Investigating causal relations by econometric models and cross spectral methods. Econometrica 37, 428–438.

CrossRef Full Text

Grassberger, P., and Procaccia, I. (1983). Estimation of the Kolmogorov entropy from a chaotic signal. Phys. Rev. A 28, 2591–2593.

CrossRef Full Text

Hadjipapas, A., Casagrande, E., Nevado, A., Barnes, G. R., Green, G., and Holliday, I. E. (2009). Can we observe collective neuronal activity from macroscopic aggregate signals? Neuroimage 44, 1290–1303.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hadjipapas, A., Hillebrand, A., Hilliday, I. E., Singh, K., and Barnes, G. R. (2005). Assessing interactions of linear and nonlinear neuronal sources using MEG beamformers: a proof of concept. Clin. Neurophysiol. 116, 1300–1313.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Haken, H. (1996). Principles of Brain Functioning. Berlin: Springer.

Hämäläinen, M., Hari, R., Ilmoniemi, R., Knuutila, J., and Lounasmaa, O. V. (1993). Magnetoencephalography – theory, instrumentation, and applications to noninvasive studies of the working human brain. Rev. Mod. Phys. 65, 413–497.

CrossRef Full Text

Hinrichs, H., Heinze, H. J., and Schoenfeld, M. A. (2006). Causal visual interactions as revealed by an information theoretic measure and fMRI. Neuroimage 31, 1051–1060.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hlavackova-Schindler, K., Palus, M., Vejmelka, M., and Bhattacharya, J. (2007). Causality detection based on information-theoretic approaches in time series analysis. Phys. Rep. 441, 1–46.

CrossRef Full Text

Jirsa, V. K., and McIntosh, A. R. (eds). (2007). Handbook of Brain Connectivity. Berlin: Springer-Verlag.

Kaffashi, F., Foglyano, R., Wilson, C. G., and Loparo, K. A. (2008). The effect of time delay on approximate and sample entropy calculations. Physica D 237, 3069–3074.

CrossRef Full Text

Kolmogorov, A. N. (1959). Entropy per unit time as a metric invariant of automorphism. Dokl. Russian Acad. Sci. 124, 754–755.

Lippé, S., Kovacevic, N., and McIntosh, A. R. (2009). Differential maturation of brain signal complexity in the human auditory and visual system. Front. Hum. Neurosci. 3:48. doi: 10.3389/neuro.09.048.2009

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Lizier, J. T., and Prokopenko, M. (2010). Differentiating information transfer and causal effect. Eur. Phys. J. B 7, 605–661.

CrossRef Full Text

McIntosh, A. R. (1999). Mapping cognition to the brain through neural interactions. Memory 7, 523–548.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

McIntosh, A. R., Kovacevic, N., and Itier, R. J. (2008). Increased brain signal variability accompanies lower behavioral variability in development. PLoS Comput. Biol. 4, e1000106. doi: 10.1371/journal.pcbi.1000106

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Mišić, B., Mills, T., Taylor, M. J., and McIntosh, A. R. (2010). Brain noise is task-dependent and region-specific. J. Neurophysiol. 104, 2667–2676.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Mišić, B., Vakorin, V., Paus, T., and McIntosh, A. R. (2011). Functional embedding predicts the variability of neural activity. Front. Syst. Neurosci. 5:90. doi: 10.3389/fnsys.2011.00090

CrossRef Full Text

Niebur, E., Schuster, H. G., and Kammen, D. M. (1991). Collective frequencies and metastability in networks of limit-cycle oscillators with time delay. Phys. Rev. Lett. 67, 2753–2756.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Nunez, P. L. (1995). Neocortical Dynamics and Human Brain Rhythms. New York: Oxford University Press.

Nunez, P. L., and Shrinivasan, R. (2005). Electric Fields in the Brain: The Neurophysics of EEG. New York: Oxford University Press.

Palus, M., Komarek, V., Hrncir, Z., and Sterbova, K. (2001). Synchronization as adjustment of information rates: detection from bivariate time series. Phys. Rev. E 63, 046211.

CrossRef Full Text

Palus, M., and Vejmelka, M. (2007). Directionality from coupling between bivariate time series: how to avoid false causalities and missed connections. Phys. Rev. E 75, 056211.

CrossRef Full Text

Pereda, E., Quiroga, R. Q., and Bhattacharya, J. (2005). Nonlinear multivariate analysis of neurophysiological signals. Prog. Neurobiol. 77, 1–37.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Pincus, S. (1995). Approximate entropy (ApEn) as a complexity measure. Chaos 5, 110–117.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Pincus, S. M. (1991). Approximate entropy as a measure of system complexity. Proc. Natl. Acad. Sci. U.S.A. 88, 2297–2301.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Prichard, D., and Theiler, J. (1995). Generalized redundancies for time series analysis. Physica D 84, 476–493.

CrossRef Full Text

Prokhorov, M. D., and Ponomarenko, V. I. (2005). Estimation of coupling between time-delay systems from time series. Phys. Rev. E 72, 016210.

CrossRef Full Text

Richman, J. S., and Moorman, J. R. (2000). Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 278, H2039–H2049.

Pubmed Abstract | Pubmed Full Text

Robinson, S. E., and Vrba, J. (1999). “Functional neuroimaging by synthetic aperture magnetometry,” in Recent Advances in Biomagnetism: Proceedings from the 11th International Conference on Biomagnetism, eds T. Yoshimine, M. Kotani, S. Kuriki, H. Karibe, and N. Nakasato (Sendai: Tohoku University Press), 302–306.

Schreiber, T. (2000). Measuring information transfer. Phys. Rev. Lett. 85, 461–464.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Sekihara, K., Nagarajan, S. S., Poeppel, D., Marantz, A., and Miyashita, Y. (2001). Reconstructing spatio-temporal activities of neural sources using an MEG vector beamformer technique. IEEE Trans. Biomed. Eng. 48, 760–771.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Shattuck, D. W., and Leahy, R. M. (2002). Brainsuite: an automated cortical surface identification tool. Med. Image Anal. 6, 129–142.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Silchenko, A. N., Adamchic, I., Pawelczyk, N., Hauptmann, C., Maarouf, M., Sturm, V., and Tass, P. A. (2010). Data-driven approach to the estimation of connectivity and time delays in the coupling of interacting neuronal subsystems. J. Neurosci. Methods 191, 32–44.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Small, M., and Tse, C. K. (2004). Optimal embedding parameters: a modeling paradigm. Physica D 194, 283–296.

CrossRef Full Text

Stam, C. J. (2005). Nonlinear dynamical analysis of EEG and MEG: review of an emerging field. Clin. Neurophysiol. 116, 2266–2301.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Taylor, M. J., Mills, T., Smith, M. L., and Pang, E. W. (2008). Face processing in adolescents with and without epilepsy. Int. J. Psychophysiol. 68, 94–103.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Vakorin, V. A., Kovacevic, N., and McIntosh, A. R. (2010a). Exploring transient transfer entropy based on a group-wise ICA decomposition of EEG data. Neuroimage 49, 1593–1600.

CrossRef Full Text

Vakorin, V. A., Ross, B., Krakovska, O. A., Bardouille, T., Cheyne, D., and McIntosh, A. R. (2010b). Complexity analysis of the neuromagnetic somatosensory steady-state response. Neuroimage 51, 83–90.

CrossRef Full Text

Vakorin, V. A., Krakovska, O. A., and McIntosh, A. R. (2009). Confounding effects of indirect connections on causality estimation. J. Neurosci. Methods 184, 152–160.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Vakorin, V. A., Lippé, S., and McIntosh, A. R. (2011). Variability of brain signals processed locally transforms into higher connectivity with brain development. J Neurosci. 31, 6405–6413.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Valdes-Sosa, P. A., Roebroeck, A., Daunizeau, J., and Friston, K. (2011). Effective connectivity: influence, causality and biophysical modeling. Neuroimage 58, 339–361.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Varela, F., Lachaux, J. P., Rodriguez, E., and Martinerie, J. (2001). The brainweb: phase synchronization and large-scale integration. Nat. Rev. Neurosci. 2, 229–239.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Vicente, R., Wibral, R., Lindner, M., and Pipa, G. (2011). Transfer entropy – a model-free measure of effective connectivity for the neurosciences. J. Comput. Neurosci. 30, 45–67.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Wibral, M., Rahm, B., Rieder, M., Lindner, M., Vicente, R., and Kaiser, J. (2011). Transfer entropy in magnetoencephalographic data: quantifying information flow in cortical and cerebellar networks. Prog. Biophys. Mol. Biol. 105, 80–97.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text