Visual cortex combines a stimulus and an error-like signal with a proportion that is dependent on time, space, and stimulus contrast

Even though the visual cortex is one of the most studied brain areas, the neuronal code in this area is still not fully understood. In the literature, two codes are commonly hypothesized, namely stimulus and predictive (error) codes. Here, we examined whether and how these two codes can coexist in a neuron. To this end, we assumed that neurons could predict a constant stimulus across time or space, since this is the most fundamental type of prediction. Prediction was examined in time using electrophysiology and voltage-sensitive dye imaging in the supragranular layers in area 18 of the anesthetized cat, and in space using a computer model. The distinction into stimulus and error code was made by means of the orientation tuning of the recorded unit. The stimulus was constructed as such that a maximum response to the non-preferred orientation indicated an error signal, and the maximum response to the preferred orientation indicated a stimulus signal. We demonstrate that a single neuron combines stimulus and error-like coding. In addition, we observed that the duration of the error coding varies as a function of stimulus contrast. For low contrast the error-like coding was prolonged by around 60–100%. Finally, the combination of stimulus and error leads to a suboptimal free energy in a recent predictive coding model. We therefore suggest a straightforward modification that can be applied to the free energy model and other predictive coding models. Combining stimulus and error might be advantageous because the stimulus code enables a direct stimulus recognition that is free of assumptions whereas the error code enables an experience dependent inference of ambiguous and non-salient stimuli.

Introduction

Since the early days of electrophysiology one goal in neuroscience has been to find a correspondence between action potentials and stimulus. Experimental studies show that correspondence is not perfect. For example repeated presentations of the same stimulus do not result in the same response amplitude (Schiller et al., 1976; Heggelund and Albus, 1978; Scobey and Gabor, 1989; Vogels et al., 1989; Snowden et al., 1992; Softky and Koch, 1993). This motivates the question why and how action potentials differ from the mere coding of the stimulus. The discrepancy between stimulus coding and action potentials may be ascribed to spontaneous fluctuations of ongoing activity (Arieli et al., 1995, 1996; Kenet et al., 2003). Spontaneous fluctuations could be the result of predictions (Ringach, 2009).

The most fundamental form of prediction is that a stimulus will repeat in space or in time. If the stimulus is repeating, the local stimulus can be used to predict a nearby or future stimulus, respectively. Thus, the error will be small. If neurons perform error coding the firing rate should drop (Koch and Poggio, 1999). The opposite is also true, i.e., when the brain is “surprised” by a stimulus, the activity should be high. For space, it has been observed that the firing rate drops when a grating stimulus becomes larger than a certain optimal radius, i.e., the stimulus repeats across space (Maffei and Fiorentini, 1976; Nelson and Frost, 1978; Angelucci et al., 2002). This effect is normally termed contextual suppression. For time, a firing rate decrease usually occurs when the visual stimulus remains constant for more than an optimal time span, i.e., the stimulus repeats across time (Kuffler, 1953). This effect is normally termed adaptation (Barlow, 1953; Muller et al., 1999; Kohn, 2007). In addition to those basic response properties, the error coding principle has explained responses to a range of stimuli such as overlapping gratings, textured surrounds, and apparent motion (Rao and Ballard, 1999; Alink et al., 2010; Spratling, 2010).

Although there is growing evidence for error coding there is also recent evidence for a true stimulus coding (Benucci et al., 2009). True stimulus coding means that the luminance pattern of the currently shown stimulus is represented by the neuronal activity. This is in contrast to error coding where not only the current luminance pattern is represented but also a prediction that was generated from a combination of previously shown stimuli and the knowledge about the environment. Interestingly, both stimulus and error coding were observed in one and the same visual area (V1). Models of predictive coding generally assume separate error and stimulus units rather than combining them (Rao and Ballard, 1999; Friston, 2008, 2010; Spratling, 2010). In contrast to these models, we postulate that both stimulus and error code can coexist in the same area and in the same neuron and that the error code can override the stimulus code.

To separate the stimulus from the error signal we have taken advantage of the orientation preference code of the neurons in the visual cortex of cats. The stimulus was constructed as such that a maximum response to the non-preferred orientation indicated an error signal, and the maximum response to the preferred orientation indicated a stimulus signal. It consisted of two images, the first image should generate a constant prediction, and the second image should violate the constancy prediction induced by the first image. The nature of that violation was that the resulting error image has an orientation that is orthogonal to that of the stimulus image.

Subsequently, we reformulated the temporal also into a spatial prediction stimulus. Using those stimuli we could examine how the proportion between error and stimulus coding varied across time and space. We could also observe that the proportion of the stimulus and error coding was dependent on the stimulus contrast. Furthermore, the prediction stimuli were used to examine the behavior of two different predictive coding models. Based on the comparison between model and experimental data we conclude that existing predictive coding models may have to be modified in order to account for a combined stimulus and error code.

Methods

The study was approved by the ethical committee for animal experimentation of the Government of Hessen. All experimental procedures were performed in accordance with the Society for Neuroscience and the German law for animal protection. Optical imaging of intrinsic signals and voltage-sensitive dye recordings were performed in area 18 of five adult (>1 years) cats. Extracellular recordings were done in eight animals.

Preparation

Anesthesia was initiated by intramuscular injection of ketamine (10 mg/kg; Ketamin, CEVA Tiergesundheit GmbH, Düsseldorf, Germany) and xylazine (1 mg/kg, Rompun, Bayer Vital, Leverkusen, Germany). After tracheotomy the anesthesia was maintained by artificial ventilation with a gas mixture of N₂O (70%), O₂ (30%), and halothane (1.2%, Halothan, Eurim-Pharm Arzneimittel GmbH, Piding, Germany) supplemented by intravenous application of a muscle relaxant (pancuronium bromide, 0.25 mg/kg/h, Pancuronium, CuraMED Pharma GmbH, Karlsruhe, Germany) to prevent eye movements. The ECG, pulmonary pressure, and CO2 content of the expired air were continuously monitored. End-tidal CO2 was kept in the range of 3–4%, and rectal temperature was maintained in the range of 37–38°C. A craniotomy was performed on one hemisphere, and a circular stainless steel chamber centered on Horsley–Clarke AP0 and AL4, 15 mm in diameter, was mounted onto the skull over the exposed region with dental cement (Paladur, Kulzer, Wehrheim, Germany).

During recording periods, the level of halothane was lowered to 0.8%. For visual stimulation, pupils were dilated and the nictitating membranes retracted with topical atropine (1%) and phenylephrinhydrochloride (1%) (Ursapharm, Saarbrücken, Germany). Corneae were protected by contact lenses with an artificial pupil of 3 mm diameter and with sufficient power to focus the retina on the stimulation monitor at a distance of 57 cm. The average eye drift during 24 h was 1.3° ± 0.3° (n = 4) (estimated from receptive field mapping during the course of the experiment).

Visual Stimulus

Visual stimuli were presented on a 21-inch computer screen (Hitachi, CM815ET, refresh rate, 100 Hz; 640 × 480 pixels resolution) at a distance of 57 cm. Stimuli were displayed using a standard graphical board (GeForce 6600-series, NVIDIA, USA) controlled by ActiveStim (www.activestim.com) and custom made software in LabVIEW.

Grating and Priming Stimulus

Two different types of stimuli were used to study near and far temporal contextual modulation, respectively. For near temporal contextual modulation a 0, 20, 50, 100, or 250 ms duration priming image was preceded by a 500 ms gray screen, and followed by a 250 ms grating. For far temporal contextual modulation the priming image always had a duration of 250 ms. Following the priming image and preceding the grating there was a blank screen of a duration of 0, 20, 40, 50, or 100 ms, i.e., a gap of different durations. The priming and grating pattern had a spatial frequency of 0.3 cyc/deg and the transition (both priming and grating pattern) were displayed with 16 different angles separated by 22.5°.

It is important to note here a fundamental difference between this and the previous study using the same stimulus (Eriksson et al., 2010). In the former study, the actual stimulus never happened to be represented by the single unit but, instead, the error was always represented. The previous study examined ferrets anesthetized with isoflurane, which suppresses single unit activity more than halothane (Villeneuve and Casanova, 2003), i.e., the anesthesia used in this study. Since firing rates are lower during stimulus coding than during error coding suppression by the anesthesia gas might have impaired the later stimulus representation in the ferret study.

Electrophysiological Recordings

Arrays of 4 × 4 Tungsten electrodes (1 MΩ, MicroProbes, Gaithersburg, MD, USA) with 300 μm inter-lead spacing were positioned touching the surface of central area 18 by using Horsley–Clarke coordinates and the retinotopic map (Tusa et al., 1978, 1979), or by previous identification of the 17/18 border with optical imaging of intrinsic signals (Rochefort et al., 2007). The craniotomy was subsequently covered with agar and bone wax. The electrodes were lowered into the brain by means of a hydraulic micromanipulator (Narishige, Japan) with a speed of 100 μm/h. We stopped moving when there were visual responses on more than 50% of the electrodes. This was typically the case after 800–1000 μm. Since the array electrode has many contact points it is difficult to avoid dimpling of the brain. Therefore, the depth of the electrode tips was less than 800–1000 μm under the cortical surface, i.e., supragranular layers or upper layer IV. Protocols were started earliest 2 h after the electrode descend had stopped. To focus on hypothetical error units only units with a transiency index (1-peak/plateau) larger than 0.5 were used for our protocol (Friston, 2008).

Spiking activity of small groups of neurons (multi-unit activity) was obtained by amplifying and band-pass filtering (MUA, 0.7–6.0 kHz; LFP, 0.7–170 Hz) the recorded signals with a customized 32 channels Plexon pre-amplifier connected to an HST16o25 headset (Plexon Inc, Dallas, TX, USA). Additional 10× signal amplification was done by onboard amplifiers (M-series acquisition boards, National Instruments, Austin, TX, USA). Signals were digitized and stored using a LabVIEW-based acquisition system developed in the institute (SPASS). Spikes were detected by amplitude thresholding (typically four standard deviations above noise level). Spike events and corresponding waveforms were sampled at 32 kS/s (spike waveform length, 1.2 ms).

Analyzes of Electrophysiological Recordings

All analyzes were done using Matlab R13 (The MathWorks, Natrick, MA, USA). Off-line spike sorting was performed using an automatic spike sorter with default parameters (Shoham et al., 2003).

Basic Analysis

For grating stimuli, an orientation tuning curve for each unit was derived from the average firing rate during 0–250 ms after the onset of 16 stationary gratings in steps of 22.5°. Responses to gratings separated by 180° were added (since the stimulus is a stationary grating a rotation of 180° results in a contrast reversal and since we couldn't find a difference between simple and complex cells). The preferred orientation was defined as the orientation that generated the highest firing frequency. We only used a unit if average firing rates (across trials) of preferred and the non-preferred orientation (90° from preferred) were highly significantly different (p < 10⁻⁸). The high significance criterion minimized the number of units that responded to the non-preferred orientation.

Stimulus for Voltage-Sensitive Dye Imaging

For VSD recording, the priming pattern transition was repeated at two different angles separated by 90°, i.e., horizontal and vertical. For studying the lateral spreading of VSD signals the pattern transition was displayed in a localized patch of 10° diameter. The position of the patch in visual space was determined by intrinsic imaging of retinotopy (see below).

Stimulus Positioning for VSD Imaging using Intrinsic Imaging

To position the stimuli and to extract an orientation map for voltage-sensitive dye imaging we did intrinsic imaging. The light from a halogen light source was passed through a band pass filter 605 ± 10 nm, and through two external light guides. Images (256 × 256 pixels) were acquired at 5 Hz with a 12 mm CCD camera (Dalsa 1M60) through a macroscope fitted with a 1× objective (Imager 3001, Optical Imaging Inc., New York, USA).

For Fourier imaging (Kalatsky and Stryker, 2003), an elongated bar was cyclically drifting over the screen into one of four different directions (left, right, up, and down). Each cycle displaying one direction lasted 8 s and was repeated 20 times. Each 20 cycle block of one direction was repeated five times. For each pixel, the phase of the stimulus induced oscillation was calculated for the four conditions. The phase in the up condition was subtracted from the phase in the down condition (the same operation was done for left and right) in order to remove a constant additive response delay in the intrinsic signals (assumed to be the same for the two conditions). The resulting time image was scaled by velocity to deliver the retinotopic positions. A similar procedure was done in order to estimate the response delay of the intrinsic signal. We found it to be around five seconds on average.

Voltage-Sensitive Dye Imaging

The exposed cortical surface was stained for 2 h with the voltage sensitive dye RH1838 (0.53 mg ml⁻¹) (Optical Imaging, Rehovot, Israel). The light from a halogen light source was band pass filtered, 630 ± 10 nm, reflected onto the brain surface with a dichroic mirror (650 nm), and collected with a high-pass emission filter (665 nm). Images (256 × 256 pixels) were acquired at 160 Hz with the Imager 3001.

Analyzes of VSD Recordings

The VSD signal was low pass filtered in time using a ±6.25 ms box filter. For the spatial low pass filtering a 200 × 200 μm box filter was weighted and normalized with a spatial blood vessel mask hand drawn in Photoshop. In order to study the population orientation coding a 800 × 800 μm low pass filter version was subtracted. Since the orientation coding for our stimuli only has two possibilities (0 and 90°) we used spatial correlation to quantify the encoded orientation. More precisely, the population response at a certain time after grating onset was correlated with the average (across time) population response evoked by that grating when preceded by a blank screen.

There is evidence that the two VSD and spiking signals may reflect the same neuronal events, e.g., action potentials. In agreement, both spike and VSD signals are spatially correlated (Tsodyks et al., 1999). A recent study suggested that the instantaneous firing rate leaks over to the voltage-sensitive dye signal but that orientation information also spreads outside the spiking region, although with a steeper decay than the absolute signal (Sharon et al., 2007; Chavane et al., 2011). Beyond a distance of one hypercolumn, the space constant of the decay was estimated to be around 1 mm (Chavane et al., 2011). We expect the space constant to be even larger in our case because our stimulus had a diameter of 10° and thus covered a six times larger area than that of Chavane et al. who proposed a positive correlation between space constant and stimulation area. We analyzed the VSD signal in the most peripheral pixels. This was done along a two step procedure.

First, the maximum extent of the lateral spreading was estimated from the VSD signal within a time interval when the stimulus orientation was encoded, i.e., 150–250 ms after the priming-actual transition. This time interval likely did not cause an underestimation (see comment below about a less conservative area estimation) of the lateral spreading since the absolute value of the correlation (see definition above) at 75 ms is almost identical to that at 170 ms. The extent of the lateral spreading was defined as those pixels whose neighboring population map (800 × 800 μm) was significantly correlated with the corresponding region in the true orientation map (calculated from intrinsic signal in response to drifting gratings). Since eye movements during the longest recording period (0.2° during 4 h; see Preparation) were smaller than the lateral spreading in visual space (more than 3°) we averaged extensively (181/801 repetitions for animal 1/2 lasted 2/4 h). Furthermore, we used false discovery rate (FDR) statistics to maximize the detected extent of the lateral spreading. The FDR was calculated at 5% making no assumptions of the underlying P value distribution. The FDR corrected criterion resulted in around 12% more pixels than obtained with a Bonferroni corrected threshold. We also tried a lower threshold generated from c(V) = 1, but this resulted in significant pixels farther away from the edge of the representation (>4 mm) than the radius of lateral connections (<3 mm). Furthermore, it did not result in significant correlations with the averaged population response, positive as well as negative, during the time of the error encoding, see second step below.

Second, the correlation values at the edge of the representation at 50–100 ms after the priming-stimulus transition were tested for significance for deviation from 0.

Discriminating between Stimulus Shown or not Shown

To test if it is possible to decide whether a given spike was evoked by a stimulus that is currently shown or a stimulus that already disappeared we did the following analysis. In order to classify all spikes, not only those during ON and OFF transients, we labelled spikes according to if a certain orientation was presented or not. The stimulus set was composed of three different transitions.

1. Checkerboard like preceding grating,
2. Grating preceded by a gray screen,
3. Grating followed by an orthogonal grating.

All the three paradigms were displayed in 16 different angles (with a resolution of 22.5°). The instantaneous firing rate was estimated for one of the angles (Ang) and for its corresponding orthogonal angle (Ang + 90).

For the two orthogonal stimulus presentations we divided the time points into two groups: the time points where the stimulus contained the orientation Ang were assigned to group “ON,” and the remaining time points were assigned to group “OFF.” The firing rate during each time point was divided by the average firing rate of the neuron. For each neuron, the normalized firing rate was averaged separately for the two ON and OFF groups. Then, the ratio between the firing rates of two neurons was calculated separately for both groups, producing one ratio for each group and each combination.

We also tried support vector machines for pairs and triplets but the supporting plane sometimes (for the cases with best classification performance) had a normal such as to classify the overall firing frequency of the pair or triplet. Although this classification resulted in a good performance on our stimulus sample, it does not allow generalizing to stimuli evoking low overall firing frequencies, i.e., of low contrast.

We also tried other—firing rate oriented—populationdecoding approaches selecting more than two optimal recording channels. Applying this method to data from two cats, we could not even classify the onset and offset of a grating let alone the sustained part of the neuronal firing. In one cat, we were able to classify the onset and offset of a grating. The resulting code could, however, not be used to classify the responses to the more complex checkerboard-grating transition and also not to the sustained part of the neuronal firing.

Stimulus for Verifying the Subtractive Operator between Previous and Current Stimulus

In order to characterize the encoding of individual cells we displayed 20 different image transitions from natural image α to natural image β. Natural images were used to estimate the operator since they have a continuum of contrasts. To this end, we extracted 40 images from collage bitmaps from the Internet. 400 × 400 pixels partial images were cut out from the original bitmaps. The average luminance of each image was chosen to be 30 cd m⁻² in order to maximize the contrast of a set of composite images (see below) that were used to test different operator hypotheses. Luminance and contrast of each partial image were adjusted such that minimum and maximum luminance were 0 and 60 cd m⁻², respectively. Different mathematical operators, such as +, −, were applied pixel wise to the pair of images, α and β, resulting in the composite images α + β and β − α. Each test image (α, β, β − α, or α + β) presentation lasted 250 ms and was preceded by a 250 ms 30 cd m⁻² blank screen. For the transition from α to β, α was preceded by a 500 ms blank screen and both images α and β lasted 250 ms.

Analysis for Verifying the Subtractive Operator between Previous and Current Stimulus

For stimulation with natural scenes, we calculated the instantaneous firing rate for a certain time point after each image transition. The resulting 20 element vector from the 20 image transitions can be viewed as an instantaneous response profile. The 20 dimensional response profile was correlated (Pearson) with four different response profiles from four test image-sets, α, β, α + β and β − α. These test images stand for four different hypotheses about what kind of image is being encoded after an image transition from image α to β. The response profile for each test image-set was calculated from the temporally averaged firing rate recorded between onset and offset of each test image. Observe that since α, β, α + β, and β − α, refer to images and not set of parameters there are no more degrees of freedom in α + β than in α or β only, and therefore it is fair to compare the correlation for α + β with that of α for example.

Analysis of Contrast

The time of switch from error to stimulus for different contrasts was calculated as follows. For each unit the peak activity of the non-preferred orientation response was calculated. This gave the amplitude and time of the peak of a Gaussian distribution that was fitted to the firing rate decay after the peak time. The Gaussian was fitted by testing 200 different standard deviations ranging from 1 to 200 in steps of 1. The standard deviation that minimized the squared error was selected. The switching time was defined as the time when the value of this Gaussian came below the average firing rate, 0–250 ms after transition, for the preferred orientation.

The duration of the error signal was calculated by adding the temporal difference between peak time and peak derivative time to the standard deviation defined above. The advantage of the maximal derivative approach over Gaussian fitting to the response upslope is that the initial firing rate immediately after the transition, that is above spontaneous, can be ignored.

Analysis of Rapid Serial Visual Presentation

For stimulation with alternating orthogonal gratings, we calculated the ratio between ON- and OFF-responses according to the following procedure. Latencies of ON- and OFF-responses varied in different cells and with stimulus contrast. Thus, the latency dependency was eliminated by extracting the amplitude information but not the phase information from the Fourier transformed PSTH. The frequency component that corresponds to a single stimulation period (one preferred orientation and one non-preferred orientation) gives the amplitude difference between ON- and OFF-responses; A₁. The first harmonic of one stimulation period corresponds to the residual amplitude of ON and OFF responses; A₂. The Fourier transform of an isolated ON response with amplitude r_ON is A₁ = r_ON, A₂ = r_ON, and for an isolated OFF response with amplitude r_OFF is A₁ = −r_OFF, A₂ = r_OFF. When both r_ON and r_OFF are non-zero; A₁ = r_ON – r_OFF, and A₂ = r_ON + r_OFF. Reformulating gives r_ON/r_OFF = (A2 − A1)/(A2 + A1).

Dynamic Expectation Maximization (DEM) Model

We have used the DEM model to study the most fundamental form of temporal prediction and how the model handles a combined stimulus and error code. Matlab code for the DEM model is freely available under the SPM 8 library and the figures we have made can be reproduced with code on the following server:

http://www.brain.mpg.de/fileadmin/user_upload/Documents/ Download/Singer_Emeritus_Group/eriksson.zip

In its most general form the model uses generalized coordinates to perform temporal prediction (Friston et al., 2008). The idea with generalized coordinates is that a signal, A, is easier to predict if we have the derivative of the signal, A', in addition to the signal A. The more different orders of derivatives the better the prediction. In many cases derivatives up to the sixth order suffice. This set of derivatives is fed into the model. The generation of the generalized coordinates was modified such that the model became causal. This was done by making sure that the derivative of the n'th order at time t was calculated using only time points equal or less than t.

Below are the equations for the model:

$\begin{array}{l}{\dot{\tilde{\mu }}}^{(i)v}=D{\tilde{\mu }}^{(i)v}-{\tilde{\epsilon }}_v^{(i)T}{\text{ξ}}^{(i)}-{\text{ξ}}^{(i+1)v}\\ {\dot{\tilde{\mu }}}^{(i)x}=D{\tilde{\mu }}^{(i)x}-{\tilde{\epsilon }}_x^{(i)T}{\text{ξ}}^{(i)}\\ {\text{ξ}}^{(i)v}={\tilde{\mu }}^{(i-1)v}-g({\tilde{\mu }}^{(i)})-{\Lambda }^{(i)z}{\text{ξ}}^{(i)}{}^v\\ {\text{ξ}}^{(i)x}=D{\tilde{\mu }}^{(i)x}-f({\tilde{\mu }}^{(i)})-{\Lambda }^{(i)w}{\text{ξ}}^{(i)}{}^x\end{array}$(1)

(i) denotes level i in the hierarchy. The set of derivatives introduced above is injected to the model at level 1 and is represented by the variable μ⁽¹⁾v (see second equation). This stimulus input is compared to the predicted input g(μ⁽¹⁾) and ʌ^(i)zξ^(i)v and the result is assigned to the error unit ξ^(i)v. The prediction of the stimulus input is based on the activity in higher levels, i.e., a feedback signal. v and x stands for prediction across hierarchical levels and within hierarchical levels across time, respectively. The resulting error ξ^(i)v is used to update the prediction μ^(i)v in the upper two equations. If the error is zero, i.e., ε^(i)T_vξ⁽ⁱ⁾ + ξ^(i+1)v = 0, it means that the prediction neurons higher up in the hierarchy represents the stimulus. As such the prediction wouldn't have to be updated. But what if the error is zero and the stimulus changes from one moment to the next? In this case the representation of the stimulus will have to change as well. The first term Dμ^(i)v handles this. D is a matrix that shift the dimensions in μ^(i)v such the first derivative becomes the second derivative, second becomes third, etc., in the generalized coordinates. This shift in derivative order of μ^(i)v on the right-hand side is mirrored on the left-hand side where, μ^(i)v, is differentiated, as indicated by the dot over μ^(i)v. Thus, assuming that the generalized coordinates are continuous in time they can be used to predict future values of the stimulus signal.

Although the free energy treatment is complex, the Laplace method (which we assume corresponds to a second order multivariate Taylor approximation), and the elimination of the Jacobian inversion for the update of the generalized coordinates (Friston, 2008), makes the DEM model surprisingly similar to the model of Rao and Ballard (Rao and Ballard, 1999).

To introduce an additional stimulus signal in the error unit we did the following. Since traditional predictive doing models strive to explain away the error signal one cannot just inject a stimulus signal to the error unit. The model will in this case just remove the stimulus signal. Therefore, a cumulative summed stimulus was injected into the error neuron:

$\text{ξ}(t)=\text{ξ}(t)+K{\displaystyle \underset{0}{\overset{t}{\int }}s(\text{τ})d\text{τ,}}$

where s(t) is the stimulus signal and K is a constant defining the strength of the stimulus signal relative to the error signal.

To handle combined error and stimulus the original Equations 1 can be re-arranged to Equations 2.

$\begin{array}{l}{\dot{\tilde{\mu }}}^{(i)v}=D{\tilde{\mu }}^{(i)v}-{\tilde{\epsilon }}_v^{(i)T}(r^{(i)}-k{\tilde{\mu }}^{(i)})-(r^{(i+1)v}-k{\tilde{\mu }}^{(i+1)}{}^v)\\ {\dot{\tilde{\mu }}}^{(i)x}=D{\tilde{\mu }}^{(i)x}-{\tilde{\epsilon }}_x^{(i)T}(r^{(i)}-k{\tilde{\mu }}^{(i)})\\ r^{(i)v}={\tilde{\mu }}^{(i-1)v}-g({\tilde{\mu }}^{(i)})-{\Lambda }^{(i)z}(r^{(i)}{}^v-k{\tilde{\mu }}^{(i)}{}^v)+k{\tilde{\mu }}^{(i)}{}^v\\ r^{(i)x}=D{\tilde{\mu }}^{(i)x}-f({\tilde{\mu }}^{(i)})-{\Lambda }^{(i)w}(r^{(i)}{}^x-k{\tilde{\mu }}^{(i)}{}^x)+k{\tilde{\mu }}^{(i)}{}^x\end{array}$(2)

where r^(i)v, r^(i)x, and r⁽ⁱ⁾ are vectors containing the “new error” units, and k is a constant that determines the proportion between stimulus (prediction unit μ) and error (error unit ξ).

V1 Model

To examine if error and stimulus coding can be dynamically allocated to different model units we used a model of the primary visual cortex (Spratling, 2010). The model was chosen because it explains the single unit responses of the primary visual cortex to a number of different stimuli. The model has two important parameters; number of iterations and a tolerance parameter e₁. In mimicking the response properties of the primary visual cortex the number of iterations was varied between 6 and 30 with a mean number of parameters equal to 13 (Spratling, 2010). Here, we used the average number of iterations, i.e., 13. The results presented in this paper become clearer with increasing number of iterations.

The tolerance parameter e₁ defines the amount of spatial suppression. Here, we tested two different values of e₁, i.e., 1e-4 (Spratling, 2010) and 1e-5 (de Meyer and Spratling, 2009). Both values generate size tuning curves and suppression indices that can be found experimentally.

We adjusted the model such that the number of different spatial phases that were represented was equal to the number of pixels of one period of the grating, i.e., six different phases and six pixels per period. This ensures that the response curve remains continuous across the model units/pixels.

For code see: http://www.brain.mpg.de/fileadmin/user_upload/Documents/ Download/Singer_Emeritus_Group/eriksson.zip

Results

Separating a Stimulus- and an Error-Like Signal

According to our hypothesis that the neuron might combine a stimulus and error code we first ought to separate those codes. This separation was done in terms of the orientation preference for the recorded unit. If the largest response was evoked by the preferred orientation we assumed that the neuron coded for stimulus. If the largest response was evoked by the non-preferred orientation we assumed that the neuron coded for error. This distinction was the result of our stimulus. We displayed a transition from a priming pattern to a grating pattern (see Figure 1A, left). The difference/error image between the priming and the grating pattern has an orientation that is orthogonal to that of the grating pattern (see Figure 1A, right). This orthogonality facilitated the classification into error and stimulus. Our assumption was that the neurons predicted the priming image better the longer it would be displayed. If neurons predicted the priming pattern there would be an error when the grating pattern were displayed. The error image would then have an orthogonal orientation to the grating image which means that the response would be maximal to the non-preferred instead of to the preferred orientation.

FIGURE 1

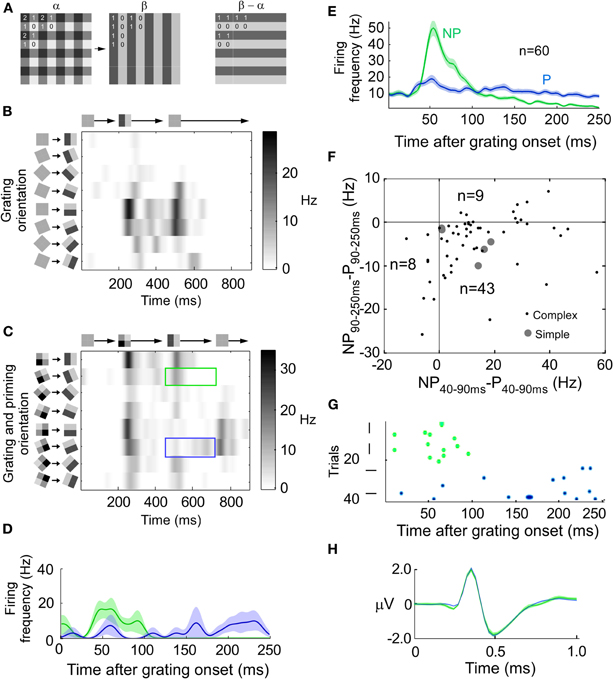
Figure 1. Combination of a stimulus and an error-like signal across time. (A) Transition from priming to grating pattern (left). The difference (error) pattern between priming and grating pattern has a horizontal orientation (right). (B) The instantaneous firing rate for a horizontally preferring complex cell when the stimulus is rotated and displayed at eight different orientations separated by 22 1/2° (y-axis). Grating onset at 200 ms and offset at 450 ms (x-axis). (C) The response of the same unit as in B, but for the priming to pattern transition (see A). The blue (green) rectangle outline indicates when the test grating matches the preferred (non-preferred) horizontal orientation of the cell. Note that the non-preferred grating orientation now generates the largest response at around 550 ms. (D) Peri-stimulus time histogram (PSTH) of the instantaneous firing rate for stimulation with, in this example, horizontal (P: preferred, blue line, stimulus) and vertical (NP: non-preferred, green line, error) gratings after the stimulus transition (at 0 ms). The transparent field around each curve denote the standard deviation of the mean. (E) Same as (D) but the average of all 60 units. (F) Scatter plot of all units. The x-coordinate is the average firing rate during 40–90 ms after transition onset for the non-preferred orientation minus the average firing rate during 40–90 ms after transition onset for the preferred orientation. The y-coordinate is like the x-coordinate but for 90–250 ms instead of 40–90 ms. (G) Spike raster plot for the preferred and non-preferred orientations for the unit shown in B–D. (H) Extracellularly recorded spike waveform from unit in G for stimulus (blue) and error (green) spikes.

Responses of a spike-sorted unit in area 18 of an anesthetized cat to a grating which was presented at eight different orientations are depicted in Figure 1B. The maximal firing rate was achieved for horizontal orientation (preferred orientation, P). For a priming-grating transition the response of the same unit is shown in Figures 1C,D. Fifty milliseconds after the transition, the maximum firing rate was achieved for vertical orientation (non-preferred orientation, NP). Only later on, after around 100 ms, the maximum firing rate was achieved for the preferred orientation. The average of all 60 units is shown in Figure 1E. In the interval between 40 and 90 ms after transition, the average firing rate was larger for the non-preferred than for the preferred orientation (p < 1e⁻⁵, n = 60, Bonferroni corrected), whereas the firing rate between 90 and 250 ms revealed the opposite relation between preferred and non-preferred (p < 1e⁻⁶, n = 60, Bonferroni corrected). Since the results were similar for simple (n = 5) and complex cells (n = 55), the two cell types were pooled (Figure 1F).

Using the transition stimulus we examined whether the same neuron could code for error and stimulus. To this end, extracelullarly recorded waveforms of one spike-sorted neuron were divided into two orientation groups. One group consisted of spikes recorded when the grating orientation matched the preference of the neuron and the other group consisted of spikes recorded when the grating orientation was orthogonal to it. We extracted the time point in the spike waveform where the amplitude difference between preferred and non-preferred waveforms was largest. If the difference at this time point was significant we concluded that the waveforms belonged to two different units (see Figures 1G and H for the example unit shown in B–D). Only four out of 60 units (6.7%) had significantly different waveforms. Since this percentage is in the range of what would be expected by chance (5%), we conclude that the same unit coded for error and stimulus.

Can the Stimulus be Extracted from the Error?

The post-synaptic membrane potential has been suggested to represent the true stimulus (Bialek et al., 1991), i.e., the membrane potential would not code for the error signal. More precisely, the linear deconvolution-transformation used to reconstruct the stimulus in the early visual system might be similar to the transformation from the pre-synaptic spike to the post-synaptic membrane potential (Bialek et al., 1991; Stanley et al., 1999; Butts et al., 2007). Thus, we studied also how our stimulus transitions would be represented in the voltage sensitive dye (VSD) signal.

Four animals entered this analysis. A typical voltage-sensitive dye signal for one animal in response to a grating stimulus is illustrated in Figure 2A. The same orientation columns are activated throughout the stimulation (p < 0.05, t-test across trials, for each of the four animals). When presenting the stimulus transition, the represented orientation changed over time (Figure 2B). The population activity was initially significantly anti-correlated, and later significantly correlated with the population activity in response to the grating (p < 0.05, t-test across trials, for each of the four animals). Similar to the instantaneous firing rate, domains responding to the orientation orthogonal to the presented one were stronger activated after the stimulus transition than domains which would normally respond to that stimulus. The correlation time course (Figure 2C) and the history dependency of the VSD signal was also similar to that of the spiking activity.

FIGURE 2

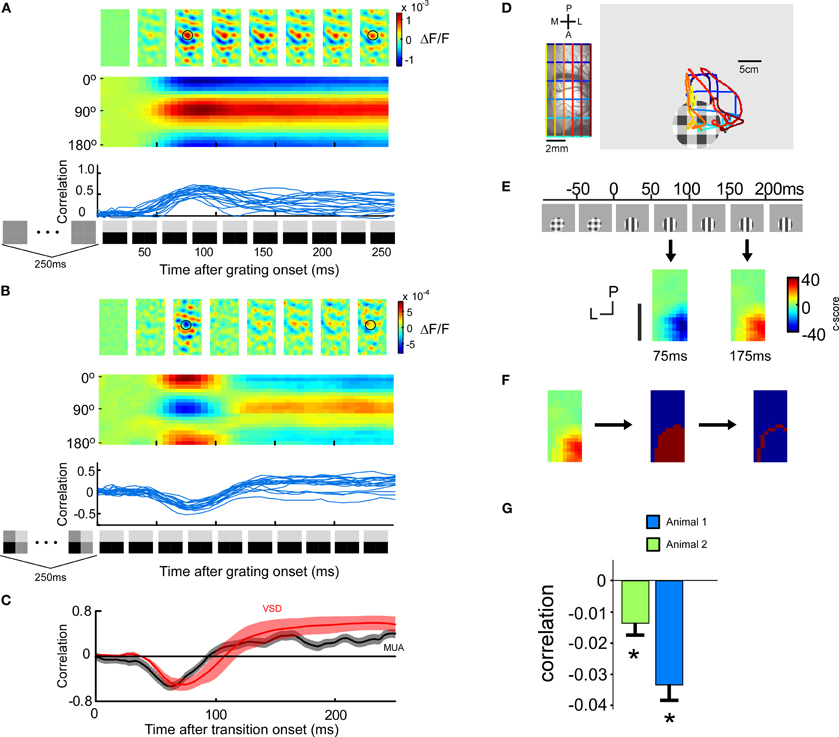
Figure 2. Voltage-sensitive dye signal after a stimulus transition. (four animals) (A) Cortical activation pattern as a function of time (upper row). VSD signal evoked by the transition from a 250 ms blank screen to a 250 ms horizontal grating. Population responses after 81 ms and 143 ms are similar. Icons on the x-axis denote stimulus sequence. Encoded orientation as a function of time (middle row). Trial by trial correlation of the population response at a certain time after grating onset with the average (across time) population response evoked by that grating when preceded by a blank screen (lower row). The correlation raises around 40 ms and stays high. (B) Same as in A, but with a 250 ms priming pattern preceding the 250 ms horizontal grating. Interestingly, the population response after 81 ms is orthogonal to that at 143 ms. (C–F) The stimulus image cannot be retrieved by the post-synaptic membrane potential. (C) Comparison of spiking and VSD response. The spiking was quantified by subtracting the non-preferred correlation from the preferred correlation. The preferred correlation was calculated as follows: for a given time point after the transition the instantaneous firing profile across the eight orientations were correlated with the instantaneous firing profile across the eight orientations for the grating preceded by a blank screen. The non-preferred correlation was calculated similarly but instead shifting the orientations by 90°. The encoding of the voltage-sensitive dye signal is represented by the correlation curve computed in B averaged across four animals (red). (D) Positioning of a patch stimulus for VSD recording using Fourier imaging retinotopy of visual cortex. Left: Imaged cortical region with superimposed retinotopic iso-lines. Blue (posterior) and green (anterior) lines indicate iso-lines for which the anterior posterior position is constant, and yellow (medial) and red (lateral) lines indicate iso-lines for which the lateral medial position is constant. Right: We have superimposed the cortical retinotopy on the stimulus monitor (left). (E) Lateral spread of the errorsignal. Upper panel: a localized stimulus (10° diameter) positioned to evoke responses in the anterior part of the imaged cortical area (guided by retinotopic imaging). Lower panel: spatial orientation coding at 75 ms and at 175 ms. Population activity evoked by the grating was pixel wise correlated with the average population activity within a 800 × 800 μm window centered around each pixel. Negative values indicate negative correlations, and thus error encoding (blue color). Positive values indicate positive correlations, and thus stimulus encoding (red color). (F) Extraction of the most peripheral pixels at time point 175 ms, i.e., when the stimulus is encoded. The peripheral pixels are those which mark the outer margin of the area containing significant information about stimulus orientation. The c-score is calculated by dividing the mean (across trials) correlation with the standard deviation (across trials) of the correlation. (G) Correlation of the peripheral pixel response at the time of error encoding (75 ms) with the averaged population response. For both animals the correlation is significantly (p < 0.05, n = 12) negative indicating that the error is encoded.

To minimize the risk that the spiking activity is leaking into the voltage-sensitive dye signal we studied the lateral spread of the VSD signal, in two additional animals. To this end, we positioned a grating patch in cortical space such that we maximized the visible lateral extent of the spread in the posterior direction (Figure 2D). The evoked response for a grating patch with a diameter of 10° was spatially confined to an area of 8–12 mm² (Figure 2E). The most peripheral pixels whose fluorescence value was significantly modulated by the stimulus orientation are illustrated in Figure 2F. In order to not underestimate the spatial extent of the lateral spread we have used extensive averaging (see methods) and false discovery rate statistics (see methods). Even the most peripheral pixels exhibited an activation pattern anti-correlated to that evoked by the grating stimulus presented alone (p < 0.05 for both animals) (Figure 2G). Pixels outside this region were not significantly modulated by stimulus orientation.

To summarize, the voltage-sensitive dye signal combines a stimulus and an error-like code. It seems unlikely that the conversion from error to stimulus can be done within V1 because the ambiguous and non-linear transformation from simple to complex neurons renders the above hypothesized linear de-convolution difficult (Benucci et al., 2007). A de-convolution could be implemented in a presumably more linear feed forward pathway from layer three (complex cells) to layer four (simple cells) of a higher area.

Another way to eliminate the error from the stimulus signal could be to detect spikes that code exclusively for the stimulus. Error coding generates spikes that are not representing the currently shown stimulus. This is because it takes time to form a prediction, i.e., the prediction builds-up over time and can therefore outlast the stimulus. It is well-known that for example OFF-responses, per definition, outlast the stimulus. Consequently, the orthogonal response can be interpreted as an OFF response since the transition consists of the disappearance of the orthogonal grating. To investigate if a population of neurons can distinguish between ON and OFF responses we defined each time point of a stimulus as containing an orientation or not (Figure 3A). We tested if this “stimulus existence code” was correlated with the population firing rate. If this would be the case the population firing rate could be used to distinguish stimulus coding spikes from spikes that codes for a disappeared stimulus. The population code was defined as the ratio between the instantaneous firing rate of one unit and the instantaneous firing rate of another unit. All possible combinations between 34 neurons and all orientations were used, i.e., 34 × 34 × 16 combinations (See red points in Figure 3B). The best combination (see encircled point in Figure 3B) is located far away from ratio 1 (origo in log-log-plot) along the diagonal meaning that the ratio for “ON” is much smaller than the ratio for “OFF” on average. Hence, the combination should be well suited to discriminate between “ON” and “OFF.” However, when inspecting individual stimulus constellations of that combination the ratios behave rather unsystematic (see Figure 3C). Whereas the firing rate is normally larger for unit 1 than for unit 2 in case of “ON”-coding, and larger for unit 2 than for unit 1 in case of “OFF” coding, there are a few time-points for the grating condition (first column in Figure 3C) where the opposite is true. Therefore, this combination does not speak in favor of a very reliable code. To be able to generalize the potential of “ON” and “OFF” coding it was compared to orientation population decoding. Instead of using three different transitions we only used the second transition, grating preceded by a screen. Instead of dividing pair-wise ratios into “ON” and “OFF” we divided them into “orientation 1” and “orientation 2”. Orientation 2 was orthogonal to orientation 1. All possible combinations between 34 neurons and all 16 orientations were used, i.e., 34 × 34 × 16 combinations (See blue points in Figure 3B). The ratios in orientation coding were around 20 times larger than those for “ON” and “OFF” coding, thus leaving the latter coding relatively unreliable.

FIGURE 3

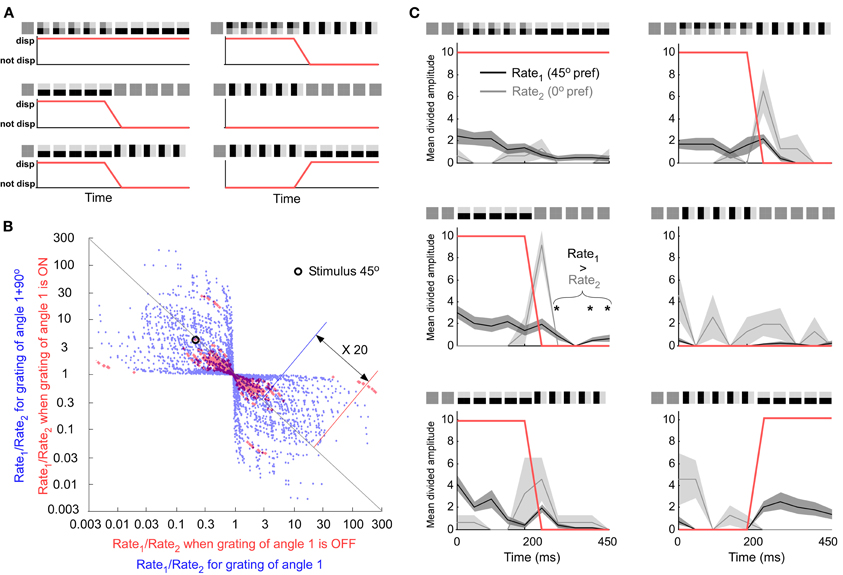
Figure 3. Comparing an orientation population code with an “ON” or “OFF” population code. (A) The three different stimulus transitions (rows). All stimulus transitions were also presented after 90° rotation (second column). Under each transition is the group assignment into ON (“up state”) and OFF (“down state”) groups (red curve). (B) All neuronal pairs and all orientations. The combination discriminating best is encircled. Best neuron combination for the “ON” and “OFF” code. (C) The preference of the first and second unit is 45° and 0°, respectively. The horizontal orientation is shown at 45° on the screen. If Rate₁ is larger than Rate₂ the orientation is on (displayed). This rule works for most cases except second row and first column when the stimulus is off (not displayed).

Rather than having to eliminate the OFF response, downstream neurons might need ON as well as OFF responses. The ON response is needed to detect increased stimulus contrast and the OFF response to detect decreased stimulus contrast. Both are necessary for a complete coverage of the subtractive error calculation (Figure 4). That also the ON response is related to error coding, in addition to the OFF response, is further motivated by the significant correlation between the transciency index of the ON response and the strength of error coding (Figure 5). To summarize, eliminating the error-like signal from the stimulus code might not be feasible. It is more likely that the brain makes use of the combined code. In the next section we examined if a combined code can be read out by a neuronal model.

FIGURE 4

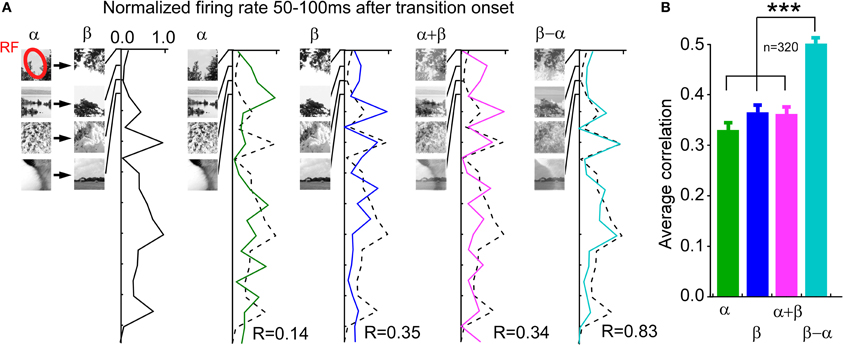
Figure 4. Operator between previous and current image, encoded by the instantaneous firing rate during the time of the ON and OFF response, is best described by a subtraction. (A) Example neuron. Different pairs of natural images where used irrespective of whether the image transition elicited ON or OFF responses. The first column shows the average firing rate between 50 and 100 ms after the transition onset. The remaining columns show the average firing rate between 50 and 100 ms after the test image onset (Observe that each test image was preceded by a blank screen). Note the high correlation in the last column. (B) Average correlations across all neurons (n = 320).

FIGURE 5

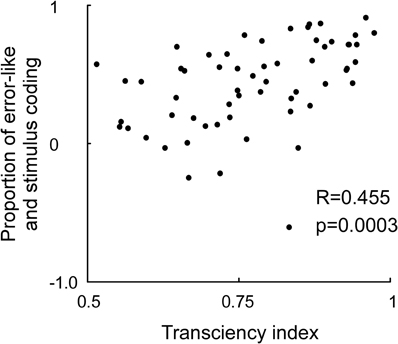
Figure 5. Correlation between the neuronal transciency index and proportion between stimulus and error-like coding. The transciency index was calculated by dividing the firing rate between 200–250 ms by the firing rate between 40 and 90 ms in response to an optimally oriented grating preceded by a gray screen (x-axis). The proportion of stimulus and error-like coding was calculated by differentiating the firing rate for the preferred and non-preffered orientation at 40–90 ms, and divide this difference with the sum of the firing rate for the preferred and non-preffered orientation at 40–90 ms (y-axis). Note that a strong transient predicts a high proportion of error coding relative to stimulus coding.

Consequence of Mixing Stimulus and Error Coding

Both the extracellular spiking signal and the voltage-sensitive dye signal showed a combination of error and stimulus coding. Since both code types are used in predictive coding models we studied how such models handle a combination of the codes. We used the dynamic expectation maximization (DEM) model because it is very general (Friston et al., 2008, see Methods). The particular version of the model applied here consists of a feed-forward network with fixed connections that forms simple edge detectors (Figure 6A). Its default response to a simple stimulus is depicted in Figure 6B. As expected from a prediction model the activity in the prediction unit follows the stimulus. The error is the difference between the stimulus and the activity in the prediction unit. Since the activity of the error units goes to zero between time steps 12 and 20, i.e., the activity for the stimulus (unit 2 with a vertical RF) is not larger than that of the error (unit 1 with a horizontal RF), it means that the stimulus is not represented during this time period. Whereas only the error signal is represented in the model, both error and stimulus signal are represented in the experimental data. Therefore, we forced the error unit to also encode a stimulus signal. This resulted in a suboptimal behavior of the model since the prediction units diverged from the stimulus (Figure 6C) and since the free energy deviated from the optimal value (low free energy is optimal) (Figure 6D).

FIGURE 6

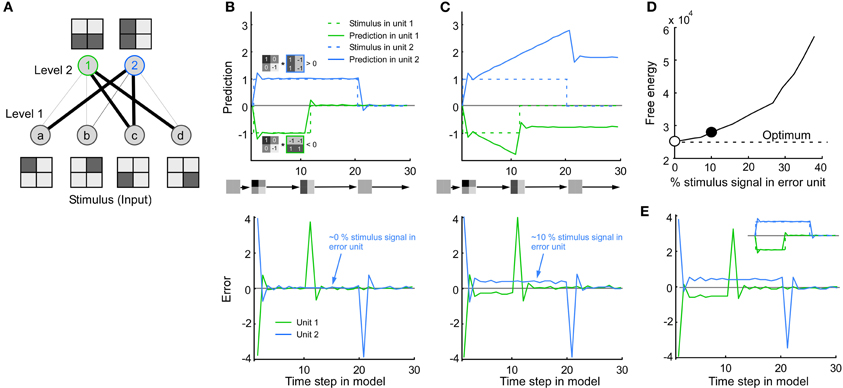
Figure 6. Consequence of mixing stimulus and error coding in a predictive coding model. (A) The model consists of four input units in level 1 (stimulus pixels) and two output units in level 2 (line detectors), where the line thickness corresponds to the connection weight. (B) Default behavior of the model. Top: Note that the activity in unit 1 and 2 follows the stimulus. The activity in unit 1/2 (green/blue line) is positive/negative since the stimulus image is positively/negatively correlated with the receptive field image of unit 1/2. Bottom: The error is the difference between the stimulus and the activity in the prediction unit. For clarity both prediction and error were taken from the line detectors in level 2, i.e., the error in level 2 was calculated by multiplying the error in level 1 by the connection weights between level 1 and 2. It is important to note that the results also hold for the error units in level 1. (C) To mimic the combination of error and stimulus signal found in this study, the error unit was made to combine stimulus and error signal (bottom). Note that the value of the prediction unit now overshoots the stimulus (top). (D) This divergence from the stimulus can also be quantified in terms of an increase in free energy. Abscissa: 0% means that only the error is represented. This corresponds to the default behavior shown in A (empty circle). Fifty percentage means that the stimulus is represented as much as the error. The example in C has a non-optimal free energy because the model is not made to combine stimulus and error coding (solid circle). (E) By a simple modification of the model the (new) error units can be made to combine stimulus and error at the same time as the prediction unit follows the stimulus (see Inset and Methods).

Next, we modified the model in a straightforward way such that it could handle the combined stimulus and error coding. To this end, the error unit was replaced with a new type of error unit in which stimulus in the multiplied by a constant was added to the error signal. The constant defines the percentage of stimulus coding in the error unit. As a consequence, the new error unit could combine stimulus and error at the same time as the prediction unit followed the stimulus (Figure 6E). The error is extracted by subtracting the stimulus prediction from the new error unit. The modification proposed here is simple and can thus most likely be applied to other predictive coding models.

Time: When the Error Signal Looks Like a Stimulus Signal

In the remaining three sections we investigated how the proportion between stimulus and error depends on stimulus history, stimulus contrast, and stimulus structure in space. To study the influence of stimulus history we ran the stimulus described above either with different durations of the priming image, or with different durations of a blank screen gap between the priming and the grating image. Five different priming image durations were used; 0, 20, 50, 100, and 250 ms. With priming image duration less than 50 ms the preferred orientation was encoded (Figure 7A).

FIGURE 7

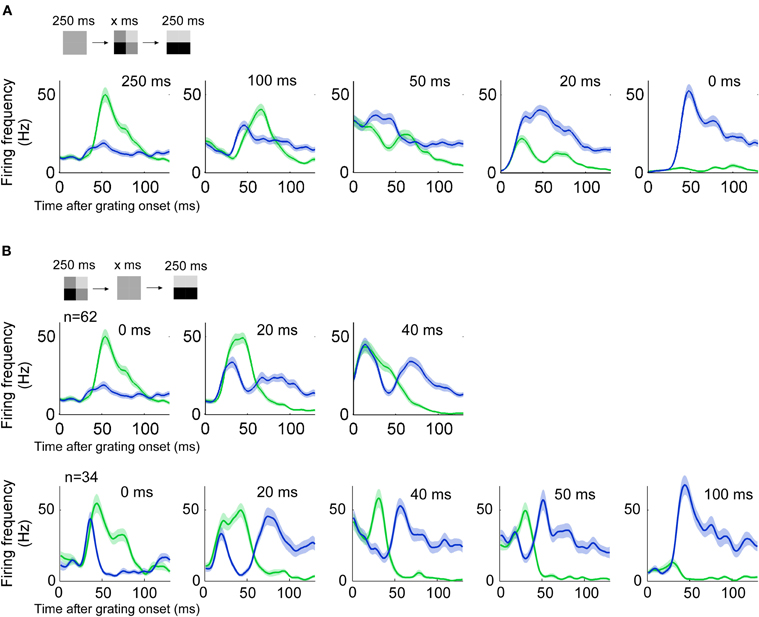
Figure 7. History dependency. (n = 60, three animals) (A) Responses to a grating preceded by a priming image of different durations. Blue (green) lines indicate the response to a grating of preferred (non-preferred) orientation. With priming lasting 20 ms the encoded image resembles more the actual stimulus image because the response to the preferred orientation dominates. Error and stimulus are equally represented when the priming duration is around 50 ms. (B) Conventions as in A. The gap between priming and stimulus image is varied. Two animals had three different gap durations (top) and one animal had five different gap durations (bottom).

We tested four different gaps between the priming image and grating pattern: 20, 40, 50, 100 ms. For a 20 ms gap, the encoded orientation was orthogonal to the orientation of the grating pattern, shortly after the onset of that grating (Figure 7B). With a 40 ms gap responses to the preferred and non-preferred stimulus were almost of equal size. Longer gaps such as 50 and 100 ms did not evoke an orthogonal (non-preferred) response related to the previous stimulus.

To study the integration time for previous stimuli we examined the combination of near and far temporal context with a rapid serial visual presentation (RSVP) stimulus consisting of orthogonal gratings alternating in different intervals. When a neuron predicts one orientation and the stimulus orientation changes to become orthogonal it results in an error that has both orientations. In other words, despite that there is an ON response to the new orientation there will also be an OFF response to the previous orthogonal orientation. This ON/OFF overlap can be seen when stimuli lasted longer than 100 ms (Figure 8, left column). Accordingly, for stimulus duration 100 and 250 ms, ON and OFF responses overlapped 30–90 ms after transition onset (Figure 8, left column). However, for shorter intervals (20 and 50 ms) the two representations were more separated (Figure 8, right column). This can also be appreciated by the fact that the OFF-response becomes smaller for the 50 ms duration than for the 100 ms duration. The longest priming duration for which the actual stimulus was represented was 50 ms. This points to an integration time of 100 ms (2 × 50 ms), as confirmed by the following argumentation. Hundred milliseconds are needed to integrate over the past two orthogonal stimuli. When two orthogonal stimuli are summed the resulting image is orientation neutral, i.e., it has both orientations. In terms of error coding, the next stimulus in the sequence will be subtracted from this orientation neutral prediction image. Since an orientation neutral stimulus minus one oriented stimulus results in an oriented stimulus, the error will correspond to the stimulus. To summarize, dependent on which stimulus history is being integrated the error might match or diverge from the stimulus.

FIGURE 8

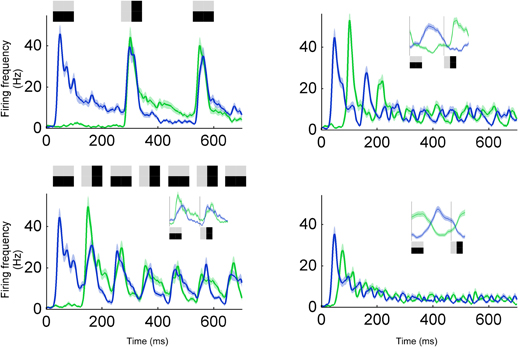
Figure 8. Integration time for a RSVP stimulus. Response to a sequence of gratings with alternating orientations, i.e., preferred and non-preferred orientations. Four different image durations were tested; 250 ms (upper left), 100 ms (lower left), 50 ms (upper right), and 20 ms (lower right). For 250 and 100 ms, the second burst (at 300 and 150 ms, respectively) encodes the difference between the horizontal and vertical grating, i.e., the error signal containing information about both horizontal and vertical grating. For 20 and 50 ms, neurons can separate between the two orientations (see inset for average across all cycles).

Contrast: Low Contrast Increases Error-Like Signal Relative to Stimulus Signal

Since low contrast has been demonstrated to increase the integration radius in a spatial context we tested if low contrast also increased the integration time. Indeed, we found that the timing between the stimulus and the error-like signal changed with contrast (Figures 9A–C). The switch from error- to stimulus coding was delayed for decreasing contrast (107 ± 18 ms, 137 ± 33 ms, and 172 ± 76 ms, p < 10⁻⁸, ANOVA, n = 52, Figure 9D). Furthermore, the duration of the error response increased with decreasing contrast (57 ± 18, 80 ± 31, and 95 ± 76 ms, p < 0.001, ANOVA, n = 52, Figure 9E). The increased integration time for low contrast was verified using a RSVP protocol. To this end, we presented alternating grating sequences according to the previous section albeit with lower contrast. According to the reasoning in the previous section, increased integration time would make the prediction image orientation neutral for longer image durations. Thus, the actual stimulus should appear for longer durations of the previous images. To detect the actual stimulus in the spike trains we calculated the number of spikes for the OFF-response divided by the number of spikes for the ON-response, OFF_ON (Figure 10A). A low value of OFF_ON indicates a relatively small OFF-response, which in turn indicates that the influence of the history is minimal, and thus that the actual stimulus is represented exclusively. The result for different contrasts is plotted in Figures 10B and C. Note that the high contrast curve (Figures 10B and C) reproduces the previous result (Figure 8), namely that the OFF-response is smallest for short image durations (in Figure 8, left column, the blue and the green lines overlap at the transients, but not for the right column). Interestingly, OFF_ON remained smaller for low contrast than for high contrast even for image durations longer than 20ms for animal 1 (Figure 10B) and 40 ms for animal 2 (Figure 10C). The increase in the full width half maximum is between 60–100%. To summarize, both integration time and error-like coding duration increased for low contrast, and this increase is so large that the actual stimulus might never be represented for some units in a 200 ms window.

FIGURE 9

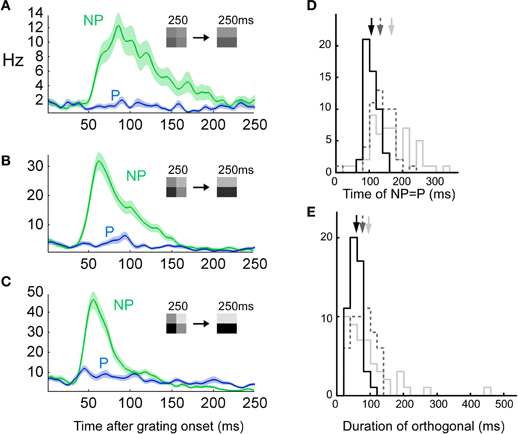
Figure 9. Low contrast prolongs error-like signal. (n = 52, two animals) See Figure 1E for plotting conventions. (A–C) Three different contrasts were tested, i.e., 25 (priming pattern) vs. 12.5% (stimulus pattern) (top row), 50 vs. 25% (middle row) and 100 vs. 50% (bottom row). (D) The time at which the error-like coding switched to stimulus coding was calculated as the intersection between a gaussian fit to the NP and a constant fit to the P (see Methods). (E) The duration of the error-like signal was increased as a function of contrast (see Methods).

FIGURE 10

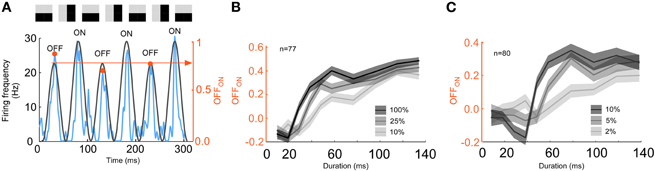
Figure 10. Integration time for a low contrast RSVP stimulus. (A) The amplitude of the OFF-response is divided by the amplitude of the ON response. A small value (yellow arrow point to the right axis) indicates that the influence of the history is minimal and thus, that the stimulus is represented. (B) Index (y-axis) as a function of priming image duration (x-axis) for three different contrasts for animal 1 (10% = light gray, 25% = gray, and 100% = black). (C) Index (y-axis) as a function of priming image duration (x-axis) for three different contrasts for the more contrast sensitive animal 2 (2% = light gray, 5%= gray, and 10% = black). Note that when the contrast is low the index remains relatively small for durations up to 50 ms.

Space: Dynamic Separation of Error and Stimulus Coding Neurons

Since predictive coding models not only work across time but also across space we examined whether the mixing of stimulus and error also occurred in space. A computer model that explains many of the response properties of single units in visual cortex was applied (Spratling, 2010). We remapped the stimulus transition from time to space. A single stimulus image was constructed by setting the checkerboard-like priming pattern and the grating pattern side-by-side in order to merge them to one stimulus image (Figure 11A). This leads to a spatial rather a temporal transition. We ran two different versions of the model; high and low spatial suppression (Figure 11B). Low spatial suppression is more representative for mice and high spatial suppression is more representative for macaque monkeys (van den denBergh et al., 2010).

FIGURE 11

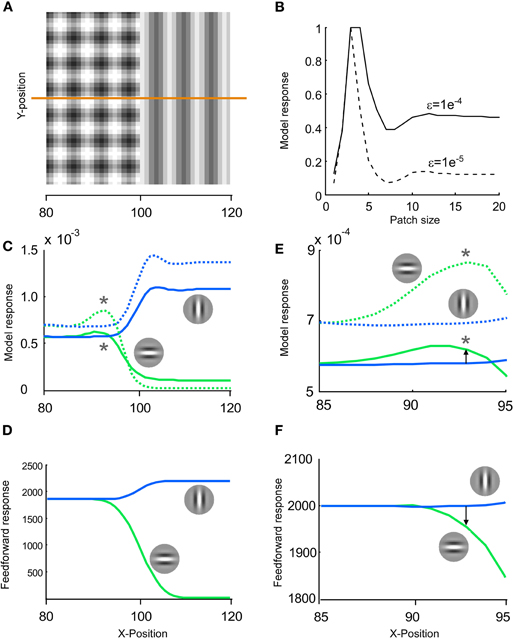
Figure 11. Blending of stimulus and error may also occur for a spatial stimulus. (A) The same stimulus image patterns that we used for a transition in time could also be used for a transition in space. To this end, a stimulus image was constructed by setting the checkerboard like pattern and the grating pattern side-by-side. (B) To study the response in space we used a computer model that explains the response of primary visual cortex to many different spatial stimuli (Spratling, 2010). We tested two different values of the epsilon parameter; generating a moderate (solid line) and strong (dashed line) spatial suppression. (C) The responses to image A were displayed separately for horizontally (green lines) and vertically preferring neurons (blue lines). At x ∼= 90 the horizontal response was larger than the vertical response, whereas when x increased the vertical was larger than the horizontal. This switch across space is similar to the switch we have shown across time in Figure 1F. (D) The results of this predictive coding model were also compared to the results of a pure feed forward model. A feed forward model was created by convolving the image with Gabor patches. (E–F) Same as in C–D but with a magnification around x = 90. Note that for the model of the primary visual cortex the horizontal unit is stronger activated than the vertical unit at x = 93 (arrow pointing upwards), whereas for a pure feed forward model the vertical unit is stronger activated than the horizontal unit at x = 93 (arrow pointing downwards).

Instead of tracing the activity from earlier to later in time, we traced the resulting activity across the neurons in space from left to right (see orange line in A). The responses for the vertical and horizontal neuron (Figure 11C) are qualitatively similar to the responses in time (Figure 1E). For the leftmost neurons, vertical and horizontal neurons are equally activated. As one gets closer to the midline the horizontal becomes more activated than the vertical neuron. Finally, to the right, the opposite activation pattern emerges. The major difference between space and time is that the peak of the horizontal unit is more toward the checkerboard pattern (to the left) in the spatial case than for the temporal case. First, this is because time is causal whereas space is not, i.e., in time the response to a stimulus can only be delayed relative to the stimulus. Second, spatial contextual modulation is more “modulatory” than temporal contextual modulation.

The results of this model were also compared to the results of a pure feed forward model (Figure 11D). A feed forward model does not have any feedback inhibition and was realized by convolving the image with Gabor patches. Note that in response to a pure feed forward model the vertical unit was stronger activated than the horizontal unit at the spatial point indicated by a star in Figure 11C, i.e., where the horizontal unit was stronger activated than the vertical unit for the V1 model (See Figures 11E and F for a magnification of 11C and D). Thus, although the feed forward evidence for a vertical orientation is stronger than for a horizontal orientation, the V1 model inverts this relation. This shows that a V1 model can make the neuronal response diverge from the stimulus when the error signal is strong. To summarize, spatial modeling suggests that blending of a stimulus and an error like signal occurs also in space, even though the spatial and temporal domain use different neuronal mechanisms, e.g., responses in the spatial domain cannot be divided into ON and OFF classes. More importantly, the proportion between stimulus and error coding is not constant across space; unit A can show stronger error coding than unit B for one stimulus and vice versa for a different stimulus.

Discussion

In this paper we hypothesized that if visual cortex does error coding, it should be possible to make the neuronal response diverge from the stimulus. By contrasting the stimulus and error we examined how the two types of codes can be combined. Our results suggest that the same neuron can code for both stimulus and error signal. We show that the strength of an error-like coding relative to a true stimulus coding changes with time, space, and stimulus contrast. Finally, we show that the combined coding presented may require a modification of existing predictive coding models.

Stimulus Motivation and Generalizations Beyond the Grating Stimulus

We have used a stimulus that enables the separation of two different components based on the neurons' orientation selectivity. This feature based separation is advantageous since a separation cannot be done on the basis of the temporal shape of the neuronal responses. The temporal shape of neuronal responses is neuron and stimulus dependent so fixed templates cannot be used for separation (Richmond and Optican, 1990; Richmond et al., 1990; Heller et al., 1995; Richmond, 2009). Furthermore, it is difficult to detect stimulus related activity because the stimulus offset can generate as complex temporal response shapes as the stimulus onset (Duysens et al., 1985, 1996; Nikolic et al., 2009). Another advantage of the feature based separation is that it allows the quantification of when in time one component becomes stronger than the other one. This is done by finding the time when the instantaneous firing rate for the preferred orientation is equal to that of the non-preferred orientation.

By using grating stimuli we suggest that neurons predict gratings which are constant across time and space (Rao and Ballard, 1999; Spratling, 2010). It might be reasonable to assume that non-grating-like stimuli such as natural movies can be better predicted and with a lower error. A lower error could be indicated if there are long periods without spiking activity. This has been shown for natural stimulus (Vinje and Gallant, 2000; Haider et al., 2010). It is, however, unlikely that “no spike” always indicates “no error.” Every spike signals an error and it is quite likely that this error will remain unchanged during silent periods until the next spike occurs. Rather, the long periods of silence in the average (across stimulus repetitions) activity are the result of a reliable firing across stimulus repetitions. That is, multiple repetitions of the same movie will result in similar spike trains, with spikes occurring at similar time points relative to the onset of the movie. This repeatability of the spike train might be the result of a better experimental control of the synaptic inputs to the recorded neuron for natural scenes than for optimized artificial stimuli. Natural scenes cover a large portion of the field of view per definition. Therefore, most neurons are stimulated and under experimental control for natural scenes. However, this might be not the only explanation for the long periods of silence for natural scene stimulation (Haider et al., 2010) and it remains to be shown if responses to natural scenes can be indicative of error coding.

In conclusion, the grating stimuli used here provide two rules that can be applied to more complex stimuli.

Once the network recognizes and can predict the stimulus, the error-like signal decreases and the stimulus signal becomes dominant (Figure 12A).

FIGURE 12

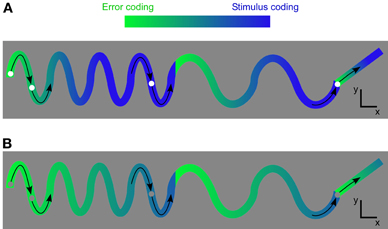
Figure 12. Example of how the results from the grating stimulus can be generalized to other types of stimuli. (A) A visual dot moves in an oscillating manner across space. In the beginning the error coding is high since the movement is new to the network. As the oscillation is repeated it is expected that the network may recognize the stimulus. The error signal decreases. The stimulus is represented if the network can recognize and predict the stimulus. (B) The same stimulus trajectory as in A, but with a low contrast dot.

For decreasing contrast the error-like signal becomes relatively stronger than the stimulus signal (Figure 12B).

High Contrast Stimulus

Our experimental results can be summarized by the following conceptual model.

$R(t)=E(t)+S(t)=[S(t)-P(t)]+S(t)=\left[S(t)-\frac{1}{T}\underset{0}{\overset{T}{{\displaystyle \int }}}S(t-\tau )d\tau \right]+S(t)$(3)

where S(t) is the stimulus and R(t) is the firing rate. E(t) corresponds to the error signal. E(t) + S(t) corresponds to the combined error and stimulus coding. P(t) is the predicted image and corresponds to the integrated history or temporal average. T defines the integration duration. The integral smoothes and delays S(t). The smoothing reduces the amplitude of S(t) if that changes quickly, i.e., the integral works like a low pass filter. A quickly changing stimulus is the case for RSVP (Reid et al., 1997; Isaak et al., 1999; Foldiak et al., 2004). Since the fluctuations in P(t) will be smaller than those in S(t) for a rapid stimulus it means that the fluctuations in S(t) will be apparent in E(t). Therefore, the error signal will be similar to the stimulus signal. This explains why the stimulus is represented during a RSVP stimulus with extra short image durations in our data and in the data of others (Benucci et al., 2009). On the other hand, if S(t) changes slower than T, P(t) will only be a delayed version of S(t). Then, the E(t) will reflect the difference between the true stimulus image and the preceding image (see also Eriksson et al., 2010).

How could the formula described above be implemented in a neuron? One mechanism could be that of adaptation. The integrated history might, for example, be encoded by intracellular calcium. Calcium has slow dynamics and the cell will, therefore, accumulate or integrate calcium over time (Baker, 1972). The amount of calcium would represent the prediction. Accumulated calcium leads to the activation of calcium dependent potassium channels and, therefore, to an increase in firing threshold (Hotson and Prince, 1980). The threshold increase corresponds to a subtraction in the firing rate, i.e., the resulting firing rate corresponds to the error. Other possibilities for creating a temporal error are synaptic depression, feedforward inhibition, inactivation of calcium channels as well as higher level mechanisms such as the action of horizontal and feedback connections onto inhibitory neurons (Gonchar and Burkhalter, 2003).

Another possibility for making a neuron represent both stimulus and error could be that error and stimulus spikes are grouped according to the phase of an oscillation. In this case, the average firing rate over at least one oscillation period would look like the sum of the stimulus and error signal. A recent evidence for this phase division is that the stimulus information is highest for spikes at a certain phase of a gamma oscillation (Womelsdorf et al., 2012). Spikes at other phases transmit considerably less stimulus information and could as such represent the error. The instantaneous firing rate at the error phase is lower than that of the stimulus phase indicating inhibition. If the neuronal network performs a prediction, the neurons will communicate with each other and therefore their activity may become correlated. This type of correlation would be called noise correlation since it is related to a prediction rather than to the stimulus and since it makes stimulus coding noisier. Consistent with this argumentation is a higher noise correlation for the error phase (Womelsdorf et al., 2012).

Contrast Dependency

For low contrast our results suggest that the integration time T in Equation 3 increases about 60–100%. This is related but not identical to the previous findings that the peak of the instantaneous firing rate, for example, is delayed in time for a low contrast stimulus (Gawne et al., 1996; Mechler et al., 1998; Reich et al., 2001). Rather, the increase in integration time might correspond to the increase in integration radius seen for spatial suppression. The optimal radius of a grating, for example, increases by 50–100% as its contrast decreases (Sceniak et al., 1999). In agreement with this notion, it has been shown also explicitly that the integration radius of a neuron increases as stimulus contrast decreases (Nauhaus et al., 2009). By this analogy between space and time we predict that equation 3 can be converted to space by replacing t (time) with r (space), T with R (integration radius), and the non-symmetric (causal) integration before t with a symmetric (acausal) integration around x.

The increased error-like coding relative to stimulus coding for low contrast might be related to the increased lateral communication across cortical neurons for low contrast (Nauhaus et al., 2009). Error coding needs a prediction and, for the spatial case, the prediction might be done in the lateral network.

Similarity between Space and Time

The similarity between space and time shown in this paper is supported by additional neuronal response properties. In this sense, the amplitude of the Gamma power in the LFP has been shown to increase both with the stimulation radius as well as with the time from stimulus onset (Gieselmann and Thiele, 2008). A further similarity is that both dimensions have also a similar relationship to the recorded cortical layer. As a consequence, the depth profile of the temporal transiency index is similar to the depth profile of the spatial suppression index. Both indices are calculated as the ratio between peak firing rate (for the optimal time or radius) and plateau firing rate (beyond the optimal time and radius). The index is higher when the peak firing rate is larger than the plateau firing rate, and lower when the peak firing rate is close to the plateau firing rate. In general, peak firing is more pronounced in the supragranular layers and less pronounced in layer V in both space (Shushruth et al., 2009; van den denBergh et al., 2010) and time (Heimel et al., 2005; Harvey et al., 2009; Eriksson et al., 2010).

In addition to the four above discussed similarities between spatial and temporal contextual influences, i.e., response shape, contrast dependency, gamma dependency, and layer dependency, we observed a fifth one in the current study. The model data indicate that the proportion of error and stimulus signal not only changes across time—as observed experimentally—but also changes across the spatial domain.

Predictive Coding Models

In this study we observed a discrepancy between the response of the error unit in the DEM model and the response measured experimentally. Model and experimental data can be compared since the model error unit is positioned in the supragranular layers (Friston, 2008, 2010) where our electrophysiology and voltage-sensitive dye data mainly originate from. The voltage-sensitive dye signal stems from the superficial part of the supragranular layers (Kleinfeld and Delaney, 1996; Petersen et al., 2003; Ferezou et al., 2006; Berger et al., 2007). Since our recordings were in the upper granular layers at deepest we conclude that the majority of our complex cells were recorded in the supragranular layers.

Whereas the experimental data showed combined stimulus and error coding, the model showed only error coding. When the error unit was forced to represent the additional stimulus signal the behavior of the model became non-optimal. To address this issue a simple modification was introduced that most likely can be applied to other predictive coding models. The modification consists of adding stimulus and error signal in a new type of error unit. The original error signal can in turn be extracted from this new error unit by simply subtracting the stimulus signal. Since we did not add or remove model features the performance and free energy is preserved. The reformulated model predicts that the target layer of the feedback signal can be the same as the source layer, which is consistent with axonal tracing studies (Rockland and Virga, 1989; Felleman and van Essen, 1991). Finally it should be noted that the presented reformulation is one of many possibilities. Future studies will reveal which biologically plausible model can best decipher a combined code.

Despite that the spatial model (Spratling, 2010) combines a stimulus and an error-like signal, this model may have to be modified in the same way as the temporal version of the DEM model. This is because this model contains error and stimulus units and the error units lack a stimulus component. The error unit responses do also not match the experimental data. With a potential modification of the model one cannot only explain more experimental data, but one can potentially also understand a combined code.

Advantage of Combining Error and Stimulus Signal

Why should a neuron encode both types of signals? To answer this question we first note that in the predictive coding framework, the error signal is the result of a generative model. It is called a generative model because “higher areas” generate a predicted image in the lower areas. The resulting predicted image is compared to the sensory input and an error is calculated. For example, when the door to my grandmother's house opens I might anticipate that her face will appear. As such, grandmother neurons in higher areas might generate a picture of grandmothers in early visual areas. This prediction is performed by a model defined by the grandmother neuron and the neurons targeted by the grandmother neuron. If it is my grandmother that is opening the door the error will be small. The error is, therefore, model dependent whereas the stimulus is model-free. A generative model might be advantageous if the stimulus is ambiguous or if the stimulus has low contrast (Wertheimer, 1923; Nauhaus et al., 2009; Ringach, 2009). On the other hand, a suboptimal model may lead to wrong inferences about the stimulus. Therefore, it could be advantageous to represent the model-free stimulus code in addition to the model-dependent error code.

The advantage of combining a model-free code with a model-dependent code can be illustrated in terms of learning. With a purely model-dependent (error) code it might be difficult for the network to improve a non-optimal representation. For example, suppose a network has two grandmother cells, which connect two error coding non-overlapping neuronal populations in the lower area, A and B, respectively. One of the grandmother cells can feed back its activation to the corresponding neuronal population in the lower area in order to predict the activity in this population, A or B, and to enable the calculation of an error in those populations. If the error is 0 there is no need to modify the model, i.e., to change the connections between grandmother cells and lower area. It is, however, easy to create a case when the error is 0, but the grandmother representation is non-optimal. This happens when we stimulate both children populations, A + B, in the lower area simultaneously. Each individual grandmother unit can predict the activity in the corresponding population, so the error is 0. Two grandmother cells are, however, non-optimal in this case as one grandmother cell alone would suffice to represent the combined children, A + B. Therefore, it would be optimal to connect the combined children to one grandmother cell instead of two. Such a change will not occur as long as the error in the children is 0 since plasticity in predictive coding models is driven by the error signal (see Equation 55 in Friston, 2008). Therefore, the required non-zero activity in the error units ought to represent the stimulus in order to enable the formation of a stimulus related connection to a more optimal grandmother cell. In this manner, a combined stimulus and error code might enable the network to improve certain suboptimal representations.

Conclusion

In this paper we have used the word “error” as a substitute for “difference between integrated stimulation history and the current stimulus,” or “difference between integrated stimulation context and the current stimulus.” One might have the objection that the word “error” is misleading because it is associated with various interpretations. To avoid this possibility we summarize our results as follows. A neuron seems to code for at least two different signals. The proportion of the two signals varies dynamically as a function of time, space and stimulus contrast. It is unclear how downstream neurons can make use of such a combined and dynamic code. Until we have the experimental tools to separate signals from different brain regions we are bound to use computer models to understand such a code. Since there is one model that has proclaimed itself to implement a general brain theory we have used that model (Friston, 2010). With this model and our modification of it we have taken one step toward understanding a combined neural code.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank Anne Schmidt and Christiane Peiker for help with experiments, Sergio Neuenschwander for the acquisition system and Danko Nicolic for visual stimulation software.

References

Alink, A., Schwiedrzik, C. M., Kohler, A., Singer, W., and Muckli, L. (2010). Stimulus predictability reduces responses in primary visual cortex. J. Neurosci. 30, 2960–2966.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Angelucci, A., Levitt, J. B., Walton, E. J., Hupe, J. M., Bullier, J., and Lund, J. S. (2002). Circuits for local and global signal integration in primary visual cortex. J. Neurosci. 22, 8633–8646.

Pubmed Abstract | Pubmed Full Text

Arieli, A., Shoham, D., Hildesheim, R., and Grinvald, A. (1995). Coherent spatiotemporal patterns of ongoing activity revealed by real-time optical imaging coupled with single-unit recording in the cat visual cortex. J. Neurophysiol. 73, 2072–2093.

Pubmed Abstract | Pubmed Full Text

Arieli, A., Sterkin, A., Grinvald, A., and Aertsen, A. (1996). Dynamics of ongoing activity: explanation of the large variability in evoked cortical responses. Science. 273, 1868–1871.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Baker, P. F. (1972). Transport and metabolism of calcium ions in nerve. Prog. Biophys. Mol. Biol. 24, 177–223.

Pubmed Abstract | Pubmed Full Text

Barlow, H. B. (1953). Action potentials from the frog's retina. J. Physiol. 119, 58–68.

Pubmed Abstract | Pubmed Full Text

Benucci, A., Frazor, R. A., and Carandini, M. (2007). Standing waves and traveling waves distinguish two circuits in visual cortex. Neuron. 55, 103–117.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Benucci, A., Ringach, D. L., and Carandini, M. (2009). Coding of stimulus sequences by population responses in visual cortex. Nat. Neurosci. 12, 1317–1324.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Berger, T., Borgdorff, A., Crochet, S., Neubauer, F. B., Lefort, S., Fauvet, B., Ferezou, I., Carleton, A., Luscher, H. R., and Petersen, C. C. (2007). Combined voltage and calcium epifluorescence imaging in vitro and in vivo reveals subthreshold and suprathreshold dynamics of mouse barrel cortex. J. Neurophysiol. 97, 3751–3762.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Bialek, W., Rieke, F., De Ruyter Van Steveninck, R. R., and Warland, D. (1991). Reading a neural code. Science. 252, 1854–1857.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Butts, D. A., Weng, C., Jin, J., Yeh, C. I., Lesica, N. A., Alonso, J. M., and Stanley, G. B. (2007). Temporal precision in the neural code and the timescales of natural vision. Nature. 449, 92–95.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Chavane, F., Sharon, D., Jancke, D., Marre, O., Fregnac, Y., and Grinvald, A. (2011). Lateral spread of orientation selectivity in V1 is controlled by intracortical cooperativity. Front. Syst. Neurosci. 5:4. doi: 10.3389/fnsys.2011.00004

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

de Meyer, K., and Spratling, M. W. (2009). A model of non-linear interactions between cortical top-down and horizontal connections explains the attentional gating of collinear facilitation. Vision Res. 49, 553–568.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Duysens, J., Orban, G. A., Cremieux, J., and Maes, H. (1985). Visual cortical correlates of visible persistence. Vision Res. 25, 171–178.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Duysens, J., Schaafsma, S. J., and Orban, G. A. (1996). Cortical off response tuning for stimulus duration. Vision Res. 36, 3243–3251.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Eriksson, D., Valentiniene, S., and Papaioannou, S. (2010). Relating information, encoding and adaptation: decoding the population firing rate in visual areas 17/18 in response to a stimulus transition. PLoS One 5:e10327. doi: 10.1371/journal.pone.0010327

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Felleman, D. J., and van Essen, D. C. (1991). Distributed hierarchical processing in the primate cerebral cortex. Cereb. Cortex 1, 1–47.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Ferezou, I., Bolea, S., and Petersen, C. C. (2006). Visualizing the cortical representation of whisker touch: voltage-sensitive dye imaging in freely moving mice. Neuron 50, 617–629.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Foldiak, P., Xiao, D., Keysers, C., Edwards, R., and Perrett, D. I. (2004). Rapid serial visual presentation for the determination of neural selectivity in area STSa. Prog. Brain Res. 144, 107–116.

Pubmed Abstract | Pubmed Full Text

Friston, K. (2008). Hierarchical models in the brain. PLoS Comput. Biol. 4:e1000211. doi: 10.1371/journal.pcbi.1000211

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Friston, K. (2010). The free-energy principle: a unified brain theory? Nat. Rev. Neurosci. 11, 127–138.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Friston, K. J., Trujillo-Barreto, N., and Daunizeau, J. (2008). DEM: a variational treatment of dynamic systems. Neuroimage 41, 849–885.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Gawne, T. J., Kjaer, T. W., and Richmond, B. J. (1996). Latency: another potential code for feature binding in striate cortex. J. Neurophysiol. 76, 1356–1360.

Pubmed Abstract | Pubmed Full Text

Gieselmann, M. A., and Thiele, A. (2008). Comparison of spatial integration and surround suppression characteristics in spiking activity and the local field potential in macaque V1. Eur. J. Neurosci. 28, 447–459.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Gonchar, Y., and Burkhalter, A. (2003). Distinct GABAergic targets of feedforward and feedback connections between lower and higher areas of rat visual cortex. J. Neurosci. 23, 10904–10912.

Pubmed Abstract | Pubmed Full Text

Haider, B., Krause, M. R., Duque, A., Yu, Y., Touryan, J., Mazer, J. A., and Mccormick, D. A. (2010). Synaptic and network mechanisms of sparse and reliable visual cortical activity during nonclassical receptive field stimulation. Neuron 65, 107–121.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Harvey, M. A., Valentiniene, S., and Roland, P. E. (2009). Cortical membrane potential dynamics and laminar firing during object motion. Front. Syst. Neurosci. 3:7. doi: 10.3389/neuro.06.007.2009

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Heggelund, P., and Albus, K. (1978). Response variability and orientation discrimination of single cells in striate cortex of cat. Exp. Brain Res. 32, 197–211.

Pubmed Abstract | Pubmed Full Text

Heimel, J. A., van Hooser, S. D., and Nelson, S. B. (2005). Laminar organization of response properties in primary visual cortex of the gray squirrel (Sciurus carolinensis). J. Neurophysiol. 94, 3538–3554.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Heller, J., Hertz, J. A., Kjaer, T. W., and Richmond, B. J. (1995). Information flow and temporal coding in primate pattern vision. J. Comput. Neurosci. 2, 175–193.

Pubmed Abstract | Pubmed Full Text

Hotson, J. R., and Prince, D. A. (1980). A calcium-activated hyperpolarization follows repetitive firing in hippocampal neurons. J. Neurophysiol. 43, 409–419.

Pubmed Abstract | Pubmed Full Text

Isaak, M. I., Shapiro, K. L., and Martin, J. (1999). The attentional blink reflects retrieval competition among multiple rapid serial visual presentation items: tests of an interference model. J. Exp. Psychol. Hum. Percept. Perform. 25, 1774–1792.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kalatsky, V. A., and Stryker, M. P. (2003). New paradigm for optical imaging: temporally encoded maps of intrinsic signal. Neuron 38, 529–545.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kenet, T., Bibitchkov, D., Tsodyks, M., Grinvald, A., and Arieli, A. (2003). Spontaneously emerging cortical representations of visual attributes. Nature 425, 954–956.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kleinfeld, D., and Delaney, K. R. (1996). Distributed representation of vibrissa movement in the upper layers of somatosensory cortex revealed with voltage-sensitive dyes. J. Comp. Neurol. 375, 89–108.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Koch, C., and Poggio, T. (1999). Predicting the visual world: silence is golden. Nat. Neurosci. 2, 9–10.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kohn, A. (2007). Visual adaptation: physiology, mechanisms, and functional benefits. J. Neurophysiol. 97, 3155–3164.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kuffler, S. W. (1953). Discharge patterns and functional organization of mammalian retina. J. Neurophysiol. 16, 37–68.

Pubmed Abstract | Pubmed Full Text

Maffei, L., and Fiorentini, A. (1976). The unresponsive regions of visual cortical receptive fields. Vision Res. 16, 1131–1139.

Pubmed Abstract | Pubmed Full Text

Mechler, F., Victor, J. D., Purpura, K. P., and Shapley, R. (1998). Robust temporal coding of contrast by V1 neurons for transient but not for steady-state stimuli. J. Neurosci. 18, 6583–6598.

Pubmed Abstract | Pubmed Full Text

Muller, J. R., Metha, A. B., Krauskopf, J., and Lennie, P. (1999). Rapid adaptation in visual cortex to the structure of images. Science 285, 1405–1408.

Pubmed Abstract | Pubmed Full Text

Nauhaus, I., Busse, L., Carandini, M., and Ringach, D. L. (2009). Stimulus contrast modulates functional connectivity in visual cortex. Nat. Neurosci. 12, 70–76.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Nelson, J. I., and Frost, B. J. (1978). Orientation-selective inhibition from beyond the classic visual receptive field. Brain Res. 139, 359–365.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Nikolic, D., Hausler, S., Singer, W., and Maass, W. (2009). Distributed fading memory for stimulus properties in the primary visual cortex. PLoS Biol. 7:e1000260. doi: 10.1371/journal.pbio.1000260

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Petersen, C. C. H., Grinvald, A., and Sakmann, B. (2003). Spatiotemporal dynamics of sensory responses in Layer 2/3 of rat barrel cortex measured in vivo by voltage-sensitive dye imaging combined with whole-cell voltage recordings and neuron reconstructions. J. Neurosci. 23, 1298–1309.

Pubmed Abstract | Pubmed Full Text

Rao, R. P., and Ballard, D. H. (1999). Predictive coding in the visual cortex: a functional interpretation of some extra-classical receptive-field effects. Nat. Neurosci. 2, 79–87.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Reich, D. S., Mechler, F., and Victor, J. D. (2001). Temporal coding of contrast in primary visual cortex: when, what, and why. J. Neurophysiol. 85, 1039–1050.

Pubmed Abstract | Pubmed Full Text

Reid, R. C., Victor, J. D., and Shapley, R. M. (1997). The use of m-sequences in the analysis of visual neurons: linear receptive field properties. Vis Neurosci. 14, 1015–1027.

Pubmed Abstract | Pubmed Full Text

Richmond, B. J. (2009). Stochasticity, spikes and decoding: sufficiency and utility of order statistics. Biol. Cybern. 100, 447–457.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Richmond, B. J., and Optican, L. M. (1990). Temporal encoding of two-dimensional patterns by single units in primate primary visual cortex. II. Information transmission. J. Neurophysiol. 64, 370–380.

Pubmed Abstract | Pubmed Full Text

Richmond, B. J., Optican, L. M., and Spitzer, H. (1990). Temporal encoding of two-dimensional patterns by single units in primate primary visual cortex. I. Stimulus-response relations. J. Neurophysiol. 64, 351–369.

Pubmed Abstract | Pubmed Full Text

Ringach, D. L. (2009). Spontaneous and driven cortical activity: implications for computation. Curr. Opin. Neurobiol. 19, 439–444.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Rochefort, N. L., Buzas, P., Kisvarday, Z. F., Eysel, U. T., and Milleret, C. (2007). Layout of transcallosal activity in cat visual cortex revealed by optical imaging. Neuroimage 36, 804–821.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Rockland, K. S., and Virga, A. (1989). Terminal arbors of individual “feedback” axons projecting from area V2 to V1 in the macaque monkey: a study using immunohistochemistry of anterogradely transported Phaseolus vulgaris-leucoagglutinin. J. Comp. Neurol. 285, 54–72.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Sceniak, M. P., Ringach, D. L., Hawken, M. J., and Shapley, R. (1999). Contrast's effect on spatial summation by macaque V1 neurons. Nat. Neurosci. 2, 733–739.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Schiller, P. H., Finlay, B. L., and Volman, S. F. (1976). Short-term response variability of monkey striate neurons. Brain Res. 105, 347–349.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Scobey, R. P., and Gabor, A. J. (1989). Orientation discrimination sensitivity of single units in cat primary visual cortex. Exp. Brain Res. 77, 398–406.

Pubmed Abstract | Pubmed Full Text

Sharon, D., Jancke, D., Chavane, F., Na'aman, S., and Grinvald, A. (2007). Cortical response field dynamics in cat visual cortex. Cereb. Cortex. 17, 2866–2877.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Shoham, S., Fellows, M. R., and Normann, R. A. (2003). Robust, automatic spike sorting using mixtures of multivariate t-distributions. J. Neurosci. Methods. 127, 111–122.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Shushruth, S., Ichida, J. M., Levitt, J. B., and Angelucci, A. (2009). Comparison of spatial summation properties of neurons in macaque V1 and V2. J. Neurophysiol. 102, 2069–2083.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Snowden, R. J., Treue, S., and Andersen, R. A. (1992). The response of neurons in areas V1 and MT of the alert rhesus monkey to moving random dot patterns. Exp. Brain Res. 88, 389–400.

Pubmed Abstract | Pubmed Full Text

Softky, W. R., and Koch, C. (1993). The highly irregular firing of cortical cells is inconsistent with temporal integration of random EPSPs. J. Neurosci. 13, 334–350.

Pubmed Abstract | Pubmed Full Text

Spratling, M. W. (2010). Predictive coding as a model of response properties in cortical area V1. J. Neurosci. 30, 3531–3543.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Stanley, G. B., Li, F. F., and Dan, Y. (1999). Reconstruction of natural scenes from ensemble responses in the lateral geniculate nucleus. J. Neurosci. 19, 8036–8042.

Pubmed Abstract | Pubmed Full Text

Tsodyks, M., Kenet, T., Grinvald, A., and Arieli, A. (1999). Linking spontaneous activity of single cortical neurons and the underlying functional architecture. Science 286, 1943–1946.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Tusa, R. J., Palmer, L. A., and Rosenquist, A. C. (1978). The retinotopic organization of area 17 (striate cortex) in the cat. J. Comp. Neurol. 177, 213–235.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Tusa, R. J., Rosenquist, A. C., and Palmer, L. A. (1979). Retinotopic organization of areas 18 and 19 in the cat. J. Comp. Neurol. 185, 657–678.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

van den Bergh, G., Zhang, B., Arckens, L., and Chino, Y. M. (2010). Receptive-field properties of V1 and V2 neurons in mice and macaque monkeys. J. Comp. Neurol. 518, 2051–2070.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Villeneuve, M. Y., and Casanova, C. (2003). On the use of isoflurane versus halothane in the study of visual response properties of single cells in the primary visual cortex. J. Neurosci. Methods 129, 19–31.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Vinje, W. E., and Gallant, J. L. (2000). Sparse coding and decorrelation in primary visual cortex during natural vision. Science 287, 1273–1276.

Pubmed Abstract | Pubmed Full Text

Vogels, R., Spileers, W., and Orban, G. A. (1989). The response variability of striate cortical neurons in the behaving monkey. Exp. Brain Res. 77, 432–436.

Pubmed Abstract | Pubmed Full Text

Wertheimer, M. (1923). Untersuchungen zur lehre von der Gestalt. Psychol. Forsch. 4, 301–350.

Womelsdorf, T., Lima, B., Vinck, M., Oostenveld, R., Singer, W., Neuenschwander, S., and Fries, P. (2012). Orientation selectivity and noise correlation in awake monkey area V1 are modulated by the gamma cycle. Proc. Natl. Acad. Sci. U.S.A. 109, 4302–4307.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text